Next Article in Journal
Effects Analysis of FAME on the Engine Characteristics of Different Polymerized Biofuels in Compression Ignition Engine
Next Article in Special Issue
Power Extraction Performance by a Hybrid Non-Sinusoidal Pitching Motion of an Oscillating Energy Harvester
Previous Article in Journal
RETRACTED: Rehman, A.u.; Lal, B. Gas Hydrate-Based CO2 Capture: A Journey from Batch to Continuous. Energies 2022, 15, 8309
Previous Article in Special Issue
Co-Gasification of Polyethylene and Biomass in Catalytic Bed Material
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 17
Issue 10
10.3390/en17102254
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine

by
Dean Sesalim
* and
Jamal Naser
*
Department of Mechanical and Product Design Engineering, Swinburne University of Technology, Hawthorn, VIC 3122, Australia
*
Authors to whom correspondence should be addressed.
Energies 2024, 17(10), 2254; https://doi.org/10.3390/en17102254
Submission received: 14 March 2024 / Revised: 4 May 2024 / Accepted: 5 May 2024 / Published: 8 May 2024
(This article belongs to the Special Issue Computational Fluid Dynamics: Technologies and Applications for Renewable Energy Systems)
Browse Figures
Versions Notes

Abstract

:
Aerodynamic noise emitted by small wind turbines is a concern due to their proximity to urban environments. Broadband airfoil self-noise has been found to be the major source, and several studies have discussed techniques to reduce airfoil leading-edge and trailing-edge noises. Reduction mechanisms inspired by owl wings and their airfoil sections were found to be most effective. However, their effect/s on the tip vortex noise remain underexplored. Therefore, this paper investigates the effects of implementing an owl airfoil design on the tip vortex noise generated by the National Renewable Energy Laboratory (NREL) Phase VI wind turbine to gain an understanding of the relationship, if any, between airfoil design and the tip vortex noise mechanism. Numerical prediction of aeroacoustics is employed using the Ansys Fluent Broadband Noise Sources function for airfoil self-noise radiation. Detailed comparisons and evaluations of the generated acoustic power levels (APLs) for two distinguished inlet velocities were made with no loss in torque. Although the owl airfoil design increased the maximum generated APL by the baseline model from 105 dB to 110 dB at the lower inlet velocity, it significantly reduced the surface area generating the noise, and reduced the maximum APL generated by the baseline model by 4 dB as the inlet velocity increased. The ability of the owl airfoil to mitigate the velocity effects along the span of the blade was found to be its main noise reduction mechanism.

1. Introduction

Small wind-turbines (SWTs), which produce less than 30 kW of power, have been increasingly implemented in rural communities and urban environments [1,2]. However, the impact of the noise emitted by SWTs on human health is severe due to their proximity to dwellings and residential areas [3,4,5,6]. Here, the aerodynamic noise due to the interaction of the wind turbine blades with the airflow was found to be the contributing noise [7,8,9,10]. And although various aerodynamic sound source mechanisms are generated by this interaction, inflow turbulence noise and airfoil self-noise were found to be the two main mechanisms [11,12,13,14]. The inflow-turbulence noise occurs due to the interaction of the turbine blades with the atmospheric turbulence, creating a broadband type of noise, and propagating as the atmospheric turbulence becomes more intense [15,16,17]. Eroded blade leading-edges, for example, were found to increase inflow-turbulence noise emission [18]. Inflow-turbulence noise does therefore depend on atmospheric turbulence, and the airfoil self-noise becomes the dominant source with less atmospheric turbulence or none. Airfoil self-noise is also of a broadband character, resulting from the interaction of the turbine blade surfaces with the turbulent boundary layer of the viscous flow [19,20,21]. The airfoil self-noise radiating from the trailing edge, for example, is increased by the thickness of the trailing edge. A trailing edge thickness of less than 1% of the chord was found to decrease the trailing edge noise [22]. However, this thickness may not be practical for small wind-turbines from a manufacturing point of view.
Moreover, cross flow due to the equalization of the pressure difference between the pressure and the suction side at the tip of a blade creates tip vortex that emits high-frequency broadband noise. As a result, tip noise is generated with the interaction between the trailing edge and the tip of the blade. This issue propagates as SWTs operate at higher tip speed in order to generate maximum power extraction [23]. Here, non-linear aerodynamics associated with low Reynolds numbers affect the performance of SWTs in general. Therefore, limiting the rotational speed of the turbine could result in much quieter operation but at the cost of reducing power output. Results show that the more efficient a SWT blade design, the less quiet it is, and the loss of power increases significantly at speeds that produce less noise [24,25]. Unexpectedly, optimization of the tip shape was found to have relatively small effects on the sound pressure level, as implementing tip shapes such as round shapes resulted in negligible contributions [26]. The chord length and twist distribution of SWTs were therefore optimized to reduce the tip speed ratio and thus the generated aerodynamic noise, but loss of power remained unpreventable [27,28].
Recently, several studies inspired by the geometrical characteristics of the owl’s wings implemented their leading edge and trailing edge serrations to achieve considerable reduction in airfoil self-noise while maintaining the power output [29,30,31,32,33,34,35]. This is owing to studies specifying wing aspects, such as the leading-edge comb and trailing-edge fringe of the owl wing as being the mechanism of the owl’s silent flights [36,37,38,39]. However, the increase of noise, especially at the tip of the blade, due to the increase in velocity remained an issue. In the meantime, the design of the airfoil was found to be fundamental in mitigating airfoil self-noise and attempts to minimize such noise while improving aerodynamic performance by utilizing various airfoil designs were successful [40,41]. Better performance was even achieved by implementing biologically inspired airfoil designs [42,43], most of which the owl airfoil inspired [44,45,46,47]. Still, in-depth investigation into such a reduction mechanism and the effects of an owl airfoil profile on the tip vortex noise in particular are yet to be investigated. Therefore, this research aims to determine the effects of an owl airfoil on the aeroacoustics of a baseline small wind-turbine model. This is performed by replacing the baseline model’s airfoil profile with an owl airfoil while keeping the chord lengths and the twist distribution of the baseline model in order to isolate the effects of the airfoil profile’s actual geometrical characteristics on the generated noise, particularly around tips of the blade. The objective is not to achieve a final solution, but to determine whether the airfoil designs have effects on the tip noise generated by the turbine blade, and the aim is to gain understanding of the mechanism leading to the reduction of noise, if any. Nevertheless, this work achieves significant reduction in the tip vortex noise generated by a small wind-turbine model and provides the evaluation and understanding of the mechanism that led to this reduction.

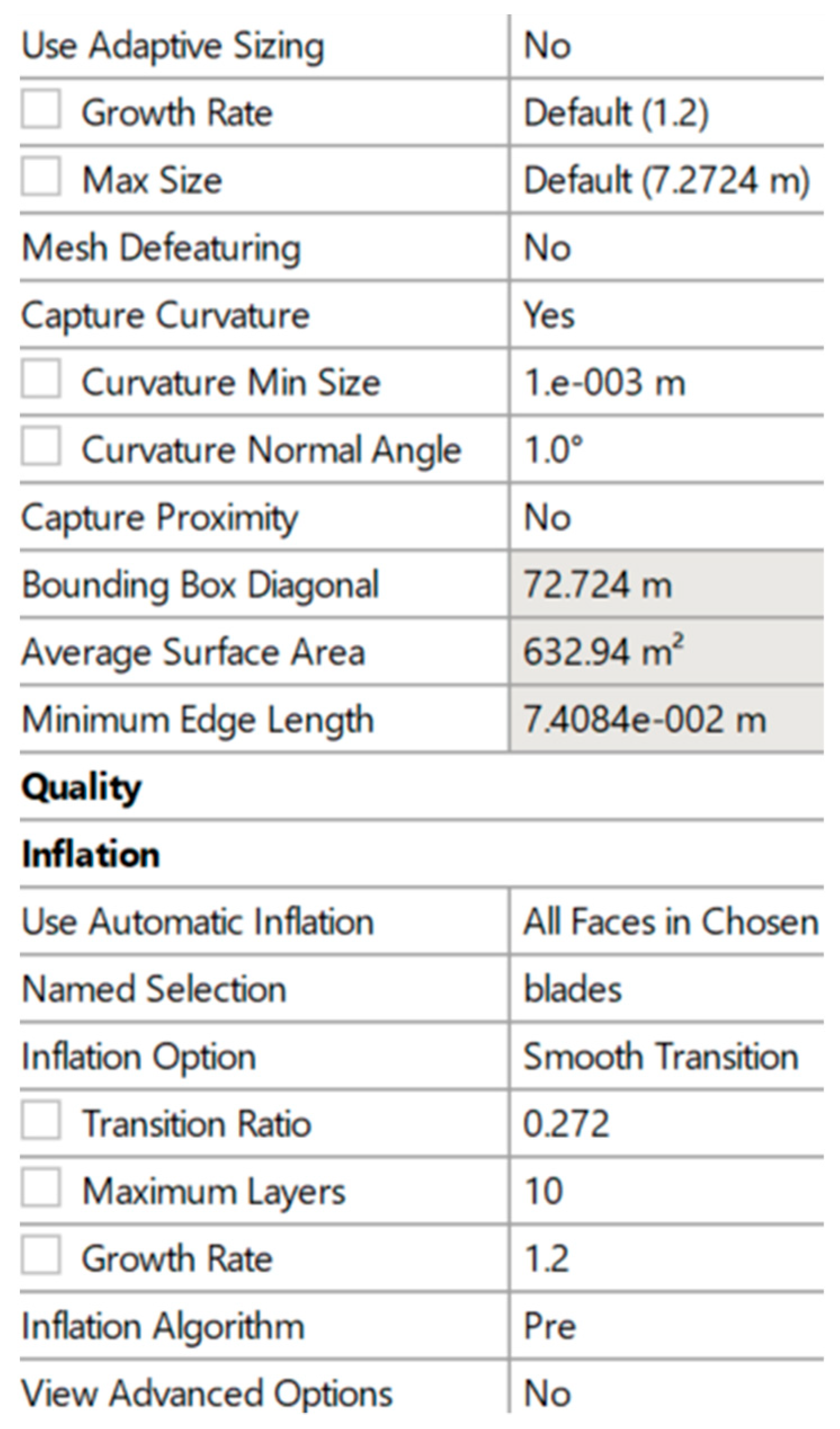
2. Numerical Setup and Conditions

Numerical analysis, and in particular computational fluid dynamics (CFD) analysis, can be much more reliable than undertaking experimental observations. This is because CFD simulations provide measurable predictions of flow properties for any expected quantities and conditions at any point of time, while experiments are limited in terms of their flow and operational conditions and are restricted to a certain number of locations. CFD simulations can also provide a larger domain of the flow and are not limited to the scale of a test section [48]. However, the reliability of a CFD analysis can be affected by propagating errors such as modelling errors. This can be due to simplified geometry, boundary conditions, or input data. Hence, experimental data are crucial in order to validate CFD analysis and ensure correct results. For example, Phase VI of the National Renewable Energy Laboratory (NREL) Unsteady Aerodynamics Experiment (UAE) experiment has been used to validate test cases for numerical analysis of wind turbines [49]. The experiment measured several quantities that provided usable data for the development and validation of modern wind turbines numerical models. The NREL Phase VI wind turbine is therefore employed in this study for validation of the analysis and the aimed-at optimization.
Similarly, the owl airfoil section employed in this optimization was captured through three-dimensional laser scanning along the span of an owl wing, with an accuracy of approximately 0.041 mm [50], in order to ensure accuracy of the optimization. A web-based tool was then used to visually extract the data from the images [51]. The WebPlotDigitizer tool is a semi-automated tool that implements extraction algorithms to extract data points. Here, a plain coordinate style containing X and Y coordinates allows the selection of points on the obtained image. Starting from the trailing edge and around the leading edge and back to the trailing edge, the data listed in Table 1 were selected and then exported into an Excel file before it was imported by Autodesk Inventor to sketch the owl airfoil shown in Figure 1. The chord lengths and pitch angles of each span station were kept in correspondence to those of the baseline model shown in Table 2.

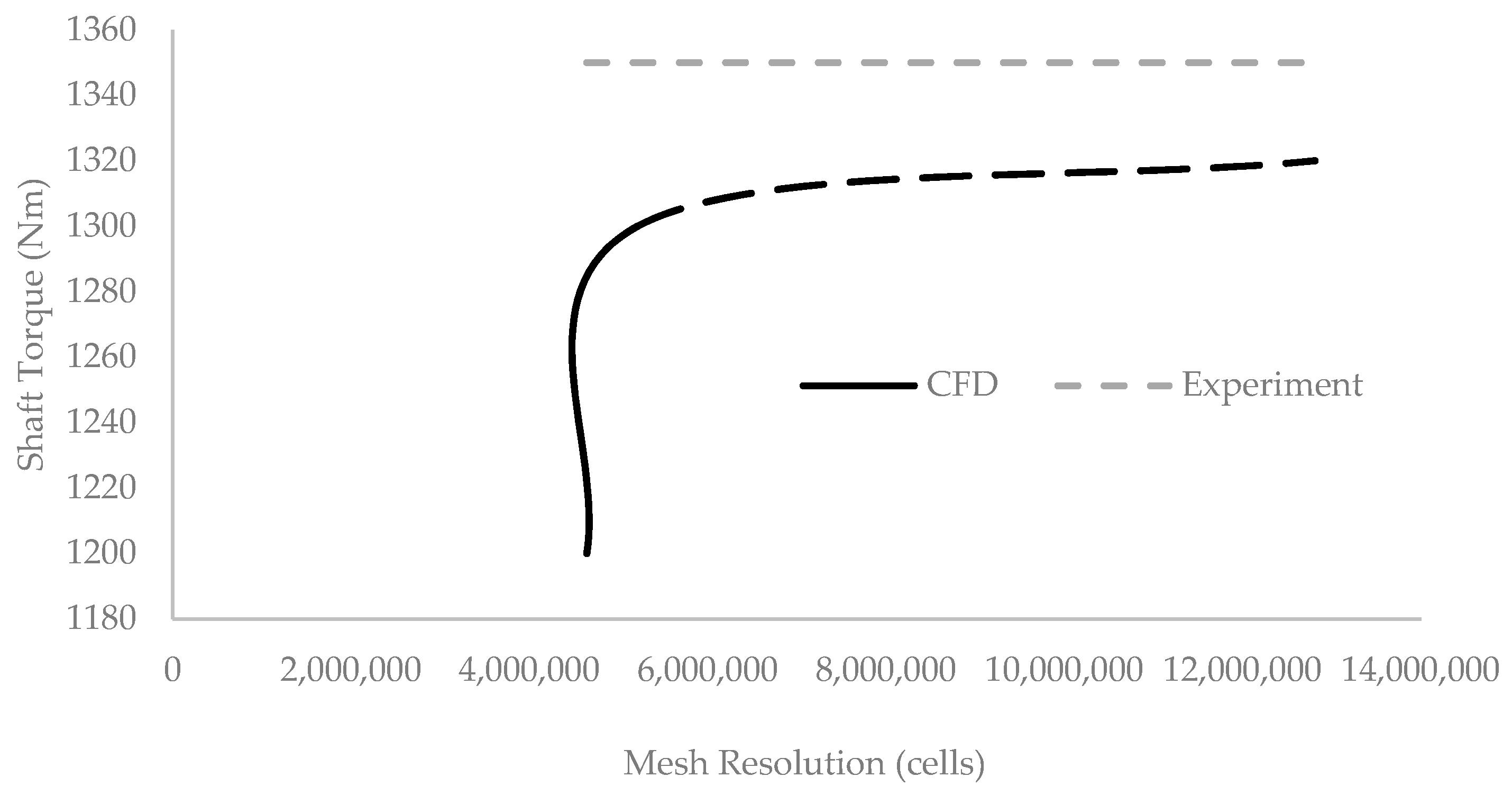
2.1. Model Validation

The NREL Phase VI experimental wind turbine is a small horizontal-axis wind turbine consisting of two blades with rotor diameters of 10.058 m and a hub height of 12.192 m. Each of the blades were formed using the S809 airfoil profile with the listed coordinates [52]. Sequence S of the experiment comprises the least-complex configuration, with a rigid upwind turbine rotor; no tip attachment; and constant 0° tilt, yaw, and cone angles. Test inlet speeds of 5, 10, 15, 20, and 25 m/s were maintained while uniformly resampling under steady flow conditions, and the rotation velocity and blade tip pitch angle were also kept constant at 72 RPM and 3°, respectively, under the default ambient conditions listed in Figure 2. Therefore, this analysis assumes a steady state simulation of the experiment. The simulation computational domain retains the 24.4 m high, 36.6 m wide and 57.912 m long dimensions of the section within which the NREL Phase VI turbine was tested [53]. However, the computational domain in the CFD model is larger by a ratio of 2:1 in the wake of the turbine. This is due to the importance of capturing the flow behavior after interaction with the blades. Also, the experimental data shows no considerable influence by the tower. And with the lack of geometrical representation of the hub, the tower and the hub are excluded from this analysis.
The 10 m/s inlet speed was found to initiate flow separation around the 30% span length of the blade, creating a challenge in simulating the turbine at this speed and span location [54,55]. Hence, selection of a suitable turbulence model and validation of this critical case is crucial to ensure correct numerical prediction. The shear stress transport (SST) k − ω turbulence model is selected for its reliability in modeling the NREL Phase VI experiment, with effective trade-off between computational cost and precision [56,57]. The model incorporates a blending function to activate the k − ω turbulence model near the surfaces and shifts to the k − ε turbulence model away from the surfaces to compensate for the sensitivity of the k − ω model to shear flow, and the limited ability of the k − ε model in near-surface regions. Hence, this allows for the simulation of the transition from laminar-to-turbulent flow as well as the flow separation and behavior away from the surface of the blade. A no-slip boundary condition is used to simulate the thin boundary layers.
To capture the effects of the geometrical variation between the baseline airfoil profile and the owl’s, correct representations of the actual geometrical models are ensured using the Control of the Curvature Min Size and the Curvature Normal Angle parameters in Ansys Mesh, as shown in Figure 3. Those values are relied upon to refine the mesh in regions of gradients while reducing the number of cells and thus, the computational cost. The effect is localized, resulting in most of the mesh resolution being concentrated on and near the blade surfaces, as regions with no curvature are not influenced by this refinement. Near-wall treatment of hexahedral layers was found necessary to produce a smoother transition and has enhanced calculation in regions of interest such as leading and trailing edges. To further reduce computational cost, the tetrahedral cells were converted to polyhedral cells in Ansys Fluent. This is because polyhedral cells have the advantage of having more neighboring cells because of the number of nodes each polyhedral cell consists of. The resulting grid is a gradient with fewer cells, as illustrated in Figure 4.
Using a three-dimensional moving reference frame model of realistically rotating blades, the mesh refinement result in Figure 5 is obtained using Curvature Min Size and Curvature Normal Angle of 3, 2, and 1 mm, and 3, 2, and 1 degree, respectively. Mesh independence was achieved with the intermediate mesh, as the higher mesh did not provide improvement of more than 5%. This may be because the different grid cases are mostly changes in the spatial grid size of the computational domain. Nonetheless, the CFD pressure distribution results for the critical location at the 30% span location are in close agreement with the measured data as shown in Figure 6, converging at 1462 of iterations using the Ansys Fluent 2022 R1 default 10 − 3 minimum residuals convergence criterion.

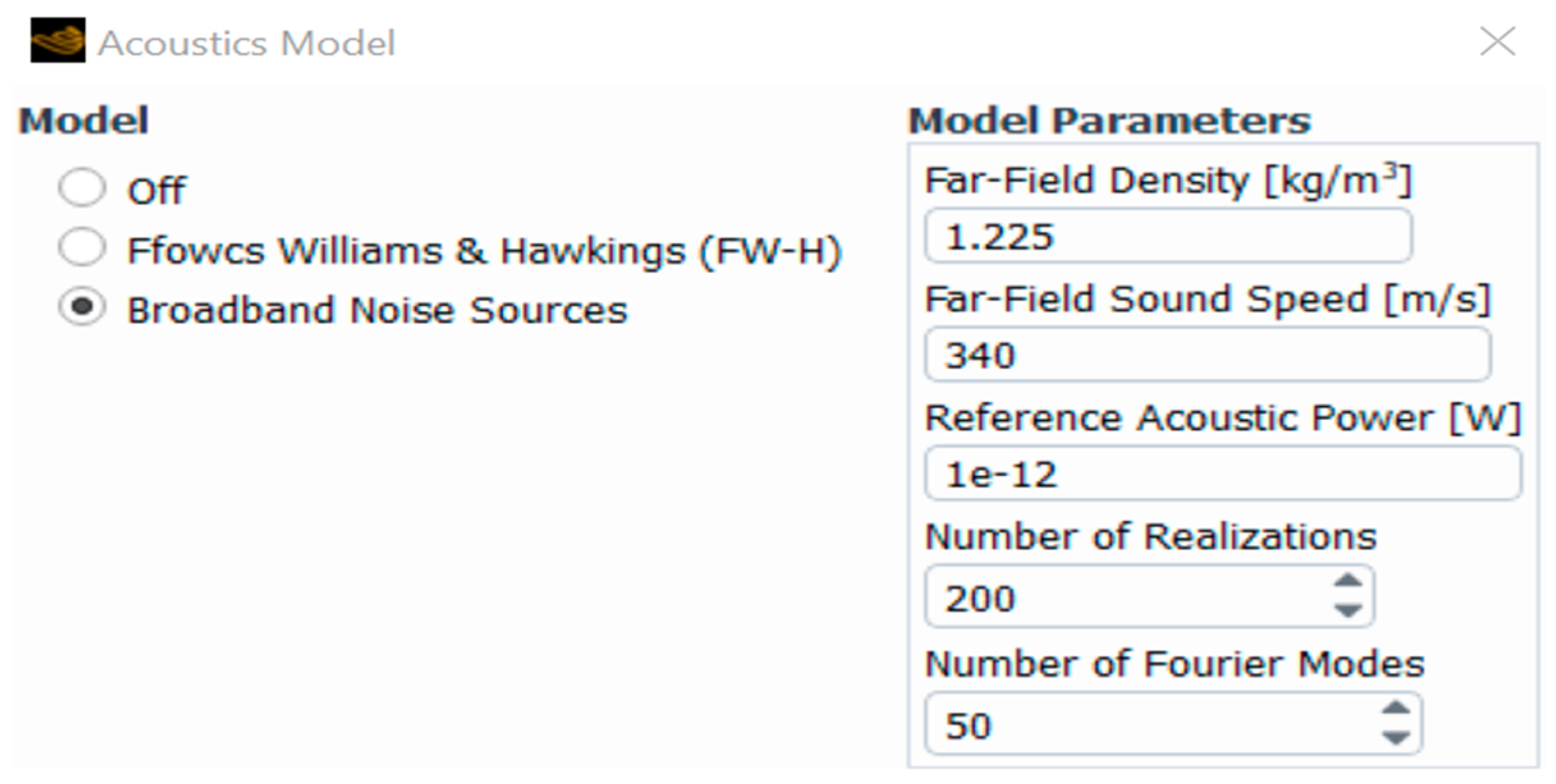
2.2. Prediction of Generated Noise

In the prediction of aerodynamically generated noise, frequency and magnitude are the two main factors for identifying the characteristics of the noise. In practical turbulent flow applications however, noise does not have definite tones, and the sound energy is constantly delivered over a wide range of frequencies. The magnitude is therefore given in term of noise power level to indicate the intensity of the noise at the source, and/or given in term of pressure level to indicate the propagation of noise as received at a distant point. The latter is not of importance in this analysis since the objective is to compare the airfoil self-noise generated by the baseline model and the model implementing the owl airfoil. Thus, the noise power level at and around both models is numerically calculated using the Ansys Fluent code approach, which utilizes a broadband noise source model. This model uses typical Reynolds-averaged Navier–Stokes equations and does not require transient solutions to the governing equations [58]. Results such as the turbulent kinetic energy (k), its rate of dissipation (ε), and the mean velocity field are all the model relies on to predict broadband noise under the pressure-based solver. Depending on the turbulence model and the flow characteristics emitting the noise, this noise prediction method is cost effective in terms of computational resources. The relevant parameters are also simplified, and the default constants such as the far field density and sound speed are maintained, as shown in Figure 7.
Here, the Reference Acoustic Power P r e f is used to compute the acoustic power outputs in decibels (dB) in the form of
P o u t = 10 log ⁡ P A P r e f
By default, the reference acoustic power is equal to 10 − 12   W / m 3 in three-dimensional environments, and P A is the acoustic power due to the isotropic turbulence. This was formulated by accounting for time difference [59], which is disregarded in the original derivation of the acoustic power formula [17]. The Number of Realizations with the default value of 200 is the number of trials used to determine the average of the source terms when applying Lighthill’s theory and linearized Euler equations to the Reynolds-averaged Navier–Stokes equations [58]. The Number of the Fourier Modes of 50 by default is used to calculate the turbulent velocity field. The result is then used to calculate linearized Euler equations. These equations are divided into mean, turbulent, and acoustic components as vector quantities in three-dimensional cases. One of the source terms constituting the formulation of the derived equations is described as self-noise, which involves only turbulent velocity components. This turbulent velocity is obtained using the stochastic noise generation and radiation method for the noise generated and radiated from a turbulent flow field. The model includes an extension for the propagation of the linearized Euler equation to handle noise generation [60]. This enables a qualitative assessment of the sound intensity and its spectral content. However, the method assumes this contribution from a single part of the turbulence field when calculating the acoustic power level. This limits the representation of turbulent fluctuations when simulating a moving noise source. To overcome this, the features are induced by relocating the volume of the noise source with velocity. The process is therefore more computationally demanding for three-dimensional cases, but remains manageable.

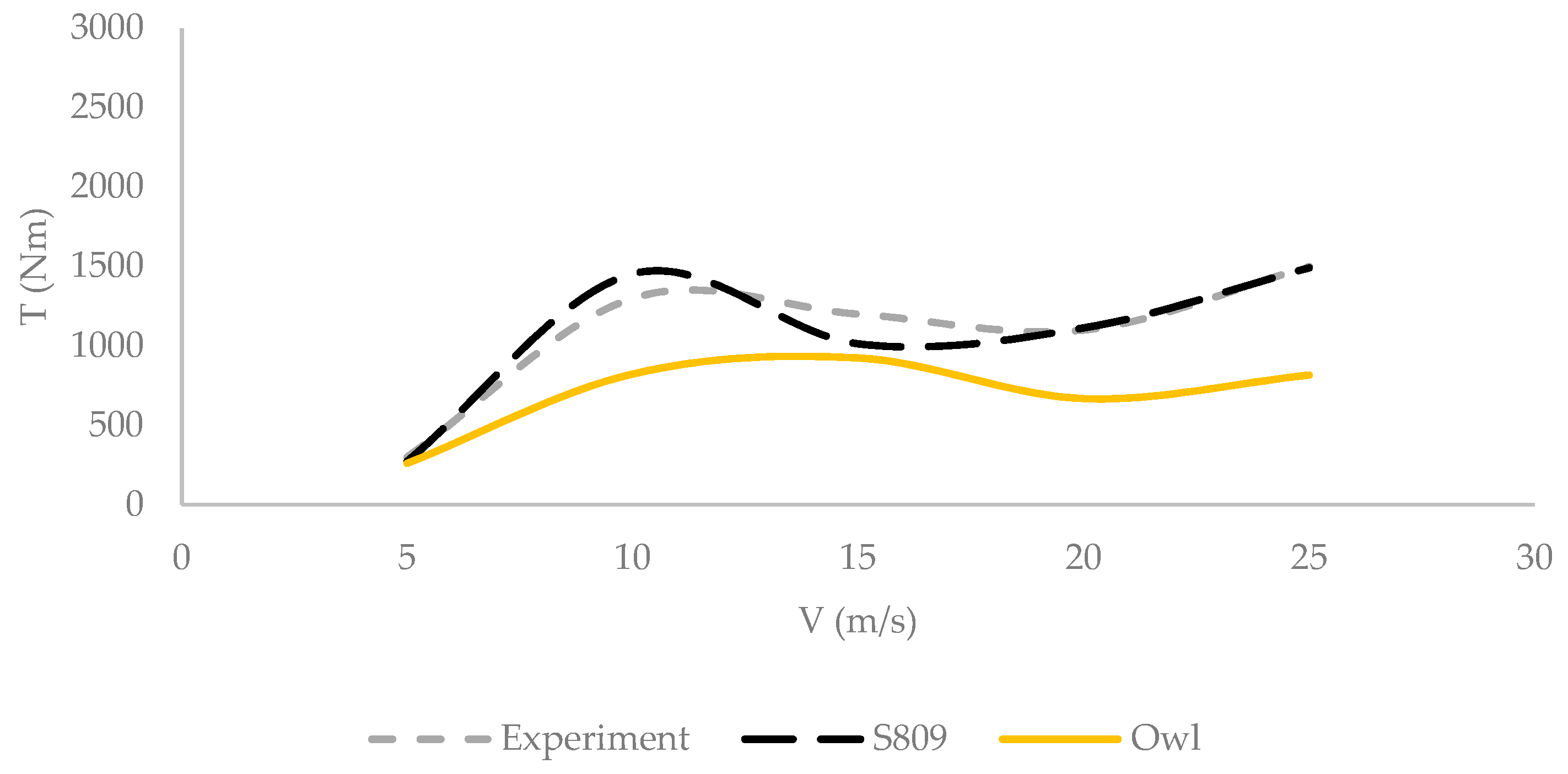
3. Results and Discussion

With the owl airfoil implemented in the NREL Phase VI wind turbine blades, the simulations of both the baseline model and the modified model are carried out under the same parameters used in the NREL Phase VI Sequence S test configurations. The torque results for each of the five inlet velocities for both models are presented in Figure 8 together with the experimental results for further validation. The comparison of the torque exerted on the rotational axis of the turbine T versus the inlet speed instead of the power coefficient C P versus the tip speed ratio is due to the fixed rotational velocity, and the direct correspondence of the two values in such case. In general, the power coefficient of a wind turbine is defined as
C P = r o t o r   p o w e r d y n a m i c   p o w e r = P 1 2 ρ A V 3 = T ω 1 2 ρ A V 3
where ρ is the air density, A is the area of the rotor disc, V is the relative wind velocity, and ω is the rotational velocity of the turbine. Since the flow velocity at the tip of a rotating turbine blade is much higher than that near its root, the turbine velocity is defined as the ratio between the velocity at the tip of the blade and the relative free stream wind speed ( ω r / V ), where r is the radius of the rotor disc or the length of the blade. Thus, the velocity is the only variable in the equation, as the rotational velocity is kept constant. In the meantime, the turbine blades impart on the wind an equal and opposite reaction torque. Most, if not all, of the energy is extracted through this torque, and therefore, it would be accurate to reference the performance characteristics in this analysis to the fluctuation in torque output. This accuracy is reflected by the considerably reduced generated torque associated with the model employing the owl airfoil at the 10, 20 and 25 m/s inlet velocities. Its performance from the 5 to 15 m/s inlet velocities has more of a moderate nature in comparison to the baseline model. It then decreases during the 20 m/s inlet velocity before it stabilizes again at the 25 m/s inlet velocity.
Similar to the baseline model at the 15 m/s inlet velocity, the modified model experienced a momentary stall before recovering. This indicates that different parameters are responsible for this stall. But the S809 airfoil is advantaged by its torque output at the 10 m/s inlet velocity. The lack of performance by the modified model at this inlet velocity in particular may not necessarily be due to the newly implemented airfoil design, but to the lack of optimization of other parameters such as chord lengths and twist distribution. However, optimization of the aerodynamic performance is outside the scope of this analysis. Nevertheless, the aim is to evaluate the ability of the owl airfoil to reduce the noise emitted by the NREL Phase VI wind turbine blades, particularly around the tip of the blade, without loss in performance in order to gain understanding of the mechanisms responsible for any reduction of noise. Therefore, the closely matched torque outputs by both models at the 5 and 15 m/s inlet velocities provide cases for direct comparison of the noise level emitted without a loss in aerodynamic performance.

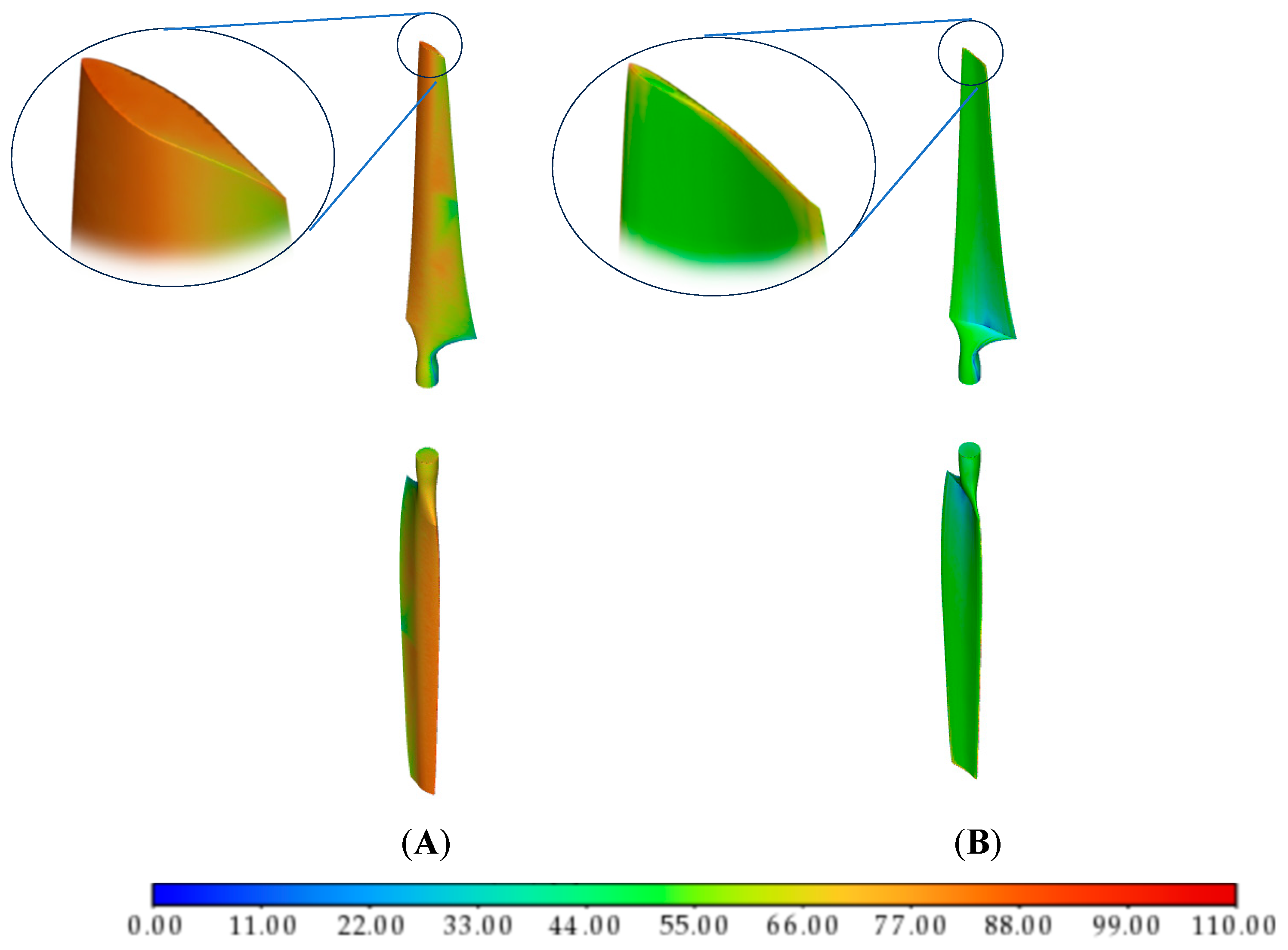
3.1. Surface Acoustic

To achieve accurate conclusions, the acoustic power levels (APLs) generated by the surfaces of both models are compared in this analysis by means of quantitative display of surface contours over the blades, as illustrated in Figure 9 and Figure 10. Here, the source location is applied to the blades only, as contributions of the test section walls are not considered. Surface areas where the maximum intensity of the noise is generated are clearly visible by the red shading, and zero generated APL is represented by the blue shading.
For the 5 m/s inlet velocity case, most of the blade surface area of the baseline model is generating around 105 dB of APL, covering almost two thirds of the chord length at the tip of the blade, as shown in the zoomed-in view of Figure 9A. On the other hand, this area is significantly reduced by the owl airfoil design at the same inlet velocity and an almost-matched power output. This is clearly illustrated by the mostly green-shaded surface area of the modified blades in Figure 9B. The reduction is also applied around the tip of the modified blade, as illustrated by the zoomed-in view of Figure 9B. Here, the 110 dB maximum generated APL by the modified blades is concentrated at a very small area of the tip. The total noise power generated by the implementation of the owl airfoil design at the 5 m/s inlet velocity is therefore significantly less than the total noise generated by the baseline model.
Propagation of the generated noise due to the velocity increase along the spans of both models is not very noticeable at this inlet velocity, as the color shading remains almost constant in both cases, except near the roots of the blades. This could be due to the relatively low relative velocity. Similarly, the effect of the sharp trailing edges of both models is not noticeable in the color shadings. This also suggests that the relative velocity plays a significant part in the relationship between the trailing edge thickness and the generated noise.
At the 15 m/s inlet velocity case, the maximum generated APL by the baseline model increases significantly to reach almost 120 dB at the tip of the blade, and mostly around areas of high curvature, as can be seen in the zoomed-in view of Figure 10A. This is not the case for the optimized model at this inlet velocity, as it generated a maximum of around 116 dB by an unnoticeable surface area at the tip of its blade. With a torque output result closely matched to that of the baseline model, the maximum APL and the surface area generating it have therefore been considerably reduced by the owl airfoil design as the velocity increased. Furthermore, a large portion of the surface area with near 0 dB blue shading extends between the root and the mid-section of the modified blade and covers more than two-thirds of its chord, as can be seen in Figure 10B. The baseline model too has generated a similar APL around the same region of its surface area, but not at the portions of high curvature where the maximum thickness of the S809 airfoil is located, as shown in Figure 10A. Here, the generated APL significantly and gradually increases as the relative velocity increases over the high curvature and further along the span of the blade. The slightly positive camber near the thin owl airfoil trailing edge has also resulted in an increase in the generated noise along the span of the modified blade, as can be seen in Figure 10A. This implies that changes in velocity have a direct and immediate impact on the locally generated noise, and the effect of the owl airfoil on mitigating the aeroacoustics of the NREL Phase VI wind turbine in the two inlet velocity cases seems to be owed to the ability of the owl airfoil geometrical characteristics to mitigate local velocity while maintaining aerodynamic performance. The inability of an airfoil design to reduce local velocities while maintaining lift is therefore crucial in the tradeoff between aerodynamic performance and the level of noise emitted. To verify this further, the aeroacoustics of the streamlines of both models are analyzed.

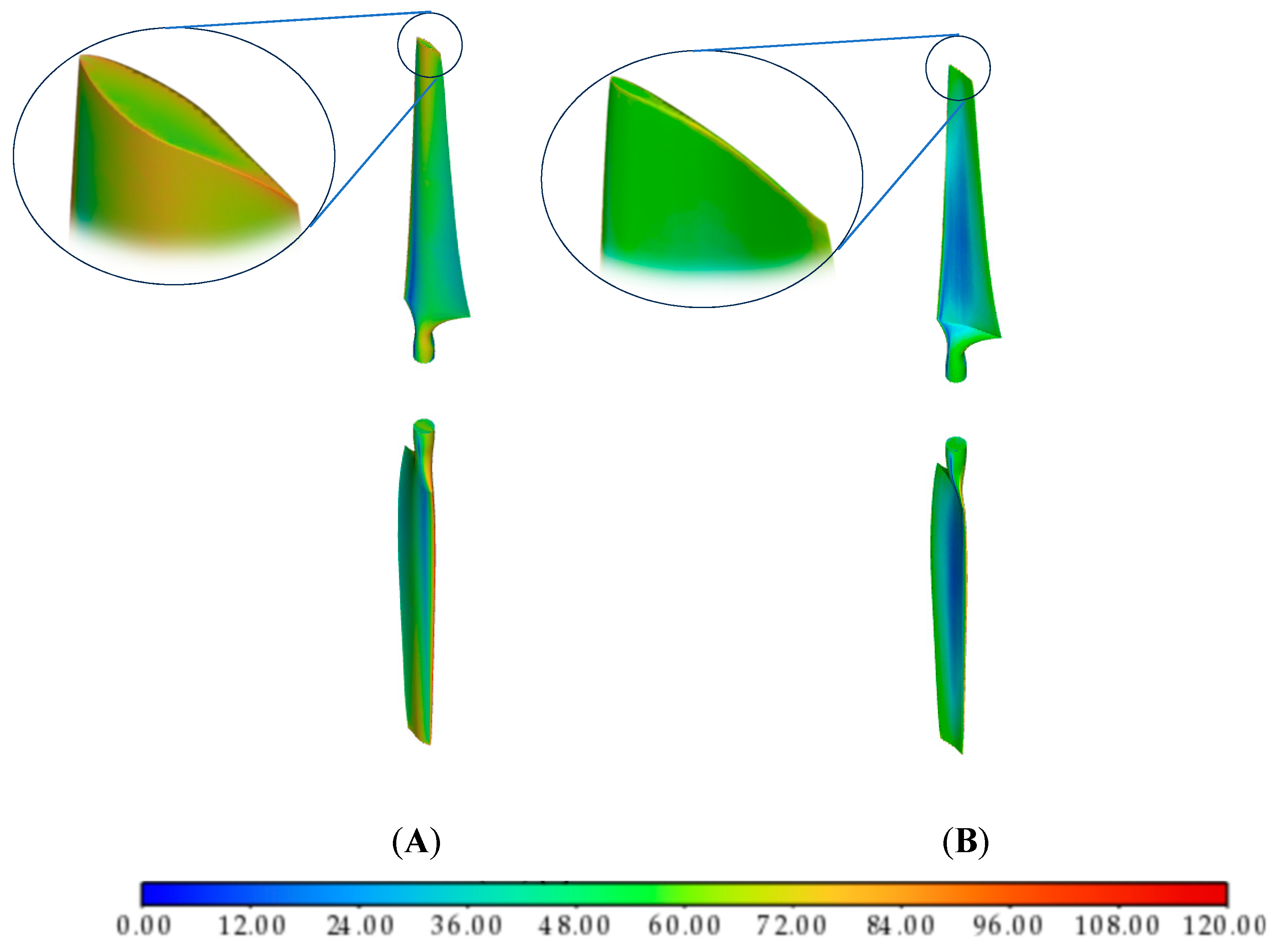
3.2. Streamlines Acoustic

By the same approach of quantitative evaluation of color shading, the aeroacoustics imparted by the blade surfaces on the local airstream and the APL generated by these streamlines are analyzed in order to verify the analyses of the surface acoustics and evaluate the streamline acoustics behavior. At a first glance at Figure 11A, the relation between the increasing velocity effects along the span and the generation of noise appears evident; this is due to the APL imparted on the airstream after interaction with the blades. Although this is contrary to the impression given by the surface acoustics in Figure 9A, it verifies the relationship between the local velocity components and the generated noise. The effect of the thin trailing edge of the modelled S809 airfoil is also verified by the blue shading in the figure, as well as the high APL contribution of the S809 leading edge due to its blunt geometrical characteristics. The level of noise carried by the airstream in the wake of the baseline turbine seems to be constant. This confirms the lack of any turbulence generated by APL at the 5 m/s inlet velocity. However, the APL imparted to the airstream by the modified blade in Figure 11B seems consistent with the generated surface APL at the 5 m/s inlet velocity in Figure 9B. Here, the velocity effect on the generated noise is minimized along the span of the blade, stabilizing at around the 30% span station, and showing no sign of propagation over the streamlines. This confirms the ability of the owl airfoil geometrical characteristics to reduce the generated noise at the tip of the blade by mitigating the local velocities along the span.
The effect of increasing the inlet velocity on the streamline acoustics is shown in Figure 12. A sudden decrease in the noise imparted at the streamlines in the wakes of both models is a distinguishing impact in this case, as the 15 m/s inlet velocity was dramatically decreased by the fixed rotation of the turbines. This further verifies the relationship between the generated noise and the increase in velocity. The zoomed-out views in the figures show that the sound energy was not, however, retained by the surfaces of the blades, as the streamline APL dramatically increased as flow velocity accelerated in the distant areas of the wake of the turbines. This phenomenon is outside the scope of this study since we are more interested in determining the different effects of the airfoil geometry and not common results. For instance, the APL of the streamline flow leaving the relatively much thinner trailing edge of the blade employing the owl airfoil is somewhat higher than that of the flow interacting with the surfaces of this blade, particularly near the root of the blade, as shown by the slight change in color shading in Figure 12B. This is possibly due to the separation of flow and its noise-generating vortices. We can therefore assume that the vortices near the root of the blades are the source of most acoustic noise generated by the modified blades. Similar but reduced vortex-generated noise can be noted at the tip of the modified blade in the figure, but still in less intensity than that imparted by the surface acoustics at the tip of the baseline blade. Further to this, the APL is distributed much more equally along the span of the baseline blades, as the structure of vortices near and around the baseline blade model is much more favorable than that around the modified blades. The advantage of the symmetrical characteristic of the S809 airfoil in reducing trailing edge vortices maybe be provided to the owl airfoil by optimizing the geometrical parameters of the owl airfoil profile. But again, this is outside the scope of this paper.
Overall, the contribution to the total generated APL by the streamlines is considerable, but the maximum value of the APL generated by the modified model at the 15 m/s inlet velocity is 4 dB less than that generated by the baseline model. Here, the acoustic of the streamline seems to be more localized and subject to the effects of the streamline velocities as mitigation of noise by the modified blades increases as the relative velocity increases.

4. Conclusions

This work covered a theoretical and numerical study of the aeroacoustics generated by a small horizontal-axis wind turbine operating in a three-dimensional environment. Extensive review of the relevant literature led to an investigation the effects of an owl airfoil design on the noise emitted by the tip of the NREL Phase VI wind turbine blade. Cases of close torque output results were selected for the comparison of the generated noise in order to achieve the objective, which was to analyze the possibility of tip vortex noise reductions attained without loss of performance. The aim, however, was not to achieve a final solution, but to determine whether there is a significant and direct effect made by the geometrical characteristics of the owl airfoil design on the noise generated by the tip of a turbine blade. This is to fill a gap in previous works, and gain understanding of the noise mitigating mechanisms of the form as a step towards obtaining a feasible solution in future work.
Substantial improvement by the owl airfoil profile was achieved, as the profile reduced the noise power generated by the tip of the NREL Phase VI wind turbine blade at two distinguished inlet velocities. Although the resulting maximum noise power generated by the modified model at the 5 m/s inlet velocity is 5 dB more than that generated by the baseline model, the owl airfoil design significantly reduced the surface area from which the maximum noise power was generated, resulting in a fraction of the total noise power generated by the baseline model. Furthermore, the mitigation of noise by the optimized blade increased as the relative velocity increased, reducing the maximum generated noise power generated by the baseline model at the 15 m/s inlet velocity by 4 dB, and generating nearly 0 dB of noise power from most of the modified blade surfaces. However, the noise generated by the near-field streamline flow was aggravated at the trailing edge of the modified blade as the velocity increased. This indicates the need for optimization of the modified blade for better aerodynamic performance. Whether or not the effect of the owl profile on the aeroacoustics of the baseline model will remain favorable or even increase after such optimization, the obtained results in this work are encouraging.

Author Contributions

Conceptualization, D.S.; methodology, D.S.; software, D.S.; validation, D.S. and J.N.; formal analysis, D.S.; investigation, D.S.; resources, D.S.; data curation, D.S.; writing—original draft preparation, D.S.; writing—review and editing, J.N.; visualization, D.S.; supervision, J.N.; project administration, D.S.; funding acquisition, J.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Alsop, A.; Eales, A.; Strachan, S.; Leary, J.; Persson, J.; Almeyda, I.R. A global market assessment methodology for small wind in the developing world. In Proceedings of the 2017 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017. [Google Scholar]
  2. Kwok, K.; Hu, G. Wind energy system for buildings in an urban environment. J. Wind. Eng. Ind. Aerodyn. 2023, 234, 105349. [Google Scholar] [CrossRef]
  3. Berg, F.V.D. Wind turbine noise: An overview of acoustical performance and effects on residents. In Proceedings of the Acoustics, Victor Harbor, Australia, 17–20 November 2013. [Google Scholar]
  4. Schmidt, J.H.; Klokker, M. Health Effects Related to Wind Turbine Noise Exposure: A Systematic Review. PLoS ONE 2014, 9, e114183. [Google Scholar] [CrossRef]
  5. Taylor, J.; Eastwick, C.; Lawrence, C.; Wilson, R. Noise levels and noise perception from small and micro wind turbines. Renew. Energy 2013, 55, 120–127. [Google Scholar] [CrossRef]
  6. Blumendeller, E.; Gaßner, L.; Müller, F.J.; Pohl, J.; Hübner, G.; Ritter, J.; Cheng, P.W. Quantification of amplitude modulation of wind turbine emissions from acoustic and ground motion recordings. Acta Acust. 2023, 7, 55. [Google Scholar] [CrossRef]
  7. Rogers, A.L.; Manwell, J.F.; Wright, S. Wind Turbine Acoustic Noise; Renewable Energy Research Laboratory: Amherst, MA, USA, 2006.
  8. Sagrillo, M. Wind Turbines and Noise; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
  9. Wagner, S.; Bareiß, R.; Guidati, G. Wind Turbine Noise; Springer: Stuttgart, Germany, 2012. [Google Scholar]
  10. Liu, W. A review on wind turbine noise mechanism and de-noising techniques. Renew. Energy 2017, 108, 311–320. [Google Scholar] [CrossRef]
  11. Zhang, C.Q.; Gao, Z.Y.; Chen, Y.Y.; Dai, Y.J.; Wang, J.W.; Zhang, L.R.; Ma, J.L. Locating and tracking sound sources on a horizontal axis wind turbine using a compact microphone array based on beamforming. Appl. Acoust. 2019, 146, 295–309. [Google Scholar] [CrossRef]
  12. Oerlemans, S.; Sijtsma, P.; López, B.M. Location and quantification of noise sources on a wind turbine. J. Sound Vib. 2007, 299, 869–883. [Google Scholar] [CrossRef]
  13. Wagner, S.; Bareiß, R.; Guidati, G. Noise Mechanisms of Wind Turbines. In Wind Turbine Noise; Springer: Berlin, Germany, 1996; pp. 67–92. [Google Scholar] [CrossRef]
  14. Lee, S.; Lee, S. Numerical and experimental study of aerodynamic noise by a small wind turbine. Renew. Energy 2014, 65, 108–112. [Google Scholar] [CrossRef]
  15. Serre, R.; Godsk, K.B.; Vronsky, T. Scales of turbulence on a wind turbine leading-edge. In Proceedings of the Wind Turbine Noise Conference, Lisbon, Portugal, 12–14 June 2019. [Google Scholar]
  16. Lilley, G.M. The Radiated Noise from Isotropic Turbulence Revisited; NASA Langley Research Center: Hampton, VA, USA, 1993.
  17. Proudman, I. The Generation of Noise by Isotropic Turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 214, 119–132. [Google Scholar] [CrossRef]
  18. Latoufis, K.; Riziotis, V.; Voutsinas, S.; Hatziargyriou, N. Effects of Leading Edge Erosion on the Power Performance and Acoustic Noise Emissions of Locally Manufactured Small Wind Turbine Blades. J. Phys. 2019, 10, 1742–6596. [Google Scholar] [CrossRef]
  19. Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; National Aeronautics and Space Administration: Washington, DC, USA, 1989.
  20. Con Doolan, D.M. Airfoil Noise Mechanisms and Control. In Flow Noise; Springer: Singapore, 2022; pp. 139–171. [Google Scholar] [CrossRef]
  21. Amirsalari, B.; Rocha, J. Recent Advances in Airfoil Self-Noise Passive Reduction. Aerospace 2023, 10, 791. [Google Scholar] [CrossRef]
  22. Zhu, W.J.; Heilskov, N.; Shen, W.Z.; Sørensen, J.N. Modeling of Aerodynamically Generated Noise from Wind Turbines. J. Sol. Energy Eng. 2005, 127, 517–528. [Google Scholar] [CrossRef]
  23. Junior, J.Y.S. Trailing-Edge Noise Development and Application of a Noise Prediction Tool for the Assessment and Design of Wind Turbine Airfoils; Escola Politécnica: São Paulo, Brasil, 2016. [Google Scholar]
  24. Clifton-Smith, M.J. Aerodynamic Noise Reduction for Small Wind Turbine Rotors. Wind. Eng. 2010, 34, 403–420. [Google Scholar] [CrossRef]
  25. Pourrajabian, A.; Rahgozar, S.; Dehghan, M.; Wood, D. A comprehensive multi-objective optimization study for the aerodynamic noise mitigation of a small wind turbine. Eng. Anal. Bound. Elements 2023, 155, 553–564. [Google Scholar] [CrossRef]
  26. Deshmukh, S.; Bhattacharya, S.; Jain, A.; Paul, A.R. Wind turbine noise and its mitigation techniques: A review. Energy Procedia 2019, 160, 633–640. [Google Scholar] [CrossRef]
  27. Rahgozar, S.; Pourrajabian, A.; Kazmi, S.M.R. Performance analysis of a small horizontal axis wind turbine under the use of linear/nonlinear distributions for the chord and twist angle. Energy Sustain. Dev. 2020, 58, 42–49. [Google Scholar] [CrossRef]
  28. Volkmer, K.; Kaufmann, N.; Carolus, T.H. Mitigation of the aerodynamic noise of small axial wind turbines—Methods and experimental validation. J. Sound Vib. 2021, 500, 116027. [Google Scholar] [CrossRef]
  29. León, C.A.; Merino-Martínez, R.; Ragni, D.; Avallone, F.; Scarano, F.; Pröbsting, S.; Snellen, M.; Simons, D.G.; Madsen, J. Effect of trailing edge serration-flow misalignment on airfoil noise emissions. J. Sound Vib. 2017, 405, 19–33. [Google Scholar] [CrossRef]
  30. Zhao, M.; Cao, H.; Zhang, M.; Liao, C.; Zhou, T. Optimal design of aeroacoustic airfoils with owl-inspired trailing-edge serrations. Bioinspiration Biomim. 2021, 16, 056004. [Google Scholar] [CrossRef] [PubMed]
  31. Rao, C.; Ikeda, T.; Nakata, T.; Liu, H. Owl-inspired leading-edge serrations play a crucial role in aerodynamic force production and sound suppression. Bioinspiration Biomim. 2017, 12, 046008. [Google Scholar] [CrossRef] [PubMed]
  32. Bodling, A.; Sharma, A. Numerical investigation of low-noise airfoils inspired by the down coat of owls. Bioinspiration Biomim. 2018, 14, 016013. [Google Scholar] [CrossRef] [PubMed]
  33. Wang, L.; Liu, X. Aeroacoustic investigation of asymmetric oblique trailing-edge serrations enlighted by owl wings. Phys. Fluids 2022, 34, 015113. [Google Scholar] [CrossRef]
  34. Wang, L.; Liu, X.; Li, D. Noise reduction mechanism of airfoils with leading-edge serrations and surface ridges inspired by owl wings. Phys. Fluids 2021, 33, 015123. [Google Scholar] [CrossRef]
  35. Li, D.; Liu, X.; Hu, F.; Wang, L. Effect of trailing-edge serrations on noise reduction in a coupled bionic aerofoil inspired by barn owls. Bioinspiration Biomim. 2019, 15, 016009. [Google Scholar] [CrossRef] [PubMed]
  36. Geyer, T.; Sarradj, E.; Fritzsche, C. Measuring owl flight noise. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
  37. Graham, R.R. The Silent Flight of Owls. J. R. Aeronaut. Soc. 1934, 38, 837–843. [Google Scholar] [CrossRef]
  38. Liang, G.Q.; Wang, J.C.; Chen, Y.; Zhou, C.H.; Liang, J.; Ren, L.Q. The Study of Owl’s Silent Flight and Noise Reduction on Fan Vane with Bionic Structure. Adv. Nat. Sci. 2010, 3, 192–198. [Google Scholar]
  39. Wagner, H.; Weger, M.; Klaas, M.; Schröder, W. Features of owl wings that promote silent flight. Interface Focus 2017, 7, 20160078. [Google Scholar] [CrossRef] [PubMed]
  40. Göçmen, T.; Özerdem, B. Airfoil optimization for noise emission problem and aerodynamic performance criterion on small scale wind turbines. Energy 2012, 46, 62–71. [Google Scholar] [CrossRef]
  41. Jones, R.; Doolan, C.J.; Teubner, M. Minimization of trailing edge noise by parametric airfoil shape modifications. In Proceedings of the 32nd AIAA Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2012. [Google Scholar]
  42. Li, D.; Wei, C. Numerical Study on Aerodynamic and Aeroacoustic Performances of Bioinspired Wings. Appl. Bionics Biomech. 2023, 2023, 9930841. [Google Scholar] [CrossRef]
  43. Bodling, A.; Sharma, A. Numerical investigation of noise reduction mechanisms in a bio-inspired airfoil. J. Sound Vib. 2019, 453, 314–327. [Google Scholar] [CrossRef]
  44. Wang, M.; Liu, X. Numerical investigation of aerodynamic and acoustic characteristics of bionic airfoils inspired by bird wing. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4004–4016. [Google Scholar] [CrossRef]
  45. Qin, S.; Cheng, L.; He, Z. Bionic Fan Blade Shape Design Based on Owl Airfoil and Analysis of Its Effect on Noise. In Advances in Mechanical Design; Springer Nature Singapore Pte Ltd.: Singapore, 2022; pp. 665–672. [Google Scholar] [CrossRef]
  46. Liu, X.; Liu, X. A Numerical Study of Aerodynamic Performance and Noise of a Bionic Airfoil Based on Owl Wing. Adv. Mech. Eng. 2014, 6, 859308. [Google Scholar] [CrossRef]
  47. Li, D.; Liu, X. A comparative study on aerodynamic performance and noise characteristics of two kinds of long-eared owl wing models. J. Mech. Sci. Technol. 2017, 31, 3821–3830. [Google Scholar] [CrossRef]
  48. Tu, J.; Yeoh, G.H.; Liu, C.; Tao, Y. Computational Fluid Dynamics: A Practical Approach, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
  49. Suárez, J.M.; Doerffer, P.; Szulc, O. CFD Validated Technique for Prediction of Aerodynamic Characteristics on Horizontal Axis Wind Energy Turbines. In Proceedings of the EWEA Offshore, Copenhagen, Denmark, 10–12 March 2015. [Google Scholar]
  50. Liu, T.; Kuykendoll, K.; Rhew, R.; Jones, S. Avian Wing Geometry and Kinematics. AIAA J. 2006, 44, 954–963. [Google Scholar] [CrossRef]
  51. WebPlotDigitizer. Available online: https://apps.automeris.io/wpd/ (accessed on 15 January 2023).
  52. Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001.
  53. BY 80-/80- BY 120-Foot Wind Tunnels. NASA Ames Research Center. Available online: https://rotorcraft.arc.nasa.gov/Research/Facilities/windtunnels.html (accessed on 15 January 2023).
  54. Song, Y.; Perot, J.B. CFD Simulation of the NREL Phase VI Rotor. Wind. Eng. 2015, 39, 299–310. [Google Scholar] [CrossRef]
  55. Yelmule, M.M.; Vsj, E.A. CFD predictions of NREL Phase VI Rotor Experiments in NASA/AMES Wind tunnel. Int. J. Renew. Energy Res. 2013, 3, 261–269. [Google Scholar]
  56. Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
  57. Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-Eddy Simulation of Flow Around the NREL Phase-VI Blade. In Proceedings of the Wind Energy Symposium, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
  58. Ansys. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v221/en/flu_ug/x1-151000023.6.1.html (accessed on 30 January 2024).
  59. Lilley, G.M. The radiated noise from isotropic turbulence. Theor. Comput. Fluid Dyn. 1994, 6, 281–301. [Google Scholar] [CrossRef]
  60. Bechara, W.; Bailly, C.; Lafon, P.; Candel, S.M. Stochastic approach to noise modeling for free turbulent flows. AIAA J. 1994, 23, 455–463. [Google Scholar] [CrossRef]
Energies 17 02254 g001
Figure 1. Modeled owl airfoil cross-section.
Figure 1. Modeled owl airfoil cross-section.
Energies 17 02254 g001
Energies 17 02254 g002
Figure 2. Reference values.
Figure 2. Reference values.
Energies 17 02254 g002
Energies 17 02254 g003
Figure 3. Reference frame motion.
Figure 3. Reference frame motion.
Energies 17 02254 g003
Energies 17 02254 g004
Figure 4. Near-surface mesh of the S809 airfoil cross-section.
Figure 4. Near-surface mesh of the S809 airfoil cross-section.
Energies 17 02254 g004
Energies 17 02254 g005
Figure 5. Mesh refinement study.
Figure 5. Mesh refinement study.
Energies 17 02254 g005
Energies 17 02254 g006
Figure 6. Pressure distribution results at 0.3R and 10 m/s inlet velocity.
Figure 6. Pressure distribution results at 0.3R and 10 m/s inlet velocity.
Energies 17 02254 g006
Energies 17 02254 g007
Figure 7. Acoustics model parameters.
Figure 7. Acoustics model parameters.
Energies 17 02254 g007
Energies 17 02254 g008
Figure 8. Torque results comparison.
Figure 8. Torque results comparison.
Energies 17 02254 g008
Energies 17 02254 g009
Figure 9. Acoustic power level (dB) at 5 m/s: S809 airfoil (A) and owl airfoil (B).
Figure 9. Acoustic power level (dB) at 5 m/s: S809 airfoil (A) and owl airfoil (B).
Energies 17 02254 g009
Energies 17 02254 g010
Figure 10. Acoustic power level (dB) at 15 m/s: S809 airfoil (A) and owl airfoil (B).
Figure 10. Acoustic power level (dB) at 15 m/s: S809 airfoil (A) and owl airfoil (B).
Energies 17 02254 g010
Energies 17 02254 g011
Figure 11. Streamline acoustic power level (dB) at 5 m/s: S809 airfoil (A) and owl airfoil (B).
Figure 11. Streamline acoustic power level (dB) at 5 m/s: S809 airfoil (A) and owl airfoil (B).
Energies 17 02254 g011
Energies 17 02254 g012
Figure 12. Streamline acoustic power level (dB) at 15 m/s: S809 airfoil (A) and owl airfoil (B).
Figure 12. Streamline acoustic power level (dB) at 15 m/s: S809 airfoil (A) and owl airfoil (B).
Energies 17 02254 g012
Table 1. Owl airfoils’ coordinate points.
Table 1. Owl airfoils’ coordinate points.
Upper SurfaceLower Surface
x/cx/c
y/cy/c
10.915
0.952460.91575
0.917580.91902
0.882690.92286
0.824820.93
0.795620.93389
0.737610.94192
0.67340.949
0.604690.955
0.569070.9575
0.498990.961
0.46410.96179
0.429220.962
0.359460.96226
0.289690.961
0.254810.96
0.219920.95841
0.185040.957
0.150160.955
0.115280.951
0.0803950.94606
0.0470980.9391
0.0264850.90258
0.0613680.90025
0.131130.90771
0.166020.914
0.20090.92018
0.235780.926
0.270660.93219
0.340430.94221
0.375310.947
0.410190.95
0.445080.952
0.479960.953
0.551040.951
0.584610.94839
0.692210.938
0.772260.92917
0.80730.925
0.882690.918
0.952460.913
10.915
Table 2. Blade chord and twist distributions [52].
Table 2. Blade chord and twist distributions [52].
Radial Distance R (m)Span Station (R/5.029)Chord Length (m)Twist (Degrees)Thickness (m) (20.95% Chord)Twist Axis (% Chord), (m)
0.00.0Hub-center of rotationHub-center of rotationHub-center of rotationHub-center of rotation
0.5080.101218 (Root hub adapter)0.0 (Root hub adapter)0.218 (Root hub adapter)50 (Root hub adapter)
0.6600.1310.2180.00.21850
0.8830.1760.1830.00.18350
1.2570.2500.73720.0400.15430, (0.221)
1.3430.2670.72818.0740.15230, (0.218)
1.5100.3000.71114.2920.14930, (0.213)
1.6480.3280.69711.9090.14630, (0.209)
1.9520.3880.6667.9790.13930, (0.199)
2.2570.4490.6365.3080.13330, (0.190)
2.3430.4660.6274.7150.13130, (0.188)
2.5620.5090.6053.4250.12630, (0.181)
2.8670.5700.5742.0830.12030, (0.172)
3.1720.6310.5431.1500.11330, (0.162)
3.1850.6330.5421.1150.11330, (0.162)
3.4760.6910.5120.4940.10730, (0.153)
3.7810.7520.482−0.0150.10030, (0.144)
4.0230.8000.457−0.3810.09530, (0.137)
4.0860.8120.451−0.4750.09430, (0.135)
4.3910.8730.420−0.9200.08830, (0.162)
4.6960.9340.389−1.3520.08130, (0.116)
4.7800.9500.381−1.4690.07930, (0.114)
5.0000.9940.358−1.7750.07530, (0.107)
5.02910.335−1.9440.07530, (0.101)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sesalim, D.; Naser, J. Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine. Energies 2024, 17, 2254. https://doi.org/10.3390/en17102254

AMA Style

Sesalim D, Naser J. Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine. Energies. 2024; 17(10):2254. https://doi.org/10.3390/en17102254

Chicago/Turabian Style

Sesalim, Dean, and Jamal Naser. 2024. "Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine" Energies 17, no. 10: 2254. https://doi.org/10.3390/en17102254

APA Style

Sesalim, D., & Naser, J. (2024). Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine. Energies, 17(10), 2254. https://doi.org/10.3390/en17102254

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop