Collaborative Operation Optimization Scheduling Strategy of Electric Vehicle and Steel Plant Considering V2G

Abstract

With the shortage of fossil fuels and the increasingly serious problem of environmental pollution, low-carbon industrial production technology has become an effective way to reduce industrial carbon emissions. Electrified steel plants based on electronic arc furnaces (EAF) can reduce most carbon emissions compared with traditional steel production methods, but the production steps have fixed electricity consumption behavior, and impact loads are easily generated in the production process, which has an impact on the stability of the power system. EV has the characteristics of a mobile energy storage unit. When a large number of EVs are connected to the power grid, they can be regarded as distributed energy storage units with scheduling flexibility. Through the orderly scheduling of EVs, the spatial–temporal transfer of EV charging and discharging load can be realized. Therefore, the EV situated in the steel plant’s distribution network node has the capacity to be utilized by providing peak shaving and valley filling services for the steel production load. This study proposes an operation optimization scheduling method for EVs and steel plants. Taking the lowest overall operating cost as the objective, an optimal scheduling model considering EVs operation, steel plant, and distributed generator is established. Based on the IEEE-33 node distribution network model considering distributed generators, the proposed model is simulated and analyzed, and the effectiveness of the EV steel plant operation optimization scheduling strategy is investigated.

1. Introduction

The shortage of fossil energy and the aggravation of environmental pollution make the decarbonization of energy an urgent issue. The Paris Climate Agreement has generated a heightened sense of urgency, compelling the world to incorporate measures to regulate greenhouse gas emissions into their growth planning [1]. The iron and steel (I and S) sector and the transportation sector are typical sectors of high carbon emissions. Large-scale deployment of electric vehicles (EV)s and the promotion of low-carbon technologies in the I and S industry could be a potential solution to the carbon emission problem.

In the I and S sector, the electric arc furnace (EAF) steelmaking technology has attracted much attention for its low carbon emissions. Compared with the blast-furnace followed basic oxygen furnace (BF-BOF) steelmaking technology, the carbon emission of the EAF steelmaking technology is only 0.6~0.7 $\mathrm{t}{\mathrm{C}\mathrm{O}}_2/\mathrm{t}\mathrm{S}$, accounting for about 30–40% of the BF-BOF steelmaking process [2,3]. Currently, the global share of EAF steel production is at 29% [4]. As the technology for electrified I and S production continues to improve, this proportion is steadily growing each year. The abbreviations and symbolic explanations of this article are shown in

Table 1. Acronyms and symbol specification table.

Interpretation	Acronyms	Interpretation	Symbol
Electric Vehicle	EV	Steel production state variable	$S_{j,l,t}^{steel}$
Vehicle to Grid	V2G	Production time	$T_l$
Blast Furnace	BF	Number of production equipment	$M_l$
Basic Oxygen Furnace	BOF	Cost coefficient of generator	$Q_i$
Iron and Steel	I and S	Generator power	$P_{i,t}^{Gen}$
Electric Arc Furnace	EAF	Upper and lower limits of generator power	$P_{i,min}^{Gen}$/$P_{i,max}^{Gen}$
Ladel Furnace	LF	EV charge and discharge state variables	$S_{k,driving}^{EVc}/S_{k,driving}^{EVd}$
Argon–Oxygen Decarburization	AOD	Charging and discharging power of EVs	$P_c^{EV}$/$P_d^{EV}$
Continuous Casting	CC	Number of charging/discharging EVs	$N_{c,t}$/$N_{d,t}$
Demand Response	DR	Electricity price of EVCharging/discharging	$P{r}_{c,t}$/$P{r}_{d,t}$
Flexible Job Shop Scheduling Problem	FJSP	State of Charge of EV	${SOC}_{k,t}$
State of Charge	SOC	EV driving power consumption	$E_{k,t-1}^{Tran}$

.

The steel production process is characterized as a large-scale, multi-layered, multi-product operation that involves parallel equipment, intricate production processes, and various energy limitations and is widely regarded as one of the most intricate industrial processes [4]. Ref. [5] analyzes the BF-BOF steel production process and separately models the oxygen consumption of BF and BOF, and finds it is achievable to reduce the imbalance caused by the random fluctuations in by-product fuel production and consumption, hence enhancing energy efficiency. In ref. [6], the author proposes a scheduling optimization model of oxygen, hydrogen, and synthetic natural gas supply systems in iron and steel plants under the EAF production route. This makes the production load of the steel plant more adjustable. Ref. [7] evaluates the economics of EAF steel production routes and models the overall production investment costs, taking into account economic and environmental costs. In ref. [8], the author proposes steel production models that incorporate the flexibility of EAF, enabling them to optimize the scheduling of energy-intensive activities and avoid peak periods. However, the current research on the regulation of the electrified steel production process is limited to the regulation of the internal production of the steel plant, and there is a lack of in-depth exploration of the complementarity of the steel plant with demand-side controllable resources such as EV to reduce the impact load. Furthermore, the production modeling methods of steel making proposed above are very complex, requiring separate modeling of production gas use and production electricity usage, making it challenging to expand the model on its original foundation.

EVs can be regarded as distributed mobile energy storage batteries in power systems [9,10,11]. Using vehicle-to-grid (V2G) technology [12], EVs can transfer peak load by optimizing charging and discharging, reducing the operating cost of generators and carbon emissions from power system operation. In general, evaluating whether V2G can operate is restricted by the state of charge (SOC) of electric vehicles that can meet their trip needs. Simultaneously, EVs can also be analyzed as mobile energy storage, as a distributed energy storage resource to provide support for the operation of the power system [13,14]. However, if a large-scale of EVs is connected to the power system, the lack of orderly management of EV charging and discharging will bring challenges to the stability of power system operation [15].

The V2G of EVs is a complex problem that involves the stability of the power system [16,17], the charging efficiency of EVs, the charging cost of EV users, and the uncertain travel willingness of EV users. A charge–discharge model for EVs is developed in ref. [18], taking into account three distinct EV user profiles and four different EV types. The results demonstrate the potential economic revenue that V2G can provide in the event of substantial fluctuations in electricity prices during different time periods. Ref. [19] proposes a demand response model of the V2G mobile energy network, which characterizes the movement of EVs in the distribution network with different network nodes. The results show that V2G technology will affect the demand response (DR) capability of a region. In ref. [20], a reliability evaluation mechanism is proposed for different charging strategies of EVs, and a dynamic random consumption model of the EV fleet is developed for reliability evaluation of the distribution network. The results show that the orderly regulation of EV charging and discharging can significantly reduce the impact on the distribution network. Ref. [21] examines the collaborative optimization scheduling problem involving EVs and wind power generators. The proposed model is a new bi-level optimization approach that addresses the issue of efficiently scheduling the charging and discharging of EVs using wind power, taking into account both temporal and spatial considerations. The results show that the positioning of EV charging and discharging loads plays a crucial role in the operational design of the distribution network. However, the current research on EV charging and discharging scheduling regards it as a controllable resource for accommodating renewable energy and providing auxiliary services for the power grid. There is a lack of research on the interaction between EVs as a mobile energy storage unit and demand-side power users to stabilize the impact load.

This work constructs a joint scheduling model of EV charging and discharging and steel plant operation based on the IEEE-33 distribution network. Considering the coupling characteristics of EV travel traffic network and distribution network nodes and the production steps of electrified steel plants, the EV charging and discharging load of distribution network nodes and adjacent nodes where the steel plant is located are optimized during the fluctuation period of the steel production load, so as to stabilize the load curve. At the same time, considering the influence of peak–valley electricity price and EV charging cost and discharge subsidy, the charging and discharging cost of EV owners and the electricity cost of steel plants are optimized. The main contributions of this paper are:

(1)

A joint operation mode of EV and steel production is proposed to reduce the impact load caused by steel production.

(2)

A linear connection approach of steel production steps is proposed, which makes the steel production model have higher scalability.

(3)

The EV charging and discharging incentive price is formulated considering the complementary mechanisms of peak–valley price and EV charging price to achieve optimal economic operation.

The rest of this paper is organized as follows. Section 2 and Section 3 introduce the steel production connection model and the EV steel plant joint scheduling model, respectively. Simulations and analysis are in Section 4. Finally, a conclusion is drawn in Section 5.

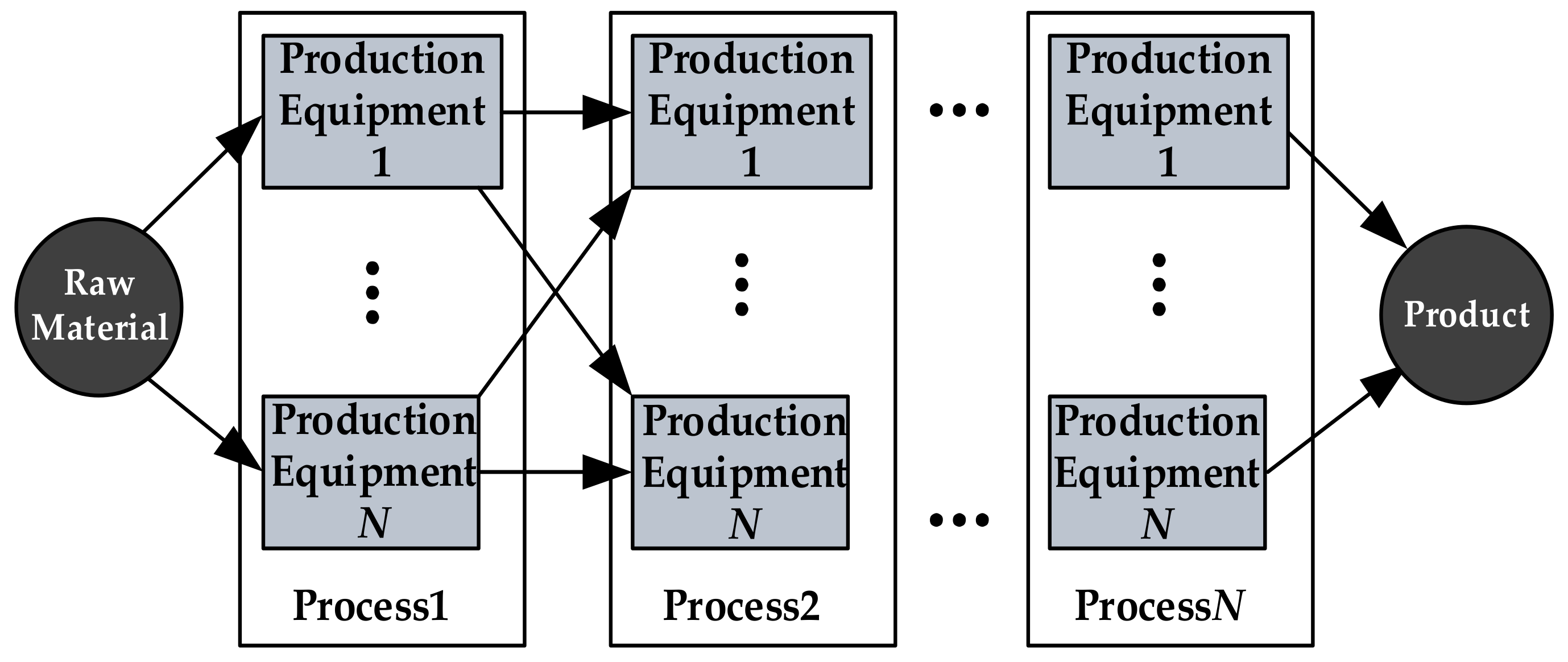
2. Establishment of Steel Production Model

2.1. EAF Steel Production Processes

The EAF steel production process can be summarized as four steel production steps [22,23].

(1)

Steel production: The scrap raw material is sent into the EAF for melting. Because of the need for electric heating, the electricity consumption of this production process is large.

(2)

Secondary metallurgy: The molten steel after EAF processing is sent to the LF furnace for refining, desulfurization and temperature control. Due to the need to control the temperature of molten steel, the electricity consumed in this process is also high.

(3)

Refining decarburization: The molten steel of the LF furnace is fed into the AOD furnace, and the decarburization process is carried out under the protection of argon and oxygen. This step does not involve heating load and consumes less electricity.

(4)

Continuous casting: In this production step, the molten steel is continuously solidified into steel, and the power consumption is less.

The sequence of EAF steel production steps is shown in Figure 1.

The fundamental principle underlying the steel production process is the methodical transformation of raw materials, specifically scrap, through a predetermined series of steps, culminating in the production of the final product. Therefore, the flexible job shop scheduling problem (FJSP) model can be used to characterize the steel production process [24]. The visual description of the FJSP model is shown in Figure 2.

2.2. Establishment of Steel Production Model

Based on the framework of FJSP, a linearized production process model of steel production is established, and a simplified method for the connection of steel production steps is proposed. We set a Boolean variable $S_{j,l,t}^{steel}$, which represents the production state of steel production heat $j$ at time $t$ on production step $l$ (1 indicates that the producing step is currently active, whereas 0 indicates that the production step is currently inactive). The constraint coupling relationship between $S_{l,j,t}$ is used to characterize the processing constraints between each production step. Set the production status change discriminant variable $Ind=S_{j,l,t}^{steel}-S_{j,l,t-1}^{steel}$ to determine the change in steel production steps in time $t$, so as to connect the overall steel production steps. When the production process begins, the steel production state variable $S_{j,l,t}^{steel}$ is constrained to 1 for the rest of the production period. When the production process ends, the steel production state variable $S_{j,l,t}^{steel}$ is constrained to 0 for the following period of transportation time.

$$S_{j,l,F_{prod}}^{steel}\ge {Ind}_{\mathrm{s}\mathrm{t}}$$

(1)

$${Ind}_1=S_{j,l,t}^{steel}-S_{j,l,t-1}^{steel}$$

(2)

$$F_{prod}=t:t+T_l-1$$

(3)

where $F_{prod}$ stands for the standard processing time length of the production step; $T_l$ is the processing time of the production step l. ${Ind}_{\mathrm{s}\mathrm{t}}$ will change with the production and processing situation $S_{j,l,t}^{steel}$ of the period t and $S_{j,l,t-1}^{steel}$ of the period $t-1$.

$$S_{j,l+1,F_{tr}}^{steel}\le 1-{Ind}_2$$

(4)

$${\sum }_{\tau =t}^{F_{Wm}}{S}_{j,l+1,\tau }^{steel}\ge 1$$

(5)

$${Ind}_2=S_{j,l,t-1}^{steel}-S_{j,l,t}^{steel}$$

(6)

$$F_{tr}=t:t+T_{trans}-1$$

(7)

$$F_{Wm}=t:t+T_{Wmax}-1$$

(8)

where $T_{trans}$ stands for the transportation time of molten steel from one production step to another. $T_{Wmax}$ represents the maximum time that liquid steel can wait.

It is necessary to limit the total production time of each manufacturing phase to ensure that production stops in each furnace once the allotted production time has elapsed.

$${\sum }_{j=1}^J{\sum }_{l=1}^L{\sum }_{t=1}^H{S}_{j,l,t}^{steel}\le M_l$$

(9)

In the process of steel production, since each heat must go through each production step in order, and the liquid steel of each production step will only be repeated once, the constraint is set so that the same heat can only be processed after the previous production step is completed.

$$S_{j,l,t}^{steel}\le \frac{\sum _{t=1}^H{S}_{j,l-1,t}^{steel}}{T_{l-1}}$$

(10)

where $S_{j,l-1,t}$ and $T_{l-1}$ represent the production state and production processing time of production step $l-1$ of heat $j$, respectively.

3. Establishment of EV Steel Plant Joint Scheduling Model

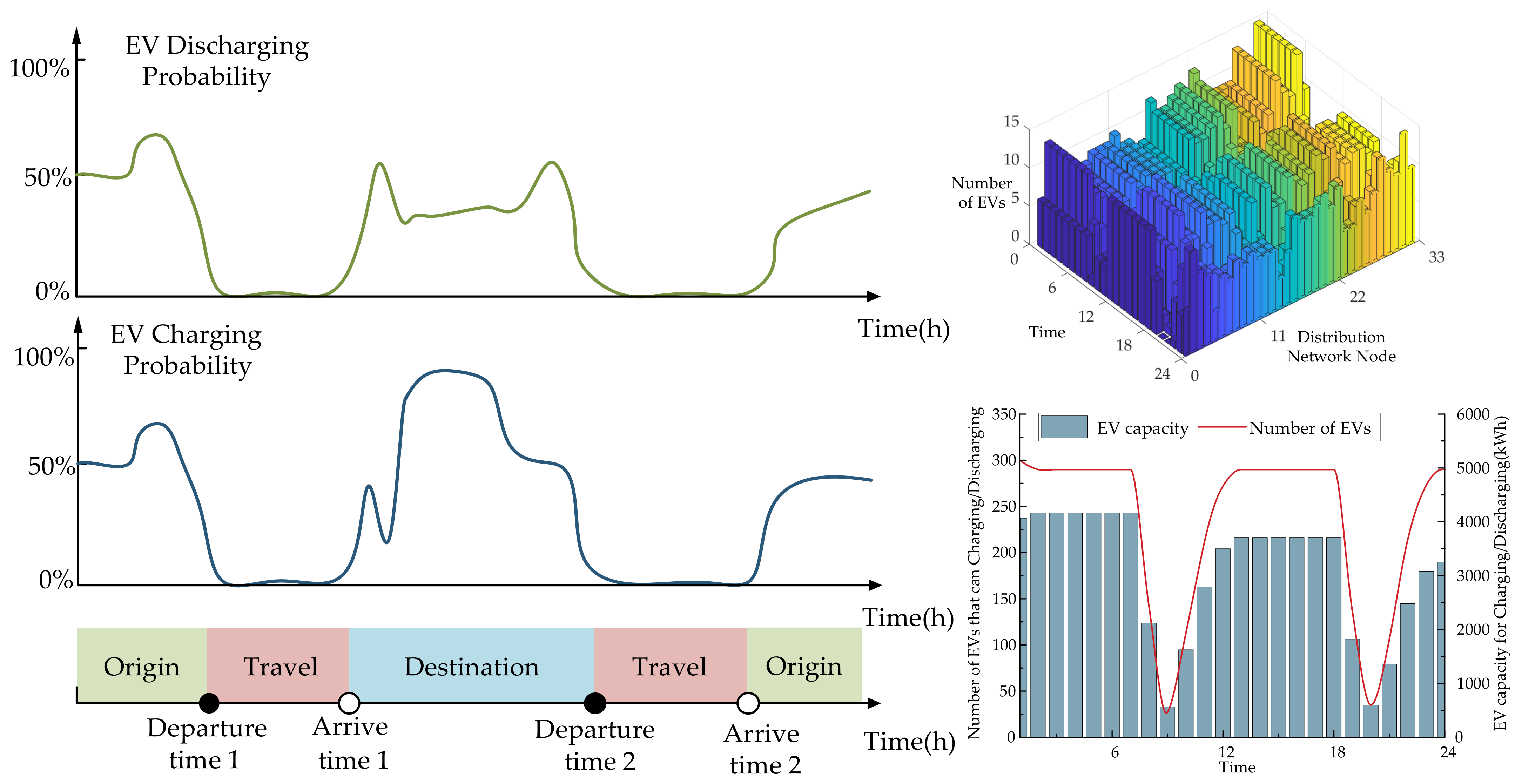
3.1. Analysis of EV Travel Characteristics

EV has the characteristics of both transportation and mobile energy storage unit. The traffic demand, travel distribution and path planning in the process of travel will be affected by traffic information such as road structure and road congestion, and its charging and discharging behavior will affect the operation of the distribution network. Therefore, in order to accurately model the operation of EV charging and discharging load, the distribution network nodes are corresponding to the traffic network one by one, and the distribution network is coupled with the traffic network, as shown in Figure 3. Because of the uncertainty and diversity of EV operation, we assume that the travel time, travel place, arrival time, and arrival place of EVs are fixed, and set the specific parameters of each EV. The model’s validity is tested by simulating the joint operation scenario of an EV and a steel plant in a dataset consisting of 500 EVs. The EV parameters considered for single EV modeling are shown in

Table 2. Explanation of operating characteristic parameters of EVs.

EV Operating Parameters	Explanation
Origin/Destination	The starting/arriving traffic nodes of EVs and the corresponding distribution network nodes.
Driving distance	The driving distance of the traffic node between the starting point and the destination of EVs.
Departure/Arrive time 1	EV departure time and arrival time from the origin to the destination.
Departure/Arrive time 2	EV departure time and arrival time from the destination to the origin.
Initial SOC state	The SOC state of EV before departure.
Charging speed	Charging speed of EV connected to charging station (considering charging efficiency).
Discharging speed	Discharging speed of EV connected to charging station (considering discharging efficiency).

.

This work sets the departure time and return time of the EV and corresponds these moments to the road network. EV cannot be charged and discharged during driving, but when EV is located at the origin and destination, it can charge and discharge according to the SOC state of the EV. In this paper, considering the influence of EV SOC state, charging and discharging price, and other factors on EV users’ charging and discharging willingness, the charging and discharging probability calculation function of a single EV at each moment is constructed. The change in EV charging and discharging probability with the influencing factors is shown in Figure 4, and the EV charging and discharging probability can be expressed as (11).

$$\left\{\begin{array}{c}{\partial }_{k,t}^{Ch}={\alpha SOC}_{k,t}+\beta Y_{k,t}+\gamma \hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ {\partial }_{k,t}^{Disch}=1-\left({\alpha SOC}_{k,t}+\beta Y_{k,t}\right)+\gamma \hfill \end{array}\right.$$

(11)

where $\alpha$ and $\beta$ are the influence coefficients of the influence of the SOC state of the EV and the travel state of the electric vehicle on the charging and discharging probability of the EV, respectively, and $\gamma$ is the random variable of the charging and discharging probability of the EV. ${SOC}_{k,t}$ is the SOC state of the EV $k$ at time $t$.

The EV charging and discharging load on the same traffic node is accumulated, and then the traffic node corresponds to the EV travel node, so that the EV charging and discharging load can be mapped to the distribution network node, and the stable operation of the distribution network can be analyzed. The specific model is established as Section 3.3 and Section 3.4.

3.2. Model Assumptions

Considering the actual production load characteristics of steel mills and the travel characteristics of EV operation, we make the following assumptions:

(1)

Because the change is small, and this work focuses on the power consumption of the steel mill, this work ignores the quality change in the finished product caused by the production decarburization during the production of 20 tons of steel per heat.

(2)

This work assumes that the charging and discharging behavior of EV users is only affected by SOC state and electricity price.

(3)

This work considers that each EV user is based on the maximum travel efficiency. It is assumed that the travel of EV users is limited to the starting point and destination and will not stop on the road.

(4)

Because the number of EVs simulated in this paper is small, this paper assumes that all EVs are the same type of working vehicles, and the travel distance of each EV is fixed.

(5)

This work mainly studies the participation of EV in the peak shaving and valley filling of the steel plant, so the remaining load in the IEEE33 node is considered as the constant load.

3.3. Objective Function

3.3.1. Power Generation Cost

The power generation cost of thermal power units can be expressed by a generator cost coefficient and power generation.

$$F_{Gen}={\sum }_t^T{\sum }_i^I{Q}_i{P}_{i,t}^{Gen}$$

(12)

where $T$ is the total time length of model simulation, $I$ is the total number of generators in the distribution network, $Q_i$ is the cost coefficient of generator $i$, and $P_{i,t}^{Gen}$ is the output power of generator $i$.

3.3.2. Charging Cost of EV Users

The charging cost of EV users represents the operating cost of all EV users in the region, which is obtained by subtracting the discharge income from the charging cost.

$$F_{EV}={\sum }_t^T(P{r}_{c,t}{N}_{c,t} P_c^{EV}-P{r}_{d,t}{N}_{d,t} P_d^{EV})$$

(13)

where $P{r}_{c,t}$ and $P{r}_{d,t}$ represent the charging price of EV at time t and the discharge subsidy at time t, respectively. $N_{c,t}$ and $N_{d,t}$ represent the total number of EVs charged and discharged at time t, respectively. $P_c^{EV}$ and $P_d^{EV}$ represent the average power of EV charging and discharging, respectively.

3.3.3. Production Cost of Steel Plant

$$F_{steel}={\sum }_{t=1}^T{\sum }_{l=1}^l{\sum }_{j=1}^J{S}_{j,l,t}^{steel}{P}_l^{steel}{Pr}_t$$

(14)

where $T$,$L$, and $J$ represent the total time granularity length, the total number of processing steps, and the total number of heats in the simulation, respectively. $S_{j,l,t}^{steel}$ is the production state of the production step $l$ of the production furnace $j$ in the period $t$. $P_l^{steel}$ is the average production power of steel production step $l$. ${Pr}_t$ represents the industrial grid electricity price ($\mathrm{\$}/\mathrm{k}\mathrm{W}\mathrm{h}$).

Therefore, the objective function can be expressed as:

$$F=\min \{F_{Gen}+F_{EV}+F_{steel}\}$$

(15)

3.4. Constraints

3.4.1. Generation Constraints

The generator set in the distribution network needs to be constrained by its maximum and minimum output power.

$$P_{i,min}^{Gen}\le P_{i,t}^{Gen}\le P_{i,max}^{Gen}$$

(16)

where $P_{i,min}^{Gen}$ and $P_{i,max}^{Gen}$ are the maximum and minimum output power of generator $i$, respectively.

3.4.2. Power Balance Constraints

Power system scheduling needs to balance power supply and demand. All power generation, EV charging and discharging, and the power of the steel plant must be balanced. This work balances the node load, EV load and steel production load of each node. The balance constraints of single node are as follows:

$$P_{n,t}^{Gen}+P_{n,t}^{trans}=P_{n,t}^{EV}+P_{n,t}^{steel}$$

(17)

where $P_{n,t}^{Gen}$ is the generator generation load in the time period $t$ of node $n$. $P_{n,t}^{trans}$ is the power transmitted by the phase node $n$ in the time period $t$of the node $n$ adjacent node. $P_{n,t}^{EV}$ and $P_{n,t}^{steel}$ are the charging and discharging load of EV on node n and the power load of steel plant, respectively.

3.4.3. Steel Production Steps Constraints

The constraints of iron and steel production steps have been described in detail above, as shown in Formulas (1), (4), (5), (9), and (10).

3.4.4. EV Charge and Discharge Constraints

The single EV needs to maintain a balance between charging and discharging, but first of all, the EV cannot be charged and discharged during driving.

$$\left\{\begin{array}{c}{S}_{k,driving}^{EVc}=0\\ S_{k,driving}^{EVd}=0\end{array}\right.$$

(18)

where $S_{k,t}^{EVc}$ is the charging state of the $k$ th EV during the period $t$. $S_{k,t}^{EVd}$ is the discharging state of the $k$ th EV during the period $t$. $driving$ represents the time period of the EV on the way, that is, a period of time between the EV from the departure time point to the destination and the EV from the destination return time point to the starting point.

3.4.5. SOC State Constraints

When charging and discharging the EV, it is also necessary to take into account its SOC state, which should be able to enable the EV to return to the starting point at a predetermined time.

$${SOC}_{k,t}={SOC}_{k,t-1}+S_{k,t-1}^{EVd}{P}_d^{EV}-S_{k,t-1}^{EVc}{P}_c^{EV}-E_{k,t-1}^{Tran}$$

(19)

$${0\le SOC}_{k,t}{\le SOC}_{kmax}$$

(20)

where ${SOC}_{k,t}$ is the SOC state of the $j$th EV at time $t$, and $E_{k,t-1}^{Tran}$ is the driving power consumption of the $j$th EV. ${SOC}_{kmax}$ is the battery capacity of EV.

By linearizing the model, the optimization problem can be transformed into a mixed integer linear programming problem. It can be solved by the Gurobi 10.2, yalmip R202306 solver in MATLAB 2020b. The optimization results include the operation state of each generator set, the output power of each generator set, the charging and discharging state of each EV and the production state of the steel plant.

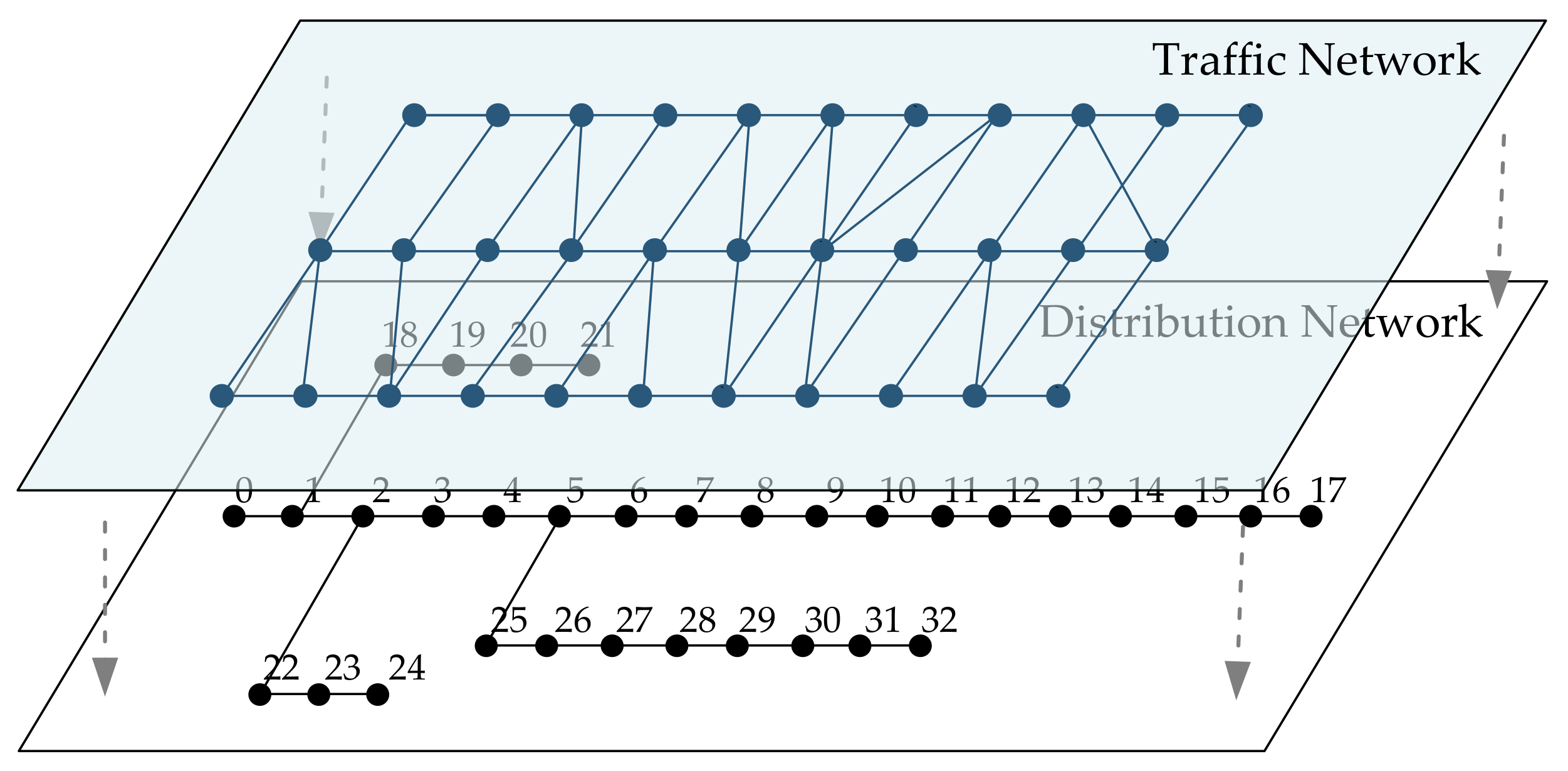
4. Analysis of Simulation Example

4.1. Analysis of Simulation Examples

In this paper, a simulation system composed of transmission network and distribution network is constructed to verify the effectiveness of the proposed steel plant EV charging and discharging optimal scheduling strategy. As shown in Figure 5, IEEE 33-bus distribution network is used to simulate the distribution network. The balance node 0 in the IEEE-33 system is the low-voltage side node of the transformer, and the high-voltage side is the node of the transmission network. Considering the electricity cost of the steel plant, the charging/discharging purchase cost of EVs and the generation cost of distributed generators installed in the distribution network, the coordinated operation mode of steel mills and electric vehicles in the distribution network is analyzed. We assumes that an electrified steel plant with medium steel production, the daily steel production plan is 200 tons. The number of EAF, LF, AODF, and CC production equipment in the steel plant is 5 units per piece of equipment, and the parameters of different equipment are shown in

Table 3. Equipment parameters of steel production line.

Parameters [25,26]	Title 3
EAF electricity consumption (kWh/tS 1)	535.7
EAF producing time (min/heat 2)	120
LF electricity consumption (kWh/tS)	121.5
LF producing time (min/heat)	120
AOD electricity consumption (kWh/tS)	25.4
AOD producing time (min/heat)	60
CC electricity consumption (kWh/tS)	31
CC producing time (min/heat)	60

¹ tS = per ton of steel. ² heat = steel filled with a ladle furnace.

. The parameters of the distributed generators are shown in

Table 4. Distributed generator parameters in distribution network.

Parameters	Maximum Output (kW)	Minimum Output (kW)	Cost Coefficient (USD/kWh)
Generator 1	300	60	14
Generator 2	300	50	30
Generator 3	300	65	40
Generator 4	300	70	20

.

In this work, we discuss the operation scenarios of the combination of steel plant operation and EV operation. Considering the multiple joint scheduling operation modes of steel plant and EV, two operation scenarios are set up. The specific electricity price data and EV travel data are shown in Figure 6.

Scenario 1: Considering the control characteristics of the steel plant, the charging of the EV in the region interacts with the power grid, and the EV operates in a charging-only state.

Scenario 2: Considering the regulation characteristics of the steel plant, the EV in the region interacts with the power grid in V2G, and the EV runs under the flexible operation state of charging and discharging.

The electricity price of the steel plant in this paper complies with the peak–valley electricity price policy for industrial electricity in Jiangsu Province. The EV charging price and EV discharge subsidy set in this paper take into account the complementary and coordinated operation ability between EV users and industrial electricity, reduce the charging price of EV users during the peak period of industrial electricity price, and increase the discharge subsidy of EV users. Improve the enthusiasm of EV users to participate in demand-side peak clipping and valley filling.

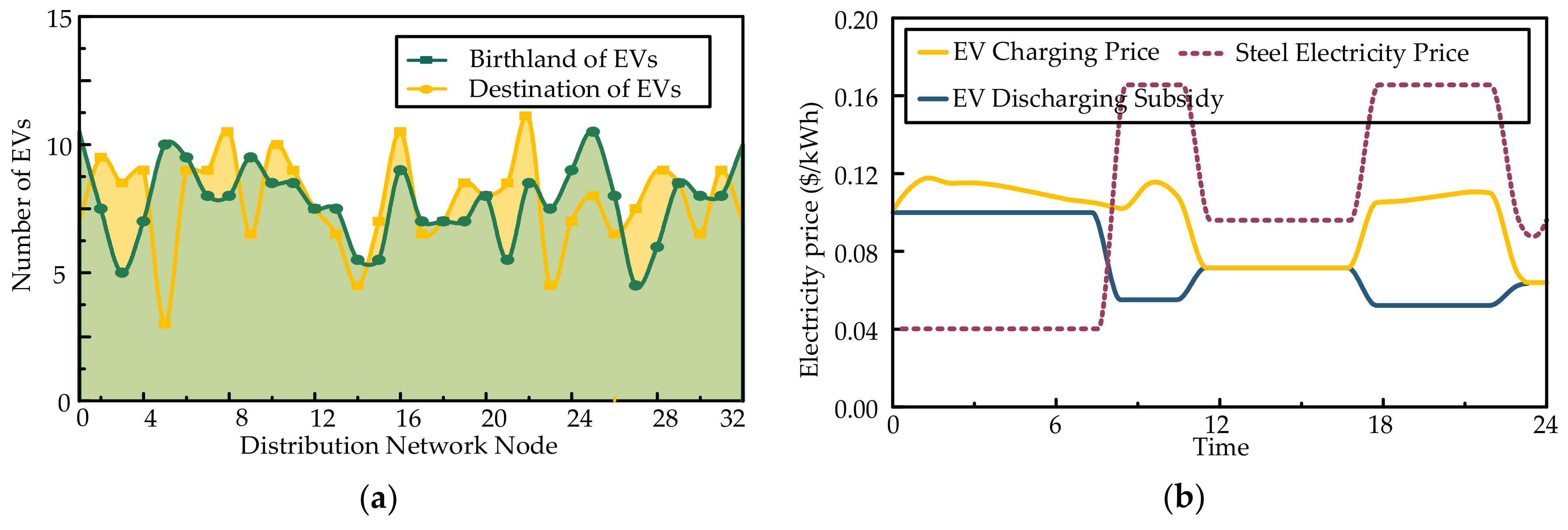
4.2. Results and Discussion

The simulation results of operating costs of EVs and steel plant in different scenarios are shown in

Table 5. Operating costs of EV and steel plant in different scenarios.

Parameters	Scenario 1	Scenario 2
EV charging cost (USD)	2606	2886
EV discharge subsidy (USD)	0	−3537
Distributed generation costs (USD)	1827	1352
Steel production cost (USD)	6105	5748
Total cost (USD)	10,538	6339

.

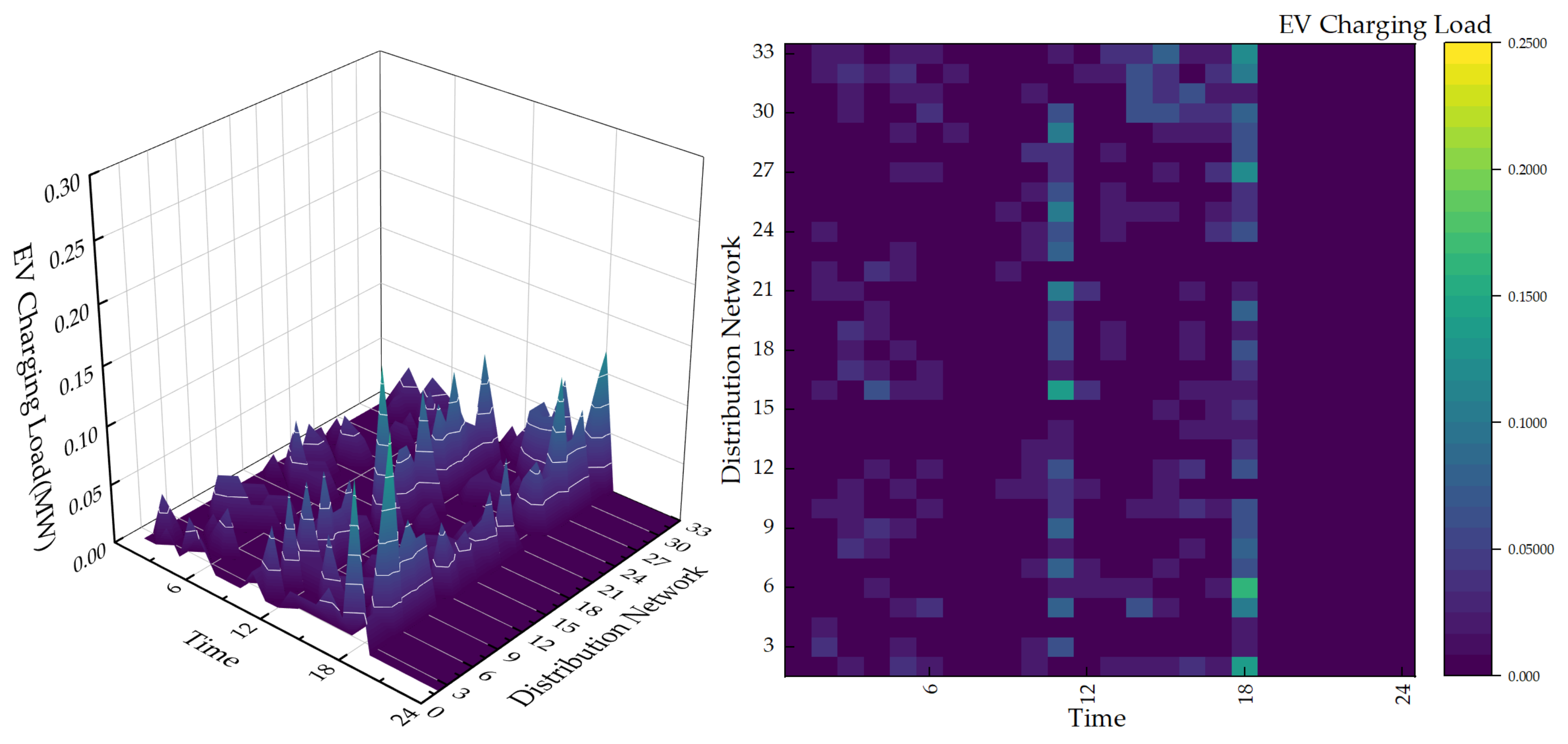
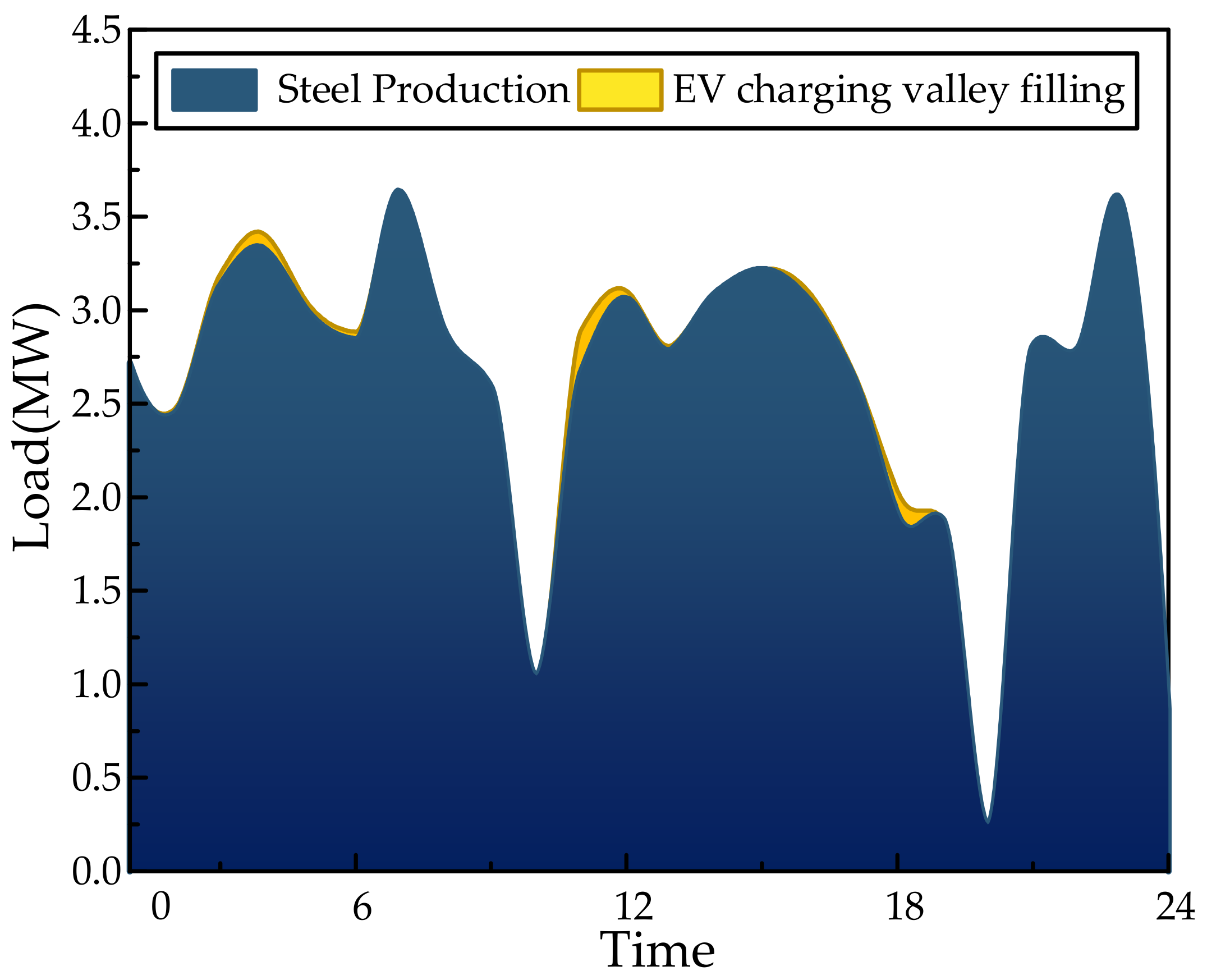
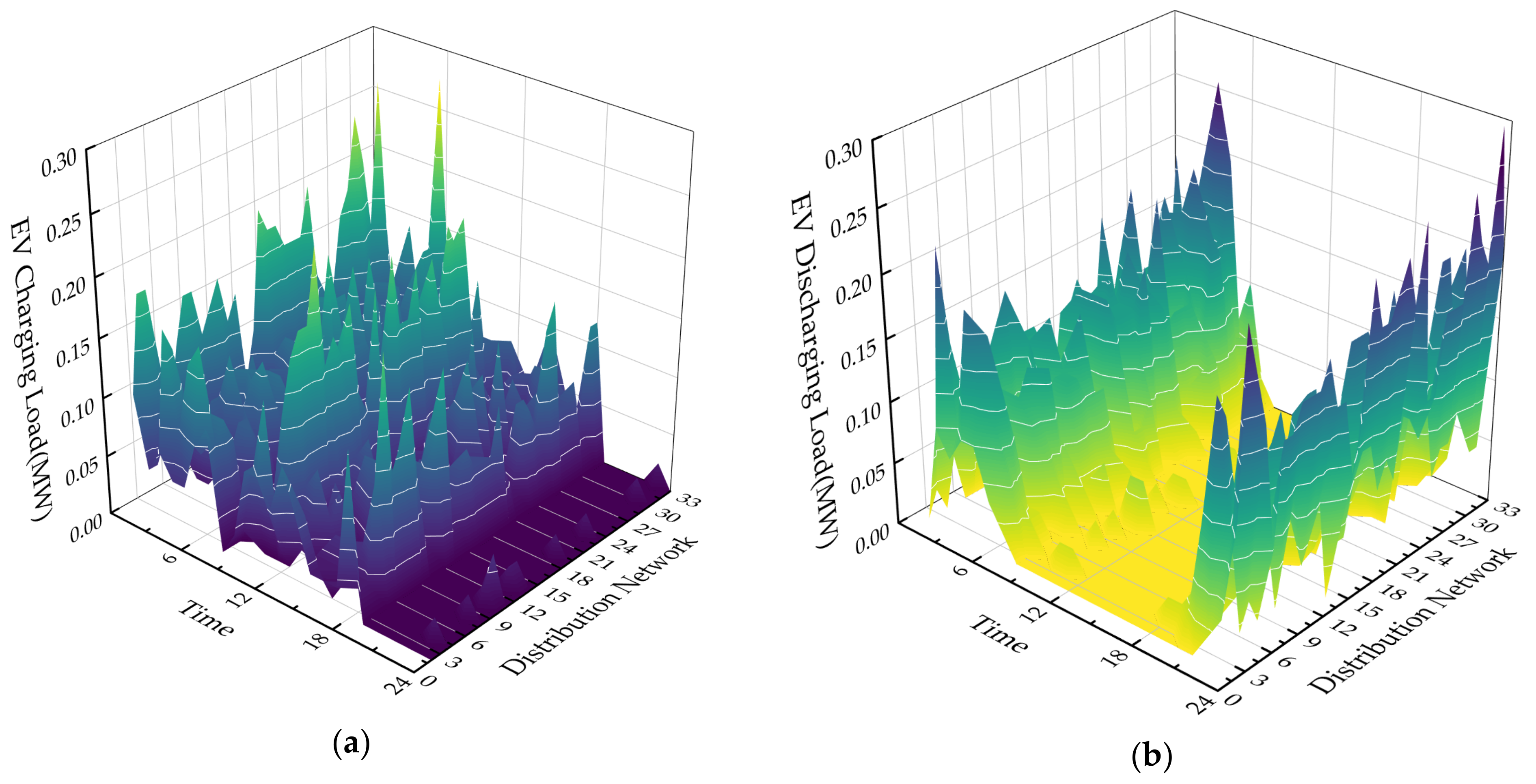
4.2.1. Scenario 1

In Scenario 1, the charging characteristics of EVs are considered. The optimization model in this paper can focus the charging time of EVs around the steel plant on the low valley period of the production load of the steel plant and use the electric vehicle load to fill the valley of the production load of the steel plant and reduce the impact of the impact load generated by the access of the steel plant.

As shown in Figure 7 and Figure 8, when EV only runs in the charging state, the load transfer advantage of EV as energy storage has not been fully utilized. The operation mode of EV is not combined with the operation of steel mills, and EV is only charged on the basis of travel demand. And because the EV does not interact with the power grid, although the charging cost of the EV is reduced, the discharge subsidy is 0, and the generators in the distribution network need more power to maintain the production of the steel plant, which makes the power generation cost higher. The peak–valley load difference of the steel plant reaches 2.76 MW, and the load variance is 0.7045. The impact load of the steel plant has not been absorbed. Therefore, in the process of iron and steel production, iron and steel enterprises will inevitably avoid the peak electricity price area for production, so as to reduce the load of iron and steel production, which will lead to the frequent start and stop of iron and steel production equipment and is the source of impact load. The disorderly operation of EV charging load without scheduling will not be able to improve or even aggravate this problem.

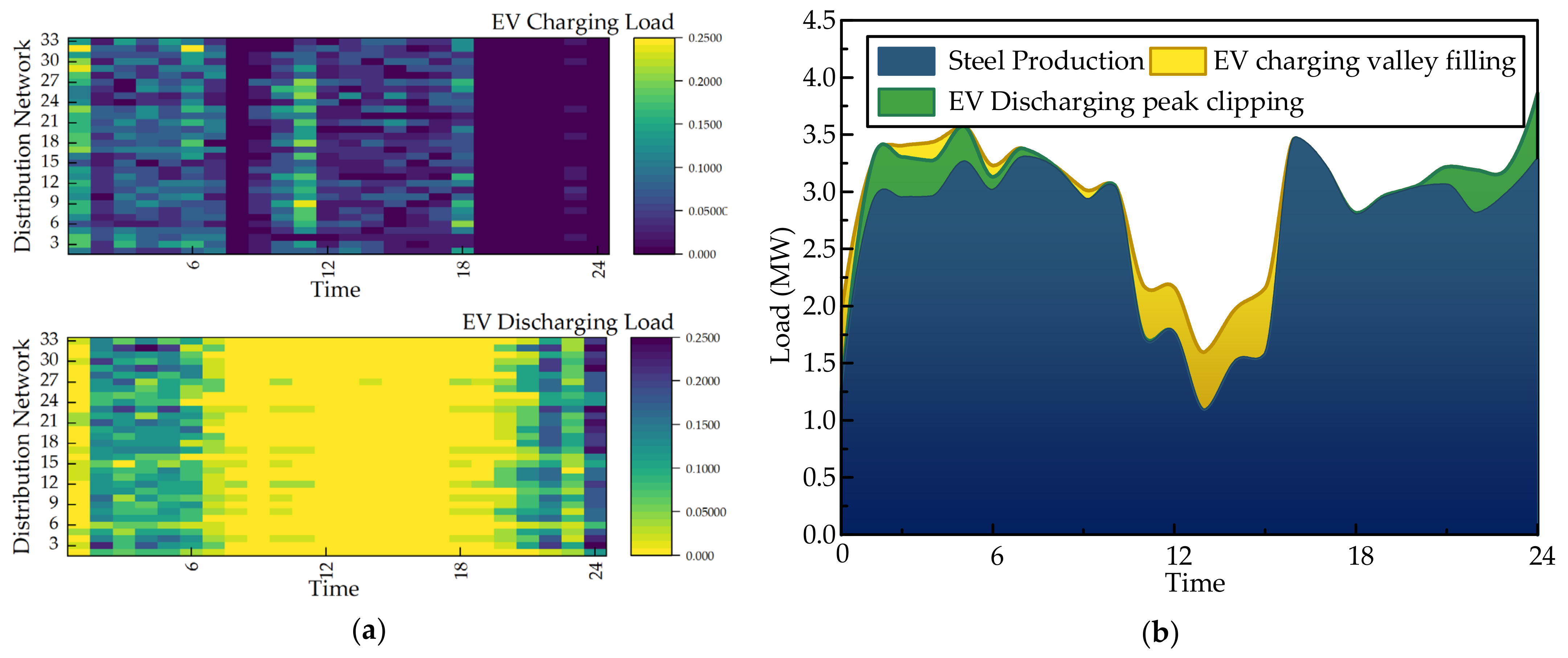
4.2.2. Scenario 2

In Scenario 2, the charging and discharging characteristics of EVs are considered. The optimization model of this paper can concentrate the charging time of EV around the steel plant during the low valley period of the production load of the steel plant and concentrate the EV during the peak period of the production load of the steel plant. Discharge, peak shaving, and valley filling of the production load of the steel plant stabilize the load of the steel plant.

As shown in Figure 9 and Figure 10, the charging and discharging load of EV not only follows the law of electricity price and can obtain the optimal charging benefit, but also concentrates on the peak shaving and valley filling demand period of the production load of the steel plant, which can provide support for the stable operation of the steel plant and the power system. In Scenario 2, the peak–valley load difference of the steel plant is reduced from 2.02 MW to 1.43 MW, which is reduced by 29.20%. The variance of production load in the steel plant is reduced by 26.5%. The load of the steel plant in this scenario is gentler and has less impact on the power system.

Compared with Scenario 1 without considering the V2G, in Scenario 2, all EV users obtain a subsidy of USD 3537 by connecting the EV to the grid for discharge, which is higher than the charging cost of USD 2886 for the overall EV users, and the zero-cost operation of the EV is realized. Due to V2G technology, the total cost of an EV is lowered by 125% compared to Scenario 1.

5. Conclusions

There has been a significant surge in the electricity usage of electrified steel enterprises, which impacts the power systems. The coordination of a large scale of EVs with steel plants may help reduce this impact. This research presents a potential optimization strategy for scheduling electric vehicles in an electric steel factory. This strategy effectively coordinates the production plan of the steel mill, the charging and discharging of electric vehicles, and the power flow operation of the distribution network, while ensuring the travel demand of electric vehicle users and the daily production plan of the steel plant are met. Based on the IEEE-33 model, an EV steel plant scheduling optimization model is constructed. The conclusions drawn from the simulation in this paper can be summarized as follows:

(a)

By adjusting the charging and discharging time of EVs, EV users can obtain discharge compensation while meeting the driving demand of EVs, so as to realize the operation “zero cost” of EV users.

(b)

In the distribution network node connected to the steel plant, the electric vehicle can cut the peak and fill the valley of the steel plant by charging and discharging, reducing the peak–valley difference of the steel plant load, and reducing the impact load of the steel plant.

(c)

Steel enterprises can use EVs as a flexible resource to reduce the production load of their steel plants during peak electricity prices, thereby lowering their electricity costs. At the same time, the addition of EVs as a flexible energy storage resource also reduces the power generation cost of distributed generators in distribution network nodes.

This work’s EV charging and discharging approach relies on predefined EV charging and discharging nodes, making the unrealistic assumption that EVs will only charge at their starting point and destination. However, in the context of discharge subsidy incentives, the majority of the charging and discharging of EVs is focused on certain locations. Exploring the EV model in depth, analyzing different types of EVs, examining various charging and discharging methods, taking into account the dynamic traffic situations during EV operation, and studying the coordinated operation of EVs with more adaptable loads will be a fruitful avenue for research.