Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method
Abstract
1. Introduction
- (a)
- The analytic hierarchy process (AHP): This method constructs a hierarchical framework for problem evaluation and assesses the relative significance of various criteria through pairwise comparisons. Among the scholars who use this method, Chen Yunfeng [13] conducted a comprehensive evaluation of transmission and transformation projects based on specific criteria such as preliminary decision making, an implementation process, construction implementation, and sustainable development using the AHP method. However, due to the sole reliance on subjective evaluation methods, there is an issue of insufficient persuasiveness in the evaluation results.
- (b)
- The fuzzy analytic hierarchy process (FAHP): This method represents an adaptation of the AHP, employing fuzzy logic to manage uncertainties and ambiguities inherent in the decision-making process. Xu Dan [14] and Gao Chao [15] utilized the FAHP to construct a social benefit evaluation model for grid engineering projects. They validated this model, and compared to the AHP, the FAHP introduces fuzziness to subjective judgments, enhancing its comprehensiveness and adaptability. However, since this method still falls under subjective evaluation, it cannot guarantee the scientific validity of indicator selection.
- (c)
- Elimination and choice expressing reality (ELECTRE): This method requires experts to establish thresholds for consistency and inconsistency among different options, ranking them according to these criteria. Given that these thresholds often derive from expert experience and intuition, the method is highly subjective. Akram, M [16] extended the ELECTRE I methodology to accommodate group decision scenarios by utilizing Pythagorean fuzzy numbers (PFNs) as attributes for each criterion, thus creating the Pythagorean Fuzzy ELECTRE I (PF-ELECTRE I) method. The integration of PFNs improves the model’s capacity to manage fuzziness and incompleteness. The efficacy of this model was demonstrated through two environmental management case studies. Although both PF-ELECTRE I and the Fuzzy AHP (FAHP) methodologies embrace fuzziness, PF-ELECTRE I is more apt for contexts characterized by conflicts, while FAHP’s simpler calculations make it more widely acceptable.
- (a)
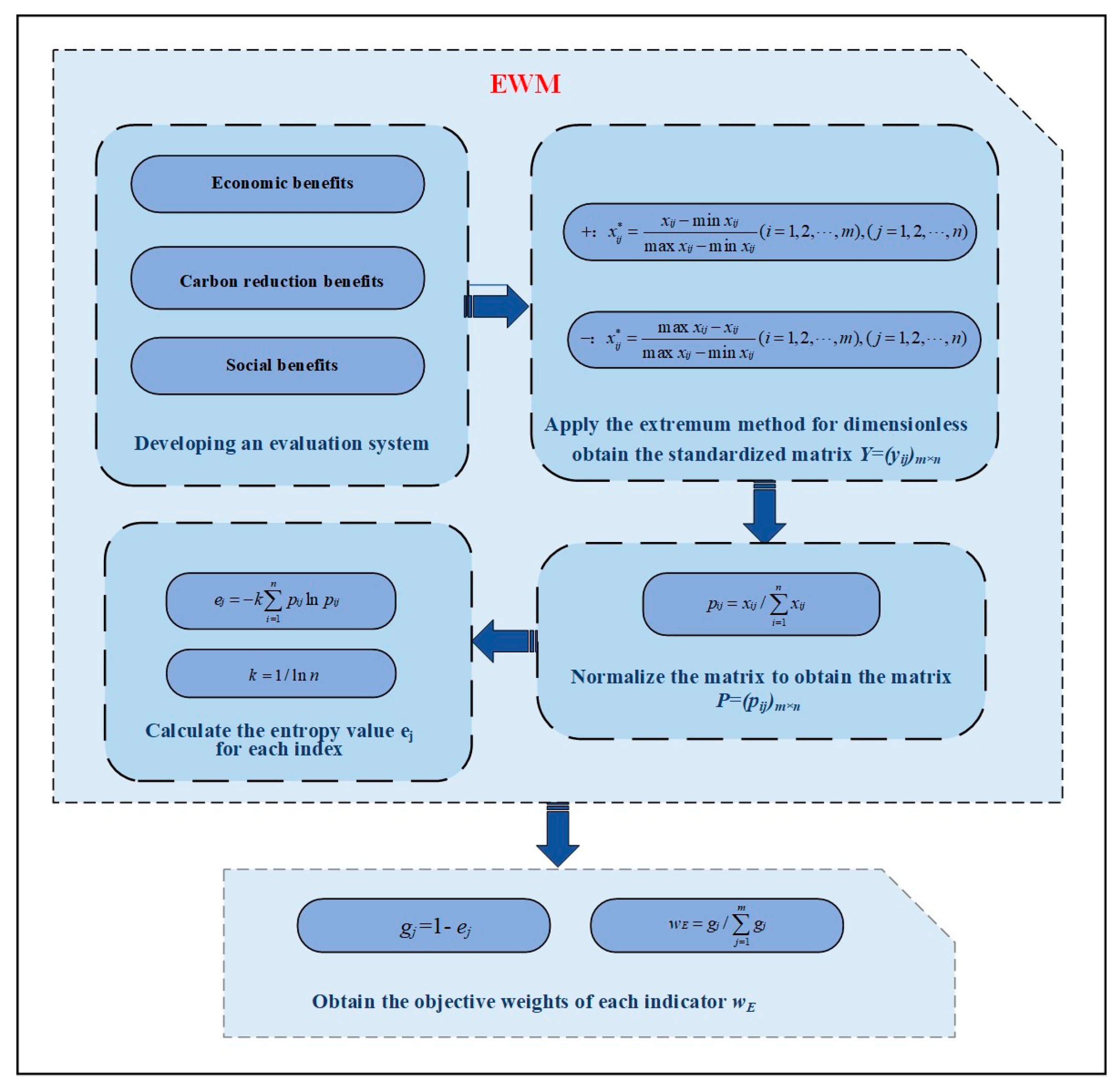
- The entropy weight method (EWM): This method employs the concept of information entropy for determining the weights of different indicators. Information entropy quantifies the degree of dispersion among criteria. Criteria with higher dispersion levels contain more information and are consequently allocated greater weights. As this method is independent of external subjective evaluations, it is broadly applicable to scenarios that demand objective assessments and decisions. Its inherent flexibility also facilitates its integration with other decision-making frameworks, including the AHP and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS). Many scholars like MRZ Banadkouki [17], Sijia Liu [18], and Minggao Chen [19] have utilized the EWM for calculating the weights of project indicators.
- (b)
- Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS): This method orders the alternatives by computing their distances to both the optimal ideal point and the least favorable nadir point, based on the evaluation criteria. While the TOPSIS method often relies on subjective techniques to ascertain weights, it can also integrate objective approaches for setting criteria weights, or employ a hybrid weighting system. Wang, Y [20] improved the TOPSIS method by constructing positive and negative ideal solutions. However, in the comprehensive evaluation of projects, this method alone is relatively singular and cannot consider the comprehensiveness of indicators. Gebrehiwet [21] proposed a method to assess the risk of delays in the entire lifecycle of transmission and transformation projects. They constructed a comprehensive model based on TOPSIS and FAHP sequential preference techniques. By establishing common standards, sub-criteria, and attributes, the impact of delay risks during the lifecycle of transmission and transformation projects was evaluated. Additionally, many scholars have modified the TOPSIS method, proposing versions that are suitable for different scenario models. Junlin Cao and Fangfang Xu [22] combined the fuzzy TOPSIS method based on fuzzy entropy weight (VEWFTOPSIS), the TOPSIS method based on entropy and interval linguistic intuitionistic fuzzy sets (EILIF-TOPSIS), and the intuitionistic fuzzy TOPSIS method based on information entropy attribute importance (IEAI-IF-TOPSIS), proposing a comprehensive MADM method to evaluate large-scale projects. Fahmi, R. Nandi, and Ali et al. [23,24,25] further improved the TOPSIS method by proposing the Fuzzy TOPSIS (F-TOPSIS) method, and applied this method to rank major projects in various fields, including agriculture and electrical engineering. Watrobski, J [26] addressed a limitation in classic MCDA, where models are based solely on a single set of input data. The TOPSIS method was enhanced by integrating the traditional approach with variability in performance measurements of alternatives, leading to the proposal of the Data Variability Assessment Technique for Order of Preference by Similarity to Ideal Solution (the DARIA-TOPSIS method).
- (c)
- Sequential Interactive Model for Urban Systems (SIMUS): This is an objective multi-criteria decision-support method primarily used for solving resource allocation issues; it is especially suitable for complex decision environments where multiple criteria or objectives need to be met simultaneously. The SIMUS method utilizes linear programming techniques to automatically allocate resources optimally, fulfilling all specified criteria and constraints. Relative to SIMUS, TOPSIS boasts a straightforward computation process that does not involve intricate optimization algorithms. In contrast, SIMUS is founded on mathematical modeling and linear programming, rendering it better suited for addressing decision-making problems characterized by intricate objectives. Using the SIMUS, scholar Svetla Stoilova [27] evaluated the container transport options via rail and road, subsequently creating a comprehensive model to assess these transportation methods.
- (d)
- The reference ideal method (RIM): This method primarily relies on fundamental data to determine the weights of various decision criteria and uses these weights to assess the relative performance of alternative options against an ideal reference point. Compared to the TOPSIS, RIM calculates only the distance between alternative options and the optimal value combination, without considering the distance to the worst value. Therefore, its comprehensiveness is less than that of the TOPSIS method.
- (e)
- Expected Solution Point–Characteristic Objects Method (ESP-COMET): This method extends the Expected Solution Point (COMET) approach and incorporates the Expected Solution Point (ESP) method to enhance individual decision-making capabilities. Additionally, the introduction of the ESP concept effectively simplifies the process of identifying expert preferences. By integrating ESP, a preference function can be shaped to assign higher preference to options that are closer to the ESP. This allows for a more efficient representation of preferences while reducing the computational burden of constructing the Matrix of Expert Judgements (MEJ). Unlike the TOPSIS method, which seeks a global optimum, ESP-COMET is better suited for ranking decisions based on the nuanced preferences of decision makers. Andrii Shekhovtsov [28] provided a detailed introduction to the ESP-COMET method in the article, validating the model’s effectiveness through multiple data calculations. The method was compared with SPOTIS and RIM, highlighting that ESP-COMET offers greater customization and complexity.
- (f)
- Stochastic Preference on TOPSIS (SPOTIS): This method expands on the traditional TOPSIS approach by integrating its foundational principles with stochastic preference theory, incorporating decision makers’ uncertain preferences into the decision-making process. Compared to the traditional TOPSIS method, the introduction of a stochastic preference model significantly reduces the subjectivity involved in determining weights. However, the incorporation of randomness also substantially increases the demands on data and the complexity of the calculation process. Dezert, J [29] provided a detailed explanation of the SPOTIS method’s calculation process in the article and used the method to rank four evaluation options.
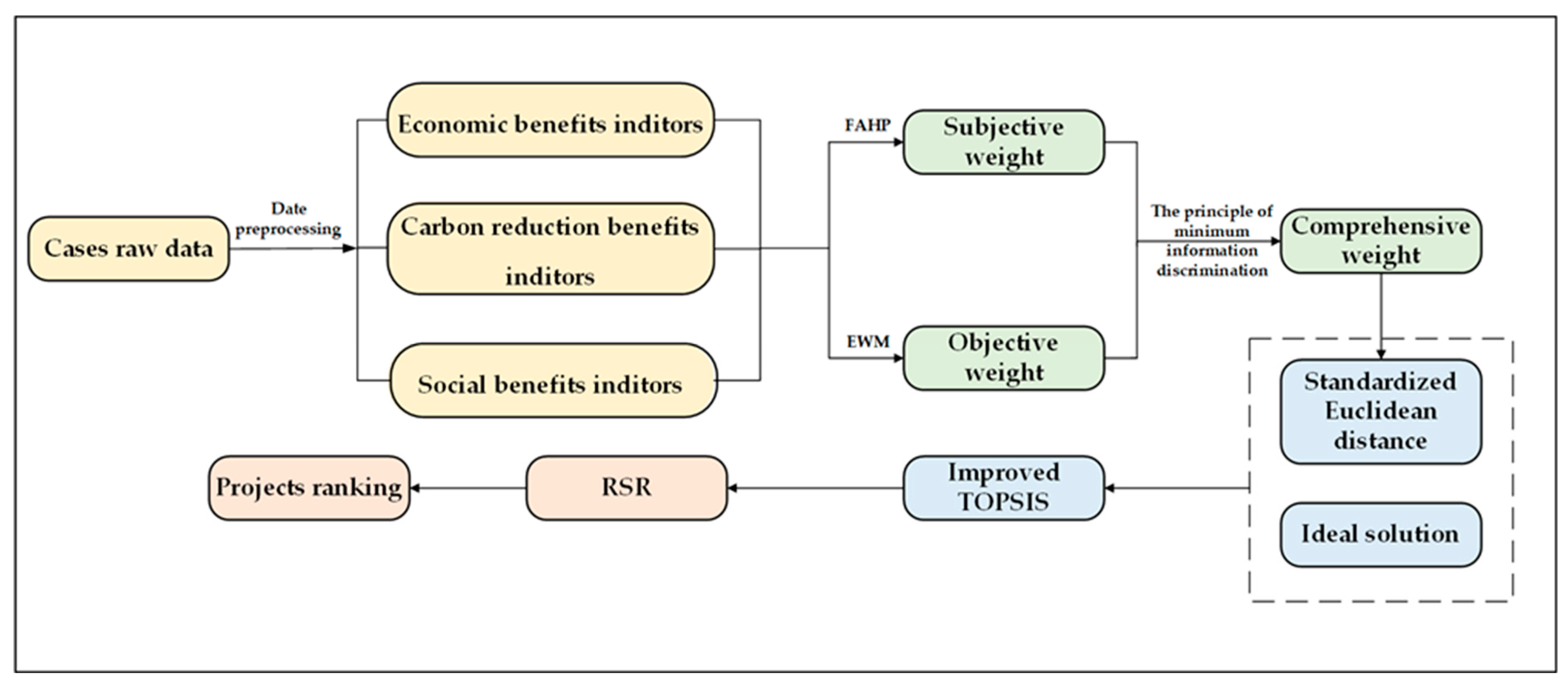
2. Methodology
2.1. Evaluation Indicators
- (a)
- Internal rate of return
- (b)
- Investment payback period
- (c)
- Return on investment
- (d)
- Asset/liability ratio
- (e)
- Current ratio
- (f)
- Quick ratio
- (g)
- Using energy-saving wires
- (h)
- Reduce SF6 gas emissions
- (i)
- Adopting distributed energy generation
- (j)
- Participation in carbon trading markets
- (k)
- Encourage low-carbon consumption by consumers
2.2. Determination of Indicators’ Weight
2.2.1. FAHP Subjective Weighting
2.2.2. EWM Objective Weighting
2.2.3. Combined Weight Optimization
2.3. Evaluation Method
2.3.1. TOPSIS
- (a)
- Construct a weighted decision matrix
- (b)
- Determine the positive ideal F+ and negative ideal solution F−
- (c)
- Obtain the separation values
- (d)
- Calculate the overall preference score
- (e)
- Ranking the results
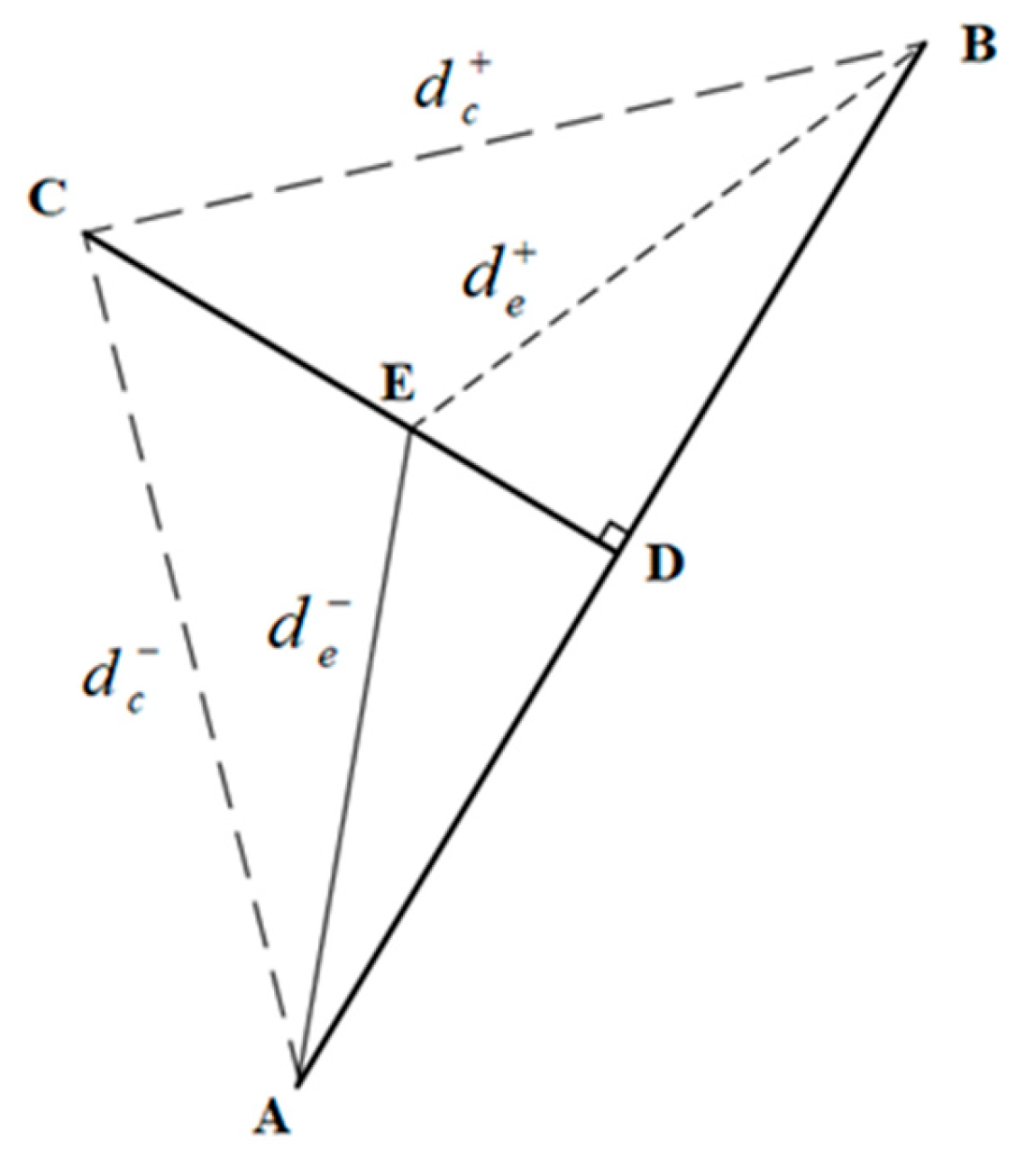
2.3.2. The Modified TOPSIS
2.3.3. TOPSIS-RSR Model
3. Results and Discussion
3.1. Cases Study
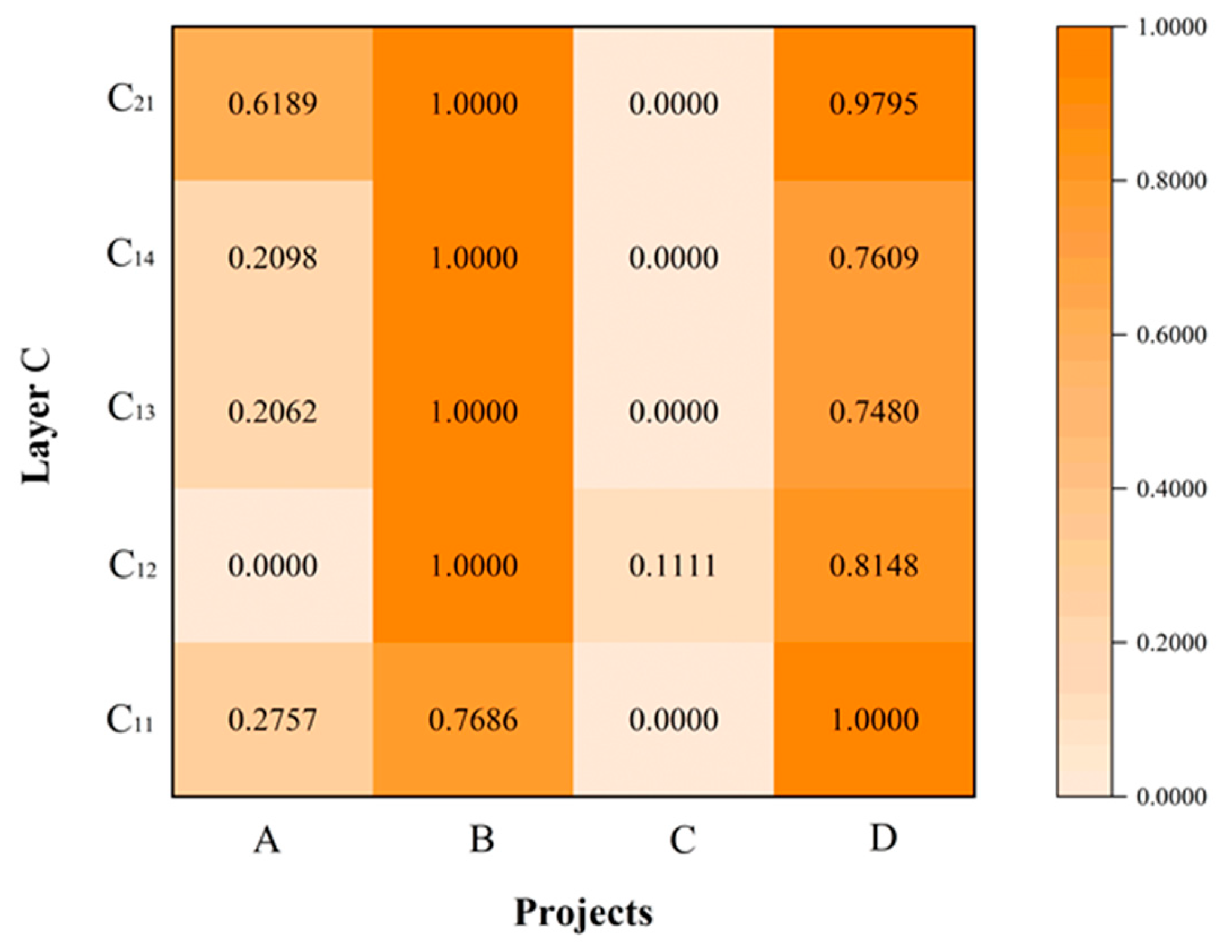
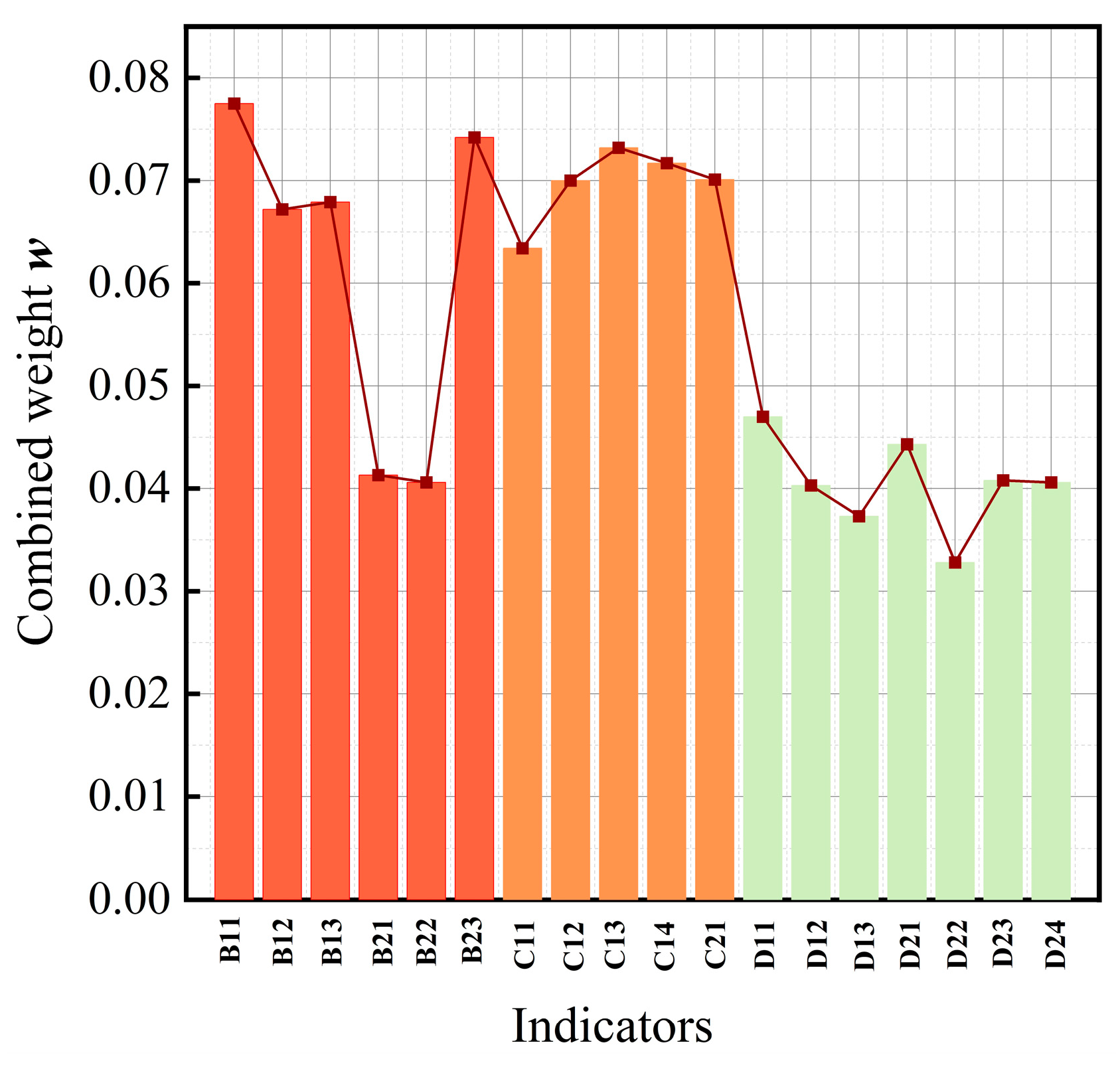
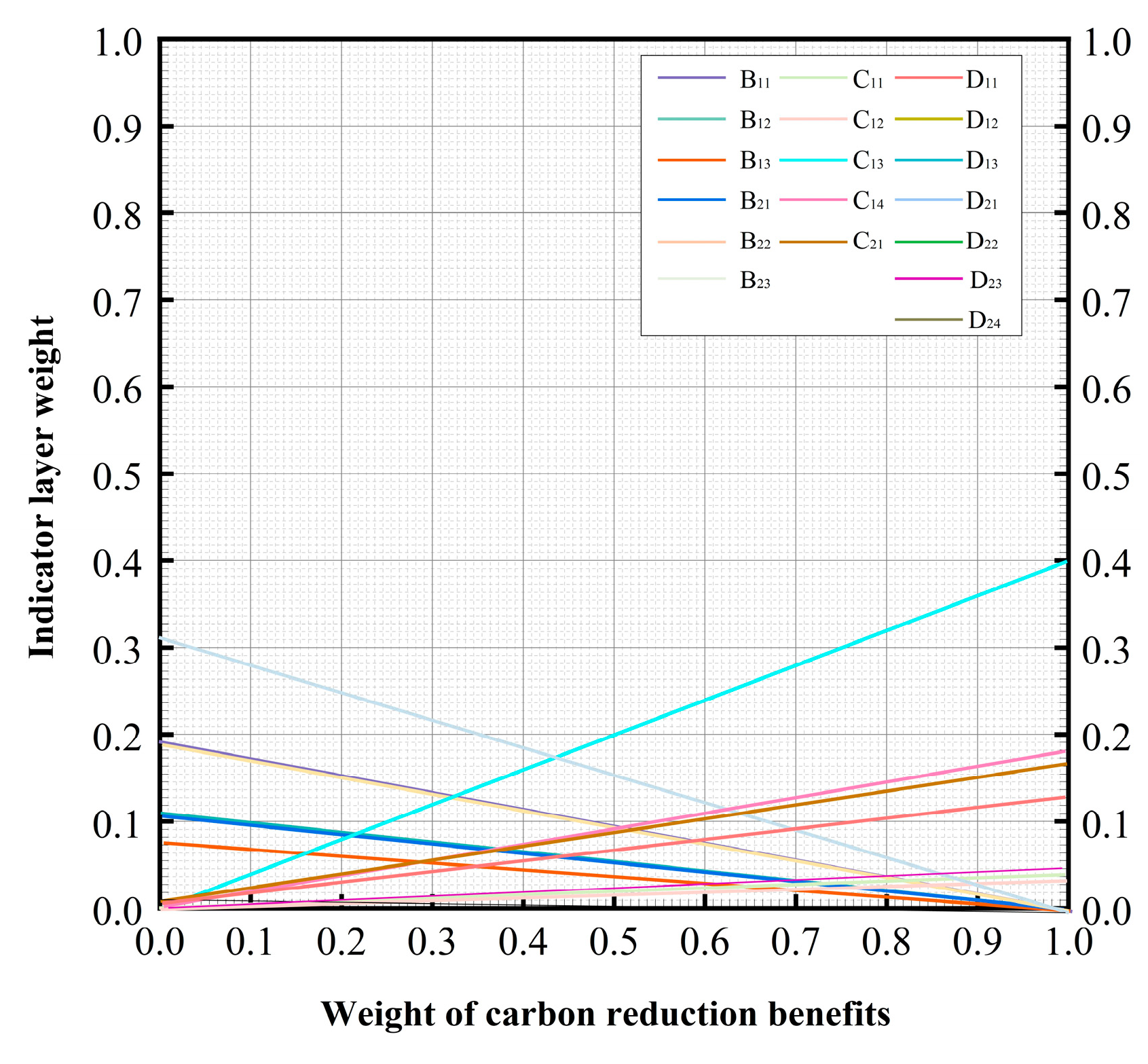
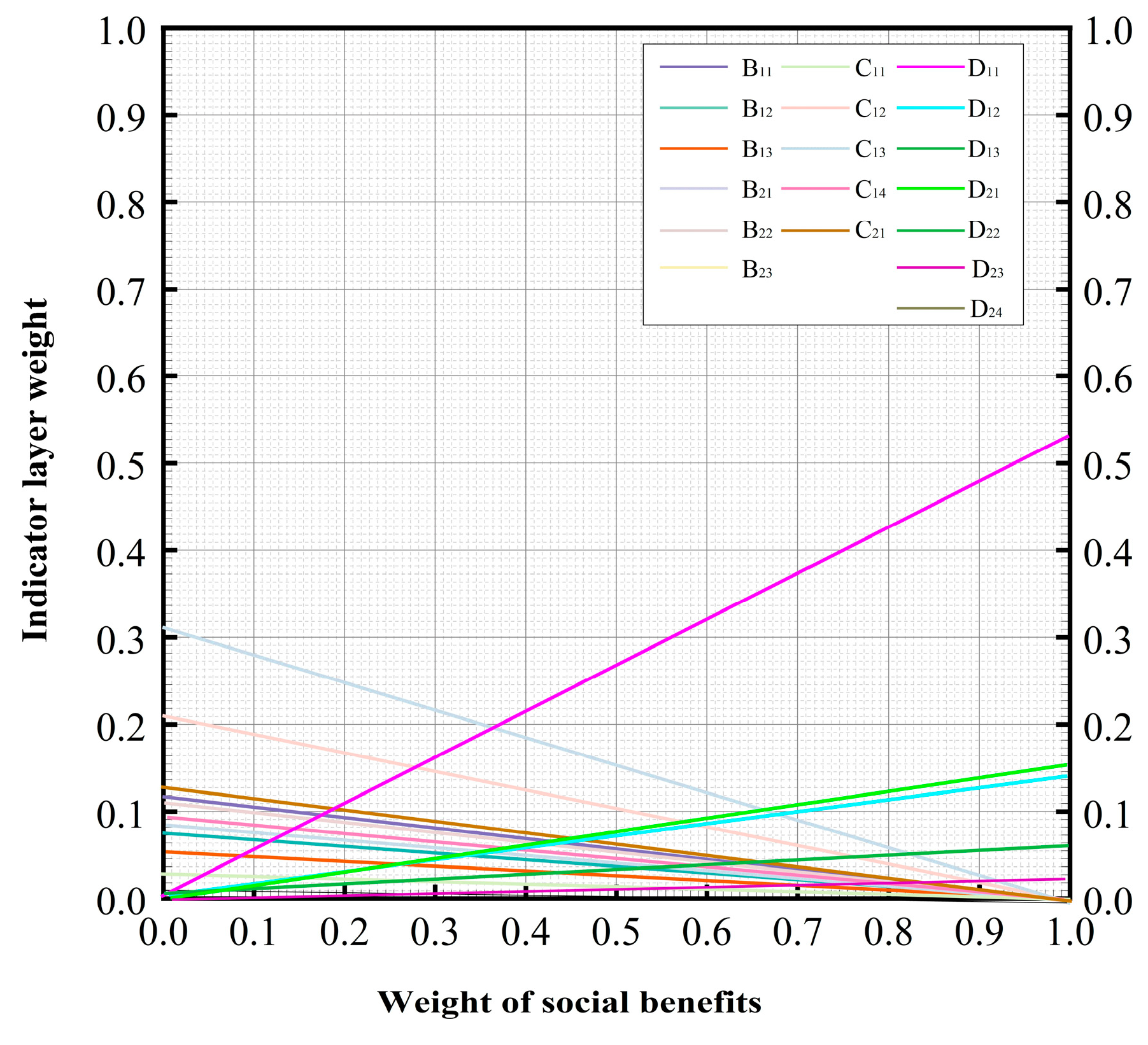
3.2. Combined Weight Analysis
3.3. Determination of Evaluation Ranks
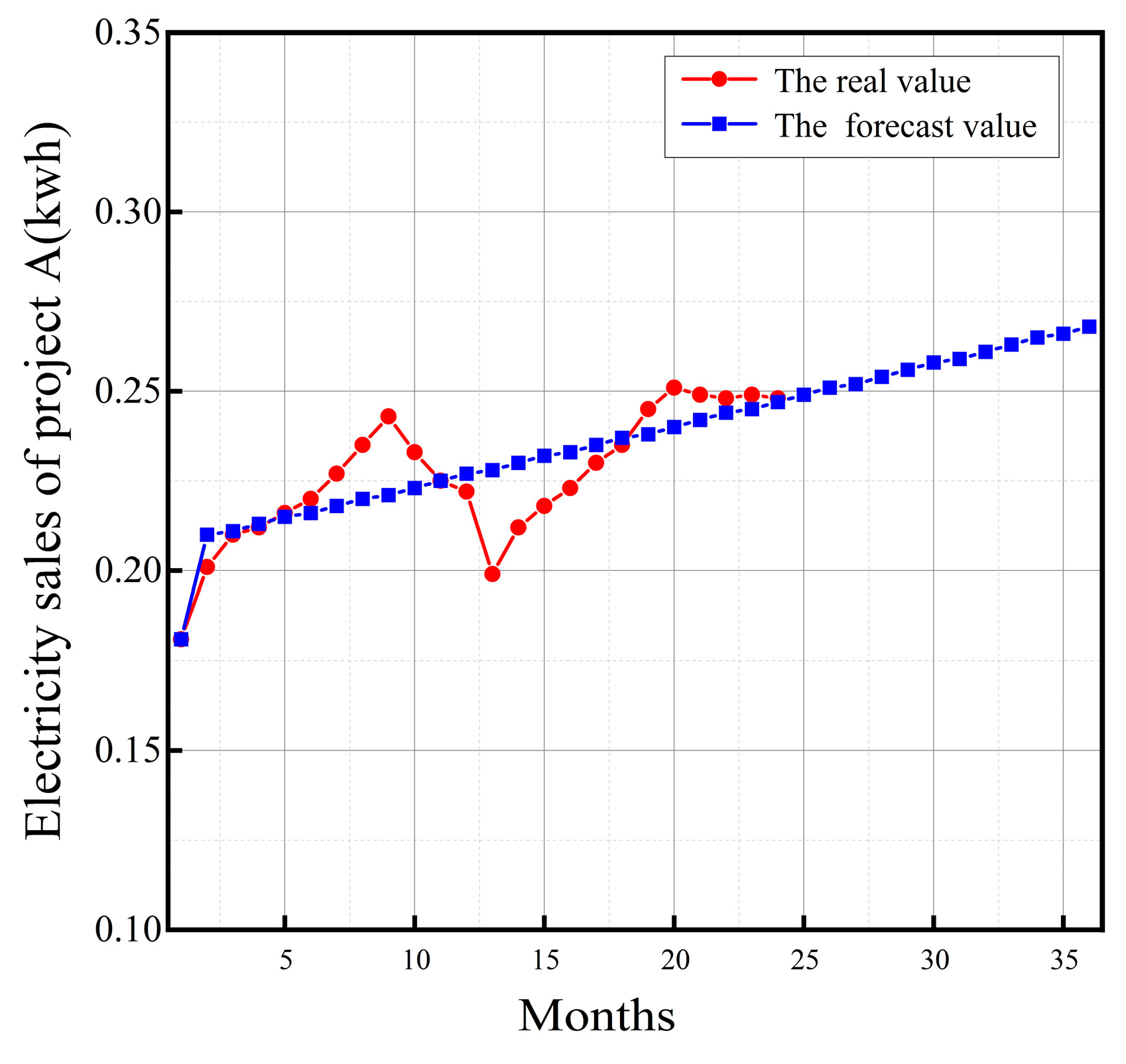
3.4. Forecast of Electricity Sales
4. Conclusions
- (a)
- A comprehensive evaluation system for carbon reduction benefits in power transmission and transformation engineering, encompassing economic, carbon reduction, and social benefits has been established. The evaluation system revealed that the most significant indicator in economic benefit B is “Internal Rate of Return B11”, accounting for 7.75% of the combined weight. In carbon reduction benefit C, the most significant indicator is “Adoption of Distributed Energy C13”, constituting 7.32% of the combined weight. Lastly, in social benefit D, the most significant indicator is “Impact on Residents’ IncomeD11”, representing 4.7% of the combined weight.
- (b)
- Introducing the TOPSIS-RSR to correct the subjectivity in the combined weights obtained from the FAHP and EWM can make the evaluation results more objective and comprehensive. Finally, using the GM (1,1) model to forecast the electricity sales of the optimal project A, a post-examination residual ratio C of 0.351 was obtained, indicating a good fit of the model.
- (c)
- While retaining the application of the TOPSIS method for deep information retrieval, the introduction of the RSR method for ranking, along with the modification of the Euclidean distance in traditional TOPSIS to standard Euclidean distance, alleviates the impact of dimensional disparities between economic and carbon reduction benefits on the evaluation results. The traditional TOPSIS method yielded a test value of p = 0.067, whereas the improved TOPSIS method resulted in a test value of p = 0.043 and an R-squared value of 0.859. Thus, the superiority of the improved TOPSIS method in linear regression of the model’s data has been validated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Zhang, H.; Zhao, H.; Wang, M.; Sun, Y.; Sun, K. New Mission and Challenge of Power Distribution and Consumption System Under Dual-carbon Target. Zhongguo Dianji Gongcheng Xuebao Proc. Chin. Soc. Electr. Eng. 2022, 42, 6931–6944. [Google Scholar]
- Li, Y.; Xia, Z.; Yang, Q.; Wang, L.; Xing, Y. Review on g-C3N4-based S-scheme heterojunction photocatalysts. J. Mater. Sci. Technol. 2022, 125, 128–144. [Google Scholar] [CrossRef]
- Acaroğlu, H.; Güllü, M.; Sivri, N.; Garcia Marquez, F.P. How can there be an economic transition to a green ecosystem by adapting plastic-to-fuel technologies through renewable energy? Sustain. Energy Technol. Assess. 2024, 64, 103691. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, J.; Ji, Q.; Liu, Y. Optimization of PCM layer height of cascaded two-layered packed-bed thermal energy storage tank with capsules of varying diameters based on genetic algorithm. J. Energy Storage 2024, 81, 110504. [Google Scholar] [CrossRef]
- Erasmus, D.J.; Sánchez-González, A.; Lubkoll, M.; Craig, K.J.; von Backström, T.W. Thermal performance characteristics of a tessellated-impinging central receiver. Appl. Therm. Eng. 2023, 229, 120529. [Google Scholar] [CrossRef]
- Olatoyan, O.J.; Kareem, M.A.; Adebanjo, A.U.; Olawale, S.O.A.; Alao, K.T. Potential use of biomass ash as a sustainable alternative for fly ash in concrete production: A review. Hybrid Adv. 2023, 4, 100076. [Google Scholar] [CrossRef]
- Osei, A.K.; Rezanezhad, F.; Oelbermann, M. Impact of freeze-thaw cycles on greenhouse gas emissions in marginally productive agricultural land under different perennial bioenergy crops. J. Environ. Manag. 2024, 357, 120739. [Google Scholar] [CrossRef]
- Dewan, S.; Bamola, S.; Lakhani, A. Addressing ozone pollution to promote United Nations sustainable development goal 2: Ensuring global food security. Chemosphere 2024, 347, 140693. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Xu, J.; Shi, C. What factors drive the temporal-spatial differences of electricity consumption in the Yangtze River Delta region of China. Environ. Impact Asses. 2023, 103, 107247. [Google Scholar] [CrossRef]
- Gür, T.M. Carbon Dioxide Emissions, Capture, Storage and Utilization: Review of Materials, Processes and Technologies. Prog. Energ. Combust. 2022, 89, 100965. [Google Scholar] [CrossRef]
- Lei, X.; Zhao, X. The synergistic effect between Renewable Portfolio Standards and carbon emission trading system: A perspective of China. Renew. Energy 2023, 211, 1010–1023. [Google Scholar] [CrossRef]
- Hansen, T.A.; Wilson, E.J.; Fitts, J.P.; Jansen, M.; Beiter, P.; Steffen, B.; Xu, B.; Guillet, J.; Münster, M.; Kitzing, L. Five grand challenges of offshore wind financing in the United States. Energy Res. Soc. Sci. 2024, 107, 103329. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, H.; Gao, Z.; Liu, J.; Zhang, F.; Wen, Z.; Sun, X. Energy autonomous electronic skin with direct temperature-pressure perception. Nano Energy 2022, 98, 107273. [Google Scholar] [CrossRef]
- He, W.; Xu, D.; Zhu, H. Study on the preparation and performance of PVDF/SMA/CdS Fenton-like membrane with both separation and dye degradation functions. J. Ind. Eng. Chem. 2024, in press. [Google Scholar] [CrossRef]
- Gao, C. Performance investigation of solar-assisted supercritical compressed carbon dioxide energy storage systems. J. Energy Storage 2024, 79, 110179. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.S.; Xia, M.M. The ELECTRE I Multi-Criteria Decision-Making Method Based on Hesitant Fuzzy Sets. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 621–657. [Google Scholar] [CrossRef]
- Zare Banadkouki, M.R. Selection of strategies to improve energy efficiency in industry: A hybrid approach using entropy weight method and fuzzy TOPSIS. Energy 2023, 279, 128070. [Google Scholar] [CrossRef]
- Liu, S.; Dong, F.; Hao, J.; Qiao, L.; Guo, J.; Wang, S.; Luo, R.; Lv, Y.; Cui, J. Combination of hyperspectral imaging and entropy weight method for the comprehensive assessment of antioxidant enzyme activity in Tan mutton. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 291, 122342. [Google Scholar] [CrossRef]
- Chen, M.J.M. Research on entropy weight multiple criteria decision-making evaluation of metro network vulnerability. Int. Trans. Oper. Res. 2024, 31, 979–1003. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.; Yao, Y. BMW-TOPSIS: A generalized TOPSIS model based on three-way decision. Inf. Sci. 2022, 607, 799–818. [Google Scholar] [CrossRef]
- Gebrehiwet, T.; Luo, H. Risk Level Evaluation on Construction Project Lifecycle Using Fuzzy Comprehensive Evaluation and TOPSIS. Symmetry 2019, 11, 12. [Google Scholar] [CrossRef]
- Cao, J.; Xu, F. Entropy-based fuzzy TOPSIS method for investment decision optimization of large-scale projects. Comput. Intell. Neurosci. 2022, 2022, 4381293. [Google Scholar] [CrossRef]
- Nandi, R.; Mondal, S.; Mandal, J.; Bhattacharyya, P. From fuzzy-TOPSIS to machine learning: A holistic approach to understanding groundwater fluoride contamination. Sci. Total Environ. 2024, 912, 169323. [Google Scholar] [CrossRef]
- Fahmi, A.; Khan, A.; Abdeljawad, T.; Alqudah, M.A. Natural gas based on combined fuzzy TOPSIS technique and entropy. Heliyon 2024, 10, e23391. [Google Scholar] [CrossRef]
- Ali, S.I.; Lalji, S.M.; Hashmi, S.; Awan, Z.; Iqbal, A.; Al-Ammar, E.A.; Gull, A. Risk quantification and ranking of oil fields and wells facing asphaltene deposition problem using fuzzy TOPSIS coupled with AHP. Ain Shams Eng. J. 2024, 15, 102289. [Google Scholar] [CrossRef]
- Watrobski, J.; Baczkiewicz, A.; Ziemba, E.; Salabun, W. Sustainable cities and communities assessment using the DARIA-TOPSIS method. Sustain. Cities Soc. 2022, 83, 103926. [Google Scholar] [CrossRef]
- Stoilova, S. Application of simus method for assessment alternative transport policies for container carriage. In Proceedings of the 18th International Scientific Conference on Engineering for Rural Development (ERD), Jelgava, Latvia, 22–24 May 2019; Malinovska, L., Osadcuks, V., Eds.; pp. 898–906. [Google Scholar]
- Shekhovtsov, A.; Kizielewicz, B.; Sałabun, W. Advancing individual decision-making: An extension of the characteristic objects method using expected solution point. Inf. Sci. 2023, 647, 119456. [Google Scholar] [CrossRef]
- Dezert, J.; Tchamova, A.; Han, D.; Tacnet, J. IEEE The SPOTIS Rank Reversal Free Method for Multi-Criteria Decision-Making Support. In Proceedings of the 2020 23rd International Conference on Information Fusion (Fusion 2020), Rustenburg, South Africa, 6–9 July 2020; pp. 195–202. [Google Scholar]
- Xie, X.; Zhang, J.; Lian, Y.; Lin, K.; Gao, X.; Lan, T.; Luo, J.; Song, F. Cloud model combined with multiple weighting methods to evaluate hydrological alteration and its contributing factors. J. Hydrol. 2022, 610, 127794. [Google Scholar] [CrossRef]
- Song, F.; Tong, S. Comprehensive evaluation of the transformer oil-paper insulation state based on RF-combination weighting and an improved TOPSIS method. Glob. Energy Interconnect. 2022, 5, 654–665. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Chen, J.; Wang, Q. Air pollution concentration forecasting based on wavelet transform and combined weighting forecasting model. Atmos. Pollut. Res. 2021, 12, 101144. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, B.; Hu, X.; Du, P.; Sun, Q. Blockchain-Based Renewable Energy Trading Using Information Entropy Theory. IEEE Trans. Netw. Sci. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, B.; Li, Y.; Sun, Q.; Pedersen, T.B.; Gao, D.W. Pricing Game and Blockchain for Electricity Data Trading in Low-Carbon Smart Energy Systems. IEEE Trans. Ind. Inform. 2024, 20, 6446–6456. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Lyapunov stability of fuzzy dynamical systems based on fuzzy-number-valued function granular differentiability. Commun. Nonlinear Sci. 2024, 133, 107984. [Google Scholar] [CrossRef]
- Santiago, L.; Bedregal, B. Multidimensional fuzzy sets: Negations and an algorithm for multi-attribute group decision making. Int. J. Approx. Reason. 2024, 169, 109171. [Google Scholar] [CrossRef]
- de Andrade, A.E.R.; Wasques, V.F. The Interactive Fuzzy Semigroup (RIC,+1/2) and its Algebraic Structure Properties. Fuzzy Set. Syst. 2024, 468, 108970. [Google Scholar] [CrossRef]
- Savari, M.; Shokati Amghani, M. SWOT-FAHP-TOWS analysis for adaptation strategies development among small-scale farmers in drought conditions. Int. J. Disaster Risk Reduct. 2022, 67, 102695. [Google Scholar] [CrossRef]
- Ahmad, R.; Gabriel, H.F.; Alam, F.; Zarin, R.; Raziq, A.; Nouman, M.; Young, H.V.; Liou, Y. Remote sensing and GIS based multi-criteria analysis approach with application of AHP and FAHP for structures suitability of rainwater harvesting structures in Lai Nullah, Rawalpindi, Pakistan. Urban Clim. 2024, 53, 101817. [Google Scholar] [CrossRef]
- Thapar, S.S.; Sarangal, H. Quantifying reusability of software components using hybrid fuzzy analytical hierarchy process (FAHP)-Metrics approach. Appl. Soft Comput. 2020, 88, 105997. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A novel approach to identifying criteria relevance based on inaccuracy expert judgments. Eng. Appl. Artif. Intell. 2023, 122, 106114. [Google Scholar] [CrossRef]
- Yu, X.; Qian, L.; Wang, W.E.; Hu, X.; Dong, J.; Pi, Y.; Fan, K. Comprehensive evaluation of terrestrial evapotranspiration from different models under extreme condition over conterminous United States. Agric. Water Manag. 2023, 289, 108555. [Google Scholar] [CrossRef]
- Han, H.; Li, X.; Gu, X.; Li, G. Urban rivers health assessment based on the concept of resilience using improved FCM-EWM-MABAC model. Ecol. Indic. 2023, 154, 110833. [Google Scholar] [CrossRef]
- Li, Y.; Lu, C.; Liu, G.; Chen, Y.; Zhang, Y.; Wu, C.; Liu, B.; Shu, L. Risk assessment of wetland degradation in the Xiong’an New Area based on AHP-EWM-ICT method. Ecol. Indic. 2023, 153, 110443. [Google Scholar] [CrossRef]
- Luo, Z.; Tian, J.; Zeng, J.; Pilla, F. Flood risk evaluation of the coastal city by the EWM-TOPSIS and machine learning hybrid method. Int. J. Disaster Risk Reduct. 2024, 106, 104435. [Google Scholar] [CrossRef]
- Wang, J.; Gu, C.; Liu, K. Anomaly electricity detection method based on entropy weight method and isolated forest algorithm. Front. Energy Res. 2022, 10, 984473. [Google Scholar]
- Wang, S.; Ge, L.; Cai, S.; Wu, L. Hybrid interval AHP-entropy method for electricity user evaluation in smart electricity utilization. J. Mod. Power Syst. Clean Energy 2018, 6, 701–711. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, L.; Xia, L.; Yang, Q.; Chen, Z.; Dong, W. Comprehensive Evaluation Technology of Photovoltaic Power Station Power Generation Performance Based on Minimum Deviation Combined Weighting Method. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; pp. 880–885. [Google Scholar]
- Ongena, S.; Paraschiv, F.; Reite, E.J. Counteroffers and Price Discrimination in Mortgage Lending. J. Empir. Financ. 2023, 74, 101431. [Google Scholar] [CrossRef]
- Kelemenis, A.; Askounis, D. A new TOPSIS-based multi-criteria approach to personnel selection. Expert. Syst. Appl. 2010, 37, 4999–5008. [Google Scholar] [CrossRef]
- Ilham, N.I.; Dahlan, N.Y.; Hussin, M.Z. Optimizing solar PV investments: A comprehensive decision-making index using CRITIC and TOPSIS. Renew. Energy Focus 2024, 49, 100551. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, L.; Liu, Z.; Sun, L.; Liu, L. Rheological performance evaluation of activated carbon powder modified asphalt based on TOPSIS method. Case Stud. Constr. Mater. 2024, 20, e2963. [Google Scholar] [CrossRef]
- Paradowski, B.; Więckowski, J.; Sałabun, W. PySensMCDA: A novel tool for sensitivity analysis in multi-criteria problems. Softwarex 2024, 27, 101746. [Google Scholar] [CrossRef]





| Goal | Level 1 | Level 2 | Level 3 | Attribute | Direction |
|---|---|---|---|---|---|
| Evaluation indicator system for carbon reduction benefits of power transmission and transformation projects A | Economic benefits B | Profitability B1 | Internal rate of return B11 | Quantitative | + |
| Investment payback period B12 | Quantitative | + | |||
| Return on investment B13 | Quantitative | + | |||
| Solvency B2 | Asset to liability ratio B21 | Quantitative | + | ||
| Current ratio B22 | Quantitative | + | |||
| Quick ratio B23 | Quantitative | + | |||
| Carbon reduction benefits C | Power companies C1 | Using energy-saving wires C11 | Quantitative | + | |
| Reduce SF6 gas emissions C12 | Quantitative | + | |||
| Adopting distributed energy generation C13 | Quantitative | + | |||
| Participation in carbon trading markets C14 | Quantitative | + | |||
| Social impact C2 | Encourage low-carbon consumption by consumers C21 | Quantitative | + | ||
| Social benefits D | Socioeconomic impact D1 | Impact on residents’ income D11 | Qualitative | + | |
| Impact on residents’ quality of life D12 | Qualitative | + | |||
| Impact on residents’ employment D13 | Qualitative | + | |||
| Interoperability D2 | Impact on the natural environment D21 | Qualitative | + | ||
| Impact on local customs and religion D22 | Qualitative | + | |||
| Impact on local science, education, culture, and health D23 | Qualitative | + | |||
| Impact on urbanization development D24 | Qualitative | + |
| Scale | Meaning |
|---|---|
| 0.100 | Element B is extremely important compared to element A |
| 0.138 | Element B is significantly more important than element A |
| 0.325 | Element B is noticeably more important than element A |
| 0.439 | Element B is slightly more important than element A |
| 0.500 | Element B is equally important as element A |
| 0.561 | Element A is slightly more important than element B |
| 0.675 | Element A is noticeably more important than element B |
| 0.862 | Element A is significantly more important than element B |
| 0.900 | Element A is extremely important compared to element B |
| Data | Project A | Project B | Project C | Project D |
|---|---|---|---|---|
| Internal rate of return/% | 12.51 | 17.39 | 11.53 | 11.47 |
| Investment payback period/year | 8.9 | 7.89 | 11.69 | 8.7 |
| Return on investment/% | 9.4 | 22.23 | 18.13 | 5.8 |
| Asset-liability ratio/% | 14.04 | 25.67 | 67 | 39.65 |
| Current ratio/% | 1.34 | 1.57 | 0.81 | 1.34 |
| Quick ratio/% | 1.21 | 1.4 | 0.73 | 1.01 |
| Electricity sales volume in year (i − 1) /billion·kWh−1 | 2.6243 | 4.612 | 1.269 | 2.133 |
| Electricity sales volume in year i/billion·kWh−1 | 2.8104 | 5.362 | 2.133 | 4.59 |
| Overall line loss rate/% | 4.69 | 4.69 | 4.69 | 4.69 |
| Grid connection and absorption ratio/% | 96 | 97 | 96 | 96 |
| Average coal consumption for power supply/g·kWh−1 | 326 | 326 | 326 | 326 |
| CO2 emission factor | 2.77 | 2.77 | 2.77 | 2.77 |
| SF6 gas emissions/t | 480 | 750 | 510 | 700 |
| SF6 gas recovery rate/% | 95 | 95 | 95 | 95 |
| SF6 gas conversion factor | 23,700 | 23,700 | 23,700 | 23,700 |
| CO2 gas recovery rate/% | 80 | 80 | 80 | 80 |
| Installed capacity of thermal power units/% | 52 | 52 | 52 | 52 |
| Percentage of carbon emissions reduced by enterprises in the carbon trading market/% | 33 | 33 | 33 | 33 |
| Project | RSR | F | ∑f | p | Probit |
|---|---|---|---|---|---|
| A | 0.5000 | 2 | 2 | 0.5000 | 5.0000 |
| B | 0.9998 | 4 | 4 | 0.9375 | 6.5341 |
| C | 0.4089 | 1 | 1 | 0.2500 | 4.3255 |
| D | 0.5699 | 3 | 3 | 0.7500 | 5.6744 |
| Project | RSR | f | ∑f | p | Probit |
|---|---|---|---|---|---|
| A | 0.9999 | 4 | 4 | 0.9375 | 6.5341 |
| B | 0.9991 | 3 | 3 | 0.7500 | 5.6744 |
| C | 0.6263 | 2 | 2 | 0.5000 | 5.0000 |
| D | 0.4571 | 1 | 1 | 0.2500 | 4.3255 |
| Level | The RSR Fitted Values | The RSR Classification Range | The Classification Results |
|---|---|---|---|
| 1 | 1.0791 | <0.2655 | — |
| 2 | 0.8486 | 0.2655~ | C, D |
| 3 | 0.6677 | 0.6678~ | B |
| 4 | 0.4869 | 1.07~ | A |
| Projects | Ci | The RSR Fitted Values | TOPSIS-RSR Joint Values | Ranking | Level |
|---|---|---|---|---|---|
| A | 0.4749 | 1.0791 | 0.7770 | 1 | 4 |
| B | 0.4736 | 0.8486 | 0.6611 | 2 | 3 |
| C | 0.2697 | 0.6677 | 0.4687 | 3 | 2 |
| D | 0.0350 | 0.4869 | 0.2609 | 4 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, H.; Zhao, S.; Fan, L.; Xin, C.; Jiang, X.; Yao, F. Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method. Energies 2024, 17, 2988. https://doi.org/10.3390/en17122988
Wang Y, Chen H, Zhao S, Fan L, Xin C, Jiang X, Yao F. Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method. Energies. 2024; 17(12):2988. https://doi.org/10.3390/en17122988
Chicago/Turabian StyleWang, Yinan, Heng Chen, Shuyuan Zhao, Lanxin Fan, Cheng Xin, Xue Jiang, and Fan Yao. 2024. "Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method" Energies 17, no. 12: 2988. https://doi.org/10.3390/en17122988
APA StyleWang, Y., Chen, H., Zhao, S., Fan, L., Xin, C., Jiang, X., & Yao, F. (2024). Benefit Evaluation of Carbon Reduction in Power Transmission and Transformation Projects Based on the Modified TOPSIS-RSR Method. Energies, 17(12), 2988. https://doi.org/10.3390/en17122988






