A Collaborative Modulation Method of Dual-Side Backflow Power Optimization and Zero-Voltage Switching for Dual Active Bridge
Abstract
1. Introduction
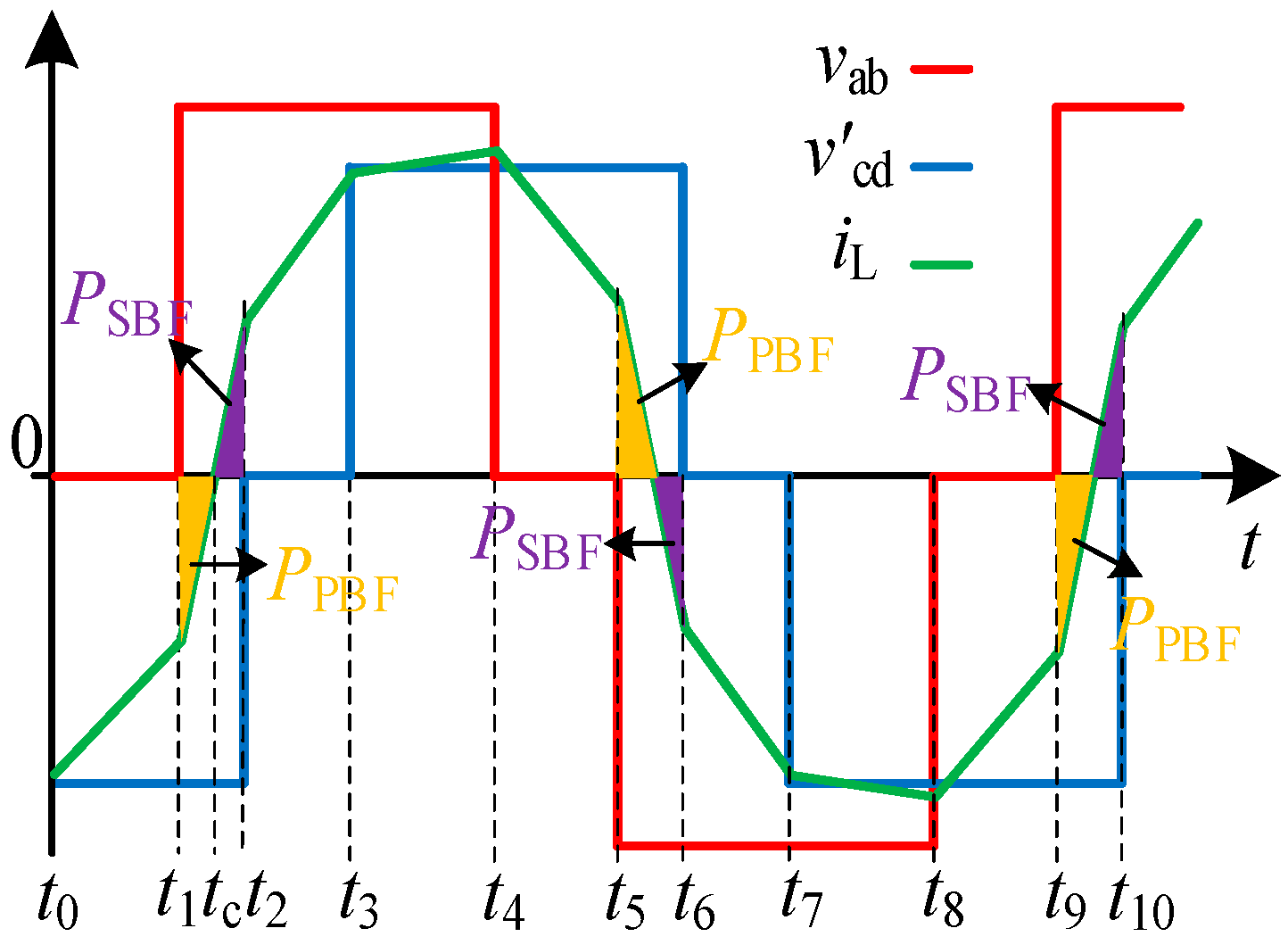
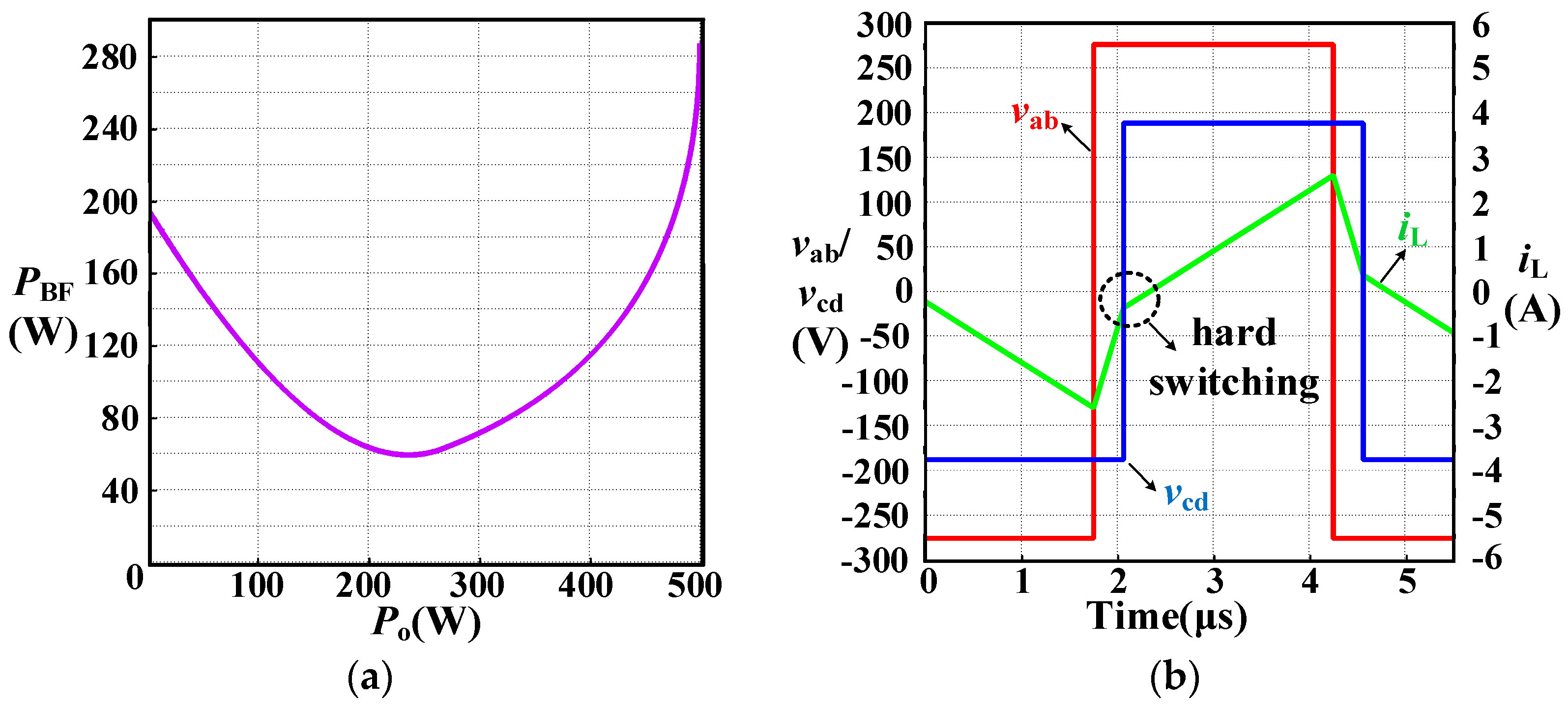
2. Backflow Power Analysis of TPS Modulation
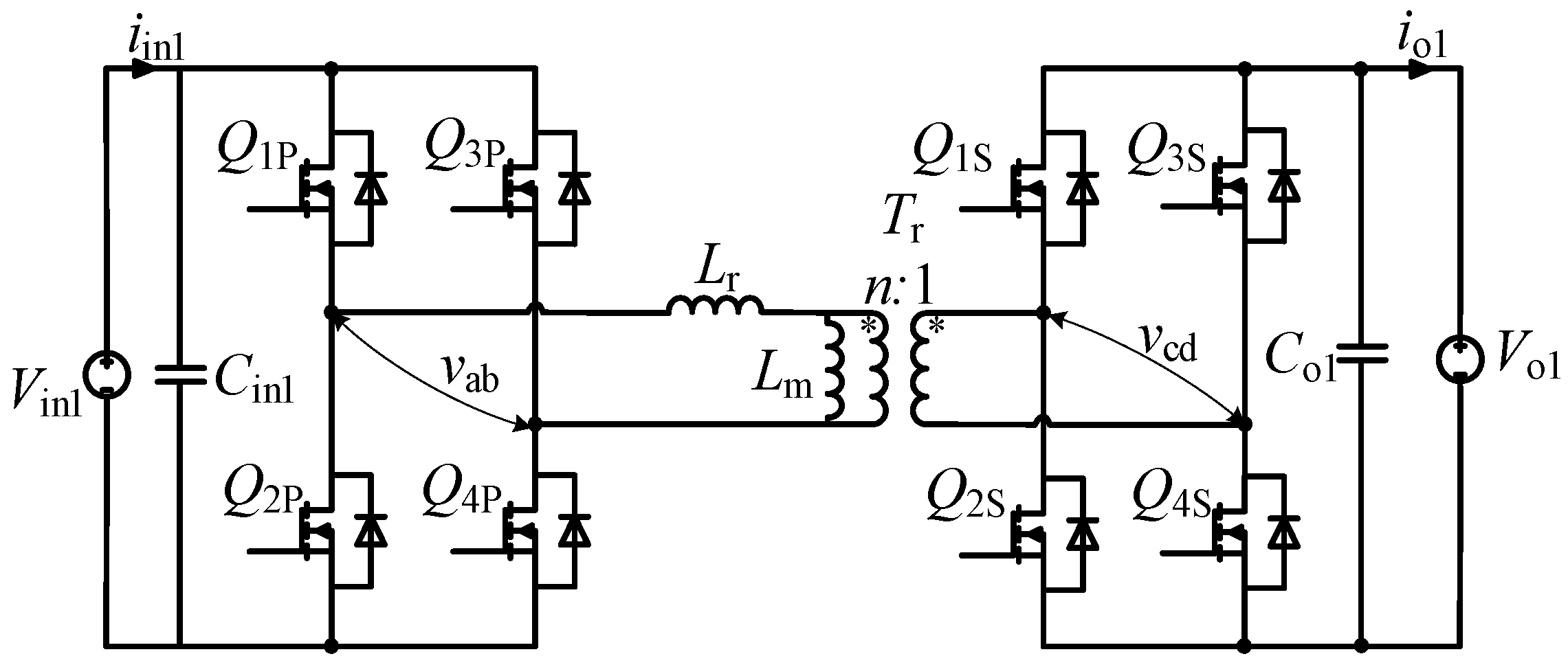
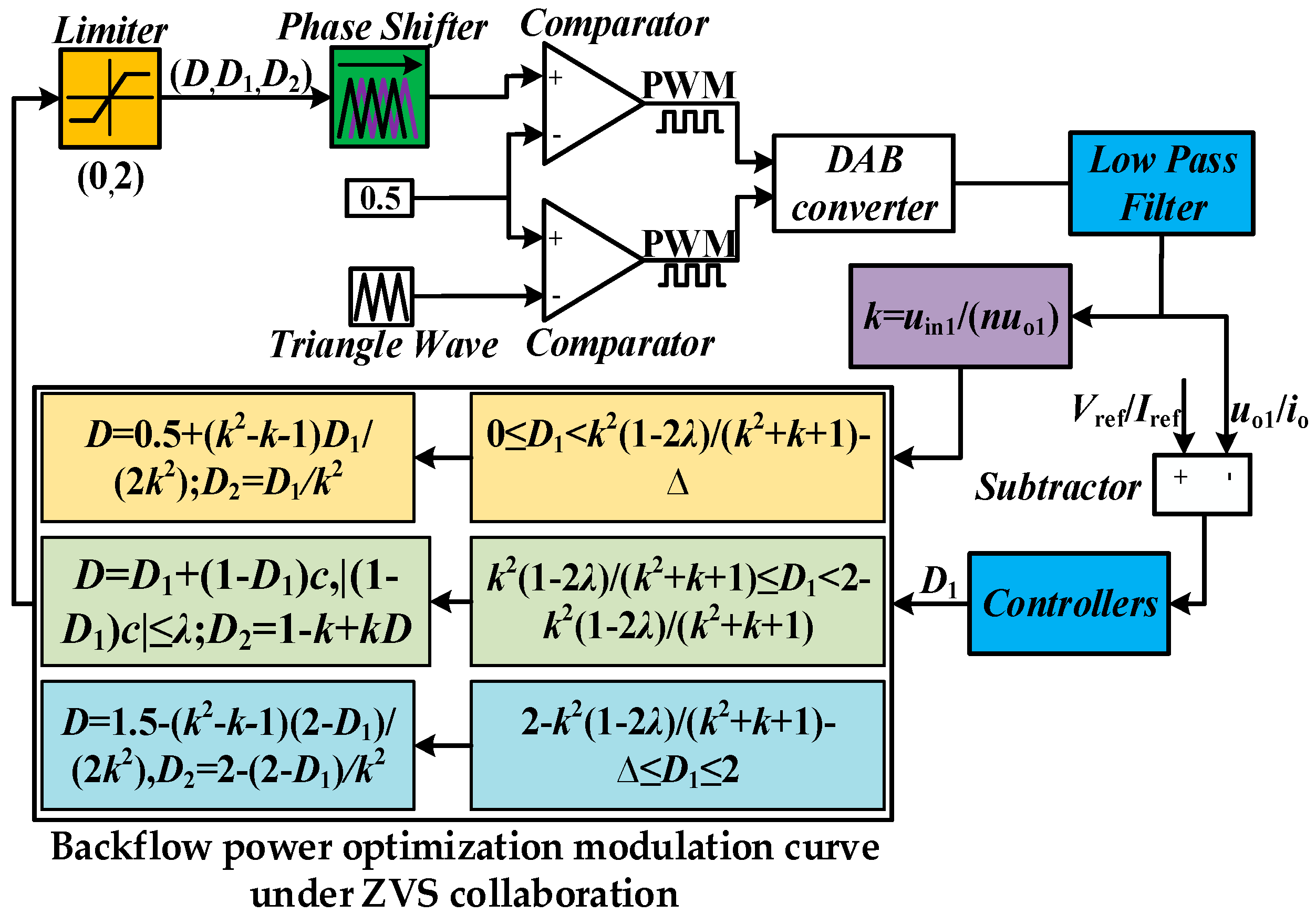
3. The Proposed Collaborative Modulation Method of Dual-Side Backflow Power Optimization and ZVS for DAB
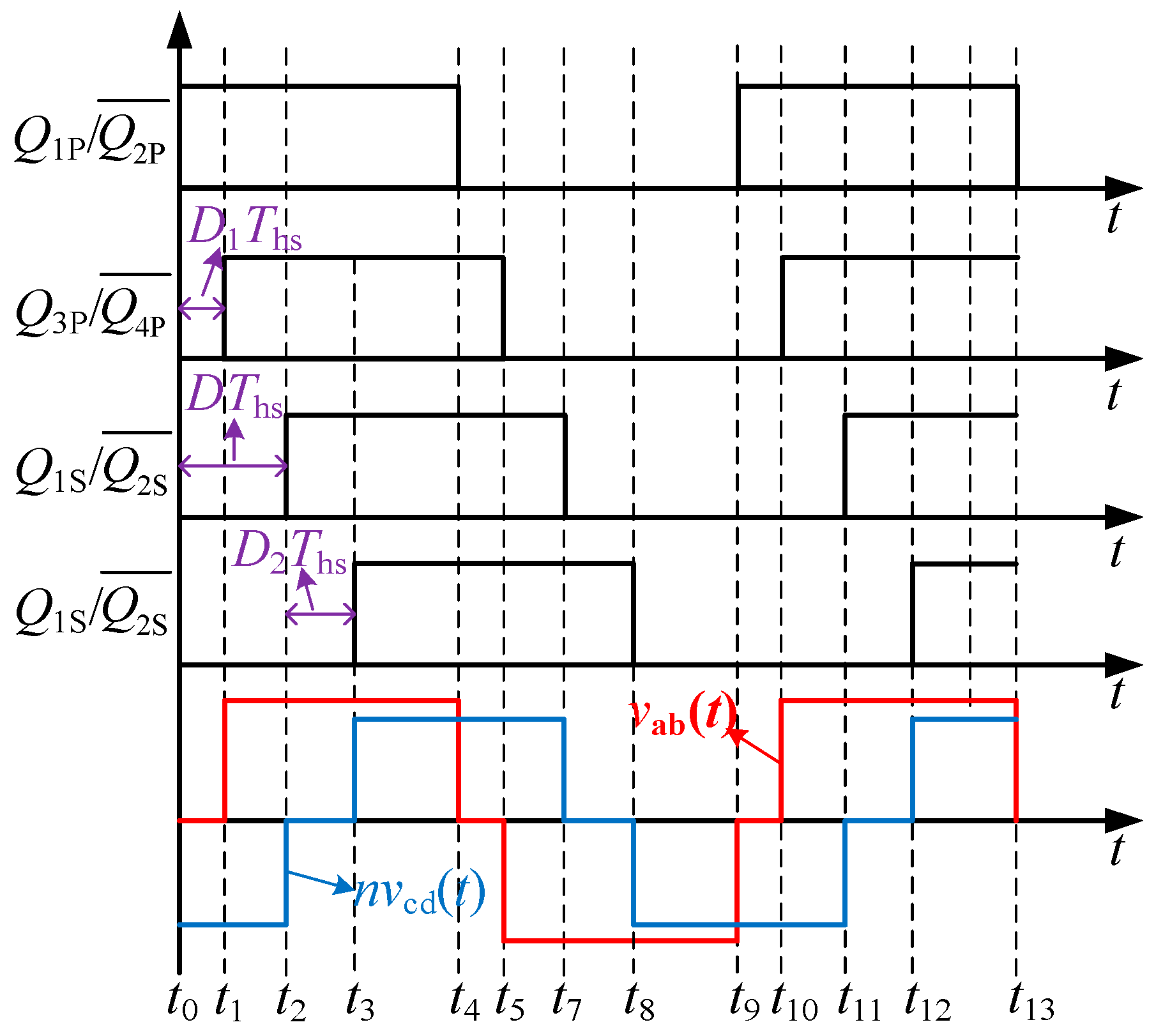
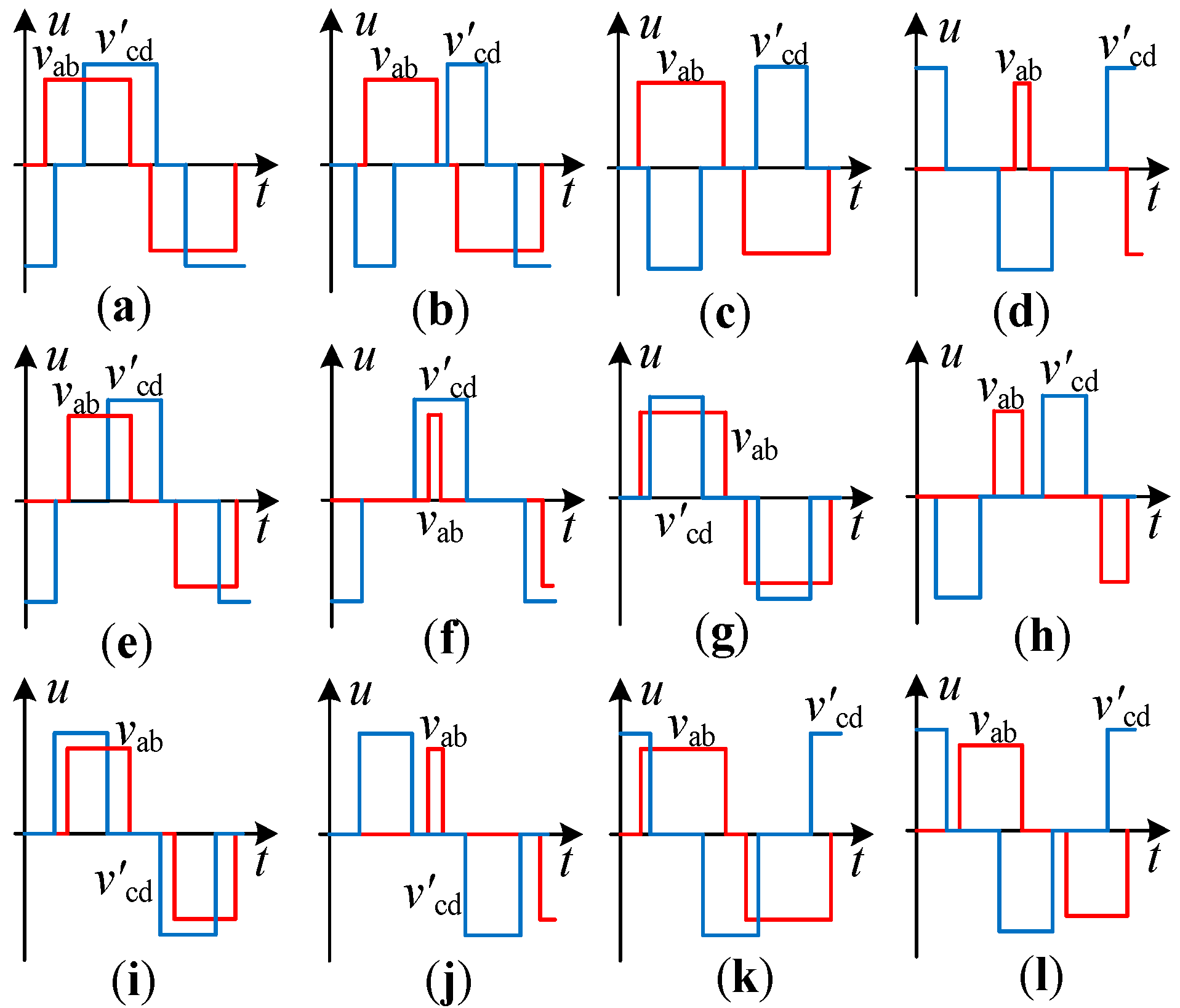
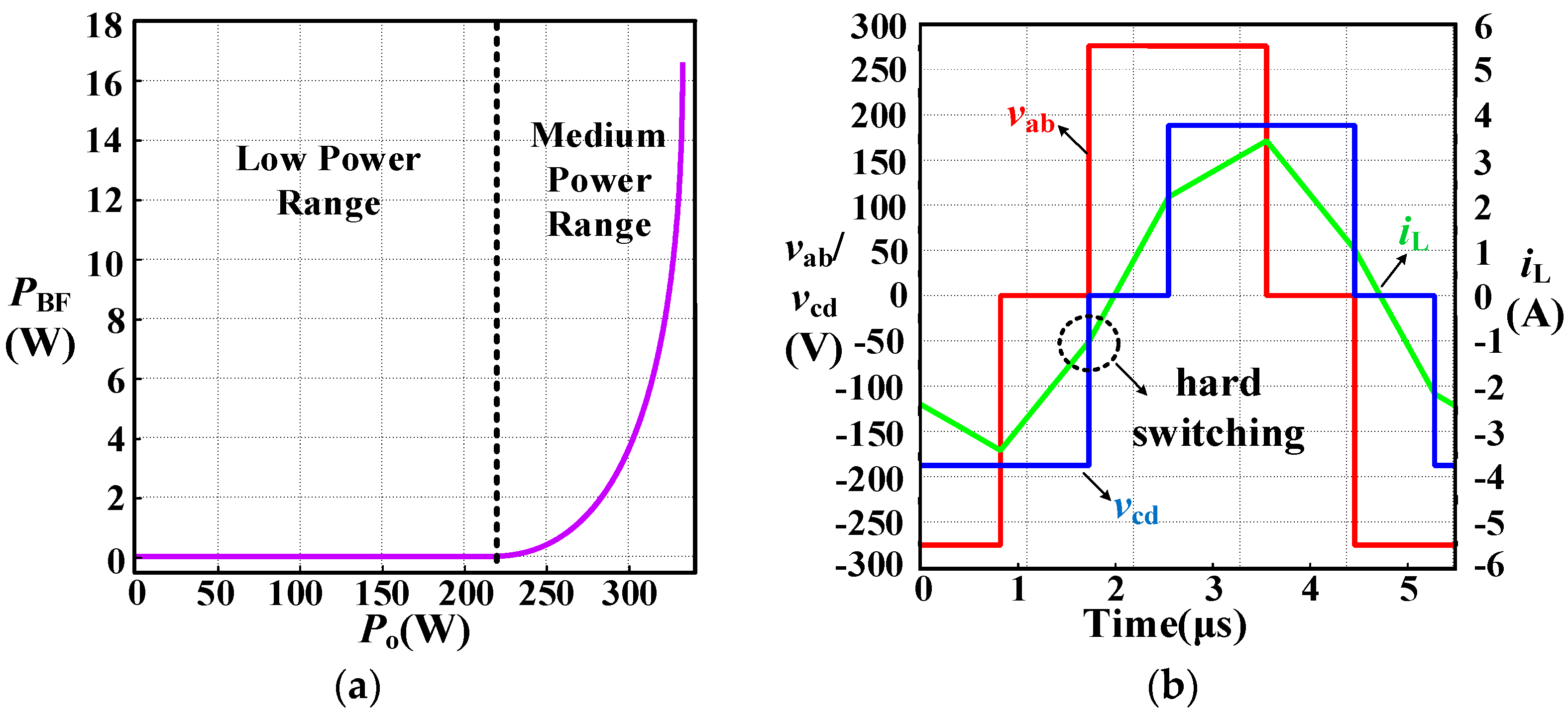
3.1. Full-Operation-Range Dual-Side Backflow Power Optimization Modulation Method
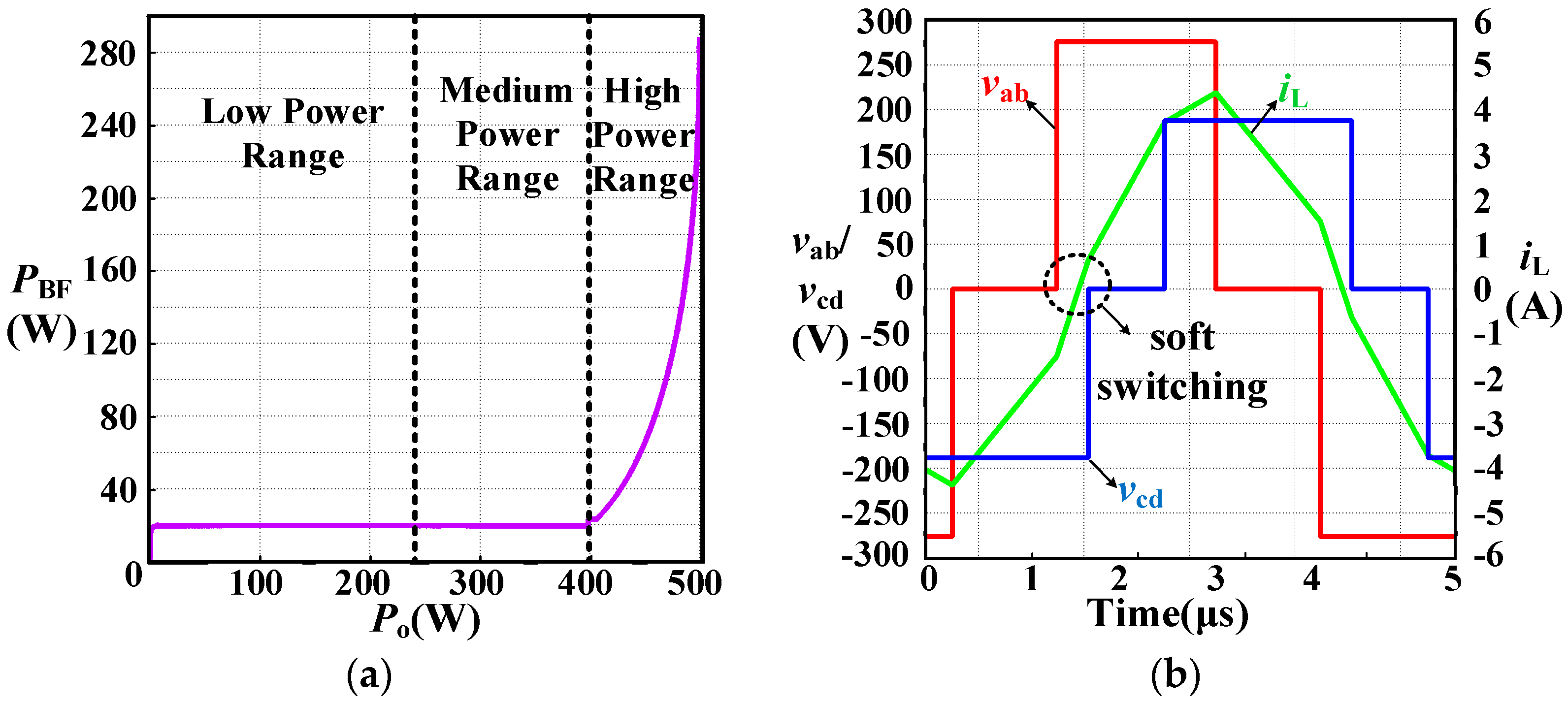
3.2. ZVS Collaborative Method Based on Backflow Power Optimization
3.3. Comparison of Backflow Power Optimization Modulation Methods for DAB
4. Simulation Analysis and Experimental Verification
4.1. Simulation Analysis
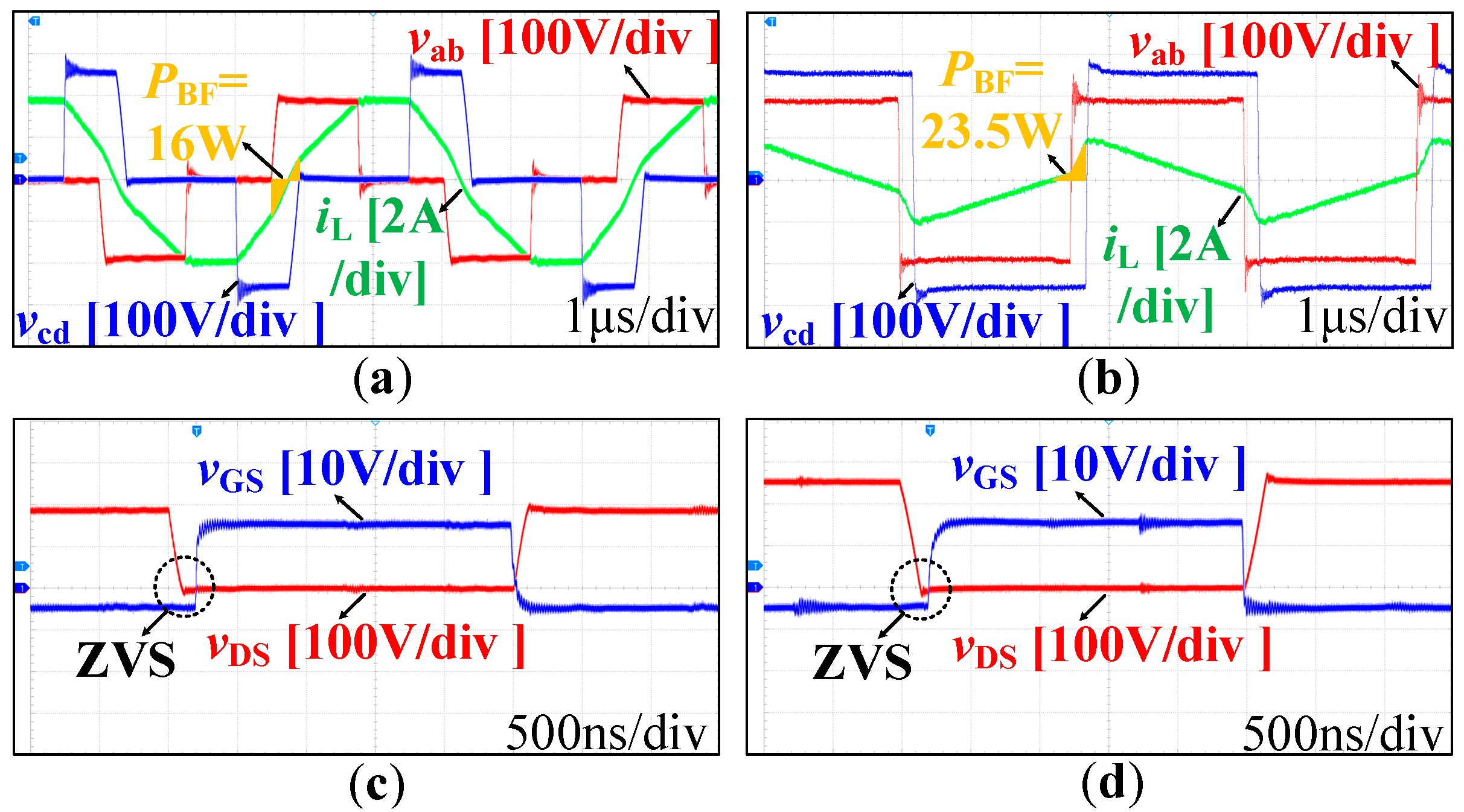
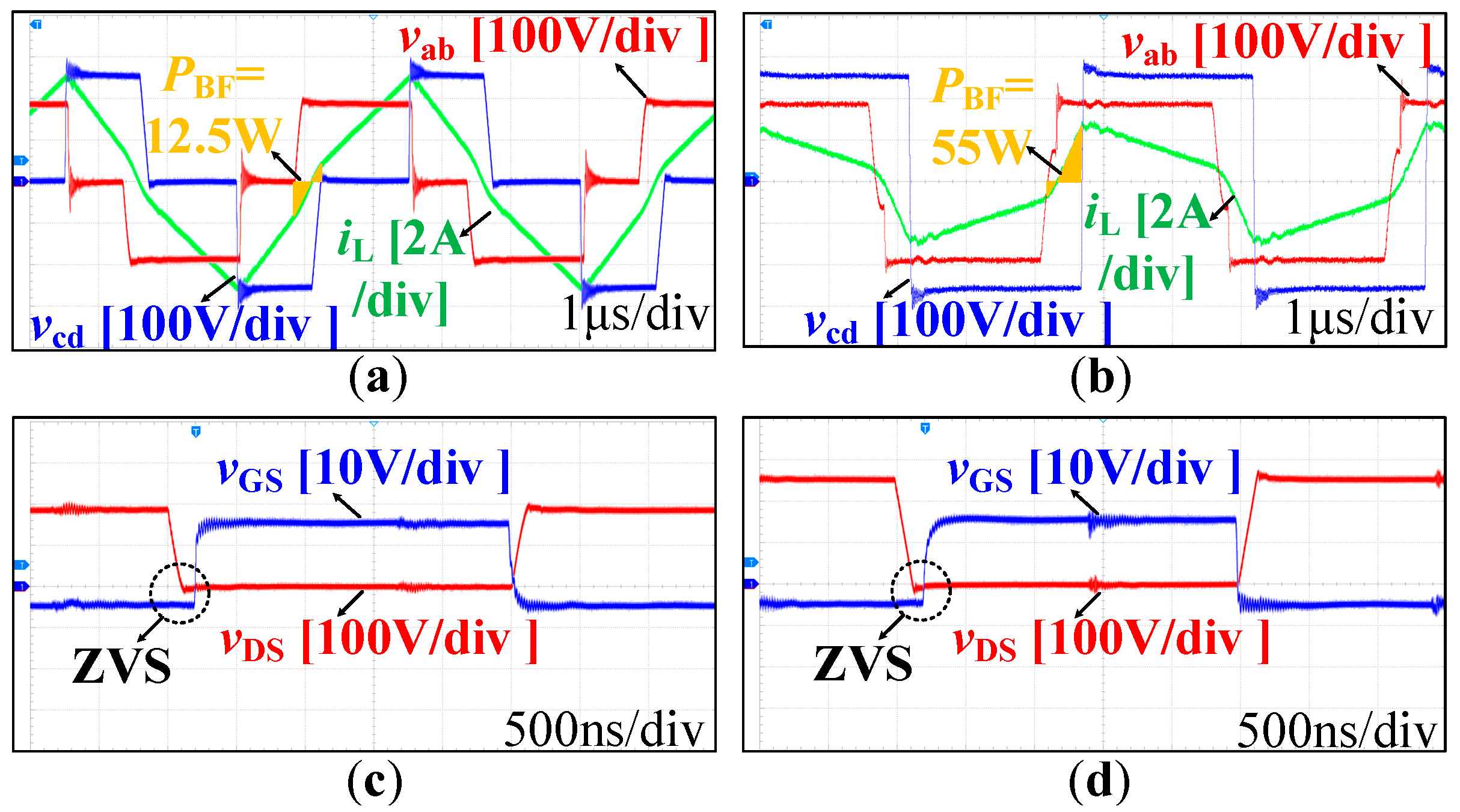
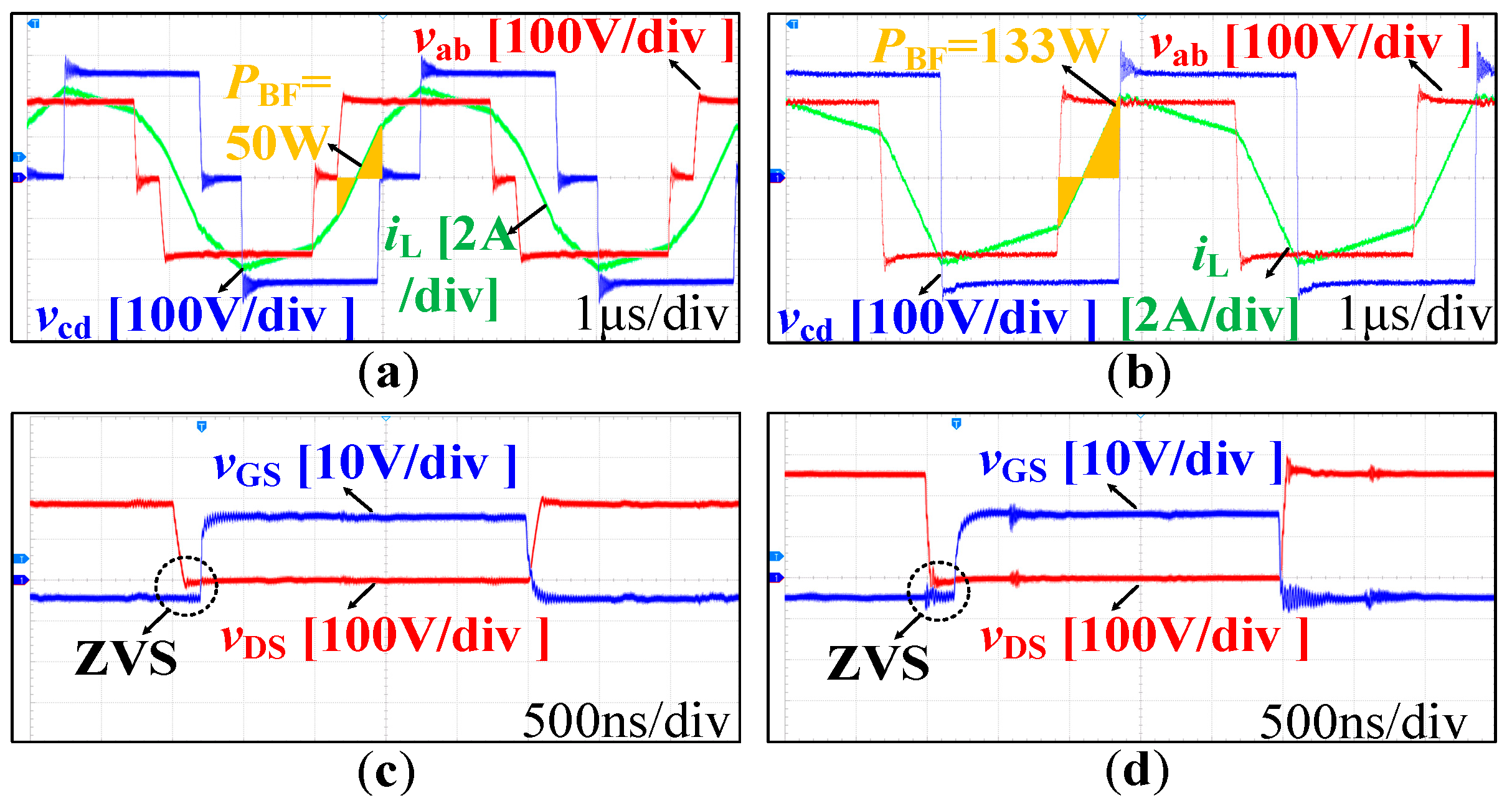
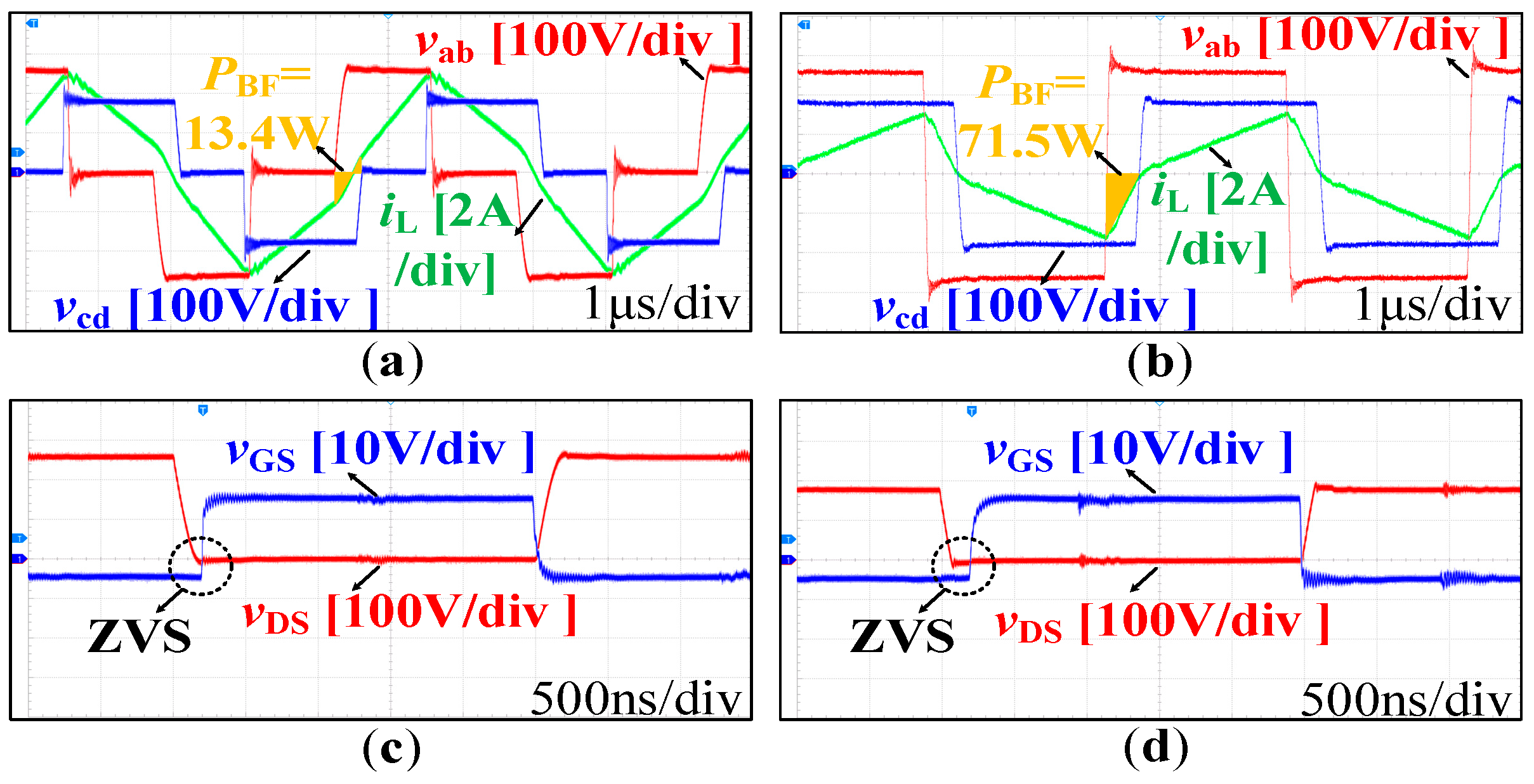
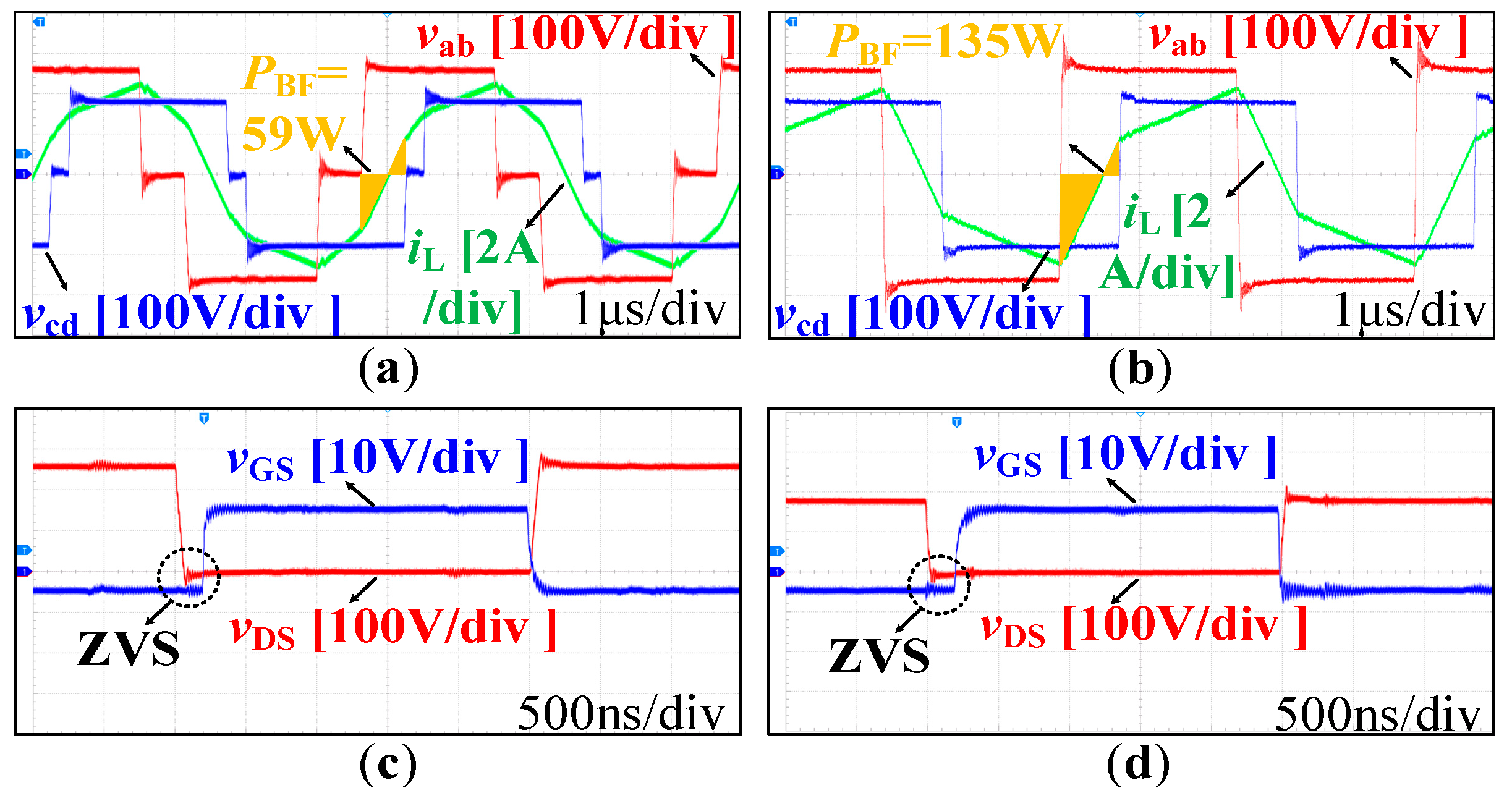
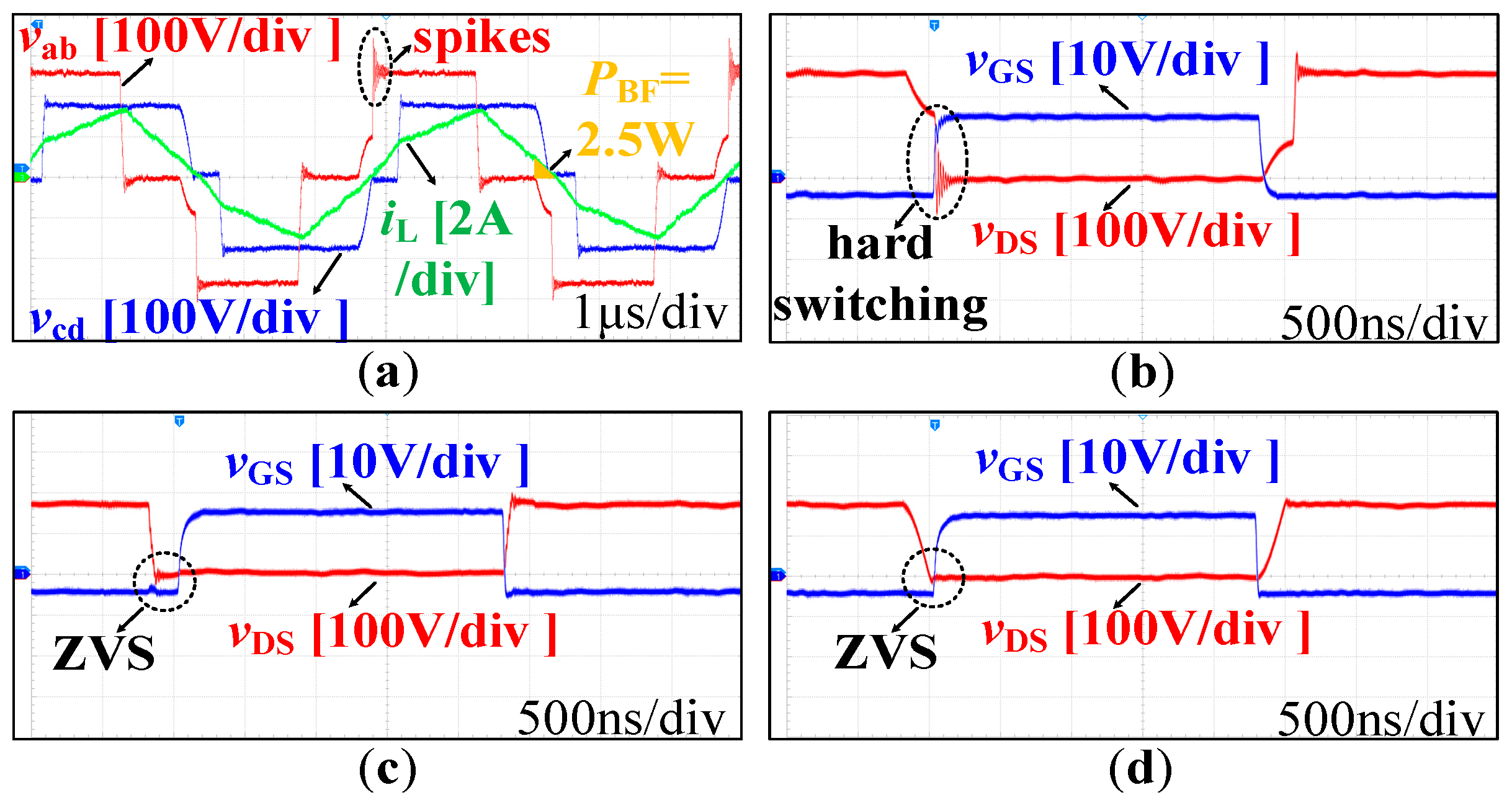
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Breyer, C.; Khalili, S.; Bogdanov, D. On the history and future of 100% renewable energy systems research. IEEE Access 2022, 10, 78176–78218. [Google Scholar] [CrossRef]
- Dragicevic, T.; Lu, X. DC microgrids—Part I: A review of control strategies and stabilization techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, P. Multicell reconfigurable multi-input multi-output energy router architecture. IEEE Trans. Power Electron. 2020, 35, 13210–13224. [Google Scholar] [CrossRef]
- Polat, H.; Hosseinabadi, F.; Hasan, M.M.; Chakraborty, S.; Geury, T.; El Baghdadi, M.; Wilkins, S.; Hegazy, O. A review of DC fast chargers with BESS for electric vehicles: Topology, battery, reliability oriented control and cooling perspectives. Batteries 2023, 9, 121. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Modeling and control simulation of power converters in automotive applications. Appl. Sci. 2024, 14, 1227. [Google Scholar] [CrossRef]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A. Design optimization and electro-thermal modeling of an off-board charging system for electric bus applications. IEEE Access 2024, 9, 84501–84519. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Electro-thermal model-based design of bidirectional on-board chargers in hybrid and full electric vehicles. Electron. 2022, 11, 112. [Google Scholar] [CrossRef]
- Kotb, R.; Chakraborty, S.; Tran, D. Power electronics converters for electric vehicle auxiliaries: State of the art and future trends. Energies 2023, 16, 1753. [Google Scholar] [CrossRef]
- Kim, I.; Jang, W.; Kim, M.; Park, J. PFM-PSM hybrid controlled CLLC resonant converter for electric vehicles. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 3386–3391. [Google Scholar]
- Dini, P.; Saponara, S.; Colicelli, A. Overview on battery charging systems for electric vehicles. Electron. 2023, 12, 4295. [Google Scholar] [CrossRef]
- Dini, P.; Ariaudo, G.; Botto, G.; Greca, F.L.; Saponara, S. Real-time electro-thermal modelling and predictive control design of resonant power converter in full electric vehicle applications. IET Power Electron. 2023, 16, 2045–2064. [Google Scholar] [CrossRef]
- Chen, X.; Xu, G.; Han, H.; Liu, D.; Sun, Y.; Su, M. Light-load efficiency enhancement of high-frequency dual-active-bridge converter under SPS control. IEEE Trans. Ind. Electron. 2021, 68, 12941–12946. [Google Scholar] [CrossRef]
- Xu, G.; Li, L.; Chen, X.; Xiong, W.; Liang, X.; Su, M. Decoupled EPS control utilizing magnetizing current to achieve full load range ZVS for dual active bridge converters. IEEE Trans. Ind. Electron. 2022, 69, 4801–4813. [Google Scholar] [CrossRef]
- Li, L.; Xu, G.; Xiong, W.; Liu, D.; Su, M. An optimized DPS control for dual-active-bridge converters to secure full-load-range ZVS with low current stress. IEEE Trans. Transp. Electrific. 2022, 8, 1389–1400. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Y.; Li, Z.; Lei, W. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC–DC converter. IEEE Trans. Ind. Electron. 2016, 63, 4169–4179. [Google Scholar] [CrossRef]
- Liu, P.; Duan, S. A hybrid modulation strategy providing lower inductor current for the DAB converter with the aid of DC blocking capacitors. IEEE Trans. Power Electron. 2020, 35, 4309–4320. [Google Scholar] [CrossRef]
- Tian, J.; Wang, F.; Zhuo, F.; Wang, Y.; Wang, H.; Li, Y. A zero-backflow-power EPS scheme with multiobjective coupled-relationship optimization in DAB-based converter. IEEE J. Emerg. Sel. Topics Power Electron. 2022, 10, 4128–4145. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H. Minimum-backflow-power scheme of DAB-based solidstate transformer with extended-phase-shift control. IEEE Trans. Ind. Appl. 2018, 54, 3483–3496. [Google Scholar] [CrossRef]
- Xu, F.; Liu, J.; Dong, Z. Minimum backflow power and ZVS design for dual-active-bridge DC–DC converters. IEEE Trans. Ind. Electron. 2023, 70, 474–484. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, X.; Li, X.; Sun, C.; Cai, W.; Zhang, Z. Automatic triple phase-shift modulation for DAB converter with minimized power loss. IEEE Trans. Ind. Appl. 2022, 58, 3840–3851. [Google Scholar] [CrossRef]
- Shao, S.; Jiang, M.; Ye, W.; Li, Y.; Zhang, J.; Sheng, K. Optimal phase-shift control to minimize reactive power for a dual active bridge DC–DC converter. IEEE Trans. Power Electron. 2019, 34, 10193–10205. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Z.; Li, C.; Wang, K.; Li, Y. Time domain analysis of reactive components and optimal modulation for isolated dual active bridge DC/DC converters. IEEE Trans. Power Electron. 2019, 34, 7143–7146. [Google Scholar] [CrossRef]
- Li, S.; Yuan, X.; Wang, Z.; Wang, K.; Zhang, Y.; Wu, X. A unified optimal modulation strategy for DAB Converters to tradeoff the backflow power reduction and all ZVS in the full operating range. IEEE J. Emerg. Sel. Topics Power Electron. 2023, 11, 5701–5723. [Google Scholar] [CrossRef]
- Jiang, L.; Sun, Y. Integrated optimization of dual-active-bridge DC–DC converter with ZVS for battery charging applications. IEEE J. Emerg. Sel. Topics Power Electron. 2023, 11, 288–300. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Z.; Chen, Y.; Feng, C.; Zhu, X. Asymmetric phase-shift modulation strategy of DAB converters for improved light-load efficiency. IEEE Trans. Power Electron. 2022, 37, 9104–9113. [Google Scholar] [CrossRef]
- Xie, F.; Wang, H.; Shu, J. Backflow power optimization of DAB based on asymmetric duty cycle and internal phase shift control. IEEE Access 2023, 11, 25682–25688. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Z.; Chen, Y.; Feng, C.; Zhu, X. Comprehensive analysis of asymmetric modulated dual-active-bridge converter and its hybrid control strategy. IEEE J. Emerg. Sel. Topics Power Electron. 2022, 10, 4218–4230. [Google Scholar] [CrossRef]
- Gu, Q.; Yuan, L.; Nie, J.; Sun, J.; Zhao, Z. Current stress minimization of dual-active-bridge DC–DC converter within the whole operating range. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 7, 129–142. [Google Scholar] [CrossRef]
- Lai, J.; Yao, X.; Su, J. Improved CTPS control for dual active bridge DC-DC converter under dead time influence. High Voltage Eng. 2023, 49, 4827–4838. [Google Scholar]
- Xiong, F.; Wu, J.; Hao, L. Backflow power optimization control for dual active bridge DC-DC converters. Energies 2017, 10, 1403. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Ye, W.; Fang, Q.; Yan, P. Dual phase shift modulation strategy for reactive power suppression of a DAB converter. Power Syst. Prot. Control 2022, 50, 14–23. [Google Scholar]
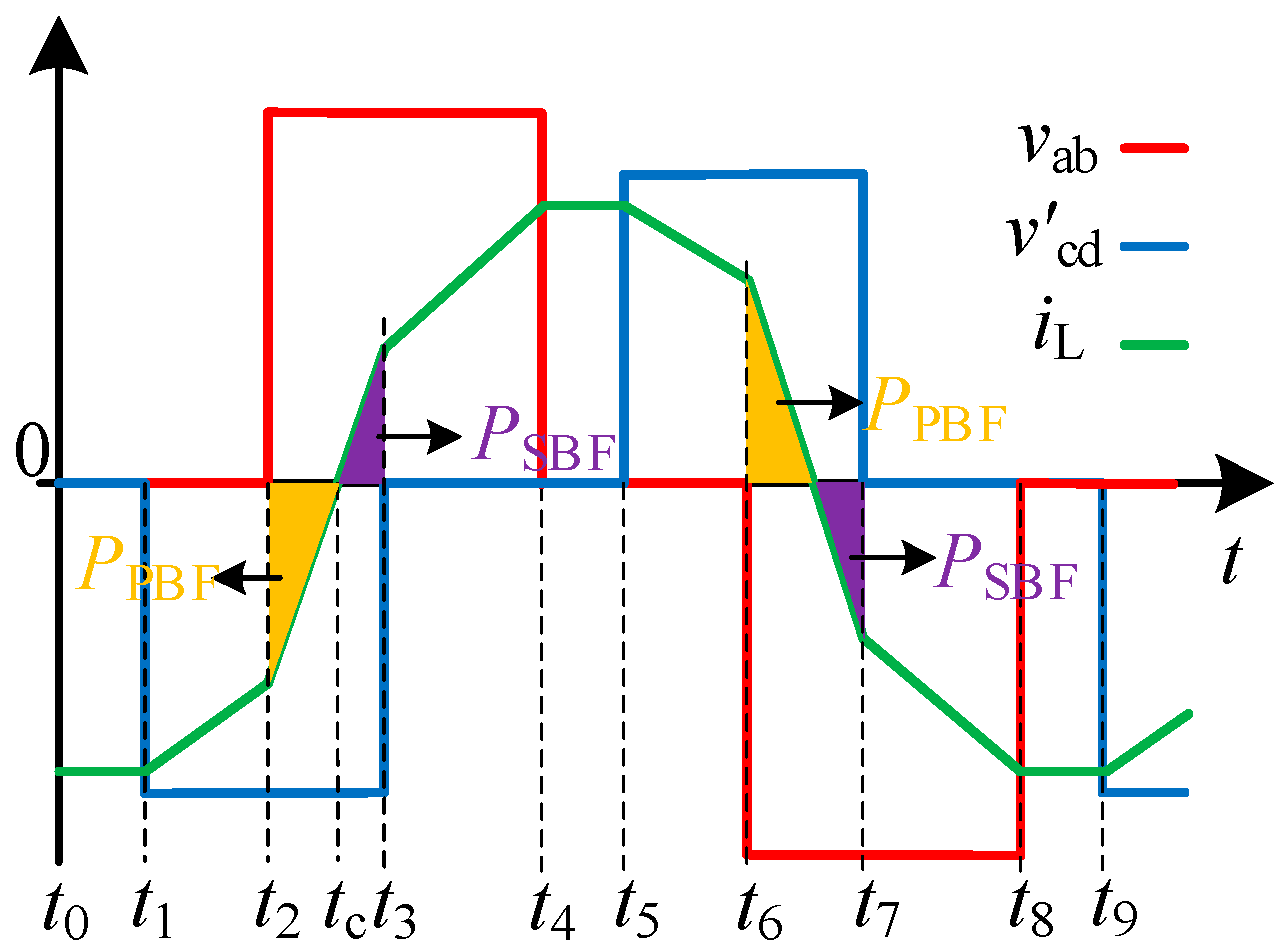
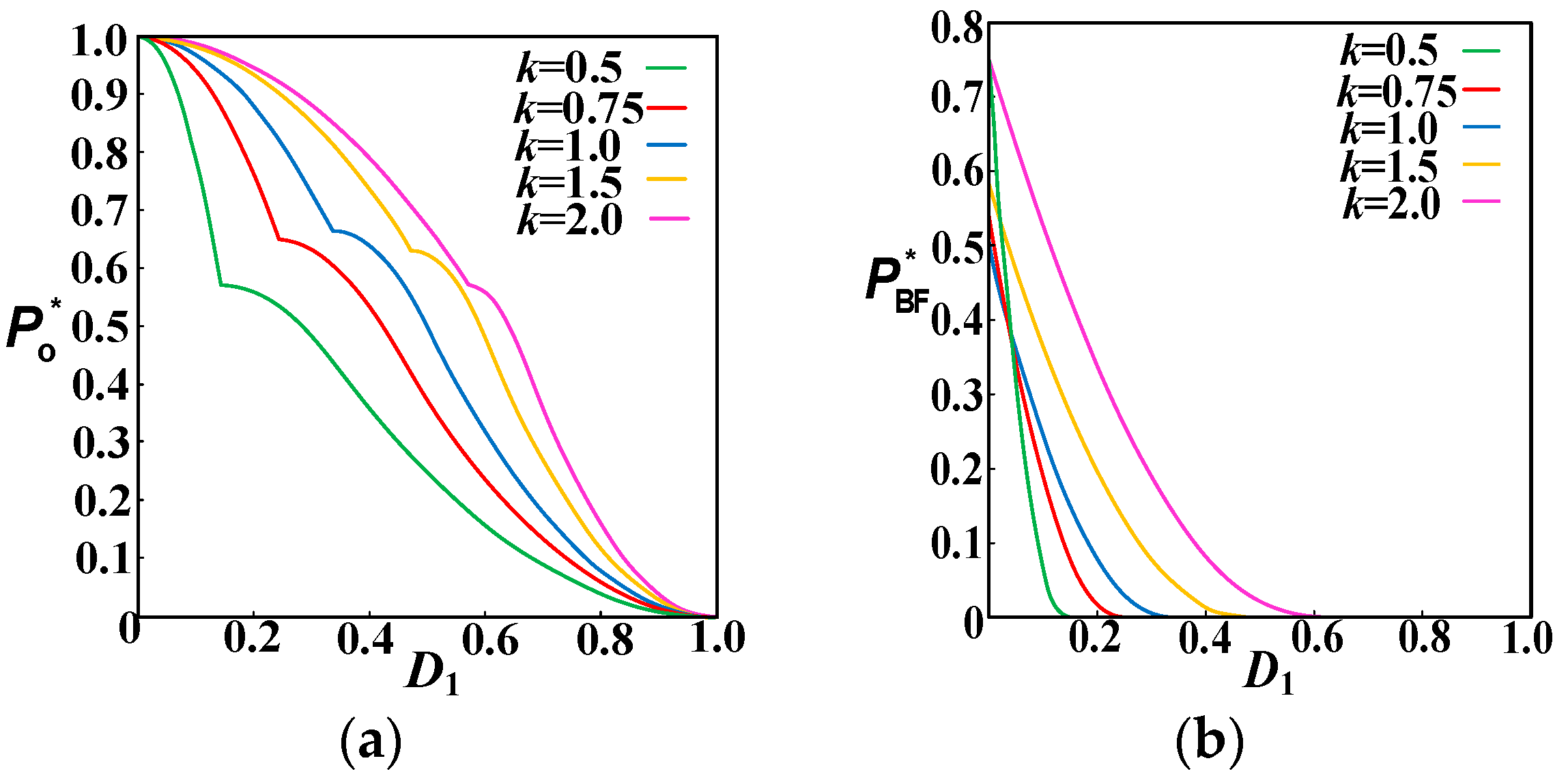
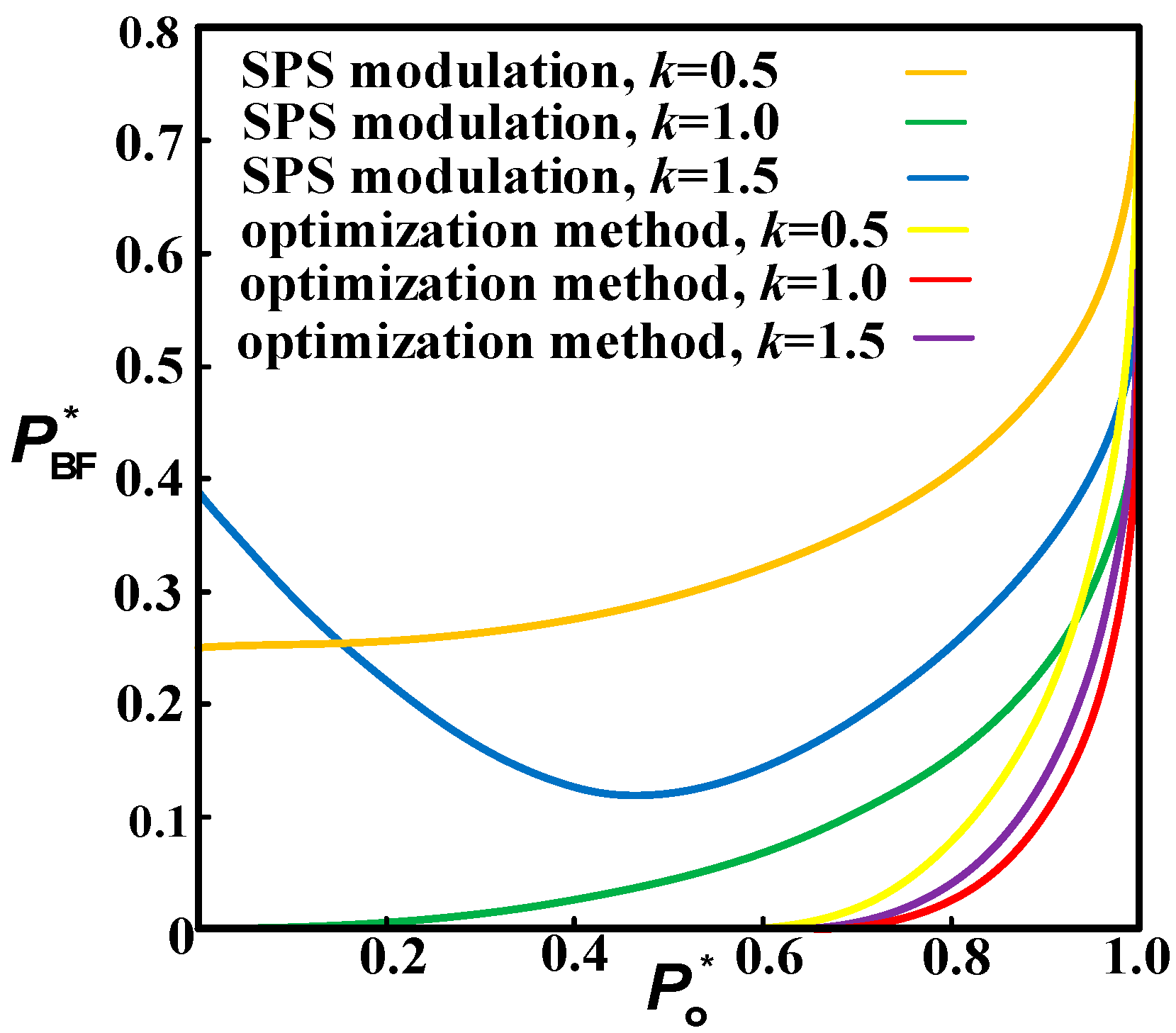
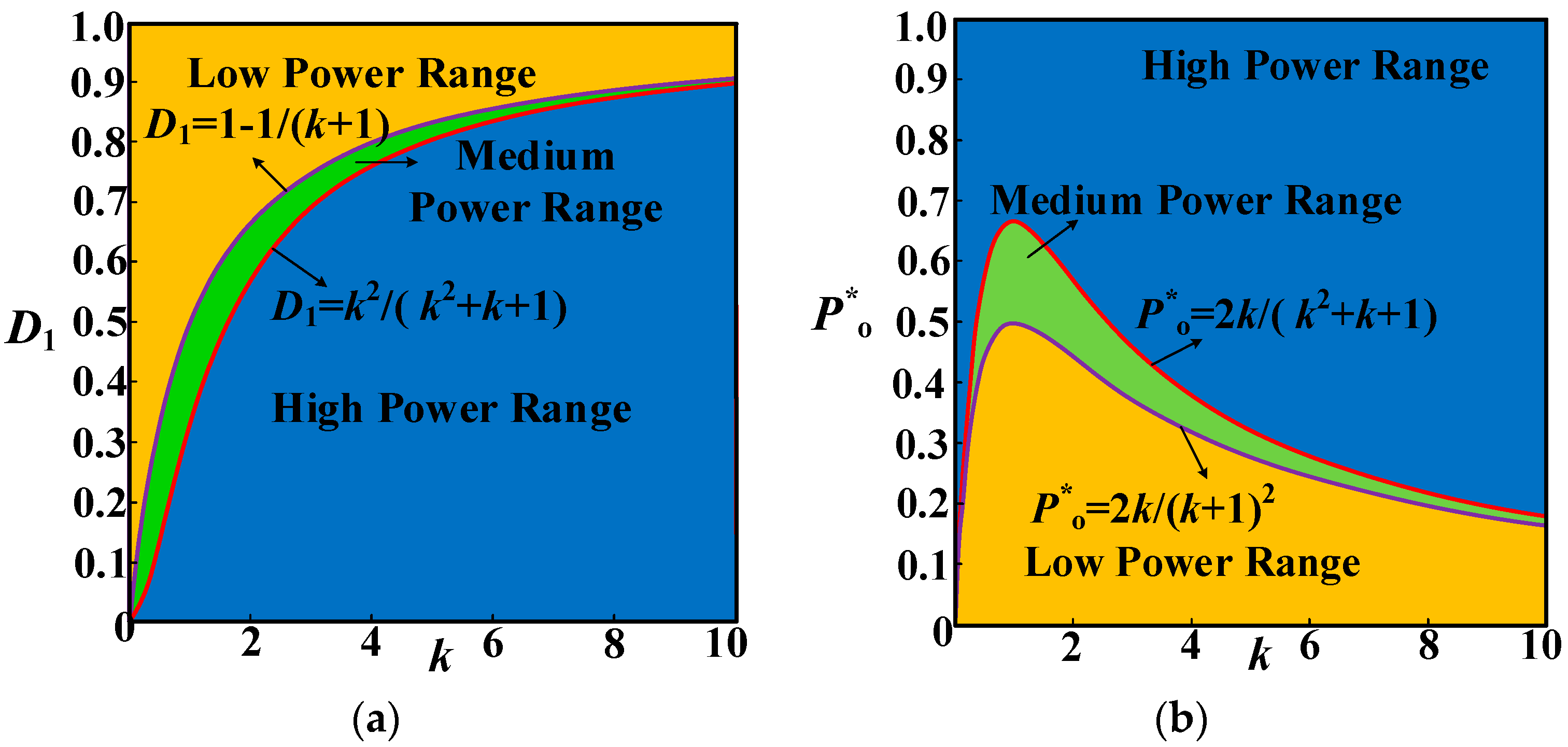



| Low-Power Range | Medium-Power Range | High-Power Range | |
|---|---|---|---|
| Range of D1 | [1 − 1/(k + 1), 1] | [k2/(k2 + k + 1), 1 − 1/(k + 1)] | [0, k2/(k2 + k + 1)] |
| D | D1 | D1 | (1 + ((k2 – k − 1)D1)/k2)/2 |
| D2 | 1 − k + kD1 | 1 − k + kD1 | D1/k2 |
| 0 | 0 | [0, (k3 + 1)/(2k2 + 2k)] | |
| Range of | [0, 2k/(k + 1)2] | [2k/(k + 1)2, 2k/(k2 + k + 1)] | [2k/(k2 + k + 1), 1] |
| Comparison Category | Backflow Power Optimization | Full-Power-Range Optimization | Collaboration with ZVS | Simple Control Interface | Continuity of Results | Unity under Different Voltage Gains | |
|---|---|---|---|---|---|---|---|
| Primary | Secondary | ||||||
| SPS | No | No | / | / | Yes | Yes | Yes |
| Optimal algorithm in [19] | Yes | No | Yes | Yes | No | No | No |
| ICTPS in [29] | Yes | Yes | No | No | No | No | No |
| GMPBC in [30] | Yes | Yes | Yes | No | No | No | Yes |
| DPS-RPS in [31] | Yes | Yes | No | No | Yes | Yes | No |
| Proposed method | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Parameter | Value |
|---|---|
| Input voltage Vin1 | 195–265 V |
| Output voltage Vo1 | 181–266 V |
| Output current io1 | 2.76 A@181 V, 1.9 A@265 V |
| Output ripple current irp | 500 mA |
| Transformer magnetic inductance Lm | 210 μH |
| Transformer turns ratio n | 1:1 |
| Leakage inductance Lr | 60.5 μH |
| Switching frequency fs | 200 kHz |
| Power switch dead time tdead | 100 ns |
| Rated power PN | 500 W |
| Power switches | C3M0120065K |
| Power switch output capacitors Coss | 45 pF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, X.; Li, T.; Huang, Z.; Chen, J. A Collaborative Modulation Method of Dual-Side Backflow Power Optimization and Zero-Voltage Switching for Dual Active Bridge. Energies 2024, 17, 3019. https://doi.org/10.3390/en17123019
Zhang Y, Liu X, Li T, Huang Z, Chen J. A Collaborative Modulation Method of Dual-Side Backflow Power Optimization and Zero-Voltage Switching for Dual Active Bridge. Energies. 2024; 17(12):3019. https://doi.org/10.3390/en17123019
Chicago/Turabian StyleZhang, Yun, Xiaodong Liu, Tong Li, Zhen Huang, and Jinrong Chen. 2024. "A Collaborative Modulation Method of Dual-Side Backflow Power Optimization and Zero-Voltage Switching for Dual Active Bridge" Energies 17, no. 12: 3019. https://doi.org/10.3390/en17123019
APA StyleZhang, Y., Liu, X., Li, T., Huang, Z., & Chen, J. (2024). A Collaborative Modulation Method of Dual-Side Backflow Power Optimization and Zero-Voltage Switching for Dual Active Bridge. Energies, 17(12), 3019. https://doi.org/10.3390/en17123019








