Abstract
Among the existing solar technologies, Concentrating Solar Power (CSP) stands out as the most efficient and adaptable option for base load applications, primarily due to its thermal storage capabilities. However, despite its potential, the implementation of this technology still lacks competitiveness compared to Photovoltaic (PV) systems. Therefore, optimizing the plant components and operational factors becomes crucial for its cost-effective utilization, particularly in the desert regions of Morocco. Hence, the objective of this study comprised two main aspects: first, to conduct a parametric analysis aimed at selecting the optimal configuration for a parabolic trough collector (PTC)-based power plant suitable for the Moroccan context. Subsequently, an environmental analysis was performed to assess the impact of soiling on the plant operation. This step aimed to refine the precision of the techno-economic analysis and enhance the project’s bankability. High-quality in situ meteorological data and soiling measurements were utilized for these analyses. Furthermore, to ensure the reliability of the results, the results from the employed simulation tool were validated against real data obtained from an operational power plant. The results indicate that Morocco holds significant potential for the integration of large-scale CSP plants. A capacity of 1 MW utilizing PTC technology could yield an annual electricity production of up to 33 GWhe, with a levelized cost of electricity (LCOE) estimated at 0.1465 EUR/kWh. However, accounting for soiling effects in the yield analysis, which is recommended for precise yield calculations, revealed a decrease in the annual production to 28 GWhe for the same 1 MW capacity. This reduction represented a 20% loss from the nominal conditions, resulting in a corresponding increase in electricity cost by 30.6 €/MWh.
1. Introduction
Nowadays, fossil fuels are the major source for the satisfaction of global energy needs. Indeed, the combustion of oil, coal and natural gas generates 81% of total primary energy and 66% of electricity. However, fossil fuels have a major role in global warming since they emit greenhouse gases during their processing and combustion [1]. In addition, the worldwide population is expected to increase rapidly to reach 9 billion by 2050, and consequently, energy consumption will rise to 30 TW in 2050 [2,3]. In order to face this challenge, many nations around the world are expanding their energy mix by using more renewable energy sources, and consequently, the worldwide capacity of renewable energy installed in 2019 reached 200 GW, which represents the highest increase [4].
Indeed, CSP technology is predicted to reach an installed capacity of 6.2 GW, which includes an expansion to new markets, with 21 GWh of thermal storage being used in combination with several CSP plants worldwide [4]. This technology, which consists of converting solar irradiance into heat and then electricity, has several promising applications, including hydrogen production [5] and industrial applications [6], which may significantly impact the prices and contribute to decreasing the LCOE.
The average LCOE of CSP plans decreased from 0.346 $/kWh in 2010 to 0.182 $/kWh in 2022, with an increase in the capacity factor from 30% to 45% for the same period due to technological improvement and the availability of high amounts of solar irradiation in the locations where CSP plants are deployed [7]. However, the deployment of CSP plants is considered modest in comparison to other renewable technologies. For instance, solar PV and wind represented 86% of the global addition in 2019 [5], which was due to the high capital investment cost of CSP plants in comparison to wind and solar PV and the fact that CSP plants are only suitable in locations with high Direct Normal Irradiation (DNI), which are mostly located in the sunbelt, like North Africa [8,9]. Nevertheless, CSP technology has tremendous potential for energy production; in fact, 2 ha/MWe of land use in North Africa has the potential to meet many times the energy demand of Europe and the MENA region combined. In addition, CSP plants generate heat at high temperature, which can be used in several industries, such as heating and cooling and the desalination of water, which is particularly interesting since CSP plants are in general installed in arid regions [8]. But the most important advantage of CSP technology over other renewables is the possibility to store high amounts of energy in the form of heat at a relatively low cost, which can be converted into electricity when needed [10]. This can provide reliable power generation, even during night or unfavorable weather conditions, that lead to the improvement of the grid connection and dispatching of such plants, as well as enhancing its capacity factor, which can reach up to 80% [11], and thus its economic competitiveness [8,12].
Indeed, CSP technology has important potential for cost reduction and performance enhancement to be competitive with other renewable energy systems or even conventional power plants [8]. In fact, several parameters should be considered for the installation of a CSP plant in any given location, and one of the most important ones is the optimal plant size according to the local values of the solar resource and the plant thermal storage. In fact, there is a delicate balance when finding the optimal design for the best management of the heat generated and to decrease the LCOE since under-sizing a solar field would result in the power block and the storage system working below their optimal capacity, while over-sizing a solar field would lead to an increase in costs, in addition to the production of more energy than the turbine and the storage capacity, which would lead to significant energy losses [7]. CSP technology uses mirrors to concentrate the Direct Normal Irradiation (DNI); then, the heat collected is transferred and used either for electricity generation via thermodynamic cycles or sent to thermal storage by means of a Heat Transfer Fluid (HTF) [13]. Therefore, the choice of an appropriate HTF is crucial in order to enhance a CSP plant’s performance, as well as leading to a reduction in the LCOE.
In recent years, much research work has been carried out to study the impact of the HTF in CSP plants; for instance, Vignarooban et al. [14] reviewed different types of HTFs, such as molten salts, thermal oils, water, liquid metals, organic fluids, air and other gases. The authors focused on the thermal characteristics of the HTF, as well as its interaction with the pipes and containing materials. Following the same direction, Benoit et al. [15] reviewed the current and future fluids to be used as HTFs in CSP plants, which include two-phase fluids, supercritical liquids, liquids and gases. The results show that at the current stage, liquid- and two-phase-based HTFs, like thermal oil, molten salt and water–steam, can achieve a thermodynamic cycle efficiency in the range of 35–42%, while an efficiency higher than 50% can be reached with new HTFs that are stable at high temperatures (700 °C and above); the candidate HTFs that can achieve this goal are supercritical water, new molten salts, pressurized gases, liquid metals, carbon dioxide and particles.
Sau et al. [16] conducted a techno-economic comparison between two CSP systems that used different HTFs; to this end, the performance of two CSP plants, each with a different heat transfer fluid (HTF), was analyzed. Both plants had a capacity of 50 MWe and 7.5 hours per day of thermal storage.
An investigation of the two plants was conducted for the location of Priolo Gargallo, Sicily in Italy. The results show that the cost of electricity production is practically the same for both HTFs, with a preference for the binary mixture of molten salts since it is more manageable. Xu et al. [17] assessed the entropy generation rate and the Carnot efficiency of five molten salt eutectic mixtures for use as high-temperature HTFs for CSP plants. The findings of this study show that carbonate salts have a higher entropy generation rate. As for the efficiency of the Carnot cycle, they found that carbonate salts have the lowest efficiency, while the efficiency is more or less similar for the other salts. Peiró et al. [18] conducted a comparative study between two HTFs that are extensively used in CSP plants, namely the thermal oil Therminol VP-1 and silicone fluid Syltherm 800. The results show that Therminol VP-1 is a better candidate than Syltherm 800 for a working temperature of up to 400 °C. In the same vein, Conroy et al. [19] investigated the performance of molten salt, liquid sodium and lead–bismuth HTFs in a CSP solar receiver. It was found that a maximum receiver thermal efficiency of approximately 92% could be achieved with sodium and lead–bismuth, whereas this efficiency was slightly lower for molten salt, at around 90%. Polimeni et al. [20] compared between different HTFs for CSP plants using CO2 power cycles. The authors found that an overall efficiency of more than 25% could be reached when using sodium as an HTF, while this efficiency was 24% and 21.5% for KCl-MgCl2 at 750 °C and Solar Salt at 565 °C, respectively.
Another important parameter that highly influences the performance of CSP plants is the climatic conditions. In fact, the most favorable locations for CSP plant installation are arid or semi-arid regions, but these locations are characterized by a considerable amount of dust deposition, which can influence the plant performance; this phenomenon, known as soiling, can cause a drop in the reflectivity of the solar field, leading to considerable energy losses, which have been reported to be around 0.5%/day. This value can vary from one location to another, as soiling is site-specific [21]; in fact, Alami Merrouni et al. [22] found that soiling in Morocco is three times higher than in Portugal, causing increases in the LCOE in Morocco and Portugal from ~0.194 €/kWh and ~0.205 €/kWh, respectively, to ~0.231 €/kWh for both locations.
Accordingly, the aim of this study is to evaluate different scenarios and configurations—based on the Solar Multiple, the thermal storage and the levelized cost of electricity—for the optimization of a 50 MWe CSP power plant based on parabolic trough collector technology for better profitability within the Moroccan context. After that, a detailed yield analysis is conducted to study the behavior of the thermal and electrical performances across a year. Finally, since Morocco has a desert semi-arid climate, the main novelty of this study is the integration of the soiling and dust impact into the techno-economic analysis. The adoption of this approach is very scarce in the literature, and very few are the studies dealing with the integration of this important parameter into the yield analysis. In fact, integrating soiling into the analysis enables the enhancement of the project’s bankability and enhances the economical calculations. This is very important for investors and for policymakers, as it provides realistic project feasibility estimation and thus good rentability for the project.
The results show that the integration of CSP power plants with 7.5 h storage in Morocco can be very beneficial, where the annual thermal production can reach 548 GWhth and 504 GWhth for Ain Beni Mathar and Benguerir, respectively. This can be translated into an electricity production of 168 GWhe and 162 GWhe and an LCOE of 0.1712 €/kWh and 0.1548 €/kWh for both locations, respectively. In addition, soiling can be a major efficiency-limiting factor for the CSP power plants, where the daily reflectivity drop can reach 32% after two weeks of exposition during the dry period of the year. Taking this into consideration, the performance of the simulated power plants decreases significantly, where the annual drop in the thermal and electrical outputs reaches 20% and 17%, which leads to an increase of 20% in the LCOE.
2. Materials and Methods
2.1. Field of Study
As mentioned above, the objective of this paper is to evaluate the performances of five different HTFs and select the most efficient one to be used for the Moroccan climate. To this end, we selected two different sites to conduct our study. The first site is located at Ain Beni Mathar (34°3′50.0″ North, 2°6′0.0″ West)—this site hosts the already operational Integrated Solar Combined Cycle power plant with a solar field gross production of 20 MWe. The second site is located at Benguerir (32°13′17.088″ North, 7°55′44.184″ West), and it hosts a 1 MWe CSP-ORC pilot with Fresnel reflectors. Both sites are characterized by semi-arid climates, and they receive annual DNI values of 2237 and 2299 kWh/m2/a, for ABM and Benguerir, respectively. This makes from them good and representative locations for evaluating the CSP performance in Morocco [23].
To conduct the simulations, ground measurement data from high-performance meteorological stations were used as inputs. These stations measure the three components of solar irradiance separately and provide the data at one-minute steps. The global and the diffuse components (GHI and DHI) were measured using a CMP11 pyranometer provided by Kipp & Zonen (Delft, The Netherlands), which is a secondary standard sensor with a measurement accuracy of 1%. The direct component (DNI) was measured using a CHP1 pyrheliometer installed into a Solys2 solar tracker. This sensor is a first-class sensor with a maximum uncertainty of 2% for hourly totals and 1% for daily totals. We need to mention that the sensors were regularly cleaned to avoid soil accumulation, and they were regularly calibrated using the ISO standards and the WMO standards. Furthermore, the collected data were carefully checked, and their quality was checked using the SERI QC protocol developed by the NREL [24].
2.2. Solar Resource Assessment
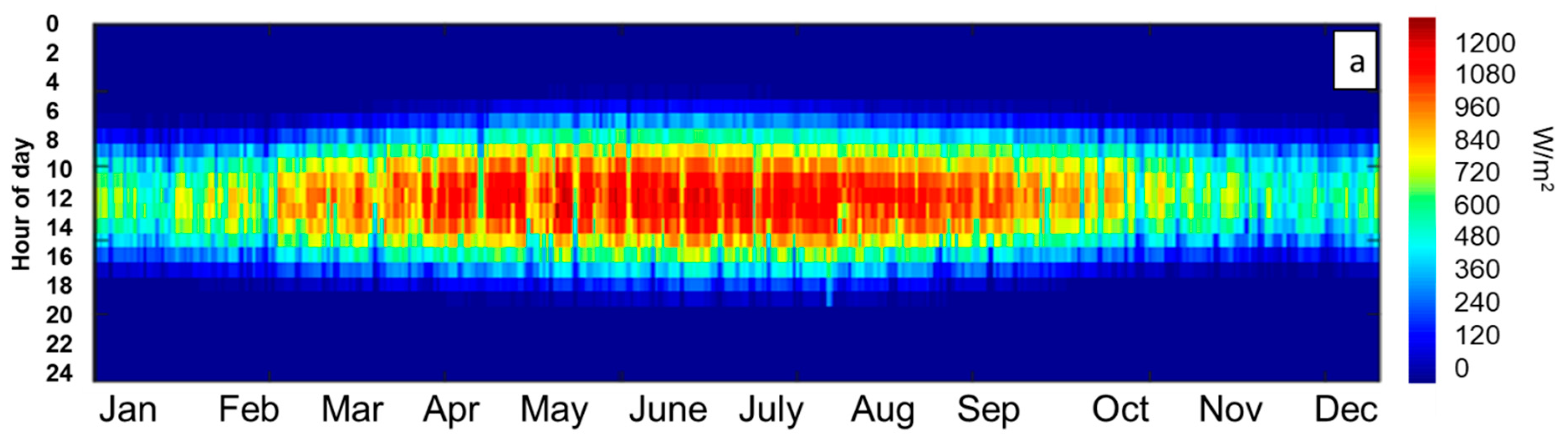
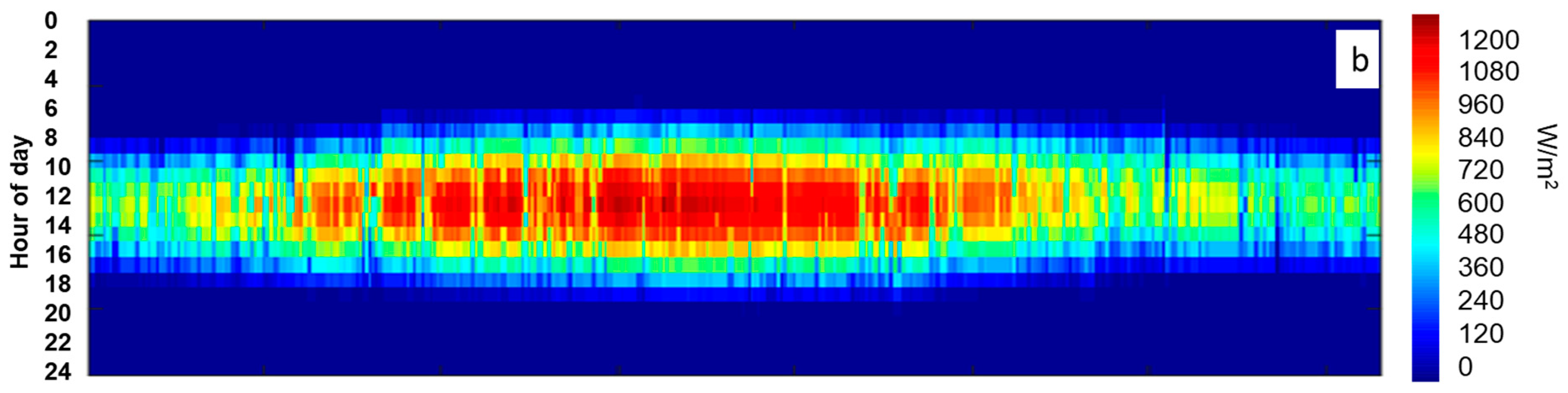
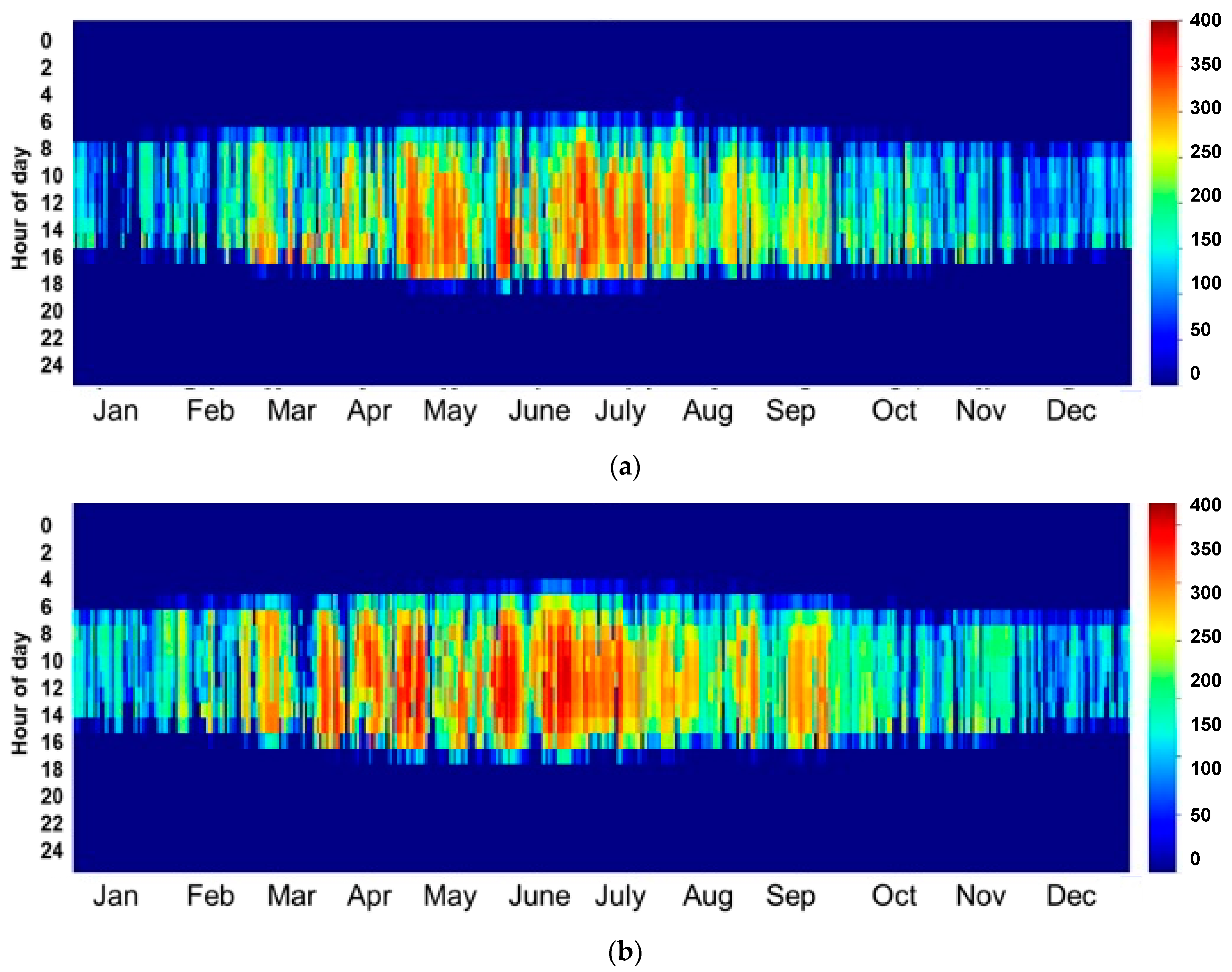
For the bankability of any solar project and to encourage investors and stockholders to invest in CSP power plants, a detailed assessment of the solar resources should be presented, preferably using in situ measurements. In this study and in order to overcome the inter-annual variation, three-year average solar irradiance data were collected from the fields of study and used as inputs for the simulation. One of the standard and most useful presentations of DNI values is a heat map. This configuration provides a clear idea of the distribution of irradiance values over the year. Figure 1 presents a heat map of the three-year average DNI data measured in the two field of study.
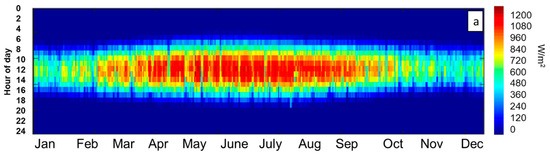
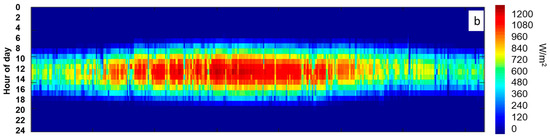
Figure 1.
DNI heat maps: (a) Ain Beni Mathar; (b) Benguerir.
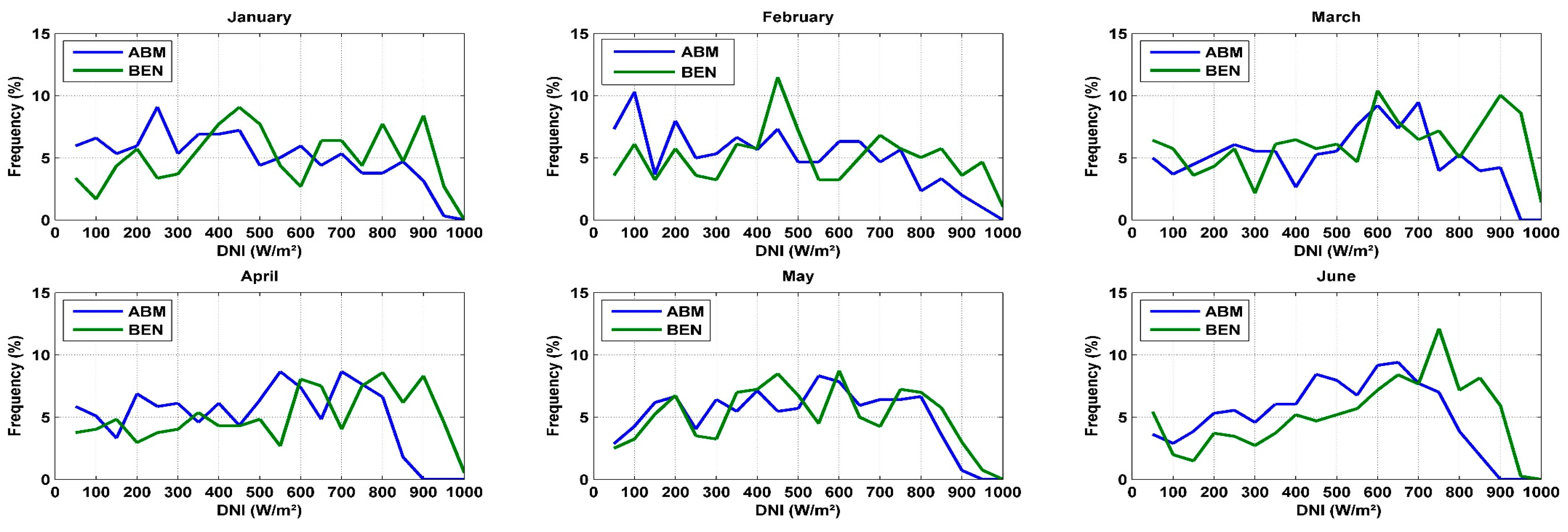
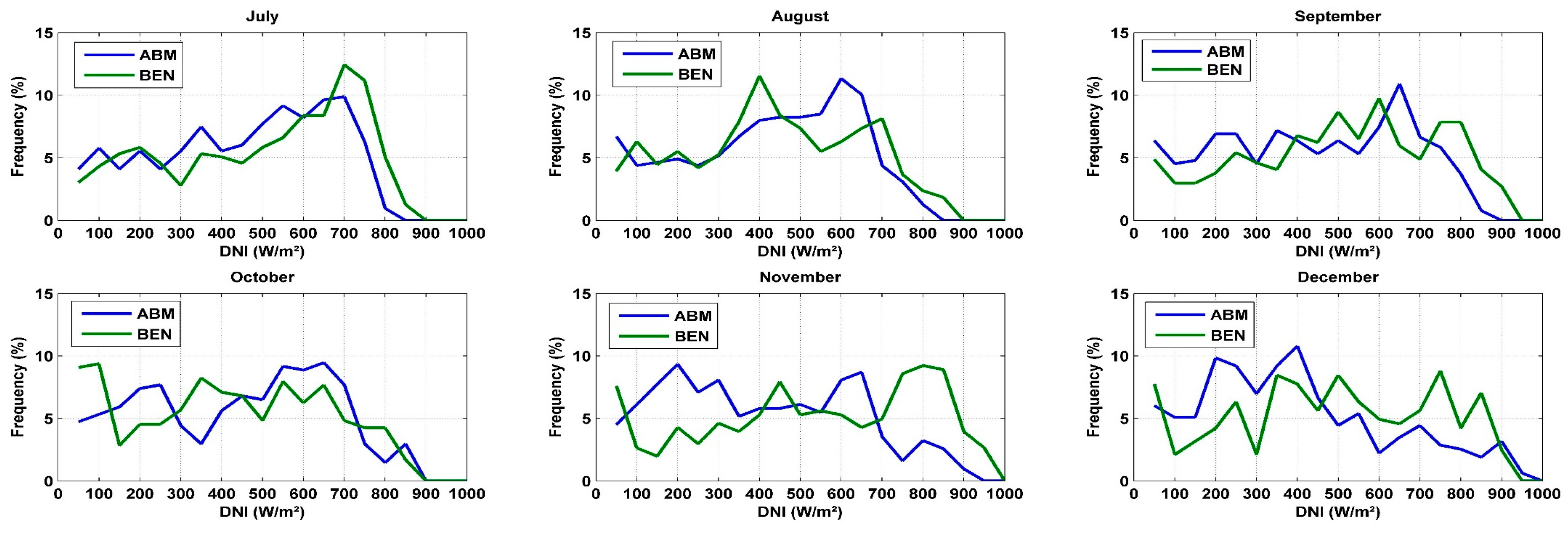
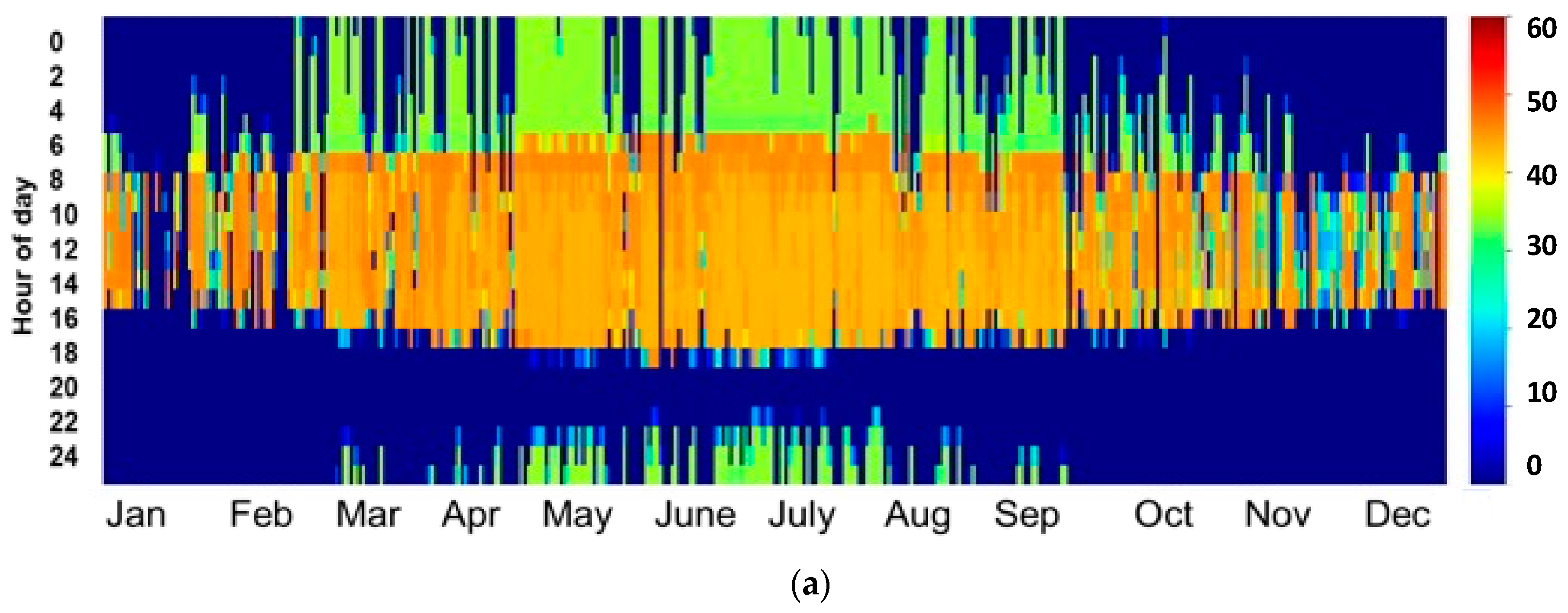
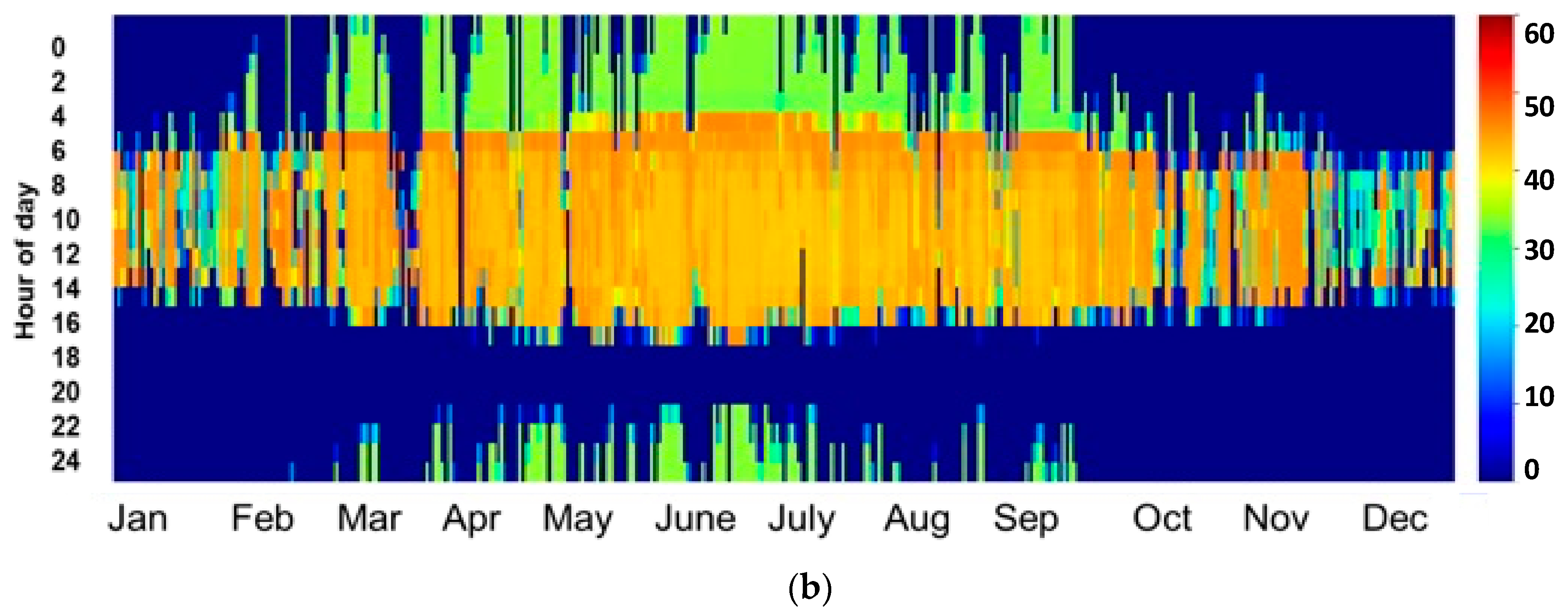
As can be observed, the site of Benguerir is highly irradiated in comparison to ABM, especially during the period from January to July. Nevertheless, both sites can be considered good CSP hosting locations, where DNI values higher than 600 W/m2 (the recommended DNI threshold for CSP applications [25]) are received for at least 6 h (from 10:00 AM to 4:00 PM) during winter and fall. During spring and summer, this period is even longer, and a CSP power plant can produce electricity for at least 11 h (from 7:00 AM to 6:00 PM). For more details about the site capacity production, the plot of the hourly DNI distribution frequency is of high importance. This information can help power plant operators to develop the optimal operation strategies and storage hours. Figure 2 presents the monthly distribution functions of the hourly DNI values for both sites. For a clear presentation, DNI values lower than 50 W/m2 were excluded. As can be illustrated, for the period from January to February, DNI values higher than 600 W/m2 represent 43% of the total daytime values for Benguerir and 32% for the site of Ain Beni Mathar. Similarly, these values present an average of 53.8% and 39.3% for the period from March to May, 44.4% and 34.7% from June to August and 39.4% and 29.7% from September to December for Benguerir and Ain Beni Mathar, respectively. With these values, we can say that the selected sites can be considered suitable for CSP hosting and that they are representative of the Moroccan case. We need to mention that for the MENA region in general and for Morocco in particular, very few are the stations that measure the DNI at the ground level; thus, the solar resource analysis and assessment presented in this section can be considered highly important for researchers and stakeholders interested by solar energy investigation in this region.

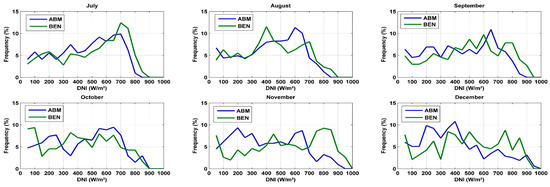
Figure 2.
Monthly distribution function of the hourly daytime DNI values.
In what follows, we will use the irradiance data described above as the input to simulate the capacity production of a 50 MWe CSP plant at both sites. Nevertheless, before moving to the simulation results, the optimization of the plant is required to find the best configuration providing the optimal techno-economic combination.
3. Model Description, Experimental Validation and Plant Optimization
In this study, we used the Greenius software (https://www.dlr.de/en/sf, last access: 6 June 2024) to conduct the simulations. This software, developed by the DLR (German Aerospace Center), is considered one of the best and most common tools used to simulate different renewable energies [26], and it is mainly recommended for CSP applications [27].
To run the simulation, this tool needs the integration of meteorological data files including the direct normal irradiance (DNI), global horizontal irradiance (GHI), diffuse horizontal irradiance (DHI), ambient temperature, humidity, pressure and wind speed. In addition, using a friendly interface, Greenius enables users to assemble their power plant by composing and choosing the collector type, the storage capacity, the solar field assembly and the power block nominal power and cooling mode. Another powerful aspect in this tool is the economical calculations, where the user can add or modify the different OPEX and CAPEX parameters to calculate the levelized cost of electricity (LCOE). To simulate the amount of solar energy collected and the power production, the software uses the following equations:
The main parameter to be calculated is the amount of energy collected by the field; thus, the energy balance is given as:
where is the energy absorbed by the field, whereas is the portion lost of the total energy . can be calculated depending on the direct normal irradiance, incidence angle modifier , optical efficiency , mirror cleanness , incidence angle , shadowing factor and end-loss factor . Furthermore, the incidence angle modifier is a function of the incidence angle given as follows:
Thus, the incidence angle is defined as follows:
where is the declination angle, is the zenith angle and the hour angle.
The optical efficiency is determined by multiplying the collector reflectance by the receiver absorbance, the transmittivity based on the reflection–refraction of beam radiation and the intercept factor:
The shadowing and end-loss factors are given as follows:
where is the distance between two parallel collectors, A is the width of the collector and is the collector focal length.
Regarding the energy losses , they are defined as the sum of the geometrical losses of the collector and the convective losses from the pipe :
and are determined as follows:
is the receiver area, is the thermal loss coefficient, is the ambient temperature, is the pipe temperature and is the difference between the heat transfer fluid and the ambient temperature.
3.1. Model Validation
Having presented the governing equations and described the simulation tool, we have arrived at the point where we need to validate the used software. To this end, we used real data collected from the Integrated Solar Combined Cycle (ISCC) power plant at Ain Beni Mathar (see Figure 3).

Figure 3.
The Ain Beni Mathar ISCC power plant.
This power plant takes up around 183.120 m2 of land use. It has a total production capacity of 452 MW, with a share of 20 MW produced by the solar field. The latter is based on parabolic trough technology, where 224 Solar Collector Assemblies (SCAs) are spread throughout 56 loops. These collectors focus the solar irradiance onto the absorber tubes to heat the working fluid, Therminol VP-1 for the studied ISCC plant.
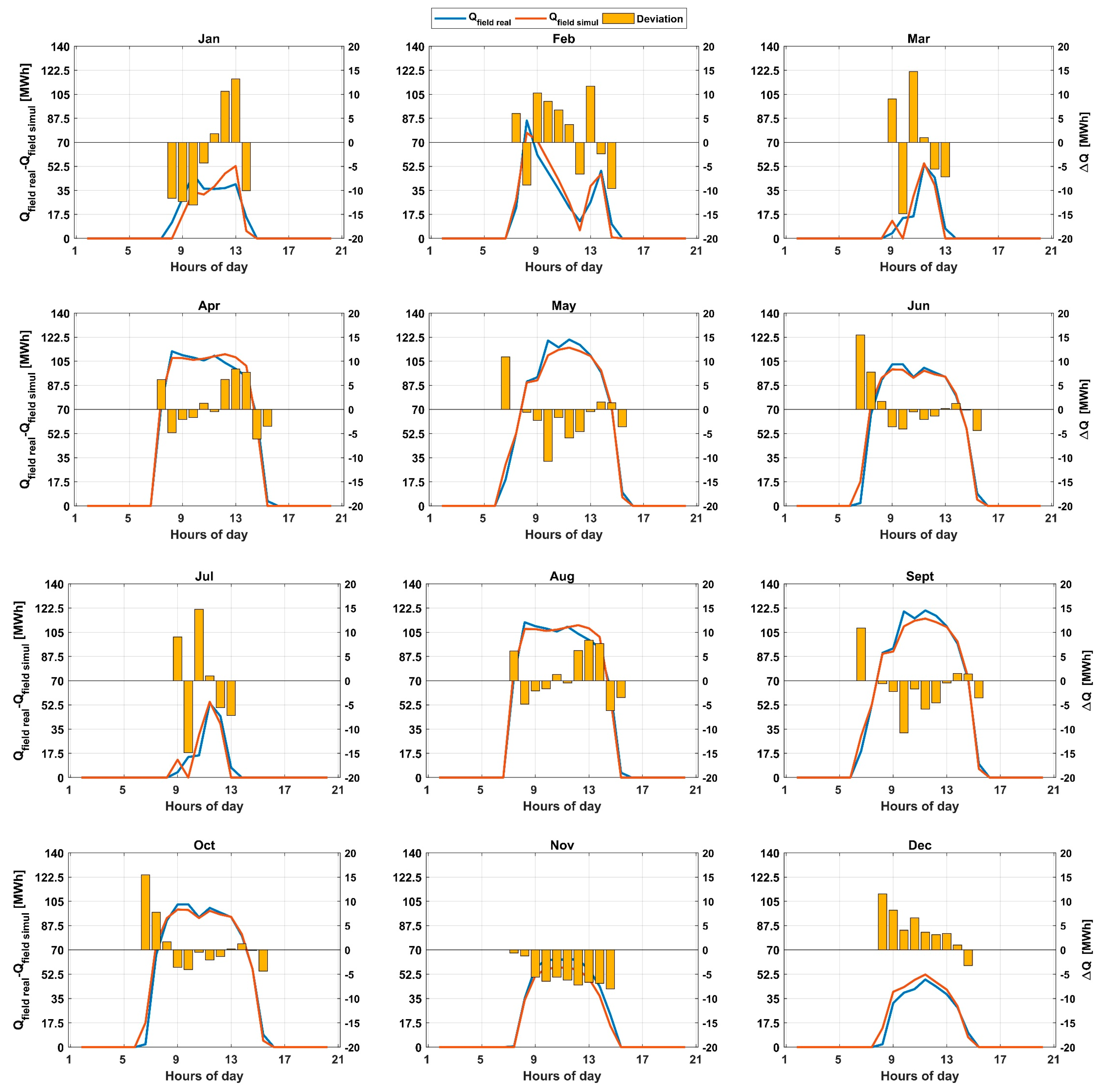
Returning to our original goal, to validate the used simulation tool, we selected 12 days (1 from each month) where the solar field was focused for the entire day, and we compared the thermal output from the simulation tool and the real measured data in situ. The deviations and validation results are denoted in Figure 4.
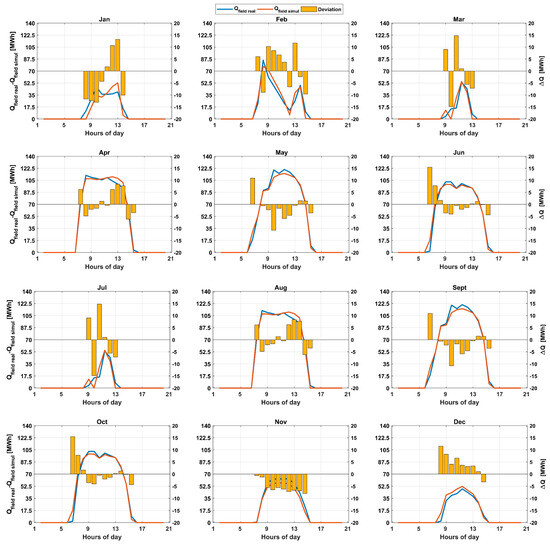
Figure 4.
Validation of the simulation tool.
As can be noticed, the average daily deviation between the simulated and real thermal production is less than 5 MW. This value is acceptable, and it is mainly derived from the first and last operation hours. Indeed, in the running power plant, the integration and defocusing of the solar depend on different technical parameters, which are not included in the software, hence why the errors are higher during these periods. Nevertheless, under regular operation conditions, the error of the simulation tool can be considered very low, especially during periods with high DNI values. For instance, in June, the deviation between 10h00 and 13h00 varies between 3.7 and 0.2 MWh with an overestimation of the simulated values. But we can say that the used simulation tool is well validated and it provides a good platform for simulating the yield of CSP power plants.
3.2. Case Study: Andasol
In the current study, we will simulate a 50 MW CSP power plant similar to Andasol 1, already operational in Aldeire Granada, Southern Spain. This power plant is parabolic-trough-collector-technology-based with a two-tank storage system that produces electricity for up to 7.5 h after sunset. Furthermore, it is one of the first demonstration sites for CSP in the Mediterranean region, and this configuration is well trusted by stakeholders. So, if a project with similar technology is considered, it will be easily bankable [28], and that is why we have chosen to use this configuration in the current study. The technical details of the 50 MWe power plant are summarized in Table 1.

Table 1.
Technical details of the reference plant.
3.3. Economical Parameters
One of the most important metrics for CSP plant performance evaluation is the levelized cost of electricity (LCOE). This parameter offers a clear idea about a plant’s total component prices, as well as its efficiency in any particular area, therefore allowing comparisons between various configurations, technologies and/or locations. To compute the LCOE, the following equation is used:
where is computed using Equation (11):
Eprod represents the annual electricity production, is the capital recovery factor, n is the project lifetime and d is the interest rate. The costs are composed of the investment Ci, operation and maintenance CO&M, replacement cost CR, fuel cost CF and taxes CT. The investment expenses consist of the solar field (including the HTF), power block (including the turbine, generator and balance of the plant), thermal storage and land. The O&M expenses evaluated include general O&M (labor), replacement and insurance. For the MENA area, these assumptions are identical to those reported by IRENA in their report on CSP cost estimations [5] (see Table 2).

Table 2.
Main economical inputs for the reference power plant.
We need to mention that to calculate the LCOE of a CSP power plant while considering the soiling impact, the difference will be based on the amount of electricity produced, which is highly impacted by this factor, as it affects the optical properties of the solar field and thus the thermal and electrical performances. More details about the soiling impact are presented in Section 4.
3.4. Power Plant Sizing and Optimization
This section will be dedicated to providing the optimal design for the 50 MWe plant with a wet cooling configuration if installed in our chosen areas of study. In reality, based on the climatic data inputs for each site, the Solar Multiple (field size), LCOE and thermal storage capacity should be adjusted to find the most optimal plant configuration. To this end, several simulation runs have been conducted in order to fill up a 2D LCOE matrix (see Table 3). In fact, for each simulation run, we fix the value of the Solar Multiple, and we increment the storage capacity using steps of 1.5 h. The values of the LCOE from each simulation run lead to filling one column of the matrix. After that, a similar procedure must be followed for the remainder of the columns by incrementing the SM by 0.25, which entails raising the SM by 0.25 from 1 to 3. The simulated results are shown in Table 3.

Table 3.
The 2D LCOE matrix for Ain Beni Mathar and Benguerir.
After completing the 2D LCOE matrices, the next step is to determine the optimal configurations for our field of studies based on the SM, the LCOE and TES. From an economic standpoint, the configuration with the lowest LCOE value should be the best one. Nonetheless, from a technical point of view, CSP power plants with a nominal capacity of 50 MWe are worked towards for base or intermediate loads; hence, large TES capabilities are required [29].
For this reason, the optimal configuration is the one providing a compromise between a low LCOE and a high storage capacity. Thus, for Ain Beni Mathar, a TES = 7.5 h and an SM = 2.5 is the optimal configuration, while the one for Benguerir has a TES = 7.5 h and an SM = 2. These combinations result in LCOEs of 0.1736 €/kWh for Ain Beni Mathar and 0.1566 €/kWh for Benguerir, respectively, and these are the ones that will be used in the rest of this study.
3.5. Heat Transfer Fluid Descriptions
To increase the efficiency of the CSP power plants, the HTF is one of the components that needs to be investigated. Different HTFs exist on the market, but not all of them are suitable for all climatic conditions. Thus, the selection of the best HTF remains important to increase a plant’s thermal and electrical output and to decrease its LCOE. In the present work, five HTFs are used for the techno-economic simulation. The HTF technical specifications are described in what follows:
3.5.1. Therminol VP-1
Therminol VP-1 is a synthetic oil composed of a blend comprising 73.5% diphenyl oxide C12H10O) and 26.5% biphenyl (C12H10) [30]. Renowned for its exceptional thermal stability and low viscosity, this HTF is adept at fulfilling the steam requirements within the temperature range of 257 °C to 400 °C. However, it is essential to note that in colder climates, close monitoring of VP-1 is imperative to prevent potential operational issues [31].
3.5.2. DOWTHERM A
DOWTHERM A comprises a blend containing 73% biphenyl oxide (C2H10O) and 27% biphenyl (C2H10), operating with identical vapor pressures. As a result, the mixture can be treated as a single compound [32]. This heat transfer fluid (HTF) boasts a freezing point of 15 °C and is utilized to operate systems under two conditions: (i) in the liquid phase, with temperatures ranging from 15 °C to 400 °C, or (ii) in the vapor phase, with temperatures between 257 °C and 400 °C.
3.5.3. Hitec-Salt
Hitec-Salt is a salt mixture comprising three components, sodium nitrate (NaNO3), potassium nitrate (KNO3) and sodium nitrite (NaNO2), with proportions of 7, 53 and 40 mol%, respectively [33]. The primary advantage of this heat transfer fluid (HTF) lies in its capacity to function at atmospheric pressure within the temperature range of 150 to 550 °C [34]. Additionally, Hitec-Salt exhibits a freezing point of 142 °C, necessitating cautious handling, particularly in regions characterized by low ambient temperature conditions.
3.5.4. Solar Salt
Similar to Hitec, Solar Salt comprises sodium nitrate and potassium nitrate at a ratio of 60% NaNO3 and 40% KNO3. This HTF is capable of achieving output temperatures of up to 600 °C. Furthermore, it is distinguished by its favorable heat exchange coefficient and high density. Additionally, Solar Salt is regarded as a cost-effective alternative compared to thermal oils. However, the utilization of this salt entails certain drawbacks, notably its high melting point of 240 °C [35].
3.5.5. Syltherm 800
This HTF is a silicone polymer renowned for its outstanding stability, although with a slight tendency to clot at elevated temperatures and under specific operating conditions [36]. Moreover, it exhibits remarkable durability, capable of lasting for more than 10 years when continuously operated within its recommended maximum temperature range of −40 °C to 400 °C. Syltherm 800 is essentially odorless and is recognized for its low toxicity [18].
3.6. Selecting the Best Heat Transfer Fluid
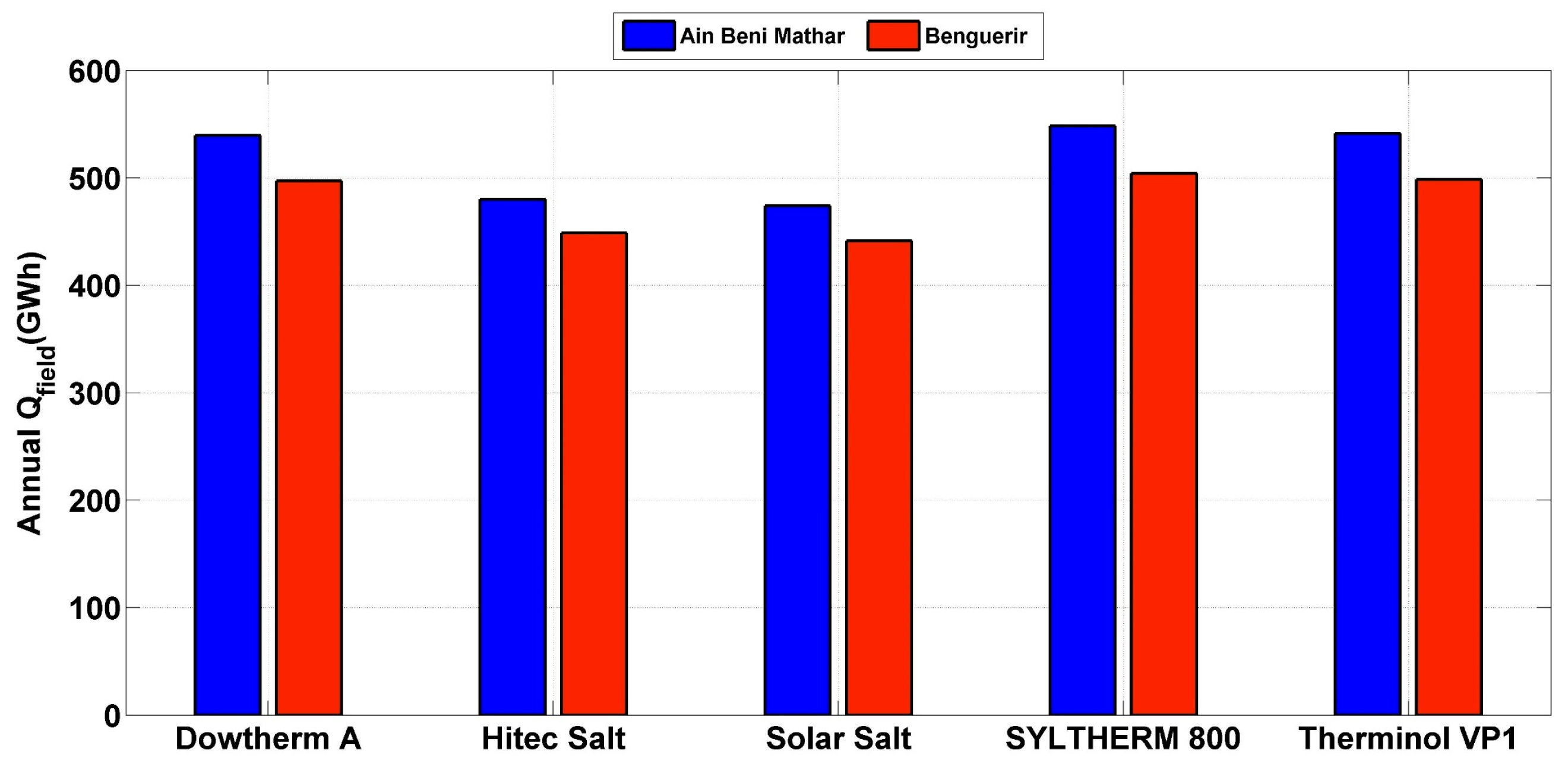
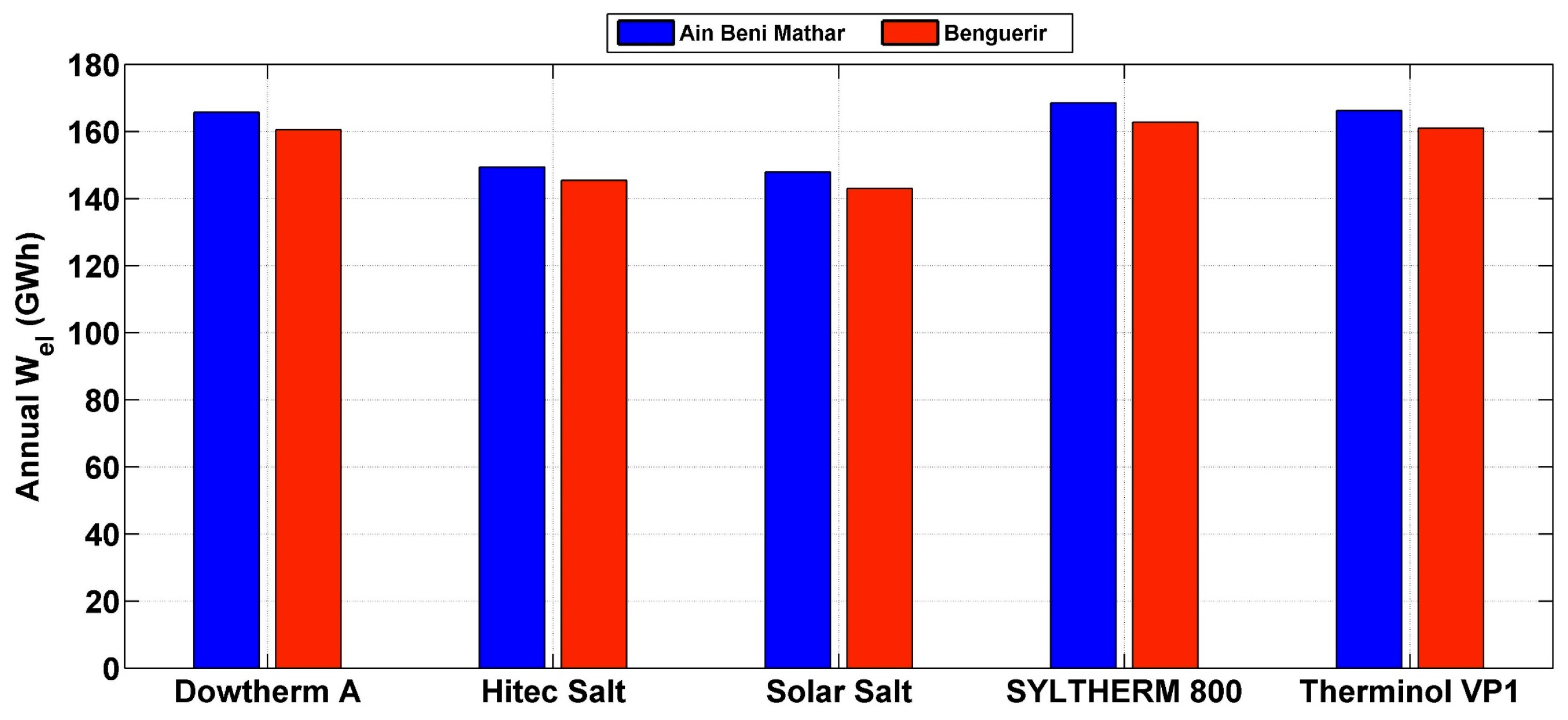
To select the optimal HTF, comparisons will be conducted based on annual thermal and electrical outputs, as well as the LCOE. Figure 5 illustrates the yearly thermal output of the 50 MW solar plant operating in the climates of Benguerir and Ain Beni Mathar, utilizing the above-described HTFs. Notably, Syltherm 800 emerges as the most favorable HTF at Ain Beni Mathar, boasting an annual thermal production of 548 GWh, followed closely by Therminol VP-1 with 541 GWh and Dowtherm A with 539.49 GWh. Conversely, Hitec-Salt and Solar Salt exhibit the lowest thermal production. This performance ranking remains consistent for electricity production (Figure 6), with Syltherm 800 leading the pack at Ain Beni Mathar with an annual production of 168.6 GWh, surpassing Therminol VP-1 and Dowtherm A by 2.4 GWhe and 2.9 GWhe, respectively. Similarly, at Benguerir, Syltherm 800 remains the preferred choice, enhancing the annual thermal and electrical productions of 504.2 GWhe and 163 GWhe, respectively. This preference is attributed to Syltherm 800’s broad working temperature range, low melting point and high thermal stability.
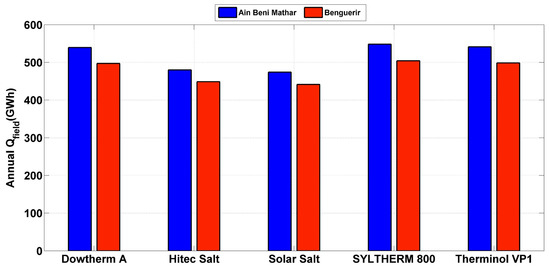
Figure 5.
Yearly thermal outputs for all HTFs at Ain Beni Mathar and Benguerir.
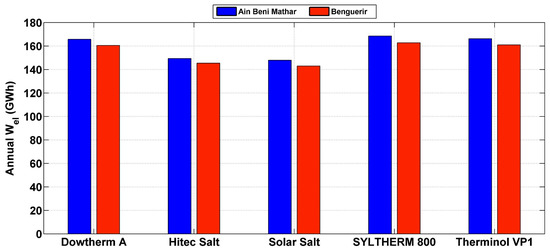
Figure 6.
Yearly electrical outputs for all HTFs at Ain Beni Mathar and Benguerir.
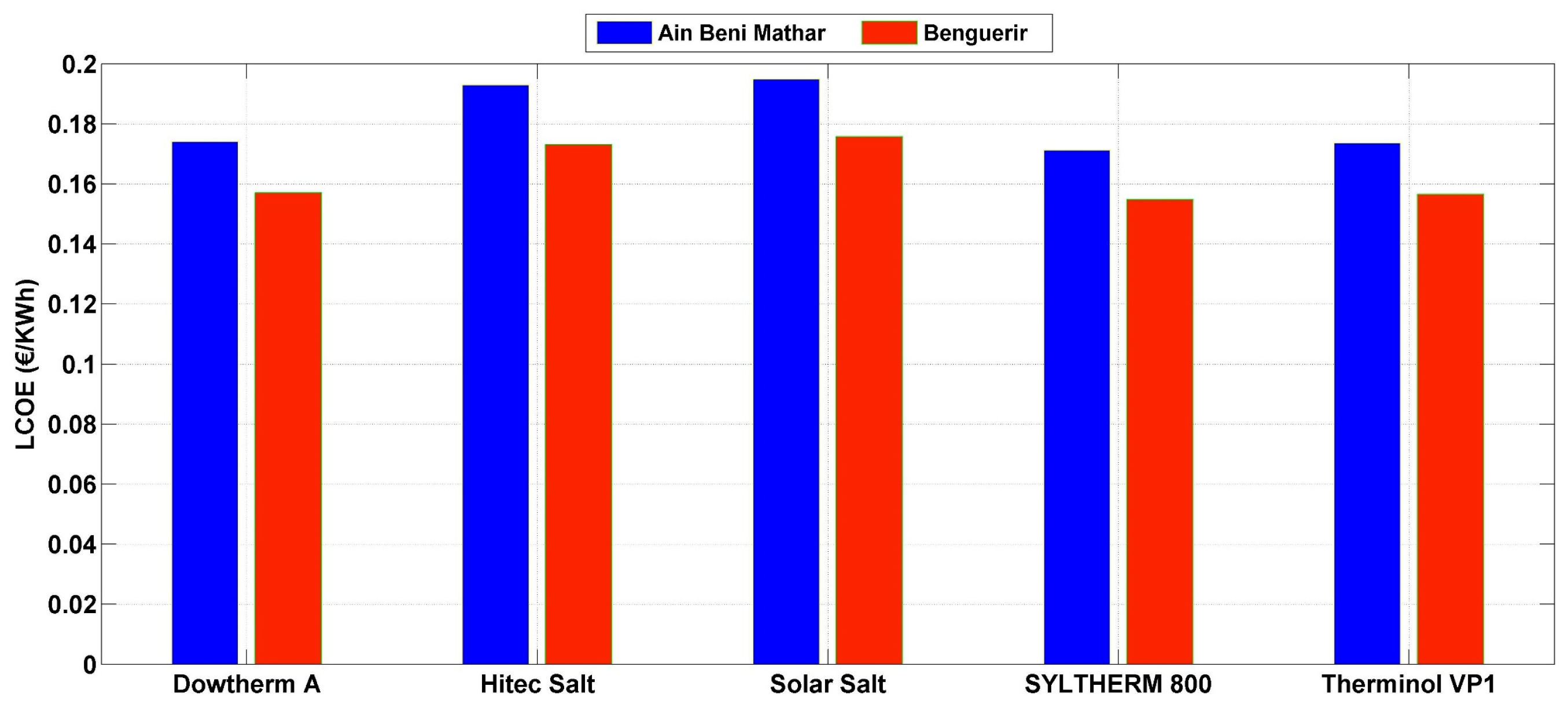
Furthermore, from an economic standpoint—as depicted in Figure 7—Syltherm 800 also emerges as the optimal choice for both locations, with costs of 0.1712 €/kWh for Ain Beni Mathar and 0.1548 €/kWh for Benguerir. Hence, Syltherm 800 emerges as the most suitable working fluid for the Moroccan climate and will be utilized in the subsequent operations.
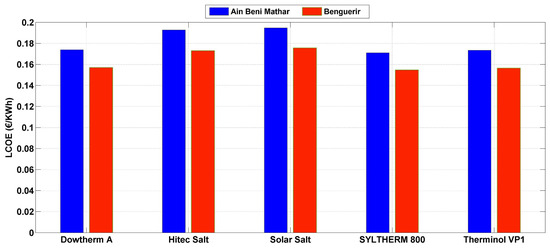
Figure 7.
LCOE for all HTFs at Ain Beni Mathar and Benguerir.
We need to highlight that Greenius software already has libraries including the different HTF types with all their parameters, including those provided by the manufacturers. Furthermore, to simulate the thermal properties, the simulation tool used empirical and semi-empirical models that have been validated.
4. Results and Discussion
After optimizing the solar field and selecting the most efficient working fluid, this section will be dedicated to presenting the simulation results describing the performances and yield of the optimized power plant in the two selected locations.
4.1. Yield and Performance Analysis
Figure 8 presents the hourly distributions of the thermal outputs across a year. The considerable solar energy received by both locations ensures excellent performance, particularly during summer. In fact, Ain Beni Mathar’s hourly thermal output reaches 360 MWhth, whereas in Benguerir, it is approximately 300 MWhth.
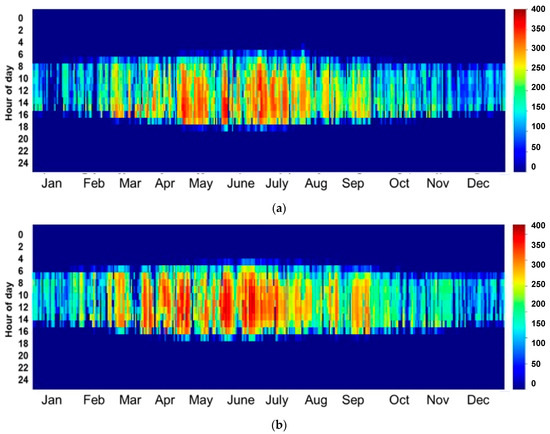
Figure 8.
The thermal outputs across the year in MWhth: (a) Ain Beni Mathar, (b) Benguerir.
During summer, more than 9 h of thermal production with high performance is possible, allowing an electricity production in nominal conditions, as well as a full storage tank for energy supply beyond sunset.
Figure 9 presents the hourly charging (in orange) and discharging cycles (in green) of the power plants in both locations. As can be observed, for both locations, the thermal storage system is very reliable, where it can keep the plant injecting electricity into the grid for up to 9 h (from 19:00 to 5:00) after sunset at Benguerir and up to 8 h (from 19:00 to 5:00) after at Ain Beni Mathar.
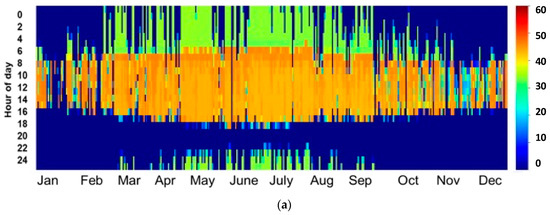
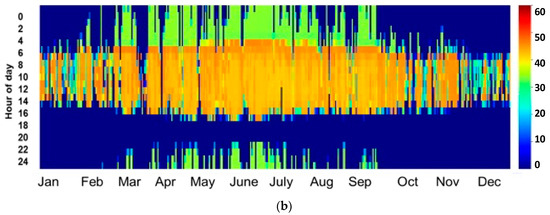
Figure 9.
Hourly charging and discharging cycles of the thermal storage system (Orange charging rate, green discharging rate; (a) ABM, (b) Benguerir).
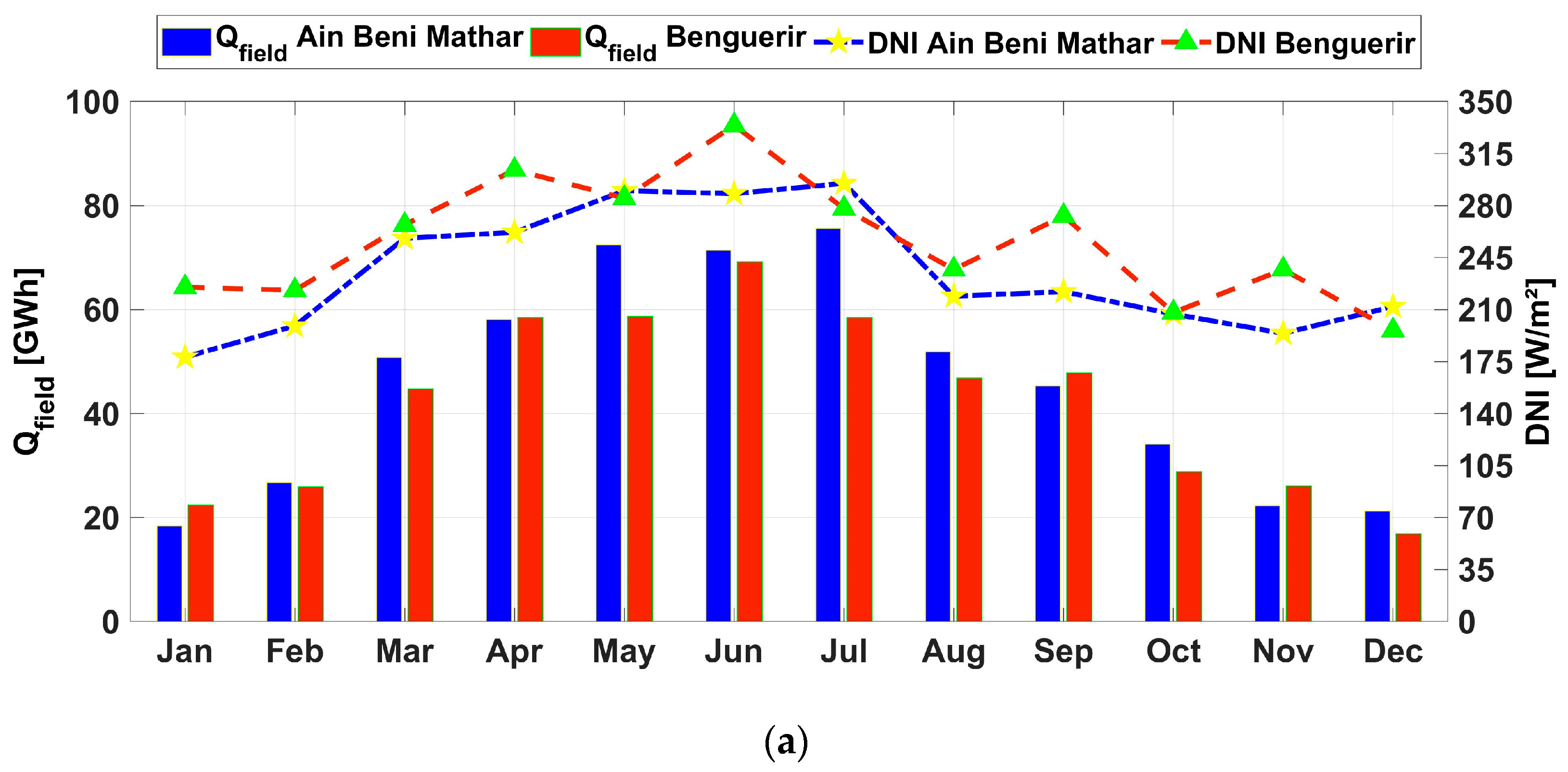
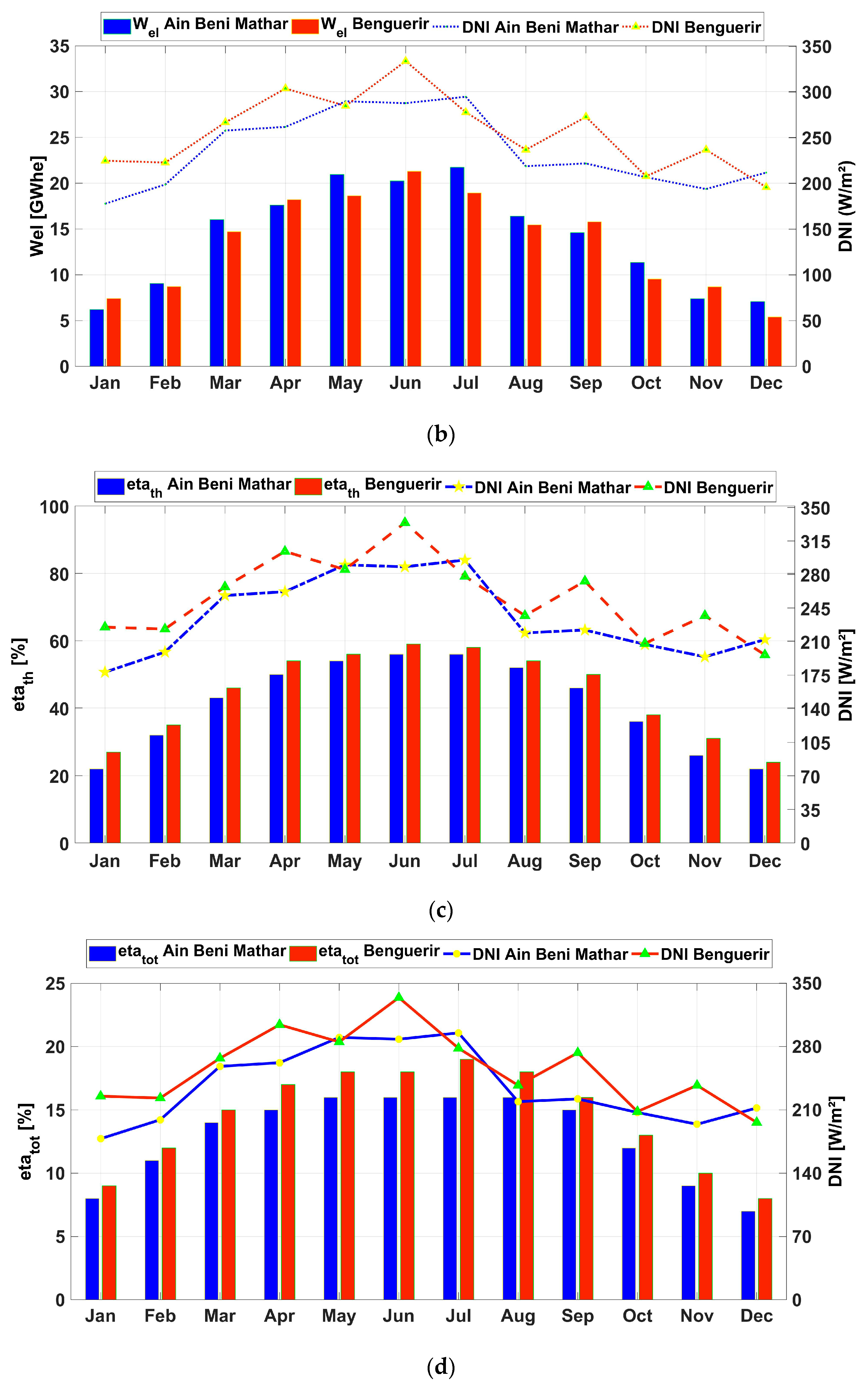
For more details about the performance of the investigated plant configuration, the monthly values of the thermal and electrical outputs are presented, together with the DNIs and the efficiencies in Figure 10. As shown in Figure 10a,b, June was the most irradiated month in Benguerir, with values reaching 334 W/m; this led to a peak in the thermal output of 70 GWh and an electrical output of 21.3 GWhe. For Ain Beni Mathar, the highest DNI values are recorded during July, with a DNI value reaching 295 W/m2, resulting in thermal and electrical generation of 75 GWh and 21.6 GWhe, respectively. The thermal and total efficiencies are illustrated in (Figure 10c,d). As can be noticed, the thermal efficiency at Benguerir is higher than the one at ABM, with the maximum values reaching 58% for Benguerir in June and 56% for Ain Beni Mathar during July. Similarly, the total efficiency reaches its max during June at Benguerir and during July at ABM, with values of 19% and 16%, respectively.
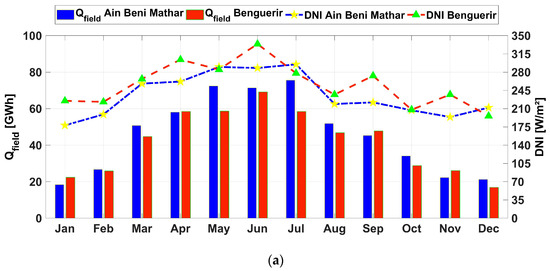
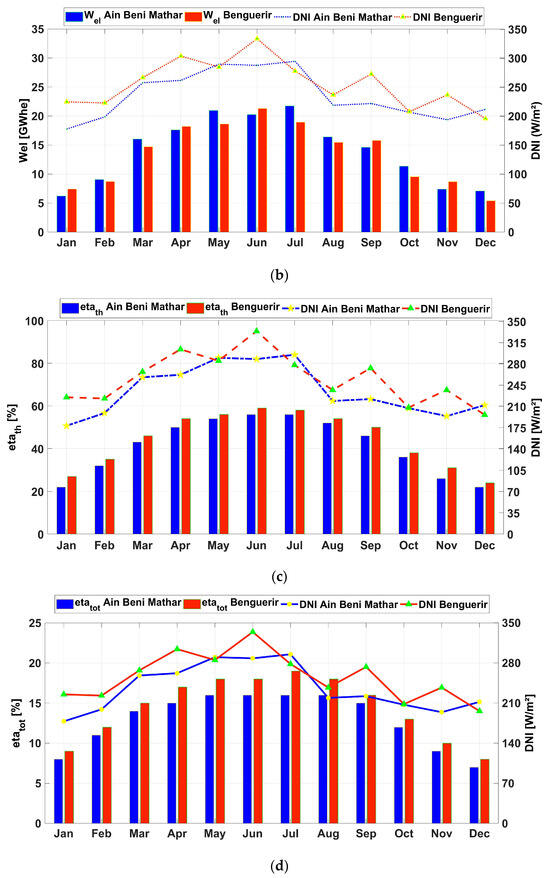
Figure 10.
The monthly values of the (a) thermal and (b) electrical outputs, (c) thermal efficiency and (d) total efficiency are presented together with the DNI.
4.2. Soiling Effect
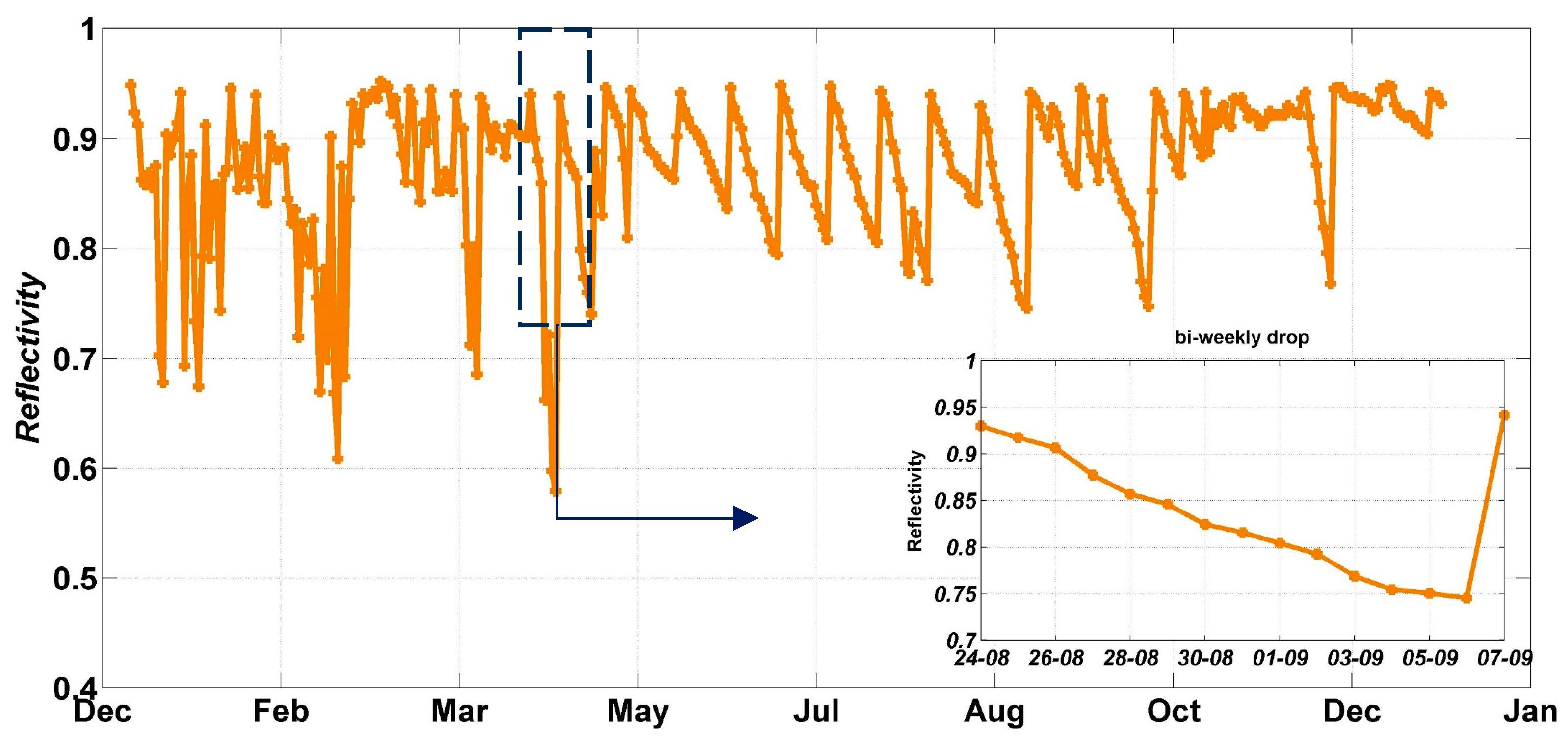
To have a realistic evaluation of the CSP yield, the impact of the environment, mainly soiling, needs to be assessed [22,37,38,39,40]. For this reason, a soiling measurement campaign has been conducted for a one-year period to evaluate the degree of the reflectivity drop due to soiling. We need to mention that due to a shortage of logistical support, the experiment was conducted only at the site of Benguerir. To measure the reflectivity, the TraCS sensor was used (see Figure 11). This sensor measures the reflectivity by dividing the reflected DNI values from the mirror over the ones coming directly from the Sun. For more details about the TraCS operation, please refer to [41]. Figure 12 presents the daily reflectivity values; as can be noticed, the drop in the mirror reflectance is considered high, where it can reach 38% even with the application of a 2-week cleaning schedule to reset the mirror reflectivity and to avoid soiling saturation [42]. But generally the drop after 2 weeks of exposition is around 20%, which is still considered high.

Figure 11.
TraCS sensor used for measuring the mirror reflectance–soiling impact.
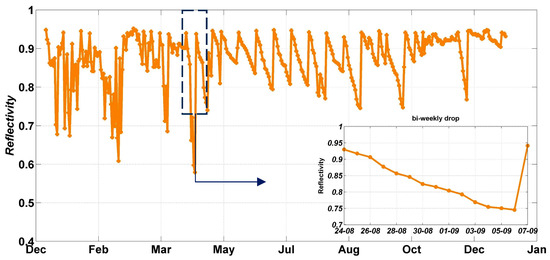
Figure 12.
The daily reflectivity measurements at Benguerir.
To assess the influence of dust on the yield, two simulations were conducted, with the first one not including the reflectivity measurements, which will be referred to as the clean scenario. Meanwhile, the second includes the reflectivity measurements, and it will be referred to as the soiled scenario.
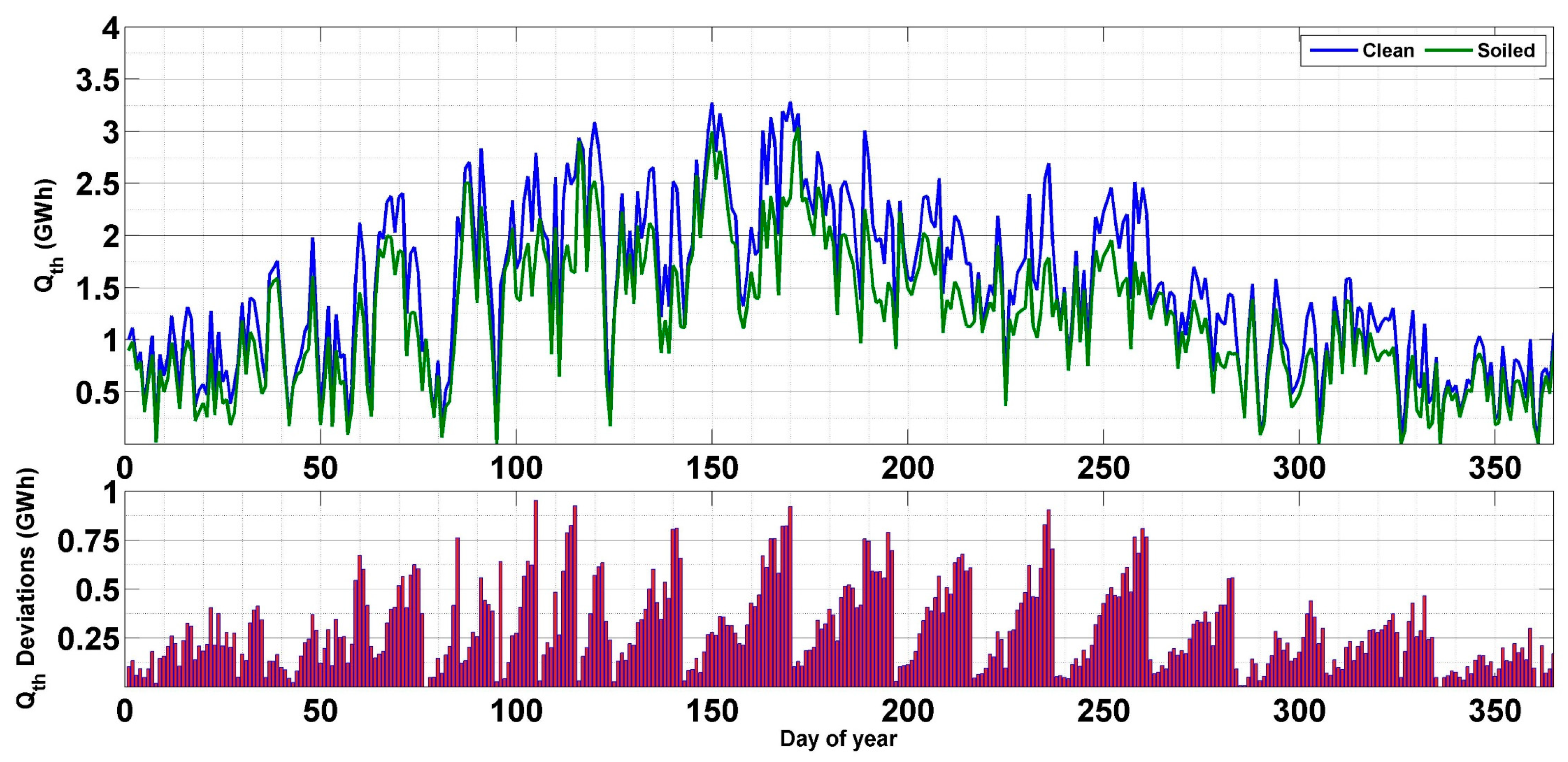
Figure 13 presents the daily thermal outputs for the two scenarios, together with the deviations between the production of the clean and soiled fields. As can be noticed, the daily difference between the thermal output of the two scenarios is very considerable, especially during the dry period of the year. In fact, during spring and summer, the daily deviation can reach 0.8 GWhth after two weeks of exposition without cleaning. Nevertheless, during fall and winter, the drop in the thermal performance due to soiling can reach 0.25 GWhth. This is completely reasonable since this period of the year is known for high rainfall values (which can be considered a natural cleaning agent) and low aerosol activity [43].
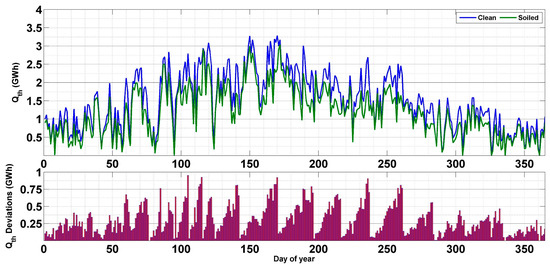
Figure 13.
The impact of soiling on the thermal performance.
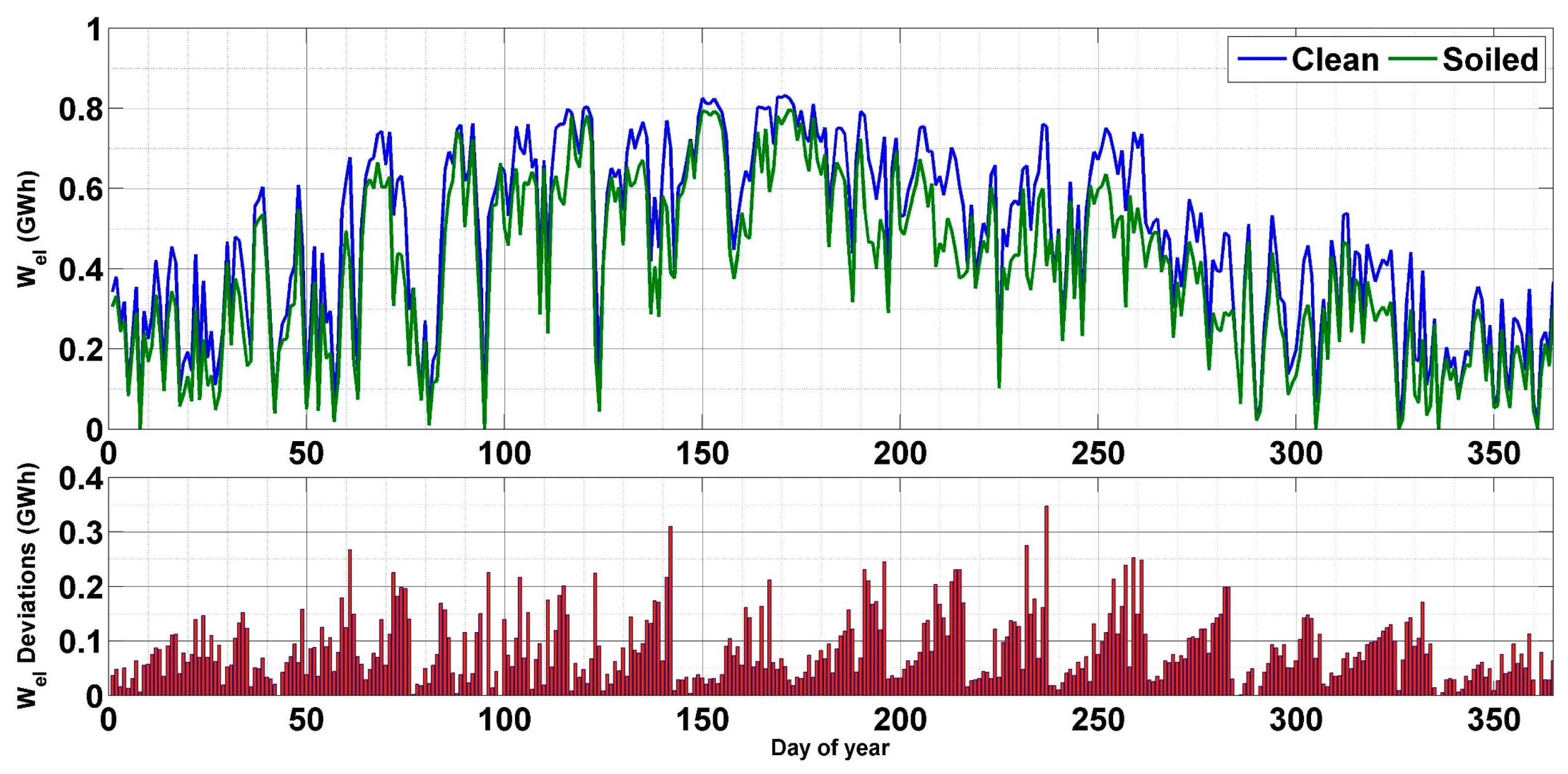
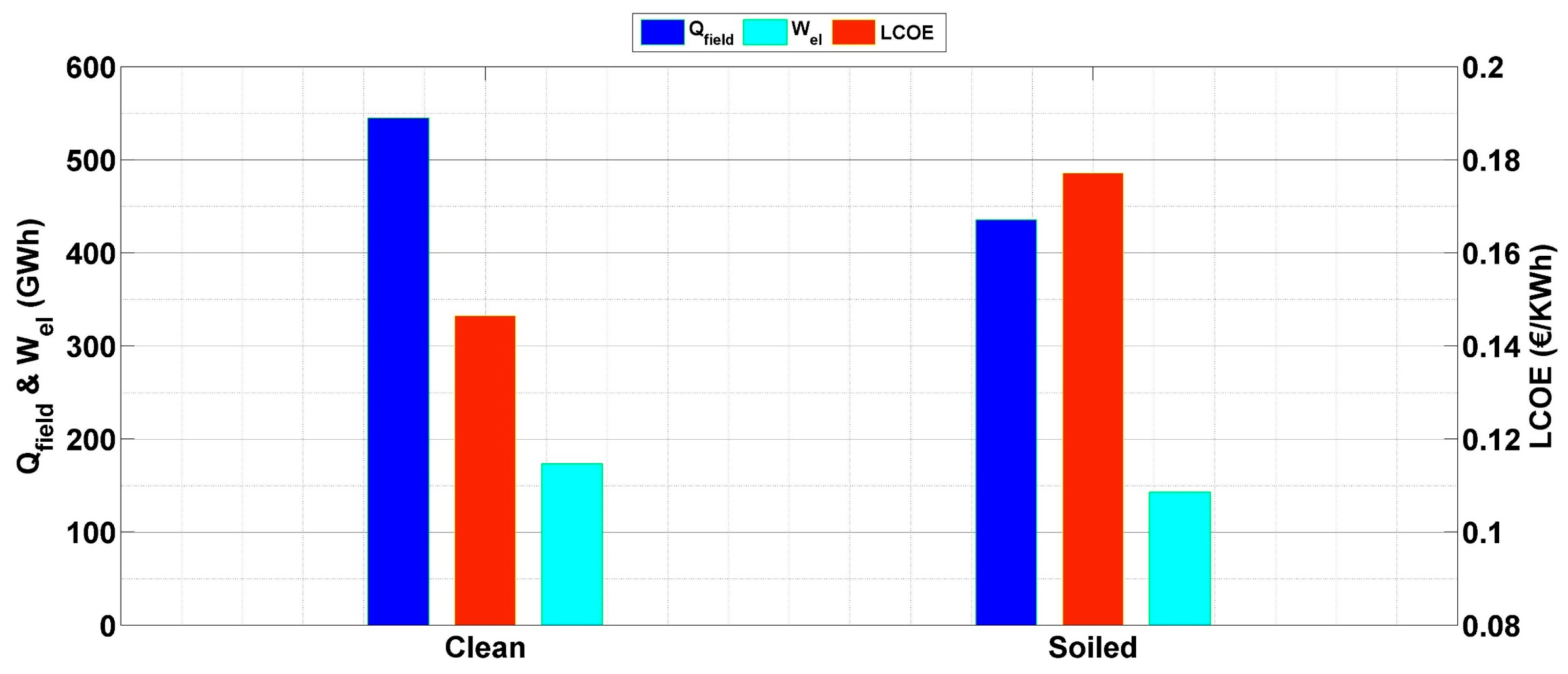
Similarly, the electrical production of the solar plant is highly affected by soiling, where the daily losses can reach 0.35 GWhe after 2 weeks of exposition during summer, and they reach 016 GWhe during fall; see Figure 14. To better evaluate the impact of soiling on both the thermal and electrical output, the annual production in both the clean and soiled scenarios is presented in Figure 15. As illustrated, more than 100 GWhth of thermal production was lost due to soiling deposition during the year. This represents about 20% of the total thermal output. Meanwhile, the yearly electrical losses due to soiling are around 30.3 GWhe, i.e., 17% of the total electricity production.
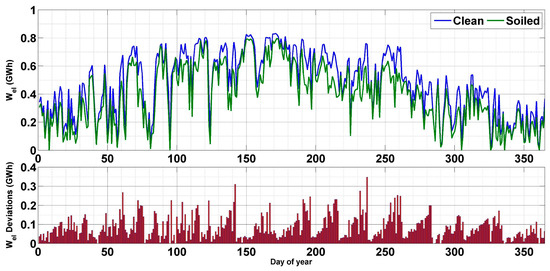
Figure 14.
The impact of soiling on the electrical performance.
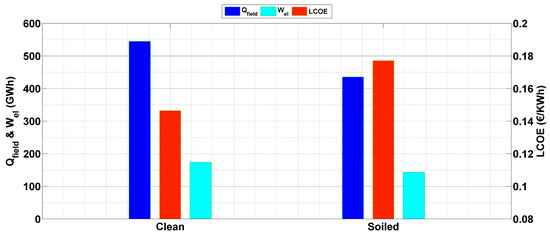
Figure 15.
The annual techno-economic performance of the CSP plants in the clean and the soiled scenarios.
Since the LCOE is related to power generation, this factor will be also affected by soiling deposition. Indeed, if soiling is considered, the LCOE increases to reach 0.1771 €/kWh instead of 0.1465 €/kWh in the clean scenario. This represents an increase of 20% in the total cost of electricity.
To wrap up, and according to these findings, soiling seems to have a significant impact on the operation of the CSP power plant, and it is recommended that all yield studies should take it into consideration to better develop a business model, develop an accurate cleaning scenario and adjust the future operation and maintenance costs.
5. Conclusions
In the last decade, due to high energy bills, Morocco has started to invest a lot in renewable energy sources, mainly solar and wind, with the objective of producing 52% of its energy needs from renewables. The introduction of green energy sources into the Moroccan energy mix will keep increasing to reach 70% in 2040 and 80% in 2050. This objective is very promising and also presents several challenges, mainly due to the intermittence of these energy sources, as well as the difficulties in selecting which is the optimal technology to use in a specific location to guarantee high production with low investment costs. In this study, we focused on CSP plants using parabolic trough collector technology and two-tank thermal storage systems with the aim of analyzing the different technical, economic and environmental parameters in order to (i) first provide an optimal design for a CSP power plant which is adaptable to the Moroccan context and (ii) to assess the impact of the weather—mainly soiling—on the production of the latter. For this reason, a 50 MWe power plant similar to Andasol 1 was selected as the reference configuration. After that, and using high-quality meteorological data measured at the ground level, the configuration of this power plant was optimized, mainly in terms of the solar field size (Solar Multiple) and the thermal storage capacity, to select the best plant design for two locations (Ain Beni Mathar and Benguerir), identified according to high DNI values, and they can be used as reference locations for hosting CSP plants in Morocco. After that, a detailed yield analysis was conducted for the optimized power plants by simulating their thermal and electrical performance under the climates of the abovementioned locations. Finally, and given the fact that Morocco has a semi-arid climate characterized by the presence of dust and sand, the impact of dust deposition on the mirror reflectivity was measured and included in the yield analysis. The key findings of this study are listed as follows:
- ▪
- For optimal operation from a techno-economic point of view, the configuration of the 50 MWe power plant at Ain Beni Mathar should have an SM of 2.5 and a TES of 7.5 h. As for Benguerir, the SM and the TES should be 7.5 h and 2.5, respectively.
- ▪
- Morocco has great potential for CSP applications, where the optimized plant configurations can produce daily thermal energy reaching 360 MWhth at Ain Beni Mathar and approximately 300 MWhth at Benguerir.
- ▪
- The daily electrical production from the proposed configurations can reach 8.47 GWhe for Ani Beni Mathar and 8.2 GWhe for Benguerir, with DNI values of 427 W/m2 and 433 W/m2, respectively.
- ▪
- The thermal storage system is considered very reliable, where it enables the plant to keep producing electricity at a medium load for up to 9 h (from 19:00 to 5:00) after sunset at Benguerir and up to 8 h (from 19:00 to 5:00) at Ain Beni Mathar.
- ▪
- For Ain Beni Mathar, the most efficient production was recorded during July, where the monthly thermal efficiency was around 56%, and the total efficiency was around 16% for a DNI average of 295 W/m2. Regarding Benguerir, June was the most efficient month with a DNI of 334 W/m2 and thermal and electrical efficiency of 58% and 19%, respectively.
- ▪
- Soiling is a highly efficiency-limiting factor, where the daily drop in the mirror reflectivity can reach 38% after only 2 weeks of exposition without cleaning during the dry period of the year.
- ▪
- Technically, soiling causes annual thermal and electrical loses of 109 GWhth and 30.3 GWhe. This represents 20% and 17% losses in annual production under the nominal conditions.
- ▪
- From an economic point of view, soiling causes a significant increase in the LCOE where the value jumps from 0.1465 €/kWh to 0.1771 €/kWh, which represents a rise of 20% due to soiling.
We believe that the results of this study are of high interest to investors and policymakers, as they demonstrate the capacity and limitation of the integration of large-scale CSP power plants into the Moroccan energy mix. Furthermore, the results on the soiling impact may provide good ideas for engineers and future project managers to enhance their economic models and precisely evaluate the O&M costs and the profitability of CSP power plants if they are installed in Morocco.
Author Contributions
N.A.: Conceptualization; software; validation; formal analysis; original draft preparation. A.A.M.: Supervision; methodology; conceptualization; formal analysis; writing—review and editing. A.M.: Writing—review and editing. E.C.: Writing—review and editing. T.W.: Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available based on reasonable usage. Any data requests should be addressed to A.A.M. due to (privacy of the row data before processing).
Acknowledgments
The authors would like to warmly acknowledge the Ain Beni Mathar power plant and the Green Energy Park research facility for providing us with the data and logistical support to conduct this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| DNI | Direct normal irradiance (W/m2) |
| GHI | Global horizontal irradiance (W/m2) |
| IAM | Incidence angle modifier (Deg°) |
| DHI | Diffuse horizontal irradiance (W/m2) |
| Wel | Electrical output (Whe) |
| Qth | Thermal output (Whth) |
| ηth | Optical efficiency (%) |
| ηtot | Total efficiency (%) |
| LCOE | Levelized cost of electricity (€/Wh) |
| CSP | Concentrated solar power plant |
| HTF | Heat transfer fluid |
| TES | Thermal energy storage |
| SM | Solar Multiple |
| N-loops | Number of loops |
References
- Kanwal, S.; Mehran, M.T.; Hassan, M.; Anwar, M.; Naqvi, S.R.; Khoja, A.H. An integrated future approach for the energy security of Pakistan: Replacement of fossil fuels with syngas for better environment and socio-economic development. Renew. Sustain. Energy Rev. 2022, 156, 111978. [Google Scholar] [CrossRef]
- Dincer, I.; Acar, C. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrogen Energy 2014, 40, 11094–11111. [Google Scholar] [CrossRef]
- Pudukudy, M.; Yaakob, Z.; Mohammad, M.; Narayanan, B.; Sopian, K. Renewable hydrogen economy in Asia—Opportunities and challenges: An overview. Renew. Sustain. Energy Rev. 2014, 30, 743–757. [Google Scholar] [CrossRef]
- REN21. Renewables 2020 Global Status Report; 2020. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2020_full_report_en.pdf (accessed on 6 June 2024).
- Yu, Q.; Hao, Y.; Ali, K.; Hua, Q.; Sun, L. Techno-economic analysis of hydrogen pipeline network in China based on levelized cost of transportation. Energy Convers. Manag. 2024, 301, 118025. [Google Scholar] [CrossRef]
- Amrani, S.-E.; Merrouni, A.A.; Touili, S.; Ouali, H.A.L.; Dekhissi, H. An AHP-GIS combination for site suitability analysis of hydrogen production units from CSP & PV solar power plants in Morocco. Int. J. Hydrogen Energy 2024, 56, 369–382. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2019; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- IRENA. Concentrating Solar Power Technology Brief; IRENA: Abu Dhabi, United Arab Emirates, 2012; Available online: https://www.irena.org/publications/2013/Jan/Concentrated-Solar-Power (accessed on 6 June 2024).
- Elmohlawy, A.E.; Ochkov, V.F.; Kazandzhan, B.I. Thermal performance analysis of a concentrated solar power system (CSP) integrated with natural gas combined cycle (NGCC) power plant. Case Stud. Therm. Eng. 2019, 14, 100458. [Google Scholar] [CrossRef]
- Calderón, A.; Palacios, A.; Barreneche, C.; Segarra, M.; Prieto, C.; Rodriguez-Sanchez, A.; Fernández, A.I. High temperature systems using solid particles as TES and HTF material: A review. Appl. Energy 2018, 213, 100–111. [Google Scholar] [CrossRef]
- IRENA. Concentrating Solar Power: Renewable Energytechnologies: Cost Analysis Series; Elsevier: Amsterdam, The Netherlands, 2020; Volume 1: PowerSector. [Google Scholar] [CrossRef]
- IRENA. Technology Roadmap Concentrating Solar Power; IRENA: Abu Dhabi, United Arab Emirates, 2010. [Google Scholar]
- Fernández, A.G.; Gomez-Vidal, J.; Oró, E.; Kruizenga, A.; Solé, A.; Cabeza, L.F. Mainstreaming commercial CSP systems: A technology review. Renew. Energy 2019, 140, 152–176. [Google Scholar] [CrossRef]
- Vignarooban, K.; Xu, X.; Arvay, A.; Hsu, K.; Kannan, A. Heat transfer fluids for concentrating solar power systems—A review. Appl. Energy 2015, 146, 383–396. [Google Scholar] [CrossRef]
- Benoit, H.; Spreafico, L.; Gauthier, D.; Flamant, G. Review of heat transfer fluids in tube-receivers used in concentrating solar thermal systems: Properties and heat transfer coefficients. Renew. Sustain. Energy Rev. 2016, 55, 298–315. [Google Scholar] [CrossRef]
- Sau, S.; Corsaro, N.; Crescenzi, T.; D’ottavi, C.; Liberatore, R.; Licoccia, S.; Russo, V.; Tarquini, P.; Tizzoni, A. Techno-economic comparison between CSP plants presenting two different heat transfer fluids. Appl. Energy 2016, 168, 96–109. [Google Scholar] [CrossRef]
- Xu, X.; Guo, P.; Liu, W.; Yang, W. Entropy generation and Carnot efficiency comparisons of high temperature heat transfer fluid candidates for CSP plants. Int. J. Hydrogen Energy 2017, 42, 20316–20323. [Google Scholar] [CrossRef]
- Peiró, G.; Gasia, J.; Miró, L.; Prieto, C.; Cabeza, L.F. Influence of the heat transfer fluid in a CSP plant molten salts charging process. Renew. Energy 2017, 113, 148–158. [Google Scholar] [CrossRef]
- Conroy, T.; Collins, M.N.; Fisher, J.; Grimes, R. Thermohydraulic analysis of single phase heat transfer fluids in CSP solar receivers. Renew. Energy 2018, 129, 150–167. [Google Scholar] [CrossRef]
- Polimeni, S.; Binotti, M.; Moretti, L.; Manzolini, G. Comparison of sodium and KCl-MgCl2 as heat transfer fluids in CSP solar tower with sCO2 power cycles. Sol. Energy 2018, 162, 510–524. [Google Scholar] [CrossRef]
- Wette, J.; Sutter, F.; Fernández-García, A. Evaluation of anti-soiling coatings for CSP reflectors under realistic outdoor conditions. Sol. Energy 2019, 191, 574–584. [Google Scholar] [CrossRef]
- Conceição, R.; Merrouni, A.A.; Lopes, D.; Alae, A.; Silva, H.G.; Bennouna, E.G.; Collares-Pereira, M.; Ghennioui, A. A comparative study of soiling on solar mirrors in Portugal and Morocco: Preliminary results for the dry season. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2126, p. 220001. [Google Scholar]
- Merrouni, A.A.; Ghennioui, A.; Wolfertstetter, F.; Mezrhab, A. The Uncertainty of the HelioClim-3 DNI Data under Moroccan Climate; AIP Publishing: Abu Dhabi, United Arab Emirates, 2017; p. 140002. [Google Scholar] [CrossRef]
- Wilcox, S.M.; McCormack, P. Implementing Best Practices for Data Quality Assessment of the National Renewable Energy Laboratory’s Solar Resource and Meteorological Assessment Project: Preprint; p. 10. Available online: https://www.nrel.gov/docs/fy11osti/50897.pdf (accessed on 6 June 2024).
- Merrouni, A.A.; Elalaoui, F.E.; Ghennioui, A.; Mezrhab, A.; Mezrhab, A. A GIS-AHP combination for the sites assessment of large-scale CSP plants with dry and wet cooling systems. Case study: Eastern Morocco. Sol. Energy 2018, 166, 2–12. [Google Scholar] [CrossRef]
- Mouaky, A.; Merrouni, A.A.; Laadel, N.E.; Bennouna, E.G. Simulation and experimental validation of a parabolic trough plant for solar thermal applications under the semi-arid climate conditions. Sol. Energy 2019, 194, 969–985. [Google Scholar] [CrossRef]
- Qoaider, L.; Liqreina, A. Optimization of dry cooled parabolic trough (CSP) plants for the desert regions of the Middle East and North Africa (MENA). Sol. Energy 2015, 122, 976–985. [Google Scholar] [CrossRef]
- Bouhal, T.; Agrouaz, Y.; Kousksou, T.; Allouhi, A.; El Rhafiki, T.; Jamil, A.; Bakkas, M. Technical feasibility of a sustainable Concentrated Solar Power in Morocco through an energy analysis. Renew. Sustain. Energy Rev. 2018, 81, 1087–1095. [Google Scholar] [CrossRef]
- Liqreina, A.; Qoaider, L. Dry cooling of concentrating solar power (CSP) plants, an economic competitive option for the desert regions of the MENA region. Sol. Energy 2014, 103, 417–424. [Google Scholar] [CrossRef]
- Mwesigye, A.; Yılmaz, I.H.; Meyer, J.P. Numerical analysis of the thermal and thermodynamic performance of a parabolic trough solar collector using SWCNTs-Therminol®VP-1 nanofluid. Renew. Energy 2018, 119, 844–862. [Google Scholar] [CrossRef]
- Merrouni, A.A.; Ouali, H.A.L.; Moussaoui, M.A.; Mezrhab, A. Analysis and comparaison of different Heat Transfer Fluids for a 1MWe Parabolic Trough Collector. In Proceedings of the 2016 International Conference on Electrical and Information Technologies (ICEIT), Tangiers, Morocco, 4–7 May 2016; pp. 510–515. [Google Scholar]
- Coco-Enríquez, L.; Muñoz-Antón, J.; Martínez-Val, J. Dual Loop line-focusing solar power plants with supercritical Brayton power cycles. Int. J. Hydrogen Energy 2017, 42, 17664–17680. [Google Scholar] [CrossRef]
- Calvet, N.; Gomez, J.C.; Faik, A.; Roddatis, V.V.; Meffre, A.; Glatzmaier, G.C.; Doppiu, S.; Py, X. Compatibility of a post-industrial ceramic with nitrate molten salts for use as filler material in a thermocline storage system. Appl. Energy 2013, 109, 387–393. [Google Scholar] [CrossRef]
- Raade, J.W.; Padowitz, D. Development of Molten Salt Heat Transfer Fluid with Low Melting Point and High Thermal Stability. J. Sol. Energy Eng. 2011, 133, 031013. [Google Scholar] [CrossRef]
- Delise, T.; Tizzoni, A.; Ferrara, M.; Corsaro, N.; D’ottavi, C.; Sau, S.; Licoccia, S. Thermophysical, environmental, and compatibility properties of nitrate and nitrite containing molten salts for medium temperature CSP applications: A critical review. J. Eur. Ceram. Soc. 2019, 39, 92–99. [Google Scholar] [CrossRef]
- Bellmann, P.; Wolfertstetter, F.; Conceição, R.; Silva, H.G. Comparative modeling of optical soiling losses for CSP and PV energy systems. Sol. Energy 2020, 197, 229–237. [Google Scholar] [CrossRef]
- Ilse, K.; Micheli, L.; Figgis, B.W.; Lange, K.; Daßler, D.; Hanifi, H.; Wolfertstetter, F.; Naumann, V.; Hagendorf, C.; Gottschalg, R.; et al. Techno-Economic Assessment of Soiling Losses and Mitigation Strategies for Solar Power Generation. Joule 2019, 3, 2303–2321. [Google Scholar] [CrossRef]
- Conceição, R.; Silva, H.G.; Collares-Pereira, M. CSP mirror soiling characterization and modeling. Sol. Energy Mater. Sol. Cells 2018, 185, 233–239. [Google Scholar] [CrossRef]
- Merrouni, A.A.; Mezrhab, A.; Ghennioui, A.; Naimi, Z. Measurement, comparison and monitoring of solar mirror’s specular reflectivity using two different Reflectometers. Energy Procedia 2017, 119, 433–445. [Google Scholar] [CrossRef]
- Conceição, R.; González-Aguilar, J.; Merrouni, A.A.; Romero, M. Soiling effect in solar energy conversion systems: A review. Renew. Sustain. Energy Rev. 2022, 162, 112434. [Google Scholar] [CrossRef]
- Wolfertstetter, F.; Pottler, K.; Geuder, N.; Affolter, R.; Merrouni, A.; Mezrhab, A.; Pitz-Paal, R. Monitoring of Mirror and Sensor Soiling with TraCS for Improved Quality of Ground based Irradiance Measurements. Energy Procedia 2014, 49, 2422–2432. [Google Scholar] [CrossRef]
- Lopes, D.; Conceição, R.; Silva, H.G.; Aranzabe, E.; Pérez, G.; Collares-Pereira, M. Anti-soiling coating performance assessment on the reduction of soiling effect in second-surface solar mirror. Sol. Energy 2019, 194, 478–484. [Google Scholar] [CrossRef]
- Conceição, R.; Silva, H.G.; Mirão, J.; Gostein, M.; Fialho, L.; Narvarte, L.; Collares-Pereira, M. Saharan dust transport to Europe and its impact on photovoltaic performance: A case study of soiling in Portugal. Sol. Energy 2018, 160, 94–102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).