An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms
Abstract
:1. Introduction
- -
- Low-energy faults promote a single-bond gas formation: for partial discharges (DP) and for low-energy thermal faults (T1);
- -
- Moderate-intensity failures, such as high-energy overheating (T2), include the formation of double-bond gases ;
- -
- Faults generated at temperatures above 1200 °C, such as low-energy electrical faults (LED) or high-energy electrical faults (HED), induce the recombination of gases with triple bonds, more precisely ;
- -
- A cellulose decomposition (CD) type of failure generally induces the reconstruction of two gases: () and ().
2. Database Construction
2.1. Used Database
2.2. Database Normalization
- -
- Min–max normalization, consists of converting the data values to a fixed range, which is generally between [0, 1] or [−1, 1].
- -
- Z-score normalization, also aims to present the initial data distribution on a scale between [0, 1].
- -
- Log transformation, scales the dataset by calculating the logarithm of each value.where , , and represent, respectively, the min, the max, the mean, and the standard deviation of the descriptor vector’s parameter.
3. Configuration of the Proposed Discrimination Model
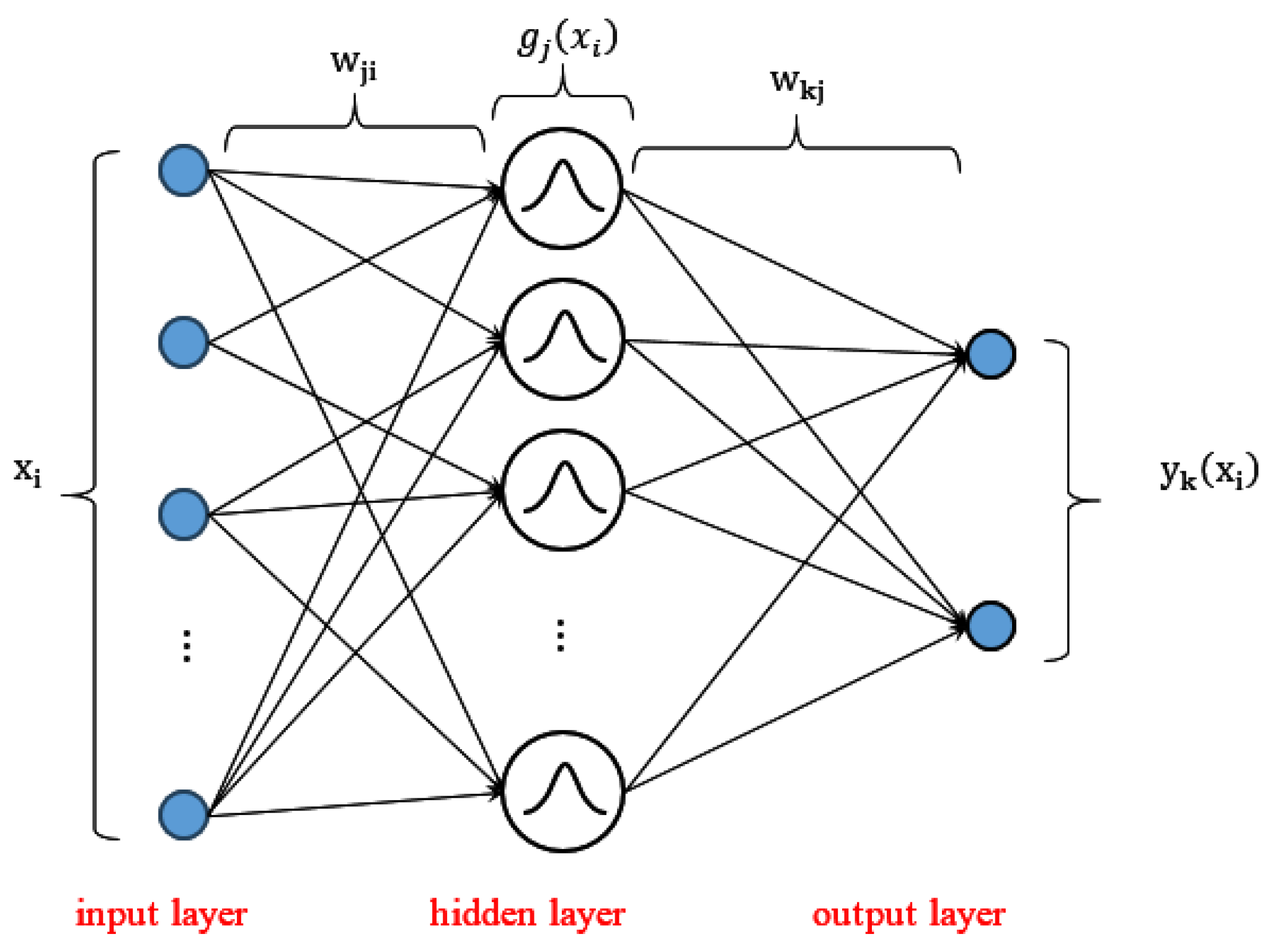
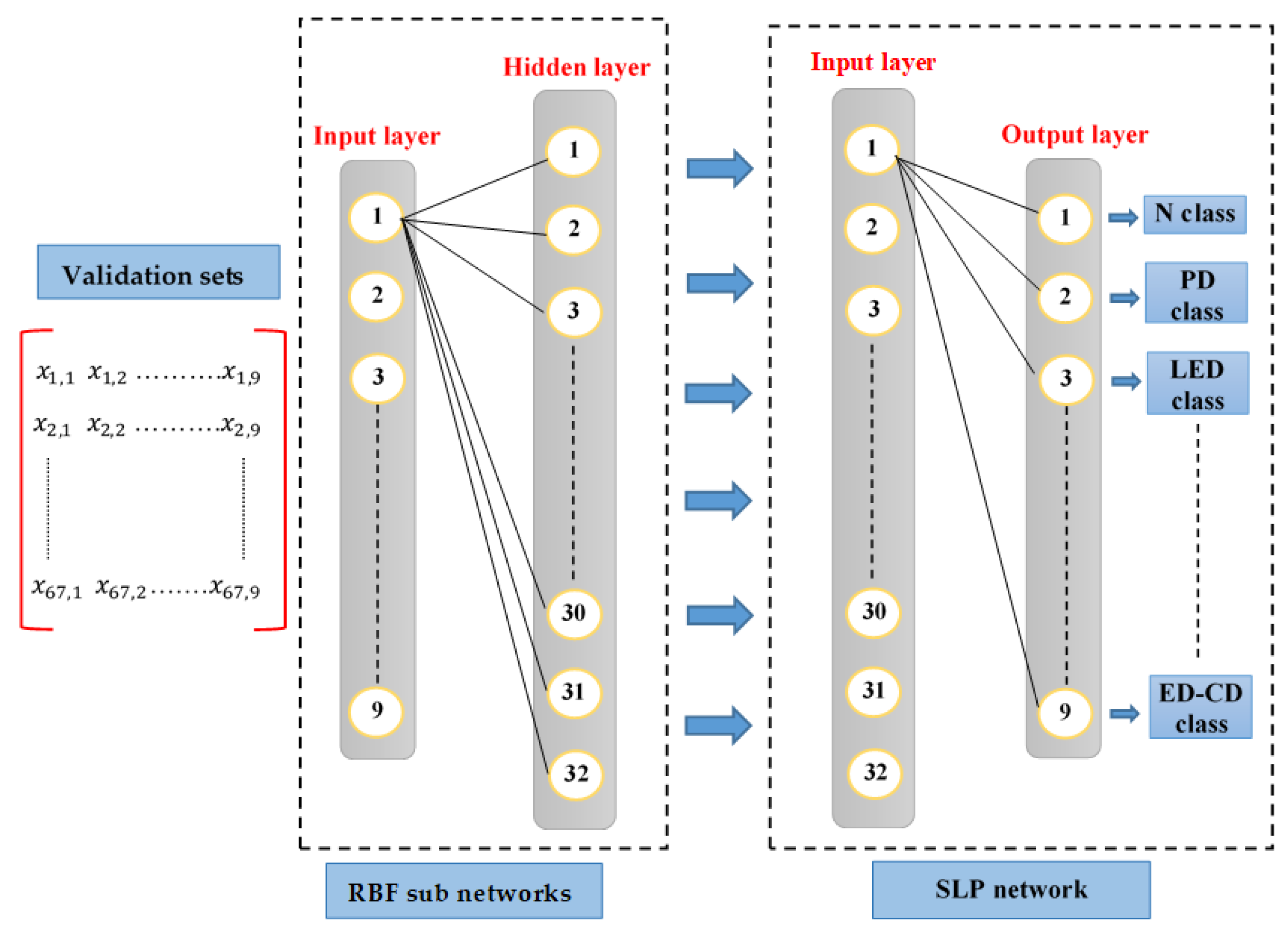
3.1. Hierarchical RBF Neural Network
- -
- An input layer that retransmits inputs without distortion and whose neuron number equals the input vector dimension. In this study, we have an input layer with nine neurons receiving the nine gas concentrations.
- -
- A hidden layer composed of Gaussian-type kernel functions with center and a receptive field . Let the example () belong to the training set , the output of the (1 ≤ j ≤ M) hidden neuron is given by
- -
- An output layer with each neuron representing a fault class or the normal class. The final output of an input vector can be calculated as follows:with as the synaptic weight between a hidden-layer neuron and the output-layer neuron , and as the output error bias. Adjusting the synaptic output weights is another critical element to ensure the good performance of an RBF-type network.
- -
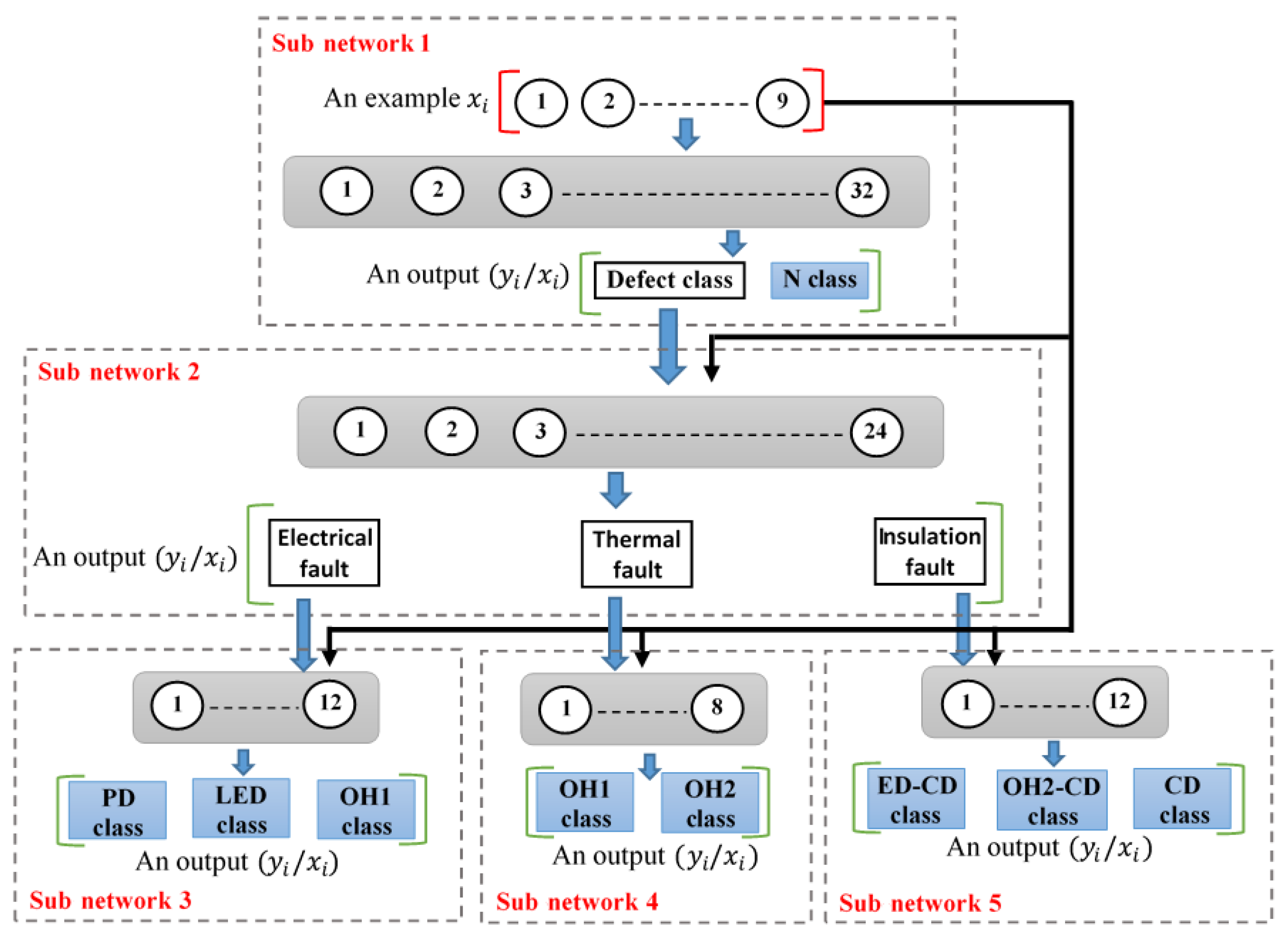
- Stage 1 consists of a single subnetwork, and it plays the role of a defect detector, effectively separating gas samples with and without defects;
- -
- Stage 2 also includes a single network, which aims to group the defect samples into three distinct categories: electrical, thermal, and cellulose decomposition;
- -
- Stage 3 is made up of subnetwork three, responsible for differentiating between electrical faults based on different discharge energy densities; subnetwork 4, able to differentiate between thermal faults according to distinct hot-spot temperatures; and subnetwork 4, which has the role of detecting cellulose decomposition defects with or without the presence of electrical or thermal damage.
3.2. Linde–Buzo–Gray Algorithm
- (A)
- Initialization
- Define an initial vector code (initial centroid):
- Measure initial distortion:
- (B)
- Dividing
- Double the codebook size by dividing each code vector as follows:
- (C)
- Iteration 1
- Determine all the similar amplitude examples with respect to each of the codebook centroids, then form clusters:
- 2.
- Update the centroids based on the new clusters:.
- 3.
- Calculate the new distortion:
- 4.
- If the threshold is lower than , then go to step (C.1).
- 5.
- Retain the distortion () and centroids (for , ) of the current iteration.
- (D)
- Iteration 2
- Repeat steps (B) and (C) until the code library size is designed.
3.3. Single-Layer Perceptron [35,36]
- -
- An input layer receiving the input vector . In this study, the middle layer outputs of a given RBF network constitute the inputs of a given SLP;
- -
- An output layer comprises threshold functions, each representing a membership category.
- (A)
- Initialization
- Randomly generate synaptic weights (weight vector) with small values;
- Set the learning rate value and the desired precision value ;
- Calculate the gradient operator on the initial mean squared error (MSE):where is a constant.
- (B)
- Iterations
- Update previous error:
- For
- 2.1.
- Compute the scalar product between the vector and the weight vector
- 2.2.
- If , update synaptic weights:where and where is an activation function, whose value is 1 if if and otherwise.
- Calculate the new MSE by referring to Equation (13).
3.4. LBG and SLP Algorithms’ Implementation Steps
- -
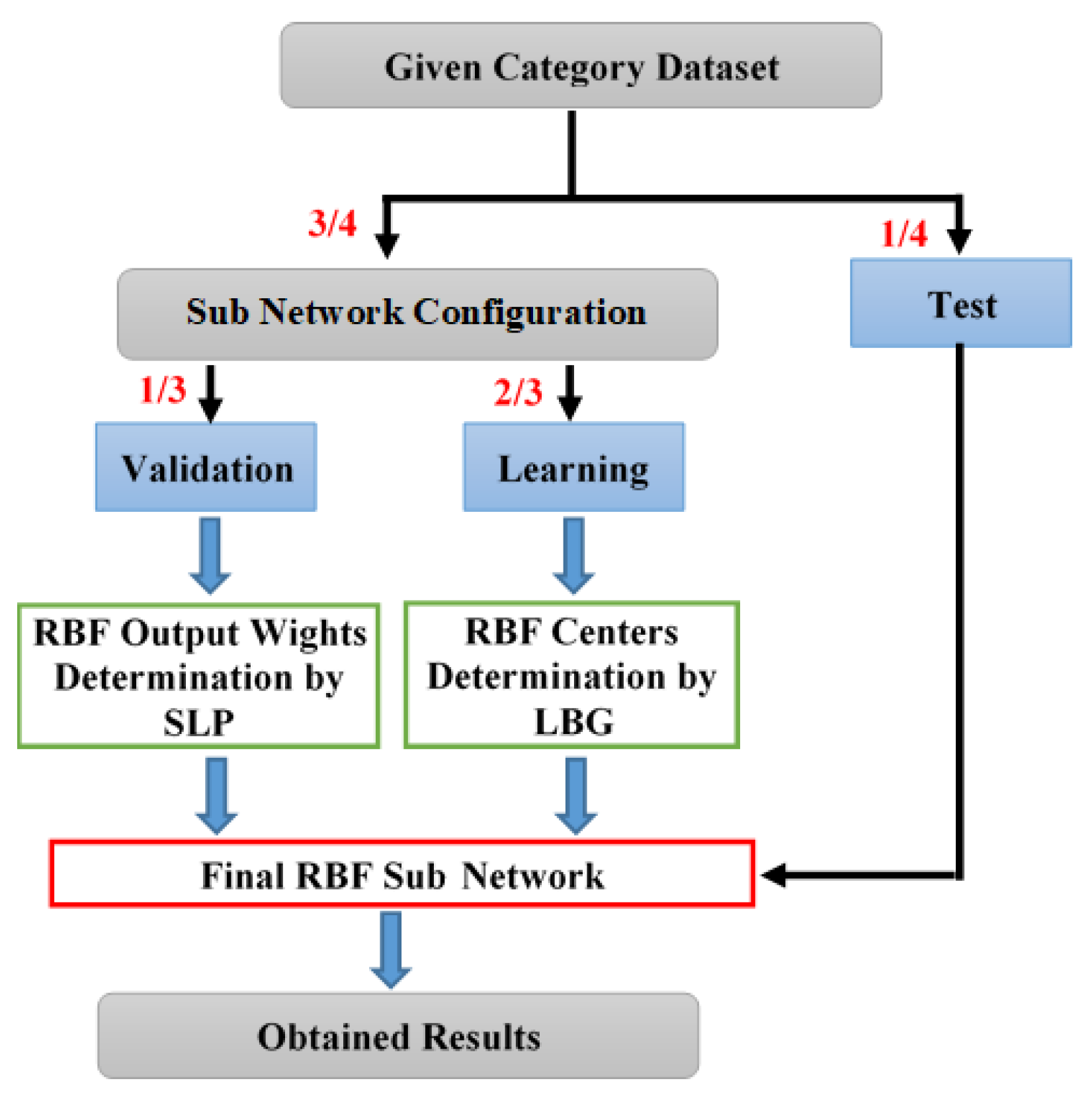
- Step 1: The examples distinguished by category (see the global database section II.A) were subdivided randomly and fairly into four parts to implement a process for four cross-validation levels.
- -
- Step 2: The three sets retained for the configuration (relative to each category) are used to construct five sub-bases, each of which allows the configuration of one of the five subnetworks.
- Sub-base 1 (for RBF subnetwork 1), includes samples classified as healthy (class 1: 33 examples) and defective (class 2: 168 examples);
- Sub-base 2 (for RBF subnetwork 2), includes defective samples classified as thermal (class 1: examples), electrical (class 2: examples), or cellulose decomposition (class 3: examples);
- Sub-base 3 (for RBF subnetwork 3), includes samples with DP defect (class 1: examples), LED defect (class 2: examples), and HED defect (class 3: examples).
- Sub-base 4 (for RBF subnetwork 4), includes samples with thermal () (class 1: examples) and thermal (t > 700 °C) (class 2: examples) defects.
- Sub-base 5 (for RBF subnetwork 5), includes samples with CD defect (class 1: examples), OH2-CD defect (class 2: examples), and ED-CD defect (class 3: 18 examples).
- -
- Step 3: The retained centroids are obtained by grouping the most similar input vectors which belong to the same cluster into a single vector using an averaging function (see Equation (11)).
- -
- Step 4: An SLP-type network is used to determine the output-layer weights of the retained RBF subnetworks. That makes it possible to overcome the weaknesses of the traditional RBF approach, which is based on a linear combination unable to deal with non-linear cases and which suffers from a fairly long convergence.
- For each cross-validation step, and each subnetwork, the centroids retained by the LBG algorithm will constitute the hidden-layer neurons of the same subnetwork;
- Each RBF subnetwork will receive the validation set as input;
- The centroids (hidden-layer) outputs constitute the SLP inputs;
- The LSP outputs constitute the membership classes the subnetwork considers;
- At the end of the learning, the weights obtained by the SLP will constitute the output weights of the final RBF subnetwork.
- -
- Step 5: Predicting the power transformer health status turns out to be a delicate and complicated task. Indeed, the diagnostic error quantification is generally irregular, complex to evaluate or fix, and varies from one expert to another and from one equipment to another. Therefore, it is preferable and more credible to implement discriminators that return the category’s belonging probabilities rather than the membership class rank (deterministic discrimination). However, RBFs are basically introduced as non-probabilistic classifiers, but it is possible to post-process their outputs in order to obtain posterior probabilities. The following formula needs to be applied to the obtained RBF outputs:
- -
- Step 6: Once all the RBF subnetworks have been formed and optimized, we proceed to the test phase as follows:
- The samples reserved during testing at each validation level and for each class (see Step 1 and Figure 3) are first merged to form a global test base;
- The verification of the proposed hierarchical network effectiveness is carried out through each example evaluation at different hierarchy levels;
- Each RBF subnetwork performance is reported separately in terms of good and bad classification numbers;
- A test results grouping (by level) is performed at the end so that all examples in the database are tested.
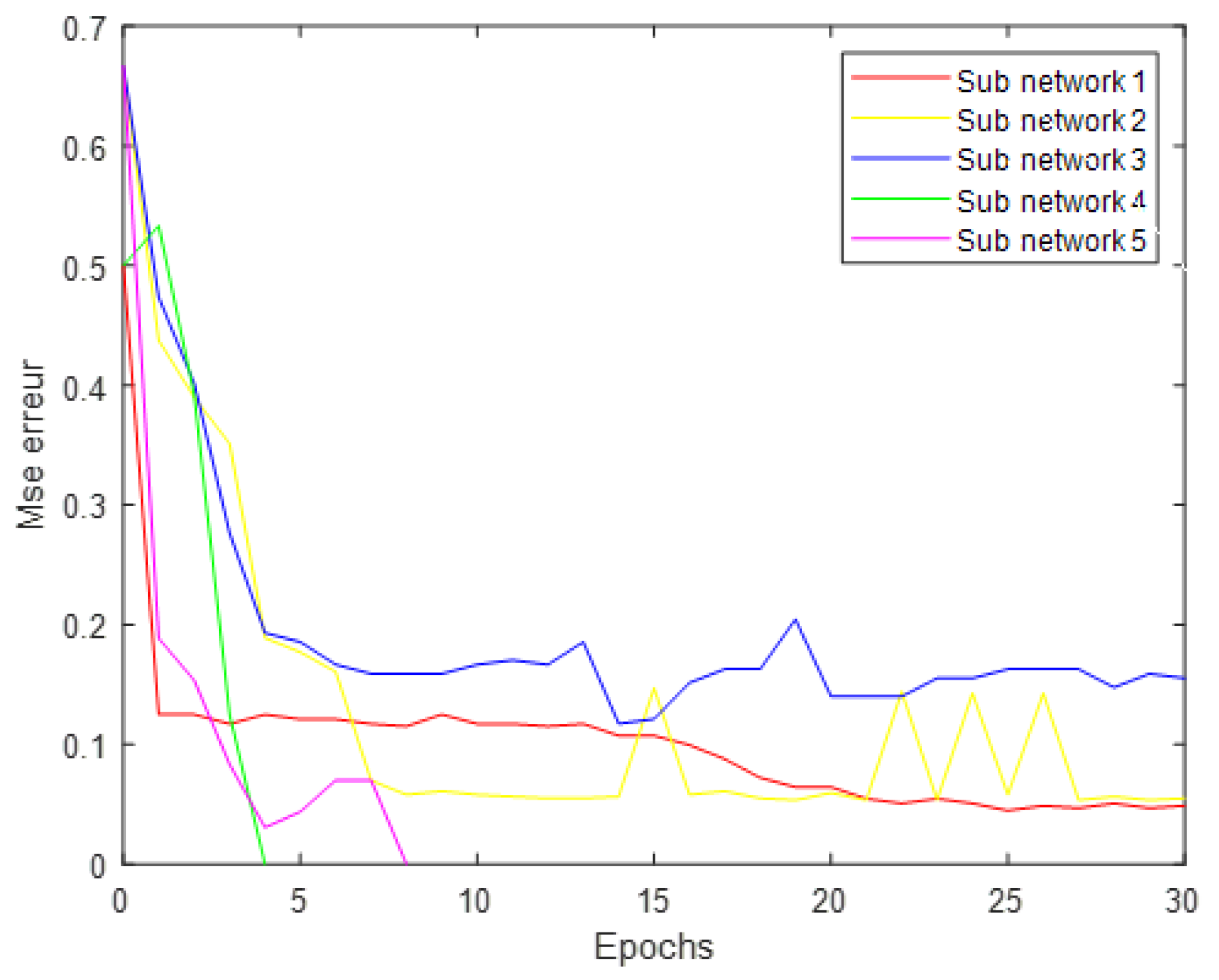
4. Results and Discussion
- -
- An input layer containing nine neurons, each receiving one dissolved gas;
- -
- A hidden layer of 72 neurons obtained by applying the LBG algorithm. The retained neuron number is the one which returns the best classification rates (sensitivity); see Table 3;
- -
- An output layer returning membership probabilities to each of the nine classes considered and whose synaptic neuron weights were optimized by the SLP network.
- -
- Sensitivity: Also called “true positive rate”, the sensitivity quantifies the portion of true positives from the total positive population (taking into consideration even those classified as negative by mistake.
- -
- Specificity: Also known as “true negative rate”, it quantifies the true negative portion in relation to the total negative population (even considering samples classified as true by error).
- -
- Positive predictive value (PPV): returns the probability that the test is indeed positive if the obtained result is true.
- -
- Negative predictive value (NPV): returns the probability that the test is truly negative if the obtained result is negative.
- -
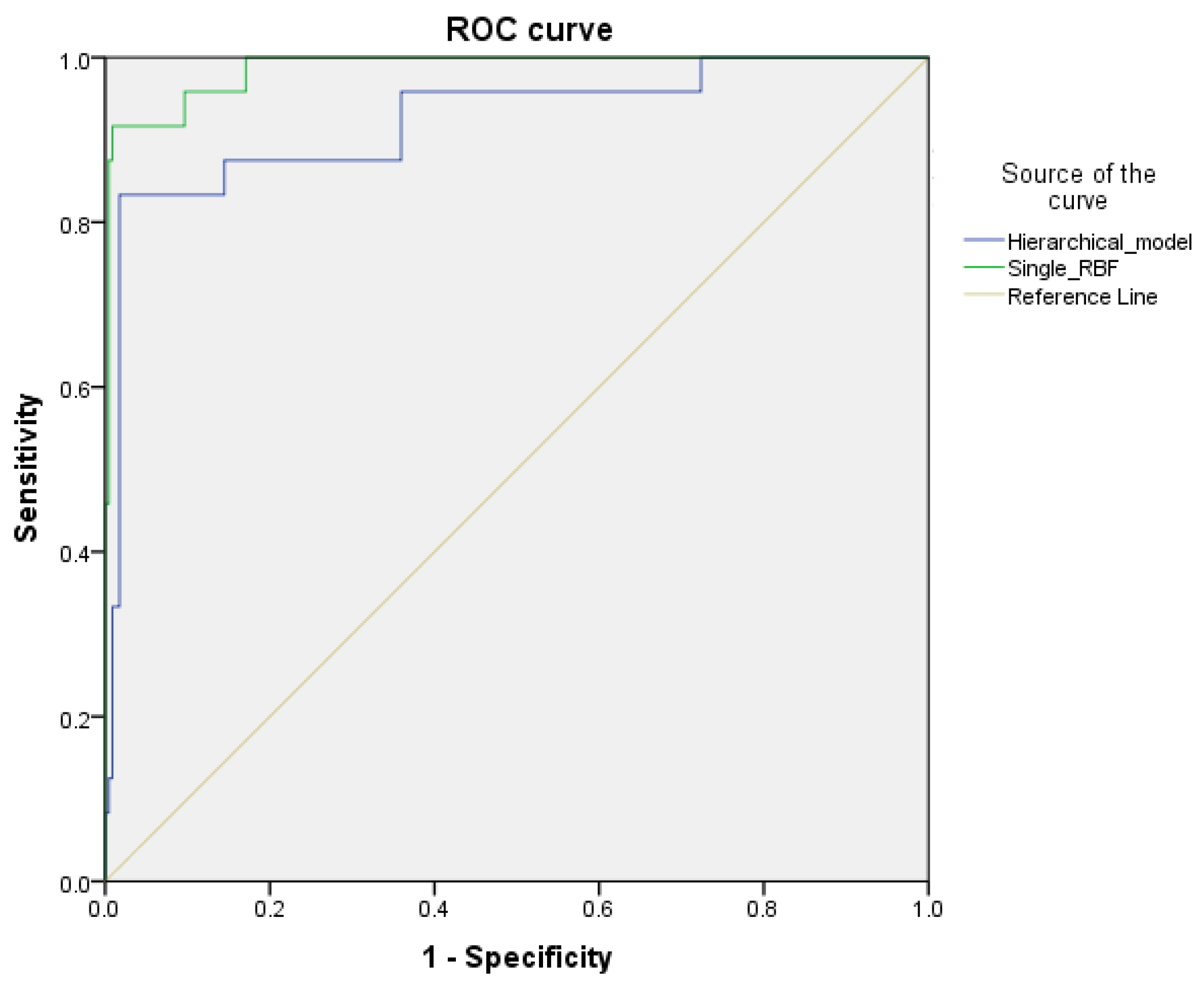
- Receiver operating characteristic (ROC) curve: allows to draw the torque values’ variation (1-specificity, sensitivity), taking into consideration all the output probabilities generated by the discriminator;
- -
- Area under the ROC curve (AUROC-95% CI): allows to fully judge the considered discriminator’s performance based on these indicators (in this study case, we refer to posterior probabilities);
- -
- Student’s test: also called “t-test”, is a parametric tool which can be used to compare the generalization averages of two statistical models, and then it allows to determine whether there exists a significant assessment of one expert over another.
- -
- Study [27] considers more examples; simultaneously, the authors obtained generalization rates higher than ours. However, the authors use a lower-class number than ours, which could facilitate the classification task and justify the high rates. Also, the present study considers statistical parameters and confidence intervals, which promise similar or even better results for a more extensive data set;
- -
- Study [31] considered more test examples but fewer categories than the present study, and it proposed a low test rate compared to ours, whereas study [32] treats the same class number as this study with more test examples and presents poorer generalization results. But once again, we recall that according to the statistical tests carried out, the results we obtained could be found with more test examples.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Liu, Y.; Chen, X.; Yan, Q.; Sui, H.; Ma, C.; Zhang, J. Power transformer fault diagnosis system based on Internet of Things. J. Wirel. Commun. Netw. 2021, 2021, 21. [Google Scholar] [CrossRef]
- Wani, S.A.; Rana, A.S.; Sohail, S.; Rahman, O.; Parveen, S.; Khan, S.A. Advances in DGA based condition monitoring of transformers: A review. Renew. Sustain. Energy Rev. 2021, 149, 111347. [Google Scholar] [CrossRef]
- Abbasi, A.R. Fault detection and diagnosis in power transformers: A comprehensive review and classification of publications and methods. Electr. Power Syst. Res. 2022, 209, 107990. [Google Scholar] [CrossRef]
- Sun, H.C.; Huang, Y.C.; Huang, C.M. Fault Diagnosis of Power Transformers Using Computational Intelligence: A Review. Energy Procedia 2012, 14, 1226–1231. [Google Scholar] [CrossRef]
- Muniz, R.N.; Costa Júnior, C.T.; Buratto, W.G.; Nied, A.; González, G.V. The Sustainability Concept: A Review Fo-cusing on Energy. Sustainability 2023, 15, 14049. [Google Scholar] [CrossRef]
- Islam, M.; Lee, G.; Hettiwatte, S.N. A nearest neighbour clustering approach for incipient fault diagnosis of power transformers. Electr. Eng. 2017, 99, 1109–1119. [Google Scholar] [CrossRef]
- Rogers, R.R. IEEE and IEC codes to interpret incipient faults in transformers, using gas in oil analysis. IEEE Trans. Electr. Insul. 1978, EL-13, 349–354. [Google Scholar] [CrossRef]
- Irungu, G.K.; Akumu, A.O.; Munda, J.L. A new fault diagnostic technique in oil-filled electrical equipment; the dual of Duval triangle. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3405–3410. [Google Scholar] [CrossRef]
- Khan, S.A.; Equbal, M.D.; Islam, T.A. Comprehensive comparative study of DGA based ANFIS models. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 590–596. [Google Scholar] [CrossRef]
- Peimankar, A.; Weddell, S.J.; Thahirah, J.; Lapthorn, A.C. Evolutionary Multi-Objective Fault Diagnosis of Power Transformers. Swarm Evol. Comput. 2017, 36, 62–75. [Google Scholar] [CrossRef]
- Abdo, A.; Liu, H.; Zhang, H.; Guo, J.; Li, Q. A new model of faults classification in power transformers based on data optimization method. Electr. Power Syst. Res. 2021, 200, 107446. [Google Scholar] [CrossRef]
- Hua, Y.; Sun, Y.; Xu, G.; Sun, S.; Wang, E.; Pang, Y. A fault diagnostic method for oil-immersed transformer based on multiple probabilistic output algorithms and improved DS evidence theory. Int. J. Electr. Power Energy Syst. 2022, 137, 107828. [Google Scholar] [CrossRef]
- Guardado, J.L.; Naredo, J.L.; Moreno, P.; Fuerte, C.R. A Comparative Study of Neural Network Efficiency in Power Transformers Diagnosis Using Dissolved Gas Analysis. IEEE Trans. Power Deliv. 2001, 16, 643–647. [Google Scholar] [CrossRef]
- Han, X.; Ma, S.; Shi, Z.; An, G.; Du, Z.; Zhao, C. A Novel Power Transformer Fault Diagnosis Model Based on Harris-Hawks-Optimization Algorithm Optimized Kernel Extreme Learning Machine. J. Electr. Eng. Technol. 2022, 17, 1993–2001. [Google Scholar] [CrossRef]
- Li, S.; Wu, G.; Gao, B.; Hao, C.; Xin, D.; Yin, X. Interpretation of DGA for Transformer Fault Diagnosis with Complementary SaE-ELM and Arctangent Transform. IEEE Trans. Dielectr. Electr. Insulation. 2016, 23, 586–595. [Google Scholar] [CrossRef]
- Le, X.; Yijun, Z.; Keyu, Y.; Mingzhen, S.; Wenbo, L.; Dong, L. Interpretation of DGA for Transformer Fault Diagnosis with Step-by-step feature selection and SCA-RVM. In Proceedings of the IEEE 16th Conference on Industrial Electronics and Applications, Chengdu, China, 1–4 August 2021. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zheng, H.; Yao, H.; Liu, J.; Zhang, C.; Peng, H.; Jiao, J. A Fault Diagnosis Model of Power Transformers Based on Dissolved Gas Analysis Features Selection and Improved Krill Herd Algorithm Optimized Support Vector Machine. IEEE Access 2019, 7, 102803–102811. [Google Scholar] [CrossRef]
- Kari, T.; Gao, W.; Zhao, D.; Abiderexiti, K.; Mo, W.; Wang, Y.; Luan, L. Hybrid feature selection approach for power transformer fault diagnosis based on support vector machine and genetic algorithm. Inst. Eng. Technol. 2018, 12, 5672–5680. [Google Scholar] [CrossRef]
- Hendel, M.; Meghnefi, F.; Senoussaoui, M.A.; Fofana, I.; Brahami, M. Using Generic Direct M-SVM Model Improved by Kohonen Map and Dempster–Shafer Theory to Enhance Power Transformers Diagnostic. Sustainability 2023, 15, 15453. [Google Scholar] [CrossRef]
- Nanfak, A.; Samuel, E.; Fofana, I.; Meghnefi, F.; Ngaleu, M.G.; Hubert Kom, C. Traditional fault diagnosis methods for mineral oil-immersed power transformer based on dissolved gas analysis: Past, present and future. IET Nanodielectrics 2024, 1–34. [Google Scholar] [CrossRef]
- Meng, K.; Dong, Z.Y.; Wang, D.H.; Wong, K.P. A Self-Adaptive RBF Neural Network Classifier for Transformer Fault Analysis. IEEE Trans. Power Syst. 2010, 25, 1350–1360. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, H.; Huang, H.; Liu, S. Electric Power Transformer Fault Diagnosis using OLS based Radial Basis Function Neural Network. In Proceedings of the IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008. [Google Scholar] [CrossRef]
- Guo, Y.J.; Sun, L.H.; Liang, Y.C.; Ran, H.C.; Sun, H.Q. The fault diagnosis of power transformer based on improved RBF neural network. In Proceedings of the IEEE Sixth International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R.M. An Algorithm for Vector Quantizer Design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Jack, R.; Knutson, Y.; Choo, C.Y. Feature based compression of vector quantized codebooks and data for optimal image compression. In Proceedings of the IEEE International Symposium on Circuits and Systems, Chicago, IL, USA, 3–6 May 1993. [Google Scholar] [CrossRef]
- Staiano, A.; Tagliaferri, R.; Pedrycz, W. Improving RBF networks performance in regression tasks by means of a supervised fuzzy clustering. Neurocomputing 2006, 69, 1570–1581. [Google Scholar] [CrossRef]
- Obulareddy, S.; Munagala, S.K. Improved Radial Basis Function (RBF) Classifier for Power Transformer Winding Fault Classification. Innov. Electr. Electron. Eng. 2022, 894, 587–601. [Google Scholar] [CrossRef]
- Chen, S.; Wu, Y.; Luk, B.L. Combined genetic algorithm optimization and regularized orthogonal least squares learning for radial basis function net works. IEEE Trans. Neural Netw. 1999, 10, 1239–1243. [Google Scholar] [CrossRef]
- Chng, E.S.; Chen, S.; Mulgrew, B. Gradient radial basis function networks for non linear and non stationary time series prediction. IEEE Trans. Neural Netw. 1996, 7, 190–194. [Google Scholar] [CrossRef]
- Cui, Y.; Ma, H.; Saha, T. Improvement of Power Transformer Insulation Diagnosis Using Oil Characteristics Data Preprocessed by SMOTEBoost Technique. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2363–2373. [Google Scholar] [CrossRef]
- Kherif, O.; Benmahamed, Y.; Teguar, M.; Boubakeur, A.; Ghoneim, S.M. Accuracy Improvement of Power Transformer Faults Diagnostic Using KNN Classifier With Decision Tree Principle. IEEE Access 2021, 9, 81693–81701. [Google Scholar] [CrossRef]
- Su, L.; Cui, Y.; Yu1, Z.; Chen, L.; Xu, P.; Hou, H.; Sheng, G. A Power Transformer Fault Diagnosis Method Based on Hierarchical Classification and Ensemble Learning. J. Phys. Conf. Ser. 2019, 1346, 012045. [Google Scholar] [CrossRef]
- Wurzberger, F.; Schwenker, F. Learning in Deep Radial Basis Function Networks. Entropy 2024, 26, 368. [Google Scholar] [CrossRef]
- Bilal, M.; Ullah, Z.; Mujahid, O.; Fouzder, T. Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation. J. Imaging 2024, 10, 124. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Khalid, S.; Tahir, M.F.; Tzes, A.; Raza, A. A novel dc fault protection scheme based on intelligent network for meshed dc grids, International. J. Electr. Power Energy Syst. 2023, 154, 109423. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Tahir, M.F.; Raza, A.; Khan, M.A.; Badshah, F. Intelligent Sensors for dc Fault Location Scheme Based on Optimized Intelligent Architecture for HVdc Systems. Sensors 2022, 22, 9936. [Google Scholar] [CrossRef]



| Defect | Abbreviation | Interpretation | Sample |
|---|---|---|---|
| Normal | N | Healthy samples category | 44 |
| Electrical | PD | Partial Discharge | 32 |
| LED | Low-energy discharge | 32 | |
| HED | High-energy discharge | 24 | |
| Thermal | OH1 | 32 | |
| OH2 | 28 | ||
| Cellulose decomposition | CD | Cellulose degradation | 32 |
| OH2-CD | Thermal (t > 700 °C) and cellulose degradation | 20 | |
| ED-CD | Energy discharge and cellulose degradation | 24 |
| Defect | Retained Category | Sub-Bases | Learning Sets | Validation Sets |
|---|---|---|---|---|
| Subnetwork 1 | Healthy samples | 33 | 22 | 11 |
| Defect samples | 168 | 112 | 56 | |
| Subnetwork 2 | Electric | 66 | 44 | 22 |
| Thermal | 45 | 30 | 15 | |
| Cellulose degradation | 57 | 38 | 19 | |
| Subnetwork 3 | PD | 24 | 16 | 8 |
| LED | 24 | 16 | 8 | |
| HED | 18 | 12 | 6 | |
| Subnetwork 4 | OH1 | 24 | 16 | 8 |
| OH2 | 21 | 14 | 7 | |
| Subnetwork 5 | CD | 24 | 16 | 8 |
| OH2-CD | 15 | 10 | 5 | |
| ED-CD | 18 | 12 | 6 |
| Defect | Retained Category | Initial Example | Retained Centers |
|---|---|---|---|
| Subnetwork 1 | Healthy samples | 22 | 16 |
| Defect samples | 112 | 16 | |
| Subnetwork 2 | Electric | 44 | 8 |
| Thermal | 30 | 8 | |
| Cellulose degradation | 38 | 8 | |
| Subnetwork 3 | PD | 16 | 4 |
| LED | 16 | 4 | |
| HED | 12 | 4 | |
| Subnetwork 4 | OH1 | 16 | 4 |
| OH2 | 14 | 4 | |
| Subnetwork 5 | CD | 16 | 4 |
| OH2-CD | 10 | 4 | |
| ED-CD | 12 | 4 |
| Kernel Functions Number | Sensitivity (%) |
|---|---|
| 9 | 65.29 |
| 18 | 77.23 |
| 36 | 81.71 |
| 72 | 91.79 |
| 134 | 83.95 |
| Class | Statistical Parameters | Hierarchical Model | Single RBF |
|---|---|---|---|
| N | AUROC | 100 [100–100] | 96.4 [92.3–100] |
| Sensitivity | 100 | 95.5 | |
| Specificity | 100 | 99.1 | |
| False positive | 0 | 0.9 | |
| False negative | 0 | 4.5 | |
| VPP | 100 | 95.5 | |
| VPN | 100 | 99.1 | |
| PD | AUROC | 99.7 [99.1–100] | 96.5 [92.6–100] |
| Sensitivity | 96.9 | 93.8 | |
| Specificity | 99.6 | 99.2 | |
| False positive | 0.4 | 0.8 | |
| False negative | 3.1 | 6.3 | |
| VPP | 96.9 | 93.8 | |
| VPN | 99.6 | 99.2 | |
| LED | AUROC | 99.3 [98.3–100] | 95 [90.4–99.6] |
| Sensitivity | 93.8 | 90.6 | |
| Specificity | 99.6 | 98.7 | |
| False positive | 0.4 | 1.3 | |
| False negative | 6.3 | 9.4 | |
| VPP | 96.8 | 90.6 | |
| VPN | 99.2 | 98.7 | |
| HED | AUROC | 98.7 [97–100] | 92.3 [85.5–99.1] |
| Sensitivity | 91.7 | 83.3 | |
| Specificity | 99.2 | 98.4 | |
| False positive | 0.8 | 1.6 | |
| False negative | 8.3 | 16.7 | |
| VPP | 91.7 | 83.3 | |
| VPN | 99.2 | 98.4 | |
| OH1 | AUROC | 100 [100–100] | 98.4 [95.7–100] |
| Sensitivity | 100 | 96.9 | |
| Specificity | 100 | 99.2 | |
| False positive | 0 | 0.8 | |
| False negative | 0 | 3.1 | |
| VPP | 100 | 93.9 | |
| VPN | 100 | 99.6 | |
| OH2 | AUROC | 94.8 [88–100] | 92.5 [85.7–99.4] |
| Sensitivity | 89.3 | 85.7 | |
| Specificity | 100 | 98.8 | |
| False positive | 0 | 1.3 | |
| False negative | 10.7 | 14.3 | |
| VPP | 100 | 88.9 | |
| VPN | 98.8 | 98.3 | |
| CD | AUROC | 100 [100–100] | 99.4 [98.5–100] |
| Sensitivity | 100 | 96.9 | |
| Specificity | 100 | 99.2 | |
| False positive | 0 | 0.8 | |
| False negative | 0 | 3.1 | |
| VPP | 100 | 93.9 | |
| VPN | 100 | 99.6 | |
| OH2-CD | AUROC | 100 [100–100] | 96.3 [91.5–100] |
| Sensitivity | 100 | 90 | |
| Specificity | 100 | 98.8 | |
| False positive | 0 | 1.2 | |
| False negative | 0 | 10 | |
| VPP | 100 | 85.7 | |
| VPN | 100 | 99.2 | |
| ED-CD | AUROC | 100 [100–100] | 96.5 [92.5–100] |
| Sensitivity | 100 | 87.5 | |
| Specificity | 99.2 | 99.2 | |
| False positive | 0.8 | 0.8 | |
| False negative | 0 | 12.5 | |
| VPP | 92.3 | 91.3 | |
| VPN | 100 | 98.8 |
| Hierarchical Model | Single RBF | |
|---|---|---|
| AUROC | 99.16 [98.04–100] | 95.92 [91.63–99.78] |
| Sensitivity | 96.85 | 91.13 |
| Specificity | 99.73 | 98.95 |
| False positive | 0.27 | 1.05 |
| False negative | 3.15 | 8.87 |
| VPP | 97.52 | 90.77 |
| VPN | 99.64 | 98.99 |
| Learning time (s) | 105 0.015 | 398 0.043 |
| Execution time (s) | 0.013 0.002 | 0.022 0.006 |
| Subnetwork 1 | Subnetwork 2 | Subnetwork 3 | Subnetwork 4 | Subnetwork 5 | |
|---|---|---|---|---|---|
| AUROC (95% CI) (p-value < 0.001) | 100 [100–100] | 99.33 [98.57–100] | 99.13 [97.83–100] | 99.45 [98.55–100] | 100 [100–100] |
| Sensitivity | 100 | 97.77 | 97.93 | 98.1 | 100 |
| Specificity | 100 | 98.9 | 98.83 | 98.1 | 100 |
| False positive | 0 | 0.5 | 1.17 | 1.9 | 0 |
| False negative | 0 | 2.23 | 2.07 | 1.9 | 0 |
| VPP | 0 | 2.23 | 2.07 | 1.9 | 0 |
| VPN | 100 | 98.87 | 98.8 | 98.5 | 100 |
| Method | Classes Number | Examples Number | Generalization Rate (%) |
|---|---|---|---|
| RBF + OLS [22] | 6 | 214 | 91 |
| RBF + k-AC method [23] | 5 | 22 | 90.90 |
| KNN classifier with decision tree principle [31] | 6 | 501 | 92.5 |
| Hierarchical classification + ensemble learning [32] | 9 | 457 | Back propagation NN: 98.59 SVM: 79.65 Random forest: 76.81 Proposed method: 90.37 |
| RBF + FCM + QPSO [21] | 4 | 50 | 82.64 |
| {SVM, C45, RBF, KNN} + SMOTE [30] | 4 | 181 | C45: 98 KNN: 84 RBF: 84 SVM: 98 |
| RBF + {PSO, Gradient, FFA, IFFA} [27] | 5 | 580 | GD: 78.73 PSO: 90.22 FFA: 92.52 IFFA: 98.27 |
| RBF + LBG + SLP | 9 | 256 | Single RBF: 91.13 Hierarchical model: 96.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hendel, M.; Bousmaha, I.S.; Meghnefi, F.; Fofana, I.; Brahami, M. An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms. Energies 2024, 17, 3171. https://doi.org/10.3390/en17133171
Hendel M, Bousmaha IS, Meghnefi F, Fofana I, Brahami M. An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms. Energies. 2024; 17(13):3171. https://doi.org/10.3390/en17133171
Chicago/Turabian StyleHendel, Mounia, Imen Souhila Bousmaha, Fethi Meghnefi, Issouf Fofana, and Mostefa Brahami. 2024. "An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms" Energies 17, no. 13: 3171. https://doi.org/10.3390/en17133171
APA StyleHendel, M., Bousmaha, I. S., Meghnefi, F., Fofana, I., & Brahami, M. (2024). An Intelligent Power Transformers Diagnostic System Based on Hierarchical Radial Basis Functions Improved by Linde Buzo Gray and Single-Layer Perceptron Algorithms. Energies, 17(13), 3171. https://doi.org/10.3390/en17133171







