Photo-Thermal Optimization of a Parabolic Trough Collector with Arrayed Selective Coatings
Abstract
:1. Introduction
2. Materials and Methods
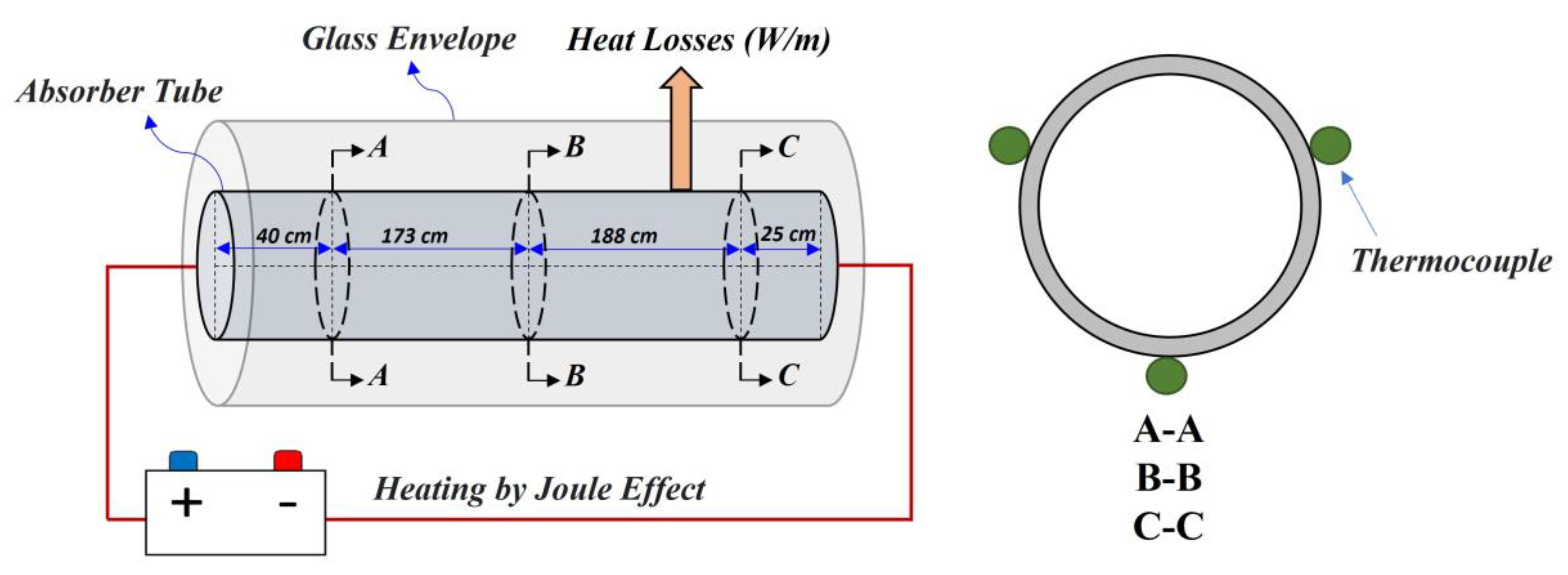
2.1. Reference System
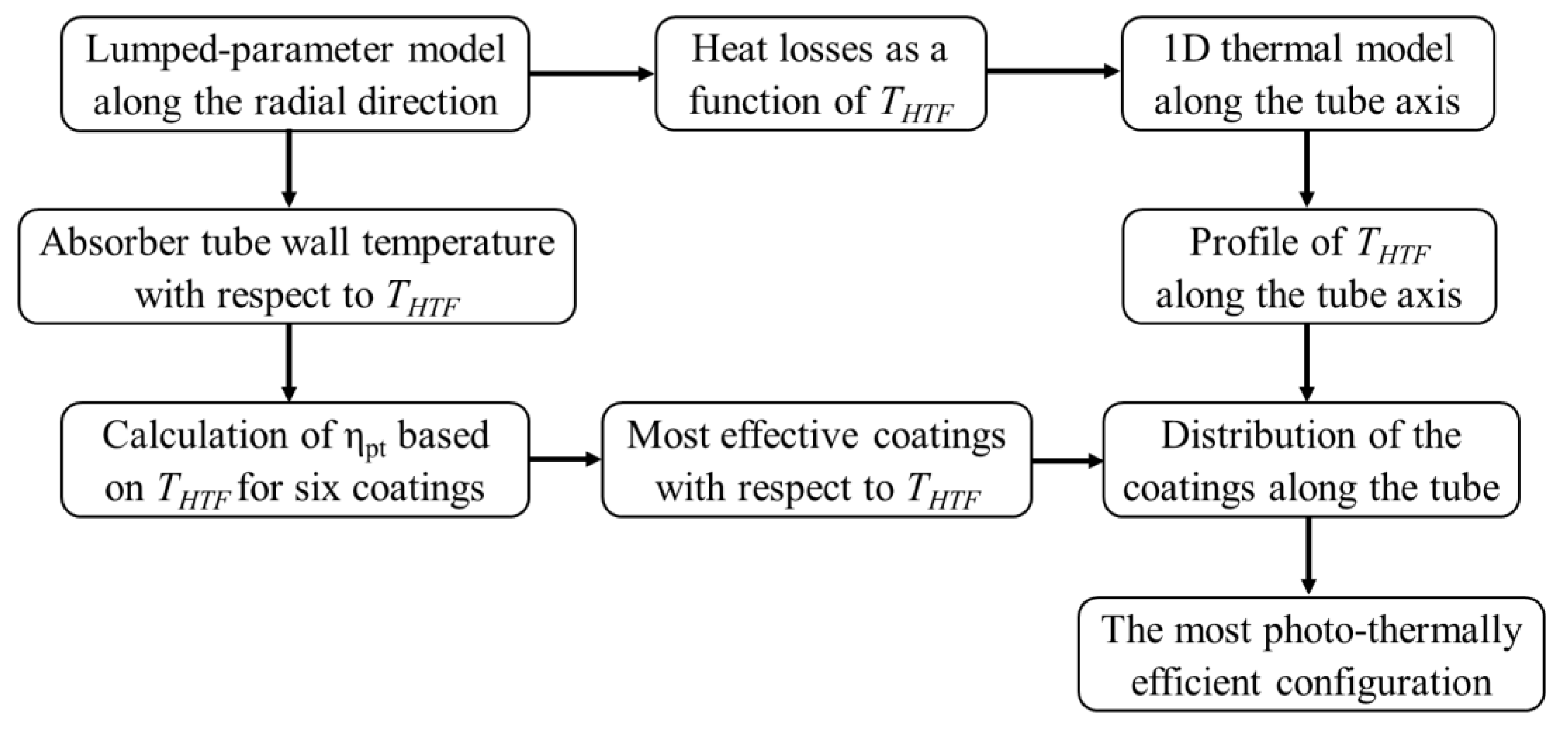
2.2. Methodology
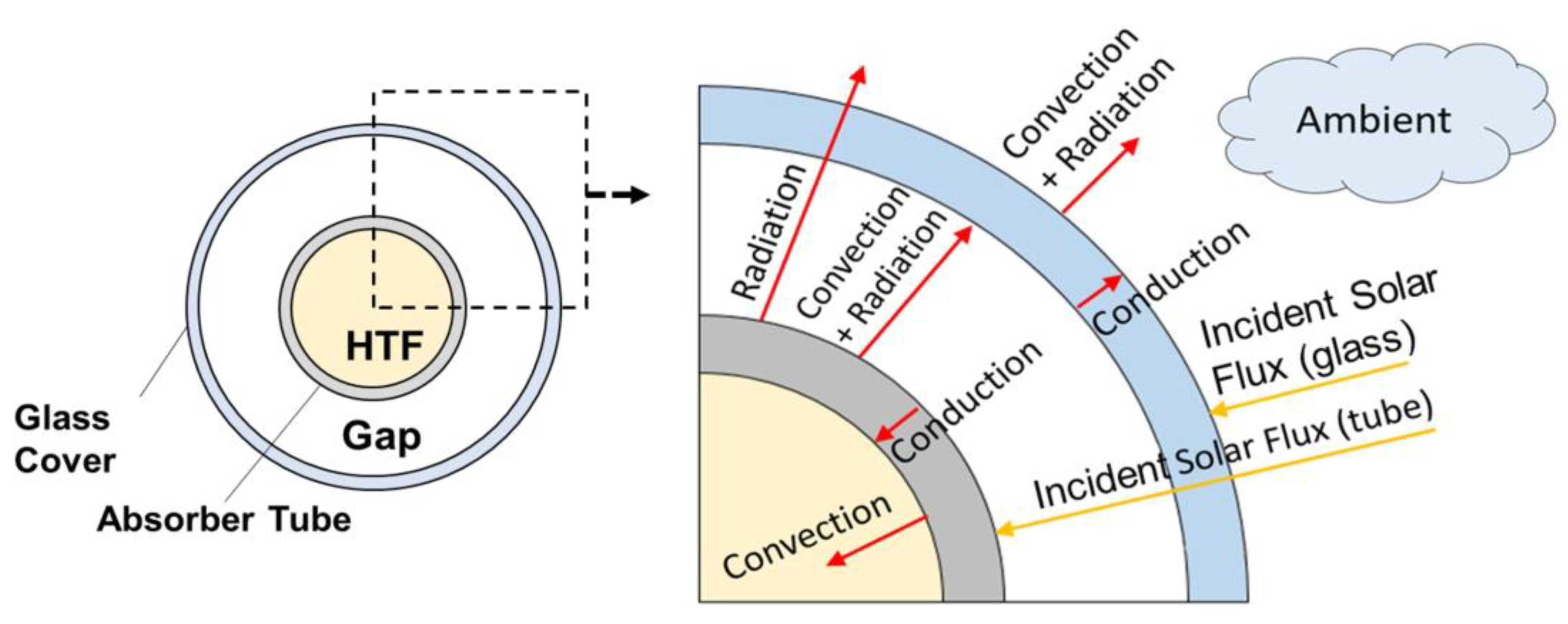
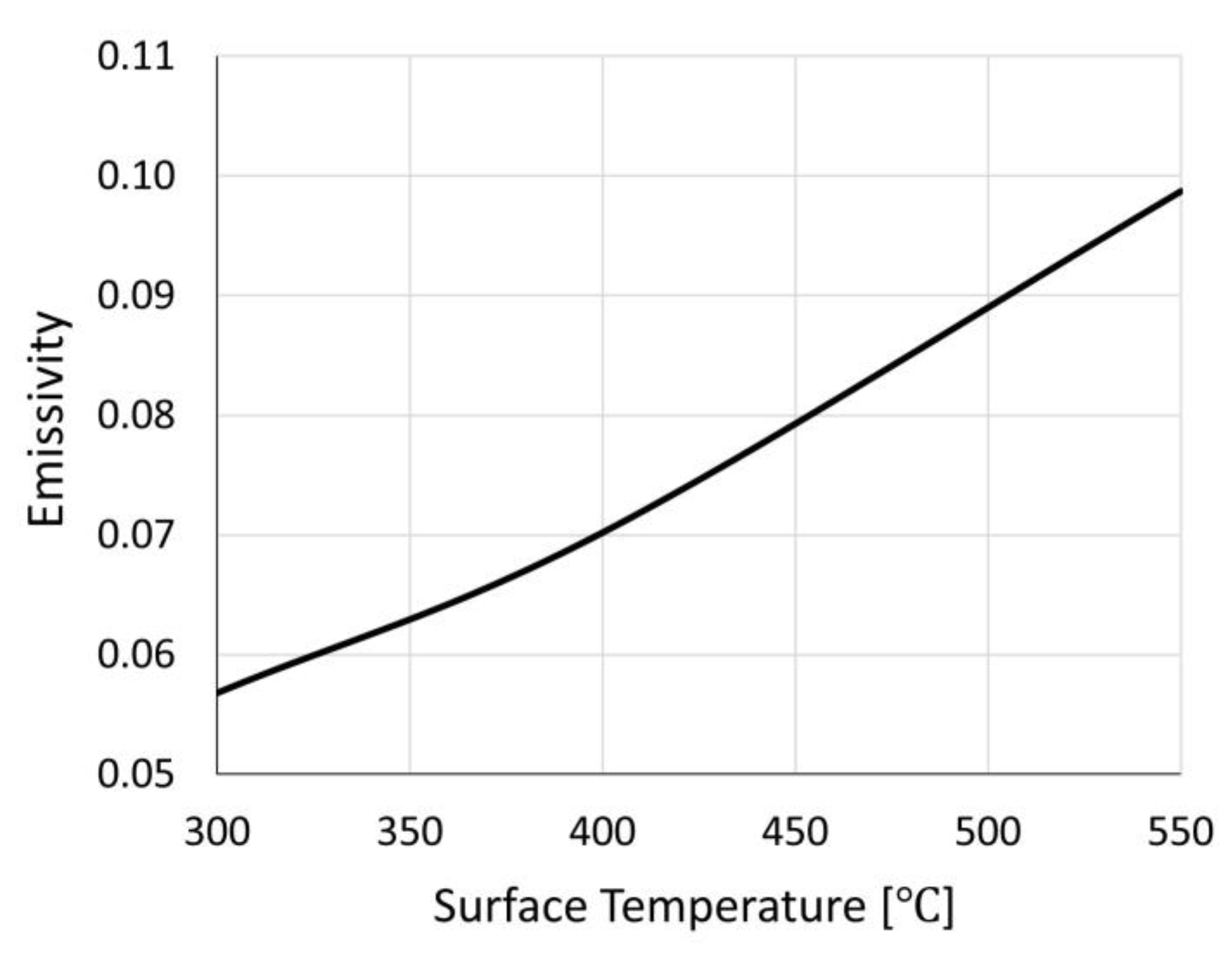
2.3. Lumped-Parameter Model
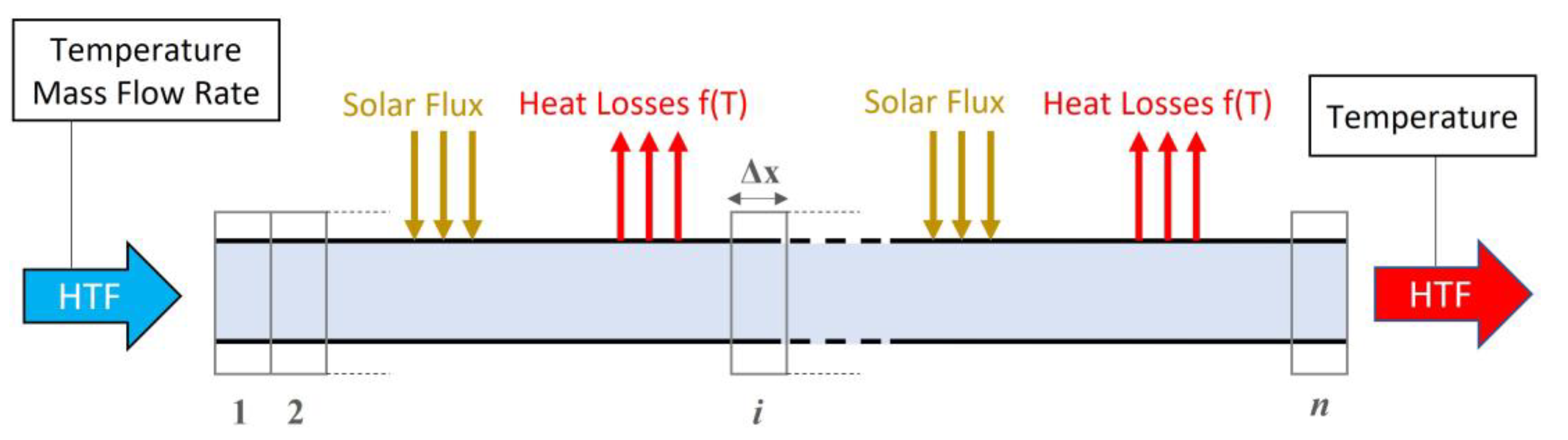
2.4. 1D Model
3. Results and Discussion
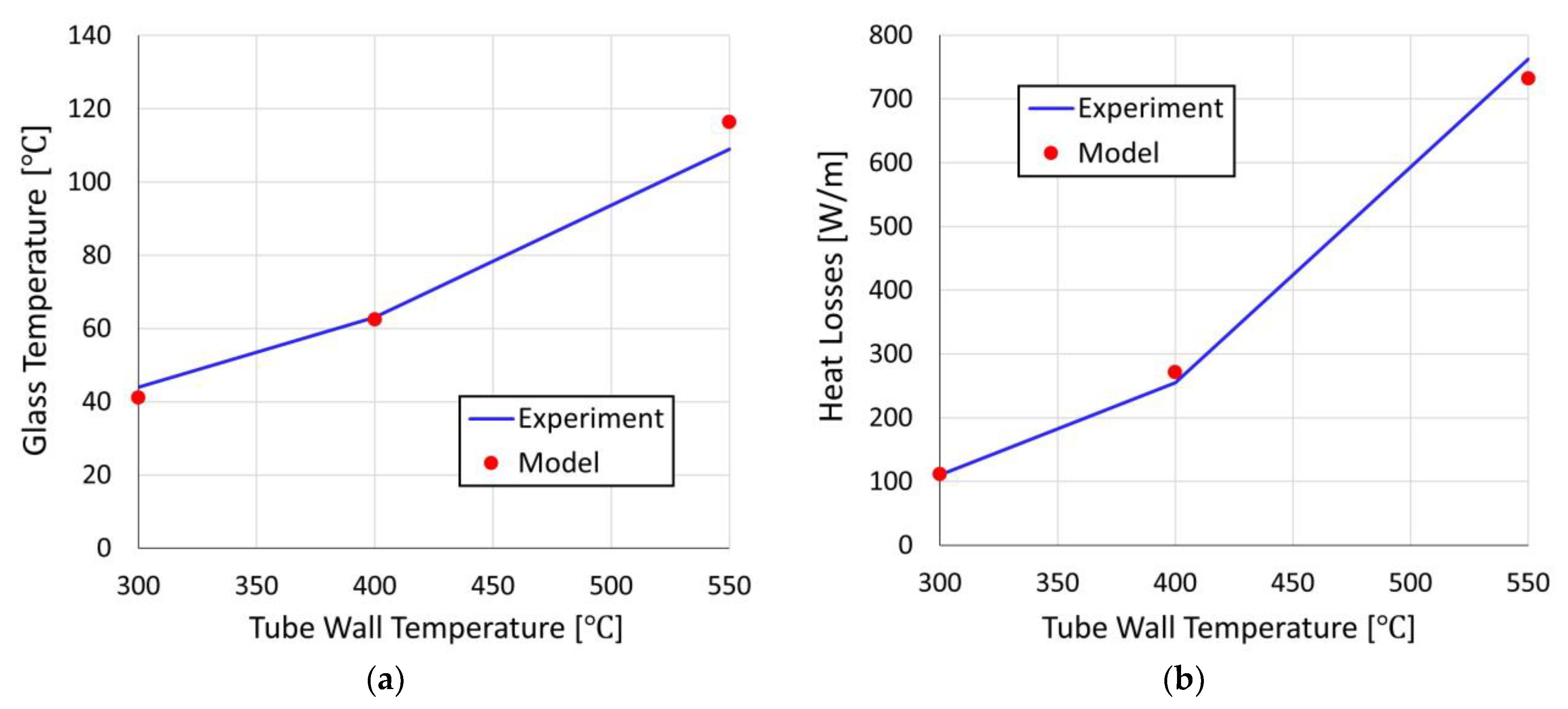
3.1. Validation
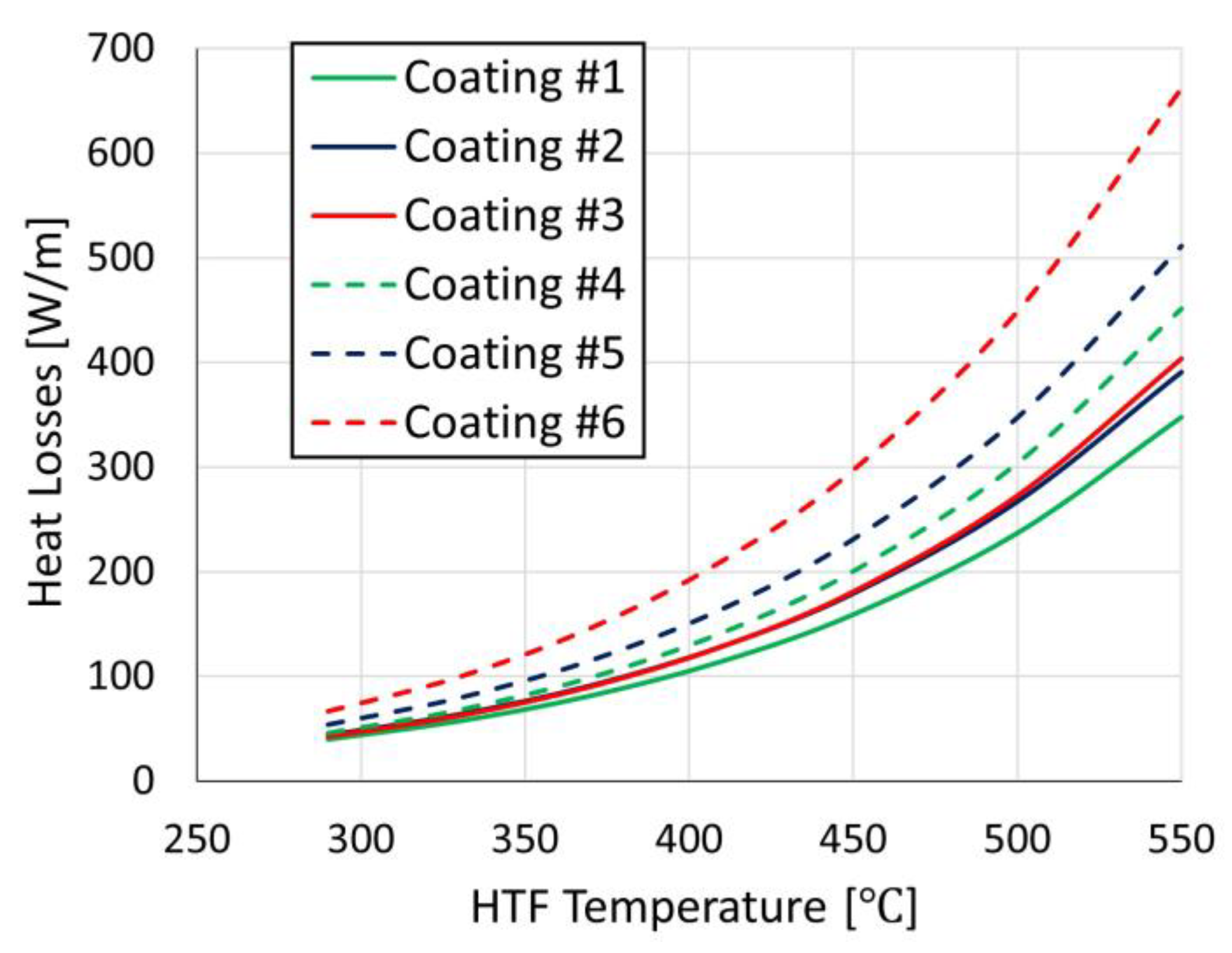
3.2. Results of the Lumped-Parameter Model
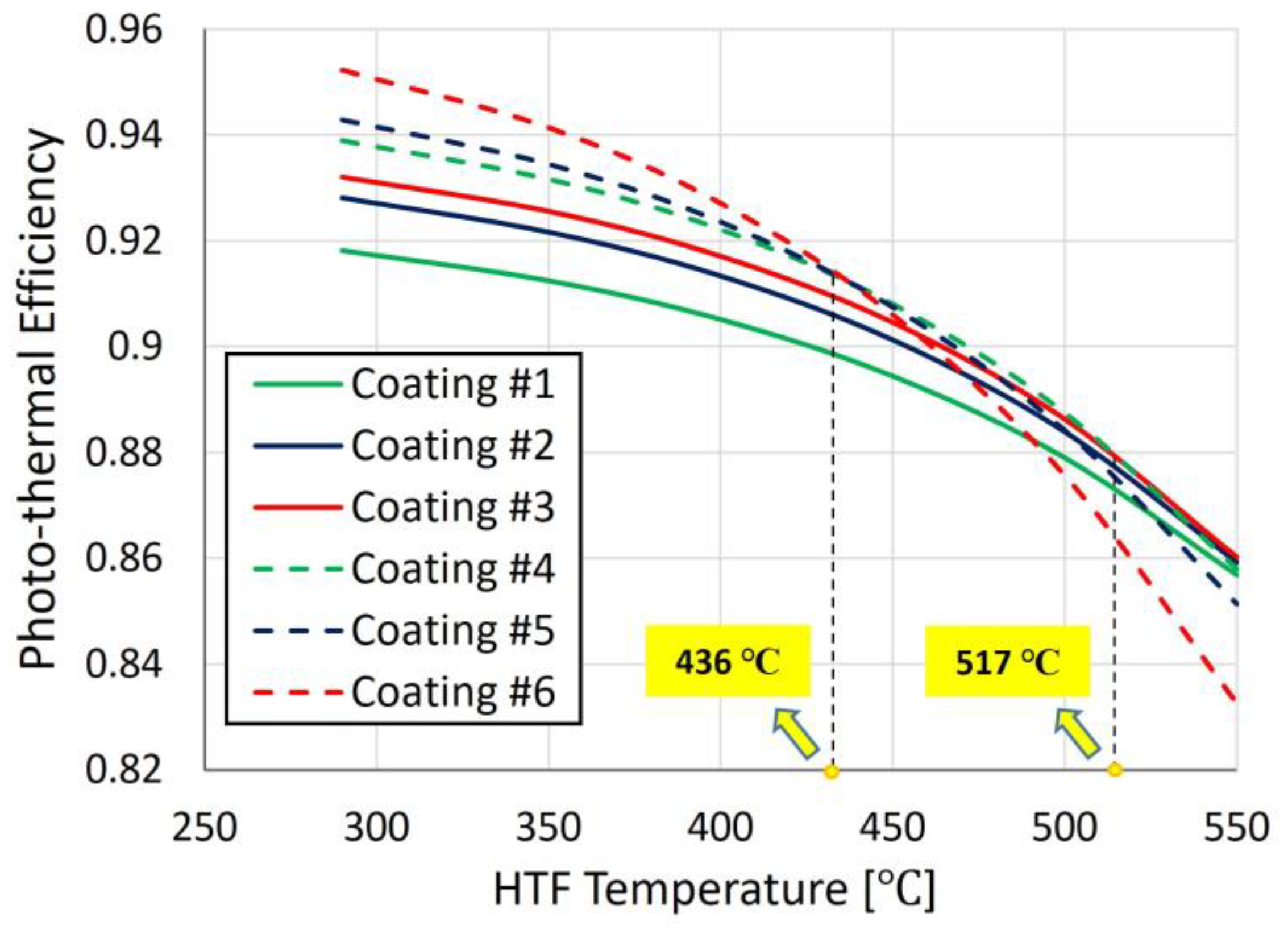
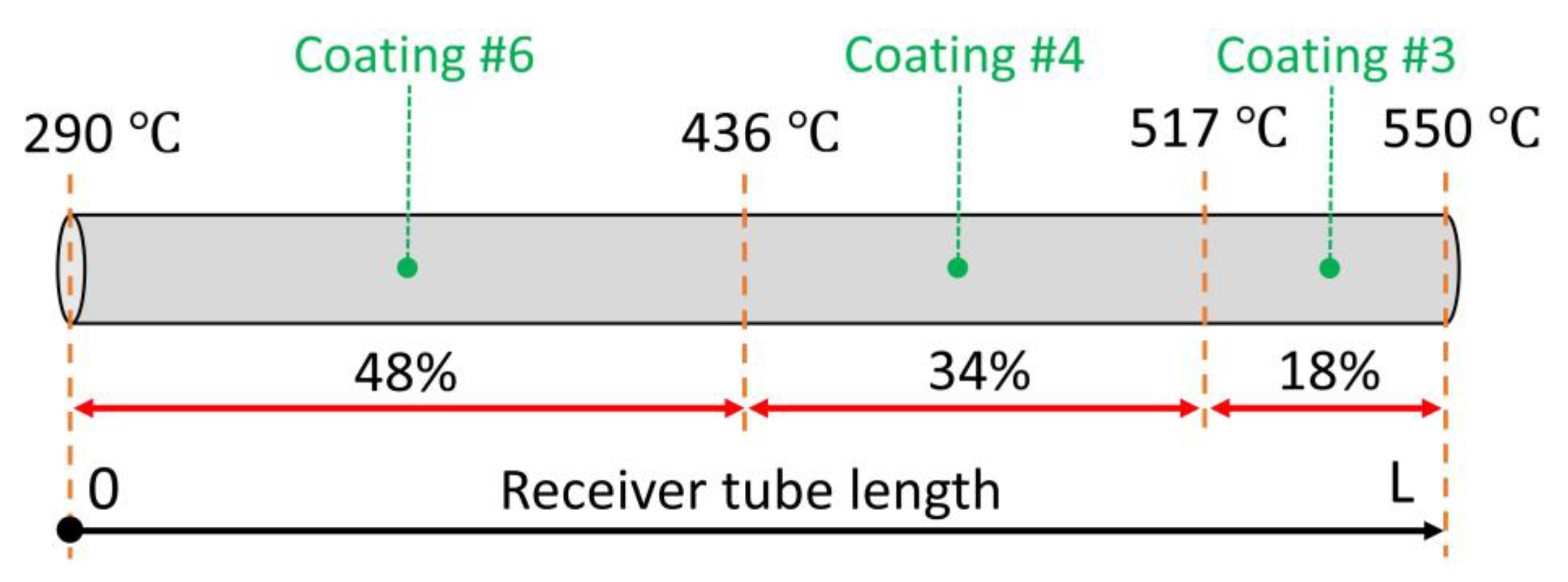
3.3. Photo-Thermal Optimization of the PTC System
- 290–436 °C → Coating #6
- 436–517 °C → Coating #4
- 517–550 °C → Coating #3
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saini, P.; Singh, S.; Kajal, P.; Dhar, A.; Khot, N.; Mohamed, M.E.; Powar, S. A Review of the Techno-Economic Potential and Environmental Impact Analysis through Life Cycle Assessment of Parabolic Trough Collector towards the Contribution of Sustainable Energy. Heliyon 2023, 9, e17626. [Google Scholar] [CrossRef]
- Shagdar, E.; Lougou, B.G.; Shuai, Y.; Anees, J.; Damdinsuren, C.; Tan, H. Performance Analysis and Techno-Economic Evaluation of 300 MW Solar-Assisted Power Generation System in the Whole Operation Conditions. Appl. Energy 2020, 264, 114744. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, M.; Liu, C.; Dai, Z. Cyclic Thermal Characterization of a Molten-Salt Packed-Bed Thermal Energy Storage for Concentrating Solar Power. Appl. Energy 2017, 195, 761–773. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, Y.; Shen, Y.; Shen, Z.; Yang, H. A Mutually Beneficial System Incorporating Parabolic Trough Concentrating Solar Power System with Photovoltaics: A Comprehensive Techno-Economic Analysis. Appl. Energy 2024, 360, 122834. [Google Scholar] [CrossRef]
- Guillén-Lambea, S.; Carvalho, M. A Critical Review of the Greenhouse Gas Emissions Associated with Parabolic Trough Concentrating Solar Power Plants. J. Clean. Prod. 2021, 289, 125774. [Google Scholar] [CrossRef]
- Al-Maliki WA, K.; Hadi, A.S.; Al-Khafaji HM, H.; Alobaid, F.; Epple, B. Novel Feedwater Preheating System for Parabolic Trough Solar Power Plant. Energy Rep. 2022, 8, 10665–10687. [Google Scholar] [CrossRef]
- Li, C.; Goswami, Y.; Stefanakos, E. Solar Assisted Sea Water Desalination: A Review. Renew. Sustain. Energy Rev. 2013, 19, 136–163. [Google Scholar] [CrossRef]
- Mohammadi, K.; Khanmohammadi, S.; Immonen, J.; Powell, K. Techno-Economic Analysis and Environmental Benefits of Solar Industrial Process Heating Based on Parabolic Trough Collectors. Sustain. Energy Technol. Assess. 2021, 47, 101412. [Google Scholar] [CrossRef]
- Xia, J.; Li, Y.; Li, C.; Wang, Y.; Xie, L.; Miao, Y.; Zhang, Q.; Hao, C.; Sun, G. Performance Evaluation of Different Solar Collectors in Building Cooling, Heating, and Hot Water Supply. J. Renew. Sustain. Energy 2020, 12, 043701. [Google Scholar] [CrossRef]
- Hamada, M.A.; Ehab, A.; Khalil, H.; Al-Sood MM, A.; Sharshir, S.W. Thermal Performance Augmentation of Parabolic Trough Solar Collector Using Nanomaterials, Fins and Thermal Storage Material. J. Energy Storage 2023, 67, 107591. [Google Scholar] [CrossRef]
- Manikandan, G.K.; Iniyan, S.; Goic, R. Enhancing the Optical and Thermal Efficiency of a Parabolic Trough Collector—A Review. Appl. Energy 2019, 235, 1524–1540. [Google Scholar] [CrossRef]
- Olson, K.D.; Talghader, J.J. Solar Selective Coating Optimization for Direct Steam Generation Parabolic Trough Designs. Sol. Energy 2016, 124, 82–88. [Google Scholar] [CrossRef]
- Esposito, S.; D’Angelo, A.; Antonaia, A.; Castaldo, A.; Ferrara, M.; Addonizio, M.L.; Guglielmo, A. Optimization Procedure and Fabrication of Highly Efficient and Thermally Stable Solar Coating for Receiver Operating at High Temperature. Sol. Energy Mater. Sol. Cells 2016, 157, 429–437. [Google Scholar] [CrossRef]
- Esposito, S.; D’Angelo, A.; Diletto, C.; Guglielmo, A.; Lanchi, M.; Rossi, G. Solar Coatings Based on Ag Infrared Reflector with High Stability at Medium and High Temperature. Energies 2021, 14, 5910. [Google Scholar] [CrossRef]
- Diletto, C.; D’Angelo, A.; Esposito, S.; Guglielmo, A.; Mirabile Gattia, D.; Lanchi, M. Materials Based on Amorphous Al2O3 and Composite W-Al2O3 for Solar Coatings Deposited by High-Rate Sputter Processes. Solar 2023, 3, 113–131. [Google Scholar] [CrossRef]
- D’Angelo, A.; Diletto, C.; Esposito, S.; Graditi, G.; Guglielmo, A.; Lanchi, M.; Rossi, G. Spectrally Selective Solar Coating Based on W-AlN Cermet Fabricated by Reactive Sputtering Processes at High Deposition Rate. AIP Conf. Proc. 2022, 2445, 020002. [Google Scholar]
- Yang, H.; Wang, Q.; Huang, Y.; Feng, J.; Ao, X.; Hu, M.; Pei, G. Spectral Optimization of Solar Selective Absorbing Coating for Parabolic Trough Receiver. Energy 2019, 183, 639–650. [Google Scholar] [CrossRef]
- Nagaraj, A. Experimental Study of Epoxy Based Graphite Coating on Parabolic Trough Solar Collector. J. Phys. Conf. Ser. 2022, 2180, 012001. [Google Scholar] [CrossRef]
- Al-Rabeeah, A.Y.; Seres, I.; Farkas, I. Experimental Investigation of Parabolic Trough Solar Collector Thermal Efficiency Enhanced with Different Absorber Coatings. Int. J. Thermofluids 2023, 19, 100386. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Q.; Huang, X.; Li, J.; Pei, G. Performance Study and Comparative Analysis of Traditional and Double-Selective-Coated Parabolic Trough Receivers. Energy 2018, 145, 206–216. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Q.; Zhong, S.; Kwan, T.H.; Feng, J.; Cao, J.; Pei, G. Spectral-Spatial Design and Coupling Analysis of the Parabolic Trough Receiver. Appl. Energy 2020, 264, 114692. [Google Scholar] [CrossRef]
- Zhao, K.; Jin, H.; Gai, Z.; Hong, H. A Thermal Efficiency-Enhancing Strategy of Parabolic Trough Collector Systems by Cascadingly Applying Multiple Solar Selective-Absorbing Coatings. Appl. Energy 2022, 309, 118508. [Google Scholar] [CrossRef]
- Singh, S.K.; Tiwari, A.K.; Paliwal, H.K. Performance Augmentation Strategy of Parabolic Trough Collector by Employing MXene-Based Solar Absorbing Coating. Process Saf. Environ. Prot. 2023, 174, 971–982. [Google Scholar] [CrossRef]
- Stanek, B.; Wang, W.; Bartela, Ł. A Potential Solution in Reducing the Parabolic Trough Based Solar Industrial Process Heat System Cost by Partially Replacing Absorbers Coatings with Non-Selective Ones in Initial Loop Sections. Appl. Energy 2023, 331, 120472. [Google Scholar] [CrossRef]
- Ferri, R.; Cammi, A.; Mazzei, D. Molten Salt Mixture Properties in RELAP5 Code for Thermodynamic Solar Applications. Int. J. Therm. Sci. 2008, 47, 1676–1687. [Google Scholar] [CrossRef]
- Esposito, S.; Antonaia, A.; Addonizio, M.L.; Aprea, S. Fabrication and Optimisation of Highly Efficient Cermet-Based Spectrally Selective Coatings for High Operating Temperature. Thin Solid Film 2009, 517, 6000–6006. [Google Scholar] [CrossRef]
- Antonaia, A.; Esposito, S.; Addonizio, M.L.; Guglielmo, A. Solar Selective Adsorber Based on Double Nitride Composite Materials and Process for Its. Preparation. Patent IPN WO/2012/172505, 20 December 2012. [Google Scholar]
- Cagnoli, M.; Mazzei, D.; Procopio, M.; Russo, V.; Savoldi, L.; Zanino, R. Analysis of the Performance of Linear Fresnel Collectors: Encapsulated vs. Evacuated Tubes. Sol. Energy 2018, 164, 119–138. [Google Scholar] [CrossRef]
- Forristall, R. Heat Transfer Analysis and Modeling of a Parabolic Trough Solar Receiver Implemented in Engineering Equation Solver; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2003; NREL/TP-550-34169. [Google Scholar]
- Rodriguez-Sanchez, M.R.; Soria, A.; Almendros-Ibáñez, J.A.; Acosta-Iborra, A.; Santana, D. Thermal Design Guidelines of Solar Power Towers. Appl. Therm. Eng. 2014, 63, 428–438. [Google Scholar] [CrossRef]
- Österholm, R.; Pålsson, J. Dynamic Modelling of a Parabolic Trough Solar Power Plant. In Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014. [Google Scholar]
- Soltigua. 1MWe CSP-ORC Pilot Plant, Solar Field Process Description; Report No.: S-F14ET001-M-B-A-2602-C; Soltigua SRL: Gambettola, Italy, 2015. [Google Scholar]
- Les, I.; Mutuberria, A.; Schöttl, P.; Nitz, P. New Functionalities for the Tonatiuh Ray-Tracing Software. In Proceedings of the 23rd SolarPACES Conference, Santiago, Chile, 26–29 September 2017. [Google Scholar]
- Qiu, Y.; He, Y.-L.; Cheng, Z.-D.; Wang, K. Study on Optical and Thermal Performance of a Linear Fresnel Solar Reflector Using Molten Salt as HTF with MCRT and FVM Methods. Appl. Energy 2015, 146, 162–173. [Google Scholar] [CrossRef]
- ASTM International. Standard G173-03: Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface. Derived from SMARTS v. 2.9.2. 2003. Available online: https://www.astm.org/standards/g173.htm (accessed on 15 May 2021).

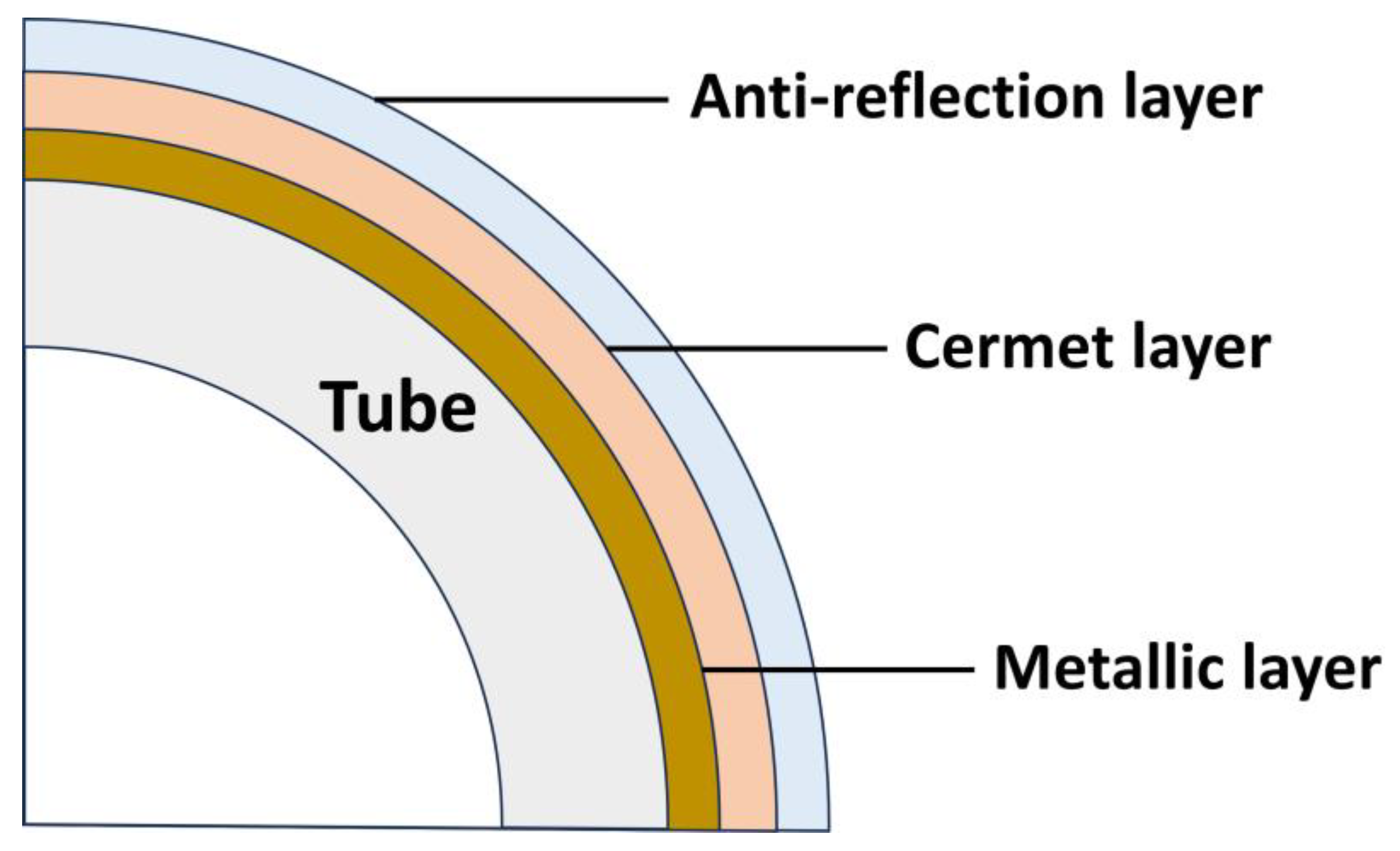
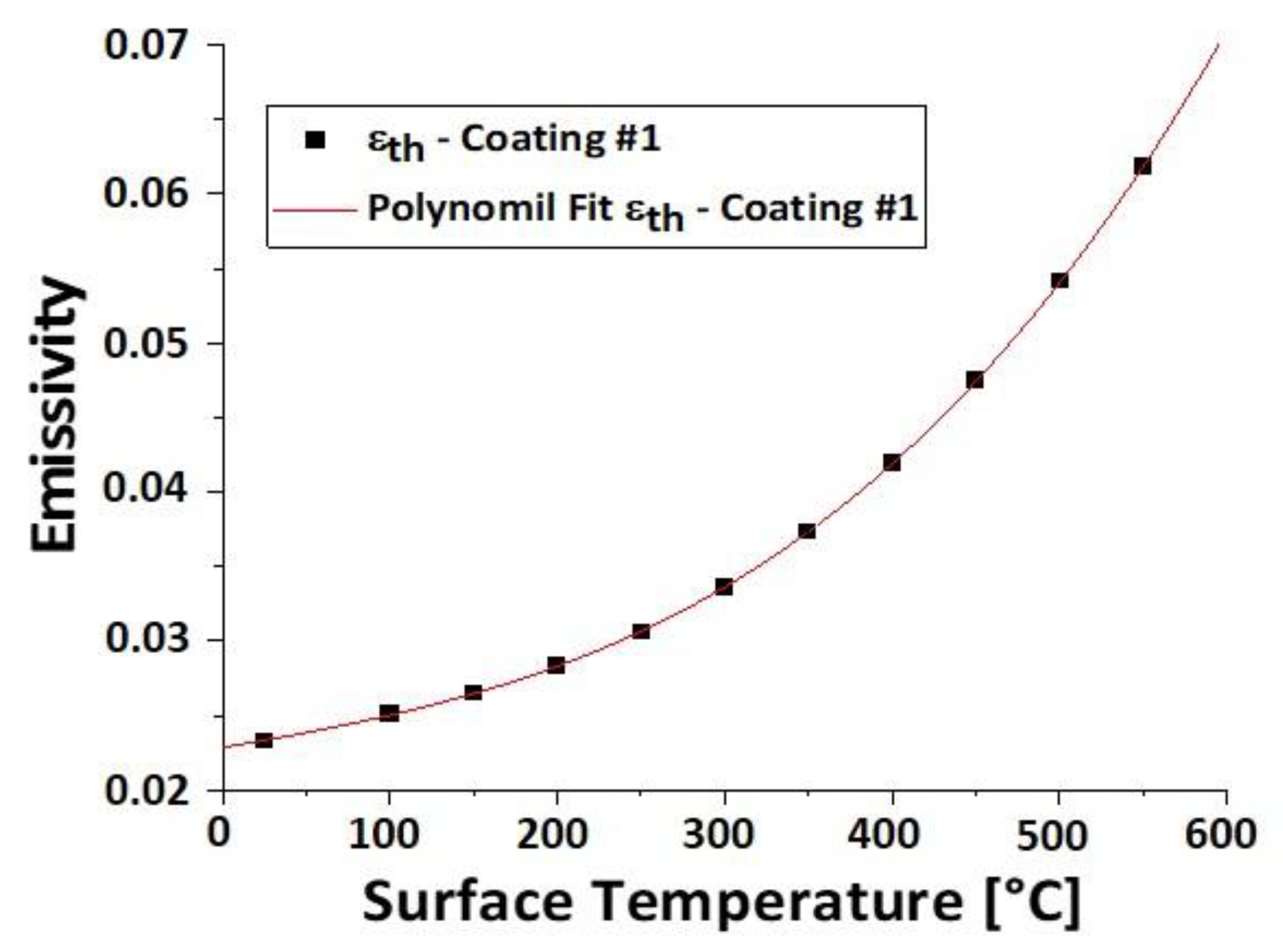
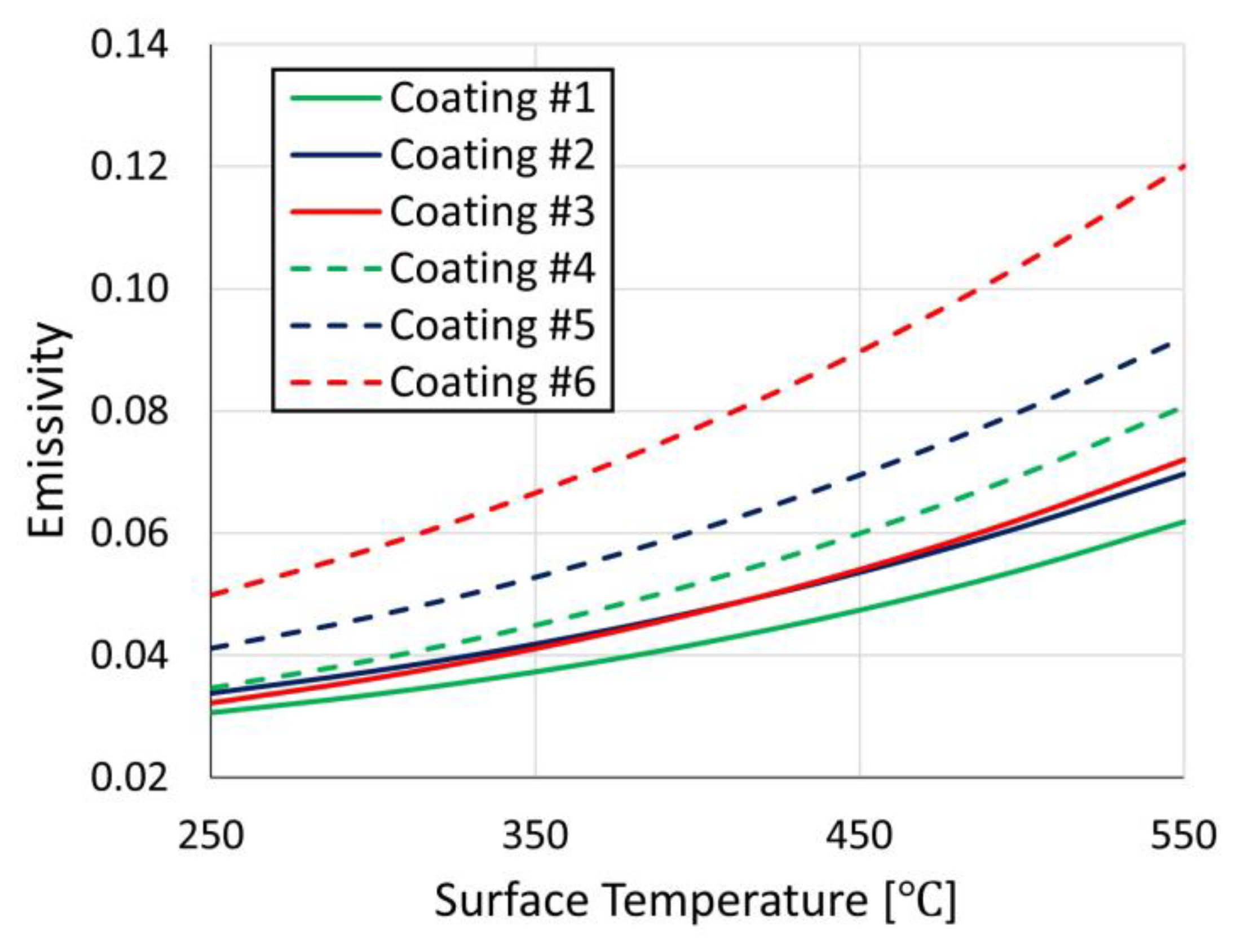


| Parameter | Value |
|---|---|
| Intercept | 0.02286 ± 0.00008 |
| B1 | 1.90641 × 10−5 ± 1.12155 × 10−6 |
| B2 | 9.95123 × 10−9 ± 4.50843 × 10−9 |
| B3 | 1.52744 × 10−10 ± 5.15498 × 10−12 |
| Residual sum of squares | 2.49034 × 10−8 |
| R-squared (COD) | 0.99998 |
| Selective Coating | Absorptance | Emissivity |
|---|---|---|
| Coating #1 | 0.9265 | ε1 = 1.53 × 10−10 T3 + 9.95 × 10−9 T2 + 1.91 × 10−5 T + 0.023 |
| Coating #2 | 0.9375 | ε2 = 1.21 × 10−10 T3 + 5.56 × 10−8 T2 + 1.40 × 10−5 T + 0.025 |
| Coating #3 | 0.9411 | ε3 = 1.62 × 10−10 T3 + 3.21 × 10−8 T2 + 2.55 × 10−5 T + 0.021 |
| Coating #4 | 0.9486 | ε4 = 1.61 × 10−10 T3 + 6.95 × 10−8 T2 + 1.73 × 10−5 T + 0.023 |
| Coating #5 | 0.9544 | ε5 = 1.01 × 10−10 T3 + 1.49 × 10−7 T2 − 9.80 × 10−7 T + 0.030 |
| Coating #6 | 0.9665 | ε6 = 1.42 × 10−10 T3 + 1.70 × 10−7 T2 + 2.66 × 10−5 T + 0.030 |
| Selective Coating | a | b | c |
|---|---|---|---|
| Coating #1 | 0.00411 ± 0.00001 | −2.299 ± 0.004 | 365.1 ± 1.7 |
| Coating #2 | 0.00458 ± 0.00001 | −2.547 ± 0.004 | 402.2 ± 1.8 |
| Coating #3 | 0.00490 ± 0.00001 | −2.770 ± 0.005 | 438.3 ± 2.0 |
| Coating #4 | 0.00555 ± 0.00001 | −3.150 ± 0.005 | 498.2 ± 2.2 |
| Coating #5 | 0.00611 ± 0.00001 | −3.425 ± 0.006 | 539.0 ± 2.3 |
| Coating #6 | 0.00796 ± 0.00002 | −4.462 ± 0.007 | 698.7 ± 3.0 |
| ΔTHTF [°C] | Selective Coating | Tube Length [m] | ||||
|---|---|---|---|---|---|---|
| = 1 kg/s | = 1.5 kg/s | = 2.2 kg/s | = 3 kg/s | |||
| 290–436 | #6 | 356 | 537 | 792 | 1070 | 1435 |
| 436–517 | #4 | 257 | 383 | 566 | 765 | 1032 |
| 517–550 | #3 | 133 | 198 | 293 | 391 | 527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokrnia, M.; Cagnoli, M.; Grena, R.; D’Angelo, A.; Lanchi, M.; Zanino, R. Photo-Thermal Optimization of a Parabolic Trough Collector with Arrayed Selective Coatings. Energies 2024, 17, 3221. https://doi.org/10.3390/en17133221
Shokrnia M, Cagnoli M, Grena R, D’Angelo A, Lanchi M, Zanino R. Photo-Thermal Optimization of a Parabolic Trough Collector with Arrayed Selective Coatings. Energies. 2024; 17(13):3221. https://doi.org/10.3390/en17133221
Chicago/Turabian StyleShokrnia, Mehdi, Mattia Cagnoli, Roberto Grena, Antonio D’Angelo, Michela Lanchi, and Roberto Zanino. 2024. "Photo-Thermal Optimization of a Parabolic Trough Collector with Arrayed Selective Coatings" Energies 17, no. 13: 3221. https://doi.org/10.3390/en17133221
APA StyleShokrnia, M., Cagnoli, M., Grena, R., D’Angelo, A., Lanchi, M., & Zanino, R. (2024). Photo-Thermal Optimization of a Parabolic Trough Collector with Arrayed Selective Coatings. Energies, 17(13), 3221. https://doi.org/10.3390/en17133221







