Thermodynamic Analysis of Chloride Corrosion in Steel for Energy System Applications in Fe-O-Cl-Na Environments
Abstract
:1. Corrosion of Iron in the Gas Phase Containing Chlorine Compounds
- The phenomenon of diffusion of gaseous Cl2/HCl through the pores or cracks present in the oxide phase of metals, up to the metal–scale interface, where the formation of ferrous chloride FeCl2(s) takes place.
- The volatilisation properties of FeCl2(s) → FeCl2(g) from the metal surface, and the diffusion of gaseous ferrous chloride through the porous and loose oxide scale layer back into the flue gas, where the chloride vapours are then oxidised to FexOy.
- Boundary conditions at the metal–oxide interface considering all components of the gas phase, which is of cognitive interest and necessary to determine the concentration gradient of the components that limit diffusion phenomena through the oxide layer in the metal–metal oxide–gas phase system.
- The influence of acting synergistically on the metal surface to form a solid iron chloride with a high tendency towards volatility () as well as a source of generated at the interface of ).
- The influence of on oxidation and reduction processes occurring at the metal–oxide interface.
- Corrosion effects related to alloy composition with respect to the carbon content in iron based on thermodynamic analysis based on a Fe-C equilibrium system with the determination of the cementite activity coefficient in iron .
- Conditions of carbon supersaturation on the surface of the iron alloy promoting potentially catastrophic pitting corrosion known in the literature as metal dusting.
- The role of water vapour in altering the oxide corrosion mechanism. In addition to chloride corrosion in this area, may be a criterion for steam-enhanced oxide corrosion, and an indicator of the susceptibility of steel to pitting corrosion associated with the decarburisation of steel.
- The action of sodium as a fuel component in the reaction space of the gas phase occurring in the form of gaseous chlorides (NaCl(g)). The technological conditions of the formation on the haematite surface of the sodium ferrate compound suggested in the literature as one of the postulates of the active oxidation model were discussed in thermodynamic terms. The effect of the formation of the liquid solution on the process of gaseous hydrogen evolution at the metal–oxide interface was determined, thus determining the composition of the gas phase in the reducing or oxidising range, regulating the corrosion phenomena associated with the direction and mechanism of the carburisation of steel. To estimate the magnitude of these phenomena, based on the thermodynamic analysis of the liquid system , the activity of was determined.
- The equilibrium composition of the gaseous phase resulting from the oxidation of hydrogen chloride, depending on the initial oxygen conditions prevailing in the system, using the author’s formalism of vector equations, thus specifying the boundary conditions at the metal oxide–gas interface.
- Trajectories of changes in partial pressures of the gaseous reactants from quasi-equilibrium to equilibrium states for the reducing and oxidising regions at the metal–metal oxide interface determining the course of corrosion.
- Iron chloride oxidation and oxide phase expansion phenomena verifying the parameters of the active oxidation postulate.
2. Fundamentals of Thermodynamic Process Analysis
3. Thermodynamic Analysis of Chloride Ions’ Role in Corrosion of Iron
3.1. Stability of Iron Compounds in the [Fe-O-Cl] System
3.2. Influence of on the Processes Occurring at the Metal–Metal Oxide Interface
3.3. Influence of the Carbon Content in Iron on the Corrosion Effects of Boiler Steel
3.3.1. The Metal Dusting Phenomenon under Carbon Supersaturation of Fe-Fe3C Alloy Surface
3.3.2. H2O(g) in Steel Decarburisation Processes
3.4. The Role of Gaseous Chlorides NaCl(g) in Steel Corrosion Processes
3.4.1. Thermodynamics of Sodium Ferrate Formation
3.4.2. Thermodynamics of Liquid Solutions Formation
3.5. Gas-Phase Composition Parameters as Boundary Conditions at the Metal Oxide–Gas Interface in Terms of the Parametric Equation Formalism
3.6. Thermodynamic Determinants of the Course of Corrosion at the Metal–Metal Oxide Interface
3.7. Verification of Iron Chloride Oxidation and Oxide Phase Expansion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission. Renewable Energy Progress Report, Brussels. 2015. Available online: http://europa.eu/rapid/press-release_IP-15-5180_en.htm (accessed on 9 May 2024).
- European Commission; Joint Research Centre; Neuwahl, F.; Brinkmann, T.; Lecomte, T.; Pinasseau, A.; Delgado Sancho, L.; Canova, M.; Jankov, I.; Roudier, S.; et al. Best Available Techniques (BAT) Reference Document for Large Combustion Plants: Industrial Emissions Directive 2010/75/EU (Integrated Pollution Prevention and Control); Publications Office: Luxembourg, Luxembourg, 2017; Available online: https://data.europa.eu/doi/10.2760/949 (accessed on 9 May 2024).
- Baxter, L.L.; Miles, T.R.; Miles, T.R., Jr.; Jenkins, B.M.; Dayton, D.C.; Milne, T.A.; Bryers, R.W.; Oden, L.L. Alkali Deposits Found in Biomass Boilers: The Behavior of Inorganic Material in Biomass-Fired Power Boilers—Field and Laboratory Experiences; Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1996; Volume 2. [Google Scholar] [CrossRef]
- Sander, B. Properties of Danish Biofuels and the Requirements for Power Production. Biomass Bioenergy 1997, 12, 177–183. [Google Scholar] [CrossRef]
- Kassman, H. Strategies to Reduce Gaseous KCl and Chlorine in Deposits during Combustion of Biomass in Fluidised Bed Boilers. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2012. Available online: http://publications.lib.chalmers.se/records/fulltext/156235.pdf (accessed on 9 May 2024).
- Ruth, L.A. Energy from Municipal Solid Waste: A Comparison with Coal Combustion Technology. Prog. Energy Combust. Sci. 1998, 24, 545–564. [Google Scholar] [CrossRef]
- Zahs, A.; Spiegel, M.; Grabke, H.J. Chloridation and Oxidation of Iron, Chromium, Nickel and Their Alloys in Chloridizing and Oxidizing Atmospheres at 400–700 °C. Corros. Sci. 2000, 42, 1093–1122. [Google Scholar] [CrossRef]
- Karlsson, S.; Pettersson, J.; Johansson, L.-G.; Svensson, J.-E. Alkali Induced High Temperature Corrosion of Stainless Steel: The Influence of NaCl, KCl and CaCl2. Oxid. Met. 2012, 78, 83–102. [Google Scholar] [CrossRef]
- Folkeson, N.; Johansson, L.-G.; Svensson, J.-E. Initial Stages of the HCl-Induced High-Temperature Corrosion of Alloy 310. J. Electrochem. Soc. 2007, 154, C515. [Google Scholar] [CrossRef]
- Viklund, P. Superheater Corrosion in Biomass and Waste Fired Boilers. Characterisation, Causes and Prevention of Chlorine-Induced Corrosion. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. Available online: https://kth.diva-portal.org/smash/get/diva2:614735/INSIDE01.pdf (accessed on 9 May 2024).
- James, P.J.; Pinder, L.W. The Impact of Coal Chlorine on The Fireside Corrosion Behaviour of Boiler Tubing: A UK Perspective. In Proceedings of the Corrosion97, New Orleans, LA, USA, 9–14 March 1997; NACE-97133. Available online: https://onepetro.org/NACECORR/proceedings-abstract/CORR97/All-CORR97/113319 (accessed on 9 May 2024).
- Nakagawa, K.; Isozaki, T. Fireside corrosion in reducing waste incineration environments. In Proceedings of the Corrosion94, Baltimore, MD, USA, 28 February–4 March 1994; NACE-94177. Available online: https://www.osti.gov/biblio/70105 (accessed on 9 May 2024).
- Spiegel, M.; Schroer, C.; Grabke, H.J. Corrosion of High Alloy Steels and Fe-Cr-Alloys Beneath Deposits from Waste Incinerator Plants. Mater. Sci. Forum 1997, 251–254, 527–534. [Google Scholar] [CrossRef]
- Daniel, P.L.; Rapp, R.A. Halogen corrosion of metals. In Advances in Corrosion Science and Technology, 1st ed.; Fontana, M.G., Staehle, R.W., Eds.; Springer: Boston, MA, USA, 1976; Volume 5, pp. 55–172. ISBN 978-1-4615-9064-4. [Google Scholar] [CrossRef]
- Mayer, P.; Manolescu, A.V. Influence of Hydrogen Chloride on Corrosion of Boiler Steels in Synthetic Flue Gas. CORROSION 1980, 36, 369–373. [Google Scholar] [CrossRef]
- Strafford, K.N.; Datta, P.K.; Forster, G. High-Temperature Chloridation of Binary FeCr Alloys at 1000 °C. Mater. Sci. Eng. A 1989, 120–121, 61–68. [Google Scholar] [CrossRef]
- Hupa, M.; Backman, P.; Backman, R.; Tran, H. Reactions between iron and HCl-bearing gases. In Incinerating Municipal and Industrial Waste, Proceedings of the International Conference on Fireside Problems While Incinerating Municipal and Industrial Waste, Palm Coast, FL, USA, 8–12 October 1989; Bryers, R.W., Ed.; Hemisphere Pub. Corp.: New York, NY, USA, 1991; ISBN 1560321458. [Google Scholar]
- Kim, A.S.; McNallan, M.J. Mixed Oxidation of Iron–Chromium Alloys in Gases Containing Oxygen and Chlorine at 900 to 1200° K. CORROSION 1990, 46, 746–755. [Google Scholar] [CrossRef]
- Lee, S.Y.; McNallan, M.J. Formation of Condensed Chlorides During Mixed Oxidation-Chlorination of Iron at 1000 K. CORROSION 1991, 47, 868–874. [Google Scholar] [CrossRef]
- Haanappel, V.A.C.; Haanappel, N.W.J.; Fransen, T.; van Corbach, H.D.; Gellings, P.J. Corrosion Kinetics of Low- and High-Alloy Steels in Chlorine-Containing Gas Atmospheres. CORROSION 1992, 48, 812–821. [Google Scholar] [CrossRef]
- Chu, H.; Datta, P.K.; Gray, J.S.; Strafford, K.N. Corrosion Mechanism of Fe(Ni)25CrAIX Type Alloys in a Bioxidant Environment at Elevated Temperature. Corros. Sci. 1993, 35, 1091–1098. [Google Scholar] [CrossRef]
- Grabke, H.J.; Reese, E.; Spiegel, M. The Effects of Chlorides, Hydrogen Chloride, and Sulfur Dioxide in the Oxidation of Steels below Deposits. Corros. Sci. 1995, 37, 1023–1043. [Google Scholar] [CrossRef]
- Grabke, H.J. Fundamental mechanisms of the attack of chlorine, HCl on steels and high temperature alloys in the temperature range 400 °C and 900 °C. In Incinerating Municipal and Industrial Waste, Proceedings of the International Conference on Fireside Problems While Incinerating Municipal and Industrial Waste, Palm Coast, FL, USA, 8–12 October 1989; Bryers, R.W., Ed.; Hemisphere Pub. Corp.: New York, NY, USA, 1991; ISBN 1560321458. [Google Scholar]
- McNallan, M. High-temperature corrosion in halogen environments. Mater. Perform. 1994, 33, 9. [Google Scholar]
- Zahs, A.; Spiegel, M.; Grabke, H. The Influence of Alloying Elements on the Chlorine-Induced High Temperature Corrosion of Fe-Cr Alloys in Oxidizing Atmospheres. Mater. Corros. 1999, 50, 561–578. [Google Scholar] [CrossRef]
- Chang, Y.-N.; Wei, F.-I. High-Temperature Chlorine Corrosion of Metals and Alloys. J. Mater. Sci. 1991, 26, 3693–3698. [Google Scholar] [CrossRef]
- Wright, I.; Krause, H.H. Assessment of Factors Affecting Boiler Tube Lifetime in Waste Fired Steam Generators: New Opportunities for Research and Technology Development; Final Report; ASME: New York, NY, USA, 1996. Available online: https://www.nrel.gov/docs/legosti/fy96/21480.pdf (accessed on 9 May 2024).
- Ihara, Y.; Ohgame, H.; Sakiyama, K.; Hashimoto, K. The Corrosion Behaviour of Iron in Hydrogen Chloride Gas and Gas Mixtures of Hydrogen Chloride and Oxygen at High Temperatures. Corros. Sci. 1981, 21, 805–817. [Google Scholar] [CrossRef]
- Harb, J.; Smith, E. Fireside Corrosion in Pc-Fired Boilers. Prog. Energy Combust. Sci. 1990, 16, 169–190. [Google Scholar] [CrossRef]
- Spiegel, M. Einfluss der Veränderungen von gasförmigem Chloranteil und Rohrwandtemperaturen auf die Korrosion unter Belägen. In Proceedings of the VDI Wissensforum: Beläge und Korrosion in Großfeuerungsanlagen, Hannover, Germany, 25–26 April 2006. [Google Scholar]
- Bramhoff, D.; Grabke, H.J.; Reese, E.; Schmidt, H.P. Einfluß von HCl und Cl2 Auf Die Hochtemperaturkorrosion des 2 1/4 Cr 1 Mo-Stahls in Atmosphären Mit Hohen Sauerstoffdrücken. Mater. Corros. 1990, 41, 303–307. [Google Scholar] [CrossRef]
- Spiegel, M. Salt Melt Induced Corrosion of Metallic Materials in Waste Incineration Plants. Mater. Corros. 1999, 50, 373–393. [Google Scholar] [CrossRef]
- Uusitalo, M.; Vuoristo, P.M.; Mäntylä, T. High Temperature Corrosion of Coatings and Boiler Steels in Oxidizing Chlorine-Containing Atmosphere. Mater. Sci. Eng. A 2003, 346, 168–177. [Google Scholar] [CrossRef]
- Sánchez Pastén, M.; Spiegel, M. High Temperature Corrosion of Metallic Materials in Simulated Waste Incineration Environments at 300–600 °C. Mater. Corros. 2006, 57, 192–195. [Google Scholar] [CrossRef]
- Latreche, H.; Doublet, S.; Schütze, M. Development of Corrosion Assessment Diagrams for High Temperature Chlorine Corrosion Part II: Development of “Dynamic” Quasi-Stability Diagrams. Oxid. Met. 2009, 72, 31–65. [Google Scholar] [CrossRef]
- Li, Y.; Niu, Y.; Wu, W. Corrosion behavior of pure Cr and two Cr-containing alloys beneath ZnCl2 and KCl-ZnCl2 deposits. J. Chin. Soc. Corr. Pro. 2002, 22, 27–31. [Google Scholar]
- Saunders, S.R.J.; Gohil, D.D.; Banks, J.P.; Sheriff, M.U.; Tortorelli, P.F.; De Van, J.H.; Wright, I.G. Behaviour of Fecralloy and Iron Aluminides Alloys in Coal Gasification Atmospheres Containing HCI. Mater. Sci. Forum 1997, 251–254, 583–590. [Google Scholar] [CrossRef]
- Zhai, W.; Yang, B.; Zhang, S.; Ni, J.; Li, S.; Li, Y. Study on High Temperature Chlorination Corrosion of Metallic Materials on The Waste Incineration Boilers. IOP Conf. Ser. Earth Environ. Sci. 2020, 450, 012006. [Google Scholar] [CrossRef]
- Zhang, K.; Niu, Y.; Zeng, C.; Wu, W. Corrosion of Iron and four commercial steels in a Cl-containing oxidizing atmosphere at 500–600 °C. J. Mater. Sci. Technol. 2004, 20, 213–216. [Google Scholar]
- Skrifvars, B.-J.; Westén-Karlsson, M.; Hupa, M.; Salmenoja, K. Corrosion of Super-Heater Steel Materials under Alkali Salt Deposits. Part 2: SEM Analyses of Different Steel Materials. Corros. Sci. 2010, 52, 1011–1019. [Google Scholar] [CrossRef]
- Skrifvars, B.-J.; Backman, R.; Hupa, M.; Salmenoja, K.; Vakkilainen, E. Corrosion of Superheater Steel Materials under Alkali Salt Deposits Part 1: The Effect of Salt Deposit Composition and Temperature. Corros. Sci. 2008, 50, 1274–1282. [Google Scholar] [CrossRef]
- Li, Y.S.; Niu, Y.; Wu, W.T. Accelerated Corrosion of Pure Fe, Ni, Cr and Several Fe-Based Alloys Induced by ZnCl2–KCl at 450 °C in Oxidizing Environment. Mater. Sci. Eng. A 2003, 345, 64–71. [Google Scholar] [CrossRef]
- Salmenoja, K.; Hupa, M.; Backman, R. Laboratory Studies on the Influence of Gaseous HCl on Superheater Corrosion. In Impact of Mineral Impurities in Solid Fuel Combustion, 1st ed.; Gupta, R.P., Wall, T.F., Baxter, L., Eds.; Springer: Boston, MA, USA, 2002; pp. 513–523. ISBN 978-1-4757-8186-1. [Google Scholar] [CrossRef]
- Janz, G.J.; Allen, C.B.; Downey, J.R.; Tomkins, R.P.T. EUTECTIC DATA: Safety, Hazards, Corrosion, Melting Points, Compositions, and Bibliography; Technical Report; US Energy Research and Development Administration: Washington, DC, USA, 1976. Available online: https://www.osti.gov/biblio/7224996 (accessed on 9 May 2024).
- Pinch, H.L.; Hirshon, J.M. Thermal Analysis of the Ferrous Chloride-Potassium Chloride System 1a. J. Am. Chem. Soc. 1957, 79, 6149–6150. [Google Scholar] [CrossRef]
- Baxter, L.L.; Nielsen, H.P. The Effects of Fuel-Bound Chlorine and Alkali on Corrosion Initiation. Fuel Energy Abstr. 1997, 42, 1091–1095. [Google Scholar] [CrossRef]
- Michelsen, H.P. Deposition and High-Temperature Corrosion in Biomass-Fired Boilers. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 1998. Available online: https://orbit.dtu.dk/en/publications/deposition-and-high-temperature-corrosion-in-biomass-fired-boiler (accessed on 9 May 2024).
- Hossain, M.K.; Noke, A.C.; Saunders, S.R.J. Oxidation of a Ni-Cr-Al Alloy at 850 °C in Air Containing HCl Gas. Oxid. Met. 1978, 12, 451–471. [Google Scholar] [CrossRef]
- Hancock, P. Vanadic and Chloride Attack of Superalloys. Mater. Sci. Technol. 1987, 3, 536–544. [Google Scholar] [CrossRef]
- Alexander, P.A. Laboratory Studies of the Effects of Sulphates and Chlorides on the Oxidation of Superheater Alloys. In The Mechanism of Corrosion by Fuel Impurities, Proceedings of the Marchwood International Conference on the Mechanism of Corrosion by Fuel Impurities, Marchwood, UK, 20–24 May 1963; Johnson, H.R., Littler, D.J., Eds.; Butterworths: London, UK, 1963. [Google Scholar]
- Gotthjælp, K.; Brøndsted, P.; Jansen, P.; Markussen, J.; Montgomery, M.; Maahn, E. High Temperature Corrosion in Biomass Incineration Plants; Final Report; Risø National Laboratory: Roskilde, Denmark, 1997. Available online: https://www.osti.gov/etdeweb/servlets/purl/510219 (accessed on 9 May 2024).
- Miller, P.D.; Krause, H.H.; Zupan, J.; Boyd, W.K. Corrosive Effects of Various Salt Mixtures Under Combustion Gas Atmospheres. CORROSION 1972, 28, 222–225. [Google Scholar] [CrossRef]
- John, R.C. Alloy Corrosion in Reducing plus Sulfidizing Gases at 600–950 °C. In High Temperature Corrosion in Energy Systems; Rothman, M.F., Ed.; Metallurgical Society of AIME: Warrendale, PA, USA, 1985; ISBN 9780895204905. [Google Scholar]
- Paul, L.D.; Daniel, P.L. Corrosion Mechanisms in oxidizing, reducing and alternating combustion gases in refuse-fired boiler environments. In Proceedings of the Corrosion93, New Orleans, LA, USA, 8–12 March 1993. NACE 93-216. [Google Scholar]
- Shinata, Y.; Takahashi, F.; Hashiura, K. NaCl-Induced Hot Corrosion of Stainless Steels. Mater. Sci. Eng. 1987, 87, 399–405. [Google Scholar] [CrossRef]
- Spiegel, M.; Grabke, H.J. High temperature corrosion of low and high alloy Steels in simulated waste incineration atmospheres. In Incinerating Municipal and Industrial Waste, Proceedings of the International Conference on Fireside Problems While Incinerating Municipal and Industrial Waste, Palm Coast, FL, USA, 8–12 October 1989; Bryers, R.W., Ed.; Hemisphere Pub. Corp.: New York, NY, USA, 1991; ISBN 1560321458. [Google Scholar]
- Nicholls, J.R.; Newton, R.; Simms, N.J.; Norton, J.F. Modelling the Oxidation of FeCrAl-RE ODS Alloys in Simulated Natural Gas Combustion Environments. Mater. High. Temp. 2003, 20, 93–108. [Google Scholar] [CrossRef]
- Ptak, W.; Sukiennik, M. Changes in the composition of the gaseous phase of a system resulting from the process of a chemical reaction. Bull. Acad. Pol. Sci. 1969, 17, 21–25. [Google Scholar]
- Ptak, W.; Sukiennik, M.; Olesinski, R.; Kaczmarczyk, R. Deformation of a properties resulting from a chemical reaction stoichiometry. Arch. Metall. 1987, 32, 355–362. [Google Scholar]
- Kaczmarczyk, R.; Gurgul, S. Model Approach of Carbon Deposition Phenomenon in Mixed H2O/CO2 Methane Reforming Process. Arch. Metall. Mater. 2014, 59, 1379–1383. [Google Scholar] [CrossRef]
- Kaczmarczyk, R.; Gurgul, S. Model Approach of Carbon Deposition Phenomenon in Steam and Dry Methane Reforming Process. Arch. Metall. Mater. 2014, 59, 145–148. [Google Scholar] [CrossRef]
- Knacke, O.; Kubaschewski, O.; Hesselmann, K. Thermochemical Properties of Inorganic Substaces, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 9783540540144. [Google Scholar]
- HSC Chemistry, Version 10.0. Metso Outotec, Espoo, Finland. Available online: http://www.hsc-chemistry.com/ (accessed on 9 May 2024).
- Chipman, J. Thermodynamics and Phase Diagram of the Fe-C System. Metall. Trans. 1972, 3, 55–64. [Google Scholar] [CrossRef]
- Richardson, F.D. The thermodynamics of metallurgical carbides and of carbon in iron. J. Iron Steel Inst. 1953, 175, 33–51. [Google Scholar]
- Krupkowski, A. Podstawowe Zagadnienia Teorii Procesów Metalurgicznych, 1st ed.; PWN: Warsaw, Poland, 1974. [Google Scholar]
- Grabke, H.; Schütze, M. Corrosion by Carbon and Nitrogen: Metal Dusting, Carburisation and Nitridation, 1st ed.; Woodhead Publishing: Sawston, UK; Cambridge, UK, 2007; ISBN 9781845692322. [Google Scholar]
- Hochman, R.F. Catastrophic deterioration of high temperature alloys in carbonaceous atmospheres. In Proceedings of the Symposium on Properties of High Temperature Alloys, with Emphasis on Environmental Effects, Proceedings of the Electrochemical Society Meeting, Las Vegas, NV, USA, 17 October 1976; Foroulis, Z.A., Pettit, F.S., Eds.; Electrochemical Society: Princeton, NJ, USA, 1977; pp. 715–732. [Google Scholar]
- Grabke, H.J.; Krajak, R.; Müller-Lorenz, E.M. Metal Dusting of High Temperature Alloys. Mater. Corros. 1993, 44, 89–97. [Google Scholar] [CrossRef]
- Grabke, H.J. Thermodynamics, Mechanisms and Kinetics of Metal Dusting. Mater. Corros. 1998, 49, 303–308. [Google Scholar] [CrossRef]
- Grabke, H.J.; Müller-Lorenz, E.M.; Eltester, B.; Lucas, M. Formation of Chromium Rich Oxide Scales for Protection against Metal Dusting. Mater. High. Temp. 2000, 17, 339–345. [Google Scholar] [CrossRef]
- Pippel, E.; Woltersdorf, J.; Schneider, R. Micromechanisms of Metal Dusting on Fe-Base and Ni-Base Alloys. Mater. Corros. 1998, 49, 309–316. [Google Scholar] [CrossRef]
- Chun, C.M.; Mumford, J.D.; Ramanarayanan, T.A. Mechanisms of Metal Dusting Corrosion of Iron. J. Electrochem. Soc. 2002, 149, B348. [Google Scholar] [CrossRef]
- Chun, C.M.; Mumford, J.D.; Ramanarayanan, T.A. Carbon-Induced Corrosion of Nickel Anode. J. Electrochem. Soc. 2000, 147, 3680. [Google Scholar] [CrossRef]
- Chun, C.M.; Mumford, J.D.; Ramanarayanan, T.A. Metal Dusting Corrosion of Cobalt. J. Electrochem. Soc. 2003, 150, B76. [Google Scholar] [CrossRef]
- Zhang, J.; Schneider, A.; Inden, G. Characterisation of the Coke Formed during Metal Dusting of Iron in CO–H2–H2O Gas Mixtures. Corros. Sci. 2003, 45, 1329–1341. [Google Scholar] [CrossRef]
- Zeng, Z.; Natesan, K.; Maroni, V. Investigation of metal-dusting mechanism in Fe-base alloys using raman spectroscopy, X-ray diffraction, and electron microscopy. Oxid. Met. 2002, 58, 147–170. [Google Scholar] [CrossRef]
- Zeng, Z.; Natesan, K. Relationship of Carbon Crystallization to the Metal-Dusting Mechanism of Nickel. Chem. Mater. 2003, 15, 872–878. [Google Scholar] [CrossRef]
- Toh, C.H.; Munroe, P.R.; Young, D.J. The Role of Cementite in the Metal Dusting of Fe–Cr and Fe–Ni–Cr Alloys. Mater. High. Temp. 2003, 20, 527–534. [Google Scholar] [CrossRef]
- Toh, C.; Munroe, P.; Young, D. Metal Dusting of Fe–Cr and Fe–Ni–Cr Alloys Under Cyclic Conditions. Oxid. Met. 2002, 58, 1–21. [Google Scholar] [CrossRef]
- Gao, W.; Li, Z. Developments in High Temperature Corrosion and Protection of Materials, 1st ed.; Woodhead Publishing: Sawston, UK; Cambridge, UK, 2008; ISBN 9781845692193. [Google Scholar]
- Cottis, R.; Graham, M.; Lindsay, R.; Lyon, S.; Richardson, J.; Scantlebury, J.; Stott, F. Shreir’s Corrosion, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 1, ISBN 978-0-444-52787-5. [Google Scholar]
- Szakálos, P. Mechanism of Metal Dusting. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2004. Available online: https://kth.diva-portal.org/smash/get/diva2:9563/FULLTEXT01.pdf (accessed on 9 May 2024).
- Wagner, C. Beitrag Zur Theorie Des Anlaufvorganges. II. Z. Für Phys. Chem. 1936, 32B, 447–462. [Google Scholar] [CrossRef]
- Norby, T. Wagner-type theory for oxidation of metals with co-transport of hydrogen ions. In High Temperature Corrosion and Materials Chemistry, Proceedings of the Per Kofstad Memorial Symposium on High Temperature Corrosion and Materials Chemistry, 1999 Joint International Meeting, Honolulu, HI, USA, 17–22 October 1999; McNallan, M., Opila, E., Maruyama, T., Narita, T., Eds.; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2000; ISBN 9781566772617. [Google Scholar]
- Kofstad, P. High Temperature Corrosion, 2nd ed.; Elsevier Applied Science: London, UK, 1988; ISBN 9781851661541. [Google Scholar]
- Khanna, A.S. Introduction to High Temperature Oxidation and Corrosion, 1st ed.; ASM International: Materials Park, OH, USA, 2002; ISBN 9780871707628. [Google Scholar]
- Grabke, H.J.; Grassl, D.; Hoffmann, F.; Liedtke, D.; Neumann, F.; Schachinger, H.; Weissohn, K.-H.; Wünning, A.; Wyss, U.; Zoch, H.-W. Die Prozeßregelung beim Gasaufkohlen und Einsatzhärten; Expert: Tübingen, Deutschland, 1997; ISBN 9783816914549. [Google Scholar]
- Grabke, H.J. Carburization: A High Temperature Corrosion Phenomenon, 1st ed.; Material Technology Institute of the Chemical Process Industries: St. Louis, MO, USA, 1998; ISBN 9781576980156. [Google Scholar]
- Grabke, H.J. Corrosion by Carbonaceous Gases, Carburization and Metal Dusting, and Methods of Prevention. Mater. High. Temp. 2000, 17, 483–487. [Google Scholar] [CrossRef]
- Birks, N.; Meier, G.H.; Pettit, F.S. Introduction to the High Temperature Oxidation of Metals, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006; ISBN 9781139163903. [Google Scholar] [CrossRef]
- Young, D.J. High Temperature Oxidation and Corrosion of Metals, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 2016; ISBN 978-0-08-100101-1. [Google Scholar] [CrossRef]
- Masuko, N. Metallurgical Chemistry in My Life. Mater. Trans. 2004, 45, 2489–2495. [Google Scholar] [CrossRef]
- Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Gheribi, A.E.; Hack, K.; Jung, I.-H.; Kang, Y.-B.; Melançon, J.; et al. FactSage Thermochemical Software and Databases, 2010–2016. Calphad 2016, 54, 35–53. [Google Scholar] [CrossRef]
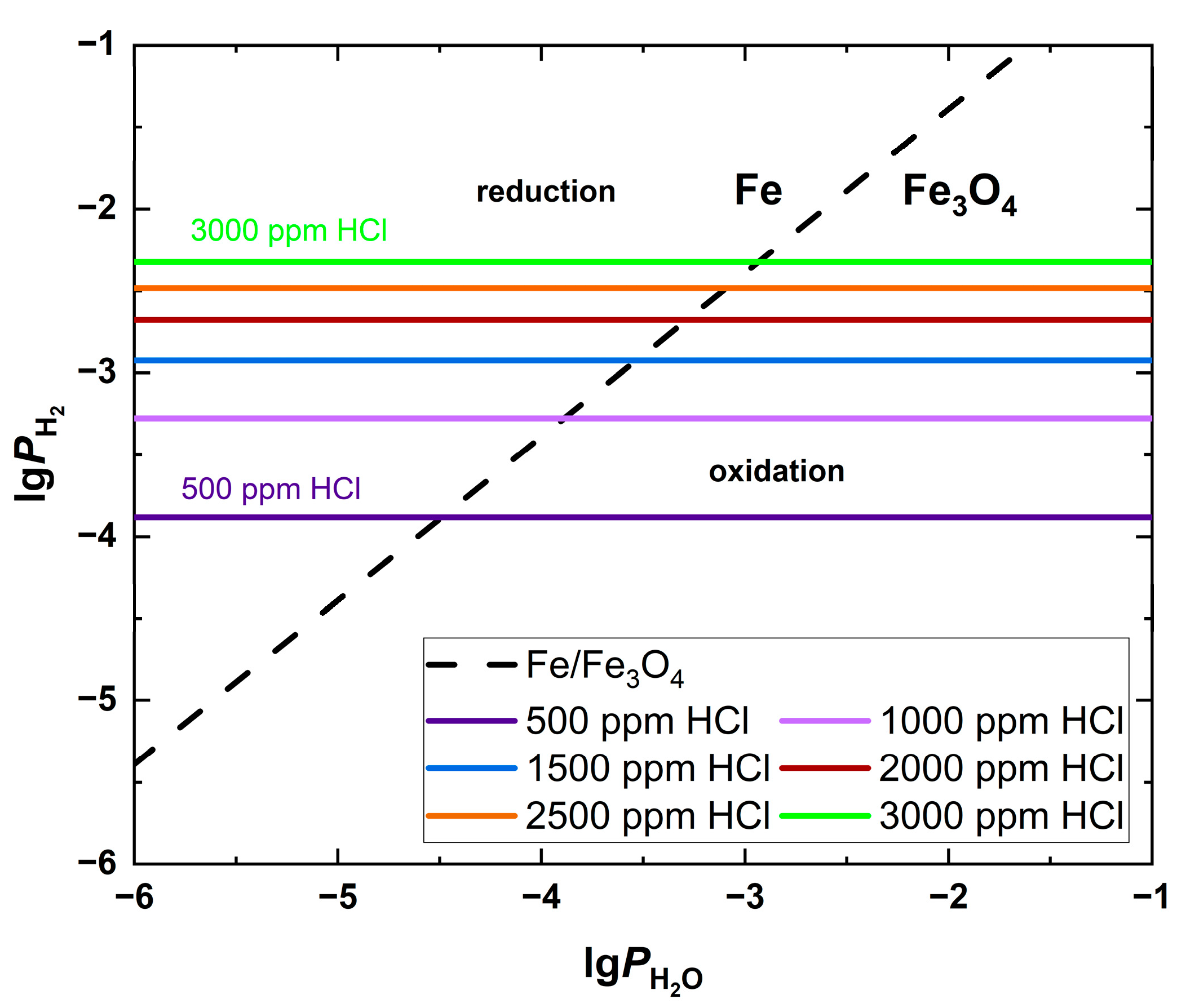
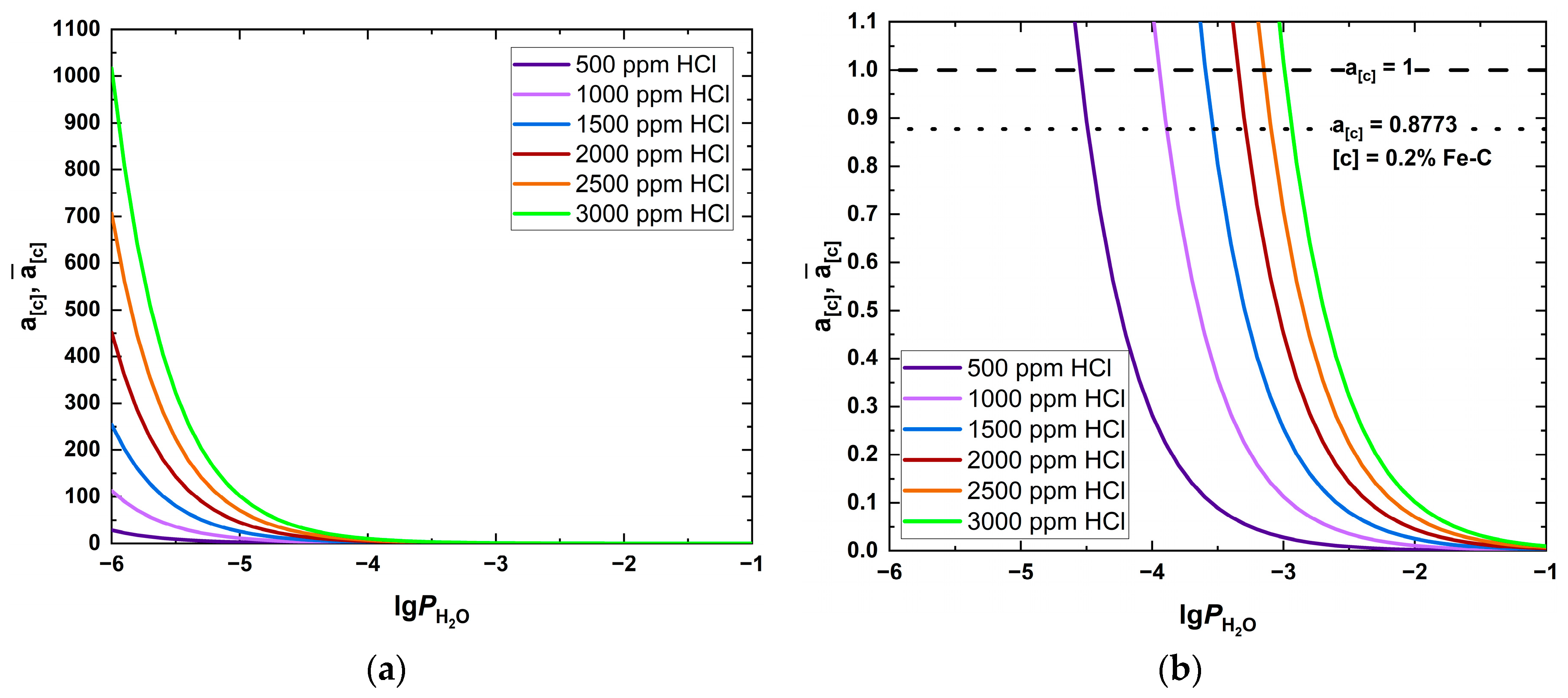
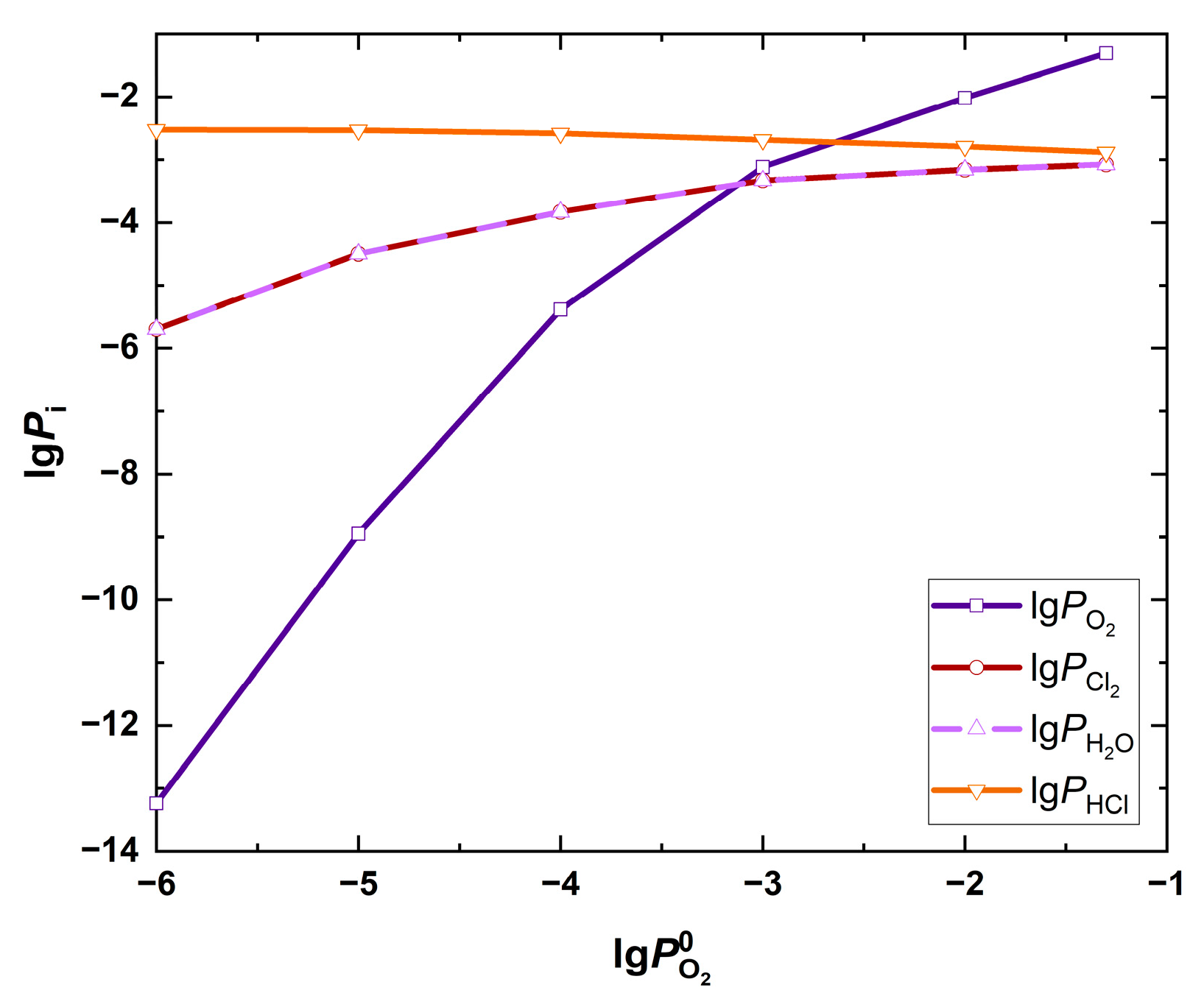
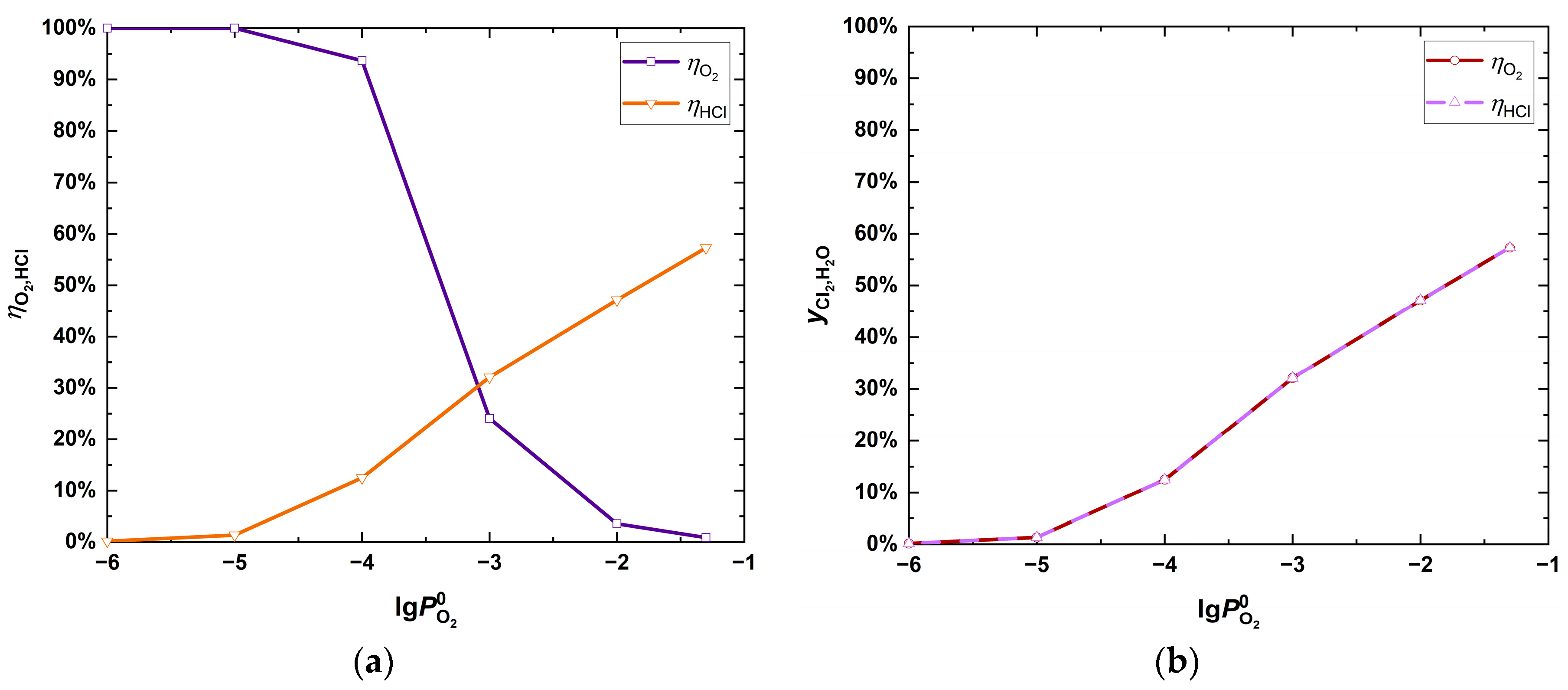
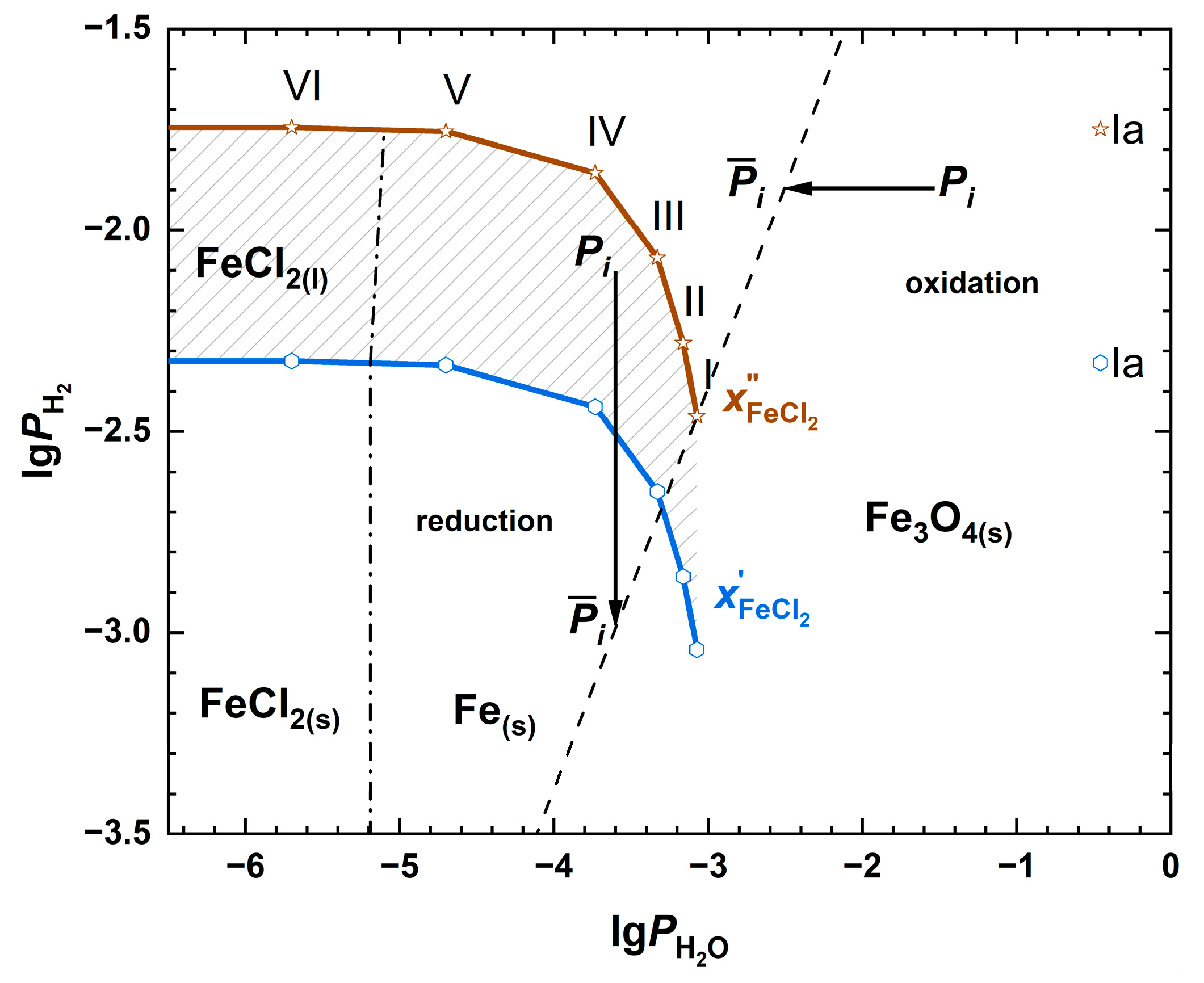

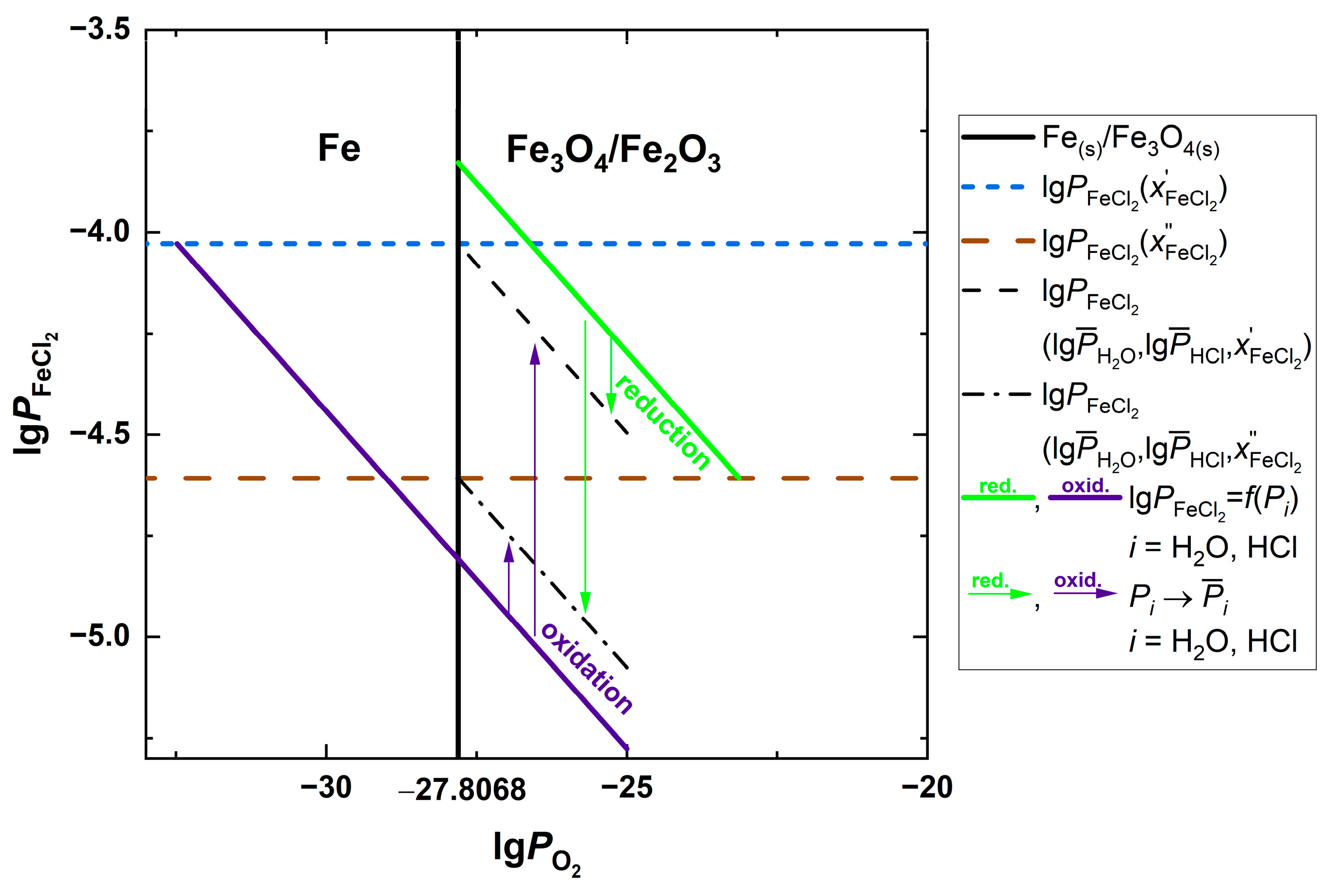
| Fuel | O2 [%] | CO2 [%] | H2O [%] | SO2 [ppm] | HCl [ppm] | KCl+NaCl [ppm] |
|---|---|---|---|---|---|---|
| Coal | ~4–5 | ~12 | ~4–16 | ~400–1200 | ~10–50 | - |
| Biomass | ~5–10 | ~8–15 | ~10–20 | ~0–70 | ~25–1000 | ~5–50 |
| Waste | ~5–11 | ~8–14 | ~10–20 | ~0–150 | ~250–1300 | <120 |
| HCl(g) 500 ppm | HCl(g) 1000 ppm | HCl(g) 1500 ppm | HCl(g) 2000 ppm | HCl(g) 2500 ppm | HCl(g) 3000 ppm | |
|---|---|---|---|---|---|---|
| −1 | 2.8 × 10−4 | 1.13 × 10−3 | 0.0025 | 0.0045 | 0.0071 | 0.0102 |
| −2 | 2.8 × 10−3 | 0.0113 | 0.0254 | 0.0452 | 0.0706 | 0.1017 |
| −3 | 0.0283 | 0.113 | 0.2543 | 0.4522 | 0.7065 | 1.02 |
| −4 | 0.2826 | 1.13 | 2.54 | 4.52 | 7.06 | 10.17 |
| −5 | 2.8 | 11.3 | 25.4 | 45.2 | 70.6 | 101.7 |
| −6 | 28 | 113 | 254 | 452 | 706 | 1017 |
| 1000 ppm | 2000 ppm | 3000 ppm | ||
|---|---|---|---|---|
| −0.4333 | −3.278/527 | −2.676/2109 | −2.324/4742 | |
| −1.0131 | −2.698/2004 | −2.096/8017 | −1.744/18,030 | |
| −0.4333 | |||
| −1.0131 |
| I | Ia | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|---|
| 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | |
| 0.05 | 0.05 | 0.01 | 0.001 | 0.0001 | 0.00001 | 0.000001 | |
| 0 | 0.35 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| −2 | 4 | ||
| −0.5 | 1 | ||
| 1 | −2 | ||
| 1 | −2 | ||
| 0 | 0 |
| I | Ia | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|---|
| −1.3010 | −1.3010 | −2 | −3 | −4 | −5 | −6 | |
| - | −0.4559 | - | - | - | - | - | |
| −1.3045 | −1.3011 | −2.0151 | −3.1158 | −5.1447 | −9.2218 | −13.2427 | |
| −3.0732 | −4.9763 | −3.1599 | −3.3292 | −3.7312 | −4.6990 | −5.6990 | |
| −3.0732 | −0.4559 | −3.1599 | −3.3292 | −3.7312 | −4.6990 | −5.6990 | |
| −2.8822 | −2.5259 | −2.7913 | −2.6854 | −2.5802 | −2.5287 | −2.5235 |
| Gas Composition | ||||
|---|---|---|---|---|
| I | 0.86% | 57.31% | 57.31% | 57.31% |
| Ia | 0.01% | 0.76% | 0.76% | 0.76% |
| II | 3.53% | 47.14% | 47.14% | 47.14% |
| III | 24.06% | 32.08% | 32.08% | 32.08% |
| IV | 93.67% | 12.49% | 12.49% | 12.49% |
| V | 99.99% | 1.33% | 1.33% | 1.33% |
| VI | 100% | 0.13% | 0.13% | 0.13% |
| Parameters | I | Ia | II | III | IV | V | VI |
|---|---|---|---|---|---|---|---|
| −3.0424 | −2.3298 | −2.8606 | −2.6488 | −2.4384 | −2.3354 | −2.325 | |
| −26.6444 | −22.835 | −27.1814 | −27.9436 | −29.1684 | −31.3100 | −33.3308 | |
| −0.6381 | −2.5428 | −0.3696 | 0.0115 | 0.6239 | 1.6947 | 2.7051 | |
| 0.2301 | 0.00286 | 0.4270 | |||||
| - | - | - | 1.03 | 4.21 | 49.51 | 507.11 | |
| −27.8069 | −27.8069 | −27.8069 | −27.8069 | −27.8069 | −27.8069 | −33.3308 | |
| −2.8822 | −2.5259 | −2.7913 | −2.7197 | −2.9207 | −3.4046 | −2.5235 | |
| −3.6544 | −2.9418 | −3.4726 | −3.3292 | −3.7312 | −4.6990 | −5.6990 | |
| −3.0424 | −2.3298 | −2.8606 | −2.7171 | −3.1192 | −4.0869 | −2.325 | |
| 0% | 0% | 0% | 7.6% | 54.3% | 86.7% | 0% | |
| 0% | 0% | 0% | 14.5% | 79.1% | 98% | 0% | |
| Parameters | I | Ia | II | III | IV | V | VI |
|---|---|---|---|---|---|---|---|
| −2.4623 | −1.7497 | −2.2805 | −2.0687 | −1.8583 | −1.7553 | −1.7449 | |
| −27.8046 | −23.9952 | −28.3256 | −29.1038 | −30.3286 | −32.4702 | −34.491 | |
| −0.058 | −1.9627 | 0.2105 | 0.5916 | 1.204 | 2.2748 | 3.2852 | |
| 0.0109 | |||||||
| - | - | 1.62 | 3.90 | 15.99 | 188.28 | 1928.41 | |
| −16.2927 | −16.2927 | −16.2927 | −16.2927 | −16.2927 | −16.2927 | −16.2927 | |
| −27.8069 | −27.8069 | −27.8069 | −27.8069 | −27.8069 | −27.8069 | −34.491 | |
| −2.8822 | −2.5259 | −2.925 | −3.0096 | −3.2106 | −3.6945 | −2.5235 | |
| −3.0743 | −2.3617 | −3.1599 | −3.3292 | −3.7312 | −4.6990 | −5.6990 | |
| −2.4623 | −1.7497 | −2.5478 | −2.7171 | −3.1191 | −4.0869 | −1.7449 | |
| 0% | 0% | 26.5% | 52.6% | 76.6% | 93.2% | 0% | |
| 0% | 0% | 45.9% | 77.5% | 94.5% | 99.5% | 0% | |
| I | Ia | II | III | IV | V | |
|---|---|---|---|---|---|---|
| −31.278 | −42.706 | −29.667 | −27.380 | −23.706 | −17.281 | |
| −27.807 | −39.227 | −26.188 | −23.902 | −20.227 | −13.802 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarczyk, R.; Gurgul, S. Thermodynamic Analysis of Chloride Corrosion in Steel for Energy System Applications in Fe-O-Cl-Na Environments. Energies 2024, 17, 3223. https://doi.org/10.3390/en17133223
Kaczmarczyk R, Gurgul S. Thermodynamic Analysis of Chloride Corrosion in Steel for Energy System Applications in Fe-O-Cl-Na Environments. Energies. 2024; 17(13):3223. https://doi.org/10.3390/en17133223
Chicago/Turabian StyleKaczmarczyk, Robert, and Sebastian Gurgul. 2024. "Thermodynamic Analysis of Chloride Corrosion in Steel for Energy System Applications in Fe-O-Cl-Na Environments" Energies 17, no. 13: 3223. https://doi.org/10.3390/en17133223
APA StyleKaczmarczyk, R., & Gurgul, S. (2024). Thermodynamic Analysis of Chloride Corrosion in Steel for Energy System Applications in Fe-O-Cl-Na Environments. Energies, 17(13), 3223. https://doi.org/10.3390/en17133223






