Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter
Abstract
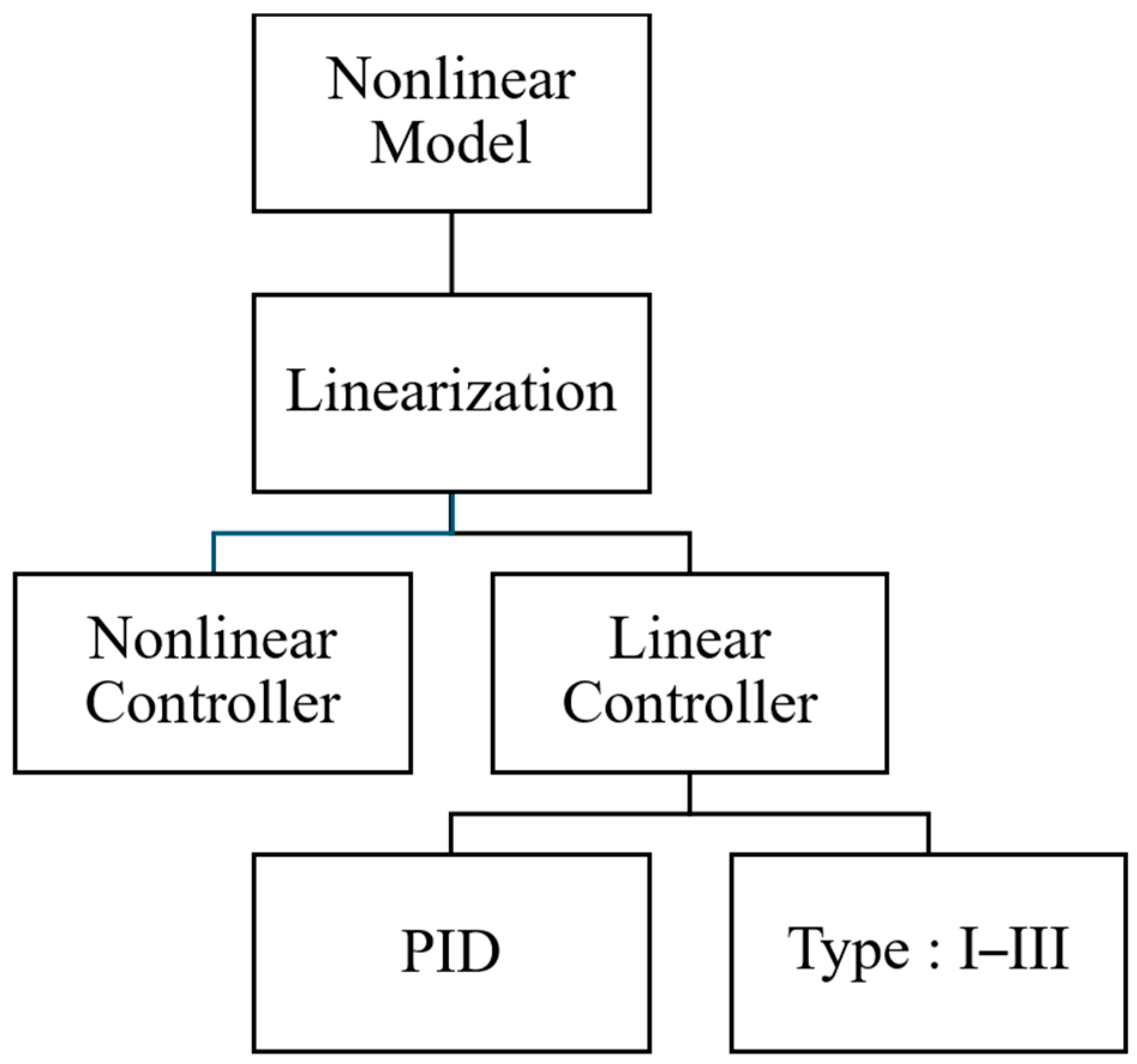
:1. Introduction
2. Material and Methods
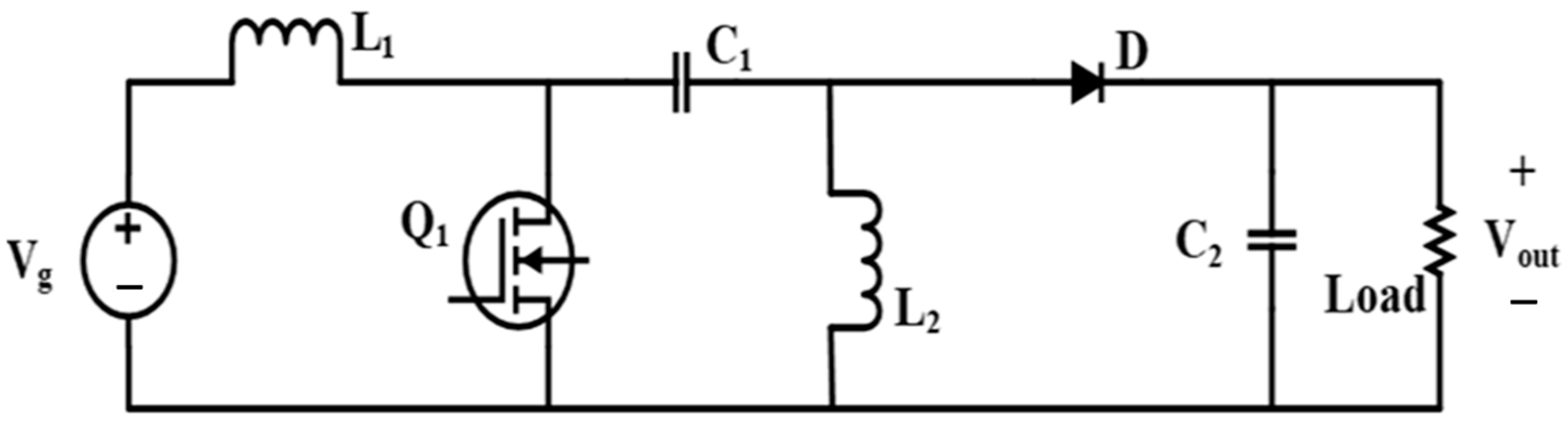
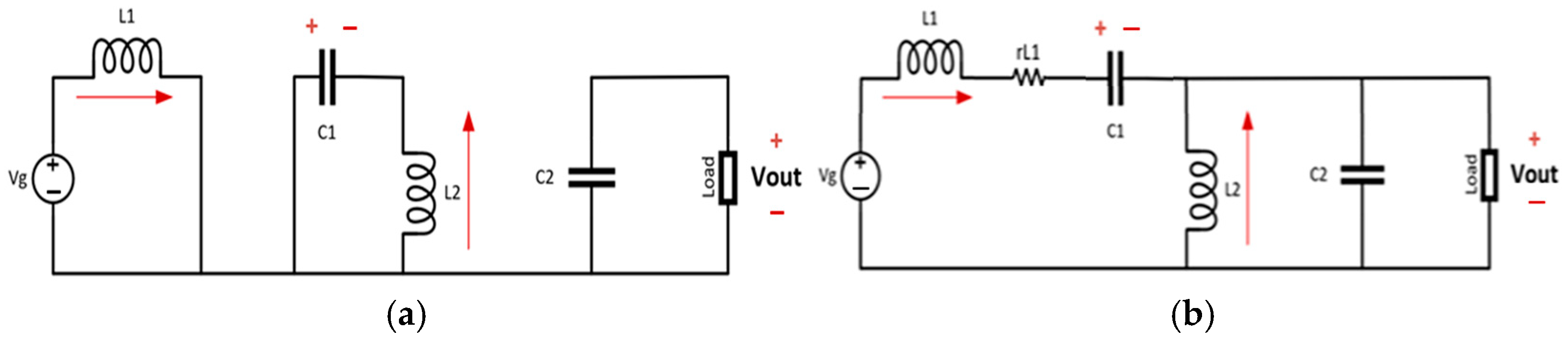
3. Mathematical Model of SEPIC
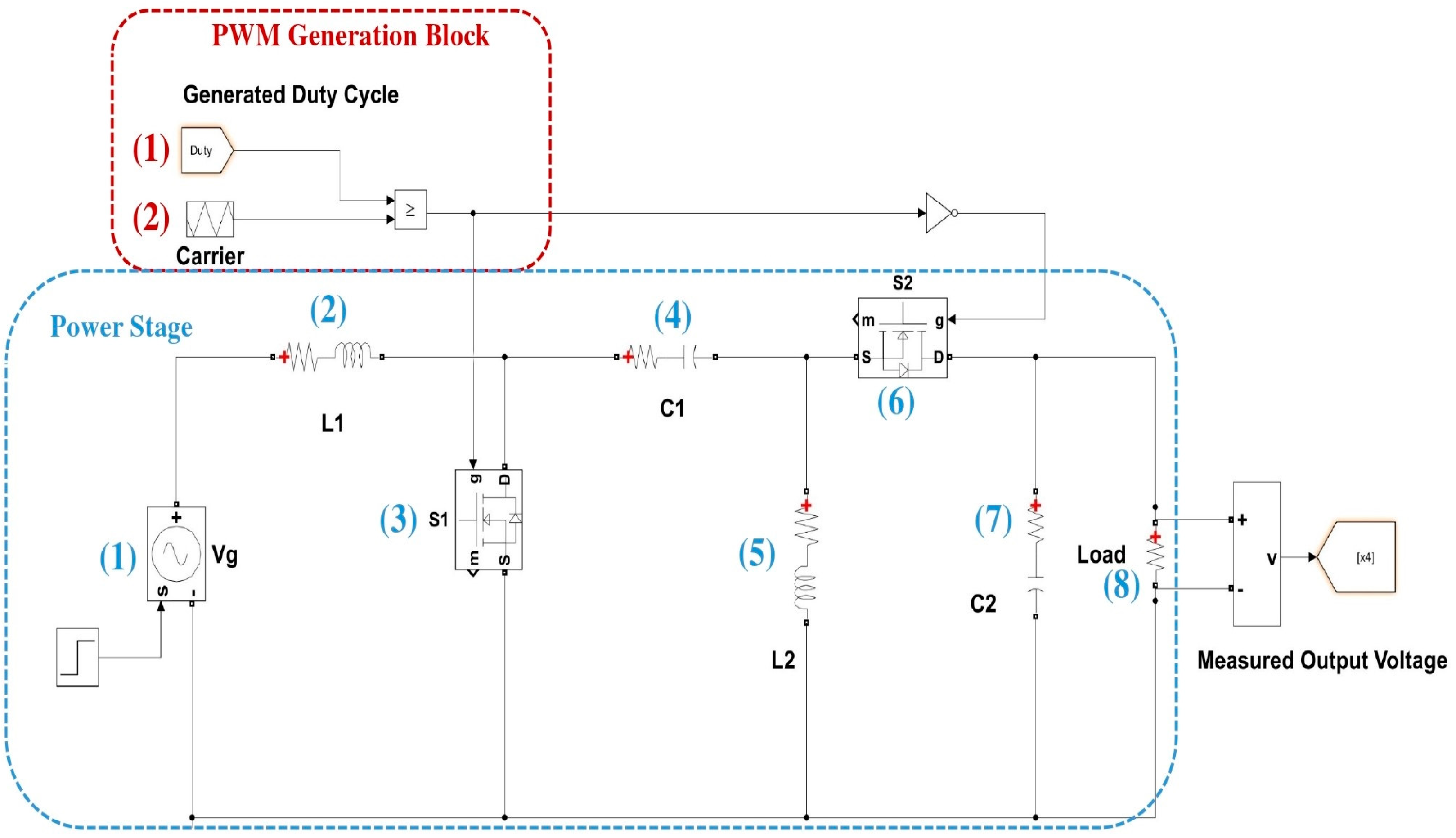
| PWM Generation Block | |
| (1) Duty cycle generated by controller | (2) Triangular reference module for duty-cycle comparison and PWM generation |
| Power Stage | |
| (1) Input voltage source | (2) Input inductor L1 with its ESR |
| (3) Primary semiconductor switch (MOSFET) | (4) Capacitor C1 |
| (5) Inductor L2 with its ESR | (6) Secondary semiconductor switch (MOSFET) is used instead of diode (synchronous connection) |
| (7) Output capacitor C2 | (8) Load (modeled as resistor) |
4. Controller Design
4.1. Type-II Compensator
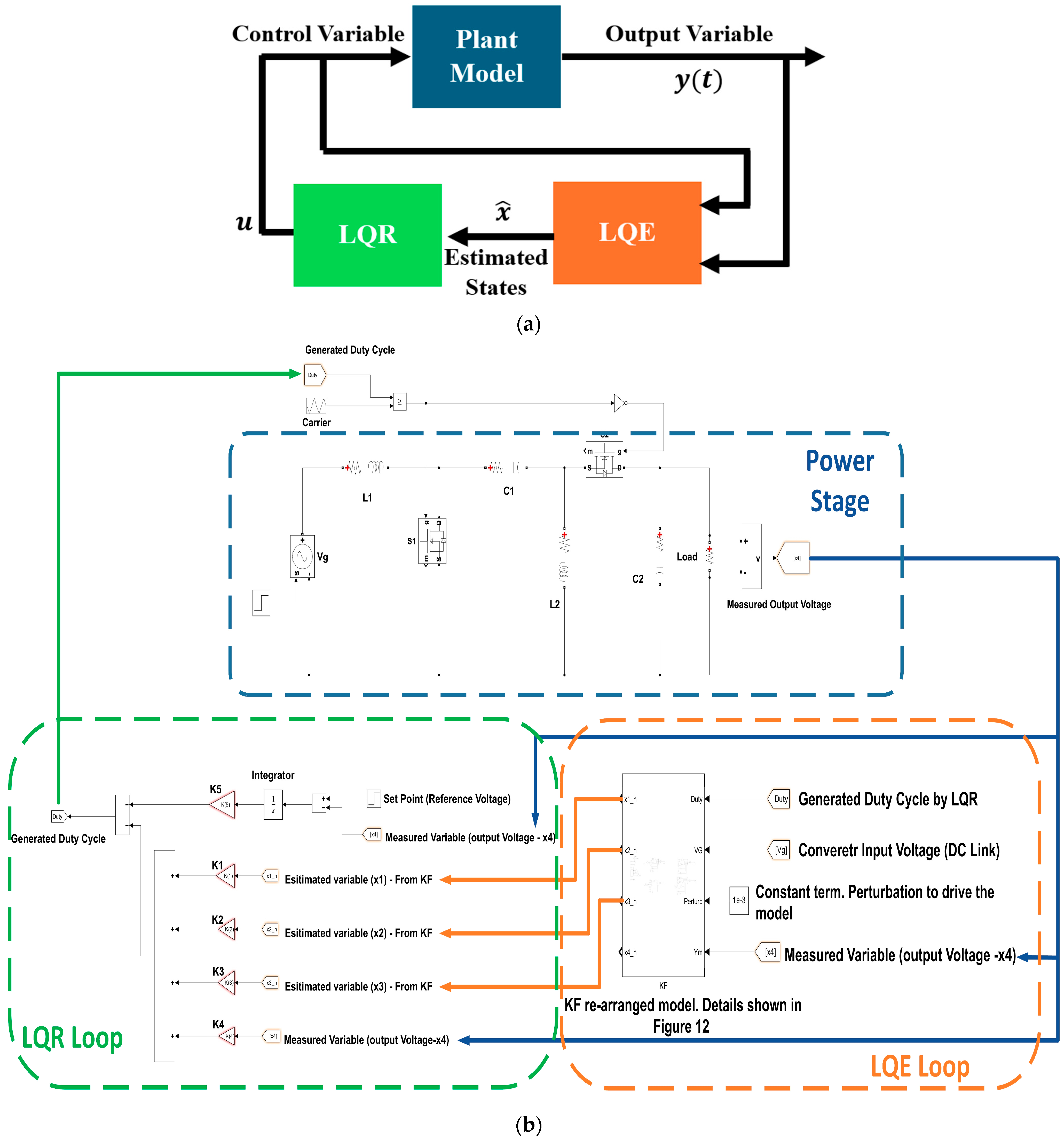
4.2. Linear Quadratic Gaussian
4.2.1. Overview of Linear Quadrature Regulator (LQR)
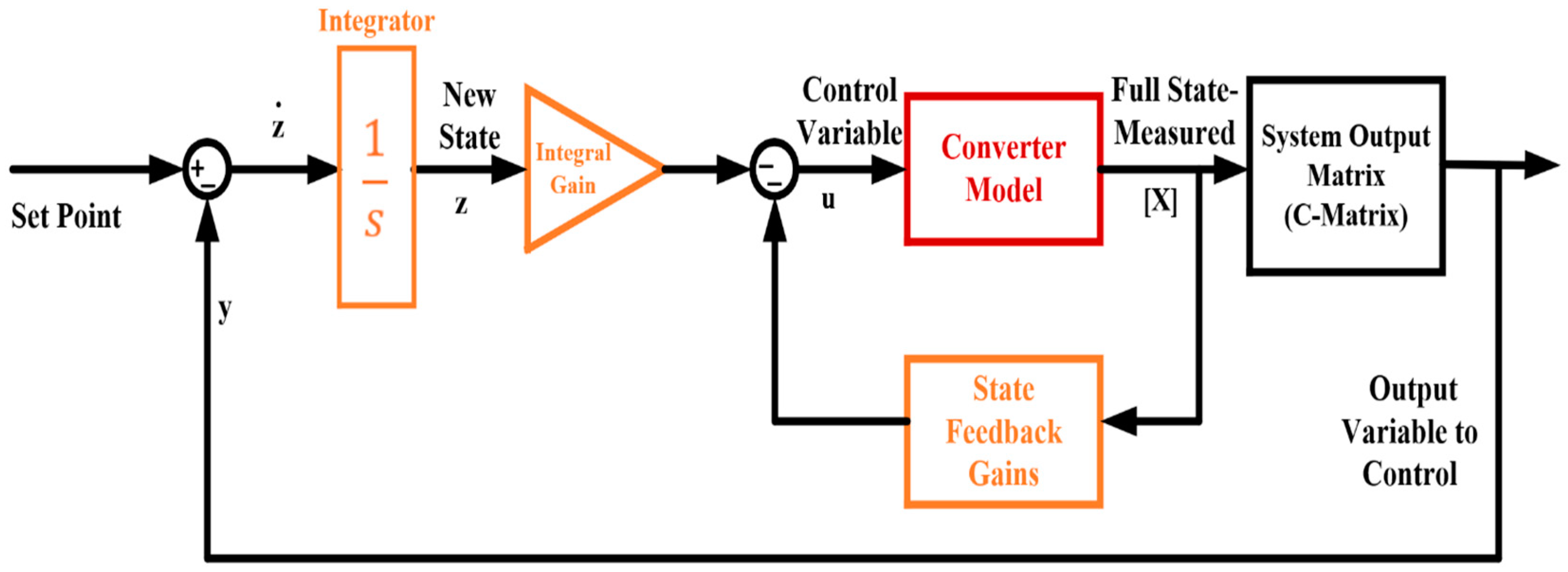
4.2.2. Integral LQR System
- (1)
- Introduce a new state variable corresponding to the pole at the origin. Let the new state variable be .
- (2)
- In Figure 9, the dynamics (the time derivative) of is characterized to be
- (3)
- The control input ( expression can be expanded by investigating the model in Figure 9, as follows:
- (4)
- Considering the generic model of the state–space equation describes a linearized system,
- (5)
4.2.3. Integral LQR Controller Design
- It must be linear or linearized.
- The state variables have a relationship with the input variable.
- Augmented system matrix ():
- Augmented input vector ():
- Augmented output matrix ():
- Designed Integral LQR Controller Parameters:
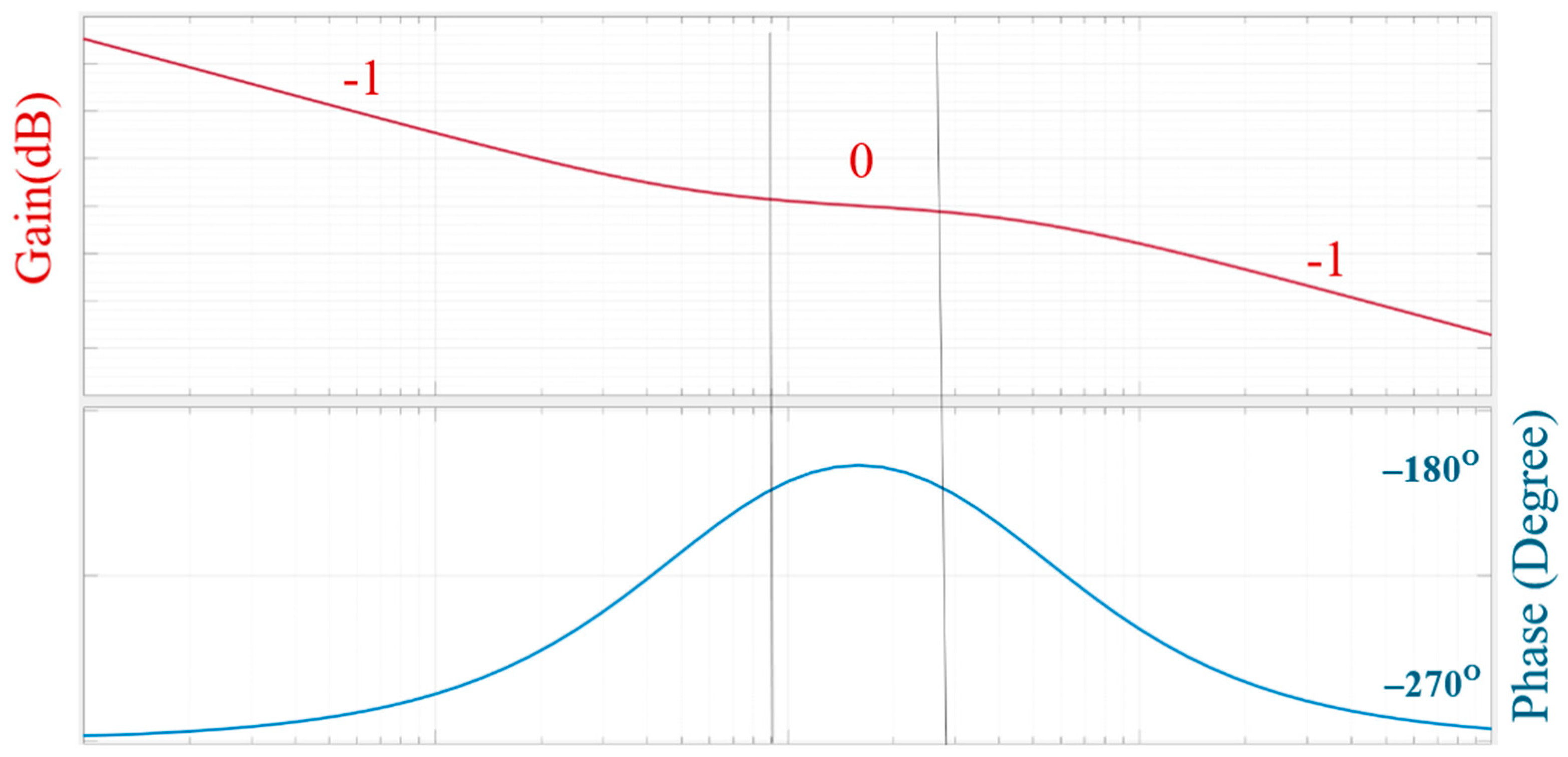
4.2.4. Stability Analysis
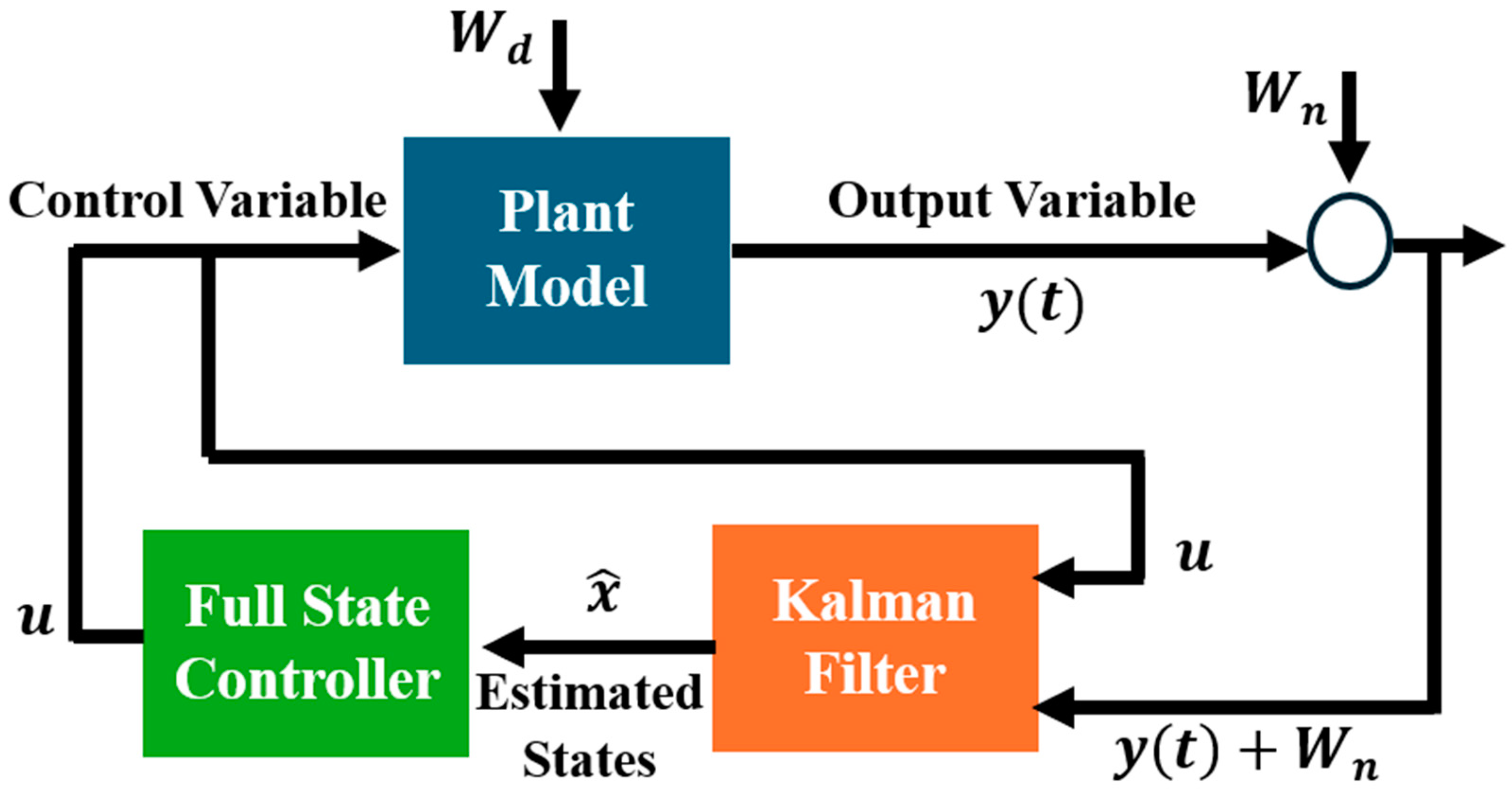
5. State Estimation Theory and Approach
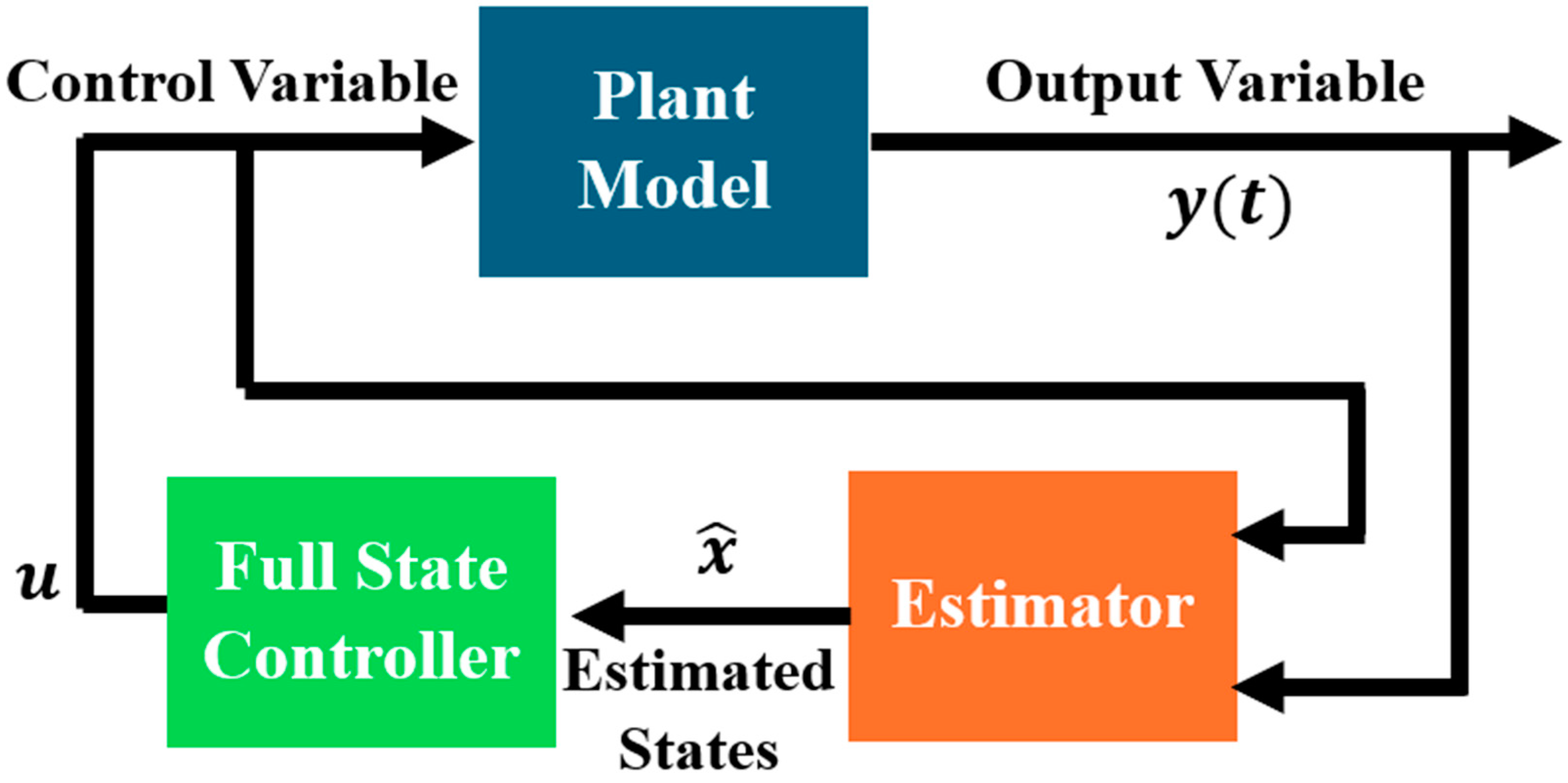
5.1. Overview
5.2. Full-State Estimation
5.2.1. Necessary Condition and Requirements
5.2.2. Measured State Variable Selection Criterion
- (1)
- Construct the system state–space representation by selecting the first state variable as the only output of the system.
- (2)
- Calculate the corresponding observability Gramian.
- (3)
- Calculate the determinant of the above derived observability Gramian.
- (4)
- Repeat the above steps with the second state variable as the system output.
- (5)
- Keep repeating the process until the determinant of the observability Gramian is calculated for all of the state variables presenting the output variable.
- The LQG system is compared to a standard Type-II controller where the output voltage is taken as feedback. Hence, to hold the comparison, both systems (Type-II and LQG) should use the feedback variable.
- The LQR controller is designed to be an integral LQR system where an additional state ( is introduced. This structure performs best if the variable of interest (to perform the tracking task) is measured directly such that the measurement is accepted with high fidelity.
5.3. Observer Design
5.3.1. Kalman Filter Design
- is the disturbance acting on the system as well as the model uncertainty. is modeled as
- ○
- Additive White Gaussian (AWG) noise.
- ○
- Has variance .
- ○
- Has size of .
- is the noise measurement. is modeled as
- ○
- Additive White Gaussian (AWG) noise.
- ○
- Has variance .
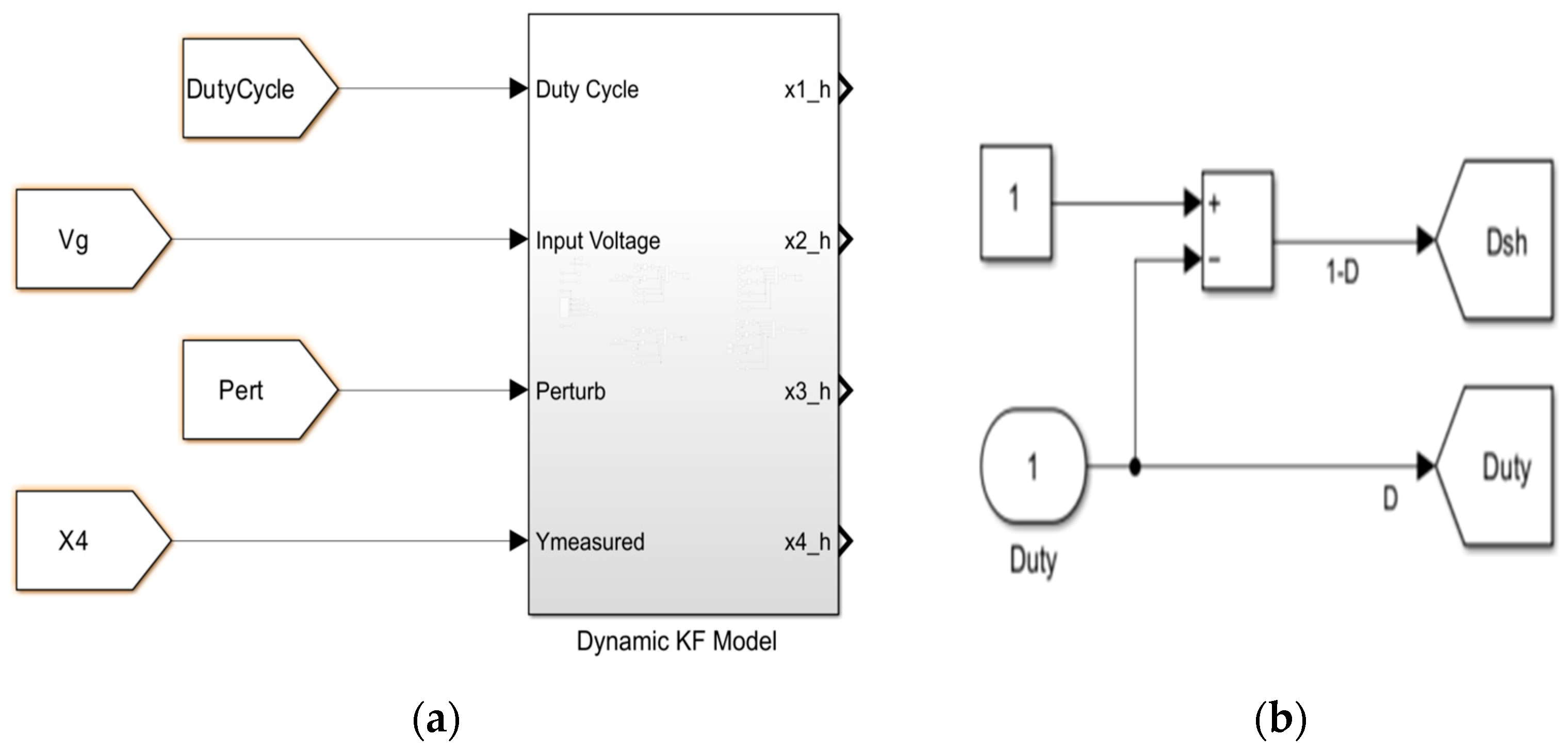
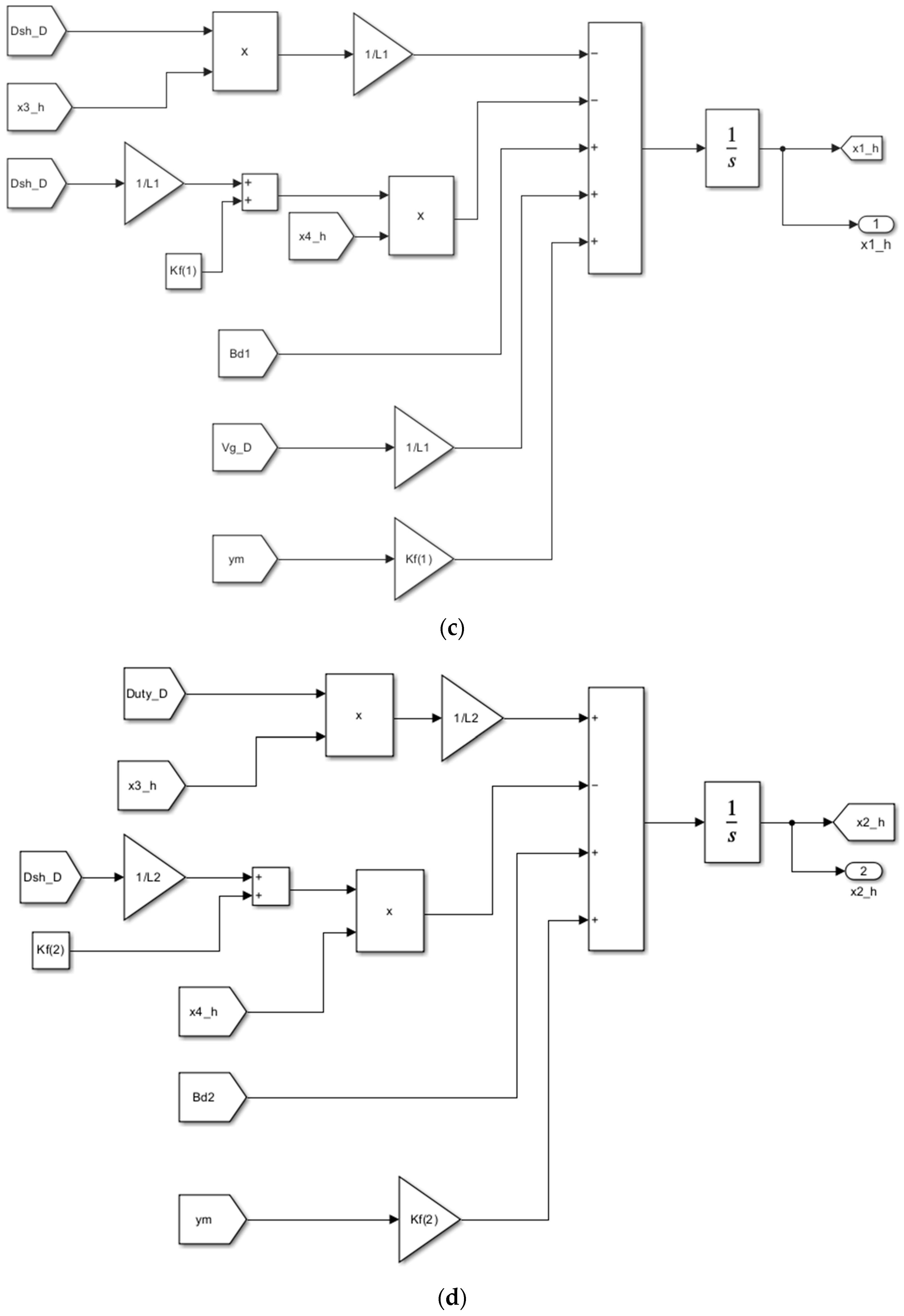
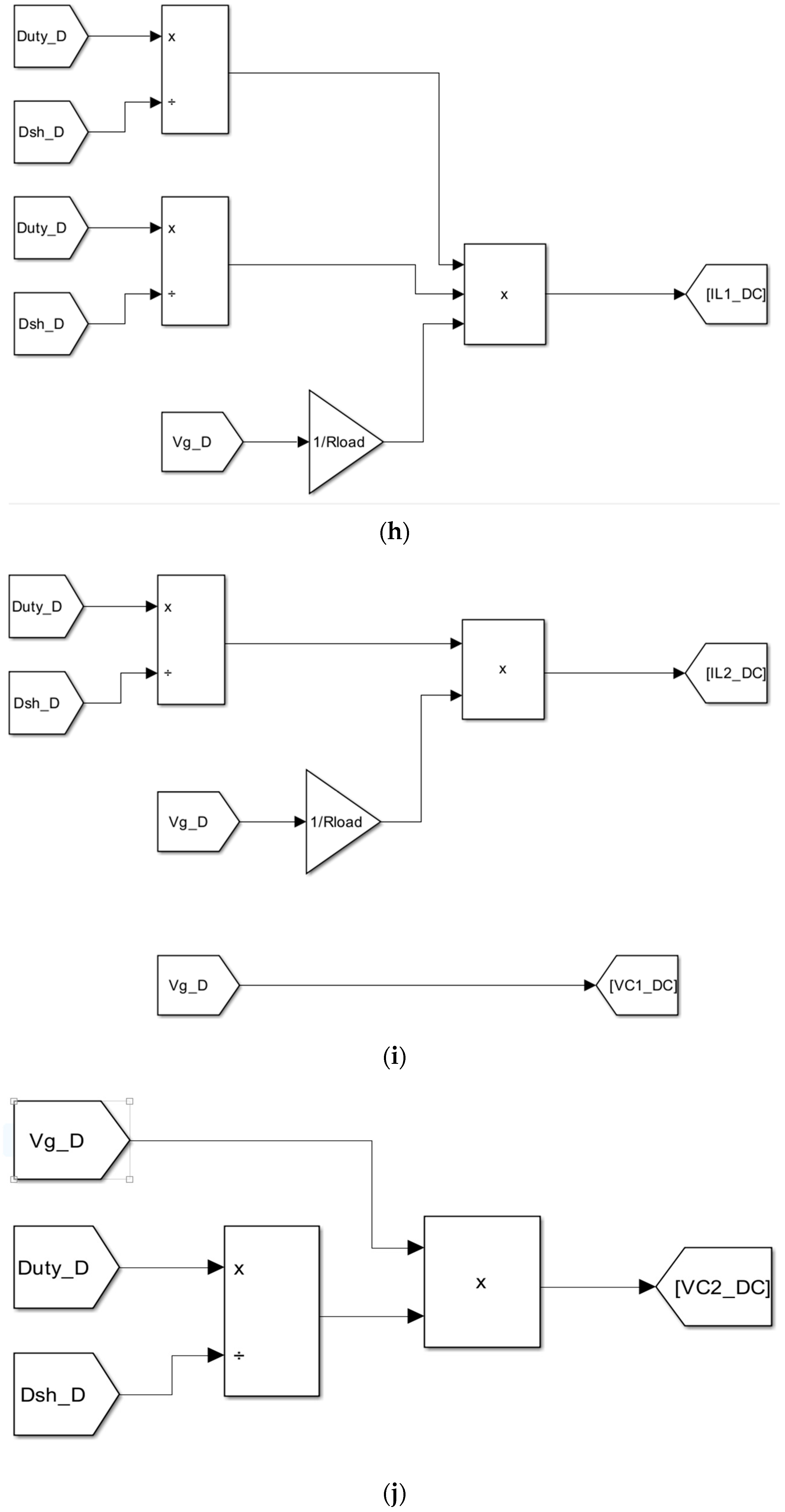
5.3.2. Kalman Filter Dynamical Model
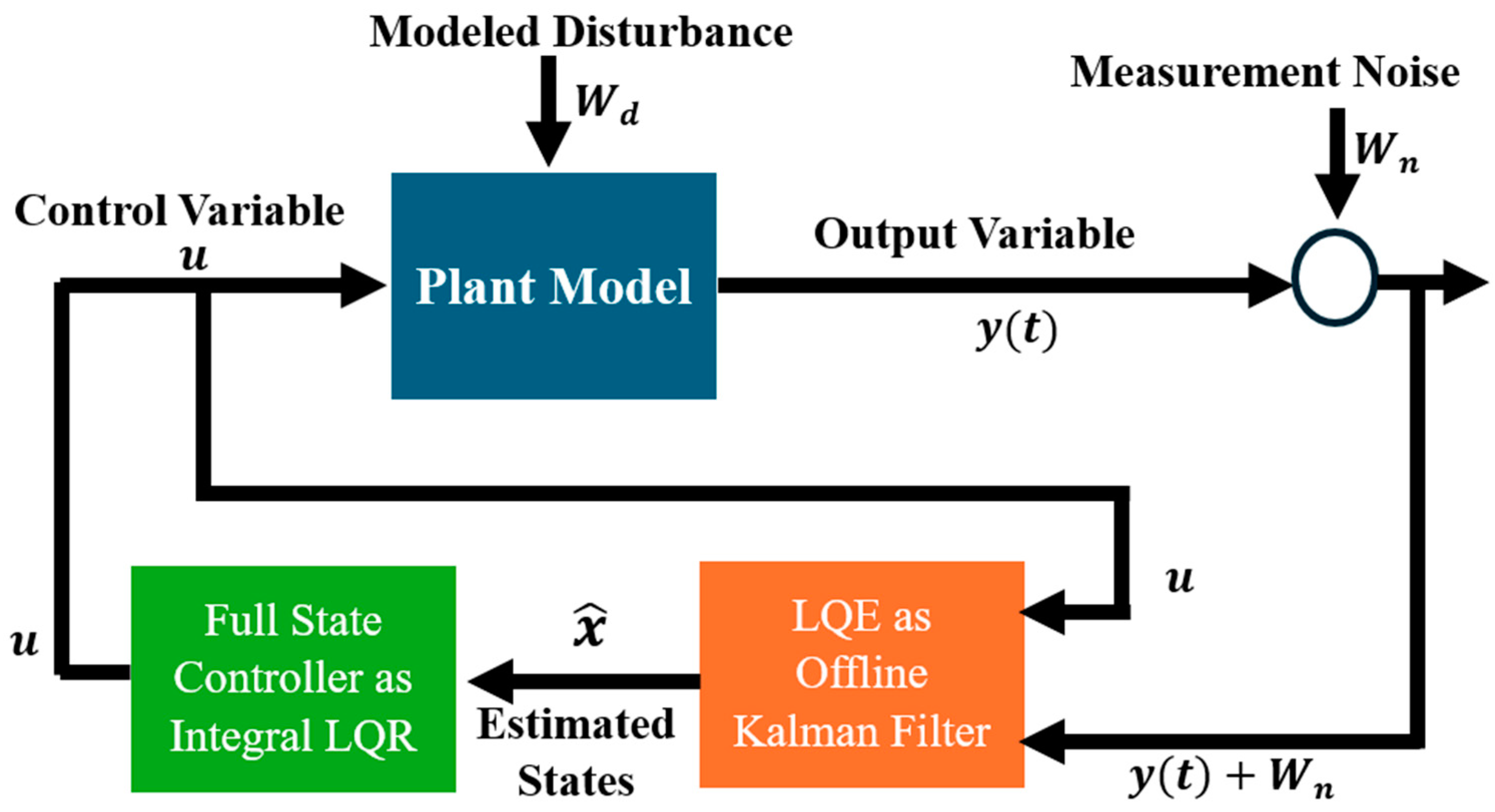
6. Linear Quadratic Gaussian (LQG)
- Design controller gains for the LQR such that the system poles (i.e., system eigen values) are placed in the desired location to obtain the desired response.
- Design estimator gains of the LQE such that the system poles (i.e., eigen values) are placed in the desired location to obtain converged estimated states.
7. Results
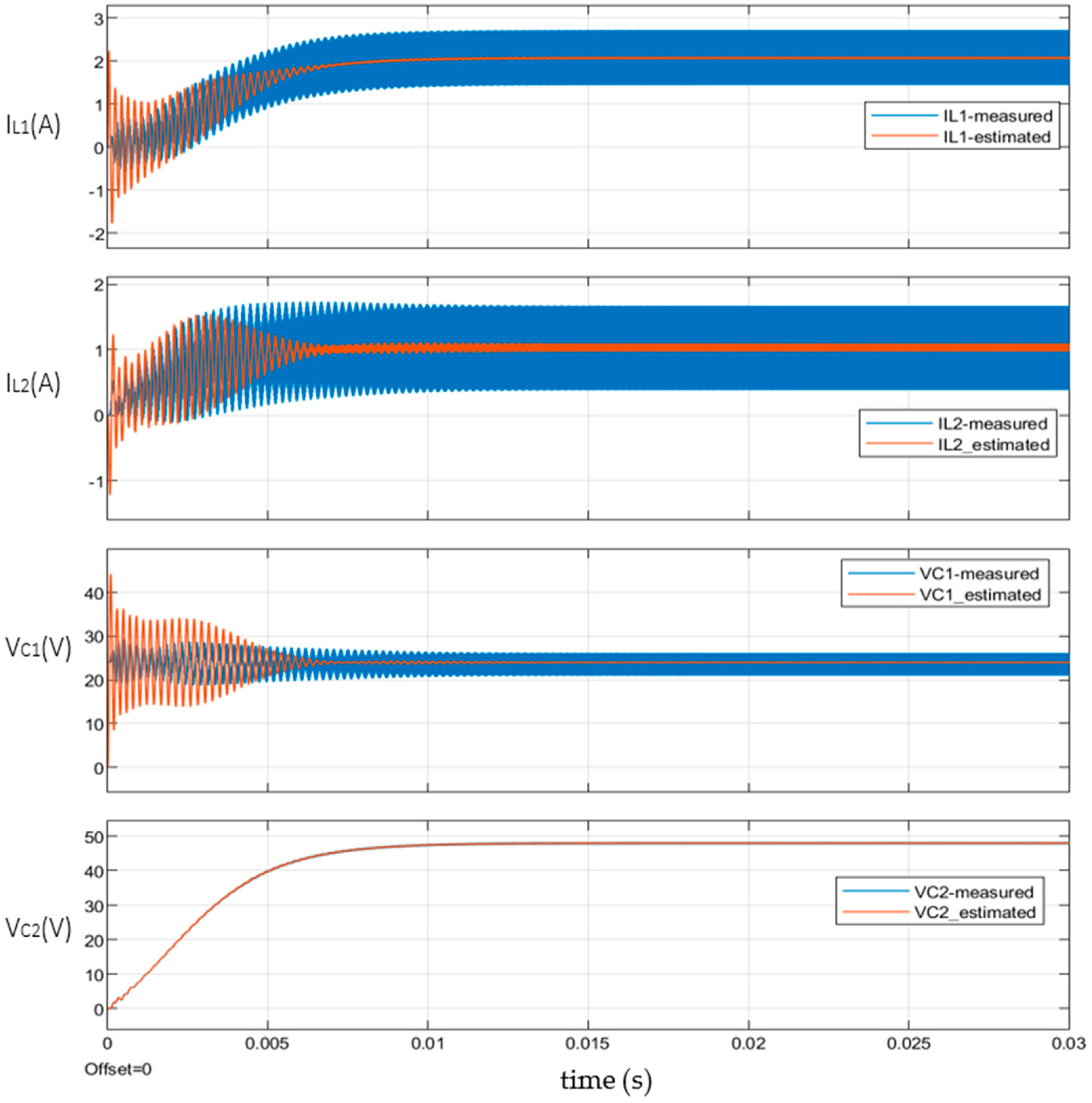
7.1. Estimated States vs. Measured Variables
7.2. Test Metrics and Comparison
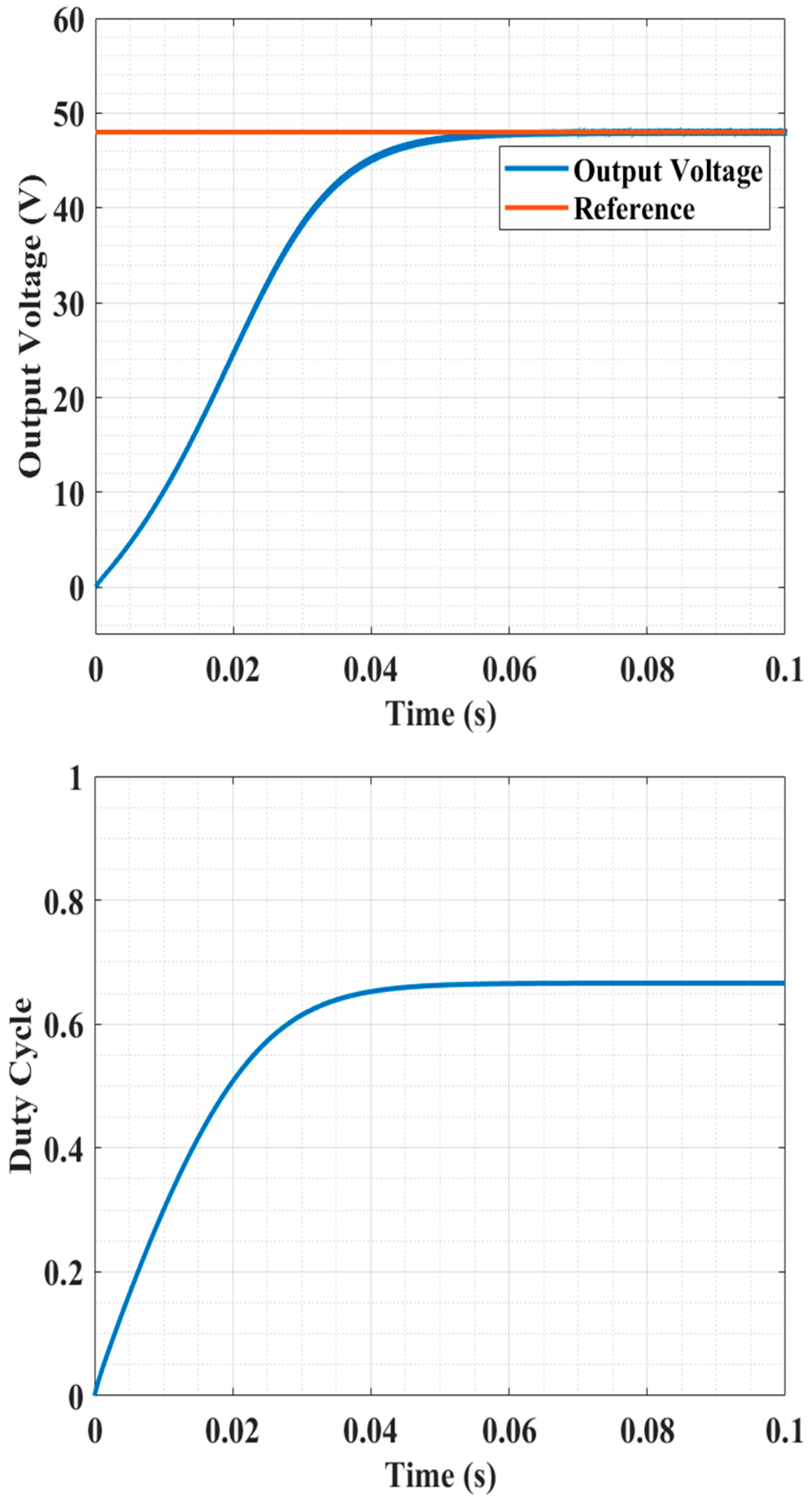
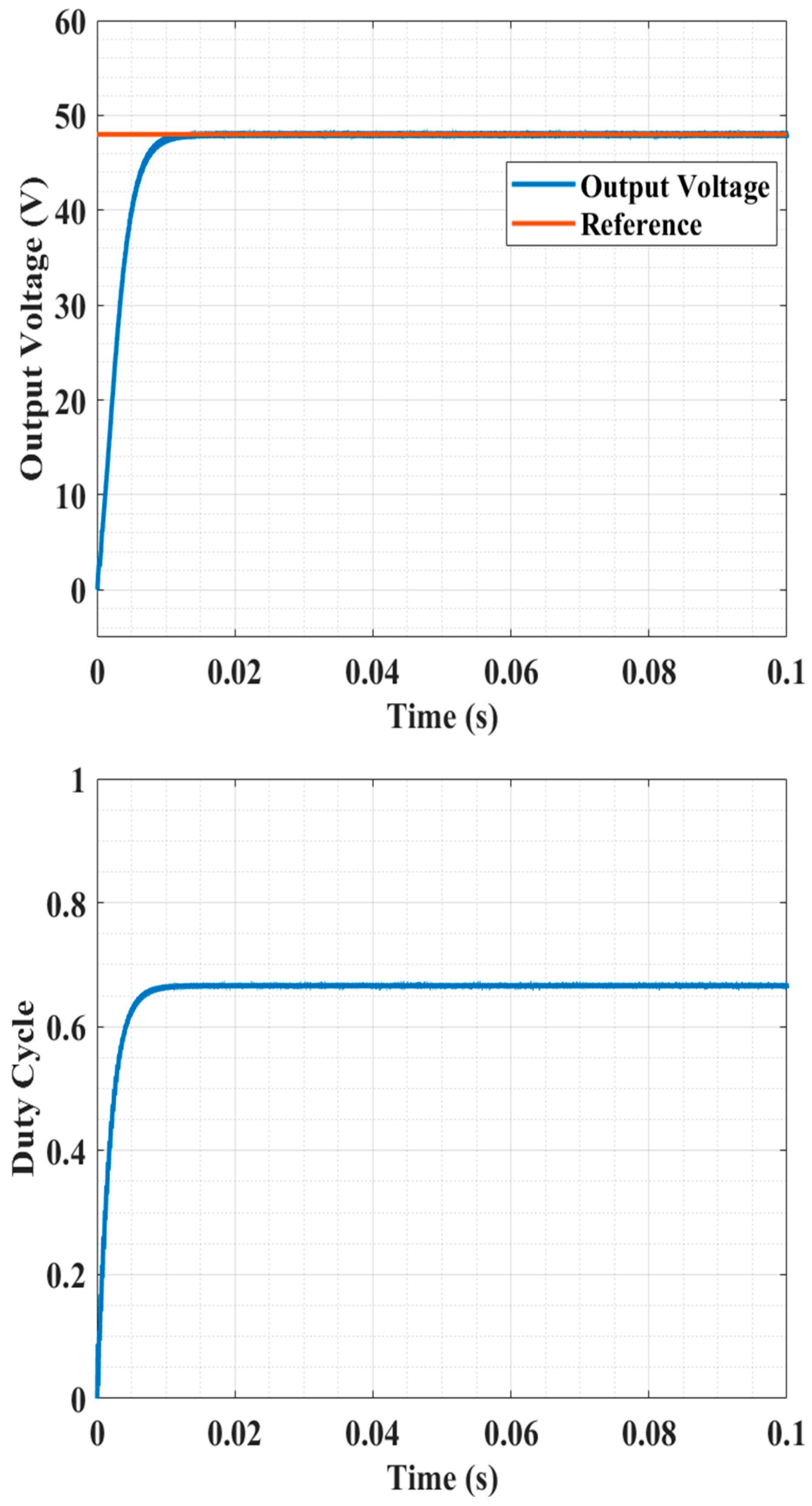
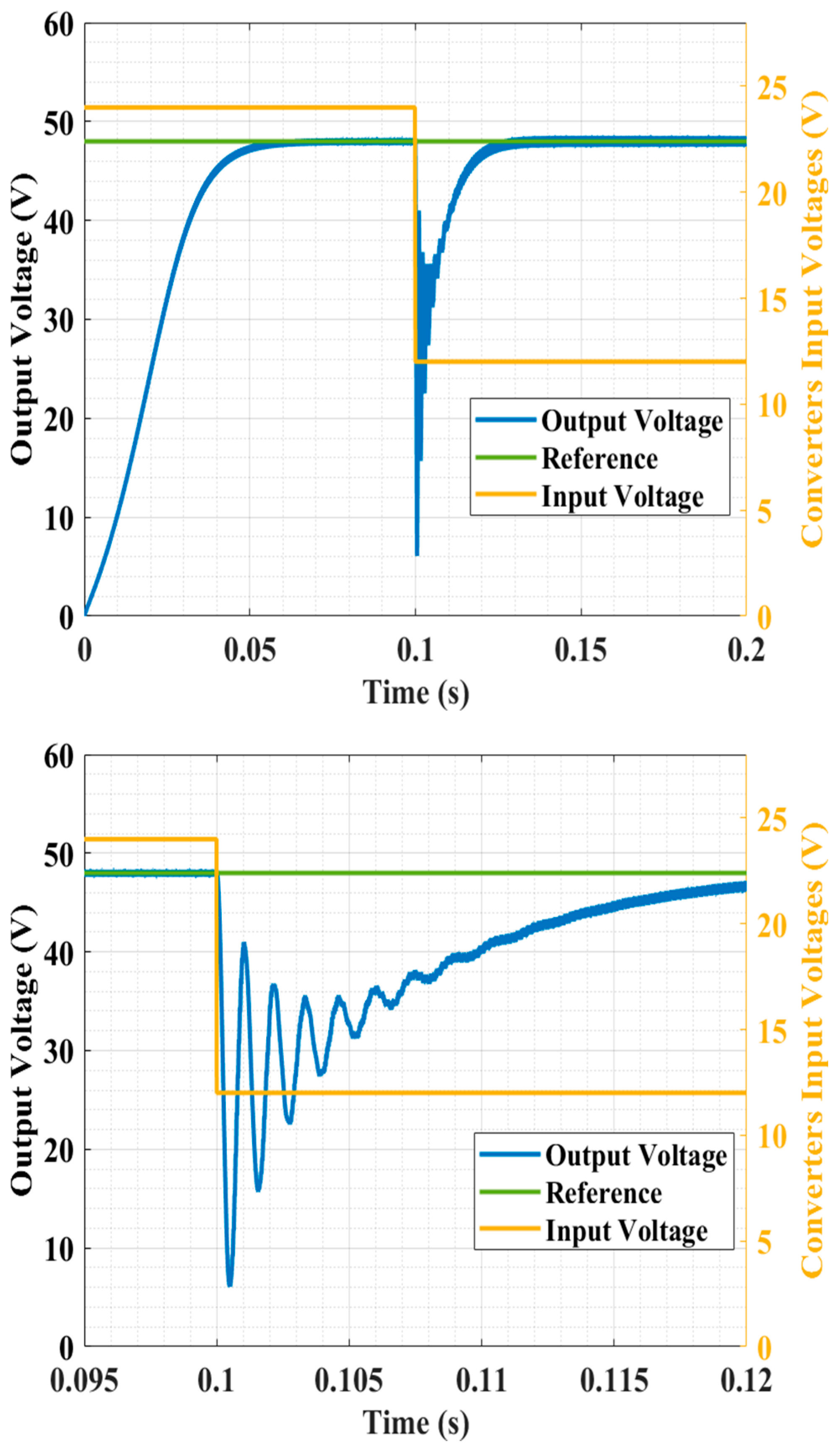
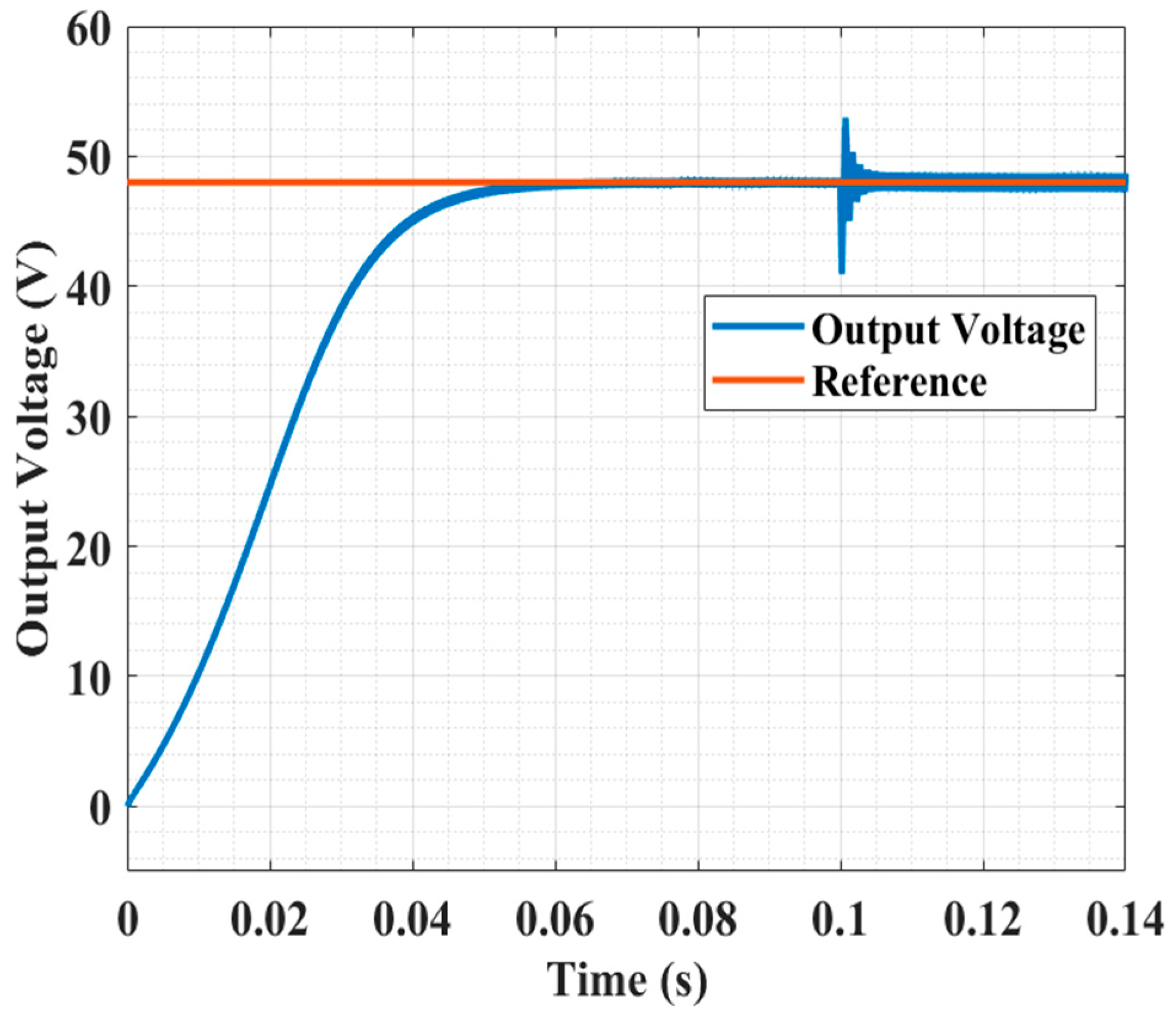
7.2.1. Cold Start Test
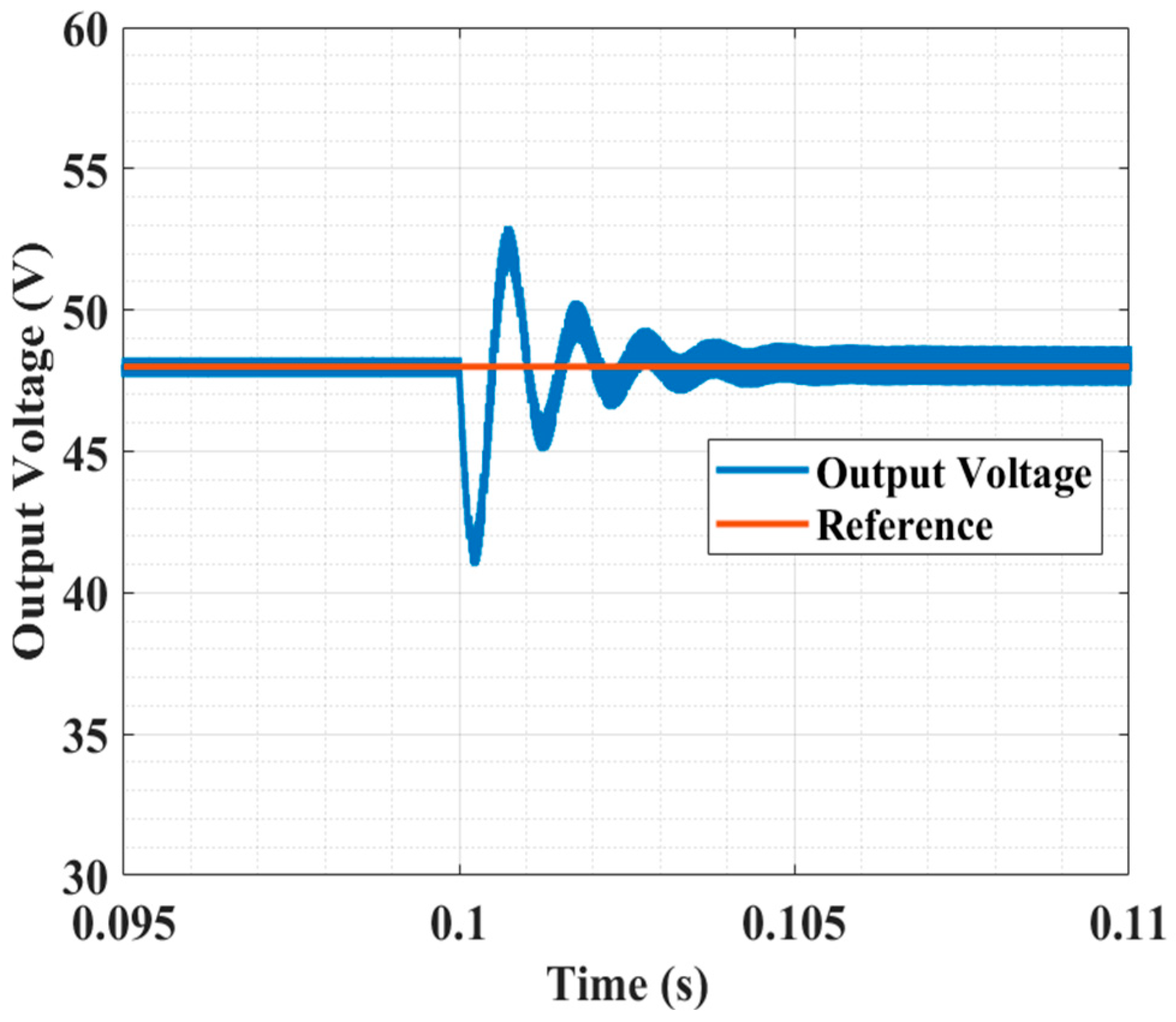
7.2.2. Disturbance Test at Input Voltage
7.2.3. Load Disturbance Test
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohan, N. Power Electronics: Converters, Applications, and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Mohan, N. Power Electronics: A First Course; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Basso, C. Switch-Mode Power Supplies, Second Edition: SPICE Simulations and Practical Designs, 2nd ed.; McGraw Hill: New York, NY, USA, 2014. [Google Scholar]
- Basso, C.P. Transfer Functions of Switching Converters; Faraday Press: Apache Junction, AZ, USA, 2021. [Google Scholar]
- Rashid, M.H. Power Electronics: Circuits, Devices, and Applications, 3rd ed.; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Boston, Inc.: Norwell, MA, USA, 2020. [Google Scholar]
- Gorji, S.A.; Sahebi, H.G.; Ektesabi, M.; Rad, A.B. Topologies and Control Schemes of Bidirectional DC–DC Power Converters: An Overview. IEEE Access 2019, 7, 117997–118019. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Ramachandaramurthy, V.K.; Padmanaban, S.; Blaabjerg, F.; Ionel, D.M.; Mitolo, M.; Almakhles, D. Survey of DC-DC Non-Isolated Topologies for Unidirectional Power Flow in Fuel Cell Vehicles. IEEE Access 2020, 8, 178130–178166. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Tofoli, F.L.; Pereira, D.d.C.; de Paula, W.J.; Júnior, D.d.S.O. Survey on non-isolated high-voltage step-up dc–dc topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef]
- Revathi, B.S.; Prabhakar, M. Non isolated high gain DC-DC converter topologies for PV applications—A comprehensive review. Renew. Sustain. Energy Rev. 2016, 66, 920–933. [Google Scholar] [CrossRef]
- Bryant, B.; Kazimierczuk, M. Derivation of the Cuk PWM DC-DC converter circuit topology. In Proceedings of the ISCAS 2003, International Symposium on Circuits and Systems, Bangkok, Thailand, 26–29 May 2003. [Google Scholar]
- Bryant, B.; Kazimierezuk, M. Derivation of the buck-boost PWM DC-DC converter circuit topology. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems, Scottsdale, AZ, USA, 26–29 May 2002. [Google Scholar]
- Wilson, T. The evolution of power electronics. IEEE Trans. Power Electron. 2000, 15, 439–446. [Google Scholar] [CrossRef]
- Bhaskar Ranjana, M.; Pandav, K.; Draxe, K. Novel Topological Derivations for DC-DC Converters. Int. J. Comput. Eng. Manag. 2013, 16, 49–53. [Google Scholar]
- Pragallapati, N.; Agarwal, V. Distributed PV Power Extraction Based on a Modified Interleaved SEPIC for Nonuniform Irradiation Conditions. IEEE J. Photovolt. 2015, 5, 1442–1453. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. An Adaptive Voltage-Sensor-Based MPPT for Photovoltaic Systems with SEPIC Converter Including Steady-State and Drift Analysis. IEEE Trans. Ind. Electron. 2015, 62, 7609–7619. [Google Scholar] [CrossRef]
- Chiang, S.J.; Shieh, H.-J.; Chen, M.-C. Modeling and Control of PV Charger System with SEPIC Converter. IEEE Trans. Ind. Electron. 2008, 56, 4344–4353. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Alghaythi, M.L.; Alshammari, M.S.; Osheba, D.S. Enhancing Photovoltaic Conversion Efficiency with Model Predictive Control-Based Sensor-Reduced Maximum Power Point Tracking in Modified SEPIC Converters. IEEE J. Mag. 2023, 11, 100769–100780. Available online: https://ieeexplore.ieee.org/document/10250777 (accessed on 3 May 2024). [CrossRef]
- Tey, K.S.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B.; Oo, A.T.; Stojcevski, A. Improved Differential Evolution-Based MPPT Algorithm Using SEPIC for PV Systems under Partial Shading Conditions and Load Variation. IEEE J. Mag. 2018, 14, 4322–4333. Available online: https://ieeexplore-ieee-org.uproxy.library.dc-uoit.ca/abstract/document/8258969 (accessed on 4 May 2024). [CrossRef]
- Elkhateb, A.; Rahim, N.A.; Selvaraj, J.; Uddin, M.N. Fuzzy-Logic-Controller-Based SEPIC Converter for Maximum Power Point Tracking. IEEE Trans. Ind. Appl. 2014, 50, 2349–2358. [Google Scholar] [CrossRef]
- Prabhakaran, P.; Agarwal, V. Novel Boost-SEPIC Type Interleaved DC–DC Converter for Mitigation of Voltage Imbalance in a Low-Voltage Bipolar DC Microgrid. IEEE Trans. Ind. Electron. 2019, 67, 6494–6504. [Google Scholar] [CrossRef]
- Veerachary, M. Power tracking for nonlinear pv sources with coupled inductor SEPTIC converter. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1019–1029. [Google Scholar] [CrossRef]
- Singh, A.K.; Badoni, M.; Tatte, Y.N. A Multifunctional Solar PV and Grid Based On-Board Converter for Electric Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 3717–3727. [Google Scholar] [CrossRef]
- Kapat, S.; Krein, P.T. A Tutorial and Review Discussion of Modulation, Control and Tuning of High-Performance DC-DC Converters Based on Small-Signal and Large-Signal Approaches. IEEE Open J. Power Electron. 2020, 1, 339–371. [Google Scholar] [CrossRef]
- Lee, S. Demystifying Type II and Type III Compensators Using Op-Amp and OTA for DC/DC Co. Application Report SLVA662-July 2014. Available online: https://www.ti.com/lit/an/slva662/slva662.pdf?ts=1720297046762&ref_url=https%253A%252F%252Fwww.google.com%252F (accessed on 4 May 2024).
- Mitchell, D.M. DC-DC Switching Regulator Analysis; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Tang, W.; Lee, F.; Ridley, R.; Cohen, I. Charge control: Modeling, analysis, and design. IEEE Trans. Power Electron. 1993, 8, 396–403. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Upper Saddle River: Prentice Hall, NJ, USA, 2010. [Google Scholar]
- Dorf, R.C. Modern Control Systems, 13th ed.; Pearson: Hoboken, NJ, USA, 2017. [Google Scholar]
- Nise, N.S. Control Systems Engineering, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Sheehan, R.; Diana, L. Switch-Mode Power Converter Compensation Made Easy; Texas Instrument: Dallas, TX, USA, 2016. [Google Scholar]
- Rahimi, A.M.; Parto, P.; Asadi, P. Compensator Design Procedure for Buck Converter with Voltage-Mode Error-Amplifier. International Rectifier. 2012. Available online: https://www.infineon.com/dgdl/an-1162.pdf?fileId=5546d462533600a40153559a8e17111a (accessed on 4 May 2024).
- OnSemi-AN-and90138-D. Available online: https://www.onsemi.com/pub/collateral/and90138-d.pdf (accessed on 30 May 2023).
- Xu, Q.; Vafamand, N.; Chen, L.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Review on Advanced Control Technologies for Bidirectional DC/DC Converters in DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1205–1221. [Google Scholar] [CrossRef]
- Pirooz, A.; Noroozian, R. Model predictive control of classic bidirectional DC-DC converter for battery applications. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 6–18 February 2016; pp. 517–522. [Google Scholar]
- Ebad, M.; Song, B.-M. Accurate model predictive control of bidirectional DC-DC converters for DC distributed power systems. In Proceedings of the 2012 IEEE Power & Energy Society General Meeting. New Energy Horizons—Opportunities and Challenges, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Hartley, E.N.; Trodden, P.A.; Richards, A.G.; Maciejowski, J.M. Model predictive control system design and implementation for spacecraft rendezvous. Control Eng. Pract. 2012, 20, 695–713. [Google Scholar] [CrossRef]
- Beccuti, A.G.; Mariethoz, S.; Cliquennois, S.; Wang, S.; Morari, M. Explicit Model Predictive Control of DC–DC Switched-Mode Power Supplies with Extended Kalman Filtering. IEEE Trans. Ind. Electron. 2009, 56, 1864–1874. [Google Scholar] [CrossRef]
- Mumtaz, F.; Yahaya, N.Z.; Meraj, S.T.; Singh, B.; Kannan, R.; Ibrahim, O. Review on non-isolated DC-DC converters and their control techniques for renewable energy applications. Ain Shams Eng. J. 2021, 12, 3747–3763. [Google Scholar] [CrossRef]
- Zhou, J. Adaptive backstepping control of uncertain systems nonsmooth nonlinearities, interactions, or time-variations. In Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Xu, Q.; Jiang, W.; Blaabjerg, F.; Zhang, C.; Zhang, X.; Fernando, T. Backstepping Control for Large Signal Stability of High Boost Ratio Interleaved Converter Interfaced DC Microgrids with Constant Power Loads. IEEE Trans. Power Electron. 2020, 35, 5397–5407. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; Taylor & Francis Group: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Ciccarelli, F.; Lauria, D. Sliding-mode control of bidirectional dc-dc converter for supercapacitor energy storage applications. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 1119–1122. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Wack, M. Observer-based higher order sliding mode control of power factor in three-phase AC/DC converter for hybrid electric vehicle applications. Int. J. Control 2014, 87, 1117–1130. [Google Scholar] [CrossRef]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Fatoorehchi, H.; Ghorbanian, S.A. Sliding Mode Control for Heartbeat Electrocardiogram Tracking Problem. J. Chem. Pet. Eng. 2019, 53, 265–272. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Y.; Liu, S.; Cai, J.; Dou, L. A sliding mode control based maximum power point tracking method of PV arrays under partially shaded conditions. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015. [Google Scholar]
- Ortega, R.; van der Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.-H.; Chen, X. Disturbance Observer-Based Control; Informa UK Limited: London, UK, 2016. [Google Scholar]
- Huangfu, Y.; Guo, L.; Ma, R.; Gao, F. An Advanced Robust Noise Suppression Control of Bidirectional DC–DC Converter for Fuel Cell Electric Vehicle. IEEE Trans. Transp. Electrif. 2019, 5, 1268–1278. [Google Scholar] [CrossRef]
- Degrees of Controllability and Gramians [Control Bootcamp]. Available online: https://www.youtube.com/watch?v=ZNHx62HbKNA (accessed on 4 May 2024).
- Engr210a Lecture 9: Controllability and Observability. Available online: https://lall.stanford.edu/engr210a/lectures/lecture9_2001_10_30_01.pdf (accessed on 4 May 2024).
- Brunton and Kutz—2017—Data Driven Science & Engineering.pdf. Available online: https://databookuw.com/databook.pdf (accessed on 4 May 2024).
- Controllability Tests, (25 February 2021). [Online Video]. Available online: https://www.youtube.com/watch?v=KZr9wga7l2U (accessed on 4 May 2024).
- Chapter 2 CONTROLLABILITY-University of Toronto. Available online: https://www.control.utoronto.ca/people/profs/kwong/ece410/2008/notes/chap2.pdf (accessed on 4 May 2024).
- ECE 5550-Applied Kalman Filtering. Available online: http://mocha-java.uccs.edu/ECE5550/ECE5550-Notes01.pdf (accessed on 4 May 2024).
- Lecture 9-The Extended Kalman Filter. Available online: https://stanford.edu/class/ee363/lectures/ekf.pdf (accessed on 4 May 2024).
- Lect25 and 26 Notes Theory of Kalman Filter.pdf. Available online: https://atmos.uw.edu/~breth/classes/AM582/lect/lect25-notes.pdf (accessed on 4 May 2024).
- Lecture 5—Observibility and State Estimation. Available online: https://stanford.edu/class/ee363/lectures/observ.pdf (accessed on 4 May 2024).
- EE363 Review Session 2: Invariant Subspaces, Sylvester Equation, PBH. Available online: https://web.stanford.edu/class/ee363/sessions/s2notes.pdf (accessed on 4 May 2024).
- Lecture 6: Invariant Subspaces. Available online: https://stanford.edu/class/ee363/lectures/inv-sub.pdf (accessed on 4 May 2024).
- Lecture 21: Filtering, State Space Models, Kalman Filter. Available online: https://ocw.mit.edu/courses/14-384-time-series-analysis-fall-2013/3dcb917d20ece78852cd398a3f7b5e64_MIT14_384F13_lec21.pdf (accessed on 4 May 2024).
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter, Course 8; University of North Carolina at Chael Hill: Chapel Hill, NC, USA, 2001. [Google Scholar]
- Motivation for Full-State Estimation [Control Bootcamp], (6 February 2017). Available online: https://www.youtube.com/watch?v=LTNMf8X21cY (accessed on 4 April 2024).
- Control Bootcamp: Observability. (6 February 2017). Available online: https://www.youtube.com/watch?v=iRZmJBcg1ZA (accessed on 4 April 2024).
- Control Bootcamp: Full-State Estimation. (6 February 2017). Available online: https://www.youtube.com/watch?v=MZJMi-6_4UU (accessed on 4 April 2024).
- The Kalman Filter [Control Bootcamp]. (6 February 2017). Available online: https://www.youtube.com/watch?v=s_9InuQAx-g (accessed on 4 April 2024).
- Control Bootcamp: Linear Quadratic Gaussian (LQG). (6 February 2017). Available online: https://www.youtube.com/watch?v=H4_hFazBGxU (accessed on 4 April 2024).
- Sel, A.; Gunes, U.; Elbir, O.; Kasnakoglu, C. Comparative analysis of performance of the SEPIC converter using LQR and PID controllers. In Proceedings of the 2017 21st International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2017; pp. 839–844. [Google Scholar]
- Meghnous, A.R.; Pham, M.T.; Lin-Shi, X. Nonlinear Observer and Lyapunov-Based Control for SEPIC Converter: Design and Experimental Results. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 5833–5838. [Google Scholar] [CrossRef]
- Sousa, S.M.; Leite, V.J.S.; Fernandes, S.W.; Oliveira, I.R.H. SEPIC DC/DC converter control by observed-state feedback. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Biricik, S.; Ngo, T.; Komurcugil, H.; Basu, M. Nonlinear control methods for single-ended primary-inductor power converters. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1337–1340. [Google Scholar]
- Meghnous, A.R.; Pham, M.T.; Lin-Shi, X. A hybrid observer for a class of DC-DC power converters. In Proceedings of the 2013 American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 6225–6230. [Google Scholar]
- Jaafar, A.; Godoy, E.; Lefranc, P.; Shi, X.L.; Fayaz, A.; Li, N. Nonlinear sliding mode observer and control of high order DC-DC converters. In Proceedings of the IECON 2010—36th Annual Conference of IEEE Industrial Electronics, Glendale, AZ, USA, 7–10 November 2010; pp. 180–186. [Google Scholar]
- SEPIC Converter Analysis and Design. Semiconductor Components Industries, LLC, 2021, Novenber 2021. Available online: https://www.onsemi.com/pub/collateral/and90136-d.pdf (accessed on 4 May 2024).
- Ridley, R. Analyzing the Sepic Converter. Power Syst. Des. Eur. 2006, 14–18. Available online: https://e2e.ti.com/cfs-file/__key/communityserver-discussions-components-files/234/Sepic-Analysis.pdf. (accessed on 4 May 2024).
- Ridley Engineering|—[002] Sepic Converter Analysis. Available online: https://ridleyengineering.com/design-center-ridley-engineering/38-control/44-002-sepic-converter-analysis.html (accessed on 19 February 2024).
- Basso, C.P. Designing Control Loops for Linear and Switching Power Supplies: A Tutorial Guide; Artech House: Boston, MA, USA, 2012. [Google Scholar]
- Ullah, M.; Ulasyar, A.; Zad, H.S.; Khattak, A. Design of Linear Quadratic Regulator Controller for Sepic Con-verter. In Proceedings of the 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2–3 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Erickson, R.W. Synthesis of switched-mode converters. In Proceedings of the 1983 IEEE Power Electronics Specialists Conference, Albuquerque, NM, USA, 6–9 June 1983; pp. 9–22. [Google Scholar]
- Venable, H.D.; Industries, V. The K Factor: A New Mathematical Tool for Stability Analysis and Synthesis. In Proceedings of the Powercon 10, San Diego, CA, USA, 22–24 March 1983. [Google Scholar]
- Venable, H.D.; Venable Instruments. Optimum Feedback Amplifier Design. Venable Instruments Technical White Paper, Number 3. pp. 1–14. Available online: https://www.venableinstruments.com/optimum-feedback-amplifier-design-wp (accessed on 4 May 2024).
- Venable, H.D.; Venable Instruments. Current Mode Control, Venable Instruments Technical White Paper, Number 5. pp. 1–12. Available online: https://www.venableinstruments.com/current-mode-control-wp (accessed on 4 May 2024).
- Slotine, J.-J.E.; Li, W. Applied Nonlinear Control; Prentice Hall International Inc.: Upper Saddle, NJ, USA, 1991. [Google Scholar]







| Required Specifications | Load R | Input Voltage Vg | Output Voltage Vo | Switching Frequency fsw |
|---|---|---|---|---|
| Value | 24 V | 48 V | 50 kHz | |
| Designed SEPIC Components | ||||
| Value | 0.25 mH | 0.25 mH | 2.78 μF | 23.15 μF |
| State–Feedback Gain | |||||
| Value | 0.00659 | 0.00375 | −1.60361 | 0.000385 | −3.87298 |
| State Variable | ||||
|---|---|---|---|---|
| Determinant of observability Gramian |
| Matrix Title | System Matrix | Input Matrix | Output Matrix | Feedforward Matrix |
|---|---|---|---|---|
| Expression |
| Cold Start | Input Voltage Disturbance | Load Disturbance | ||||||
|---|---|---|---|---|---|---|---|---|
| Response | Settling Time | Response | Settling Time | Drop in o/p Voltage Rail | Response | Settling Time | Drop in o/p Voltage Rail | |
| Type-II | Over- damped | 0.05 s | Severe Oscillation | 0.025 s | 42 V | Severe Oscillation | 0.004 s | 7 V |
| LQG system | Over- damped | 0.01 s | Overdamped | 0.006 s | 14 V | Overdamped | 0.003 s | 5.5 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Haj, Y.; Sood, V.K. Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter. Energies 2024, 17, 3385. https://doi.org/10.3390/en17143385
El Haj Y, Sood VK. Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter. Energies. 2024; 17(14):3385. https://doi.org/10.3390/en17143385
Chicago/Turabian StyleEl Haj, Youssef, and Vijay K. Sood. 2024. "Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter" Energies 17, no. 14: 3385. https://doi.org/10.3390/en17143385
APA StyleEl Haj, Y., & Sood, V. K. (2024). Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter. Energies, 17(14), 3385. https://doi.org/10.3390/en17143385







