Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach
Abstract
1. Introduction
1.1. Motivation
1.2. Background
1.3. Main Contributions
- Unlike many existing studies that focus solely on isolated aspects of forecasting, this methodology addresses the entire trajectory of EV charging behavior prediction. It bridges various stages, including data pre-processing, feature selection, and feature engineering, alongside the utilization and comparison of diverse forecasting methods, followed by a thorough validation and performance evaluation. This framework aims to harmonize and optimize every stage of the predictive process, enhancing the overall accuracy and reliability of EV charging behavior forecasting.
- This methodology places specific emphasis on forecasting both the plugged-in status and the power consumption of EVs at CSs, recognizing the significance of understanding both aspects for effective grid management. This is particularly important to determine the flexibility of the charging process, enabling the smart charging of the EVs.
1.4. Paper Organization
2. Methodology
2.1. Inputs
- Time series data:The initial dataset contains EVs’ charging sessions for a single CS. The data should include at least the following:Start date time (time stamp): The date and time at which the EV is connected for charging.End date time (time stamp): The date and time at which the EV is disconnected. It includes both the periods for which the EV is connected and actively charging and the periods for which the EV is connected, but no longer charging.Charging duration (minutes): The number of minutes the EV is connected and actively charging.Energy consumed (kWh): The amount of energy that has been dispensed by the CS to the EV during the charging session.The size of the dataset can vary, but the more data available, the better.
- Number of days to forecast:It is necessary to define the time horizon of the forecast (in days), e.g., 1 day, 7 days (a week), and 30 days (a month).
- Starting date of the forecast:It is necessary to define the starting date for the forecast period. All the data available before this date are used for training, and from this point onward, the specified number of days is forecasted.
2.2. Pre-Processing
2.2.1. Data Preparation
2.2.2. Missing Data
- If the missing data gap consists of less than one hour of missing values, linear interpolation is utilized to bridge the gap. Linear interpolation is widely used in time series analysis and data imputation due to its simplicity and effectiveness [18] for handling short gaps of missing data.
- If the missing data gap spans over an hour of missing values, it remains unfilled. This decision is made to avoid introducing artificial values for extended time periods, which could potentially and adversely affect the accuracy of the forecasting process. However, in the dataset used in the present paper, the missing values are always lower than 1 h. For other datasets, the methods proposed in [18] can be applied.
2.2.3. Outliers
2.3. Feature Engineering
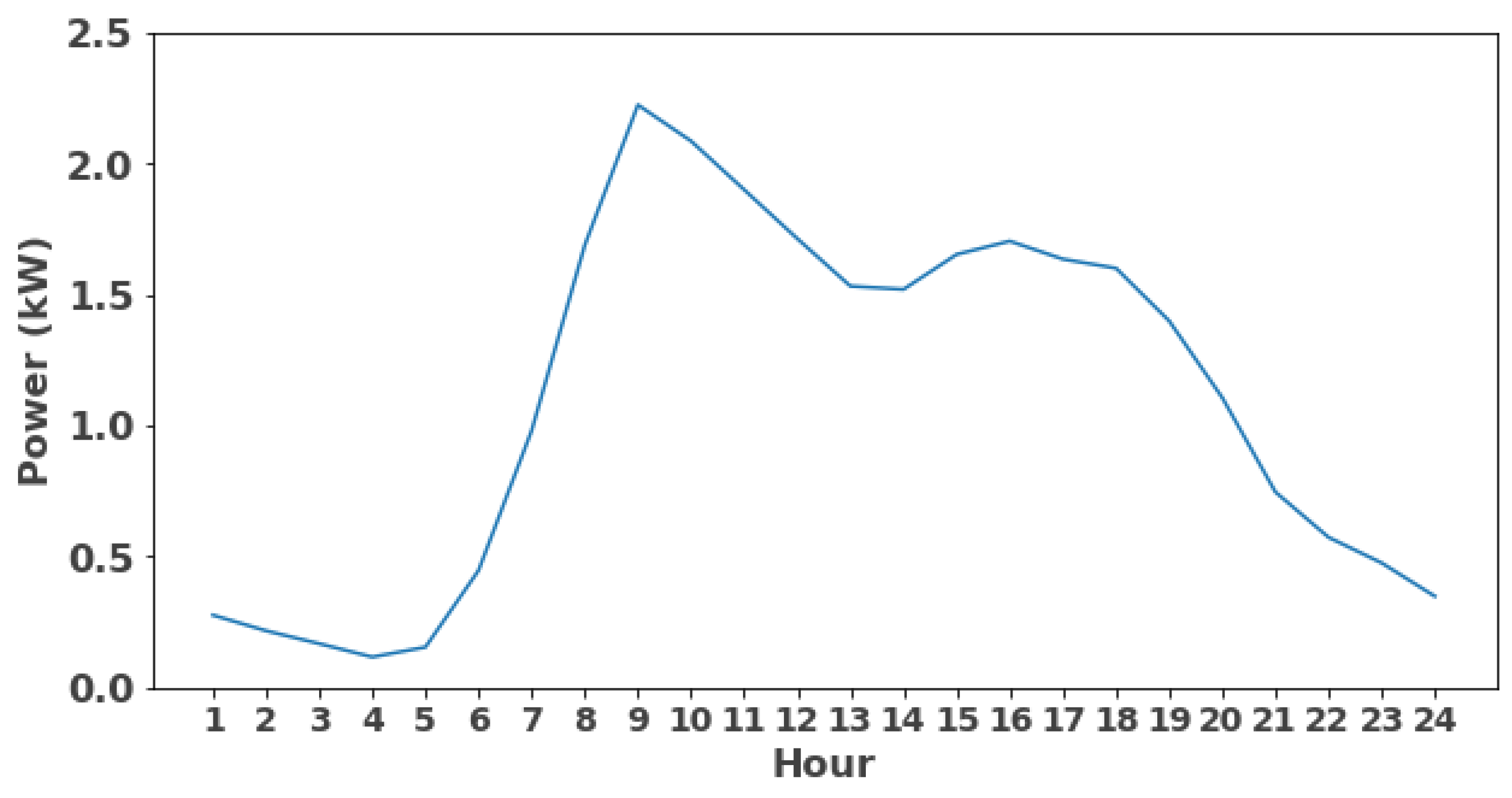
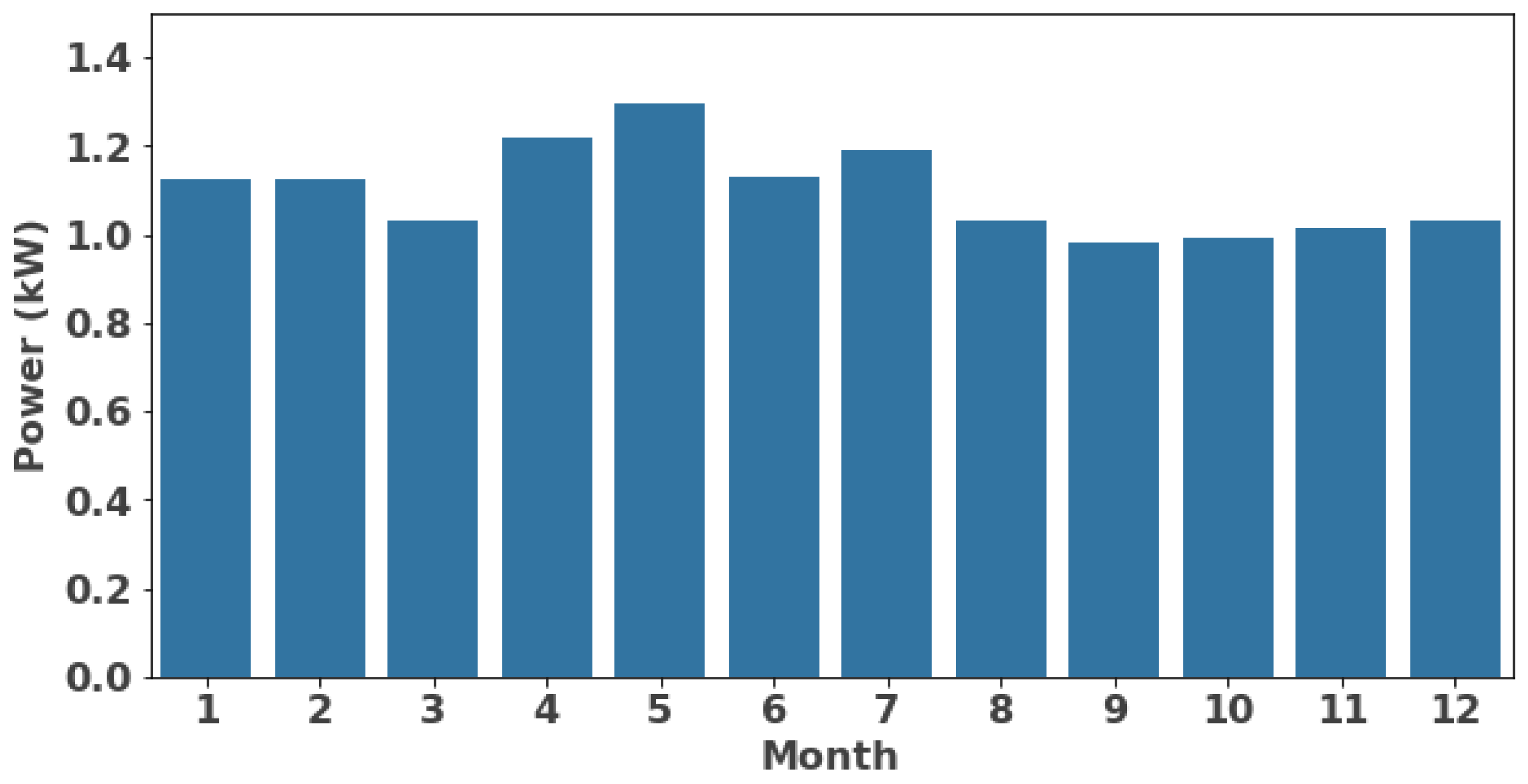
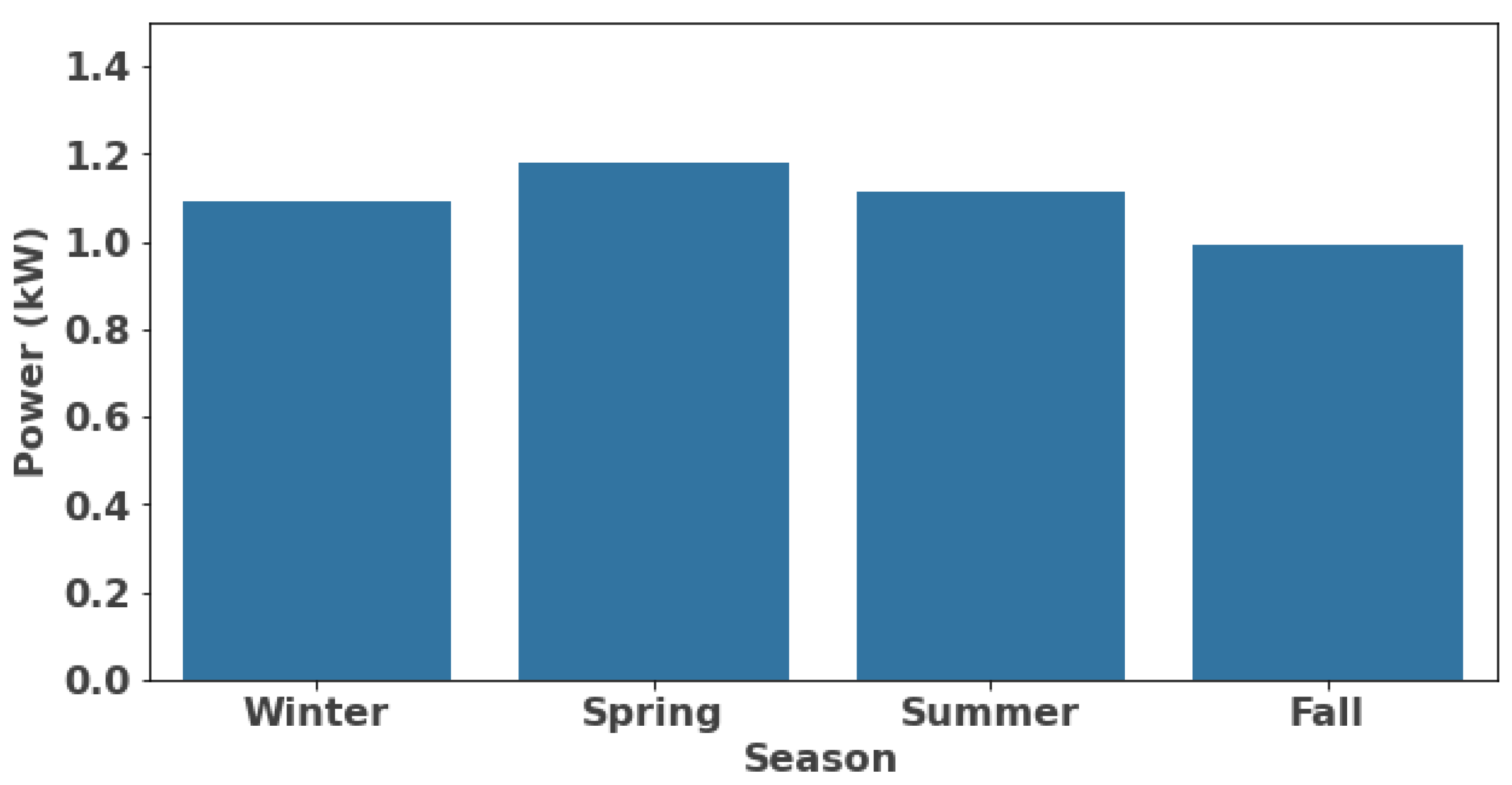
2.3.1. Date/Time Features
- Week of year: 1–52.
- Day of year: 1–365.
- Season: 1–4 (winter = 1, spring = 2, summer = 3, fall = 4).
- Month: 1–12.
- Day of month: 1–30/31.
- Day of week: 1–7 (Monday-Sunday).
- Weekend: 1 if weekend, 0 if not.
- Holiday: 1 if holiday, 0 if not.
- Hour: 1–24.
- Minute: 15, 30 or 45.
2.3.2. Lag Features
- Power lag 1: power consumption 1 day prior.
- Power lag 5: power consumption 5 days prior.
- Power lag 7: power consumption 7 days prior.
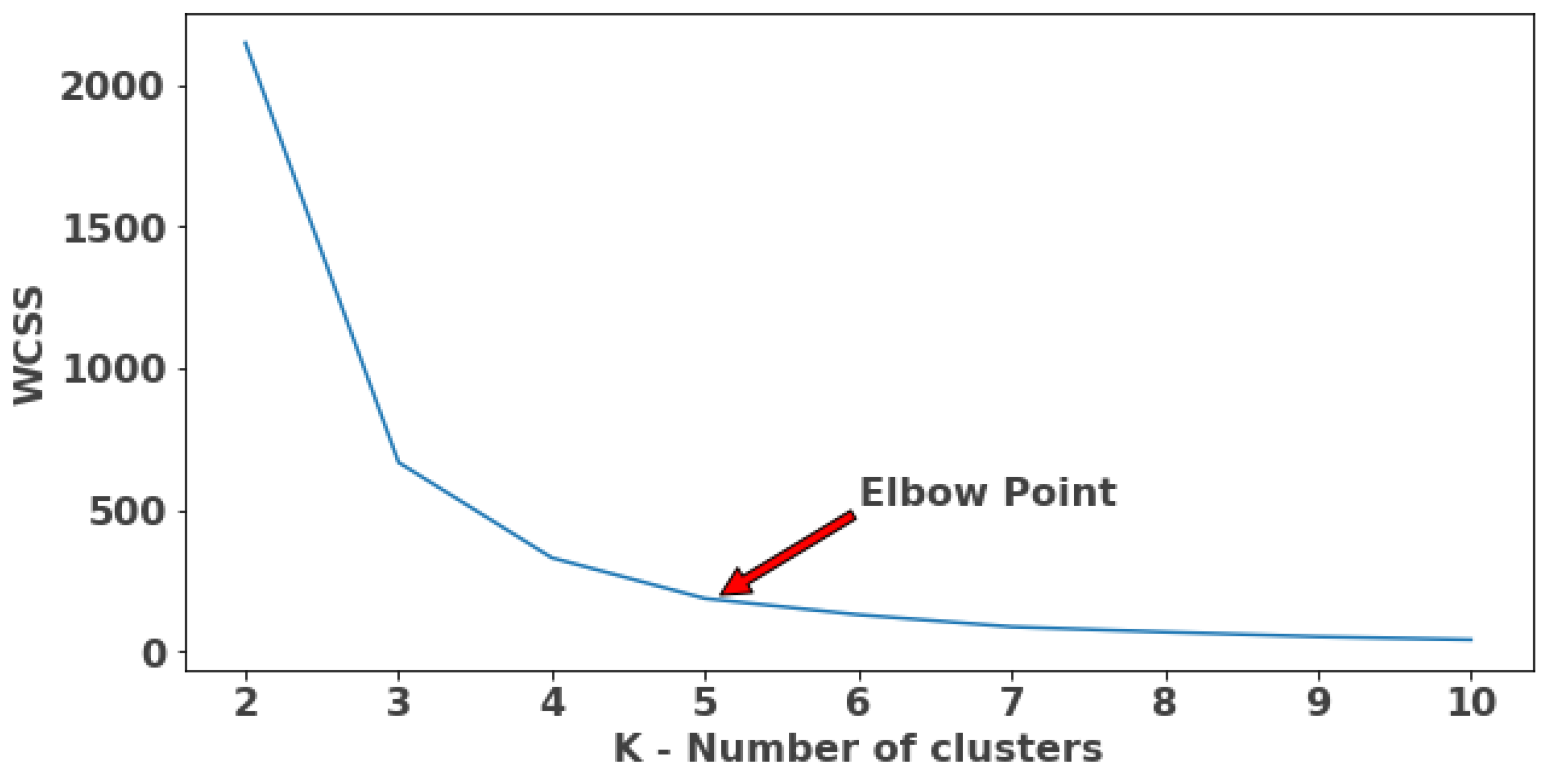
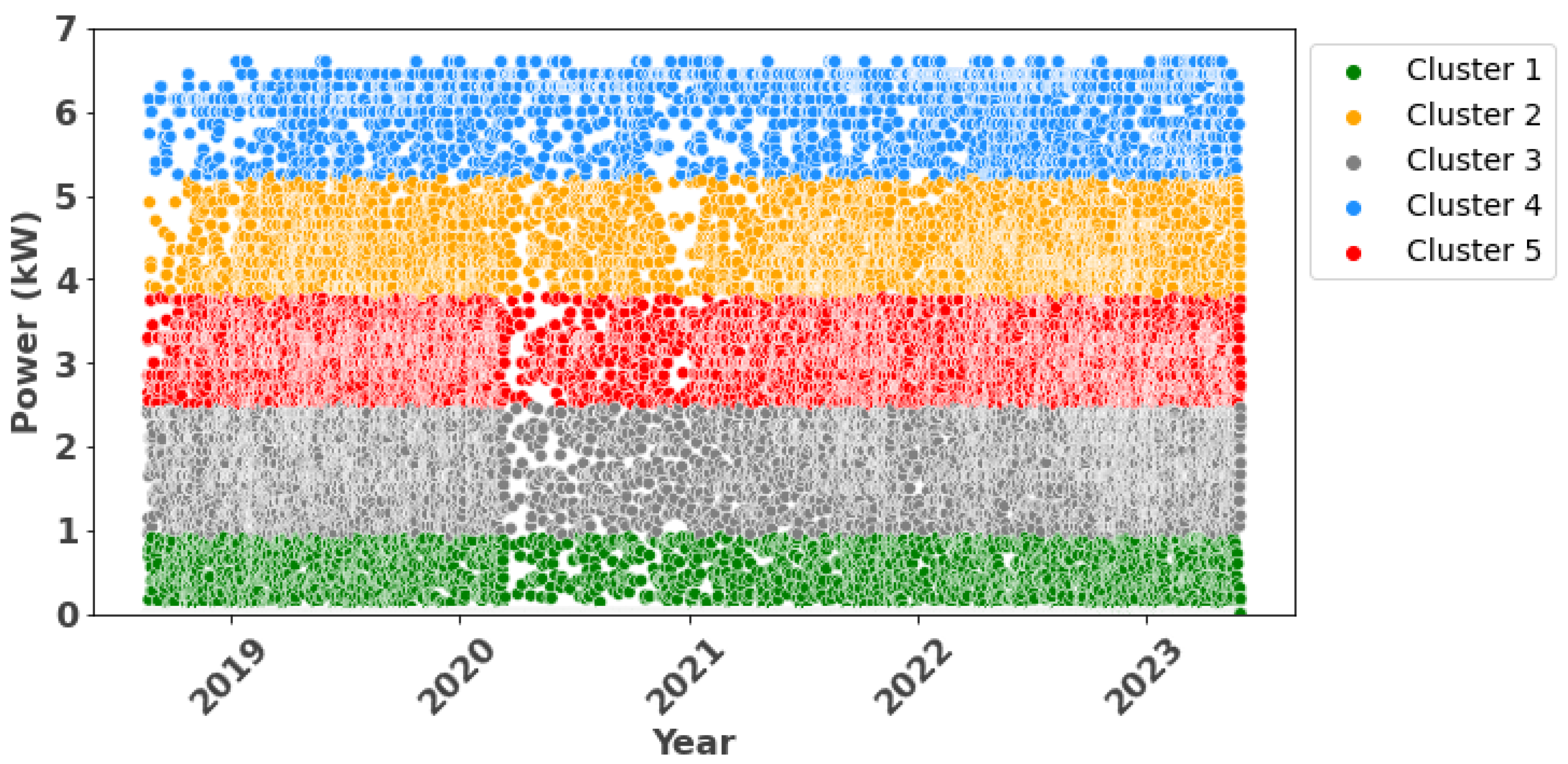
2.3.3. Clustering
2.4. Feature Selection
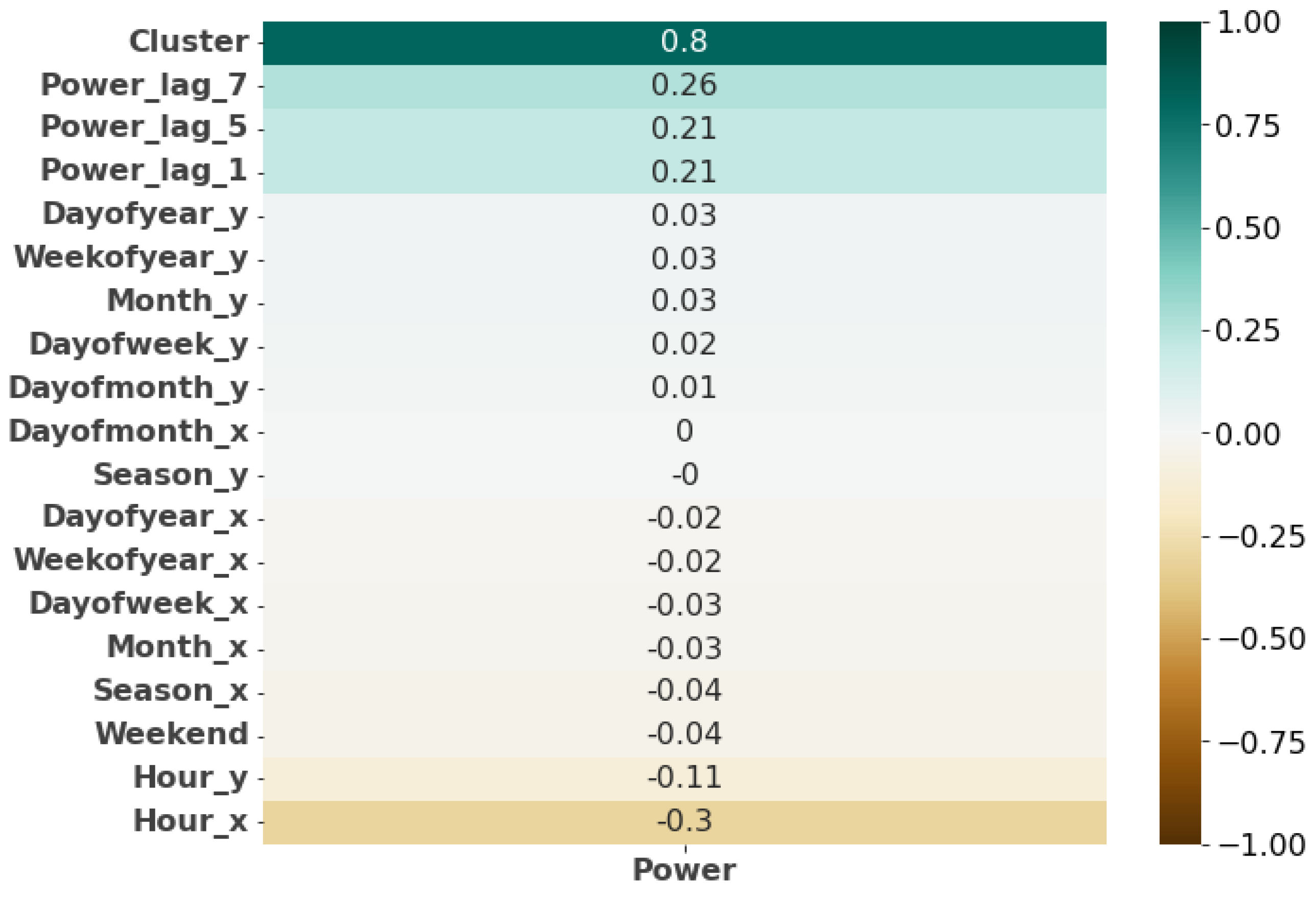
2.4.1. Correlation Matrix
2.4.2. Filter Method: K Best
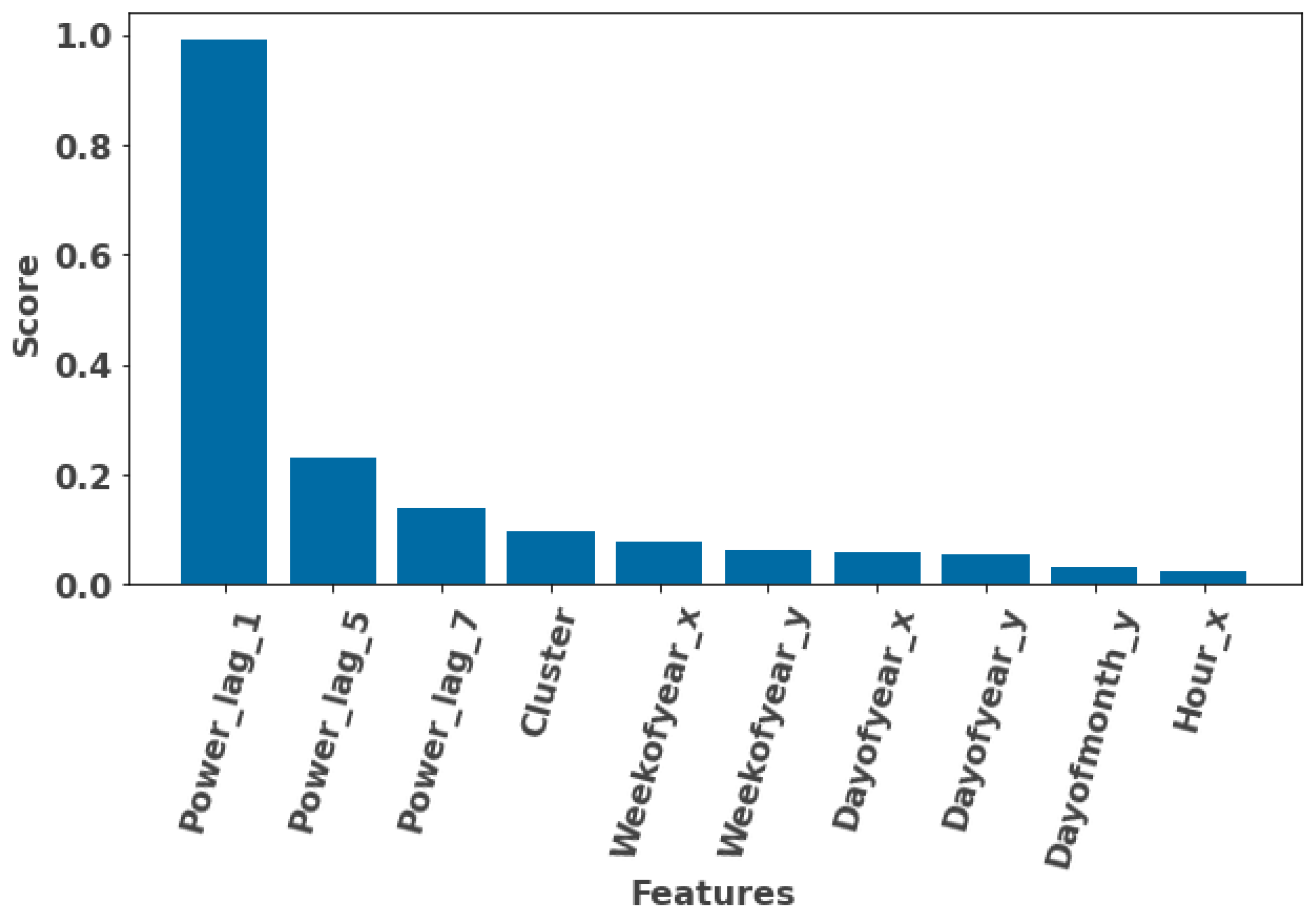
2.4.3. Embedded Method (Feature Importance)
2.5. Forecasting Methods
2.5.1. Multiple Linear Regression (MLR)
2.5.2. Decision Trees (DT)
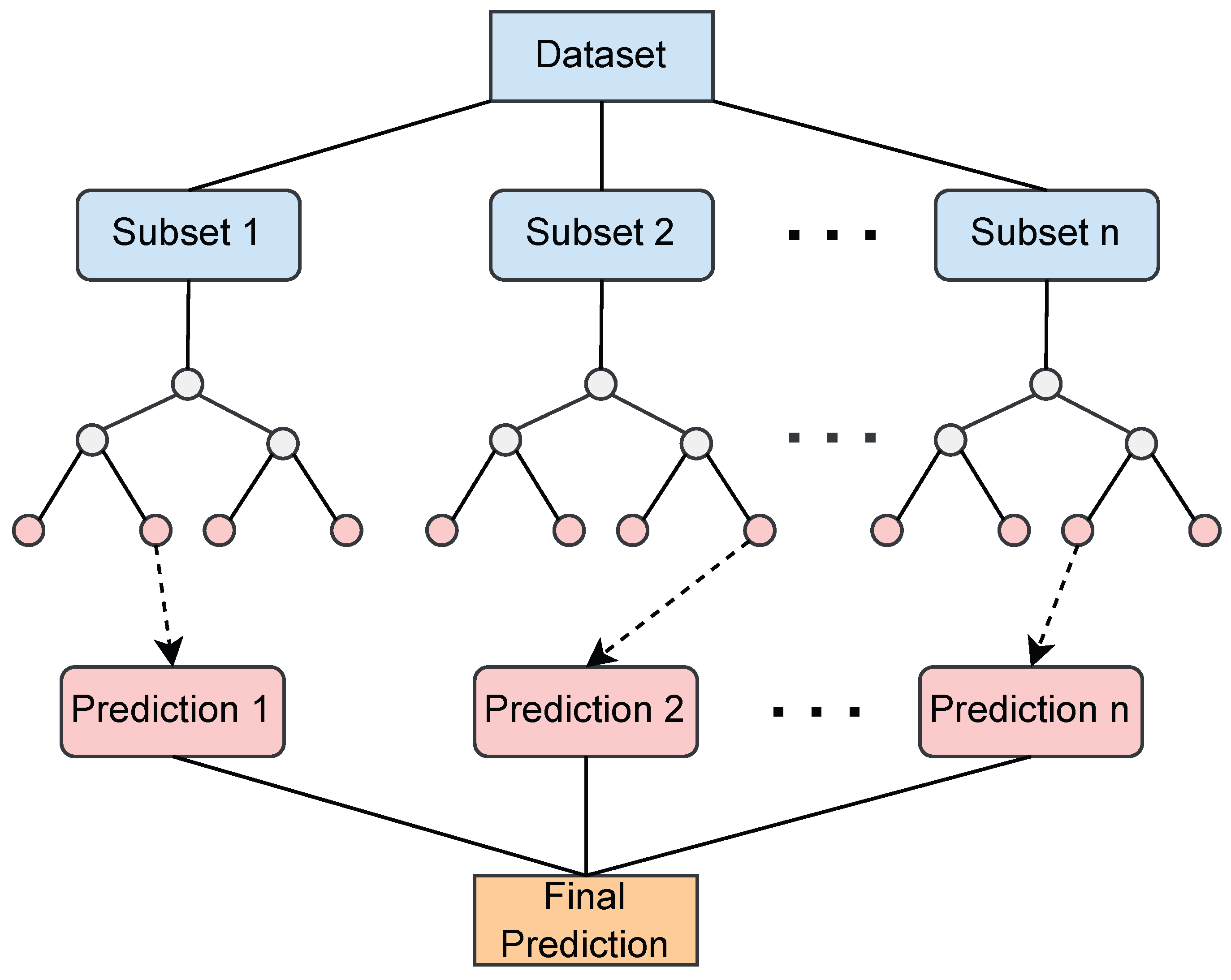
2.5.3. Random Forest (RF)
- Parameters: (number of decision trees to be included), (maximum depth allowed for each decision tree), and (minimum number of samples required to split an internal node).
- Building of decision trees: Each decision tree in the RF is constructed using a subset of the original dataset. For each tree, a random subset of samples is selected with replacement, known as bootstrapping [30].
- Recursive binary splitting: If the stopping criterion is met (e.g., maximum depth reached or minimum number of samples for splitting not satisfied), a leaf node is created, and it is assigned the average target value of the samples in that node. Otherwise, the best feature and the split point that minimizes the mean-squared error (MSE) or any other splitting criterion are determined.
- Final prediction: Once all the decision trees are constructed, the predictions are made by aggregating the individual predictions from each tree, and the final prediction is obtained by averaging the predictions from all decision trees.
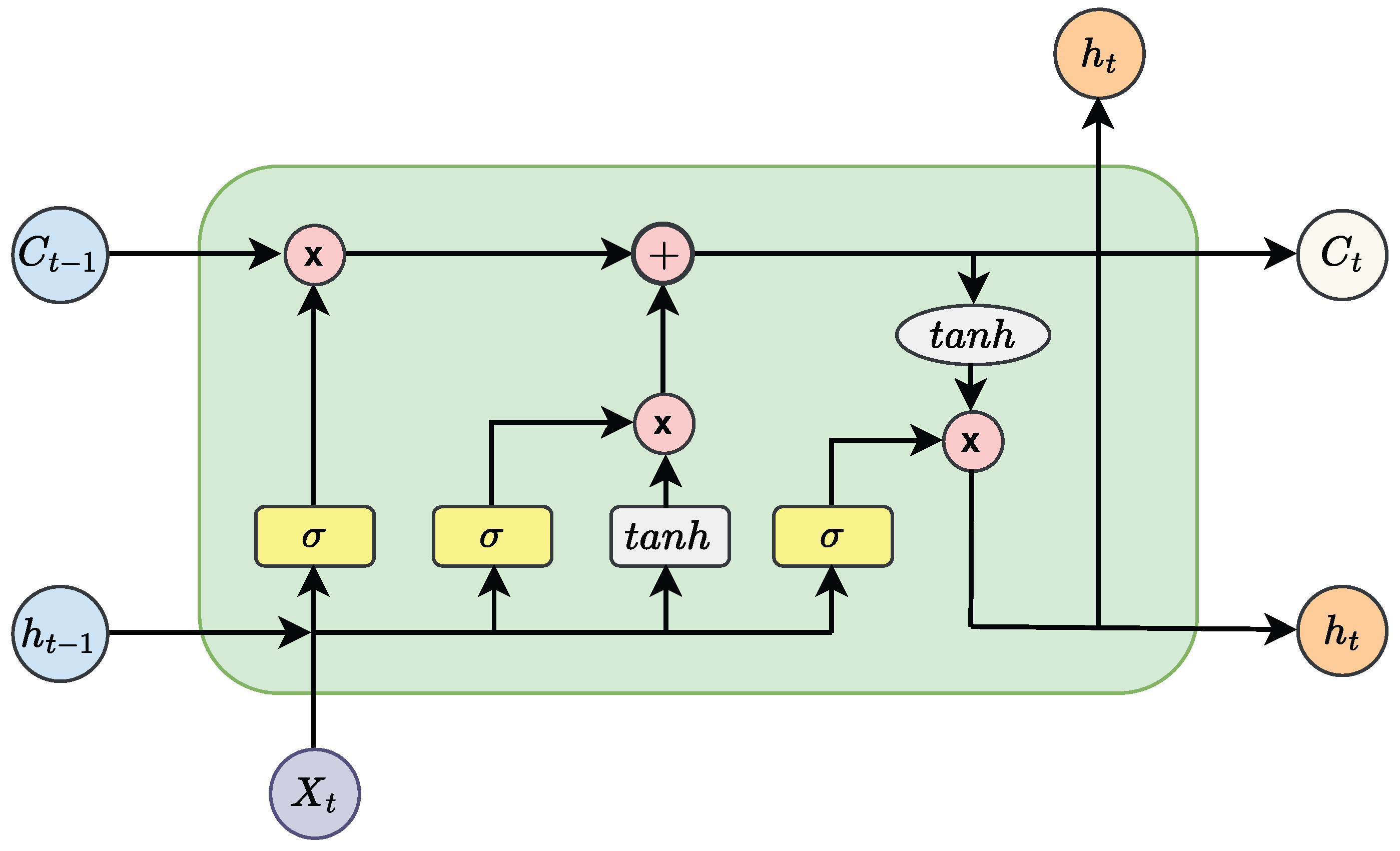
2.5.4. Long Short-Term Memory Neural Network (LSTM-NN)
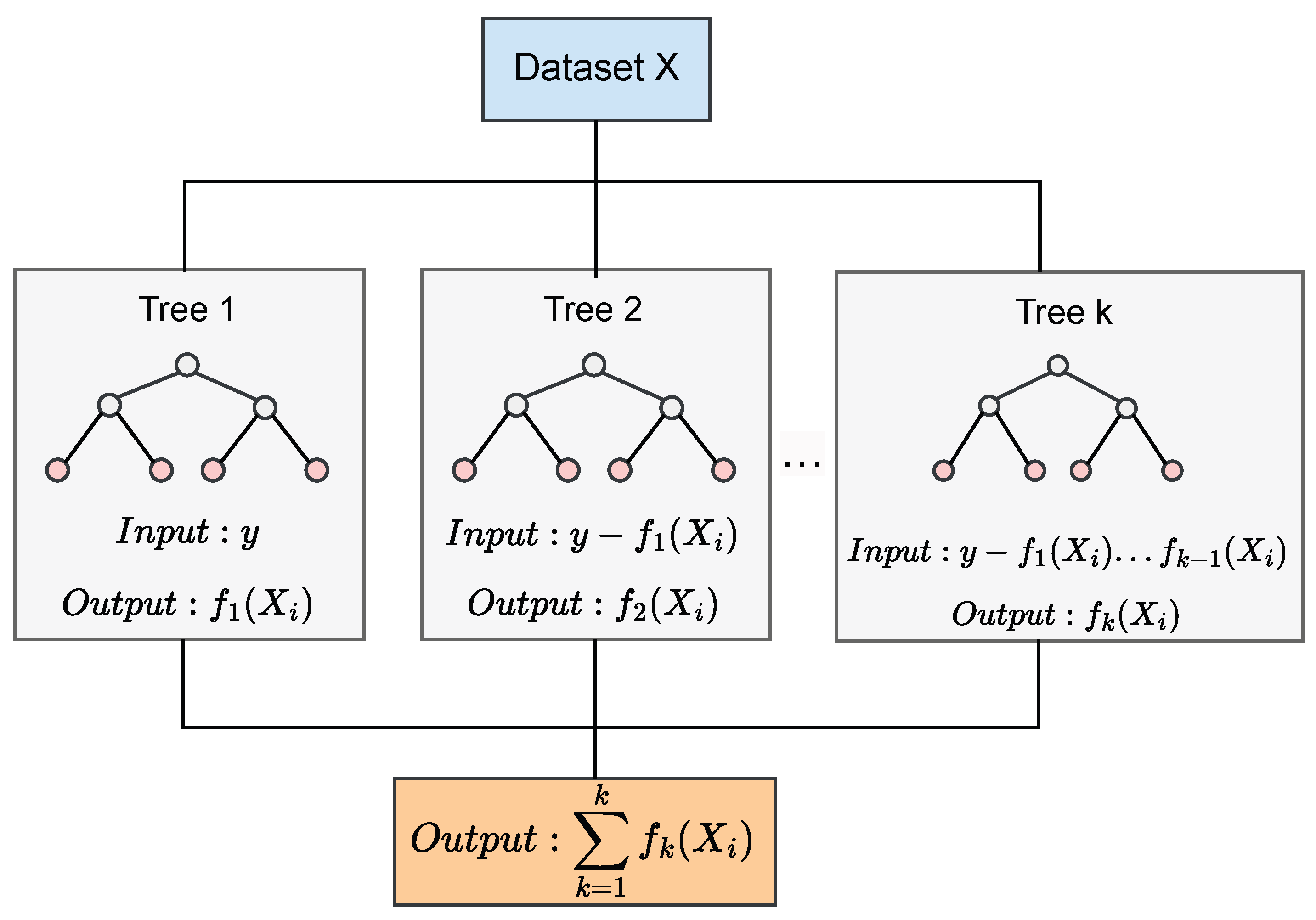
2.5.5. Extreme Gradient Boosting (XGBoost)
2.5.6. Light Gradient Boosting Machine (LightGBM)
2.6. Hyperparameter Tuning
2.6.1. RF Hyperparameters
- Minimum samples leaf: 3;
- Number of estimators: 500;
- Minimum samples split: 7;
- Maximum depth: 30.
2.6.2. LSTM Hyperparameters
- Number of layers: 2;
- First layer: LSTM with 42 neurons and sigmoid activation function;
- Second layer: Dense with 16 neurons and ReLU activation function;
- Number of epochs: 10;
- Learning rate: 0.001.
2.6.3. XGBoost Hyperparameters
- Number of estimators: 500;
- Learning rate: 0.01;
- Minimum child weight: 1;
- Subsample: 0.7;
- Colsample by tree: 1;
- Regularization Alpha: 0;
- Regularization Lambda: 1;
- Objective: reg:linear;
- Booster: gbtree.
2.6.4. LightGBM Hyperparameters
- Number of leaves: 50;
- Learning rate: 0.1;
- Maximum depth: 5;
- Feature fraction: 0.9;
- Bagging fraction: 0.7;
- Bagging frequency: 10;
- Number of iterations: 50;
- Objective: regression.
2.7. Validation
2.7.1. Post-Processing
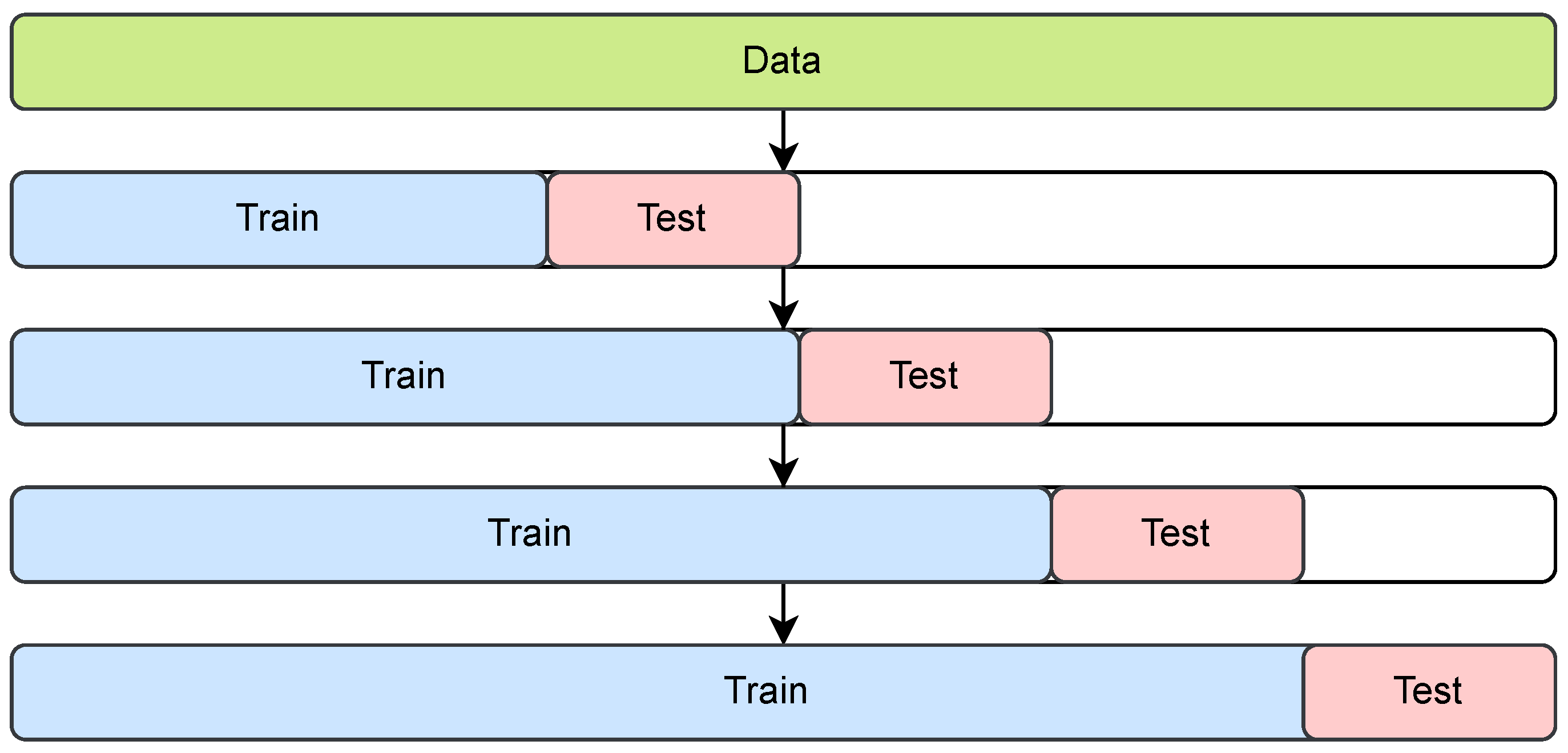
2.7.2. Cross-Validation
2.7.3. Performance Evaluation
- F1-score:
- Mean Absolute Error (MAE):
- Normalized root-mean-squared error (NRMSE)
- Coefficient of determination ():
- Execution time (in seconds):
3. Case Study
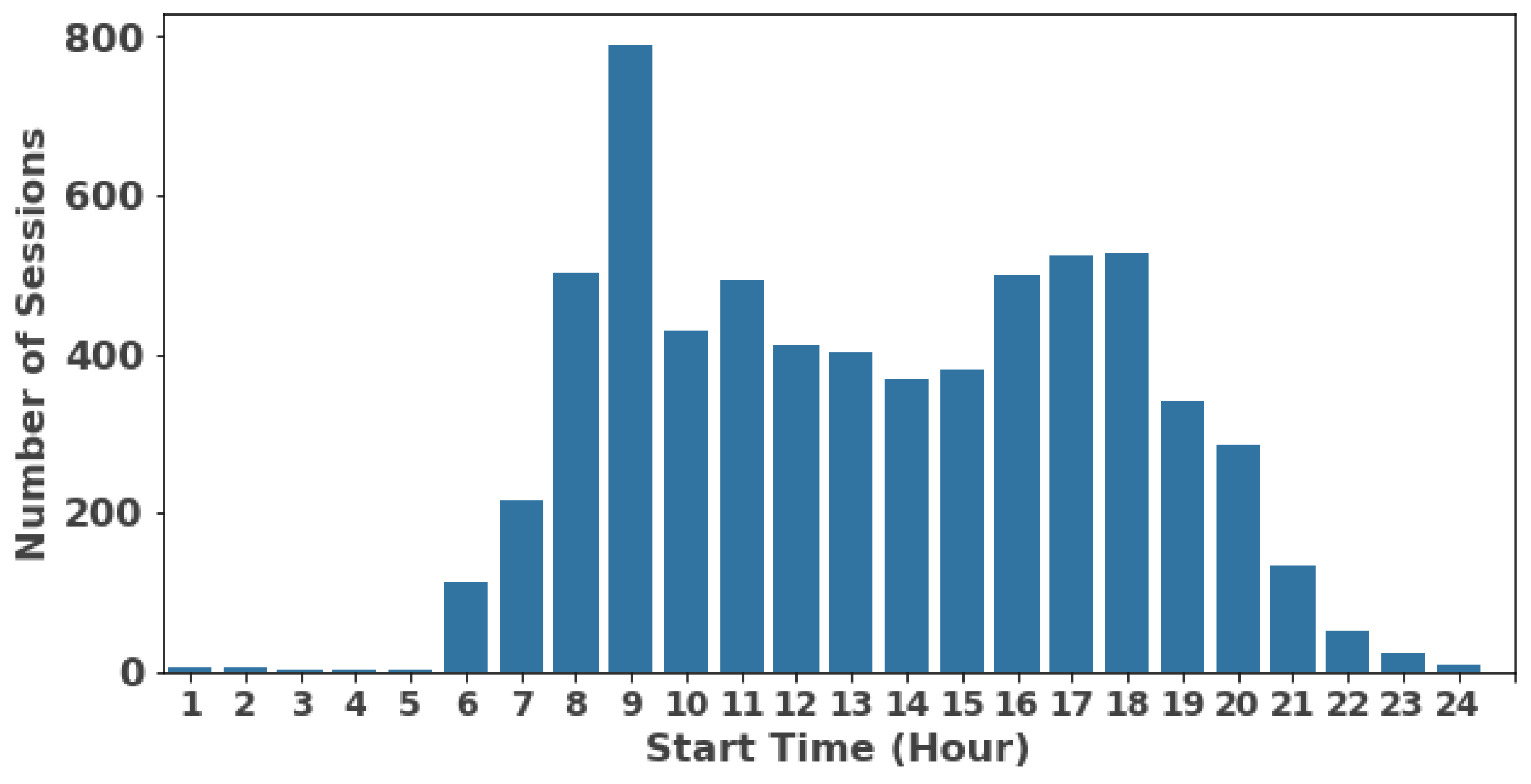
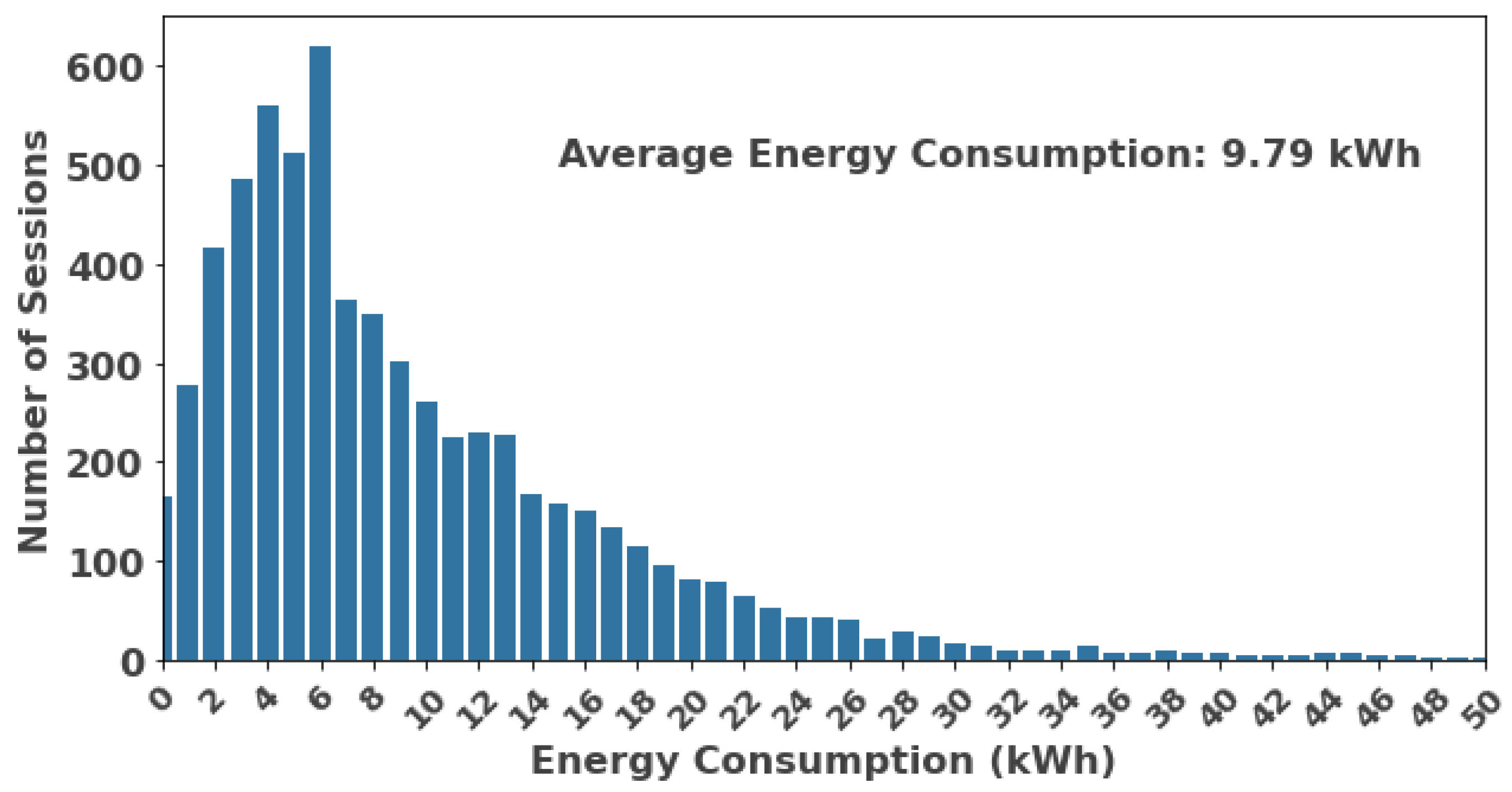
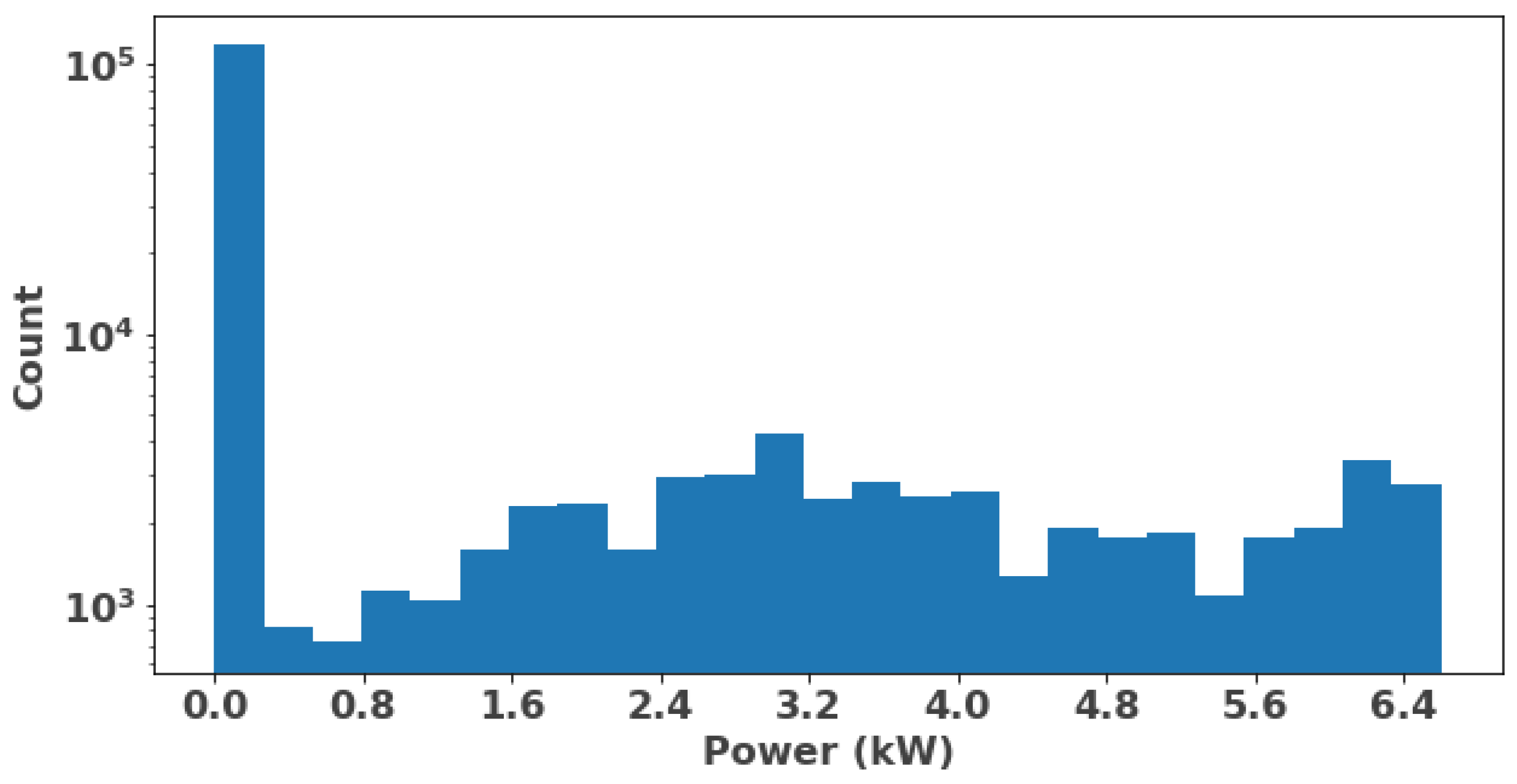
3.1. Data Description and Inputs
3.2. Pre-Processing
3.3. Feature Engineering
3.3.1. Feature Selection
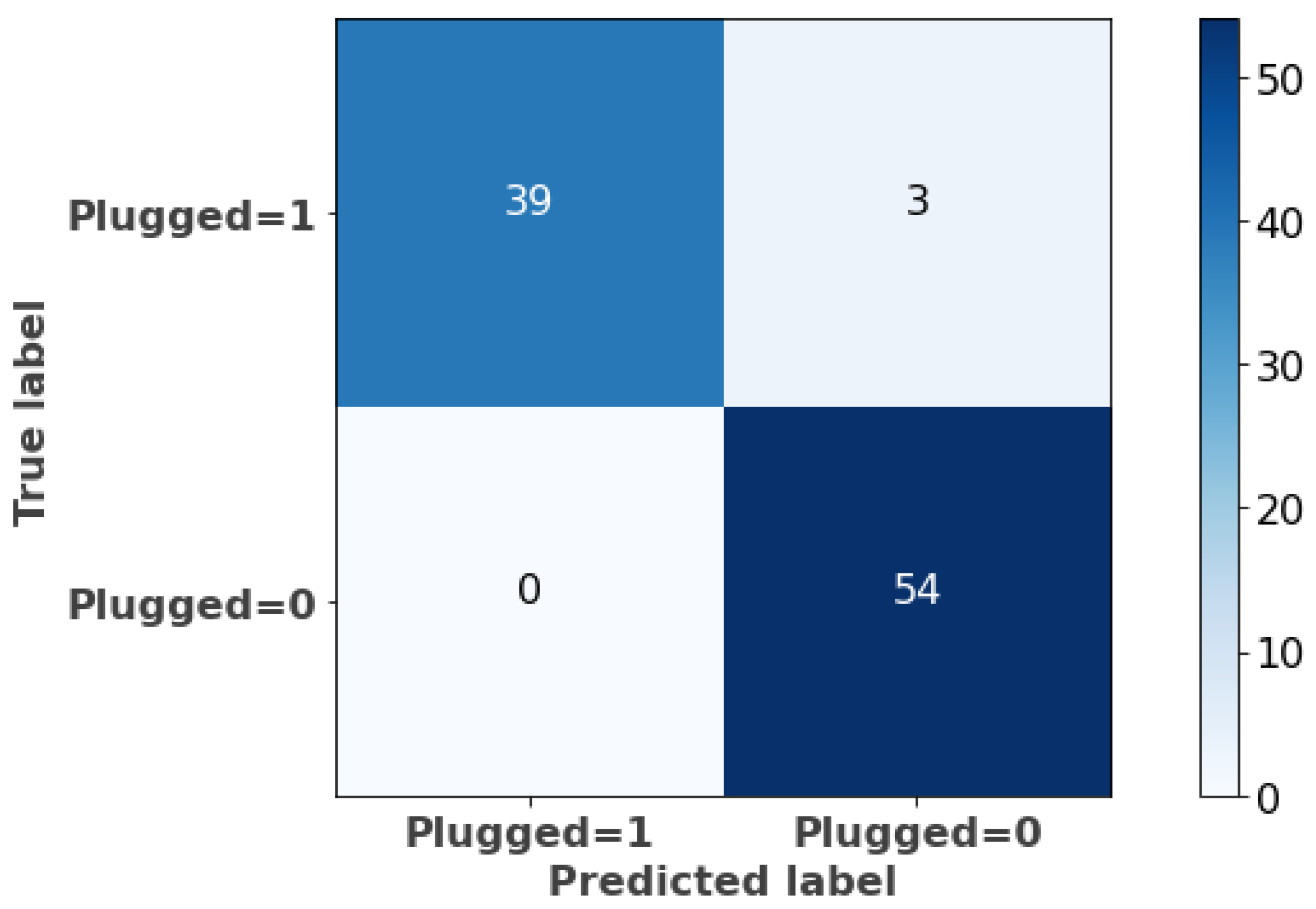
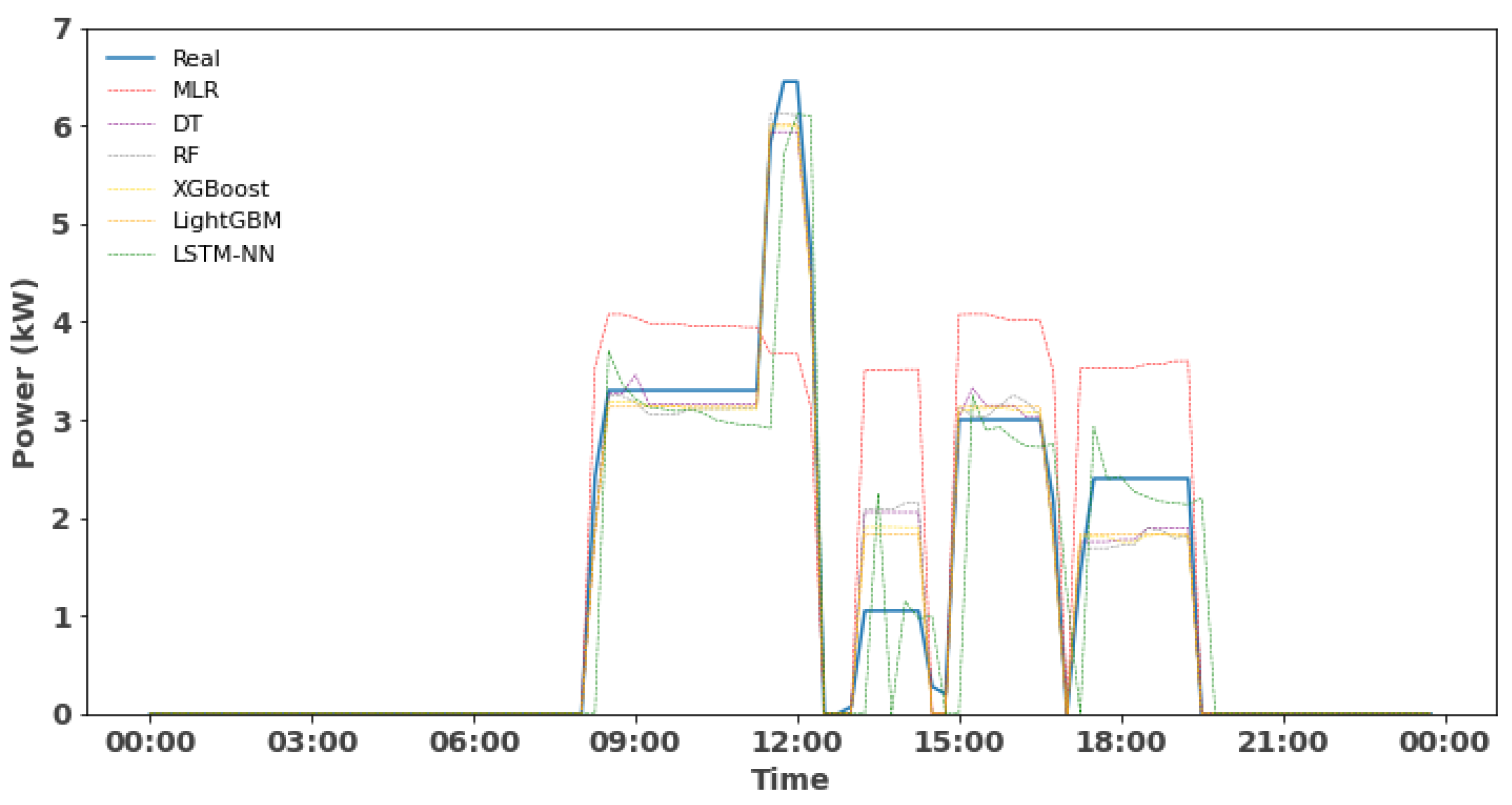
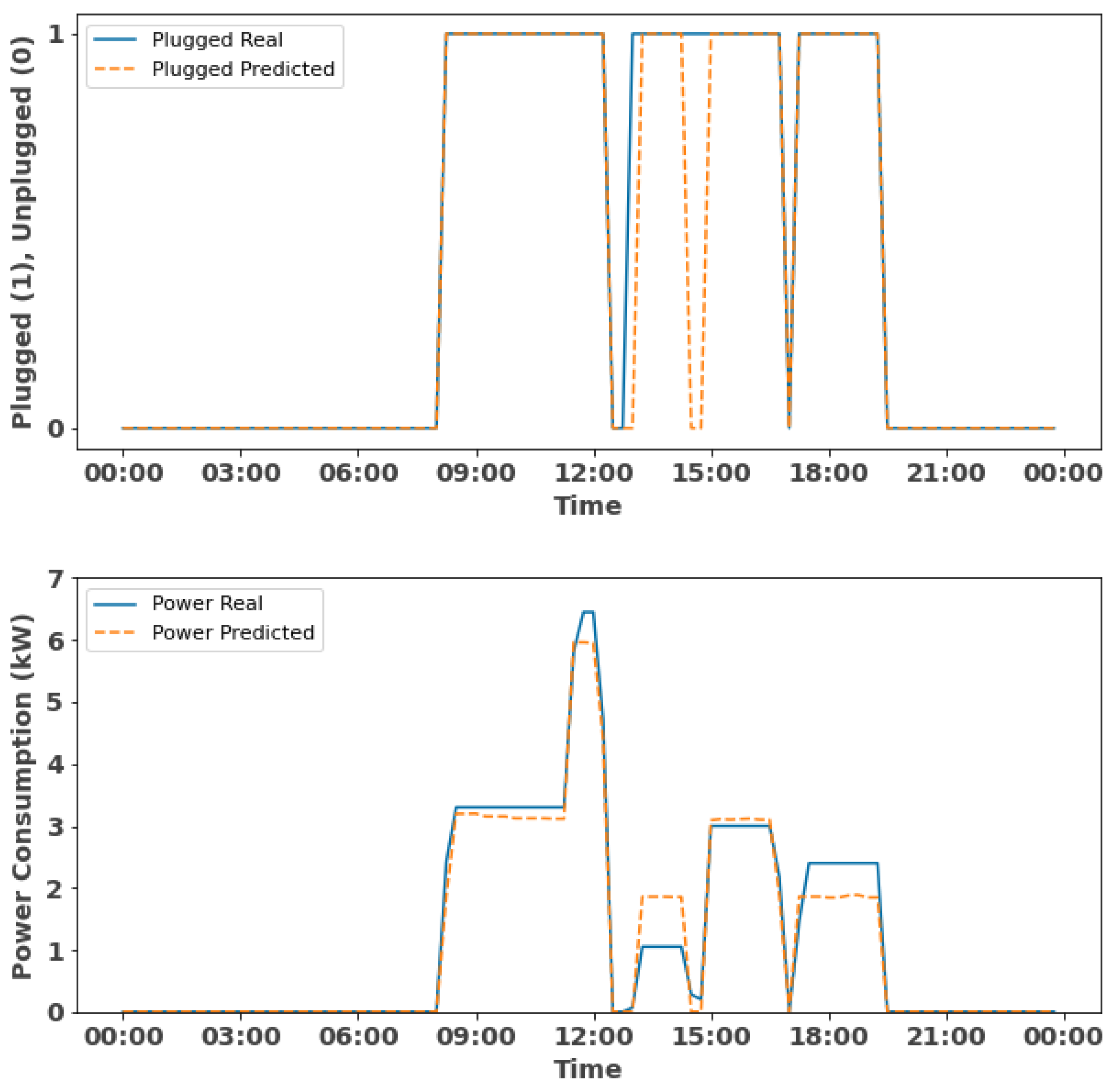
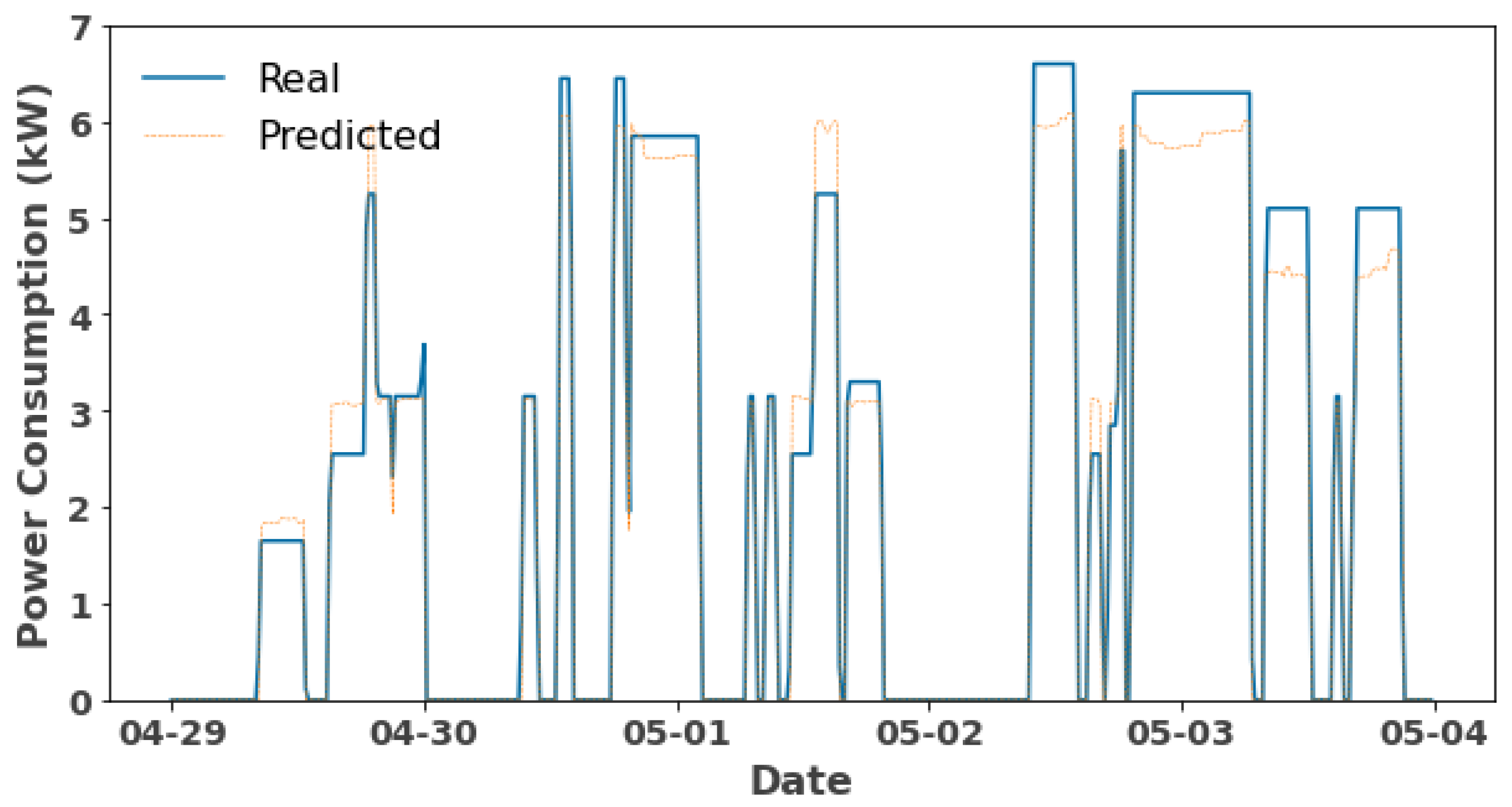
3.3.2. Forecasting and Evaluation
- True positives (TPs): There are 39 instances where the actual class was plugged-in (1) and the model has correctly predicted them as plugged-in (1).
- False positives (FPs): The model has predicted three instances as unplugged (0), when the actual class was plugged (1).
- False negatives (FNs): The model did not predict any instances as plugged-in (1), when the actual class was unplugged (0).
- True negatives (TNs): The model has correctly predicted 54 instances as unplugged (0), when the actual class was unplugged (0).
3.3.3. Cross-Validation
4. Conclusions and Limitations
4.1. Main Conclusions
4.2. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. Global EV Outlook 2023: Catching Up with Climate Ambitions; International Energy Agency: Paris, France, 2023; pp. 1–142. [Google Scholar]
- Fit for 55: MEPs Back Objective of Zero Emissions for Cars and Vans in 2035 | News | European Parliament, 2022. Available online: https://www.europarl.europa.eu/news/en/press-room/20220603IPR32129/fit-for-55-meps-back-objective-of-zero-emissions-for-cars-and-vans-in-2035 (accessed on 7 May 2024).
- Deliverable D1.1 Electric Road Mobility Evolution Scenarios. Available online: https://cordis.europa.eu/project/id/101056765 (accessed on 12 March 2024).
- Guzman, C.P.; Bañol Arias, N.; Franco, J.F.; Rider, M.J.; Romero, R. Enhanced coordination strategy for an aggregator of distributed energy resources participating in the day-ahead reserve market. Energies 2020, 13, 1965. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, Z.; Mourshed, M.; Guo, Y.; Zhou, Y.; Chang, Y.; Wei, Y.; Feng, S. Electric vehicle charging load forecasting: A comparative study of deep learning approaches. Energies 2019, 12, 2692. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Morais, H.; Castro, R.; Vale, Z. Simulated annealing to handle energy and ancillary services joint management considering electric vehicles. Electr. Power Syst. Res. 2016, 136, 383–397. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Machine learning approaches for EV charging behavior: A review. IEEE Access 2020, 8, 168980–168993. [Google Scholar] [CrossRef]
- Abbas, F.; Feng, D.; Habib, S.; Rasool, A.; Numan, M. An improved optimal forecasting algorithm for comprehensive electric vehicle charging allocation. Energy Technol. 2019, 7, 1900436. [Google Scholar] [CrossRef]
- Jia, Z.; Li, J.; Zhang, X.P.; Zhang, R. Review on Optimization of Forecasting and Coordination Strategies for Electric Vehicle Charging. J. Mod. Power Syst. Clean Energy 2022, 11, 389–400. [Google Scholar] [CrossRef]
- Xing, Y.; Li, F.; Sun, K.; Wang, D.; Chen, T.; Zhang, Z. Multi-type electric vehicle load prediction based on Monte Carlo simulation. Energy Rep. 2022, 8, 966–972. [Google Scholar] [CrossRef]
- Ullah, I.; Liu, K.; Yamamoto, T.; Al Mamlook, R.E.; Jamal, A. A comparative performance of machine learning algorithm to predict electric vehicles energy consumption: A path towards sustainability. Energy Environ. 2022, 33, 1583–1612. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Zhang, Y.; Jian, L. A systematic methodology for mid-and-long term electric vehicle charging load forecasting: The case study of Shenzhen, China. Sustain. Cities Soc. 2020, 56, 102084. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y.; Xie, D.; Wei, E.; Bao, X.; Chen, H.; Zhong, X. The application of improved random forest algorithm on the prediction of electric vehicle charging load. Energies 2018, 11, 3207. [Google Scholar] [CrossRef]
- Gruosso, G.; Mion, A.; Gajani, G.S. Forecasting of electrical vehicle impact on infrastructure: Markov chains model of charging stations occupation. ETransportation 2020, 6, 100083. [Google Scholar] [CrossRef]
- Douaidi, L.; Senouci, S.M.; El Korbi, I.; Harrou, F. Predicting Electric Vehicle Charging Stations Occupancy: A Federated Deep Learning Framework. In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; pp. 1–5. [Google Scholar]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Prediction of EV charging behavior using machine learning. IEEE Access 2021, 9, 111576–111586. [Google Scholar] [CrossRef]
- Jeon, Y.E.; Kang, S.B.; Seo, J.I. Hybrid Predictive Modeling for Charging Demand Prediction of Electric Vehicles. Sustainability 2022, 14, 5426. [Google Scholar] [CrossRef]
- Kim, T.; Ko, W.; Kim, J. Analysis and impact evaluation of missing data imputation in day-ahead PV generation forecasting. Appl. Sci. 2019, 9, 204. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Ghosh, J.; Liu, A. K-means. The Top Ten Algorithms in Data Mining; CRC Press: Boca Raton, FL, USA, 2009; pp. 21–35. [Google Scholar]
- Cui, M. Introduction to the k-means clustering algorithm based on the elbow method. Account. Audit. Financ. 2020, 1, 5–8. [Google Scholar] [CrossRef]
- Ganti, A. Correlation coefficient. Corp. Financ. Acc. 2020, 9, 145–152. [Google Scholar]
- Khalid, N.H.M.; Ismail, A.R.; Aziz, N.A.; Hussin, A.A.A. Performance Comparison of Feature Selection Methods for Prediction in Medical Data. In Proceedings of the International Conference on Soft Computing in Data Science, Online, 24–25 January 2023; pp. 92–106. [Google Scholar]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Costa, V.G.; Pedreira, C.E. Recent advances in decision trees: An updated survey. Artif. Intell. Rev. 2023, 56, 4765–4800. [Google Scholar] [CrossRef]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
- Afzal, A.; Aabid, A.; Khan, A.; Khan, S.A.; Rajak, U.; Verma, T.N.; Kumar, R. Response surface analysis, clustering, and random forest regression of pressure in suddenly expanded high-speed aerodynamic flows. Aerosp. Sci. Technol. 2020, 107, 106318. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M.; Alaraj, M.; Alsaidan, I. A machine learning-based gradient boosting regression approach for wind power production forecasting: A step towards smart grid environments. Energies 2021, 14, 5196. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM–a tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Essam, Y.; Ahmed, A.N.; Ramli, R.; Chau, K.W.; Idris Ibrahim, M.S.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Investigating photovoltaic solar power output forecasting using machine learning algorithms. Eng. Appl. Comput. Fluid Mech. 2022, 16, 2002–2034. [Google Scholar] [CrossRef]
- Liu, J.J.; Liu, J.C. Permeability predictions for tight sandstone reservoir using explainable machine learning and particle swarm optimization. Geofluids 2022, 2022, 2263329. [Google Scholar] [CrossRef]
- Torres-Barrán, A.; Alonso, Á.; Dorronsoro, J.R. Regression tree ensembles for wind energy and solar radiation prediction. Neurocomputing 2019, 326, 151–160. [Google Scholar] [CrossRef]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine learning models for predicting the residual value of heavy construction equipment: An evaluation of modified decision tree, LightGBM, and XGBoost regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- Al Daoud, E. Comparison between XGBoost, LightGBM and CatBoost using a home credit dataset. Int. J. Comput. Inf. Eng. 2019, 13, 6–10. [Google Scholar]
- Guo, J.; Yun, S.; Meng, Y.; He, N.; Ye, D.; Zhao, Z.; Jia, L.; Yang, L. Prediction of heating and cooling loads based on light gradient boosting machine algorithms. Build. Environ. 2023, 236, 110252. [Google Scholar] [CrossRef]
- Weerts, H.J.; Mueller, A.C.; Vanschoren, J. Importance of tuning hyperparameters of machine learning algorithms. arXiv 2020, arXiv:2007.07588. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Srinivas, P.; Katarya, R. hyOPTXg: OPTUNA hyper-parameter optimization framework for predicting cardiovascular disease using XGBoost. Biomed. Signal Process. Control 2022, 73, 103456. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Shrivastava, S. Cross Validation in Time Series, 2020. Available online: https://medium.com/@soumyachess1496/cross-validation-in-time-series-566ae4981ce4 (accessed on 7 May 2024).
- Mehdiyev, N.; Enke, D.; Fettke, P.; Loos, P. Evaluating forecasting methods by considering different accuracy measures. Procedia Comput. Sci. 2016, 95, 264–271. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Lateko, A.A.H.; Yang, H.T.; Huang, C.M. Short-Term PV Power Forecasting Using a Regression-Based Ensemble Method. Energies 2022, 15, 4171. [Google Scholar] [CrossRef]
- Zainab, A.; Syed, D.; Ghrayeb, A.; Abu-Rub, H.; Refaat, S.S.; Houchati, M.; Bouhali, O.; Bañales Lopez, S. A Multiprocessing-Based Sensitivity Analysis of Machine Learning Algorithms for Load Forecasting of Electric Power Distribution System. IEEE Access 2021, 9, 31684–31694. [Google Scholar] [CrossRef]
- City of Colorado. Electric Vehicle Charging Station Energy Consumption in the City of Boulder, Colorado, 2023. Available online: https://bouldercolorado.gov/services/electric-vehicle-charging-stations (accessed on 7 May 2024).



| Reference | Plugged-in Forecasting | Power Consumption Forecasting | Pre-Processing | Feature Engineering | Feature Selection | Forecasting Methods | Validation |
|---|---|---|---|---|---|---|---|
| [10] | ✓ | ✓ | |||||
| [12] | ✓ | ✓ | |||||
| [14] | ✓ | ||||||
| [13] | ✓ | ✓ | ✓ | ✓ | |||
| [11] | ✓ | ✓ | ✓ | ✓ | |||
| [16] | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [17] | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| This work | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| RF | XGBoost | LightGBM |
|---|---|---|
| Cluster | Power lag 7 | Power lag 7 |
| Day of year_y | Power lag 1 | Power lag 5 |
| Day of month_y | Power lag 5 | Power lag 1 |
| Power lag 1 | Hour_x | Cluster |
| Power lag 7 | Hour_y | Hour_y |
| Hour_x | Cluster | Hour_x |
| Power lag 5 | Month_y | Day of year_x |
| Model | NRMSE (%) Top Ranked Features | ||||||
|---|---|---|---|---|---|---|---|
| Top 2 | Top 3 | Top 4 | Top 5 | Top 6 | Top 7 | Top 8 | |
| MLR | 14.28 | 14.28 | 14.48 | 14.58 | 14.53 | 14.72 | 14.86 |
| DT | 4.32 | 4.50 | 4.31 | 4.18 | 4.80 | 4.25 | 4.37 |
| RF | 4.60 | 4.10 | 4.59 | 4.94 | 5.03 | 4.80 | 4.81 |
| XGBoost | 4.48 | 4.45 | 4.53 | 4.58 | 4.42 | 4.26 | 4.26 |
| LightGBM | 4.36 | 4.38 | 4.49 | 4.42 | 4.22 | 4.29 | 4.27 |
| LSTM | 9.92 | 9.90 | 10.01 | 10.20 | 9.40 | 9.87 | 9.91 |
| Average | 6.99 | 6.94 | 7.07 | 7.15 | 7.07 | 7.03 | 7.08 |
| Model | Performance Evaluation | |||
|---|---|---|---|---|
| NRMSE (%) | MAE (kW) | Execution Time (s) | ||
| LightGBM | 4.22 | 0.15 | 0.97 | 5.0 |
| XGBoost | 4.42 | 0.15 | 0.97 | 50.0 |
| DT | 4.80 | 0.16 | 0.96 | 0.5 |
| RF | 5.03 | 0.16 | 0.96 | 180.0 |
| LSTM-NN | 9.40 | 0.25 | 0.86 | 780.0 |
| MLR | 14.53 | 0.59 | 0.58 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amezquita, H.; Guzman, C.P.; Morais, H. Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach. Energies 2024, 17, 3396. https://doi.org/10.3390/en17143396
Amezquita H, Guzman CP, Morais H. Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach. Energies. 2024; 17(14):3396. https://doi.org/10.3390/en17143396
Chicago/Turabian StyleAmezquita, Herbert, Cindy P. Guzman, and Hugo Morais. 2024. "Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach" Energies 17, no. 14: 3396. https://doi.org/10.3390/en17143396
APA StyleAmezquita, H., Guzman, C. P., & Morais, H. (2024). Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach. Energies, 17(14), 3396. https://doi.org/10.3390/en17143396







