A Novel Non-Isolated Bidirectional DC-DC Converter with Improved Current Ripples for Low-Voltage On-Board Charging
Abstract
:1. Introduction
- One approach is to increase the inductance of the inductors. This reduces the current ripple, but it can slow down the dynamic response, cost, and size of the converter due to the larger inductor size [20].
- Using a large capacitor can solve the ripple issues, but it increases the size and cost of the converter.
- Increasing the switching frequency can help reduce ripple current and allow for smaller inductors. However, the switching frequency increase is constrained by gate drive circuit limitations, switching losses, and electromagnetic compliance requirements.
- Implementing DCM in converters can lower inductor size. However, the higher inductor current in DCM mode increases switch stress, leading to increased power loss.
- The inductor ripple can be reduced by employing the interleaving technique [21]. Although effective, this method increases the number of switches and inductors, thereby complicating control and increasing the converter cost.
- Utilizing cascaded converters with phase shifts can also decrease inductor ripples [19]. However, this approach may raise the complexity and cost due to an increase in the component count. The converter must also operate within a fixed duty cycle.
- Low-output ripple current;
- The inductor operates at twice the switching frequency;
- Reduced inductor size;
- Low-voltage stresses on power switches;
- Common ground between LVS and HVS;
- No additional RC snubber circuit is required;
- No shoot-through or dead time issue;
- Less component count and reduced overall size.
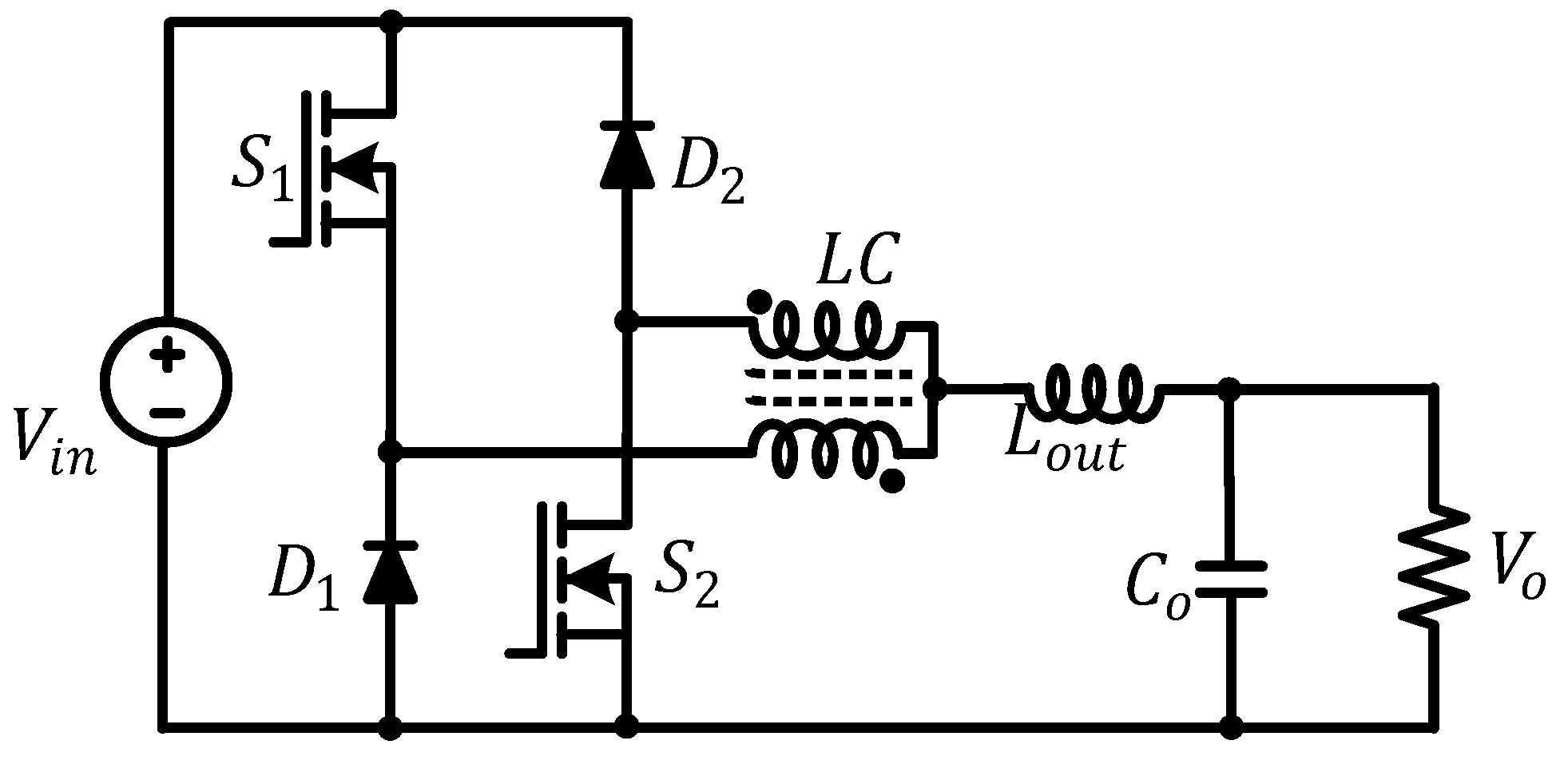
2. Proposed Buck Converter Topology and Switching Scheme
2.1. Proposed Topology
2.2. Proposed Switching Scheme
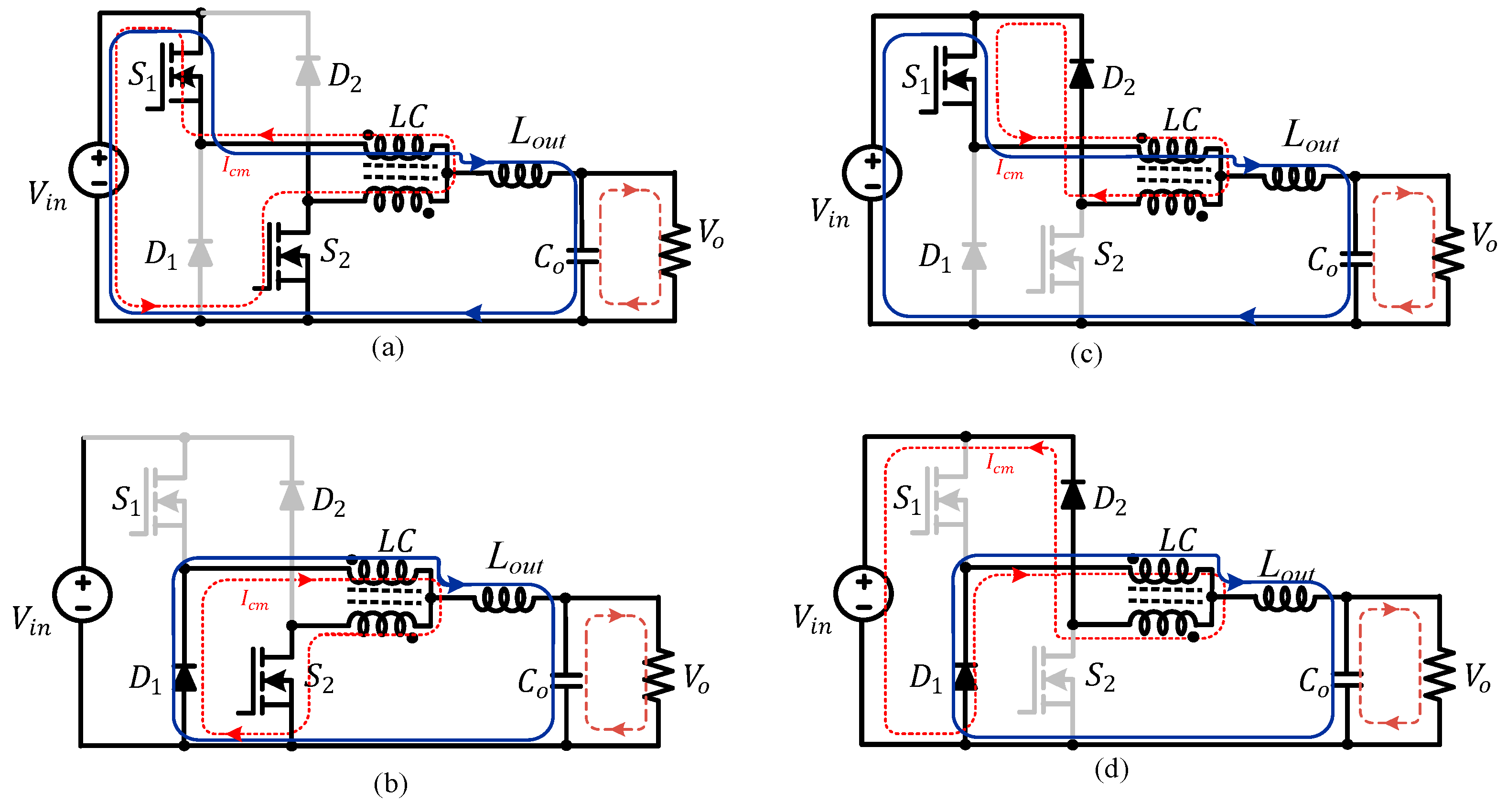
3. Modes of Operation
3.1. Operation Mode for D < 0
3.2. Operation Modes for D > 0
4. Ripple Current Analysis and Component Selection
4.1. Inductor Design
4.2. Output Inductor Ripple
4.3. Comparison of Current Ripples
4.4. Couple Inductor Design
4.5. Output Inductor Comparison
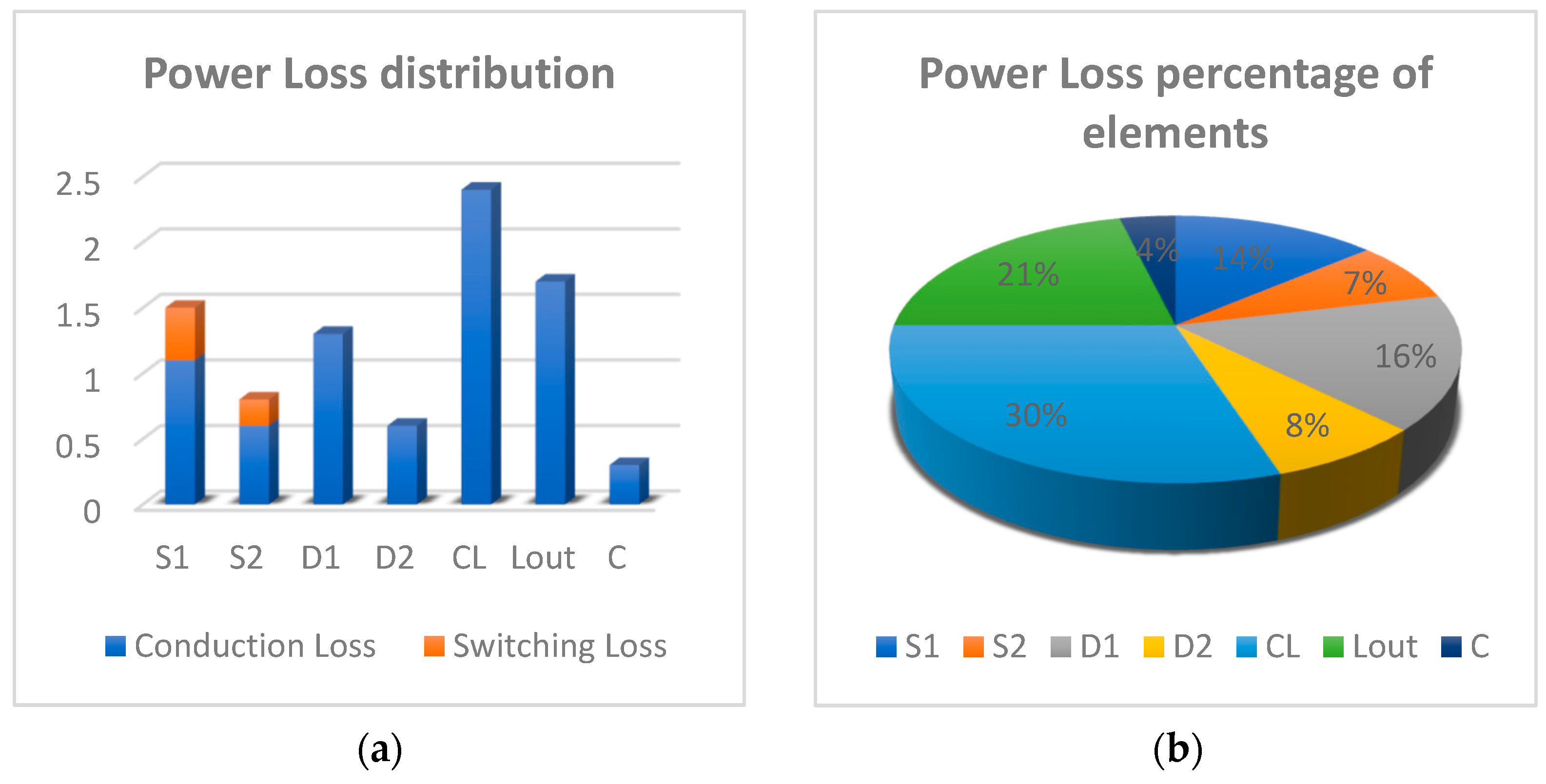
5. Stress and Power Loss Analysis
5.1. Voltage and Current Stress
5.2. Power Loss Analysis
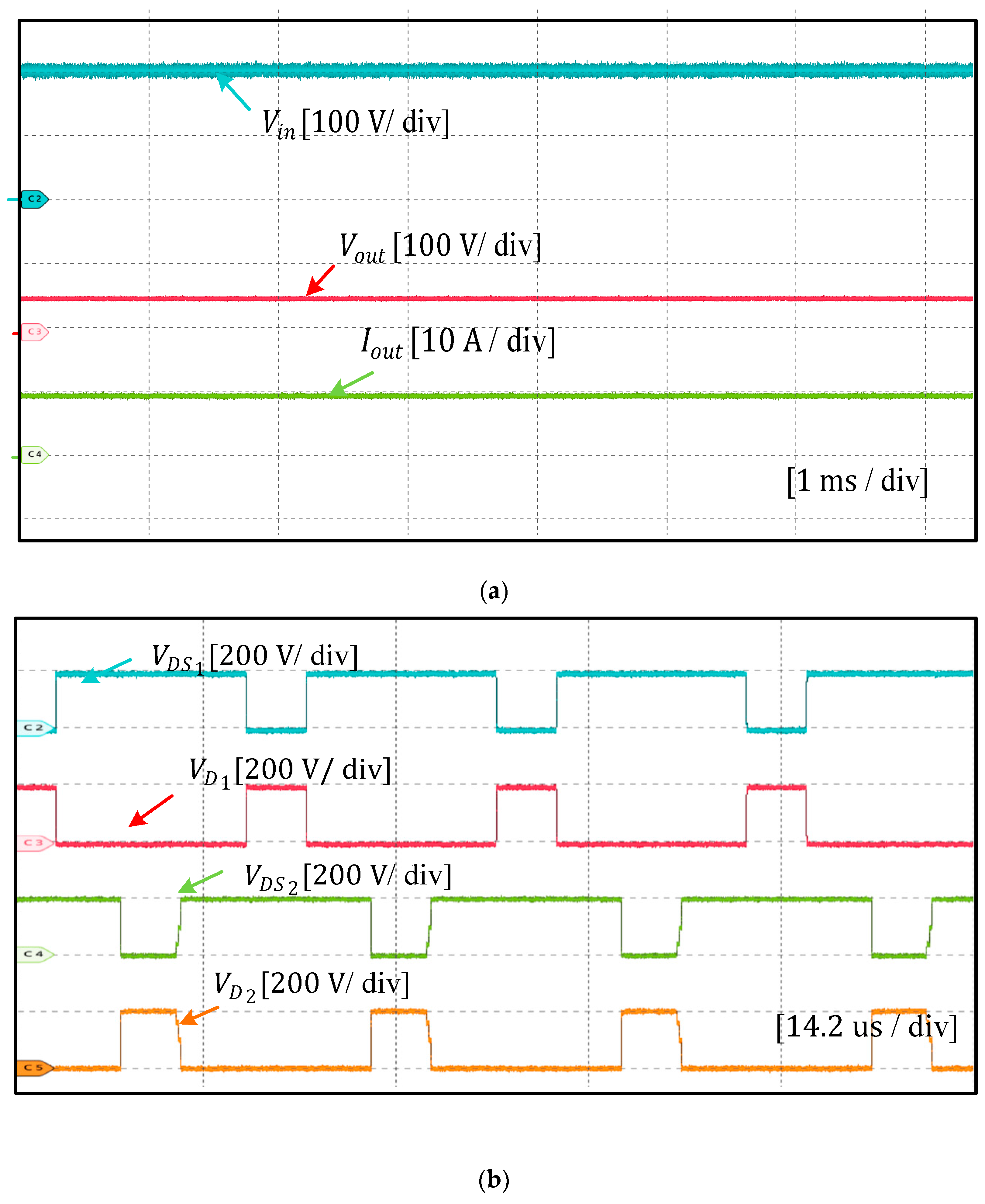
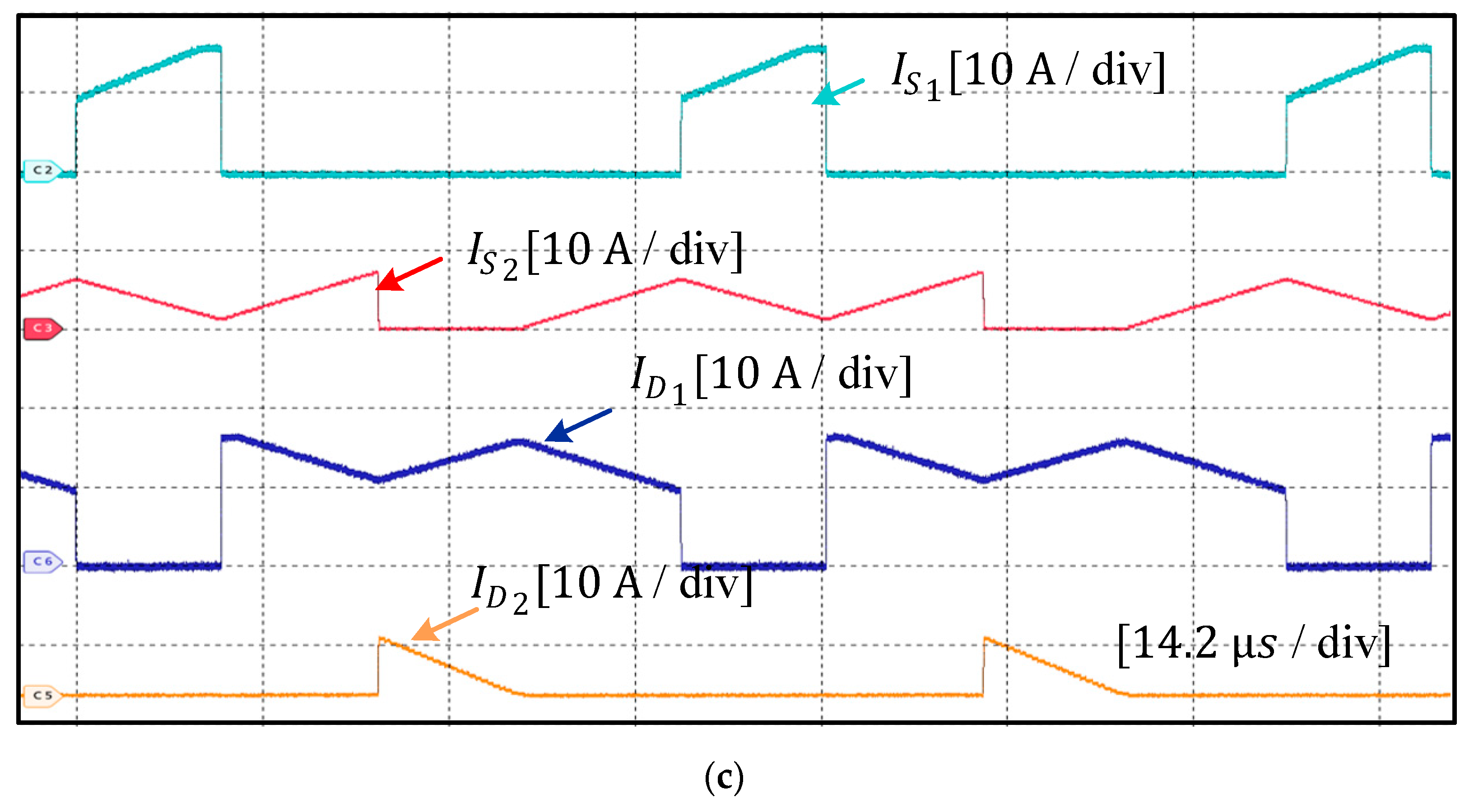
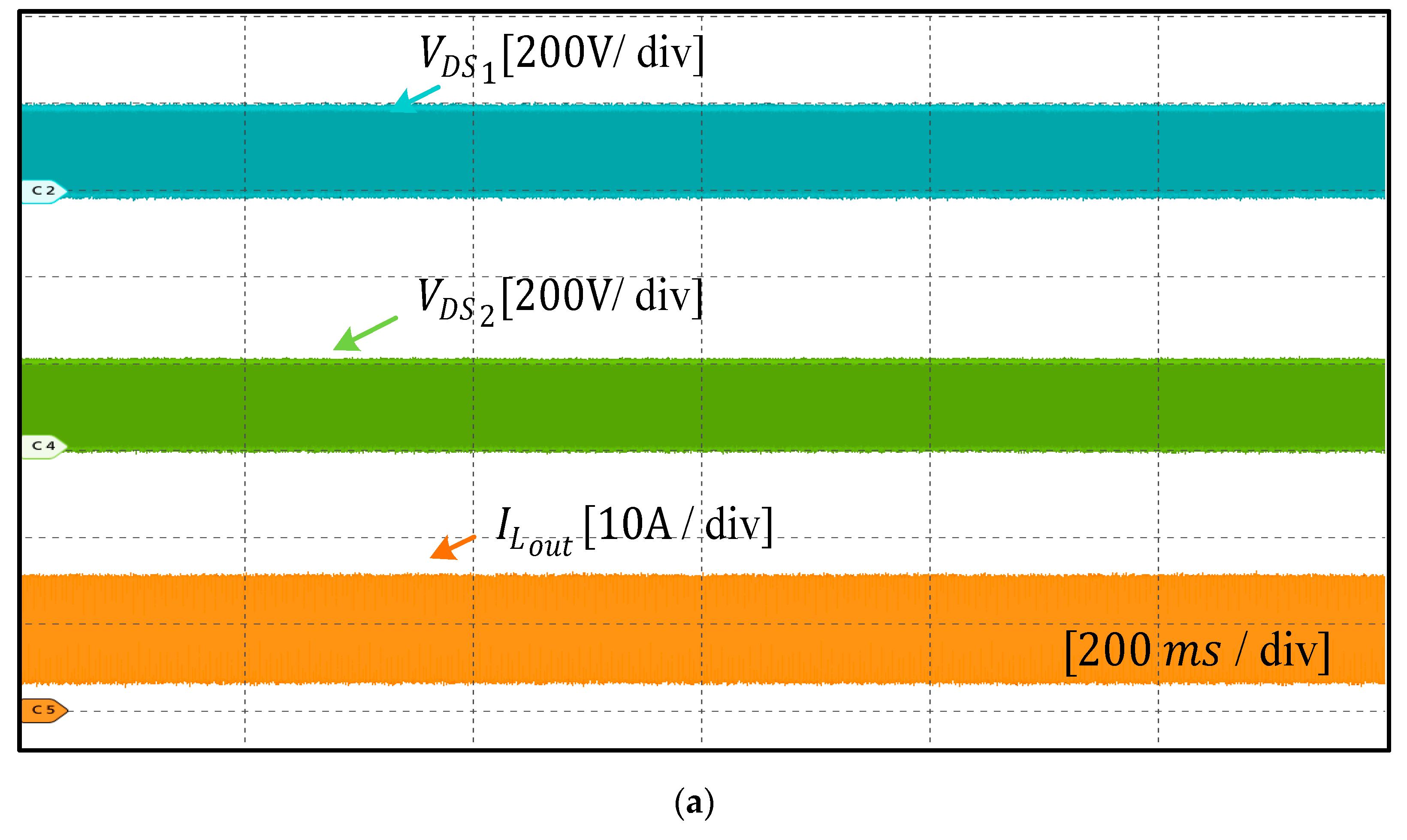
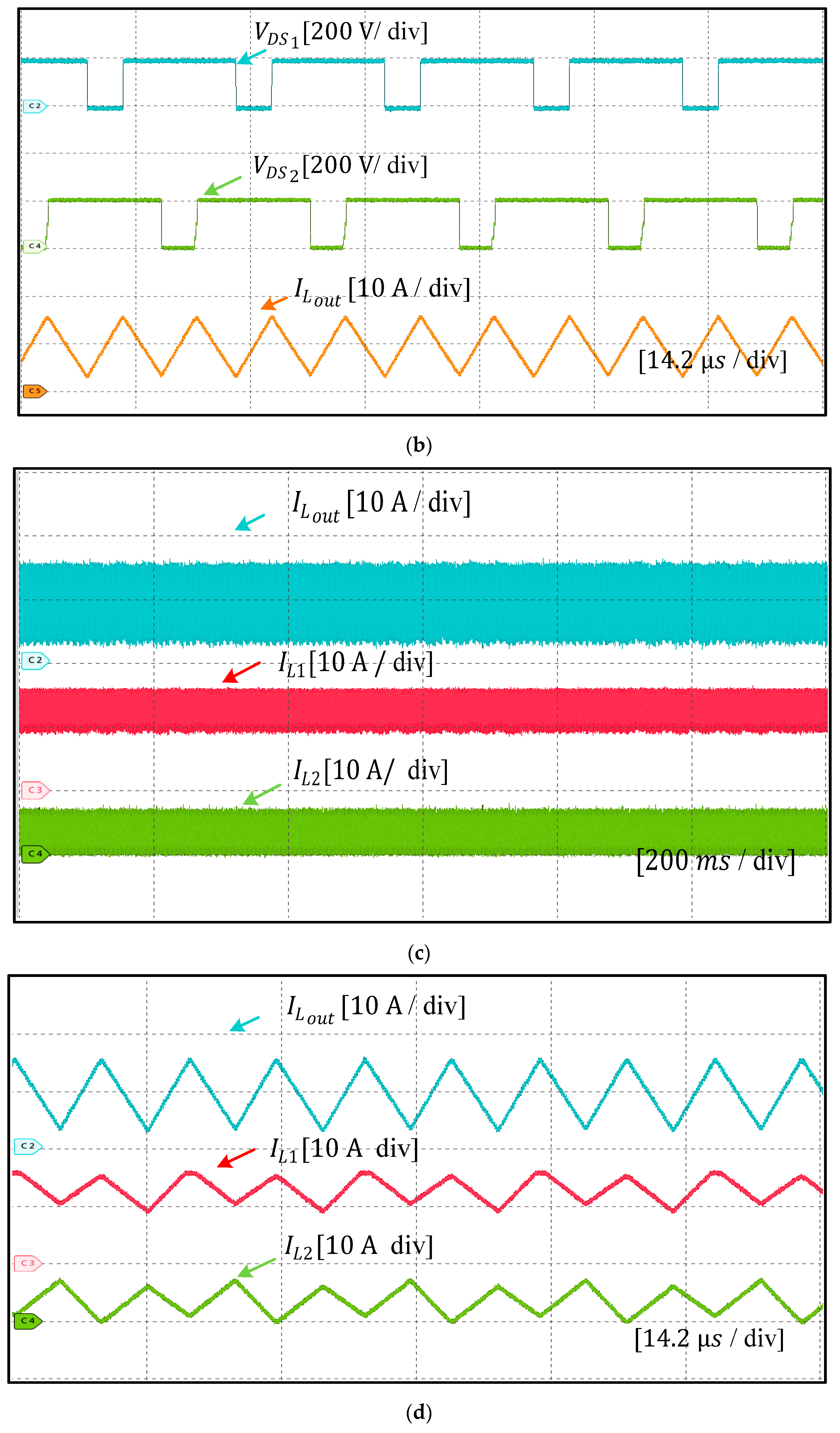
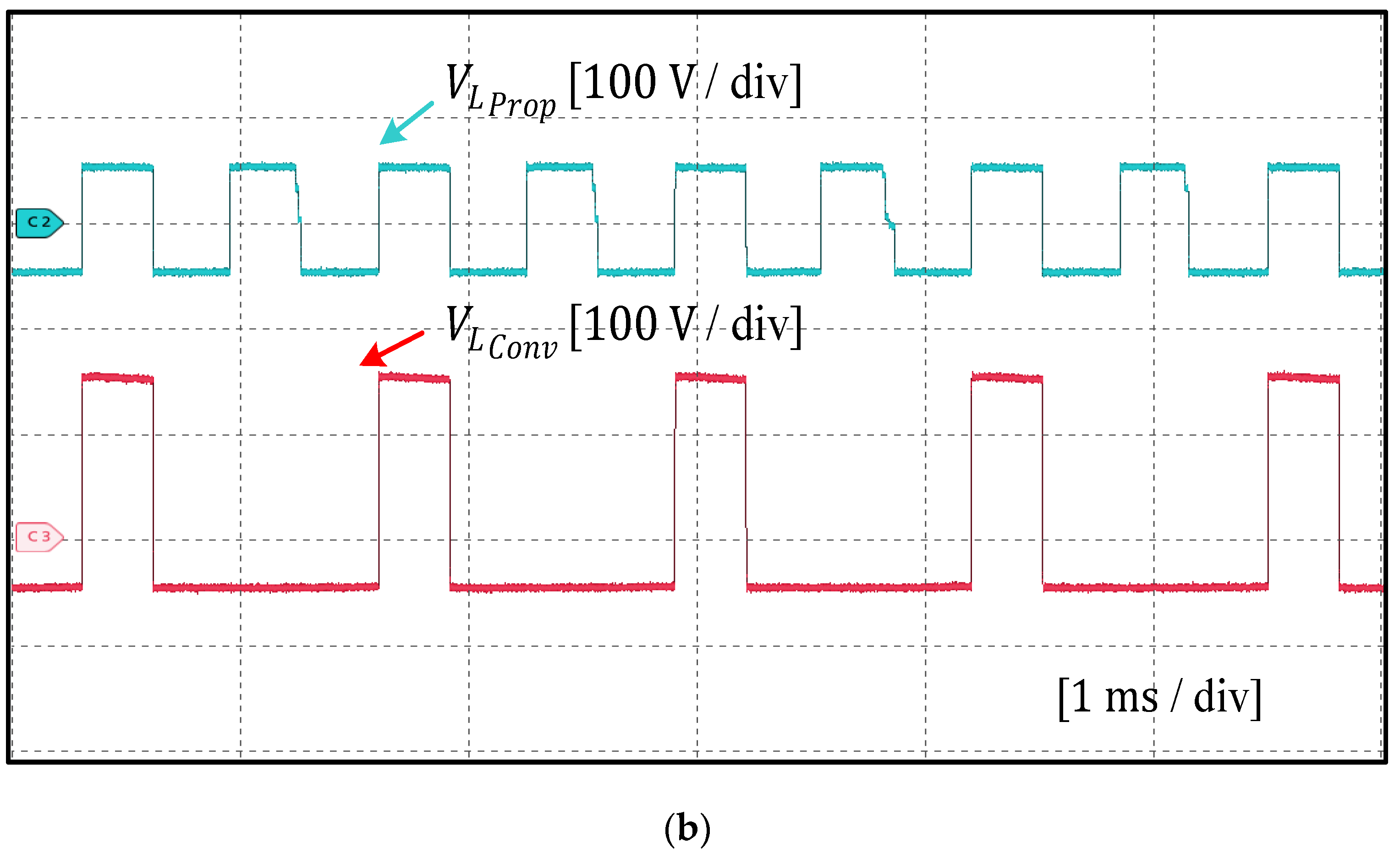
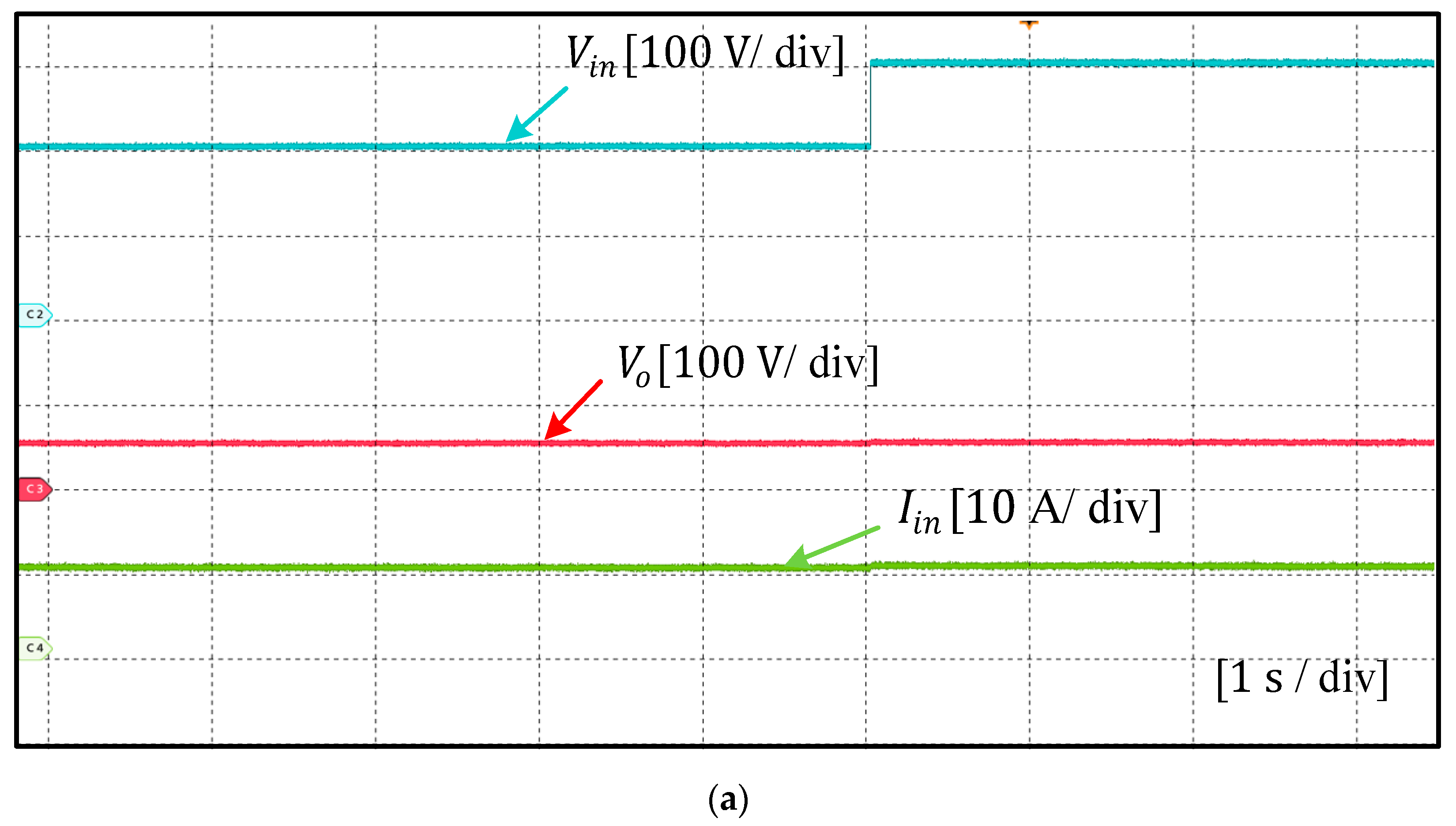
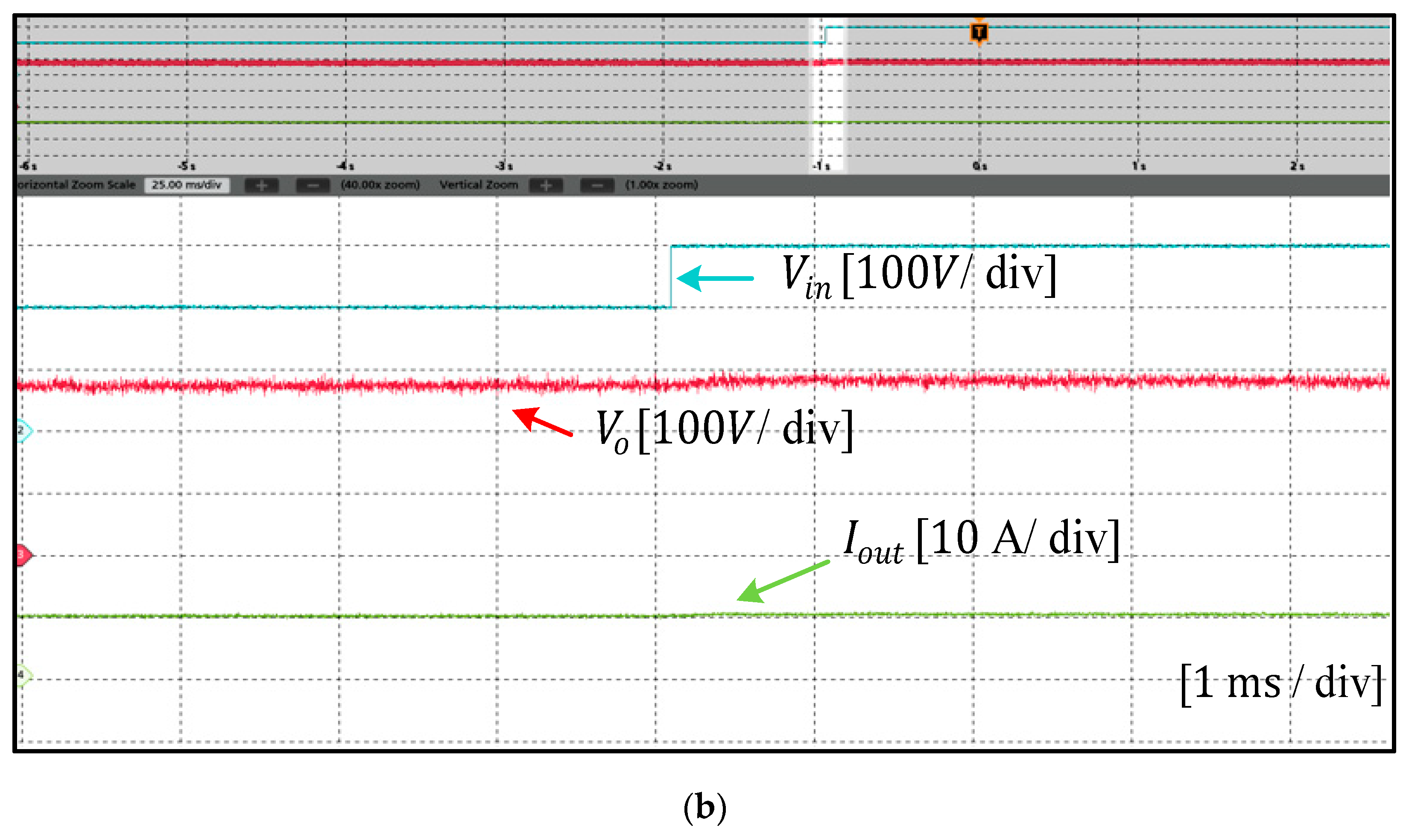
6. Experimental Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Edenhofer, O.; Pichs Madruga, R.; Sokona, Y.; IPCC (Eds.) Renewable Energy Sources and Climate Change Mitigation: Summary for Policymakers and Technical Summary; International Panel of Climate Change: Geneva, Switzerland, 2011; ISBN 978-92-9169-131-9. [Google Scholar]
- Wang, S.-P.; Liao, H.; Chen, J.-F. Design and Implementation of a Novel Bidirectional DC-DC Converter with Coupled Inductor. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 644–649. [Google Scholar] [CrossRef]
- Esmaeili, S.; Shekari, M.; Rasouli, M.; Hasanpour, S.; Khan, A.A.; Hafezi, H. High Gain Magnetically Coupled Single Switch Quadratic Modified SEPIC DC-DC Converter. IEEE Trans. Ind. Appl. 2023, 59, 3593–3604. [Google Scholar] [CrossRef]
- Reddy, B.M.; Samuel, P. A comparative analysis of non-isolated bi-directional dc-dc converters. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Mumtaz, F.; Zaihar Yahaya, N.; Tanzim Meraj, S.; Singh, B.; Kannan, R.; Ibrahim, O. Review on non-isolated DC-DC converters and their control techniques for renewable energy applications. Ain Shams Eng. J. 2021, 12, 3747–3763. [Google Scholar] [CrossRef]
- Parimalasundar, E.; Maneesha, S.; Hanish, R.; Reddy, P.M.; Harish, P.K.; Rao, P.K. Performance Analysis of DC-DC Converter for Electric Vehicle Charging Applications. In Proceedings of the 2023 7th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 23–25 February 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1543–1546. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, P.; Li, B.; Ma, X.; Wang, P. A Bidirectional DC–DC Converter with High Voltage Conversion Ratio and Zero Ripple Current for Battery Energy Storage System. IEEE Trans. Power Electron. 2021, 36, 8012–8027. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Kosenko, R.; Liivik, E.; Galkin, I. Bidirectional DC–DC Converter for Modular Residential Battery Energy Storage Systems. IEEE Trans. Ind. Electron. 2020, 67, 1944–1955. [Google Scholar] [CrossRef]
- Santra, S.B.; Chatterjee, D.; Siwakoti, Y.P. Coupled Inductor Based Soft Switched High Gain Bidirectional DC-DC Converter with Reduced Input Current Ripple. IEEE Trans. Ind. Electron. 2023, 70, 1431–1443. [Google Scholar] [CrossRef]
- Filsoof, K.; Lehn, P.W. A Bidirectional Modular Multilevel DC–DC Converter of Triangular Structure. IEEE Trans. Power Electron. 2015, 30, 54–64. [Google Scholar] [CrossRef]
- Ahmad, A.; Singh, R.K.; Mahanty, R. Bidirectional quadratic converter for wide voltage conversion ratio. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Khan, A.A.; Cha, H.; Lai, J.-S. Cascaded Dual-Buck Inverter with Reduced Number of Inductors. IEEE Trans. Power Electron. 2018, 33, 2847–2856. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Fardahar, S.M.; Sabahi, M. New Expandable Switched-Capacitor/Switched-Inductor High-Voltage Conversion Ratio Bidirectional DC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 2480–2487. [Google Scholar] [CrossRef]
- Hulea, D.; Muntean, N.; Gireada, M.; Cornea, O.; Serban, E. Bidirectional Hybrid Switched-Inductor Switched-Capacitor Converter Topology with High Voltage Gain. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Khan, A.A.; Eberle, W.; Wang, L.; Akbar, F.; Khan, U.A.; Lu, Y.W.; Agamy, M. Coupled-Inductor Buck–Boost Inverter with Reduced Current Ripple. IEEE Trans. Power Electron. 2020, 35, 7933–7946. [Google Scholar] [CrossRef]
- Ismail, A.H.; Ma, Z.; Al-Hmoud, A.; Zhao, Y. A High Frequency Coupled Inductor Design for High Power Density DC-DC Converters. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3275–3280. [Google Scholar] [CrossRef]
- Zhu, G.-R.; Tan, S.-C.; Chen, Y.; Tse, C.K. Mitigation of Low-Frequency Current Ripple in Fuel-Cell Inverter Systems through Waveform Control. IEEE Trans. Power Electron. 2013, 28, 779–792. [Google Scholar] [CrossRef]
- Abeywardana, D.B.W.; Hredzak, B.; Fletcher, J.E.; Konstantinou, G. A cascaded boost inverter based battery energy storage system with reduced battery ripple current. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2733–2738. [Google Scholar]
- Lee, P.-W.; Lee, Y.-S.; Cheng, D.K.W.; Liu, X.-C. Steady-state analysis of an interleaved boost converter with coupled inductors. IEEE Trans. Ind. Electron. 2000, 47, 787–795. [Google Scholar] [CrossRef]
- Leal, W.C.; Godinho, M.O.; Bastos, R.F.; De Aguiar, C.R.; Fuzato, G.H.F.; Machado, R.Q. Cascaded Interleaved DC–DC Converter for a Bidirectional Electric Vehicle Charging Station. IEEE Trans. Ind. Electron. 2024, 71, 3708–3717. [Google Scholar] [CrossRef]
- Scire, D.; Lullo, G.; Vitale, G. Design and Modeling of an Interleaving Boost Converter with Quasi-Saturated Inductors for Electric Vehicles. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 18–20 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Sferlazza, A.; Garraffa, G.; Vitale, G.; D’Ippolito, F.; Alonge, F.; Lullo, G.; Busacca, A.; Giaconia, G.C.; Scirè, D. Robust Disturbance Rejection Control of DC/DC Interleaved Boost Converters with Additional Sliding Mode Component. In Proceedings of the 2023 Asia Meeting on Environment and Electrical Engineering (EEE-AM), Hanoi, Vietnam, 13–15 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Akbar, F.; Cha, H.; Ahmed, H.F.; Khan, A.A. A Family of Single-Stage High-Gain Dual-Buck Split-Source Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1701–1713. [Google Scholar] [CrossRef]
- Khan, A.A.; Cha, H.; Ahmed, H.F. An Improved Single-Phase Direct PWM Inverting Buck–Boost AC–AC Converter. IEEE Trans. Ind. Electron. 2016, 63, 5384–5393. [Google Scholar] [CrossRef]
- Khan, A.A.; Cha, H.; Ahmed, H.F. High-Efficiency Single-Phase AC–AC Converters without Commutation Problem. IEEE Trans. Power Electron. 2016, 31, 5655–5665. [Google Scholar] [CrossRef]









| Components | Values |
|---|---|
| ) | 200 V |
| 48 V | |
| Rated output power | 460 W |
| ) | NTHL065N65S3HF (ONSEMI, St.John’s, NL, Canada) |
| Switching frequency | 50 Khz |
| ) | BYC30JT-600PSQ |
| Controller | TMS320F28335 |
| ) | 0.1 mH |
| ) | 100 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, J.M.; Khan, A.A.; Jamil, M. A Novel Non-Isolated Bidirectional DC-DC Converter with Improved Current Ripples for Low-Voltage On-Board Charging. Energies 2024, 17, 3570. https://doi.org/10.3390/en17143570
Khan JM, Khan AA, Jamil M. A Novel Non-Isolated Bidirectional DC-DC Converter with Improved Current Ripples for Low-Voltage On-Board Charging. Energies. 2024; 17(14):3570. https://doi.org/10.3390/en17143570
Chicago/Turabian StyleKhan, Jamil Muhammad, Ashraf Ali Khan, and Mohsin Jamil. 2024. "A Novel Non-Isolated Bidirectional DC-DC Converter with Improved Current Ripples for Low-Voltage On-Board Charging" Energies 17, no. 14: 3570. https://doi.org/10.3390/en17143570
APA StyleKhan, J. M., Khan, A. A., & Jamil, M. (2024). A Novel Non-Isolated Bidirectional DC-DC Converter with Improved Current Ripples for Low-Voltage On-Board Charging. Energies, 17(14), 3570. https://doi.org/10.3390/en17143570







