A Hybrid Commutation Technique for Reducing Zero-Crossing Distortion in a Sliding Mode Controller for Single-Phase Grid-Tied Full-Bridge Inverters
Abstract
1. Introduction
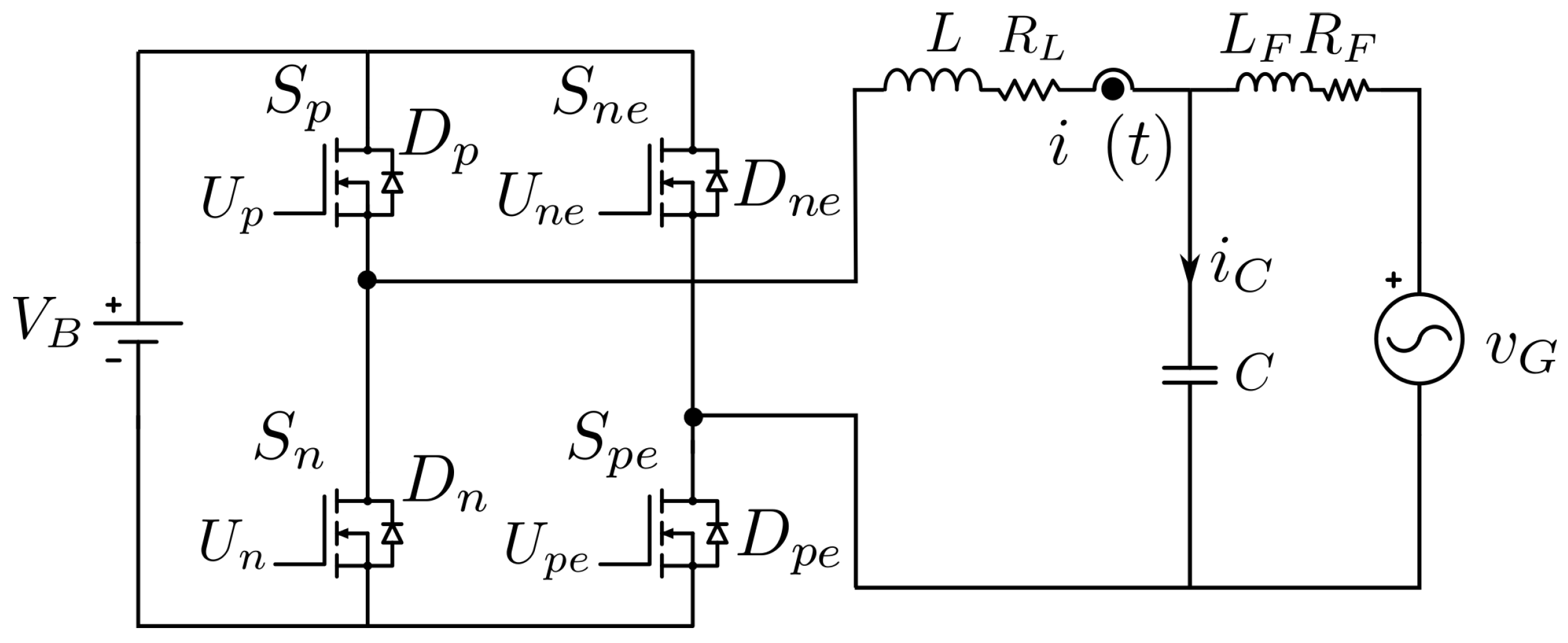
2. Full-Bridge Inverter Operation
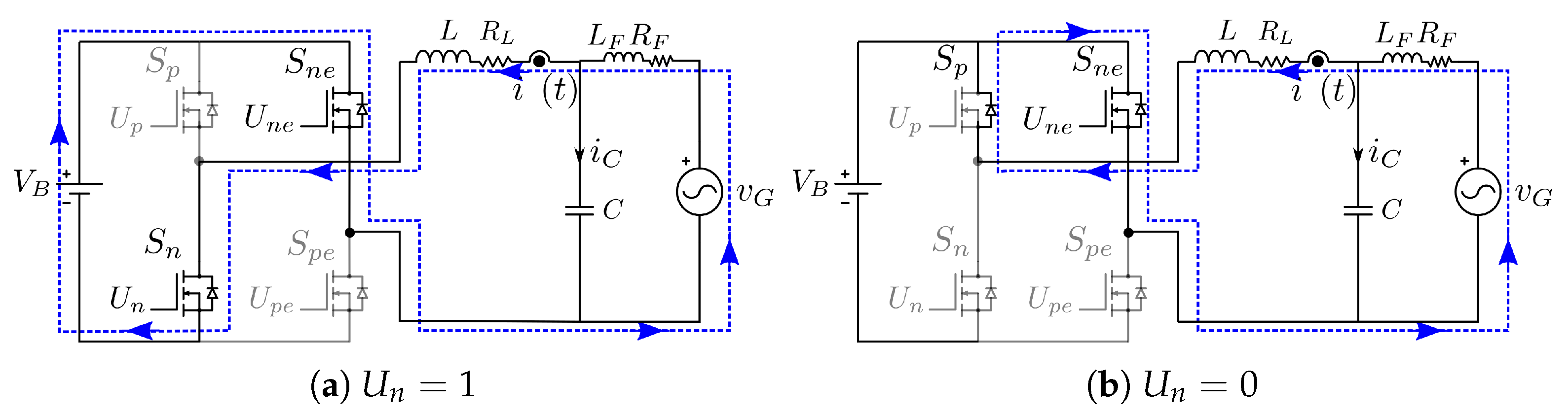
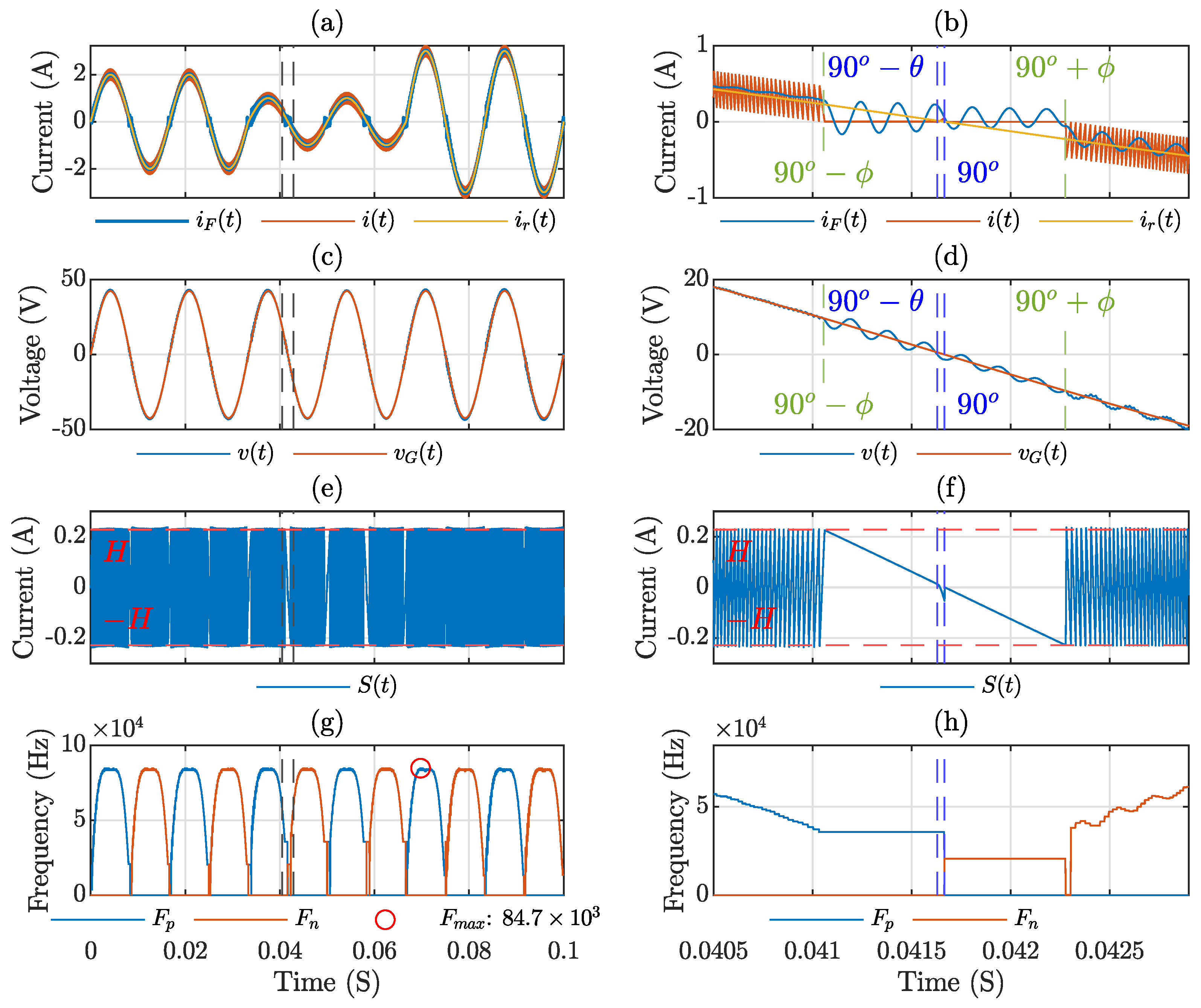
2.1. Inverter Operation with Unipolar Commutation (FB-U)
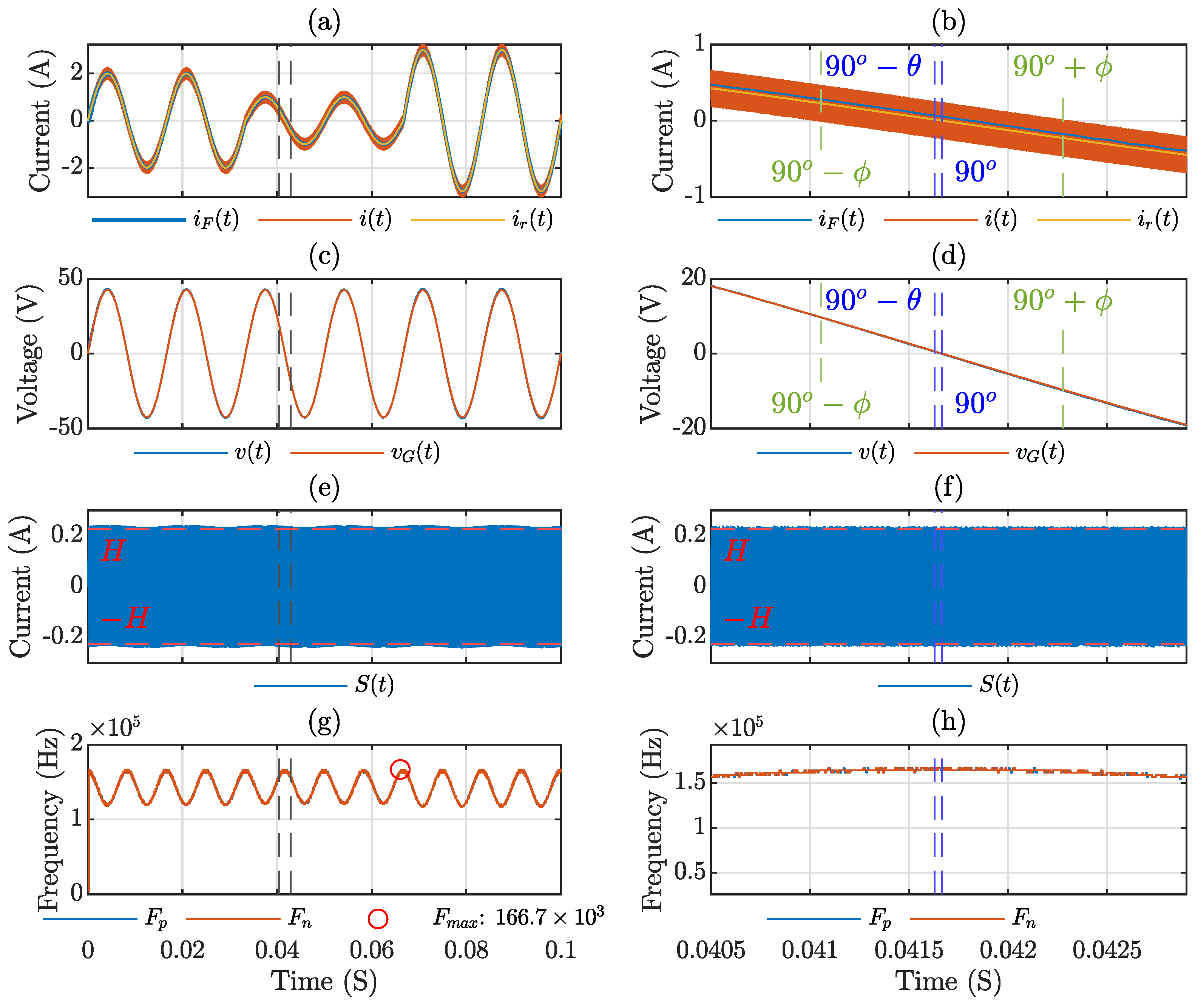
2.2. Inverter Operation with Bipolar Commutation (FB-B)
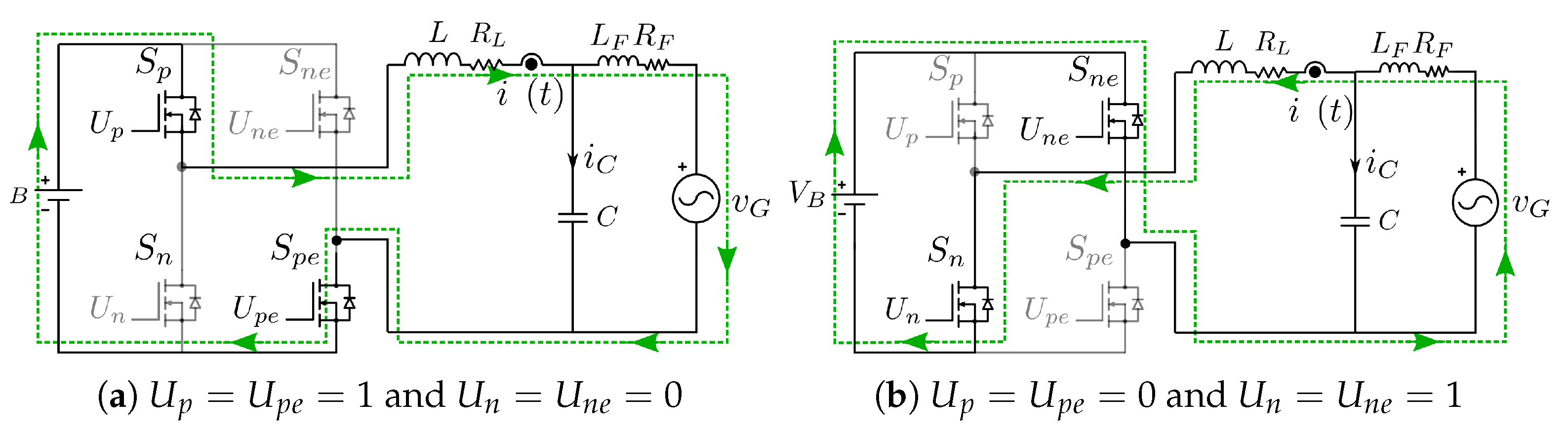
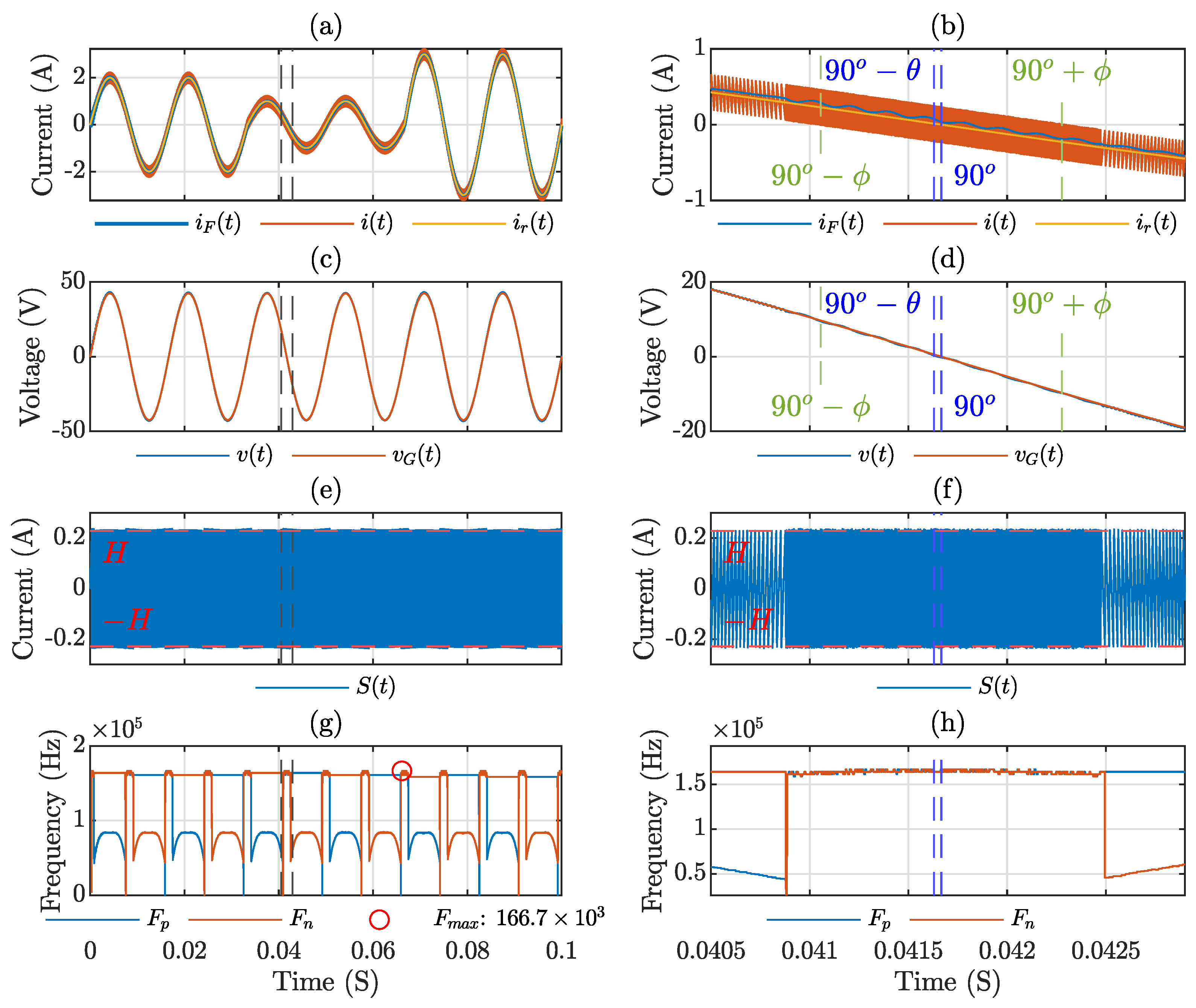
2.3. Inverter Operation with Hybrid Commutation (FB-H)
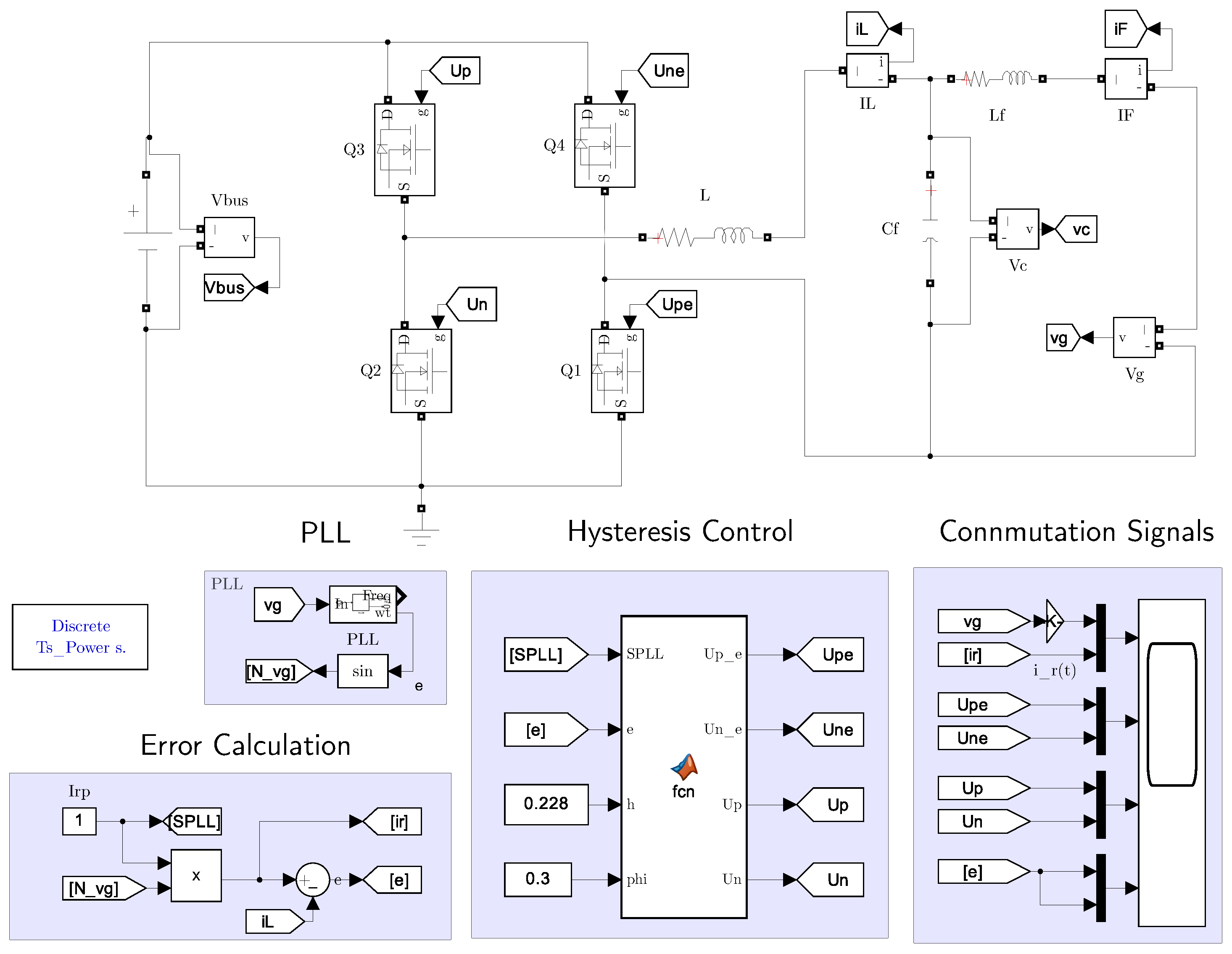
3. FB Inverter Control Strategy
3.1. Control Scheme Functionality
3.2. Sliding Mode Control Analysis
3.2.1. Sliding Mode Surface
3.2.2. Transversality Condition
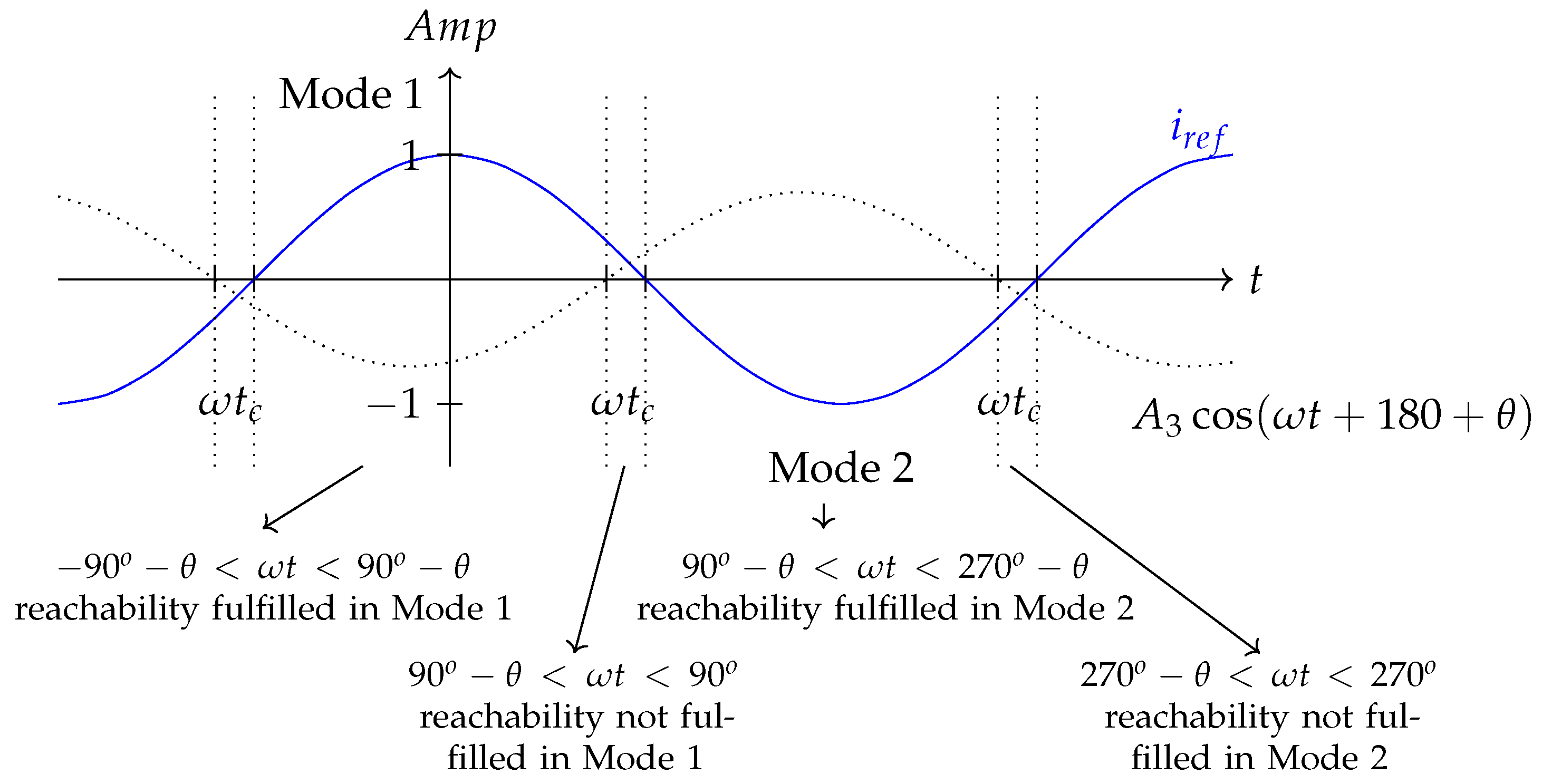
- Mode 1: then and then ;
- Mode 2: then and then
- Mode 3: results in , while leads to
3.2.3. Reachability Condition
3.3. Design of Parameters—Guidelines
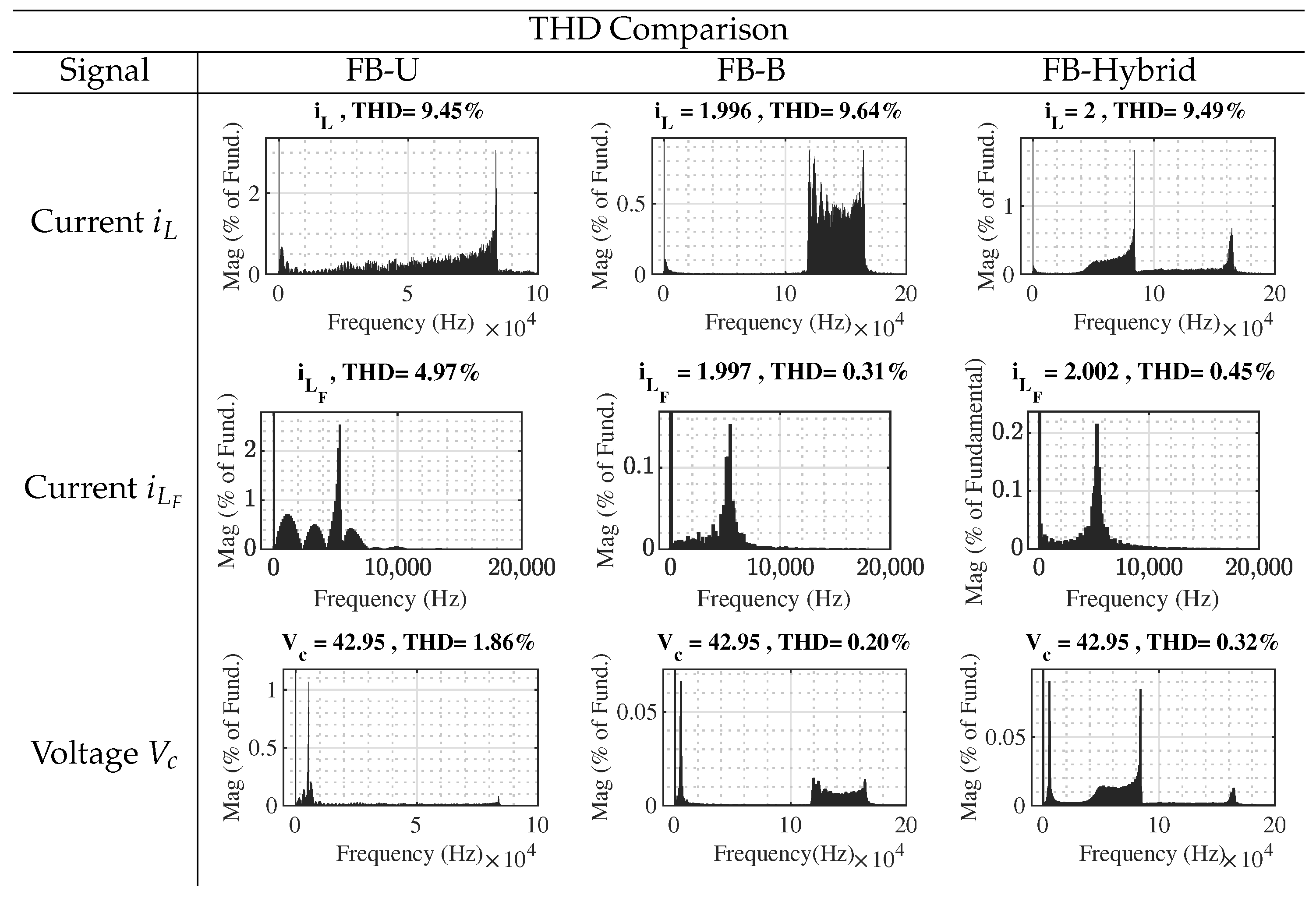
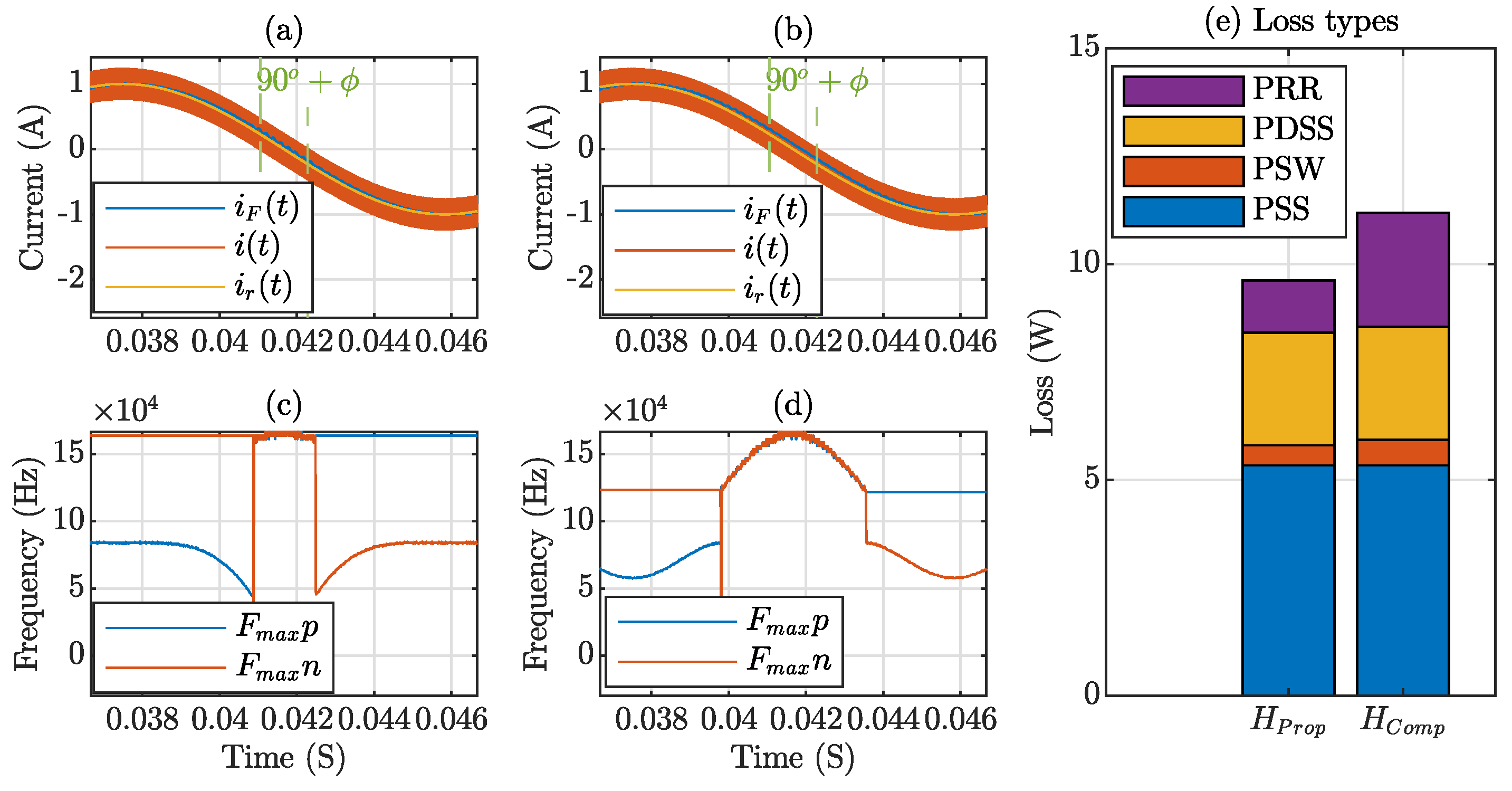
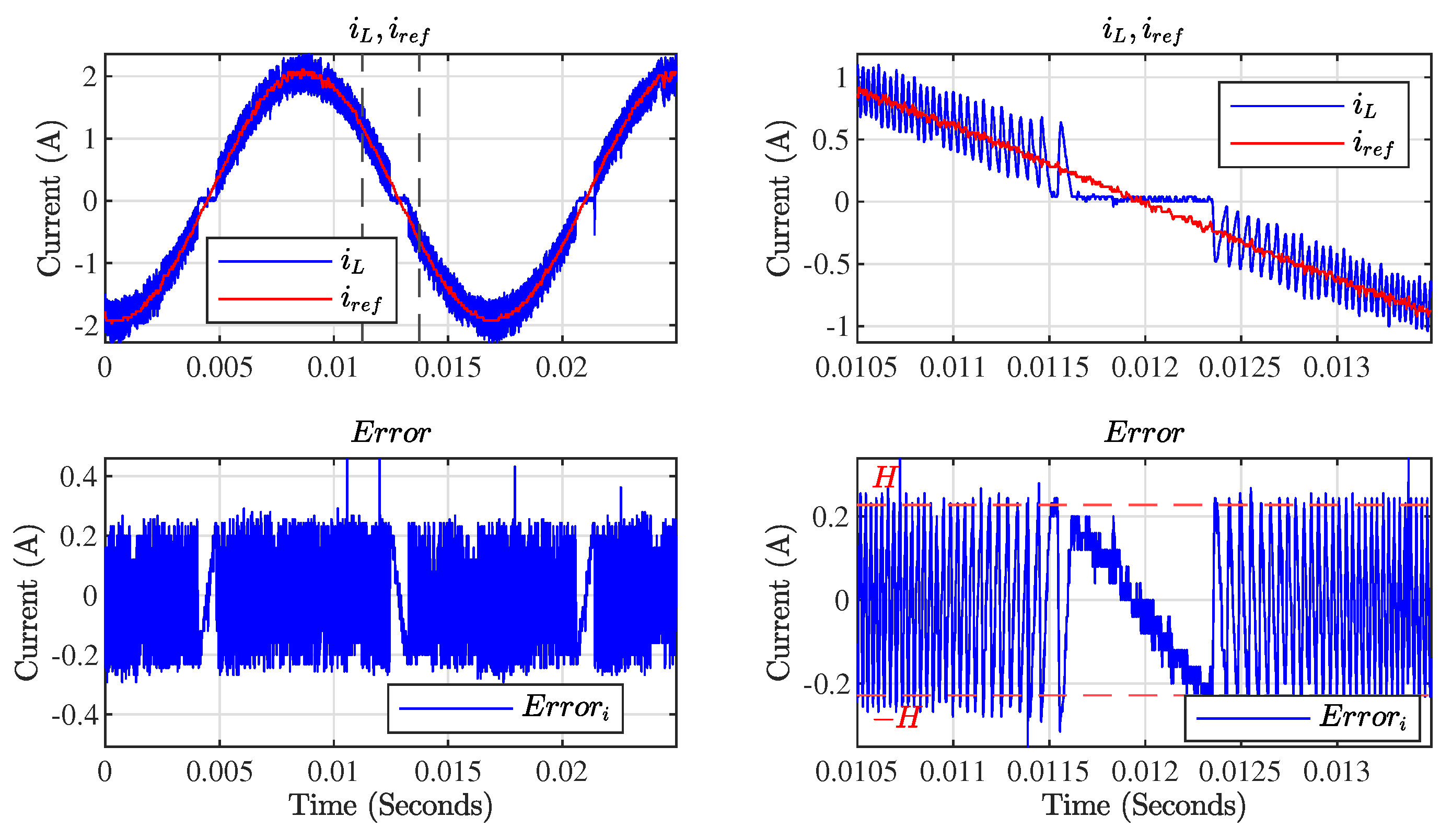
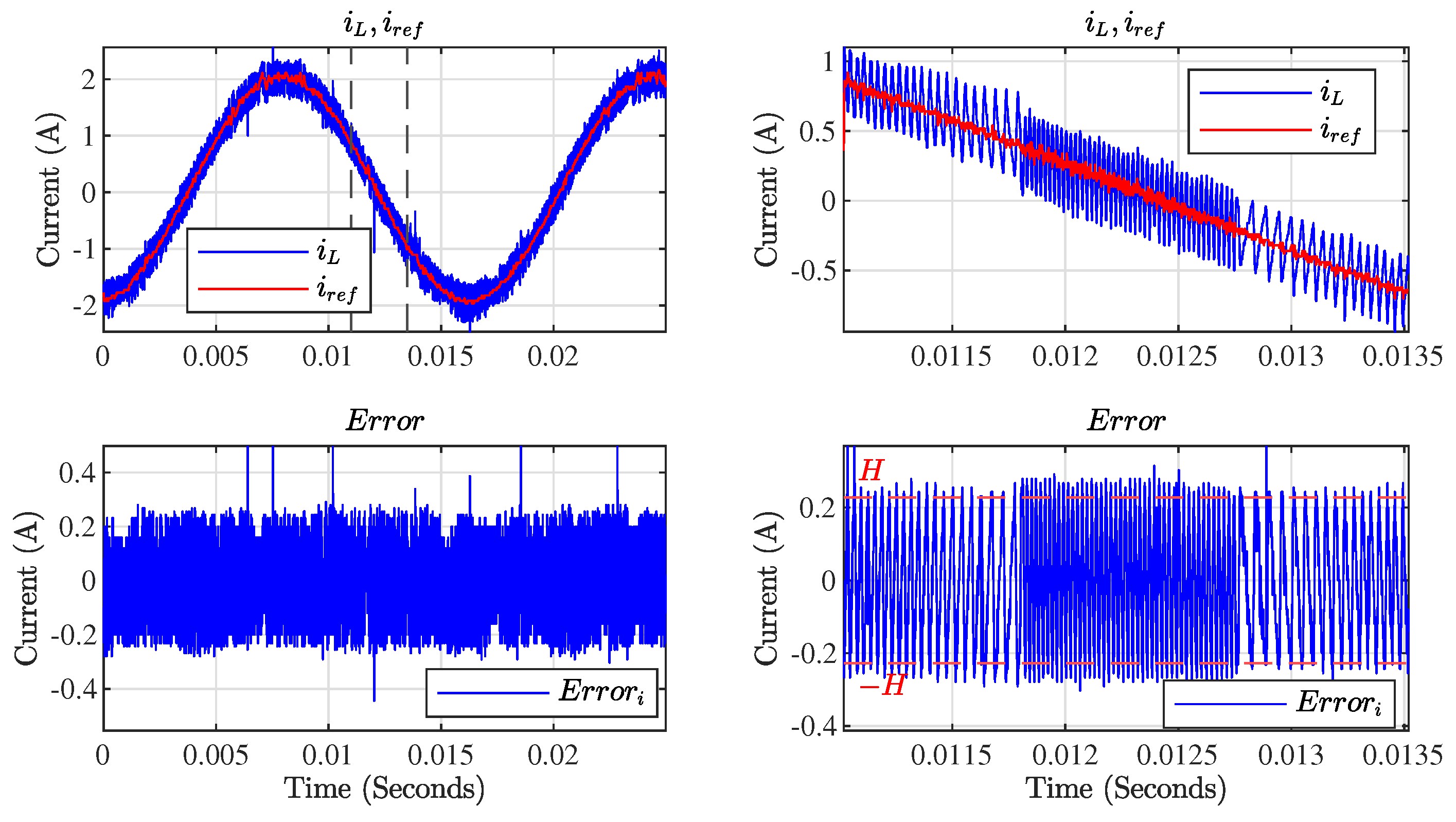
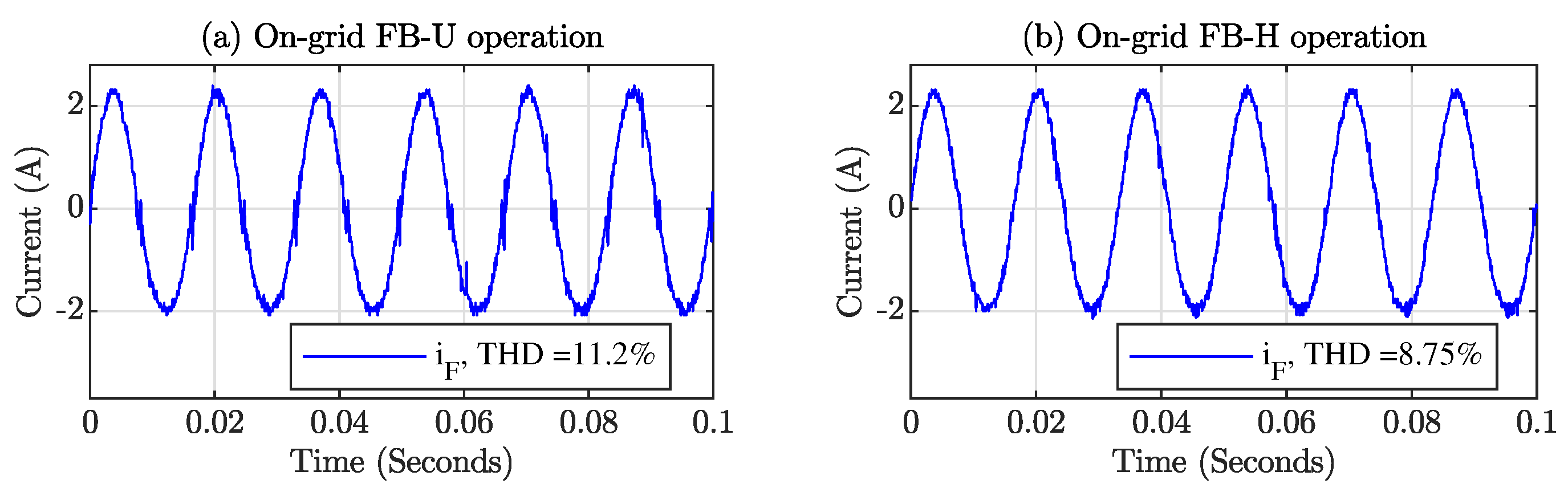
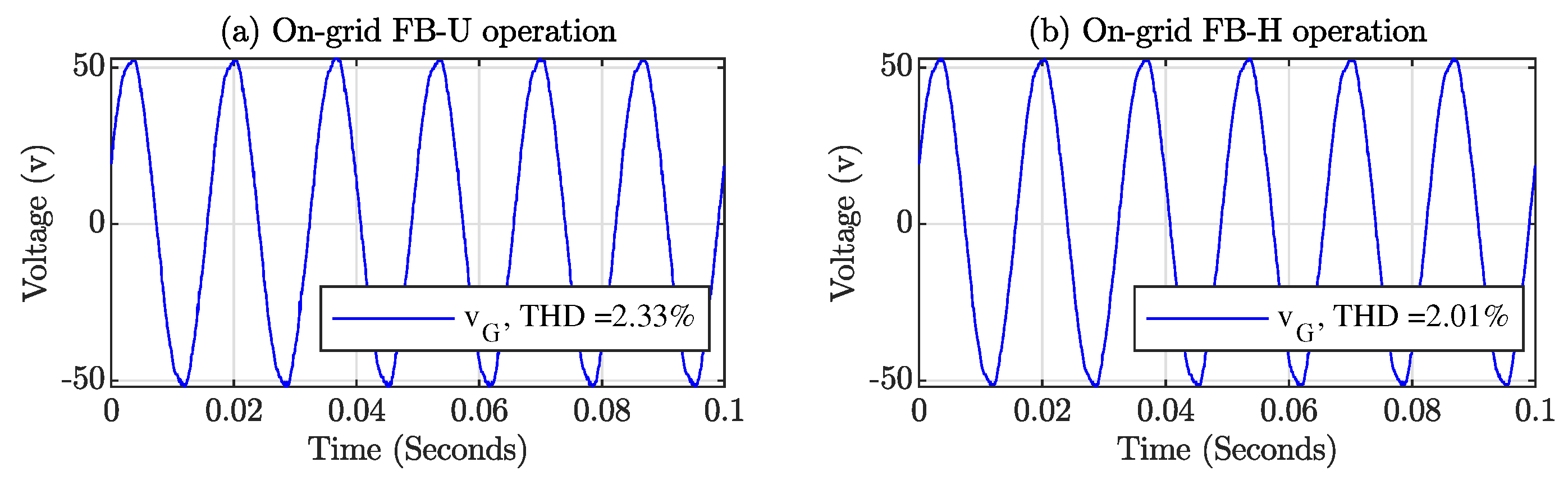
4. Simulation and Experimental Results
Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kabalcı, E. Review on novel single-phase grid-connected solar inverters: Circuits and control methods. Sol. Energy 2020, 198, 247–274. [Google Scholar] [CrossRef]
- Hong, F.; Liu, J.; Ji, B.; Zhou, Y.; Wang, J.; Wang, C. Single Inductor Dual Buck Full-Bridge Inverter. IEEE Trans. Ind. Electron. 2015, 62, 4869–4877. [Google Scholar] [CrossRef]
- Khan, M.Y.A.; Liu, H.; Yang, Z.; Yuan, X. A comprehensive review on grid connected photovoltaic inverters, their modulation techniques, and control strategies. Energies 2020, 13, 4185. [Google Scholar] [CrossRef]
- Brinker, T.; Hoffmann, L.; Friebe, J. Comparison of Modulation Techniques for a Single-Phase Full-Bridge Photovoltaic Micro-Inverter Considering Reactive Power Capability. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 841–846. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, C.; Guo, Y.; Sun, H.; Jiang, L. Optimization of Zero-Crossing Distortion for Unipolar BCM Grid-Tied Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3680–3691. [Google Scholar] [CrossRef]
- Wu, T.F.; Kuo, C.L.; Sun, K.H.; Hsieh, H.C. Combined unipolar and bipolar PWM for current distortion improvement during power compensation. IEEE Trans. Power Electron. 2014, 29, 1702–1709. [Google Scholar] [CrossRef]
- Tang, Z.; Su, M.; Sun, Y.; Cheng, B.; Yang, Y.; Blaabjerg, F.; Wang, L. Hybrid UP-PWM Scheme for HERIC Inverter to Improve Power Quality and Efficiency. IEEE Trans. Power Electron. 2019, 34, 4292–4303. [Google Scholar] [CrossRef]
- Liu, B.; Su, M.; Yang, J.; Song, D.; He, D.; Song, S. Combined Reactive Power Injection Modulation and Grid Current Distortion Improvement Approach for H6 Transformer-Less Photovoltaic Inverter. IEEE Trans. Energy Convers. 2017, 32, 1456–1467. [Google Scholar] [CrossRef]
- Zeng, B.; Xu, H.B.; Chen, K.; Chen, J.G. Suppression of zero-crossing distortion for single-phase grid-connected photovoltaic inverters with unipolar modulation. Rev. Sci. Instrum. 2013, 84, 104705. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Sun, B.; Zhao, K.; Sun, L. Analysis and Solution of Current Zero-Crossing Distortion with Unipolar Hysteresis Current Control in Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2013, 60, 4450–4457. [Google Scholar] [CrossRef]
- Wu, F.; Li, X.; Duan, J. Improved Elimination Scheme of Current Zero-Crossing Distortion in Unipolar Hysteresis Current Controlled Grid-Connected Inverter. IEEE Trans. Ind. Inform. 2015, 11, 1111–1118. [Google Scholar] [CrossRef]
- Xie, R.; Zeng, Q.; Yang, F.; Lin, B.; Xu, O.; He, Y. Decoupled Unipolar Hysteresis Current Control for Single-Phase Grid-Tied Inverter Without Current Zero-Crossing Distortion. IEEE Access 2024, 12, 21453–21463. [Google Scholar] [CrossRef]
- Shimada, R.; Huang, C.; Mannen, T.; Isobe, T. Unipolar/Bipolar Mixed Modulation for Discontinuous Current Mode Single-Phase Grid-tied Inverter with Off-time Discrete Control. In Proceedings of the 2021 IEEE International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 16–19 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, X.; Li, Q. Hybrid Modulation Method for Single Phase Full Bridge CRM Inverter to Improve Reactive Power Capability. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2314–2319. [Google Scholar] [CrossRef]
- Lai, J.C.T.; Yeung, S.C.R.; Chung, H.S.H. Achieving Fast Dynamic Response and Output Filter Condition Monitoring in Hybrid PWM Inverters Using a Low-Computational State Trajectory Prediction Algorithm Incorporating With Reduced-Order Switching Surfaces. IEEE Trans. Power Electron. 2024, 39, 6941–6960. [Google Scholar] [CrossRef]
- Chen, J.; Wu, C.; Li, J.; Shao, Z.; Wang, J.; Wang, Y. A Low Distortion Collaborative Modulation for Zero-Crossing Distortion Pseudo DC Link Single-Stage Isolated Inverter. IEEE Trans. Power Electron. 2024, 39, 9132–9137. [Google Scholar] [CrossRef]
- Yao, R.; Wei, C.; Li, R. A Quasi-Trapezoidal Modulation Method with Zero-Voltage Switching for Single-Phase Inverters. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2088–2092. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, J.; Shao, S. A Variable Switching Frequency Multimode Control Scheme for Single-Phase Grid-Tied Multilevel PV Microinverters. IEEE Trans. Power Electron. 2023, 38, 11543–11555. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Xiao, S.; Balog, R.S. Hybrid hysteresis current control and low-frequency current harmonics mitigation based on proportional resonant in dc/ac inverter. IET Power Electron. 2018, 11, 2093–2101. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Zhang, H. Hybrid-Modulation Hysteresis Scheme Based Decoupled Power Control of Grid-Connected Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 276–287. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, L.; Liu, X.; He, Y.; Shi, J.; Wang, C. Half-Cycle Control Method of the Bidirectional Three-Phase Dual-Buck Inverter without Zero-Crossing Distortion. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2088–2097. [Google Scholar] [CrossRef]
- Sabi, K.; Costinett, D. Design and implementation of a bipolar-unipolar switched boundary current mode (BCM) Control GaN-Based single-phase inverter. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition, ECCE 2019, Baltimore, MD, USA, 29 September–3 October 2019; pp. 6473–6480. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Tian, Y.; Zhao, H. Optimization of Boundary Current Mode Control Strategy for Reducing Zero-crossing Distortion in a H-bridge Inverter. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Kumar, H.; Banerjee, S.; Mishra, S.K. A Method to Compensate for the Distortion of the Output Voltage of an H-Bridge Inverter Under Sinusoidal Unipolar PWM. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Haruna, J.; Masubuchi, N.; Iwase, S.; Funato, H. Loss analysis and efficiency enhancing method for a unipolar hysteresis-Controlled single-phase grid-connected inverter. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1182–1188. [Google Scholar] [CrossRef]
- Bolaños-Navarrete, M.A.; Bastidas-Rodríguez, J.D.; Osorio, G.A. Hysteresis control for a grid connected dual-buck inverter. Rev. UIS Ing. 2020, 20, 1–10. [Google Scholar] [CrossRef]
- Bolaños, M.A.; Osorio, G.; Bastidas-Rodriguez, J.D.; Revelo-Fuelagan, E. Computational Model of a Two-stage Microinverter With Flyback Active Clamp and Dual Buck. In Proceedings of the 2019 IEEE 4th Colombian Conference on Automatic Control (CCAC), Medellin, Colombia, 15–18 October 2019. [Google Scholar]



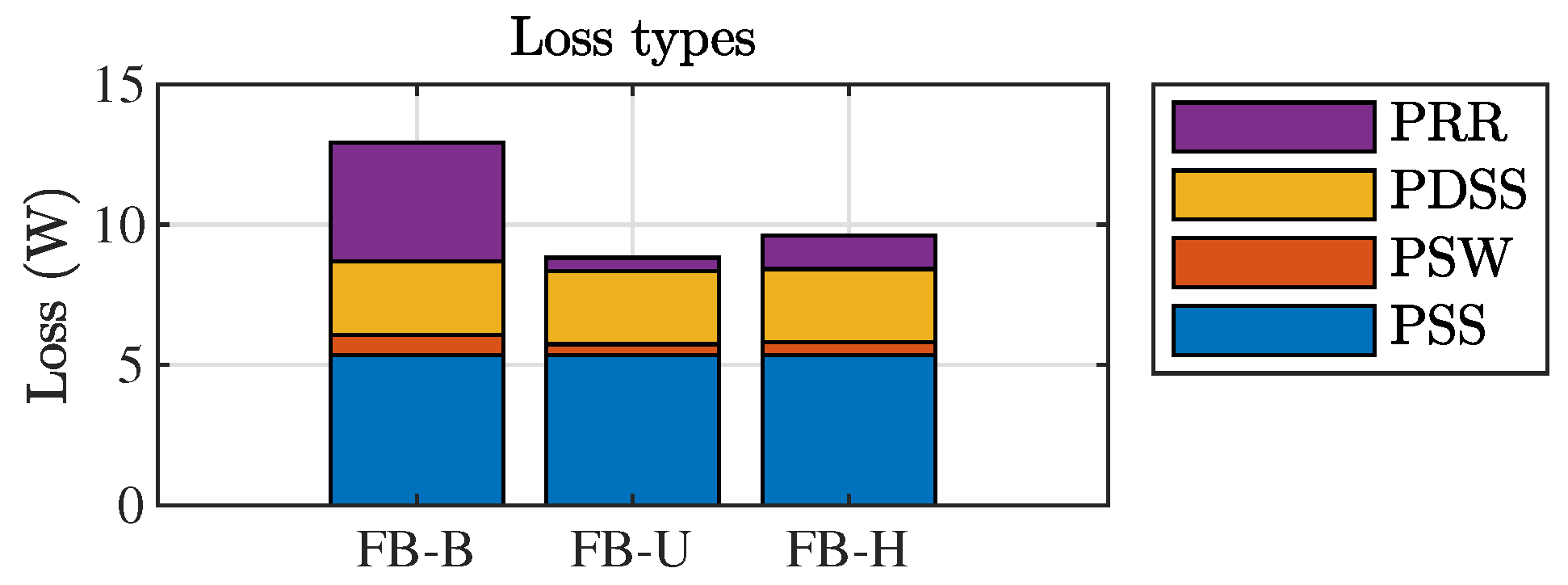



| Component | Value | Units | |
|---|---|---|---|
| Component | L | 540 | H |
| 0.320 | |||
| 270 | H | ||
| 0.160 | |||
| C | 3.3 | f | |
| 21.21 | |||
| 88 | V | ||
| Control Parameters | 13.18 | ∘ | |
| θ | 0.8065 | ∘ | |
| 2, 1, 3 | A | ||
| H | 228 m | A | |
| 1 k | Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolaños-Navarrete, M.A.; Bastidas-Rodríguez, J.D.; Osorio, G. A Hybrid Commutation Technique for Reducing Zero-Crossing Distortion in a Sliding Mode Controller for Single-Phase Grid-Tied Full-Bridge Inverters. Energies 2024, 17, 3671. https://doi.org/10.3390/en17153671
Bolaños-Navarrete MA, Bastidas-Rodríguez JD, Osorio G. A Hybrid Commutation Technique for Reducing Zero-Crossing Distortion in a Sliding Mode Controller for Single-Phase Grid-Tied Full-Bridge Inverters. Energies. 2024; 17(15):3671. https://doi.org/10.3390/en17153671
Chicago/Turabian StyleBolaños-Navarrete, Mario Andrés, Juan David Bastidas-Rodríguez, and Gustavo Osorio. 2024. "A Hybrid Commutation Technique for Reducing Zero-Crossing Distortion in a Sliding Mode Controller for Single-Phase Grid-Tied Full-Bridge Inverters" Energies 17, no. 15: 3671. https://doi.org/10.3390/en17153671
APA StyleBolaños-Navarrete, M. A., Bastidas-Rodríguez, J. D., & Osorio, G. (2024). A Hybrid Commutation Technique for Reducing Zero-Crossing Distortion in a Sliding Mode Controller for Single-Phase Grid-Tied Full-Bridge Inverters. Energies, 17(15), 3671. https://doi.org/10.3390/en17153671







