Turbulent Boundary Layer Control with Multi-Scale Riblet Design
Abstract
:1. Introduction
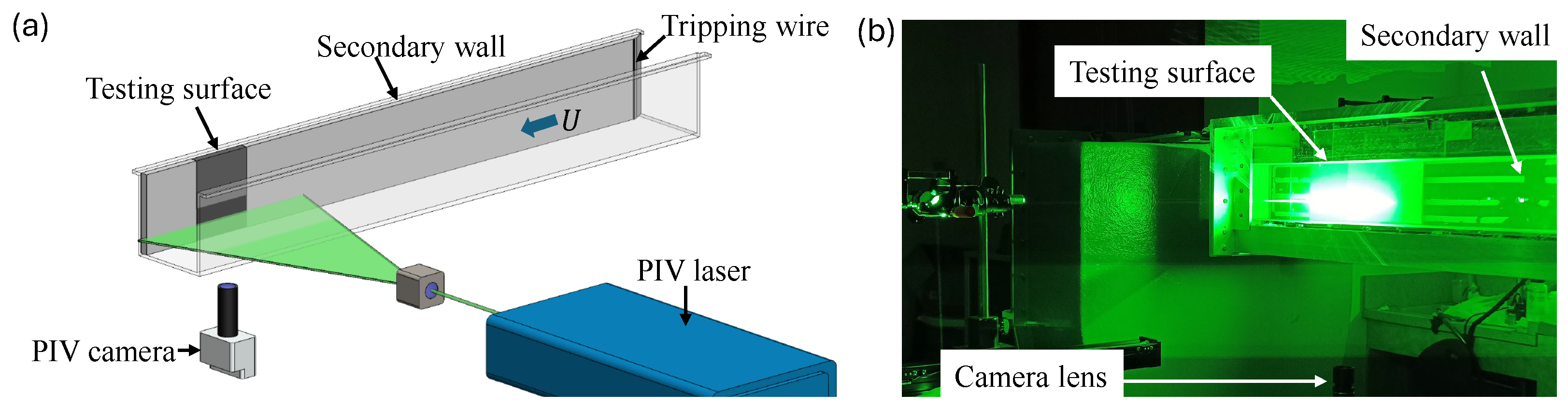
2. Experimental Setup
3. Results and Discussion
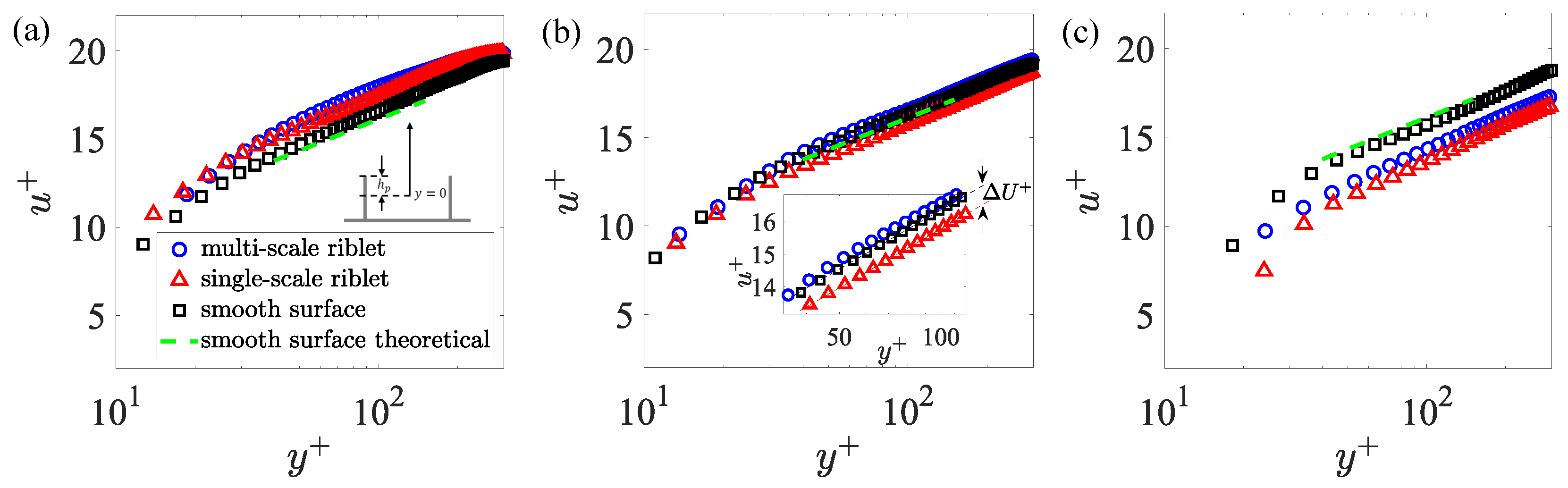
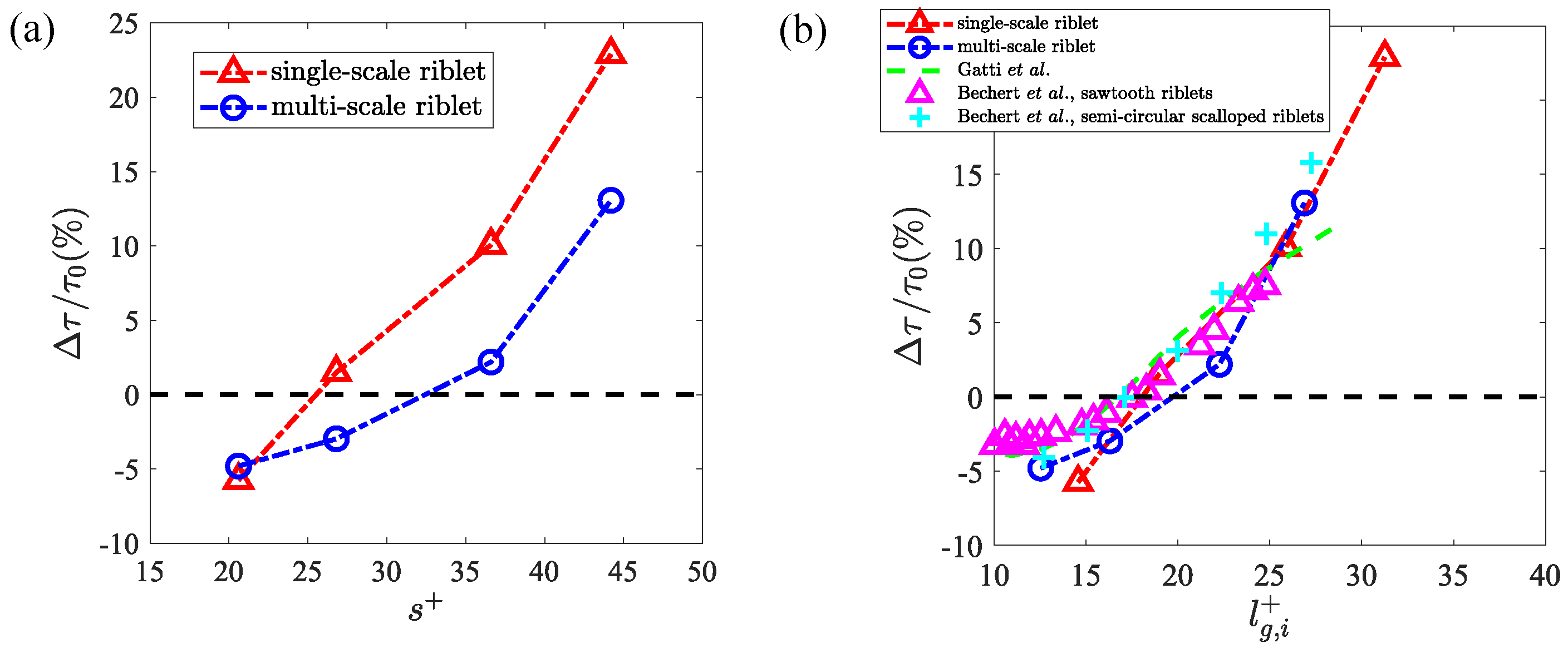
3.1. Drag Reduction Effectiveness and Large-Scale Structures
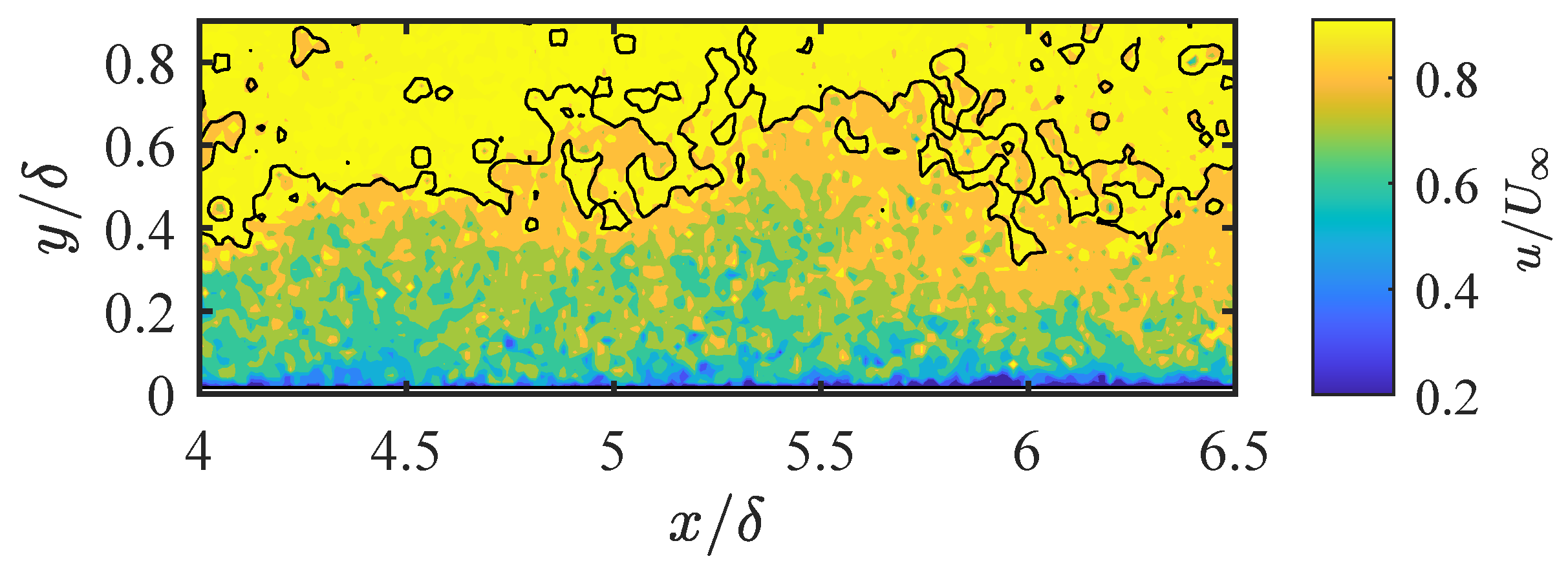
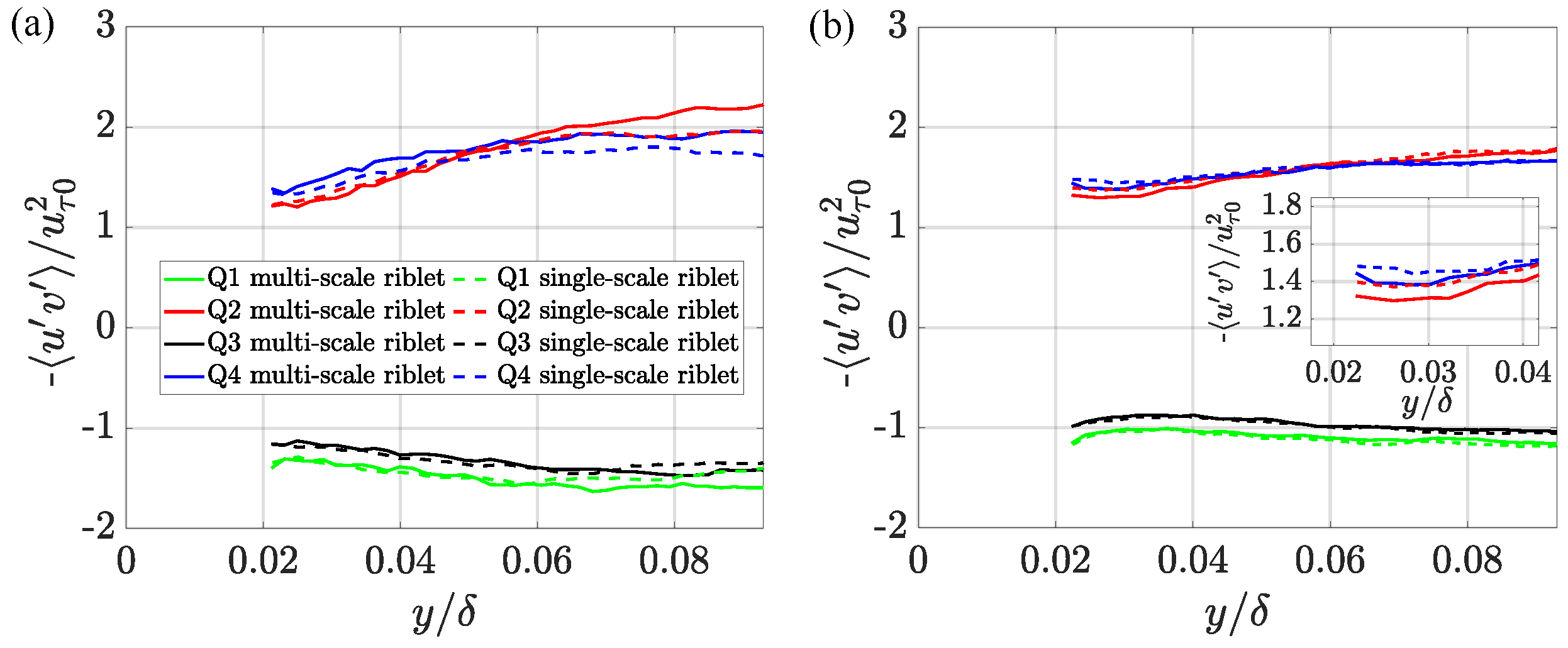
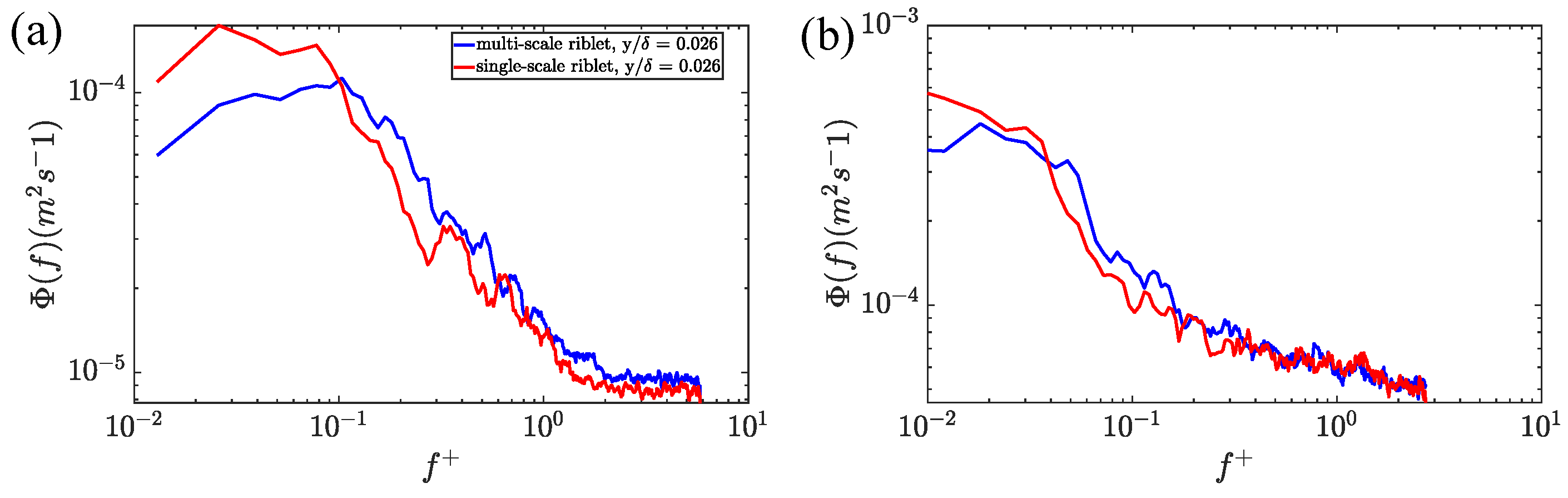
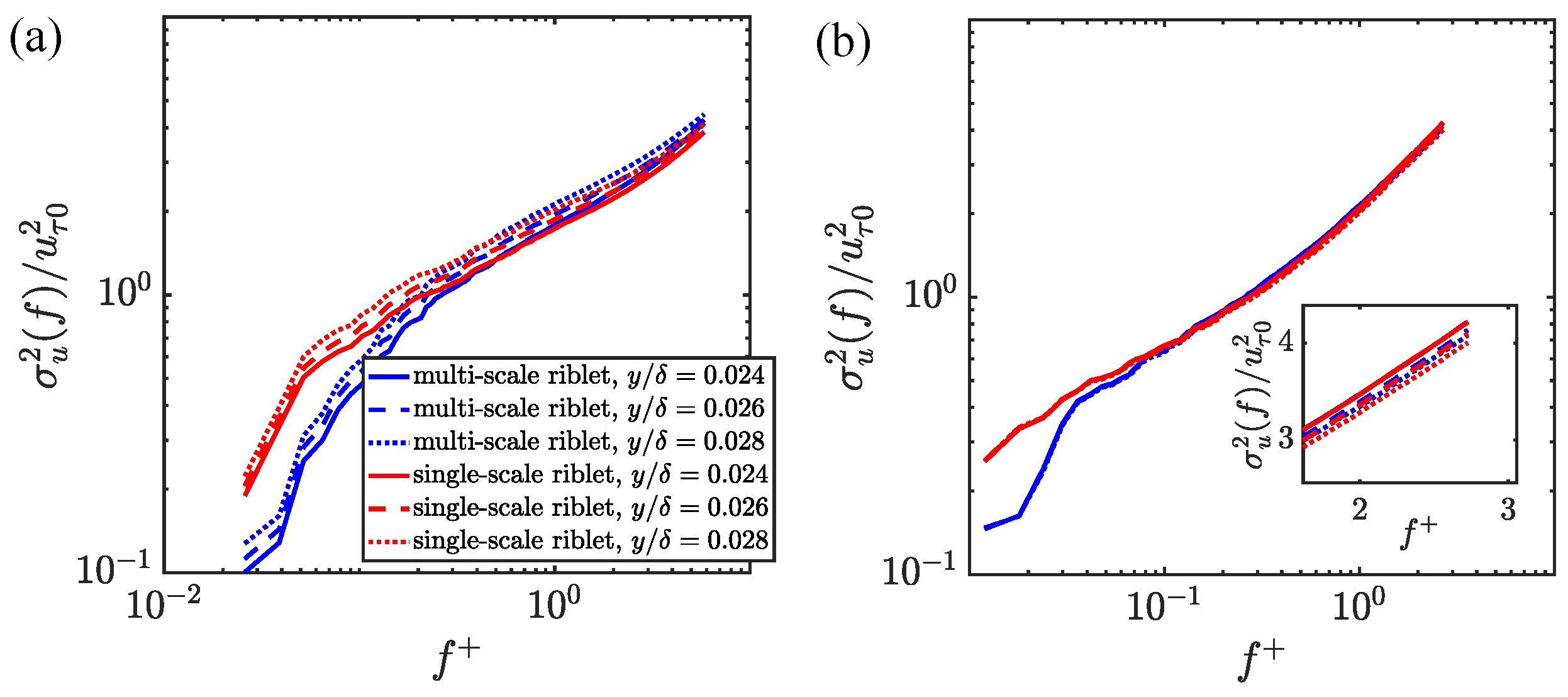
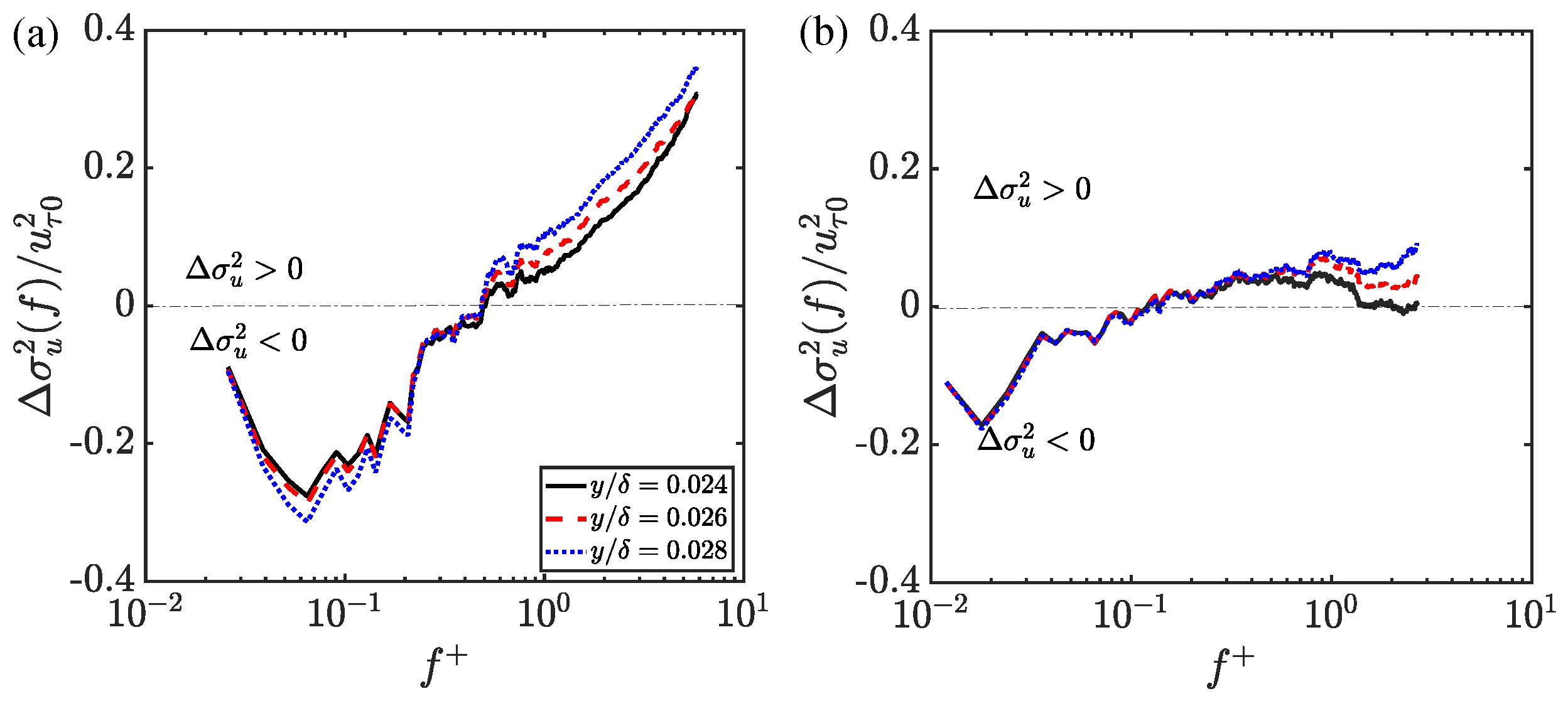
3.2. Near-Wall Flow Dynamics
4. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, L.; Huang, P.; LeBeau, R.; Hauser, T. Numerical study of blowing and suction control mechanism on NACA0012 airfoil. J. Aircr. 2004, 41, 1005–1013. [Google Scholar] [CrossRef]
- Chng, T.; Rachman, A.; Tsai, H.; Zha, G.C. Flow control of an airfoil via injection and suction. J. Aircr. 2009, 46, 291–300. [Google Scholar] [CrossRef]
- Moussavi, S.A.; Ghaznavi, A. Effect of boundary layer suction on performance of a 2 MW wind turbine. Energy 2021, 232, 121072. [Google Scholar] [CrossRef]
- Greenblatt, D.; Schulman, M.; Ben-Harav, A. Vertical axis wind turbine performance enhancement using plasma actuators. Renew. Energy 2012, 37, 345–354. [Google Scholar] [CrossRef]
- Guoqiang, L.; Weiguo, Z.; Yubiao, J.; Pengyu, Y. Experimental investigation of dynamic stall flow control for wind turbine airfoils using a plasma actuator. Energy 2019, 185, 90–101. [Google Scholar] [CrossRef]
- You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 2008, 24, 1349–1357. [Google Scholar] [CrossRef]
- Tang, H.; Salunkhe, P.; Zheng, Y.; Du, J.; Wu, Y. On the use of synthetic jet actuator arrays for active flow separation control. Exp. Therm. Fluid Sci. 2014, 57, 1–10. [Google Scholar] [CrossRef]
- Belamadi, R.; Djemili, A.; Ilinca, A.; Mdouki, R. Aerodynamic performance analysis of slotted airfoils for application to wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2016, 151, 79–99. [Google Scholar] [CrossRef]
- Beyhaghi, S.; Amano, R.S. A parametric study on leading-edge slots used on wind turbine airfoils at various angles of attack. J. Wind Eng. Ind. Aerodyn. 2018, 175, 43–52. [Google Scholar] [CrossRef]
- Park, S.; Hristov, G.; Balasubramanian, S.; Goza, A.; Ansell, P.J.; Matlack, K. Design and analysis of phononic material for passive flow control. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3330. [Google Scholar]
- Hussein, M.I.; Biringen, S.; Bilal, O.R.; Kucala, A. Flow stabilization by subsurface phonons. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140928. [Google Scholar] [CrossRef]
- Willey, C.L.; Barnes, C.J.; Chen, V.W.; Rosenberg, K.; Medina, A.; Juhl, A.T. Multi-input multi-output phononic subsurfaces for passive boundary layer transition delay. J. Fluids Struct. 2023, 121, 103936. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Arndt, R.; Sotiropoulos, F. Drag reduction of large wind turbine blades through riblets: Evaluation of riblet geometry and application strategies. Renew. Energy 2013, 50, 1095–1105. [Google Scholar] [CrossRef]
- Sareen, A.; Deters, R.W.; Henry, S.P.; Selig, M.S. Drag reduction using riblet film applied to airfoils for wind turbines. J. Sol. Energy Eng. 2014, 136, 021007. [Google Scholar] [CrossRef]
- Viswanath, P. Aircraft viscous drag reduction using riblets. Prog. Aerosp. Sci. 2002, 38, 571–600. [Google Scholar] [CrossRef]
- Modesti, D.; Endrikat, S.; Hutchins, N.; Chung, D. Dispersive stresses in turbulent flow over riblets. J. Fluid Mech. 2021, 917, A55. [Google Scholar] [CrossRef]
- Chavarin, A.; Luhar, M. Resolvent analysis for turbulent channel flow with riblets. AIAA J. 2020, 58, 589–599. [Google Scholar] [CrossRef]
- Tubije, J.; Jin, Y.; Leonardi, S. Numerical investigation of effects of riblets on wind turbine performance. J. Phys. Conf. Ser. 2024, 2767, 022023. [Google Scholar] [CrossRef]
- Park, S.R.; Wallace, J.M. Flow alteration and drag reduction by riblets in a turbulent boundary layer. AIAA J. 1994, 32, 31–38. [Google Scholar] [CrossRef]
- Bechert, D.; Hage, W. Drag reduction with riblets in nature and engineering. In WIT Transactions on State-of-the-Art in Science and Engineering; WIT Press: Southampton, UK, 2006; Volume 4. [Google Scholar]
- Buttner, C.C.; Schulz, U. Shark skin inspired riblet structures as aerodynamically optimized high temperature coatings for blades of aeroengines. Smart Mater. Struct. 2011, 20, 094016. [Google Scholar] [CrossRef]
- Choi, K.S. Near-wall structure of a turbulent boundary layer with riblets. J. Fluid Mech. 1989, 208, 417–458. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bruse, M.; Hage, W.v.; Van der Hoeven, J.T.; Hoppe, G. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- Dean, B.; Bhushan, B. Shark-skin surfaces for fluid-drag reduction in turbulent flow: A review. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 4775–4806. [Google Scholar] [CrossRef]
- Walsh, M.J. Riblets as a viscous drag reduction technique. AIAA J. 1983, 21, 485–486. [Google Scholar] [CrossRef]
- Garcia-Mayoral, R.; Jiménez, J. Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 2011, 678, 317–347. [Google Scholar] [CrossRef]
- Lee, S.J.; Choi, Y.S. Decrement of spanwise vortices by a drag-reducing riblet surface. J. Turbul. 2008, 9, N23. [Google Scholar] [CrossRef]
- Walsh, M. Turbulent Boundary Layer Drag Reduction Using Riblets. In Proceedings of the 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982; p. 169. [Google Scholar]
- Lee, S.J.; Lee, S.H. Flow field analysis of a turbulent boundary layer over a riblet surface. Exp. Fluids 2001, 30, 153–166. [Google Scholar] [CrossRef]
- Wang, J.j.; Lan, S.l.; Chen, G. Experimental study on the turbulent boundary layer flow over riblets surface. Fluid Dyn. Res. 2000, 27, 217–229. [Google Scholar] [CrossRef]
- Robinson, S.K. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Goldstein, D.; Handler, R.; Sirovich, L. Direct numerical simulation of turbulent flow over a modeled riblet covered surface. J. Fluid Mech. 1995, 302, 333–376. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 1993, 255, 503–539. [Google Scholar] [CrossRef]
- El-Samni, O.; Chun, H.; Yoon, H. Drag reduction of turbulent flow over thin rectangular riblets. Int. J. Eng. Sci. 2007, 45, 436–454. [Google Scholar] [CrossRef]
- Choi, K.S. European drag-reduction research—Recent developments and current status. Fluid Dyn. Res. 2000, 26, 325. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kasagi, N. Turbulent drag reduction mechanism above a riblet surface. AIAA J. 1994, 32, 1781–1790. [Google Scholar] [CrossRef]
- Hou, J.; Hokmabad, B.V.; Ghaemi, S. Three-dimensional measurement of turbulent flow over a riblet surface. Exp. Therm. Fluid Sci. 2017, 85, 229–239. [Google Scholar] [CrossRef]
- Guangyao, C.; Chong, P.; Di, W.; Qingqing, Y.; Jinjun, W. Effect of drag reducing riblet surface on coherent structure in turbulent boundary layer. Chin. J. Aeronaut. 2019, 32, 2433–2442. [Google Scholar]
- Li, W.; Peng, S.; Xi, H.; Schröder, W. Experimental investigation on the degradation of turbulent friction drag reduction over semi-circular riblets. Exp. Fluids 2022, 63, 190. [Google Scholar] [CrossRef]
- Bechert, D.; Bartenwerfer, M. The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 1989, 206, 105–129. [Google Scholar] [CrossRef]
- Luchini, P.; Manzo, F.; Pozzi, A. Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 1991, 228, 87–109. [Google Scholar] [CrossRef]
- Wang, H.; Fan, Y.; Yan, Z.; Li, W. Direct numerical simulations of turbulent flow over the converging and diverging riblets. Phys. Fluids 2023, 35, 075121. [Google Scholar]
- Koeltzsch, K.; Dinkelacker, A.; Grundmann, R. Flow over convergent and divergent wall riblets. Exp. Fluids 2002, 33, 346–350. [Google Scholar] [CrossRef]
- Xu, F.; Zhong, S.; Zhang, S. Statistical analysis of vortical structures in turbulent boundary layer over directional grooved surface pattern with spanwise heterogeneity. Phys. Fluids 2019, 31, 085110. [Google Scholar] [CrossRef]
- Xu, F.; Zhong, S.; Zhang, S. Experimental study on secondary flow in turbulent boundary layer over spanwise heterogeneous microgrooves. Phys. Fluids 2020, 32, 035109. [Google Scholar] [CrossRef]
- Bai, H.; Gong, J.; Lu, Z. Energetic structures in the turbulent boundary layer over a spanwise-heterogeneous converging/diverging riblets wall. Phys. Fluids 2021, 33, 075113. [Google Scholar] [CrossRef]
- Guo, T.; Fang, J.; Zhong, S.; Moulinec, C. Energy-based drag decomposition analyses for a turbulent channel flow developing over convergent–divergent riblets. Phys. Fluids 2022, 34, 025115. [Google Scholar] [CrossRef]
- Martin, S.; Bhushan, B. Modeling and optimization of shark-inspired riblet geometries for low drag applications. J. Colloid Interface Sci. 2016, 474, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.; Tuan, T.C. Secondary flow induced by riblets. J. Fluid Mech. 1998, 363, 115–151. [Google Scholar] [CrossRef]
- Endrikat, S.; Modesti, D.; MacDonald, M.; García-Mayoral, R.; Hutchins, N.; Chung, D. Direct numerical simulations of turbulent flow over various riblet shapes in minimal-span channels. Flow Turbul. Combust. 2021, 107, 1–29. [Google Scholar] [CrossRef]
- Endrikat, S.; Modesti, D.; García-Mayoral, R.; Hutchins, N.; Chung, D. Influence of riblet shapes on the occurrence of Kelvin–Helmholtz rollers. J. Fluid Mech. 2021, 913, A37. [Google Scholar] [CrossRef]
- Endrikat, S.; Modesti, D.; Garcia-Mayoral, R.; Hutchins, N.; Chung, D. Only certain riblets experience the Kelvin-Helmholtz instability. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, Virtual, 22–24 November 2020; p. G07-008. [Google Scholar]
- Endrikat, S.; Newton, R.; Modesti, D.; García-Mayoral, R.; Hutchins, N.; Chung, D. Reorganisation of turbulence by large and spanwise-varying riblets. J. Fluid Mech. 2022, 952, A27. [Google Scholar] [CrossRef]
- Wong, J.; Camobreco, C.; García-Mayoral, R.; Hutchins, N.; Chung, D. A viscous vortex model for predicting the drag reduction of riblet surfaces. J. Fluid Mech. 2024, 978, A18. [Google Scholar] [CrossRef]
- Wilkinson, S.; Anders, J.; Lazos, B.; Bushnell, D. Turbulent drag reduction research at NASA langley: Progress and plans. Int. J. Heat Fluid Flow 1988, 9, 266–277. [Google Scholar] [CrossRef]
- Bhamitipadi Suresh, D.; Aju, E.J.; Pham, D.T.; Jin, Y. On the incipient sediment suspension downstream of three-dimensional wall-mounted obstacles. Phys. Fluids 2021, 33, 083307. [Google Scholar] [CrossRef]
- Aju, E.J.; Gong, P.; Pham, D.T.; Kaushik, K.; Jin, Y. On the wake dynamics and thrust generation of a foil flapping over solid and sedimentary beds. Exp. Fluids 2022, 63, 32. [Google Scholar] [CrossRef]
- Gatti, D.; von Deyn, L.; Forooghi, P.; Frohnapfel, B. Do riblets exhibit fully rough behaviour? Exp. Fluids 2020, 61, 81. [Google Scholar] [CrossRef]
- Chauhan, K.; Philip, J.; De Silva, C.M.; Hutchins, N.; Marusic, I. The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 2014, 742, 119–151. [Google Scholar] [CrossRef]
- de Silva, C.M.; Hutchins, N.; Marusic, I. Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 2016, 786, 309–331. [Google Scholar] [CrossRef]
- Wallace, J.M.; Eckelmann, H.; Brodkey, R.S. The wall region in turbulent shear flow. J. Fluid Mech. 1972, 54, 39–48. [Google Scholar] [CrossRef]

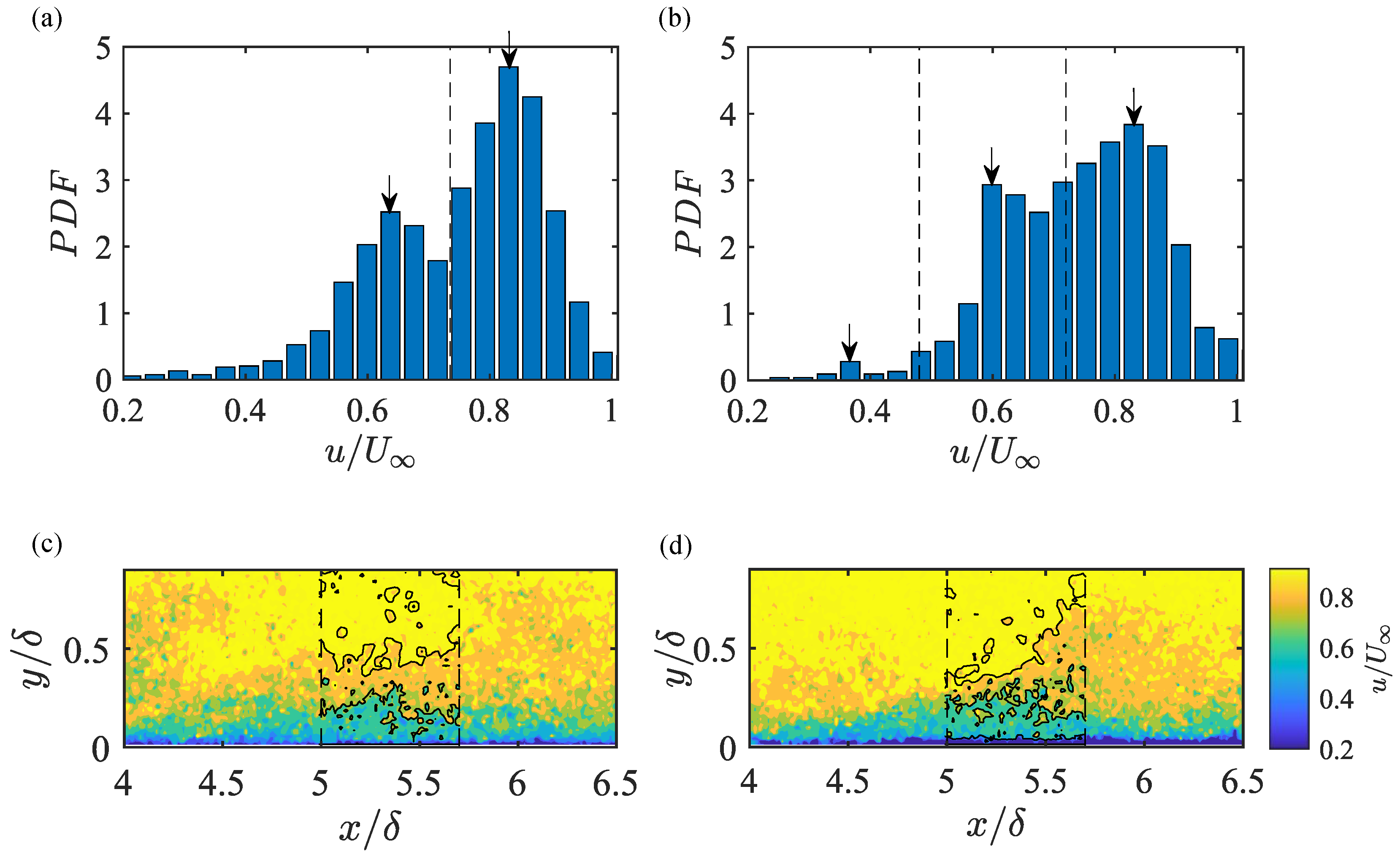
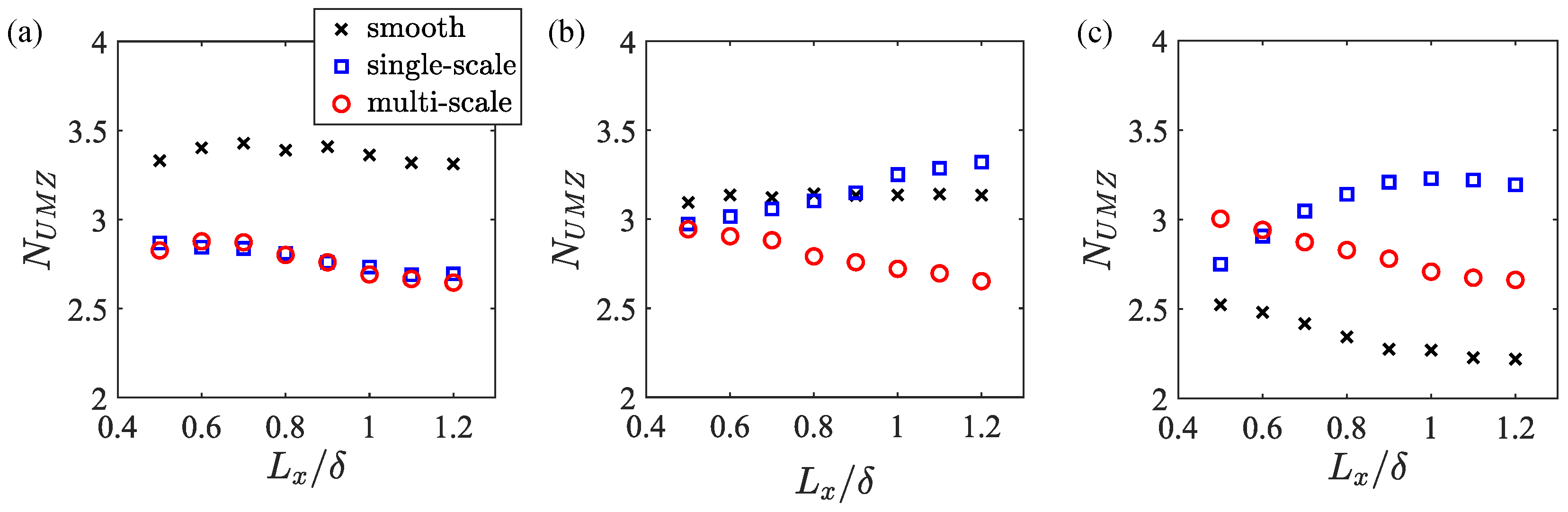
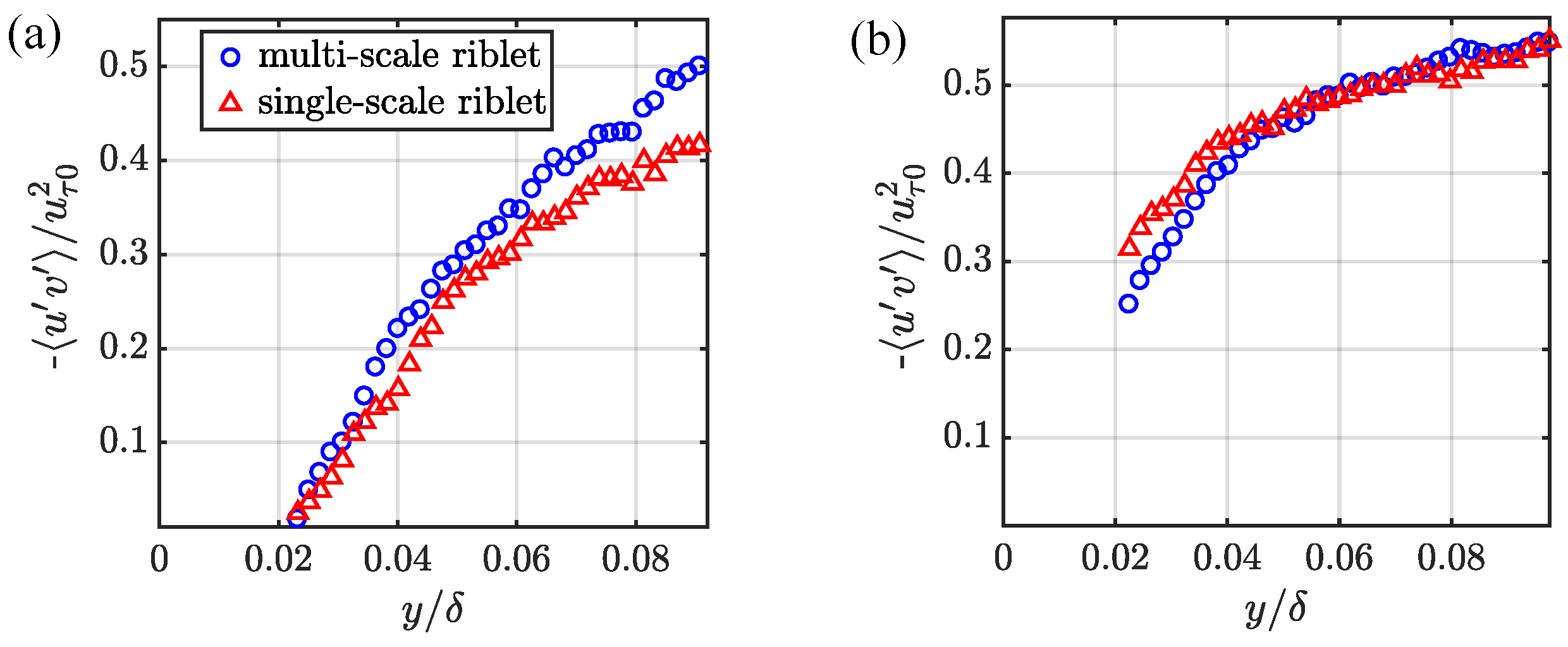
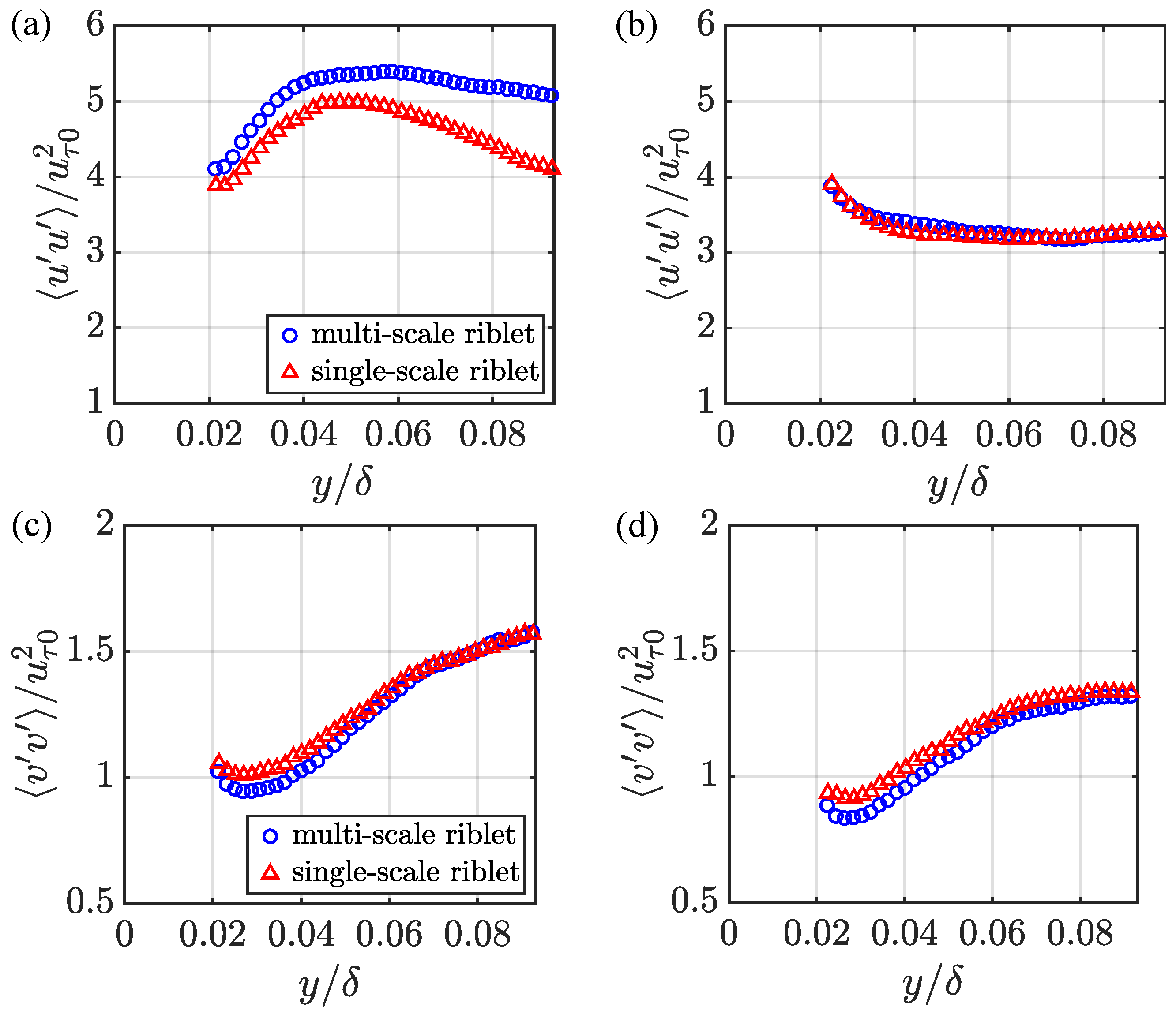

| (m s−1) | (mm) | (m s−1) | |||
|---|---|---|---|---|---|
| 0.20 | 32.40 | 0.0103 | 20.6 | 334 | 0.0053 |
| 0.26 | 31.90 | 0.0134 | 26.8 | 427 | 0.0053 |
| 0.36 | 30.35 | 0.0183 | 36.6 | 555 | 0.0052 |
| 0.44 | 30.76 | 0.0221 | 44.2 | 686 | 0.0051 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zani, M.R.; Maor, N.S.; Bhamitipadi Suresh, D.; Jin, Y. Turbulent Boundary Layer Control with Multi-Scale Riblet Design. Energies 2024, 17, 3827. https://doi.org/10.3390/en17153827
Zani MR, Maor NS, Bhamitipadi Suresh D, Jin Y. Turbulent Boundary Layer Control with Multi-Scale Riblet Design. Energies. 2024; 17(15):3827. https://doi.org/10.3390/en17153827
Chicago/Turabian StyleZani, Md. Rafsan, Nir Saar Maor, Dhanush Bhamitipadi Suresh, and Yaqing Jin. 2024. "Turbulent Boundary Layer Control with Multi-Scale Riblet Design" Energies 17, no. 15: 3827. https://doi.org/10.3390/en17153827
APA StyleZani, M. R., Maor, N. S., Bhamitipadi Suresh, D., & Jin, Y. (2024). Turbulent Boundary Layer Control with Multi-Scale Riblet Design. Energies, 17(15), 3827. https://doi.org/10.3390/en17153827







