Linear Active Disturbance Rejection Control for Flexible Excitation System of Pumped Storage Units
Abstract
:1. Introduction
2. Control Strategy for Flexible Excitation System of PSU Based on LADRC
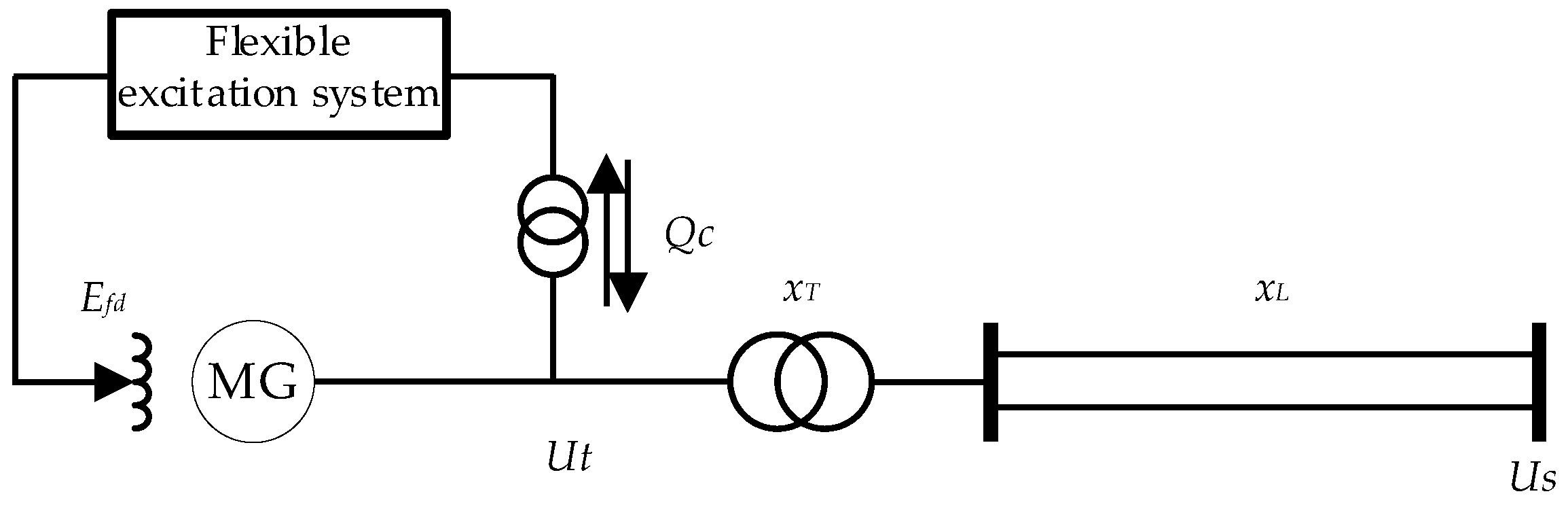
2.1. Structure of Single-Machine Infinite Bus System Based on Flexible Excitation System
2.2. Mathematical Model of Pumped Storage Unit Based on Flexible Excitation System
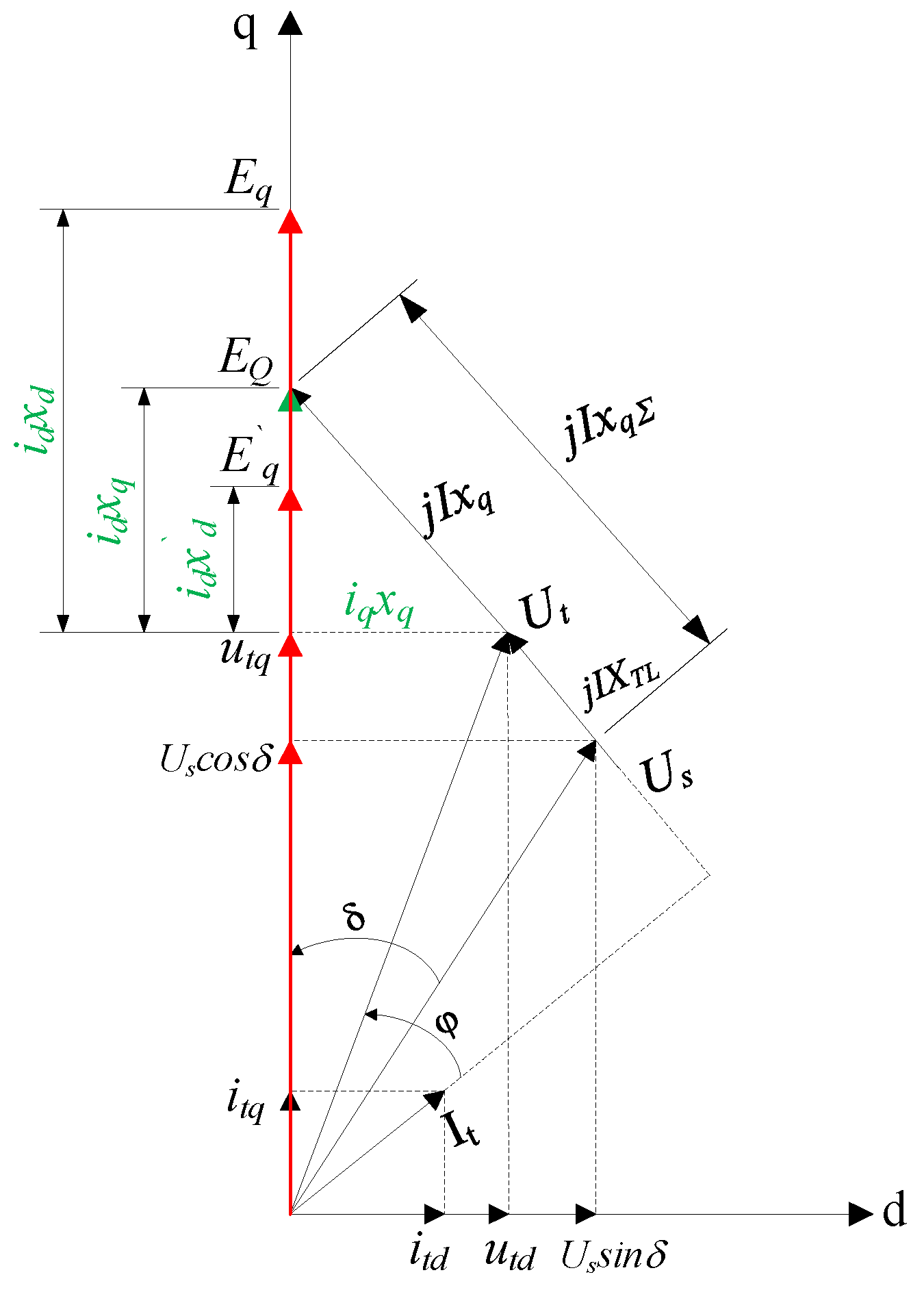
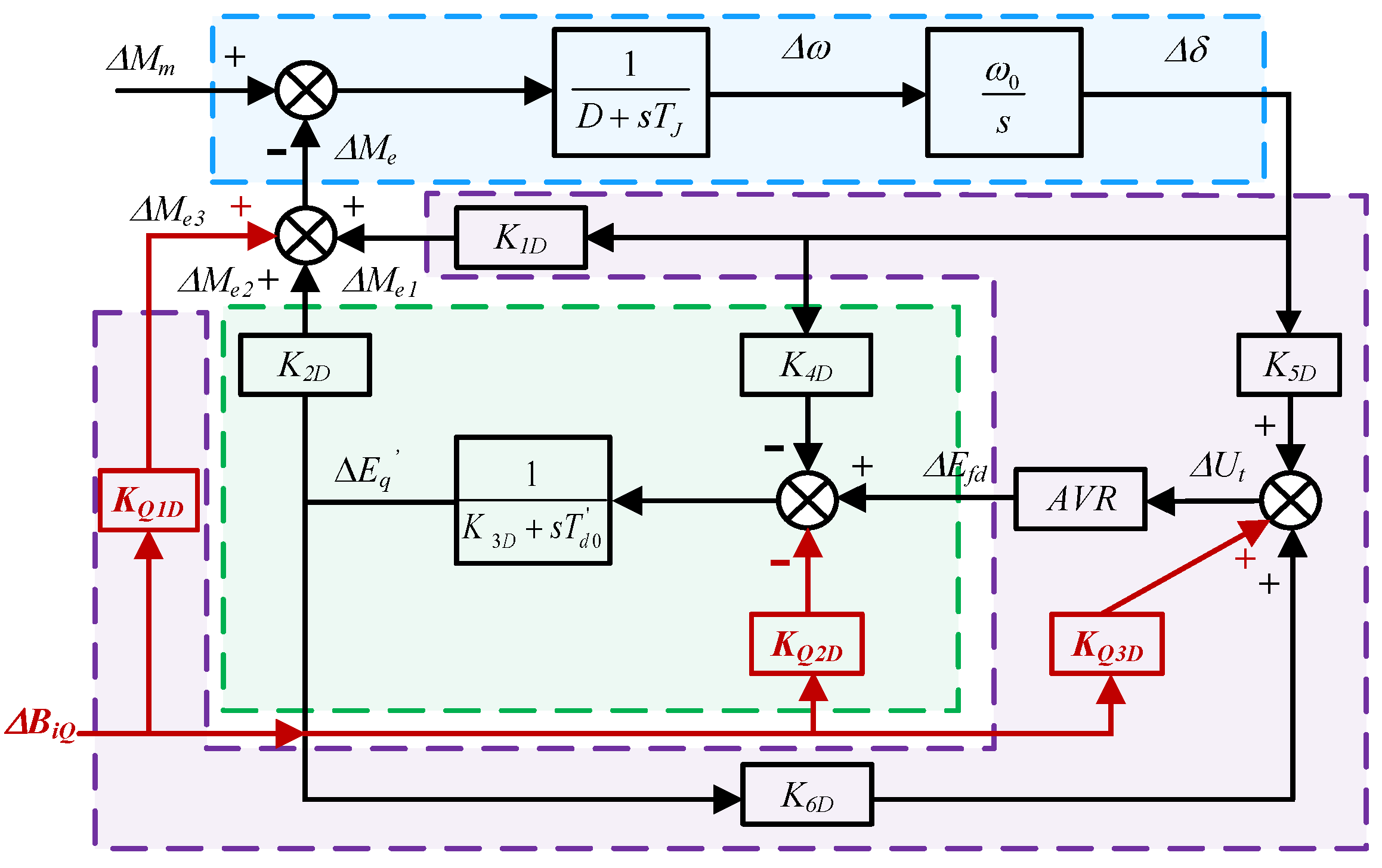
2.2.1. Mathematical Model of Generation/Motor
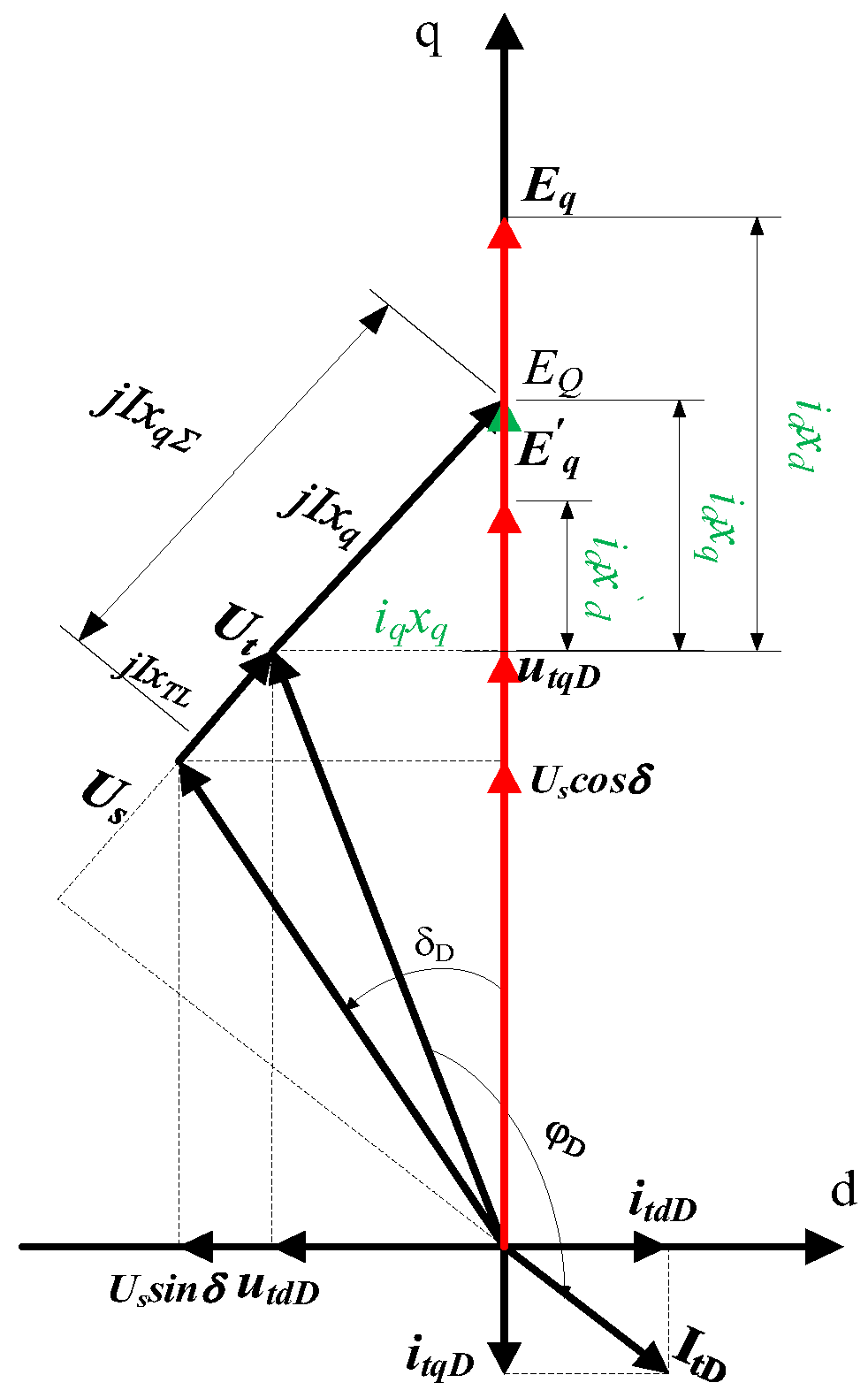
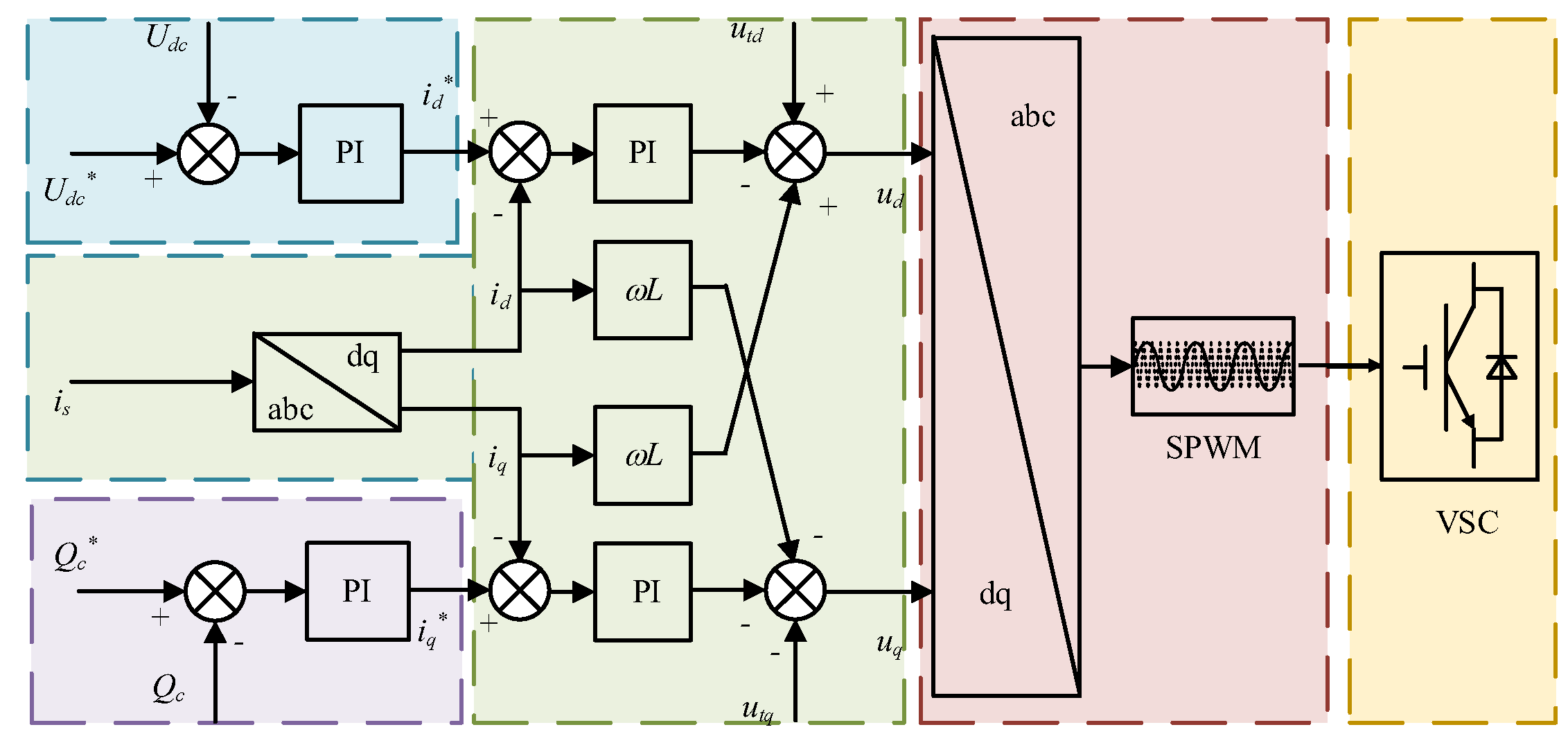
2.2.2. Mathematical Model of Flexible Excitation System
- (1)
- Generating conditions
- (2)
- Pumping conditions
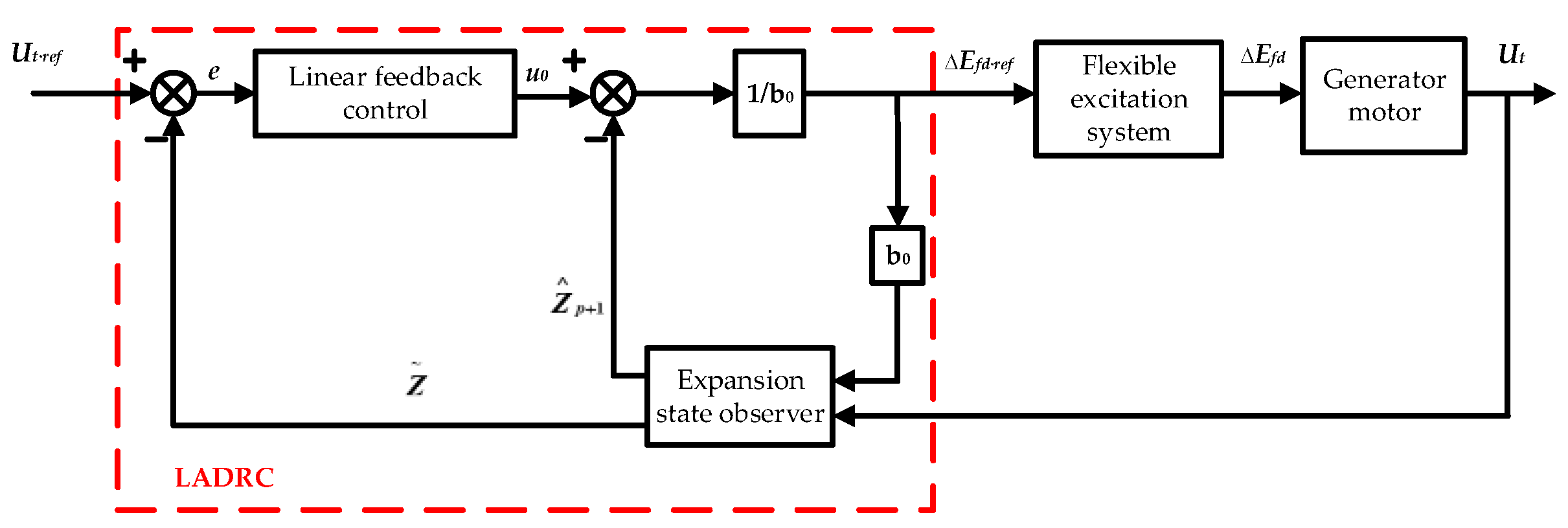
2.3. Principle of LADRC
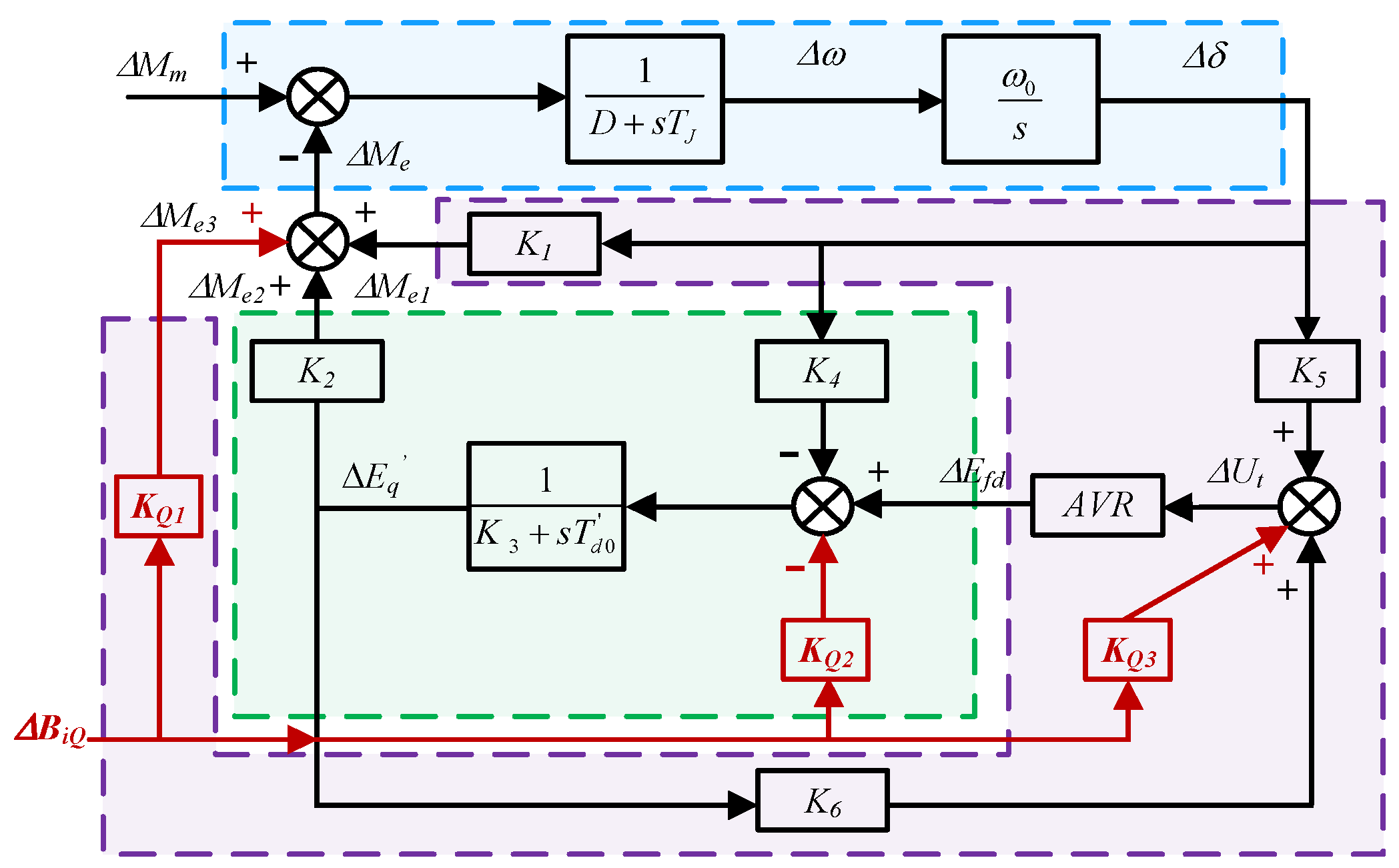
2.4. LADRC Scheme for Flexible Excitation System of PSU
3. LADRC Parameter Tuning Based on Tree Seed Optimizer Algorithm
3.1. Establishing System Performance Indicators
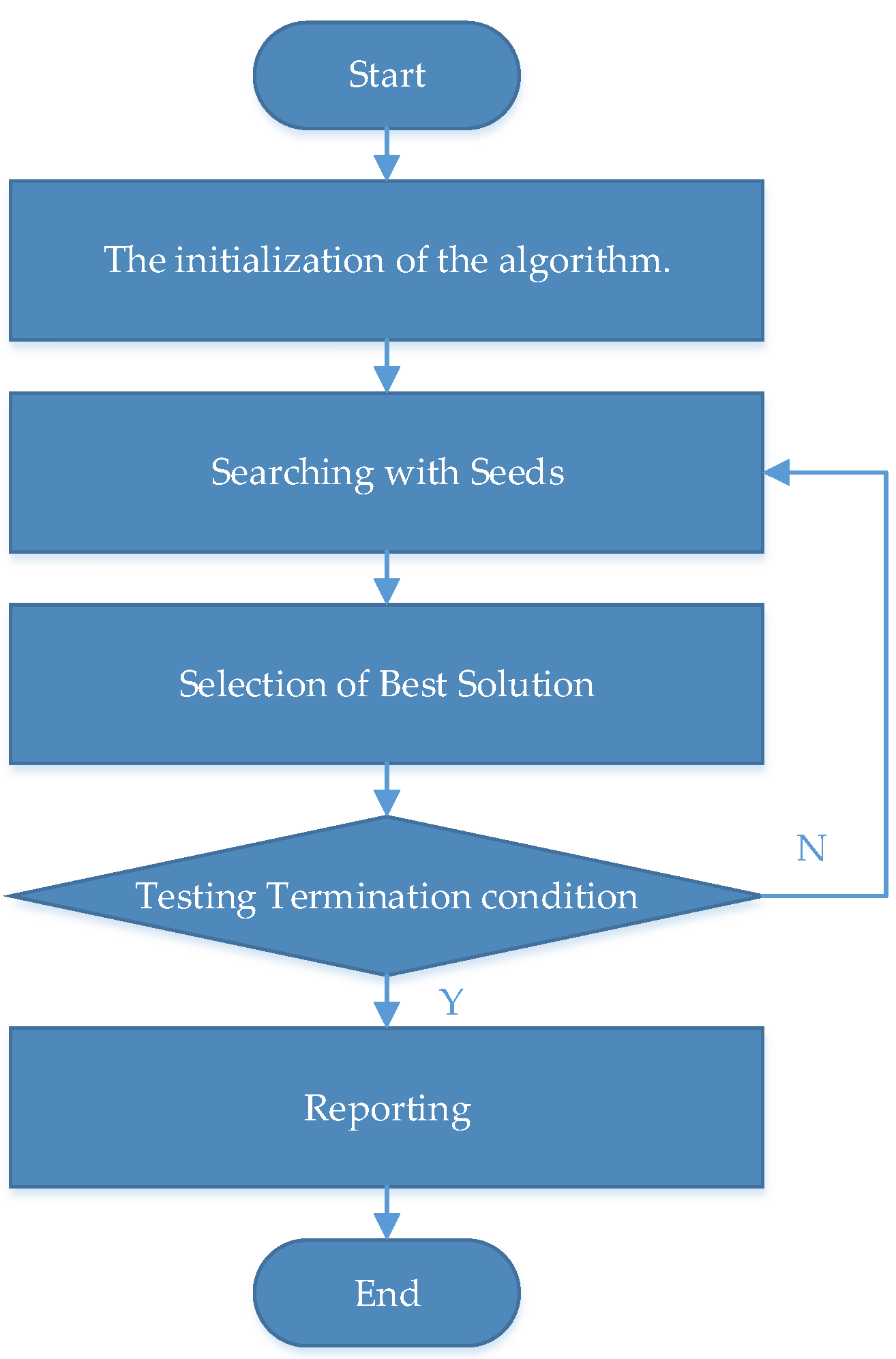
3.2. Solution Methods and Processes for TSO Algorithms
4. Simulation Verification
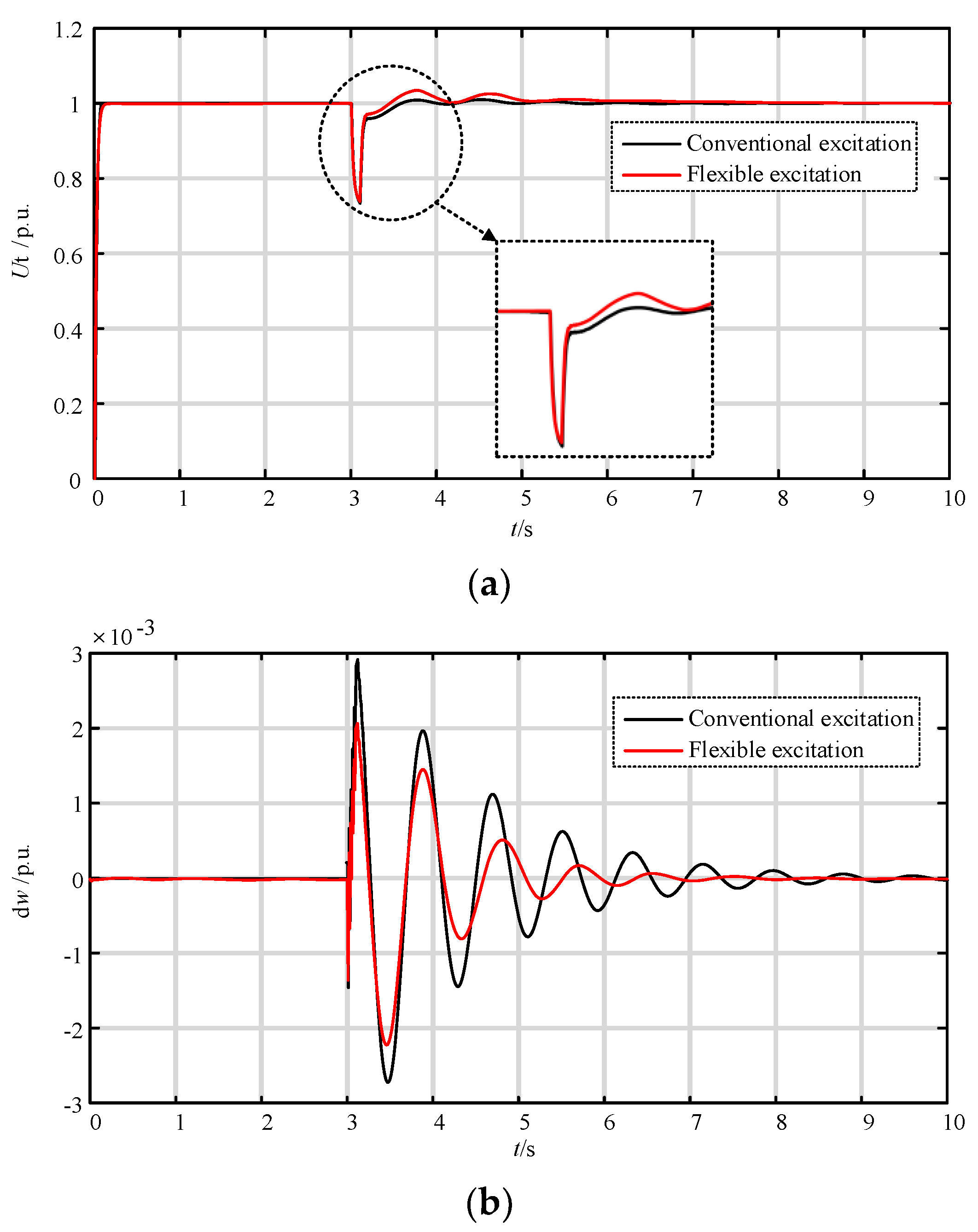
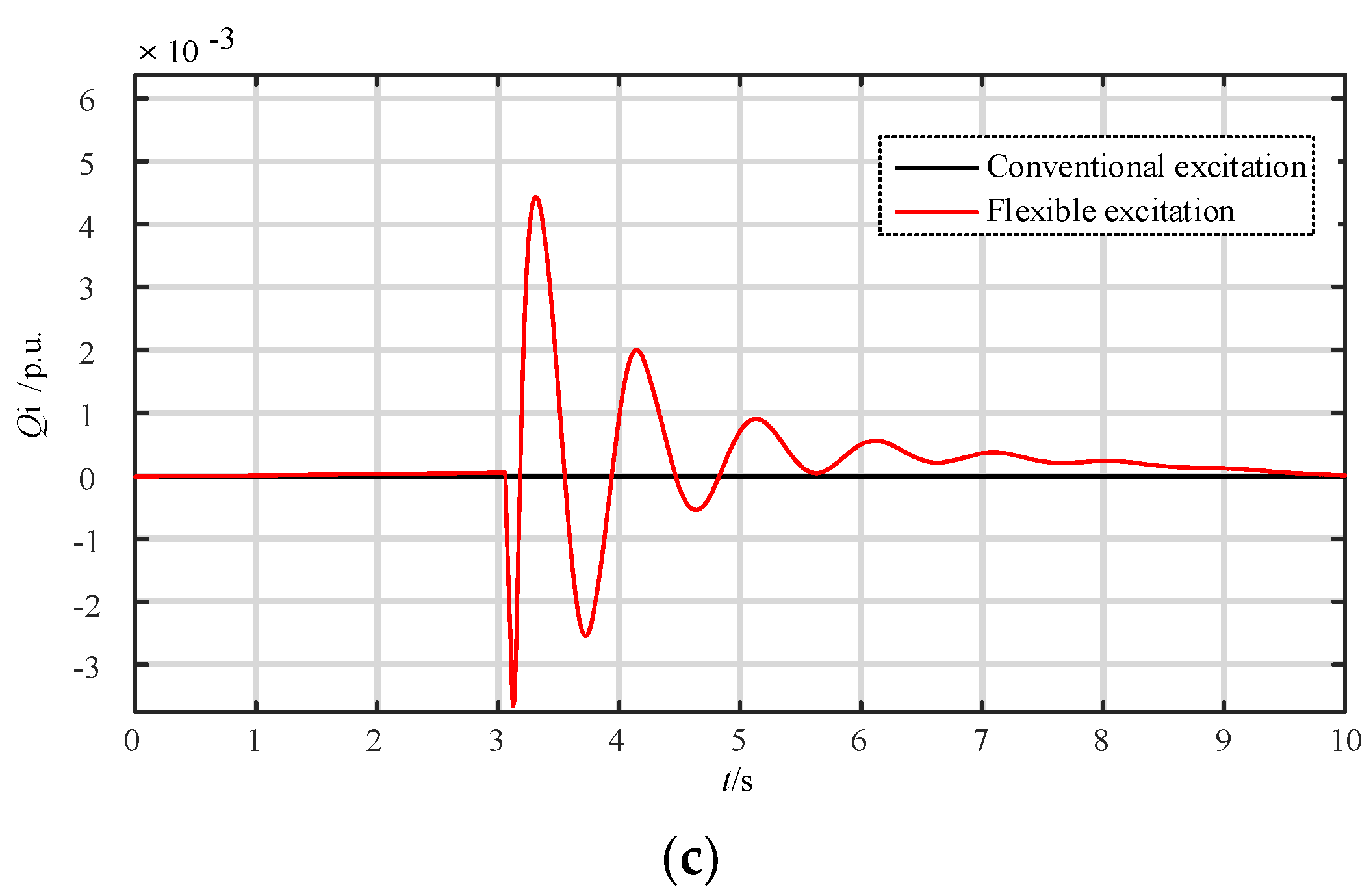
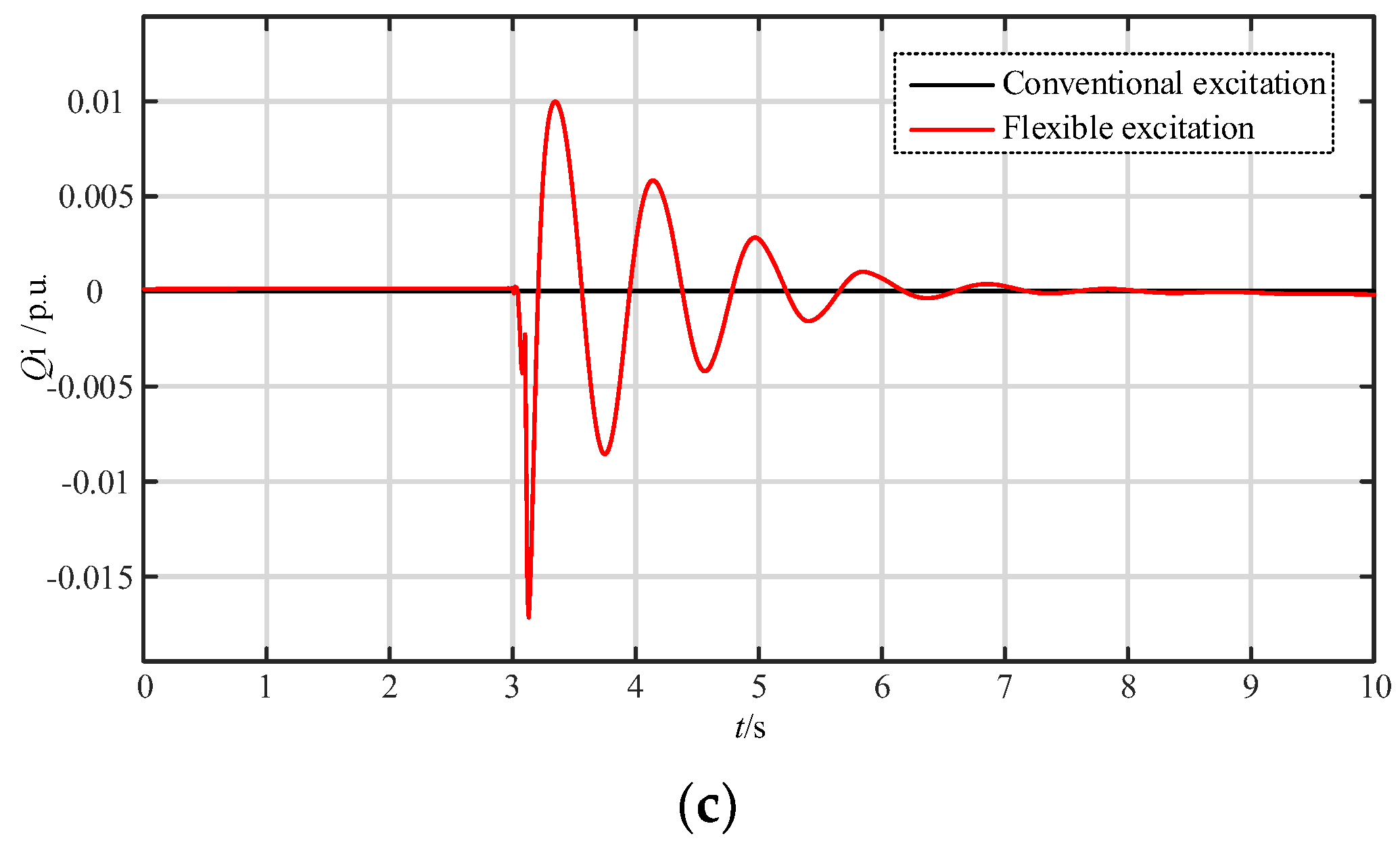
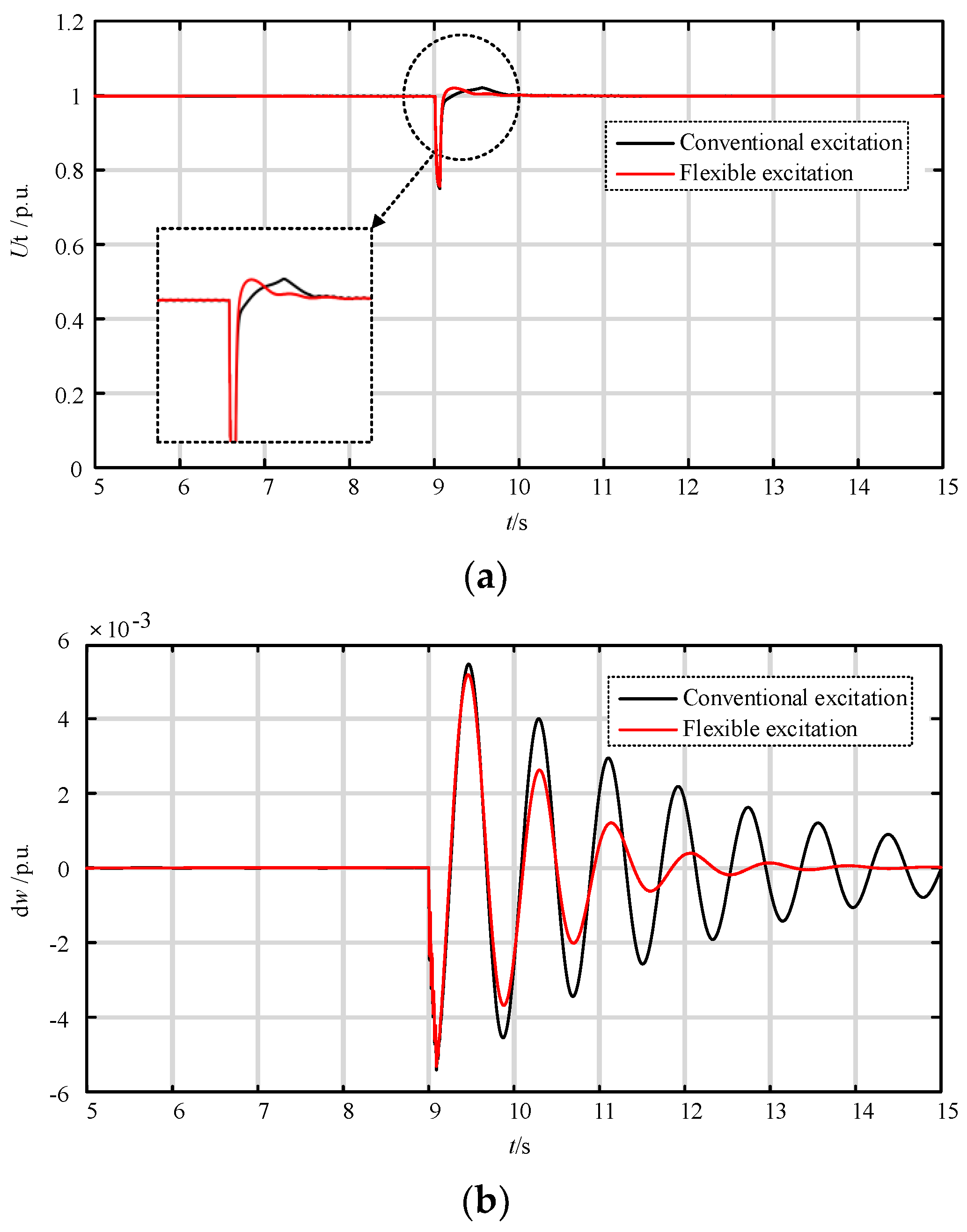
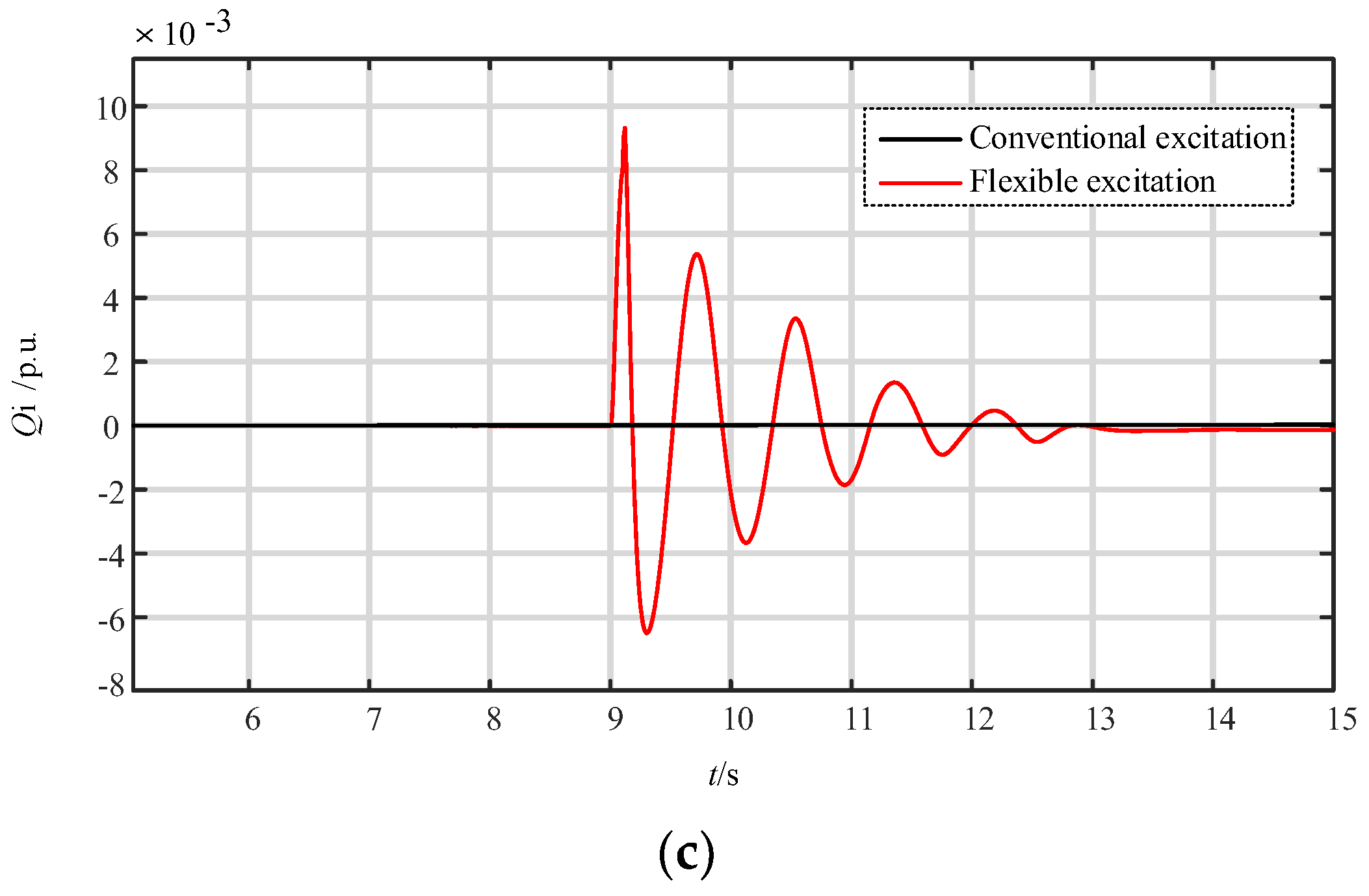
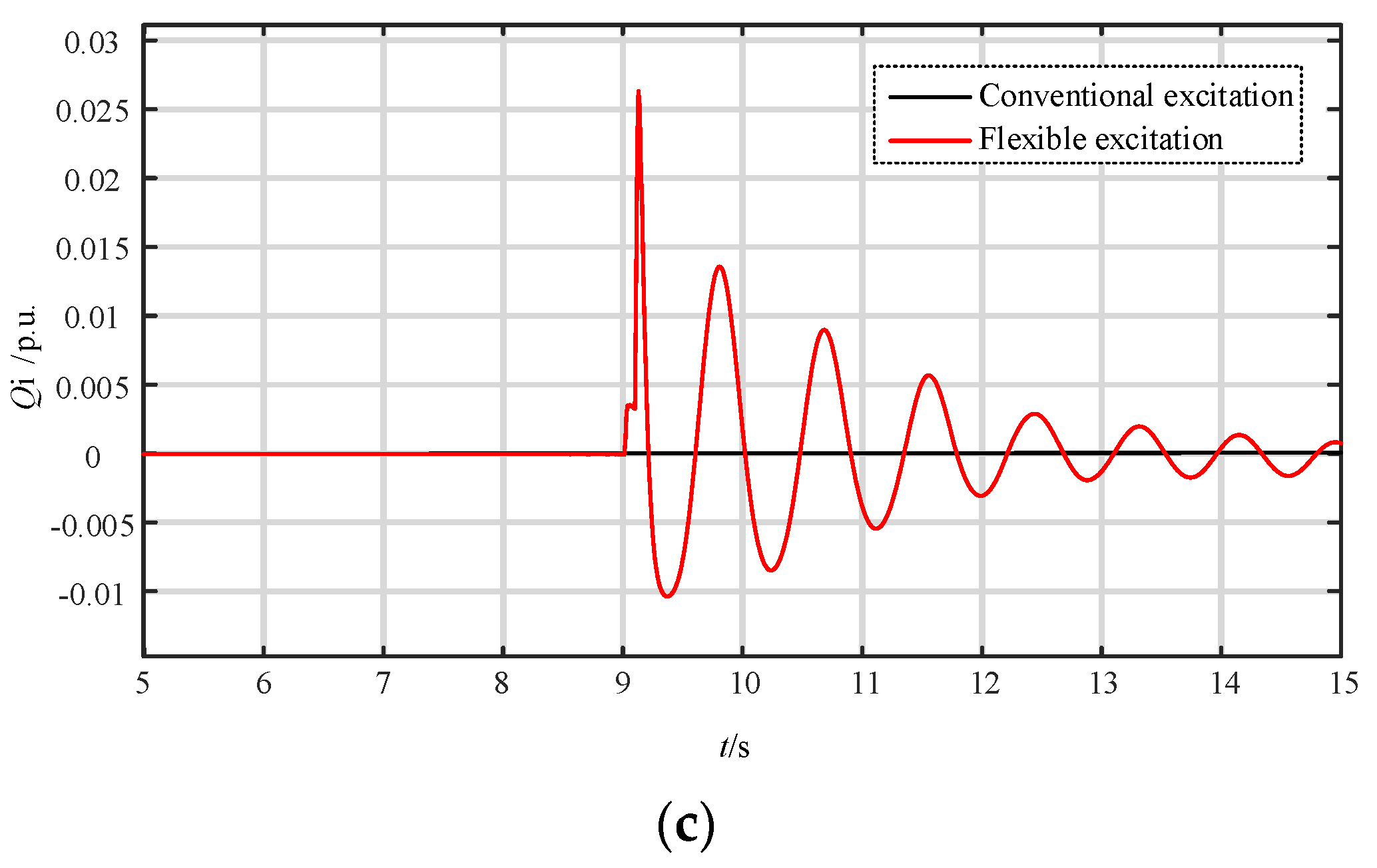
4.1. Simulation of Operating Characteristics of Flexible Excitation System
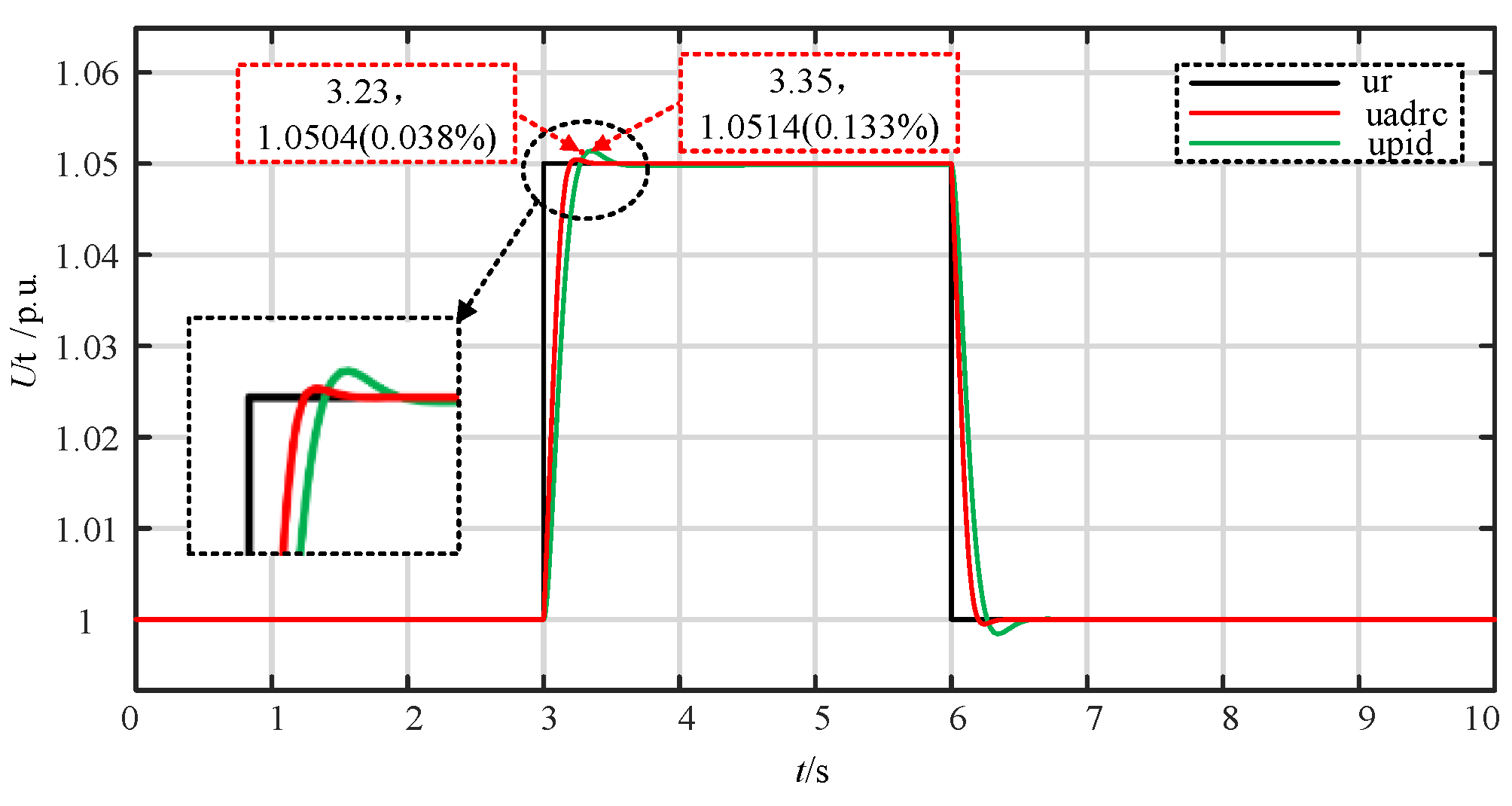
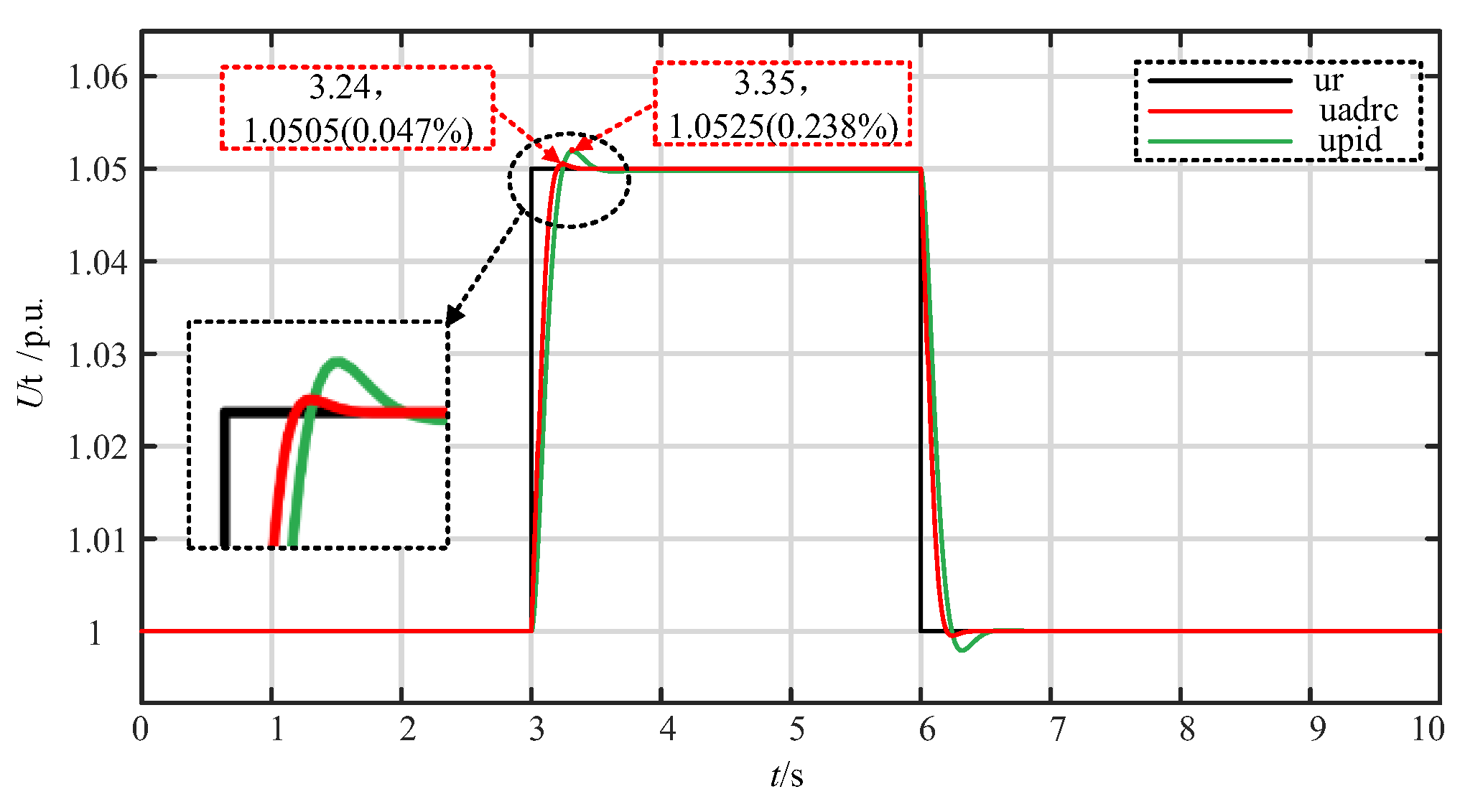
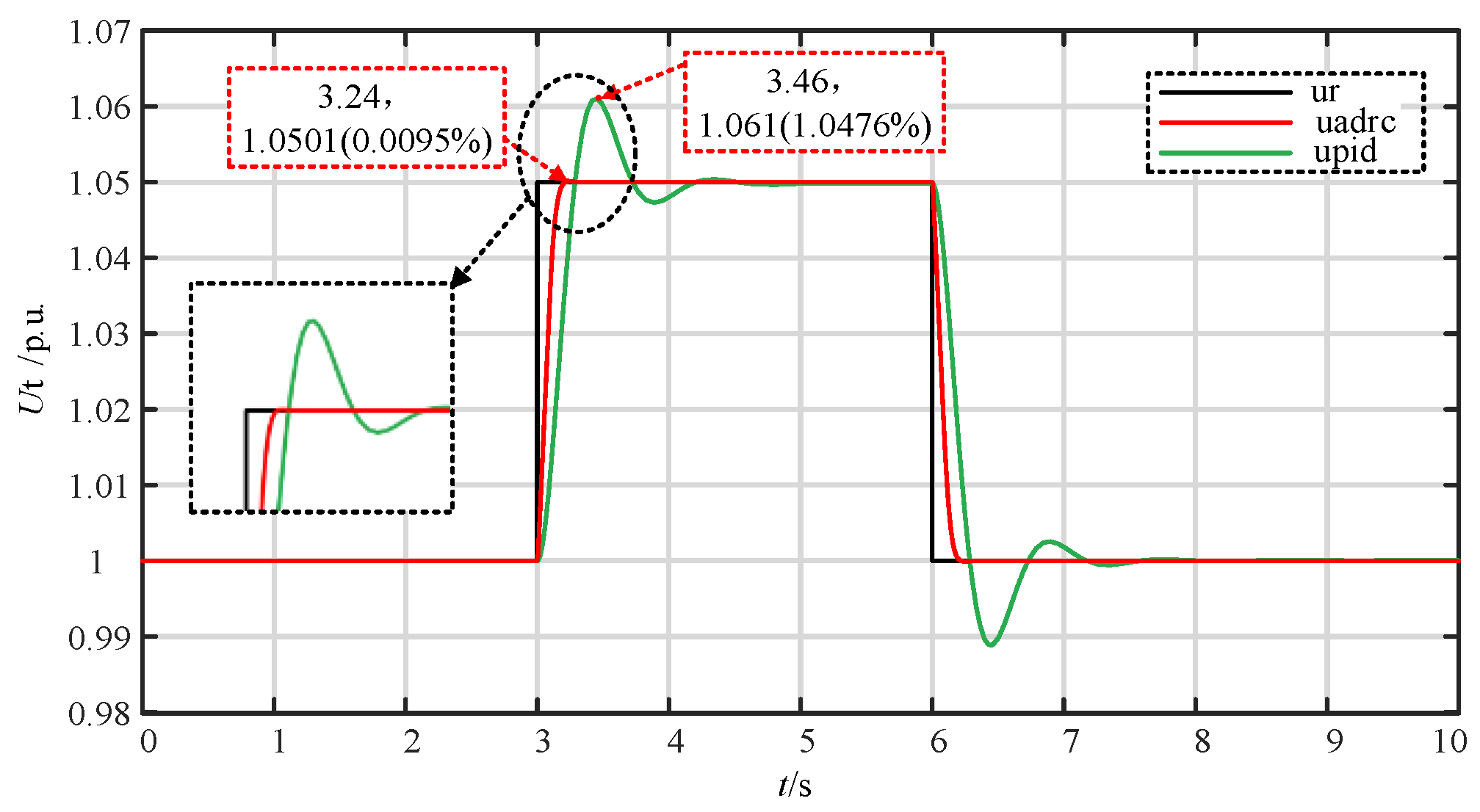
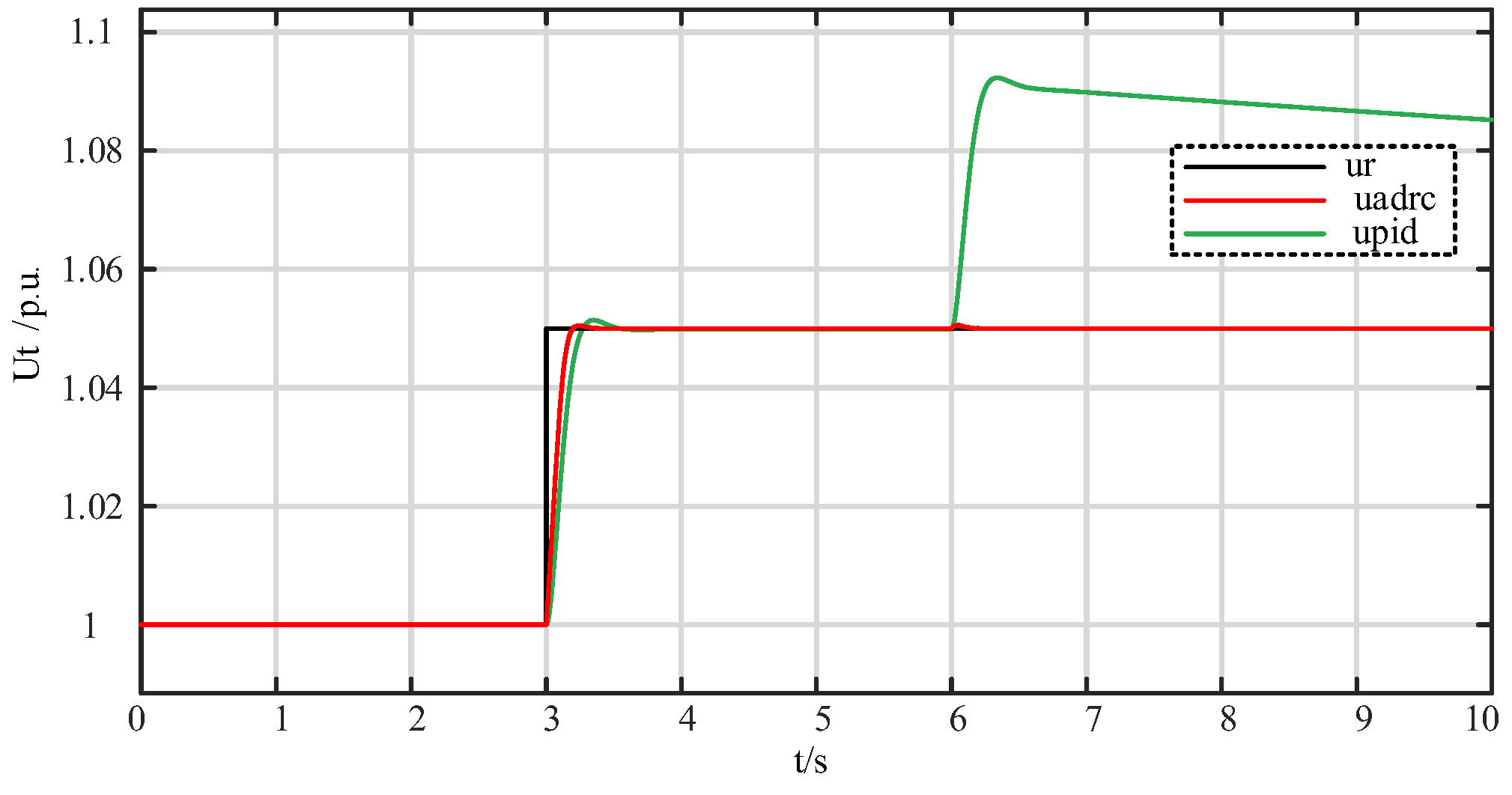
4.2. Performance Experiment of Linear Self-Disturbance Rejection Control System
- (1)
- Step response experiment
- (2)
- Robustness experiment
- (3)
- Anti interference experiment
5. Conclusions
- (1)
- After adopting the flexible excitation system based on fully controlled devices, compared with traditional conventional excitation systems based on thyristors, the voltage support capacity and oscillation suppression ability of PSU are significantly improved;
- (2)
- The flexible excitation system of pumped storage adopts the LADRC controller, which has better performance than the PID controller, can effectively alleviate the contradiction between response speed and overshoot, and has better robustness and anti-interference.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Compiled by State Grid Xinyuan Holdings Co., Ltd. Technology of Pumped Storage Units and Their Auxiliary Equipment; Electric Power Press: Beijing, China, 2019. [Google Scholar]
- National Energy Administration of China. Medium and Long Term Development Plan for Pumped Storage Energy (2021–2035) [EB/OL]. 2021. Available online: https://www.nea.gov.cn/2021-09/09/c_1310177087.htm (accessed on 21 June 2024).
- Lu, J.; Mao, C.; Fan, S.; Wang, D. Microcomputer-Based Excitation Control for Synchronous Generators; Electric Power Press: Beijing, China, 2005. [Google Scholar]
- He, L.; Mao, C.; Lu, J. Novel Excitation System Using High Power Electronics Full Controlled Devices Rectifier. High Volt. Eng. 2009, 35, 1711–1717. [Google Scholar]
- Wu, J.; He, L.; Mao, C.; Lu, J.; Wang, D. Novel excitation system for synchronous generators. J. Electr. Power Sci. Technol. 2009, 24, 12–18. [Google Scholar]
- He, J.; Mao, C.; Lu, J.; Wang, D.; Yang, J. Control Strategy of Voltage Source Converter Excitation System Based on Full Controlled Device. Trans. China Electrotech. Soc. 2012, 27, 240–247+263. [Google Scholar]
- Peng, Y.; Zhang, J.; Mao, C.; Xiong, H.; Zhang, T.; Wang, D. A Coordinated Optimal Strategy for Voltage and Reactive Power Control with Adaptive Amplitude Limiter Based on Flexible Excitation System. Energies 2021, 14, 5212. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, J.; Wu, L. Novel Flexible Excitation System Based on Multilevel Topology Technology. Electr. Power 2019, 52, 100–106. [Google Scholar]
- Mao, C.; He, J.; Wang, D.; Lu, J. Multivariable Feedback Linearization Scheme for New Excitation Systems Based on Full Controlled Devices. Proc. CSEE 2013, 33, 53–60+10. [Google Scholar]
- Wu, K.; Zhang, T.; Zhang, J.; Yu, M.; Mao, C.; Xion, H.; Wang, D. Optimum design method of flexible excitation system for improving damping of low frequency oscillation. Electr. Mach. Control. 2020, 24, 105–114. [Google Scholar]
- Zhang, T.; Cheng, L.; He, S.; Yu, M.; Mao, C.; Wang, D.; Zhang, J.; Han, B.; Tao, Z. Optimal Design Method of Flexible Excitation System for Improving Power System Stability. IEEE Trans. Ind. Appl. 2021, 57, 2120–2128. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Wang, B.; Zhuo, G.; Hua, W.; Xiong, H. Research on the improvement of transient stability characteristics of the receiving end power grid by flexible excitation. Zhejiang Electr. Power 2022, 41, 72–77. [Google Scholar]
- Zhang, T.; Mao, C.; Zhang, J.; Tian, J.; Yu, M.; Wu, K.; Xiong, H.; Wu, L.; Yu, H. Design and Field Application of Flexible Excitation System Damping Controllers. IEEE Trans. Ind. Electron. 2021, 68, 949–959. [Google Scholar] [CrossRef]
- Han, J. Active Disturbance Rejection Controller and Its Application. Control. Decis. 1998, 13, 19–23. [Google Scholar]
- Gao, Z. Active disturbance rejection control: A parallel shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2399–2405. [Google Scholar]
- Cheng, L. Optimization Control Strategy for Excitation System of Energy Storage Type Fully Controlled Device. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2023. [Google Scholar]
- Yu, M. Analysis of Operating Characteristics of Flexible Excitation System. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Zhang, T. Damping Control Method and Field Application of Flexible Excitation System. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2023. [Google Scholar]
- Wu, L.; Mou, W.; Shi, Y.; Han, B. Research and Application of PSS for Pump Working Condition of Large Pumping and Storage Power Station Unit. Hydroelectr. Pumped Storage 2022, 8, 40–44. [Google Scholar]
- Liu, Q. Power System Stability and Generator Excitation Control; Electric Power Press: Beijing, China, 2007. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Zheng, Q.; Gao, L.D.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Chen, Z.; Sun, M.; Yang, R. Onthe stability of linear active disturbance rejection control. Acta Autom. Sin. 2013, 39, 574–580. [Google Scholar] [CrossRef]
- Tian, G.; Gao, Z. Frequency response analysis of active disturbance rejection based control system. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1595–1599. [Google Scholar]
- Köse, E. Optimal Control of AVR System With Tree Seed Algorithm-Based PID Controller. IEEE Access 2020, 8, 89457–89467. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]




| Step | Specific Algorithm |
|---|---|
| Step 1. The initialization of the algorithm. | Set the number of population size (N). |
| Set the ST parameter for the method. | |
| Set the dimensionality of the problem (D). | |
| Decide the termination condition | |
| Generate Nrandom tree location on the D-dimensional search space. | |
| Evaluate the tree location using objective function specified for the problem. | |
| Step 2. Searching with Seeds | FOR all trees Decide the number of seeds produced for this tree. FOR all seeds FOR all dimensions IF (rand < ST) Update the dimension ELSE Update the dimension END IF END FOR END FOR Select the best seed and compare it with the tree. If the seed location is better than tree location, the seed substitutes for this tree. END FOR |
| Step 3. Selection of Best Solution | Select the best solution of population. |
| If new best solution is better than the previous best solution, new best solution | |
| substitutes for the previous best solution. | |
| SStep 4. Testing Termination condition | If termination condition is not met, go to Step 2. |
| Step 5. Reporting | Report the best solution. |
| Model | Parameter Name (Unit) | Parameter Value |
|---|---|---|
| Synchronous generator motor | Rated capacity SGN (MVA) | 334 |
| Rated voltage UGN (kV) | 15.75 | |
| Excitation winding time constant T′d0 (s) | 13.123 | |
| Inertia constant TJ (s) | 8.6 | |
| Polar logarithm p | 7 | |
| Rated excitation voltage UfN (V) | 330 | |
| Rated excitation current IFn (A) | 1600 | |
| Main transformer | Rated capacity STN (MVA) | 400 |
| Transformation ratio | 15.75/242 | |
| Excitation transformer | Rated capacity STEN (MVA) | 5 |
| Transformation ratio (kV) | 15.75/0.38 | |
| Flexible excitation | DC voltage (V) | 660 |
| Infinite system | Rated voltage USN (kV) | 220 |
| Parameter Name | Parameter Values | Line Length |
|---|---|---|
| Resistance per unit length r0 (Ω/km) | 0.01273 | 300 km |
| Inductance per unit length l0 (mH/km) | 0.9337 | |
| Inductance per unit length c0 (μF/km) | 12.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Zheng, J.; Qin, J.; Wang, D.; Li, J.; Cheng, X.; Jia, S. Linear Active Disturbance Rejection Control for Flexible Excitation System of Pumped Storage Units. Energies 2024, 17, 3838. https://doi.org/10.3390/en17153838
Zhao B, Zheng J, Qin J, Wang D, Li J, Cheng X, Jia S. Linear Active Disturbance Rejection Control for Flexible Excitation System of Pumped Storage Units. Energies. 2024; 17(15):3838. https://doi.org/10.3390/en17153838
Chicago/Turabian StyleZhao, Bo, Jiandong Zheng, Jun Qin, Dan Wang, Jiayao Li, Xinyu Cheng, and Sisi Jia. 2024. "Linear Active Disturbance Rejection Control for Flexible Excitation System of Pumped Storage Units" Energies 17, no. 15: 3838. https://doi.org/10.3390/en17153838
APA StyleZhao, B., Zheng, J., Qin, J., Wang, D., Li, J., Cheng, X., & Jia, S. (2024). Linear Active Disturbance Rejection Control for Flexible Excitation System of Pumped Storage Units. Energies, 17(15), 3838. https://doi.org/10.3390/en17153838






