Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines
Abstract
1. Introduction
- The reliability and availability of the studied wind turbine will be improved, thereby an increased useful lifetime can be ensured. This advantage was confirmed through the various simulation validation tests and the assessment of the obtained detection indices on actuators and fault sensors.
- The risks from the internal and external operation tasks are minimized. This is due to the capabilities of the proposed fault diagnosis approach to characterize, evaluate, and analyze faults to prevent and reduce the risk of faults in time. Indeed, the obtained results confirm clearly the effectiveness of the proposed process based on the evaluation of the detection time, sensitivity, and detection thresholds.
- The implementation simplicity of the proposed approach in real-time due to its simple structure.
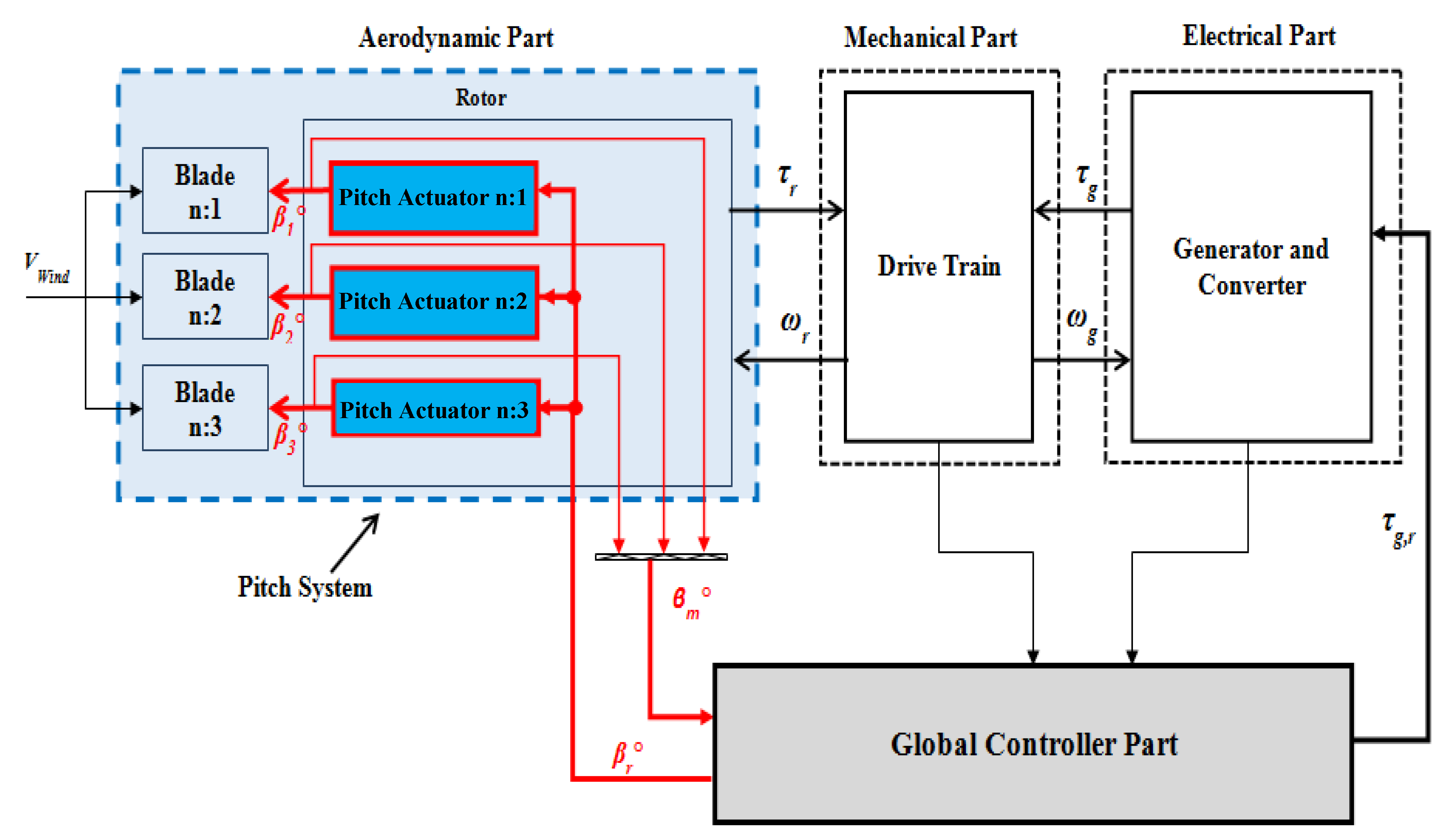
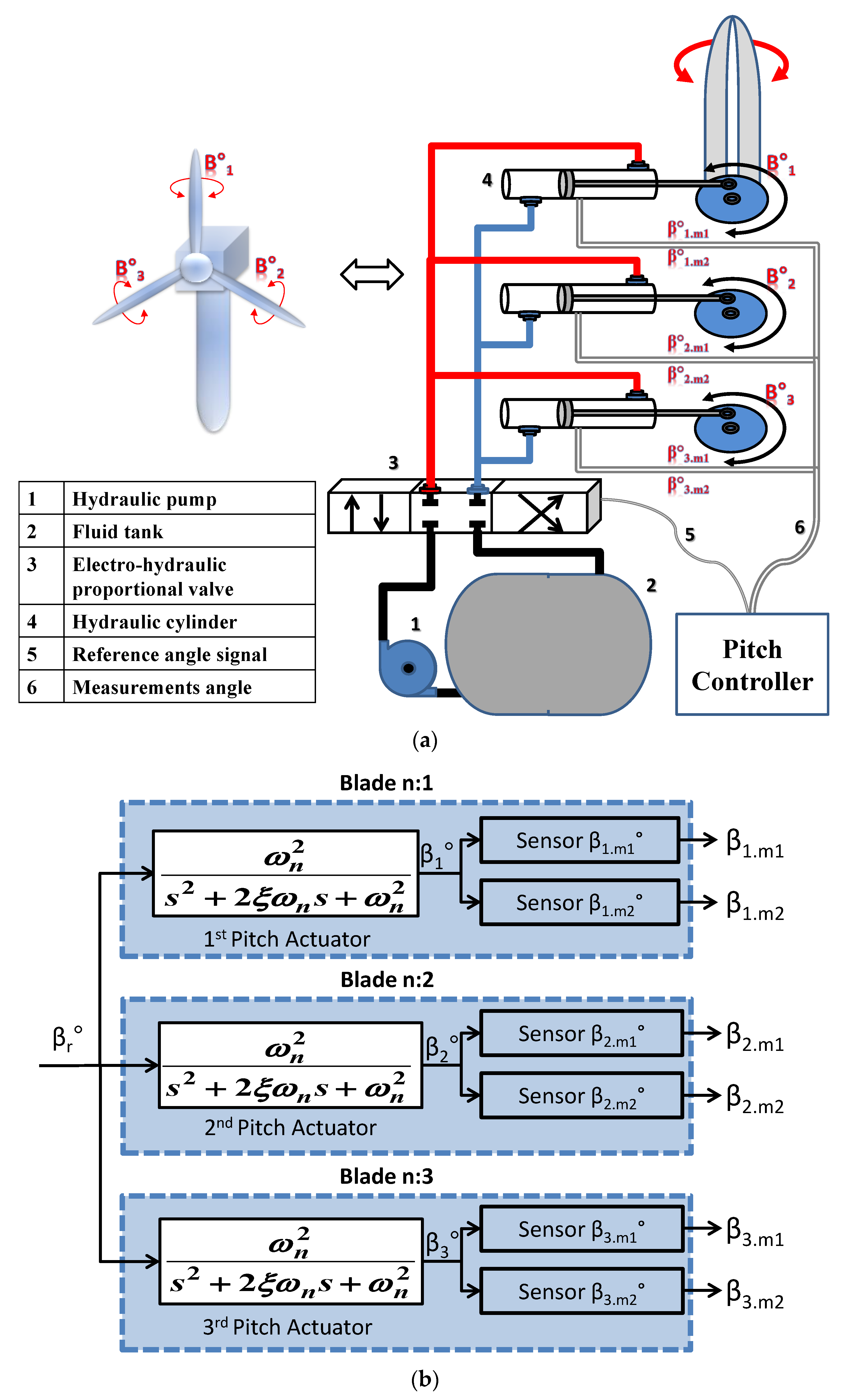
2. Pitch System Model
- -
- When the hydraulic head increases, the bulk modulus (resistance to compression) of the fluid also increases. This can lead to higher internal damping within the system.
- -
- At a higher hydraulic head, the pump might work harder, potentially leading to an increased heat generation in the fluid, whereas it is obvious that thinner fluids with lower viscosity tend to damp less than thicker, higher-viscosity fluids.
- -
- The hydraulic head provokes pressure fluctuations that can affect the pressure pulsations within the system, where pulsations can arise from pump imperfections or rapid load changes. The pressure difference caused by the hydraulic head itself can be added to these pulsations, potentially making them worse.
- -
- At a decreased damping factor, the piston will vibrate more and take longer to settle after hydraulic pressure change.
- -
- At an increased frequency, the piston moves more rapidly, causing pressure fluctuations and increased pulsation frequency due to air compression and expansion. This can lead to erratic movement and reduced control accuracy.
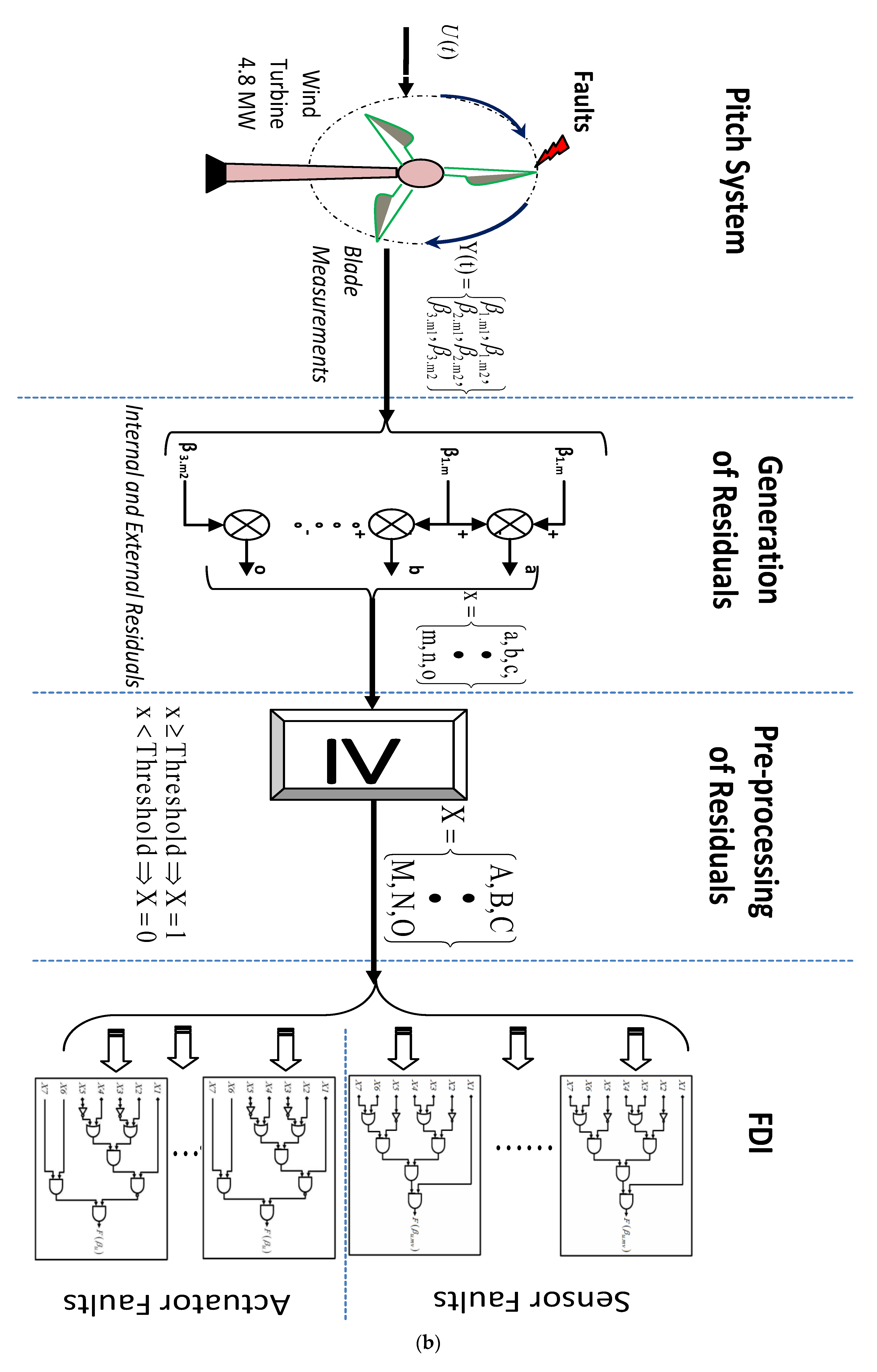
3. Development of a Digital Algorithm for the Detection of the Pitch Angle System Faults
3.1. Faults Affecting the Pitch Angle Sub-System
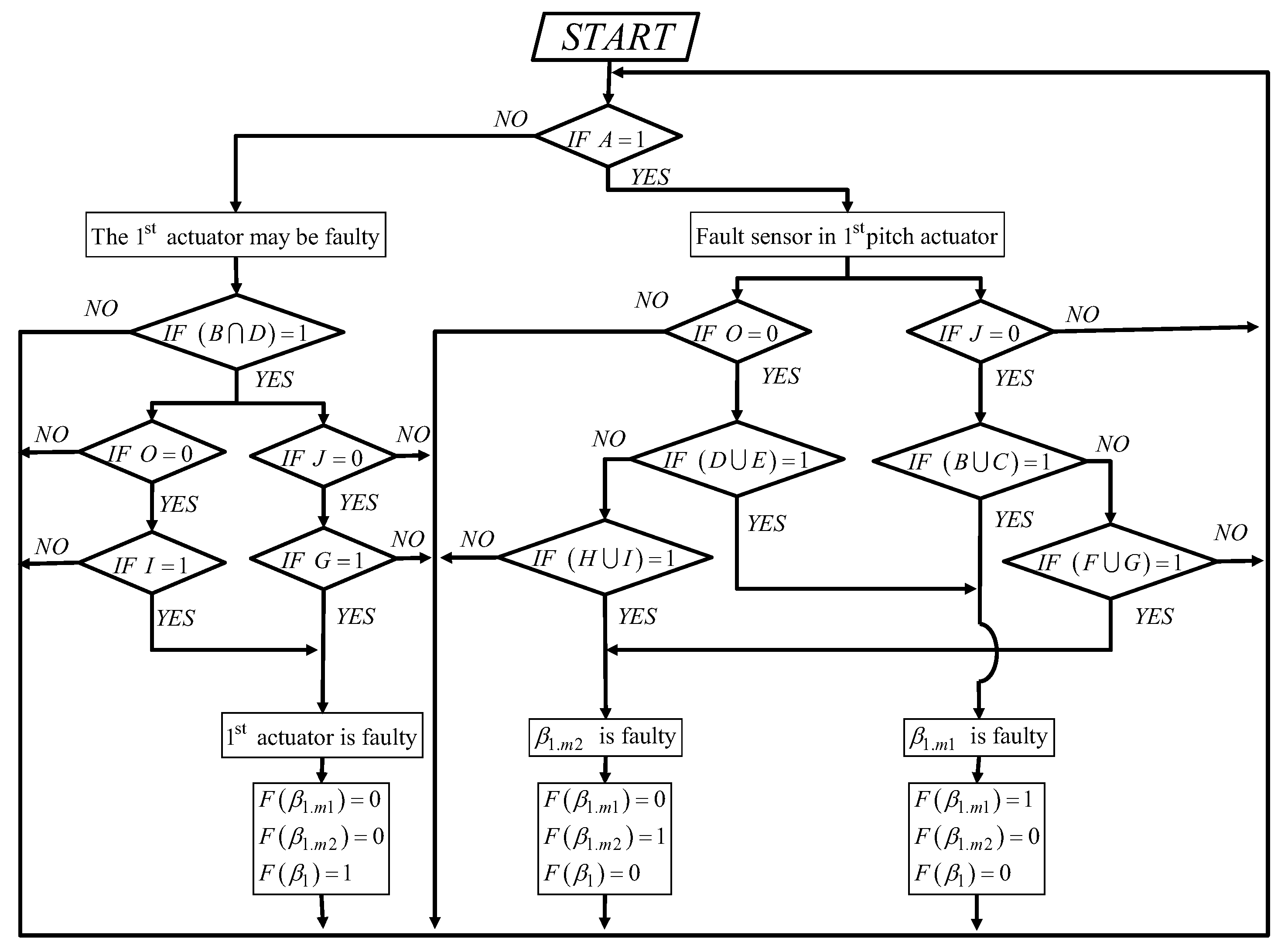
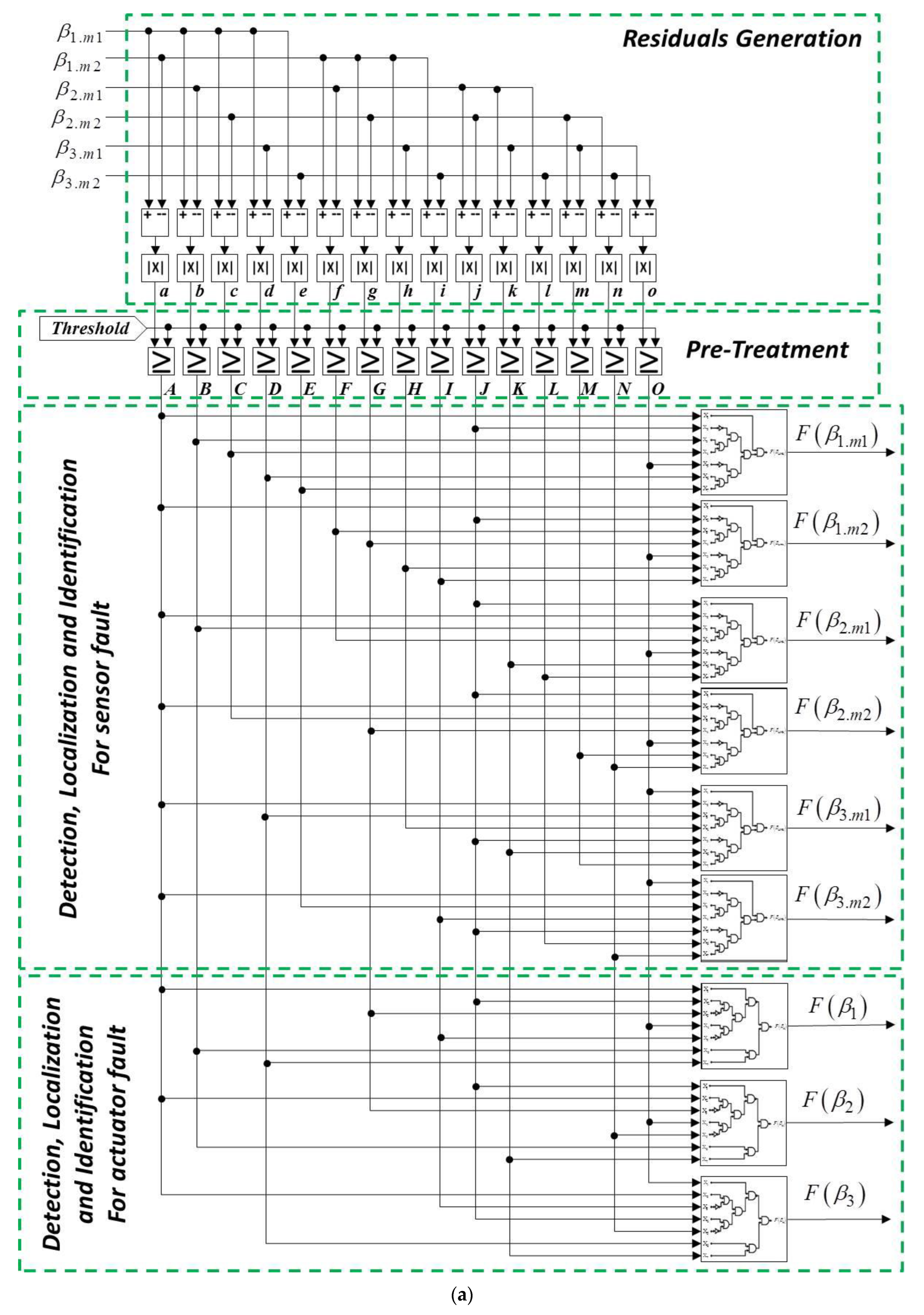
3.2. Pitch System Diagnostics Using the Proposed Digital Detection Algorithm
- To avoid incorrect and failure detection, the threshold is greater than the marginal variation in uninfluenced residual values.
- To detect faults correctly, the threshold should be smaller than the values of all the influenced residues of the occurred defect.
- To avoid delayed and imprecise detections, the detection time (TD) must be decreased continuously.
- A.
- Generation of residues and pre-processing of detection
- B.
- Fault detection, localization, and identification steps
- a.
- Sensors’ faults
- a.1
- Scenario: Fault sensor in the 1st actuator A = 1
- a.2
- Scenario: Fault sensor in the 2nd actuator J = 1
- a.3
- Scenario: Fault sensor in the 3rd actuator O = 1
- b. Actuators’ Faults
- b.1 Scenario: Fault in the 1st actuator A = 0, B = 1, and D = 1
- b.2
- Scenario: Fault in the 2nd actuator J = 0, K = 1, and B = 1:
- b.3
- Scenario: Fault in the 3rd actuator O = 0, D = 1, and K = 1:
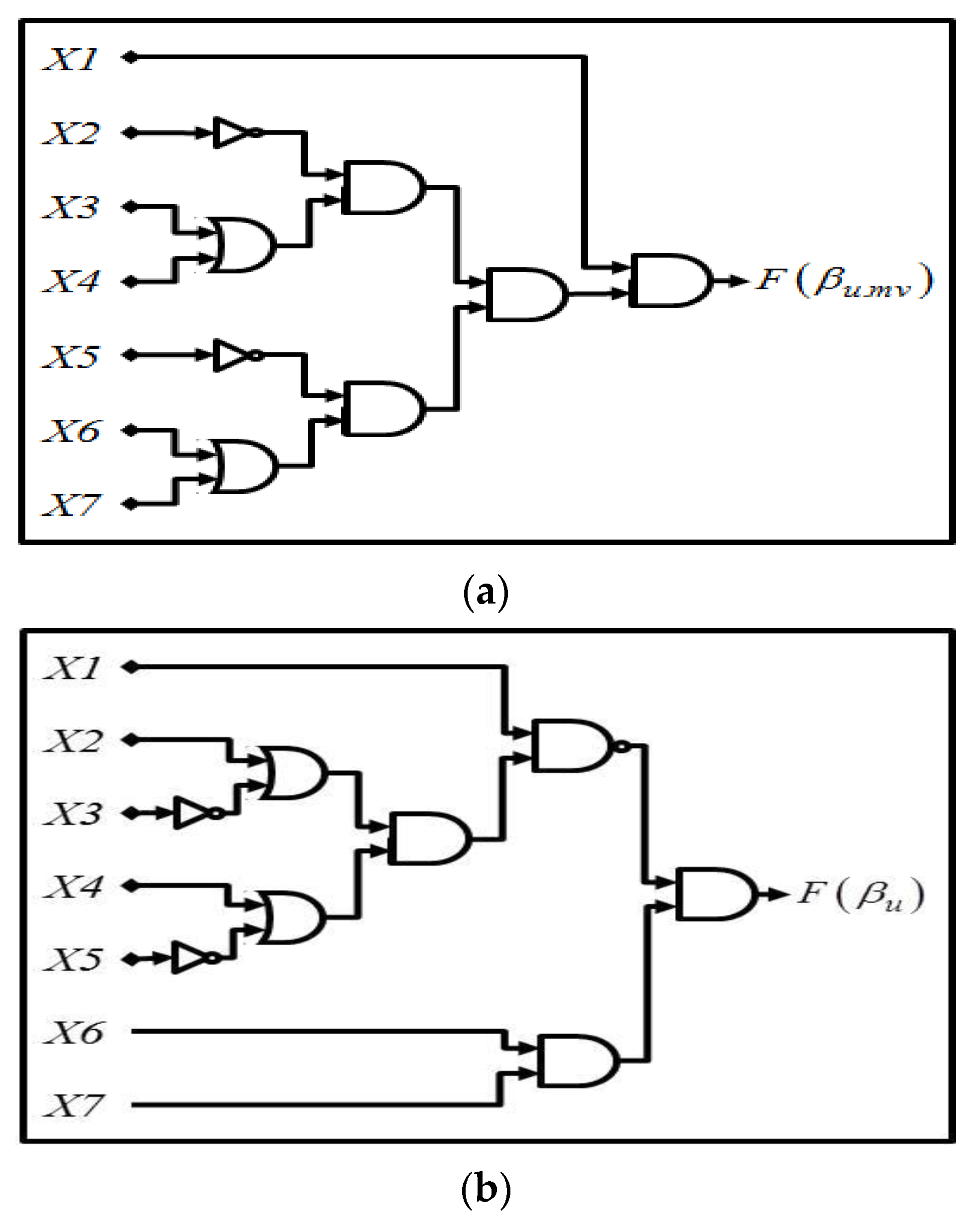
3.3. Construction of the Diagnostic System Using the Equivalent Electronic Logic Diagrams
4. Obtained Results and Investigations
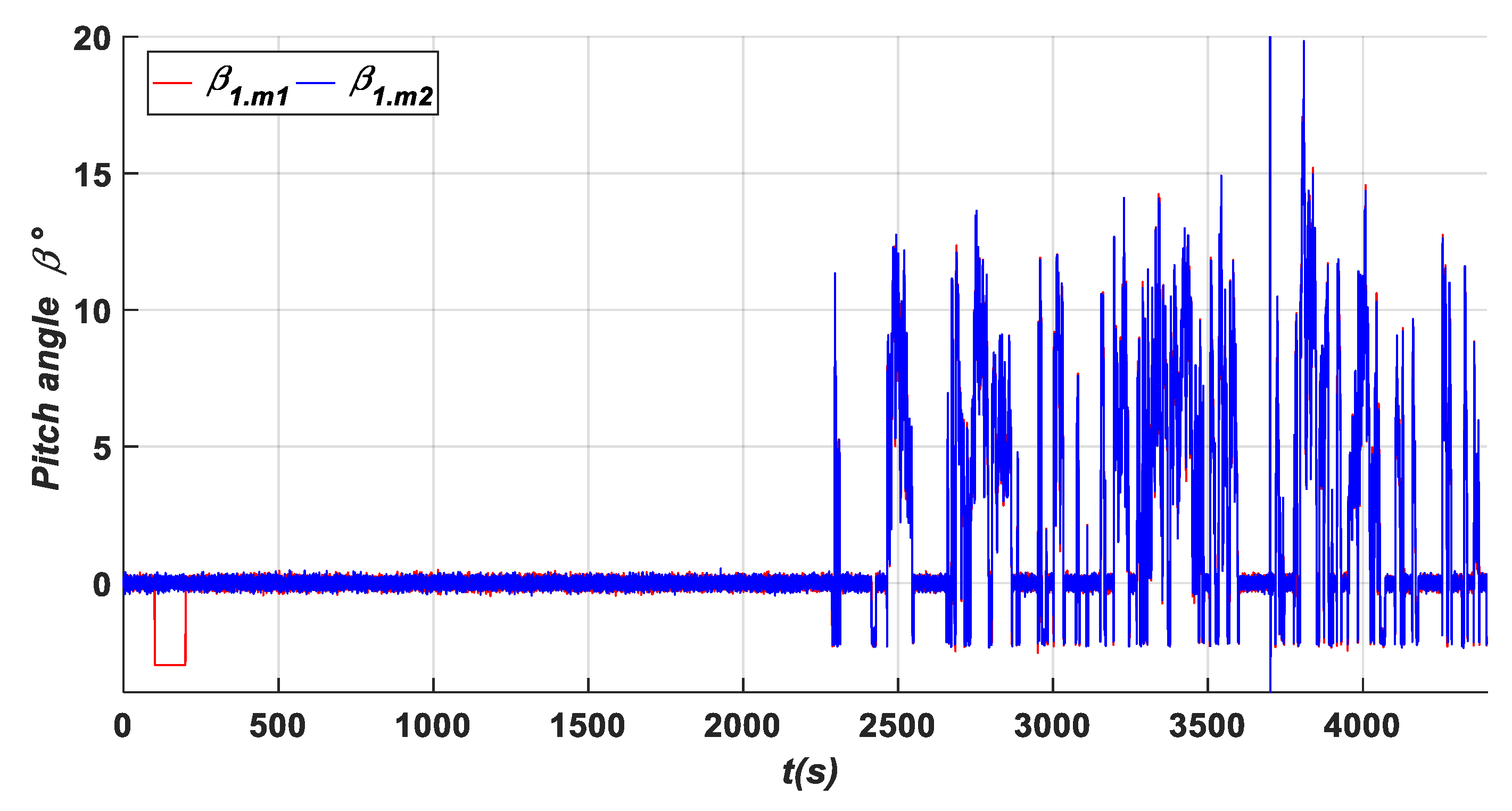
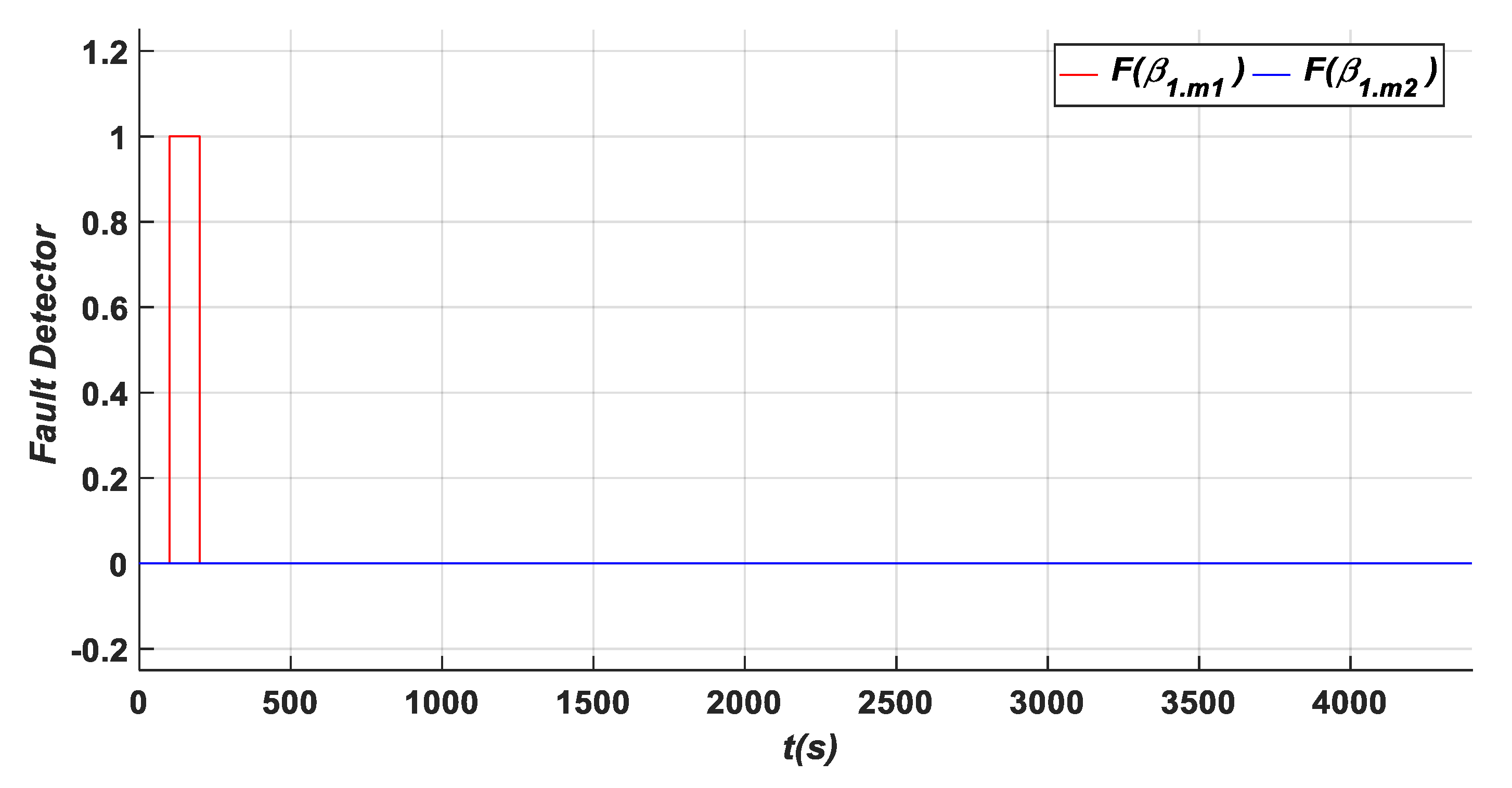
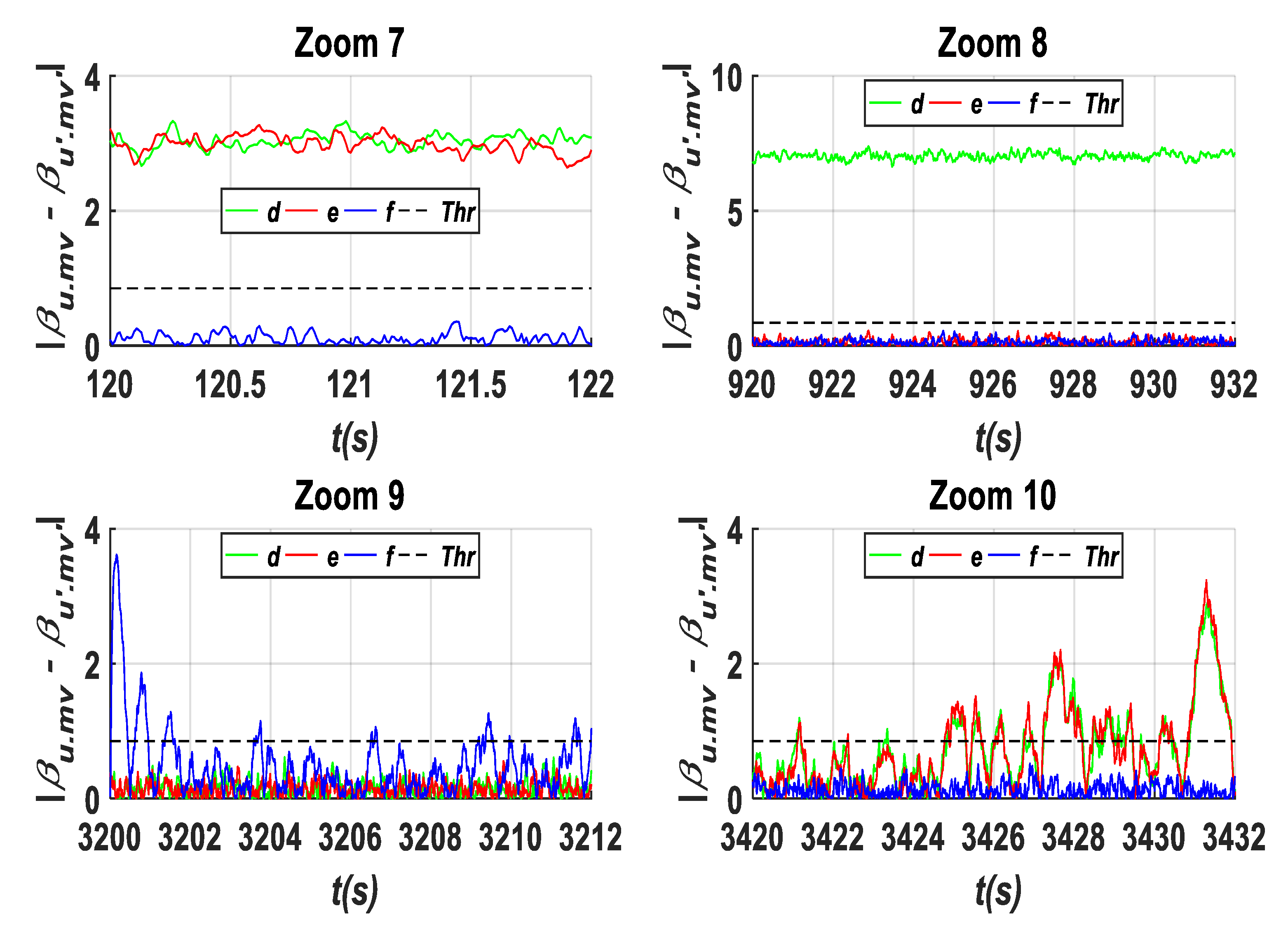
- A fixed value (A1) in β1.m1 (−3°) within an interval time: [100–200 s]: This fault influences the residuals {a, b, and c} as shown in Figure 11 and Zoom 4 of Figure 12, and the residuals {d and e} as shown in Figure 14 and Zoom 7 of Figure 15. These residuals exceed the predefined threshold, while the residual {f} presented in Figure 14 and Zoom7 of Figure 15 is less than the predefined threshold due to no influence of this fault type on these residuals. In this case, the fault detection signals are determined based on F (β1.m1) as shown in Figure 13, where the detection time in this case is TD = 0.02 s.
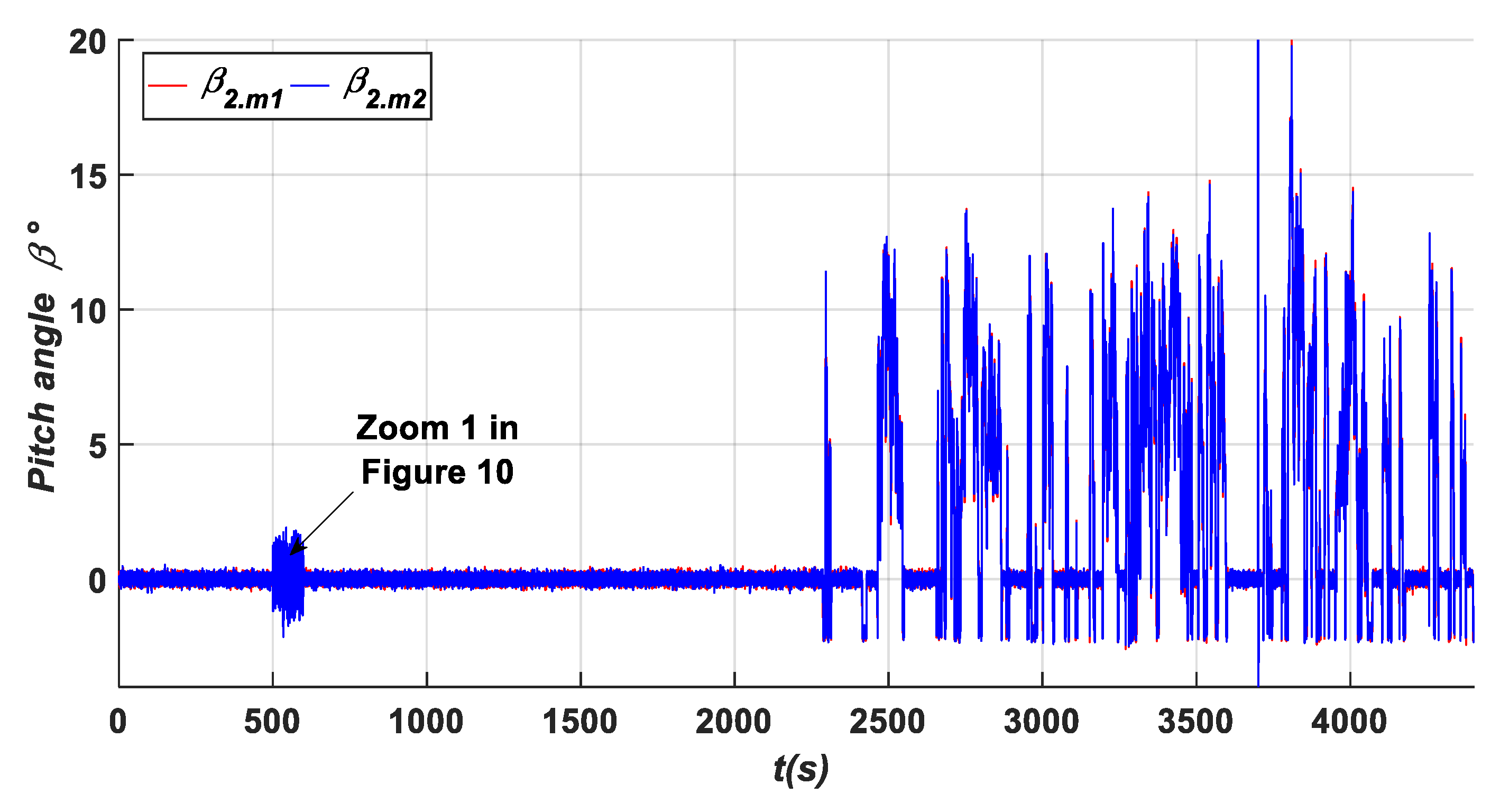
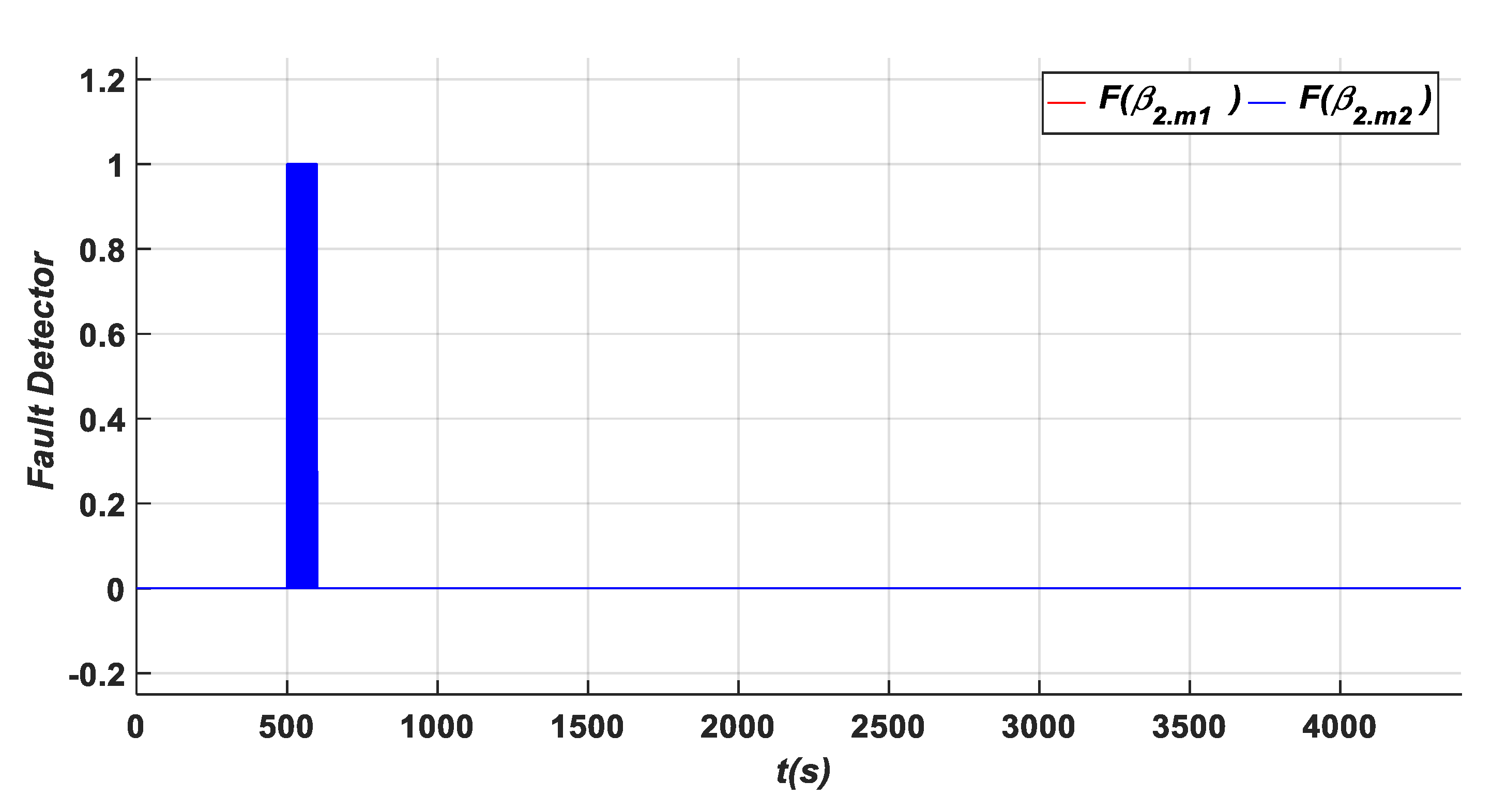
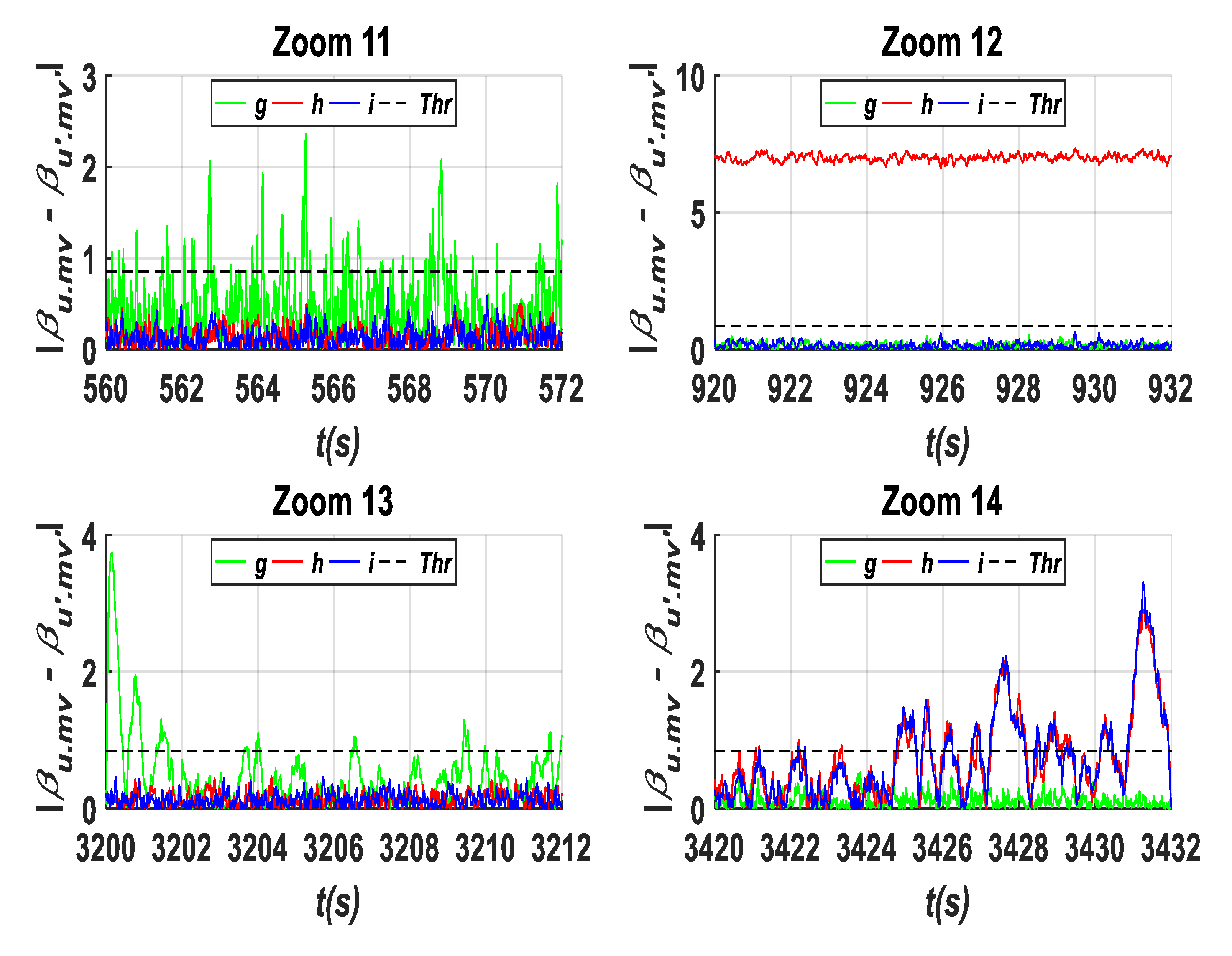
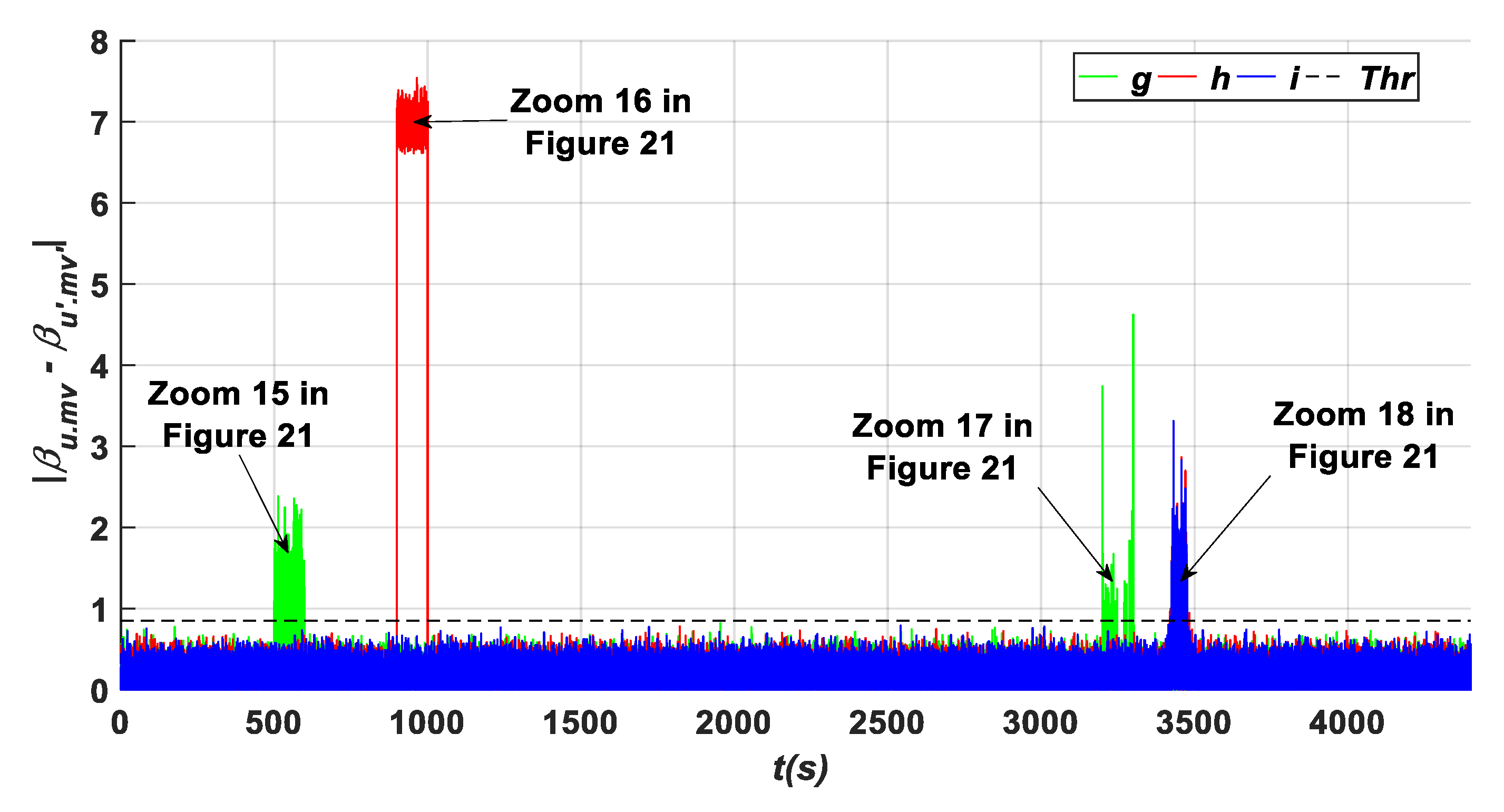
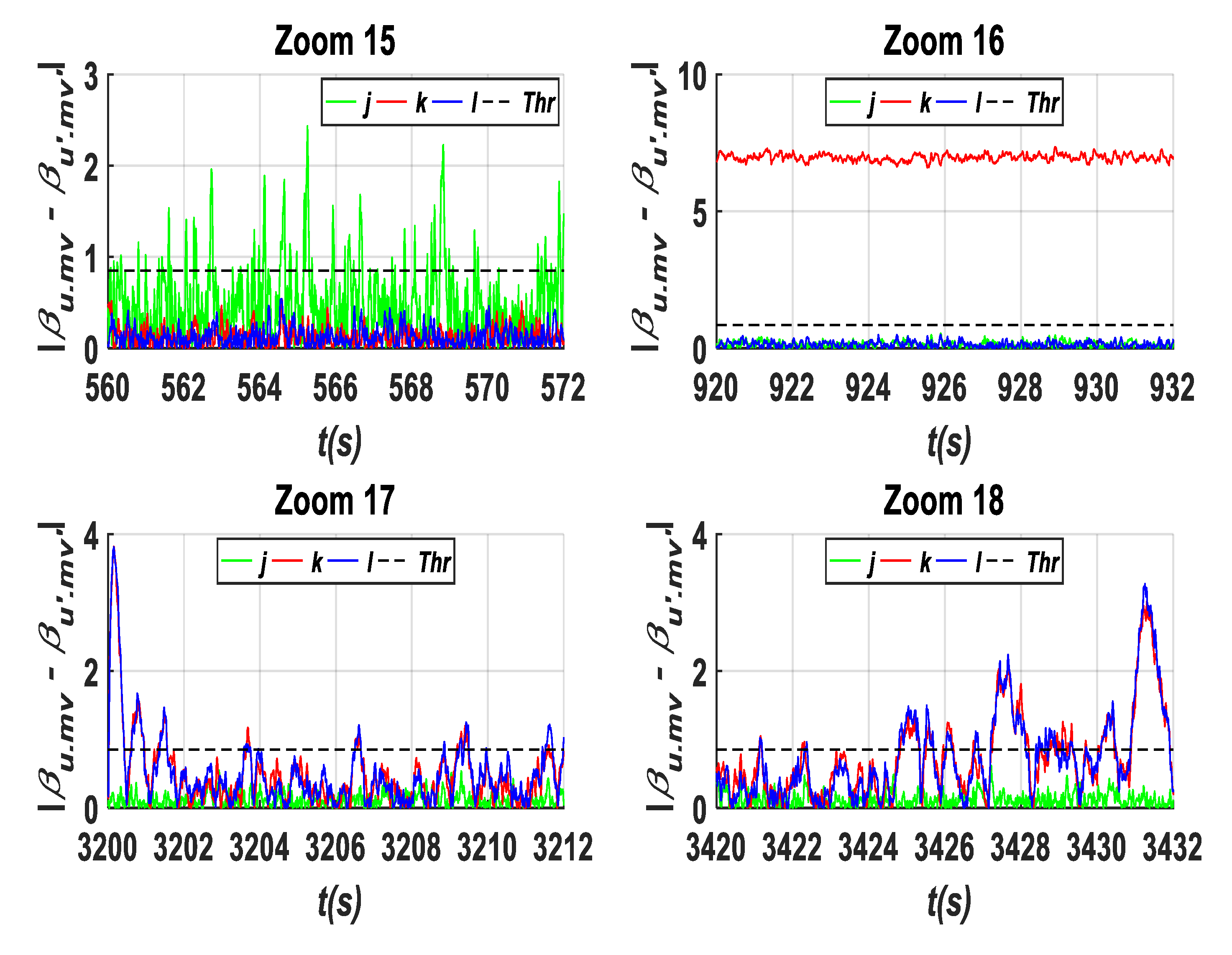
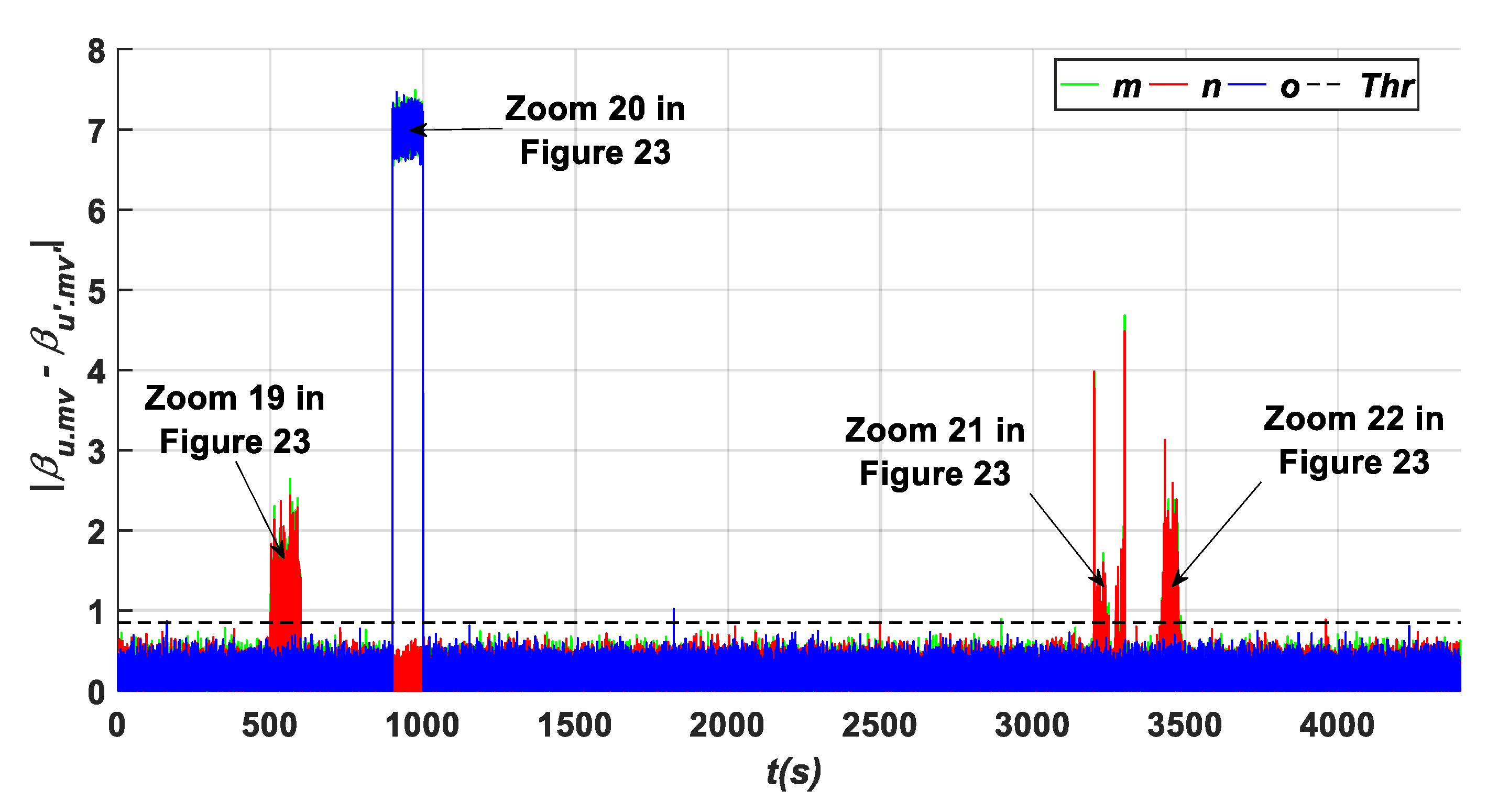
- A gain factor (A2) in β2.m2 is equal to (5.β2.m2) within an interval time of [500 s–600 s]. As it can be observed from Figure 11, Figure 17, Figure 20 and Figure 22, it is obvious that the residuals {c, g, j, m, and n} have been influenced by this fault type, where they exceed the predefined threshold. To show their high exceedance of the predefined threshold during each time interval of the fault occurrence, specific zooms are elaborated as shown in Zooms 5, 11, 15, and 19 of Figure 12, Figure 18, Figure 21 and Figure 23, respectively, whereas the residuals {a, and o} have been detected to be less than the predefined threshold as shown in Zoom. 5 of Figure 11 and Zoom 19 of Figure 23. In this case, the fault detection signal is determined by F (β2.m2) as shown in Figure 16 with a detection time TD = 0.08 s.
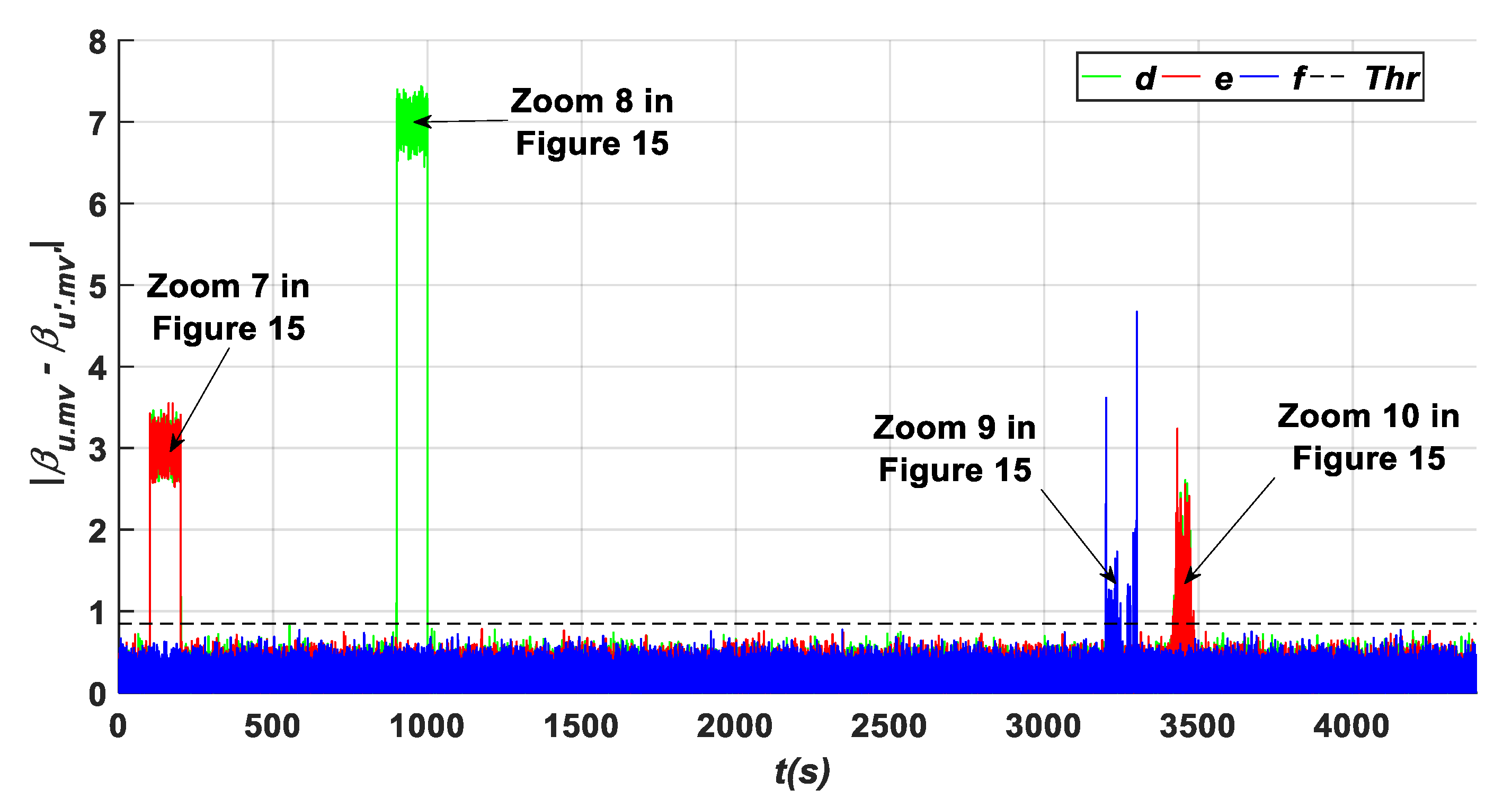
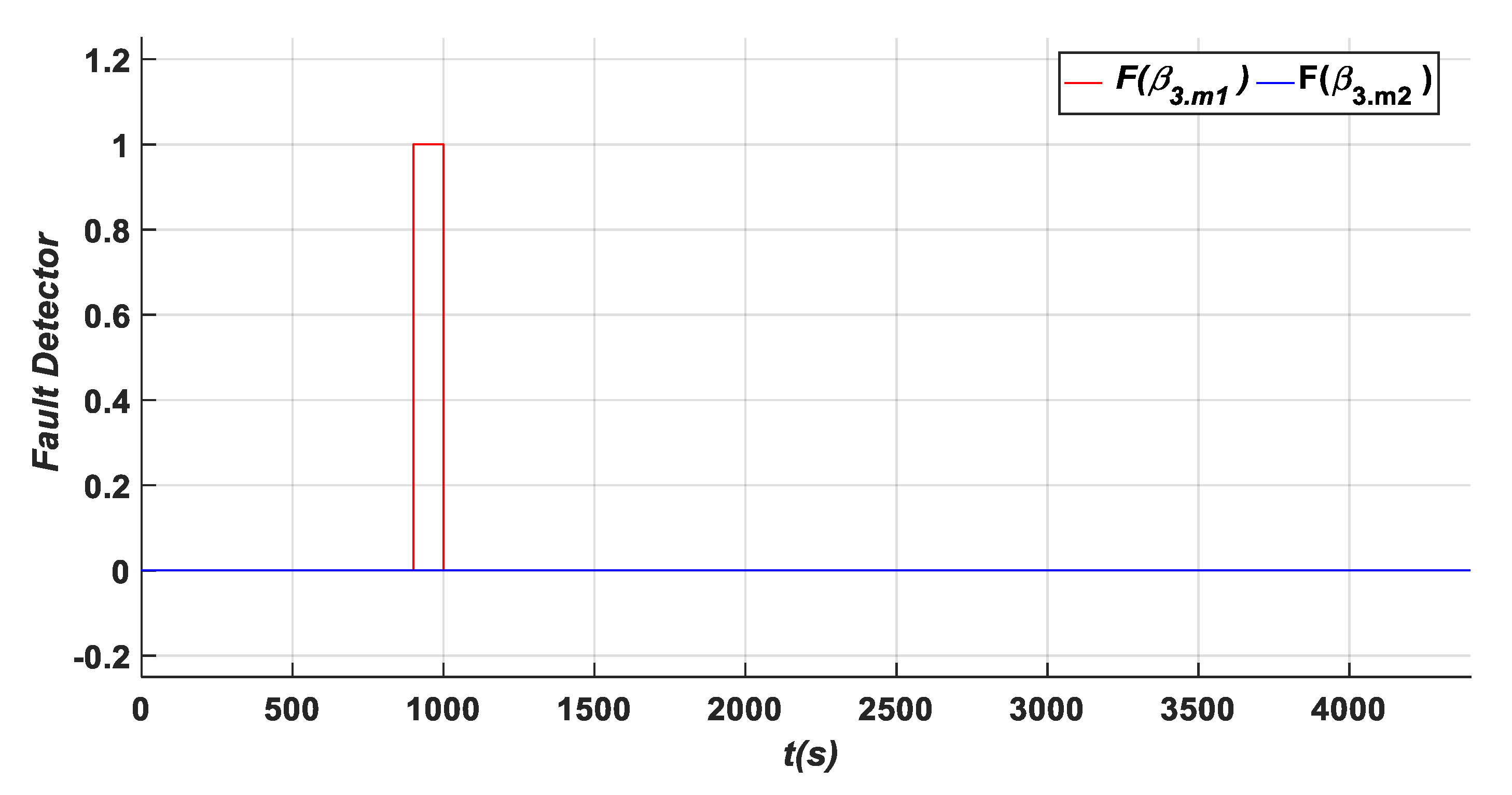
- A fixed value (A1) in β3.m1 with a value of (7°) within an interval time of [900 s–1000 s]. Based on the results shown in Figure 14, Figure 17, Figure 20 and Figure 22, it is clear that this fault type has influences on the residuals {d, h, k, m, and o}, where their values exceed the predefined threshold. Specifically captured zooms within the mentioned time interval are shown in Zooms 8, 12, 18, and 20 in Figure 15, Figure 18, Figure 21 and Figure 23, respectively. However, the residuals {a and j} remain less than the predefined threshold value as presented in Figure 11 and Zoom 16 of Figure 21. In this case, the fault detection signal is determined by F (β3.m1) as shown in Figure 19 with a time of detection (TD = 0.01 s).
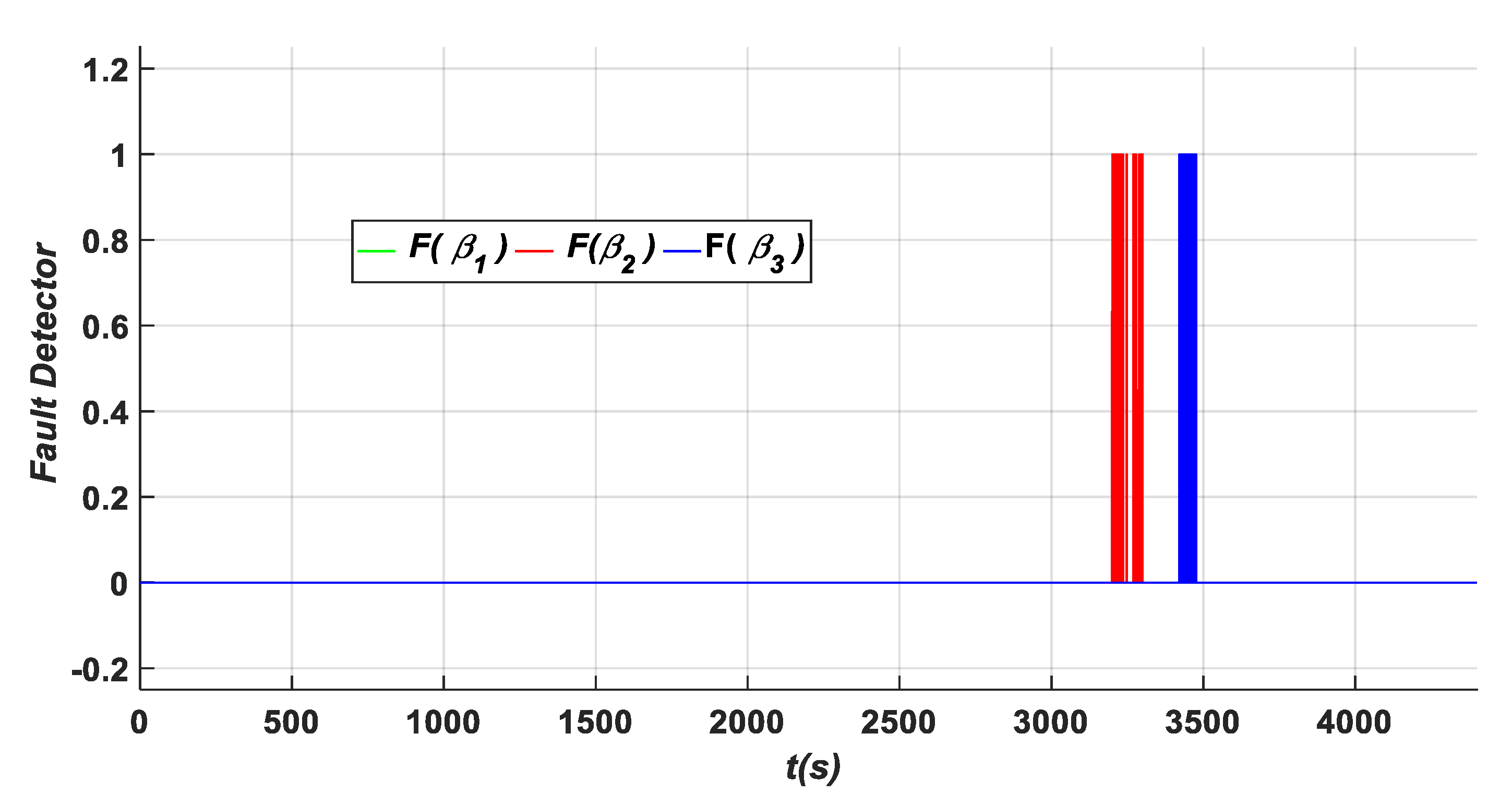
- Hydraulic pressure drops (B3) is an actuator fault that occurs in the second actuator β2 within the time interval of [3200 s–3300 s]. As shown in Figure 11, Figure 14, Figure 17, Figure 20 and Figure 22, this fault type influences the residuals {b, c, f, g, k l, m, and n}. The zooms carried out at each fault occurrence within the specified duration show that the measured values of these signals infer the decision related to the occurring fault as the aforementioned residuals exceed the predefined threshold as shown in Zooms 6, 9, 13, 17, and 21 of Figure 12, Figure 15, Figure 18, Figure 21 and Figure 23, respectively, while the residuals {a, e, d, j, and o} have their values less than the predefined threshold during the mentioned duration [3200 s to 3300 s] as depicted in Zoom 6 of Figure 12, Zoom 9 of Figure 15, Zoom 13 of Figure 18, Zoom 17 of Figure 21, and Zoom 21 of Figure 23. In this case, the fault detection signal is determined by F (β2) as shown in Figure 24 with a time of detection (TD = 0.01 s).
- Increasing air content (B4) in the third actuator (β3) within the time interval [3400 s–3500 s]. This fault type influences the residuals {d, e, h, i, k, l, m, and n} as shown in Figure 14, Figure 17, Figure 20 and Figure 22, leading to exceeding the predefined threshold value as it can be seen clearly in the captured zooms within the defined time interval [3400 s to 3500 s] such as Zooms 10, 14, 18, and 22 of Figure 15, Figure 18, Figure 21 and Figure 23, respectively, whereas the signals {f, g, j, and o} remain less than the predefined threshold within the specified duration as shown in Zoom 10 of Figure 15, Zoom 14 of Figure 18, Zoom 18 of Figure 21, and Zoom 22 of Figure 23. In this case, the fault detection signal is determined by F (β3) as shown in Figure 24 with a time of detection (TD = 22.01 s).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WT | Wind turbine |
| PV | Photovoltaic |
| FTC | Fault-tolerant control approach |
| FDI | Fault detection and identification |
| FFT | Fast Fourier transform |
| FSK-MBCNN | Fast spectral kurtosis multi-branch convolutional neural network method |
| PI | Proportional-Integrator controllers |
| WPT | Wireless Power Transfer |
| MEPT | Maximum Efficiency Point Tracking control |
| Vwind | Wind speed |
| β1, β2, β3 | The real values of the pitch angle of the first, second, and third wind turbine blades |
| βm | Pitch angle signal measurements |
| βr | Pitch angle signal reference |
| τr | Rotor torque |
| ωr | Rotor speed (turbine speed) |
| τg | Generator torque |
| τg.r | Reference of generator torque |
| ωg | Generator speed |
| ωn | The pulsation frequency factor of second-order transfer function |
| ξ | The damping factor of the second-order transfer function |
| TD | The time of Detection |
| Thr | Threshold value |
| x = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o} | Internal and external residual signals obtained in Residual Generation. |
| X = {A, B, C, D, E, F, G, H, I, J, K, L, M, N, and O} | Binary states of internal and external residuals obtained in the pre-treatment stage |
| {nbr: blade} | Blade number (uth = {1st, 2nd, or 3rd}) |
| {nbr: sensor} | Sensor number (vth = {1st, or 2nd}) in the uth blade |
| βu.mv | Measurements of the vth sensor on the uth pitch angle sub-system. |
| F(βu.mv) | Sensor fault in vth sensor of uth actuator |
| F(βu) | Actuator fault in the uth actuator. |
| “A” | An indication for sensor faults in different parts of the proposed model of the WT system. |
| “A1” | The first sensor fault class: “fixed value” in a sensor in the pitch angle system into the aerodynamic part. |
| “A2” | The second sensor fault class: “gain factor” in a sensor in the pitch angle system into the aerodynamic part. |
| “B” | An indication for actuator faults in different parts of the proposed model of the WT system. |
| “B3” | The third actuator fault class: “changed dynamics” as a hydraulic head in a hydraulic pitch angle sub-system into the aerodynamic part. |
| “B4” | The fourth actuator fault class: “changed dynamics” as an increasing air in a hydraulic pitch angle sub-system into the aerodynamic part. |
References
- Gao, Z.; Liu, X. An overview on fault diagnosis, prognosis and resilient control for wind turbine systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault Tolerant Control of Wind Turbines—A benchmark model. IFAC Proc. Vol. 2009, 42, 155–160. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. A Benchmark evaluation of fault tolerant wind turbine control concepts. IEEE Trans. Control Syst. Technol. 2015, 23, 1221–1228. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Kusiak, A.; Verma, A. A Data-Driven approach for monitoring blade pitch faults in wind turbines. IEEE Trans. Sustain. Energy 2011, 2, 87–96. [Google Scholar] [CrossRef]
- Fernandez-Canti, R.M.; Blesa, J.; Tornil-Sin, S.; Puig, V. Fault detection and isolation for a wind turbine benchmark using a mixed Bayesian/Set-membership approach. Annu. Rev. Control 2015, 40, 59–69. [Google Scholar] [CrossRef]
- Azizi, A.; Nourisola, H.; Shoja-Majidabad, S. Fault tolerant control of wind turbines with an adaptive output feedback sliding mode controller. Renew. Energy 2019, 135, 55–65. [Google Scholar] [CrossRef]
- Colombo, L.; Corradini, M.L.; Ippoliti, G.; Orlando, G. Pitch angle control of a wind turbine operating above the rated wind speed: A sliding mode control approach. ISA Trans. 2020, 96, 95–102. [Google Scholar] [CrossRef]
- Sanchez, H.; Escobet, T.; Puig, V.; Odgaard, P.F. Fault diagnosis of an advanced wind turbine benchmark using interval-based ARRs and observers. IEEE Trans. Ind. Electron. 2015, 62, 3783–3793. [Google Scholar] [CrossRef]
- Blesa, J.; Rotondo, D.; Puig, V.; Nejjari, F. FDI and FTC of wind turbines using the interval observer approach and virtual actuators/sensors. Control Eng. Pract. 2014, 24, 138–155. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Natili, F. Wind turbine generator slip ring damage detection through temperature data analysis. Diagnostyka 2019, 20, 3–9. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Castaldi, P. Fault diagnosis of a wind turbine benchmark via identified fuzzy models. IEEE Trans. Ind. Electron. 2015, 62, 3775–3782. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Castaldi, P. Residual generator fuzzy identification for wind turbine Benchmark fault diagnosis. Machines 2014, 2, 275–298. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Chen, M.Z.Q. Takagi–Sugeno Fuzzy Model Based Fault Estimation and Signal Compensation with Application to Wind Turbines. IEEE Trans. Ind. Electron. 2017, 64, 5678–5689. [Google Scholar] [CrossRef]
- Civelek, Z. Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm. Eng. Sci. Technol. Int. J. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Stetco, A.; Ramirez, J.M.; Mohammed, A.; Djurović, S.; Nenadic, G.; Keane, J. An End-to-End, Real-Time Solution for Condition Monitoring of Wind Turbine Generators. Energies 2020, 13, 1825–1840. [Google Scholar] [CrossRef]
- Habib Chaouki Ben Djoudi, Ahmed Hafaifa, Dalila Djoudi and Mouloud Guemana, Fault tolerant control of wind turbine via identified fuzzy models prototypes. Diagnostyka 2020, 21, 3–13. [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Tan, Q.; Yu, H. A fault diagnosis method for wind turbines gearbox based on adaptive loss weighted meta-ResNet under noisy labels. Mech. Syst. Signal Process. 2021, 161, 107963. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, B.; Wang, Z.; Zhang, J. An FSK-MBCNN based method for compound fault diagnosis in wind turbine gearboxes. Measurement 2021, 172, 108933. [Google Scholar] [CrossRef]
- Jiang, N.; Li, N. A wind turbine frequent principal fault detection and localization approach with imbalanced data using an improved synthetic oversampling technique. Int. J. Electr. Power Energy Syst. 2021, 126 Pt A, 106595. [Google Scholar] [CrossRef]
- Sellami, T.; Berriri, H.; Jelassi, S.; Darcherif, A.M.; Mimouni, M.F. Performance analysis of grid-connected wind turbine system under inter-turn-short-circuit fault conditions. Int. J. Renew. Energy Res. 2018, 8, 374–383. [Google Scholar]
- Sahoo, S.; Subudhi, B.; Panda, G. Comparison of output power control performance of wind turbine using PI, fuzzy logic and model predictive controllers. Int. J. Renew. Energy Res. 2018, 8, 1062–1070. [Google Scholar]
- Zeng, H.; Chen, D. A voltage fed single stage multi-input inverter for hybrid wind/photovoltaic power generation system. J. Power Electron. 2022, 22, 593–602. [Google Scholar] [CrossRef]
- Gao, W.; Fan, Y.; Wang, C.; Wang, K.; Li, H. Operating area analysis and design of WPT systems with MEPT control. J. Power Electron. 2022, 22, 702–710. [Google Scholar] [CrossRef]
- Saci, A.; Cherroun, L.; Hafaifa, A.; Mansour, O. Effective fault diagnosis method for the pitch system, the drive train, and the generator with converter in a wind turbine system. Electr. Eng. 2022, 104, 1967–1983. [Google Scholar] [CrossRef]
- Zemali, Z.; Cherroun, L.; Hadroug, N.; Hafaifa, A.; Iratni, A.; Alshammari, O.S.; Colak, I. Robust intelligent fault diagnosis strategy using Kalman observers and neuro-fuzzy systems for a wind turbine benchmark. Renew. Energy 2023, 205, 873–898. [Google Scholar] [CrossRef]
- Mazzeo, F.; Micheletto, D.; Talamelli, A.; Segalini, A. An Experimental Study on a Wind Turbine Rotor Affected by Pitch Imbalance. Energies 2022, 15, 8665. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, W.; Zhang, G.; Shu, L. Wind turbine fault diagnosis based on transfer learning and convolutional autoencoder with small-scale data. Renew. Energy 2021, 171, 103–115. [Google Scholar] [CrossRef]
- Liu, Y.; Ferrari, R.; Wu, P.; Jiang, X.; Li, S.; van Wingerden, J.-W. Fault diagnosis of the 10MW Floating Offshore Wind Turbine Benchmark: A mixed model and signal-based approach. Renew. Energy 2021, 164, 391–406. [Google Scholar] [CrossRef]
- Pang, Y.; Jia, L.; Zhang, X.; Liu, Z.; Li, D. Design and implementation of automatic fault diagnosis system for wind turbine. Comput. Electr. Eng. 2020, 87, 106754. [Google Scholar] [CrossRef]
- Kong, Y.; Qin, Z.; Wang, T.; Han, Q.; Chu, F. An enhanced sparse representation-based intelligent recognition method for planet bearing fault diagnosis in wind turbines. Renew. Energy 2021, 173, 987–1004. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.S.; Yao, L.; Qi, X.; Zhang, J. Data-driven fault diagnosis for wind turbines using modified multiscale fluctuation dispersion entropy and cosine pairwise-constrained supervised manifold mapping. Knowl.-Based Syst. 2021, 228, 107276. [Google Scholar] [CrossRef]
- Jaramillo, F.; Gutiérrez, J.M.; Orchard, M.; Guarini, M.; Astroza, R. A Bayesian approach for fatigue damage diagnosis and prognosis of wind turbine blades. Mech. Syst. Signal Process. 2022, 174, 109067. [Google Scholar] [CrossRef]
- Guang, W.; Huang, Z. Data-driven fault-tolerant control design for wind turbines with robust residual generator. IET Control Theory Appl. 2015, 9, 1173–1179. [Google Scholar]
- Vidal, Y.; Tutivén, C.; Rodellar, J.; Acho, L. Fault diagnosis and fault-tolerant control of wind turbines via a discrete time controller with a disturbance compensator. Energies 2015, 8, 4300–4316. [Google Scholar] [CrossRef]
- Alexandre Magno Ferreira Diniz, Cristiano Hora de Oliveira Fontes, Caiuby Alves Da Costa, Gloria Meyberg Nunes Costa, Dynamic modeling and simulation of a water supply system with applications for improving energy efficiency. Energy Effic. 2015, 8, 417–432. [CrossRef]
- Arif, A.; Javed, F.; Arshad, N. Integrating renewables economic dispatch with demand side management in micro-grids: A genetic algorithm-based approach. Energy Effic. 2014, 7, 271–284. [Google Scholar] [CrossRef]
- Zemali, Z.; Cherroun, L.; Hadroug, N.; Nadour, M.; Hafaifa, A. Fault Diagnosis-Based Observers using Kalman Filters and Luenberger Estimators: Application to the Pitch System Fault Actuators. Diagn. J. 2023, 24, 2022110. [Google Scholar] [CrossRef]
- Laouti, N.; Othman, S.; Alamir, M.; Sheibat-Othman, N. Combination of model-based observer and support vector machines for fault detection of wind turbines. Int. J. Autom. Comput. 2014, 11, 274–287. [Google Scholar] [CrossRef]
- Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar] [CrossRef]
- Esfahani, P.S.; Pieper, J.K. Machine learning based model linearization of a wind turbine for power regulation. Int. J. Green Energy 2021, 18, 1565–1583. [Google Scholar] [CrossRef]
- Laouti, N.; Sheibat-Othman, N.; Othman, S. Support vector machines for fault detection in wind turbines. In Proceedings of the 18th IFAC World Congress, IFAC, Universit´a Cattolica del Sacro Cuore, Milan, Italy, 28 August–2 September 2011; pp. 7067–7072. [Google Scholar]
- Zare, S.; Ayati, M. Simultaneous fault diagnosis of wind turbine using multichannel convolutional neural networks. ISA Trans. 2021, 108, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Kandukuri, S.T.; Klausen, A.; Karimi, H.R.; Robbersmyrc, K.G. A review of diagnostics and prognostics of low-speed machinery towards wind turbine farm-level health management. Renew. Sustain. Energy Rev. 2016, 53, 697–708. [Google Scholar] [CrossRef]
- Yu, W.X.; Lu, Y.; Wang, J.N. Application of small sample virtual expansion and spherical mapping model in wind turbine fault diagnosis. Expert Syst. Appl. 2021, 183, 115397. [Google Scholar] [CrossRef]
- Lan, J.; Patton, R.J.; Zhu, X. Fault-tolerant wind turbine pitch control using adaptive sliding mode estimation. Renewable Energy 2018, 116, 219–231. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F. Tommy Andy Tameghe and Gabriel Ekemb, Wind turbine condition monitoring: State-of-the-art review, new trends, and future challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Gao, S.; Liu, J. Adaptive fault-tolerant vibration control of a wind turbine blade with actuator stuck. Int. J. Control 2020, 93, 713–724. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A Survey on wind turbine condition monitoring and fault diagnosis. Part I: Components and subsystems. IEEE Trans. Ind. Electron. 2015, 62, 6536–6545. [Google Scholar] [CrossRef]
- Yang, S.; Wang, R.; Zhou, J.; Chen, B. Intermediate-Variable-Based Distributed Fusion Estimation for Wind Turbine Systems. Actuators 2022, 11, 15. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, Z.; Liu, Y.; Zhang, A.; Yin, X. Actuator and sensor fault classification for wind turbine systems based on fast fourier transform and uncorrelated multi-linear principal component analysis techniques. Processes 2020, 8, 1066. [Google Scholar] [CrossRef]
- Park, J.; Kim, C.; Dinh, M.-C.; Park, M. Design of a Condition Monitoring System for Wind Turbines. Energies 2022, 15, 464. [Google Scholar] [CrossRef]
- Meyer, A. Vibration Fault Diagnosis in Wind Turbines based on Automated Feature Learning. Energies 2022, 15, 1514. [Google Scholar] [CrossRef]
- Howard, H.H.; Simani, S. Wind Turbine Pitch Actuator Regulation for Efficient and Reliable Energy Conversion: A Fault-Tolerant Constrained Control Solution. Actuators 2022, 11, 102. [Google Scholar] [CrossRef]
- Jing, X.; Wu, Z.; Zhang, L.; Li, Z.; Mu, D. Electrical Fault Diagnosis From Text Data: A Supervised Sentence Embedding Combined With Imbalanced Classification. IEEE Trans. Ind. Electron. 2024, 71, 3064–3073. [Google Scholar] [CrossRef]
- Zhi, S.; Shen, H.; Wang, T. Gearbox localized fault detection based on meshing frequency modulation analysis. Appl. Acoust. 2024, 219, 109943. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Z.; Hu, J.; Zou, X.; Kang, Y.; Guerrero, J.M. Rethinking Fault Ride-Through Control of DFIG-Based Wind Turbines From New Perspective of Rotor-Port Impedance Characteristics. IEEE Trans. Sustain. Energy 2024, 15, 2050–2062. [Google Scholar] [CrossRef]
- Zhao, D.; Cui, L.; Liu, D. Bearing Weak Fault Feature Extraction Under Time-Varying Speed Conditions Based on Frequency Matching Demodulation Transform. IEEE/ASME Trans. Mechatron. 2023, 28, 1627–1637. [Google Scholar] [CrossRef]
- Hu, X.; Tang, T.; Tan, L.; Zhang, H. Fault Detection for Point Machines: A Review, Challenges, and Perspectives. Actuators 2023, 12, 391. [Google Scholar] [CrossRef]
- Liu, K.; Nie, G.; Jiao, S.; Gao, B.; Ma, H.; Fu, J.; Mu, J.; Wu, G. Research on fault diagnosis method of vehicle cable terminal based on time series segmentation for graph neural network model. Measurement 2024, 237, 114999. [Google Scholar] [CrossRef]
- Yang, J.; Yang, F.; Zhou, Y.; Wang, D.; Li, R.; Wang, G.; Chen, W. A data-driven structural damage detection framework based on parallel convolutional neural network and bidirectional gated recurrent unit. Inf. Sci. 2021, 566, 103–117. [Google Scholar] [CrossRef]

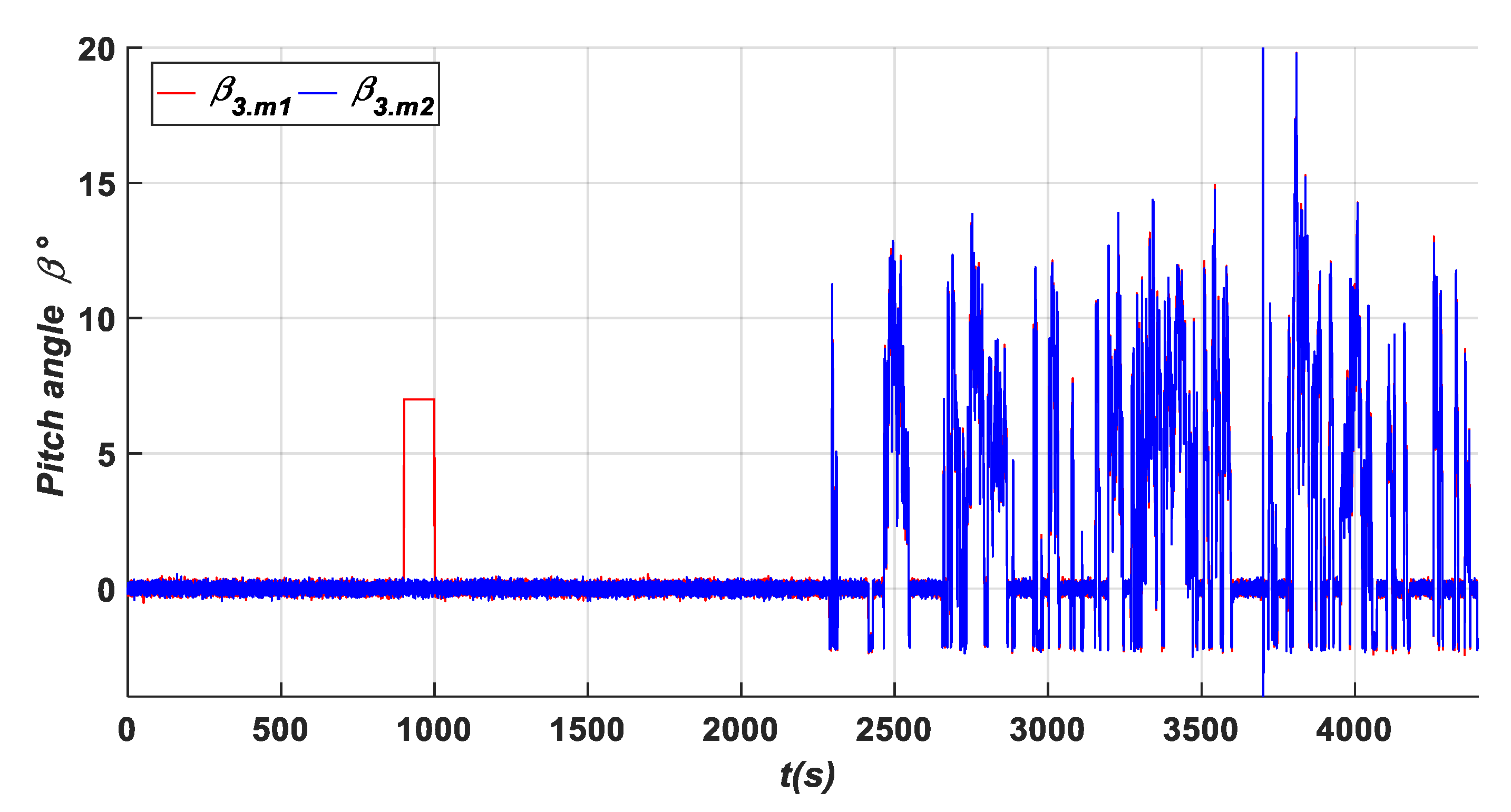
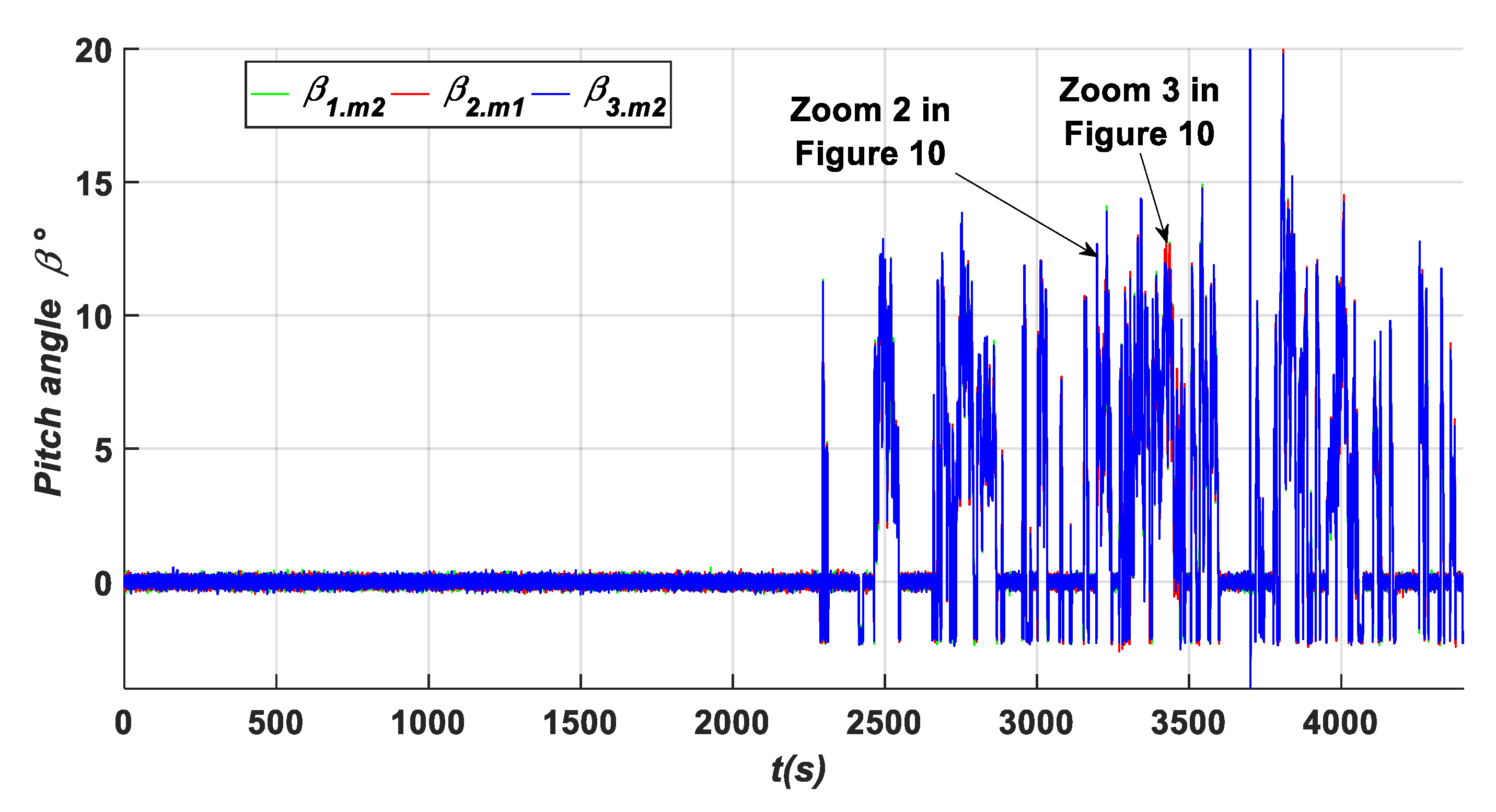
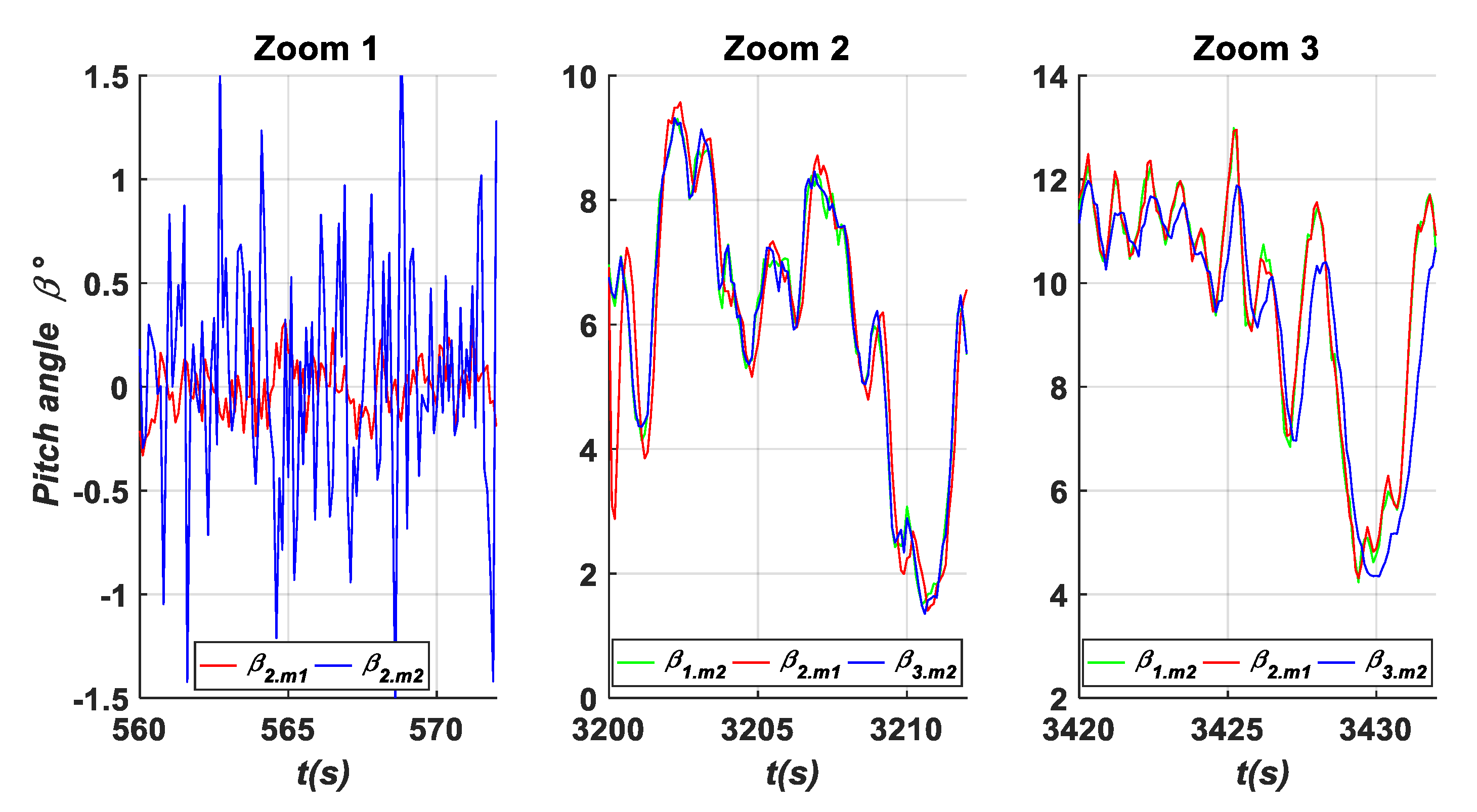

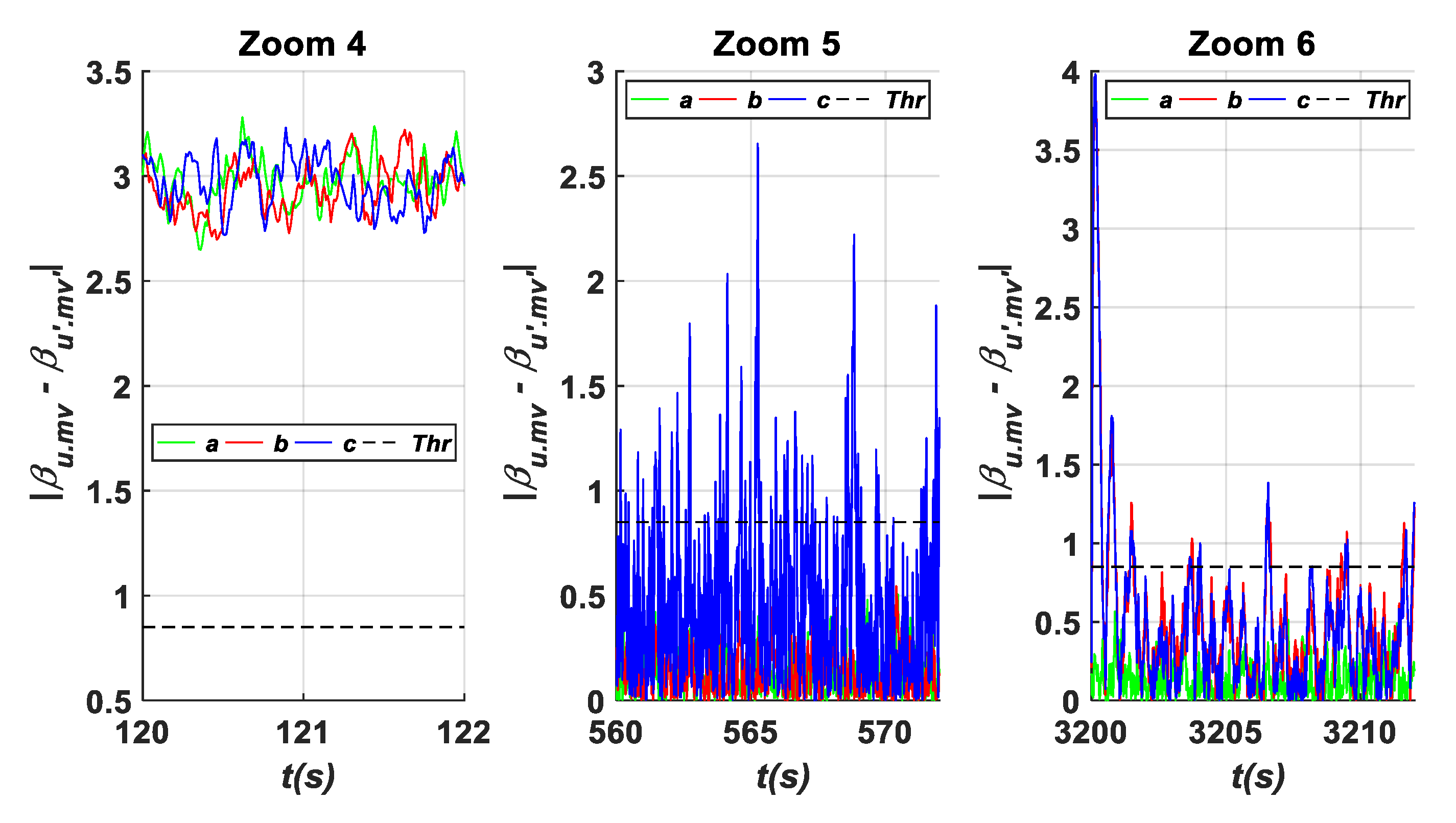


| Faults | Fault Class | Fault Type | Fault’s Location | TD(s) |
|---|---|---|---|---|
| Sensor faults: | A1 | Fixed Value | Pitch Position Sensors | TD < 10 s |
| A2 | Gain Factor | |||
| Actuator faults’: , , | B3 | Changed Dynamics | Pitch Actuators | TD < 8 s |
| B4 | Changed Dynamics | TD < 100 s |
| Fault | Fault Type | Class | Site | Fault Time |
|---|---|---|---|---|
| F (β1.m1) | Fixed value | A1 | β1.m1 | [100 s: 200 s] |
| F (β2.m2) | Gain factor | A2 | β2.m2 | [500 s: 600 s] |
| F (β3.m1) | Fixed value | A1 | β3.m1 | [900 s: 1000 s] |
| F(β2) | Changed dynamics | B3 | β2 | [3200 s: 3300 s] |
| F(β3) | Changed dynamics | B4 | β3 | [3400 s: 3500 s] |
| Pitch Sensor and Actuator Faults | ||||||||
|---|---|---|---|---|---|---|---|---|
| Fault | Detection Values | |||||||
| Site | Type | Class | Value | Period | Influenced Residuals | Residual Max Value | Criterion Detector | TD (s) |
| β1.m1 | Fixed value | A1 | −3 | [100–200 s] | a, b, c, d, e | 3.4469 | F(β1.m1) | 0.02 |
| β2.m2 | Gain factor | A2 | 5 × β2.m2 | [500–600 s] | c, g, j, m, n | 2.4911 | F(β2.m2) | 0.08 |
| β3.m1 | Fixed value | A1 | 7 | [900–1000 s] | d, h, k, m, o | 7.4727 | F(β3.m1) | 0.01 |
| β2 | Increase in air content changes | B3 | ζ3 = 0.9 ωn3 = 3.42 | [3200–3300 s] | b, c, f, g, k, l, m, n | 4.2610 | F(β2) | 0.01 |
| β3 | Hydraulic head loss changes | B4 | ζ3 = 0.45 ωn3 = 5.73 | [3400–3500 s] | d, e, h, i, k, l, m, n | 3.1461 | F(β3) | 22.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saci, A.; Nadour, M.; Cherroun, L.; Hafaifa, A.; Kouzou, A.; Rodriguez, J.; Abdelrahem, M. Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines. Energies 2024, 17, 4016. https://doi.org/10.3390/en17164016
Saci A, Nadour M, Cherroun L, Hafaifa A, Kouzou A, Rodriguez J, Abdelrahem M. Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines. Energies. 2024; 17(16):4016. https://doi.org/10.3390/en17164016
Chicago/Turabian StyleSaci, Abdelmoumen, Mohamed Nadour, Lakhmissi Cherroun, Ahmed Hafaifa, Abdellah Kouzou, Jose Rodriguez, and Mohamed Abdelrahem. 2024. "Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines" Energies 17, no. 16: 4016. https://doi.org/10.3390/en17164016
APA StyleSaci, A., Nadour, M., Cherroun, L., Hafaifa, A., Kouzou, A., Rodriguez, J., & Abdelrahem, M. (2024). Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines. Energies, 17(16), 4016. https://doi.org/10.3390/en17164016












