Predicting the Remaining Life of Centrifugal Pump Bearings Using the KPCA–LSTM Algorithm
Abstract
1. Introduction
2. KPCA Principle
- (1)
- Suppose the processed data is a m matrix composed of X bar-dimensional n data, which is the introduced kernel function; the formula is as follows:
- (2)
- Centering on, represents i the average value of the th-dimension.
- (3)
- Calculated covariance matrix.
- (4)
- The eigenvectors and eigenvalues of Q, the covariance matrix, and define the matrix C as a collection of eigenvectors .
- (5)
- Let the data be reduced to the k dimension, and take the front column of the matrix as kQ′.
- (6)
- Calculate the output matrix Y′.
3. LSTM-Based Bearing Remaining Life Prediction Model
- (1)
- Forgotten Gate
- (2)
- Input gate
- (3)
- Output gate
4. Experimental Verification
4.1. Validation of the Bearing Life-Degradation Characteristics Index
4.1.1. Experimental Platform
4.1.2. Experimental Data Analysis
- (1)
- Time-domain feature analysis
- (2)
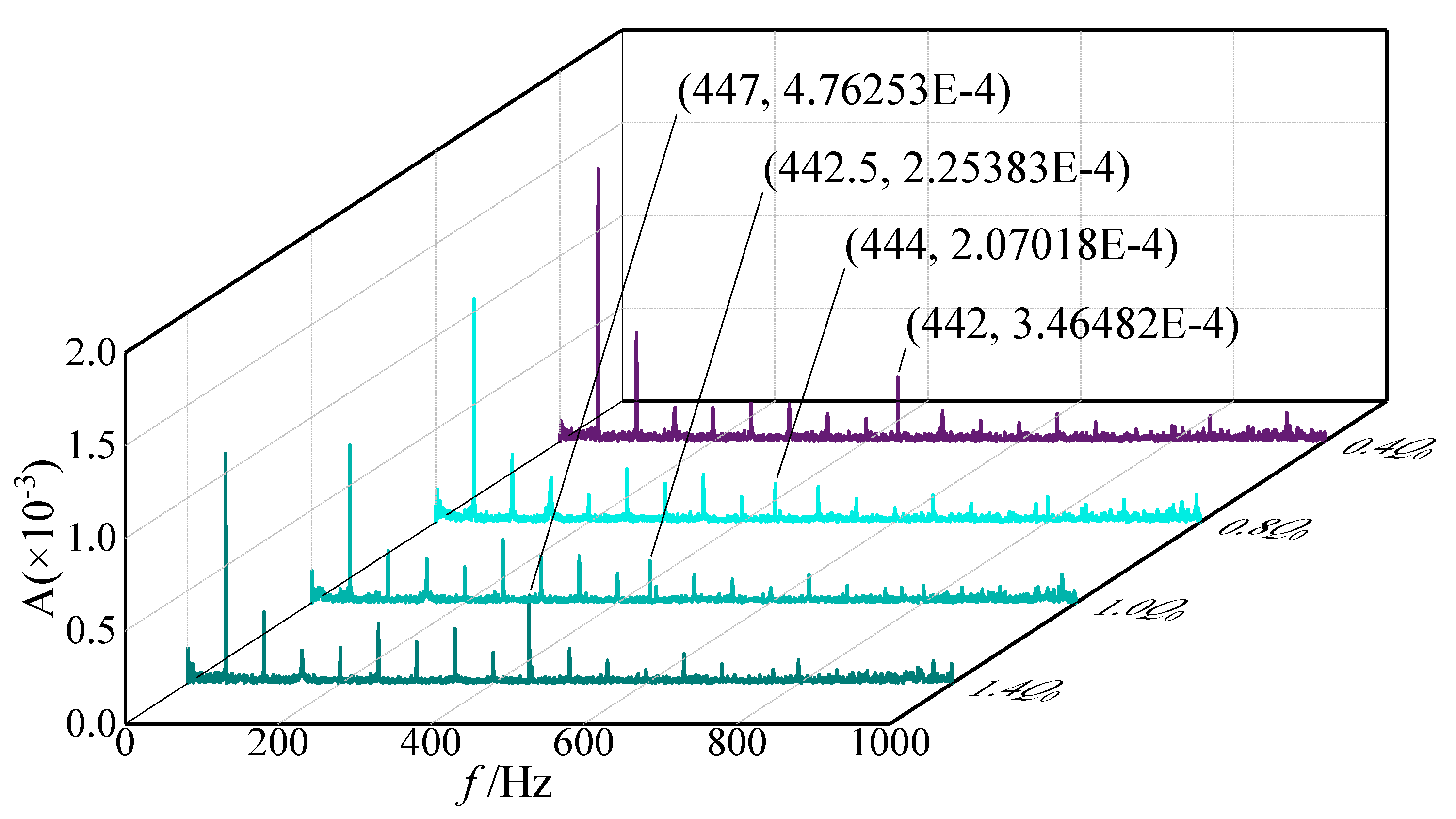
- Frequency-domain feature analysis
- (3)
- Characteristic Analysis of Wavelet Packet Decomposition
- (4)
- CEEMDAN characteristic analysis
4.2. Verification of the Bearing Remaining Life Prediction Model
4.2.1. Experiment Platform
4.2.2. Experimental Data Analysis
- (1)
- Monotonicity
- (2)
- Trend
- (3)
- Robustness
4.3. Centrifugal Pump Rolling-Bearing Life Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mand Hare, A.; Karunamurthy, K.; Ismail, S. Compendious review on “Internal Flow Physics and Minimization of Flow Instabilities Through Design Modifications in a Centrifugal Pump”. J. Press. Vessel. Technol. 2019, 141, 5–16. [Google Scholar]
- Lei, Y.G.; Han, T.Y.; Wang, B.; Li, N.; Yan, T.; Yang, J. Interpretation of XJTU-SY Rolling Bearing Accelerated Life Test Dataset. Chin. J. Mech. Eng. 2019, 55, 1–6. [Google Scholar]
- Guo, Z.; Li, Y.; Li, G. Research progress on equipment system remaining service life prediction technology. J. Nanjing Univ. Aeronaut. Astronaut. 2022, 54, 341–364. [Google Scholar]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 372–378. [Google Scholar]
- Pei, H.; Hu, C.; Si, X. Review of machine learning-based equipment remaining life prediction methods. Chin. J. Mech. Eng. 2019, 55, 1–13. [Google Scholar] [CrossRef]
- Lu, N.; Li, T.; Ren, X.; Miao, H. A deep learning scheme for motor imagery classification based on restricted Boltzmann machines. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Weerakody, P.B.; Wong, K.W.; Wang, G.; Ela, W. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing 2021, 441, 161–178. [Google Scholar] [CrossRef]
- Lu, W.; Duan, J.; Wang, P.; Ma, W.; Fang, S. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214, 118980. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, J.; Jiang, Y.; Huang, G.; Chen, R. A text sentiment classification modeling method based on coordinated CNN-LSTM-Attention model. Chin. J. Electron. 2019, 28, 120–126. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Li, H. Rolling bearing fault monitoring method based on wavelet packet energy characteristics. J. Syst. Simul. 2003, 15, 6. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Luo, X. Forecasting Foreign Exchange Rate Based on Convolutional Neural Network; Guizhou University: Guiyang, China, 2020. [Google Scholar]












| Serial Number | Feature |
|---|---|
| T1 | average |
| T2 | standard deviation |
| T3 | square root amplitude |
| T4 | RMS (root mean square) |
| T5 | peak-to-peak |
| T6 | Skewness |
| T7 | Kurtosis |
| T8 | crest factor |
| T9 | margin factor |
| T10 | form factor |
| T11 | pulse index |
| Condition | Bearing Number | Total Number of Samples | Actual Life | Failure Location |
|---|---|---|---|---|
| Speed: 2100 (r/min) Radial force: 12 kN | A1 | 123 | 2 h 3 min | Outer ring |
| A2 | 161 | 2 h 41 min | Outer ring | |
| A3 | 158 | 2 h 32 min | Outer ring | |
| A4 | 122 | 2 h 2 min | Cage | |
| A5 | 52 | 52 min | inner ring, outer ring |
| Serial Number | Trend Score | Robustness Score | Monotonicity Score | Comprehensive Index Score |
|---|---|---|---|---|
| T2 | 0.863 | 0.898 | 0.302 | 0.533 |
| T3 | 0.856 | 0.907 | 0.273 | 0.516 |
| T4 | 0.863 | 0.898 | 0.302 | 0.533 |
| F1 | 0.893 | 0.905 | 0.325 | 0.554 |
| F6 | 0.904 | 0.939 | 0.299 | 0.548 |
| F13 | 0.902 | 0.923 | 0.312 | 0.552 |
| X4 | 0.772 | 0.853 | 0.266 | 0.485 |
| X5 | 0.886 | 0.856 | 0.231 | 0.487 |
| X7 | 0.881 | 0.827 | 0.263 | 0.499 |
| C1 | 0.890 | 0.837 | 0.269 | 0.507 |
| C2 | 0.830 | 0.858 | 0.201 | 0.458 |
| C5 | 0.683 | 0.856 | 0.133 | 0.388 |
| Sample | RMSE | MAPE | T (s) |
|---|---|---|---|
| A3 | 0.155 | 0.386 | 28.8 |
| A4 | 0.072 | 0.272 | 28.8 |
| A5 | 0.112 | 0.233 | 28.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Zhang, X.; Huang, Q.; Li, S.; Fu, Q. Predicting the Remaining Life of Centrifugal Pump Bearings Using the KPCA–LSTM Algorithm. Energies 2024, 17, 4167. https://doi.org/10.3390/en17164167
Zhu R, Zhang X, Huang Q, Li S, Fu Q. Predicting the Remaining Life of Centrifugal Pump Bearings Using the KPCA–LSTM Algorithm. Energies. 2024; 17(16):4167. https://doi.org/10.3390/en17164167
Chicago/Turabian StyleZhu, Rongsheng, Xinyu Zhang, Qian Huang, Sihan Li, and Qiang Fu. 2024. "Predicting the Remaining Life of Centrifugal Pump Bearings Using the KPCA–LSTM Algorithm" Energies 17, no. 16: 4167. https://doi.org/10.3390/en17164167
APA StyleZhu, R., Zhang, X., Huang, Q., Li, S., & Fu, Q. (2024). Predicting the Remaining Life of Centrifugal Pump Bearings Using the KPCA–LSTM Algorithm. Energies, 17(16), 4167. https://doi.org/10.3390/en17164167






