Slow-Scale Bifurcation Analysis of a Single-Phase Voltage Source Full-Bridge Inverter with an LCL Filter
Abstract
1. Introduction
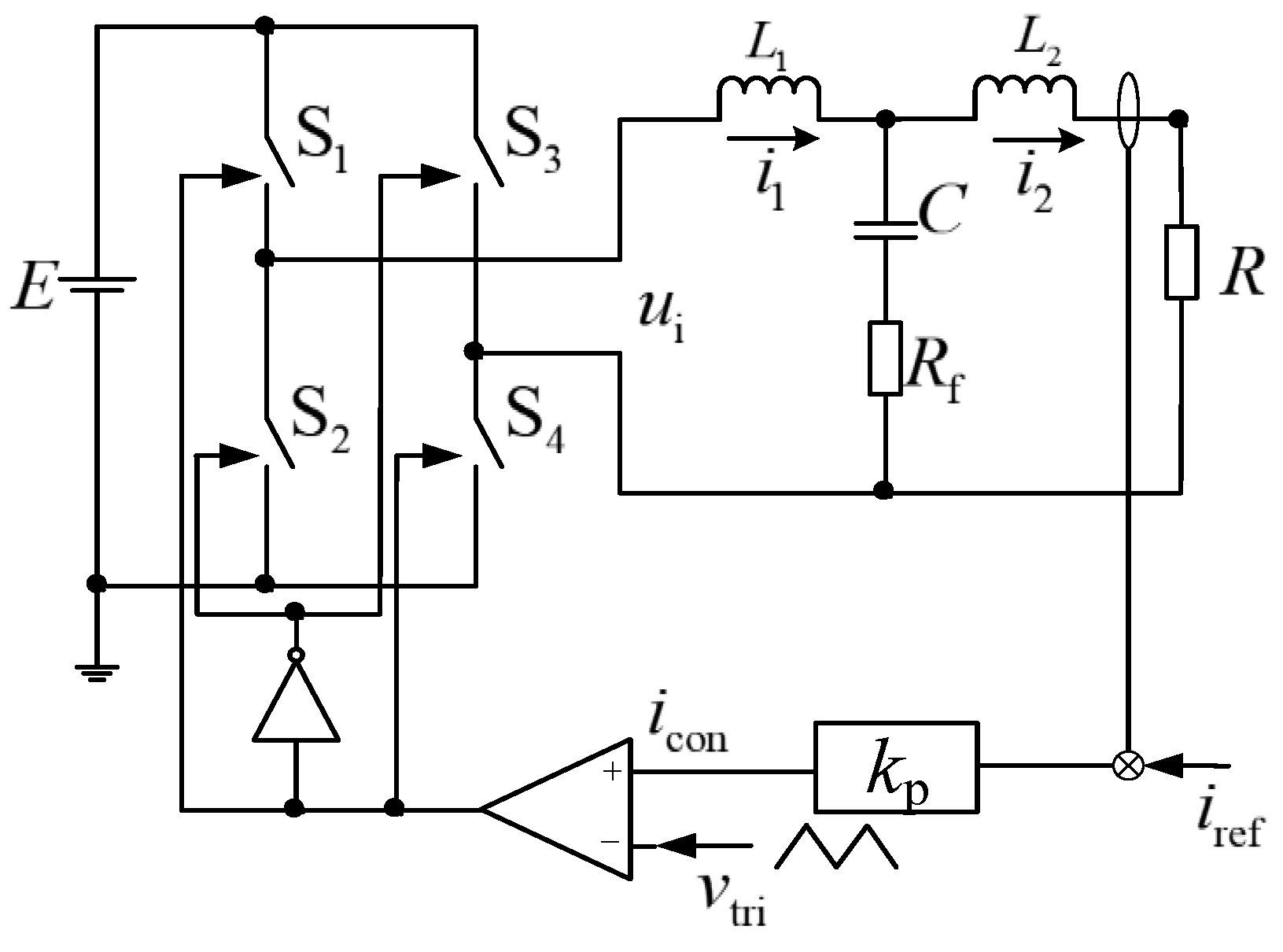
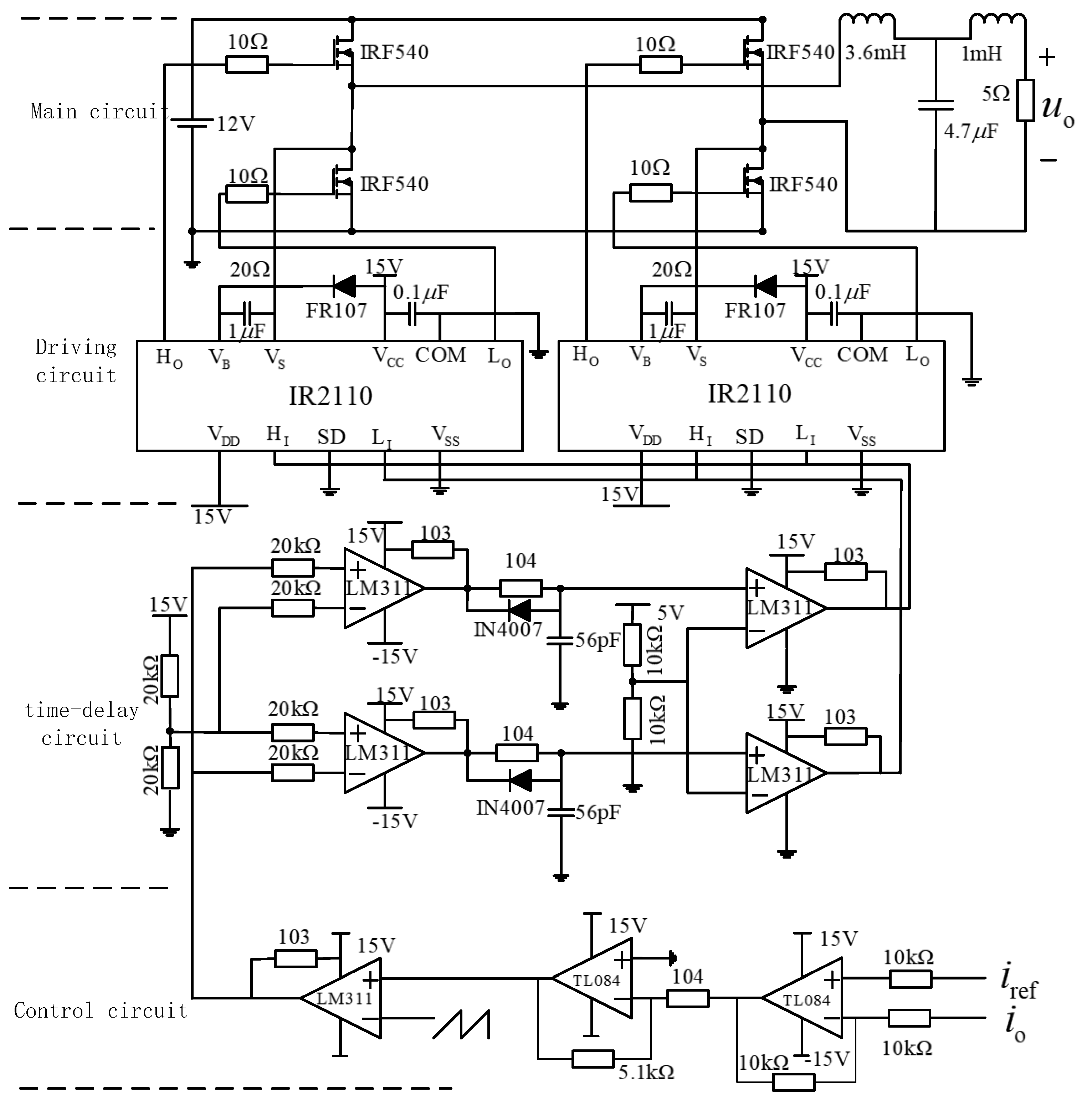
2. Circuit Description
2.1. Circuit Operation
2.2. State Equation
2.3. Linearized Switching Model
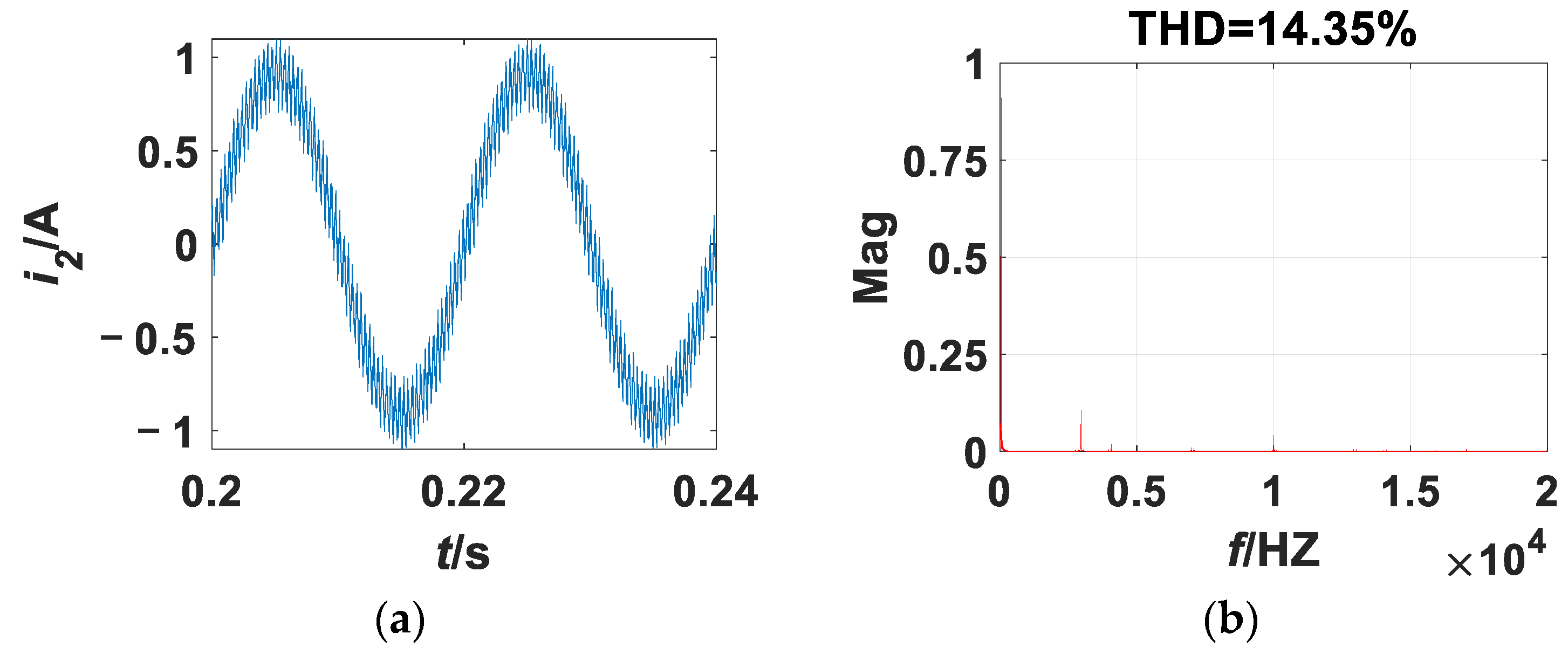
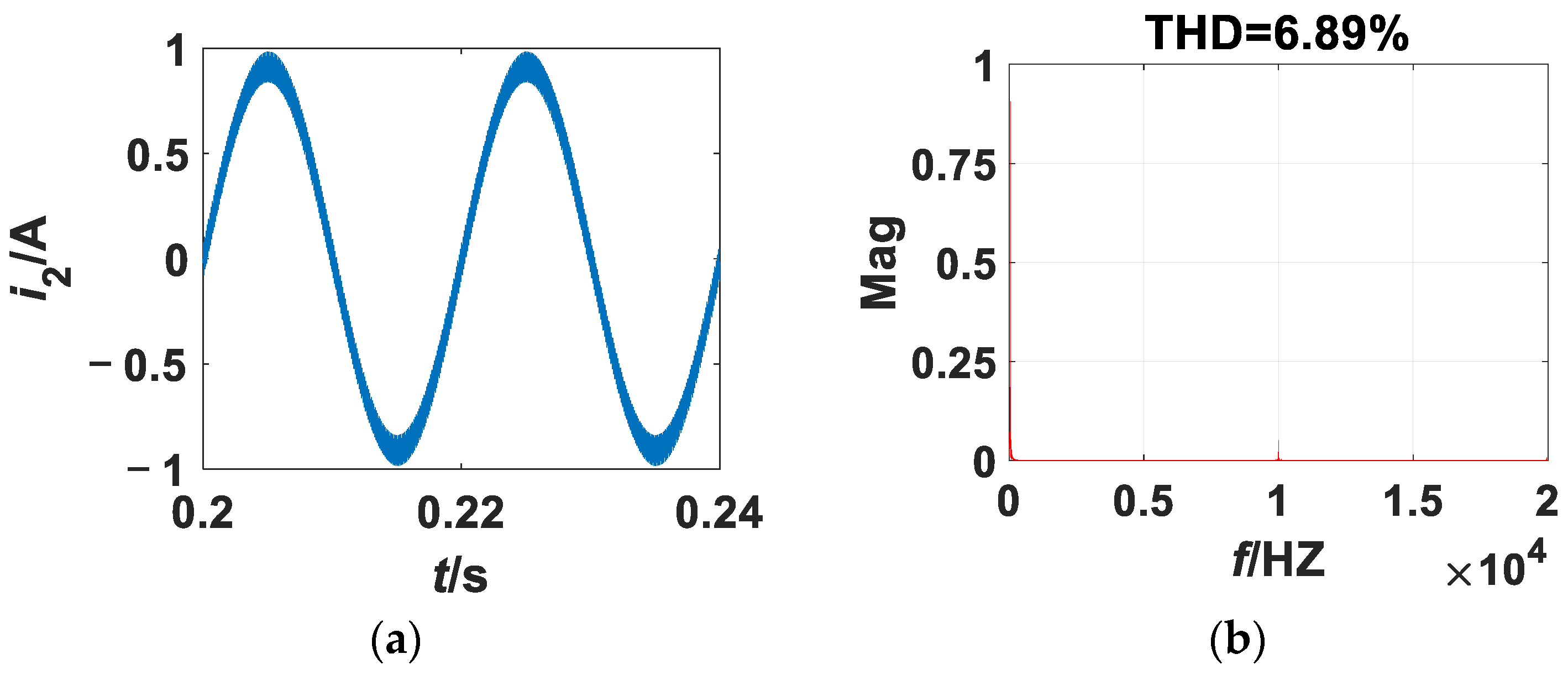
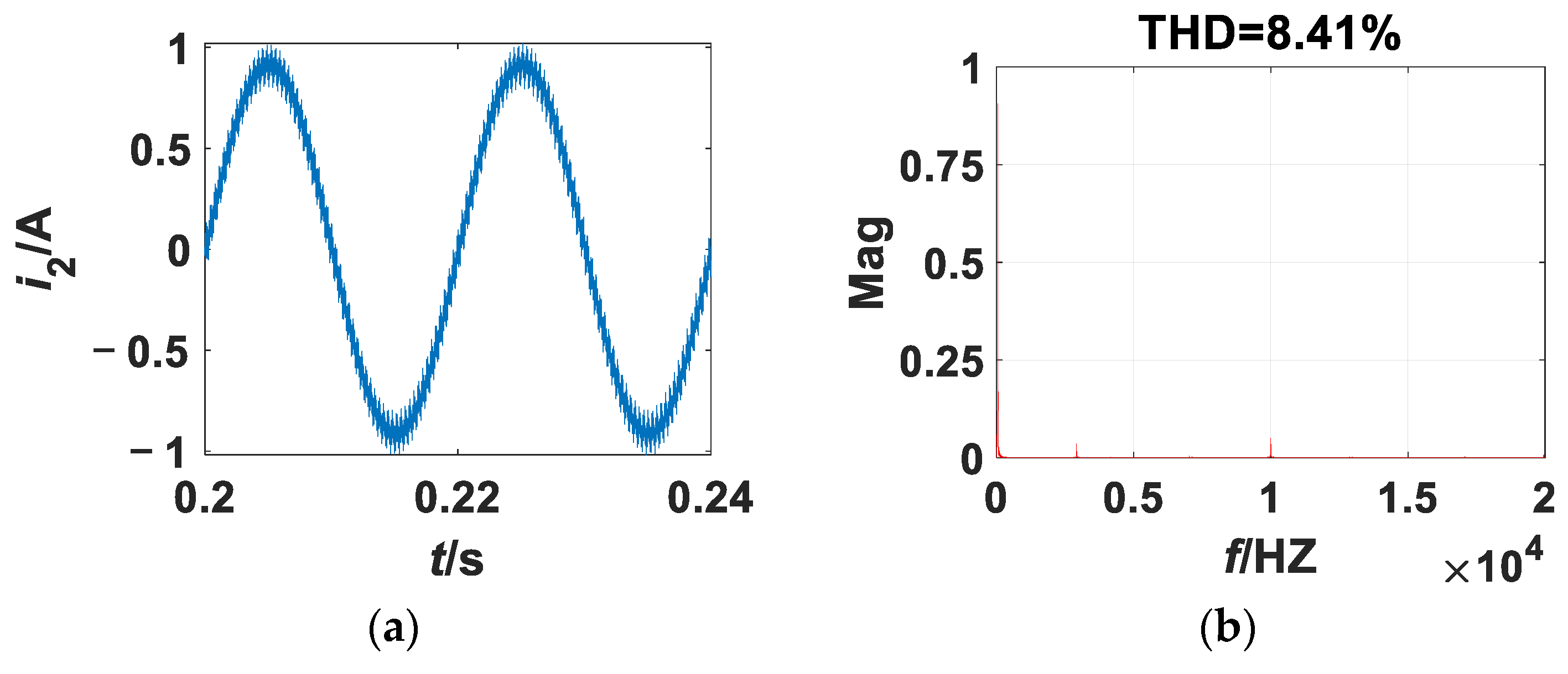
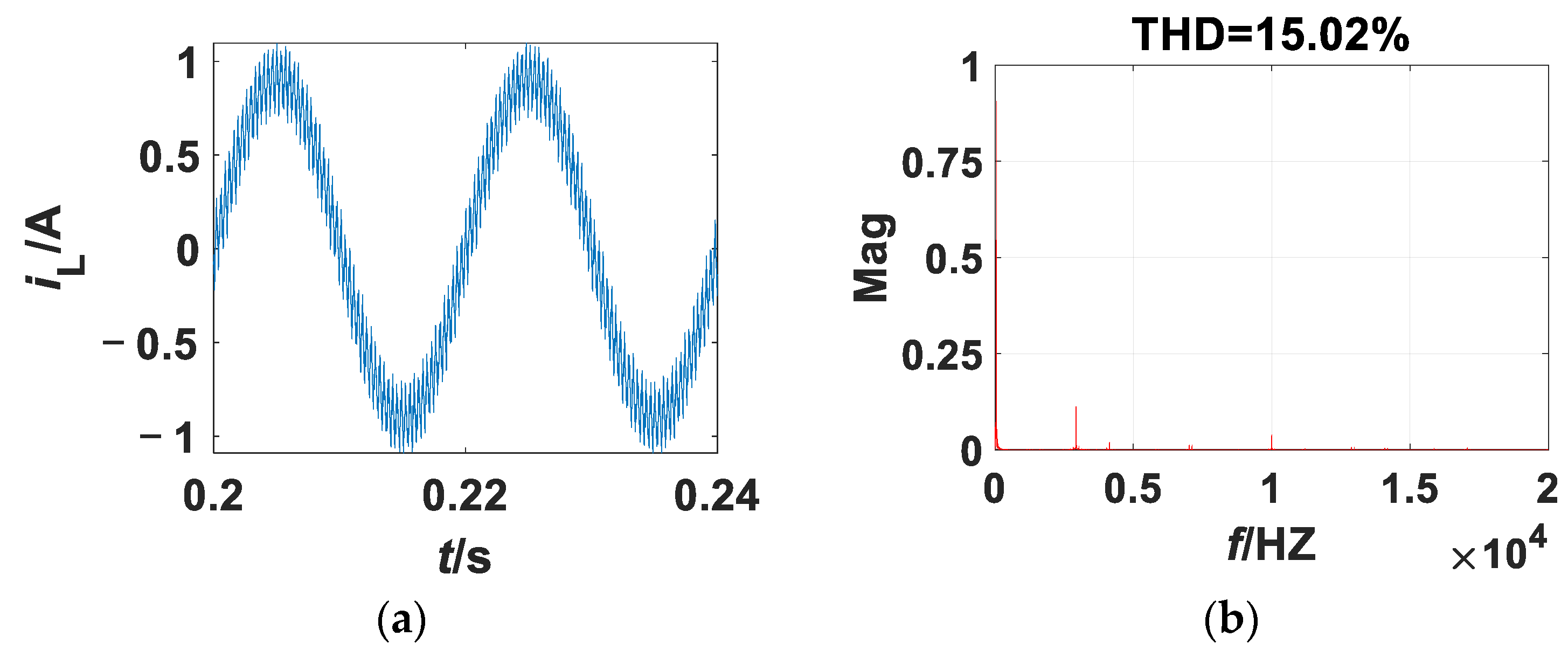
3. Numerical Simulations
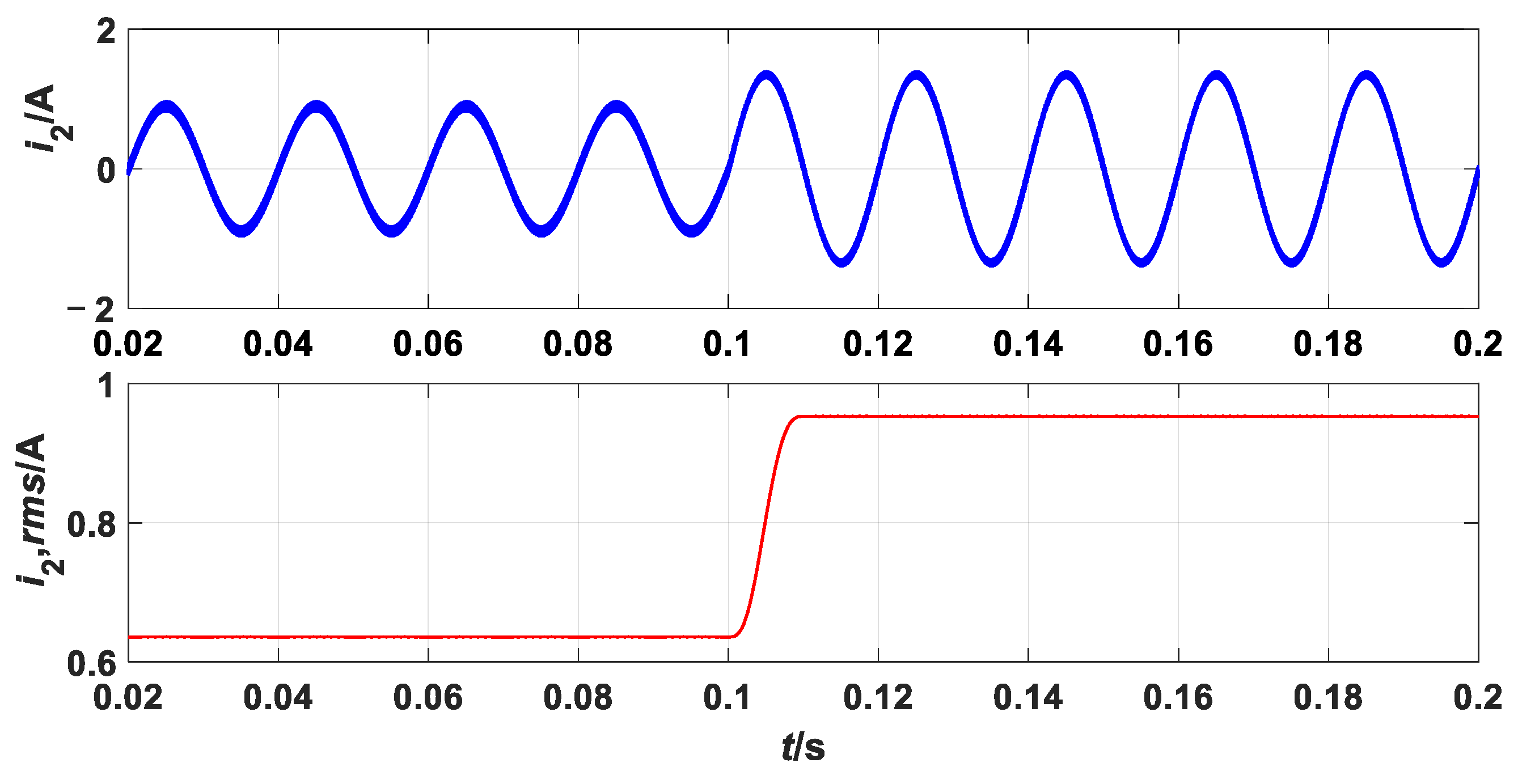
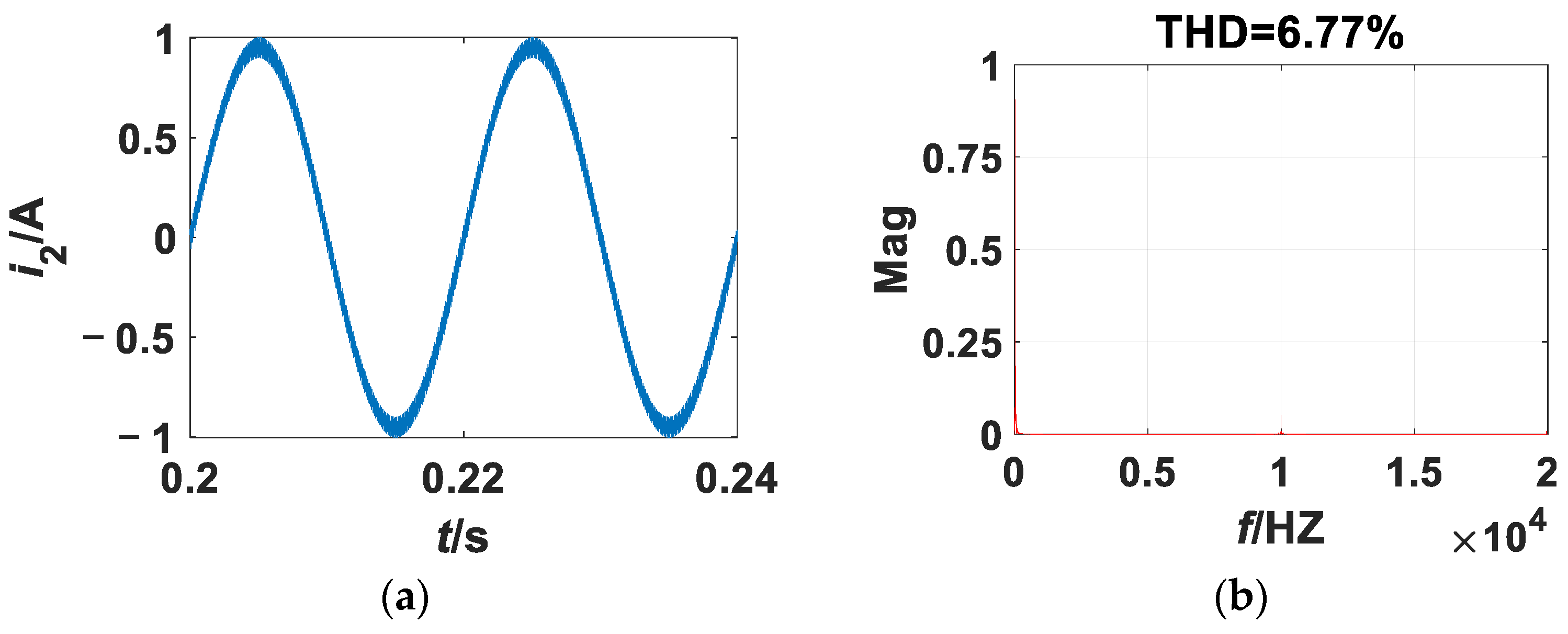
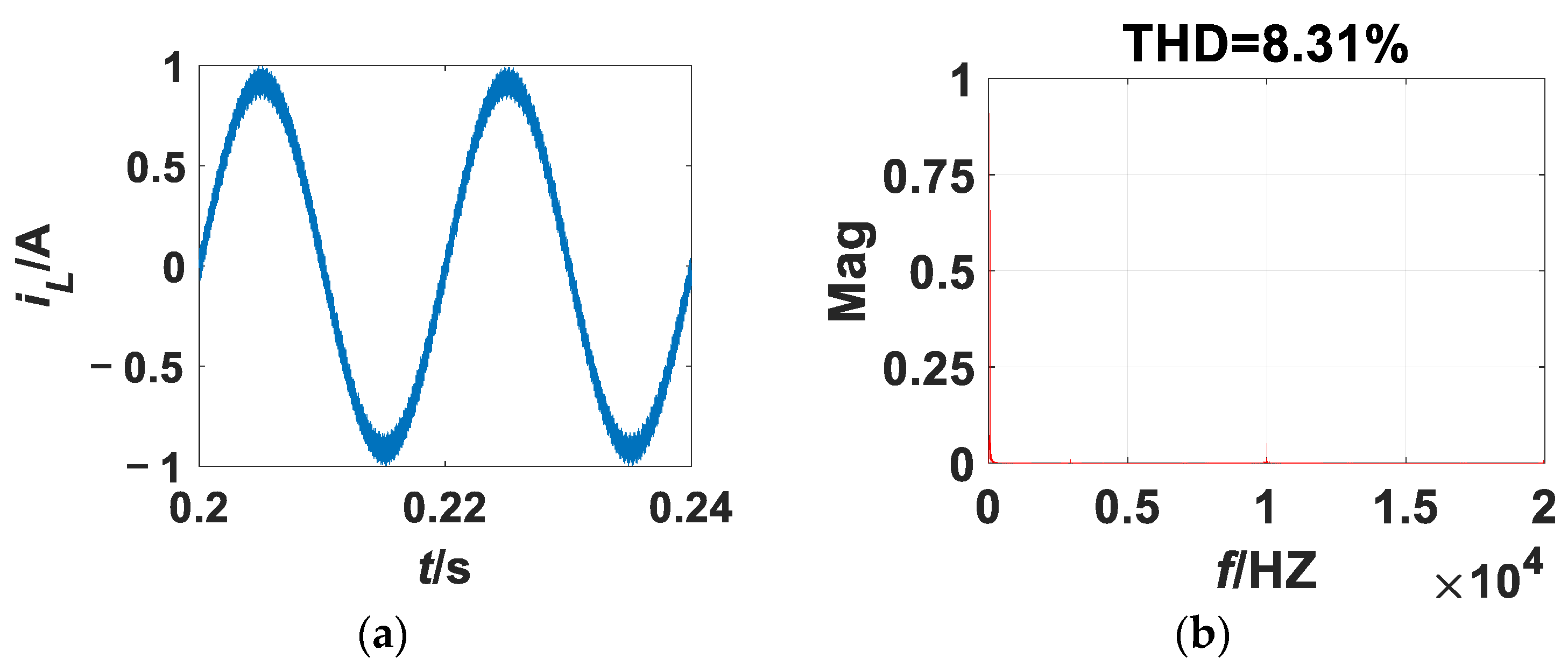
3.1. Transient-State Simulation
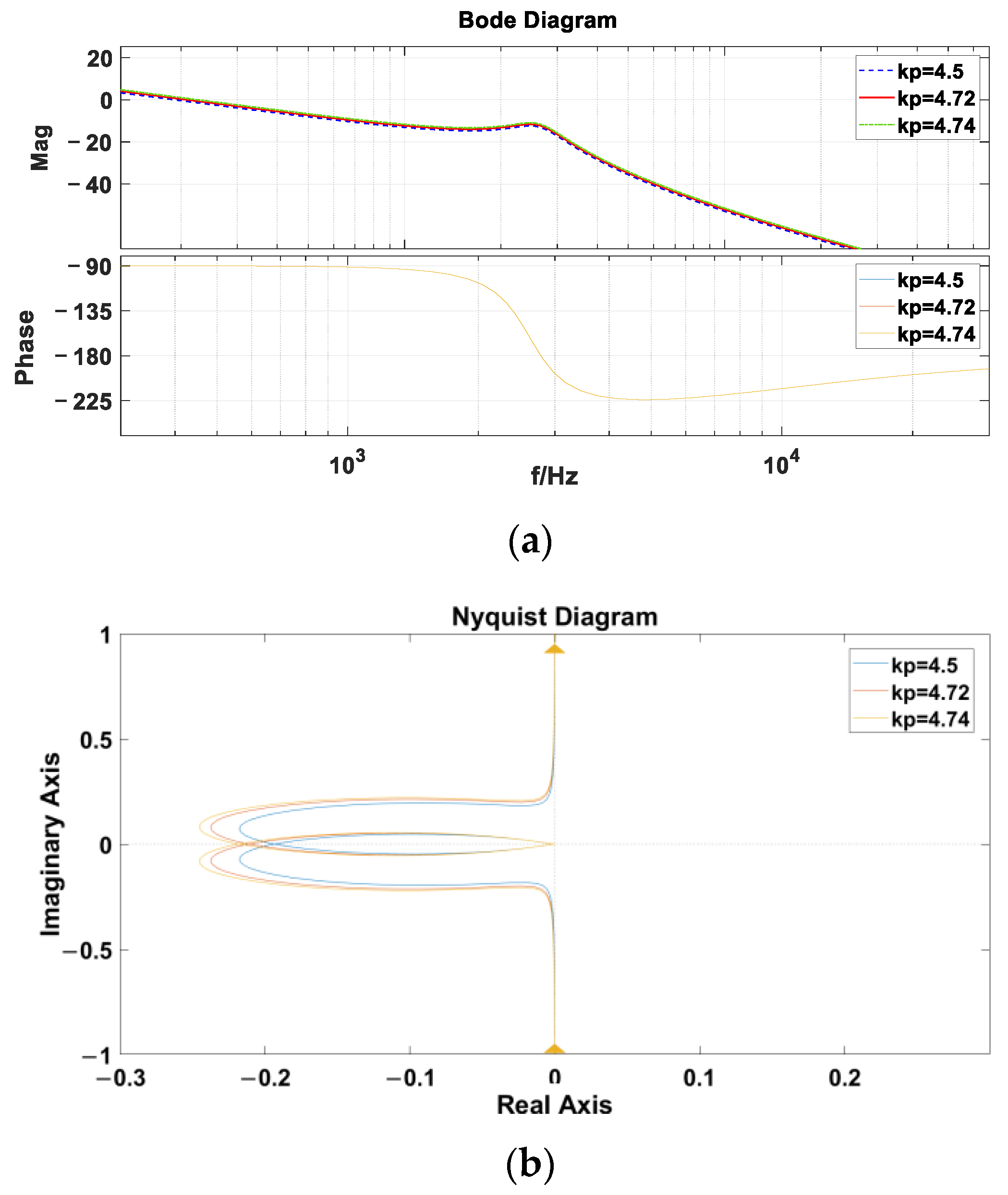
3.2. kp as the Bifurcation Parameter
3.2.1. kp as the Bifurcation Parameter
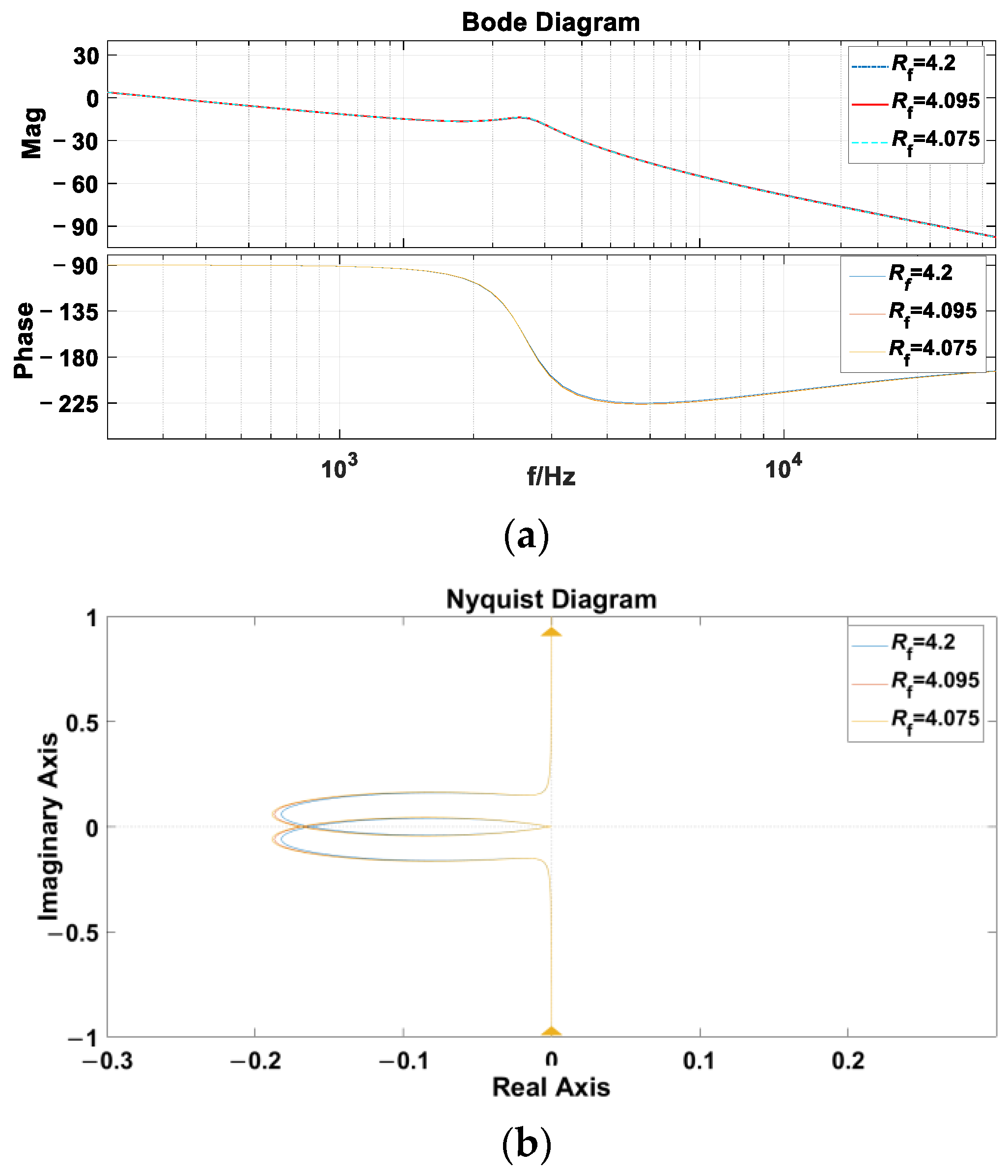
3.2.2. Rf as the Bifurcation Parameter
4. Theoretical Analysis
4.1. Stability Analysis Based on Linearized Switching Model
4.2. Stability Analysis Based on Nonlinear Dynamics
4.2.1. Average Model of the Circuit
4.2.2. Hopf Bifurcation Analysis
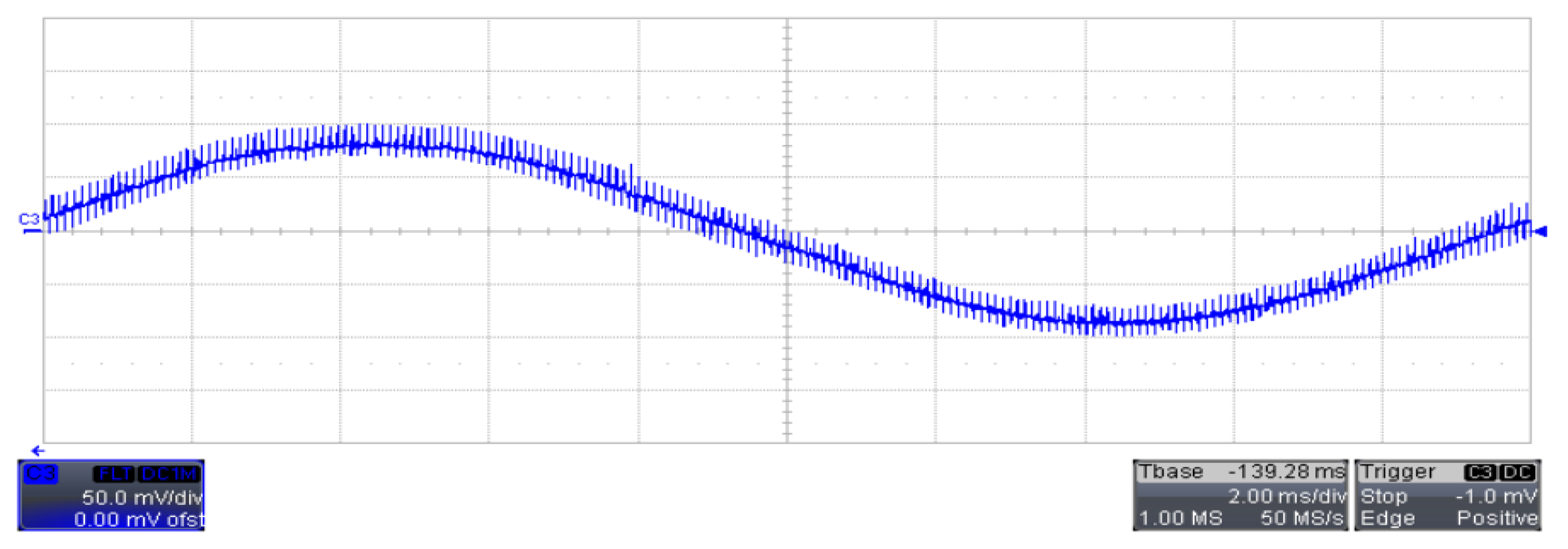
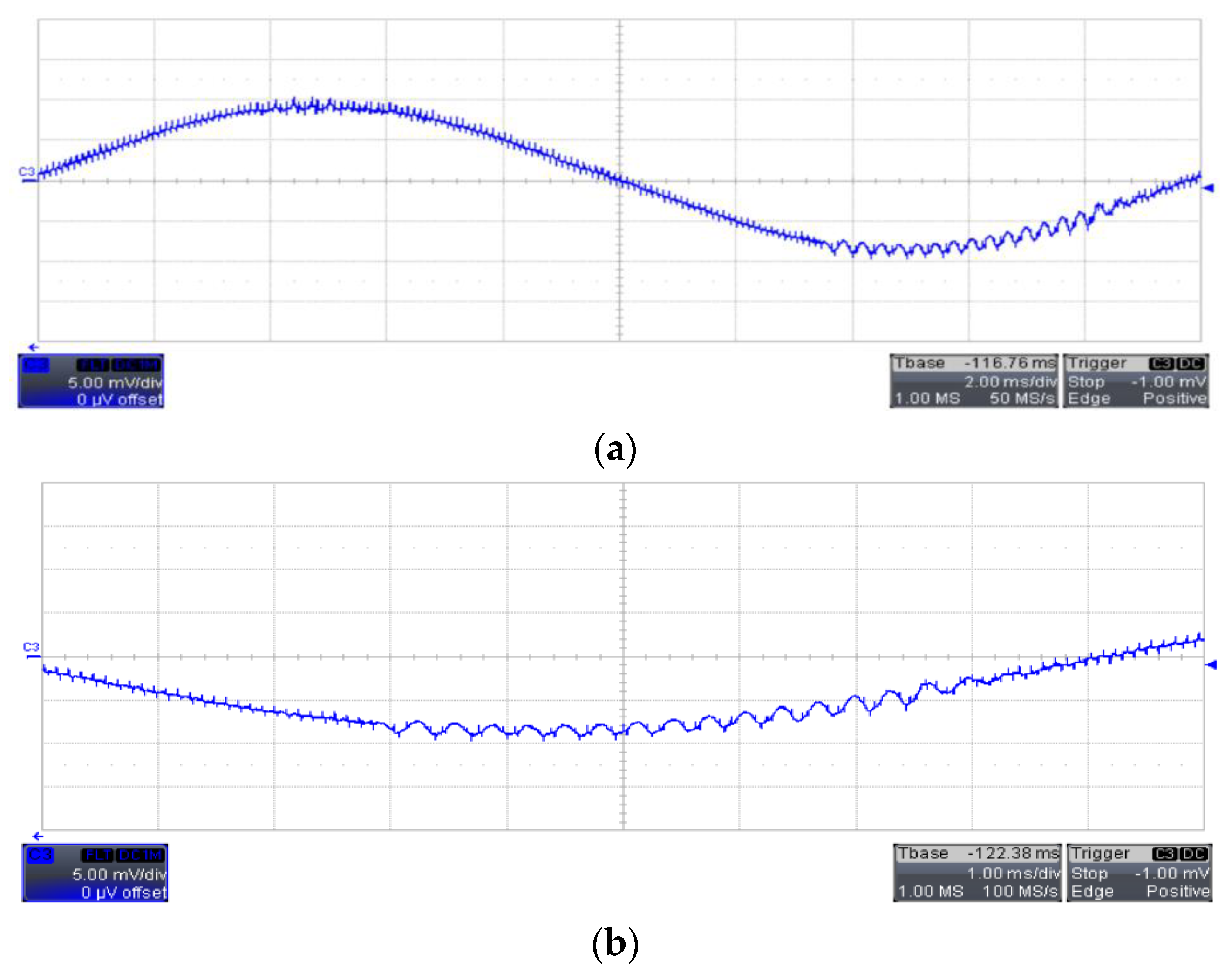
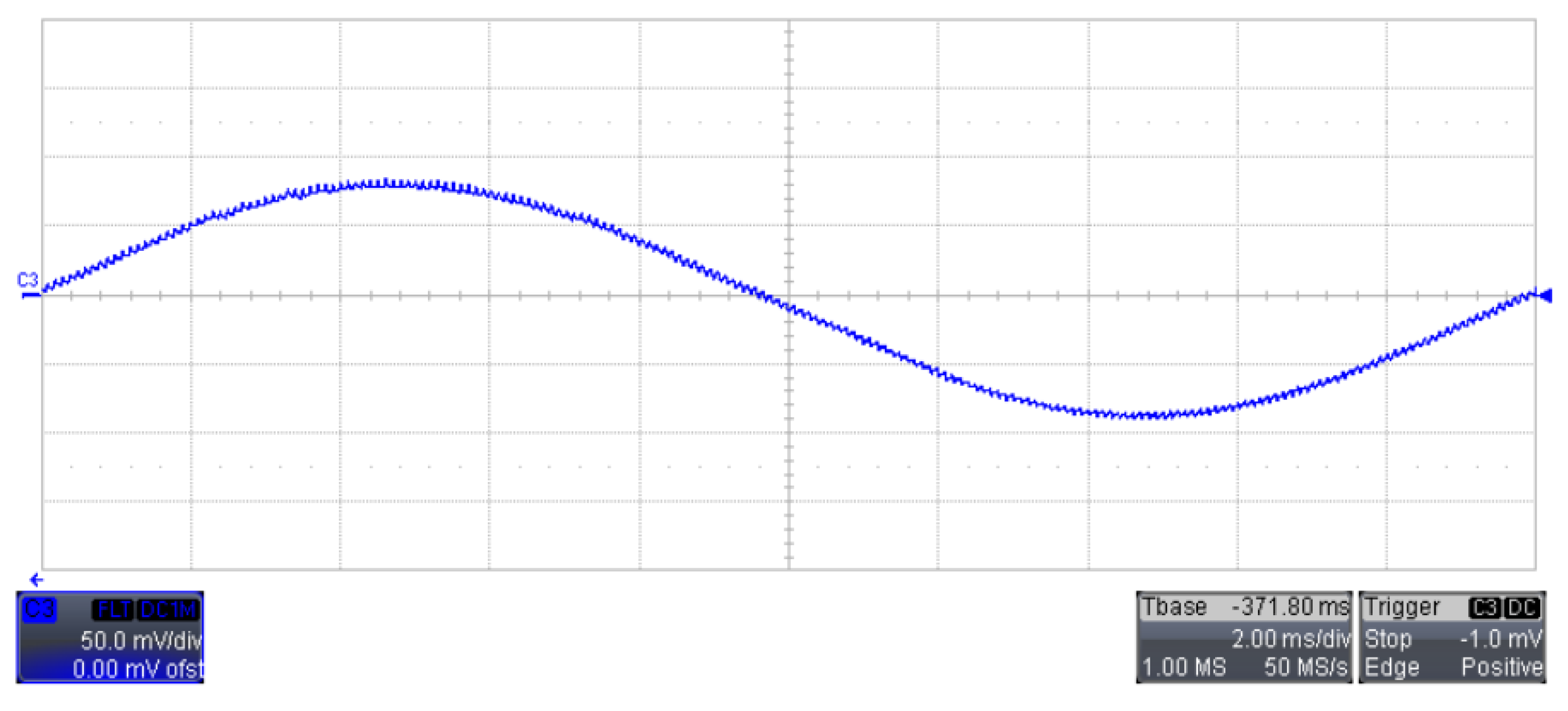
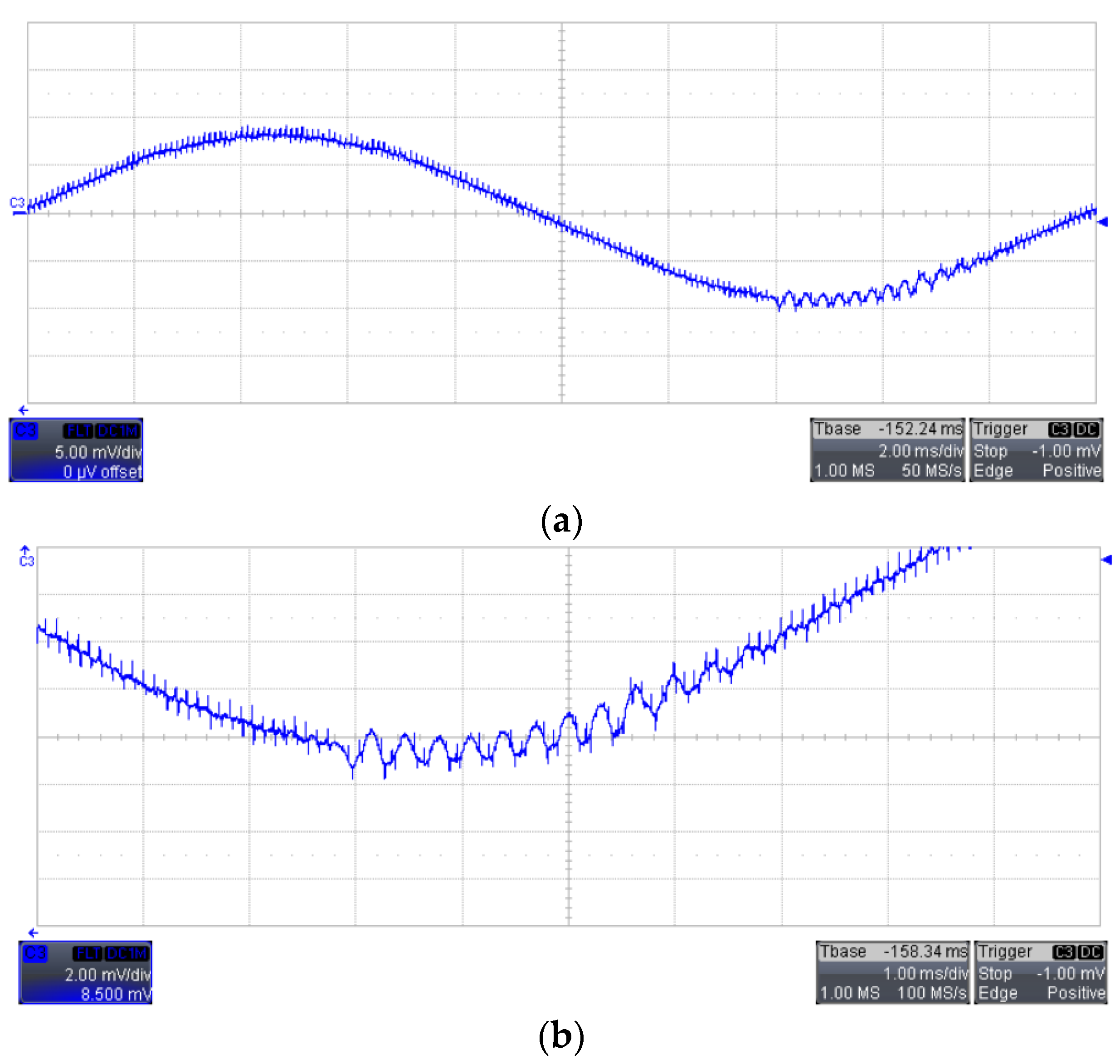
5. Experimental Verification
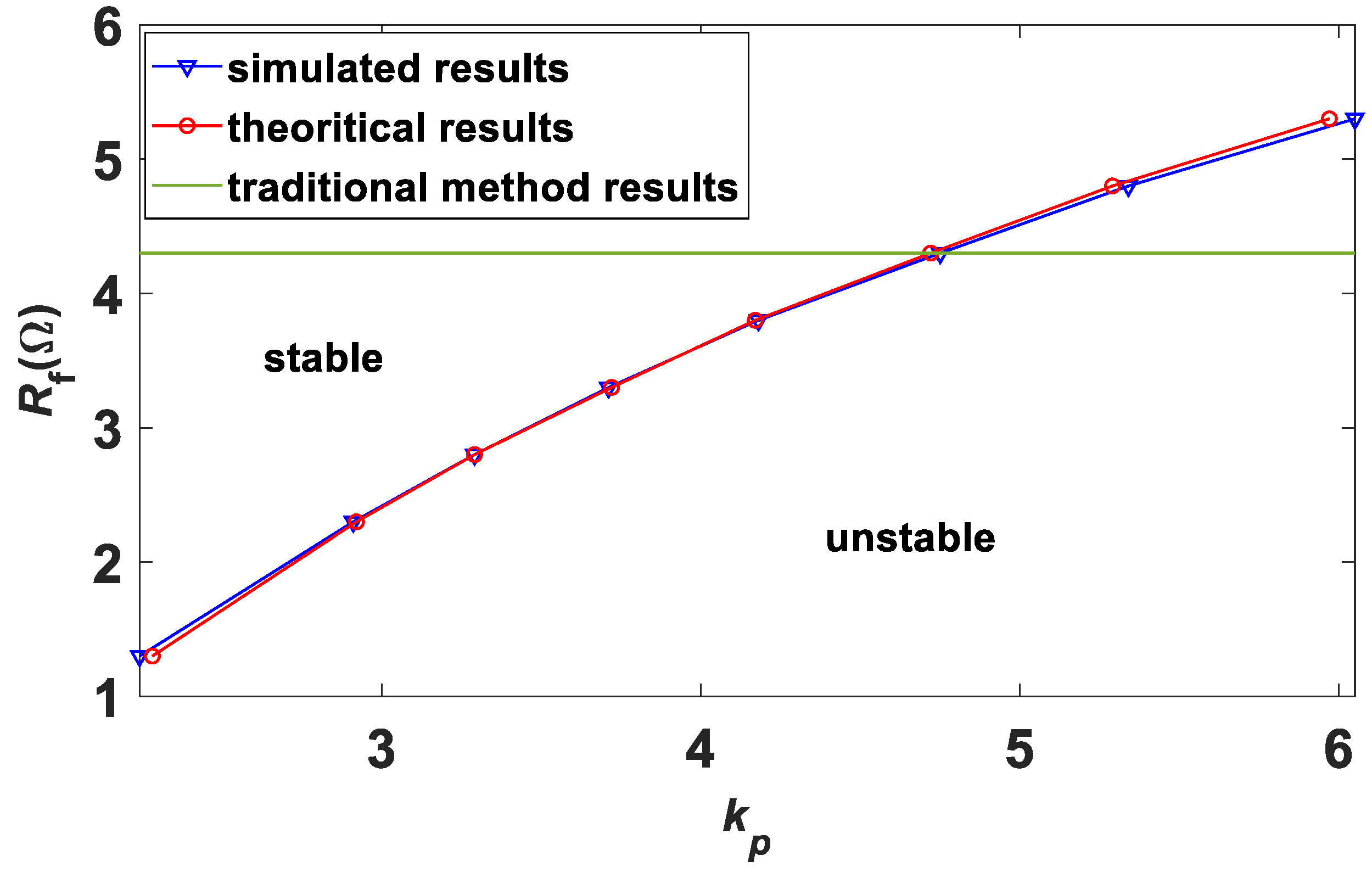
5.1. kp as the Bifurcation Parameter
5.2. Rf as the Bifurcation Parameter
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of Multilevel Inverters for PV Energy System Applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
- Cai, Y.; He, Y.; Zhou, H.; Liu, J. Active-Damping Disturbance-Rejection Control Strategy of LCL Grid-Connected Inverter Based on Inverter-Side-Current Feedback. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7183–7198. [Google Scholar]
- Singh, J.K.; Prakash, S.; Al Jaafari, K.; Al Zaabi, O.; Al Hosani, K.; Behera, R.K.; Muduli, U.R. Active Disturbance Rejection Control of Photovoltaic Three-Phase Grid Following Inverters Under Uncertainty and Grid Voltage Variations. IEEE Trans. Power Delivery 2023, 38, 3155–3168. [Google Scholar]
- Ma, G.D.; Xie, C.; Li, C.; Zou, J.X.; Guerrero, J.M. Passivity-Based Design of Passive Damping for LCL-Type Grid-Connected Inverters to Achieve Full-Frequency Passive Output Admittance. IEEE Trans. Power Electron. 2023, 38, 16048–16060. [Google Scholar]
- Ye, J.; Wang, H.Z.; Li, B.J.; Huang, Y.K.; Xu, J.B.; Shen, A.W. Passivity-Based Controller Design of PCC Voltage Feedforward Active Damping for Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2023, 38, 16048–16060. [Google Scholar]
- Zhe, W.; Ishak, D.; Hamidi, M.N. A Grid-Connected Inverter with Grid-Voltage-Weighted Feedforward Control Based on the Quasi-Proportional Resonance Controller for Suppressing Grid Voltage Disturbances. Energies 2024, 17, 885. [Google Scholar] [CrossRef]
- Zhang, J.S.; Yang, X.; Chen, W.J.; Zhou, H.W.; Luo, J. A Multifrequency Small-Signal Model for the MLCL-Filtered Grid-Connected Inverter Considering the FCE of Nonlinear Inductors. IEEE Trans. Ind. Electron. 2023, 70, 4901–4911. [Google Scholar]
- Zhang, R.; Zhang, C.H.; Xing, X.Y.; Chi, S.M.; Liu, C.; Fang, J.Y. Modeling and Attenuation of Common Mode Resonance Current for Improved LCL-Type Parallel Inverters in PV Plants. IEEE Trans. Ind. Inform. 2023, 20, 5193–5205. [Google Scholar] [CrossRef]
- Han, Y.; Mengling, Y.; Li, H.; Yang, P.; Xu, L.; Coelho, E.A.; Guerrero, J.M. Modeling and Stability Analysis of LCL -Type Grid-Connected Inverters: A Comprehensive Overview. IEEE Access 2019, 7, 114975–115001. [Google Scholar]
- Pea-Alzola, R.; Liserre, M.; Blaabjerg, F.; Sebastián, R.; Dannehl, J.; Fuchs, F.W. Analysis of the passive damping losses in LCL-filter based grid converters. IEEE Trans. Power Electron. 2013, 28, 2642–2646. [Google Scholar]
- Wu, W.; Liu, J.; Li, Y.; Blaabjerg, F. Individual Channel Design-Based Precise Analysis and Design for Three-Phase Grid-Tied Inverter With LCL-Filter Under Unbalanced Grid Impedance. IEEE Trans. Power Electron. 2020, 35, 5381–5396. [Google Scholar]
- Khan, D.; Qais, M.; Hu, P. A reinforcement learning-based control system for higher resonance frequency conditions of grid-integrated LCL-filtered BESS. J. Energy Storage 2024, 93, 112373. [Google Scholar]
- Yang, Z.; Shah, C.; Chen, T.; Yu, L.; Joebges, P.; De Doncker, R.W. Stability Investigation of Three-Phase Grid-Tied PV Inverter Systems Using Impedance Models. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2672–2684. [Google Scholar]
- Li, X.Q.; Wu, X.J.; Geng, Y.W.; Zhang, Q. Stability Analysis of Grid-Connected Inverters with an LCL Filter Considering Grid Impedance. J. Power Electron. 2013, 13, 896–908. [Google Scholar]
- Zhu, T.; Huang, G.; Ouyang, X.; Zhang, W.; Wang, Y.; Ye, X.; Wang, Y.; Gao, S. Analysis and Suppression of Harmonic Resonance in Photovoltaic Grid-Connected Systems. Energies 2024, 17, 1218. [Google Scholar] [CrossRef]
- Yang, J.X.; Tse, C.K.; Liu, D. Sub-Synchronous Oscillations and Transient Stability of Islanded Microgrid. IEEE Trans. Power Syst. 2023, 38, 3760–3774. [Google Scholar]
- Cao, H.B.; Wang, F.Q.; Liu, J.J. Analysis of Fast-Scale Instability in Three-Level T-Type Single-Phase Inverter Feeding Diode-Bridge Rectifier With Inductive Load. IEEE Trans Power Electron. 2022, 37, 15066–15083. [Google Scholar]
- Luo, C.; Liu, T.; Wang, X.F.; Ma, X.K. Design-Oriented Analysis of DC-Link Voltage Control for Transient Stability of Grid-Forming Inverters. IEEE Trans. Ind. Electron. 2024, 71, 3698–3707. [Google Scholar]
- Yang, F.; Yang, L.H.; Ma, X.K. Fast-Scale Bifurcation Analysis in One-Cycle Controlled H-Bridge Inverter. Int. J. Bifurcat. Chaos 2016, 26, 1650199. [Google Scholar]
- Cheng, C.; Xie, S.; Qian, Q.; Xu, J. On Absolute Stability of Open-Loop Synchronized Single-Phase Grid-Following Inverters. IEEE Trans. Ind. Electron. 2023, 70, 10239–10248. [Google Scholar]
- Cheng, C.; Xie, S.; Xu, J.; Qian, Q. Universal Absolute Stability Criterion for Single-Phase Grid-Following Inverters Equipped With Orthogonal-Normalization-Based Grid Synchronizer. IEEE Trans. Power Electron. 2023, 38, 9090–9099. [Google Scholar]
- Avrutin, V.; Zhusubaliyev, Z.T.; Suissa, D.; El Aroudi, A. Non-observable chaos in piecewise smooth systems. Nonlinear Dyn. 2020, 99, 2031–2048. [Google Scholar]
- Zhusubaliyev, Z.T.; Avrutin, V.; Kucherov, A.S.; Haroun, R.; El Aroudi, A. Period adding with symmetry breaking/recovering in a power inverter with hysteresis control. Physica D 2023, 444, 133600. [Google Scholar]
- Yin, Z.; Gong, R.; Lu, Y. Slow-Scale Nonlinear Control of a H-Bridge Photovoltaic Inverter. Electronics 2023, 12, 2000. [Google Scholar] [CrossRef]
- Keyvani-Boroujeni, B.; Shahgholian, G.; Fani, B. A Distributed Secondary Control Approach for Inverter Dominated Microgrids with Application to Avoiding Bifurcation Triggered Instabilities. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3361–3371. [Google Scholar]
- Ji, H.; Xie, F.; Shen, L.; Yang, R.; Zhang, B. Unstable behavior analysis and stabilization of double-loop proportional-integral control H-bridge inverter with inductive impedance load. Int. J. Circuit Theory Appl. 2022, 50, 904–925. [Google Scholar]
- Lei, B.; Xiao, G.C.; Wu, X.L.; Zheng, L. A unified “scalar” discrete-time model for enhancing bifurcation prediction in digitally controlled H-bridge grid-connected inverter. Int. J. Bifurcat. Chaos 2013, 23, 1350126. [Google Scholar]

| Name | Simulation Parameter |
|---|---|
| DC-side voltage | E = 12 V |
| Load resistance | R = 5 Ω |
| Inverter LCL filter parameters | L1 = 3.6 mH, C = 4.7 μF, L2 = 1 mH |
| Carrier amplitude | Vtri = 1 |
| Line frequency | f = 50 Hz |
| Invert switching frequency | fs = 10 kHz |
| Reference current amplitude | Iref = 1 A |
| kp | Rf | Simulation Results | System Status |
|---|---|---|---|
| 4.5 | 4.3 | not oscillate | stable |
| 4.72 | low-frequency oscillation | unstable | |
| 4.74 | oscillation increases | unstable | |
| 4.5 | 4.2 | not oscillate | stable |
| 4.095 | low-frequency oscillation | unstable | |
| 4.075 | oscillation increases | unstable |
| kp | Characteristic Root | System Status |
|---|---|---|
| 4.2 | −313.8650 ± 1.8214 × 104i, −9.8667 × 103 | equilibrium point |
| 4.3 | −247.3777 ± 1.8288 × 104i, −9.9997 × 103 | equilibrium point |
| 4.4 | −182.1180 ± 1.8363 × 104i, −1.0130 × 103 | equilibrium point |
| 4.5 | −118.0462 ± 1.8436 × 104i, −1.0258 × 103 | equilibrium point |
| 4.6891 | 0.00027 ± 1.8576 × 104i, −1.0494 × 103 | Hopf bifurcation |
| 4.76 | 43.2502 ± 1.8627 × 104i, −1.0581 × 103 | unstable |
| Rf | Characteristic Root | System Status |
|---|---|---|
| 4.4 | −185.7460 ± 1.8443 × 104, −1.0251 × 104 | equilibrium point |
| 4.3 | −118.0462 ± 1.8436 × 104i, −1.0258 × 104 | equilibrium point |
| 4.2 | −50.3659 ± 1.8430 × 104i, −1.0266 × 104 | equilibrium point |
| 4.1 | −16.5331 ± 1.8427 × 104i, −1.0270 × 104 | equilibrium point |
| 4.12556 | 0.0027 ± 1.8425 × 104i, −1.0272 × 104 | Hopf bifurcation |
| 4.09 | 24.0600 ± 1.8423 × 104i, −1.0274 × 104 | unstable |
| Rf | Traditional Method/Rf′ | Simulation Results/kp | Theoretical Results/kp |
|---|---|---|---|
| 2.3 Ω | 4.3 Ω | 2.91 | 2.92 |
| 2.8 Ω | 4.3 Ω | 3.29 | 3.29 |
| 3.3 Ω | 4.3 Ω | 3.71 | 3.72 |
| 3.8 Ω | 4.3 Ω | 4.18 | 4.17 |
| 4.3 Ω | 4.3 Ω | 4.75 | 4.72 |
| 4.8 Ω | 4.3 Ω | 5.34 | 5.39 |
| 5.3 Ω | 4.3 Ω | 6.05 | 5.97 |
| 1.3 Ω | 4.3 Ω | 2.24 | 2.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Bai, W.; Huang, X.; Wang, Y.; Liu, J.; Kang, Z. Slow-Scale Bifurcation Analysis of a Single-Phase Voltage Source Full-Bridge Inverter with an LCL Filter. Energies 2024, 17, 4168. https://doi.org/10.3390/en17164168
Yang F, Bai W, Huang X, Wang Y, Liu J, Kang Z. Slow-Scale Bifurcation Analysis of a Single-Phase Voltage Source Full-Bridge Inverter with an LCL Filter. Energies. 2024; 17(16):4168. https://doi.org/10.3390/en17164168
Chicago/Turabian StyleYang, Fang, Weiye Bai, Xianghui Huang, Yuanbin Wang, Jiang Liu, and Zhen Kang. 2024. "Slow-Scale Bifurcation Analysis of a Single-Phase Voltage Source Full-Bridge Inverter with an LCL Filter" Energies 17, no. 16: 4168. https://doi.org/10.3390/en17164168
APA StyleYang, F., Bai, W., Huang, X., Wang, Y., Liu, J., & Kang, Z. (2024). Slow-Scale Bifurcation Analysis of a Single-Phase Voltage Source Full-Bridge Inverter with an LCL Filter. Energies, 17(16), 4168. https://doi.org/10.3390/en17164168






