On the Influence of H2 Addition on NH3 Laminar Flame Speed under Engine-like Conditions
Abstract
1. Introduction
2. The Model
2.1. Governing Equations
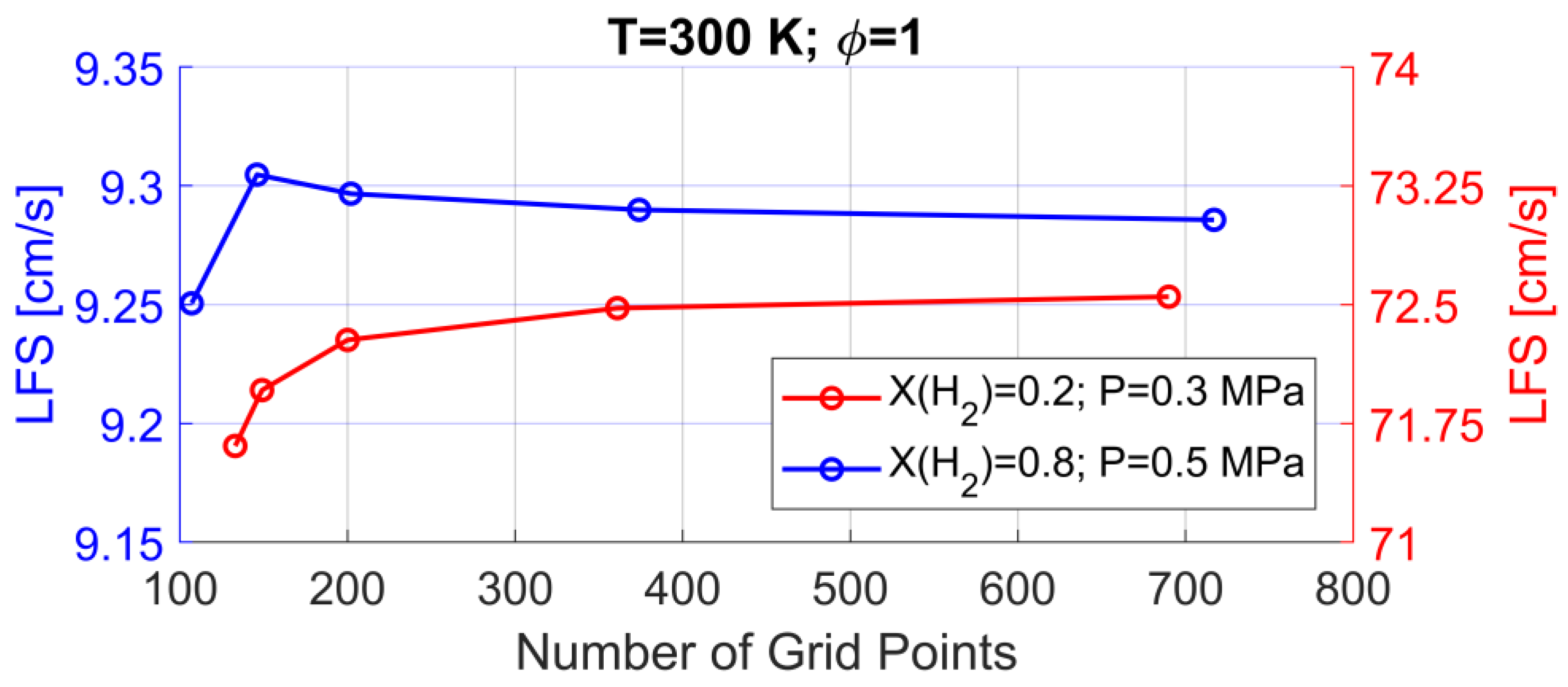
2.2. Numerical Method
3. Results and Discussion
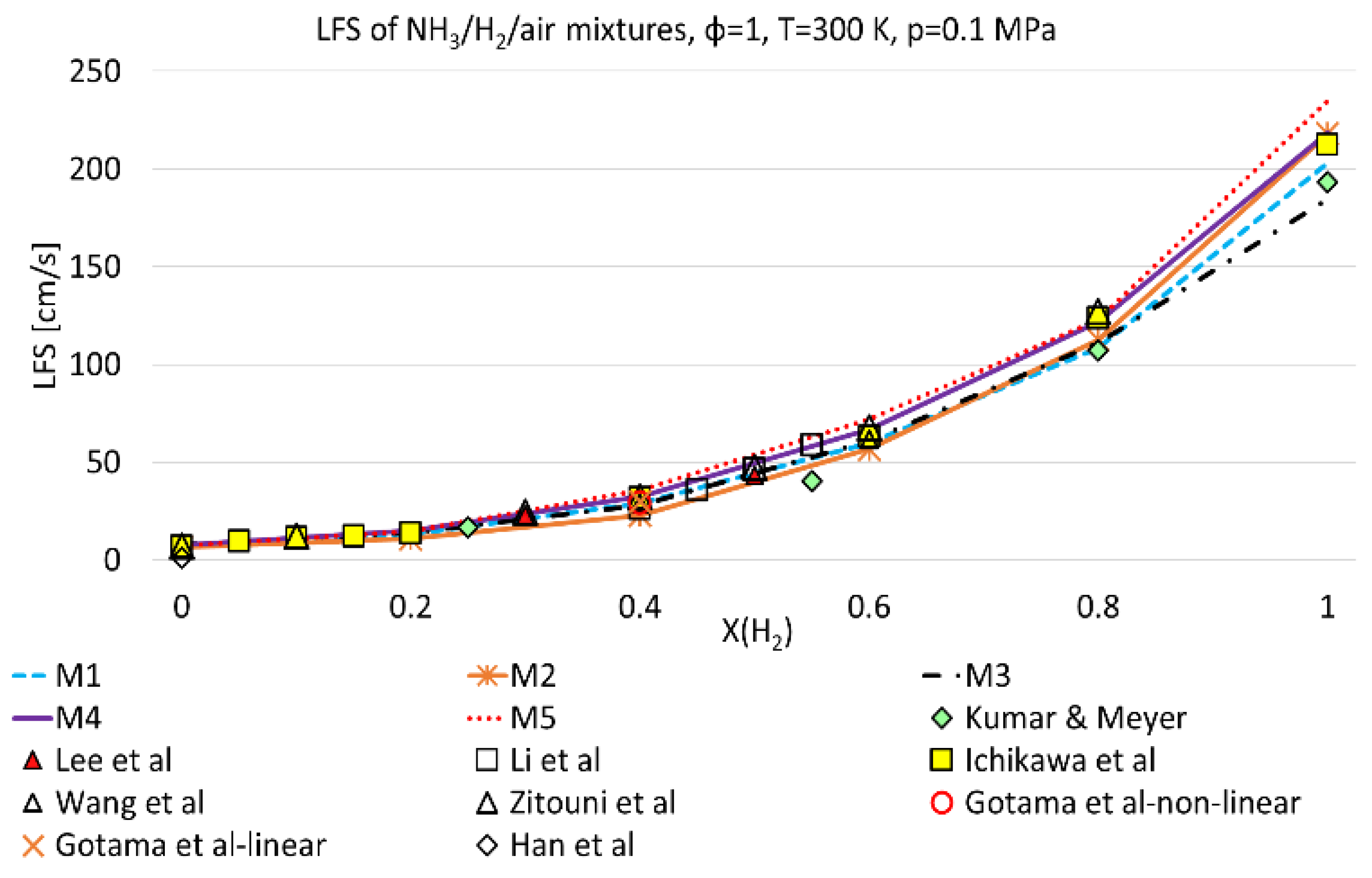
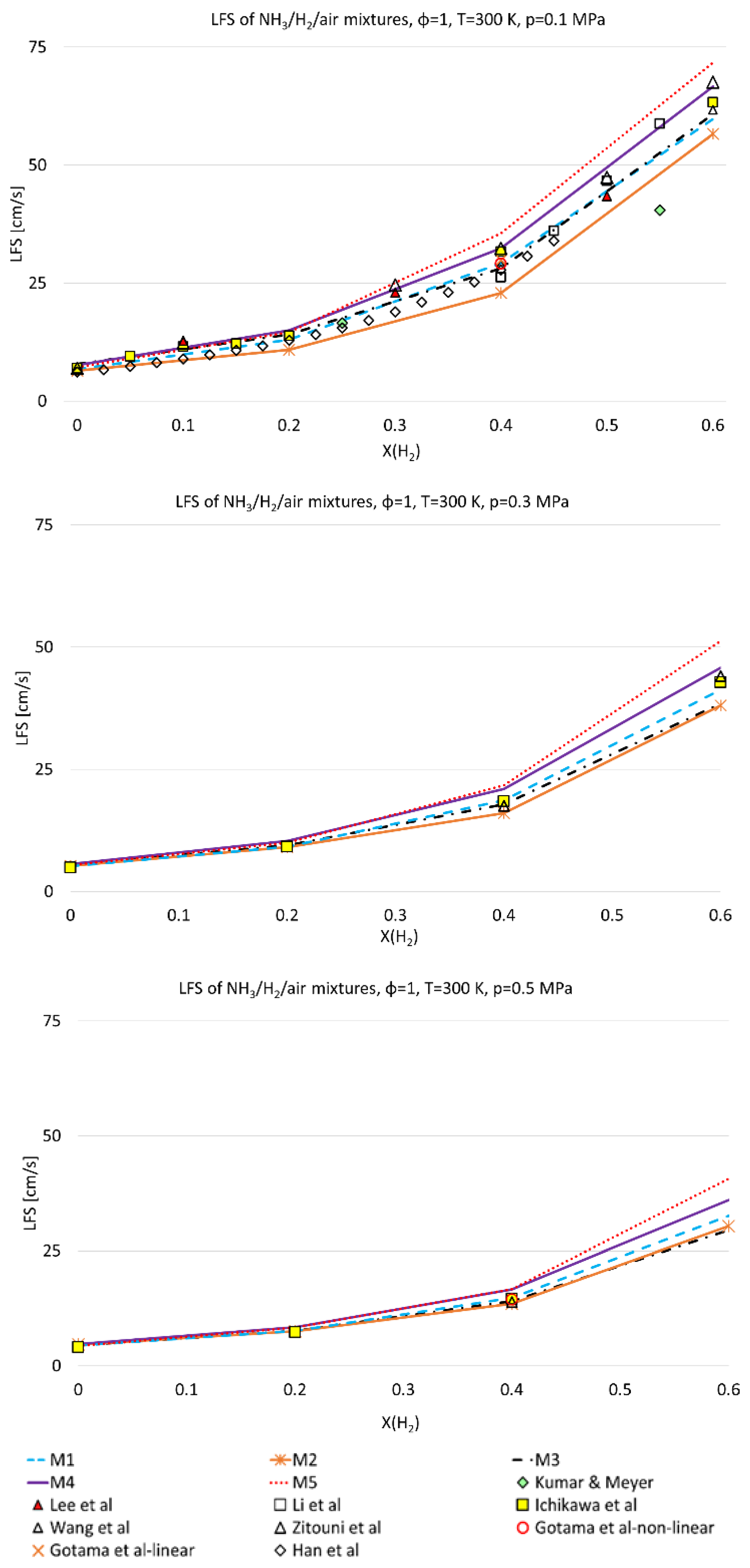
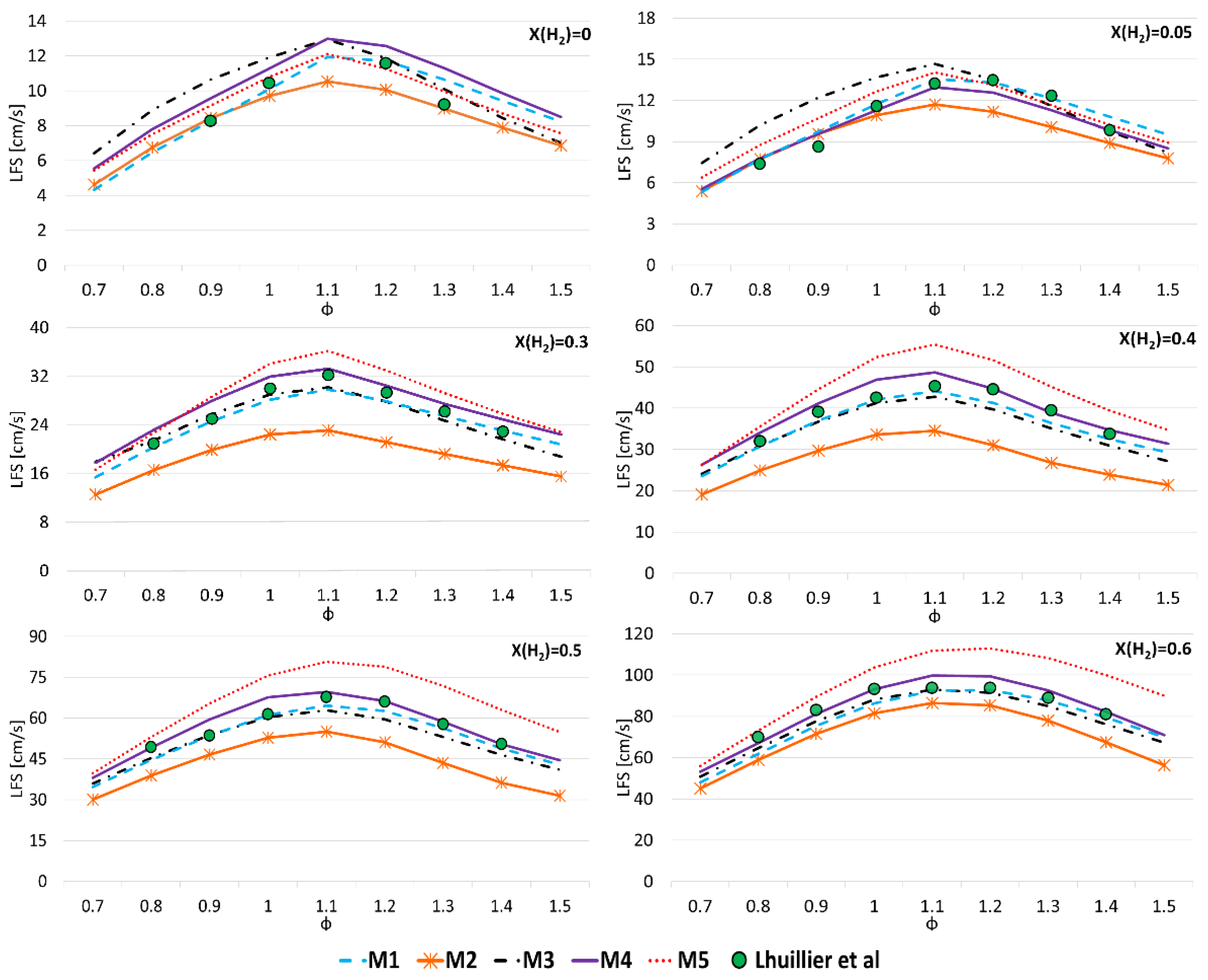
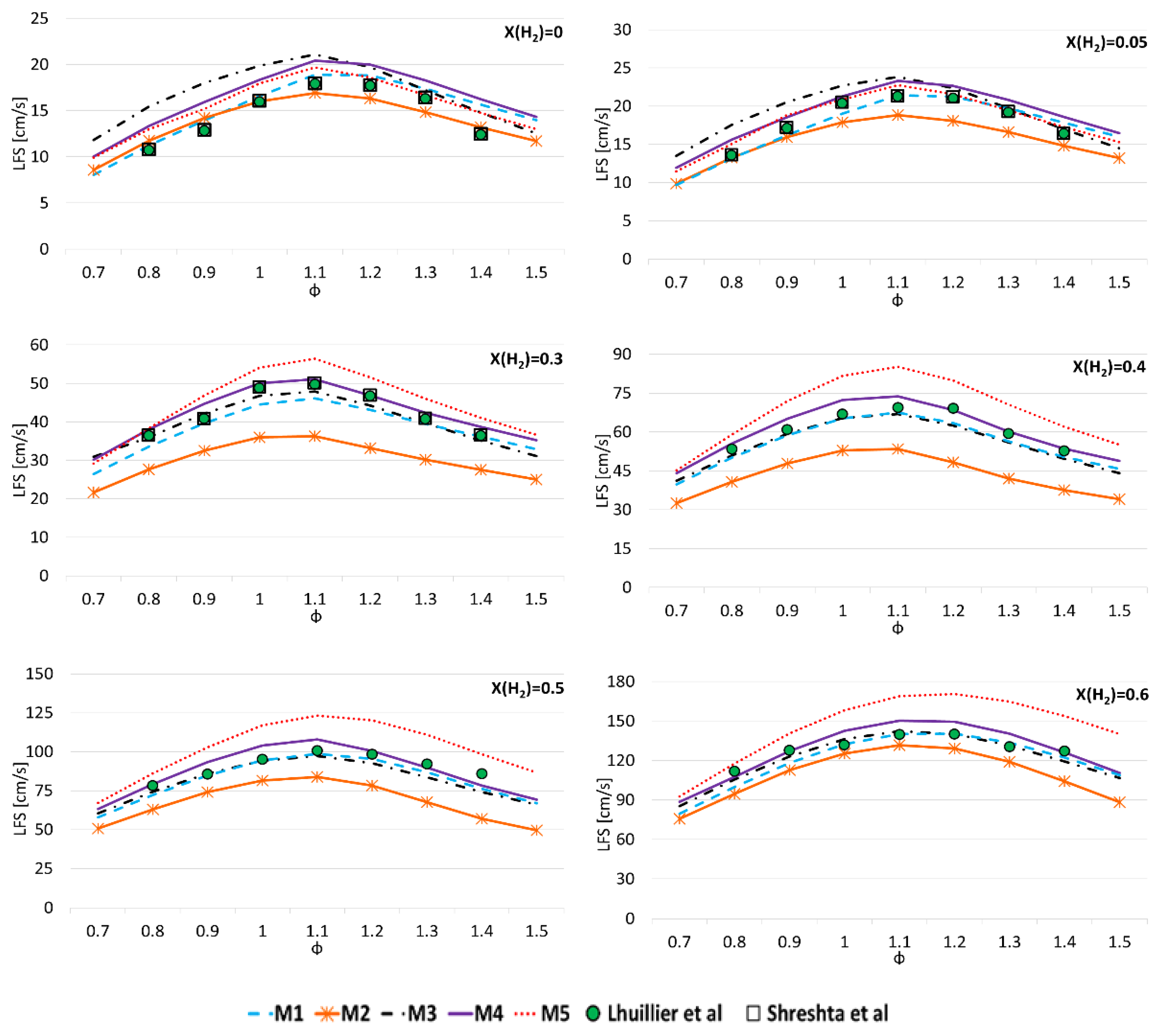
3.1. Model Validation
3.2. A Parametric Analysis
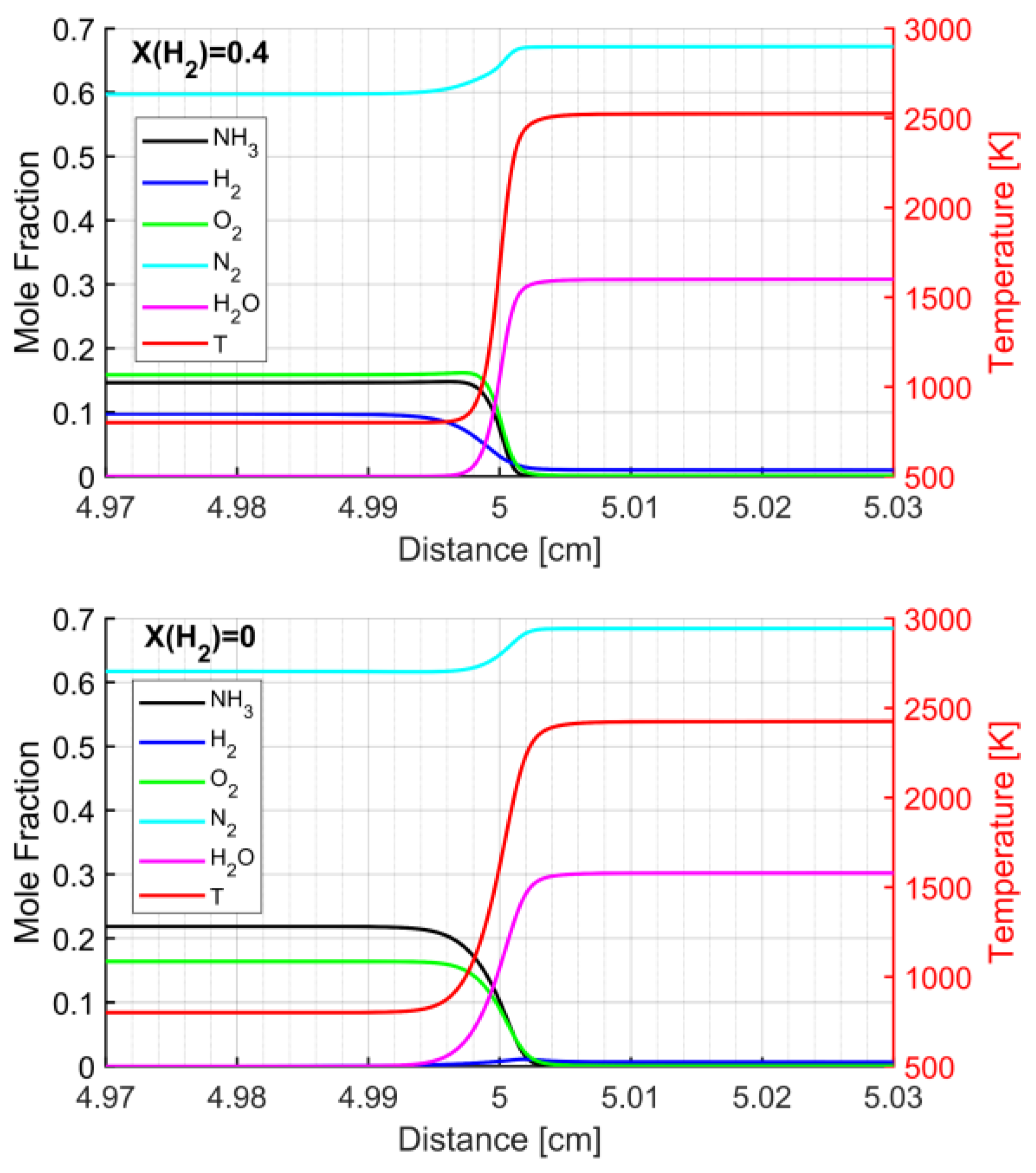
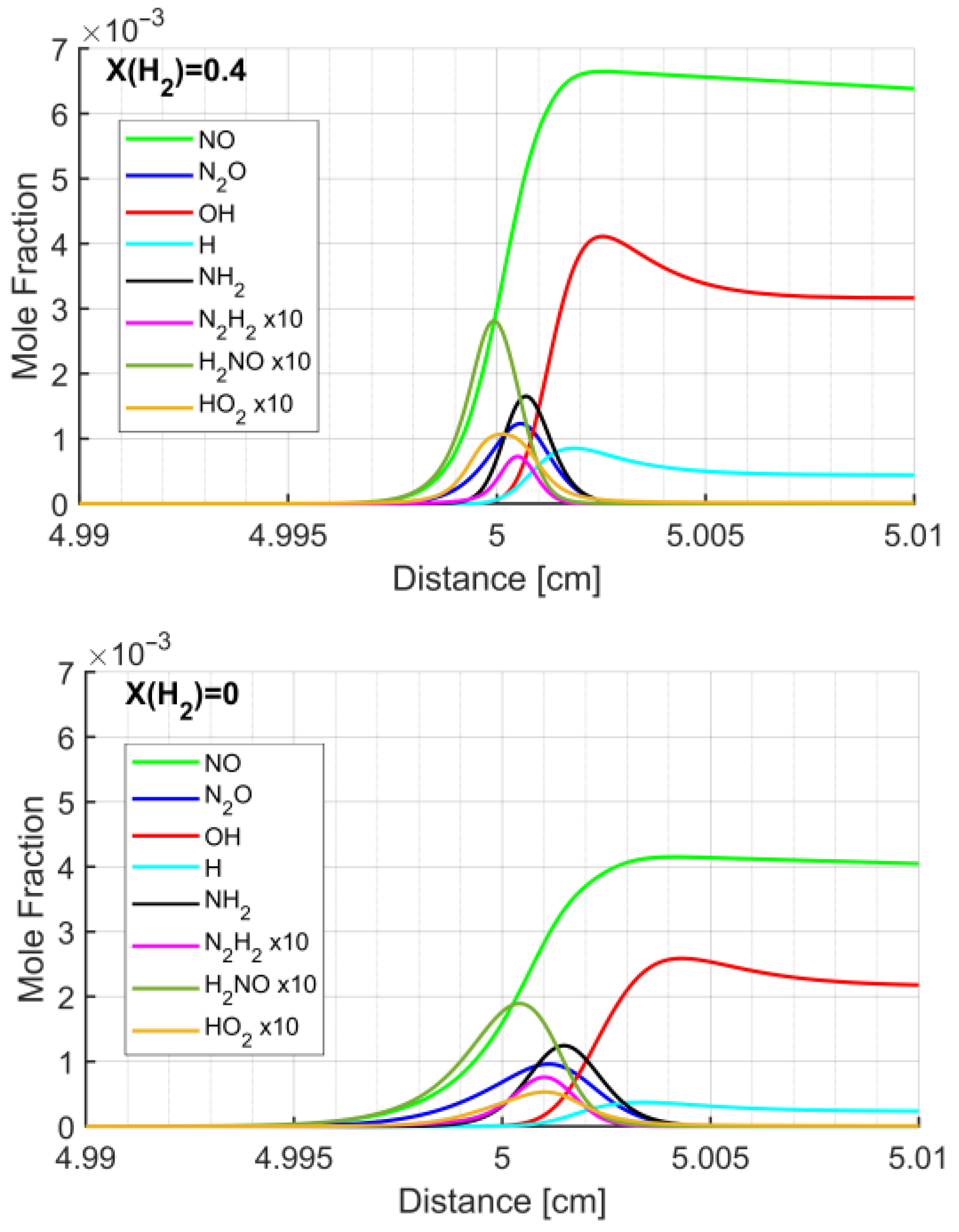
3.3. Structure of the NH3/H2 Flame
4. Conclusions
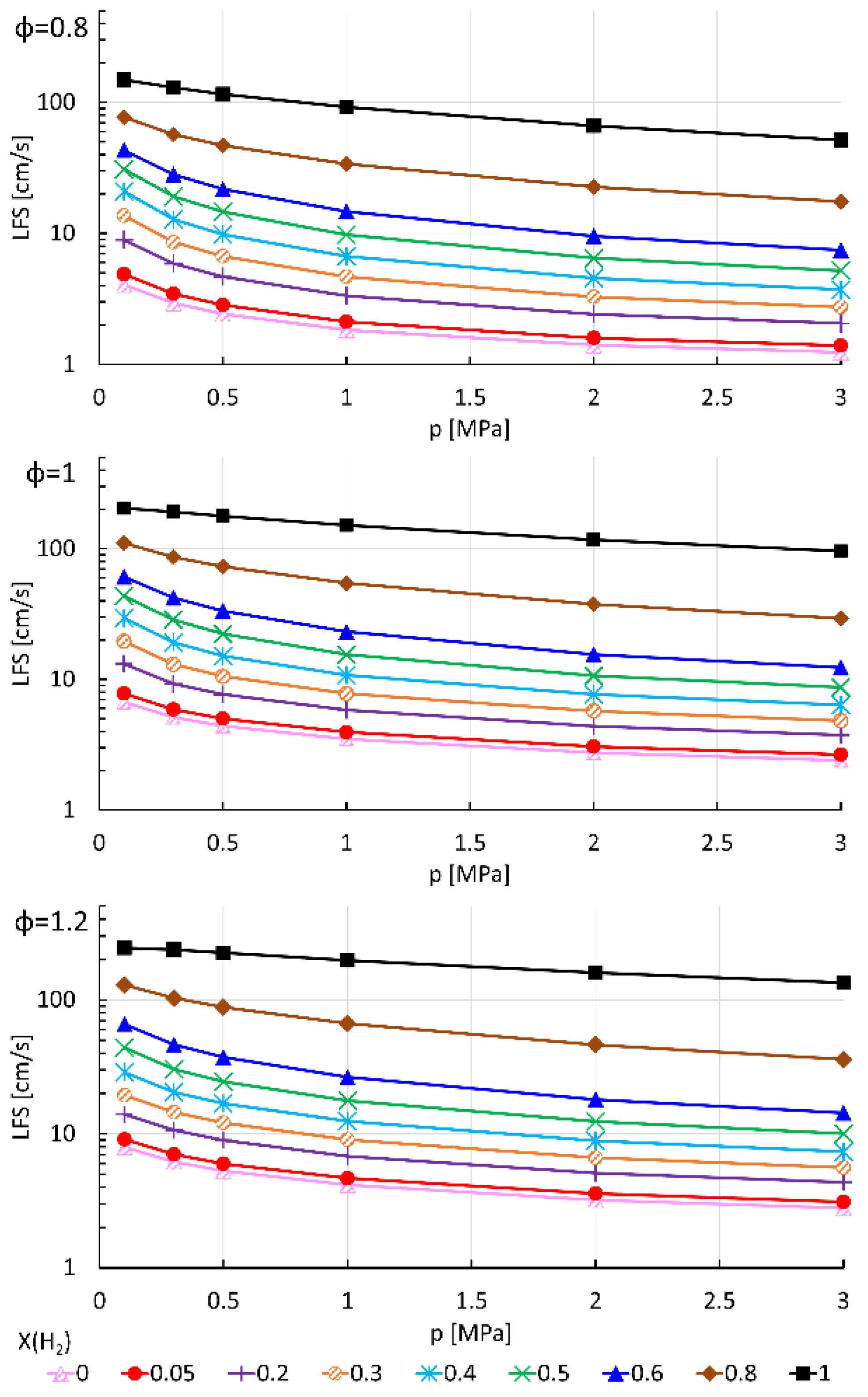
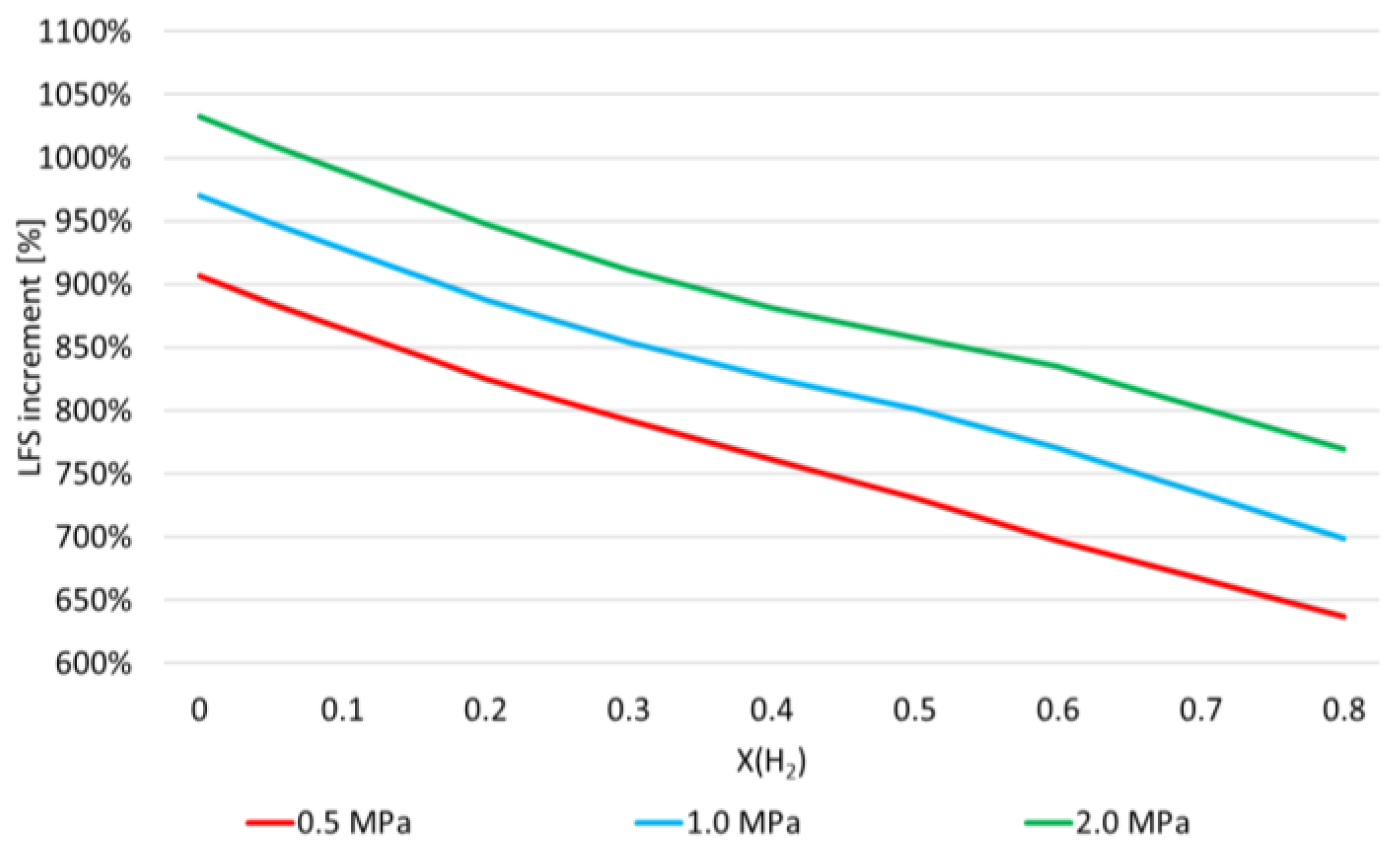
- LFS exponentially increases with H2 mole fraction, at 300 K and 800 K and for all pressures and equivalence ratios considered in this work;
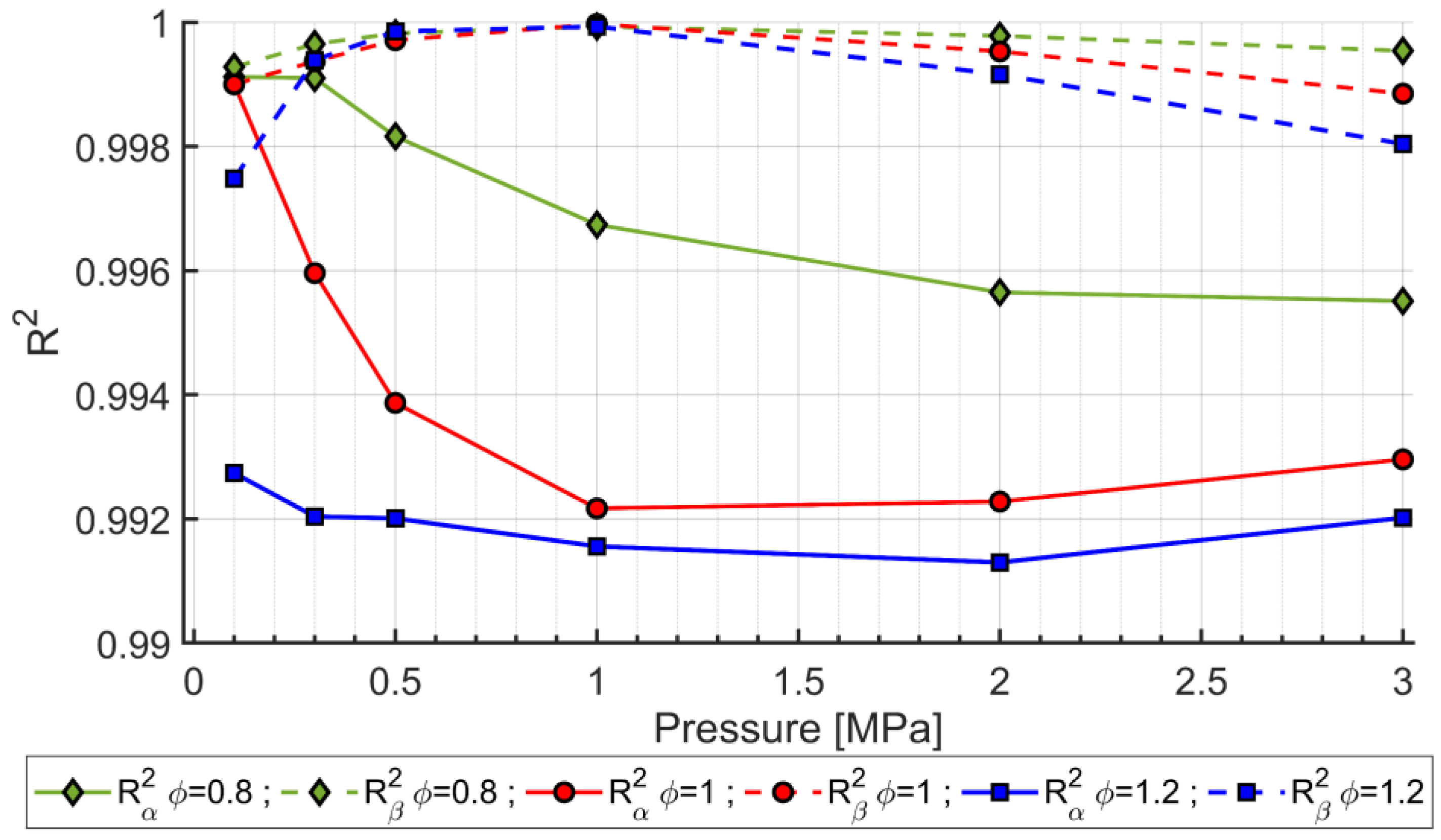
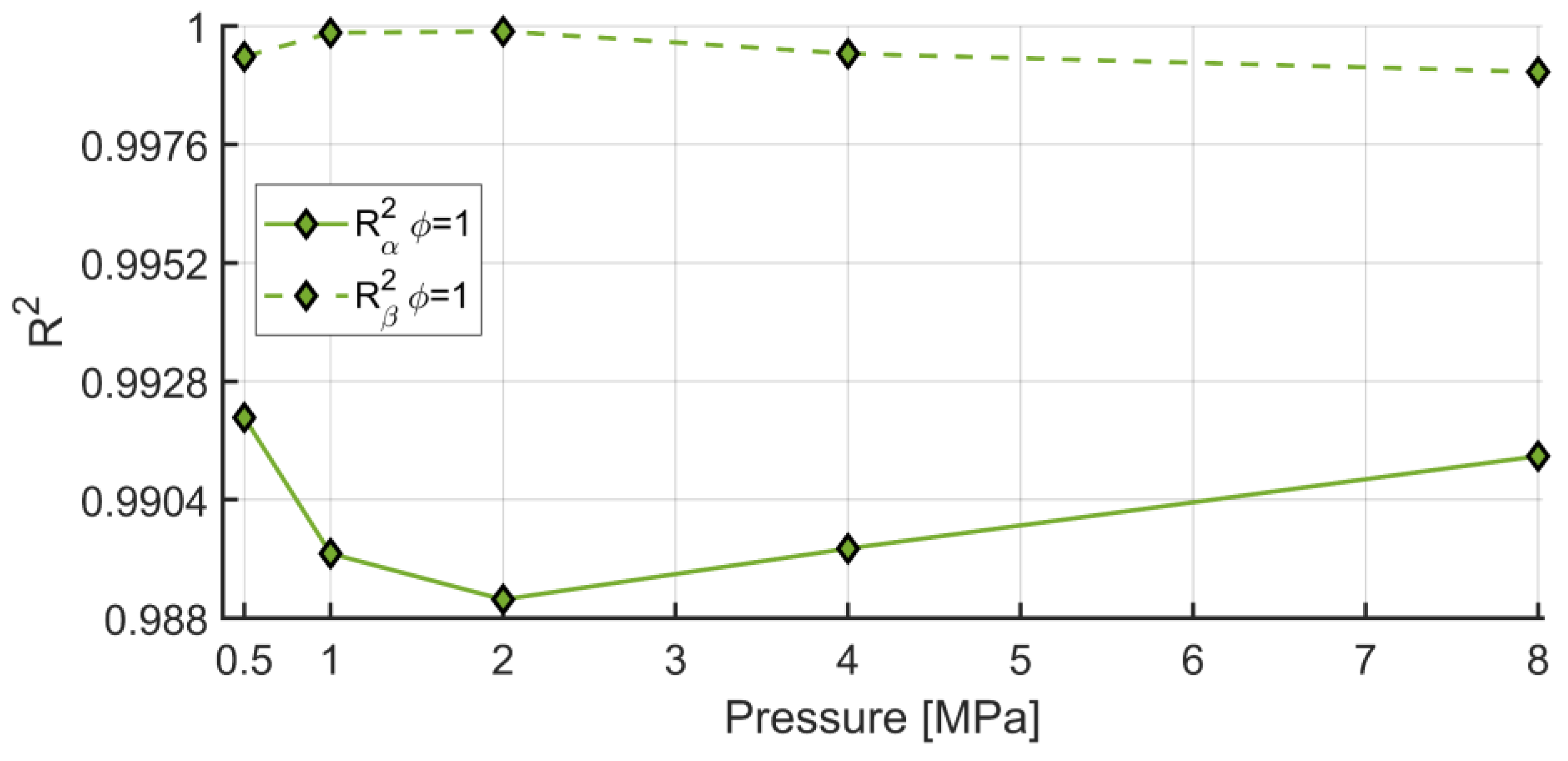
- In a semi-logarithmic scale, a second-degree polynomial regression accurately predicts the numerical results, with varying in the range of 0.99748–0.99997. However, even a linear regression provides a good accuracy with H2 mole fractions in the range of 0.0–0.6, and such a regression may be employed for less time-consuming computations. Both regressions may be used for further studies, specifically for CFD simulations of engines fueled with synthetic fuels;
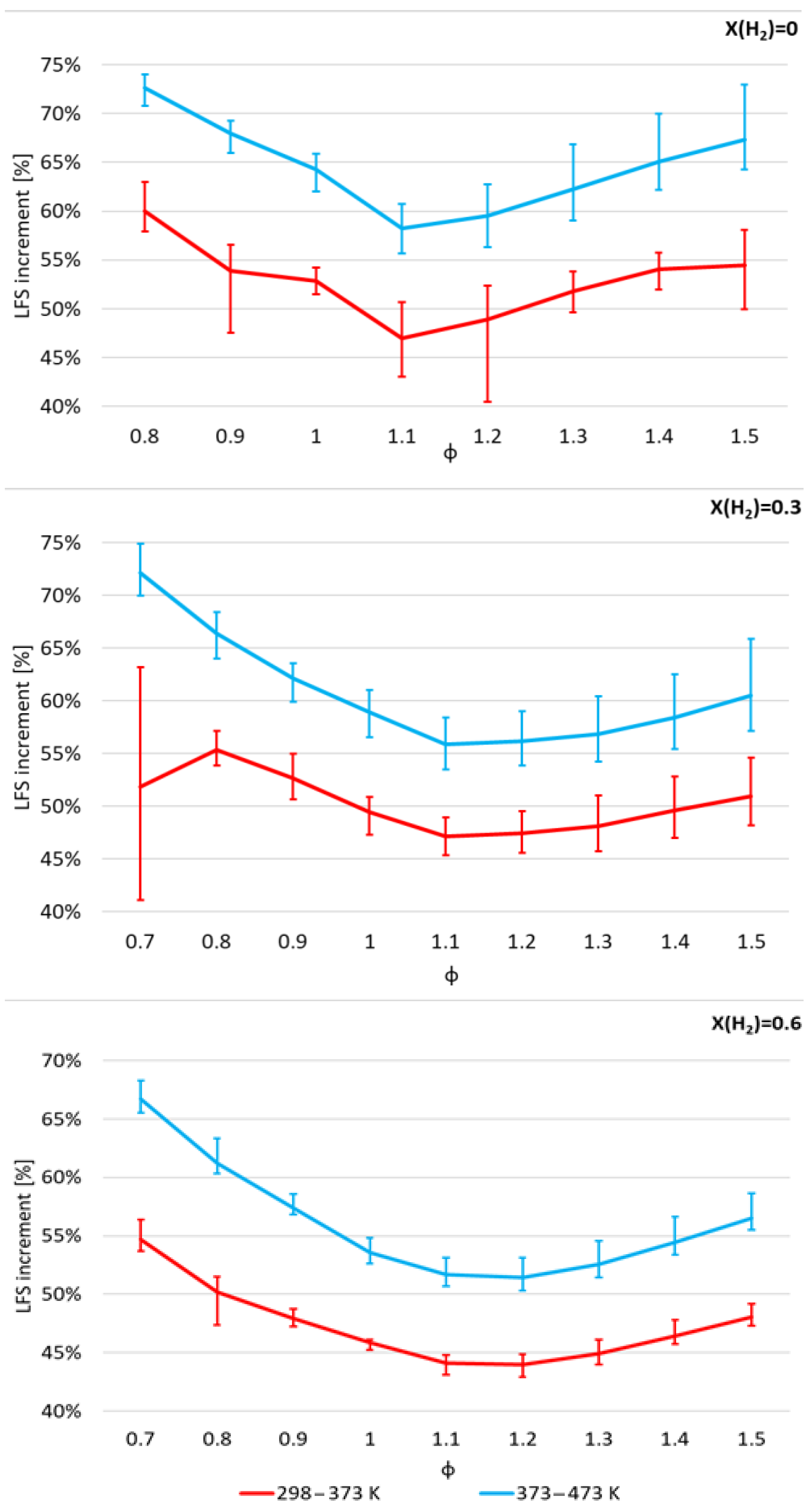
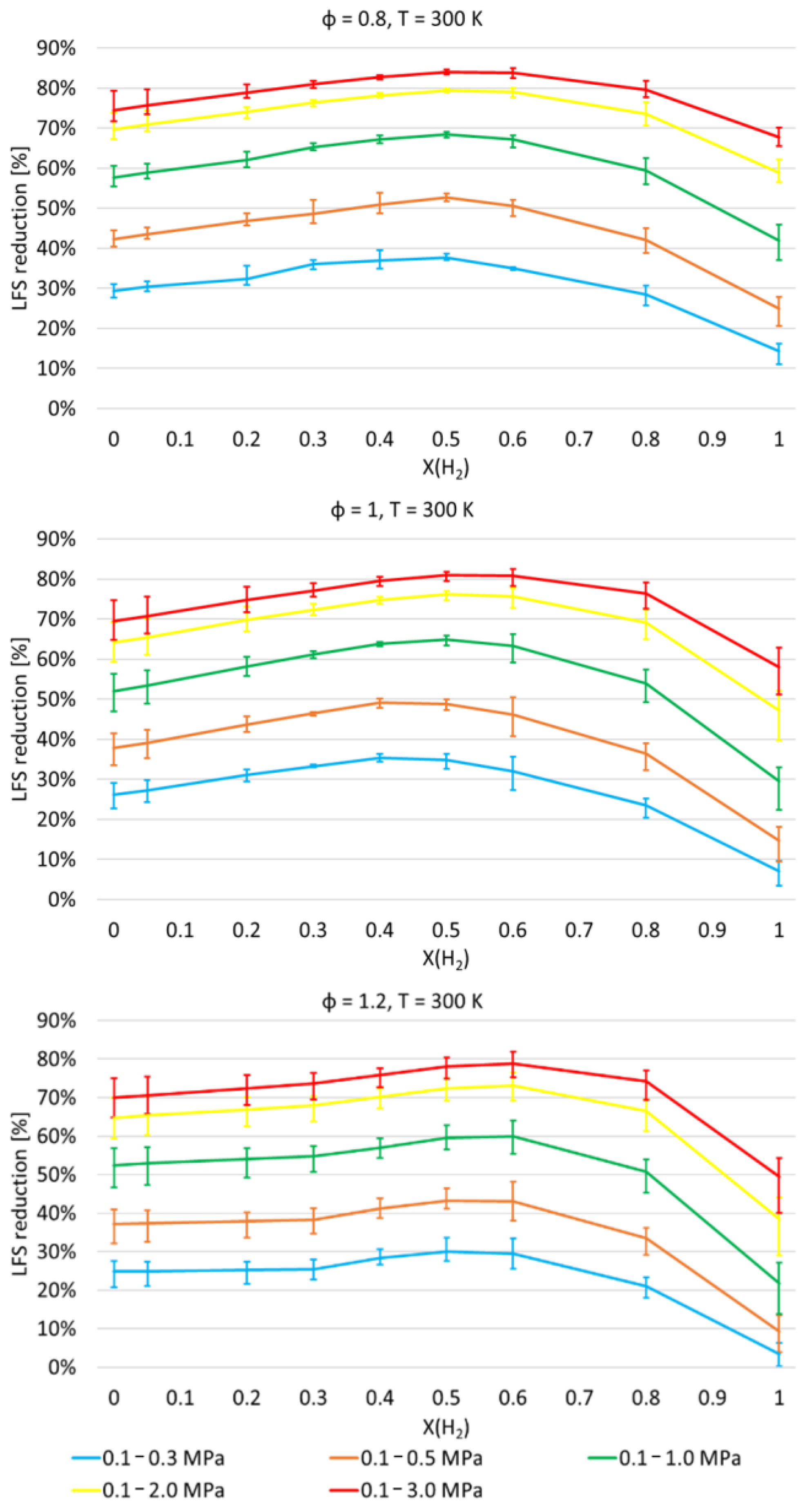
- α values show that the enhancement of LFS as the H2 mole fraction increases in the range of 0.0–0.6 is lower as pressure and temperature increase, and as ϕ increases from 0.8 to 1.2;
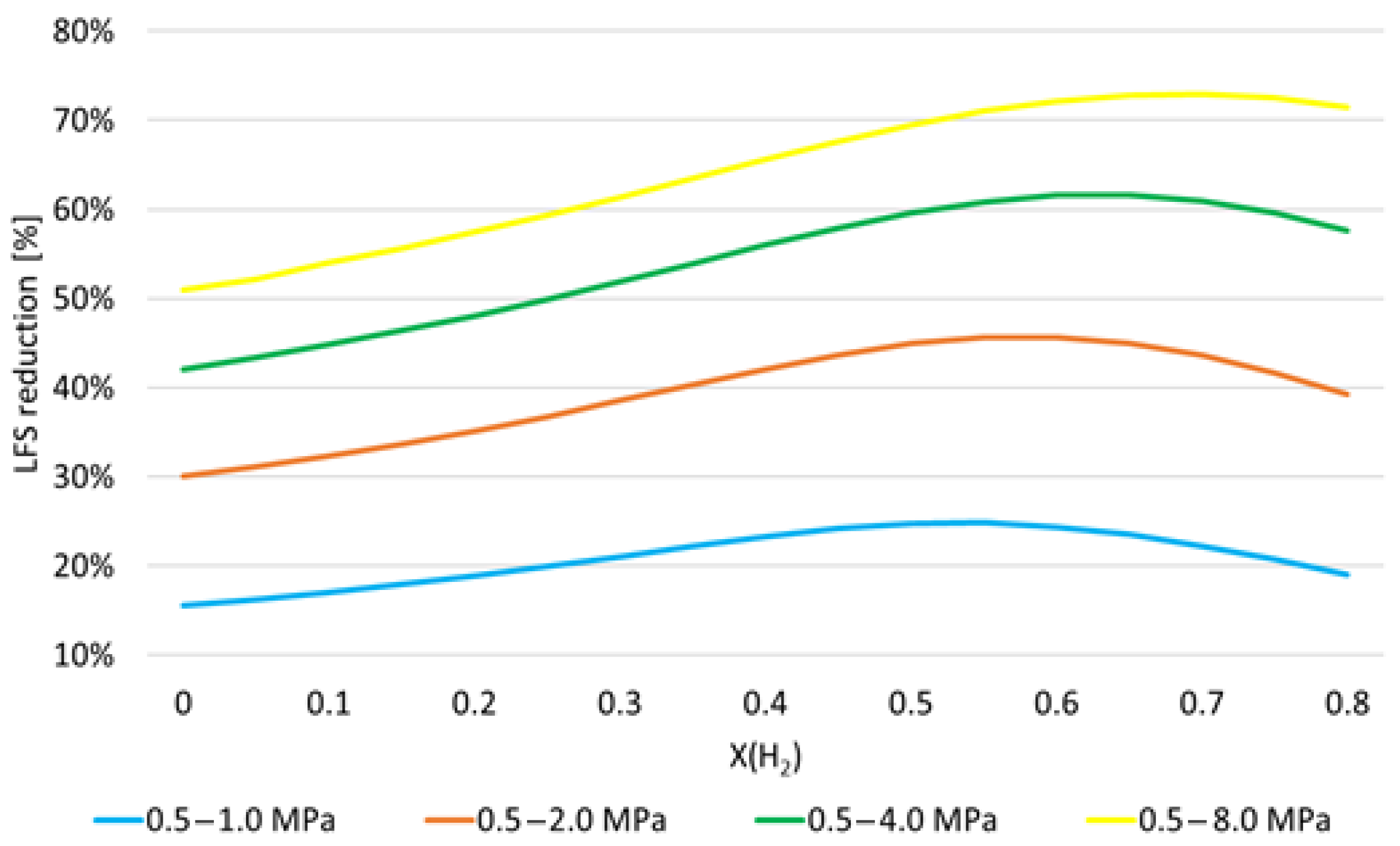
- As expected, LFS decreases as pressure increases. However, the more pressure increases, the less it influences the LFS. Furthermore, the increase in LFS with temperature is higher as pressure increases and H2 mole fraction decreases;
- Under thermodynamic engine-relevant conditions, i.e., 800 K and 4.0 MPa, the flame thickness for a stoichiometric mixture of with 40% by mole of H2 in the fuel blend is halved compared to the case of pure ammonia;
- The analysis of the flame structure shows the kinetics that leads to LFS enhancement by H2: the presence of hydrogen in the fuel mixture enhances the formation of radicals, such as H, O and OH, thus increasing the reactivity of the mixture and, subsequently, the laminar flame speed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Incer-Valverde, J.; Korayem, A.; Tsatsaronis, G.; Morosuk, T. Colors of hydrogen: Definitions and carbon intensity. Energy Convers. Manag. 2023, 291, 117294. [Google Scholar] [CrossRef]
- Shinde, B.J.; Karunamurthy, K. Recent progress in hydrogen fuelled internal combustion engine (H2ICE)—A comprehensive outlook. Mater. Today Proc. 2022, 51, 1568–1579. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. Thermophysical Properties of Fluid Systems, NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar] [CrossRef]
- Ichikawa, A.; Kitagawa, Y.; Hayakawa, A.; Somarathne, K.D.K.A.; Kudo, T.; Kobayashi, H. Laminar burning velocity and Markstein length of ammonia/hydrogen/air premixed flames at elevated pressures. Int. J. Hydrogen Energy 2015, 40, 9570–9578. [Google Scholar] [CrossRef]
- Han, X.; Wang, Z.; Costa, M.; Sun, Z.; He, Y.; Cen, K. Experimental and kinetic modeling study of laminar burning velocities of NH3/air, NH3/H2/air, NH3/CO/air and NH3/CH4/air premixed flames. Comb. Flame 2019, 206, 214–226. [Google Scholar] [CrossRef]
- Li, R.; Konnov, A.A.; He, G.; Qin, F.; Zhang, D. Chemical mechanism development and reduction for combustion of NH3/H2/CH4 mixtures. Fuel 2019, 257, 116059. [Google Scholar] [CrossRef]
- Pessina, V.; Berni, F.; Fontanesi, S.; Stagni, A.; Mehl, M. Laminar flame speed correlations of ammonia/hydrogen mixtures at high pressure and temperature for combustion modeling applications. Int. J. Hydrogen Energy 2022, 47, 25780–25794. [Google Scholar] [CrossRef]
- Shrestha, K.P.; Lhuillier, C.; Barbosa, A.A.; Brequigny, P.; Contino, F.; Mounaïm-Rousselle, C.; Seidel, L.; Mauss, F. An experimental and modeling study of ammonia with enriched oxygen content and ammonia/hydrogen laminar flame speed at elevated pressure and temperature. Proc. Combust. Inst. 2021, 38, 2163–2174. [Google Scholar] [CrossRef]
- Zhang, X.; Moosakutty, S.P.; Rajan, R.P.; Younes, M.; Sarathy, S.M. Combustion chemistry of ammonia/hydrogen mixtures: Jet-stirred reactor measurements and comprehensive kinetic modeling. Comb. Flame 2021, 234, 111653. [Google Scholar] [CrossRef]
- Otomo, J.; Koshi, M.; Mitsumori, T.; Iwasaki, H.; Yamada, K. Chemical kinetic modeling of ammonia oxidation with improved reaction mechanism for ammonia/air and ammonia/hydrogen/air combustion. Int. J. Hydrogen Energy 2018, 43, 3004–3014. [Google Scholar] [CrossRef]
- Gotama, G.J.; Hayakawa, A.; Okafor, E.C.; Kanoshima, R.; Hayashi, M.; Kudo, T.; Kobayashi, H. Measurement of the laminar burning velocity and kinetics study of the importance of the hydrogen recovery mechanism of ammonia/hydrogen/air premixed flames. Comb. Flame 2022, 236, 111753. [Google Scholar] [CrossRef]
- Stagni, A.; Cavallotti, C. H-abstractions by O2, NO2, NH2, and HO2 from H2NO: Theoretical study and implications for ammonia low-temperature kinetics. Proc. Combust. Inst. 2023, 39, 633–641. [Google Scholar] [CrossRef]
- Singh, A.S.; Dash, S.K.; Reddy, V.M. Chemical kinetic analysis on influence of hydrogen enrichment on the combustion characteristics of ammonia air using newly proposed reaction model. Int. J. Engine Res. 2022, 46, 6144–6163. [Google Scholar] [CrossRef]
- Ansys® Academic Research Chemkin-Pro, Release 20.2. Available online: https://www.ansys.com/products/fluids/ansys-chemkin-pro (accessed on 13 November 2020).
- Dixon-Lewis, G. Flame structure and flame reaction kinetics II. Transport phenomena in multicomponent systems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1968, 307, 111–135. [Google Scholar] [CrossRef]
- Curtiss, C.F.; Hirschfelder, J.O. Transport properties of multicomponent gas mixtures. J. Chem. Phys. 1949, 17, 550–555. [Google Scholar] [CrossRef]
- Smallbone, A.; Tsuneyoshi, K.; Kitagawa, T. Turbulent and Stable/Unstable Laminar Burning Velocity Measurements from Outwardly Propagating Spherical Hydrogen-Air Flames at Elevated Pressures. J. Therm. Sci. Technol. 2006, 1, 31–41. [Google Scholar] [CrossRef][Green Version]
- Lee, J.H.; Lee, S.I.; Kwon, O.C. Effects of ammonia substitution on hydrogen/air flame propagation and emissions. Int. J. Hydrogen Energy 2010, 35, 11332–11341. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Kobayashi, N.; He, Z.; Nagai, Y. Study on using hydrogen and ammonia as fuels: Combustion characteristics and NOx formation. Int. J. Engine Res. 2014, 38, 1214–1223. [Google Scholar] [CrossRef]
- Kumar, P.; Meyer, T.R. Experimental and modeling study of chemical-kinetics mechanisms for H2–NH3–air mixtures in laminar premixed jet flames. Fuel 2013, 108, 166–176. [Google Scholar] [CrossRef]
- Zitouni, S.; Brequigny, P.; Mounaїm-Rousselle, C. Influence of hydrogen and methane addition in laminar ammonia premixed flame on burning velocity, Lewis number and Markstein length. Comb. Flame 2023, 253, 112786. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Elbaz, A.M.; Han, X.; He, Y.; Costa, M.; Konnov, A.A.; Roberts, W.L. Experimental study and kinetic analysis of the laminar burning velocity of NH3/syngas/air, NH3/CO/air and NH3/H2/air premixed flames at elevated pressures. Comb. Flame 2020, 221, 270–287. [Google Scholar] [CrossRef]
- Lhuillier, C.; Brequigny, P.; Lamoureux, N.; Contino, F.; Mounaïm-Rousselle, C. Experimental investigation on laminar burning velocities of ammonia/hydrogen/air mixtures at elevated temperatures. Fuel 2020, 263, 116653. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.H.; Park, J.H.; Kwon, O.C. Studies on properties of laminar premixed hydrogen-added ammonia/air flames for hydrogen production. Int. J. Hydrogen Energy 2010, 35, 1054–1064. [Google Scholar] [CrossRef]
- Mei, B.; Zhang, X.; Ma, S.; Cui, M.; Guo, H.; Cao, Z.; Li, Y. Experimental and kinetic modeling investigation on the laminar flame propagation of ammonia under oxygen enrichment and elevated pressure conditions. Comb. Flame 2019, 210, 236–246. [Google Scholar] [CrossRef]
- Zakaznov, V.F.; Kursheva, L.A.; Fedina, Z.I. Determination of normal flame velocity and critical diameter of flame extinction in ammonia-air mixture. Combust. Explos. Shock. Waves 1978, 14, 710–713. [Google Scholar] [CrossRef]





| Pressure [MPa] | Temperature [K] | Equivalence Ratio | H2 Mole Fraction in the Fuel Mixture |
|---|---|---|---|
| 0.1, 0.3, 0.5, 1.0, 2.0, 3.0, 4.0, 8.0 | 300, 373, 473, 800 | [0.7–1.5] | [0.0–1.0] |
| Reference | Label | Number of Species | Number of Reactions |
|---|---|---|---|
| Zhang et al. [9] | M1 | 38 | 263 |
| Otomo et al. [10] | M2 | 32 | 231 |
| Gotama et al. [11] | M3 | 32 | 165 |
| Stagni et al. [12] | M4 | 41 | 203 |
| Singh et al. [13] | M5 | 32 | 259 |
| Grid Refinement | Gradient Parameter | Curvature Parameter |
|---|---|---|
| 0 | 0.1 | 0.5 |
| 1 | 0.08 | 0.3 |
| 2 | 0.06 | 0.1 |
| 3 | 0.03 | 0.07 |
| 4 | 0.01/0.015 | 0.05 |
| Reference | p [MPa] | T [K] | X(H2) | ϕ |
|---|---|---|---|---|
| Ichikawa et al. [4] | 0.1, 0.3, 0.5 | 298 | [0–1] | [0.8–1.2] |
| Han et al. [5] | 0.1 | 298 | [0–0.45] | [0.8–1.4] |
| Shrestha et al. [8] | 0.1 | 473 | [0–0.3] | [0.8–1.4] |
| Smallbone et al. [17] | 0.1 | 298 | 1 | 1 |
| Lee et al. [18] | 0.1 | 298 | 0.1, 0.3, 0.5 | 1 |
| Li et al. [19] | 0.1 | 293 | [0.4–0.6] | 1, 1.3, 1.4 |
| Kumar and Meyer [20] | 0.1 | 298 | 0.25, 0.55, 0.8, 1 | 1 |
| Zitouni et al. [21] | 0.1 | 298 | [0–0.8] | [0.8–1.4] |
| Wang et al. [22] | 0.1, 0.3, 0.5 | 298 | 0.4, 0.6 | [0.7–1.5] |
| Gotama et al. [11] | 0.1, 0.5 | 298 | 0.4 | [0.8–1.4] |
| Lhuillier et al. [23] | 0.1 | 298, 373, 473 | [0–0.6] | [0.8–1.4] |
| Lee et al. [24] | 0.1 | 298 | 0.5 | 0.8, 1 |
| Mei et al. [25] | 0.1 | 300 | 0 | [0.9–1.3] |
| Zakaznov et al. [26] | 0.1 | 293 | 0 | [0.8–1.3] |
| p [MPa] | α | β1 | β2 | ||
|---|---|---|---|---|---|
| ϕ = 0.8 | |||||
| 0.1 | 4.01535 | 0.99912 | 4.46199 | −0.85382 | 0.99928 |
| 0.3 | 3.78417 | 0.99910 | 3.66447 | 0.13347 | 0.99965 |
| 0.5 | 3.65400 | 0.99816 | 3.28495 | 0.57963 | 0.99982 |
| 1.0 | 3.44229 | 0.99674 | 2.76635 | 1.13354 | 0.99993 |
| 2.0 | 3.16464 | 0.99565 | 2.24763 | 1.56685 | 0.99978 |
| 3.0 | 2.97080 | 0.99551 | 1.98115 | 1.69605 | 0.99954 |
| ϕ = 1.0 | |||||
| 0.1 | 3.74508 | 0.99900 | 4.01731 | −0.54984 | 0.99900 |
| 0.3 | 3.51541 | 0.99596 | 3.21302 | 0.45000 | 0.99937 |
| 0.5 | 3.35729 | 0.99387 | 2.77596 | 0.94952 | 0.99971 |
| 1.0 | 3.10613 | 0.99217 | 2.18010 | 1.57654 | 0.99997 |
| 2.0 | 2.84256 | 0.99228 | 1.65541 | 2.04374 | 0.99953 |
| 3.0 | 2.69021 | 0.99296 | 1.41644 | 2.19024 | 0.99885 |
| ϕ = 1.2 | |||||
| 0.1 | 3.51514 | 0.99274 | 3.38537 | 0.14472 | 0.99748 |
| 0.3 | 3.31057 | 0.99204 | 2.73452 | 0.96245 | 0.99939 |
| 0.5 | 3.20450 | 0.99201 | 2.41179 | 1.35772 | 0.99985 |
| 1.0 | 3.03999 | 0.99156 | 1.94449 | 1.89475 | 0.99993 |
| 2.0 | 2.82580 | 0.99130 | 1.44550 | 2.38350 | 0.99916 |
| 3.0 | 2.67350 | 0.99202 | 1.16852 | 2.58980 | 0.99804 |
| p [MPa] | α | β1 | β2 | ||
|---|---|---|---|---|---|
| ϕ = 1.0 | |||||
| 0.5 | 3.00838 | 0.99207 | 2.33794 | 1.07392 | 0.99938 |
| 1 | 2.79248 | 0.98931 | 1.85683 | 1.54954 | 0.99986 |
| 2 | 2.53740 | 0.98838 | 1.45236 | 1.82900 | 0.99989 |
| 4 | 2.27164 | 0.98941 | 1.19617 | 1.82809 | 0.99944 |
| 8 | 2.01777 | 0.99128 | 1.08260 | 1.59253 | 0.99907 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bochicchio, F.; D’Amato, M.; Magi, V.; Viggiano, A. On the Influence of H2 Addition on NH3 Laminar Flame Speed under Engine-like Conditions. Energies 2024, 17, 4181. https://doi.org/10.3390/en17164181
Bochicchio F, D’Amato M, Magi V, Viggiano A. On the Influence of H2 Addition on NH3 Laminar Flame Speed under Engine-like Conditions. Energies. 2024; 17(16):4181. https://doi.org/10.3390/en17164181
Chicago/Turabian StyleBochicchio, Flavio, Marco D’Amato, Vinicio Magi, and Annarita Viggiano. 2024. "On the Influence of H2 Addition on NH3 Laminar Flame Speed under Engine-like Conditions" Energies 17, no. 16: 4181. https://doi.org/10.3390/en17164181
APA StyleBochicchio, F., D’Amato, M., Magi, V., & Viggiano, A. (2024). On the Influence of H2 Addition on NH3 Laminar Flame Speed under Engine-like Conditions. Energies, 17(16), 4181. https://doi.org/10.3390/en17164181






