The Influence of Stops on the Selected Route of the City ITS on the Energy Efficiency of the Public Bus
Abstract
1. Introduction
- The first part provides an introduction;
- The second part presents the energy balance of the bus;
- In the third part, the examined case is described and a statistical analysis of the vehicle’s motion profile is made;
- The fourth part presents the simulation of energy consumption;
- The fifth part summarizes the paper.
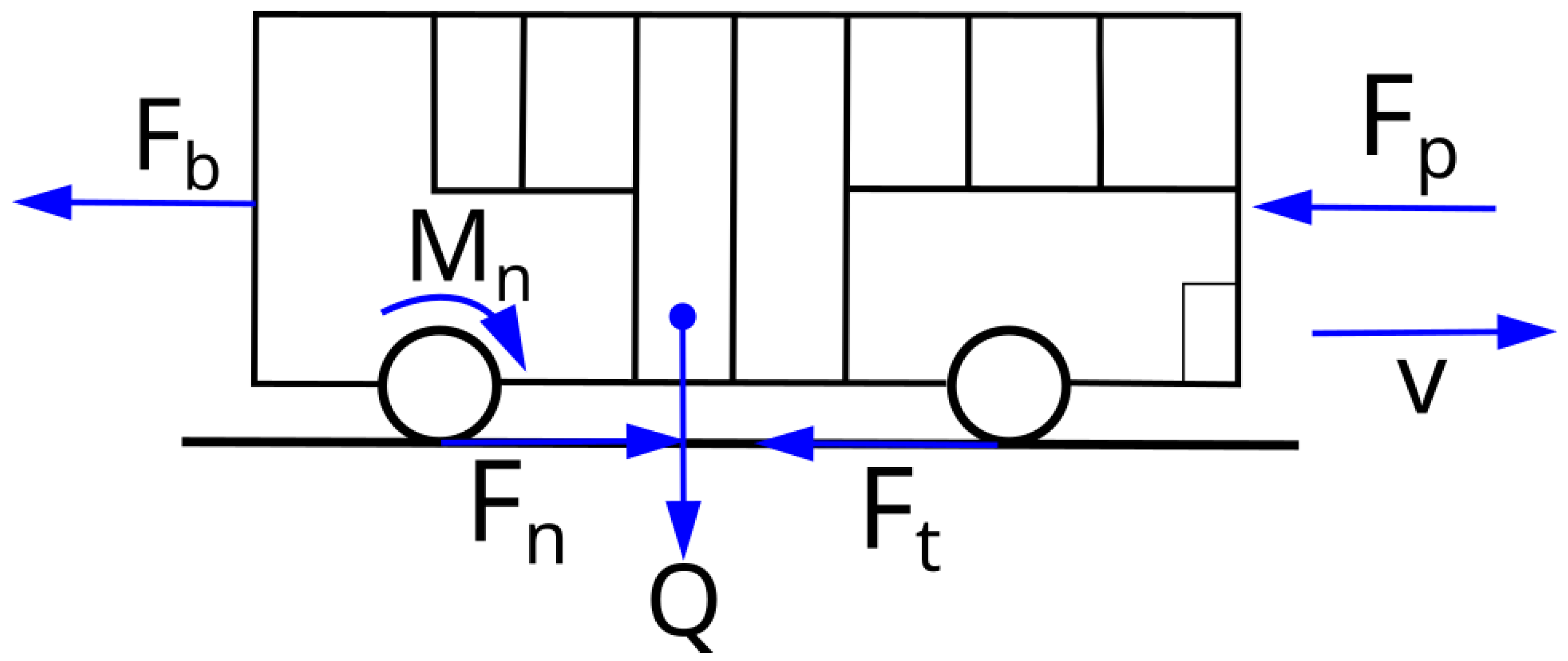
2. Energy Balance of the Bus
- cx—air resistance coefficient;
- A—vehicle frontal area, [m2];
- ρ—air density, [kg/m3];
- v—vehicle speed, [m/s];
- ft—rolling resistance coefficient;
- m—vehicle weight, [kg];
- g—acceleration due to gravity, [m/s2].
- su—length of a road section of a steady-state motion, [m];
- cx—air resistance coefficient;
- A—vehicle frontal area, [m2];
- ρ—air density, [kg/m3];
- vu—speed of steady-state motion, [m/s];
- ft—rolling resistance coefficient;
- m—vehicle weight, [kg];
- g—acceleration due to gravity, [m/s2].
- sb—length of braking distance, [m];
- ab—deceleration, [m/s2];
- tb—braking time, [s];
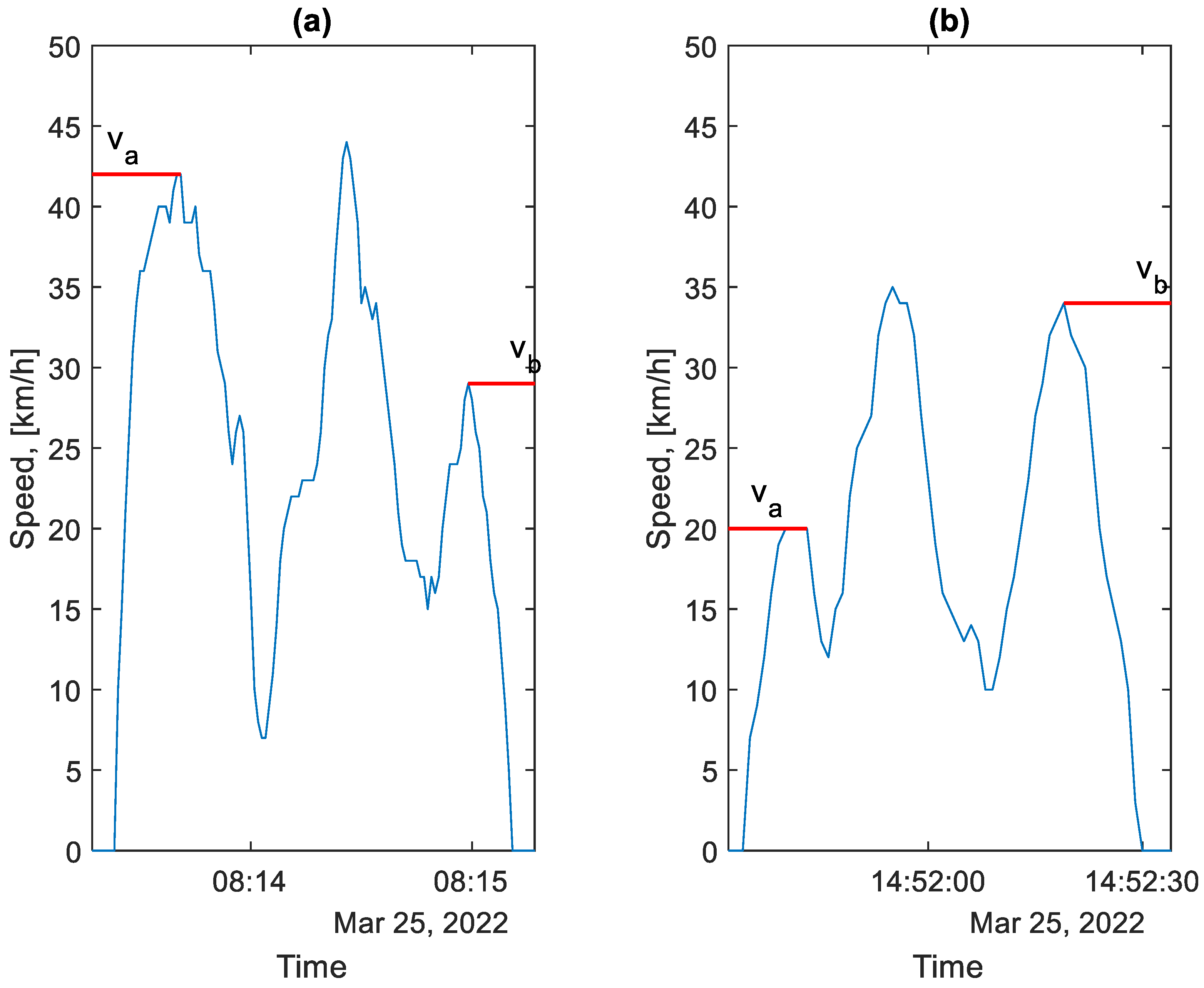
- vb—the speed at which braking is initiated, [m/s].
3. Case Description and Analysis of Parameters Related to Vehicle Movement
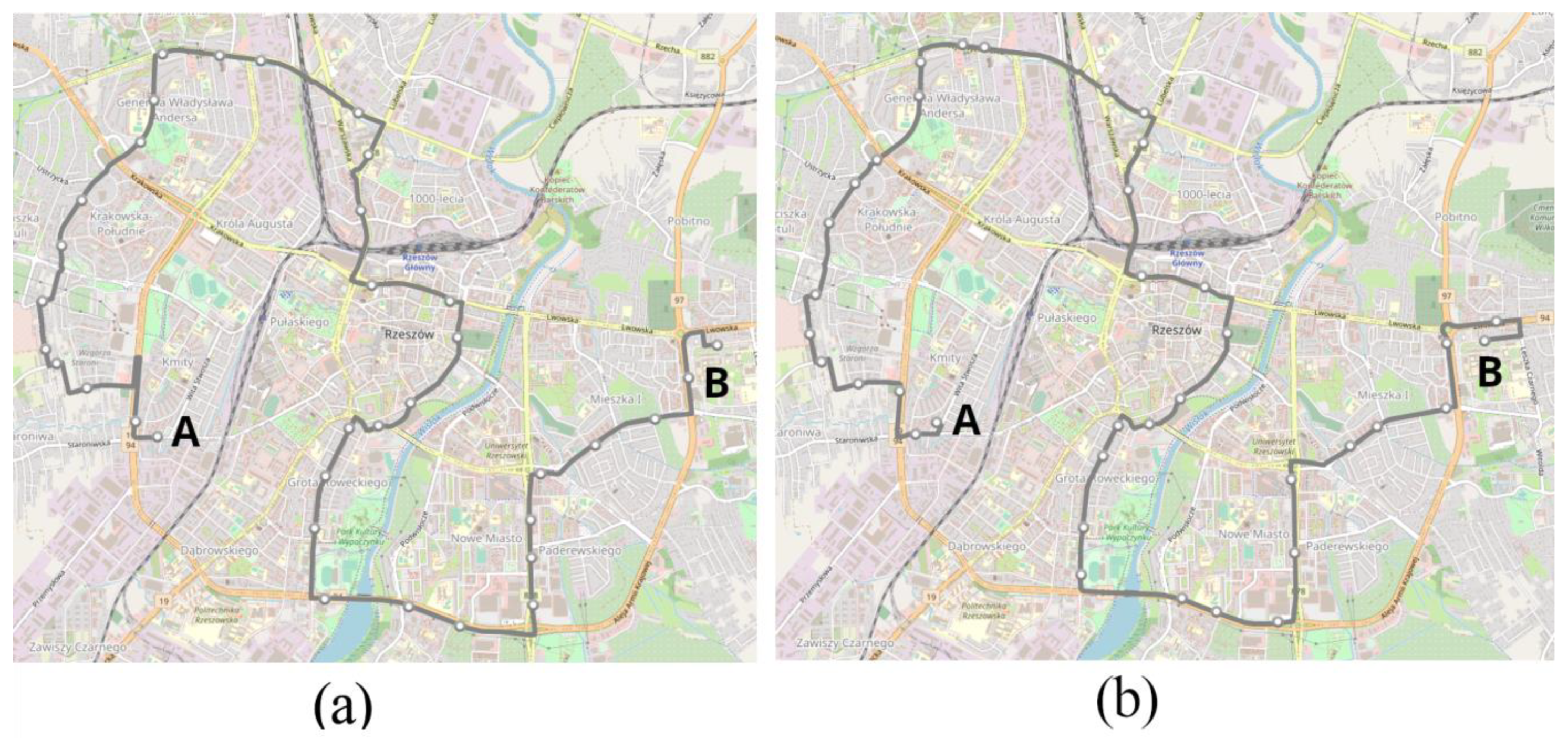
3.1. Intelligent Transport System in Rzeszów
3.2. Characteristics of the Considered Route
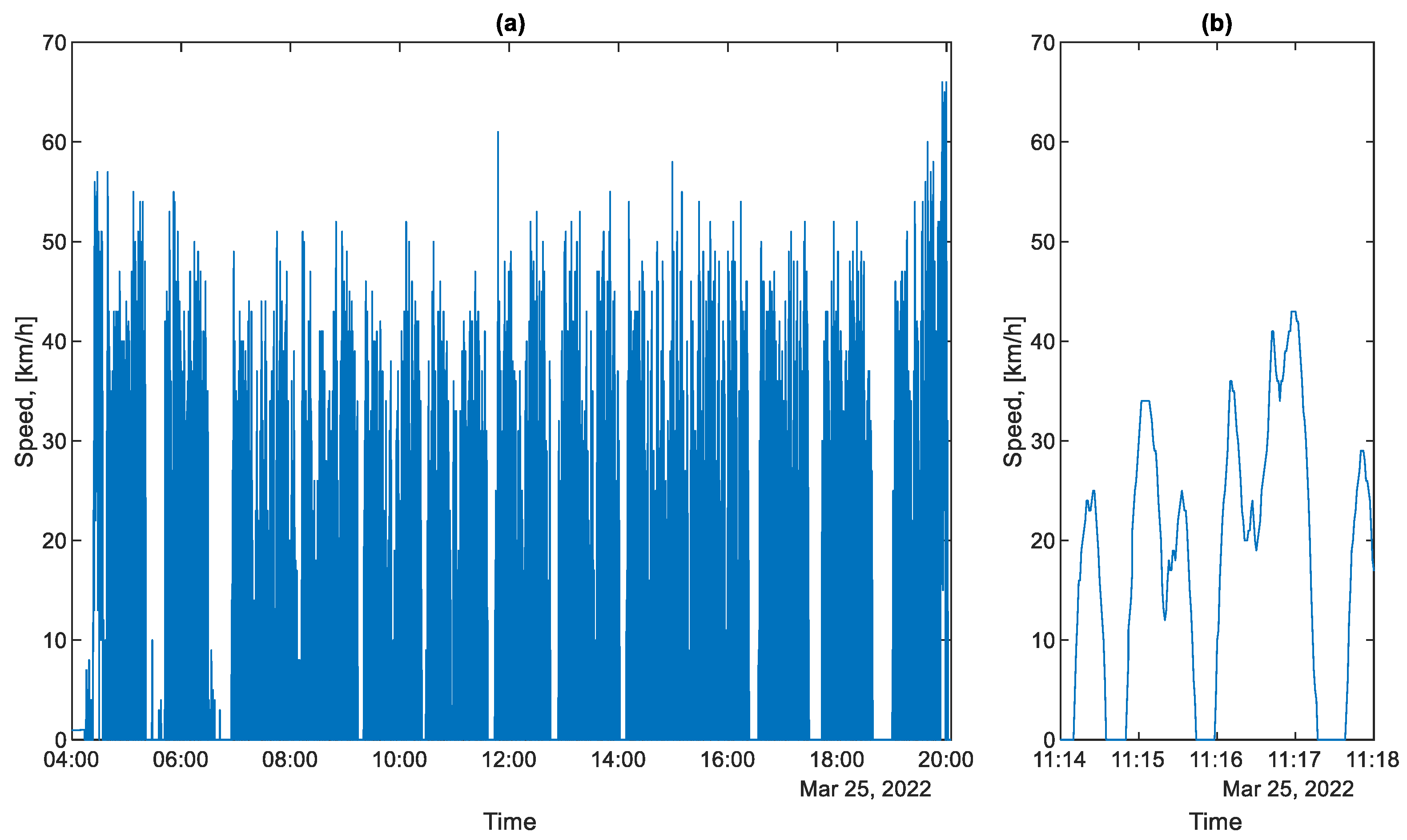
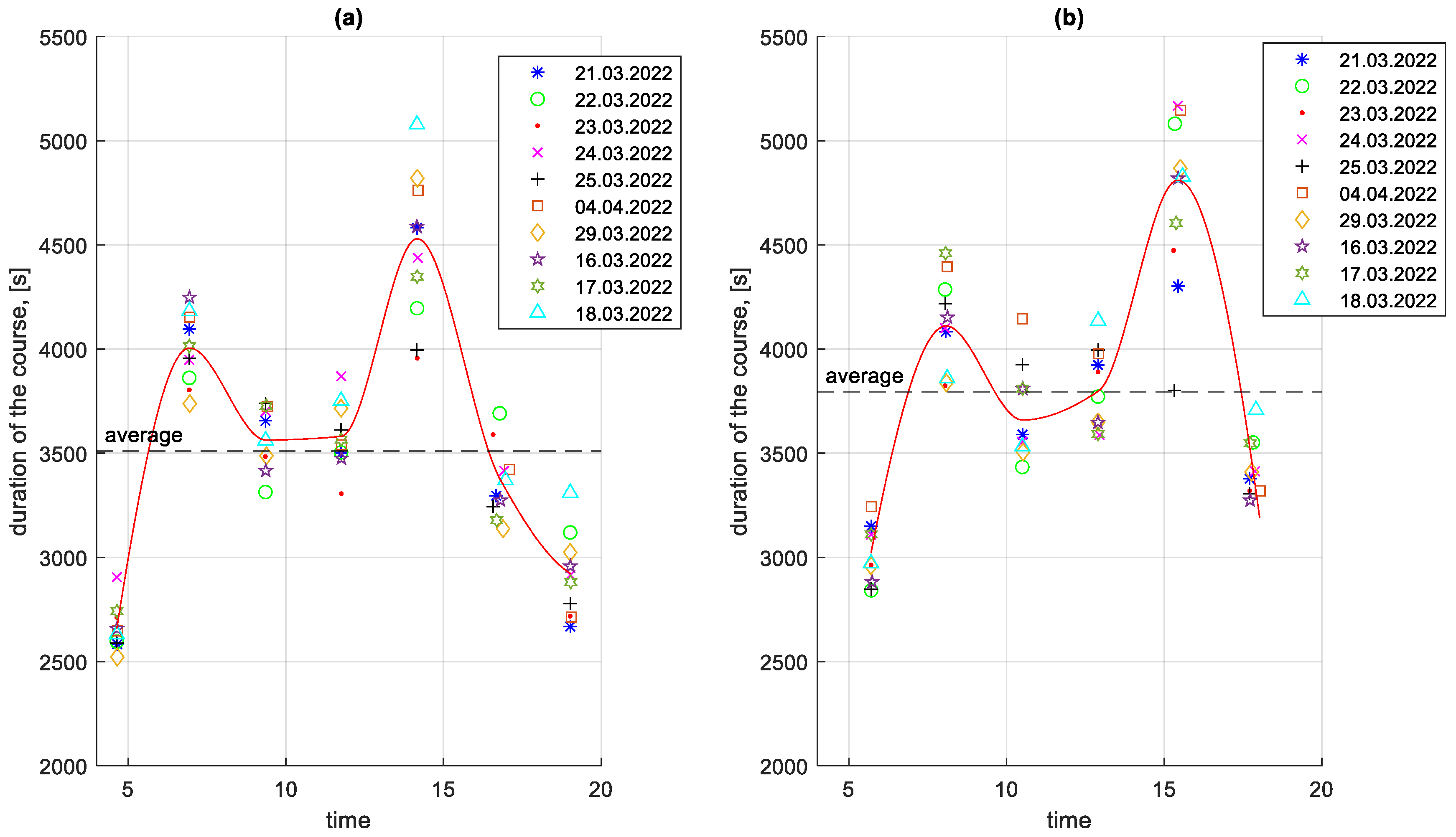
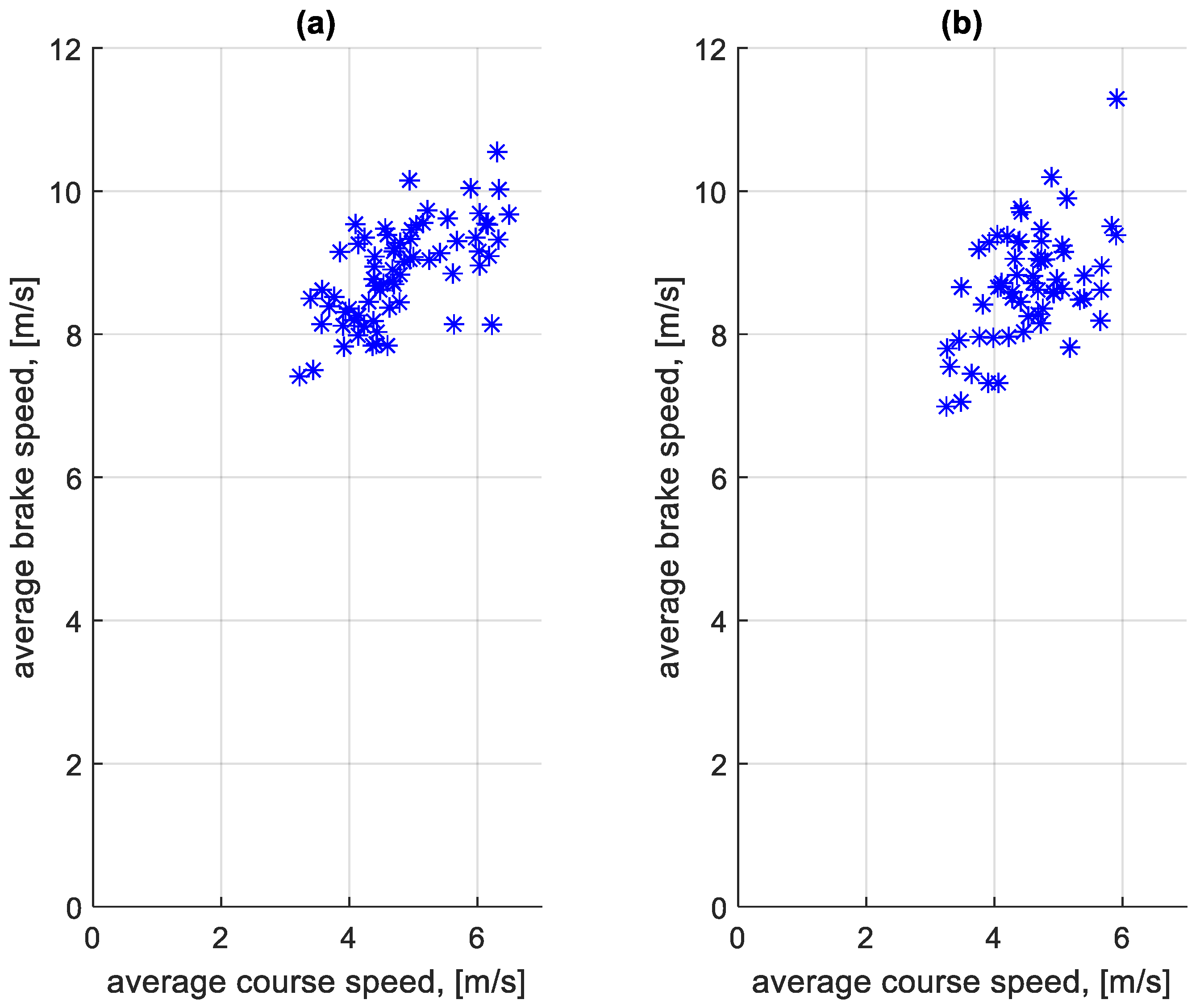
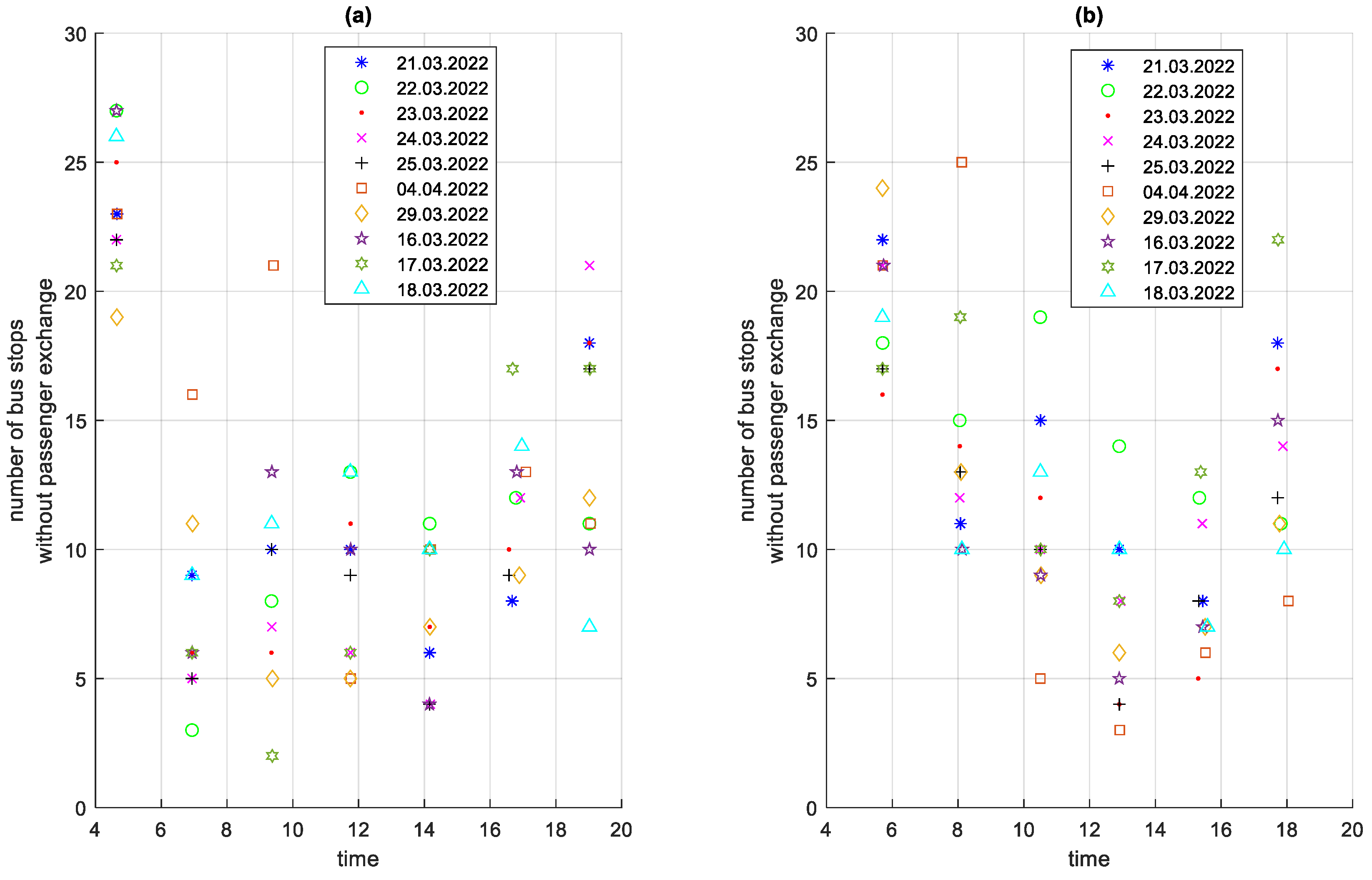
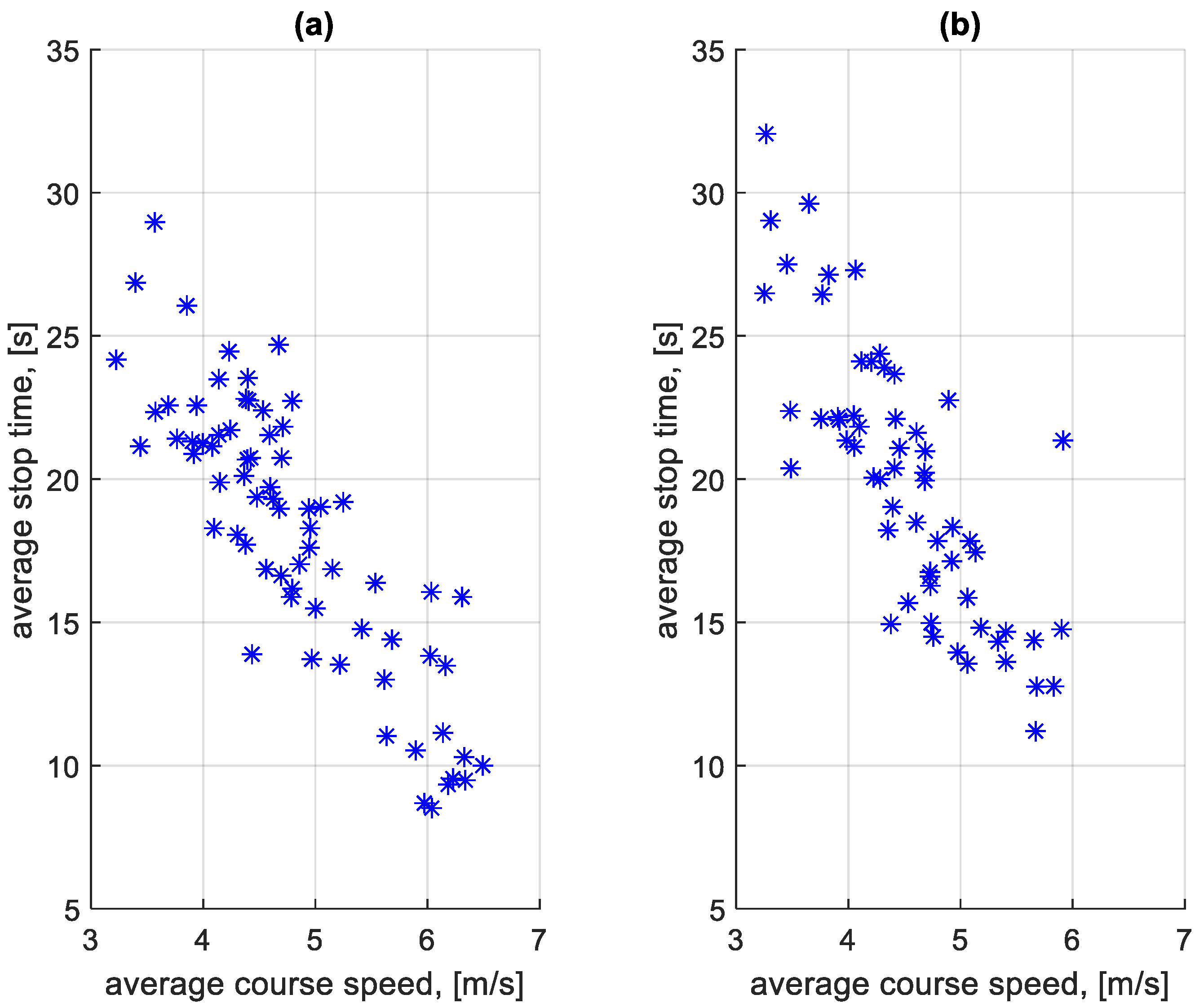
3.3. Characteristics of the Traffic Profile
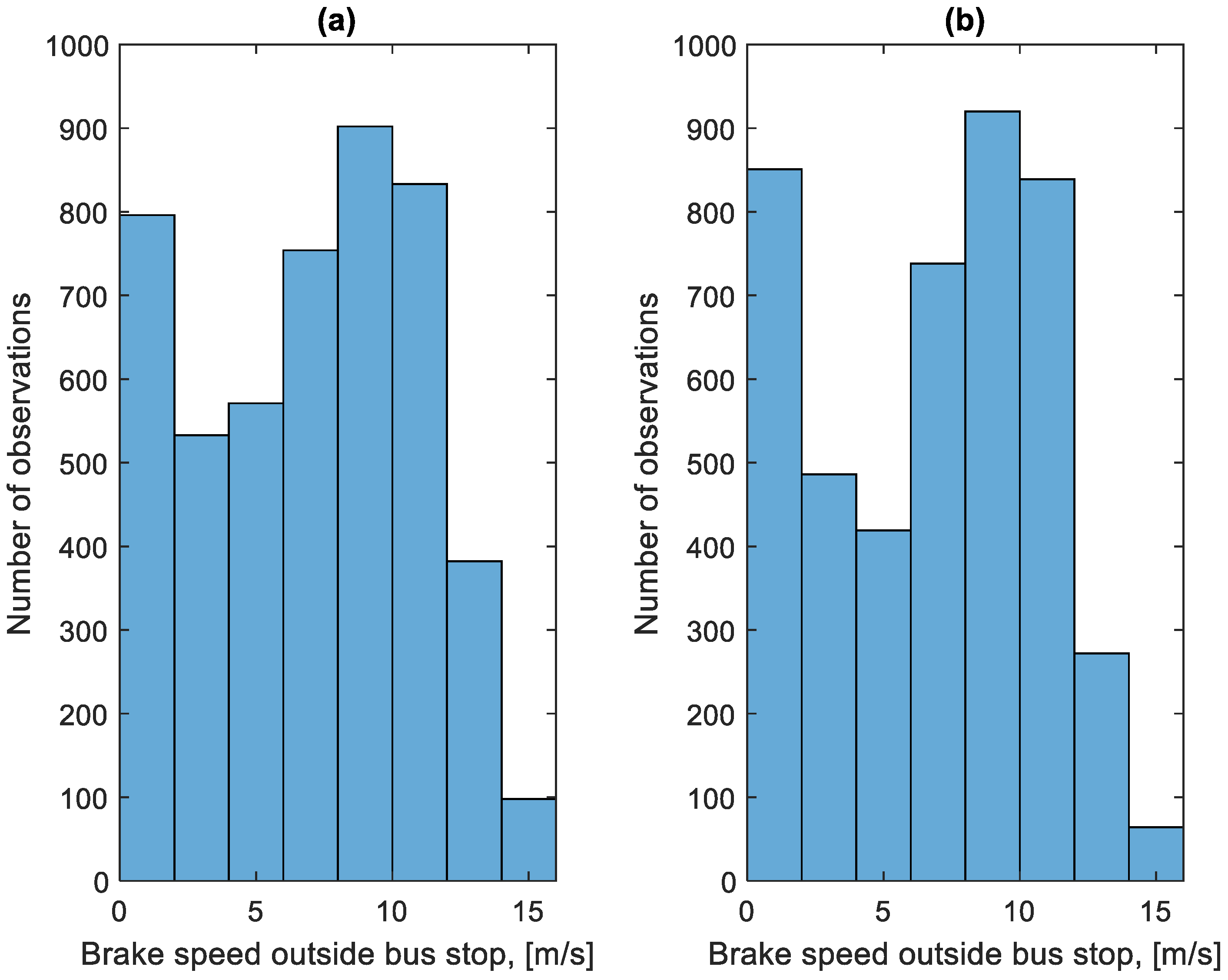
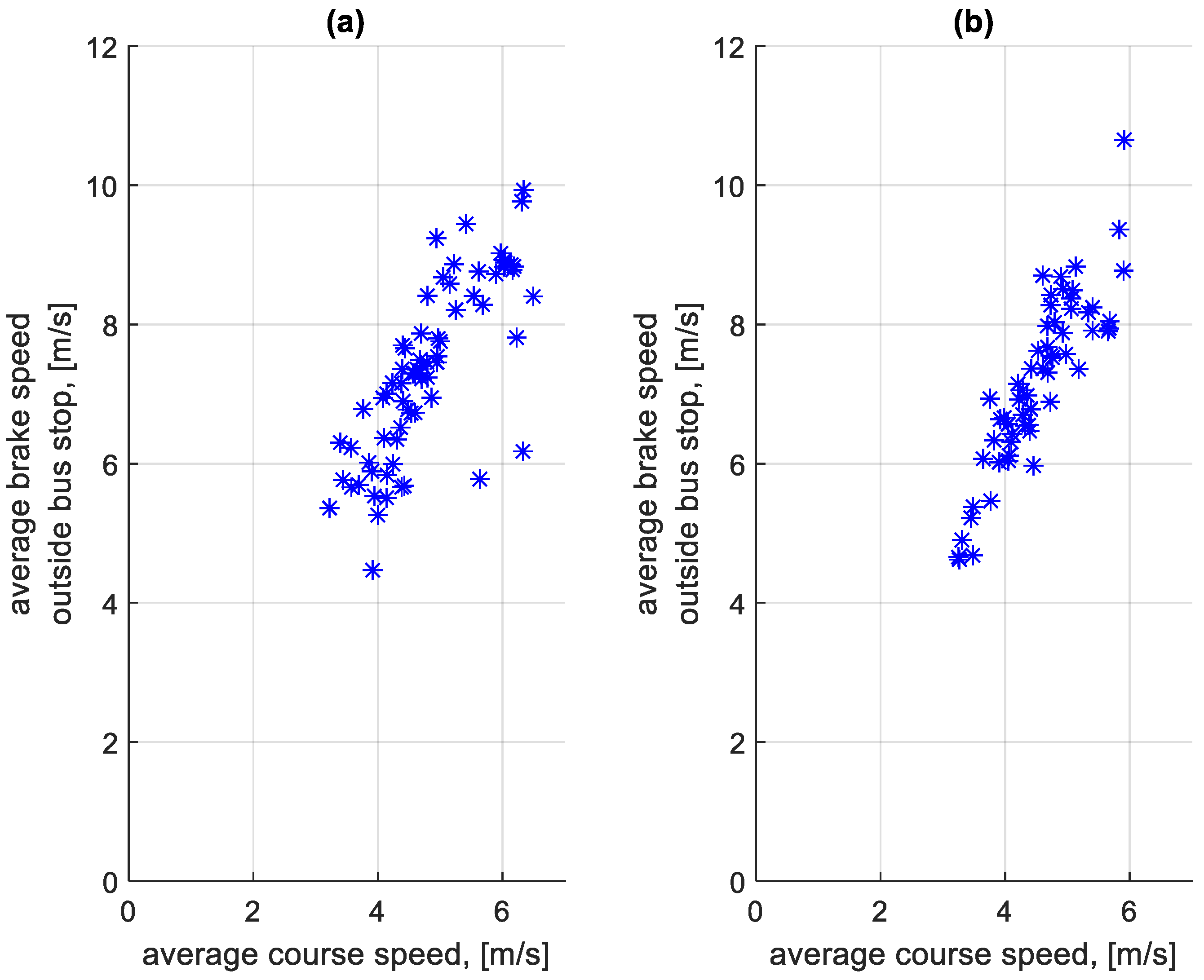
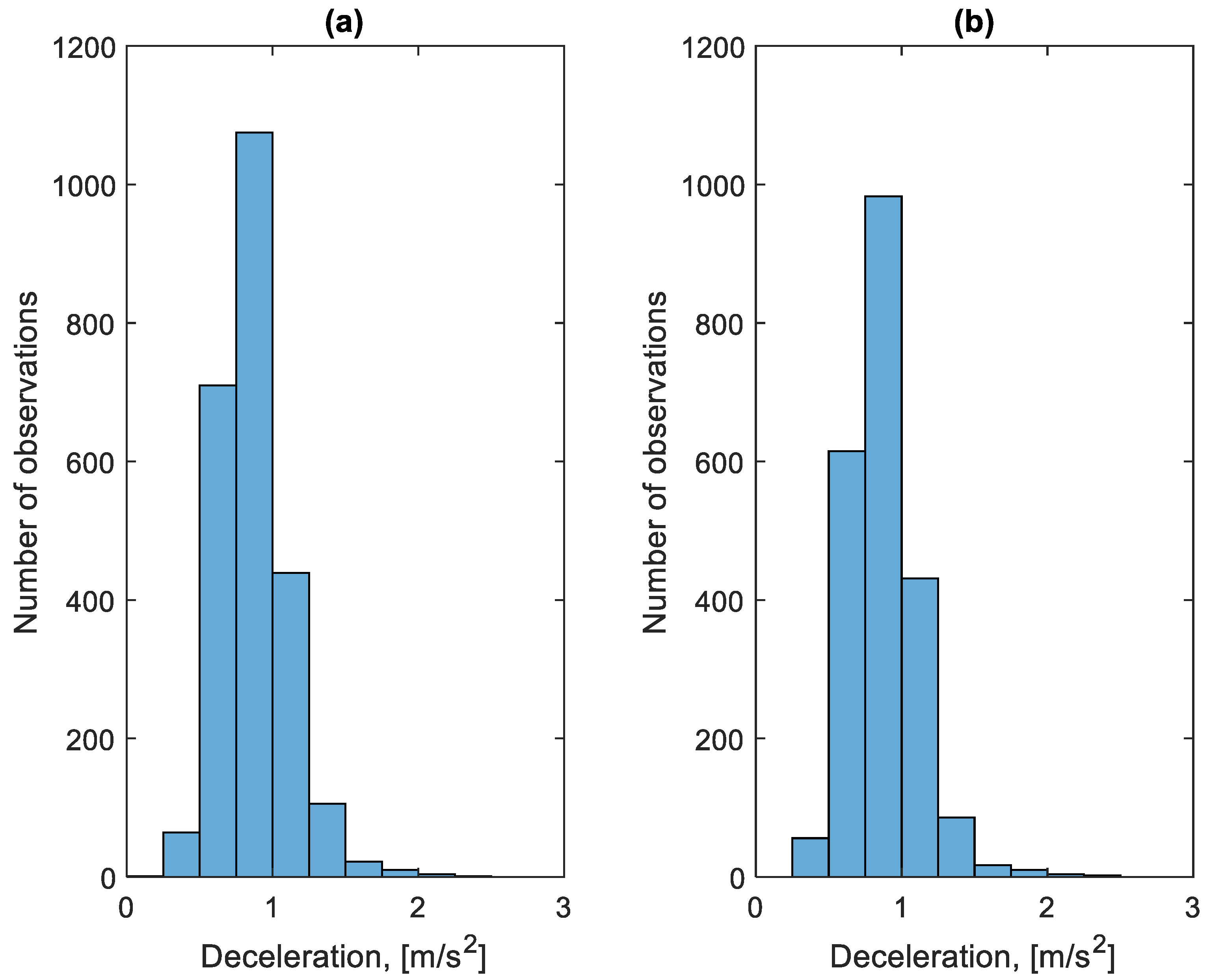
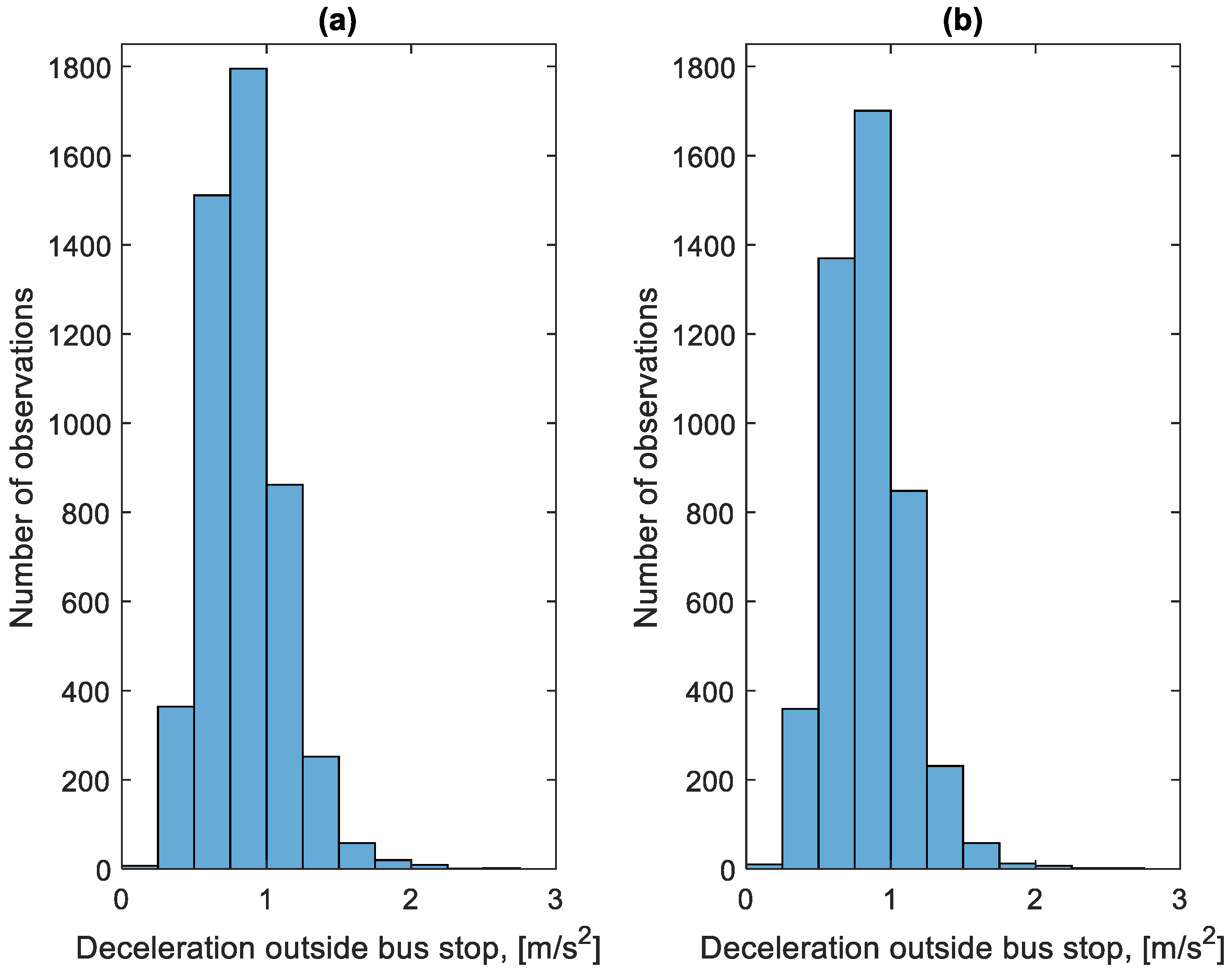
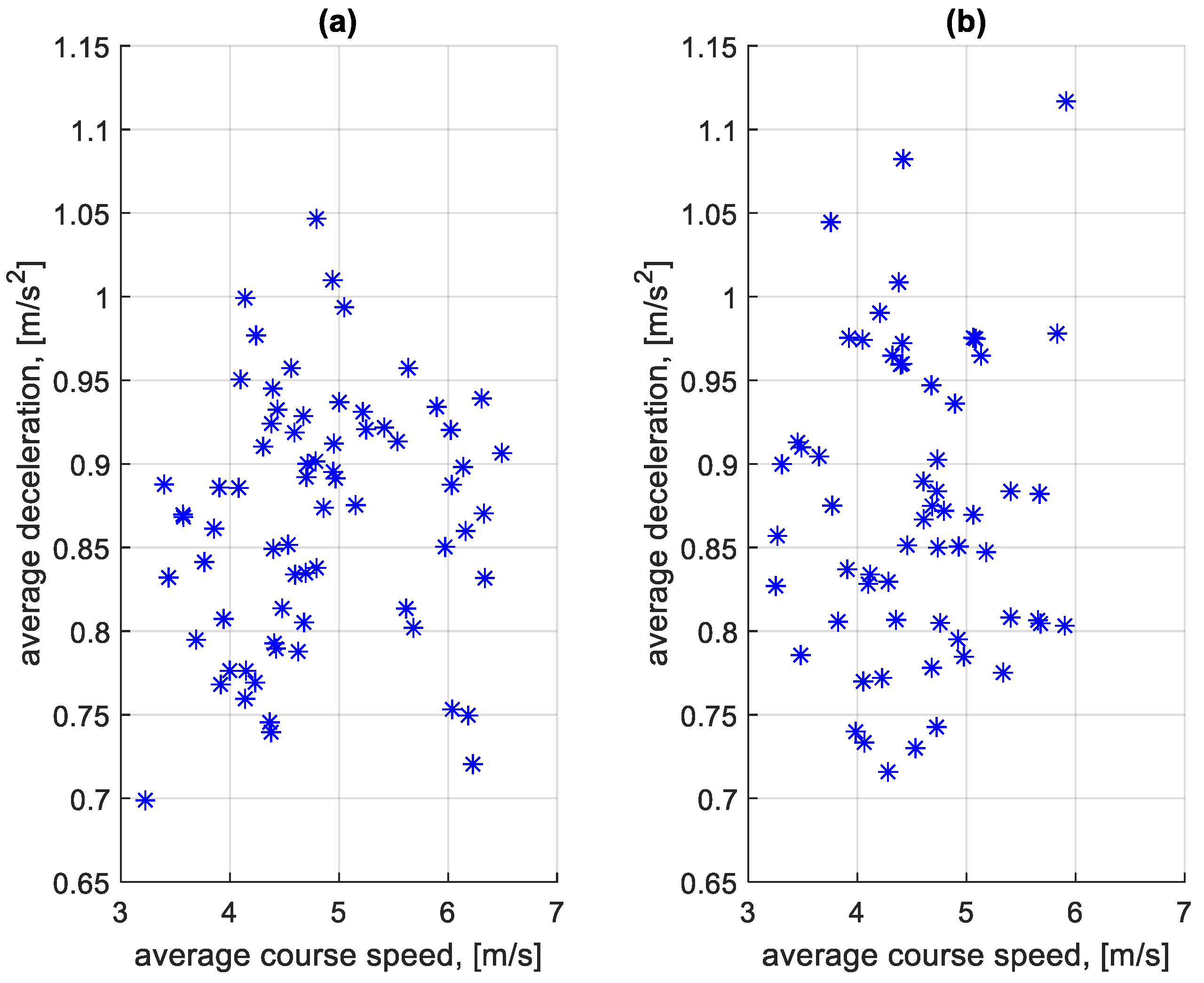
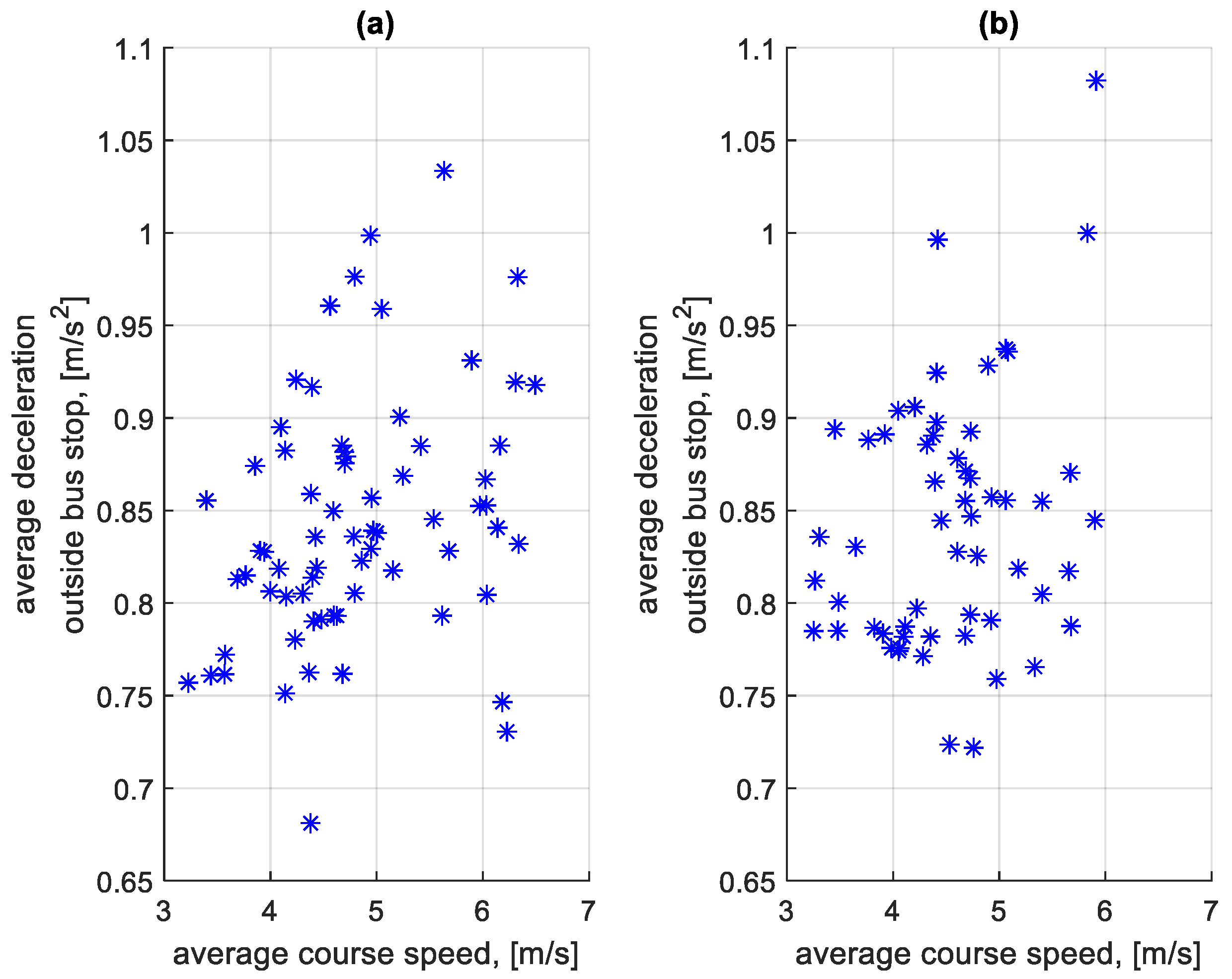
3.4. Analysis of Braking Process Parameters
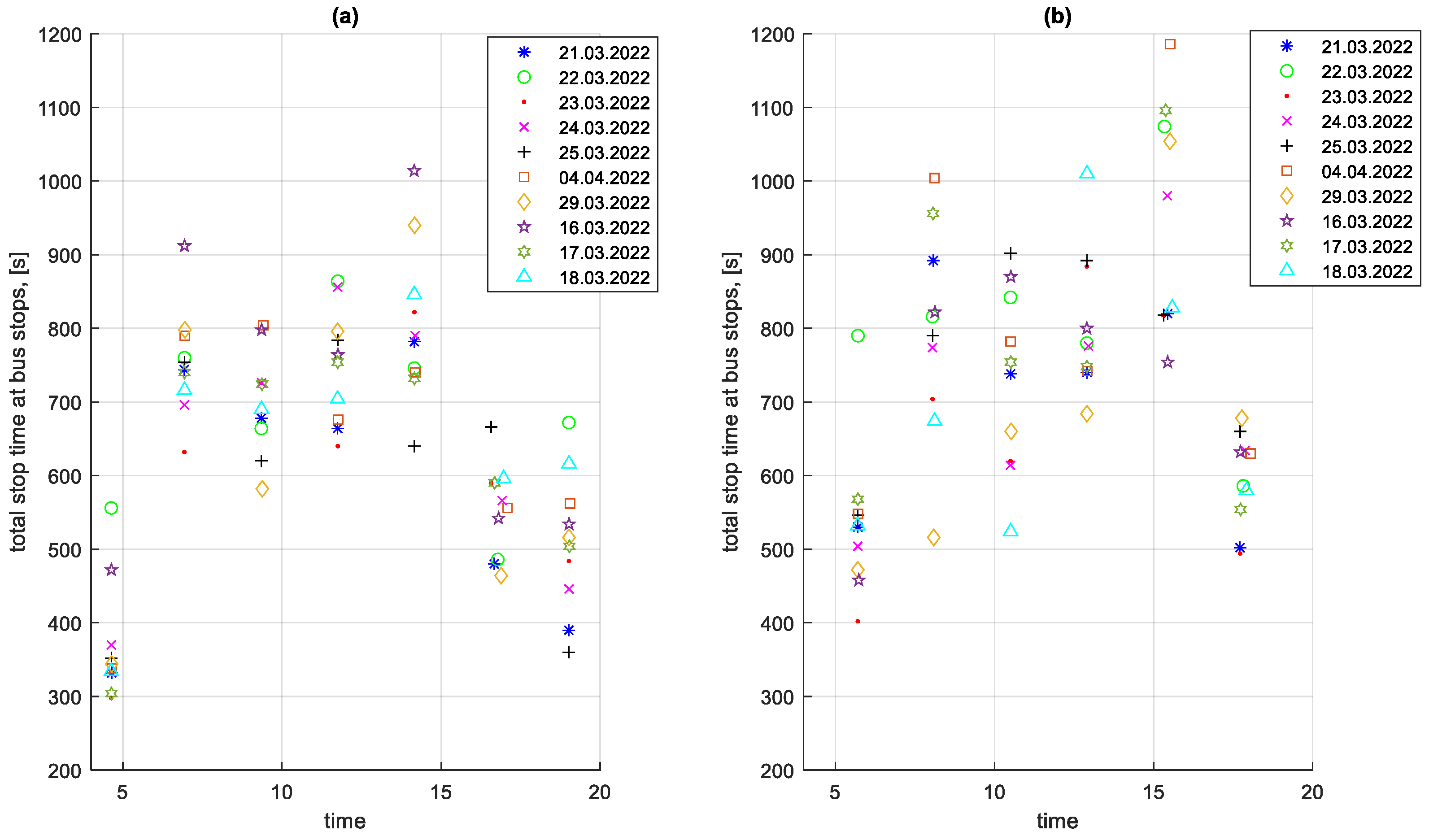
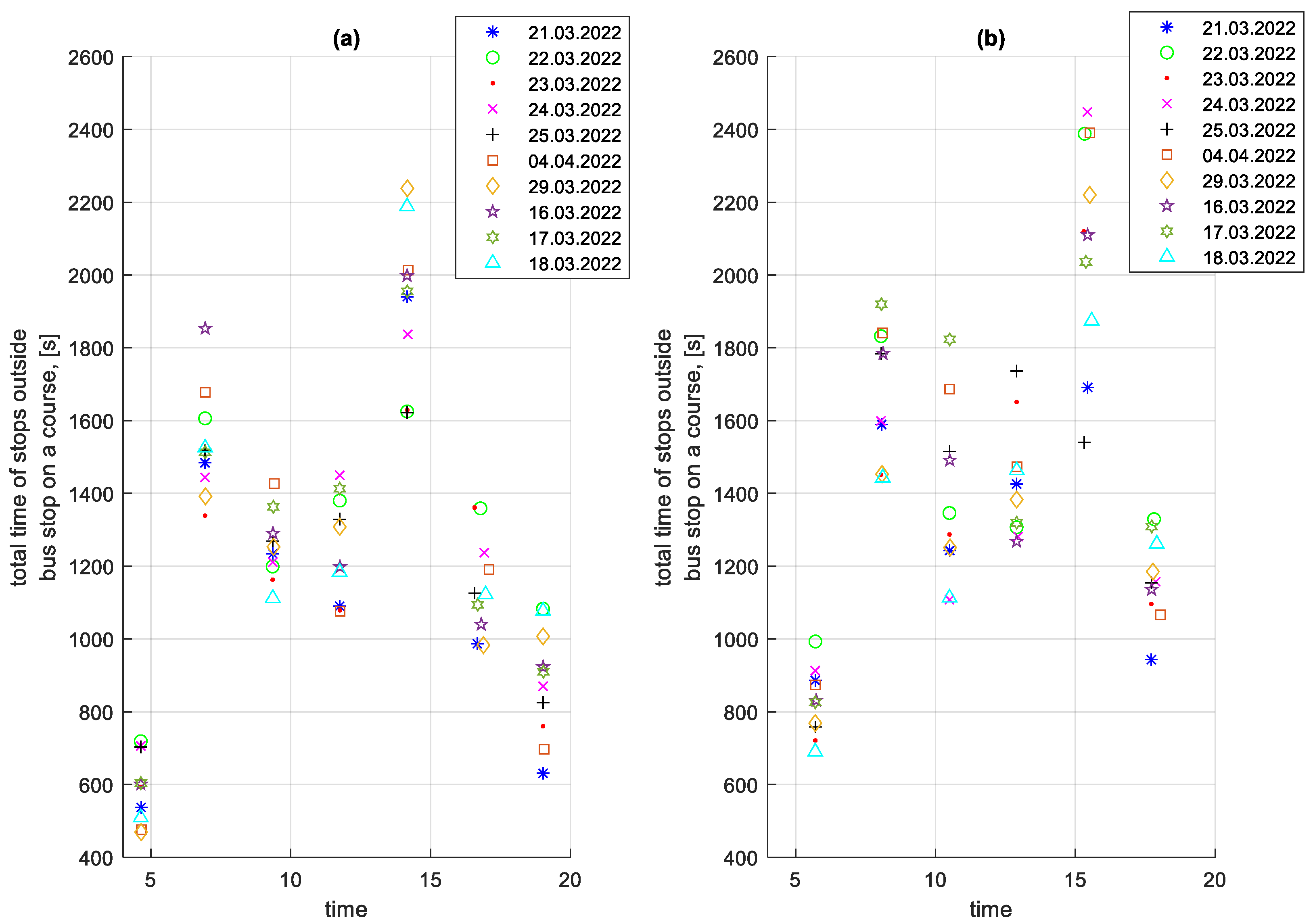
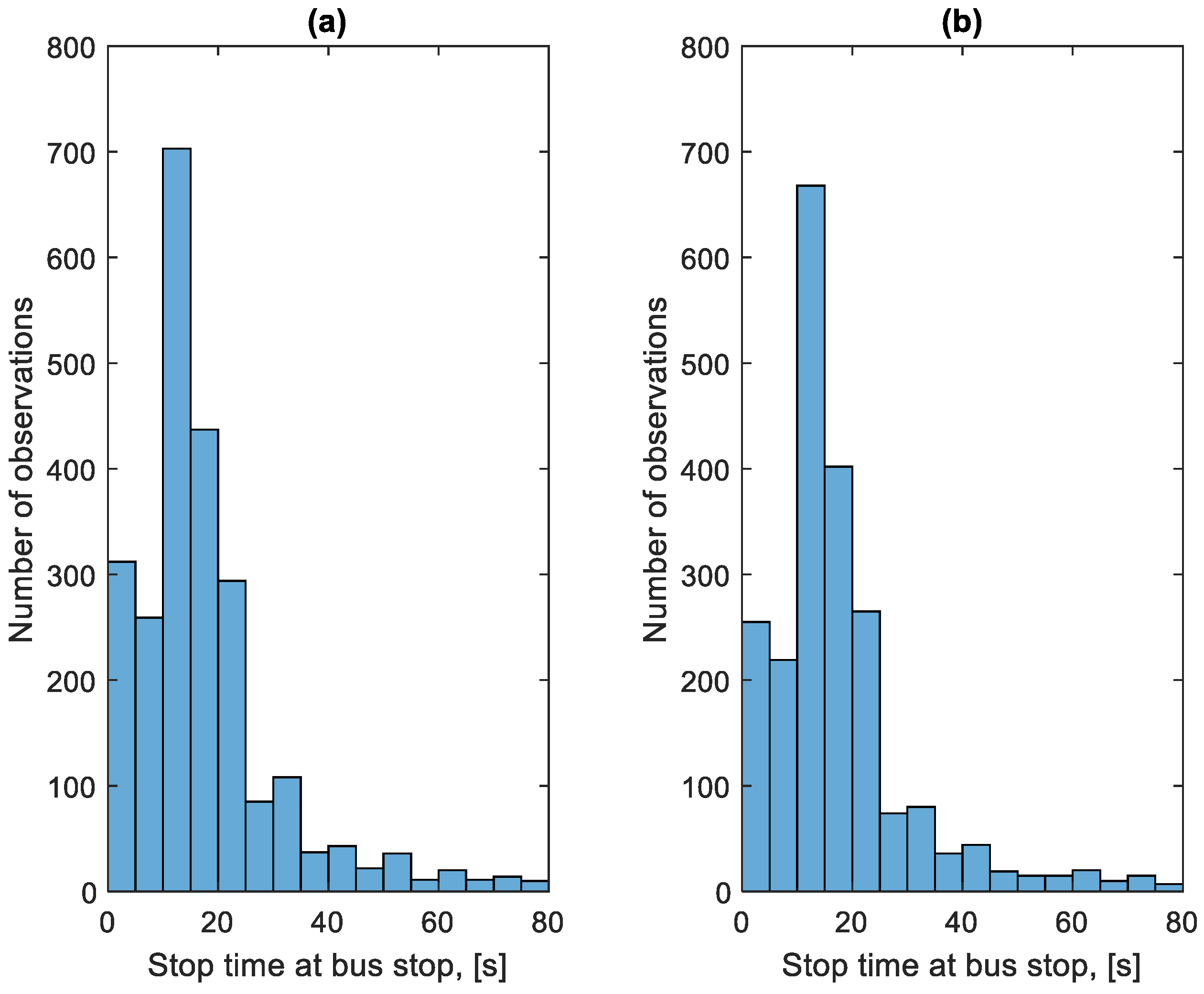
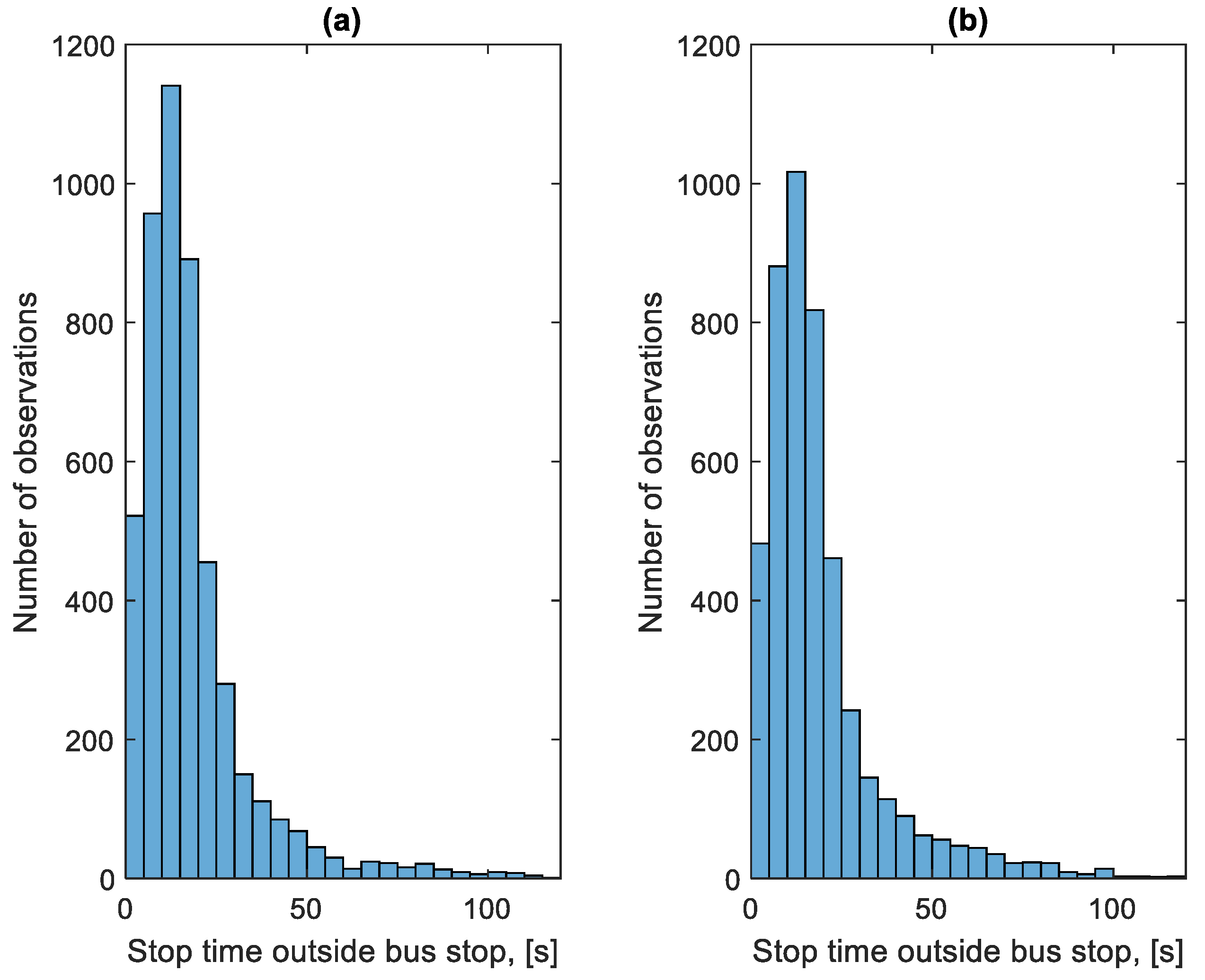
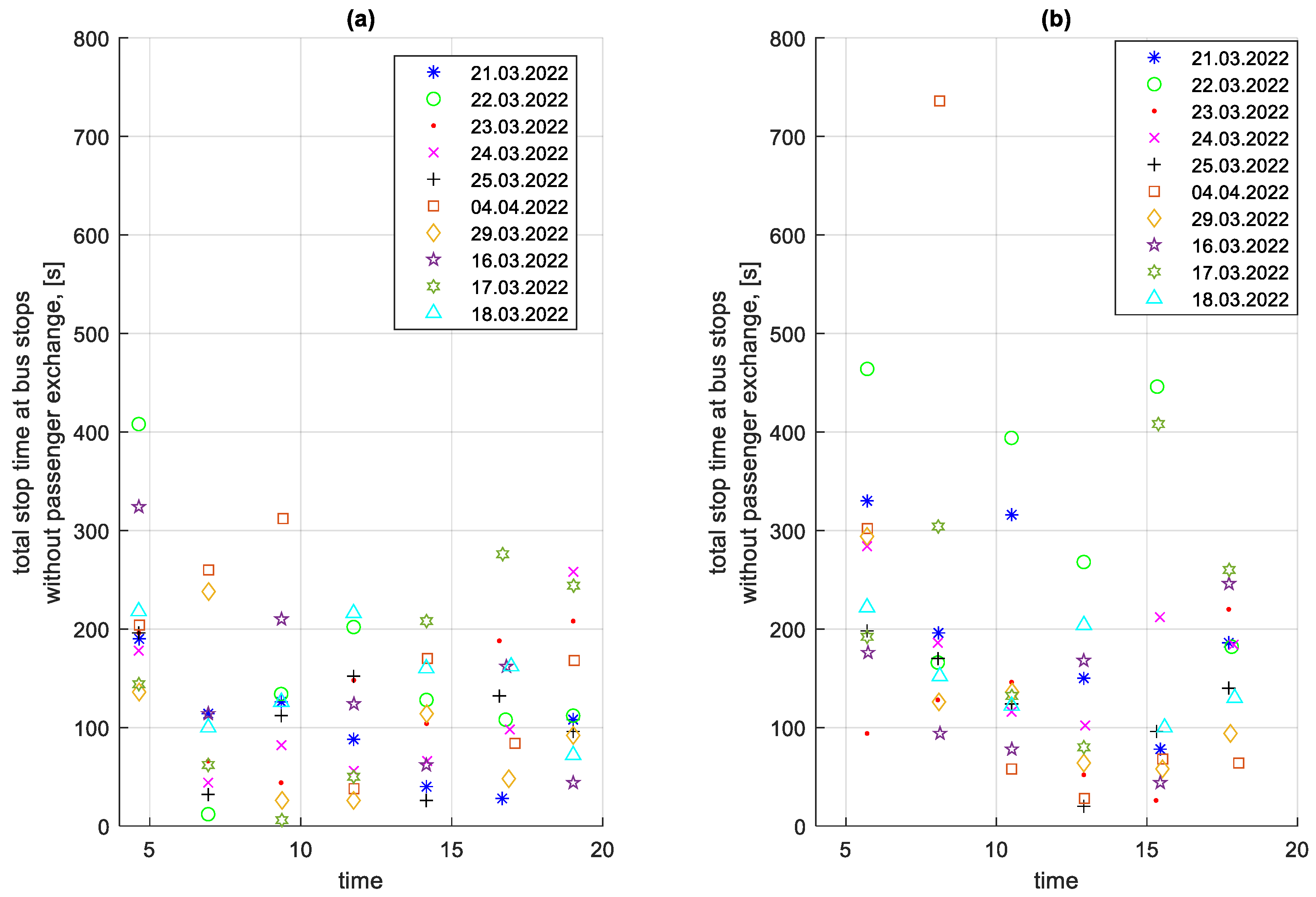
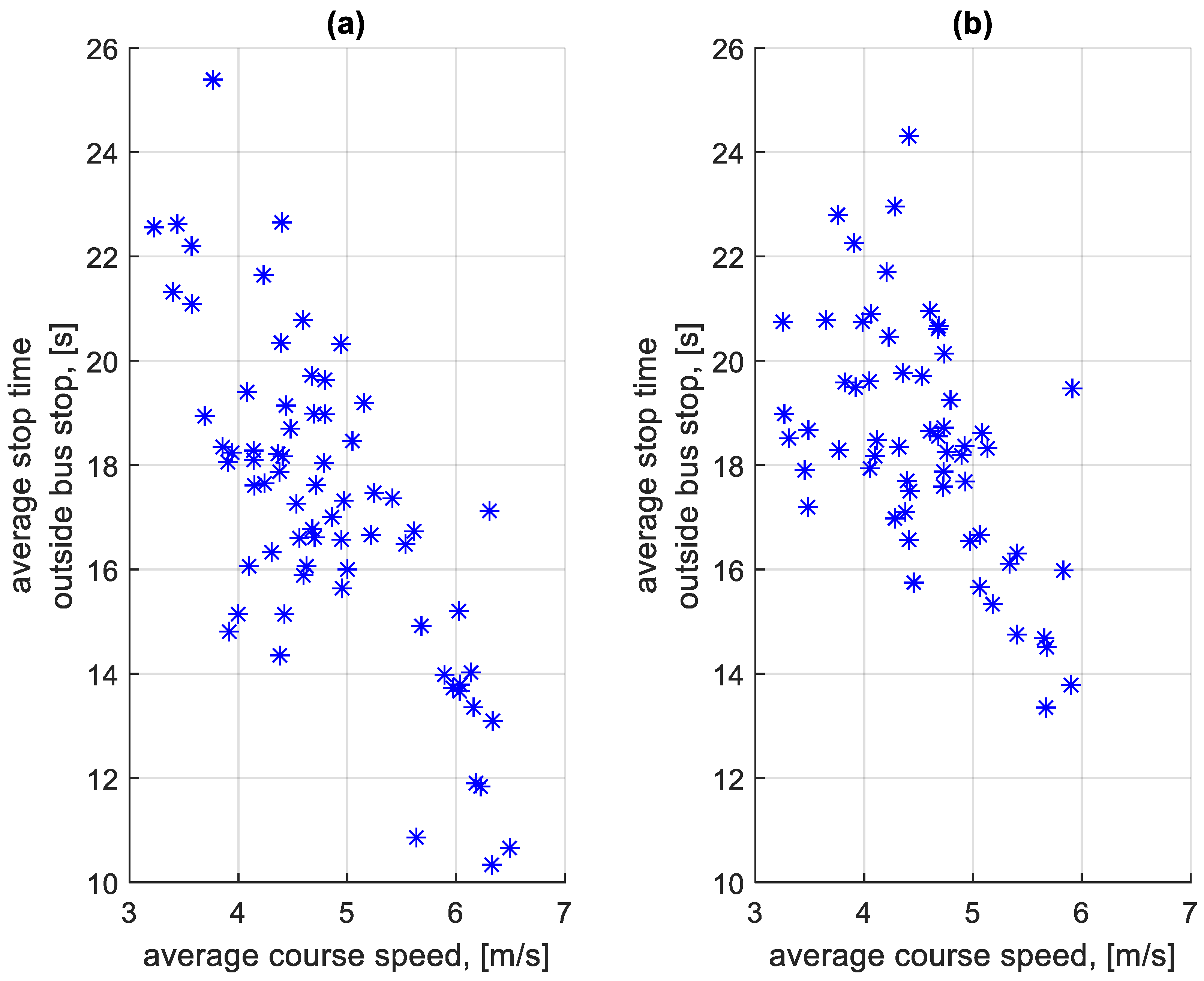
3.5. Analysis of Stop Times
4. Determining Energy Consumption
4.1. Assumptions
- —total energy lost;
- —lost kinetic energy.
- m—bus weight, m = 13,000 kg;
- —the speed at which the bus brakes, m/s;
- g—acceleration due to gravity, g = 9.81 m/s2;
- ft—rolling resistance coefficient, ft = 0.01;
- —braking distance, m;
- —efficiency of the drive system, ;
- —engine efficiency, ;
- —energy lost during standstill.
- —bus standstill time, s;
- —fuel consumption per second during standstill, g/s;
- —calorific value of fuel, .
- —energy lost on the ith stop;
- n—number of all stops.
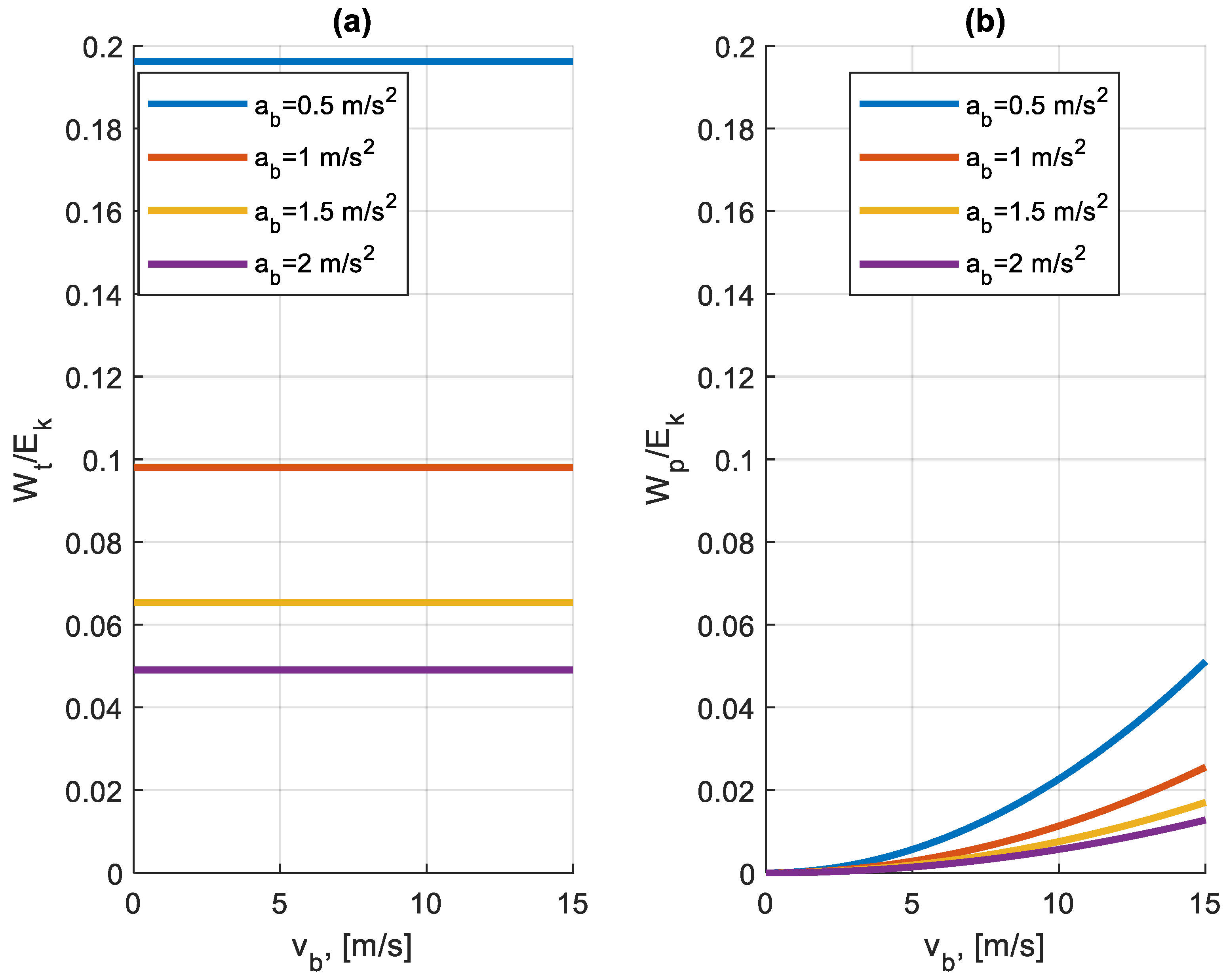
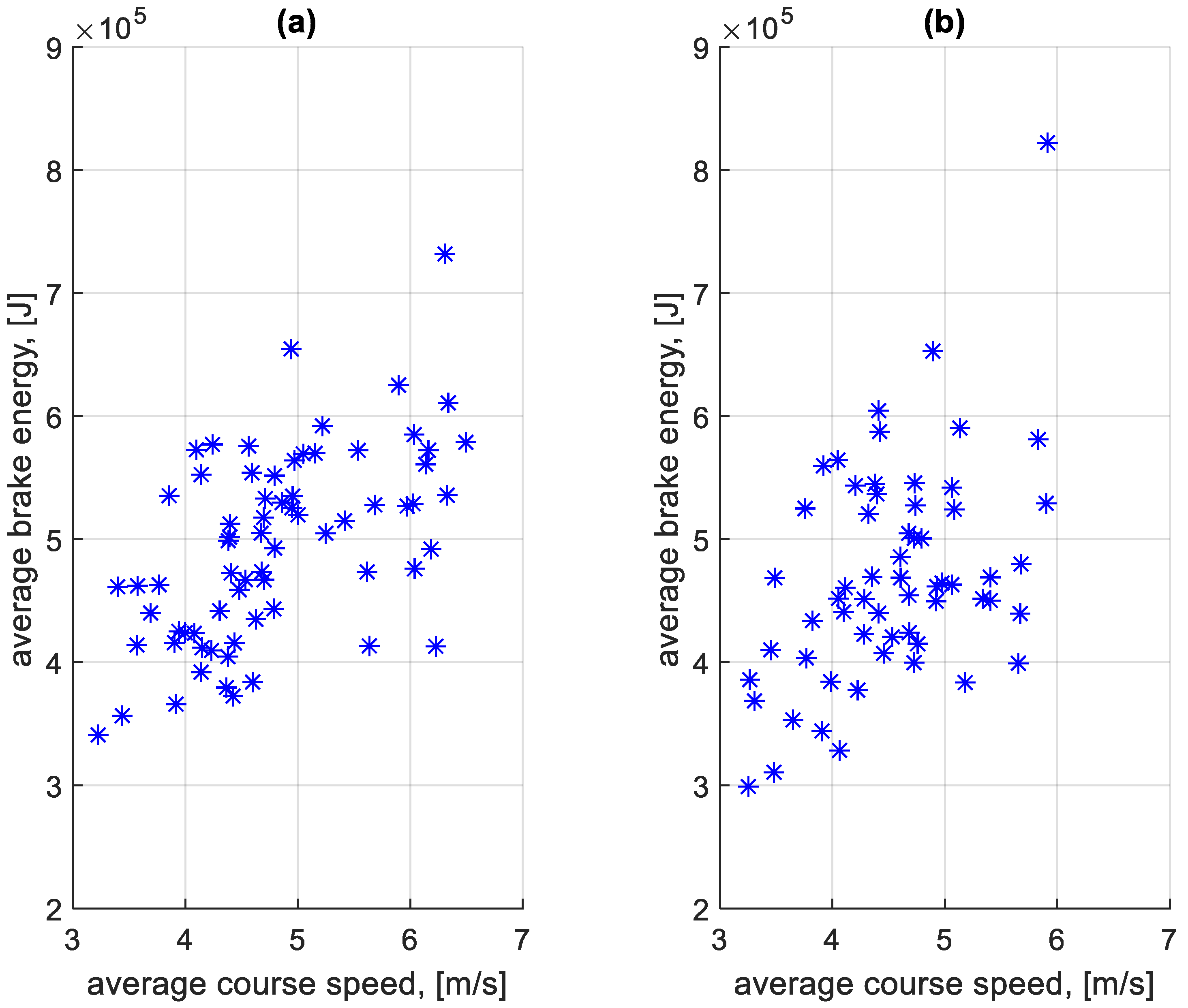
4.2. Simulation of Energy Loss in the Braking Process
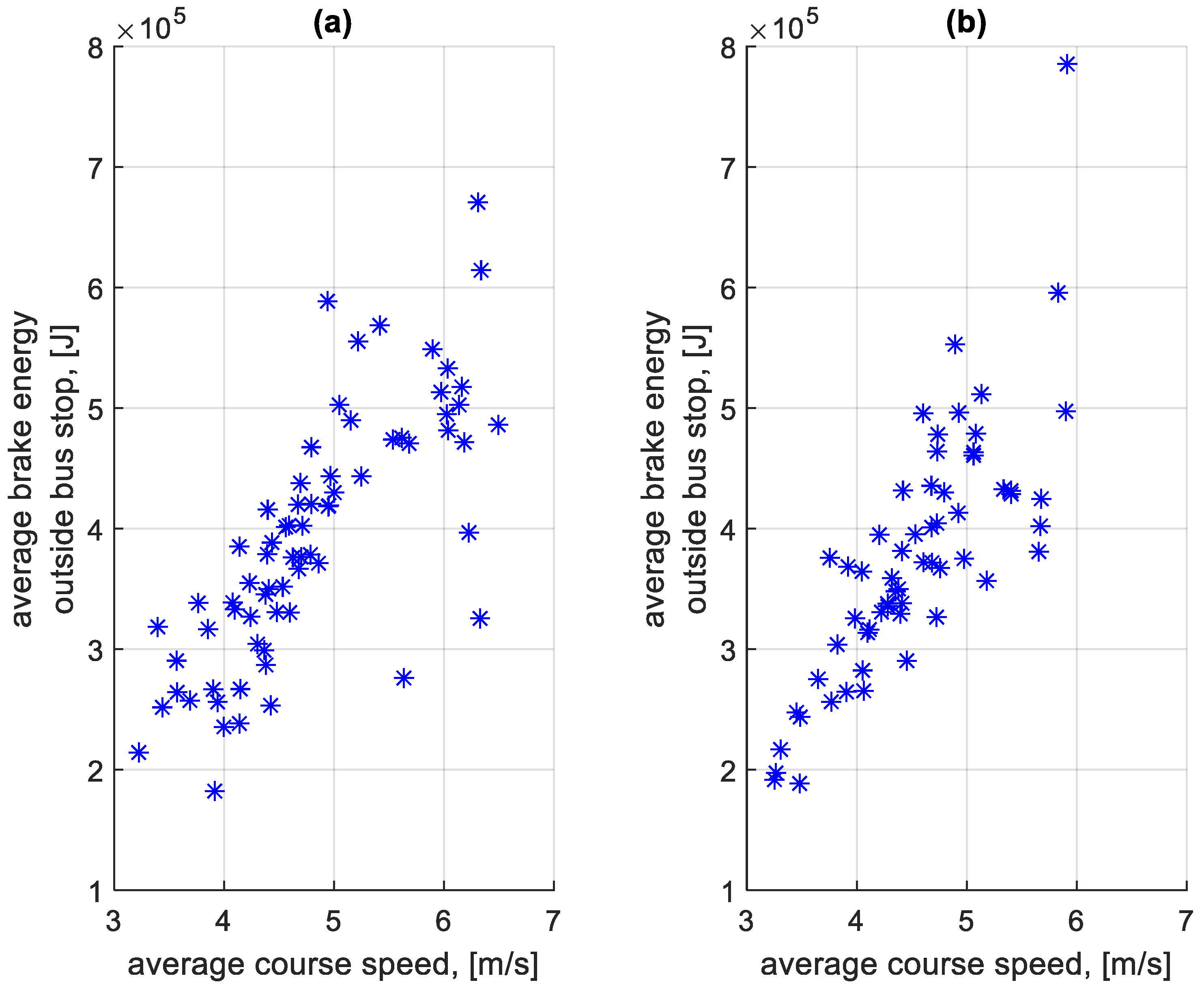
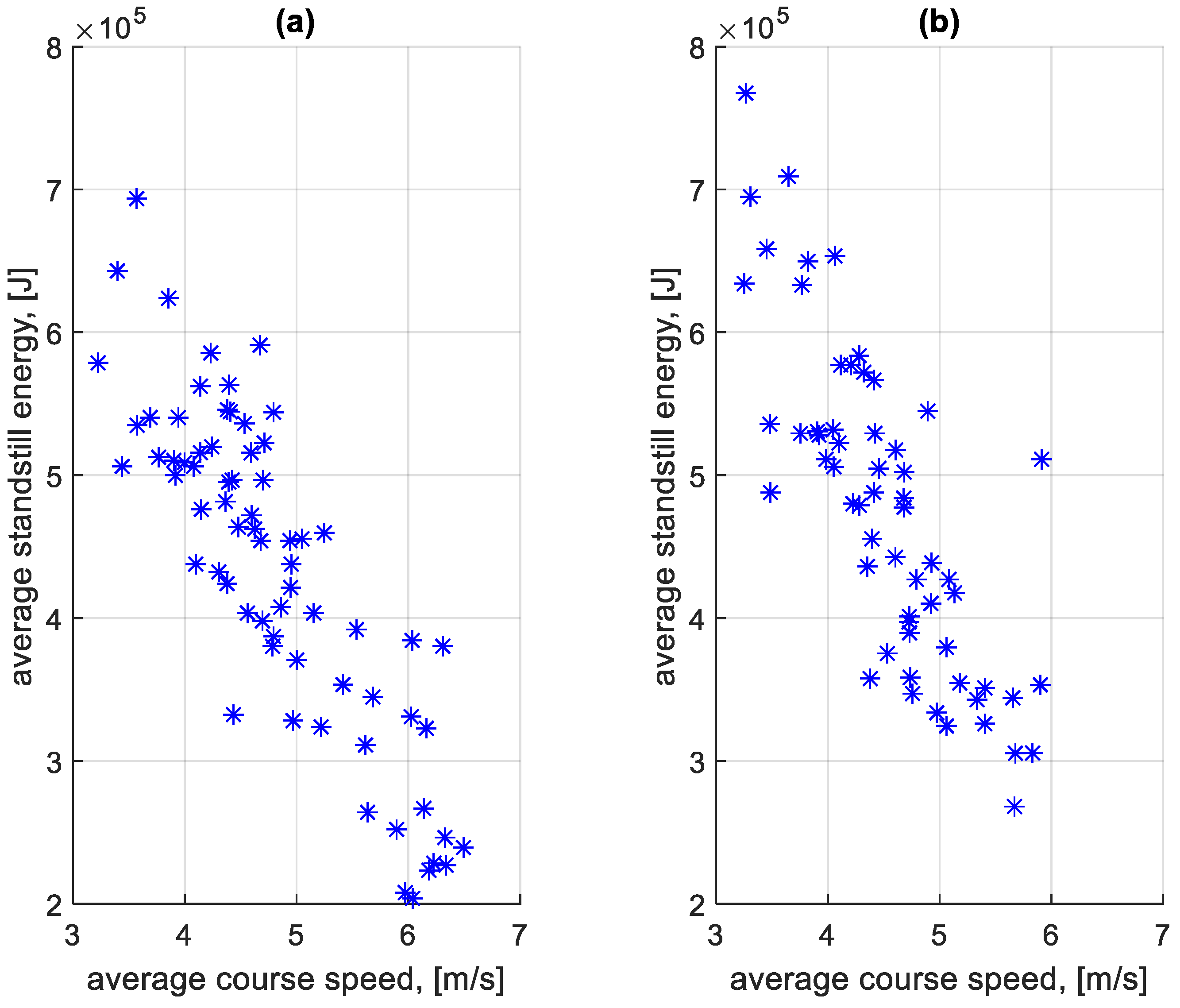
4.3. Total Energy Losses and Their Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, X.; Zhang, L. Ecodriving for reduction of bus transit emission with vehicle’s Hybrid dynamic model. Math. Probl. Eng. 2015, 2015, 543429. [Google Scholar] [CrossRef]
- Alshayeb, S.; Stevanovic, A.; Effinger, J.R. Investigating impacts of various operational conditions on fuel consumption and stop penalty at signalized intersections. Int. J. Transp. Sci. Technol. 2022, 11, 690–710. [Google Scholar] [CrossRef]
- Abdelaty, H.; Al-Obaidi, A.; Mohamed, M.; Farag, H.E.Z. Machine learning prediction models for battery-electric bus energy consumption in transit. Transp. Res. Part D Transp. Environ. 2021, 96, 102868. [Google Scholar] [CrossRef]
- Grabowski, L. Modeling research of city bus fuel consumption for different driving cycles. J. Phys. Conf. Ser. 2021, 2130, 012001. [Google Scholar] [CrossRef]
- Frey, H.C.; Rouphail, N.M.; Zhai, H.; Farias, T.L.; Gonçalves, G.A. Comparing real-world fuel consumption for diesel- and hydrogen-fueled transit buses and implication for emissions. Transp. Res. Part D Transp. Environ. 2007, 12, 281–291. [Google Scholar] [CrossRef]
- Rosero, F.; Fonseca, N.; López, J.-M.; Casanova, J. Effects of passenger load, road grade, and congestion level on real-world fuel consumption and emissions from compressed natural gas and diesel urban buses. Appl. Energy 2021, 282, 116195. [Google Scholar] [CrossRef]
- Shahariar, G.M.H.; Bodisco, T.A.; Zare, A.; Sajjad, M.; Jahirul, M.I.; Chu Van, T.; Bartlett, H.; Ristovski, Z.; Brown, R.J. Impact of driving style and traffic condition on emissions and fuel consumption during real-world transient operation. Fuel 2022, 319, 123874. [Google Scholar] [CrossRef]
- Rodríguez, R.A.; Virguez, E.A.; Rodríguez, P.A.; Behrentz, E. Influence of driving patterns on vehicle emissions: A case study for latin american cities. Transp. Res. Part D Transp. Environ. 2016, 43, 192–206. [Google Scholar] [CrossRef]
- Wang, Y.; Boggio-Marzet, A. Evaluation of eco-driving training for fuel efficiency and emissions reduction according to Road Type. Sustainability 2018, 10, 3891. [Google Scholar] [CrossRef]
- Özener, O.; Özkan, M. Fuel consumption and emission evaluation of a rapid bus transport system at different operating conditions. Fuel 2020, 265, 117016. [Google Scholar] [CrossRef]
- Sun, R.; Chen, Y.; Dubey, A.; Pugliese, P. Hybrid electric buses fuel consumption prediction based on real-world driving data. Transp. Res. Part D Transp. Environ. 2021, 91, 102637. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, Y.; Liu, H.; Huang, R.; Yang, L.; Li, Z.; Fu, L.; Hao, J. Real-world fuel consumption and CO2 emissions of Urban Public Buses in Beijing. Appl. Energy 2014, 113, 1645–1655. [Google Scholar] [CrossRef]
- Rosero, F.; Fonseca, N.; López, J.-M.; Casanova, J. Real-world fuel efficiency and emissions from an urban diesel bus engine under transient operating conditions. Appl. Energy 2020, 261, 114442. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, B.; Wang, S.; Ma, Y. Analysis and estimation of energy consumption of electric buses using real-world data. Transp. Res. Part D Transp. Environ. 2024, 126, 104017. [Google Scholar] [CrossRef]
- Ji, J.; Bie, Y.; Zeng, Z.; Wang, L. Trip Energy Consumption Estimation for electric buses. Commun. Transp. Res. 2022, 2, 100069. [Google Scholar] [CrossRef]
- Ghaffarpasand, O.; Talaie, M.R.; Ahmadikia, H.; Khozani, A.T.; Shalamzari, M.D.; Majidi, S. Real-world assessment of Urban Bus Transport in a medium-sized city of the Middle East: Driving behavior, emission performance, and Fuel Consumption. Atmos. Pollut. Res. 2021, 12, 113–124. [Google Scholar] [CrossRef]
- Ma, X.; Miao, R.; Wu, X.; Liu, X. Examining influential factors on the energy consumption of electric and diesel buses: A data-driven analysis of large-scale public transit network in Beijing. Energy 2021, 216, 119196. [Google Scholar] [CrossRef]
- Wang, A.; Ge, Y.; Tan, J.; Fu, M.; Shah, A.N.; Ding, Y.; Zhao, H.; Liang, B. On-road pollutant emission and fuel consumption characteristics of buses in Beijing. J. Environ. Sci. 2011, 23, 419–426. [Google Scholar] [CrossRef]
- de Abreu e Silva, J.; Moura, F.; Garcia, B.; Vargas, R. Influential vectors in fuel consumption by an urban bus operator: Bus route, driver behavior or vehicle type? Transp. Res. Part D Transp. Environ. 2015, 38, 94–104. [Google Scholar] [CrossRef]
- Macián, V.; Tormos, B.; Ruíz, S.; Ramírez, L. Potential of low viscosity oils to reduce CO2 emissions and fuel consumption of urban buses fleets. Transp. Res. Part D Transp. Environ. 2015, 39, 76–88. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Zhang, Y.; Zhang, K.; Jiang, M. The effects of dynamic traffic conditions, route characteristics and environmental conditions on trip-based electricity consumption prediction of electric bus. Energy 2021, 218, 119437. [Google Scholar] [CrossRef]
- Yang, X.; Liu, L. Analysis of the influence of passenger load on bus energy consumption a vehicle-engine combined model-based simulation framework. Sci. Rep. 2022, 12, 14535. [Google Scholar] [CrossRef] [PubMed]
- Abdelaty, H.; Mohamed, M. A prediction model for battery electric bus energy consumption in transit. Energies 2021, 14, 2824. [Google Scholar] [CrossRef]
- Stankiewicz, J.; Michalski, K. Rozwiązania Z Zakresu Inteligentnych systemów transportowych W Wybranych Miastach w Polsce. Ekon. I Organ. Logistyki 2018, 3, 79–91. [Google Scholar] [CrossRef]
- W Rzeszowie na Wszystkich Skrzyżowaniach Z Sygnalizacją Świetlną będą Detektory Ruchu. (In Polish). Available online: https://nowiny24.pl/w-rzeszowie-na-wszystkich-skrzyzowaniach-z-sygnalizacja-swietlna-beda-detektory-ruchu/ar/c4-16359805 (accessed on 24 April 2024).
- Kilka Słów O Rzeszowskim inteligentnym Systemie Transportowym: Wiadomości: Focus on Business—Created by Pro Progressio. (In Polish). Available online: https://focusonbusiness.eu/pl/wiadomosci/kilka-slow-o-rzeszowskim-inteligentnym-systemie-transportowym/11213 (accessed on 24 April 2024).
- Śmieszek, M.; Mateichyk, V. Determining the fuel consumption of a public city bus in urban traffic. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1199, 012080. [Google Scholar] [CrossRef]
- Smieszek, M.; Kostian, N.; Mateichyk, V.; Mosciszewski, J.; Tarandushka, L. Estimation of the public transport operating performance: Example of a selected city bus route. Commun.-Sci. Lett. Univ. Zilina 2023, 25, B7–B21. [Google Scholar] [CrossRef]
- Śmieszek, M.; Kostian, N.; Mateichyk, V.; Mościszewski, J.; Tarandushka, L. Determination of the model basis for assessing the vehicle energy efficiency in urban traffic. Energies 2021, 14, 8538. [Google Scholar] [CrossRef]
- Wang, J.; Rakha, H.A. Fuel consumption model for conventional diesel buses. Appl. Energy 2016, 170, 394–402. [Google Scholar] [CrossRef]
- Rahman, S.M.A.; Masjuki, H.H.; Kalam, M.A.; Abedin, M.J.; Sanjid, A.; Sajjad, H. Impact of idling on fuel consumption and exhaust emissions and available idle-reduction technologies for diesel vehicles—A Review. Energy Convers. Manag. 2013, 74, 171–182. [Google Scholar] [CrossRef]



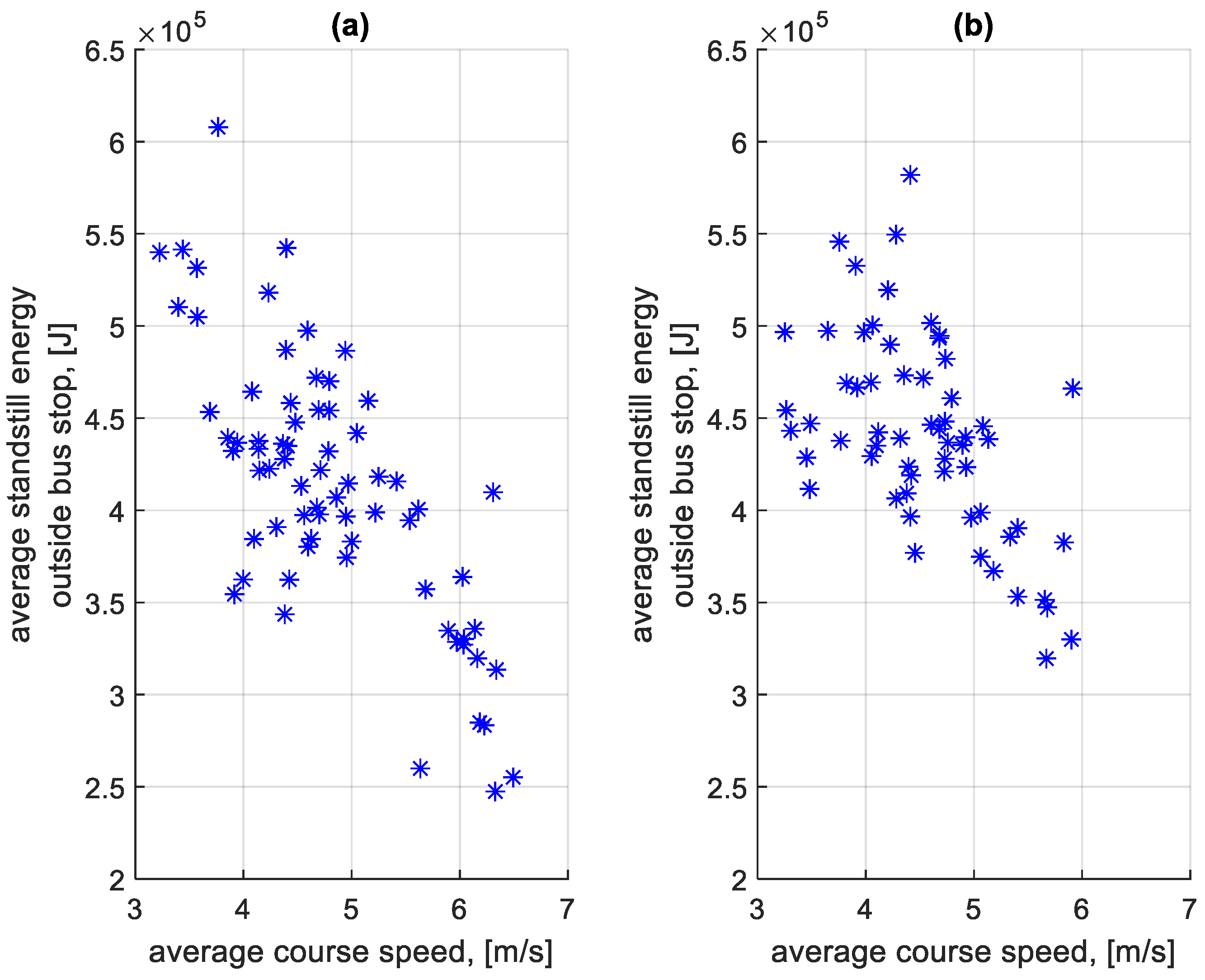
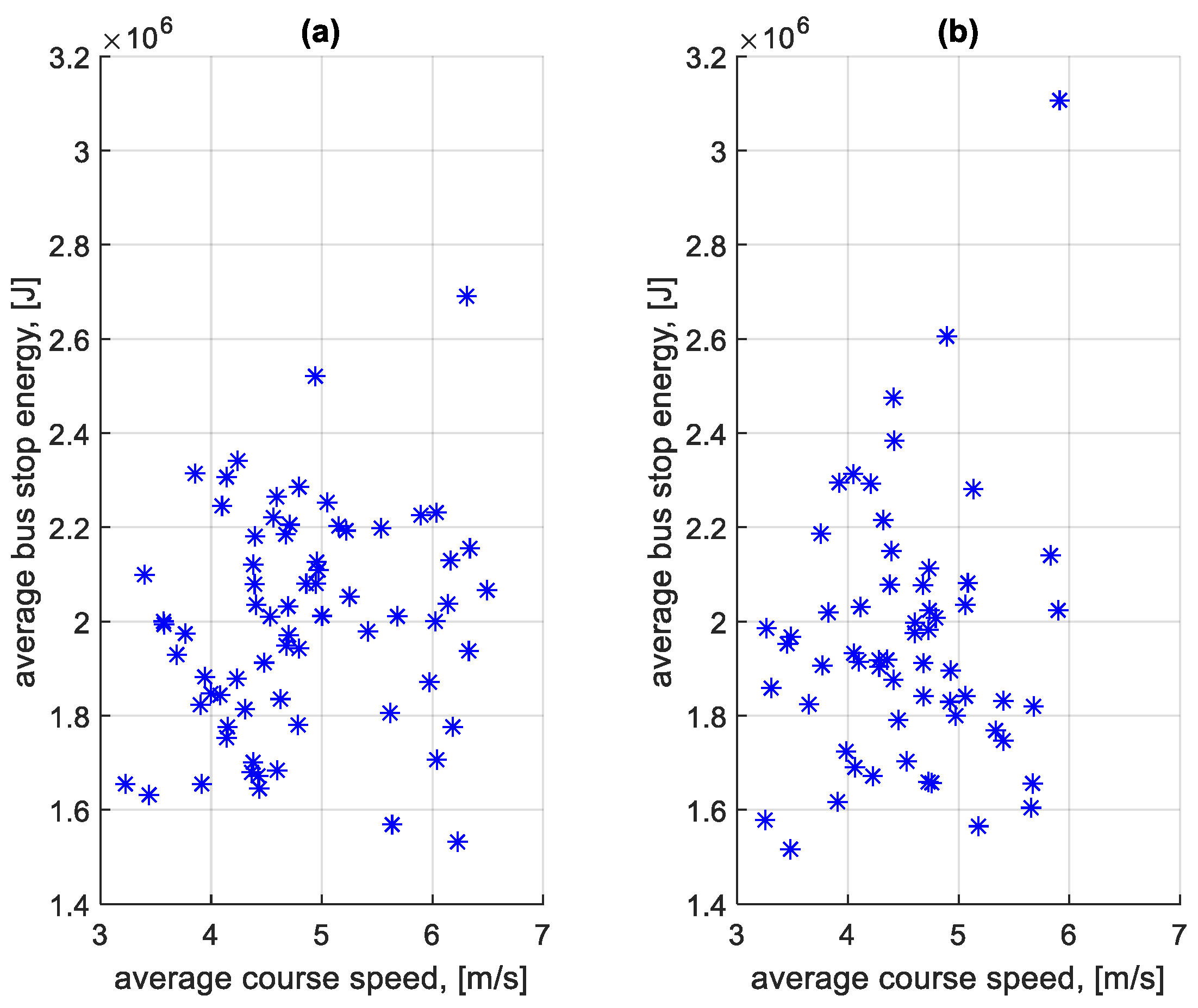
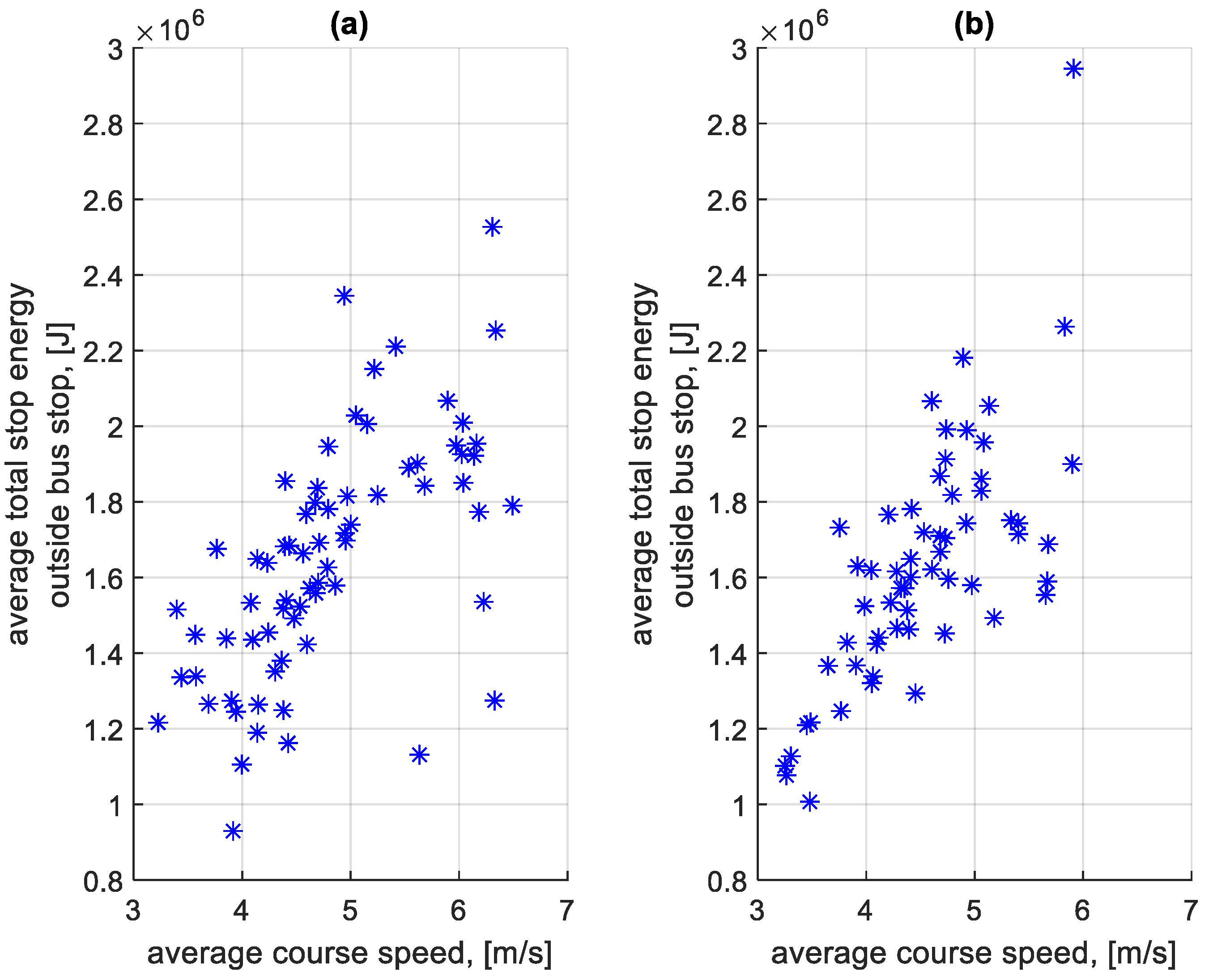
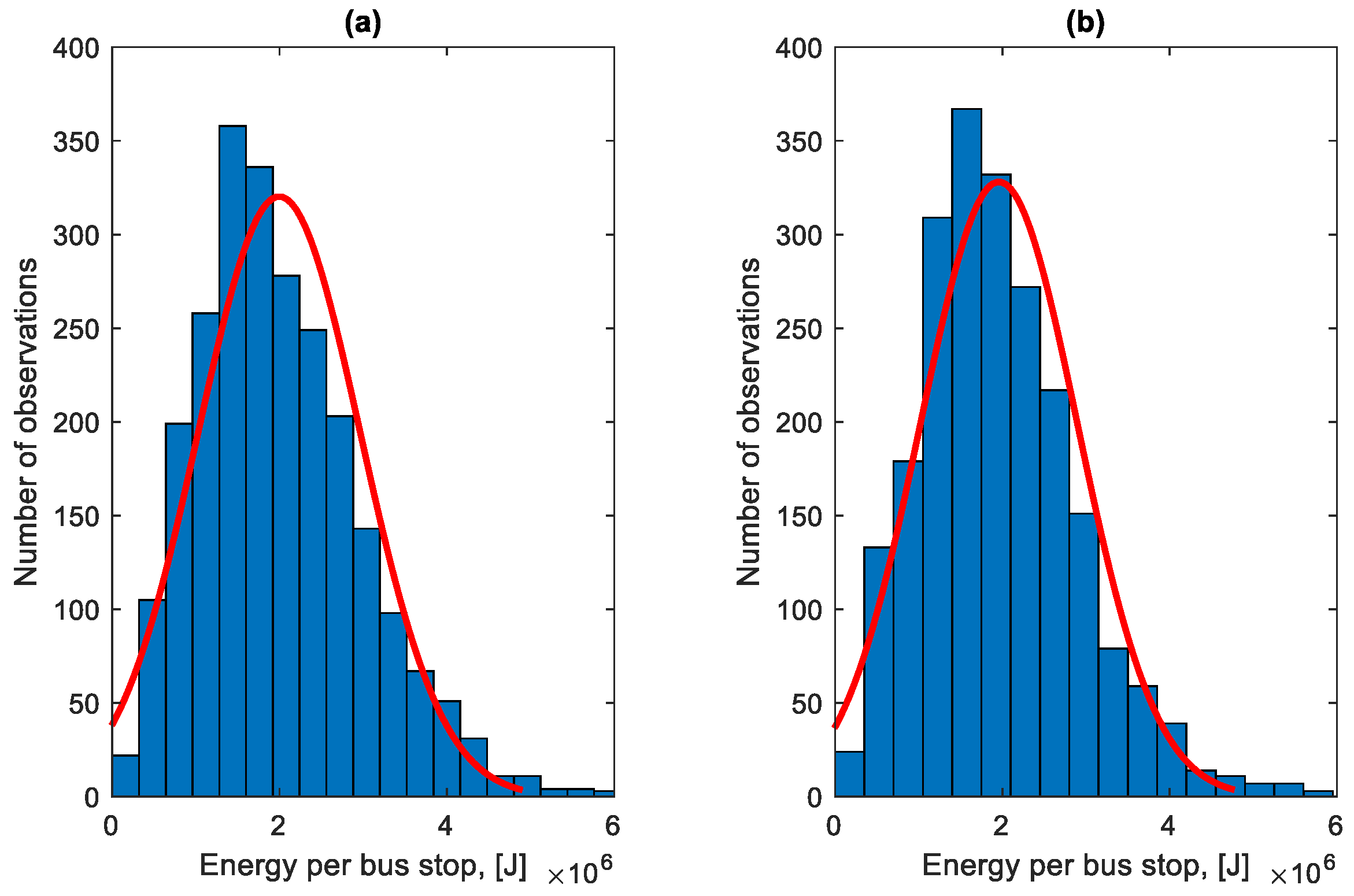
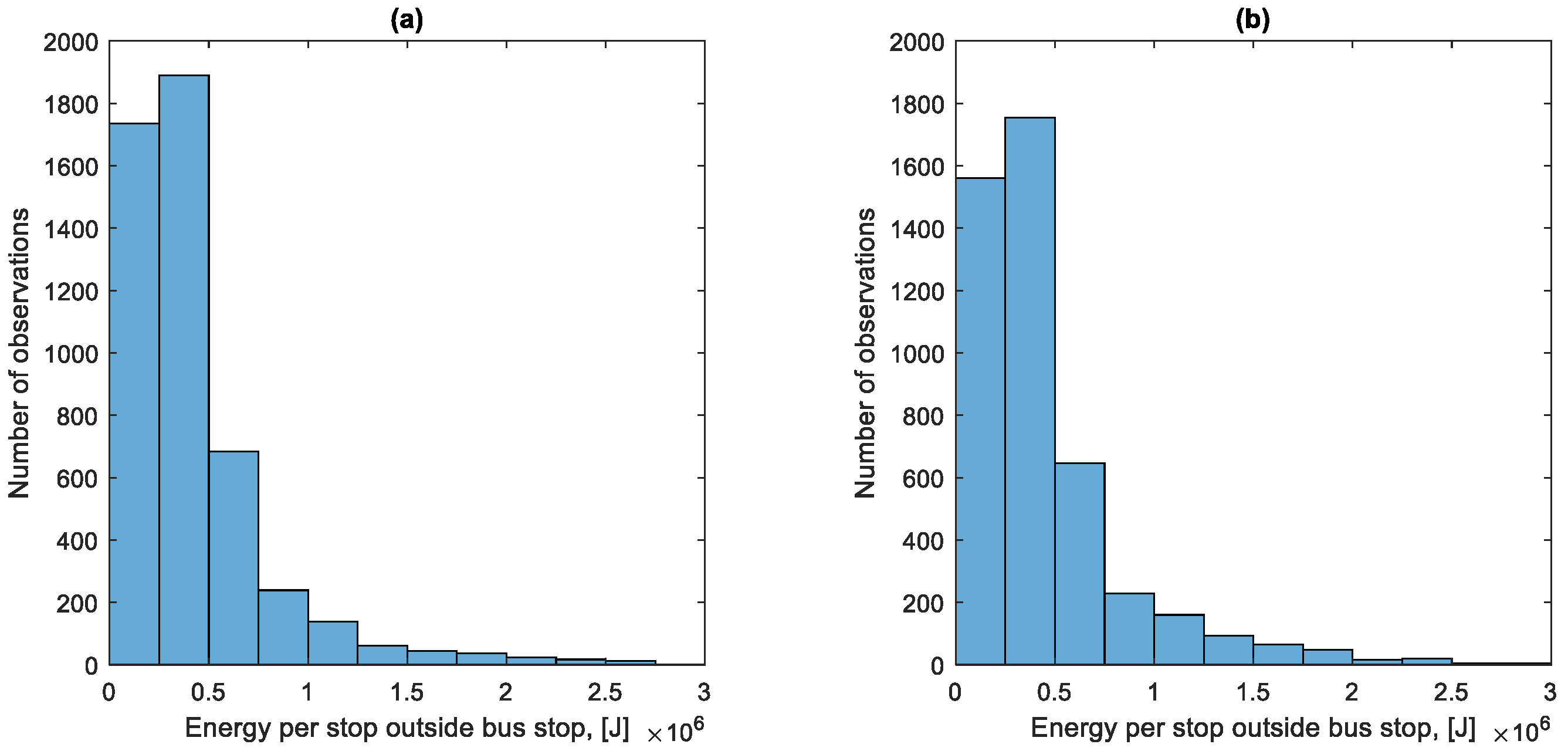
| Direction | Share of Braking Energy [%] | Share of Standstill Energy [%] |
|---|---|---|
| A to B | 78.35 | 21.65 |
| B to A | 75.89 | 24.11 |
| Direction | Share of Braking Energy [%] | Share of Standstill Energy [%] |
|---|---|---|
| A to B | 23.32 | 76.68 |
| B to A | 22.74 | 77.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smieszek, M.; Mateichyk, V.; Mosciszewski, J. The Influence of Stops on the Selected Route of the City ITS on the Energy Efficiency of the Public Bus. Energies 2024, 17, 4179. https://doi.org/10.3390/en17164179
Smieszek M, Mateichyk V, Mosciszewski J. The Influence of Stops on the Selected Route of the City ITS on the Energy Efficiency of the Public Bus. Energies. 2024; 17(16):4179. https://doi.org/10.3390/en17164179
Chicago/Turabian StyleSmieszek, Miroslaw, Vasyl Mateichyk, and Jakub Mosciszewski. 2024. "The Influence of Stops on the Selected Route of the City ITS on the Energy Efficiency of the Public Bus" Energies 17, no. 16: 4179. https://doi.org/10.3390/en17164179
APA StyleSmieszek, M., Mateichyk, V., & Mosciszewski, J. (2024). The Influence of Stops on the Selected Route of the City ITS on the Energy Efficiency of the Public Bus. Energies, 17(16), 4179. https://doi.org/10.3390/en17164179






