Study on the Gas Phase Liquid Carrying Velocity of Deep Coalbed Gas Well with Atomization Assisted Production
Abstract
:1. Introduction
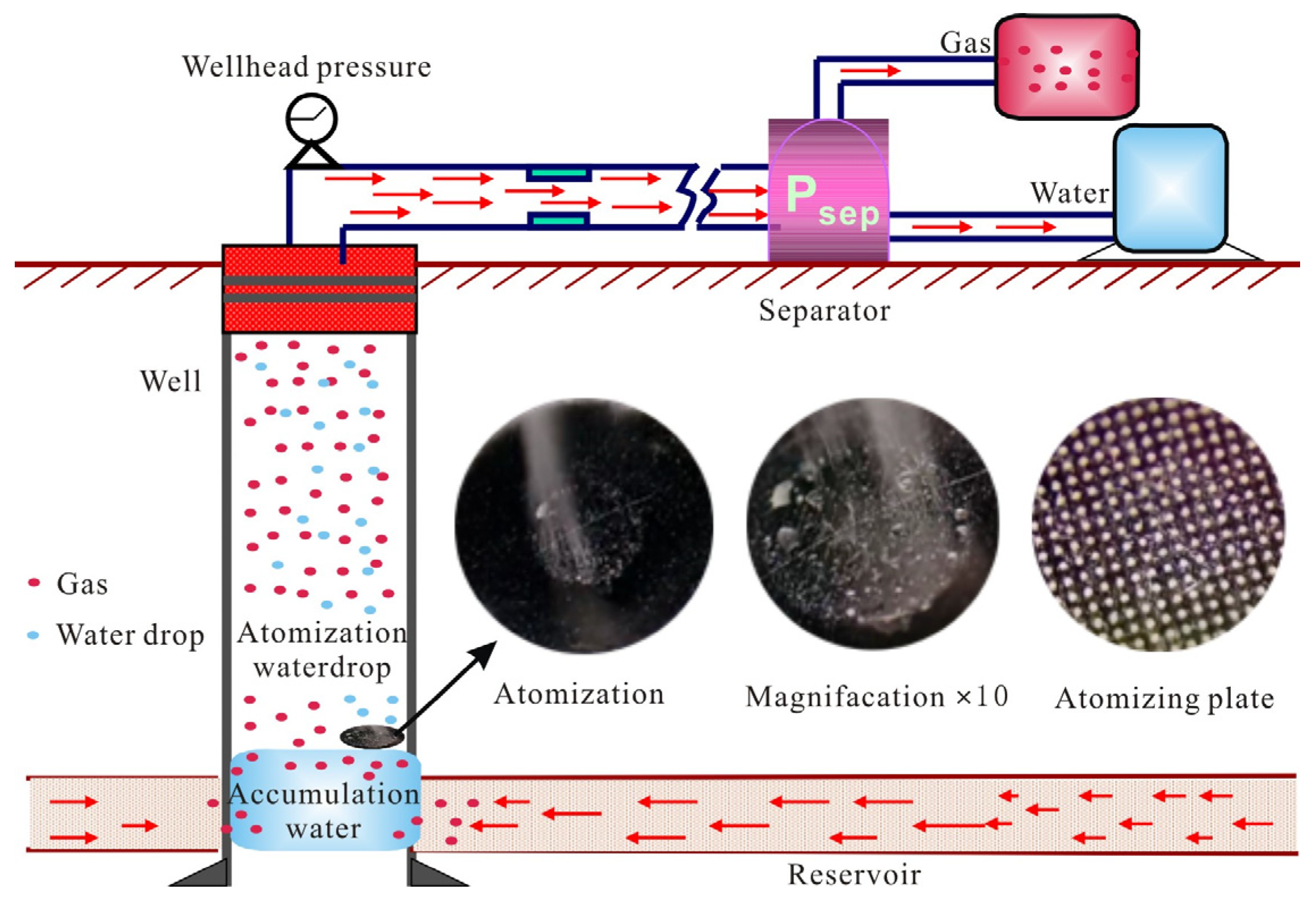
2. Function and Principle of Production by Atomizing
3. Modeling of Gas-Phase Carrying Droplet
3.1. Force Analysis of Droplet Flow
3.2. Pressure Gradient and Calculation Method for Two-Phase Flow in Wellbore
3.2.1. Hypothesis
3.2.2. Gas-Liquid Two-Phase Transient Flow Modeling
3.2.3. Numerical Model
3.2.4. Solution Step
- (1)
- First, the underlying computational parameters should be specified, and then the initial and boundary conditions should be circled;
- (2)
- Discretize the fixed solution domain;
- (3)
- Give a set of m + 1 moments and j + 1 nodes at the corresponding and calculate the unknown quantity , , ;
- (4)
- The mist flow pattern and several physical parameters calculated in the previous step are used to calculate and ;
- (5)
- Comparison with , , and , view the error of both, if less than 98%, from step (3), recalculate and ; on the contrary, if the calculated value is accurate, you can continue to calculate until the calculation is made to the ground wellhead.

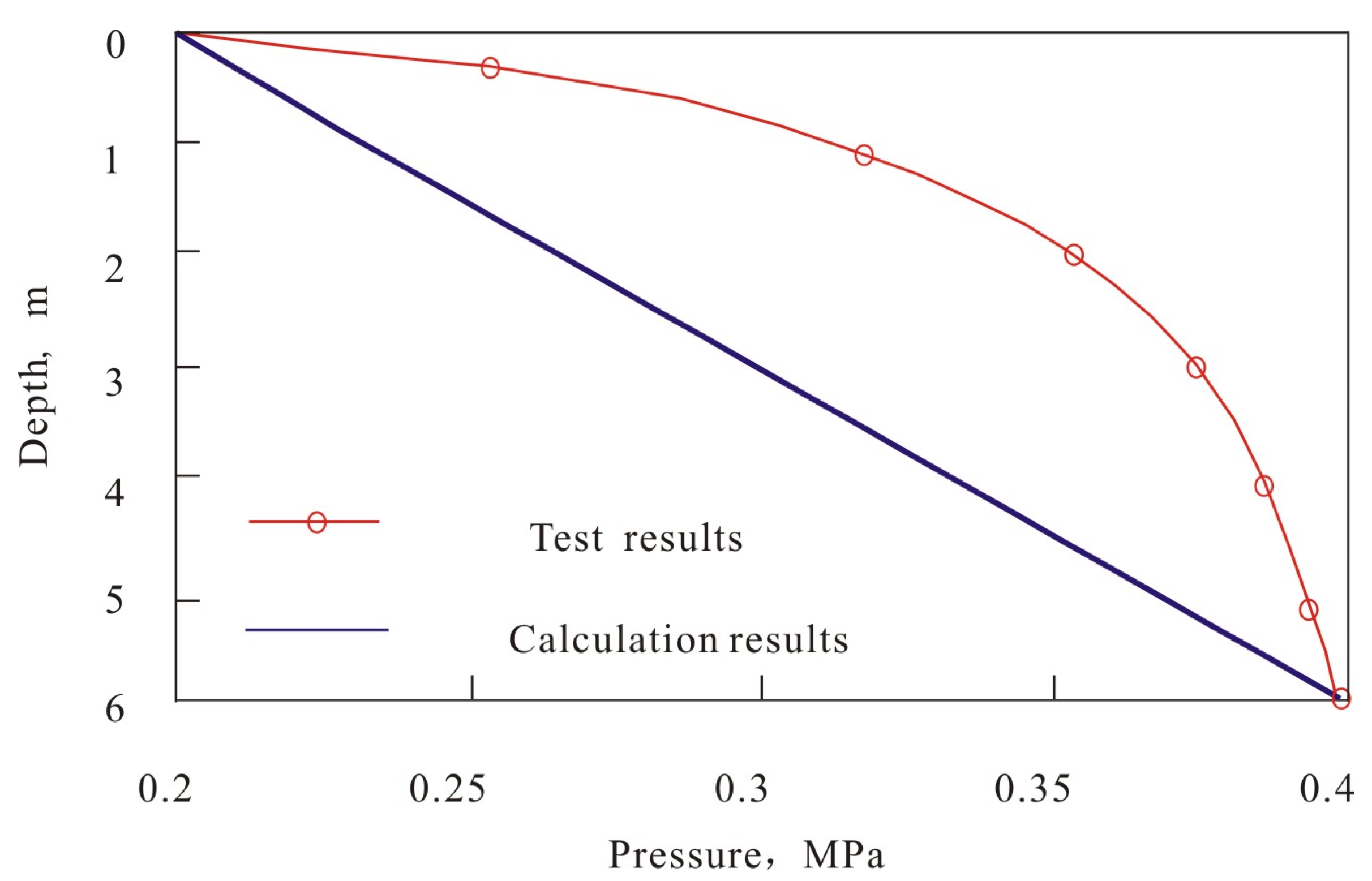
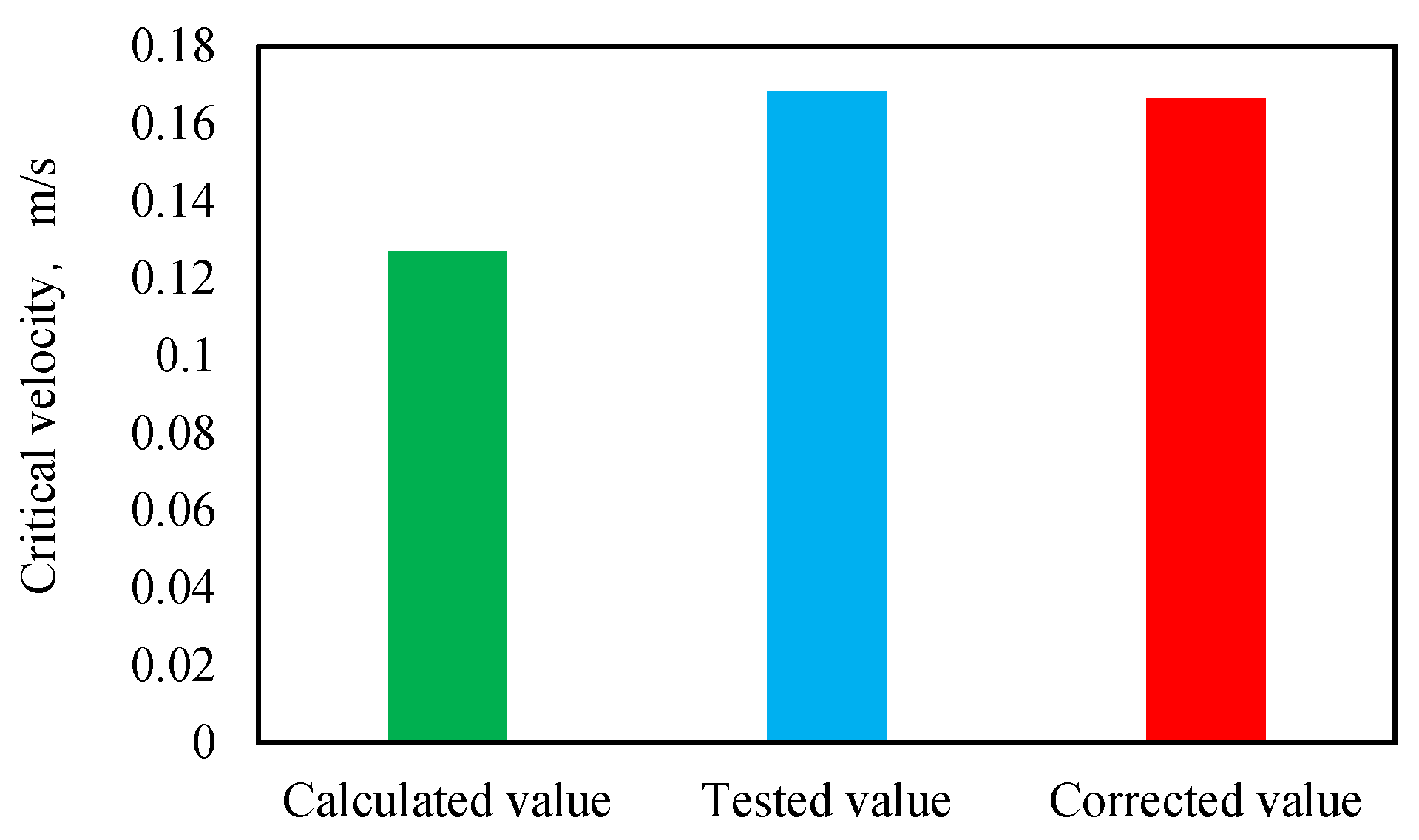
3.2.5. Model Validation
- (1)
- First, the liquid is injected through the injection hole at the lowest part of the wellbore to simulate wellbore liquid accumulation, and the liquid should be injected slowly to prevent liquid splashing. After liquid injection, wait for the liquid accumulation speed to reach a stable in the tube;
- (2)
- Next, open the atomizer (droplet aperture diameter of 0.1 mm) and observe whether the accumulated liquid is going to droplets. If droplets form, proceed to the next step. On the contrary, check the atomizer.
- (3)
- Then, open the valve of the gas tank and set an injection pressure difference of 0.1 MPa. Pay attention to the observation that the gas flow rate at this time is small and does not reach the critical liquid-carrying state. After a period of stability, liquid accumulation may occur again in the wellbore.
- (4)
- The injection pressure was increased step by step (0.02 MPa each time) until no liquid accumulation occurred in the wellbore, the minimum liquid-carrying velocity was measured, and the pressure distribution along the wellbore was recorded, as shown in the red line in Figure 4.
4. Analysis of Factors Affecting the Fluid-Carrying Process in Gas Wells
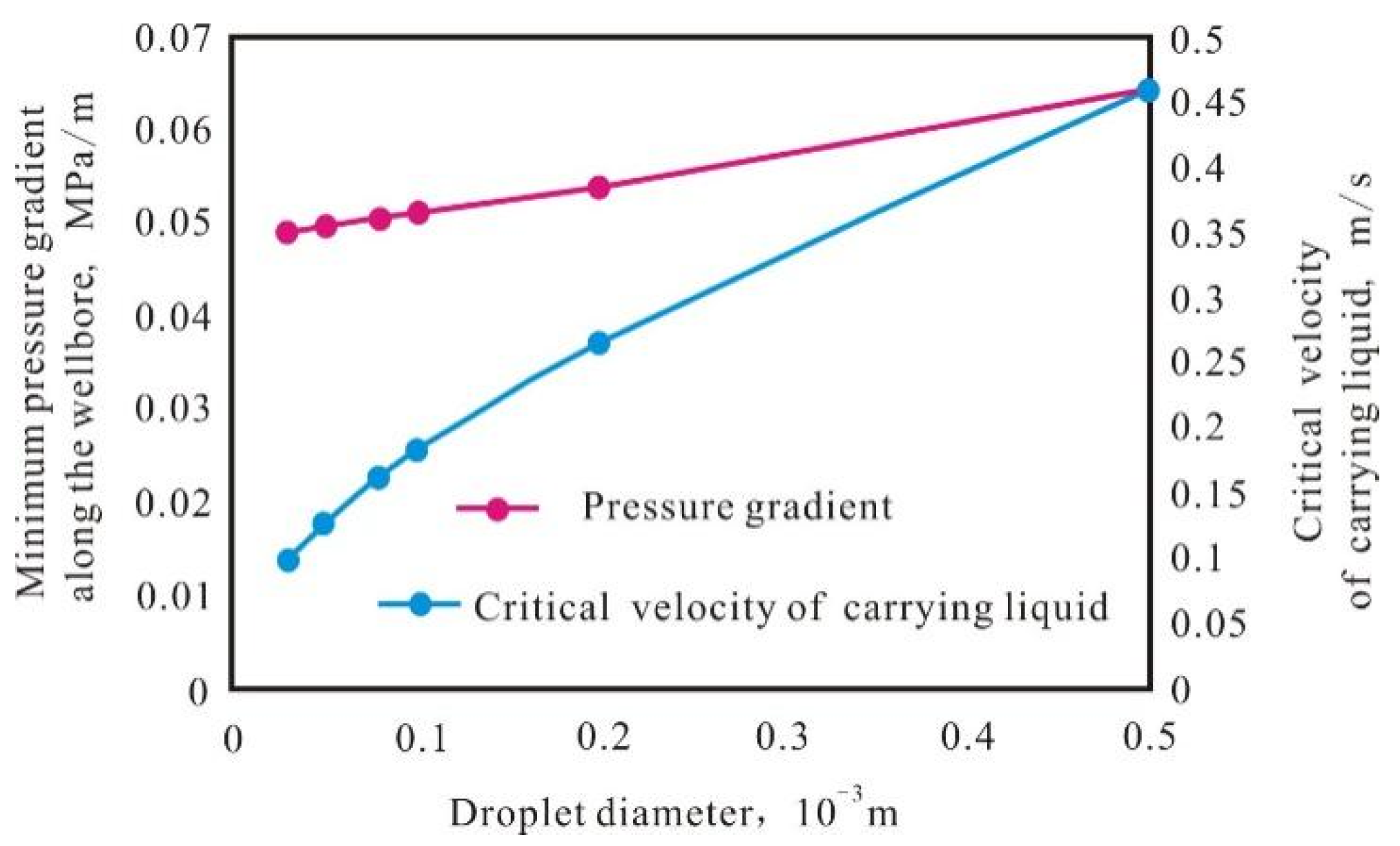
4.1. Droplet Size
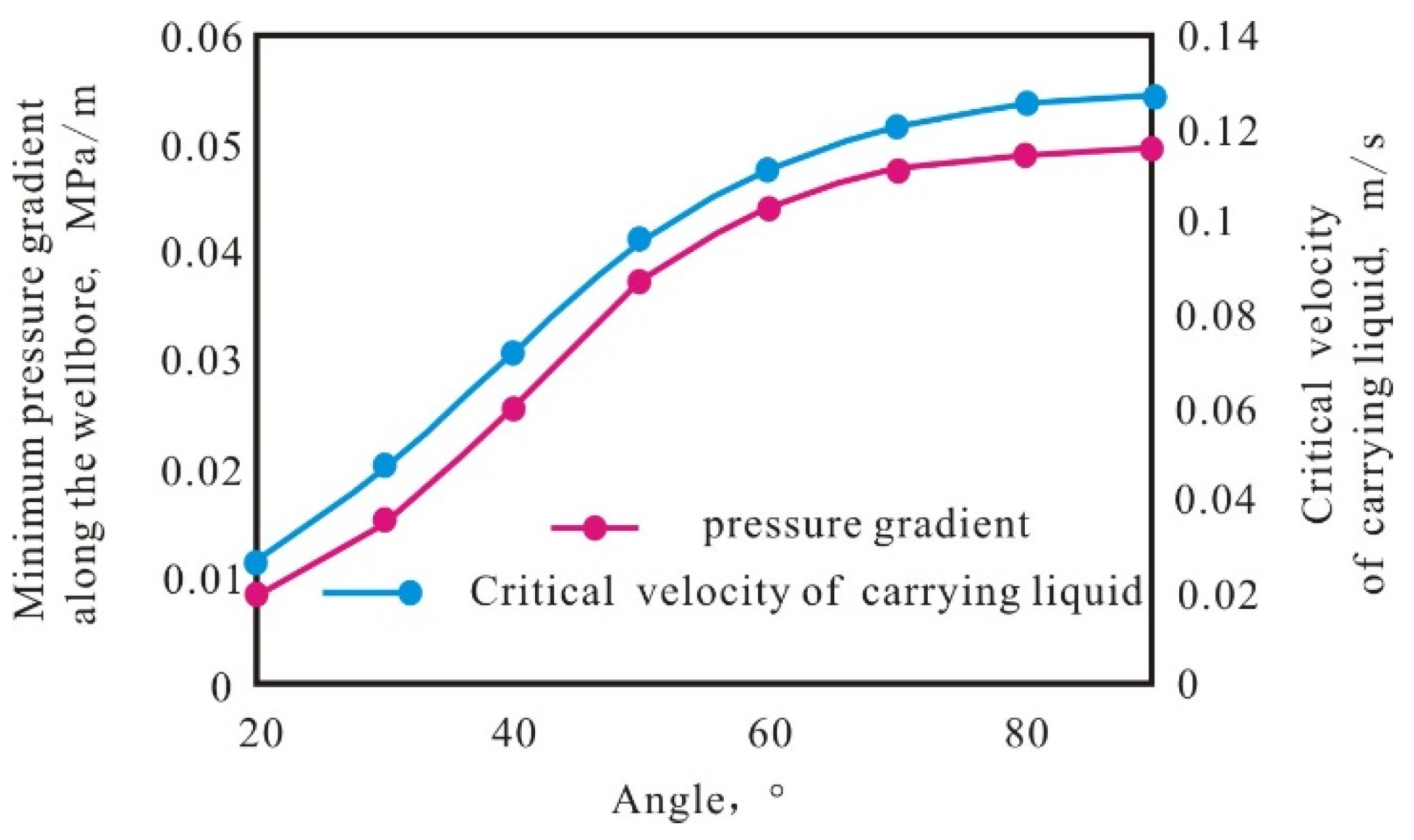
4.2. Wellbore Inclination Angle
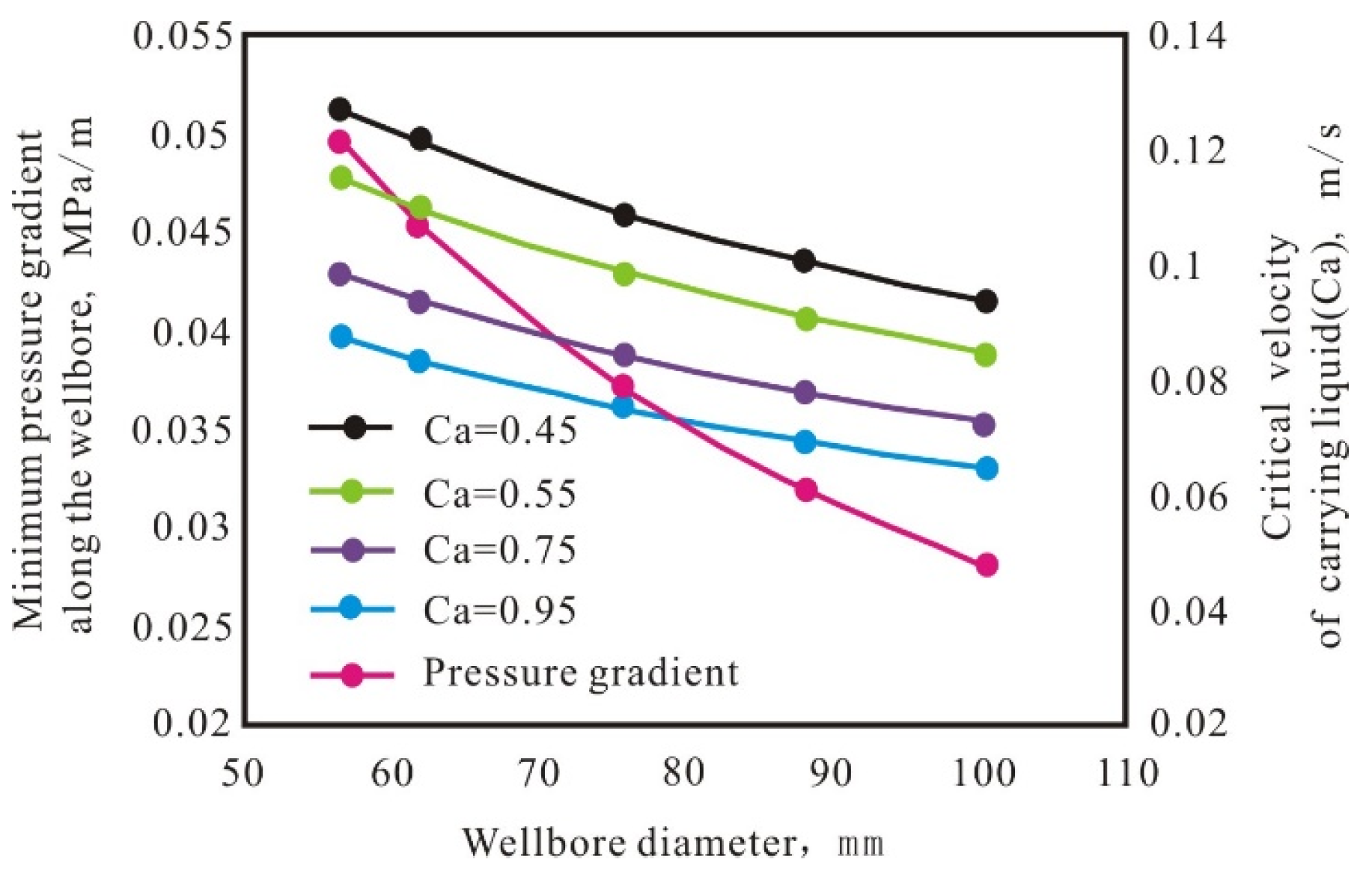
4.3. Wellbore Diameter
4.4. Wellhead Pressure
5. Field Scale Application Prediction
6. Conclusions
- (1)
- The wellbore droplet mechanics flow equilibrium equations were established, making it clear that the driving force on the droplets in the wellbore is the pressure difference between the upstream and downstream of the droplet flow as well as the buoyancy of the gas phase in the wellbore, and the resistance of the droplets is its own gravity and its resistance to the over-flow of the gas phase traversing the wellbore. Those are balanced, mutual games and indispensable, and it reveals that the reason for the accumulation of fluid in gas wells lies in the fact that the driving force on the droplets is less than the resistance to the flow, and the capacity of the gas phase to carry the fluid increases with the increase in the driving force.
- (2)
- The pressure gradient in the wellbore is the core of whether the gas phase can carry droplets from the bottom of the well to the wellhead, and the influencing factors of the liquid-carrying capacity should be considered: droplet size, wellbore inclination, wellbore diameter, wellhead backpressure; the pressure gradient decreases with the increase in droplet diameter, and the liquid-carrying speed needs to be increased by 1.45 times when the diameter increases by one time, and the liquid-carrying speed needs to be increased by 1.27 times when the inclination increases by one time. Moreover, the liquid-carrying capacity increases with the increase in wellbore diameter and decreases with the increase in wellhead backpressure.
- (3)
- Fogging-assisted production is a newly developed method for the gas well’s outflowing water, which can break well water into tiny droplets that can be more easily carried by the gas phase in the wellbore. It is conducive to prolonging the gas production time and providing an effective period of transitioning from self-flowing to pump production. It has a good prospect and potential for practical application.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Description of Symbols
| Resistance factor, dimensionless | |
| Droplet diameter, | |
| Tube diameter, | |
| Resistance factor, dimensionless | |
| Gravitational acceleration, | |
| Porosity, dimensionless | |
| Liquid retention rate, dimensionless | |
| Molecular weight of gases, dimensionless | |
| Fluid pressure, MPa | |
| Universal gas constant | |
| Fluid temperature, °C | |
| Gas phase velocity, | |
| Liquid phase velocity, | |
| Mixing speed, | |
| Gas compression factor, dimensionless | |
| Gas phase density, | |
| Liquid phase density, | |
| Mixture density, | |
| Wellbore inclination, ° | |
| Gas–water interface tension, |
References
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Wang, F.; Wu, J.; Usman Tahir, M.; Li, Q.; Yuan, L.; Liu, Z. Effect of thickener and reservoir parameters on the filtration property of CO2 fracturing fluid. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 42, 1705–1715. [Google Scholar] [CrossRef]
- Wang, F.J.; Xu, H.; Liu, Y.K.; Meng, X.H.; Liu, L.H.F. Mechanism of Low Chemical Agent Adsorption by High Pressure for Hydraulic Fracturing-Assisted Oil Displacement Technology: A Study of Molecular Dynamics Combined with Laboratory Experiments. Langmuir 2023, 39, 16628–16636. [Google Scholar] [CrossRef]
- Yun, J.; Xu, F.; Liu, L.; Zhong, N.; Wu, X. New progress and future prospects of CBM exploration and development in China. Int. J. Min. Sci. Technol. 2012, 22, 363–369. [Google Scholar] [CrossRef]
- Xu, F.; Yan, X.; Wang, F.; Ma, X.; Yun, J.; Wang, H.; Xu, B.; Zhang, S.; Mao, D. Development Strategy and Countermeasures of China’s CBM Industry under the Goal of “Carbon Peak and Neutrality”. J. Earth Sci. 2023, 34, 975–984. [Google Scholar] [CrossRef]
- Gao, L.-J.; Tang, D.-Z.; Xu, H.; Meng, S.Z.; Zhang, W.Z.; Meng, Y.J.; Wang, J.J. Geologically controlling factors on coal bed methane (CBM) productivity in Liulin. J. Coal Sci. Eng. 2012, 18, 362–367. [Google Scholar] [CrossRef]
- Li, X.; Fu, X.; Yang, X.; Ge, Y.; Quan, F. Coalbed methane accumulation and dissipation patterns: A Case study of the Junggar Basin, NW China. J. Asian Earth Sci. 2018, 160 (Suppl. S1), 13–26. [Google Scholar] [CrossRef]
- Liu, X.F.; Qi, Y.G.; Liu, C.H.; Zhao, P.H.; Yang, L. Calculation of dynamic loads of the sucker rod pumping system in CBM wells. J. Coal Sci. Eng. (China) 2010, 16, 170–175. [Google Scholar] [CrossRef]
- Yan, Y.W.; Li, Z.G.; Liu, K.; Li, F.; Zhang, Z. Application of hydrodynamic drive rodless pump drainage gas production technology in Bao-Ping 10 horizontal multilateral well. Oil Field Equip. 2021, 50, 61–65. [Google Scholar]
- Li, C.; An, Y.; Yang, Y.; Jiang, W.; Peng, L.; Liu, Y. Research on the Application of Double-Tube Gas Lift Drainage Recovery in Coalbed Methane Wells: A Case Study of the Hancheng Block, China. Lithophere 2022, 12, 9886330. [Google Scholar]
- Yan, X.; Zhang, S.; Tang, S.; Li, Z.; Zhang, Q.; Wang, J.; Deng, Z. Quantitative optimization of drainage strategy of coalbed methane well based on the dynamic behavior of coal reservoir permeability. Sci. Rep. 2020, 20, 202306. [Google Scholar] [CrossRef] [PubMed]
- Kurteev, V.A. Diaphragms for pneumatic pumps. Chem. Pet. Eng. 2011, 47, 550–556. [Google Scholar] [CrossRef]
- Liu, C.; Hu, C.; Chen, T. Wear analysis and life prediction of sucker rod and tubing under ternary emulsion lubrication in Daqing oilfield: A case study in block H. J. Pet. Explor. Prod. Technol. 2024, 14, 271–287. [Google Scholar] [CrossRef]
- Wang, H.; Dong, S. Research on the Coupled Axial-Transverse Nonlinear Vibration of Sucker Rod String in Deviated Wells. J. Vib. Eng. Technol. 2020, 9, 115–129. [Google Scholar] [CrossRef]
- Doty, D.R.; Schmidt, Z. An Improved Model for Sucker Rod Pumping. Soc. Pet. Eng. J. 1983, 23, 33–41. [Google Scholar] [CrossRef]
- Fakher, S.; Khlaifat, A.; Hossain, M.E.; Nameer, H. A comprehensive review of sucker rod pumps’ components, diagnostics, mathematical models, and common failures and mitigations. J. Pet. Explor. Prod. Technol. 2021, 11, 3815–3839. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, S.; Ni, Y.; Zhang, G.; Li, L.; Meng, Z. Key technology for treating slack coal blockage in CBM recovery: A case study from multi-lateral horizontal wells in the Qinshui Basin. Nat. Gas Ind. B 2016, 3, 66–70. [Google Scholar] [CrossRef]
- Katagiri, N.; Kioka, A.; Nonoyama, M.; Hayashi, Y. Inhibiting flow-accelerated copper corrosion under liquid jet impingement by utilizing nanobubbles. Surf. Interfaces 2023, 40, 103067. [Google Scholar] [CrossRef]
- Wang, H.W.; Liu, C.J. Process parameters design method of drainage gas recovery technology in gas-driven pump for coalbed methane production. J. Pet. Sci. Eng. 2021, 207, 109167. [Google Scholar]
- Wu, D.; Tang, Z.; Dong, L.; Li, G.; Li, D.; Wang, L.; Shi, T.; Rahman, M.M.; Zhang, X. Enhanced ultrasonic spray ionization for direct mass spectrometry analysis of aqueous solution and complex samples using a single-orifice piezoelectric atomizer. Talanta 2023, 255, 124237. [Google Scholar] [CrossRef]
- Wang, W.; Cui, G.; Wei, Y.; Pan, J. A new model for predicting the critical liquid-carrying velocity in inclined gas wells. Pet. Explor. Dev. 2021, 48, 1218–1226. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Wang, Q.; Ye, C.; Yu, F. A simple and accurate model to predict pressure drop in vertical gas wells. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 1245–1259. [Google Scholar] [CrossRef]



| Formulas | E | F | G |
|---|---|---|---|
| (8) | 0 | ||
| (9) | 0 | ||
| (10) |
| Parameter Category | Parameter Value | Parameter Category | Parameter Value |
|---|---|---|---|
| well depth, m | 6 | specific gravity of gas | 0.63 |
| Inner diameter of oil pipe, mm | 62 | specific gravity of a liquid | 1 |
| Resistance coefficient, Ca | 0.45 | Atomizing droplet diameter, mm | 0.05 |
| Wellbore Inclination, ° | 90 | bottoming-out pressure, MPa | 0.4 |
| Tube wall roughness | 0.00834 | Wellhead back pressure, MPa | 0.2 |
| Well Bottom Flowing Pressure MPa | Wellhead Pressure MPa | Minimum Pressure Gradient in the Wellbore. MPa/m | Fluid Accumulation | Critical Liquid-Carrying Velocity m/s | Whether or Not to Atomize |
|---|---|---|---|---|---|
| 7.5 | 4.0 | 0.00362 | No fluid accumulation | 0.020973 | yes |
| 7 | 3.5 | 0.0034 | No fluid accumulation | 0.019096 | yes |
| 6.5 | 3 | 0.0031 | No fluid accumulation | 0.016189 | yes |
| 6 | 2.5 | 0.00286 | No fluid accumulation | 0.013418 | yes |
| 5.5 | 2 | 0.00256 | No fluid accumulation | 0.008803 | yes |
| 5 | 1.5 | 0.00239 | No fluid accumulation | 0.004401 | yes |
| 4.5 | 1 | 0.00216 | fluid accumulation | / | yes |
| 4.5 | 0.5 | 0.00222 | fluid accumulation | / | yes |
| 4.5 | 0.1 | 0.00233 | fluid accumulation | / | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.; Wang, H.; Song, G.; Duan, D.; Zhang, C.; Zhu, W.; Liu, Y. Study on the Gas Phase Liquid Carrying Velocity of Deep Coalbed Gas Well with Atomization Assisted Production. Energies 2024, 17, 4185. https://doi.org/10.3390/en17164185
Wu R, Wang H, Song G, Duan D, Zhang C, Zhu W, Liu Y. Study on the Gas Phase Liquid Carrying Velocity of Deep Coalbed Gas Well with Atomization Assisted Production. Energies. 2024; 17(16):4185. https://doi.org/10.3390/en17164185
Chicago/Turabian StyleWu, Ruidong, Haidong Wang, Gangxiang Song, Dongping Duan, Chunguang Zhang, Wenjuan Zhu, and Yikun Liu. 2024. "Study on the Gas Phase Liquid Carrying Velocity of Deep Coalbed Gas Well with Atomization Assisted Production" Energies 17, no. 16: 4185. https://doi.org/10.3390/en17164185
APA StyleWu, R., Wang, H., Song, G., Duan, D., Zhang, C., Zhu, W., & Liu, Y. (2024). Study on the Gas Phase Liquid Carrying Velocity of Deep Coalbed Gas Well with Atomization Assisted Production. Energies, 17(16), 4185. https://doi.org/10.3390/en17164185








