Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges
Abstract
:1. Introduction
2. Advanced Monitoring and Control for Optimised Exploitation
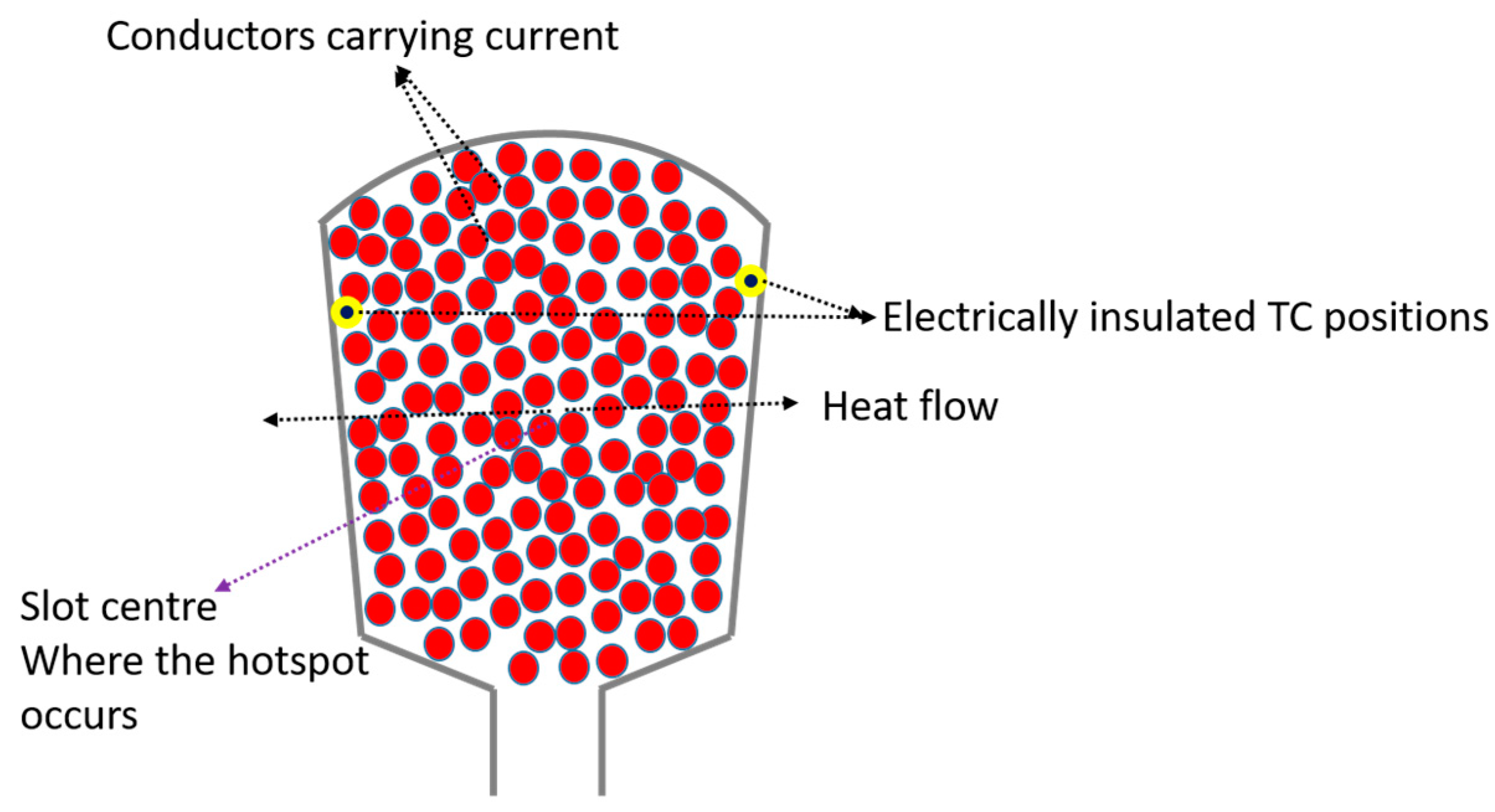
2.1. Wind Turbine Thermal Condition Monitoring
2.2. Thermal Design Limits and Margins
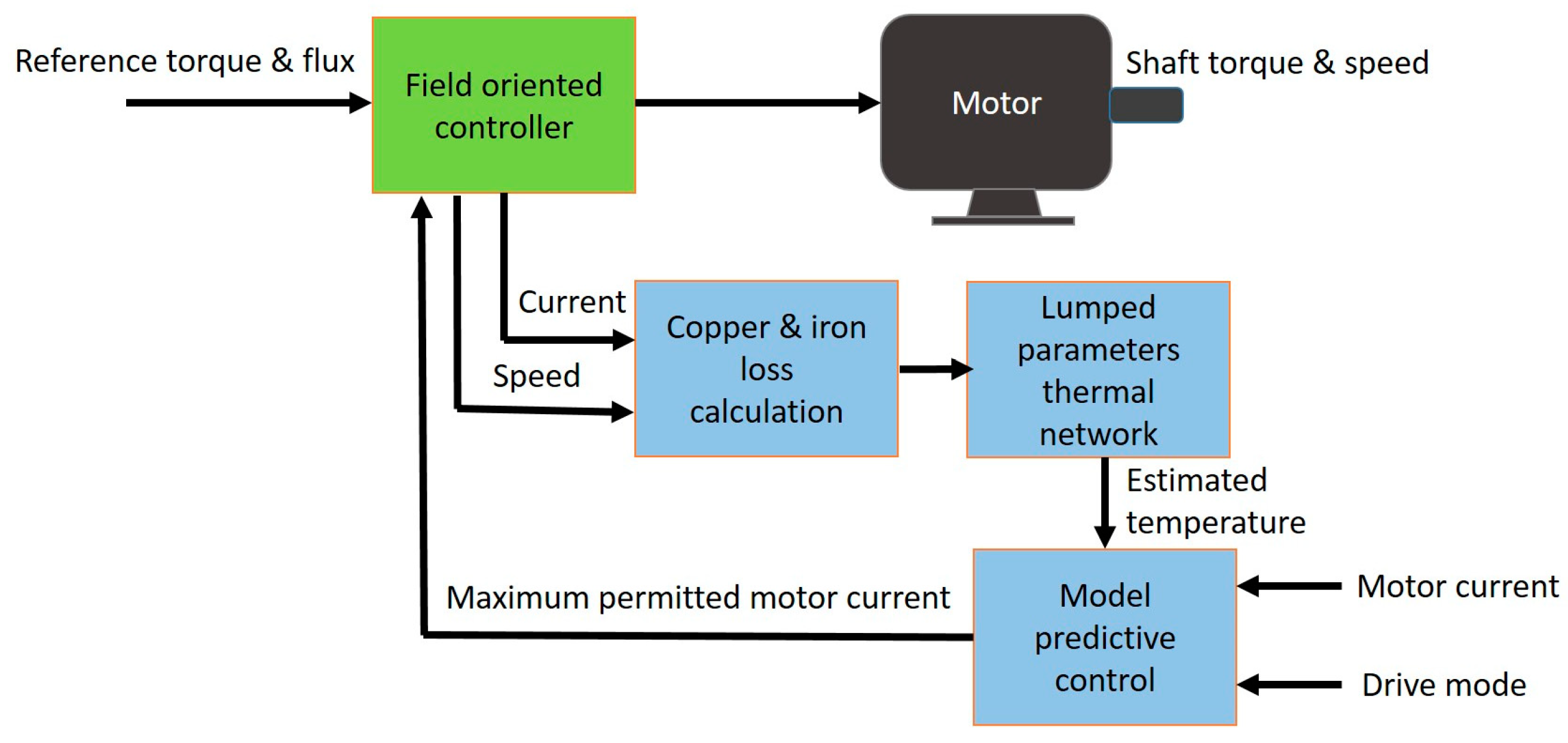
2.3. Integration of Closed-Loop Thermal Feedback with Electrical Machine Control
2.4. Wind Turbine Overload Capability and Extracting More Energy
- (a)
- Operating close to or at the thermal design limit in conditions of high wind, so the WT energy yield is increased;
- (b)
- Temporarily exceeding the thermal design limit in a controlled fashion in scenarios requiring a sudden and large power injection into the grid, for grid frequency support, or to compensate for the failure of another WT.
2.5. Discussion and Summary
3. Optimal Power Flow with Machine Learning
3.1. Machine Learning Methods for OPF
3.2. OPF Based on Objective Functions
3.2.1. Operating Cost Minimisation
3.2.2. Voltage Deviation Minimisation
3.2.3. Emission Cost Minimisation
3.2.4. Increasing System Reliability
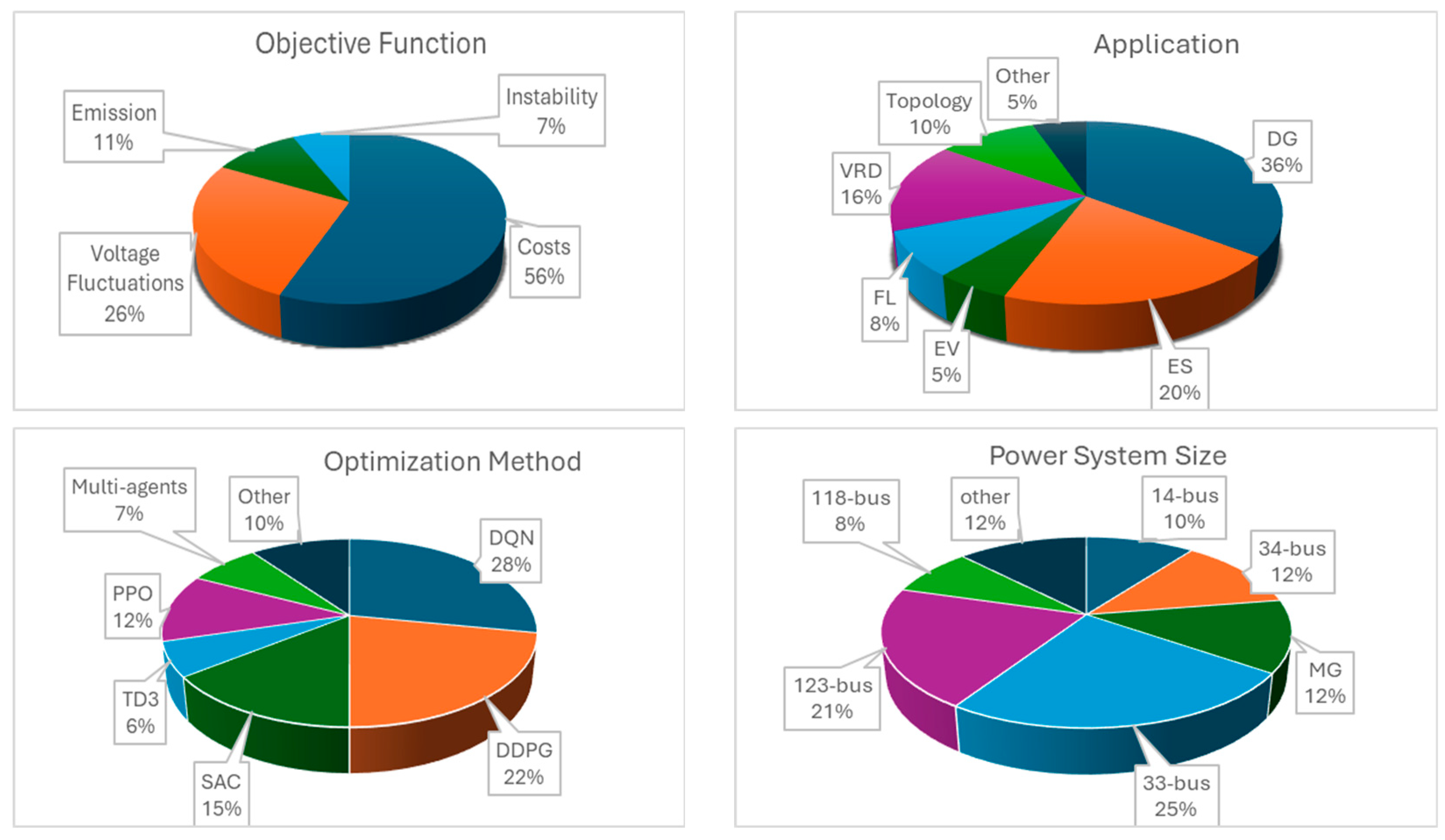
3.3. Discussion and Summary
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- RUSI. How Will Growth in Renewables Change the UK’s Approach to Energy Security? Available online: https://rusi.org/explore-our-research/publications/commentary/how-will-growth-renewables-change-uks-approach-energy-security (accessed on 31 January 2024).
- NEMA. NEMA MG-1 Motor-Generator Standard. Available online: https://law.resource.org/pub/us/cfr/ibr/005/nema.mg-1.2009.pdf (accessed on 12 June 2023).
- Baker, N.; Liserre, M.; Dupont, L.; Avenas, Y. Improved reliability of power modules: A review of online junction temperature measurement methods. IEEE Ind. Electron. Mag. 2014, 8, 17–27. [Google Scholar] [CrossRef]
- Siemens Gamesa. Asset Optimization Services. Available online: https://www.siemensgamesa.com/global/en/home/products-and-services/service-wind/asset-optimization.html (accessed on 8 April 2023).
- Vestas. Fleet Optimisation. Available online: https://www.vestas.com/en/services/fleet-optimisation#accordion-d626793722-item-03a4e4001e (accessed on 5 April 2023).
- Ghafoor, A.; Apsley, J.; Djurović, S. Thermal Margin Exploitation for Increased Energy Yield in Wind Turbine Permanent Magnet Synchronous Generators. In Proceedings of the 12th International Conference on Power Electronics, Machines and Drives (PEMD), Brussels, Belgium, 23–24 October 2023; pp. 1–6. [Google Scholar]
- DNVGL. Certification of Condition Monitoring. Available online: https://www.dbassetservices.com/images/DNVGL-SE-0439.pdf (accessed on 12 June 2023).
- Mohammed, A.; Djurović, S. Stator Winding Internal Thermal Monitoring and Analysis Using In Situ FBG Sensing Technology. IEEE Trans. Energy Convers. 2018, 33, 1508–1518. [Google Scholar] [CrossRef]
- Suryandi, A.A.; Sarma, N.; Mohammed, A.; Peesapati, V.; Djurović, S. Fiber Optic Fiber Bragg Grating Sensing for Monitoring and Testing of Electric Machinery: Current State of the Art and Outlook. Machines 2022, 10, 1103. [Google Scholar] [CrossRef]
- Liton Hossain, M.; Abu-Siada, A.; Muyeen, S.M. Methods for Advanced Wind Turbine Condition Monitoring and Early Diagnosis: A Literature Review. Energies 2018, 11, 1309. [Google Scholar] [CrossRef]
- Fabian, M.; Hind, D.M.; Gerada, C.; Sun, T.; Grattan, K.T.V. Comprehensive Monitoring of Electrical Machine Parameters Using an Integrated Fiber Bragg Grating-Based Sensor System. J. Light. Technol. 2018, 36, 1046–1051. [Google Scholar] [CrossRef]
- Chen, S.; Vilchis-Rodriguez, D.; Barnes, M.; Djurović, S. Direct On-Chip IGBT Thermal Sensing Using Adhesive Bonded FBG Sensors. IEEE Sens. J. 2023, 23, 22507–22516. [Google Scholar] [CrossRef]
- Chen, S.; Vilchis-Rodriguez, D.; Djurovic, S.; Barnes, M.; McKeever, P.; Jia, C. Direct on Chip Thermal Measurement in IGBT Modules Using FBG Technology—Sensing Head Interfacing. IEEE Sens. J. 2022, 22, 1309–1320. [Google Scholar] [CrossRef]
- Chen, S.; Vilchis-Rodriguez, D.; Barnes, M.; Djurovic, S. A Comparison of Chip Temperature Acquisition Technologies of IGBT Power Modules. IEEE Sens. J. 2024, 24, 19107–19116. [Google Scholar] [CrossRef]
- Qi, F.; Ralev, I.; Stippich, A.; De Doncker, R.W. Model Predictive Overload Control of an Automotive Switched Reluctance Motor for Frequent Rapid Accelerations. In Proceedings of the 19th International Conference on Electrical Machines and Sytems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Sun, T.; Wang, J.; Griffo, A.; Sen, B. Active Thermal Management for Interior Permanent Magnet Synchronous Machine (IPMSM) Drives Based on Model Predictive Control. IEEE Trans. Ind. Appl. 2018, 54, 4506–4514. [Google Scholar] [CrossRef]
- Qi, F.; Stippich, A.; Koschik, S.; De Doncker, R.W. Model Predictive Overload Control of Induction Motors. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 999–1005. [Google Scholar]
- Han, X.; Mu, C.; Yan, J.; Niu, Z. An Autonomous Control Technology Based on Deep Reinforcement Learning for Optimal Active Power Dispatch. Int. J. Electr. Power Energy Syst. 2023, 145, 108686. [Google Scholar] [CrossRef]
- Woo, J.H.; Wu, L.; Park, J.B.; Roh, J.H. Real-Time Optimal Power Flow Using Twin Delayed Deep Deterministic Policy Gradient Algorithm. IEEE Access 2020, 8, 213611–213618. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Xu, X.; Wu, Q.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep Reinforcement Learning Based Approach for Optimal Power Flow of Distribution Networks Embedded with Renewable Energy and Storage Devices. J. Mod. Power Syst. Clean Energy 2021, 9, 1101–1110. [Google Scholar] [CrossRef]
- Al-Saffar, M.; Musilek, P. Reinforcement Learning-Based Distributed BESS Management for Mitigating Overvoltage Issues in Systems with High PV Penetration. IEEE Trans. Smart Grid 2020, 11, 2980–2994. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D.; Yang, X. Wind Turbine Generator Condition-Monitoring Using Temperature Trend Analysis. IEEE Trans. Sustain. Energy 2012, 3, 124–133. [Google Scholar] [CrossRef]
- De Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A Review of Wind Turbine Bearing Condition Monitoring: State of the Art and Challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Benbouzid, M.; Berghout, T.; Sarma, N.; Djurović, S.; Wu, Y.; Ma, X. Intelligent Condition Monitoring of Wind Power Systems: State of the Art Review. Energies 2021, 14, 5967. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind Turbine Condition Monitoring: Technical & Commercial Challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef]
- Tavner, P.; Ran, L.; Crabtree, C. Condition Monitoring of Rotating Electrical Machines, 3rd ed.; Institution of Engineering and Technology: London, UK, 2020; ISBN 978-1-78561-866-6. [Google Scholar]
- Siemens.Siplus CMS. Available online: https://cache.industry.siemens.com/dl/files/350/36815350/att_58847/v1/ION_SIMATIC_S7_PN_OperatingInstructions_2011-09_EN.pdf (accessed on 5 July 2021).
- Mohammed, A.; Djurovic, S. FBG Thermal Sensing Features for Hot Spot Monitoring in Random Wound Electric Machine Coils. IEEE Sens. J. 2017, 17, 3058–3067. [Google Scholar] [CrossRef]
- Mohammed, A.; Djurovic, S. In-Situ Thermal and Mechanical Fibre Optic Sensing for in-Service Electric Machinery Bearing Condition Monitoring. In Proceedings of the IEEE International Conference on Electric Machines and Drives (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 37–43. [Google Scholar]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Crabtree, C.; Zappalá, D.; Tavner, P. Survey of Commercially Available Condition Monitoring Systems for Wind Turbines. Available online: https://dro.dur.ac.uk/12497/1/12497.pdf?DDD10+ttsd23+dul4eg (accessed on 12 June 2023).
- Mohammed, A.; Djurović, S. FBG Thermal Sensing Ring Scheme for Stator Winding Condition Monitoring in PMSMs. Trans. Transp. Electrif. 2019, 5, 1370–1382. [Google Scholar] [CrossRef]
- Mohammed, A.; Djurović, S. Rotor Condition Monitoring Using Fibre Optic Sensing Technology. In Proceedings of the 10th IET International Conference on Power Electronics, Machines and Drives (PEMD), Nottingham, UK, 1–3 December 2020; pp. 1–6. [Google Scholar]
- Mohammed, A.; Djurovic, S. Electric Machine Bearing Health Monitoring and Ball Fault Detection by Simultaneous Thermo-Mechanical Fibre Optic Sensing. IEEE Trans. Energy Convers. 2021, 36, 71–80. [Google Scholar] [CrossRef]
- Shang, K.; Zhang, Y.; Galea, M.; Brusic, V.; Korposh, S. Fibre Optic Sensors for the Monitoring of Rotating Electric Machines: A Review. Opt. Quantum Electron. 2021, 53, 75. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Lusuardi, L.; Cavallini, A.; Gerada, C.; Galea, M. Thermal Overload and Insulation Aging of Short Duty Cycle, Aerospace Motors. IEEE Trans. Ind. Electron. 2020, 67, 2618–2629. [Google Scholar] [CrossRef]
- IEEE 112-2017; IEEE Standard Test Procedure for Polyphase Induction Motors and Generators. IEEE: Piscataway, NJ, USA. Available online: https://ieeexplore.ieee.org/document/8291810 (accessed on 12 June 2023).
- TOSHIBA. MOTORS & DRIVES Temperature Rise. Available online: https://www.toshiba.com/tic/datafiles/app_notes/Temperature_Rise_1605749858.pdf (accessed on 1 June 2023).
- Werneck, M.M.; Célia, R.; Allil, B.; Ribeiro, B.A. Calibration and Operation of a Fibre Bragg Grating Temperature Sensing System in a Grid-Connected Hydrogenerator. IET Sci. Meas. Technol. 2013, 7, 59–68. [Google Scholar] [CrossRef]
- Lemmens, J.; Vanassche, P.; Driesen, J. Optimal Control of Traction Motor Drives Under Electrothermal Constraints. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 249–263. [Google Scholar] [CrossRef]
- Hales, K.; Spruce, C.; BJerregaard, S.L.; Rasmussen, P.O. Over-Rating Control of a Wind Turbine Generator. Available online: https://patentimages.storage.googleapis.com/65/03/8d/acc8695a2e154e/US10544779.pdf (accessed on 22 June 2024).
- Ghafoor, A.; Djurović, S.; Apsley, J. A Coupled Electromagnetic-thermal Dynamic Model for Wind Turbine Permanent Magnet Synchronous Generator Operation Analysis. In Proceedings of the 32nd International Symposium Industrial Electronics (IEEE ISIE), Helsinki, Finland, 19–21 June 2023; pp. 1–6. [Google Scholar]
- Dommel, H.W.; Tinney, W.F. Optimal Power Flow Solutions. IEEE Trans. Power Appar. Syst. 1968, 10, 1866–1876. [Google Scholar] [CrossRef]
- Ghaddar, B.; Marecek, J.; Mevissen, M. Optimal Power Flow as a Polynomial Optimization Problem. IEEE Trans. Power Syst. 2015, 31, 539–546. [Google Scholar] [CrossRef]
- Grover-Silva, E.; Heleno, M.; Mashayekh, S.; Cardoso, G.; Girard, R.; Kariniotakis, G. A Stochastic Optimal Power Flow for Scheduling Flexible Resources in Microgrids Operation. Appl. Energy 2018, 229, 201–208. [Google Scholar] [CrossRef]
- Madrigal, M.; Ponnambalam, K.; Quintana, V.H. Probabilistic Optimal Power Flow. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, Waterloo, ON, Canada, 25–28 May 1998. [Google Scholar]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Faster Evolutionary Algorithm Based Optimal Power Flow Using Incremental Variables. Int. J. Electr. Power Energy Syst. 2014, 54, 198–210. [Google Scholar] [CrossRef]
- Kang, Q.; Zhou, M.; An, J.; Wu, Q. Swarm Intelligence Approaches to Optimal Power Flow Problem with Distributed Generator Failures in Power Networks. IEEE Trans. Autom. Sci. Eng. 2012, 10, 343–353. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 2012, 28, 52–63. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine Learning: Trends, Perspectives, and Prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep Reinforcement Learning: An Overview. In Proceedings of the SAI Intelligent Systems Conference (IntelliSys) 2016; Springer International Publishing; Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Pham, Q.V.; Liyanage, M.; Deepa, N.; VVSS, M.; Reddy, S.; Maddikunta, P.K.R.; Hwang, W.J. Deep Learning for Intelligent Demand Response and Smart Grids: A Comprehensive Survey. arXiv 2021. preprint. [Google Scholar] [CrossRef]
- Aldahmashi, J.; Ma, X. Real-Time Energy Management in Smart Homes Through Deep Reinforcement Learning. IEEE Access 2024, 12, 43155–43172. [Google Scholar] [CrossRef]
- Ullah, Z.; Wang, S.; Wu, G.; Hasanien, H.M.; Jabbar, M.W.; Qazi, H.S.; Elkadeem, M.R. Advanced Studies for Probabilistic Optimal Power Flow in Active Distribution Networks: A Scientometric Review. IET Gener. Transm. Distrib. 2022, 16, 3579–3604. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Real-Time Optimal Power Flow: A Lagrangian Based Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 2020, 35, 3270–3273. [Google Scholar] [CrossRef]
- da Silva André, J.; Stai, E.; Stanojev, O.; Hug, G. Battery Control with Lookahead Constraints in Distribution Grids Using Reinforcement Learning. Electr. Power Syst. Res. 2022, 211, 108551. [Google Scholar] [CrossRef]
- Alabdullah, M.H.; Abido, M.A. Microgrid Energy Management Using Deep Q-Network Reinforcement Learning. Alex. Eng. J. 2022, 61, 9069–9078. [Google Scholar] [CrossRef]
- Hua, H.; Qin, Z.; Dong, N.; Qin, Y.; Ye, M.; Wang, Z.; Cao, J. Data-Driven Dynamical Control for Bottom-Up Energy Internet System. IEEE Trans. Sustain. Energy 2021, 13, 315–327. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Xu, X.; Li, T.; Zhang, Z.; Chen, Z. Physical-Model-Free Intelligent Energy Management for a Grid-Connected Hybrid Wind-Microturbine-PV-EV Energy System Via Deep Reinforcement Learning Approach. Renew. Energy 2022, 200, 433–448. [Google Scholar] [CrossRef]
- Jin, J.; Xu, Y. Optimal Policy Characterization Enhanced Actor-Critic Approach for Electric Vehicle Charging Scheduling in a Power Distribution Network. IEEE Trans. Smart Grid 2020, 12, 1416–1428. [Google Scholar] [CrossRef]
- Xing, Q.; Chen, Z.; Zhang, T.; Li, X.; Sun, K. Real-Time Optimal Scheduling for Active Distribution Networks: A Graph Reinforcement Learning Method. Int. J. Electr. Power Energy Syst. 2023, 145, 108637. [Google Scholar] [CrossRef]
- Wang, B.; Li, Y.; Ming, W.; Wang, S. Deep Reinforcement Learning Method for Demand Response Management of Interruptible Load. IEEE Trans. Smart Grid 2020, 11, 3146–3155. [Google Scholar] [CrossRef]
- Bui, V.H.; Su, W. Real-Time Operation of Distribution Network: A Deep Reinforcement Learning-Based Reconfiguration Approach. Sustain. Energy Technol. Assess. 2022, 50, 101841. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, W.; Shi, J.; Yu, N. Batch-Constrained Reinforcement Learning for Dynamic Distribution Network Reconfiguration. IEEE Trans. Smart Grid 2020, 11, 5357–5369. [Google Scholar] [CrossRef]
- Aldahmashi, J.; Ma, X. Advanced Machine Learning Approach of Power Flow Optimization in Community Microgrid. In Proceedings of the 2022 27th International Conference on Automation and Computing (ICAC), Bristol, UK, 1–3 September 2022; pp. 1–6. [Google Scholar]
- Li, X.; Han, X.; Yang, M. Day-Ahead Optimal Dispatch Strategy for Active Distribution Network Based on Improved Deep Reinforcement Learning. IEEE Access 2022, 10, 9357–9370. [Google Scholar] [CrossRef]
- Kushwaha, D.S.; Biron, Z.; Abdollahi, R. Economic Energy Dispatch of Microgrid Using DeepLSTM-Based Deep Reinforcement Learning. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Li, X.; Wang, J.; Lu, Z.; Cai, Y. A Cloud Edge Computing Method for Economic Dispatch of Active Distribution Network with Multi-Microgrids. Electr. Power Syst. Res. 2023, 214, 108806. [Google Scholar] [CrossRef]
- Gao, Z.; Zheng, Z.; Wu, J.; Qi, L.; Li, W.; Yang, Y. Reactive Power Optimization of Distribution Network Based on Deep Reinforcement Learning and Multi Agent System. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 1052–1057. [Google Scholar]
- Yang, Z.; Yang, F.; Min, H.; Tian, H.; Hu, W.; Liu, J.; Eghbalian, N. Energy Management Programming to Reduce Distribution Network Operating Costs in the Presence of Electric Vehicles and Renewable Energy Sources. Energy 2023, 263, 125695. [Google Scholar] [CrossRef]
- Hai, D.; Zhu, T.; Duan, S.; Huang, W.; Li, W. Deep Reinforcement Learning for Volt/VAR Control in Distribution Systems: A Review. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE) IEEE, Chongqing, China, 22–24 April 2022; pp. 596–601. [Google Scholar]
- Sun, X.; Qiu, J.; Zhao, J. Optimal Local Volt/VAR Control for Photovoltaic Inverters in Active Distribution Networks. IEEE Trans. Power Syst. 2021, 36, 5756–5766. [Google Scholar] [CrossRef]
- Beyer, K.; Beckmann, R.; Geißendörfer, S.; von Maydell, K.; Agert, C. Adaptive Online-Learning Volt-VAR Control for Smart Inverters Using Deep Reinforcement Learning. Energies 2021, 14, 1991. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Zhao, J.; Huang, Q.; Chen, Z.; Blaabjerg, F. A Multi-Agent Deep Reinforcement Learning Based Voltage Regulation Using Coordinated PV Inverters. IEEE Trans. Power Syst. 2020, 35, 4120–4123. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Two-Stage Deep Reinforcement Learning for Inverter-Based Volt-VAR Control in Active Distribution Networks. IEEE Trans. Smart Grid 2020, 12, 2037–2047. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, B.; Xu, C.; Lan, T.; Diao, R.; Shi, D.; Wang, Z.; Lee, W.-J. A Data-Driven Method for Fast AC Optimal Power Flow Solutions Via Deep Reinforcement Learning. J. Mod. Power Syst. Clean Energy 2020, 8, 1128–1139. [Google Scholar] [CrossRef]
- Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering Smart Grid: A Comprehensive Review of Energy Storage Technology and Application with Renewable Energy Integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, N.; Cao, Z.; Chen, Y.; Wang, M.; Liu, Y. Voltage Regulation Based on Deep Reinforcement Learning Algorithm in Distribution Network with Energy Storage System. In Proceedings of the 2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE) IEEE, Chongqing, China, 23–25 April 2021; pp. 892–896. [Google Scholar]
- Wang, Y.; Mao, M.; Chang, L.; Hatziargyriou, N.D. Intelligent Voltage Control Method in Active Distribution Networks Based on Averaged Weighted Double Deep Q-Network Algorithm. J. Mod. Power Syst. Clean Energy 2022, 11, 132–143. [Google Scholar] [CrossRef]
- Kelker, M.; Quakernack, L.; Haubrock, J. Multi agent deep Q-reinforcement learning for autonomous low voltage grid control. In In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–6. [Google Scholar]
- Hossain, R.; Lakouraj, M.M.; Ghasemkhani, A.; Livani, H.; Ben–Idris, M. Deep Reinforcement Learning-Based Volt-VAR Optimization in Distribution Grids with Inverter-Based Resources. In Proceedings of the 2021 North American Power Symposium (NAPS) IEEE, College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar]
- Moy, K.; Tae, C.; Wang, Y.; Henri, G.; Bambos, N.; Rajagopal, R. An OpenAI-OpenDSS Framework for Reinforcement Learning on Distribution-Level Microgrids. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM) IEEE, Washinton, DC, USA, 25–29 July 2021; pp. 1–5. [Google Scholar]
- Yang, Q.; Wang, G.; Sadeghi, A.; Giannakis, G.B.; Sun, J. Two-Timescale Voltage Control in Distribution Grids Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 11, 2313–2323. [Google Scholar] [CrossRef]
- Tahir, Y.; Khan, M.F.N.; Sajjad, I.A.; Martirano, L. Optimal Control of Active Distribution Network Using Deep Reinforcement Learning. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar]
- Wang, W.; Yu, N.; Gao, Y.; Shi, J. Safe Off-Policy Deep Reinforcement Learning Algorithm for Volt-VAR Control in Power Distribution Systems. IEEE Trans. Smart Grid 2019, 11, 3008–3018. [Google Scholar] [CrossRef]
- Li, W.; Huang, W.; Zhu, T.; Wu, M.; Yan, Z. Deep Reinforcement Learning Based Continuous Volt-VAR Optimization in Power Distribution Systems with Renewable Energy Resources. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 682–686. [Google Scholar]
- Cao, D.; Zhao, J.; Hu, W.; Ding, F.; Huang, Q.; Chen, Z.; Blaabjerg, F. Data-Driven Multi-Agent Deep Reinforcement Learning for Distribution System Decentralized Voltage Control with High Penetration of PVs. IEEE Trans. Smart Grid 2021, 12, 4137–4150. [Google Scholar] [CrossRef]
- Kundačina, O.B.; Vidović, P.M.; Petković, M.R. Solving Dynamic Distribution Network Reconfiguration Using Deep Reinforcement Learning. Electr. Eng. 2022, 104, 1487–1501. [Google Scholar] [CrossRef]
- Rahman, J.; Jacob, R.A.; Paul, S.; Chowdhury, S.; Zhang, J. Reinforcement Learning Enabled Microgrid Network Reconfiguration Under Disruptive Events. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022; pp. 1–6. [Google Scholar]
- Zhang, J.; Lu, C.; Fang, C.; Ling, X.; Zhang, Y. Load Shedding Scheme with Deep Reinforcement Learning to Improve Short-Term Voltage Stability. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Beijing, China, 22–25 May 2018; pp. 13–18. [Google Scholar]
- Zhang, B.; Hu, W.; Ghias, A.M.Y.M.; Xu, X.; Chen, Z. Multi-Agent Deep Reinforcement Learning-Based Coordination Control for Grid-Aware Multi-Buildings. Appl. Energy 2022, 328, 120215. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Liu, W.; Ferrese, F. Multiagent-Based Reinforcement Learning for Optimal Reactive Power Dispatch. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 1742–1751. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Wang, C.; Wu, Z.; Gao, L. Safe Deep Reinforcement Learning-Based Constrained Optimal Control Scheme for Active Distribution Networks. Appl. Energy 2020, 264, 114772. [Google Scholar] [CrossRef]
- Diao, R.; Wang, Z.; Shi, D.; Chang, Q.; Duan, J.; Zhang, X. Autonomous Voltage Control for Grid Operation Using Deep Reinforcement Learning. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Cao, D.; Zhao, J.; Hu, W.; Yu, N.; Ding, F.; Huang, Q.; Chen, Z. Deep Reinforcement Learning Enabled Physical-Model-Free Two-Timescale Voltage Control Method for Active Distribution Systems. IEEE Trans. Smart Grid 2021, 13, 149–165. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J. A Customized Voltage Control Strategy for Electric Vehicles in Distribution Networks with Reinforcement Learning Method. IEEE Trans. Ind. Inform. 2021, 17, 6852–6863. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, C.; Si, J.; Song, J.; Su, Y. Deep Reinforcement Learning for Short-Term Voltage Control by Dynamic Load Shedding in China Southern Power Grid. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Kocer, M.C.; Cengiz, C.; Gezer, M.; Gunes, D.; Cinar, M.A.; Alboyaci, B.; Onen, A. Assessment of Battery Storage Technologies for a Turkish Power Network. Sustainability 2019, 11, 3669. [Google Scholar] [CrossRef]
- Wei, T.; Chu, X.; Yang, D.; Ma, H. Power Balance Control of RES Integrated Power System by Deep Reinforcement Learning with Optimized Utilization Rate of Renewable Energy. Energy Rep. 2022, 8, 544–553. [Google Scholar] [CrossRef]
- Kabir, F.; Gao, Y.; Yu, N. Reinforcement Learning-Based Smart Inverter Control with Polar Action Space in Power Distribution Systems. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), San Diego, CA, USA, 8–11 August 2021; pp. 315–322. [Google Scholar]
- Pei, Y.; Yao, Y.; Zhao, J.; Ding, F.; Wang, J. Multi-Agent Deep Reinforcement Learning for Realistic Distribution System Voltage Control Using PV Inverters. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Zhu, Z.; Weng, Z.; Zheng, H. Optimal Operation of a Microgrid with Hydrogen Storage Based on Deep Reinforcement Learning. Electronics 2022, 11, 196. [Google Scholar] [CrossRef]
- Qiu, D.; Wang, Y.; Sun, M.; Strbac, G. Multi-Service Provision for Electric Vehicles in Power-Transportation Networks Towards a Low-Carbon Transition: A Hierarchical and Hybrid Multi-Agent Reinforcement Learning Approach. Appl. Energy 2022, 313, 118790. [Google Scholar] [CrossRef]
- Gao, Y.; Shi, J.; Wang, W.; Yu, N. Dynamic Distribution Network Reconfiguration Using Reinforcement Learning. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019; pp. 1–7. [Google Scholar]
- Li, Y.; Hao, G.; Liu, Y.; Yu, Y.; Ni, Z.; Zhao, Y. Many-Objective Distribution Network Reconfiguration via Deep Reinforcement Learning Assisted Optimization Algorithm. IEEE Trans. Power Deliv. 2021, 37, 2230–2244. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Duan, J.; Qiu, G.; Liu, T.; Liu, J. DDPG-Based Multi-Agent Framework for SVC Tuning in Urban Power Grid with Renewable Energy Resources. IEEE Trans. Power Syst. 2021, 36, 5465–5475. [Google Scholar] [CrossRef]
- Zhou, Y.; Lee, W.-J.; Diao, R.; Shi, D. Deep Reinforcement Learning Based Real-Time AC Optimal Power Flow Considering Uncertainties. J. Mod. Power Syst. Clean Energy 2021, 10, 1098–1109. [Google Scholar] [CrossRef]
- Jung, Y.; Han, C.; Lee, D.; Song, S.; Jang, G. Adaptive Volt–Var Control in Smart PV Inverter for Mitigating Voltage Unbalance at PCC Using Multiagent Deep Reinforcement Learning. Appl. Sci. 2021, 11, 8979. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, W.; Xu, X.; Liu, H.; Pan, L.; Fan, H.; Zhang, Z.; Chen, Z. Optimal Scheduling of a Wind Energy Dominated Distribution Network Via a Deep Reinforcement Learning Approach. Renew. Energy 2022, 201, 792–801. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Li, J.; Cao, D.; Huang, R.; Huang, Q.; Chen, Z.; Blaabjerg, F. Dynamic Energy Conversion and Management Strategy for an Integrated Electricity and Natural Gas System with Renewable Energy: Deep Reinforcement Learning Approach. Energy Convers. Manag. 2020, 220, 113063. [Google Scholar] [CrossRef]
- Velamuri, S.; Kantipudi, M.V.V.P.; Sitharthan, R.; Kanakadhurga, D.; Prabaharan, N.; Rajkumar, A. A Q-Learning Based Electric Vehicle Scheduling Technique in a Distribution System for Power Loss Curtailment. Sustain. Comput. Inform. Syst. 2022, 36, 100798. [Google Scholar] [CrossRef]
- Wang, S.; Du, L.; Fan, X.; Huang, Q. Deep Reinforcement Scheduling of Energy Storage Systems for Real-Time Voltage Regulation in Unbalanced LV Networks with High PV Penetration. IEEE Trans. Sustain. Energy 2021, 12, 2342–2352. [Google Scholar] [CrossRef]
- Huang, R.; Chen, Y.; Yin, T.; Li, X.; Li, A.; Tan, J.; Yu, W.; Liu, Y.; Huang, Q. Accelerated Derivative-Free Deep Reinforcement Learning for Large-Scale Grid Emergency Voltage Control. IEEE Trans. Power Syst. 2021, 37, 14–25. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Wang, X.; Pu, T. Load Shedding Control Strategy in Power Grid Emergency State Based on Deep Reinforcement Learning. CSEE J. Power Energy Syst. 2021, 8, 1175–1182. [Google Scholar] [CrossRef]
- Matavalam, A.R.R.; Guddanti, K.P.; Weng, Y.; Ajjarapu, V. Curriculum Based Reinforcement Learning of Grid Topology Controllers to Prevent Thermal Cascading. IEEE Trans. Power Syst. 2022, 38, 4206–4220. [Google Scholar] [CrossRef]
- Oh, S.H.; Yoon, Y.T.; Kim, S.W. Online Reconfiguration Scheme of Self-Sufficient Distribution Network Based on a Reinforcement Learning Approach. Appl. Energy 2020, 280, 115900. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Choi, D.-H. Three-Stage Inverter-Based Peak Shaving and Volt-VAR Control in Active Distribution Networks Using Online Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 3266–3277. [Google Scholar] [CrossRef]
- Horri, R.; Roudsari, H.M. Reinforcement-Learning-Based Load Shedding and Intentional Voltage Manipulation Approach in a Microgrid Considering Load Dynamics. IET Gener. Transm. Distrib. 2022, 16, 3384–3401. [Google Scholar] [CrossRef]
- Hagmar, H.; Tuan, L.A.; Eriksson, R. Deep Reinforcement Learning for Long-Term Voltage Stability Control. arXiv 2022. Preprint. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, H.; He, X.; Tang, J.; Yuan, X.; Wang, G. Emergency Frequency Control Strategy Using Demand Response Based on Deep Reinforcement Learning. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjin, China, 20–23 September 2020; pp. 1–5. [Google Scholar]


| NEMA Insulation Class Rating Measured by Resistance Method | Temperature Rise in Degrees, °C Starting from the Ambient Temperature of 40 °C | |
|---|---|---|
| Insulation class | SF 1 | SF 1.15 |
| A | 60 | 65 |
| B | 80 | 85 |
| F | 105 | 110 |
| H | 125 | 135 |
| NEMA Insulation Class Rating Measured by Slot-Embedded Sensors | Temperature Rise in Degrees, °C Starting from the Ambient Temperature of 40 °C | |
|---|---|---|
| Insulation class | SF 1 | SF 1.15 |
| A | 65 | 75 |
| B | 85 | 95 |
| F | 110 | 120 |
| H | 135 | 145 |
| Ref. | Optimisation Method | Objective Function | Application | Action | Power System Size |
|---|---|---|---|---|---|
| [18] | Lagrange multiplier SAC | Maximise operational rewards, minimise generation costs, maintain system constraints (power balance, voltage limits) | Optimal active power dispatch for DGs in systems with renewable energy | Discrete actions | IEEE 118-bus power system |
| [56] | Lagrangian-based DDPG | Minimise total generation cost | Optimising real-time power flow in systems with intermittent distributed renewable generators | Continuous action | IEEE 118-bus power system |
| [19] | TD3 and Levenberg–Marquardt | Minimise total generation cost | Real-time optimal power flow management, controlling DG outputs | Continuous action | IEEE 118-bus power system |
| [57] | DDPG with safety layer and dual replay buffer | Minimise expected time average cost over control horizon, accounting for monetary costs at PCC and dispatch plan deviation cost | Real-time control of ES in active distribution grids with distributed energy resources | Continuous action | 34-bus Swiss grid |
| [58] | DQN | Minimise operational costs of microgrid | Management of conventional generators, DGs, ESs, and grid interactions | Discrete actions | Microgrid (size not specified) |
| [59] | A2C with Curriculum Learning | Minimise overall operational costs of microgrids, considering generation costs, storage management, and penalties for operational constraint violations. | Energy management of controllable DGs in a network of microgrids | Continuous action | Network of interconnected microgrids (size not specified) |
| [60] | TD3 | Minimise operating costs, including generation, transaction, and EV charging costs, with incentives for renewable energy use | Intelligent energy management in a hybrid DG and EV system | Continuous action | Microgrid (size not specified) |
| [61] | SAC with nodal multi-target (NMT) approach | Minimise energy costs and penalties related to EV charging non-completion | EV charging scheduling in a power distribution network | Continuous action | IEEE 37-node test feeder with 2500 EV stations |
| [62] | Graph RL with Graph Attention Networks (GAT) and DDPG | Minimise costs, including network transactions, power losses, load control, and voltage deviations | Real-time optimal scheduling of FLs, DGs, ES systems, and SVCs in active distribution networks | Continuous action | Modified IEEE 33-bus system |
| [63] | DDQN | Maximise long-term profit by managing interruptible loads to reduce peak demand and operation costs while maintaining voltage limits | Demand response management of interruptible load (FL) in power distribution networks | Discrete actions | Enhanced IEEE 33-node test feeder system |
| [64] | Three-stage DDQN and DDPG | Minimise operational costs while ensuring network stability and reliability, reducing power losses, managing load demands, and optimising distributed energy resources (DERs) | Real-time operation of distribution networks, controlling DGs, load points, switches, and ESSs | Discrete and continuous actions | IEEE 33-bus |
| [65] | Batch-constrained soft actor-critic (BCSAC) | Minimise overall operational costs, including electricity consumption, line losses, and switching operations | Dynamic distribution network reconfiguration, controlling remotely operable switches | Discrete actions | 119-bus distribution network |
| [20] | PPO | Minimise the cost of power loss across the distribution network with constraints related to renewable energy and storage device operations | Optimal power flow in networks with DGs and ESs | Continuous actions | Modified IEEE 33-bus network with added renewables and storage |
| [66] | TD3 | Minimise total power loss within a community microgrid | Power flow optimisation in community microgrids, controlling DERs and ESS | Continuous actions | IEEE 14-bus test system |
| [67] | Improved DRL | Minimise operational costs in day-ahead dispatch, including costs from power purchases, network losses, and curtailment of renewable energy | Day-ahead optimal dispatch in active distribution networks, controlling DGs, ESS, and CBs | Discrete and continuous actions | IEEE 33-bus test system |
| [68] | Deep LSTM-based DQN | Minimise overall daily operational cost of the grid-tied microgrid, optimising power flow from BESS and managing grid interactions to reduce costs and maximise revenue | Economic energy dispatch of ES systems in a grid-tied microgrid | Discrete actions | Residential microgrid (specific size not provided |
| [69] | Multi-agent deep deterministic policy gradient (MADDPG) | Minimise total generation and interaction costs, balancing production costs and revenue/costs associated with power flow between microgrids and the main grid | Economic dispatch of ES and DG in active distribution networks with multiple microgrids | Continuous actions | Multiple microgrids, unspecified the size |
| [70] | Double DQN | Minimise reactive power-related losses and voltage deviations, expressed as a weighted sum of costs associated with line losses and voltage deviations | Reactive power optimisation in distribution networks, controlling reactive power compensators | Discrete actions | IEEE 37-bus test system |
| [71] | DQN | Minimise annual operational costs, including energy losses and the operation of dispersed generation units | Energy management in distribution networks with EVs and DGs | Discrete actions | 57-bus IEEE grid |
| Ref. | Optimisation Method | Objective Function | Application | Action | Power System Size |
|---|---|---|---|---|---|
| [74] | DDPG | Minimise voltage fluctuations | DGs | Continuous action | IEEE 21-bus |
| [75] | MADDPG | Minimise voltage fluctuations | DGs | Continuous action | 123-bus systems |
| [76] | JASAC | Minimise voltage deviation and active power loss | DGs | Continuous action | IEEE 123-bus |
| [77] | PPO with IL | Minimise voltage deviation and generator costs | Conventional generators | Continuous action | IEEE 200-bus |
| [79] | DQN | Minimising the average voltage fluctuation and maximising the SoC of energy storage | ESs | Discrete action | IEEE 33-bus |
| [21] | RL with MPC | Minimise voltage deviation, active power loss, and overall cost | ESs | Continuous action | IEEE 33-bus |
| [80] | AWDDQN | Minimise voltage fluctuations | EVs and DGs | Discrete action | IEEE 123-bus system |
| [81] | MADQN | Increase the proportion of PV power generation used locally and minimise voltage fluctuations | EVs and ESs | Discrete action | Low voltage grid |
| [82] | DDPG | Voltage regulation and power loss minimisation | DGs and ESs | Continuous action | IEEE-34 |
| [83] | DQN | Minimise voltage deviation | CBs | Discrete action | 13-bus |
| [84] | DQN | Minimising the long and short-term average voltage deviation | DGs and CBs | Discrete action | The Southern California Edison 47-bus |
| [85] | DDPG | Minimising the voltage swell and power losses | TCs | Continuous action | IEEE 33-bus system |
| [86] | Constrained SAC | Minimising voltage deviation and generating costs | TCs and CBs | Discrete action | 123-bus |
| [87] | SAC | Minimising voltage deviation and power loss and generating cost | DG inverters and CBs | Continuous action | 33-bus |
| [88] | Multi-agent SAC and sparse pseudo-Gaussian process | Minimising the voltage deviation and PV curtailment | ESs, DGs, and SVCs | Continuous action | IEEE 123-bus |
| [93] | Multi-agent RL algorithms | Minimising voltage deviation and active power loss | Conventional generators and capacitor bank | Discrete action | IEEE 162-bus |
| [94] | DDPG | Minimising voltage deviation and active power loss | TCs | Continuous action | IEEE 123-bus |
| [95] | DQN | Minimising the voltage deviation | Conventional generators, CBs, and TCs | Discrete action | IEEE 14-bus |
| [96] | Multi-agent SAC | Minimising the voltage deviation | DGs, CBs, and TCs | Continuous action | IEEE 123-bus |
| [97] | DDPG and Monte Carlo | Minimising voltage deviation and power loss | EVs, CBs, and TCs | Continuous action | IEEE 123-bus |
| [89] | DQN | Minimising voltage deviation, power loss and switch action cost | Topology | Discrete action | Taiwan power company 84-bus |
| [90] | PPO | Minimising voltage deviation and power loss | Topology | Discrete action | IEEE 34-bus |
| [91] | DDPG with CNN | Minimising voltage deviation | Load shedding (FL) | Continuous action | New England 39-bus system |
| [92] | Multi-agent SAC | Minimising voltage deviation, energy cost and indoor thermal discomfort | Load shedding (FL) | Continuous action | Low-voltage network 6-bus |
| [98] | Convolutional LSTM with DQN | Minimising short-term voltage deviation | Load shedding (FL) | Discrete action | China Southern Power Grid 23-bus |
| Ref. | Optimisation Method | Objective Function | Application | Action | Power System Size |
|---|---|---|---|---|---|
| [100] | Duelling DQN | Minimising operating costs and curtailment of RE | DGs | Discrete actions | IEEE 14-bus |
| [101] | DDPG and model-based approach | Minimising line losses, voltage deviations, and curtailment of RE | DGs | Continuous action | IEEE 34-bus |
| [102] | MASAC | Minimising voltage deviations and curtailment of RE | DGs | Continuous action | Colorado U.S. grid 759-bus |
| [103] | DDPG | Minimising operating and emission cost | DGs and ES | Continuous action | Microgrid |
| [104] | MAPPO with parameter-sharing | Minimising operating and emission cost | EVs | Continuous + discrete action | 15-bus radial distribution |
| [105] | DQN | Minimising line losses, voltage deviations, and curtailment of RE | Reconfiguration (Topology) | Discrete action | 16-bus |
| [106] | DQN with multi-objective bacterial foraging optimisation | Minimising PV power curtailment, power loss, and generation cost | Reconfiguration (Topology) | Discrete action | IEEE 118-bus |
| [107] | MADDPG | Minimising line losses, voltage deviations, and curtailment of RE | SVC | Continuous action | IEEE 300-bus and China 157-node |
| Ref. | Optimisation Method | Objective Function | Application | Action | Power System Size |
|---|---|---|---|---|---|
| [108] | PPO | Maximise power system security | Conventional generators | Continuous action | 200-bus |
| [109] | PPO | Minimise voltage unbalance at the PCC | DGs | Continuous action | IEEE 34 bus |
| [110] | DDPG | Minimising the power fluctuations and power cost | ESs | Continuous action | IEEE 14 bus |
| [111] | DDPG | Minimising the operating cost and net load fluctuations | ESs | Continuous action | 11 bus |
| [118] | Safety-constrained SAC | Peak shaving and voltage regulation | DG inverters and ESs | Continuous action | IEEE 123-bus |
| [112] | Q-learning algorithm and enhanced Grasshopper optimisation | Peak shaving and minimising the power loss | DG and EVs | Discrete action | IEEE 33-bus |
| [113] | SAC | Minimising the total daily cost and voltage regulation in unbalanced grid | ESs | Continuous action | IEEE 34-bus |
| [114] | PARS with LSTM | Minimising the total load-shedding amount and the voltage violations | Load shedding (FL) | Continuous action | IEEE 300-bus |
| [115] | DDPG | Minimising voltage violations | Load shedding (FL) | Continuous action | IEEE 39-bus |
| [116] | A3C | Minimising the total line loading | Topology | Discrete action | IEEE 14-bus |
| [117] | DQN | Mitigating line congestion and voltage violations | Topology | Discrete action | IEEE 123-bus |
| [119] | Q-learning | Minimising the load shedding cost and frequency instability | DGs, ES, and demand response (FL) | Discrete action | IEEE 37-node MG |
| [120] | Clipped PPO | Maximising long-term voltage stability | ES and demand response (FL) | Continuous action | Nordic 32-bus |
| [121] | Q-learning with CNN | Maximising frequency stability after the fault | Load shedding (FL) | Discrete action | IEEE 39-bus |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafoor, A.; Aldahmashi, J.; Apsley, J.; Djurović, S.; Ma, X.; Benbouzid, M. Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges. Energies 2024, 17, 4399. https://doi.org/10.3390/en17174399
Ghafoor A, Aldahmashi J, Apsley J, Djurović S, Ma X, Benbouzid M. Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges. Energies. 2024; 17(17):4399. https://doi.org/10.3390/en17174399
Chicago/Turabian StyleGhafoor, Aras, Jamal Aldahmashi, Judith Apsley, Siniša Djurović, Xiandong Ma, and Mohamed Benbouzid. 2024. "Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges" Energies 17, no. 17: 4399. https://doi.org/10.3390/en17174399
APA StyleGhafoor, A., Aldahmashi, J., Apsley, J., Djurović, S., Ma, X., & Benbouzid, M. (2024). Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges. Energies, 17(17), 4399. https://doi.org/10.3390/en17174399









