Reliable Energy Optimization Strategy for Fuel Cell Hybrid Electric Vehicles Considering Fuel Cell and Battery Health
Abstract
1. Introduction
1.1. Background and Literature Survey
1.2. Objectives
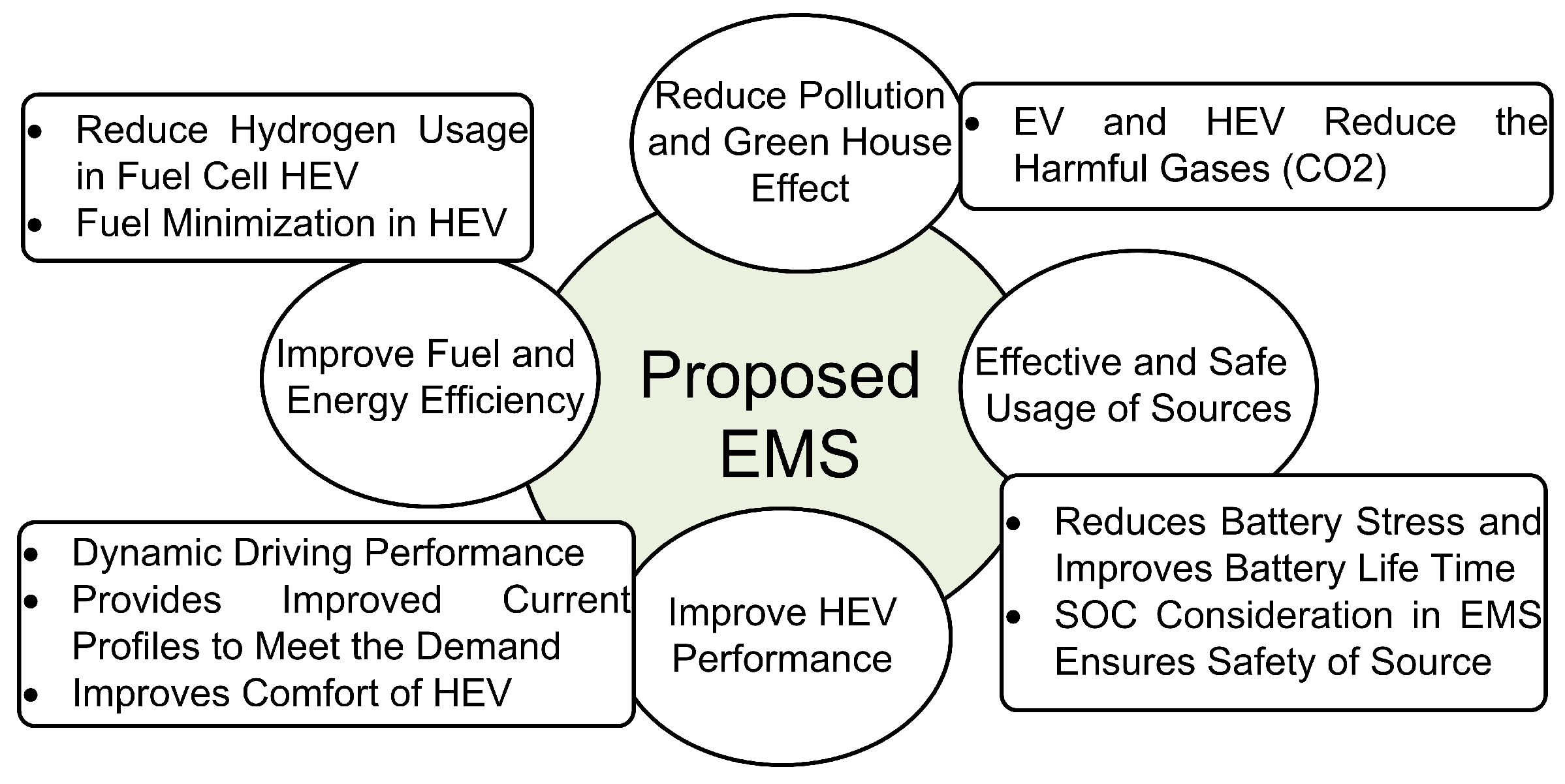
1.3. Main Contributions
- The problem is the instantaneous distribution of the electrical power requested from the two energy sources while optimizing as much as possible the global consumption of hydrogen on a given mission profile. Energy management strategies based on improved energy management methods based on dynamic programming (DP) are developed. Then, we present a method of Pontryagin’s minimum principle (PMP). These strategies lead the fuel cell to operate at the points of best performance while maintaining the SOC of the battery function. We then compare our method with two other strategies based on a fuzzy-logicstrategy-based EMS (FLS) and an equivalent consumption minimization strategy (ECMS).
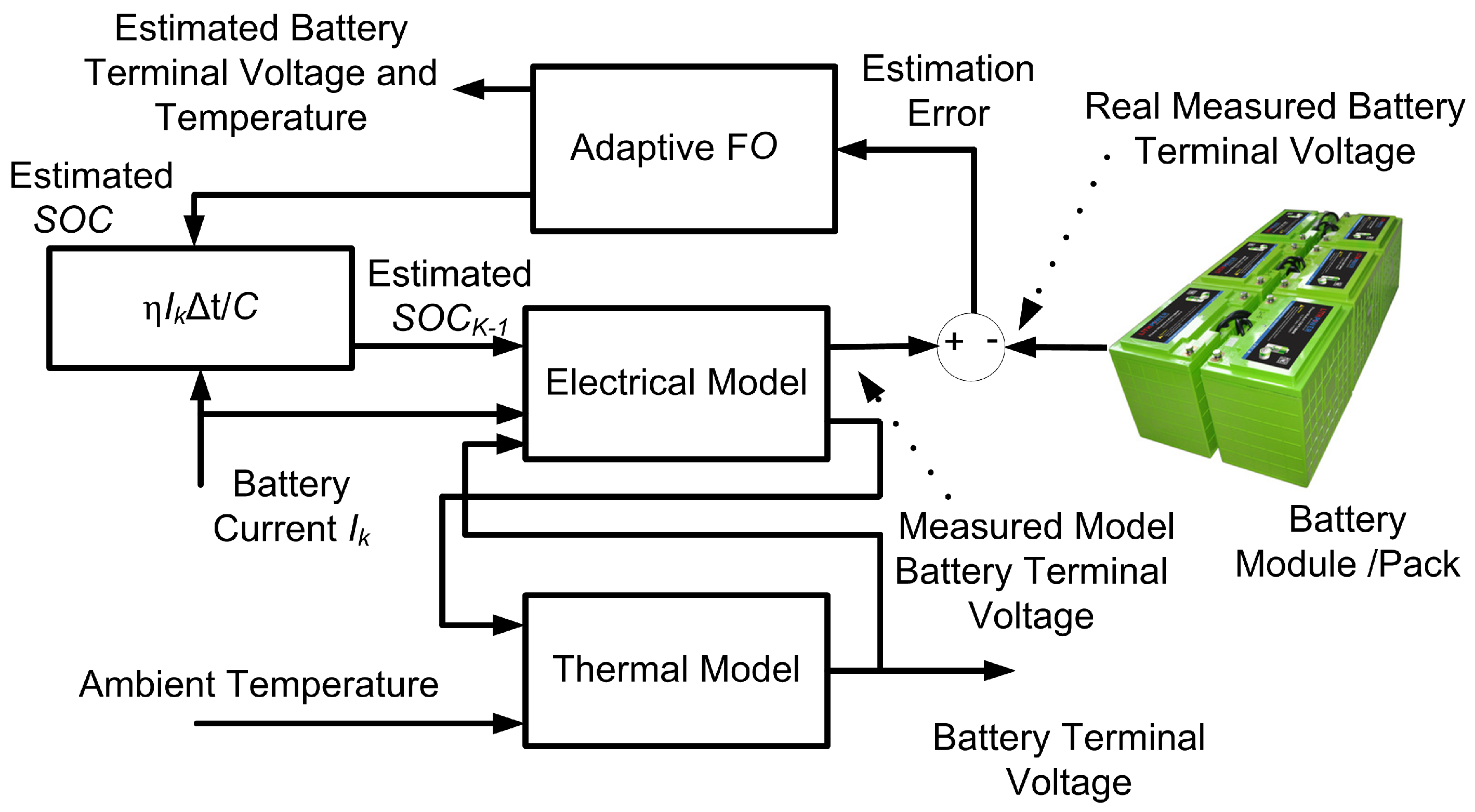
- The estimation of the SOC of the battery is proposed. An algorithm supported by a theory from the field of advanced control is used for the first time for the estimation of the SOC. It is chosen for its accuracy and its low computational resources required, which make it well-suited for the characteristics required for light electric vehicles.
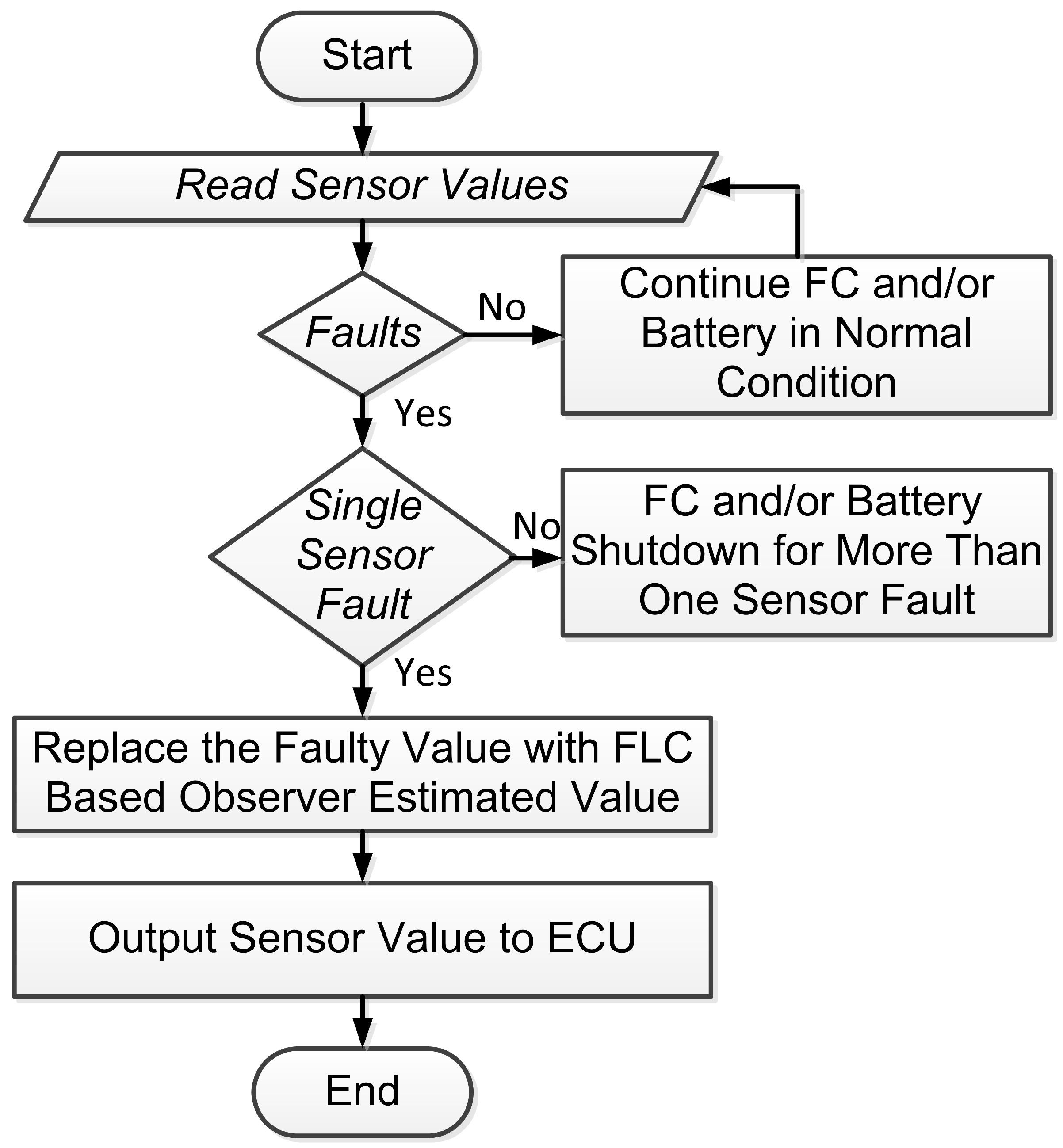
- The work presented in this manuscript concerns the implementation of a better BFCMS methodology that takes into account the occurrence of PEMFC and battery faults. The developed strategy is FTC that aims to limit the occurrence of and reduce the effects of faults. FTC based on an adaptive fuzzy observer (AFO) using the linear matrix inequality (LMI) allows for sufficiently early mitigation of the fault to reduce its consequences (performance decrease and degradations).
- Simulation results using TruckMaker/MATLAB software confirm that the proposed approach leads to optimal energy consumption of the vehicle for any unknown driving cycles and compensates for battery fault effects.
1.4. Plan of the Document
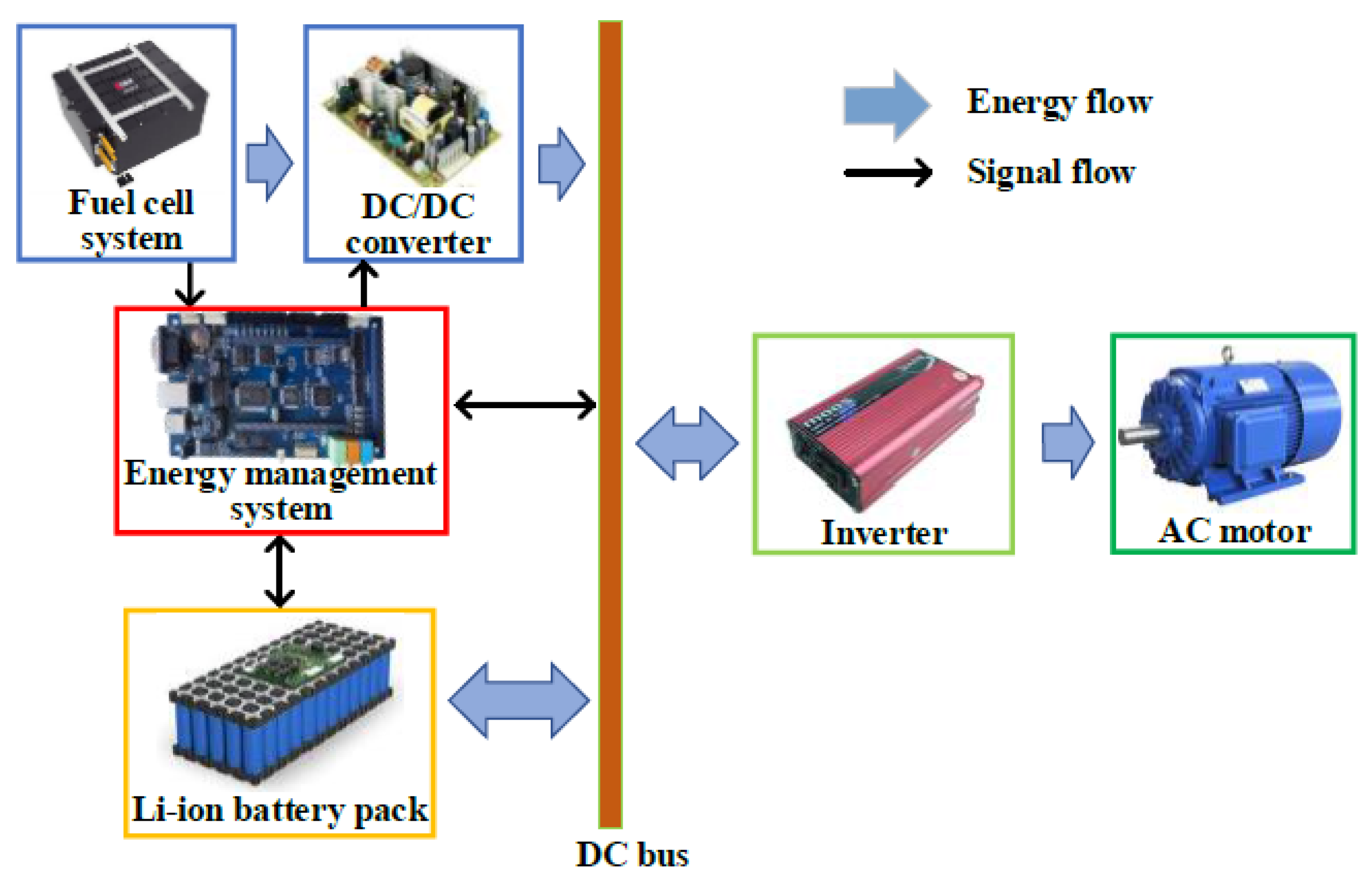
2. Modeling of the Studied Vehicle
2.1. Dynamics of the Vehicle
2.2. Fuel Cell System Model
2.3. The Battery Model
2.4. FCHEV Design Using TruckMaker
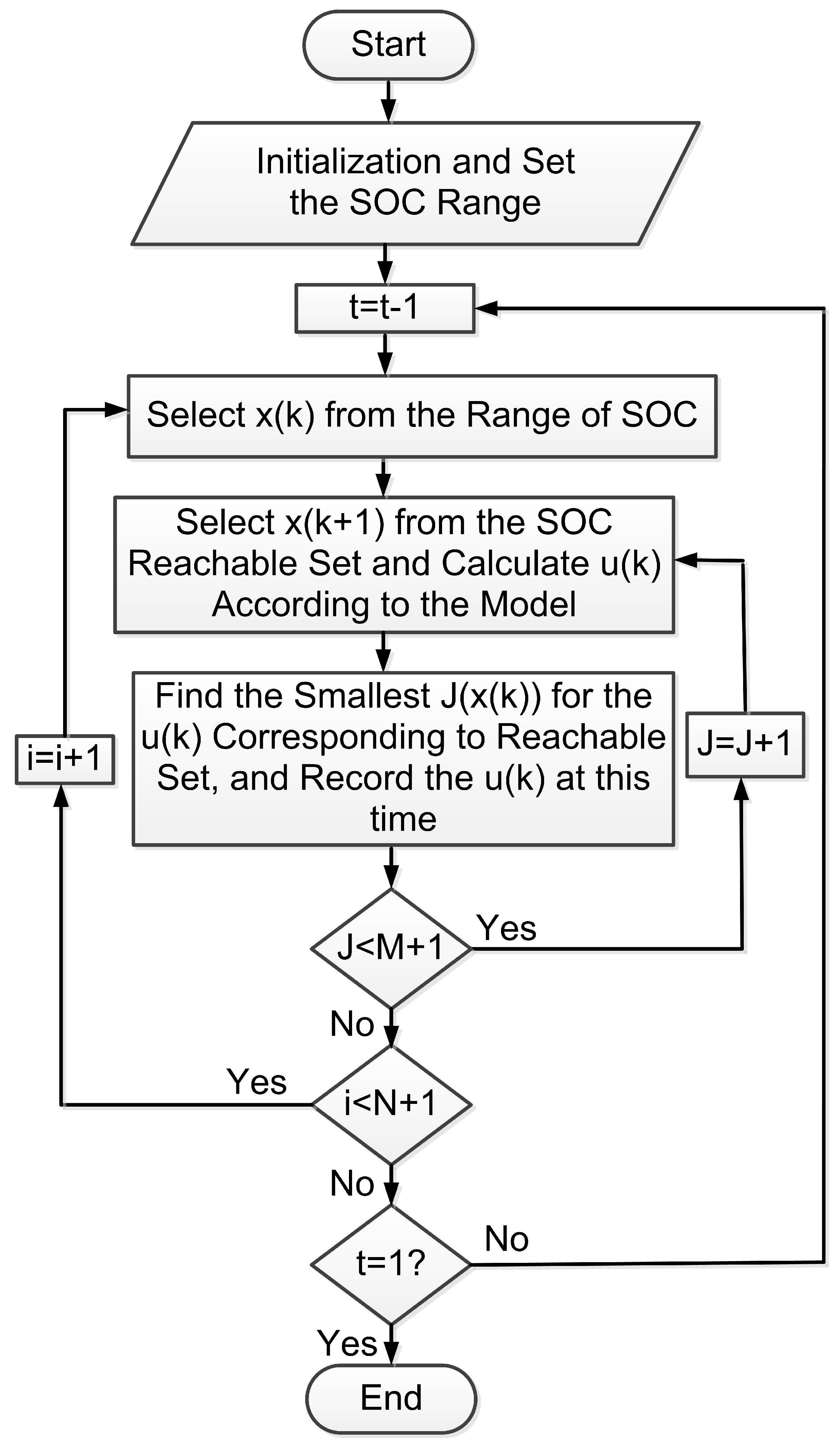
3. Formulation of the Optimization Problem
4. Overall Proposed Control Architecture and Main Components
4.1. Supervisory Fuzzy FTC and Prediction Strategy (Level 2: SFFTC)
4.1.1. Supervisory Fuzzy FTC
- a.
- Observer Design
- b.
- Proposed fuzzy fault-tolerant control
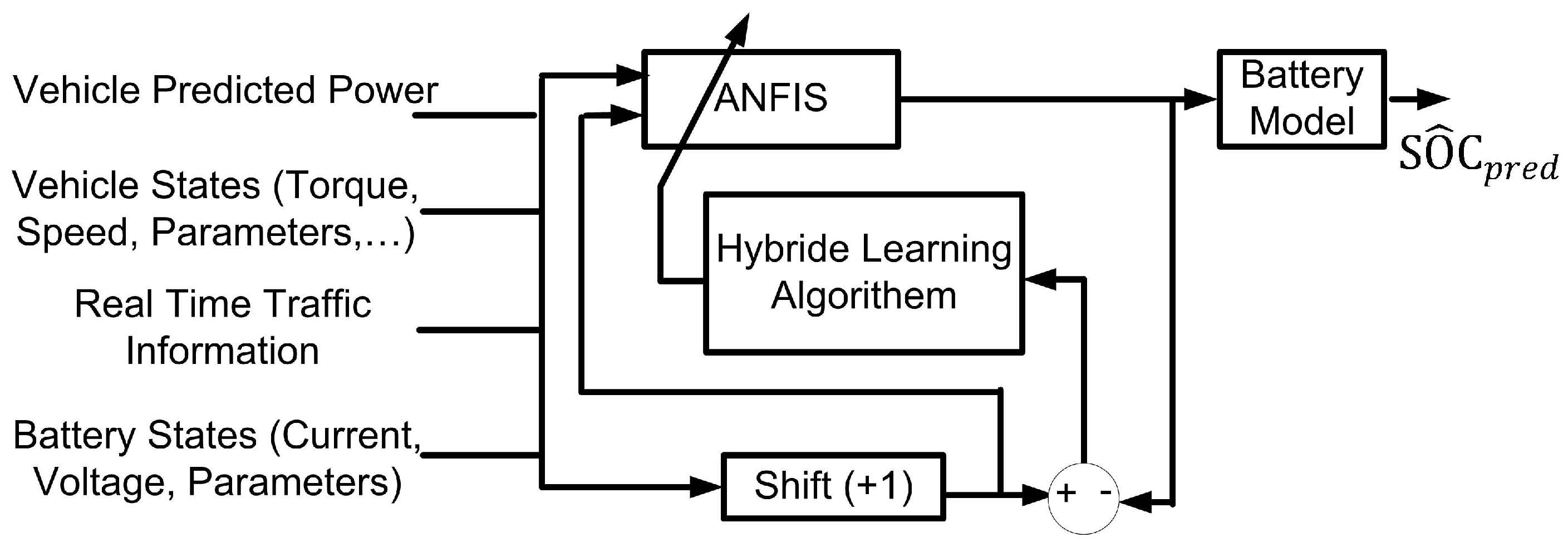
4.1.2. Estimation of the SOC and Its Predicted Progress
- a.
- Estimation Results for the SOC Based on an AFO
- b.
- Estimation Results for the SOC Based on the ANFIS
4.2. Hybrid System Energy Management Algorithms (Level 1: HSEMA)
4.2.1. EMS Optimization Based on Dynamic Programming
4.2.2. Robust Adaptive Fuzzy Controller
5. EMS Optimization Based on Rule-Based Strategy and ECMS
5.1. Improved EMS Based on PMP
5.2. Improved EMS Based on ECMS
5.3. Improved Fuzzy-Logic-Strategy-Based EMS
6. Simulation and Validation Results
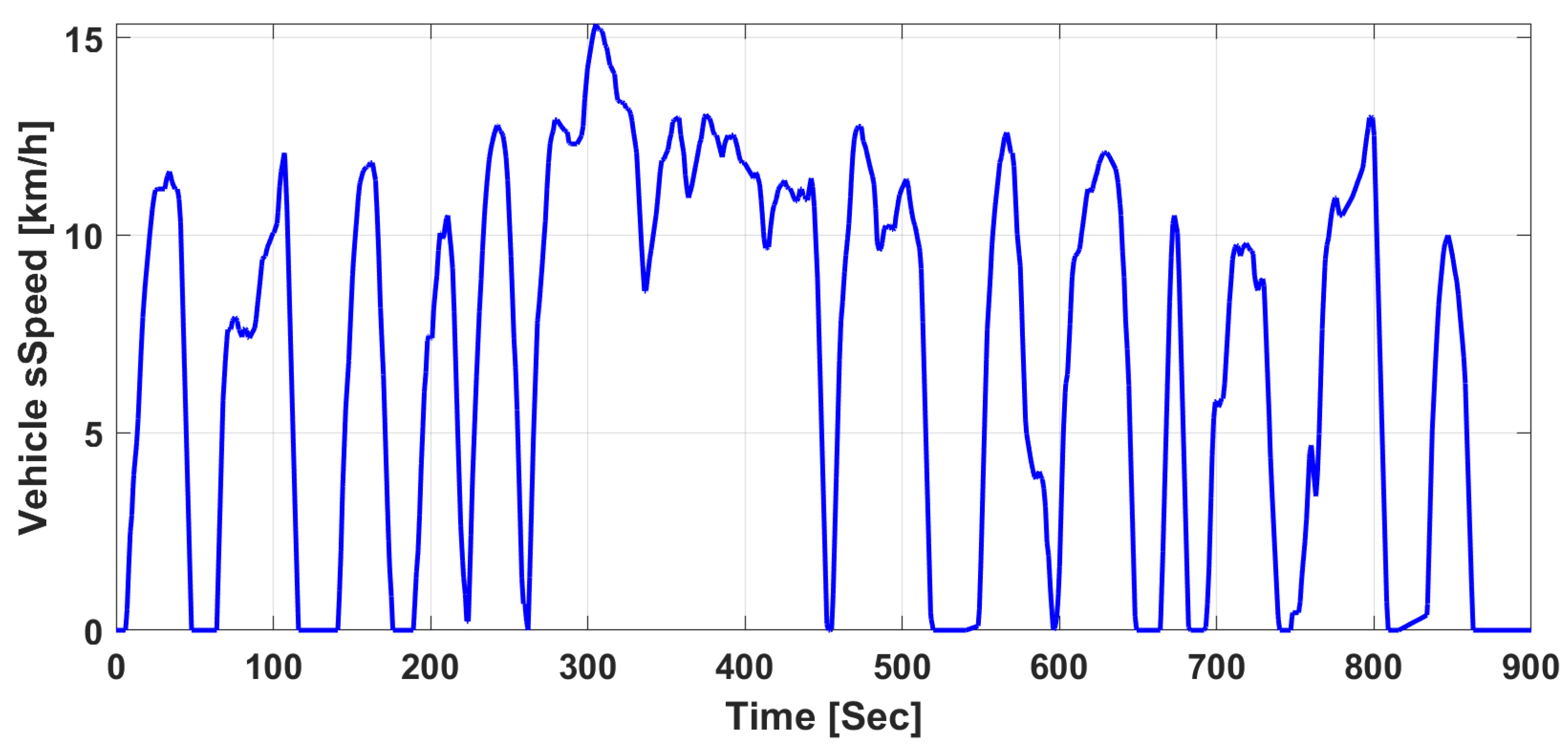
6.1. Simulation 1: Overall HSEM Validation with and without FTC
6.2. Simulation 2: Comparisons of the Different Energy Management Strategies
7. Conclusions
- Increasing the bus’s energy efficiency and minimizing total energy consumption;
- Detecting and compensating for the effects of sensor and/or actuator faults in the PEMFC and battery;
- Reducing hydrogen consumption by 9.8% and 8.86%, respectively, compared to the FLS strategy under the same driving conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| v | bus speed |
| traction force | |
| slope | |
| air density | |
| m | bus mass |
| A | frontal area |
| drag coefficient (a constant) | |
| r | wheel radius |
| wheel torque | |
| rotation speed | |
| transmission efficiency | |
| gear ratio | |
| power demand | |
| motor efficiency | |
| total power demand | |
| consumption by the auxiliaries | |
| N | number of cells |
| molar mass of hydrogen | |
| n | transferred electrons |
| F | Faraday’s constant |
| fuel cell stack current | |
| efficiency of the PEMFC | |
| instantaneous hydrogen consumption | |
| PEMFC power | |
| open-circuit voltage of the battery | |
| ohmic resistance | |
| equivalent capacitor | |
| battery voltage | |
| battery current | |
| battery capacity | |
| battery power | |
| total hydrogen consumption | |
| instantaneous hydrogen consumption | |
| PEMFC power supplied | |
| prediction length | |
| current time step | |
| total PEMFC efficiency | |
| DC/DC efficiency | |
| SOC set-points | |
| SOC at the end of the mission | |
| SOC at the initial time | |
| PEMFC maximum power | |
| PEMFC minimum power | |
| battery maximum power | |
| battery minimum power | |
| SOC maximum power | |
| SOC minimum power | |
| state vector | |
| control input vector | |
| output vector | |
| fuzzy sets | |
| p | number of rules |
| system matrix | |
| input matrix | |
| output matrix | |
| actuator faults | |
| E | actuator fault matrix |
| and | observer gains |
| and | controller gains |
References
- Venkatesan, R.; Savio, A.D.; Balaji, C.; Narayanamoorthi, R.; Kotb, H.; ELrashidi, A.; Nureldeen, W. A Comprehensive Review on Efficiency Enhancement of Wireless Charging System for an Electric Vehicles Application. IEEE Access 2024, 12, 46967–46994. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Pahon, E.; Pera, M.-C.; Gao, F. Multi-timescale lifespan prediction for PEMFC systems under dynamic operating conditions. IEEE Trans. Transp. Electrific. 2022, 8, 345–355. [Google Scholar] [CrossRef]
- Soumeur, M.A.; Gasbaoui, B.; Abdelkhalek, O.; Ghouili, J.; Toumi, T.; Chakar, A. Comparative study of energy management strategies for hybrid proton exchange membrane fuel cell four wheel drive electric vehicle. J. Power Sources 2020, 462, 228167. [Google Scholar] [CrossRef]
- Chi, X.; Lin, F.; Wang, Y.-X. Disturbance and uncertainty-immune onboard charging batteries with fuel cell by using equivalent load fuzzy logic estimation-based backstepping sliding-mode control. IEEE Trans. Transp. Electrific. 2021, 7, 1249–1259. [Google Scholar] [CrossRef]
- Tan, X.; Chen, Y.; Zeng, J.; Liao, W.; Liu, J. An Integrated Self-Modularized Battery Equalizer and Supercapacitor Charger for Hybrid Electric Vehicle Energy Storage System. IEEE Trans. Veh. Technol. 2024, 73, 9865–9877. [Google Scholar] [CrossRef]
- Gan, J.; Li, S.; Lin, X.; Tang, X. Multi-Agent Deep Reinforcement Learning-Based Multi-Objective Cooperative Control Strategy for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2024, 1–13. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, J.; Wang, L. Cost-Based Research on Energy Management Strategy of Electric Vehicles Using Hybird Energy Storage System. Tsinghua Sci. Technol. 2024, 29, 684–697. [Google Scholar] [CrossRef]
- Shen, Y.; Xie, J.; He, T.; Yao, L.; Xiao, Y. CEEMD-Fuzzy Control Energy Management of Hybrid Energy Storage Systems in Electric Vehicles. IEEE Trans. Energy Convers. 2024, 39, 555–566. [Google Scholar] [CrossRef]
- Mehraban, A.; Ghanbari, T.; Farjah, E. AI-Based Control of Storage Capacity in High-Power-Density Energy Storage Systems, Used in Electric Vehicles. IEEE Trans. Transp. Electrif. 2024, 10, 2293–2301. [Google Scholar] [CrossRef]
- Shuai, B.; Hua, M.; Li, Y.; Shuai, S.; Xu, H.; Zhou, Q. Optimal Energy Management of Plug-in Hybrid Electric Vehicles Through Ensemble Reinforcement Learning With Exploration-to-Exploitation Ratio Control. IEEE Trans. Intell. Veh. 2024, 1–11. [Google Scholar] [CrossRef]
- Sun, X.; Dong, Z.; Jin, Z.; Tian, X. System-Level Energy Management Optimization Based on External Information for Power-Split Hybrid Electric Buses. IEEE Trans. Ind. Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Munsi, M.S.; Chaoui, H. Energy Management Systems for Electric Vehicles: A Comprehensive Review of Technologies and Trends. IEEE Access 2024, 12, 60385–60403. [Google Scholar] [CrossRef]
- Xu, P.; Wang, C.; Ye, J.; Ouyang, T. State-of-Charge Estimation and Health Prognosis for Lithium-Ion Batteries Based on Temperature-Compensated Bi-LSTM Network and Integrated Attention Mechanism. IEEE Trans. Ind. Electron. 2024, 71, 5586–5596. [Google Scholar] [CrossRef]
- Xu, P.; Liu, B.; Hu, X.; Ouyang, T.; Chen, N. State-of-charge estimation for lithium-ion batteries based on fuzzy information granulation and asymmetric Gaussian membership function. IEEE Trans. Ind. Electron. 2022, 69, 6635–6644. [Google Scholar] [CrossRef]
- Sun, Q.; Lv, H.; Wang, S.; Gao, S.; Wei, K. Optimized State of Charge Estimation of Lithium-Ion Battery in SMES/Battery Hybrid Energy Storage System for Electric Vehicles. IEEE Trans. Appl. Supercond. 2021, 31, 1–6. [Google Scholar] [CrossRef]
- Karnehm, D.; Samanta, A.; Anekal, L.; Pohlmann, S.; Neve, A.; Williamson, S. Comprehensive Comparative Analysis of Deep Learning-based State-of-charge Estimation Algorithms for Cloud-based Lithium-ion Battery Management Systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 597–604. [Google Scholar] [CrossRef]
- Bao, Z.; Nie, J.; Lin, H.; Gao, K.; He, Z.; Gao, M. TTSNet: State-of-Charge Estimation of Li-ion Battery in Electrical Vehicles with Temporal Transformer-based Sequence Network. IEEE Trans. Veh. Technol. 2024, 73, 7838–7851. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, J.; Shi, D.; Zhang, X. A Model-Based Battery Dataset Recovery Method Considering Cell Aging in Real-World Electric Vehicles. IEEE Trans. Ind. Inform. 2024, 20, 7904–7914. [Google Scholar] [CrossRef]
- Lucero, J.N.E.; Sujan, V.A.; Onori, S. An experimentally validated electro-thermal EV battery pack model incorporating cycle-life aging and cell-to-cell variations. IEEE Trans. Transp. Electrif. 2024, 1. [Google Scholar] [CrossRef]
- Sun, H.; Tao, F.; Fu, Z.; Gao, A.; Jiao, L. Driving-Behavior-Aware Optimal Energy Management Strategy for Multi-Source Fuel Cell Hybrid Electric Vehicles Based on Adaptive Soft Deep-Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4127–4146. [Google Scholar] [CrossRef]
- Ali, A.M.; Moulik, B.; Söffker, D. Intelligent Real-Time Power Management of Multi-Source HEVs Based on Driving State Recognition and Offline Optimization. IEEE Trans. Intell. Transp. Syst. 2023, 24, 247–257. [Google Scholar] [CrossRef]
- Ali, A.M.; Shivapurkar, R.; Söffker, D. Optimal Situation-Based Power Management and Application to State Predictive Models for Multi-Source Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 11473–11482. [Google Scholar] [CrossRef]
- Venkatasatis, R.; Dhanamjayulu, C. Reinforcement learning based energy management systems and hydrogen refuelling stations for fuel cell electric vehicles: An overview. Int. J. Hydrogen Energy 2022, 47, 27646–27670. [Google Scholar] [CrossRef]
- Oladosu, T.L.; Pasupuleti, J.; Kiong, T.S.; Koh, S.P.J.; Yusaf, T. Energy management strategies, control systems, and artificial intelligence-based algorithms development for hydrogen fuel cell-powered vehicles: A review. Int. J. Hydrogen Energy 2024, 61, 1380–1404. [Google Scholar] [CrossRef]
- Wang, D.; Mei, L.; Xiao, F.; Song, C.; Qi, C.; Song, S. Energy management strategy for fuel cell electric vehicles based on scalable reinforcement learning in novel environment. Int. J. Hydrogen Energy 2024, 59, 668–678. [Google Scholar] [CrossRef]
- Nie, Z.; Huang, J.; Lian, Y.; Yang, W. Hierarchical control-based energy management strategy of intelligent battery/supercapacitor/ fuel cell hybrid vehicles. Int. J. Hydrogen Energy 2024, 61, 1092–1106. [Google Scholar] [CrossRef]
- Machacek, D.T.; Yasar, N.O.; Huber, T.; Onder, C.H. Energy management of hydrogen hybrid electric vehicles—A potential analysis. Int. J. Hydrogen Energy 2024, 58, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, R.; Zhao, D.; Huangfu, Y.; Liu, W. An Online Efficiency Optimized Energy Management Strategy for Fuel Cell Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 3203–3217. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar]
- Zhao, X.; Wang, L.; Zhou, Y.; Pan, B.; Wang, R.; Wang, L.; Yan, X. Energy management strategies for fuel cell hybrid electric vehicles: Classification, comparison, and outlook. Energy Convers. Manag. 2022, 270, 116179. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, X.; Liu, Q.; Li, S.; Xu, Y. Review article: A comprehensive review of energy management strategies for hybrid electric vehicles. Mech. Sci. 2022, 13, 147–188. [Google Scholar] [CrossRef]
- Li, Q.; Su, B.; Pu, Y.; Han, Y.; Wang, T.; Yin, L.; Chen, W. A state machine control based on equivalent consumption minimization for fuel cell/supercapacitor hybrid tramway. IEEE Trans. Transp. Electrific. 2019, 5, 552–564. [Google Scholar] [CrossRef]
- Maria, C.; Suja, S.; Sajini, M.L.M. Effective Energy Management in Grid Integrated with Renewable Resources Using Finite State Machine Model. In Proceedings of the 2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 1–3 March 2022. [Google Scholar]
- Garcia, P.; Fernandez, L.M.; Garcia, C.A.; Jurado, F. Energy management system of fuel-cell-battery hybrid tramway. IEEE Trans. Ind. Electron. 2010, 57, 4013–4023. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, W.; Liu, J.; Li, Q.; Chen, W. The Control Strategy of Fuel Cell Hybrid Tram Based on State Machine Control. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 699–703. [Google Scholar]
- Khanafari, A.; Alasty, A.; Kermani, M.J.; Asghari, S. Experimental study of water management of a three-cell PEM fuel cell stack using adaptive neuro-fuzzy approximation and fuzzy control. Int J. Hydrogen Energy 2024, 50, 931–944. [Google Scholar] [CrossRef]
- Hemi, H.; Ghouili, J.; Cheriti, A. A real time fuzzy logic power management strategy for a fuel cell vehicle. Energy Convers. Manag. 2014, 80, 63–70. [Google Scholar] [CrossRef]
- Martínez, J.S.; Mulot, J.; Harel, F.; Hissel, D.; Pera, M.C.; John, R.I.; Amiet, M. Experimental validation of a type-2 fuzzy logic controller for energymanagement in hybrid electrical vehicles. Eng. Appl. Artif. Intell. 2013, 26, 1772–1779. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C.; Wu, C.; Xu, W. Adaptive fuzzy logic control of fuel-cell-battery hybrid systems for electric vehicles. IEEE Trans. Ind. Inform. 2018, 14, 292–300. [Google Scholar] [CrossRef]
- Shen, J.; Khaligh, A. A supervisory energy management control strategy in a battery/ultracapacitor hybrid energy storage system. IEEE Trans. Transp. Electrific. 2015, 1, 223–231. [Google Scholar] [CrossRef]
- Duhr, P.; Balerna, C.; Onder, C.H. Time-optimal gearshift and energy management strategies for a hybrid electric race car. Appl. Energy 2021, 282, 115980. [Google Scholar] [CrossRef]
- Biswas, A.; Emadi, A. Energy management systems for electrified powertrains: State-of-the-art review and future trends. IEEE Trans. Veh. Technol. 2019, 68, 6453–6467. [Google Scholar] [CrossRef]
- Lin, X.; Xu, X.; Lin, H. Predictive-ECMS based degradation protective control strategy for a fuel cell hybrid electric vehicle considering uphill condition. eTransportation 2022, 12, 1–19. [Google Scholar] [CrossRef]
- Jia, C.; Qiao, W.; Cui, J.; Qu, L. Adaptive Model-Predictive-Control-Based Real-Time Energy Management of Fuel Cell Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2023, 38, 2681–2694. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.; Gong, X.; Cao, R.; Guo, L.; Chen, H. Energy Management Strategy for Fuel Cell Hybrid Electric Vehicles Considering the Inaccuracy of Predicted Vehicle Speed. IEEE Trans. Transp. Electrif. 2024, 1. [Google Scholar] [CrossRef]
- Hou, Z.; Chu, L.; Guo, Z.; Hu, J.; Jiang, J.; Yang, J.; Chen, Z.; Zhang, Y. A Learning-and-Tube-Based Robust Model Predictive Control Strategy for Plug-In Hybrid Electric Vehicle. IEEE Trans. Intell. Veh. 2024, 9, 579–592. [Google Scholar] [CrossRef]
- Song, K.; Huang, X.; Xu, H.; Sun, H.; Chen, Y.; Huang, D. Model predictive control energy management strategy integrating long short-term memory and dynamic programming for fuel cell vehicles. Int. J. Hydrogen Energy 2024, 56, 1235–1248. [Google Scholar] [CrossRef]
- Soldo, J.; Škugor, B.; Deur, J. Model Predictive Control of a Parallel Plug-In Hybrid Electric Vehicle Relying on Dynamic Programming and Extended Backward-Looking Model. IEEE Trans. Control. Syst. Technol. 2024, 32, 581–594. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Wang, Y.; Xu, L.; Lei, S. Energy Management Optimization and Validation of a Hydrogen Fuel Cell-Powered Agricultural Tractor Based on Hierarchical Dynamic Programming. IEEE Access 2024, 12, 21382–21401. [Google Scholar] [CrossRef]
- Tang, W.; Wang, Y.; Jiao, X.; Ren, L. Hierarchical energy management strategy based on adaptive dynamic programming for hybrid electric vehicles in car-following scenarios. Energy 2023, 265, 126264. [Google Scholar] [CrossRef]
- Ma, M.; Xu, E.; Zheng, W.; Qin, J.; Huang, Q. The optimized real-time energy management strategy for fuel-cell hybrid trucks through dynamic programming. Int. J. Hydrogen Energy 2024, 59, 10–21. [Google Scholar] [CrossRef]
- Chen, B.-C.; Wu, Y.-Y.; Tsai, H.-S. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming. Appl. Energy 2014, 113, 1764–1774. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Jianqiu, L.; Yang, F.; Lu, L.; Hua, J. Application of Pontryagin’s minimal principle to the energy management strategy of plugin fuel cell electric vehicles. Int. J. Hydrogen Energy 2013, 38, 10104–10115. [Google Scholar] [CrossRef]
- Volkan, S.; Metin, G.; Seta, B. A novel ECMS and combined cost map approach for high-efficiency series hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 3557–3570. [Google Scholar]
- Li, S.; Chu, L.; Hu, J.; Li, J.; Hou, Z.; Sun, W. A novel A-ECMS energy management strategy based on dragonfly algorithm for plug-in FCEVs. Sensors 2023, 23, 1192. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Du, X.; Wang, W.; Yang, L.; Zha, M. A Rolling Convergent Equivalent Consumption Minimization Strategy for Plug-in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2024, 73, 3340–3353. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. A novel equivalent consumptionminimization strategy for hybrid electric vehicle powered by fuel cell, battery and supercapacitor. J. Power Sources 2018, 395, 262–270. [Google Scholar] [CrossRef]
- Tian, X.; Cai, Y.; Sun, X.; Zhu, Z.; Xu, Y. An adaptive ECMS with driving style recognition for energy optimization of parallel hybrid electric buses. Energy 2019, 189, 116151. [Google Scholar] [CrossRef]
- Kim, N.; Jeong, J.; Zheng, C.H. Adaptive energy management strategy for plug-in hybrid electric vehicles with pontryagin’s minimum principle based on daily driving patterns. Int. J. Precis. Eng. -Manuf.-Green Technol. 2019, 6, 539–548. [Google Scholar] [CrossRef]
- Liu, C.; Liu, L. Optimal power source sizing of fuel cell hybrid vehicles based on Pontryagin’s minimum principle. Int. J. Hydrogen Energy 2015, 40, 8454–8464. [Google Scholar] [CrossRef]
- Zheng, C.; Liang, Q. An energymanagement strategy of hybrid energy storage systems for electric vehicle applications. IEEE Trans. Sustain. Energy 2018, 9, 1880–1888. [Google Scholar] [CrossRef]
- Meng, X.; Li, Q.; Chen, W.; Zhang, G. A layered energy management method for a fuel cell hybrid power system based on Pontryagin’s principle of minimum value. Proc. Chin. Soc. Elect. Eng. 2019, 39, 782–792. [Google Scholar]
- Li, X.; Wang, Y.; Yang, D.; Chen, Z. Adaptive energy management strategy for fuel cell/battery hybrid vehicles using Pontryagin’s minimal principle. J. Power Sources 2019, 440, 227105. [Google Scholar] [CrossRef]
- Yang, C.; Du, S.; Li, L.; You, S.; Yang, Y.; Zhao, Y. Adaptive realtime optimal energy management strategy based on equivalent factors optimization for plug-in hybrid electric vehicle. Appl. Energy 2017, 203, 883–896. [Google Scholar] [CrossRef]
- Onori, S.; Tribioli, L. Adaptive Pontryagin’s minimum principle supervisory controller design for the plug-in hybrid GM chevrolet volt. Appl. Energy 2015, 147, 224–234. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Ouyang, M.; Hua, J.; Li, X. Active fault tolerance control system of fuel cell hybrid city bus. Int. J. Hydrog. Energy 2010, 35, 12510. [Google Scholar] [CrossRef]
- Li, J.; Zhou, T. Active fault-tolerant coordination energy management for a proton exchange membrane fuel cell using curriculum-based multiagent deep meta-reinforcement learning. Renew. Sustain. Energy Rev. 2023, 185, 1–16. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, X. Fault-tolerant control systems: A comparative study between active and passive approaches. Annu. Rev. Control. 2012, 36, 60–72. [Google Scholar] [CrossRef]
- Zhong, Z.; Huo, H.; Zhu, X.; Cao, G.; Ren, Y. Adaptive maximum power point tracking control of fuel cell power plants. J. Power Sources 2008, 176, 259–269. [Google Scholar] [CrossRef]
- Aubry, J.; Steiner, N.Y.; Morando, S.; Zerhouni, N.; Hissel, D. Fault tolerant control of a Proton Exchange Membrane Fuel Cell based on a Modified Failure Mode and Effect Analysis. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 February 2021; pp. 1–5. [Google Scholar]
- Dijoux, E.; Benne, M.; Péra, M.-C.; Grondin-Perez, B. Experimental Validation of an Active Fault Tolerant Control Strategy Applied to a Proton Exchange Membrane Fuel Cell. Electrochem 2022, 3, 633–652. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, X.; Dong, Z.; Fan, N.; Cao, S. Fixed time adaptive fault tolerant sliding mode control of PEMFC air supply system. Int. J. Hydrogen Energy 2024, 55, 1434–1444. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Chen, Z. Robust fault diagnosis and fault tolerant control for PEMFC system based on an augmented LPV observer. Int. J. Hydrogen Energy 2020, 45, 13508–13522. [Google Scholar] [CrossRef]
- Rout, S.; Das, S. Online State-of-Charge Estimation of Lithium-Ion Battery using a Fault Tolerant and Noise Immune Threefold Modified Adaptive Extended Kalman Filter. IEEE Trans. Transp. Electrif. 2024, 1. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, Z.; Wang, Y.; Zuo, Z. Event-Triggered Sensor Fault Estimation for Lithium-Ion Battery Packs. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3101–3105. [Google Scholar] [CrossRef]
- Lebreton, C.; Benne, M.; Damour, C.; Yousfi-Steiner, N.; Grondin-Perez, B.; Hissel, D.; Chabriat, J.-P. Fault Tolerant Control Strategy applied to PEMFC water management. Int. J. Hydrogen Energy 2015, 40, 10636–10646. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main factors affecting the lifetime of proton exchange membrane fuel cells in vehicle applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Robin, C.; Gérard, M.; Quinaud, M.; d’Arbigny, J.; Bultel, Y. Proton exchange membrane fuel cell model for aging predictions: Simulated equivalent active surface area loss and comparisons with durability tests. J. Power Sources 2016, 326, 417–427. [Google Scholar] [CrossRef]
- Song, K.; Chen, H.; Wen, P.; Zhang, T.; Zhang, B.; Zhang, T. A comprehensive evaluation framework to evaluate energy management strategies of fuel cell electric vehicles. Electrochim. Acta 2018, 292, 960–973. [Google Scholar] [CrossRef]
- Wang, T.; Li, Q.; Wang, X.; Chen, W.; Breaz, E.; Gao, F. A power allocation method for multistack PEMFC system considering fuel cell performance consistency. IEEE Trans. Ind. Appl. 2020, 56, 5340–5351. [Google Scholar] [CrossRef]
- Zhang, R.; Tao, J. GA-based fuzzy energy management system for FC/SC-powered HEV considering H2 consumption and load variation. IEEE Trans. Fuzzy Syst. 2018, 26, 1833–1843. [Google Scholar] [CrossRef]
- Florescu, A.; Bacha, S.; Munteanu, I.; Bratcu, A.L.; Rumeau, A. Adaptive frequency-separation-based energy management system for electric vehicles. J. Power Sources 2015, 280, 410–421. [Google Scholar] [CrossRef]
- Behling, N.; Williams, M.C.; Managi, S. Fuel cells and the hydrogen revolution: Analysis of a strategic plan in Japan. Econ. Anal. Policy 2015, 48, 204–221. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Cocquempot, V. Adaptive observer-based fast fault estimation. Int. J. Control. 2008, 6, 320–326. [Google Scholar]
- Cai, C.H.; Du, D.; Liu, Z.Y. Battery state-of-charge (SOC) estimation using adaptive neuro-fuzzy inference system (ANFIS). In Proceedings of the 12th IEEE International Conference on Fuzzy Systems, FUZZ ’03, St. Louis, MO, USA, 25–28 May 2003; pp. 1068–1073. [Google Scholar]
- Lin, X.; Sun, D.; Qin, D.; Yin, Y. Development of Power-balancing Global Optimization Control Strategy for a Series-Parallel Hybrid Electric City Bus. China Mech. Eng. 2011, 22, 2259–2263. [Google Scholar]
- Zhou, H.; Yu, Z.; Wu, X.; Fan, Z.; Yin, X.; Zhou, L. Dynamic programming improved online fuzzy power distribution in a demonstration fuel cell hybrid bus. Energy 2023, 284, 128549. [Google Scholar] [CrossRef]
- Xie, C.; Ogden, J.; Quan, S.; Chen, Q. Optimal power management for fuel cell-battery full hybrid powertrain on a test station. Int. J. Electr. Power Energy Syst. 2013, 53, 307–320. [Google Scholar] [CrossRef]
- Lin, W.-M.; Tu, C.-S.; Tsai, M.-T. Energy Management Strategy for Microgrids by Using Enhanced Bee Colony Optimization. Energies 2016, 9, 5. [Google Scholar] [CrossRef]
- Ramya, A.; Imtiaz, A.; Balaji, M. Hybrid self tuned fuzzy PID controller for speed control of brushless DC motor. Automatika 2016, 57, 672–679. [Google Scholar] [CrossRef]
- Shi, D.; Liu, S.; Cai, Y.; Wang, S.; Li, H.; Chen, L. Pontryagin’s minimum principle based fuzzy adaptive energy management for hybrid electric vehicle using real-time traffic information. Appl. Energy 2021, 286, 116467. [Google Scholar] [CrossRef]






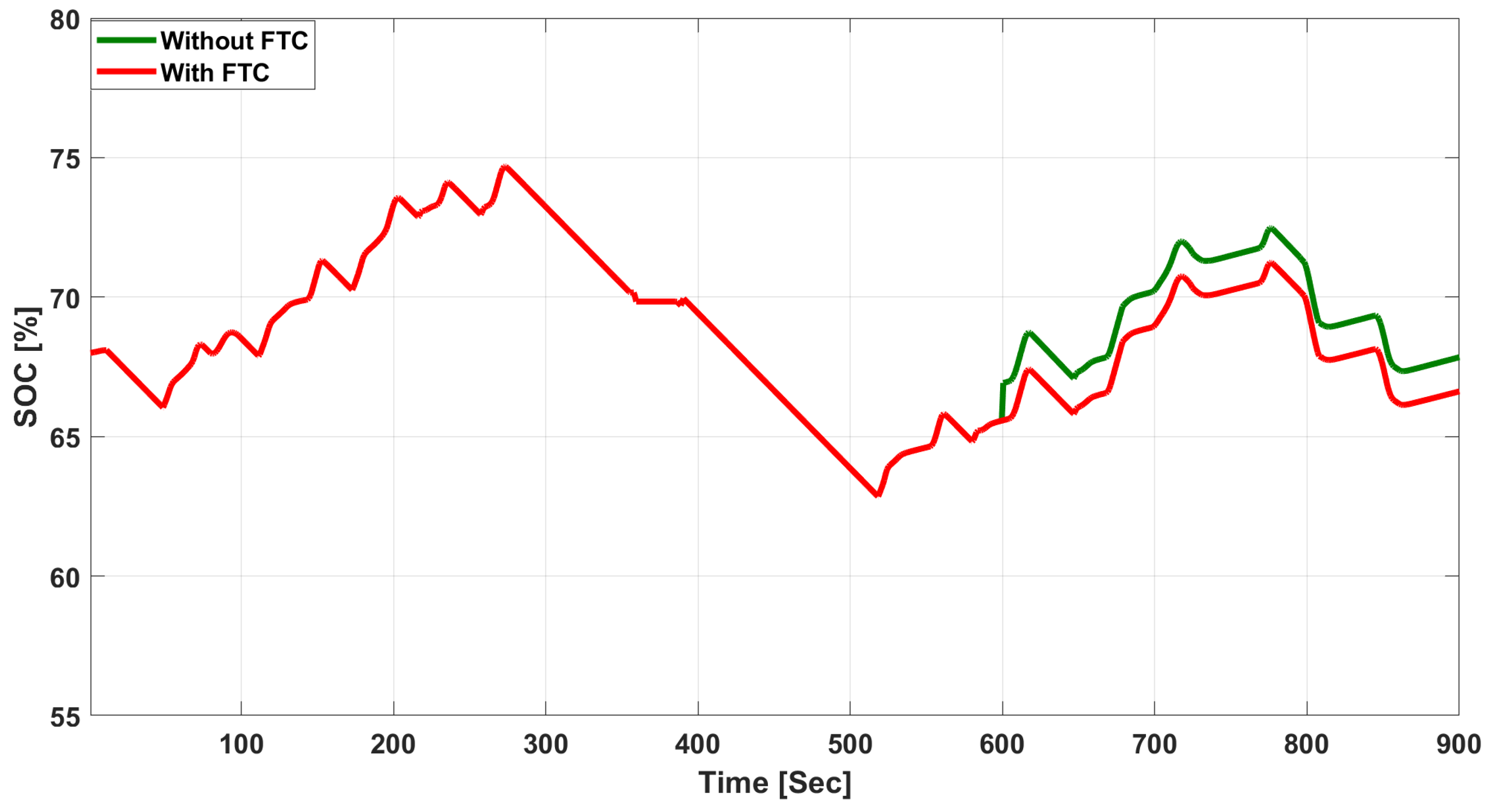

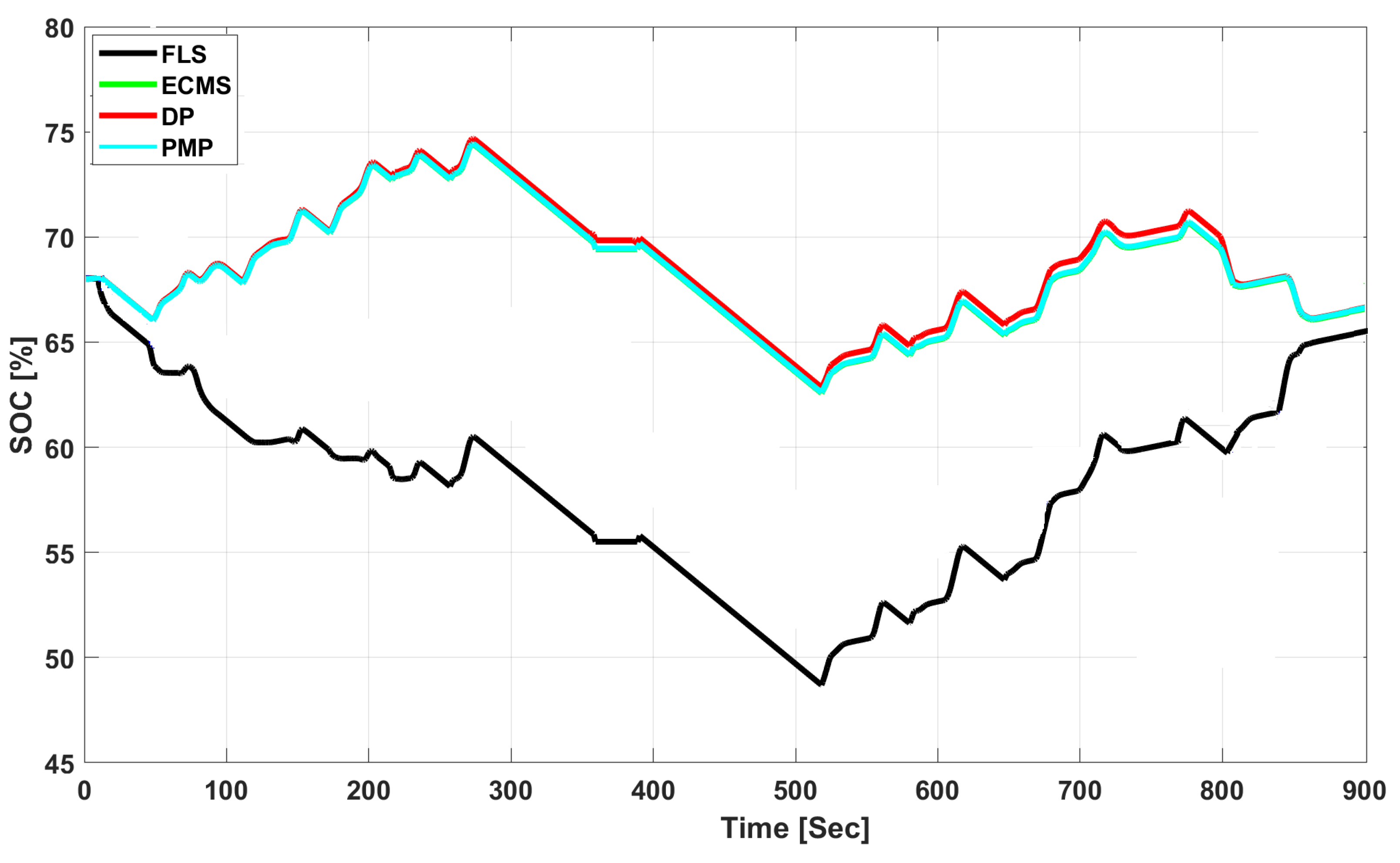
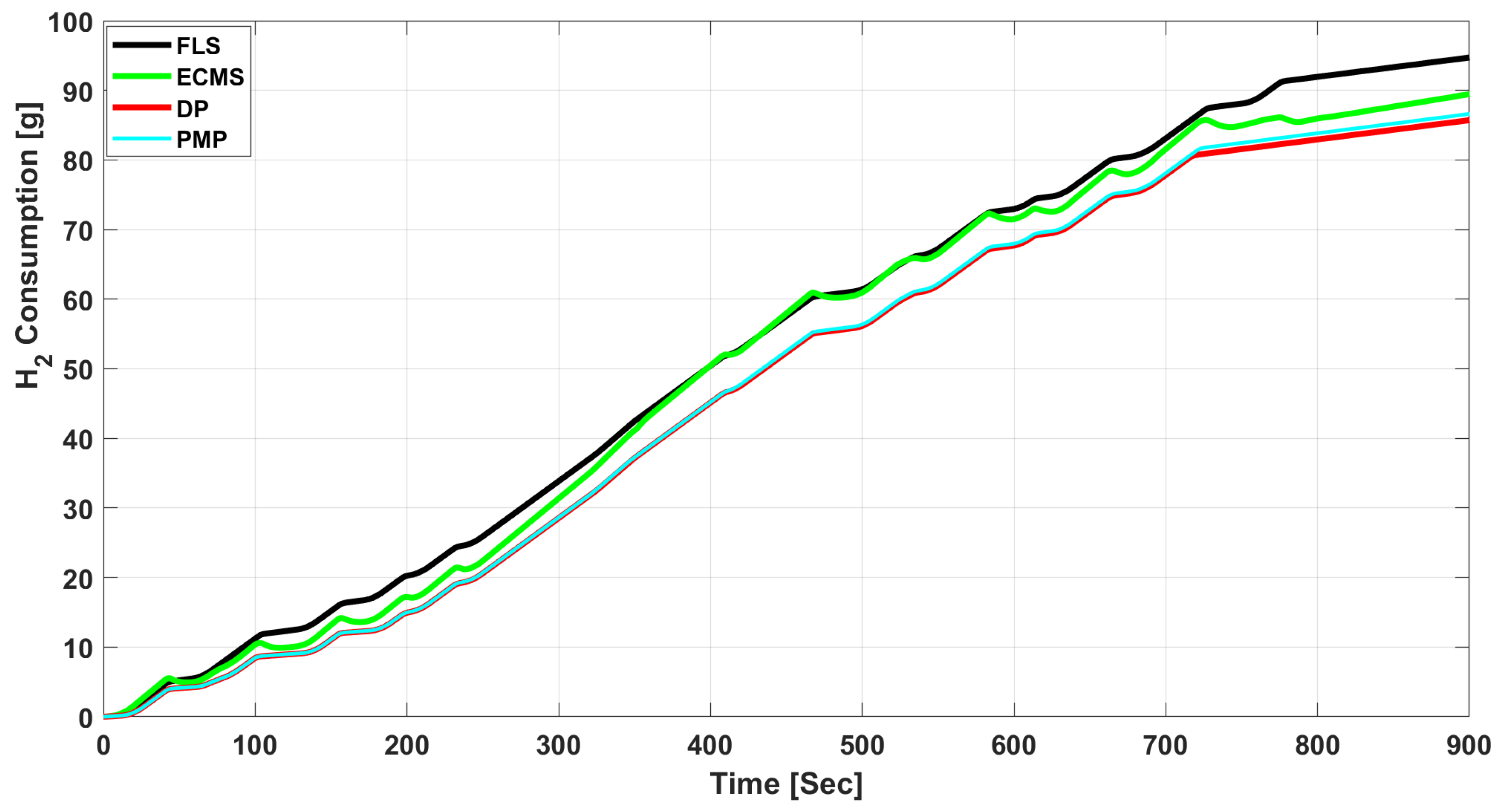
| DP Strategy | SOC [%] | Consumption [g] |
|---|---|---|
| Without FTC | 69.2654 | 90.000 |
| With FTC | 67.9912 | 84.3681 |
| EMS Strategy | SOC [%] | Consumption [g] | Economy (Relative to FLS) % |
|---|---|---|---|
| FLS | 66.8731 | 91.9412 | - |
| ECMS | 67.9528 | 85.9618 | 6.5035 |
| PMP | 67.9311 | 83.7993 | 8.8556 |
| DP | 67.9912 | 82.9303 | 9.8007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, C.; Kamal, E.; Ghorbani, R. Reliable Energy Optimization Strategy for Fuel Cell Hybrid Electric Vehicles Considering Fuel Cell and Battery Health. Energies 2024, 17, 4686. https://doi.org/10.3390/en17184686
Ji C, Kamal E, Ghorbani R. Reliable Energy Optimization Strategy for Fuel Cell Hybrid Electric Vehicles Considering Fuel Cell and Battery Health. Energies. 2024; 17(18):4686. https://doi.org/10.3390/en17184686
Chicago/Turabian StyleJi, Cong, Elkhatib Kamal, and Reza Ghorbani. 2024. "Reliable Energy Optimization Strategy for Fuel Cell Hybrid Electric Vehicles Considering Fuel Cell and Battery Health" Energies 17, no. 18: 4686. https://doi.org/10.3390/en17184686
APA StyleJi, C., Kamal, E., & Ghorbani, R. (2024). Reliable Energy Optimization Strategy for Fuel Cell Hybrid Electric Vehicles Considering Fuel Cell and Battery Health. Energies, 17(18), 4686. https://doi.org/10.3390/en17184686






