Comparative Analysis of PWM Techniques for Interleaved Full Bridge Converter in an AC Battery Application
Abstract
1. Introduction
2. PWM Method Principle
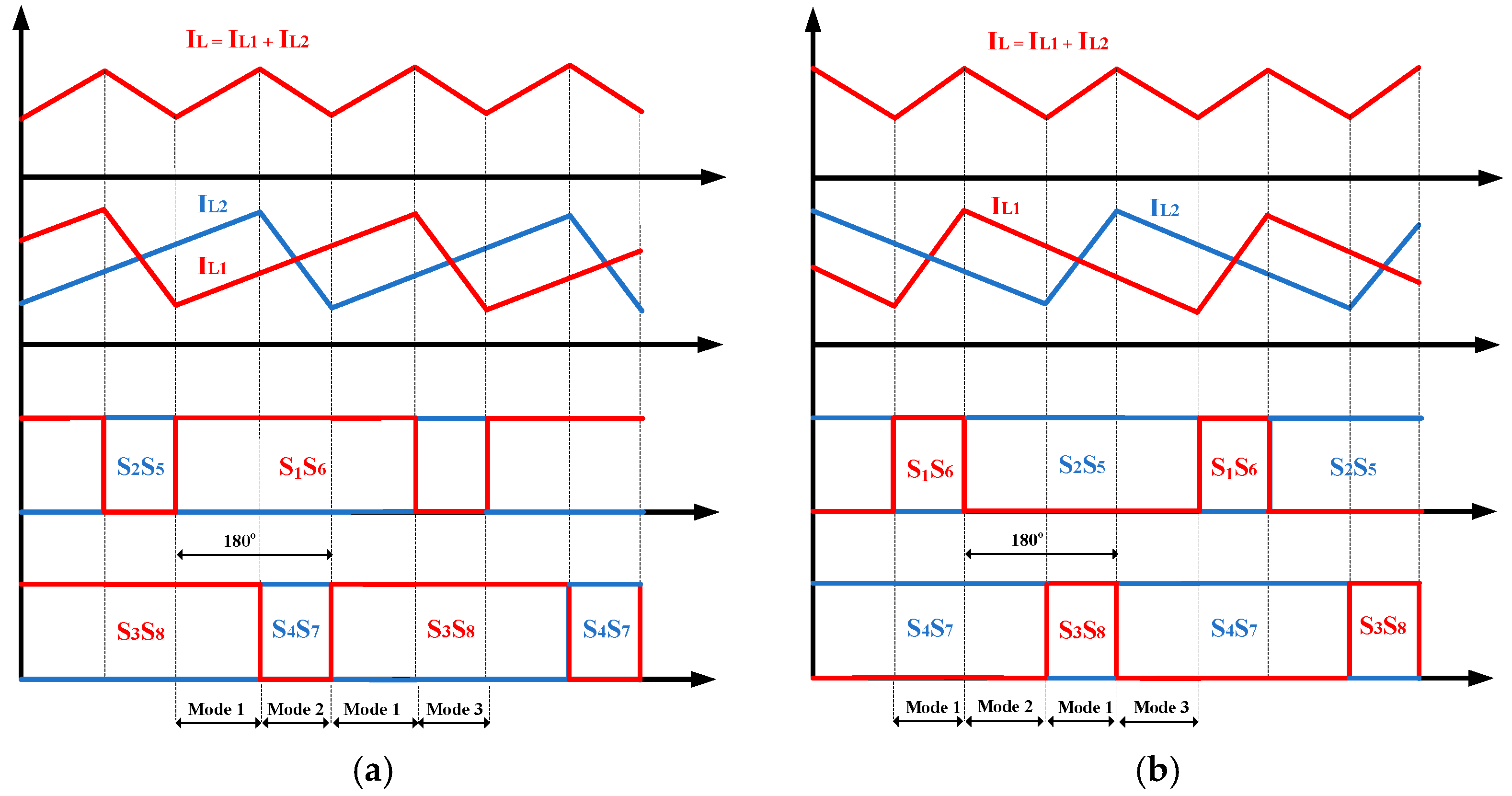
2.1. Interleaved Bipolar PWM
- Pulse pattern analysis
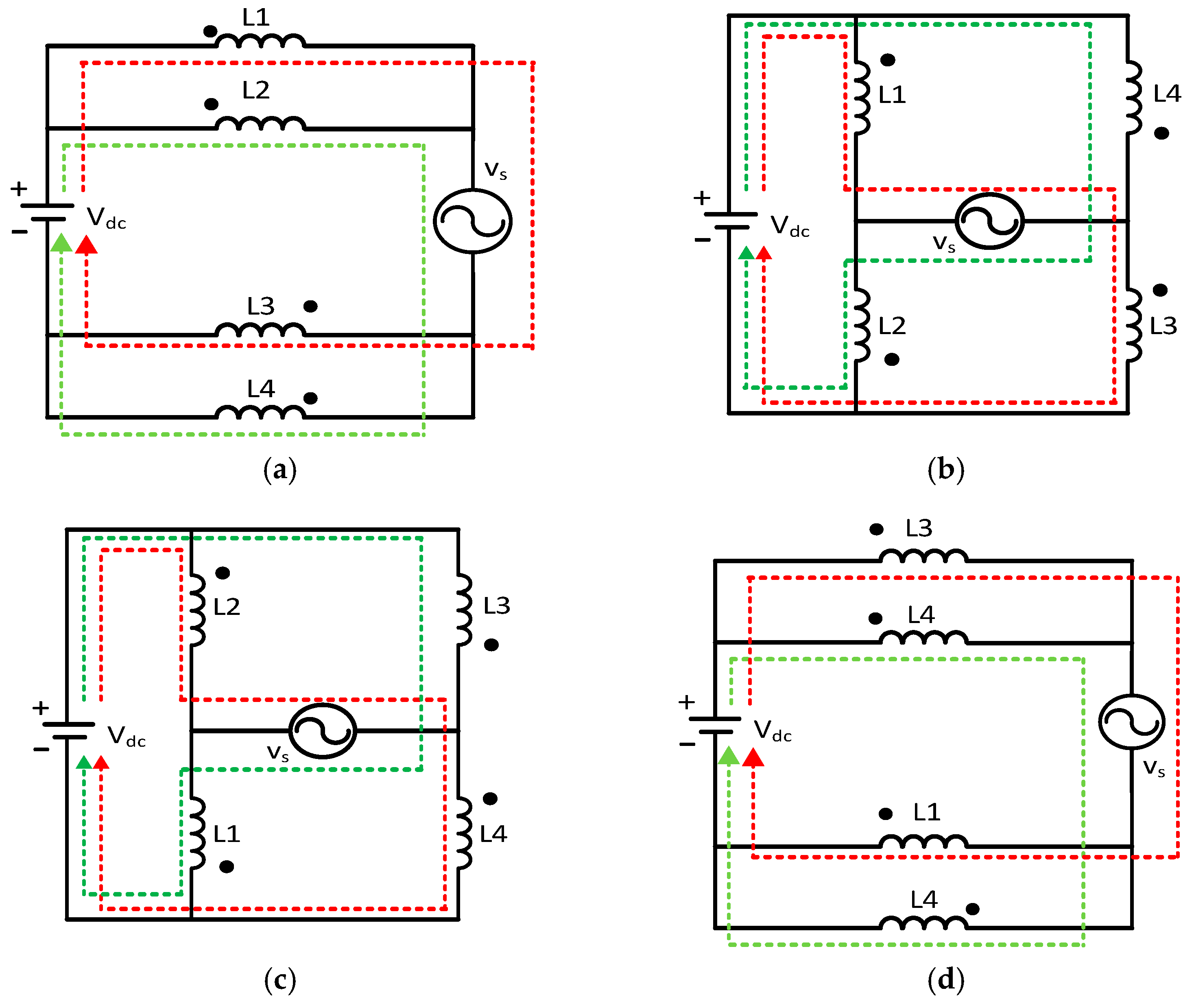
- Common-mode voltage analysis
- Ripple of the split-inductor current and the output current
- -
- With D > 0.5 (Vs > 0): The IFB converter works in modes 1, 2, and 3.
- -
- With D < 0.5 (Vs < 0): the IFB converter operates in modes 2, 3, and 4.
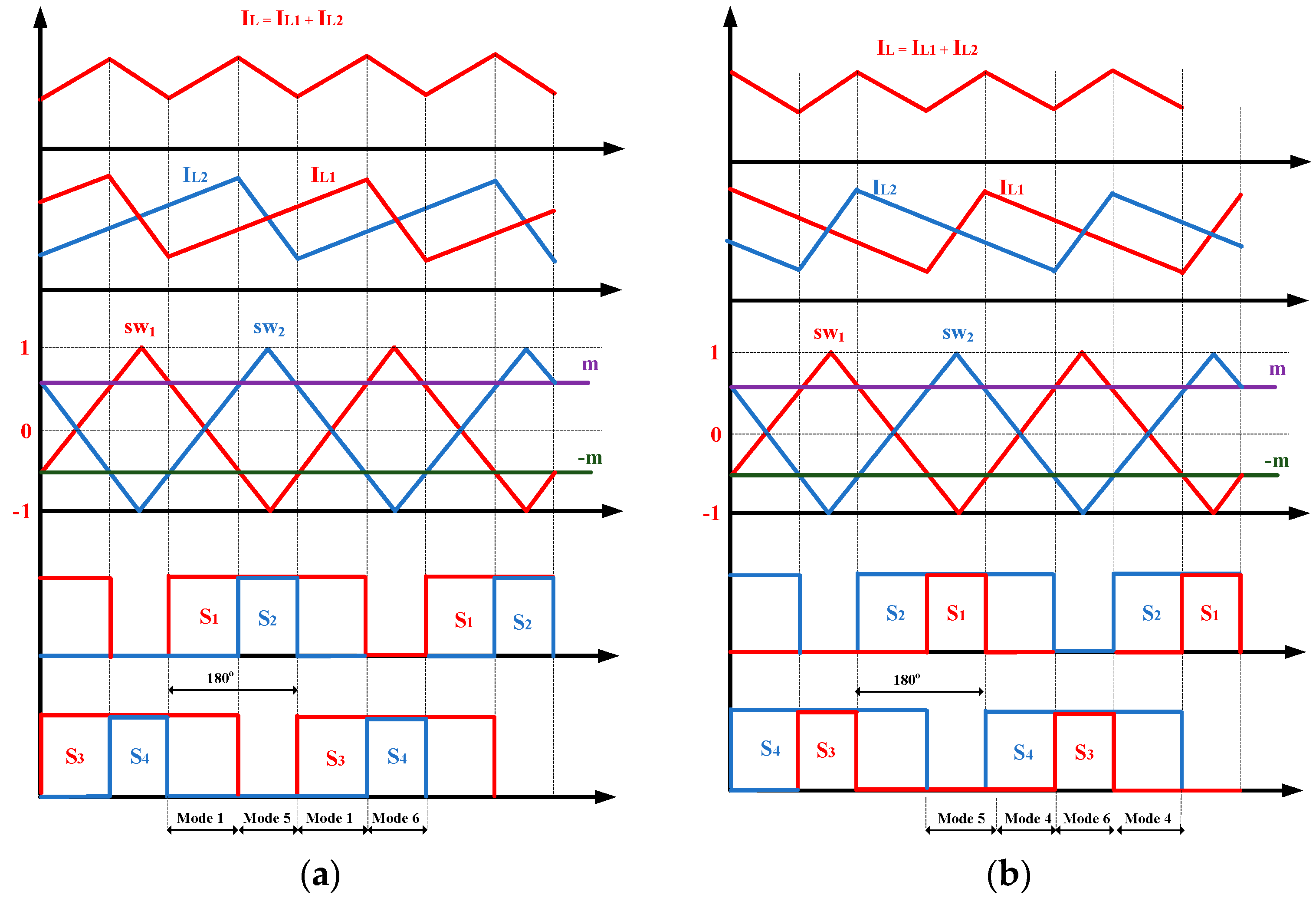
2.2. Interleaved Unipolar PWM
- Pulse pattern analysis
- Ripple of the split-inductor current and the output current
- -
- With D > 0.5 (Vs > 0): The IFB converter operates in modes 1, 5, and 6.
- -
- With D < 0.5 (Vs < 0): The IFB converter operates in modes 4, 5, and 6.
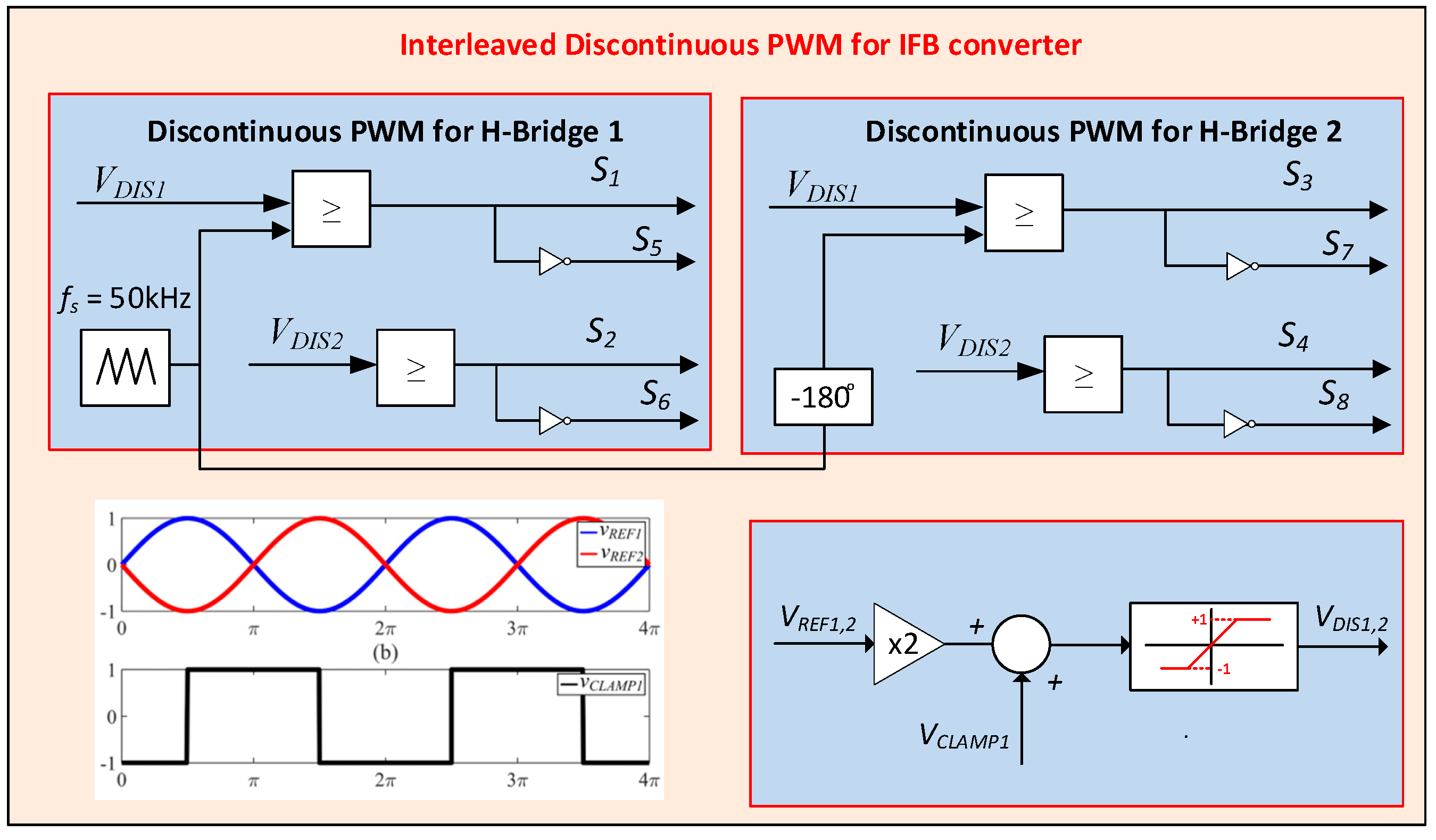
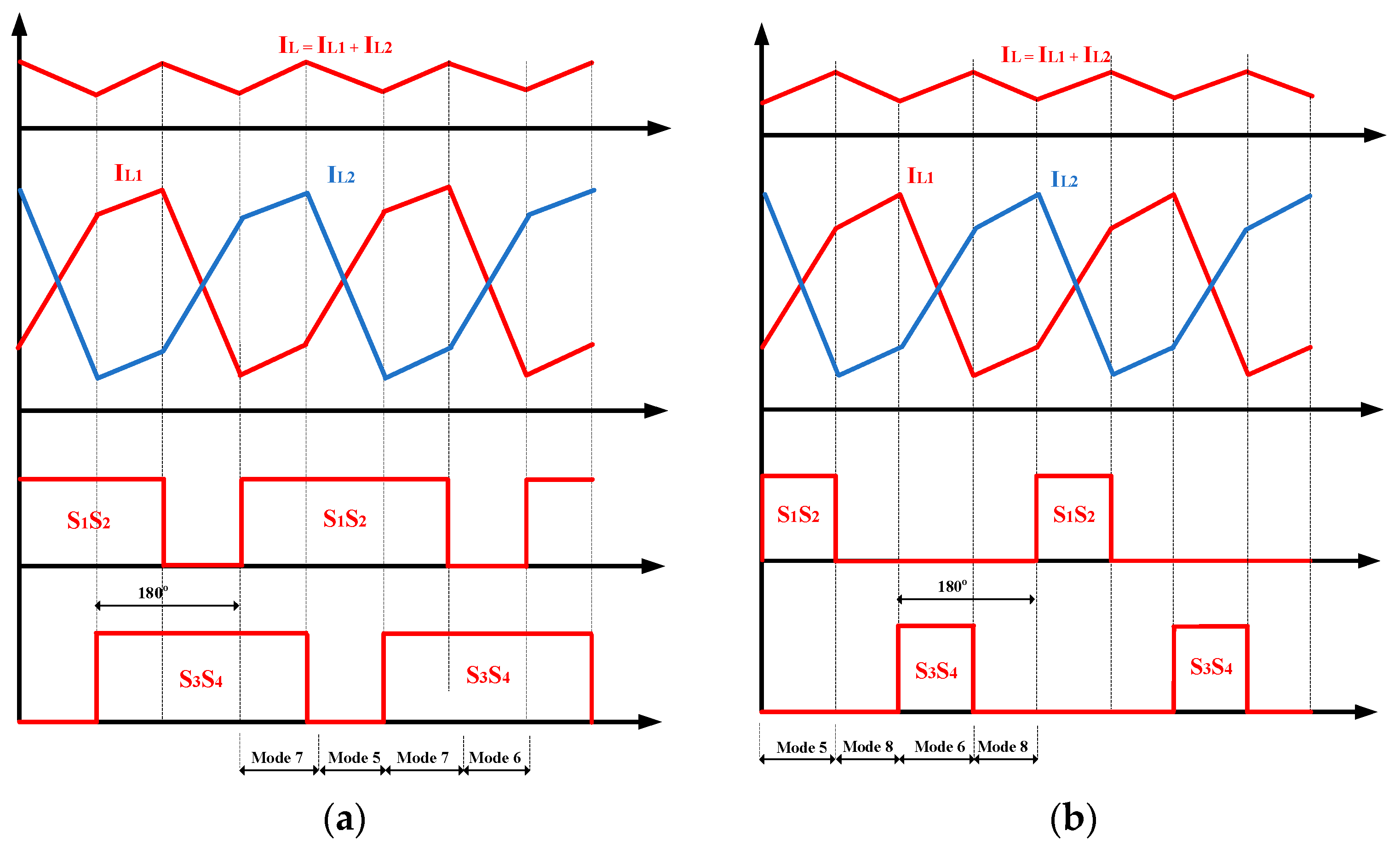
2.3. Interleaved Discontinuous PWM
- Pulse pattern analysis
- Common-mode voltage analysis
- Ripple of the split-inductor current and output current
- Non-switching interval: Due to the discontinuous PWM rule, all the upper switches S1, S2, S3, and S4 are on or off in this interval, hence, the currents through the four split-inductors are in phase and the current ripples seem to be zero.
- Switching interval: In some modes of this interval, the currents only flow through the inductor and Vs. Therefore, the sign of Vs decides whether the current increases or decreases. In this section, the current ripples are analyzed when Vs < 0, while the analysis when Vs > 0 is similar. Unlike the previous interleaved PWM method, the inductor currents with the ID-PWM increase or decrease with the different rates in the different modes.
- -
- With D > 0.5: The IFB converter operates in modes 5, 6, and 7.
- -
- With D < 0.5: The IFB converter operates in modes 5, 6, and 8.
2.4. Theorectical Comparion among Three Interleaved PWM Methods for the IFB Converter
3. Simulation Verification
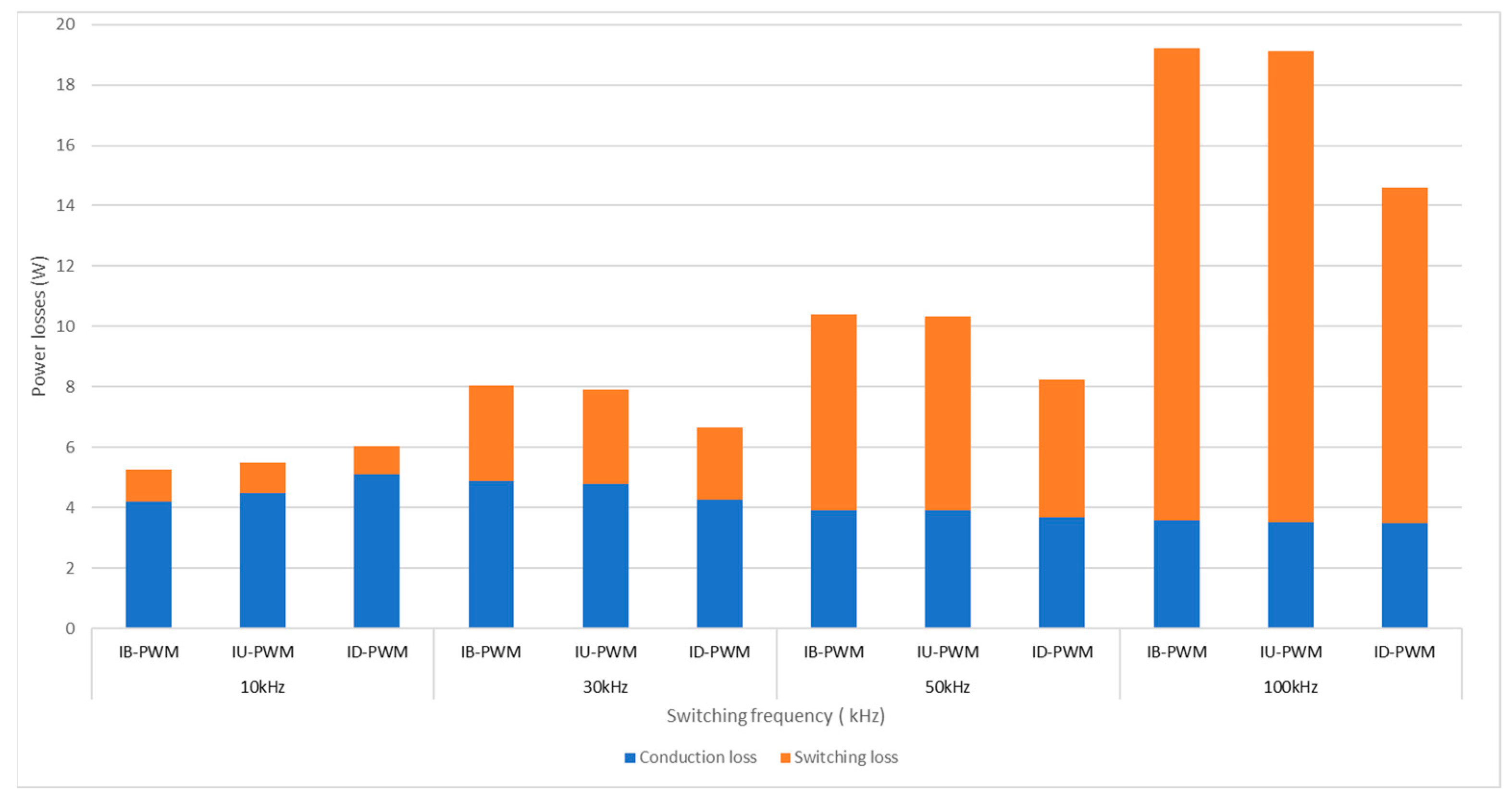
3.1. Power Losses Evaluation
- Scenario 1:
- Scenario 2:
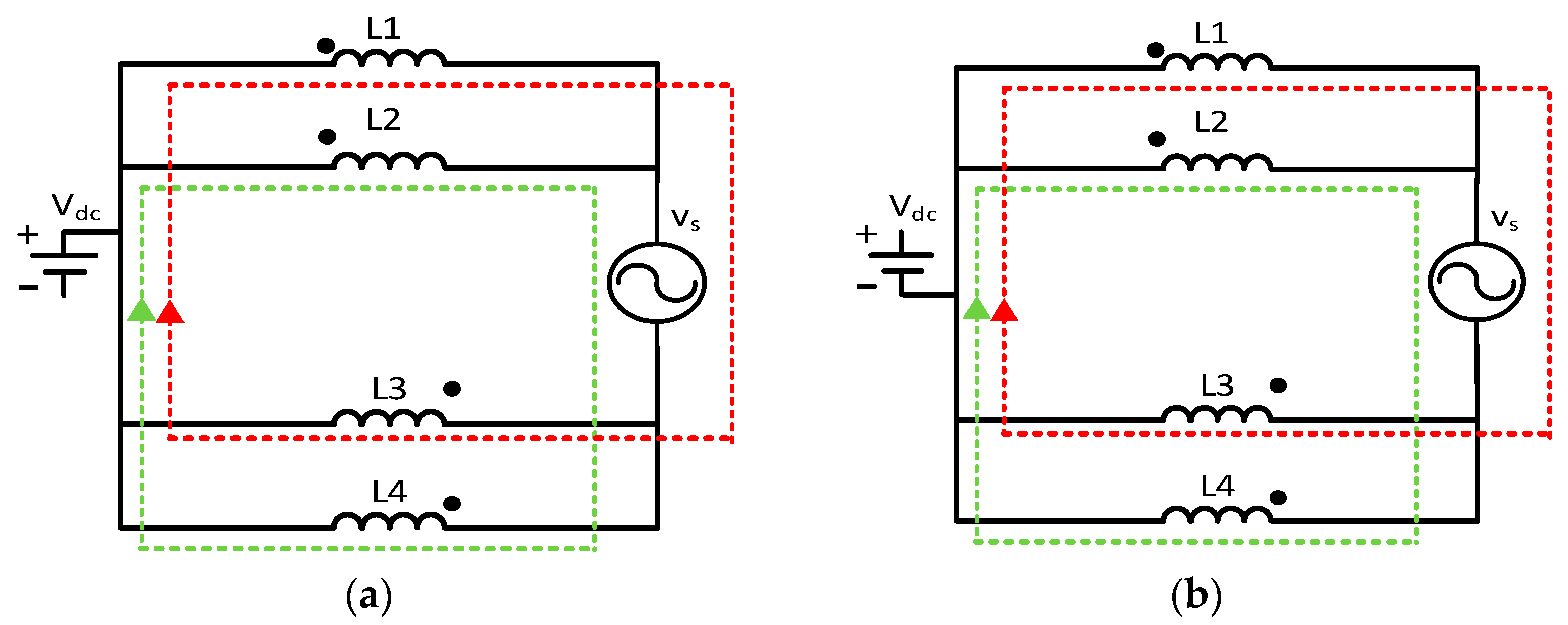
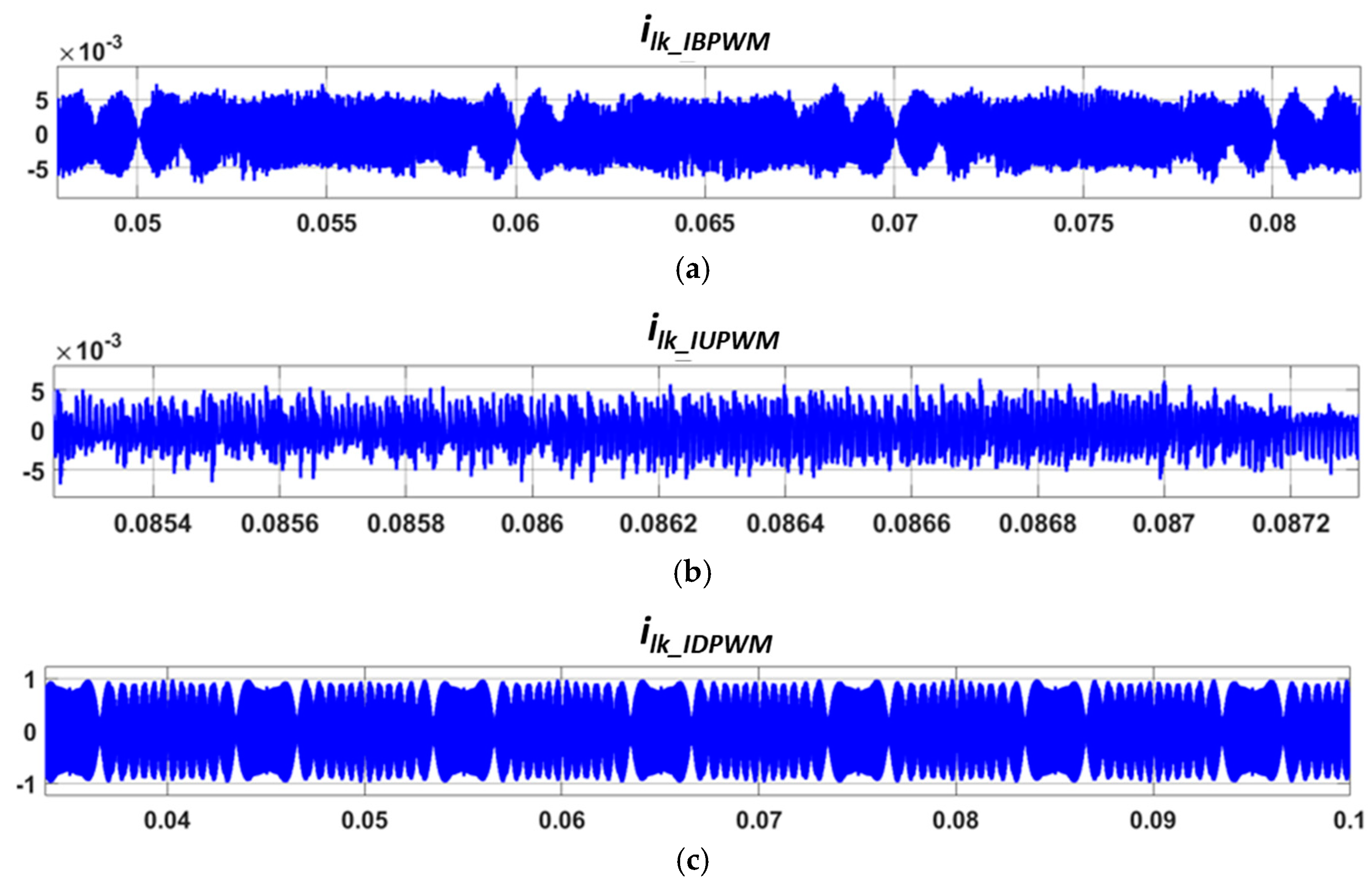
3.2. Leakage Current Comparisons
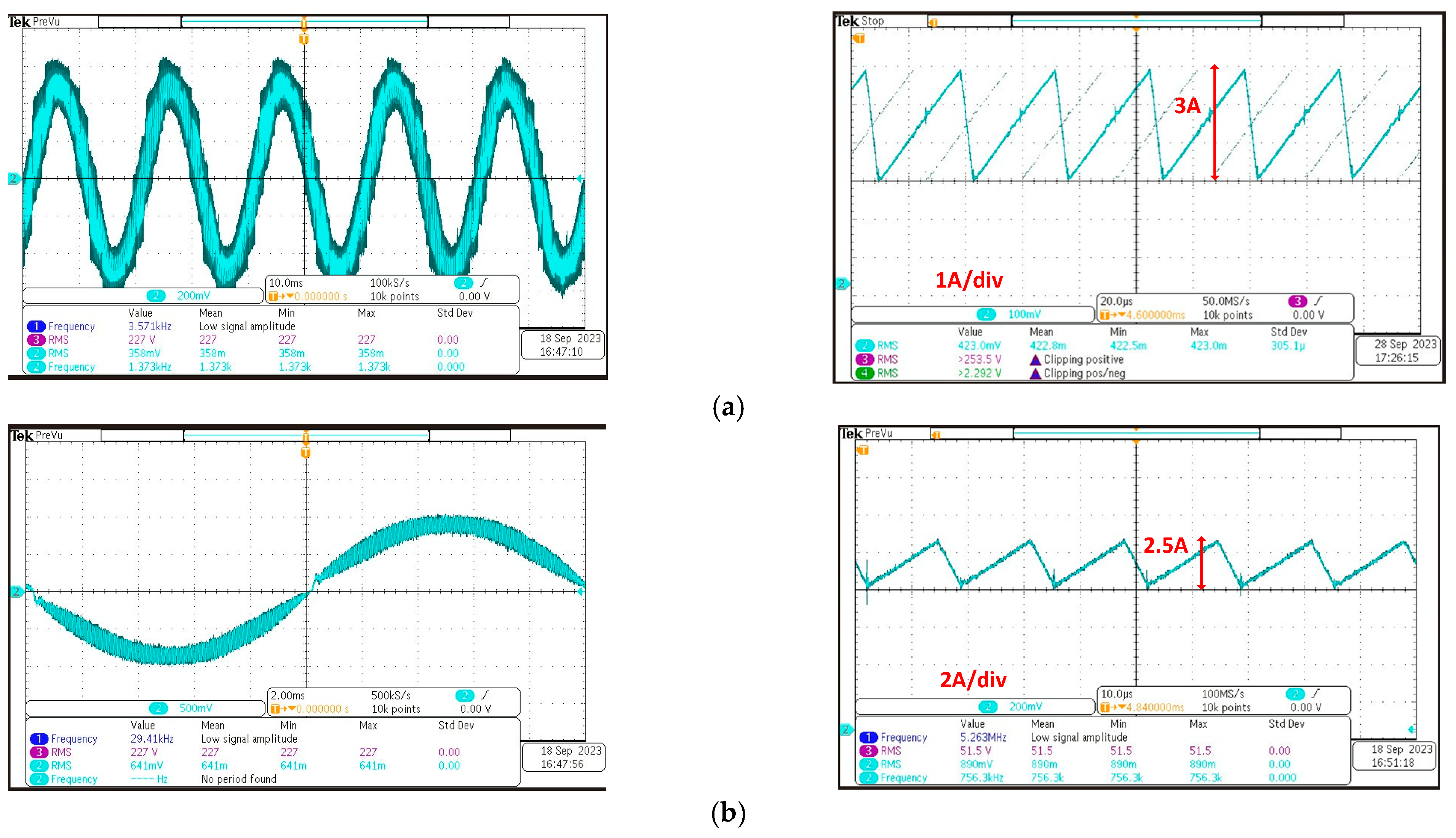
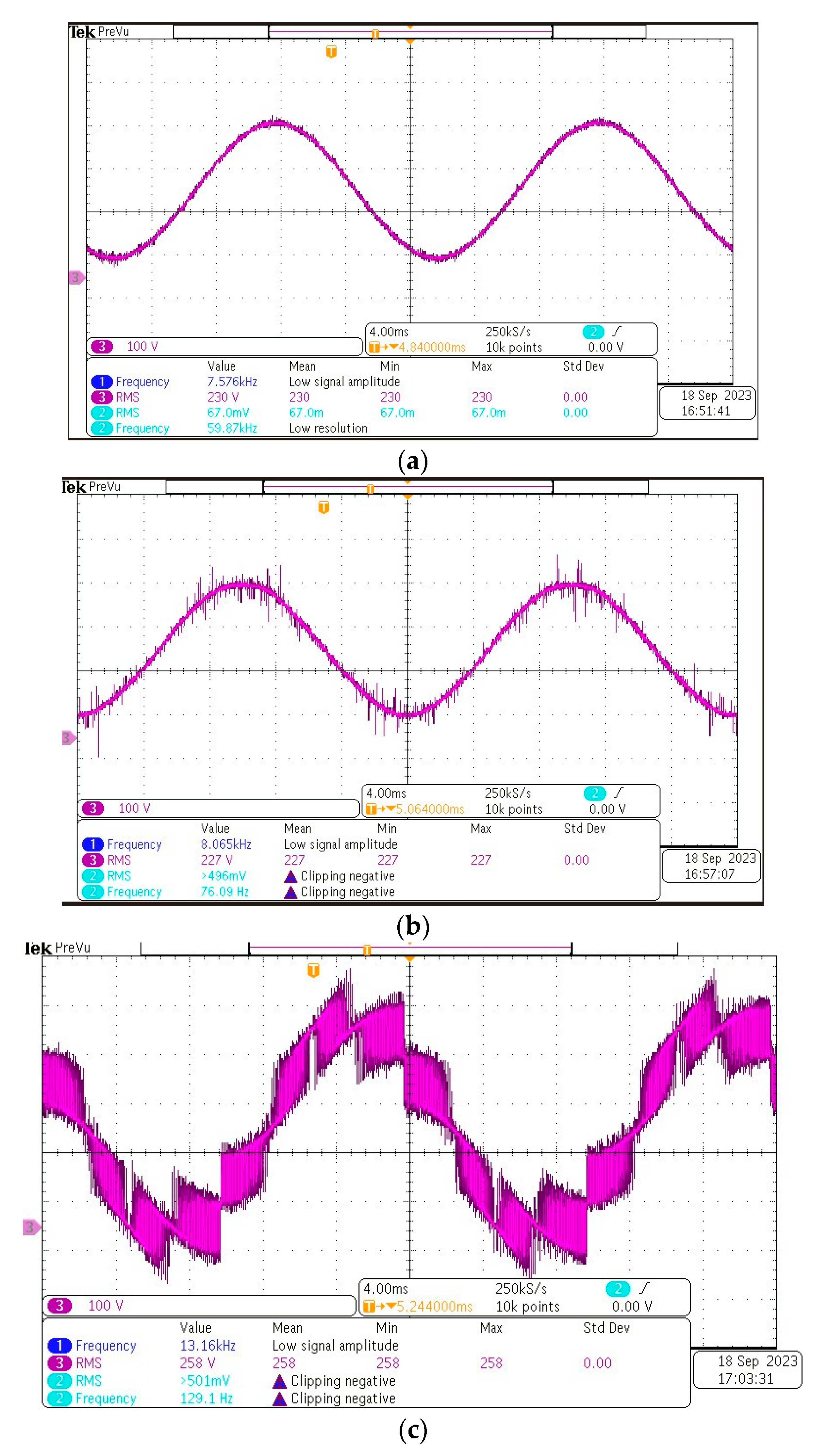
4. Experiment Verification
- Output current performance evaluation
- Common-mode voltage discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; He, S.; Yang, Q.; Wei, Z.; Li, Y.; He, H. A Comprehensive Review of Second Life Batteries Towards Sustainable Mechanisms: Potential, Challenges, and Future Prospects. IEEE Trans. Transp. Electrif. 2022, 9, 4824–4845. [Google Scholar] [CrossRef]
- Zhao, Y.; Pohl, O.; Bhatt, A.I.; Collis, G.E.; Mahon, P.J.; Rüther, T.; Hollenkamp, A.F. A Review on Battery Market Trends, Second-Life Reuse, and Recycling. Sustain. Chem. 2021, 2, 167–205. [Google Scholar] [CrossRef]
- Simatupang, D.; Benshatti, A.; Park, S.-Y. Embedded Electrochemical Impedance Spectroscopy into Battery Management System. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Hu, X.; Deng, X.; Wang, F.; Deng, Z.; Lin, X.; Teodorescu, R.; Pecht, M.G. A Review of Second-Life Lithium-Ion Batteries for Stationary Energy Storage Applications. Proc. IEEE 2022, 110, 735–753. [Google Scholar] [CrossRef]
- Yang, S.; Ma, X.; Bao, W.; Liu, J. Multiple-Function Control Strategy for Hybrid SLB-NB Energy Storage System. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 318–323. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Alyasseri, Z.A.A.; Abasi, A.K.; Khader, A.T.; Damaševičius, R.; Mohammed, M.A.; Abdulkareem, K.H. Smart Home Battery for the Multi-Objective Power Scheduling Problem in a Smart Home Using Grey Wolf Optimizer. Electronics 2021, 10, 447. [Google Scholar] [CrossRef]
- Zich, J.; Jandik, J. Active Battery Management System for Home Battery Energy Storage. In Proceedings of the 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 19–21 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, X. Research on the Participation of Household Battery Energy Storage in the Electricity Peak Regulation Ancillary Service Market. Processes 2023, 11, 794. [Google Scholar] [CrossRef]
- Inamdar, S.; Thosar, A.; Mante, S. Literature Review of 3.3kW On Board Charger Topologies. In Proceedings of the 2019 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 276–281. [Google Scholar]
- FMusavi, F.; Eberle, W.; Dunford, W.G. A high-performance single-phase AC-DC power factor corrected boost converter for plug in hybrid electric vehicle battery chargers. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3588–3595. [Google Scholar] [CrossRef]
- Xia, Y.; Ayyanar, R. Comprehensive comparison of THD and common mode leakage current of bipolar, unipolar and hybrid modulation schemes for single phase grid connected full bridge inverters. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 743–750. [Google Scholar] [CrossRef]
- Marandi, D.; Sowmya, T.N.; Babu, B.C. Comparative study between unipolar and bipolar switching scheme with LCL filter for single-phase grid connected inverter system. In Proceedings of the 2012 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Awais, M.; Yasin, A.R.; Riaz, M.; Saqib, B.; Zia, S.; Yasin, A. Robust Sliding Mode Control of a Unipolar Power Inverter. Energies 2021, 14, 5405. [Google Scholar] [CrossRef]
- Algaddafi, A.; Elnaddab, K.; Ma’Mari, A.; Esgiar, A.N. Comparing the Performance of Bipolar and Unipolar Switching Frequency to Drive DC-AC Inverter. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference, Marrakech, Morocco, 14–17 November 2016. [Google Scholar] [CrossRef]
- Behera, P.K.; Das, S.; Pattnaik, M. Performance Comparison Between Bipolar and Unipolar Switching Scheme for a Single-Phase Inverter Based Stand-alone Photovoltaic System. In Proceedings of the 2019 IEEE 16th India Council International Conference, Rajkot, India, 13–15 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Ferrer-Arnau, L.; Berbel, N.; Capella, G.J.; Zaragoza, J. Study of modulation techniques applied to full bridge single-phase inverters based on wide-bandgap semiconductors. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 2032–2037. [Google Scholar] [CrossRef]
- Fernandez, M.; Robles, E.; Aretxabaleta, I.; Kortabarria, I.; Martín, J.L. Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation. Machines 2023, 11, 404. [Google Scholar] [CrossRef]
- Hossameldin, A.A.; Abdelsalam, A.K.; Ibrahim, A.A.; Williams, B.W. Enhanced Performance Modified Discontinuous PWM Technique for Three-Phase Z-Source Inverter. Energies 2020, 13, 578. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Xing, Y.; Zhao, J. Parallel Operation of Modular Single-Phase Transformerless Grid-Tied PV Inverters with Common DC Bus and AC Bus. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 858–869. [Google Scholar] [CrossRef]
- Kiranmai, K.S.P.; Damodaran, R.V.; Hushki, M.; Shareef, H. An alternate hybrid PWM for uniform thermal sharing in single phase voltage-source inverter. Sci. Rep. 2023, 13, 3348. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.elipse.eu/wp-content/uploads/2020/10/White-Paper-Safety-Standards-Elipse-Oct-2020.pdf (accessed on 1 September 2023).
- Yang, Y.; Blaabjerg, F.; Wang, H. Low voltage ride-through of single-phase transformerless photovoltaic inverters. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 4762–4769. [Google Scholar] [CrossRef]
- Trzynadlowski, A.M. EMI Effects of power converters. In Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Wu, W.; Sun, Y.; Lin, Z.; He, Y.; Huang, M.; Blaabjerg, F.; Chung, H.S.-H. A Modified LLCL Filter With the Reduced Conducted EMI Noise. IEEE Trans. Power Electron. 2014, 29, 3393–3402. [Google Scholar] [CrossRef]
- Hedayati, M.H.; John, V. EMI and Ground Leakage Current Reduction in Single-Phase Grid-Connected Power Converter. IET Power Electron. 2017, 10, 938–944. [Google Scholar] [CrossRef]
- Figueredo, R.S.; de Carvalho, K.C.M.; Matakas, L. Integrated common and differential mode filter applied to a single-phase transformerless PV microinverter with low leakage current. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 2618–2625. [Google Scholar]
- Barater, D.; Buticchi, G.; Lorenzani, E.; Concari, C. Active common-mode filter for ground leakage current reduction in grid-connected PV converters operating with arbitrary power factor. IEEE Trans. Ind. Electron. 2014, 61, 3940–3950. [Google Scholar] [CrossRef]
- Barater, D.; Buticchi, G.; Crinto, A.S.; Franceschini, G.; Lorenzani, E. A New Proposal for Ground Leakage Current Reduction in Transformerless Grid-Connected Converters for Photovoltaic Plants. In Proceedings of the 35th Annual Conference of IEEE Industrial Electronics (IECON), Porto, Portugal, 3–5 November 2009; pp. 4567–4572. [Google Scholar]
- Gonzalez, R.; Lopez, J.; Sanchis, P.; Marroyo, L. Transformerless inverter for single-phase photovoltaic systems. IEEE Trans. Power Electron. 2007, 22, 693–697. [Google Scholar] [CrossRef]











| Mode | H-Bridge 1 | H-Bridge 2 | Method |
|---|---|---|---|
| 1 | S1 on, S2 off, S5 off, S6 on | S3 on, S4 off, S7 off, S8 on | IB-PWM 1,2, IU-PWM 1 |
| 2 | S1 on, S2 off, S5 off, S6 on | S3 off, S4 on, S7 on, S8 off | IB-PWM 1,2 |
| 3 | S1 off, S2 on, S5 on, S6 off | S3 on, S4 off, S7 off, S8 on | IB-PWM 1,2 |
| 4 | S1 off, S2 on, S5 on, S6 off | S3 off, S4 on, S7 on, S8 off | IB-PWM 1,2, IU-PWM 2 |
| 5 | S1 on, S2 on, S5 off, S6 off | S3 off, S4 off, S7 on, S8 on | IU-PWM 1,2,ID-PWM 2 |
| 6 | S1 off, S2 off, S5 on, S6 on | S3 on, S4 on, S7 off, S8 off | IU-PWM 1, ID-PWM 2 |
| 7 | S1 on, S2 on, S5 off, S6 off | S3 on, S4 on, S7 off, S8 off | ID-PWM 1 |
| 8 | S1 off, S2 off, S5 on, S6 on | S3 off, S4 off, S7 on, S8 on | ID-PWM 2 |
| Pulse Width Modulation Method | ||||
|---|---|---|---|---|
| Criteria | IB-PWM | IU-PWM | ID-PWM | |
| Parameter | Unit | Value |
|---|---|---|
| Nominal power | kW | 10 |
| AC voltage | V | 220 |
| AC frequency | Hz | 50 |
| DC voltage | V | 400 |
| Switching frequency | kHz | 30 |
| L filter | μH | 330 |
| DC-link capacitor | μF | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, T.A.; Nguyen, Q.D.; Vu, P.; Ngo, M.D.; Ahn, S.-J. Comparative Analysis of PWM Techniques for Interleaved Full Bridge Converter in an AC Battery Application. Energies 2024, 17, 375. https://doi.org/10.3390/en17020375
Do TA, Nguyen QD, Vu P, Ngo MD, Ahn S-J. Comparative Analysis of PWM Techniques for Interleaved Full Bridge Converter in an AC Battery Application. Energies. 2024; 17(2):375. https://doi.org/10.3390/en17020375
Chicago/Turabian StyleDo, Tuan Anh, Quang Dich Nguyen, Phuong Vu, Minh Duc Ngo, and Seon-Ju Ahn. 2024. "Comparative Analysis of PWM Techniques for Interleaved Full Bridge Converter in an AC Battery Application" Energies 17, no. 2: 375. https://doi.org/10.3390/en17020375
APA StyleDo, T. A., Nguyen, Q. D., Vu, P., Ngo, M. D., & Ahn, S.-J. (2024). Comparative Analysis of PWM Techniques for Interleaved Full Bridge Converter in an AC Battery Application. Energies, 17(2), 375. https://doi.org/10.3390/en17020375






