Evaluation of a Simplified Model for Three-Phase Equilibrium Calculations of Mixed Gas Hydrates

Abstract

In this study, we perform an extensive evaluation of a simple model for hydrate equilibrium calculations of binary, ternary, and limited quaternary gas hydrate systems that are of practical interest for separation of gas mixtures. We adopt the model developed by Lipenkov and Istomin and analyze its performance at temperature conditions higher than the lower quadruple point. The model of interest calculates the dissociation pressure of mixed gas hydrate systems using a simple combination rule that involves the hydrate dissociation pressures of the pure gases and the gas mixture composition, which is at equilibrium with the aqueous and hydrate phases. Such an approach has been used extensively and successfully in polar science, as well as research related to space science where the temperatures are very low. However, the particular method has not been examined for cases of higher temperatures (i.e., above the melting point of the pure water). Such temperatures are of interest to practical industrial applications. Gases of interest for this study include eleven chemical components that are related to industrial gas-mixture separations. Calculations using the examined methodology, along with the commercial simulator CSMGem, are compared against experimental measurements, and the range of applicability of the method is delineated. Reasonable agreement (particularly at lower hydrate equilibrium pressures) between experiments and calculations is obtained considering the simplicity of the methodology. Depending on the hydrate-forming mixture considered, the percentage of absolute average deviation in predicting the hydrate equilibrium pressure is found to be in the range 3–91%, with the majority of systems having deviations that are less than 30%.

1. Introduction

Under conditions of low temperatures or high pressures, water molecules can self-assemble in forming three-dimensional crystalline structures that contain cavities/cages. These cavities can be stabilized if a fraction (i.e., rendering hydrate non-stoichiometric materials) of them, which belong to the hydrate crystal unit cell, are occupied by certain types of guest molecules that have an appropriate size to fit within them (e.g., CH₄, CO₂, N₂, etc.). Such ice-like, solid materials are known as clathrate hydrates or simply “hydrates” [1,2,3].

Hydrates are very important compounds due to their involvement in a number of major energy-related industrial [4,5,6,7,8] and environmental [9,10] applications. Depending on the particular application, the appearance/formation of hydrates can be seen either as a major nuisance or as acting beneficially for the process of interest.

For example, hydrate formation is a major concern for safety and flow assurance in gas/oil pipelines [11,12,13], as well as unit operations where pressure and temperature conditions exist, such that hydrate formation is possible [3]. Significant effort and financial resources are dedicated in order to either completely avoid hydrate formation or to effectively control hydrate formation and the subsequent hydrate particle agglomeration. In a related context, during oil/gas exploration/exploitation operations, drilling through hydrate layers requires special care, since uncontrolled hydrate dissociation can be the cause of serious industrial accidents [14,15].

On the other hand, the hydrate characteristic to incorporate/store large volumes of gases within the hydrate crystal can be beneficial. In particular, hydrates are studied as a possible source of energy [4,5,6,7], since an enormous amount of carbon is deposited in worldwide accumulations of hydrates, containing predominantly methane, both on-shore (under the permafrost), and off-shore (in marine sediments). The recoverable amount of methane is, however, an issue that is currently under debate [16,17,18]. Methane production from the dissociation of hydrates confined within marine sediments requires a better understanding of the interactions between the dissociation thermodynamics occurring under different types of confinement, hydrate saturations, and the different production schemes (i.e., depressurization, thermal stimulation, hydrate inhibitor injection) [19,20,21,22,23]. Significant challenges need to be addressed in an adequate manner in order to incorporate hydrate deposits into the future energy mix in use [7,24]. Furthermore, hydrates can be used for storage and transportation of “energy carrier” gases (e.g., methane [25,26], hydrogen [27,28,29]). The characteristic of hydrates to selectively incorporate gases in their solid structure has been considered in order to achieve gas-mixture separation [30,31,32,33]. Similarly, the exclusion of ions from the hydrate crystals makes the use of hydrate-based technologies attractive for water desalination as well [34,35].

The particular aspect of hydrates to selectively incorporate gases in their solid structure and its use in hydrate-based applications for gas-mixture separations is the main focus of the current study. In order to design gas-mixture separation processes, such as natural gas purification or CO₂ capture from flue-gas streams that are based on hydrates, accurate thermodynamic, transport, and kinetic properties are required for all the involved pure components and their mixtures [8]. As discussed extensively in [36,37], there are three major approaches that have been employed in order to obtain such properties, namely, (i) experimental measurements, (ii) atomistic scale simulations, and (iii) continuum-scale theories. It should be noted that each one of the approaches for property estimation has advantages and disadvantages, including the following:

(i)

When fluid mixtures are involved, performing experiments that consider all the possible mixture compositions can be significantly expensive and time-consuming. Therefore, it is of utmost importance to develop alternative thermodynamic tools that can be used to calculate the required properties of the pure components and their mixtures. Such are the cases of atomistic scale simulations, and the models based on continuum-scale theories.

(ii)

Molecular simulations (e.g., Molecular Dynamics [38,39,40,41,42,43,44,45,46] or Monte Carlo [47,48,49,50,51,52,53,54,55,56,57] simulations) can use very detailed physics at the microscopic level; however, they are very computationally demanding, and therefore, the size of the system under consideration is very small, and the considered times are usually short (e.g., up to several microseconds). Therefore, such types of simulations are hard to use during process design or process-optimization schemes.

(iii)

Models based on continuum-scale (macroscopic) theories, which are related to hydrate-forming systems, include those developed for the calculation of the three-phase (Hydrate–Liquid water–Vapor; H–L_w–V) equilibrium pressure and temperature conditions via a methodology that couples the van der Waals and Platteeuw statistical theory [58] with an Equation of State (EoS) [59,60,61,62,63,64]. The particular coupling is considered as one of the best examples of the application of Statistical Thermodynamic Theory toward the solution of a real industrial problem. Parrish and Prausnitz [59] pioneered the earlier development of the methodology, and an extensive review of the earlier studies was provided by Holder et al. [61] and Englezos [65]. While a significant number of studies considered the use of cubic EoS [59,60,61,62,66,67,68,69,70], during recent years, non-cubic EoS (e.g., SAFT-type [63,64,71,72]) has also been considered. Medeiros et al. [73] and Khan et al. [74] provided comprehensive reviews of hydrate equilibrium calculations using the van der Waals–Platteeuw theory, while the aspects of the particular theory under confinement have been discussed in [19,75].

A major requirement of the macroscopic tools developed for hydrate equilibrium calculations, in addition to their accuracy, is their computational efficiency. An accurate and computationally fast tool, at the macroscopic level, can be used for initial screening purposes in the optimization of a given separation process. Therefore, the motivation of the current study is to identify/develop such a reliable macroscopic tool that can accurately describe the hydrate equilibrium pressure of hydrates of gas mixtures, while being computationally efficient.

The objective of the current study is to perform an extensive evaluation of a simple model for three-phase equilibrium calculations of mixed gas hydrates that are of practical interest for gas-mixture separations. The model considered in this study calculates the equilibrium pressure of the mixed gas hydrate using a simple combination rule that employs (i) the hydrate dissociation pressures of the pure gases involved, and (ii) the gas mixture composition. In particular, we examine the methodology presented by Lipenkov and Istomin [76]. The particular approach has been used extensively and successfully in polar science studies [76,77], as well as research related to space science [78,79] where the temperatures are very low (i.e., below the freezing point of pure water, which is also close to the lower quadruple point, Q₁, of the corresponding hydrate systems). However, to the best of our knowledge, the particular method has not been examined systematically for cases of higher temperatures (i.e., above the Q₁), which are going to be of interest to practical industrial applications of gas-mixture separations. Gases of interest for the current study include those that are indicated in

Table 1. Parameters for the correlation of the dissociation pressure of pure gases using Equation (3). Temperature is in K and pressure is in kPa. T range denotes the temperature range of applicability of the parameters. N/A denotes not applicable.

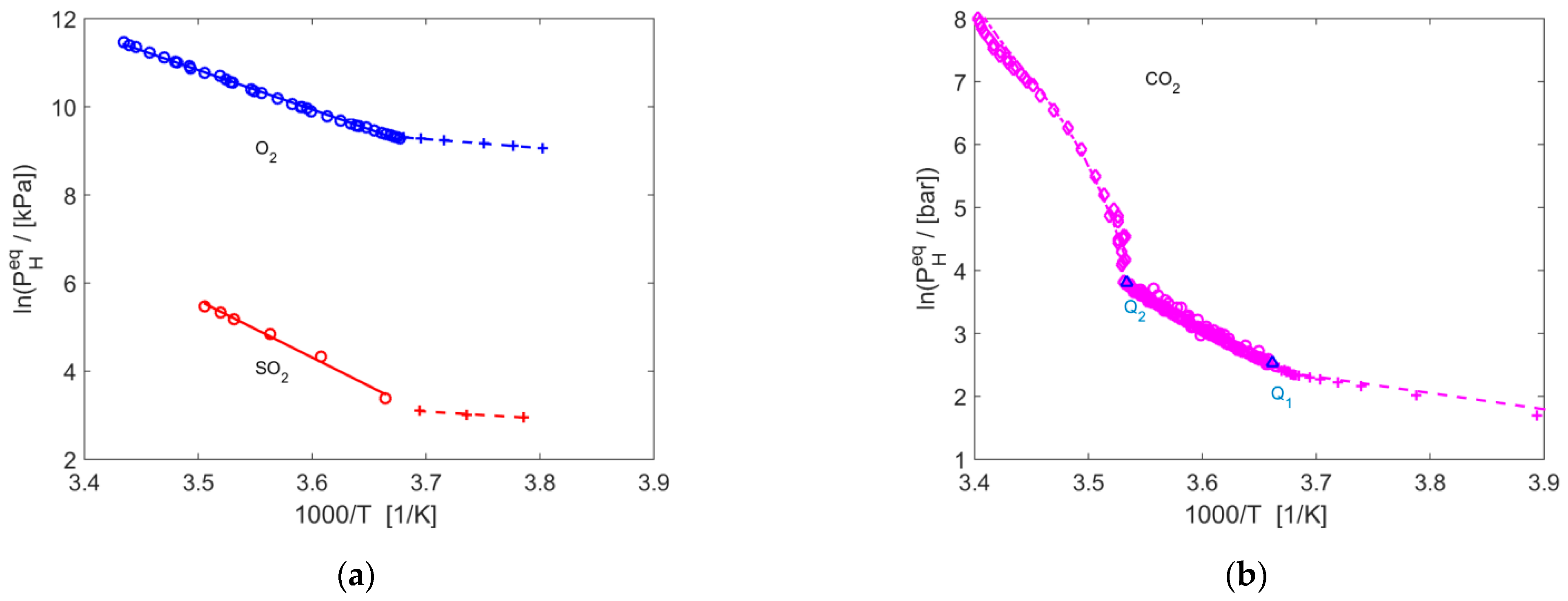
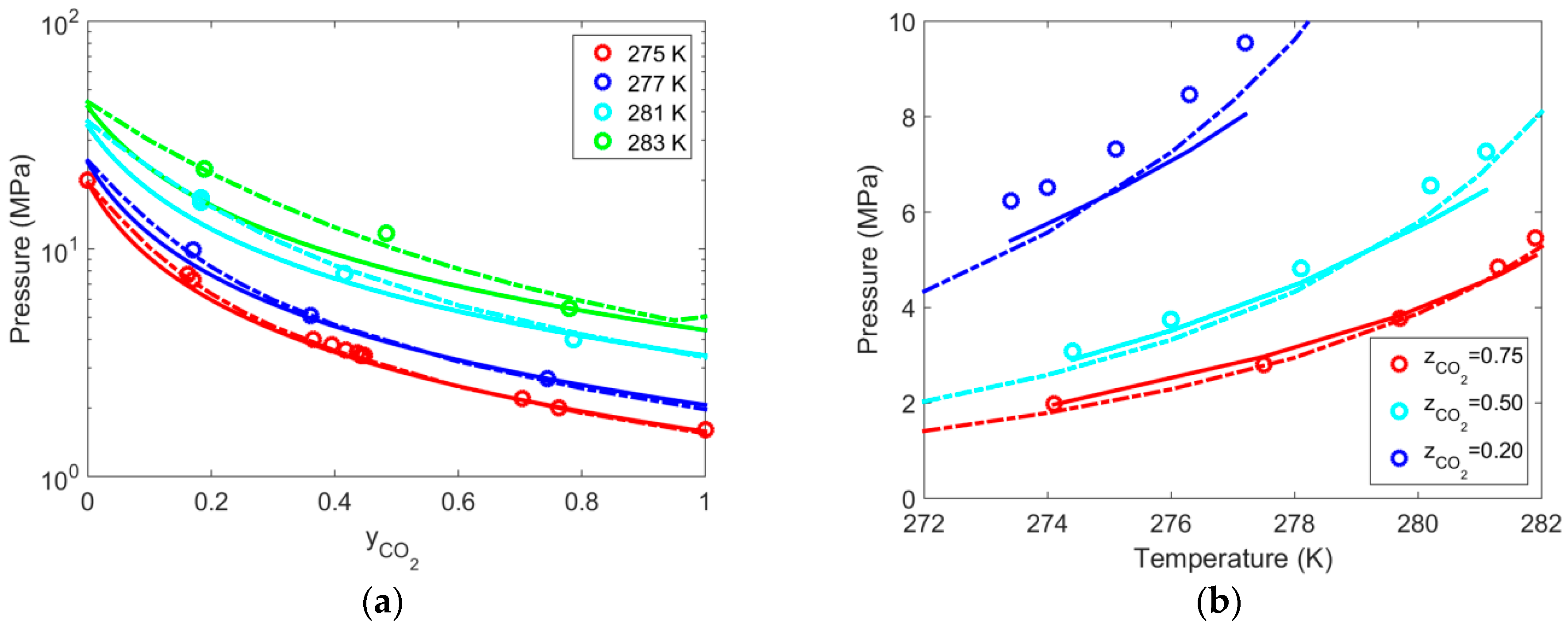
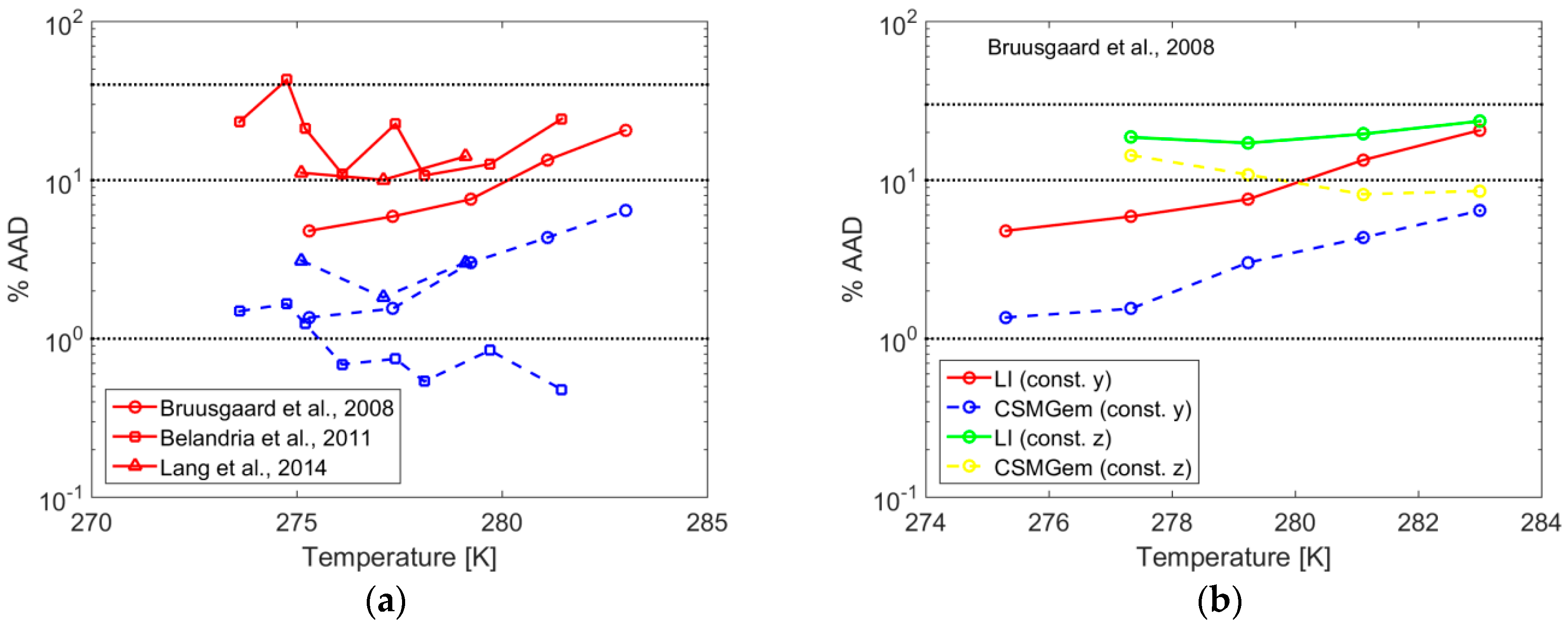
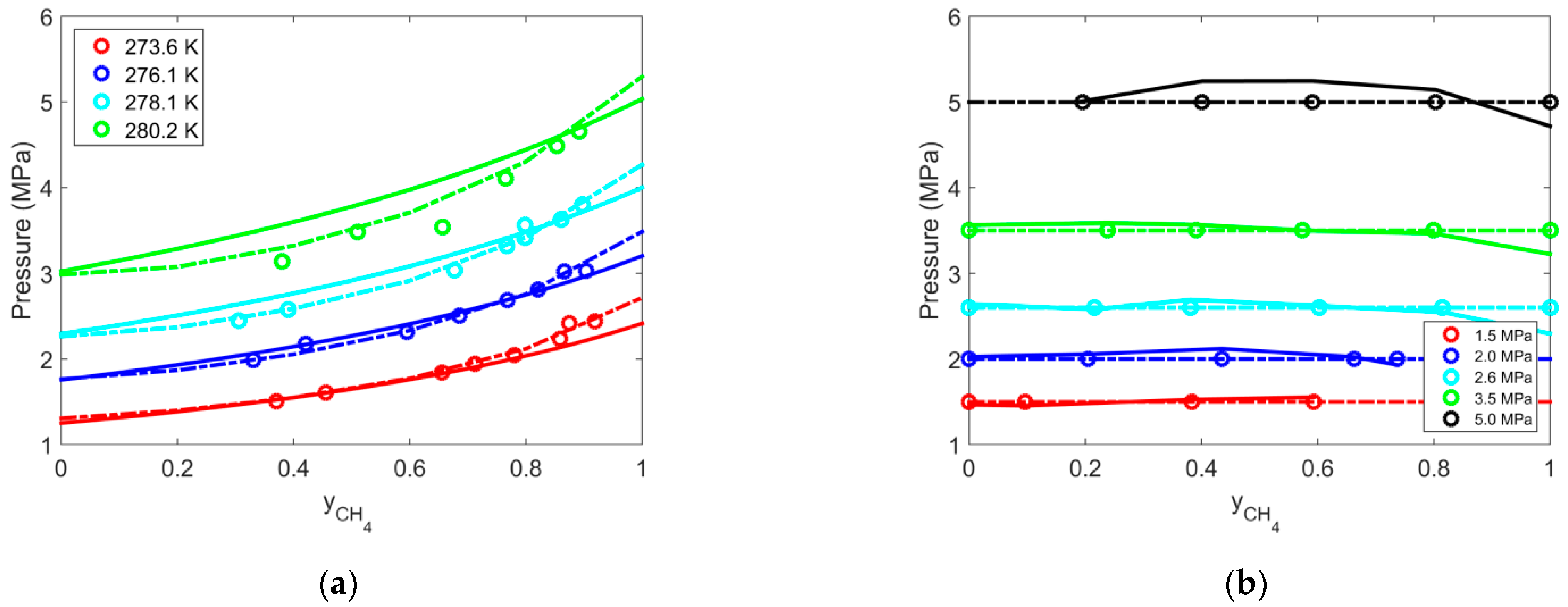
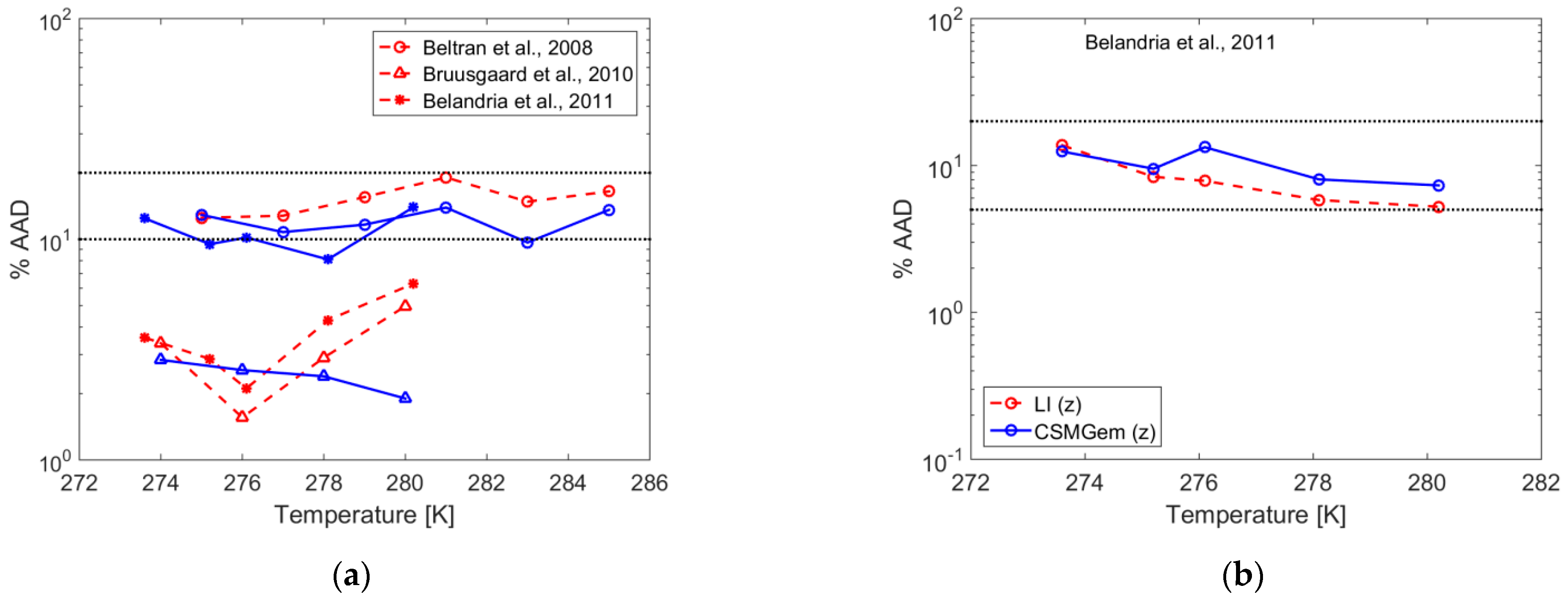
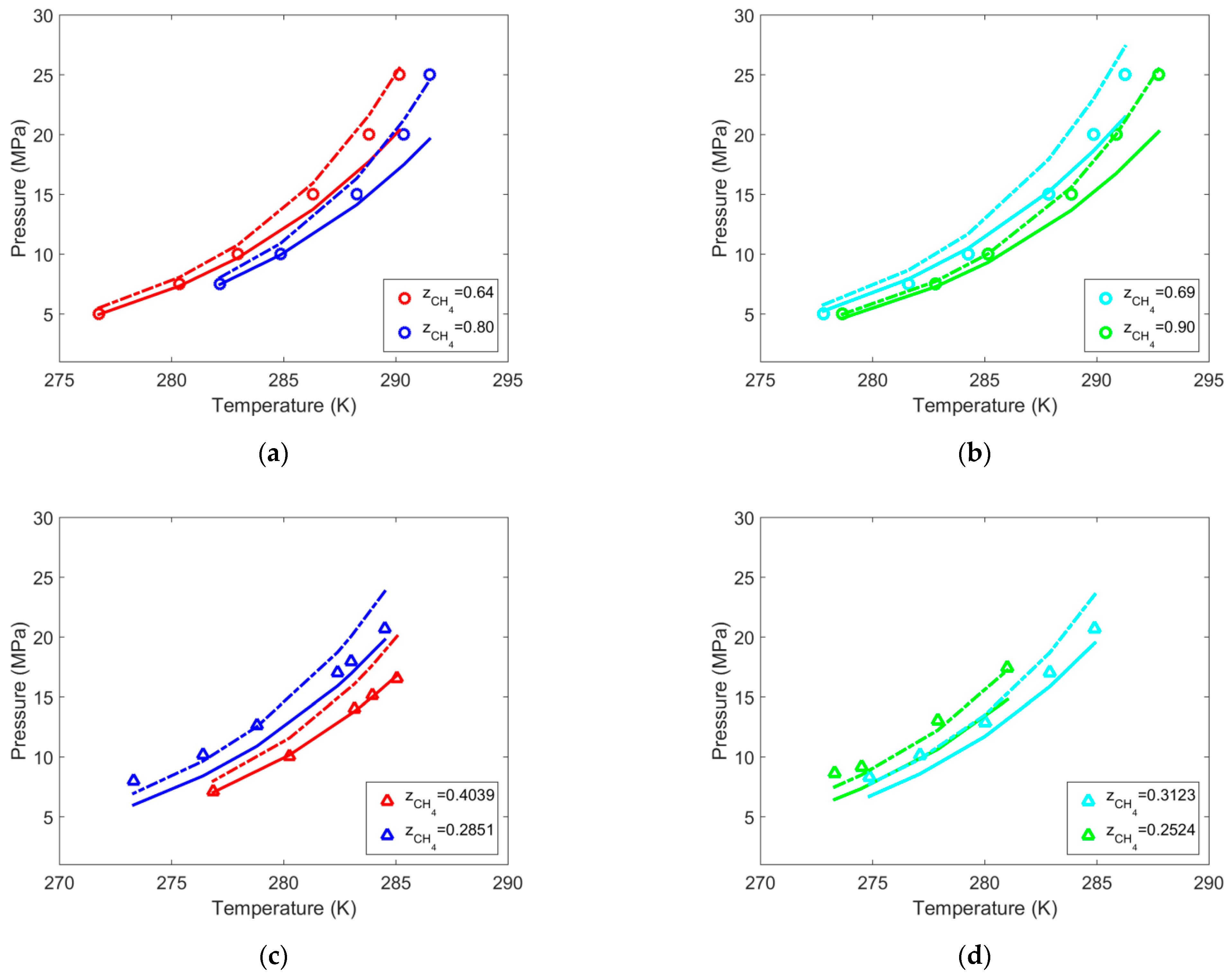
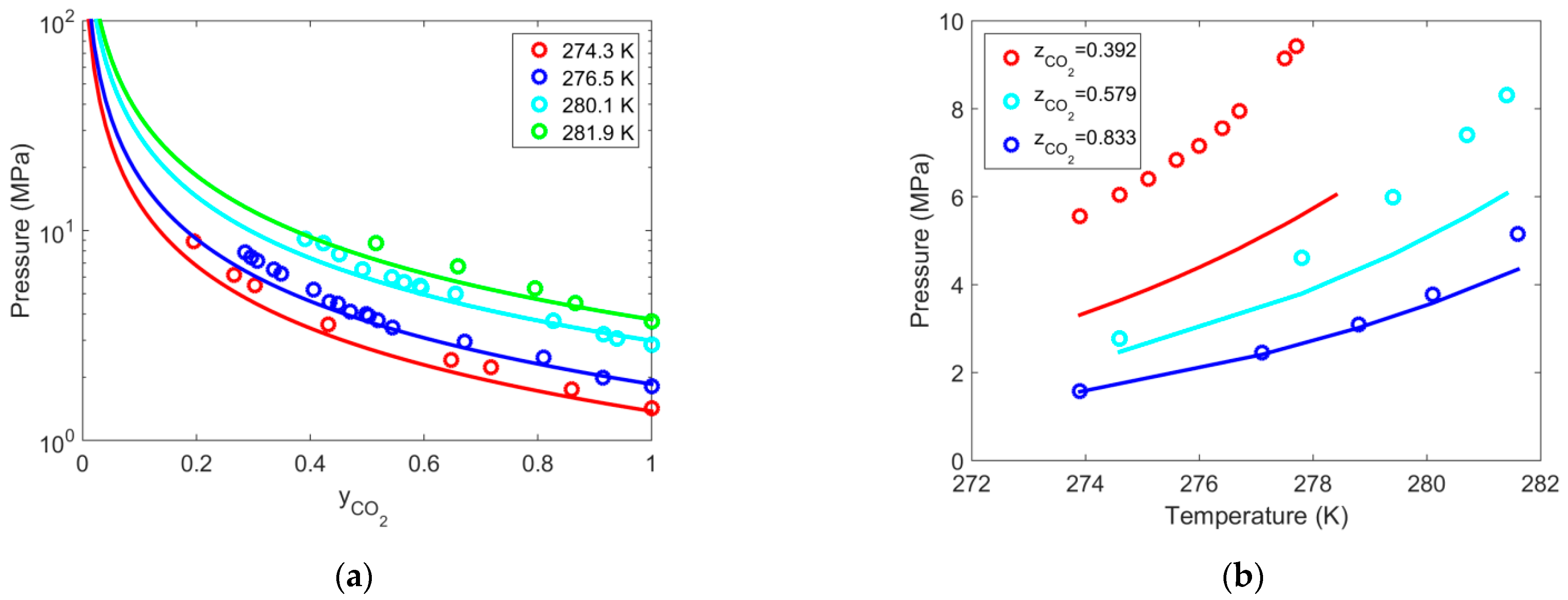
Gas	T Range (K)	Type of Equilibria	Ai (−)	Bi (K)	Source	Refs.
CH4	248–273	H–I–V	14.7170	−1886.79	Holder et al. [61]	N/A
CH4	273–298	H–Lw–V	38.9803	−8533.80	Holder et al. [61]	N/A
C2H6	248–273	H–I–V	17.5110	−3104.535	Holder et al. [61]	N/A
C2H6	273–287	H–Lw–V	44.2728	−10,424.248	Holder et al. [61]	N/A
C2H6	287–304	H–Lw–LH	$14.5831 \pm$ 0.0367	$-1860.741 \pm$ 10.867	This work	[81]
C2H4	269–274	H–Lw–V	$24.7929 \pm$ 1.7055	$-5016.239 \pm$ 466.056	This work	[82,83,84]
C2H4	274–286	H–Lw–V	$47.1247 \pm$ 1.7384	−11,138.677$\pm$ 490.000	This work	[83,84,85]
C2H4	286–291	H–Lw–V	$42.6159 \pm$ 0.3859	$-9941.235 \pm$ 109.283	This work	[83,84,85]
C2H4	291–295	H–Lw–LH	$120.9001 \pm$ 2.8681	−32,679.321$\pm$ 838.367	This work	[83,85]
C3H8	248–273	H–I–V	17.1560	−3269.646	Holder et al. [61]	N/A
C3H8	273–278	H–Lw–V	67.1301	−16,921.840	Holder et al. [61]	N/A
C3H8	278–303	H–Lw–LH	$14.5533 \pm$ 0.0684	$-2286.93 \pm$ 19.215	This work	[86,87]
CO	274–285	H–Lw–V	$32.4755 \pm$ 0.1108	$-8199.692 \pm$ 31.071	This work	[88]
CO2	248–273	H–I–V	18.5939	−3161.410	Holder et al. [61]	N/A
CO2	273–284	H–Lw–V	44.5776	−10,245.010	Holder et al. [61]	N/A
CO2	283–292	H–Lw–LH	$118.5425 \pm$ 4.0947	−31,030.579$\pm$ 1171.400	This work	[1]
N2	248–273	H–I–V	15.1289	−1504.276	Holder et al. [61]	N/A
N2	273–298	H–Lw–V	37.8079	−7688.626	Holder et al. [61]	N/A
H2S	248–273	H–I–V	16.5597	−3270.409	Holder et al. [61]	N/A
H2S	273–298	H–Lw–V	34.8278	−8266.102	Holder et al. [61]	N/A
O2	268–271.7	H–I–V	$16.7315 \pm$ 0.0871	$-2017.949 \pm$ 23.298	This work	[89,90,91]
O2	271.7–291	H–Lw–V	$41.9589 \pm$ 0.1963	$-8894.429 \pm$ 54.799	This work	[89,90,92]
SO2	T < 270.65	H–I–V	$8.9306 \pm$1.3650	$-1579.951 \pm$ 365.068	This work	[93,94,95]
SO2	270.7–286	H–Lw–V	$50.8949 \pm$ 2.3810	−12,940.097$\pm$ 667.712	This work	[93,94,95]
H2	267–273.7	H–I–V	$53.0775 \pm$ 0.9598	−11,120.167$\pm$ 259.541	This work	[96]
H2	273.7–348	H–Lw–V	$19.3750 \pm$ 0.2126	$-1769.473 \pm$ 64.707	This work	[96]

. Such gases are encountered in typical industrial applications. Some preliminary results considering some limited binary gas mixtures have been reported in an earlier study [80]. Therefore, the current work is a systematic extension of the aforementioned paper.

The purpose of the current study is two-fold: (i) to extend the Lipenkov–Istomin methodology to mixed gas hydrate systems of industrial interest by calculating the parameters of pure components that are not available, with emphasis on conditions above the Q₁, and (ii) to evaluate the quality of the predictions of the three-phase equilibrium conditions by comparing to experimental measurements. To this purpose, reported experimental measurements (i.e., the recent experimental data collection reported by Kastanidis et al. [97] is utilized) of hydrate equilibrium pressures are compared against (i) calculations using the examined Lipenkov–Istomin methodology [76], and (ii) calculations based on a commercial simulator (CSMGem [1]). As a result, the range of applicability of the Lipenkov–Istomin method is delineated.

The remainder of the manuscript is organized as follows: Initially, the Lipenkov–Istomin methodology is briefly discussed, followed by the presentation of the extensive series of calculations for the examined hydrate-forming gas mixtures. Finally, the conclusions are presented.

2. Methodology

2.1. Calculation of Hydrate Dissociation Pressures

Lipenkov and Istomin [76] introduced a simplified methodology for calculating the hydrate dissociation pressure of a gas mixture to a first approximation, and after assuming that (i) the clathrate of the gas mixture behaves as an ideally dilute solid solution, and (ii) that the ratio of occupancies for the small and large cages is constant and the same for all guest molecules. According to the proposed methodology, the hydrate dissociation pressure of a gas mixture can be expressed as a function of the hydrate dissociation pressures of the pure gases and the corresponding mole fractions of the gas phase as follows:

$${\left(P_H^{eq}\right)}_{gas-mixture}={\left({\displaystyle \sum _{i=1}^n\frac{y_i}{{(P_H^{eq})}_i}}\right)}^{-1}$$

(1)

where ${\left(P_H^{eq}\right)}_i$ is the hydrate dissociation pressure of the pure gas i (with $i=1, 2, \dots , n$), and y_i is the equilibrium gas-phase mole fraction of the gas i, which belongs to a gas mixture that contains n different components. It should be pointed out that y_i used in Equation (1) corresponds to the vapor phase that is part of the three-phase equilibrium system (i.e., Hydrate—Liquid water (or ice)—Vapor). However, a number of experimental studies, instead of reporting the measured y_i values, report the initial feed composition z_i values, which may be different compared to y_i. In the current study, we also examine the cases when z_i values are reported (i.e., y_i is replaced by z_i in Equation (1), which is a reasonable assumption) and present the corresponding results separately. Also, it should be noted that CSMGem needs the overall composition, z_i, as an input parameter and upon completion of the calculation, the resulting y_i values are very close to the corresponding z_i values. In summary, Equation (1) is a simple empirical model according to which the hydrate dissociation pressure of a gas mixture can be expressed as a function of the hydrate dissociation pressures of the pure gases and the corresponding mole fractions of the gas phase. On the other hand, CSMGem is a specifically designed model for the prediction of thermodynamically stable hydrate structures and cage occupancy. The model utilizes Gibbs energy minimization principles, providing insights into hydrate formation conditions for gas.

The hydrate dissociation pressure of the pure gas i is a function of temperature:

$${\left(P_H^{eq}\right)}_i=f\left(T\right)$$

(2)

Within the narrow temperature ranges of interest for this study, the three-phase (H–L_w–V) equilibrium curves can be obtained rather accurately through the following simple empirical relation:

$$\ln {\left(P_H^{eq}\right)}_i=A^i+\frac{B_i}{T}+\frac{C_i}{T^2}+\frac{D_i}{T^3}+\dots$$

(3)

where A_i, B_i, C_i, D_i, etc., are component-specific parameters that are usually obtained from fitting Equation (3) to available experimental data. All of the hydrate-forming gases considered in the current study use a first-degree polynomial (with respect to $1/T$) for the description of the RHS of Equation (3), namely an Arrhenius-type description. Notice however, that a higher-degree polynomial can be used if it is deemed necessary to improve the accuracy.

2.2. Parameter Estimation

In the current study, the values for the parameters A_i and B_i are either (i) obtained from Holder et al. [61], or (ii) they are calculated in the current study using available experimental measurements. A schematic showing the steps followed in the current study is shown in Figure 1. We consider two or three different zones, depending on whether a particular hydrate-forming gas has only the lower quadruple point, Q₁ (e.g., methane), or there is also an upper quadruple point, Q₂ (e.g., propane, carbon dioxide). Therefore, for conditions below Q₁, the type of phase equilibria observed is Hydrate–Ice water–Vapor, H–I–V. For conditions above Q₁ (when no Q₂ is present) or between Q₁ and Q₂ (when Q₂ is present), the type of phase equilibria observed is Hydrate–Liquid water–Vapor, H–L_w–V. Finally, for conditions above Q₂ (when Q₂ is present), the type of phase equilibria observed is Hydrate–Liquid water–Liquid hydrocarbon/gas, H–L_w–L_H. Figure 2a is a typical example of the particular calculation for the cases of oxygen and sulfur dioxide where a first-degree polynomial is used, while Figure 2b shows the cases of carbon dioxide where a higher-degree polynomial is required for the description of the H–L_w–L_CO2 zone.

Table 1 gives the values of the parameters A_i, and B_i, for the cases of all gases that are of interest for the current study. The parameters have been calculated by performing a regression analysis on the published experimental data (also shown in Table 1) for each pure gas hydrate, as implemented using Excel 2021. Shown also in Table 1 are the corresponding errors that resulted from the parameter estimation, as well as the temperature ranges of applicability of the empirical relation for all hydrate-forming components. The last column of Table 1 indicates the references for the experimental data that were used in the current study for obtaining the component-specific parameters.

3. Results and Discussion

As discussed in the previous section, Lipenkov and Istomin [76] introduced a simplified methodology for calculating the hydrate dissociation pressure of a gas mixture at low temperatures (i.e., Ts corresponding to values below the lower quadruple point, Q₁). This methodology is used in order to examine binary, ternary, and some limited quaternary mixed gas hydrates that are of industrial interest. The emphasis in the current study is on conditions above the lower quadruple point, Q₁. In this work, we use experimental data obtained from the data collection reported by Kastanidis et al. [97]. In particular, we examine the experimental hydrate systems that are indicated in

Table 2. Hydrate-forming gas mixtures considered in the current study and the corresponding experimental studies.

Notation	System	Comment	References Examined
GM–1	CO2 + N2	“Flue Gas” A	[98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118]
GM–2	CO2 + N2 + O2	“Flue Gas” B	[113]
GM–3	CO2 + H2	Methane steam reforming	[101,119,120,121,122,123,124,125,126,127,128,129]
GM–4	CO2 + CH4	Biogas upgrade	[99,103,106,108,110,112,115,117,127,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154]
GM–5	CO2 + gas (other)	CO2-containing mixtures	[108,112,155,156,157,158]
GM–6	CH4 + H2	–	[125,148,159,160,161,162,163]
GM–7	CH4 + N2	–	[115,164,165,166,167,168,169,170]
GM–8	CH4 + N2 + O2	“Coal-mine” gas mixture	[171]
GM–9	CH4 + CO2 + N2	–	[117,148,154,166,172,173,174,175,176,177,178,179]
GM–10	CH4 + hydrocarbon gas mixtures	CH4-containing mixture A	[166,180,181,182,183,184]
GM–11	CH4 + gas (other)	CH4-containing mixture B	(No system considered)
GM–12	Light hydrocarbon binaries	Other cases	[166,185,186]
GM–13	H2S + gas (other)	H2S-containing mixtures	[128,142,187,188,189]
GM–14	H2 + natural gas mixtures	H2-containing mixtures	[128,148,160,161,190]
GM–15	Air + gas (other)	Air/N2-containing mixtures	[91,92,191,192]

. Namely, 98 publications, reporting 135 experimental mixed hydrate systems, were considered, containing a total of 2516 experimental data points.

Two different comparisons are reported. In particular, we compare the hydrate dissociation pressure values that were obtained using (i) the Lipenkov–Istomin methodology (LI), and (ii) the commercial simulator CSMGem [1], against the aforementioned experimental values. The overall results of both comparisons are reported in

Table 3. Percentage average absolute deviation (% AAD) during the calculation of hydrate equilibrium pressure, $P_H^{eq}$, for the hydrate mixture systems considered (i.e., cases of y-values or z-values reported). The number of experimental data points is denoted as ndp. N/A denotes that the corresponding CSMGem parameters for O₂, H₂, CO, and SO₂ are not available.

Gas Mixture System		# of Exper. Studies Examined	Total ndp	$\% \mathit{ADD} \mathbf{in} {\mathit{P}}_{\mathit{H}}^{\mathit{e}\mathit{q}}$		$\% \mathit{ADD} \mathbf{in} {\mathit{P}}_{\mathit{H}}^{\mathit{e}\mathit{q}}$
				CSMGem		Lipenkov–Istomin
				y-Values	z-Values	y-Values	z-Values
GM–1: CO2 + N2		20	432	15.73	25.74	7.40	17.54
GM–2: CO2 + N2 + O2		1	4	N/A	N/A	-	14.85
GM–3: CO2 + H2		12	194	N/A	N/A	9.24	34.45
GM–4: CO2 + CH4		36	719	10.79	14.12	7.44	13.23
GM–5: CO2 + gas (other)	CO2 + C2H6	3	127	1.40	3.42	5.66	6.11
	CO2 + C3H8	2	66	-	18.18	-	19.37
	CO2 + C2H6 + C3H8	1	5	-	15.68	-	31.81
	CO2 + CO	1	6	N/A	N/A	-	91.45
	CO2 + SO2	2	75	N/A	N/A	-	21.38
GM–6: CH4 + H2		7	338	N/A	N/A	9.38	27.61
GM–7: CH4 + N2		8	93	4.61	7.21	12.77	9.50
GM–8: CH4 + N2 + O2		1	6	N/A	N/A	-	25.31
GM–9: CH4 + CO2 + N2		12	146	33.77	14.11	15.79	9.66
GM–10: CH4 + hydrocarbon gas mixtures	CH4 + C2H6	3	35	3.15	18.72	14.38	17.30
	CH4 + C3H8	3	38	-	13.17	-	85.03
	CH4 + C2H6 + C3H8	2	20	-	6.87	-	65.16
GM–11: CH4 + gas (other)		-	-	-	-	-	-
GM–12: Light hydrocarbon binary	C2H6 + C3H8	3	78	-	13.16	-	25.28
GM–13: H2S + gas (other)	H2S + CO2	2	19	90.97	25.92	3.11	15.02
	H2S + CH4	2	11	-	8.75	-	14.58
	H2S + CH4 + CO2	2	13	8.60	9.93	15.52	3.30
	H2S + CH4 + C3H8	1	10	-	128.72	-	78.83
	H2S + H2 + CO2	1	4	N/A	N/A	24.65	48.74
GM–14: H2 + natural gas mixtures	H2 + CH4 + C3H8	1	22	N/A	N/A	49.51	-
	H2 + CH4 + C2H6 + C3H8	1	16	N/A	N/A	82.69	-
	H2 + C2H4	1	6	N/A	N/A	21.49	-
	H2 + CH4 + C2H4	1	4	N/A	N/A	37.33	3.73
	H2 + CO2 + CH4	1	5	N/A	N/A	33.13	-
	H2 + CO2 + H2S	1	4	N/A	N/A	32.41	15.42
GM–15: Air + gas (other)		4	20	N/A	N/A	-	13.90

, while additional more detailed results are reported in the Supplementary Material file. We report in Table 3 the total number of available experimental data points (ndp) and the percentage of the absolute average deviation in predicting the hydrate equilibrium pressure (% AAD) for calculations using either the equilibrium gas-phase mole fraction (y_i) or the initial feed composition (z_i), or both, depending on the information provided by each experimental study, which is calculated as follows:

$$\% AAD=\frac{100}{ndp}\times {\displaystyle \sum _{i=1}^{ndp}\left|\frac{{\left(P_H^{eq}\right)}_i^{\exp }-{\left(P_H^{eq}\right)}_i^{calc}}{{\left(P_H^{eq}\right)}_i^{\exp }}\right|}$$

(4)

Initially, some general conclusions are presented. For cases of hydrate-forming systems that both computational methods can be applied to, the CSMGem method performs better than the LI for gas mixtures GM–1, GM–5, GM–7, and GM–10. On the other hand, the LI approach performs better for the cases of mixtures GM–4, GM–9, GM–12, and GM–13. The better performance of the CSMGem should be expected since the parameters of the methodology are optimized in order to minimize the error in predicting the three-phase equilibrium conditions (it should also be noted that the quality of the experimental measurement affects the performance of the CSMGem approach). On the other hand, the LI is a simplified mixing rule of the equilibrium pressures of the corresponding pure components of the mixture.

A more detailed comparison between the two computational approaches and the experimental data is presented in the Supplementary Material file (i.e., tables included in Sections S1–S15) where a distinction is made for experimental studies published either before or after 2008. The particular year is selected since it is the year that CSMGem was made available. Therefore, experimental data that were published during earlier years could have been included (in principle) in the development of CSMGem (i.e., during parameter optimization). On the other hand, experimental data that are published after 2008 can serve only for testing the accuracy of the considered model. In the tables included in Sections S1–S15, we report for each study the total number of available experimental data points, ndp, and the percentage of the absolute average deviation in predicting the hydrate equilibrium pressure, % AAD.

It should be noted that for gas mixtures containing either one of the gases O₂ (GM–2, GM–8, GM–15), H₂ (GM–3, GM–6, GM–13, GM–14), CO (GM–5), and SO₂ (GM–5) (also see Table 3 for particular cases considered in the current study), we report calculations in the current study only with the LI method, since optimized parameters for those components are not available in the CSMGem simulator [1].

Next, some characteristic comparison examples are plotted in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, and are further discussed. Figure 3 shows the comparison between experimental (denoted with circles) and calculated values with (i) the LI method (shown with solid lines), and (ii) the CSMGem simulator (shown with dashed lines), for the hydrate equilibrium pressures of the binary gas mixture: CO₂ + N₂ (GM–1). In particular, Figure 3a shows the case of the experimental data for $P_H^{eq}$, which are plotted as a function of $y_{C{O}_2}$, that were reported by Bruusgaard et al. [102], which were measured at constant temperature, T. Similarly, Figure 3b shows the case of the experimental data for $P_H^{eq}$ plotted as a function of T that were reported by Olsen et al. [98], which were measured at constant feed composition, z. Reasonable agreement is found between the computational approaches examined (LI and CSMGem) and the two aforementioned studies.

In order to further quantify the performance of the two calculation methodologies under consideration, we plotted in Figure 4 the overall % AAD corresponding to the calculation of the three-phase equilibrium pressure for different experimental studies for varying T, y, and z. Figure 4a shows the % AAD plotted as a function of T, for the experimental data of Bruusgaard et al. [102], Belandria et al. [104], and Lang et al. [105] for which studies’ y-values have been reported. For the case of the binary gas mixture CO₂ + N₂, the CSMGem method results, in most cases, in lower % AAD values (i.e., less than 4%). On the other hand, for the case of the LI method, the resulting % AAD values vary in the range 5–30%. Furthermore, no clear/systematic trend for the % AAD values can be identified. For example, the % AAD increases when T increases for the experimental data of Bruusgaard et al. [102], while the % AAD decreases when T increases for the experimental data of Belandria et al. [104].

The corresponding figures for % AAD plotted as a function of $y_{C{O}_2}$ (Figure S1a) or $z_{C{O}_2}$ (Figure S1b) are shown in Figure S1 of the Supplementary Material. For most cases shown, the % AAD values are lower than 20% for the case of the CSMGem method, while on the other hand, they are lower than 40% for the case of the LI method. It should be noted that for the case of the experimental data of Herri et al. [103], the LI method results in lower % AAD values when compared to CSMGem values, which is a notable exception for the gas mixture GM–1. Additional exceptions include the experimental data of Belandria et al. [104] and Le Quang et al. [106].

Figure 4b utilizes the experimental data reported by Bruusgaard et al. [102] in order to assess the effect of using the available initial feed composition z_i values in Equation (1), instead of the required measured y_i values. For the particular experimental data set, it is clear that for both methods (i.e., LI and CSMGem) we obtain lower values for % AAD when y_i values are used. The difference in % AAD is higher at lower Ts. As T increases and the upper quadruple point, Q₂, for CO₂ is approached (i.e., T = 283.0 K), we observe that the % AAD for the cases of y_i or z_i values is converging asymptotically. A more detailed discussion on Q₂ for the case of CO₂ can be found in Kastanidis et al.’s report [193]. In addition, from Table 3, we can observe that for the vast majority of cases, the % AAD values when y_i values are reported are lower than those when z_i values are reported.

Similarly, Figure 5 shows the comparison between experimental and calculated values for the hydrate equilibrium pressures of the binary gas mixture: CO₂ + CH₄ (GM–4). In particular, Figure 5a shows the case of the experimental data of Belandria et al. [138], which were measured at constant temperature, T, while Figure 5b shows the case of the experimental data of Seo et al. [135], which were measured at constant pressure, P. For both cases, experimental values for y_i have been reported.

A general observation that can be made from the figures shown, as well as from all the calculations that were performed, is that the % AAD in hydrate equilibrium predictions increases as the hydrate equilibrium pressure (or temperature) increases. For hydrate equilibrium pressures that are below 10 MPa, the % AAD is kept well below 8–10%. Therefore, the accuracy of the methodology deteriorates as we go with higher pressures.

We can further observe in Table 3 that for the case of gas mixture GM–4, the LI method gives lower overall % AAD values. Some typical examples are also shown in Figure 6, where we plot the % AAD as a function of T for several experimental studies, which provide y-values (Figure 6a) or z-values (Figure 6b). Additional plots showing the % AAD as a function of $y_{C{H}_4}$(Figure S2a) or $z_{C{H}_4}$ (Figure S2b,c) are shown in Figure S2 of the Supplementary Material. It is evident that for most cases of experimental data sets (e.g., Adisasmito et al. [131] (e.g., see Figure S2a), Unruh et al. [130], Servio et al. [194], Lee et al. [146], Belandria et al. [138,145], Sfaxi et al. [110], Sadeq et al. [115] (e.g., see Figure S2b,c)), the % AAD values are lower than 10%, or in the range 10–20% (e.g., Beltran et al. [136], Bruusgaard et al. [137], Belandria et al. [138] (e.g., see Figure 6a,b)). Only a few exceptions to the aforementioned rule have been identified. Namely, the experimental data of Obanijesu et al. [148] and Legoix et al. [117,151] have % AAD values in the range 30–60% (see Figure S2b and Tables in Section S4 of the Supplementary Material). Given that the calculations (LI or CSMGem) for the other experimental data sets result in % AADs with significantly lower values, this could lead to the conclusion that the three particular data sets may have problematic experimental measurements that could be resolved by performing additional experimental measurements under similar conditions.

Figure 7 examines the case of the binary gas hydrate CH₄ + N₂ (GM–7). It shows the case of the experimental data for $P_H^{eq}$ plotted as a function of T, measured at constant feed composition, z. In particular, Figure 7a,b show the experimental data of Sadeq et al. [115], while Figure 7c,d show the experimental data of Lee et al. [167]. As can be seen from Figure 7 and also Table S7 of the Supplementary Material for the particular experimental data sets, both methods considered in the current study give similar results. Overall, for the case of gas mixture GM–7, CSMGem performs slightly better than the LI method. In particular, CSMGem has a % AAD equal to 4.48% with the corresponding LI equal to 12.57% for cases when y is reported. On the other hand, CSMGem has a % AAD equal to 9.50% with the corresponding LI equal to 7.20% for cases when z is reported. Additional comparisons are provided in Figure S3 of the Supplementary Material, where the % AAD values are plotted as a function of $z_{C{H}_4}$. The majority of cases result in % AAD values that are less than 10%, while a limited number of cases are in the range 10–20%.

Figure 8 shows the comparison between experimental and calculated (LI method) values for the hydrate equilibrium pressures of the binary gas mixture CO₂ + H₂ (GM–3). In particular, Figure 8a shows the case of the experimental data for $P_H^{eq}$ as a function of $y_{C{O}_2}$ that were reported by Sugahara et al. [119], which were measured at constant temperature, T. Similarly, Figure 8b shows the case of the experimental data for $P_H^{eq}$ as a function of T that were reported by Kumar et al. [120], which were measured at constant feed composition, z.

Figure S4 of the Supplementary Material shows additional comparisons for the gas mixture GM–3. Namely, Figure S4a shows the % AAD values for the prediction of the three-phase equilibrium pressure of three experimental studies (Sugahara et al. [119], Belandria et al. [121] (reporting y-values), and Belandria et al. [121] (reporting z-values)) plotted as a function of T. Figure S4b shows the corresponding % AAD values of all available experimental data (Table S3 of the Supplementary Material) plotted as a function of $z_{C{O}_2}$. The majority of the cases result in % AAD values in the range 10–50%, while for the case of Belandria et al. (y-values), the % AAD values are lower than 8%.

Figure 9 shows the comparison between experimental and calculated (LI method) values for the hydrate equilibrium pressures of the binary gas mixture CH₄ + H₂ (GM–6). Figure 9a shows the case of the experimental data for $P_H^{eq}$ as a function of T that were reported by Pang et al. [125], which were measured at constant feed composition, z, while Figure 9b shows the corresponding cases of the experimental data of Zhang et al. [161], and Obanijesu et al. [148].

Additional comparisons are provided in Figure S5 of the Supplementary Material, where the % AAD values for the prediction of the three-phase equilibrium pressure of four experimental studies (Zhang et al. [161], Skiba et al. [162], Pang et al. [125], and Obanijesu et al. [148]) are plotted as a function of $z_{C{H}_4}$. The majority of cases result in % AAD values that are less than 10%, while a limited number of cases have % AAD values that are in the range 10–20%.

4. Model Limitations

Macroscopic tools developed for hydrate equilibrium calculations need to be (i) accurate, and (ii) computationally efficient. An accurate and computationally fast tool can be used for initial screening purposes in the optimization of a given separation process. The identification/development of such a reliable macroscopic tool that can accurately describe the hydrate equilibrium pressure of hydrates of gas mixtures, while being computationally efficient, is the main motivation of the current study. The current section summarizes the limitations of the examined/proposed LI methodology.

(1) In the current study, the vast majority of the experimental data that were examined have P and T conditions that are between the upper and lower quadruple points of the participating pure components in the hydrate-forming gas mixtures. From the analysis in this work, we can conclude that the presence of a component exhibiting an upper quadruple point, Q₂, results in calculations of the hydrate equilibrium pressures with the LI method that have usually higher values of % AAD, particularly at the proximity or above Q₂. Therefore, it would be of interest to conduct a more systematic study of such hydrate systems (i.e., containing CO₂, H₂S, C₂H₄, C₃H₆, etc.), particularly at the proximity or above Q₂. Such aspects, however, which may also include structural transition phenomena (i.e., sII to sI), are beyond the scope of the current study and are left for the future.

(2) The examined LI methodology is not capable of providing any information regarding cage occupancies. For the case of methods that couple the van der Waals–Platteeuw statistical theory with an EoS, such as the CSMGem method, the calculation of cage occupancies is a side result obtained during the calculation of three-phase equilibrium conditions.

(3) The LI methodology is applicable to mixtures with components for which the parameters A_i and B_i, for calculating the equilibrium pressure (via Equation (3)) of the pure component, are available. Namely, the methodology is limited to hydrate-forming components listed in Table 1. Therefore, in order to extend the methodology to other components, an approach such as the one described in the flowchart, shown in Figure 1, should be followed.

5. Conclusions

In this work, we have considered a simple methodology, called LI, for the calculation of the hydrate equilibrium pressure of gas mixtures. Gas mixtures of interest for this study were binary, ternary, and limited quaternary mixtures that were made up of different combinations of eleven components (i.e., CH₄, C₂H₆, C₂H₄, C₃H₈, CO, CO₂, N₂, H₂S, O₂, SO₂, and H₂). In total, 98 publications, reporting 135 experimental mixed hydrate systems, were considered, containing a total of 2516 experimental data points. Such gas mixtures are encountered in practical industrial applications of gas-mixture separations.

An extensive series of calculations using the examined LI methodology were performed and the calculations were compared against available experimental measurements, as well as with the CSMGem simulator. It should be noted that the intent of the study is not to replace the CSMGem simulator with the proposed methodology but to examine if a simpler and more computationally efficient approach can produce reasonable results (at least within some specific temperature, pressure, and composition range) that can be used during the preliminary stage of the design of processes. After all, the theoretical basis behind CSMGem or other similar van der Waals–Platteeuw-based models is significantly stronger than the simplified LI approach.

Reasonable agreement between experiments and calculations with the LI methodology was obtained, considering its simplicity. The agreement was found to be better at lower hydrate equilibrium pressures.

Finally, higher deviations have been observed for hydrate-forming gas mixtures that contain a component exhibiting an upper quadruple point, Q₂, particularly at the proximity of Q₂. Such systems require a more detailed study in order to examine if the performance of the LI method can be further improved. This aspect is left for a future study.