An Investigation of Structural Strength of Nuclear Fuel Spacer Grid
Abstract
:1. Introduction
2. Materials and Methodologies
2.1. Review of APR1400 FA Spacer Grid Mechanical Strength Assessments
2.2. Method of Obtaining Optimized FA Model
3. Reduced Model of PLUS7 FA
3.1. Development of FEA Model
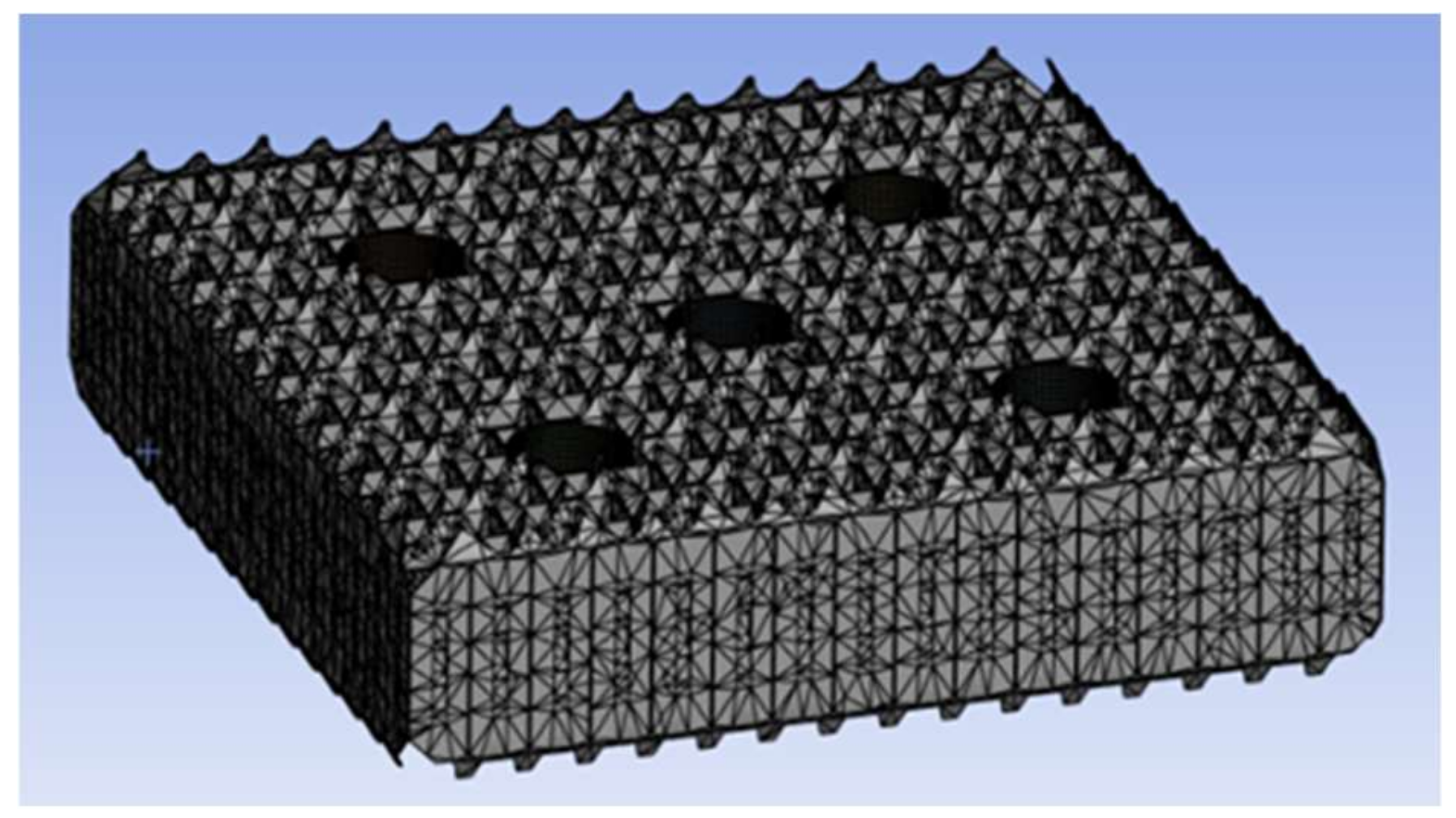
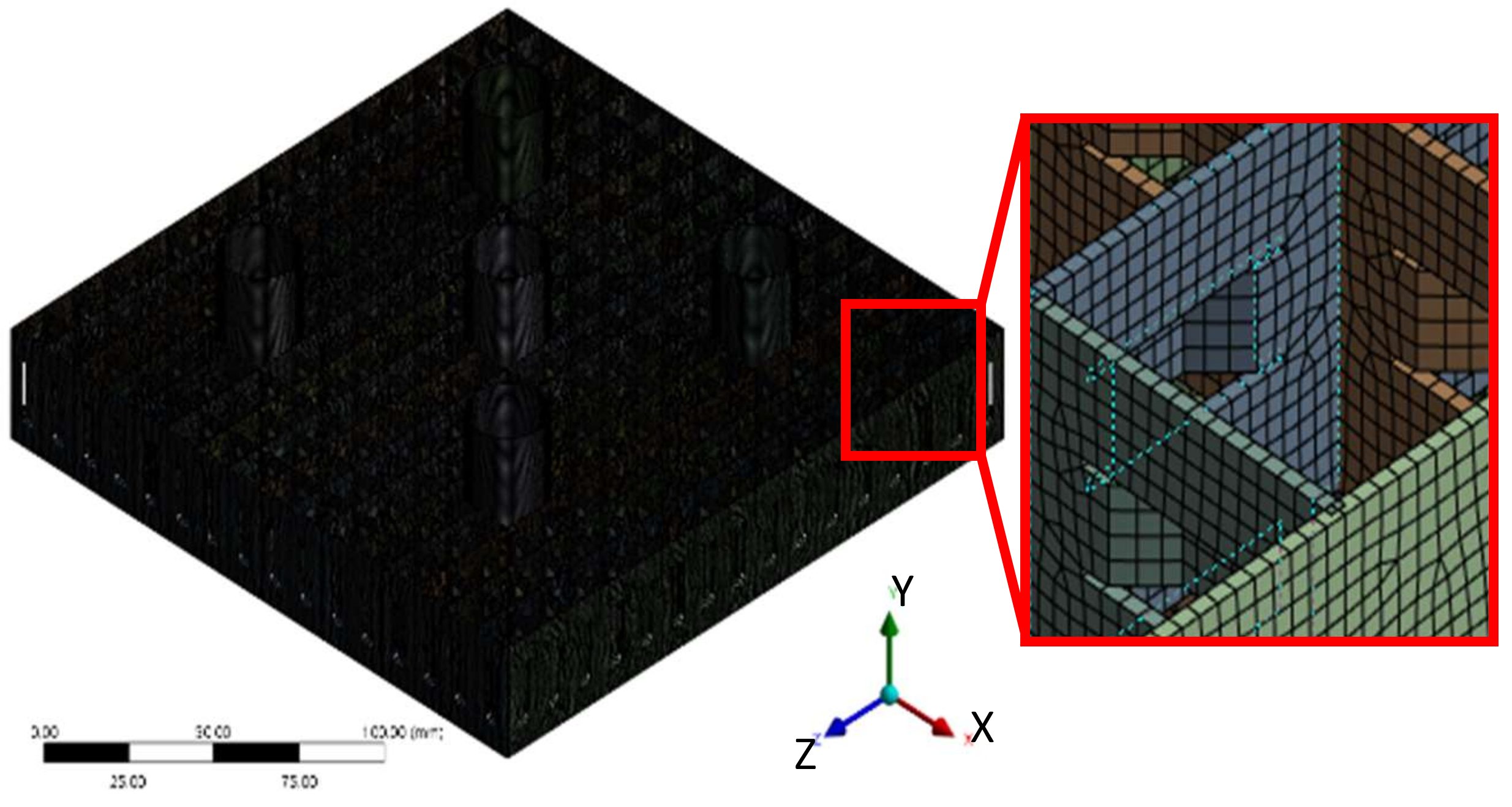
3.2. Meshing
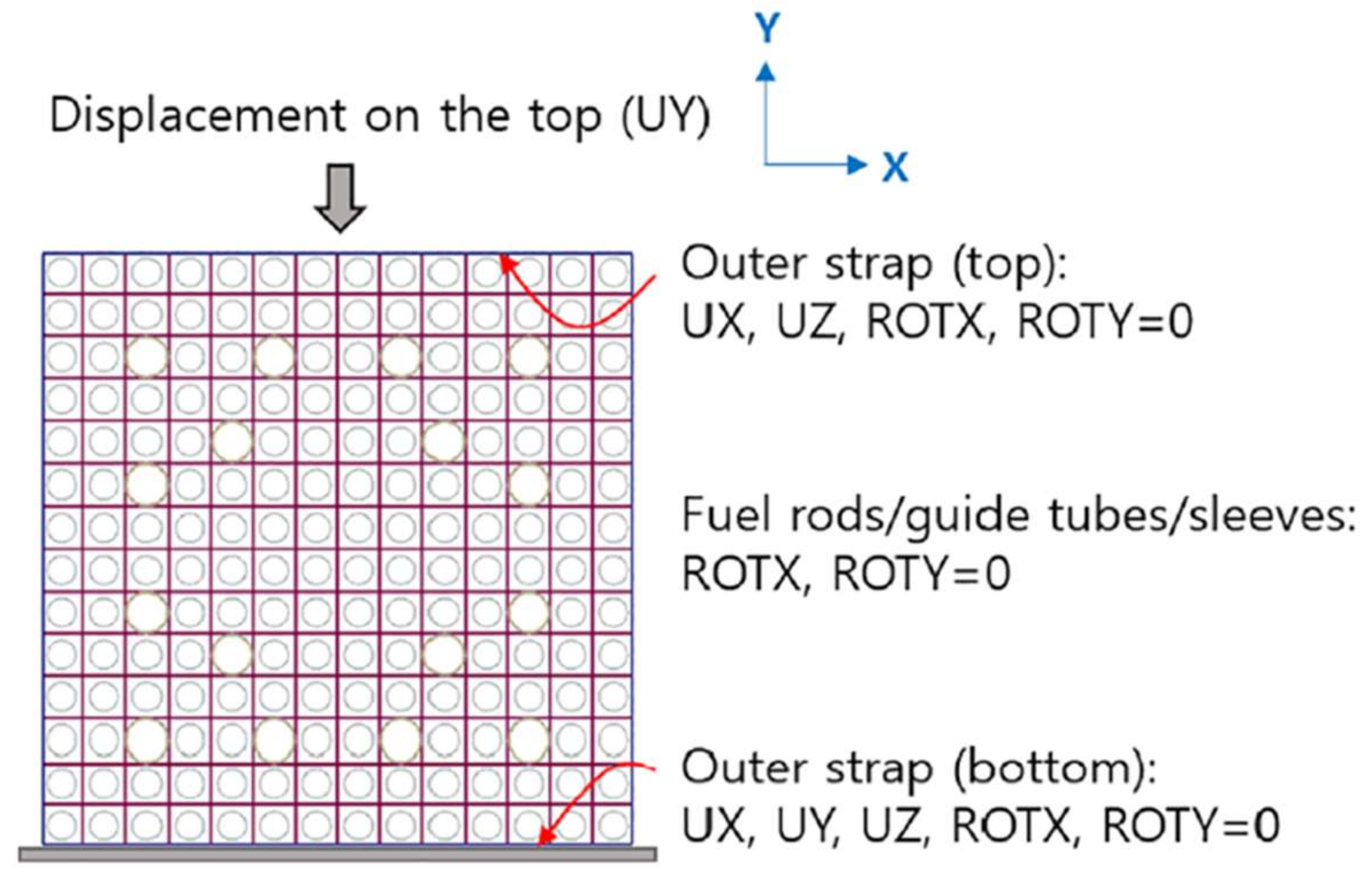
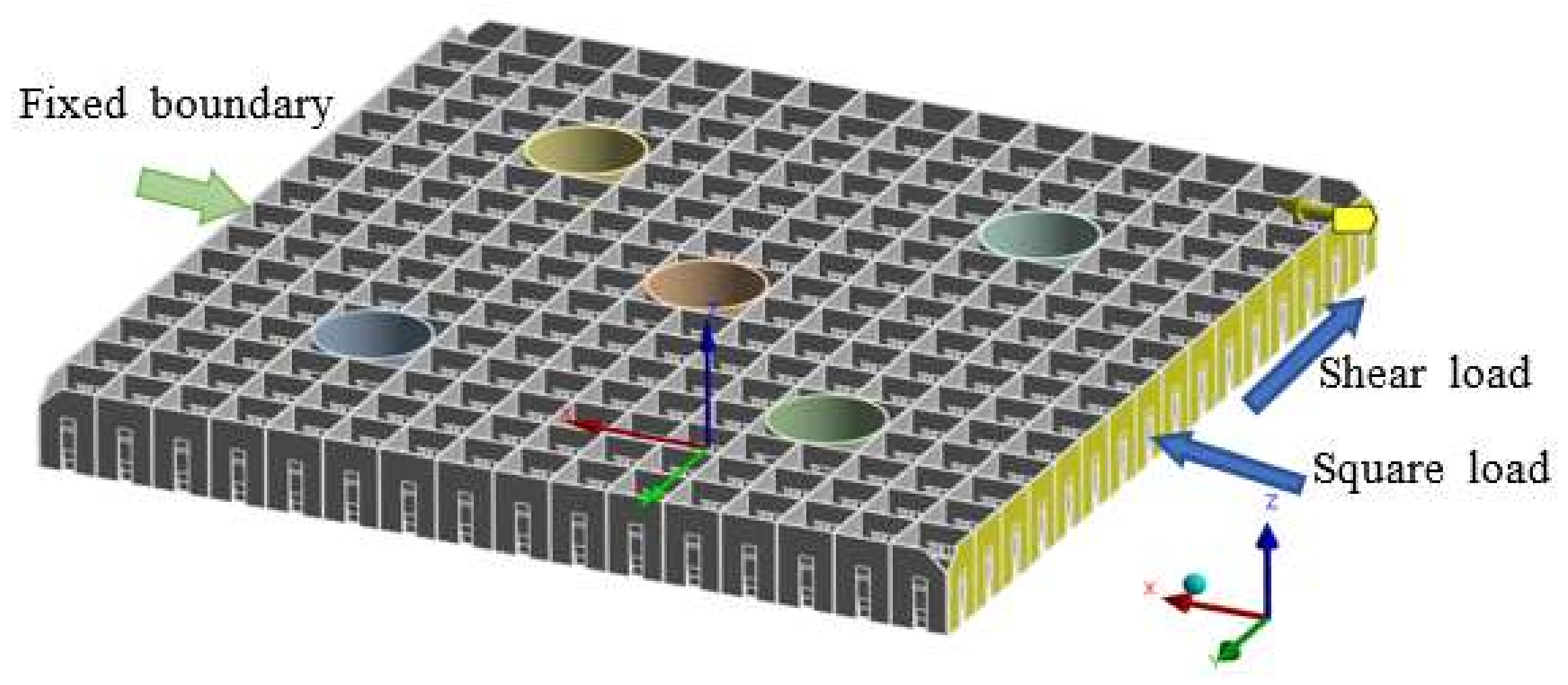
3.3. Boundary Conditions
3.4. Zircaloy Material Engineering Data
4. Results and Discussions
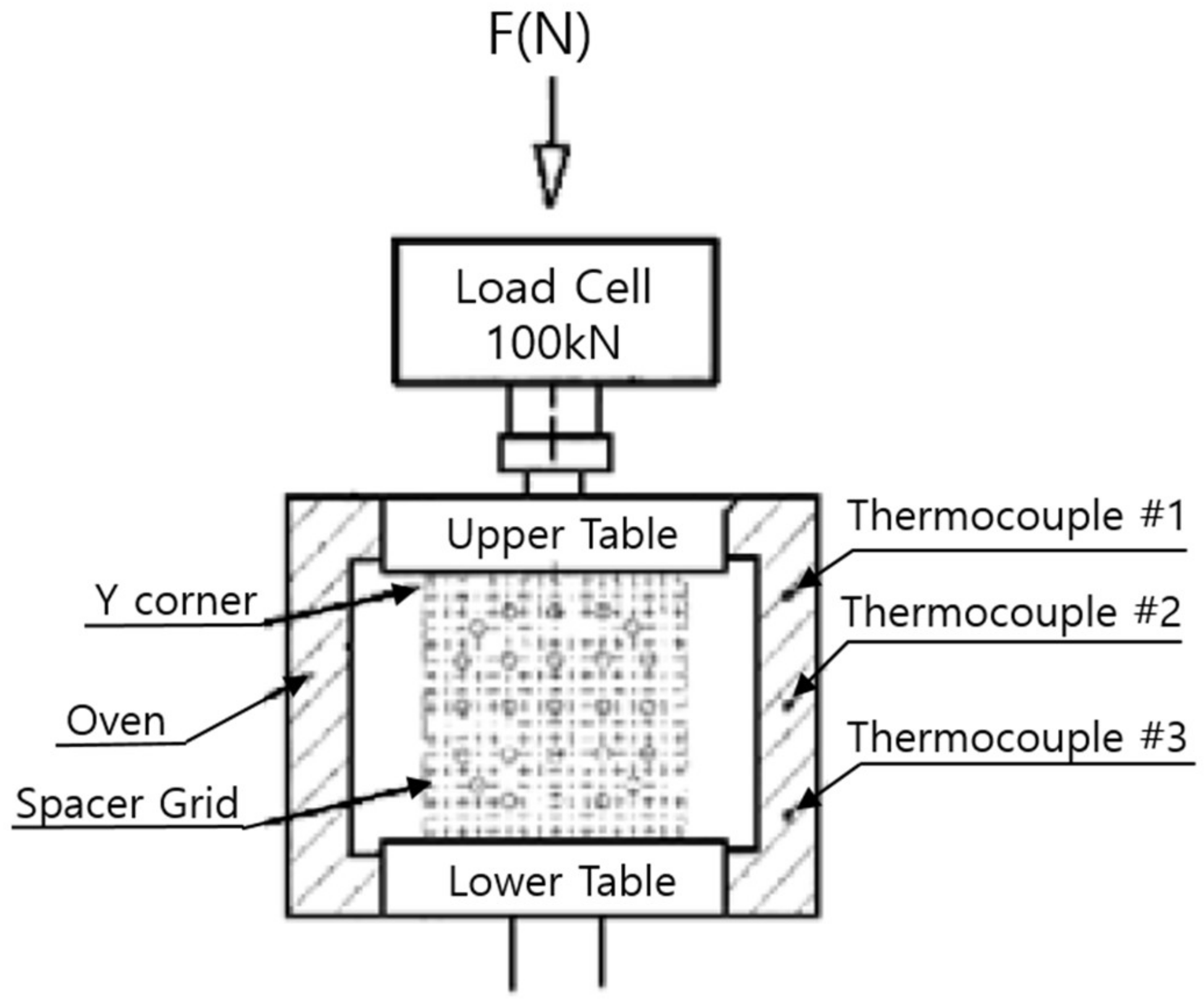
4.1. Review of Spacer Grid Test Results
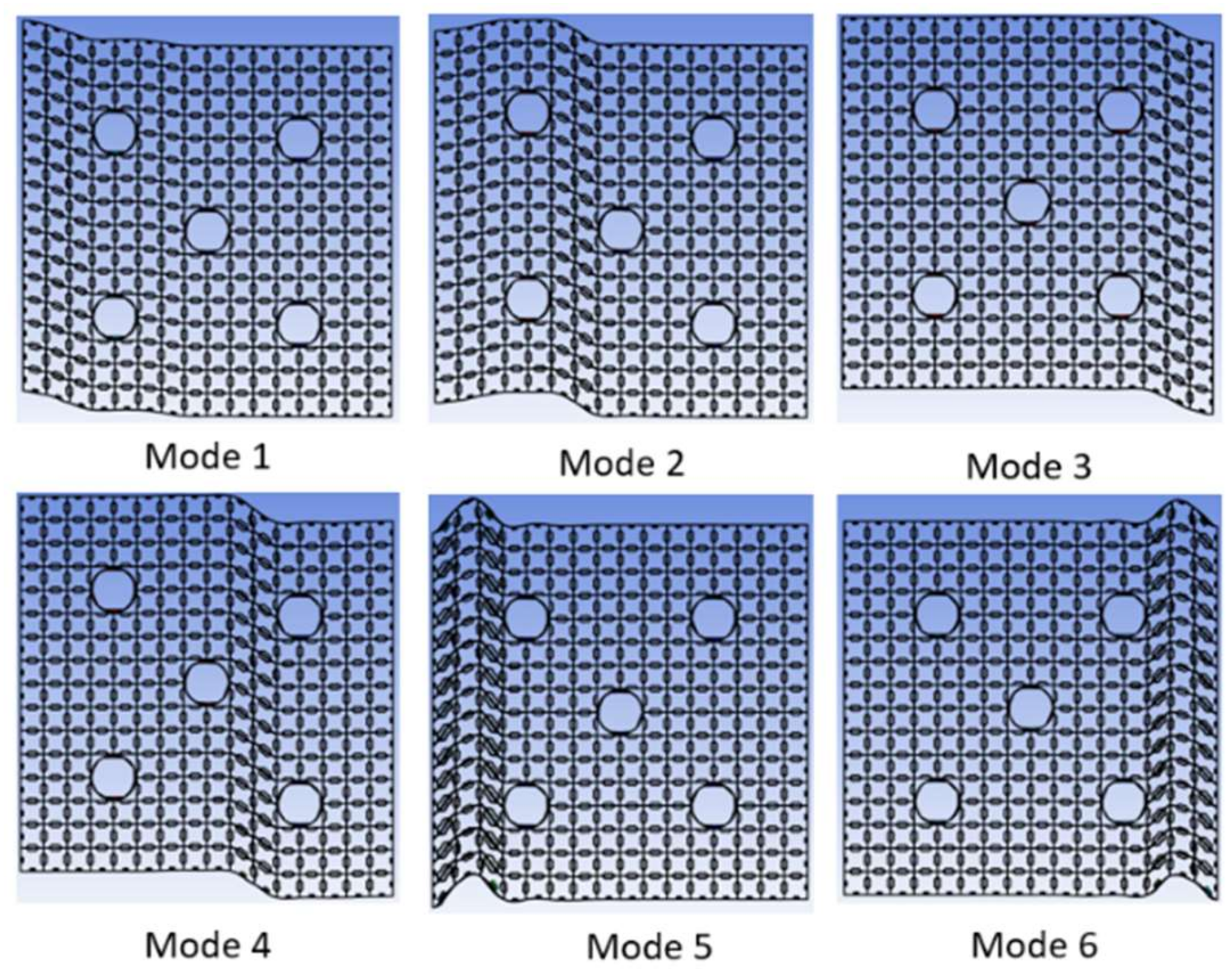
4.2. FEA Results of the Reduced Spacer Grid Models
5. Conclusions and Further Considerations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Subhan, M.; Namgung, I. Development of nuclear fuel assembly 3D reduced model and modal analysis. Ann. Nucl. Energy 2023, 181, 109561. [Google Scholar] [CrossRef]
- ASME. ASME Boiler and Pressure Vessel Code, Section III, Non-Mandatory Appendix F, Rules for Evaluation of Service Loadings with Level D Service Limits; American Society of Mechanical Engineers: New York, NY, USA, 2021. [Google Scholar]
- Namgung, I. An investigation of structural strength of PWR fuel assembly spacer grid with fuel rod clad. Ann. Nucl. Energy 2024, 195, 110124. [Google Scholar]
- Song, K.N.; Lee, S.B.; Shin, M.K.; Lee, J.J.; Park, G.J. New spacer grid to enhance mechanical/structural performance. Nucl. Sci. Technol. 2010, 47, 295–303. [Google Scholar] [CrossRef]
- Yoo, Y.; Kim, K.; Eom, K.; Lee, S. Finite element analysis of the mechanical behavior of a nuclear fuel assembly spacer grid. Nucl. Eng. Des. 2019, 352, 110179. [Google Scholar] [CrossRef]
- IAEA. Structural behavior of fuel assemblies for water cooled reactors. In Proceedings of the Technical Meeting, Cadarache, France, 22–26 November 2004; IAEA-TECDOC-1454. IAEA: Vienna, Austria, 2004. [Google Scholar]
- Areva. PWR Fuel Assembly Structural Response to Externally Applied Dynamic Excitations; Topical Report to NRC; AREVA Inc.: Columbia, MD, USA, 2015. [Google Scholar]
- Yoon, K.H.; Heo, S.P.; Song, K.N.; Jung, Y.H. Dynamic impact analysis of the grid structure using multi-point constraint (MPC) equation under the lateral impact load. Comput. Struct. 2004, 82, 2221–2228. [Google Scholar] [CrossRef]
- Shin, M.K.; Lee, H.A.; Lee, J.J.; Song, K.N.; Park, G.J. Optimization of a nuclear fuel spacer grid spring using homology constraints. Nucl. Eng. Des. 2008, 238, 2624–2634. [Google Scholar] [CrossRef]
- Schettino, C.F.M.; Gouvêa, J.P.; Medeiros, N. Analysis of spacer grid compression strength and fuel assembly structural behavior. Nucl. Eng. Des. 2013, 260, 93–103. [Google Scholar] [CrossRef]
- Kim, K.T.; Suh, J.M. Development of an advanced PWR fuel for OPR1000s in Korea. Nucl. Eng. Des. 2008, 238, 2606–2613. [Google Scholar] [CrossRef]
- Yoo, Y.; Kim, J.; Park, J.; Kim, H. Development of nuclear fuel assembly finite element model for mechanical integrity evaluation. Nucl. Eng. Des. 2023, 413, 112523. [Google Scholar] [CrossRef]
- Choi, Y.; Park, J.B.; Lee, S.J.; Park, N.C.; Park, Y.P.; Kim, J.S.; Roh, W.J. Seismic analysis of the APR 1400 reactor vessel internals using the model reduction method. J. Nucl. Sci. Technol. 2016, 53, 1701–1714. [Google Scholar] [CrossRef]
- CATIA, 3D computer aided design software, CATIA V.5. Release 2023.
- ANSYS. Mechanical Properties, Data Compiled by the Granta Design Team at ANSYS, Incorporating Various Sources Including JAHM and MagWeb; ANSYS R2 Version; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Siefken, L.J.; Coryell, E.W.; Harvego, E.A.; Hohorst, J.K. MATPRO—A Library of Materials Properties for Light-Water-Reactor Accident Analysis; Idaho National Engineering and Environmental Laboratory for NRC: Idaho Falls, ID, USA, 2001. [Google Scholar]
- Oh, Y.J.; Baek, J.H.; Lee, S.H.; Jeong, Y.H. The Measurement of Basic Thermal and Mechanical Properties of HANA Cladding Tubes. In Proceedings of the KNS Fall Conference, Busan, Republic of Korea, 27–28 October 2005. [Google Scholar]
- IAEA. Thermophysical Properties of Materials for Water Cooled Reactors; IAEA-TECDOC-949; IAEA: Vienna, Austria, 1997. [Google Scholar]
- Geelhood, K.J.; Neyer, C.E.; Luscher, W.G. PNNL Stress/Strain Correlation for Zircaloy; Pacific North-West National Laboratory Report PNNL-17700; U.S. DOE: Washington, DC, USA, 2008.





| Temp. (°C) | Young’s Modulus (GPa) | Shear Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| 21 | 105.678 | 38.999 | 0.355 |
| 290 | 89.005 | 32.436 | 0.372 |
| 325 | 86.836 | 31.577 | 0.375 |
| Input Square Disp. (mm) | Reaction Force (kN) | ||
|---|---|---|---|
| 21 °C | 290 °C | 325 °C | |
| 0.2 | 8 | 7 | 7 |
| 0.5 | 20 | 17 | 17 |
| 1 | 40 | 34 | 33 |
| 1.5 | 60 | 51 | 50 |
| 2 | 80 | 68 | 66 |
| 2.5 | 101 | 85 | 83 |
| 3 | 121 | 102 | 99 |
| 3.5 | 141 | 119 | 116 |
| 4 | 161 | 136 | 132 |
| 4.5 | 181 | 153 | 149 |
| 5 | 201 | 170 | 166 |
| 5.5 | 221 | 187 | 182 |
| 6 | 241 | 204 | 199 |
| 6.5 | 261 | 220 | 215 |
| 7 | 281 | 237 | 232 |
| 7.5 | 302 | 254 | 248 |
| 8 | 322 | 271 | 265 |
| 8.5 | 342 | 288 | 281 |
| 9 | 362 | 305 | 298 |
| 9.5 | 382 | 322 | 314 |
| 10 | 402 | 339 | 331 |
| Input Shear Disp. (mm) | Reaction Force (N) | ||
|---|---|---|---|
| 21 °C | 290 °C | 325 °C | |
| 0.5 | 45 | 39 | 38 |
| 1 | 91 | 77 | 75 |
| 2 | 182 | 154 | 151 |
| 3 | 272 | 232 | 226 |
| 4 | 363 | 309 | 302 |
| 5 | 454 | 386 | 377 |
| 6 | 545 | 463 | 453 |
| 7 | 636 | 540 | 528 |
| 8 | 726 | 618 | 604 |
| 9 | 817 | 695 | 679 |
| 10 | 908 | 772 | 755 |
| 11 | 999 | 849 | 830 |
| 12 | 1090 | 926 | 905 |
| 13 | 1180 | 1004 | 981 |
| 14 | 1271 | 1081 | 1056 |
| 15 | 1362 | 1158 | 1132 |
| 16 | 1453 | 1235 | 1207 |
| 17 | 1544 | 1312 | 1283 |
| 18 | 1634 | 1390 | 1358 |
| 19 | 1725 | 1467 | 1434 |
| 20 | 1816 | 1544 | 1509 |
| Mode | Force (kN) | ||
|---|---|---|---|
| 21 °C | 290 °C | 325 °C | |
| 1 | 14.5 | 12.4 | 12.1 |
| 2 | 14.6 | 12.4 | 12.1 |
| 3 | 15.2 | 12.9 | 12.6 |
| 4 | 15.3 | 13.0 | 12.7 |
| 5 | 18.3 | 15.6 | 15.2 |
| 6 | 18.5 | 15.7 | 15.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adli, N.H.; Namgung, I. An Investigation of Structural Strength of Nuclear Fuel Spacer Grid. Energies 2024, 17, 458. https://doi.org/10.3390/en17020458
Adli NH, Namgung I. An Investigation of Structural Strength of Nuclear Fuel Spacer Grid. Energies. 2024; 17(2):458. https://doi.org/10.3390/en17020458
Chicago/Turabian StyleAdli, Naqeeb Hakam, and Ihn Namgung. 2024. "An Investigation of Structural Strength of Nuclear Fuel Spacer Grid" Energies 17, no. 2: 458. https://doi.org/10.3390/en17020458
APA StyleAdli, N. H., & Namgung, I. (2024). An Investigation of Structural Strength of Nuclear Fuel Spacer Grid. Energies, 17(2), 458. https://doi.org/10.3390/en17020458




