Photovoltaic-Based q-ZSI STATCOM with MDNESOGI Control Scheme for Mitigation of Harmonics
Abstract
1. Introduction
- The suggested architecture improves upon the existing SOGI approach by connecting two analogous filter loops for prominent harmonic components in parallel with the prime loop.
- The suggested structure necessitates a reduced sampling time requirement, hence facilitating expedited creation of reference currents across diverse operating conditions.
- Power quality challenges including reactive power, load balancing, power factor, and DC link voltage stabilization are addressed using the established technique.
- The suggested architecture is developed, and its performance is evaluated and verified in the laboratory on a real-time platform.
2. Related Works
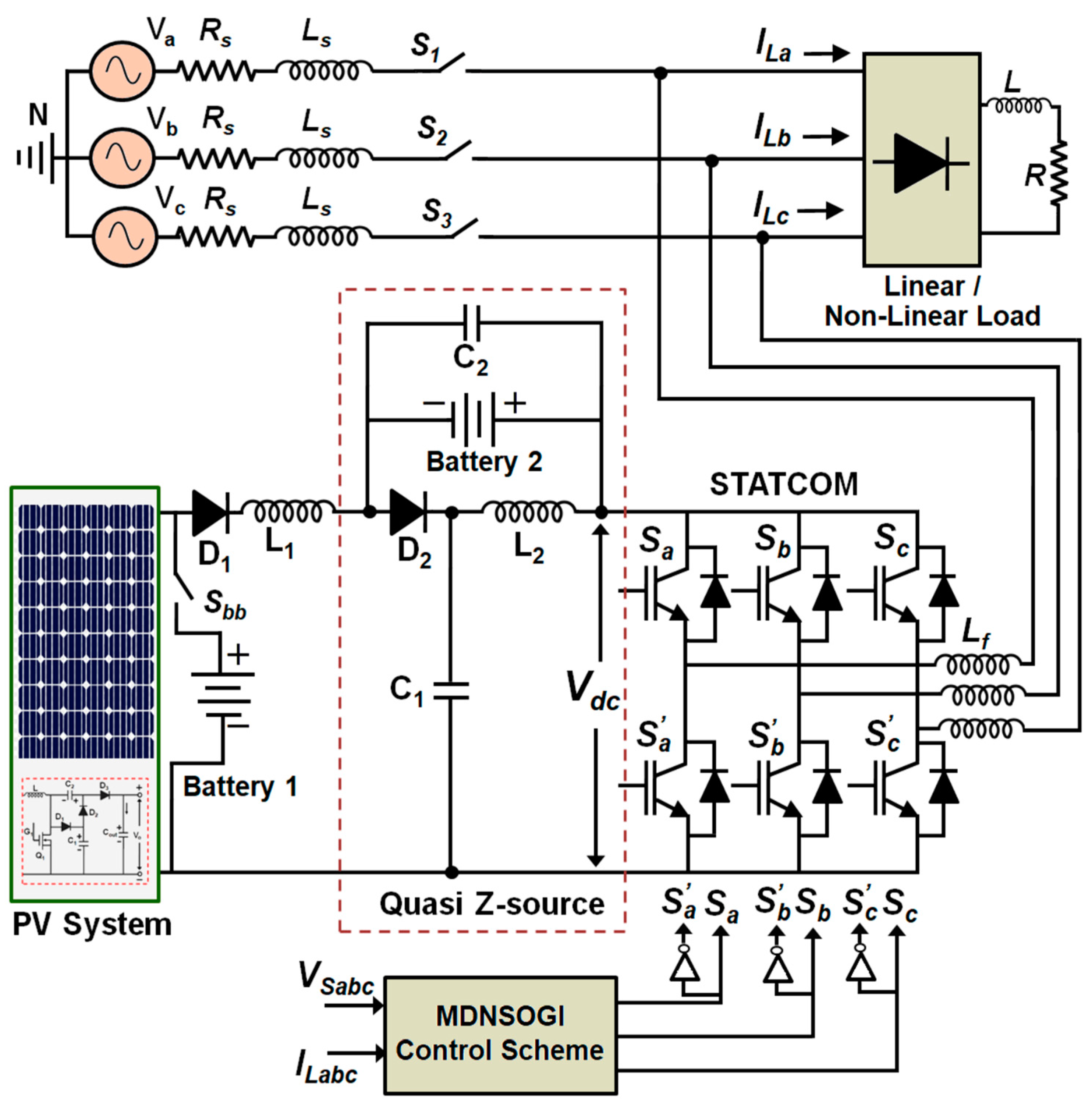
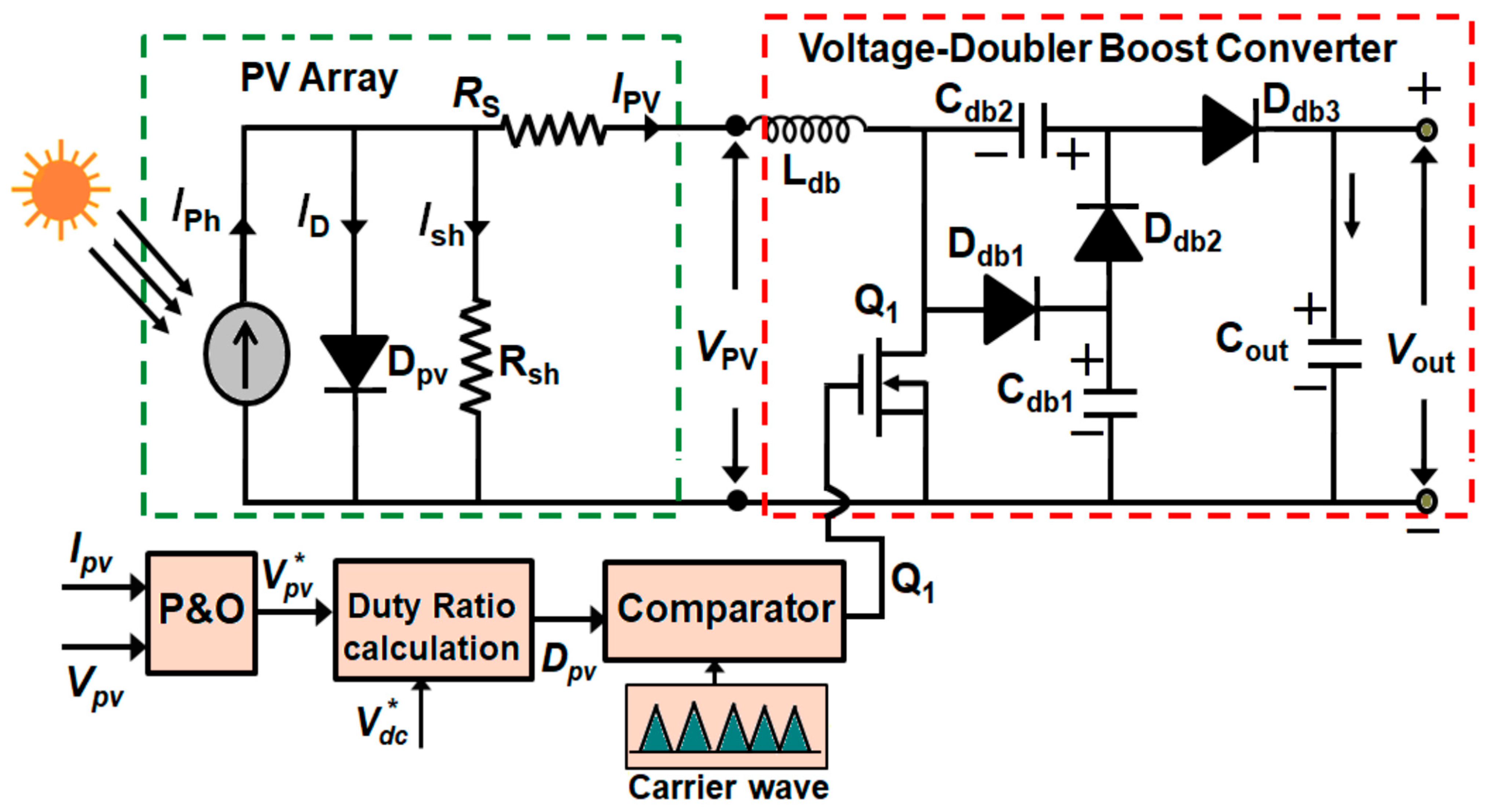
3. System Description
4. Different Operating Modes of PV-Based qZSI-STATCOM
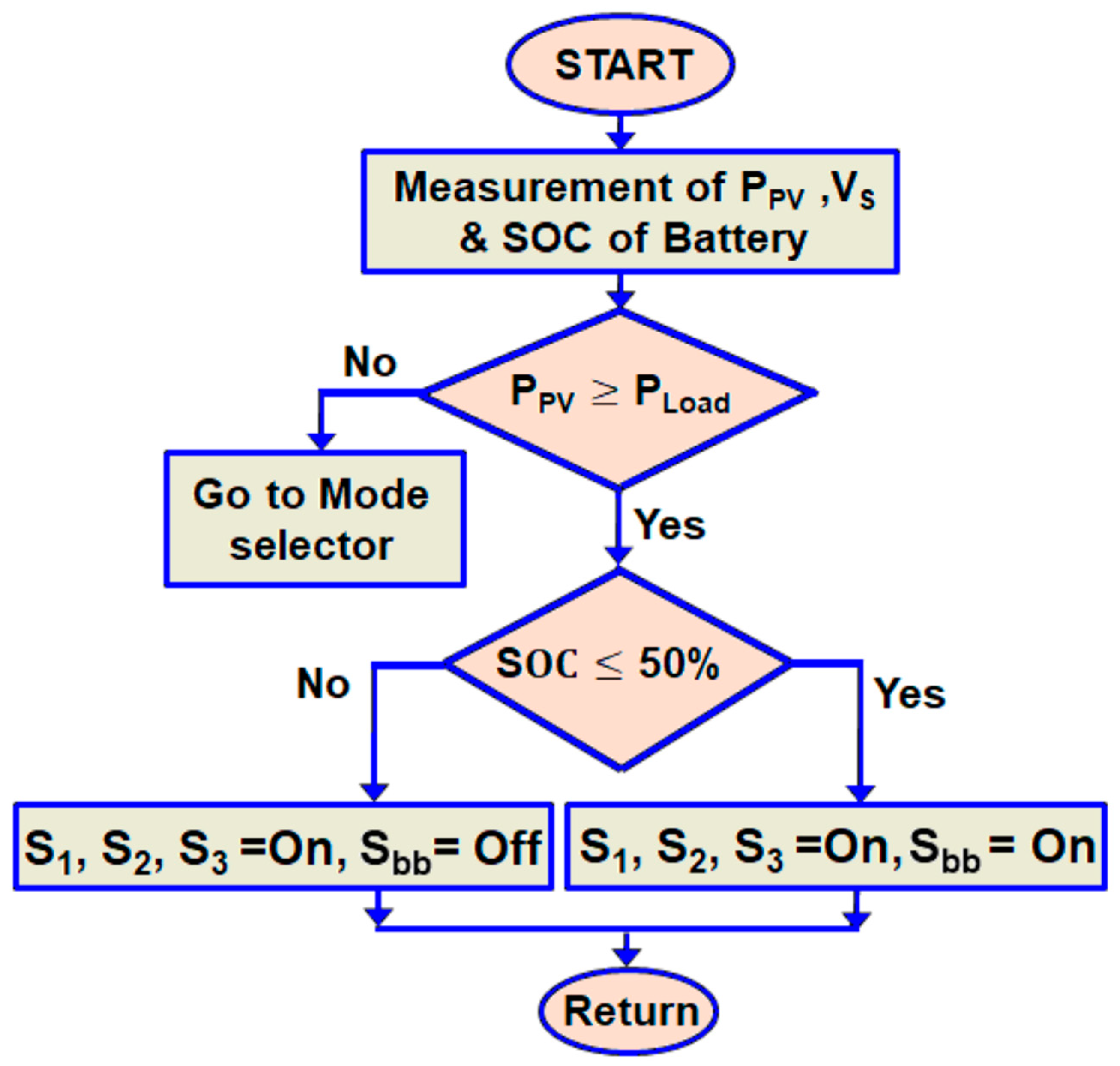
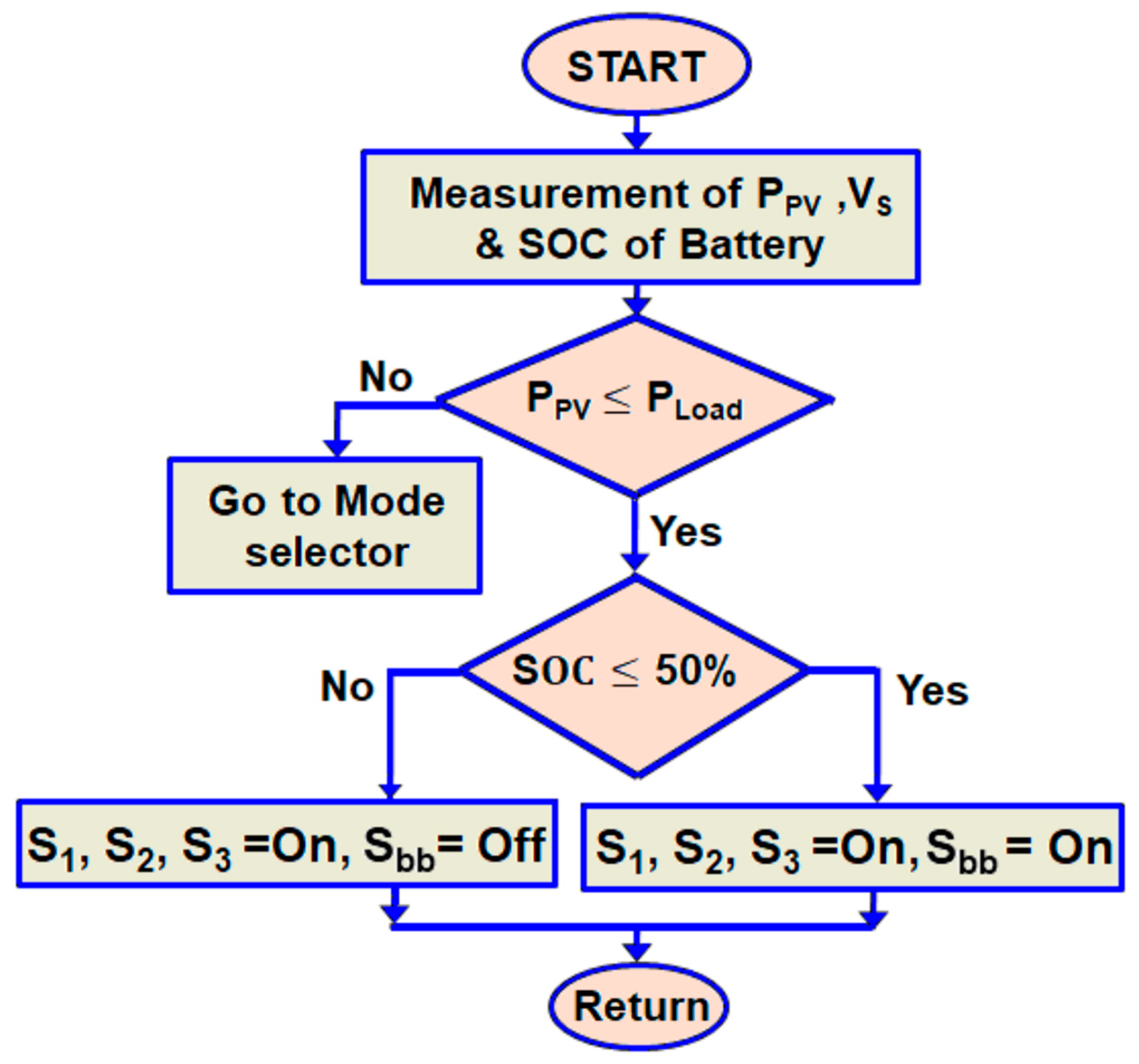
4.1. Mode: 1
4.2. Mode: 2
4.3. Mode: 3
4.4. Mode: 4
5. Control Scheme of PV-qZSI-STATCOM
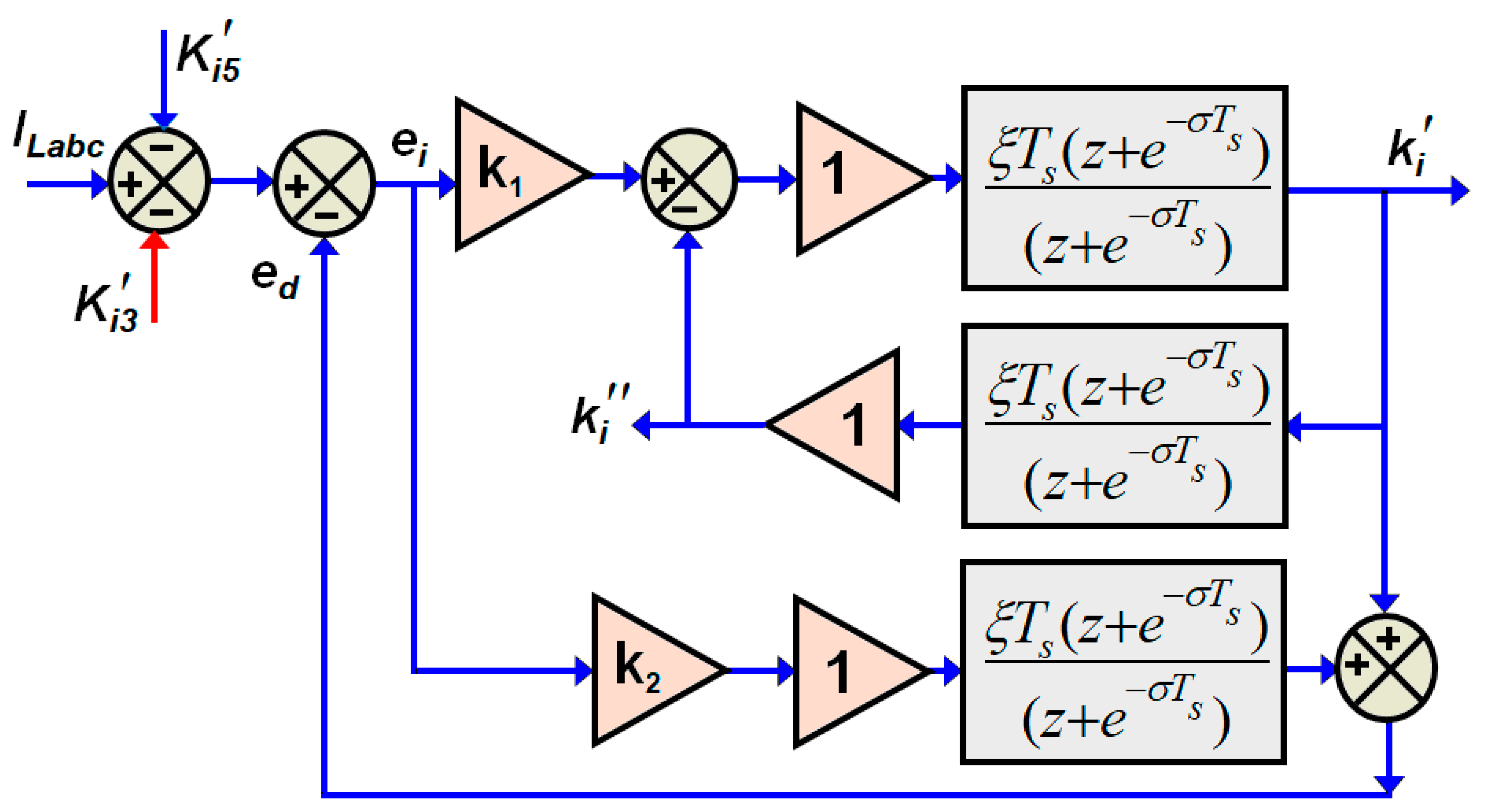
5.1. Current Control Scheme
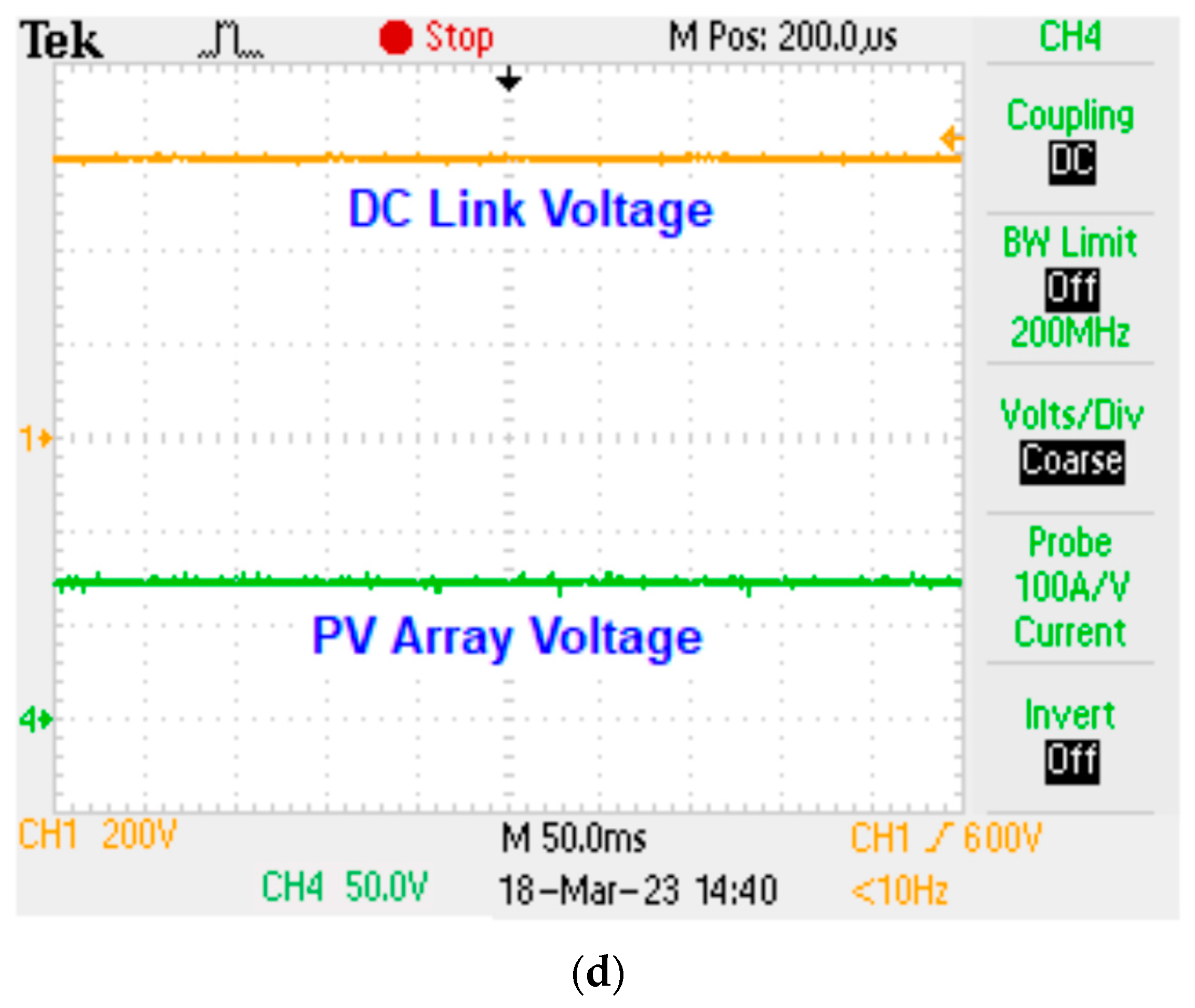
5.2. DC Link Voltage Control
5.3. AC Voltage Control
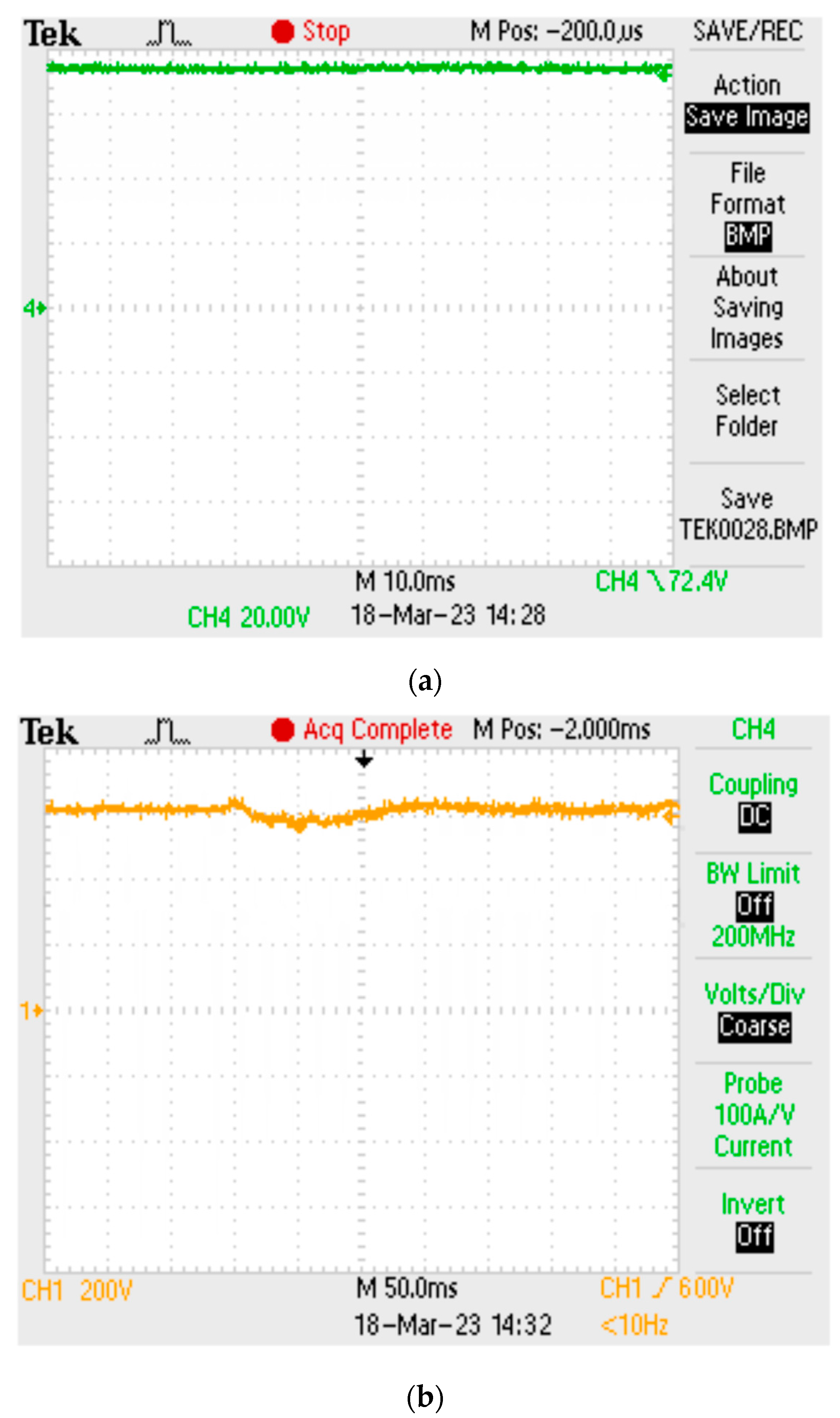
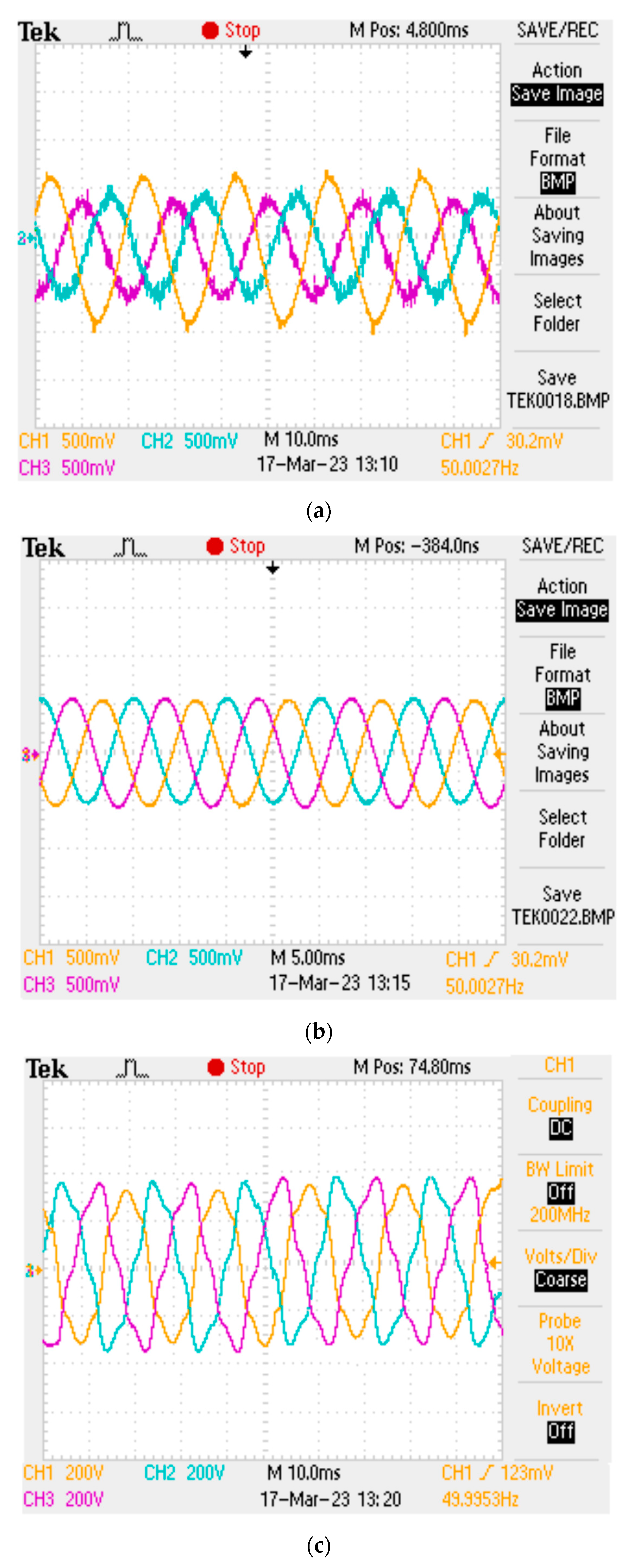
6. Experimental Results and Discussion
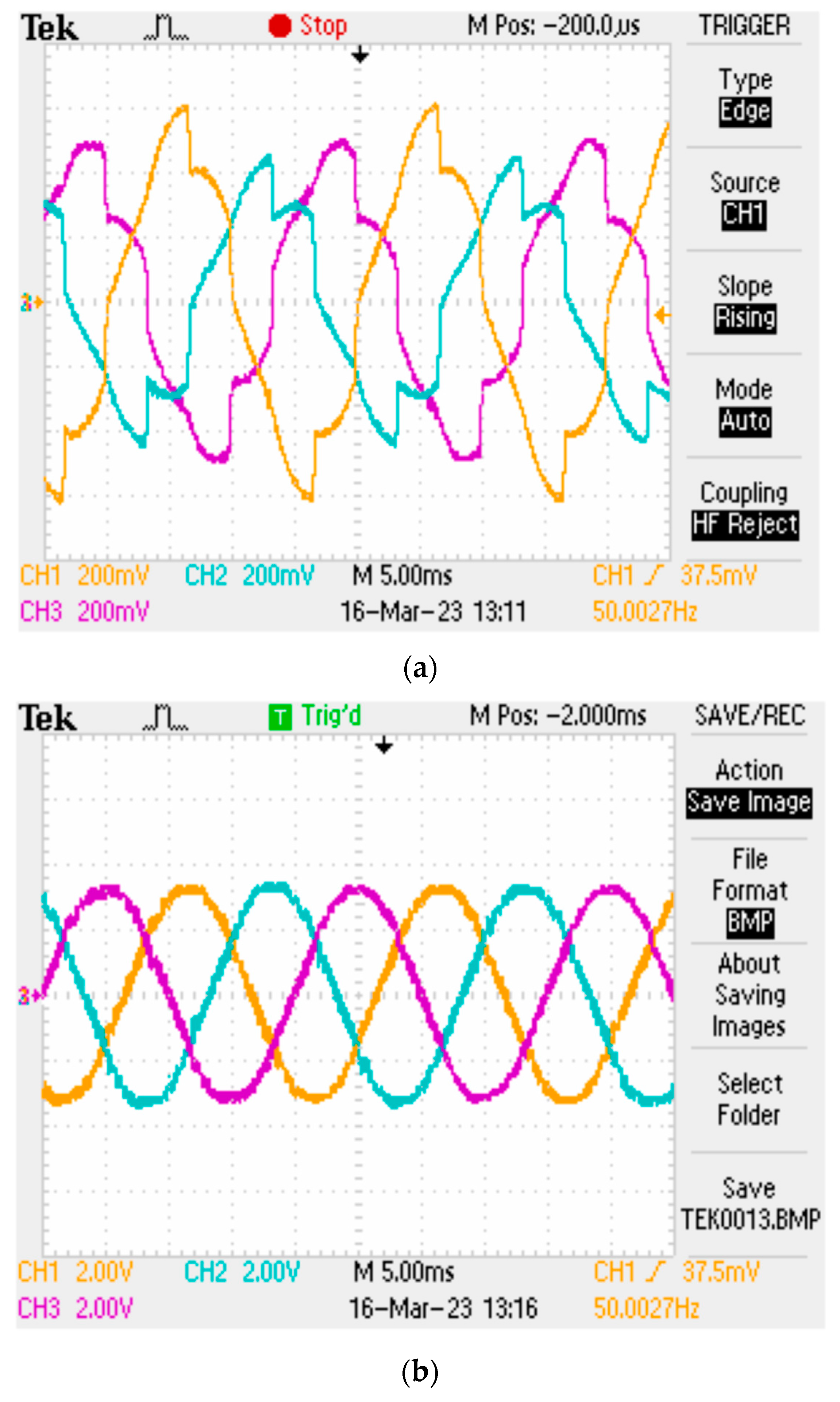
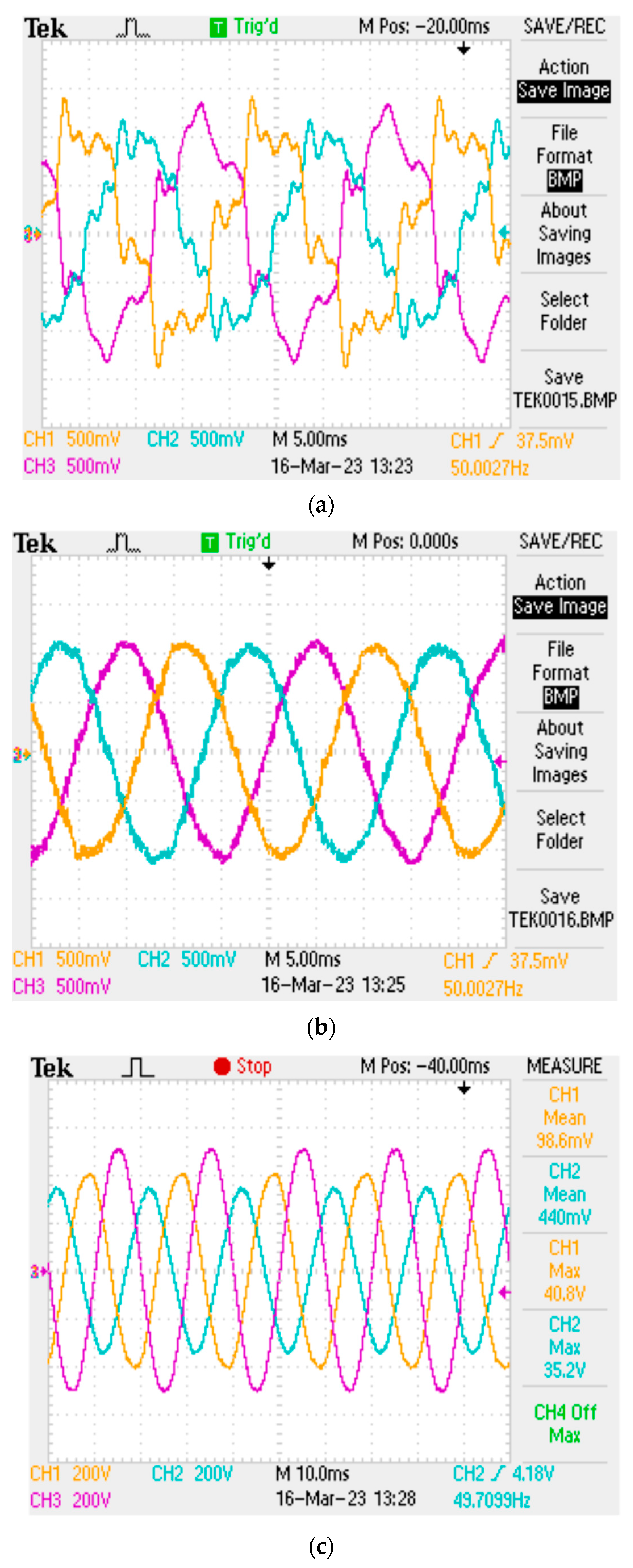
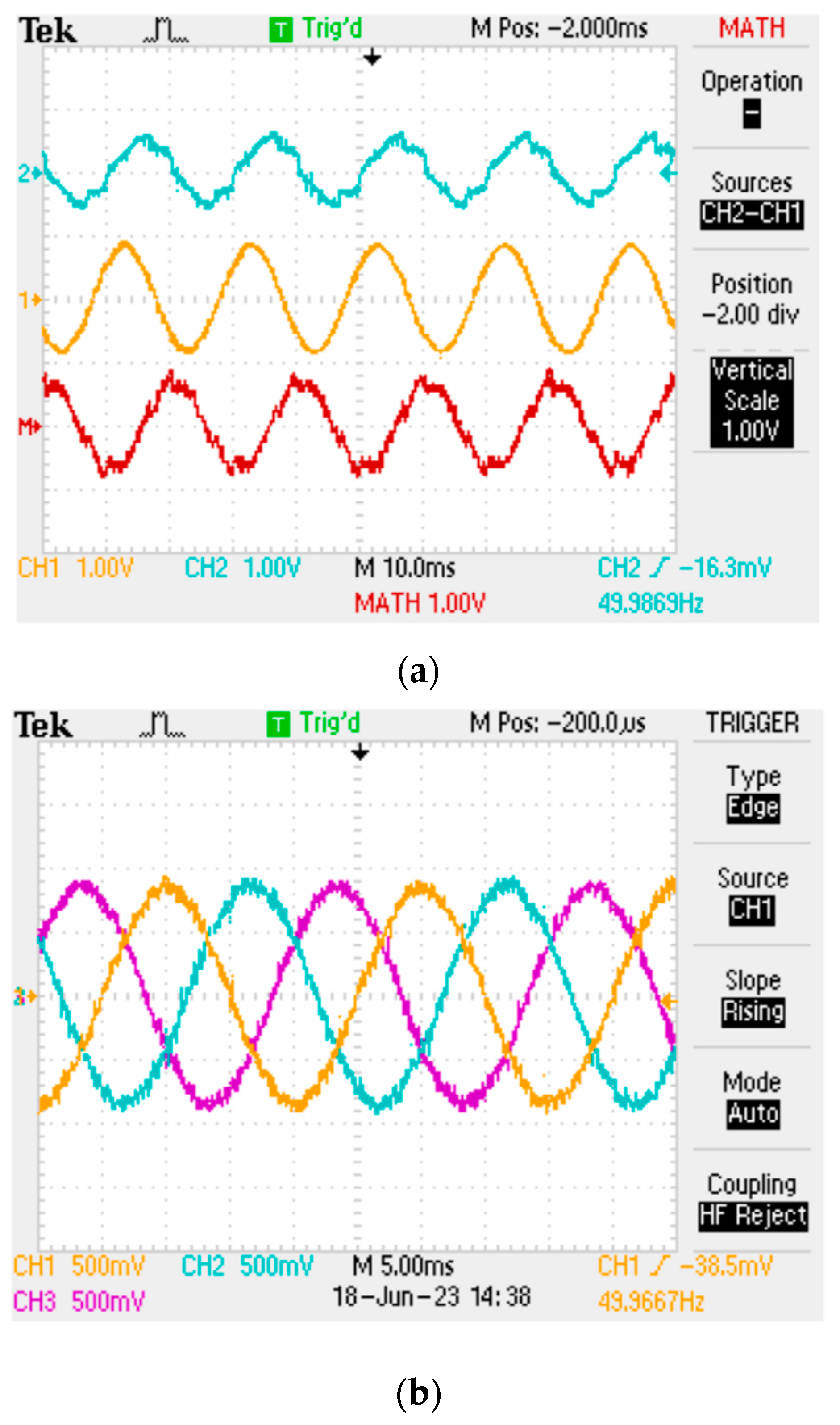
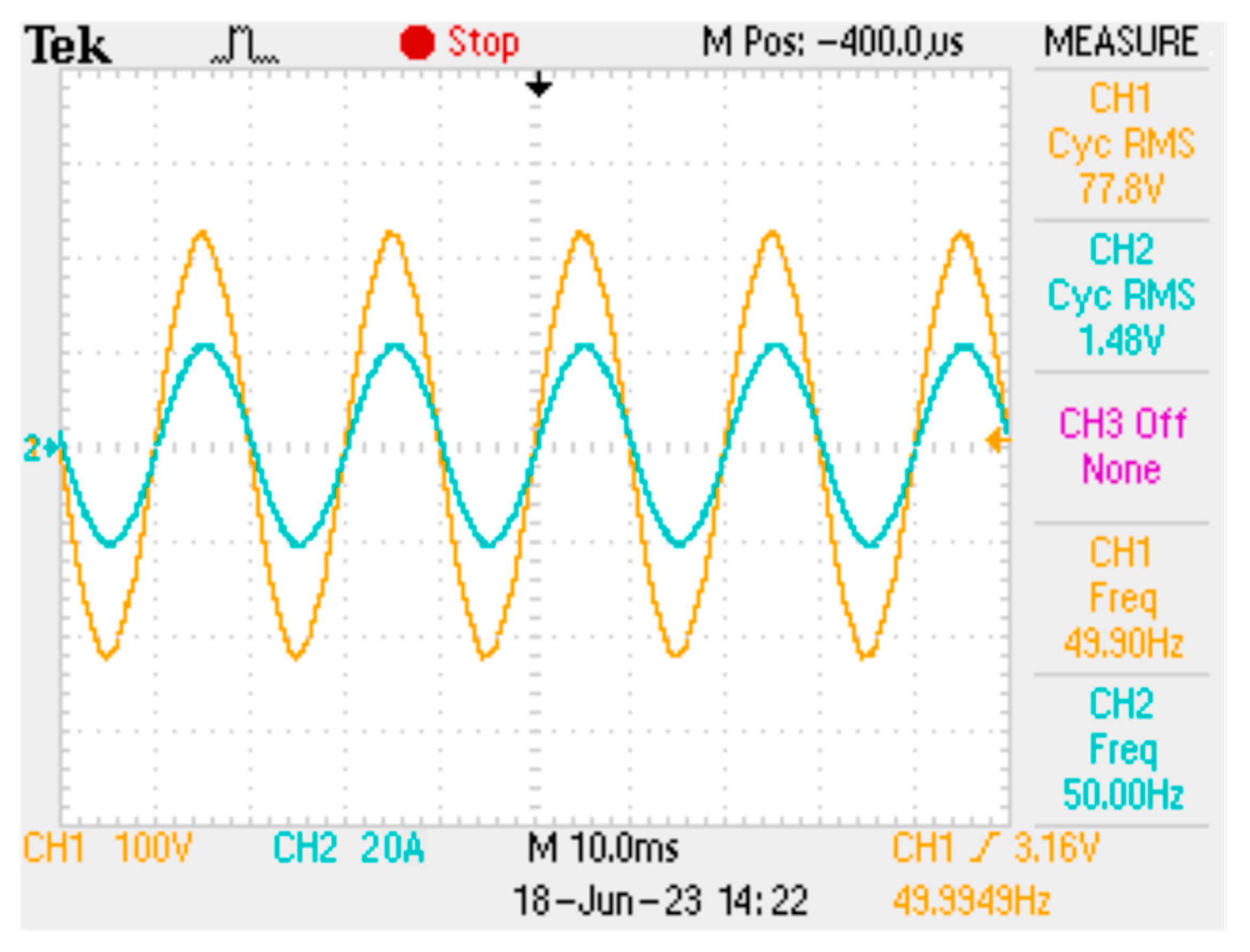
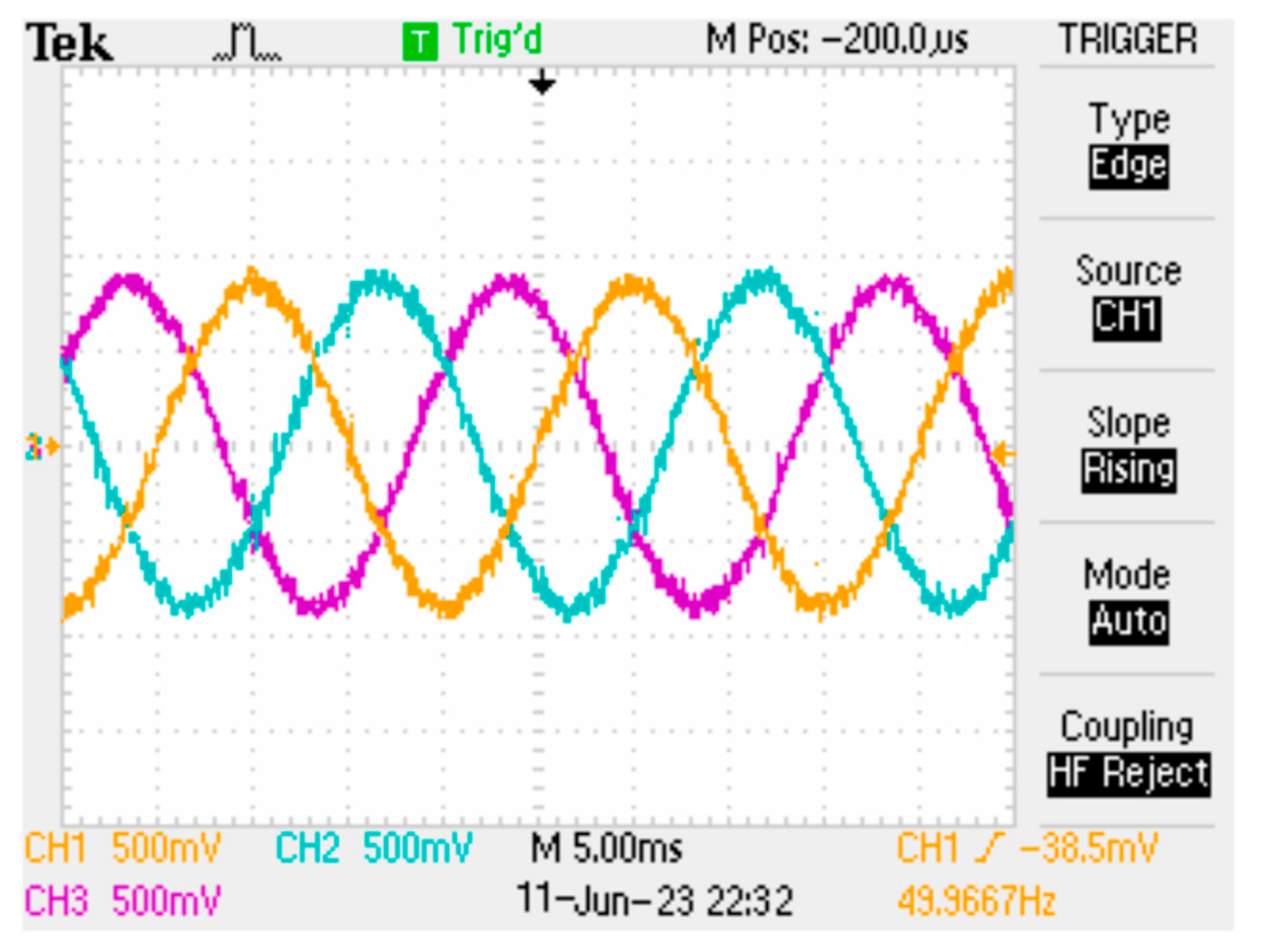
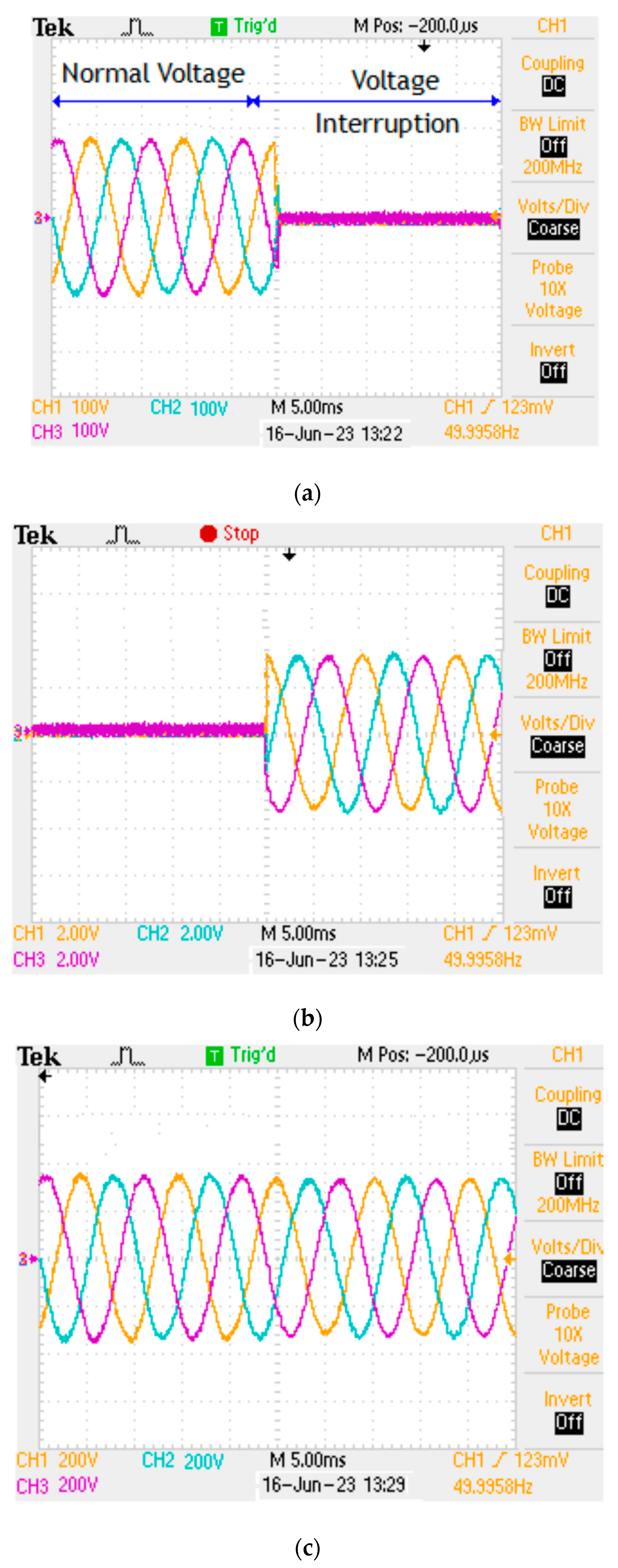
6.1. Case 1: Balanced Voltages with Unbalanced Loads
6.2. Case 2: Unbalanced Voltages with Unbalanced Loads
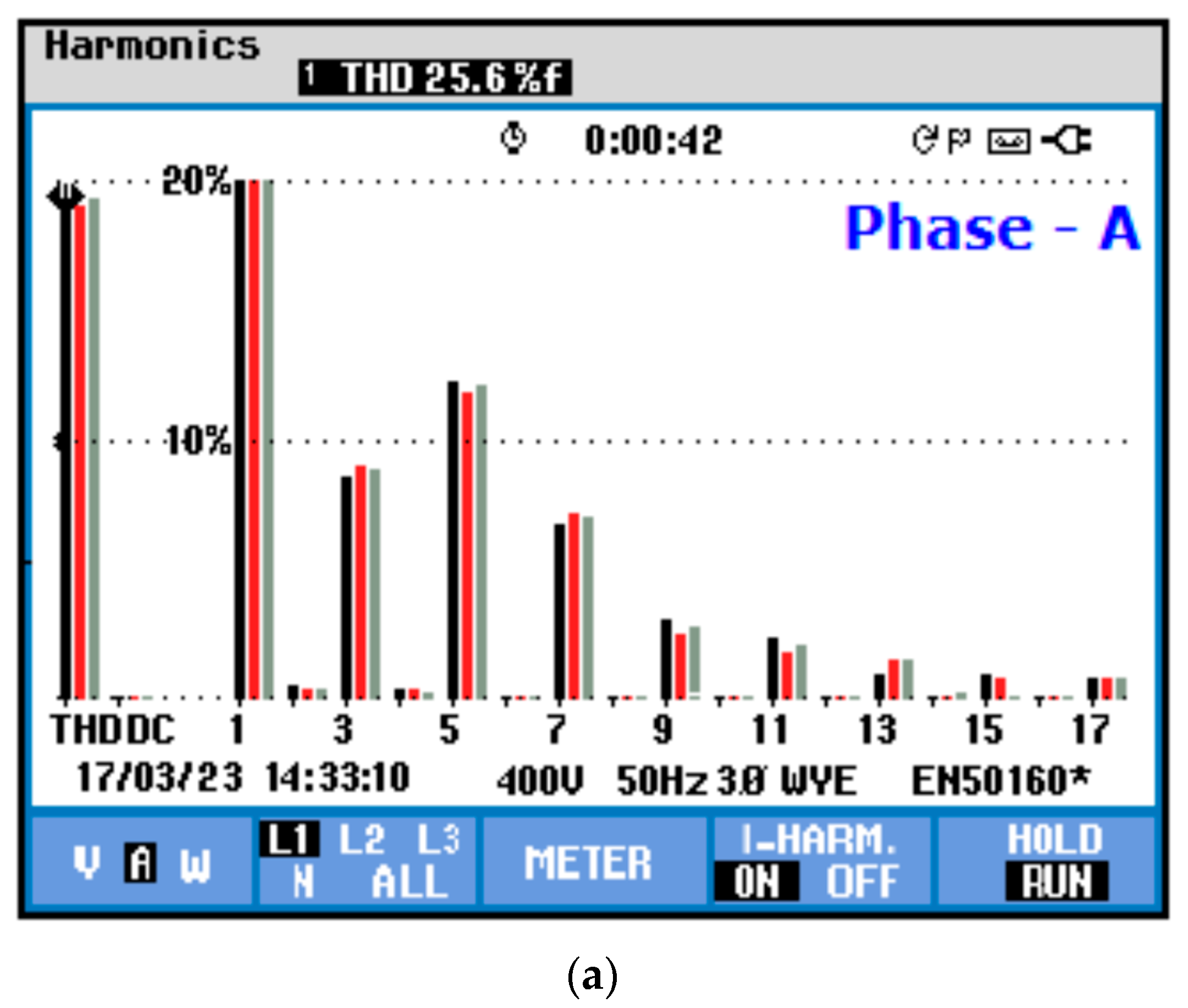
6.3. Case 3: Distorted Voltages with Unbalanced Loads
7. Performance Comparison of Proposed and Conventional Controllers
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Srivastava, M.; Goyal, S.K.; Saraswat, A.; Shekhawat, R.S.; Gangil, G. A Review on Power Quality Problems, Causes and Mitigation Techniques. In Proceedings of the 2022 1st International Conference on Sustainable Technology for Power and Energy Systems (STPES), Srinagar, India, 4–6 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Bollen, M.H. Understanding Power Quality Problems-Voltage Sags and Interruptions; IEEE Press: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Gao, M.; Awodele, K. Investigation of power electronics solutions to power quality problems in distribution networks. In Proceedings of the AFRICON 2015, Addis Ababa, Ethiopia, 14–17 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sepasi, S.; Talichet, C.; Pramanik, A.S. Power Quality in Microgrids: A Critical Review of Fundamentals, Standards, and Case Studies. IEEE Access 2023, 11, 108493–108531. [Google Scholar] [CrossRef]
- Ezhiljenekkha, B.; MarsalineBeno, M. Review of Power Quality Issues in Solar and Wind Energy. Mater. Today Proc. 2020, 24, 2137–2143. [Google Scholar] [CrossRef]
- Gupta, A. Power quality evaluation of photovoltaic grid interfaced cascaded H-bridge nine-level multilevel inverter systems using D-STATCOM and UPQC. Energy 2022, 238, 121707. [Google Scholar] [CrossRef]
- Houran, M.A.; Sabzevari, K.; Hassan, A.; Oubelaid, A.; Tostado-Véliz, M.; Khosravi, N. Active power filter module function to improve power quality conditions using GWO and PSO techniques for solar photovoltaic arrays and battery energy storage systems. J. Energy Storage 2023, 72, 108552. [Google Scholar] [CrossRef]
- Harirchi, F.; Simões, M.G. Enhanced Instantaneous Power Theory Decomposition for Power Quality Smart Converter Applications. IEEE Trans. Power Electron. 2018, 33, 9344–9359. [Google Scholar] [CrossRef]
- Han, Y.; Fang, X.; Yang, P.; Wang, C.; Xu, L.; Guerrero, J.M. Stability Analysis of Digital-Controlled Single-Phase Inverter with Synchronous Reference Frame Voltage Control. IEEE Trans. Power Electron. 2018, 33, 6333–6350. [Google Scholar] [CrossRef]
- Yallamilli, R.S.; Mishra, M.K. Instantaneous Symmetrical Component Theory Based Parallel Grid Side Converter Control Strategy for Microgrid Power Management. IEEE Trans. Sustain. Energy 2019, 10, 682–692. [Google Scholar] [CrossRef]
- Liang, X. Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Azbe, V.; Mihalic, R. STATCOM control strategies in energy-function-based methods for the globally optimal control of renewable sources during transients. Int. J. Electr. Power Energy Syst. 2022, 141, 108145. [Google Scholar] [CrossRef]
- Patel, N.; Gupta, N.; Babu, B.C. Photovoltaic system operation as DSTATCOM for power quality improvement employing active current control. IET Gener. Trans. Distrib. 2020, 14, 3518–3529. [Google Scholar] [CrossRef]
- Badoni, M.; Singh, A.; Singh, B. Comparative Performance of Wiener Filter and Adaptive Least Mean Square-Based Control for Power Quality Improvement. IEEE Trans. Ind. Electron. 2016, 63, 3028–3037. [Google Scholar] [CrossRef]
- Singh, B.; Solanki, J. A Comparison of Control Algorithms for DSTATCOM. IEEE Trans. Ind. Electron. 2009, 56, 2738–2745. [Google Scholar] [CrossRef]
- Liu, A.; Li, H. Stabilization of Delayed Boolean Control Networks with State Constraints: A Barrier Lyapunov Function Method. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2553–2557. [Google Scholar] [CrossRef]
- Giri, A.K.; Arya, S.R.; Maurya, R.; Babu, B.C. VCO-Less PLL Control-Based Voltage-Source Converter for Power Quality Improvement in Distributed Generation System. IET Electr. Power Appl. 2019, 13, 1114–1124. [Google Scholar] [CrossRef]
- Ram, A.; Sharma, P.R.; Ahuja, R.K. Enhancement of power quality using U-SOGI based control algorithm for DSTATCOM. Ain Shams Eng. J. 2023, 2023, 102296. [Google Scholar] [CrossRef]
- Astero, P.; Söder, L. Improving PV Dynamic Hosting Capacity Using Adaptive Controller for STATCOMs. IEEE Trans. Energy Convers. 2019, 34, 415–425. [Google Scholar] [CrossRef]
- Rashad, A.; Kamel, S.; Jurado, F.; Abdel-Nasser, M.; Mahmoud, K. ANN-Based STATCOM Tuning for Performance Enhancement of Combined Wind Farms. Electr. Power Compon. Syst. 2019, 47, 10–26. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Cao, D.; Yi, J.; Huang, Q.; Liu, Z.; Chen, Z.; Blaabjerg, F. A Data-Driven Approach for Designing STATCOM Additional Damping Controller for Wind Farms. Int. J. Electr. Power Energy Syst. 2020, 117, 105620. [Google Scholar] [CrossRef]
- Kamel, O.M.; Diab, A.A.Z.; Do, T.D.; Mossa, M.A. A Novel Hybrid Ant Colony-Particle Swarm Optimization Techniques Based Tuning STATCOM for Grid Code Compliance. IEEE Access 2020, 8, 41566–41587. [Google Scholar] [CrossRef]
- Bakir, H.; Kulaksiz, A.A. Modelling and Voltage Control of the Solar-Wind Hybrid Micro-grid with Optimized STATCOM Using GA and BFA. Eng. Sci. Technol. Int. J. 2020, 23, 576–584. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.; Ashfaq, H. Stability Enhancement of Induction Generator–Based Series Compensated Wind Power Plants by Alleviating Subsynchronous Torsional Oscillations Using BFOA-Optimal Controller Tuned STATCOM. Wind Energy 2020, 23, 1846–1867. [Google Scholar] [CrossRef]
- Fatama, A.Z.; Khan, M.A.; Kurukuru, V.S.B.; Haque, A.; Blaabjerg, F. Coordinated Reactive Power Strategy Using Static Synchronous Compensator for Photovoltaic Inverters. Int. Trans. Electr. Energy Syst. 2020, 30, 1–18. [Google Scholar] [CrossRef]
- Sonawane, A.J.; Umarikar, A.C. Voltage and Reactive Power Regulation with Synchronverter-Based Control of PV-STATCOM. IEEE Access 2023, 11, 52129–52140. [Google Scholar] [CrossRef]
- Raja, A.; Vijayakumar, M.; Karthikeyan, C. Solar Photovoltaic Interconnected ZSI-Unified Power Quality Conditioner to Enhance Power Quality. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e140015. [Google Scholar] [CrossRef]
- Muthuvel, K.; Vijayakumar, M. Solar PV Sustained Quasi Z-Source Network-Based Unified Power Quality Conditioner for Enhancement of Power Quality. Energies 2020, 13, 2657. [Google Scholar] [CrossRef]
- Xie, M.; Wen, H.; Zhu, C.; Yang, Y. DC Offset Rejection Improvement in Single-Phase SOGI-PLL Algorithms: Methods Review and Experimental Evaluation. IEEE Access 2017, 5, 12810–12819. [Google Scholar] [CrossRef]
- Varma, R.K.; Siavashi, E.M. PV-STATCOM: A New Smart Inverter for Voltage Control in Distribution Systems. IEEE Trans. Sustain. Energy 2018, 9, 1681–1691. [Google Scholar] [CrossRef]
- Gawhade, P.; Ojha, A. Recent Advances in Synchronization Techniques for Grid-Tied PV System: A Review. Energy Rep. 2021, 7, 6581–6599. [Google Scholar] [CrossRef]
- IEEE Std. 519-1992; IEEE Recommended Practices and Requirement for Harmonic Control on Electric Power System. IEEE Std.: New York, NY, USA, 1992; p. 519.
- European Standard EN50160 (1999). Voltage Characteristics of Electricity Supplied by Public Distribution System. CENELEC: Brussels, Belgium, 1999.
- Jahnavi, B.; Karanki, S.B.; Kar, P.K. Power Quality Improvement with D-STATCOM Using Combined PR and Comb Filter-Controller. In Proceedings of the 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sayahi, K.; Kadri, A.; Bacha, F.; Marzougui, H. Implementation of a D-STATCOM Control Strategy Based on Direct Power Control Method for Grid Connected Wind Turbine. Int. J. Electr. Power Energy Syst. 2020, 121, 106105. [Google Scholar] [CrossRef]
- Alvaro, R.; Águila Téllez, A.; Ortiz, L. Optimal Location and Sizing of a D-STATCOM in Electrical Distribution Systems to Improve the Voltage Profile Considering the Restriction of Harmonic Injection through the JAYA Algorithm. Energies 2023, 16, 7683. [Google Scholar] [CrossRef]






| Design Approach | Control Technique | Remarks |
|---|---|---|
| Adaptive law [20] | Adaptive Control | The performance of the controller is contingent upon the state of the system. |
| ANN [21] | Soft computing | It takes a lot of time and energy to train an agent and fine-tune the control parameters. |
| DDPG [22] | Soft computing | The process of agent training and control parameter tuning necessitates a substantial investment of time and effort. |
| ACO and PSO [23] | Soft computing | The procedure of tuning requires additional time. |
| GA and BFA [24] | Soft computing | Tuning is a time-consuming procedure. |
| BFA [25] | Soft computing | The design of the controller is founded upon the utilization of a linearized model or an equivalent circuit. |
| Coordinated control of STATCOM and PV inverter [26] | Coordinated control | The complexity of computations arises from the utilization of SVM for fault classification. |
| Synchronverter-based PV system [27] | Synchronverter | Need improvement in dynamic characteristics. |
| Modes | Status of the Mode Selector Switches | |||
|---|---|---|---|---|
| S1 | S2 | S3 | Sbb | |
| Mode 1 | ON | ON | ON | ON/OFF |
| Mode 2 | ON | ON | ON | ON/OFF |
| Mode 3 | ON | ON | ON | OFF |
| Mode 4 | OFF | OFF | OFF | ON/OFF |
| Parameter | Rating | Symbol |
|---|---|---|
| Nominal voltage | 400 V, 230 V | VL, Vph |
| Frequency of the system | 50 Hz | f |
| STATCOM | ||
| Filter inductance | 26 mH | Lf |
| Resistance | 1.5 Ω | Rf |
| Switching frequency | 10 kHz | fs |
| IGBT | 600 V, 20 A, reactive power range: 2000 kVAR | |
| MOSFET | 60 A, 300 V | |
| Gate Driver | LM5112 | |
| Voltage-Current Sensor | Maximum sample rate: 1 kHz Voltage Range: ±10 V | |
| Battery | ||
| Battery capacity | 500 Ah | Ah |
| PV Array | ||
| Power output of PV array | 400 w | PVw |
| PV nominal voltage | 72 V | VPV |
| Voltage Doubler | ||
| Inductance | 48 µH | Ldb |
| Capacitance | 3.151 µF, 1.062 µF, 1000 µF | Cdb, Cdb, Cout |
| Switching frequency | 20 kHz | fsD |
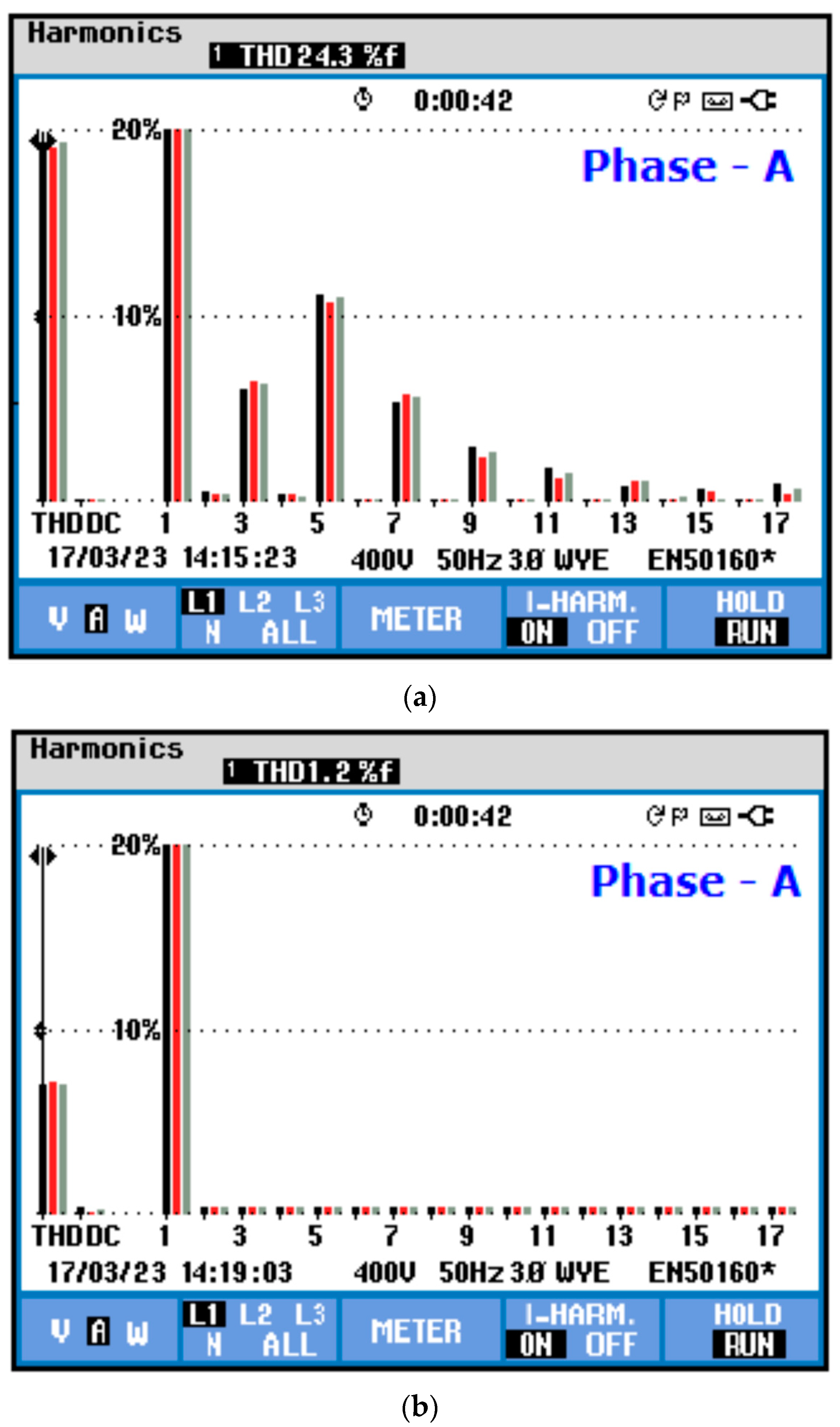
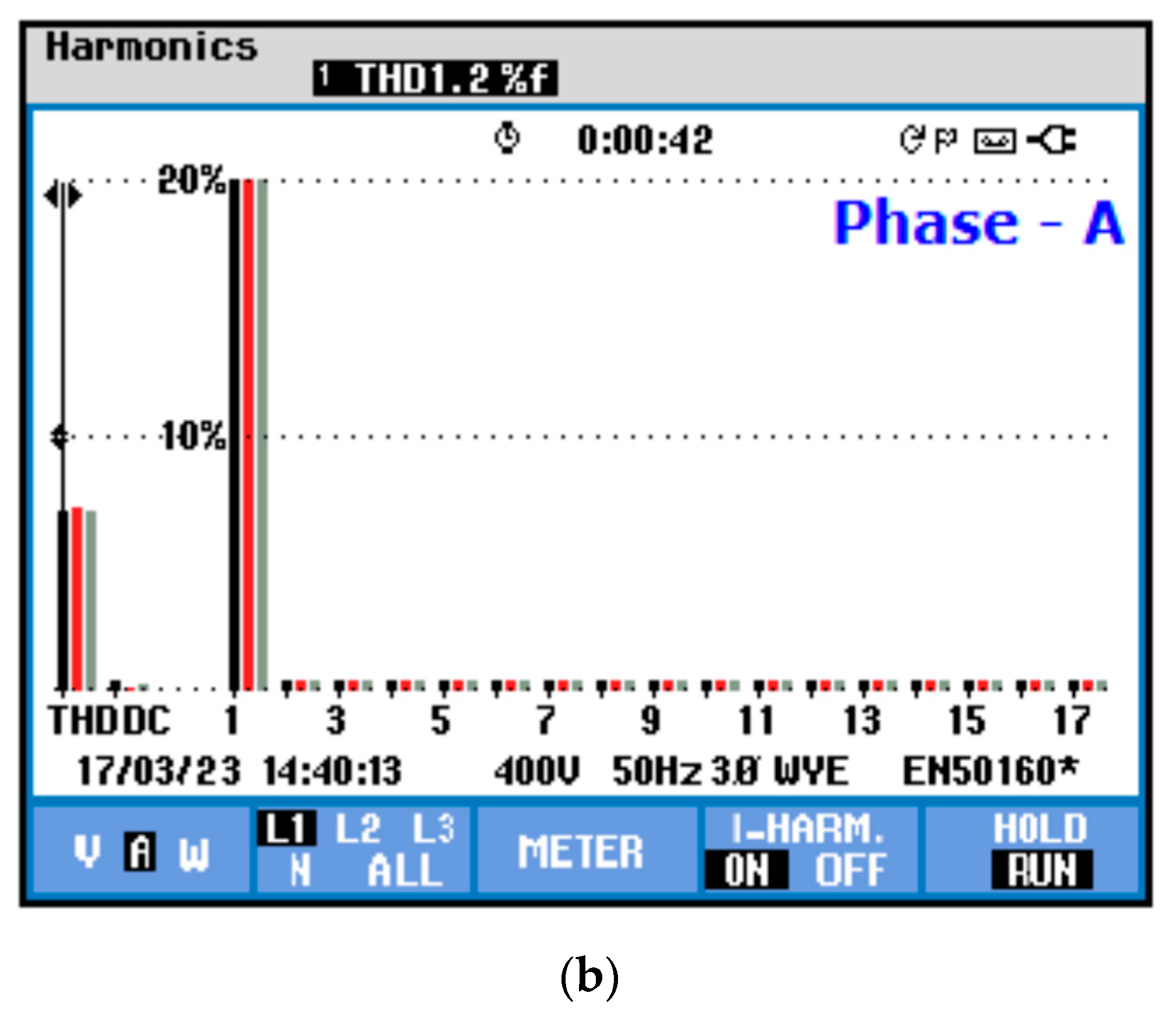
| THD Results of Experimentation | ||||||
|---|---|---|---|---|---|---|
| Case Study | Before Compensation THD (%) | After Compensation THD (%) | ||||
| Phase-A | Phase-B | Phase-C | Phase-A | Phase-B | Phase-C | |
| 1 | 24.3 | 24.4 | 24.3 | 1.2 | 1.2 | 1.2 |
| 2 | 25.7 | 25.5 | 25.6 | 1.2 | 1.2 | 1.2 |
| 3 | 25.6 | 25.5 | 25.5 | 1.2 | 1.2 | 1.2 |
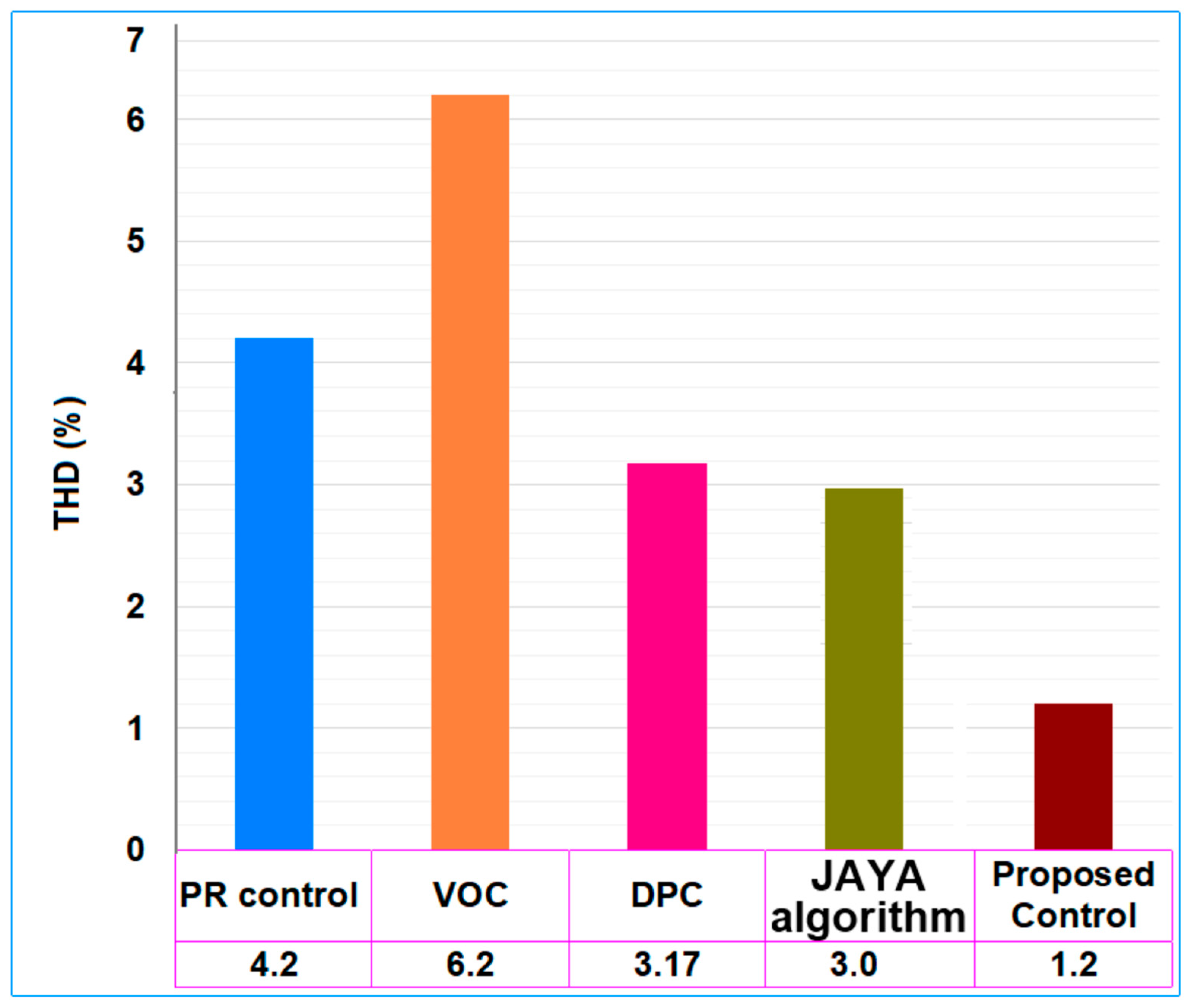
| Control Strategy | THD (%) | Proficiency of DC Offset Rejection | Steady-State Error | Compensation Capability | Power Loss | Energy Source/Energy Storage |
|---|---|---|---|---|---|---|
| Proportional Resonant (PR) Controller [34] | 4.2 | No | Slow | Short-term | High | Capacitor |
| Voltage Oriented Control [35] | 6.20 | Less Rejection | Moderate | Short-term | Moderate | Capacitor |
| Direct Power Control [35] | 3.17 | No | Moderate | Short-term | Moderate | Capacitor |
| JAYA Algorithm [36] | 3.0 | No | Moderate | Short-term | Moderate | Battery |
| Proposed Control Scheme | 1.2 | More rejection | Quick response | Long-term | Low | PV/Battery |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nallaiyagounder, K.; Madhaiyan, V.; Murugesan, R.; Aldosari, O. Photovoltaic-Based q-ZSI STATCOM with MDNESOGI Control Scheme for Mitigation of Harmonics. Energies 2024, 17, 534. https://doi.org/10.3390/en17020534
Nallaiyagounder K, Madhaiyan V, Murugesan R, Aldosari O. Photovoltaic-Based q-ZSI STATCOM with MDNESOGI Control Scheme for Mitigation of Harmonics. Energies. 2024; 17(2):534. https://doi.org/10.3390/en17020534
Chicago/Turabian StyleNallaiyagounder, Kanagaraj, Vijayakumar Madhaiyan, Ramasamy Murugesan, and Obaid Aldosari. 2024. "Photovoltaic-Based q-ZSI STATCOM with MDNESOGI Control Scheme for Mitigation of Harmonics" Energies 17, no. 2: 534. https://doi.org/10.3390/en17020534
APA StyleNallaiyagounder, K., Madhaiyan, V., Murugesan, R., & Aldosari, O. (2024). Photovoltaic-Based q-ZSI STATCOM with MDNESOGI Control Scheme for Mitigation of Harmonics. Energies, 17(2), 534. https://doi.org/10.3390/en17020534






