Asymmetric Operation of Power Networks, State of the Art, Challenges, and Opportunities
Abstract
:1. Introduction
2. Definitions
2.1. Symmetry in Power Systems
2.2. Needs for Asymmetric Operation of Power Lines
2.3. Security of Supply Enhancement by Asymmetrical Operation of Transmission Lines
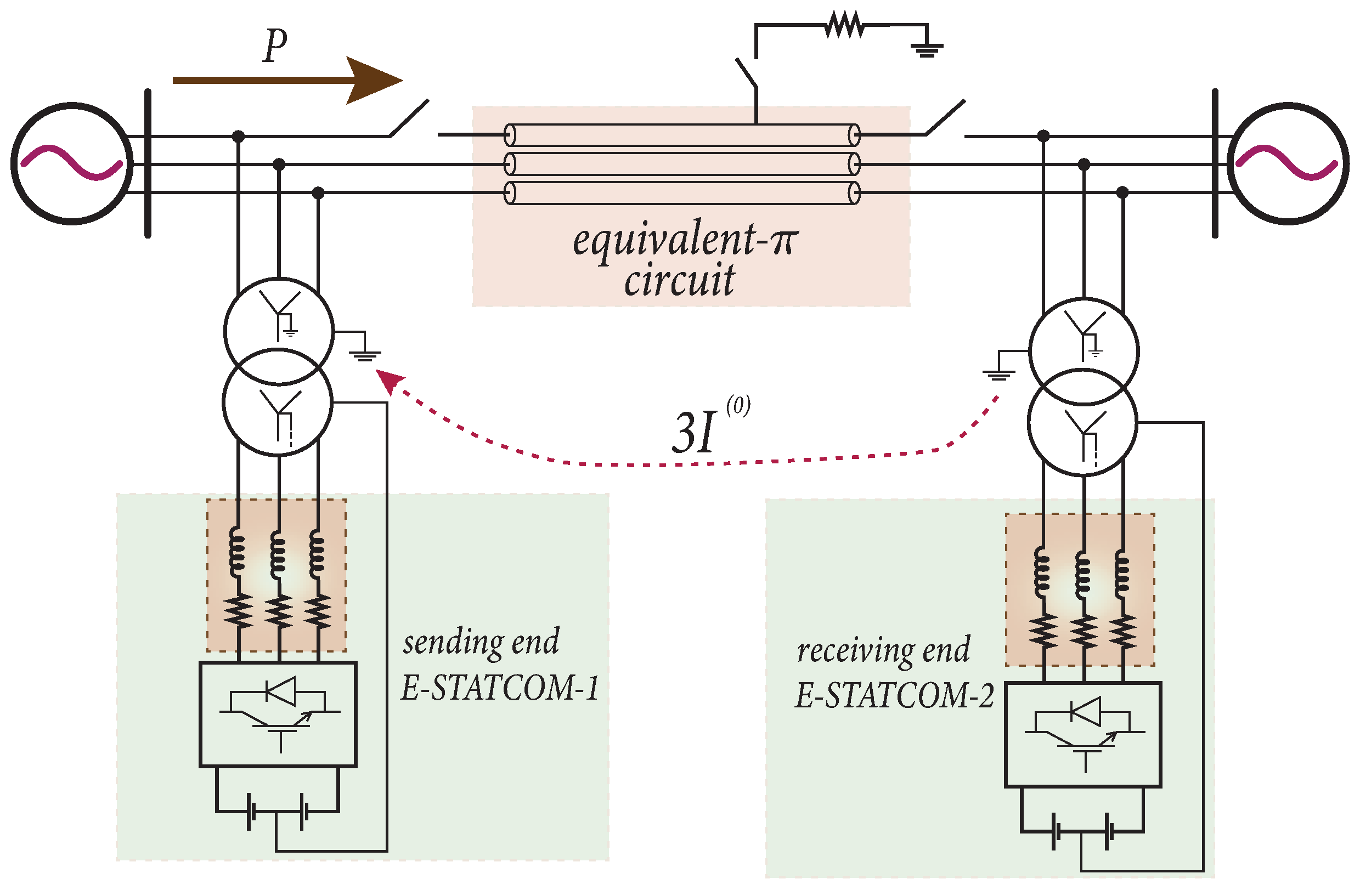
3. Historical Approaches to Power Line Asymmetrical Operation
3.1. Conceptual Approach
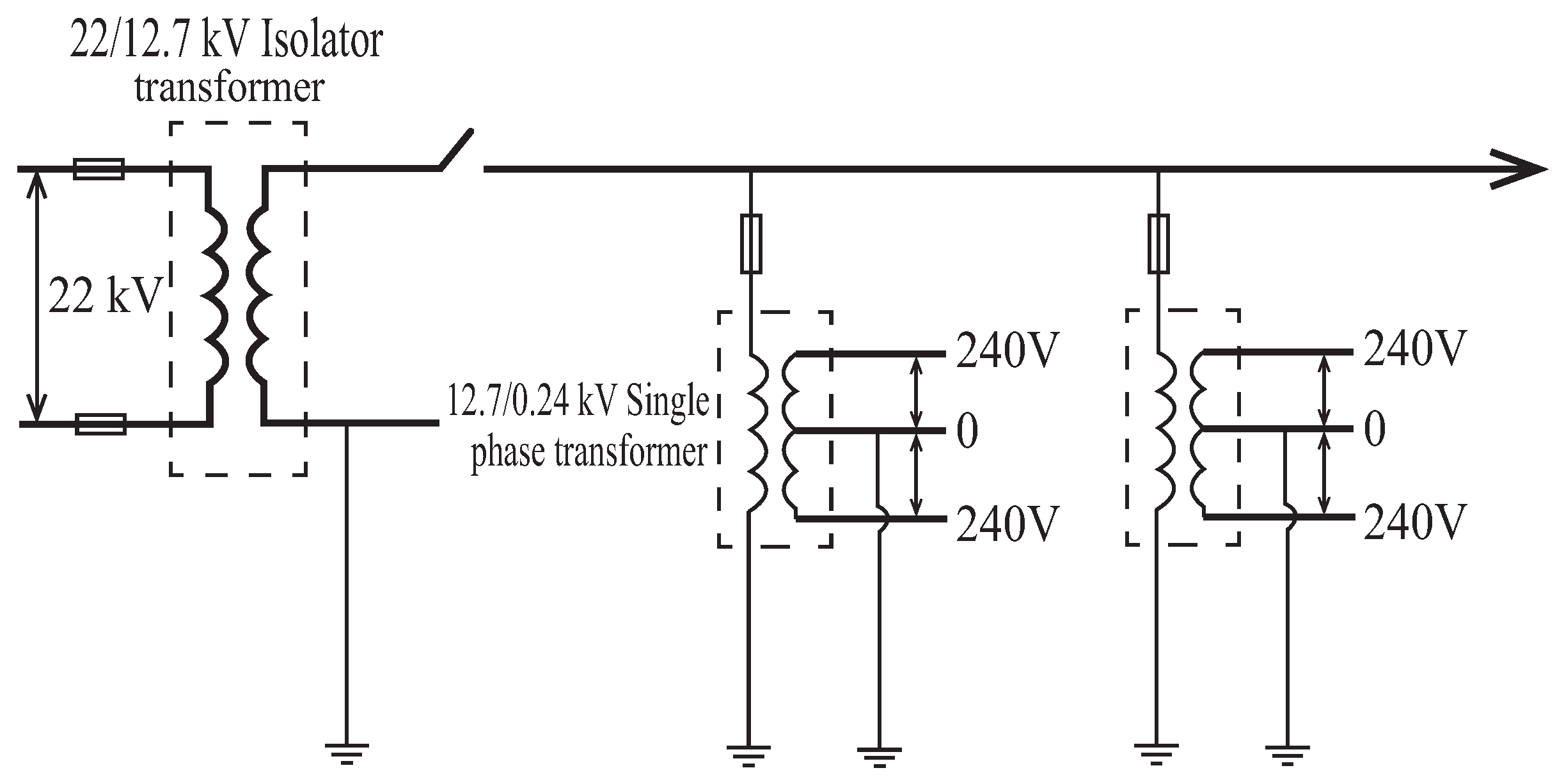
3.2. Unbalanced and Asymmetric Operation in Low-Voltage and Distribution Systems
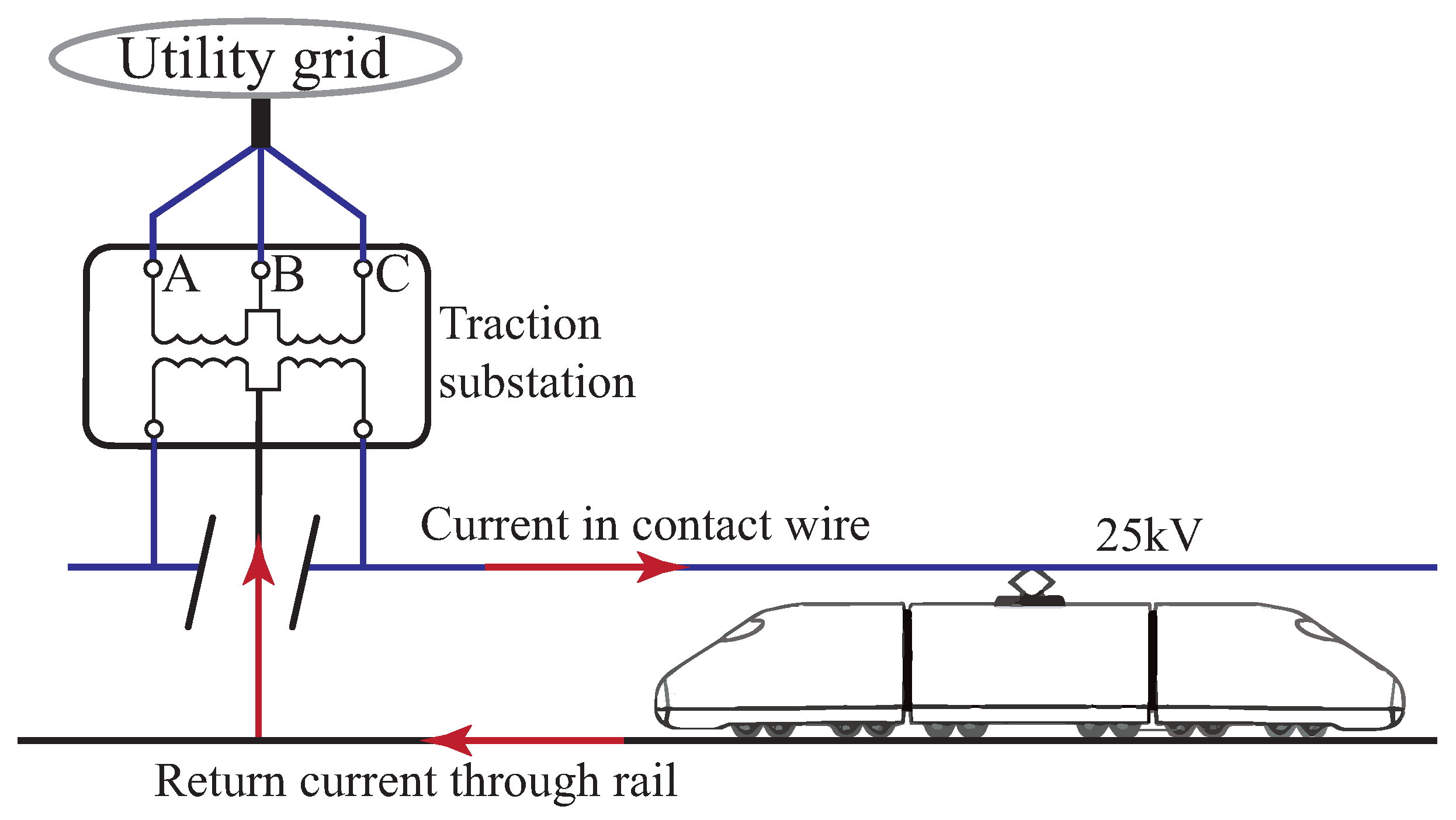
3.3. Practically Realized Medium-Voltage (2.4–69 kV) Asymmetric Systems
3.4. Passive-Element Filters and Specific Transformers
3.5. Y-Connected Passive Filter
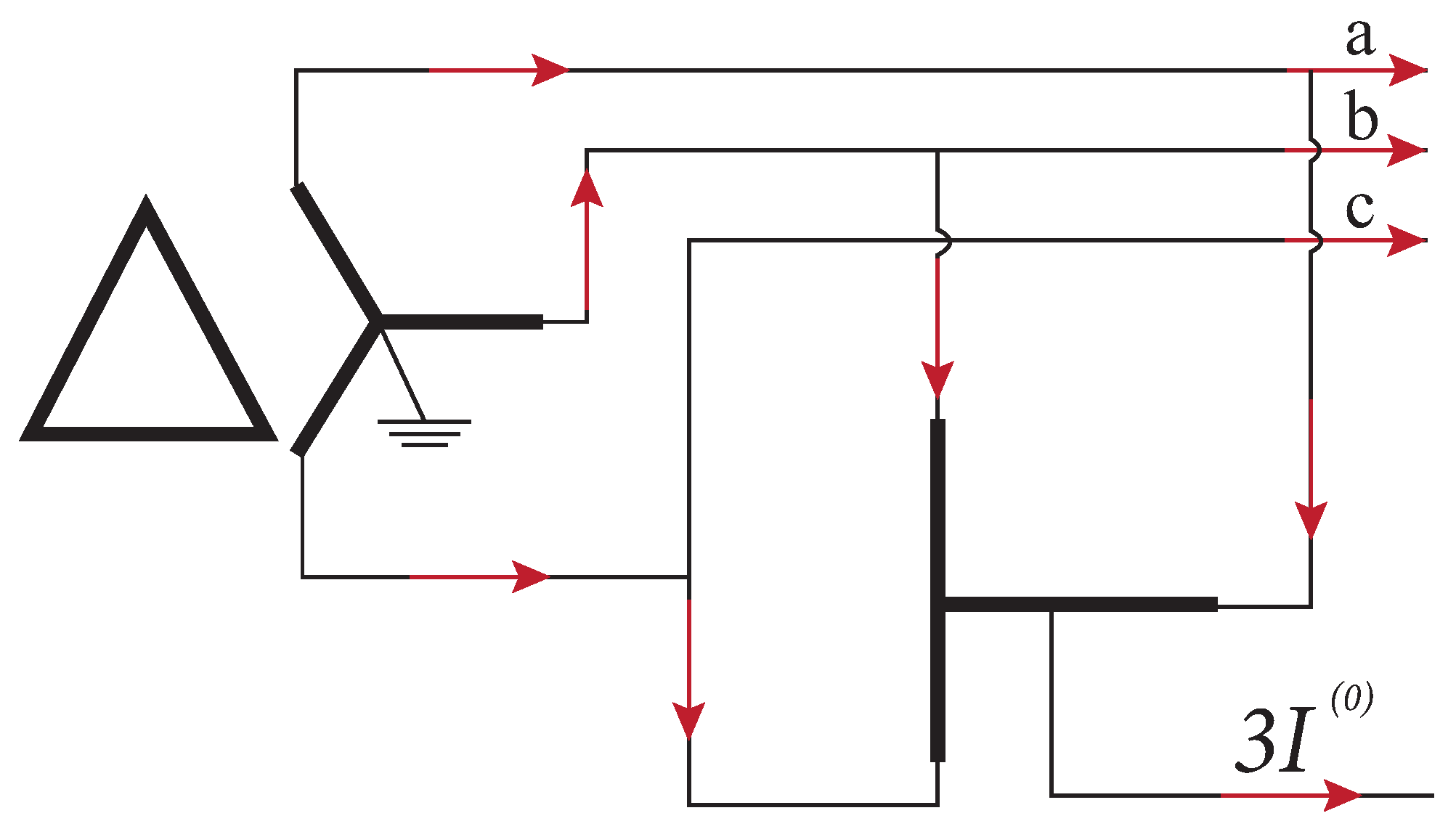
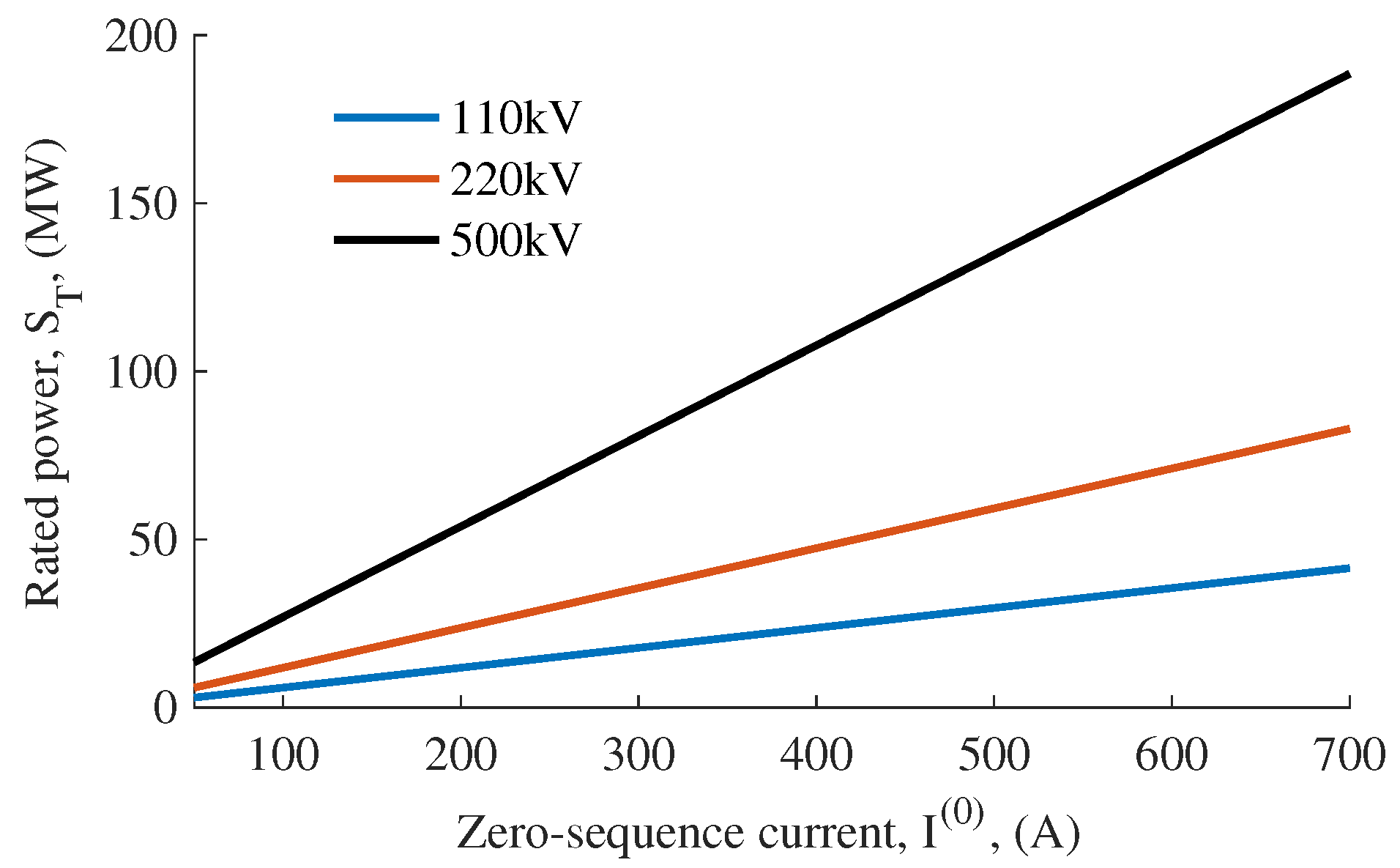
3.6. Specific Transformers for Suppressing Zero-Sequence Currents
3.7. Comparison of Passive Element with Power Electronic Filters
4. Review of Latest Academic Literature on the Asymmetrical Operation Subject
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| APF | Active Power Filter |
| DG | Distributed Generation |
| DSSC | Distributed Static Series Compensator |
| EHV | Extra-High Voltage |
| FACTS | Flexible Alternating Current Transmission System |
| IBR | Inverter-Based Resources |
| IPC | Interphase Power Controller |
| NPS | National Power System |
| OPL | Overhead Power Line |
| PCC | Point of Common Coupling |
| PP | Power Plant |
| RES | Renewable Energy Sources |
| SIL | Surge Impedance Loading |
| SWER | Single-Wire-Earth Return |
| UHV | Ultra-High Voltage |
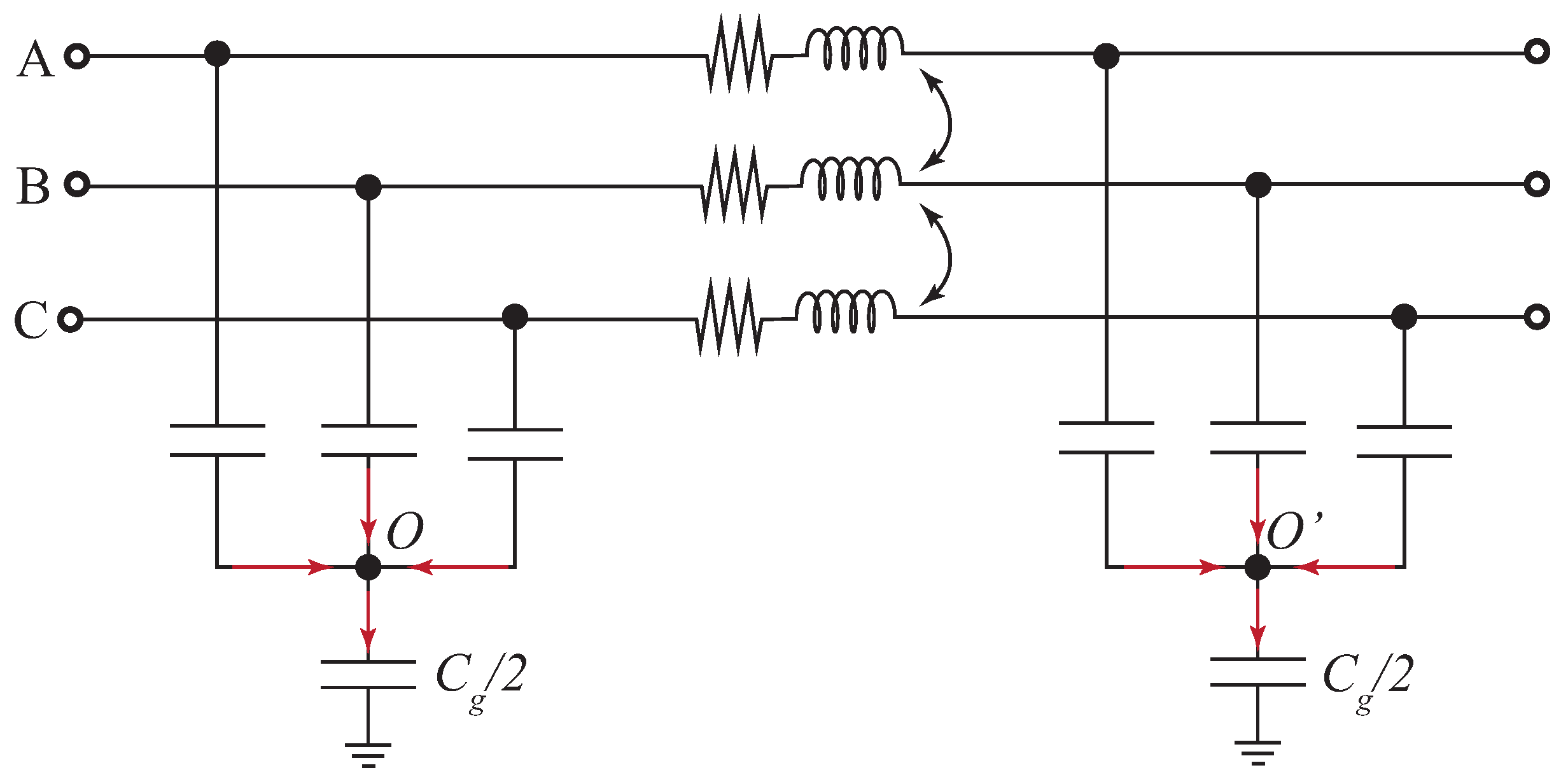
Appendix A. Generic Three-Phase Power Line Model
References
- Whelan, M.; Rockwell, S.; Blalock, T. Great Barrington 1886: Inspiring an Industry Toward AC Power. Available online: https://edisontechcenter.org/GreatBarrington.html (accessed on 28 August 2024).
- Harnessing Niagara Falls: The Adams Power Station. The Most Famous of Early Hydroelectric Power Stations. Available online: https://edisontechcenter.org/Niagara.htm#:~:text=President%20Adams%20and%20Forbes%of,phase%2C%four-wire%2Dgenerators (accessed on 28 August 2024).
- IEA. Renewables 2023; Licence: CC BY 4.0; IEA: Paris, France, 2024. [Google Scholar]
- Meserve, B.E. Fundamental Concepts of Algebra; Dover Publications: Mineola, NY, USA, 1982; originally published: Cambridge, MA, USA, in 1953. [Google Scholar]
- Todde, C.; Marceau, R.J.; McGillis, D.; Lefebvre, S.; Sana, A.R. An investigation into the compensation of asymmetric systems. In Proceedings of the Engineering Solutions for the Next Millennium. 1999 IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No. 99TH8411), Edmonton, AB, Canada, 9–12 May 1999; Volume 2, pp. 1187–1190. [Google Scholar]
- Sana, A.R.; McGillis, D.; Marccau, R.; Do, X.D.; Olivier, G. Asymmetrical operation of corridor with one single line. In Proceedings of the 2000 Canadian Conference on Electrical and Computer Engineering. Conference Proceedings. Navigating to a New Era (Cat. No. 00TH8492), Halifax, NS, Canada, 7–10 May 2000; Volume 2, pp. 936–940. [Google Scholar]
- Sana, A.R.; Marceau, R.J.; McGillis, D.T.; Todde, C.; Do, X.D. On the asymmetrical operation of transmission systems. In Proceedings of the CIGRE Symposium on Working Plant and Systems Harder, London, UK, 7–9 June 1999; pp. 400.011–400.016, ARRAY(0x5587225ee388). [Google Scholar]
- Marceau, R.; McGillis, D.; Sana, A. The role of asymmetric operation in enhancing the flexibility of power system operation. In Proceedings of the CCECE 2003—Canadian Conference on Electrical and Computer Engineering Toward a Caring and Humane Technology (Cat. No.03CH37436), Montreal, QC, Canada, 4–7 May 2003; Volume 1, pp. 509–514. [Google Scholar] [CrossRef]
- Belyakov, N.N.; Volchek, V.L.; Ilyinichin, V.V.; Losev, S.B.; Lyskov, Y.I.; Novella, V.N.; Rashkes, V.S.; Strelkov, V.M.; Fokin, G.G.; Khoroshev, M.I. Application of Single-Phase Autoreclosing in a Complex EHV Network Containing 1200 kV Transmission Lines. In Protection and Automation (B5) Committee Session Materials; CIGRE: Paris, France, 1990; pp. 34–207. [Google Scholar]
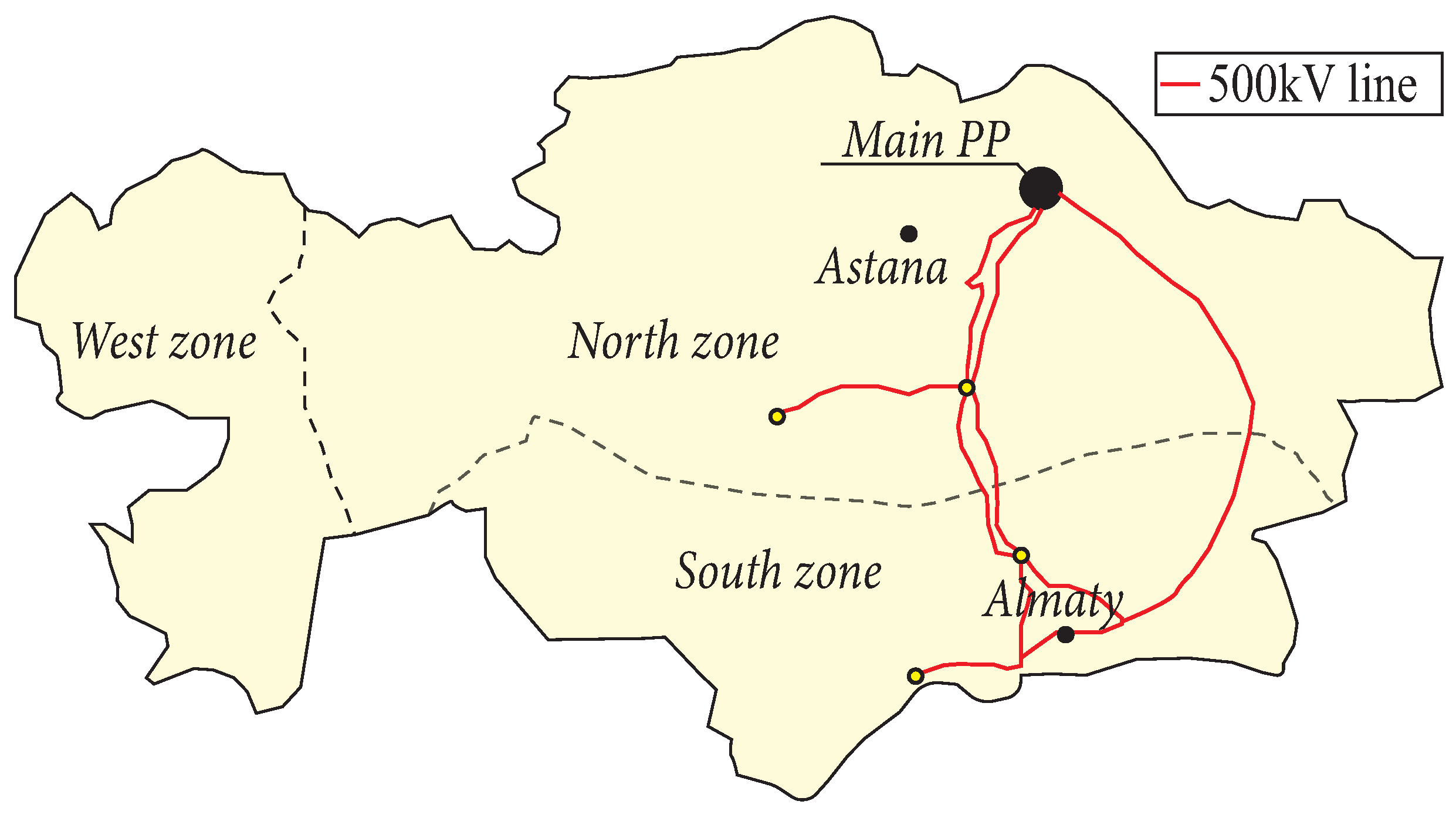
- Kazakhstan Government. Concept on Transition towards Green Economy until 2050. 2013. Available online: https://policy.asiapacificenergy.org/sites/default/files/Concept%20on%20Transition%20towards%20Green%20Economy%20until%202050%20%28EN%29.pdf (accessed on 10 September 2024).
- Pruski, P.; Paszek, S. Analysis of transient waveforms in a power system at asymmetrical short-circuits. Prz. Elektrotech. 2020, 2, 26–29. [Google Scholar] [CrossRef]
- Marceau, R.J.; McGillis, D.T.; Sana, A.R. Asymmetric Operation of AC Power Transmission Systems: The Key to Optimizing Power System Reliability and Economics; Presses inter Polytechnique: Montréal, QC, Canada, 2006. [Google Scholar]
- Sana, A.R.; Marceau, R.; Todde, C.; Do, D.; Mahseredjian, J.; Joos, G. The exploitation of asymmetry in electric power transmission networks. In Proceedings of the Conference Proceedings. IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No.98TH8341), Waterloo, ON, Canada, 25–28 May 1998; Volume 2, pp. 485–488. [Google Scholar] [CrossRef]
- Glover, J.D. Power System Analysis & Design, 7th ed.; Cengage: Boston, MA, USA, 2023. [Google Scholar]
- Berdygozhin, A.; Pepper, B.; Campos-Gaona, D. Asymmetric Operation of Power Lines by Using E-STATCOM and Internal Model Controllers. In Proceedings of the 2024 IEEE 15th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Luxembourg, 23–26 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- EPRI. HVDC Ground Electrode Overview; Technical report; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2010. [Google Scholar]
- Holt, R.J.; Dabkowski, J.; Hauth, R.L. HVDC Power Transmission Electrode Siting and Design; Technical report; New England Power Service Company: Westborough, MA, USA, 1997. [Google Scholar]
- CIGRÉ. General Guidelines for HVDC Electrode Design; Tech. Brochure WG B4.61; CIGRÉ: Paris, France, 2017. [Google Scholar]
- Mishra, M.K. Power Quality in Power Distribution Systems: Concepts and Applications; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Yin, F.; Zhao, P.; Wang, Y.; Li, Z.; Wang, Y.; Xiao, X. Coordinated central and local voltage control in low voltage distribution network with photovoltaic generation. In Proceedings of the 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 298–302. [Google Scholar] [CrossRef]
- Papachristou, A.C.; Awad, A.S.A.; Turcotte, D.; Wong, S.; Prieur, A. Impact of DG on Voltage Unbalance in Canadian Benchmark Rural Distribution Networks. In Proceedings of the 2018 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 10–11 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Akagi, H. Instantaneous Power Theory and Applications to Power Conditioning; IEEE Press Series on Power Engineering; Wiley: Hoboken, NJ, USA; IEEE Press: Piscataway, NJ, USA, 2007. [Google Scholar]
- Campos-Gaona, D.; Peña-Alzola, R.; Monroy-Morales, J.L.; Ordonez, M.; Anaya-Lara, O.; Leithead, W.E. Fast Selective Harmonic Mitigation in Multifunctional Inverters Using Internal Model Controllers and Synchronous Reference Frames. IEEE Trans. Ind. Electron. 2017, 64, 6338–6349. [Google Scholar] [CrossRef]
- Khoshooei, A.; Moghani, J.S.; Candela, I.; Rodriguez, P. Control of D-STATCOM During Unbalanced Grid Faults Based on DC Voltage Oscillations and Peak Current Limitations. IEEE Trans. Ind. Appl. 2018, 54, 1680–1690. [Google Scholar] [CrossRef]
- Merritt, N.R.; Chakraborty, C.; Bajpai, P. An E-STATCOM Based Solution for Smoothing Photovoltaic and Wind Power Fluctuations In a Microgrid Under Unbalanced Conditions. IEEE Trans. Power Syst. 2022, 37, 1482–1494. [Google Scholar] [CrossRef]
- Edison, O.E. Regulation of Open Delta Connected Transformers; The University of Nebraska-Lincoln: Lincoln, NE, USA, 1915. [Google Scholar]
- Roux, G.P. Delta-Cross Connections of Transformers. Trans. Am. Inst. Electr. Eng. 1915, 34, 2141–2155. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Zaninelli, D. Electrical Railway Transportation Systems, 1st ed.; IEEE Press Series on Power Engineering; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Chen, M.; Liu, S.; Zhu, J.; Xie, C.; Tian, H.; Li, J. Effects and Characteristics of AC Interference on Parallel Underground Pipelines Caused by an AC Electrified Railway. Energies 2018, 11, 2255. [Google Scholar] [CrossRef]
- Samra, B.S. An Analysis of Single Wire Earth Return (SWER) System for Rural Electrification; University of Missouri: Rolla, MO, USA, 1972. [Google Scholar]
- Karhammar, R.; Sanghvi, A.; Fernstrom, E.; Aissa, M.; Arthur, J.; Tulloch, J.; Davies, I.; Bergman, S.; Mathur, S. Sub-Saharan Africa: Introducing Low-Cost Methods in Electricity Distribution Networks; ESMAP Technical Paper 104; ESMAP: Washington, DC, USA, 2006. [Google Scholar]
- Da Silva, I. The Use of Single Wire Earth Return (SWER) as a Potential Solution to Reduce the Cost of Rural Electrification in Uganda. 2001. Available online: https://www.researchgate.net/profile/Izael-Da-Silva/publication/236216354_The_use_of_single_wire_earth_return_SWER_as_a_potential_solution_to_reduce_the_cost_of_rural_electrification_in_Uganda/links/00b7d539b0c84a40bc000000/The-use-of-single-wire-earth-return-SWER-as-a-potential-solution-to-reduce-the-cost-of-rural-electrification-in-Uganda.pdf (accessed on 5 June 2024).
- Benar, P.P. Electric power transmission «two wires—earth». Elektrichestvo 1933, 13–20. (In Russian) [Google Scholar]
- Buryanina, N.; Korolyuk, Y.; Lesnykh, E. Using “Two Wires-Earth” Power Transmission Lines. Proc. Irkutsk State Tech. Univ. 2017, 21, 91–99. [Google Scholar] [CrossRef]
- Bouchard, R.P.; Olivier, G. Electrotechnique; Presses Inter Polytechnique: Montréal, QC, Canada, 1999. [Google Scholar]
- Mathur, R.M. Thyristor-Based FACTS Controllers for Electrical Transmission Systems/[internet Resource]; IEEE Press Series on Power Engineering; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Dekka, A.; Wu, B.; Fuentes, R.L.; Perez, M.; Zargari, N.R. Evolution of Topologies, Modeling, Control Schemes, and Applications of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1631–1656. [Google Scholar] [CrossRef]
- Ch, A.B.; Maiti, S. Modular multilevel E-STATCOM considering distributed energy storage at the dc link. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Bharadwaj, A.; Maiti, S. 18—Multilevel converter-based STATCOM with hybrid storage system. In Emerging Trends in Energy Storage Systems and Industrial Applications; Prabhansu, Kumar, N., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 521–534. [Google Scholar] [CrossRef]
- Kilic, H.; Asker, M.E.; Haydaroglu, C. Enhancing power system reliability: Hydrogen fuel cell-integrated D-STATCOM for voltage sag mitigation. Int. J. Hydrogen Energy 2024, 75, 557–566. [Google Scholar] [CrossRef]
- Eroğlu, F.; Kurtoğlu, M.; Eren, A.; Vural, A.M. Multi-objective control strategy for multilevel converter based battery D-STATCOM with power quality improvement. Appl. Energy 2023, 341, 121091. [Google Scholar] [CrossRef]
- Kamarposhti, M.A.; Colak, I.; Thounthong, P.; Eguchi, K. Modeling and Simulation of DVR and D-STATCOM in Presence of Wind Energy System. Comput. Mater. Contin. 2022, 74, 4547–4570. [Google Scholar] [CrossRef]
- Mohamedi, R.; Lefebvre, S.; Ba, A.O.; Houle, A. Comparative Study of the Symmetric and Asymmetric Approaches to Increase Power Transfer Capacity of a Corridor. In Proceedings of the 2007 iREP Symposium—Bulk Power System Dynamics and Control—VII. Revitalizing Operational Reliability, Charleston, SC, USA, 19–24 August 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Mohamedi, R.; Lefebvre, S.; Ba, A.O.; Houle, A. Increasing the Transfer Capacity of a Corridor through Power Flow Control. In Proceedings of the 2007 IEEE Canada Electrical Power Conference, Montreal, QC, Canada, 25–26 October 2007; pp. 507–513. [Google Scholar] [CrossRef]
- Mougnol Assala, G.R.; Mandeng, J.J.; Kom, C.H.; Mbihi, J. Grid-tied PV system-based power compensation of a grid equipped with dual interphase power controllers (IPC) 240 with three branches: Case of a short transmission line. Energy Syst. 2023, 1–21. [Google Scholar] [CrossRef]
- Steva, K.C.C.; Ghislain, M.M.; Joseph, K.K.; Jeannot, B.G.; Leandre, N.N. Contribution to Asymmetrical Compensation through Parallel Controllers of FACTS (STATCOM)—IPC 240 Dual for a Power Transmission Line. World J. Eng. Technol. 2022, 11, 20–40. [Google Scholar] [CrossRef]
- Yadav, D.S.; Jaiswal, B.; Gautam, M.; Agrawal, M. Soil Acidification and Its Impact on Plants; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–26. [Google Scholar]
- MathWorks. Three-Phase PI Section Line. Available online: https://uk.mathworks.com/help/sps/powersys/ref/threephasepisectionline.html (accessed on 26 July 2024).

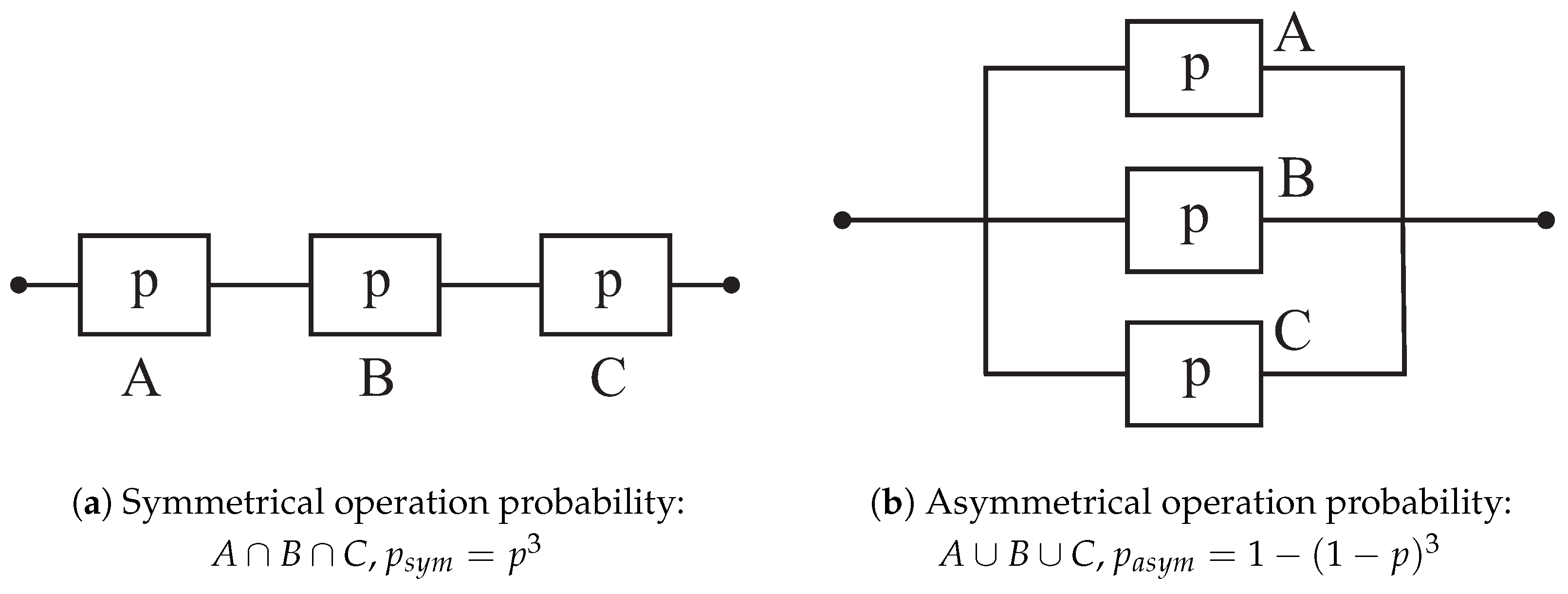
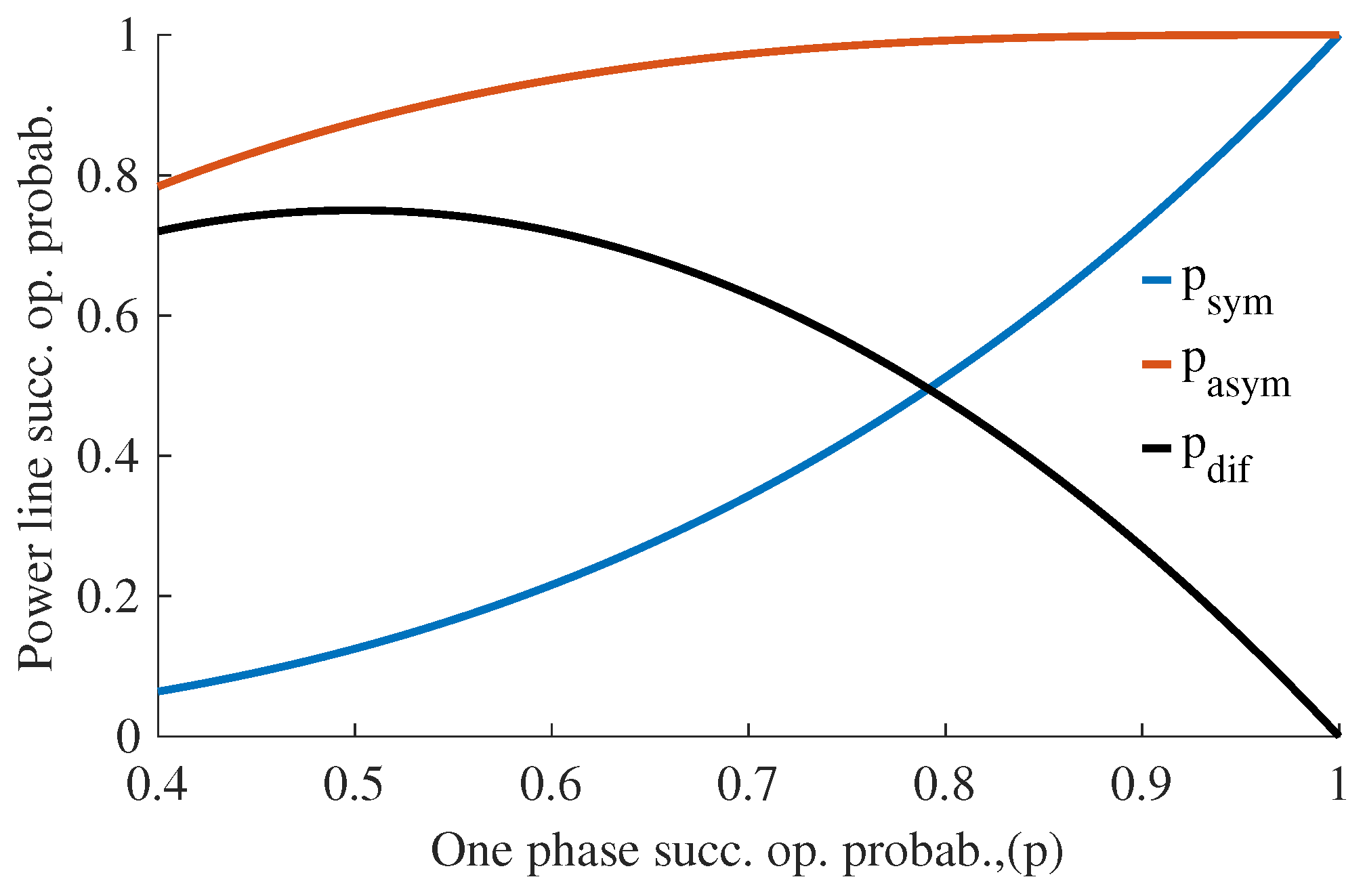
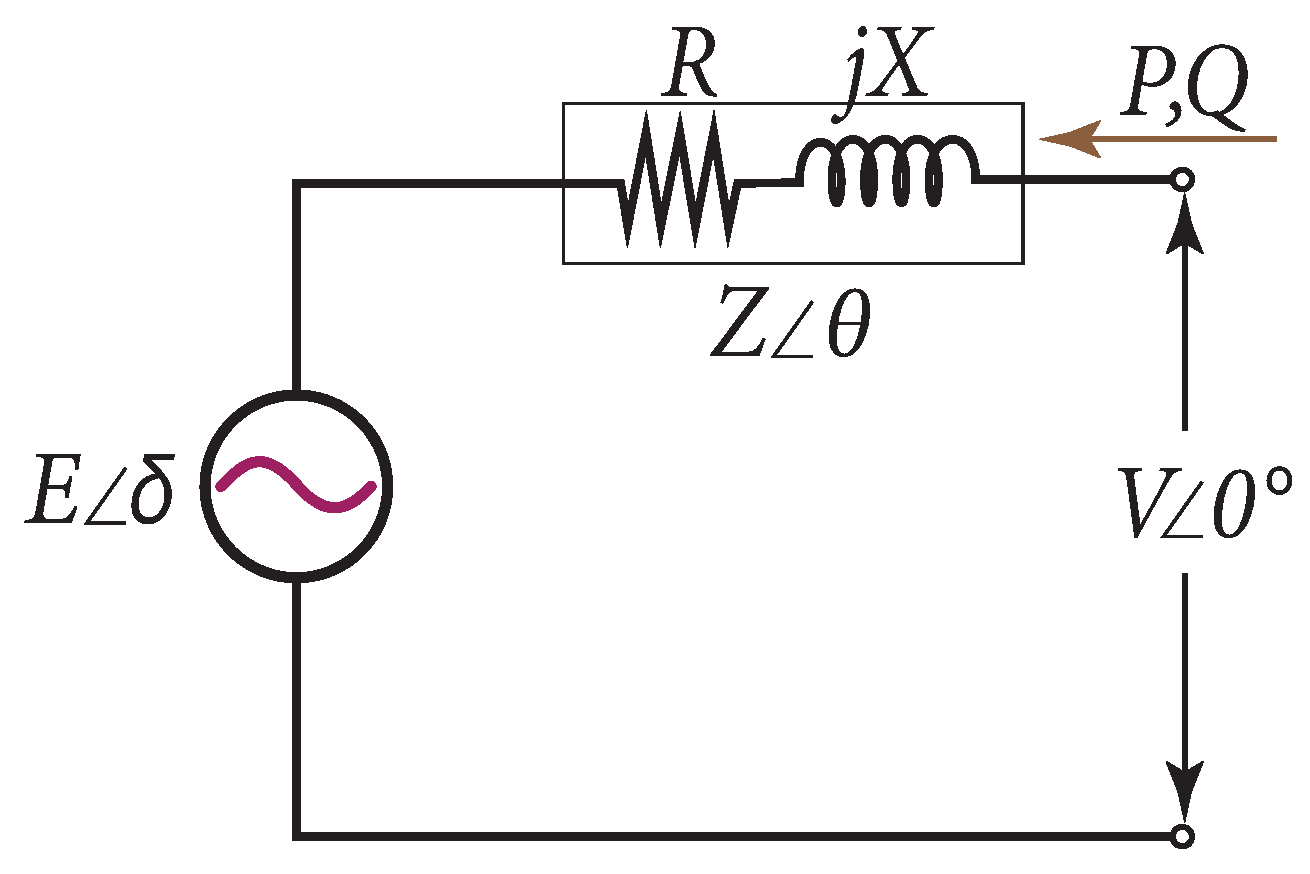
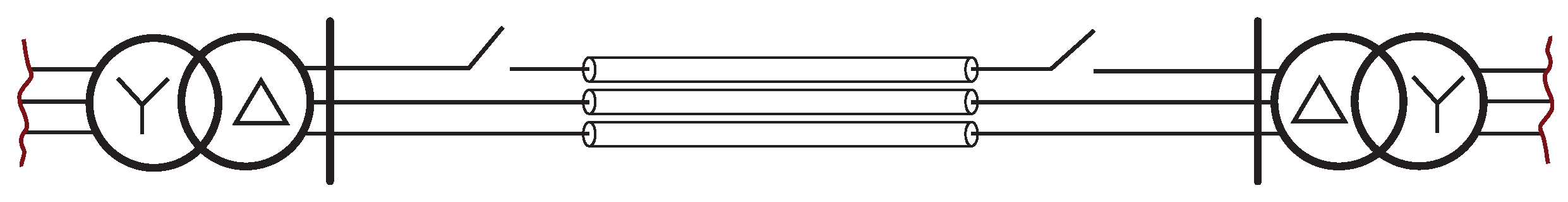



| Passive-Element Filters | Power Electronic Filters | |
|---|---|---|
| Pros | Can be located anywhere along the line | IBRs can be used in fault conditions Flexible to the power flow changes High controllability |
| Cons | Low controllability of controllable shunt reactors [36] Different devices for negative- and zero-sequence current components | Complicated implementation along the line |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berdygozhin, A.; Campos-Gaona, D. Asymmetric Operation of Power Networks, State of the Art, Challenges, and Opportunities. Energies 2024, 17, 5021. https://doi.org/10.3390/en17205021
Berdygozhin A, Campos-Gaona D. Asymmetric Operation of Power Networks, State of the Art, Challenges, and Opportunities. Energies. 2024; 17(20):5021. https://doi.org/10.3390/en17205021
Chicago/Turabian StyleBerdygozhin, Ansar, and David Campos-Gaona. 2024. "Asymmetric Operation of Power Networks, State of the Art, Challenges, and Opportunities" Energies 17, no. 20: 5021. https://doi.org/10.3390/en17205021
APA StyleBerdygozhin, A., & Campos-Gaona, D. (2024). Asymmetric Operation of Power Networks, State of the Art, Challenges, and Opportunities. Energies, 17(20), 5021. https://doi.org/10.3390/en17205021







