Wall Shading Losses of Photovoltaic Systems
Abstract
:1. Introduction
2. Methods and Materials
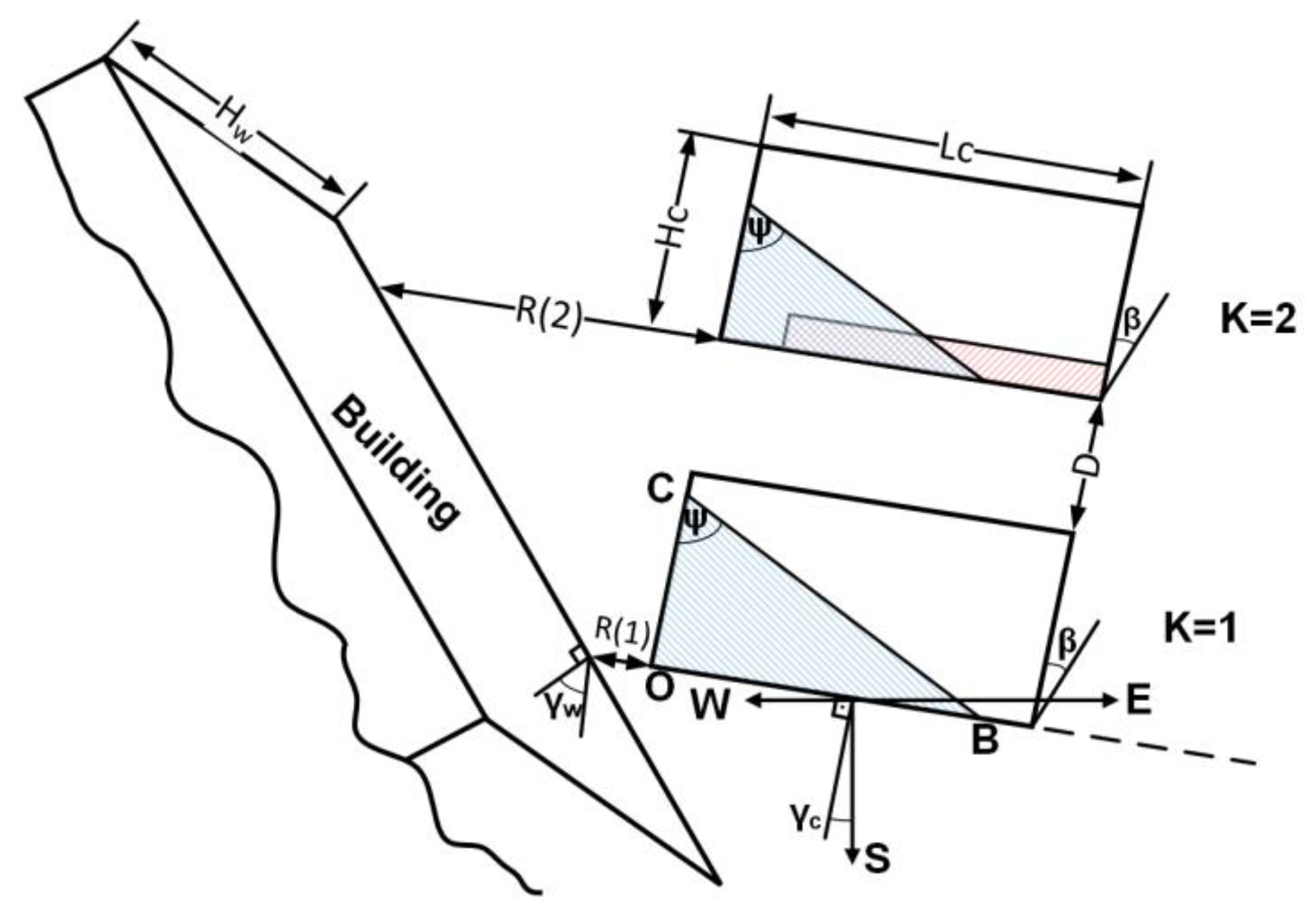
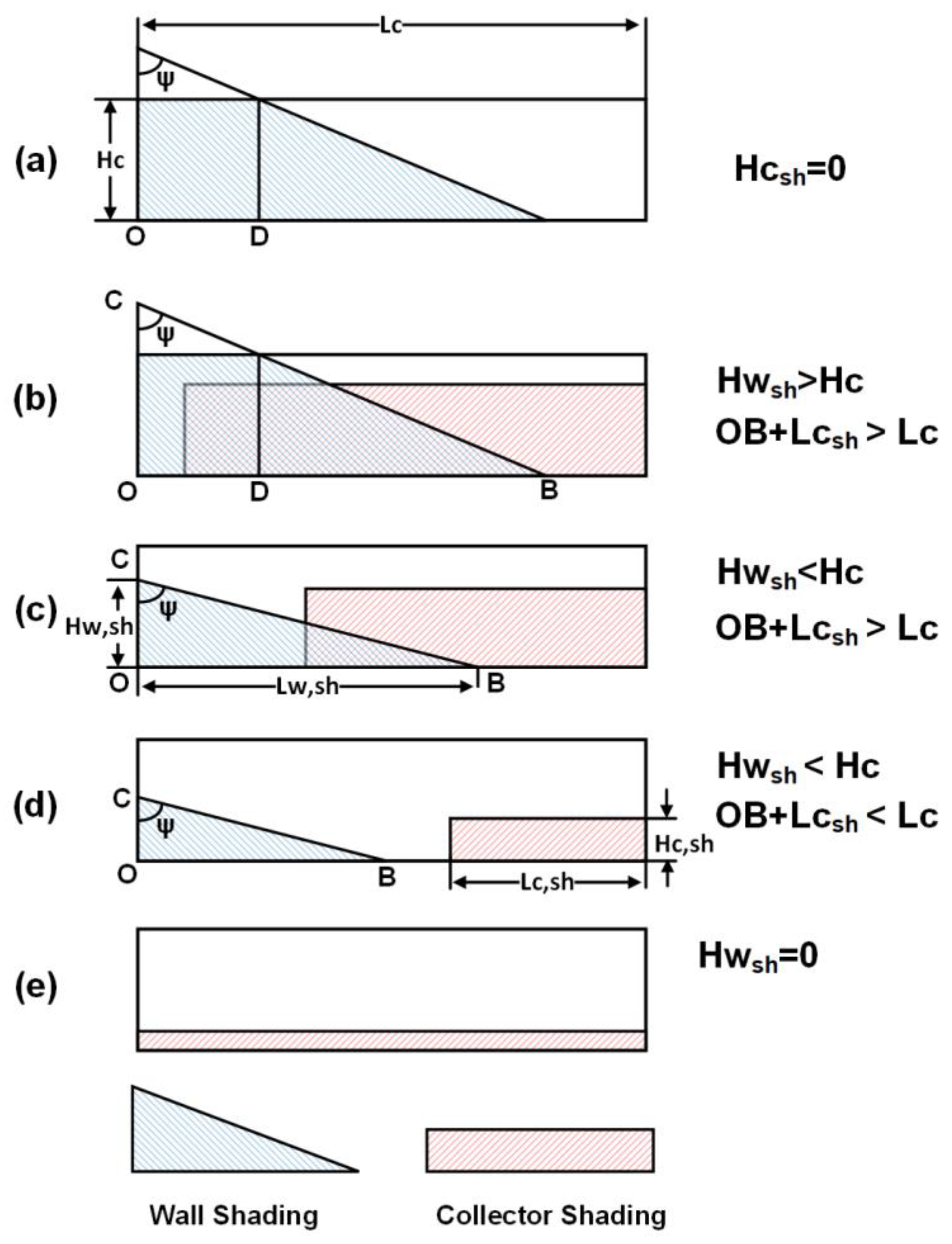
2.1. Wall Shading on the First Collector,
2.2. Inter-Row Shading on the Second Collector,
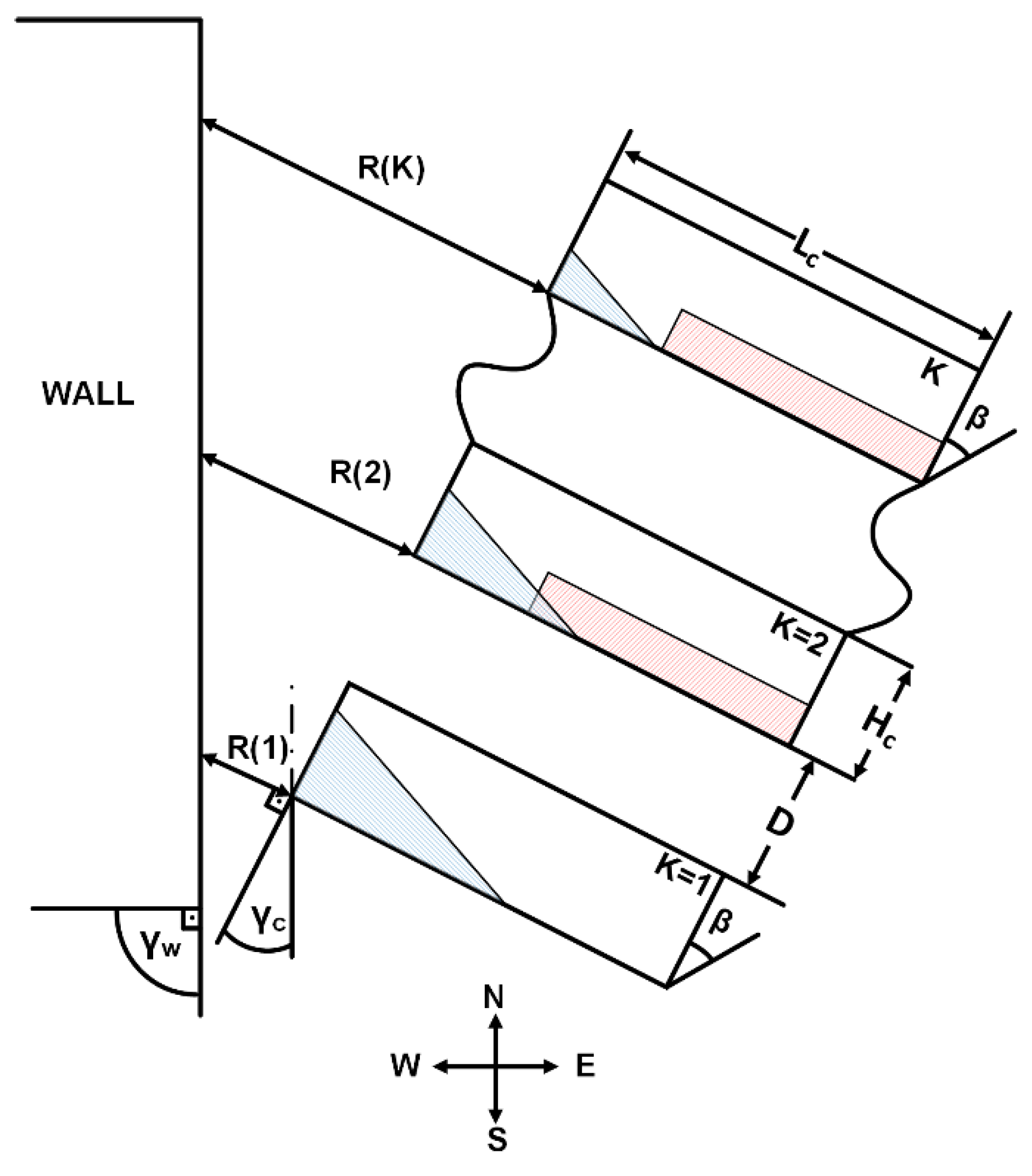
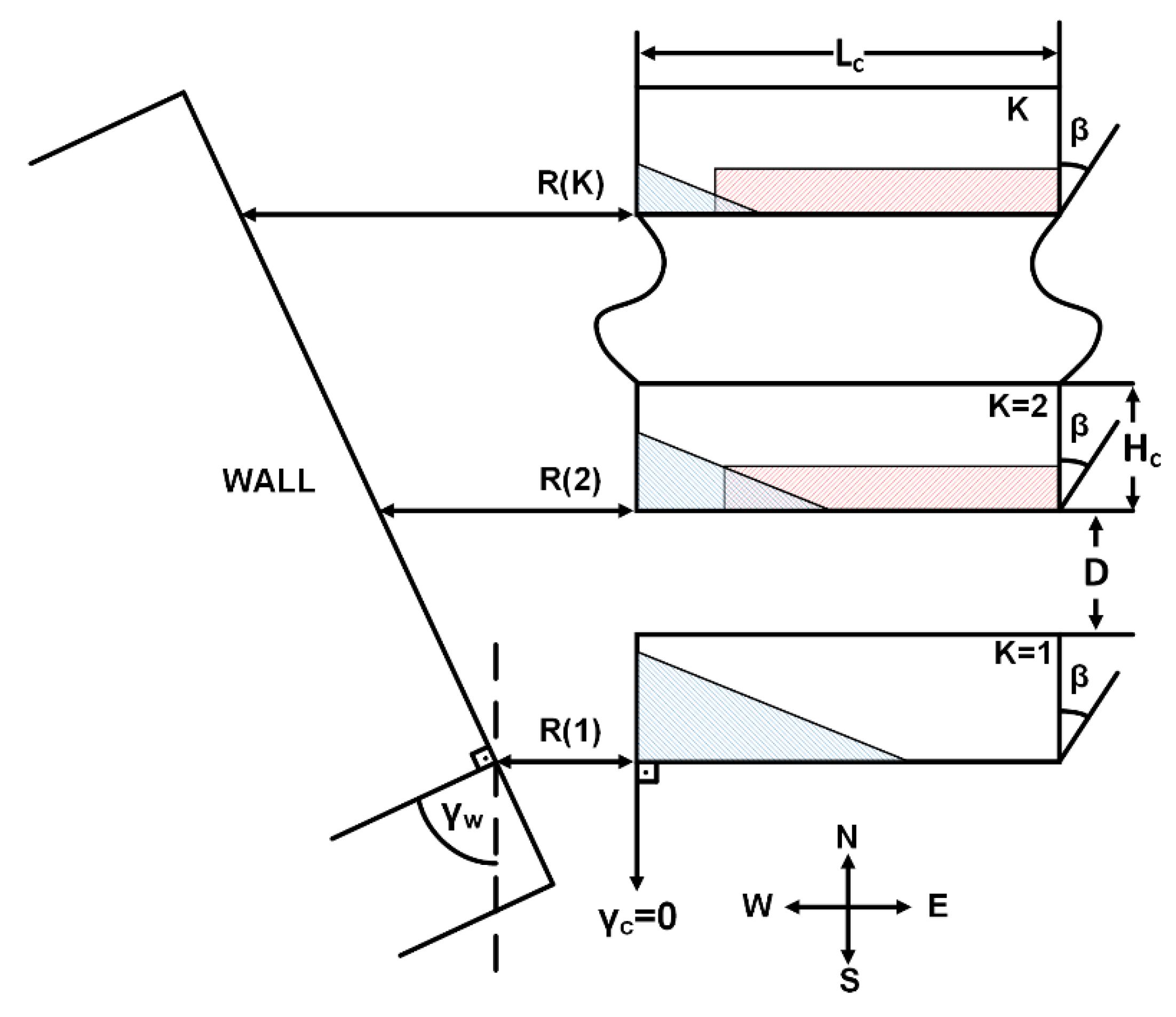
2.3. General Deployment of PV Collectors near a Wall
2.4. Combined Shading—Collectors Deployed in East–West Direction , and a Vertical Wall in North–South Direction, Shading on the Second Collector, Figure 6
2.5. Combined Shading—Collectors Deployed in East–West Direction with an Angle and a Vertical Wall in North–South Direction, , Shading on the Second Collector Row, Figure 7
2.6. Combined Shading—Collectors Deployed in East–West Direction and a Vertical Wall in North–South Direction with an Angle with Respect to South, Figure 8, Shading on the Second and on the Subsequent Collector Rows
3. Results
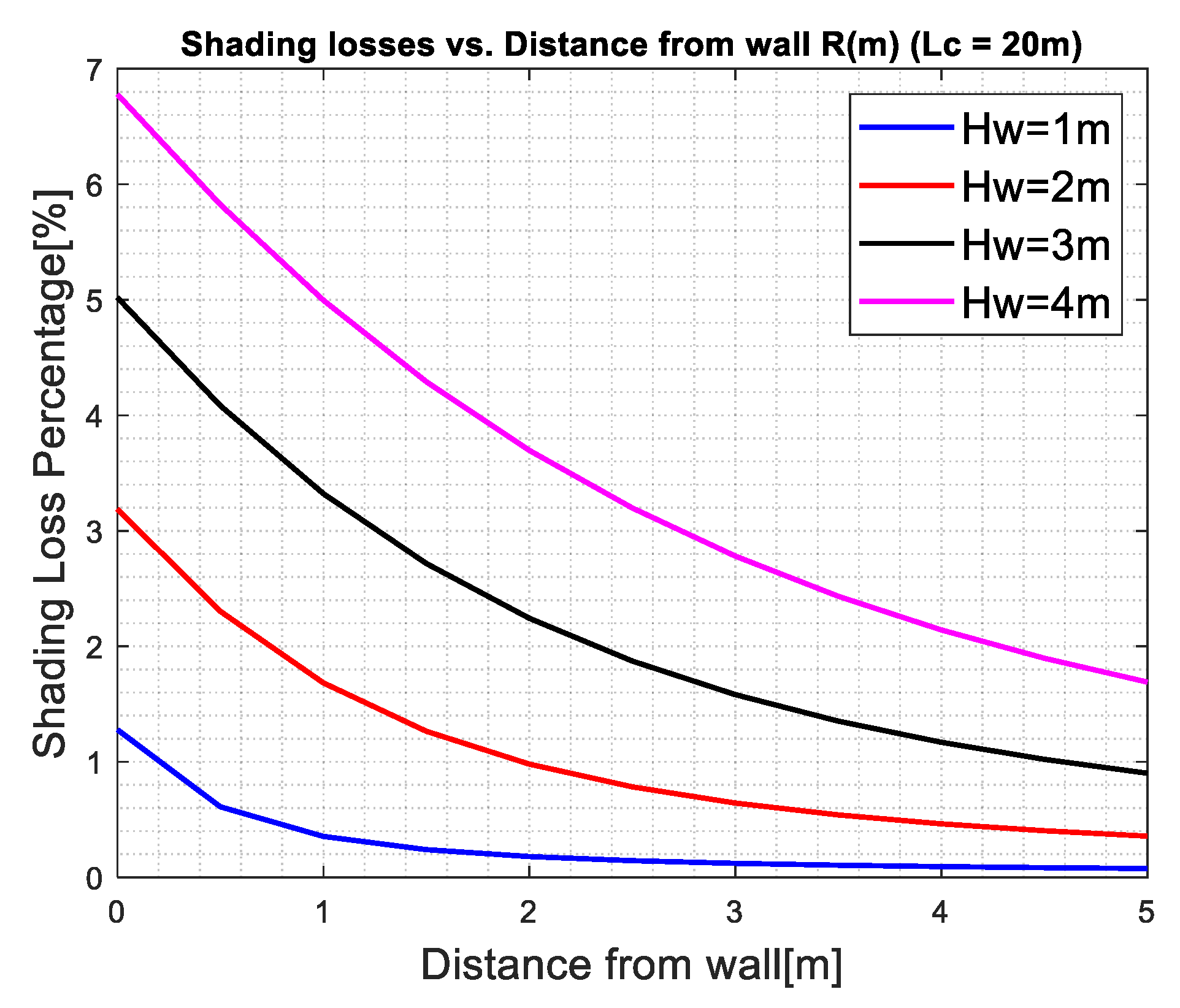
3.1. Wall Shading—Vertical Wall in North–South Direction, , Collectors Facing South, Figure 6
3.2. Inter-Row Shading—Collectors in East–West Direction, , Figure 6, Shading on the Second Collector
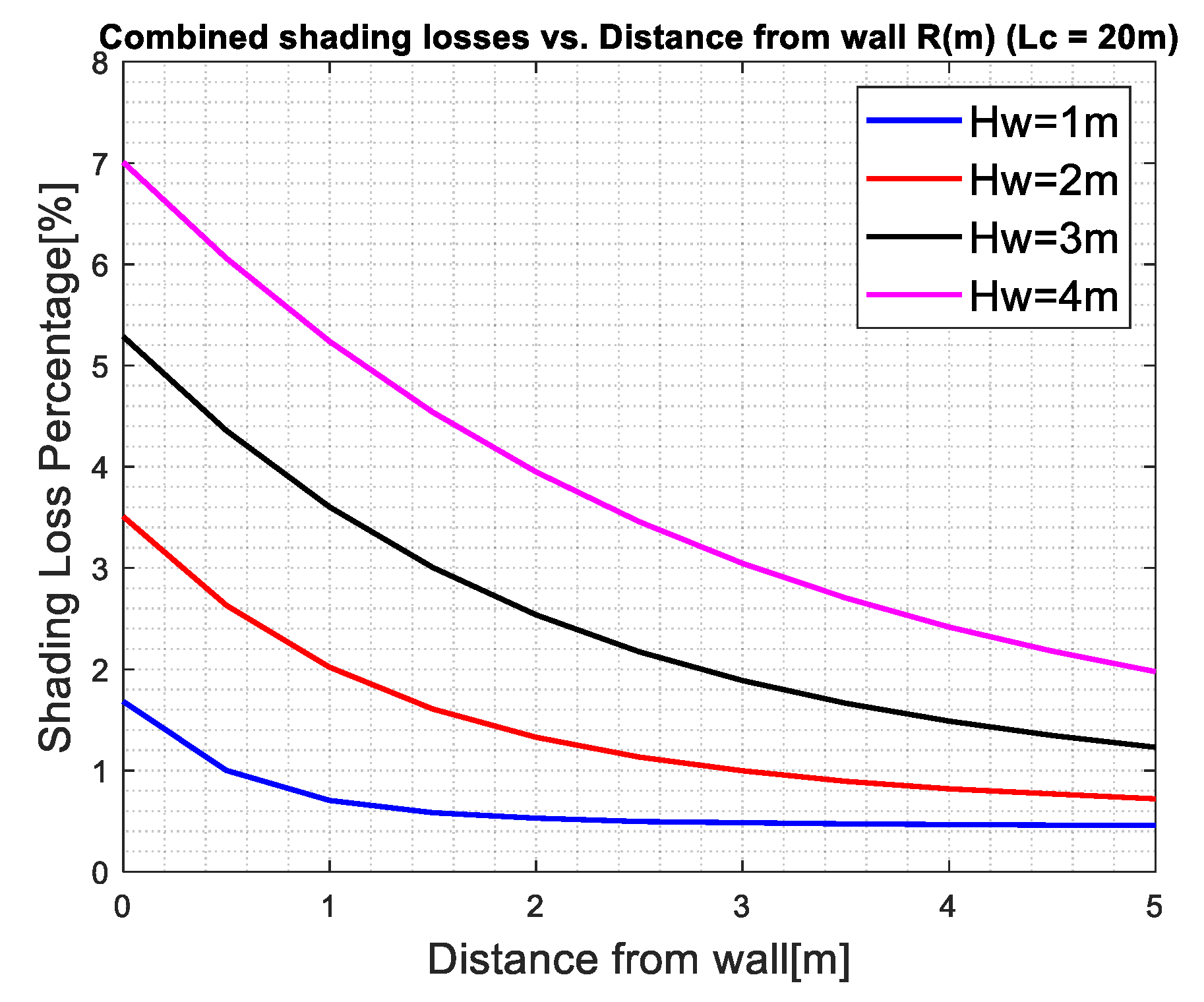
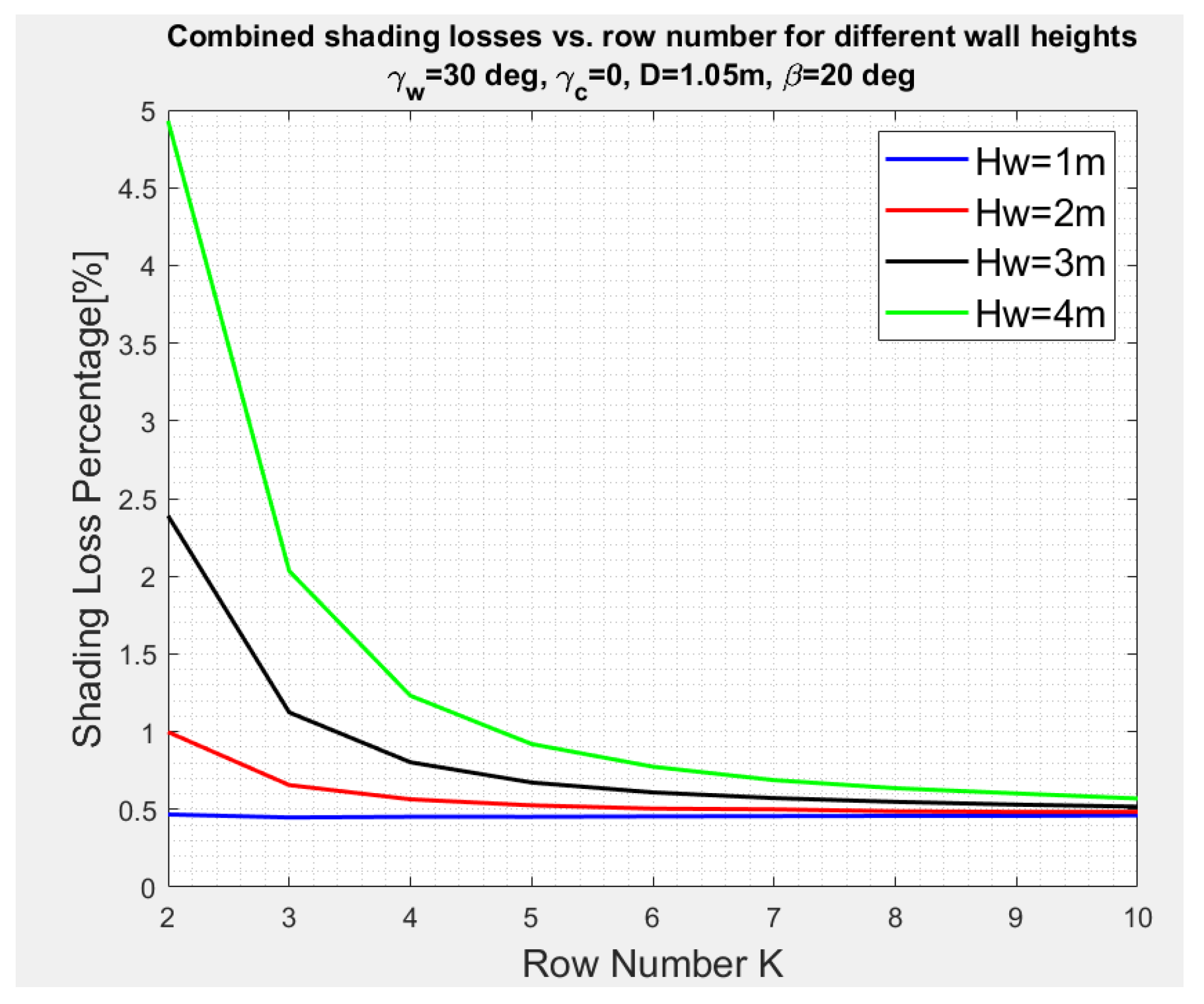
3.3. Combined Shading—Collectors in East–West Direction, and a Vertical Wall in North–South Direction, , Figure 6
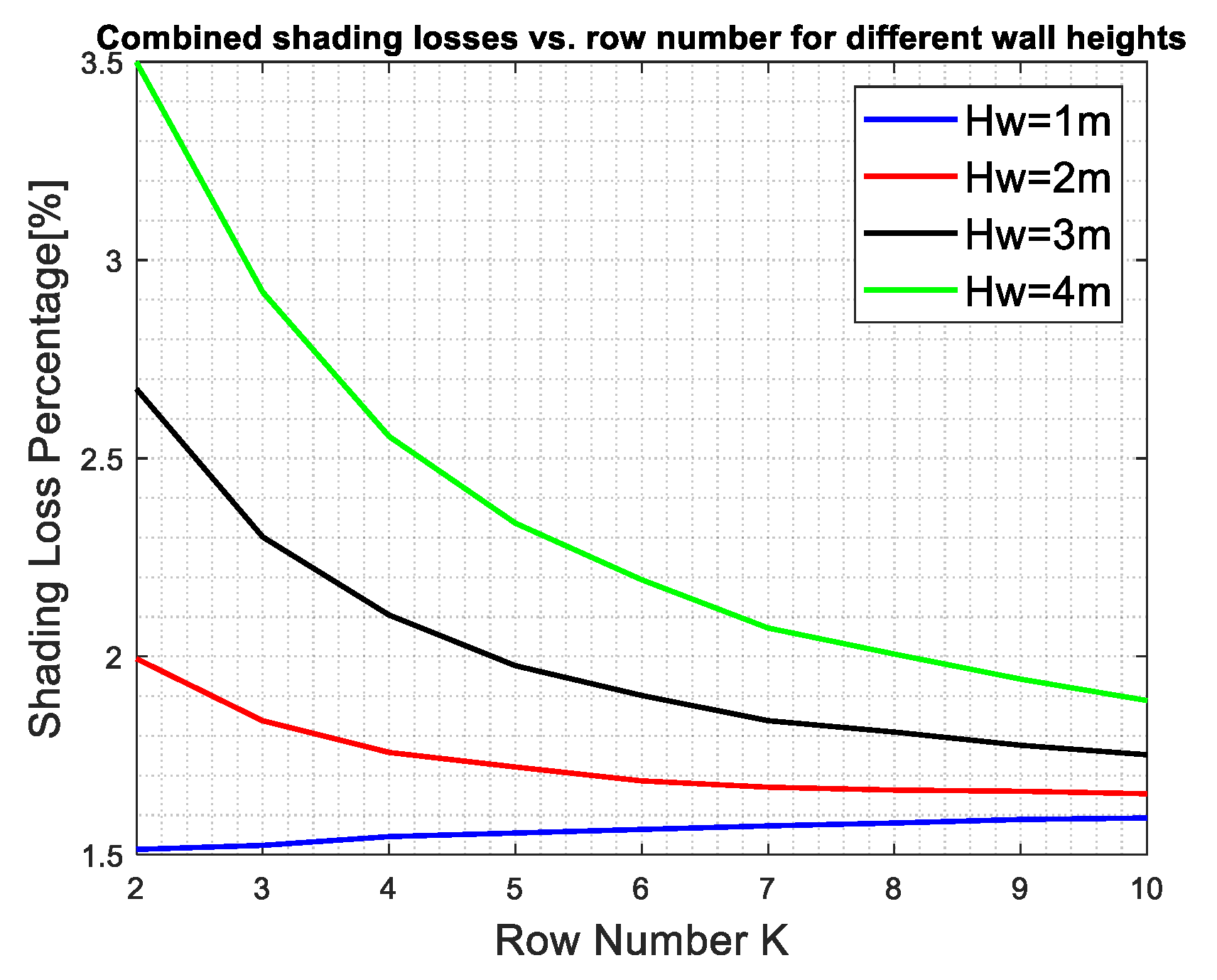
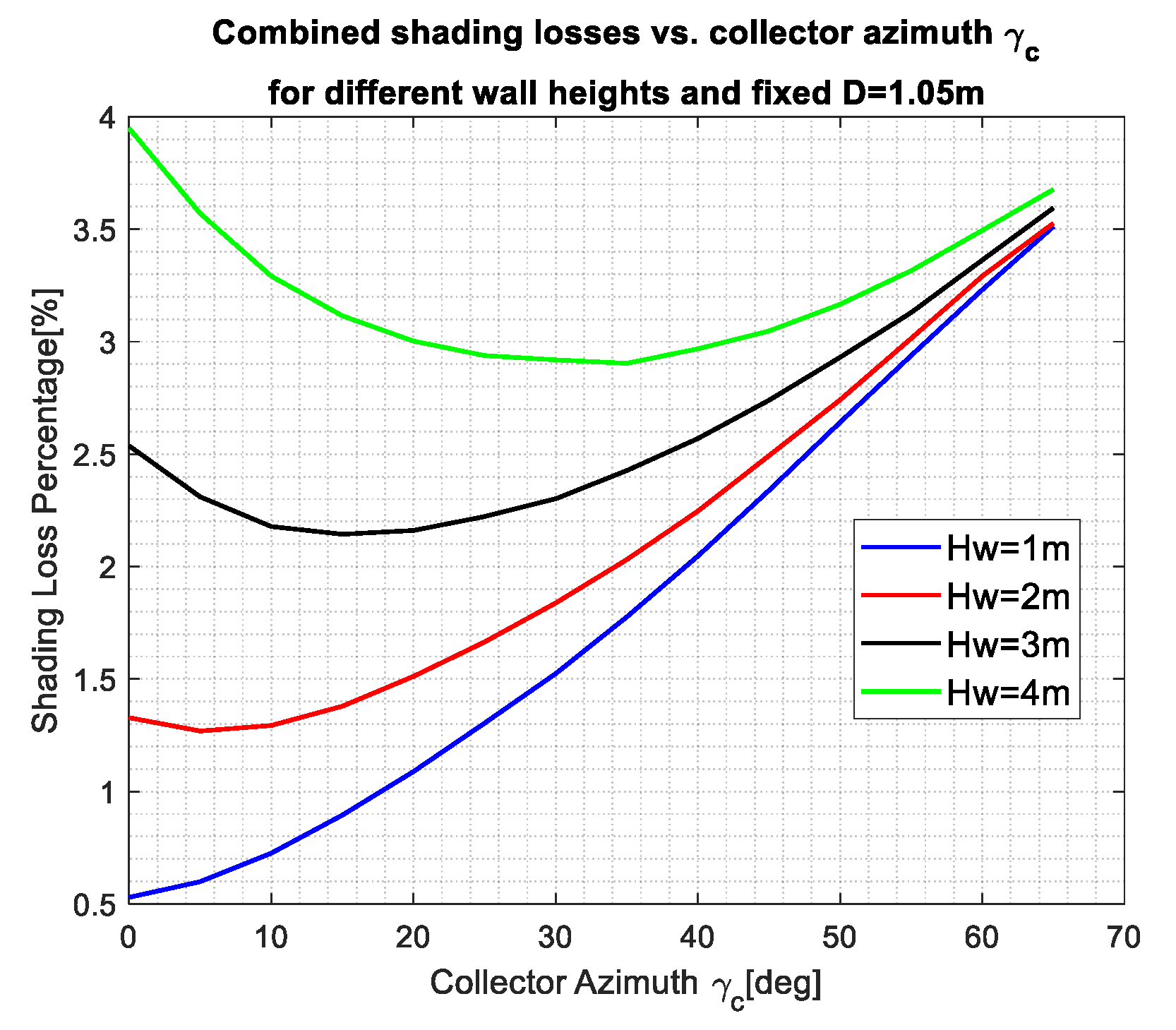
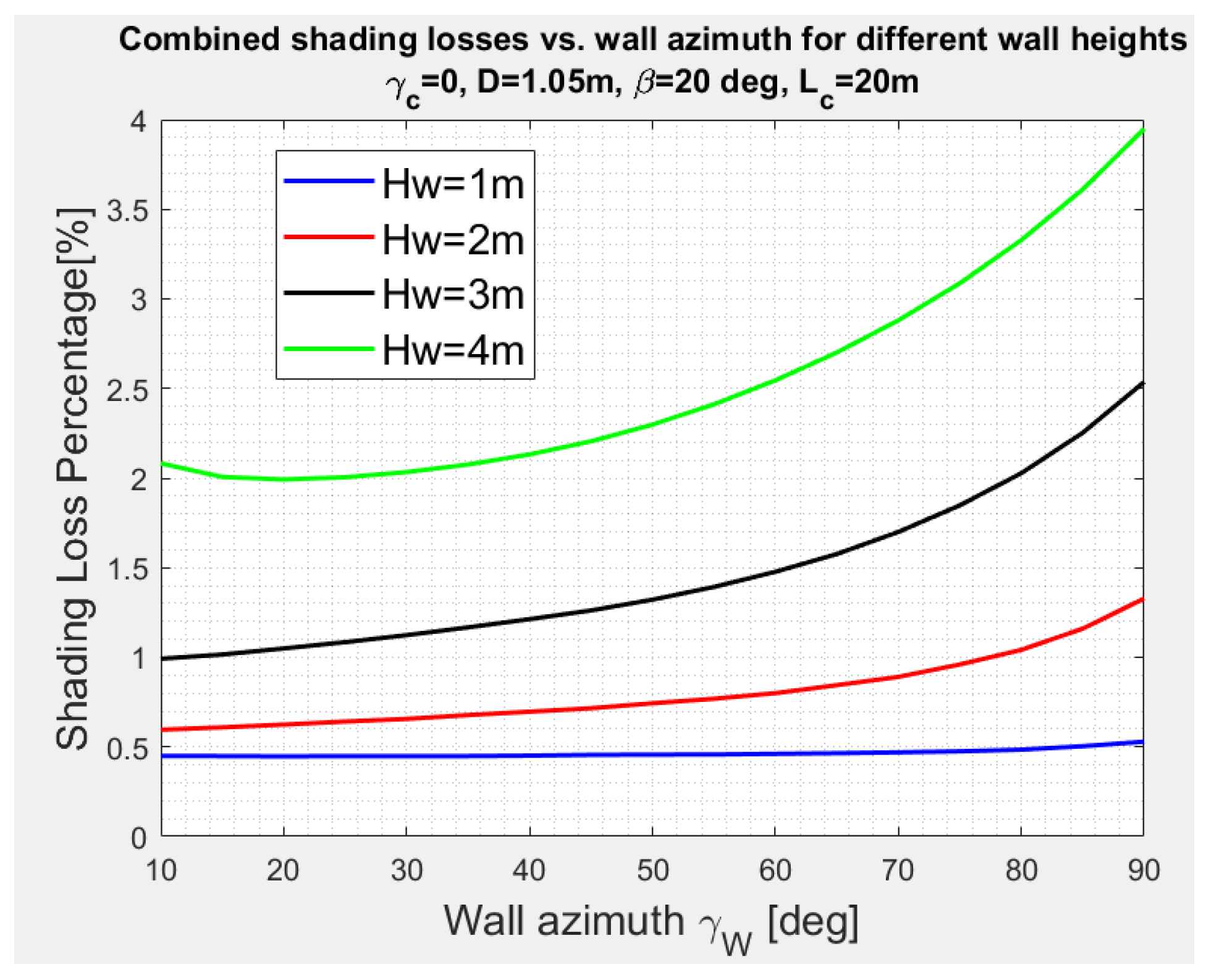
3.4. Combined Shading, Collectors Deployed in East–West Direction Facing the South with an Azimuth Angle , and a Vertical Wall in North–South Direction , Figure 7
3.5. Combined Shading, Collectors Deployed in East–West Direction Facing the South with an Angle , and a Vertical Wall in North–South Direction with an Azimuth Angle , Figure 8
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Collector width | |
| Shadow height on a collector for inter-row shading | |
| Wall height | |
| Shadow height on a collector for wall shading | |
| Number of collector rows | |
| Collector length | |
| Shadow length on a collector for inter-row shading | |
| Shadow length on a collector for wall shading | |
| Distance between wall and collector | |
| Distance between walls and collector number | |
| View factor of first collector | |
| Solar altitude angle | |
| Collector inclination angle | |
| Collector latitude | |
| Declination angle | |
| Collector azimuth angle | |
| Solar azimuth angle | |
| Wall angle | |
| Hour angle | |
| Shading angle |
References
- Sailor, D.J.; Anard, J.; King, R.R. Photovoltaics in the built environment: A critical review. Energy Build. 2021, 253, 111479. [Google Scholar] [CrossRef]
- Annathurai, V.; Gan, C.K.; Baharim, K.A.; Ghani, M.R.A. Shading analysis for the siting of solar PV power plant. APRN J. Eng. Appl. Sci. 2016, 11, 5021–5027. [Google Scholar]
- Sun, Y.; Li, X.; Hong, R.; Shen, H. Analysis on the Effect of Shading on the Characteristics of Large-scale on-grid PV System in China. Energy Power Eng. 2013, 5, 215–218. [Google Scholar] [CrossRef]
- Li, D.; Liu, G.; Liao, S. Solar potential in urban residential buildings. Sol. Energy 2015, 11, 225–235. [Google Scholar] [CrossRef]
- Redweik, P.; Catita, C.; Brito, M. Solar energy potential on roofs and facades in an urban landscape. Sol. Energy 2013, 97, 332–341. [Google Scholar] [CrossRef]
- Masa-Bote, D.; Caamaño-Martín, E. Methodology for estimating building integrated photovoltaics electricity production under shadowing conditions and case study. Renew. Sustain. Energy Rev. 2014, 31, 492–500. [Google Scholar] [CrossRef]
- Groumpos, P.P.; Kouzam, K.Y. A Generic approach to the shadow effect in large solar power systems. Sol. Cells 1987, 22, 29–46. [Google Scholar] [CrossRef]
- Hanitsch, R.E.; Schultz, D.; Siegfried, U. Shading effect on output power of grid connected photovoltaic generated systems. Rev. Energ. Ren. Power Eng. 2001, 93–99. Available online: https://www.cder.dz/download/upec-12.pdf (accessed on 2 August 2024).
- Martinez-Moreno, F.; Munoz, J.; Lorenzo, E. Experiment model to estimate shading losses on PV arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 2298–2303. [Google Scholar] [CrossRef]
- Karatepe, E.; Boztepe, M.; Colak, M. Development of a suitable model for Characterizing photovoltaic arrays with shaded solar cells. Sol. Energy 2007, 81, 977–992. [Google Scholar] [CrossRef]
- Alsadi, S.Y.; Nassar, Y.F. A general expression for the shadow geometry for fixed mode horizontal, step-like structure and inclined solar fields. Sol. Energy 2019, 181, 53–69. [Google Scholar] [CrossRef]
- Varga, N.; Mayer, M.J. Model-based analysis of shading losses in ground-mounted photovoltaic power plant. Sol. Energy 2021, 216, 428–438. [Google Scholar] [CrossRef]
- Dhimish1, M.; Silvestre, S. Estimating the impact of azimuth-angle variations on photovoltaic annual energy production. Clean Energy 2019, 3, 47–58. [Google Scholar] [CrossRef]
- Aronescu, A.; Appelbaum, J. Shading on photovoltaic collectors on rooftops. Appl. Sci. 2020, 10, 2977. [Google Scholar] [CrossRef]
- Bany, J.; Appelbaum, J. The Effect of Shading on the Design of a Field of Solar Collectors. Sol. Cells 1987, 20, 201–228. [Google Scholar] [CrossRef]
- Aronescu, A.; Appelbaum, J. The Effect of Collector Azimuth on Inter-Row Shading in Photovoltaic Fields—A Comprehensive Point of View. Energies 2023, 16, 4876. [Google Scholar] [CrossRef]






| Annual Percentage of Wall Shading Losses | |||
|---|---|---|---|
| Collector Length [m] | Hw = 2 m | Hw = 3 m | Hw = 4 m |
| 10 | 1.8 | 4.1 | 6.8 |
| 20 | 1.0 | 2.3 | 3.7 |
| 30 | 0.7 | 1.6 | 2.6 |
| 40 | 0.5 | 1.2 | 2.0 |
| Collector Length [m] | Annual Percentage Inter-row Shading Losses [%] |
|---|---|
| 10 | 0.39 |
| 20 | 0.47 |
| 30 | 0.50 |
| 40 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Appelbaum, J.; Peled, A.; Aronescu, A. Wall Shading Losses of Photovoltaic Systems. Energies 2024, 17, 5089. https://doi.org/10.3390/en17205089
Appelbaum J, Peled A, Aronescu A. Wall Shading Losses of Photovoltaic Systems. Energies. 2024; 17(20):5089. https://doi.org/10.3390/en17205089
Chicago/Turabian StyleAppelbaum, Joseph, Assaf Peled, and Avi Aronescu. 2024. "Wall Shading Losses of Photovoltaic Systems" Energies 17, no. 20: 5089. https://doi.org/10.3390/en17205089
APA StyleAppelbaum, J., Peled, A., & Aronescu, A. (2024). Wall Shading Losses of Photovoltaic Systems. Energies, 17(20), 5089. https://doi.org/10.3390/en17205089





