Active Battery Voltage Equalization Based on Chain-Loop Comparison Strategy
Abstract
:1. Introduction
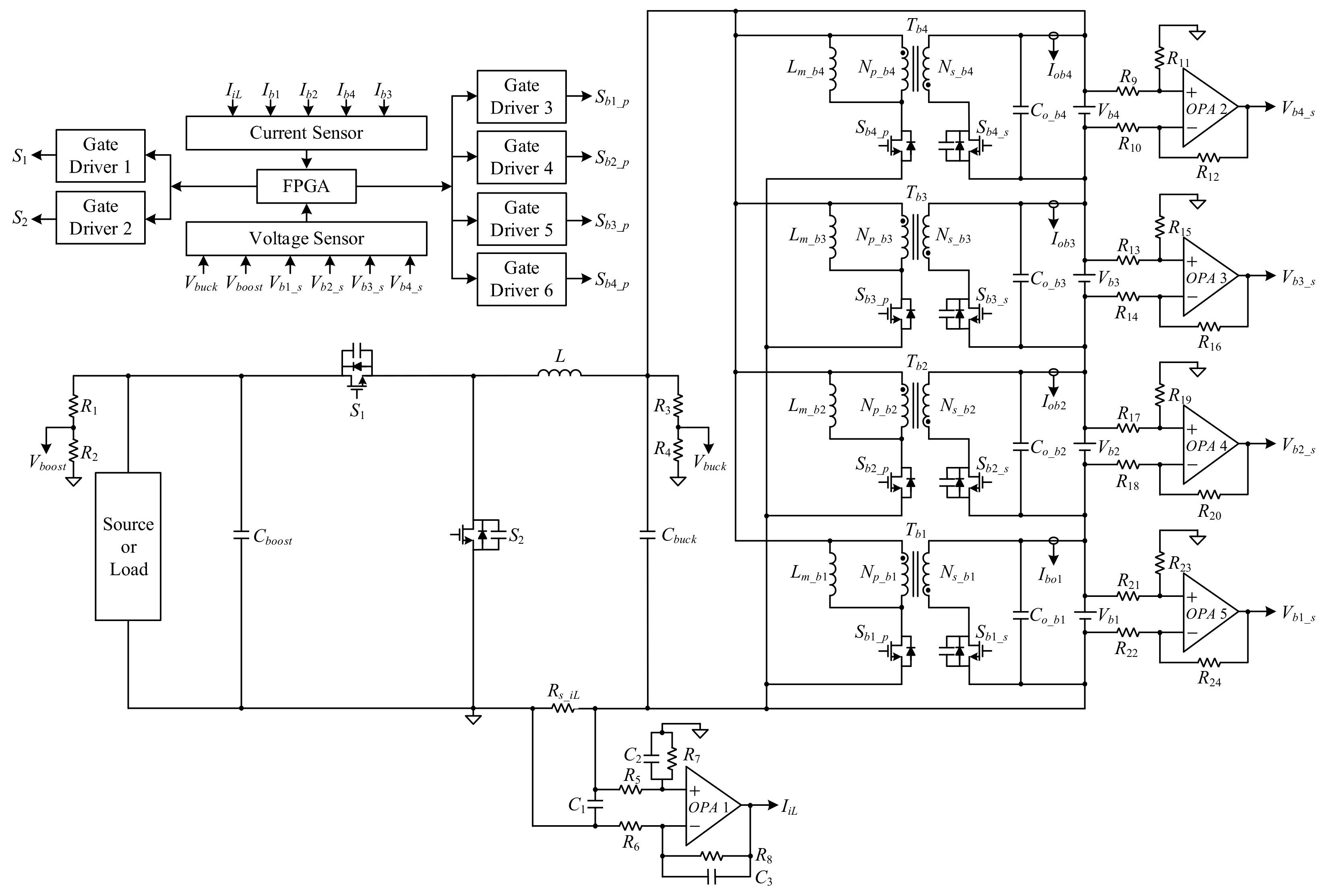
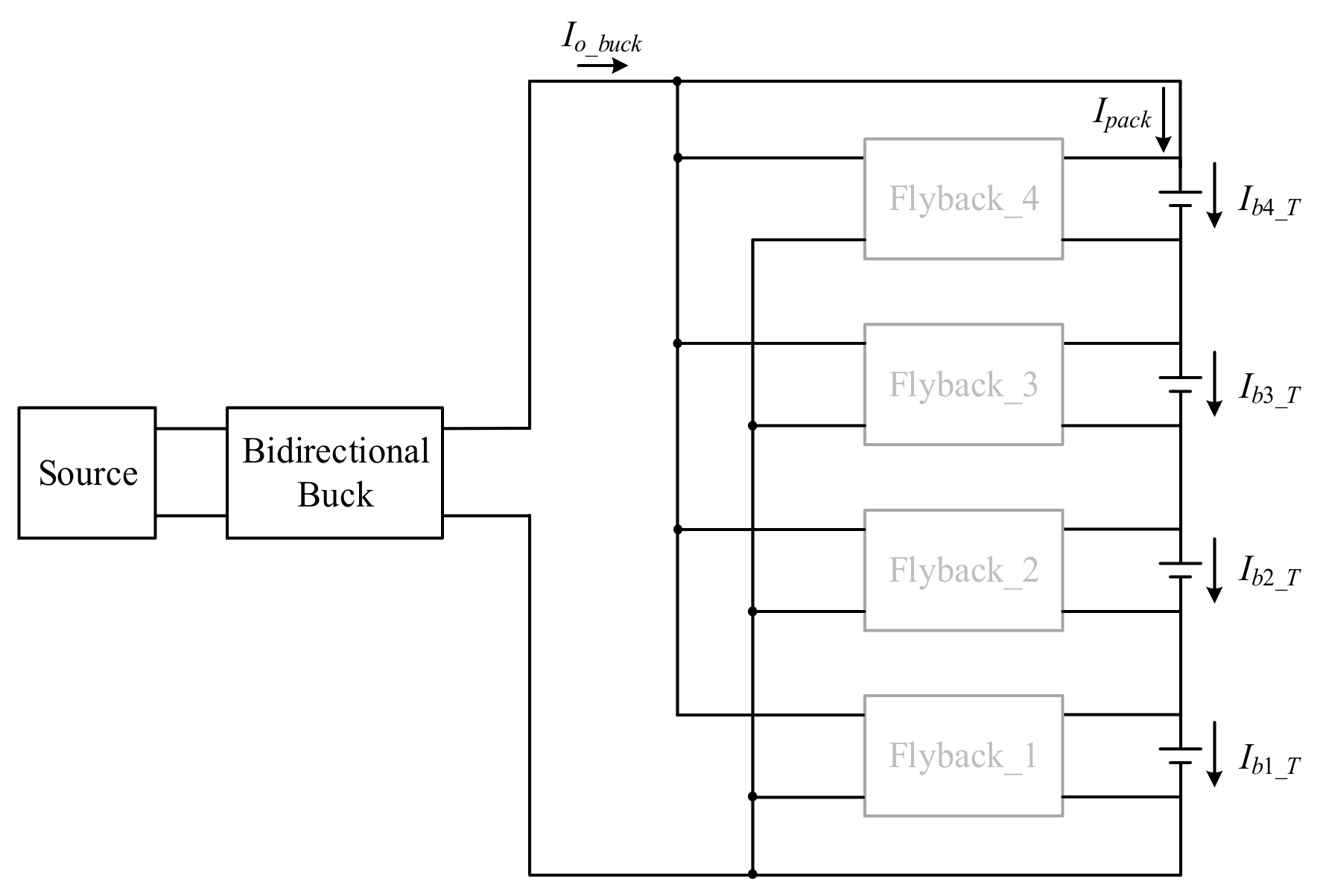
2. System Configuration
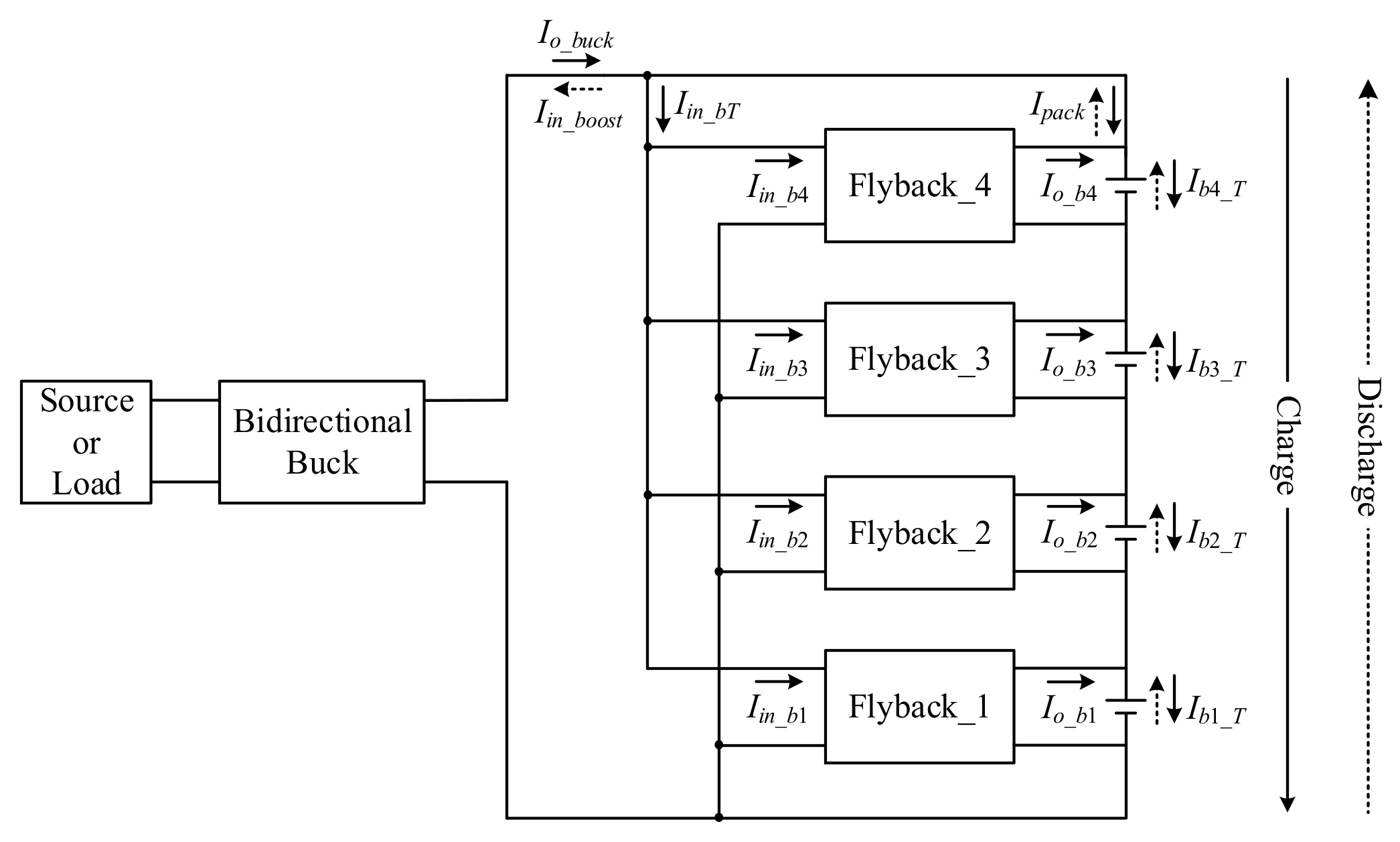
3. Operating Principle of the Battery Voltage Equalizer
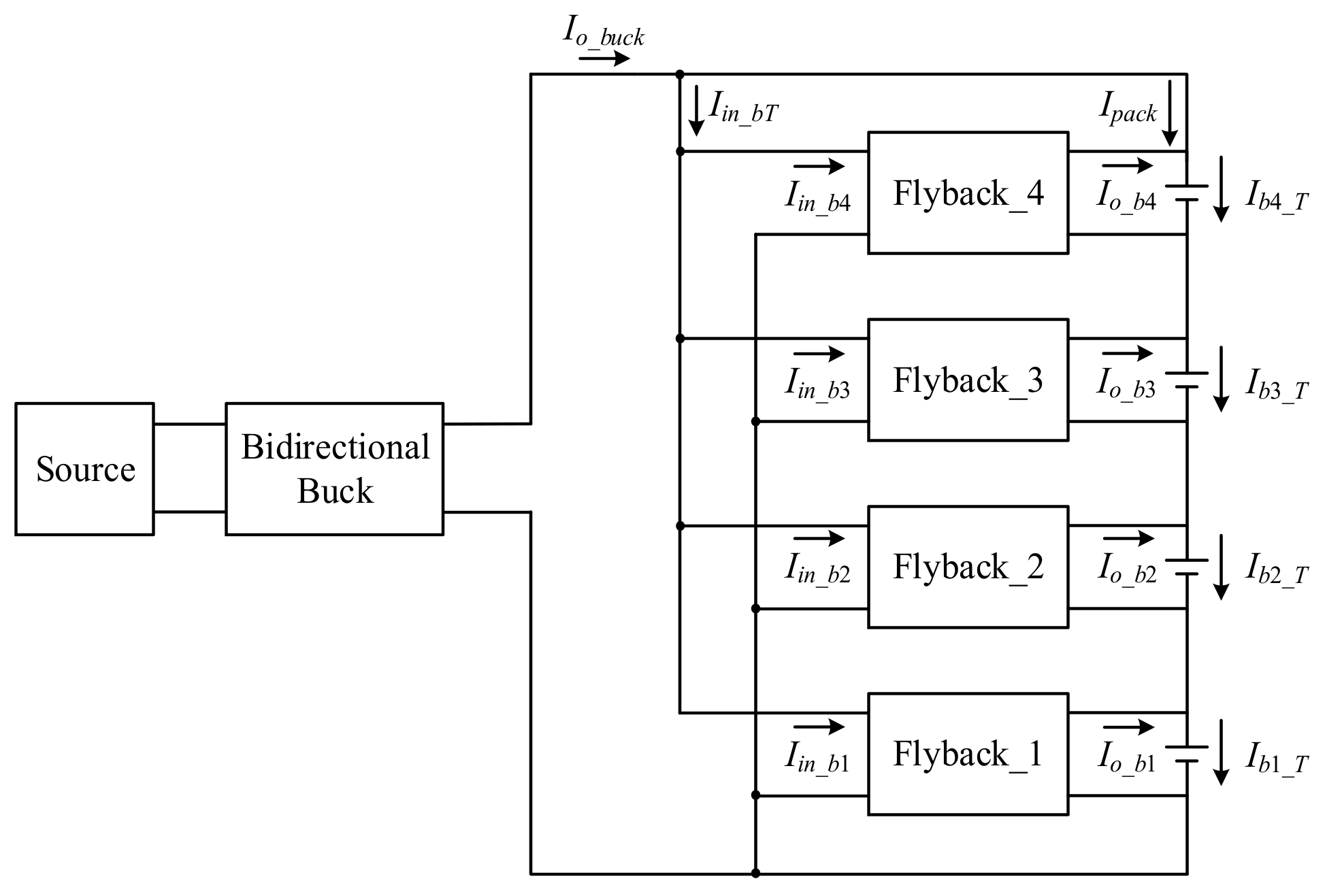
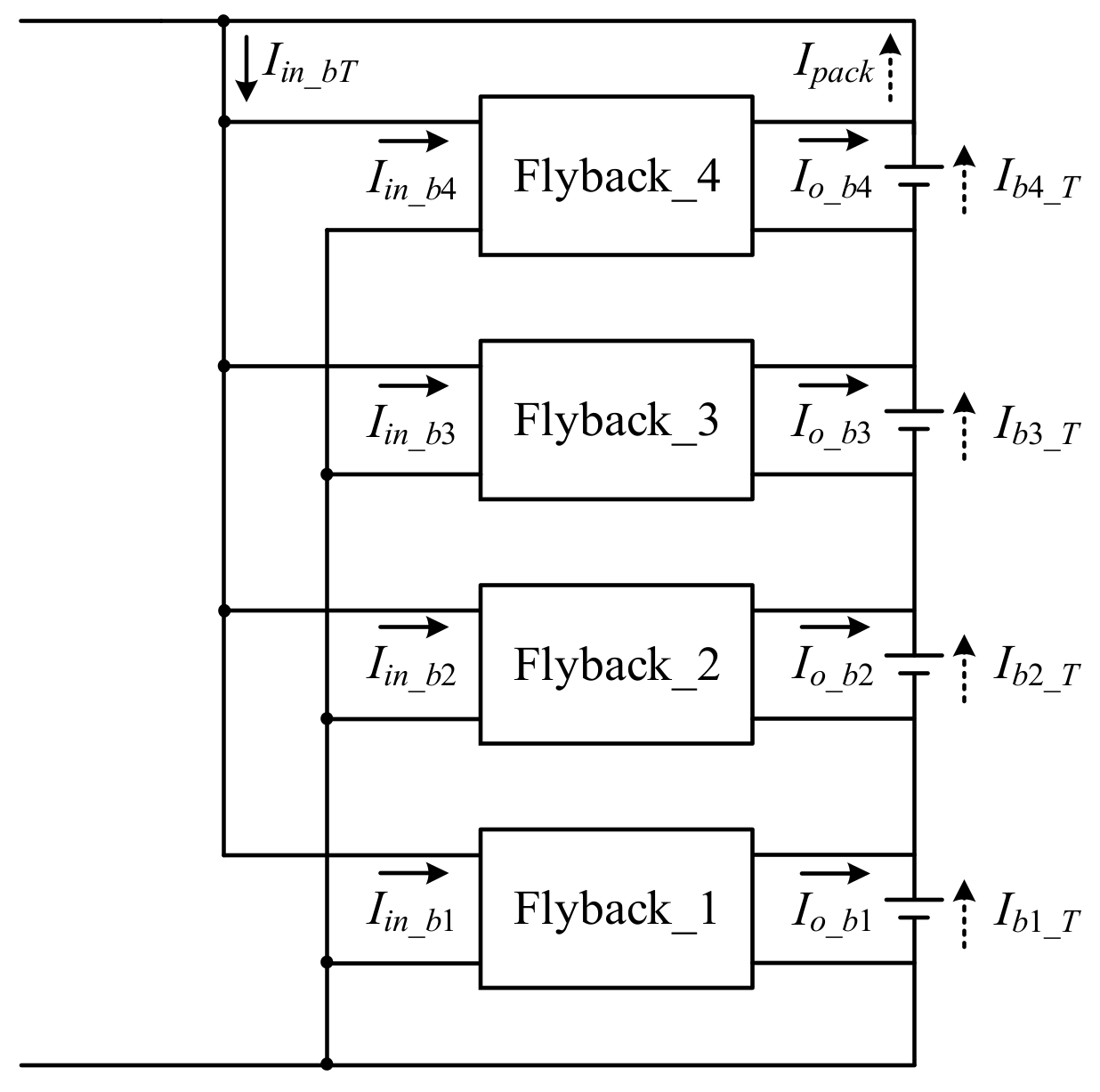
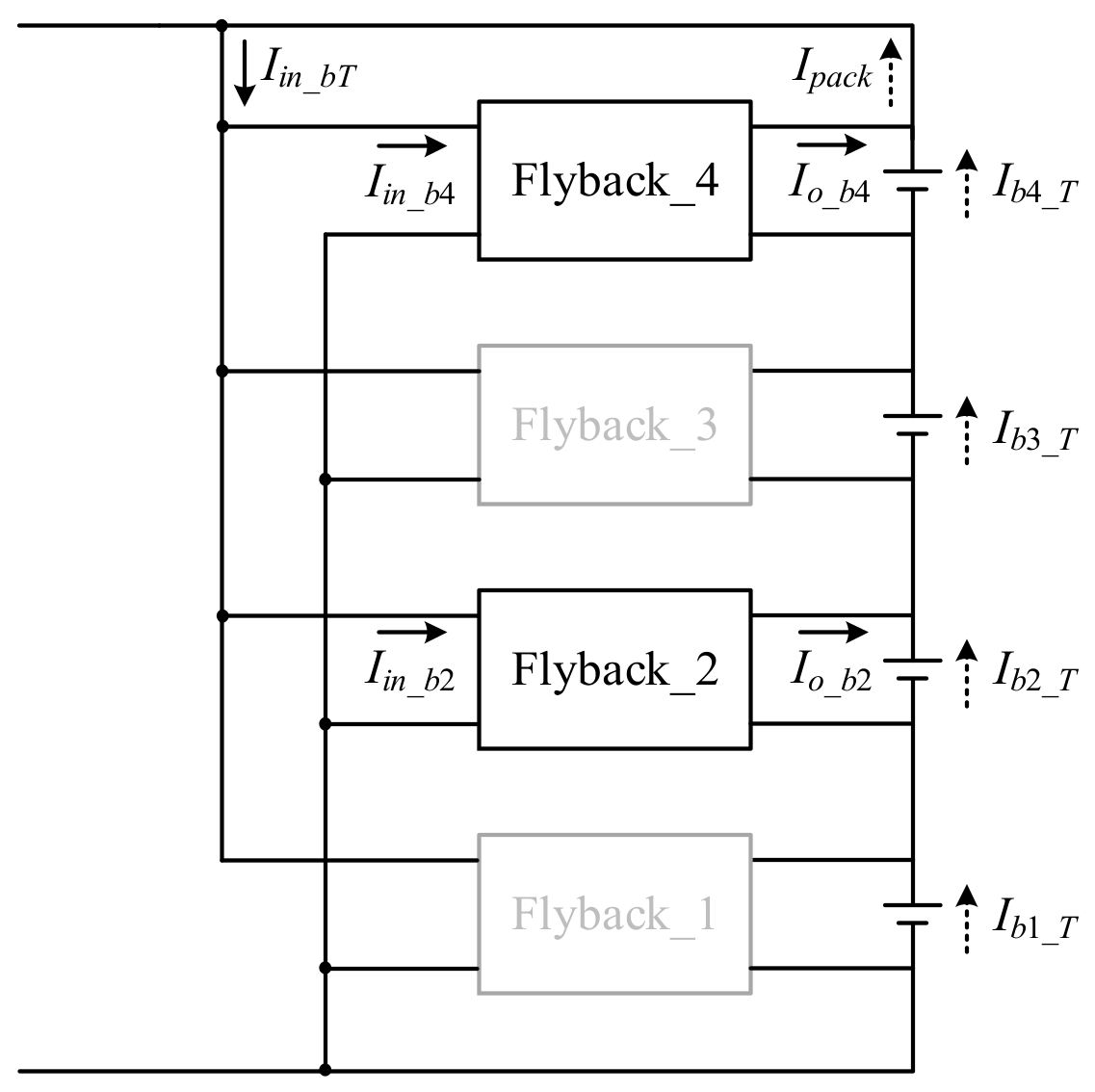
3.1. Charging Balance
3.2. Discharging Balance
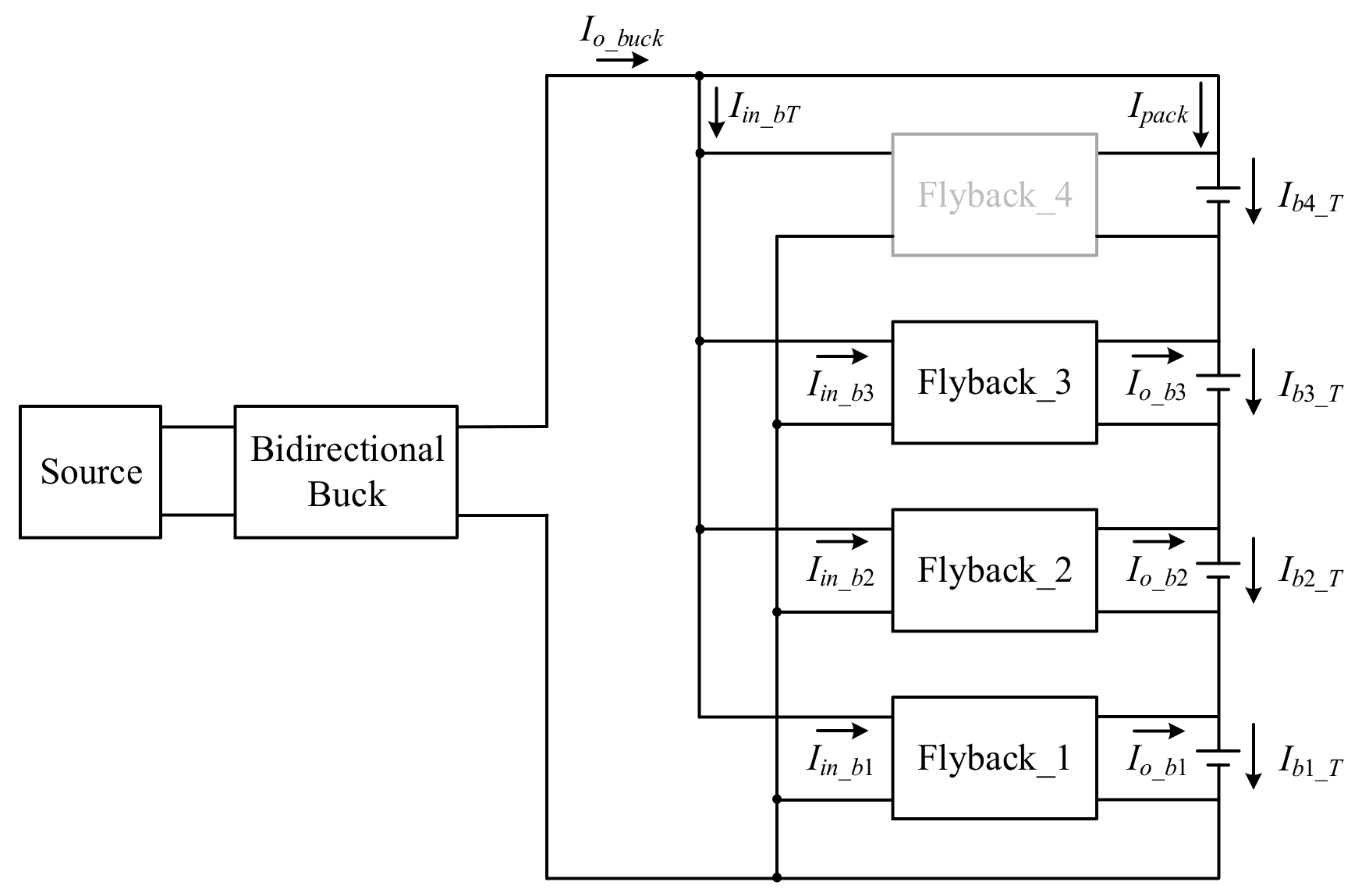
3.3. Static Balance
4. Design Considerations
4.1. Circuit Parameter Design
4.1.1. Inductance Design for Bidirectional Buck Converter
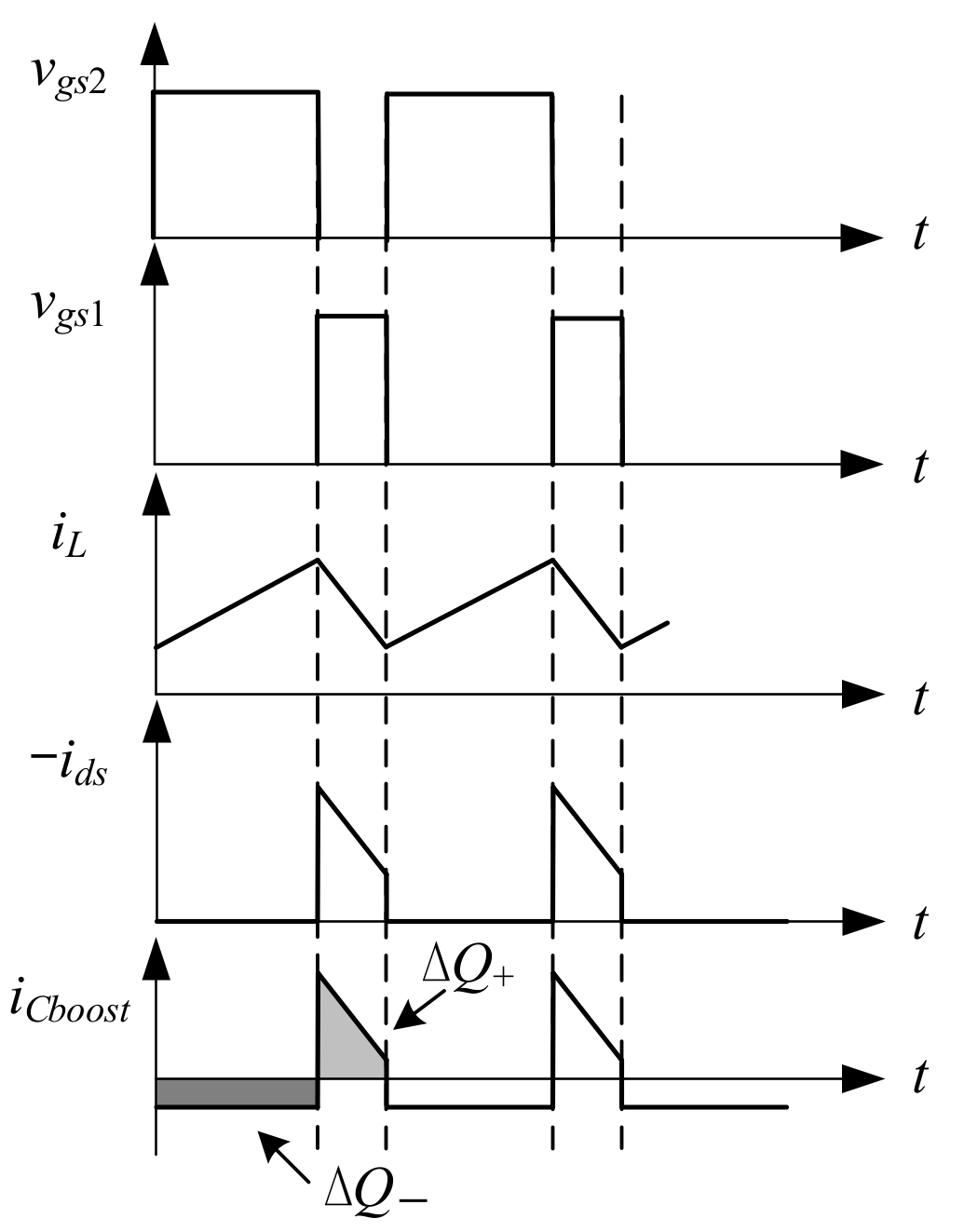
4.1.2. Output Capacitance Design for the Bidirectional Buck Converter
Output Capacitance Cbuck in Buck Mode
Output Capacitance Cbuck in Boost Mode
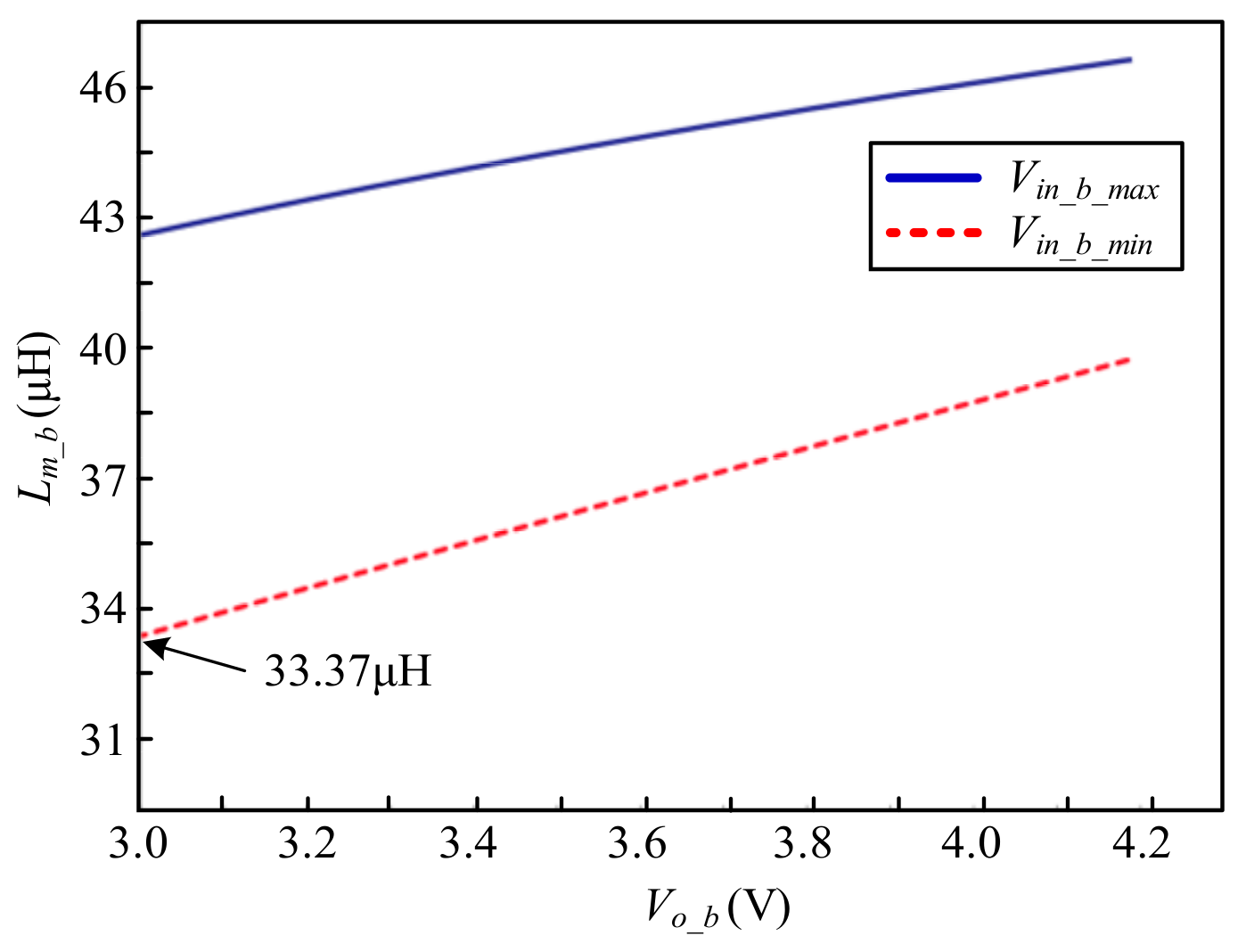
4.1.3. Magnetizing Inductance Design for Flyback Converter
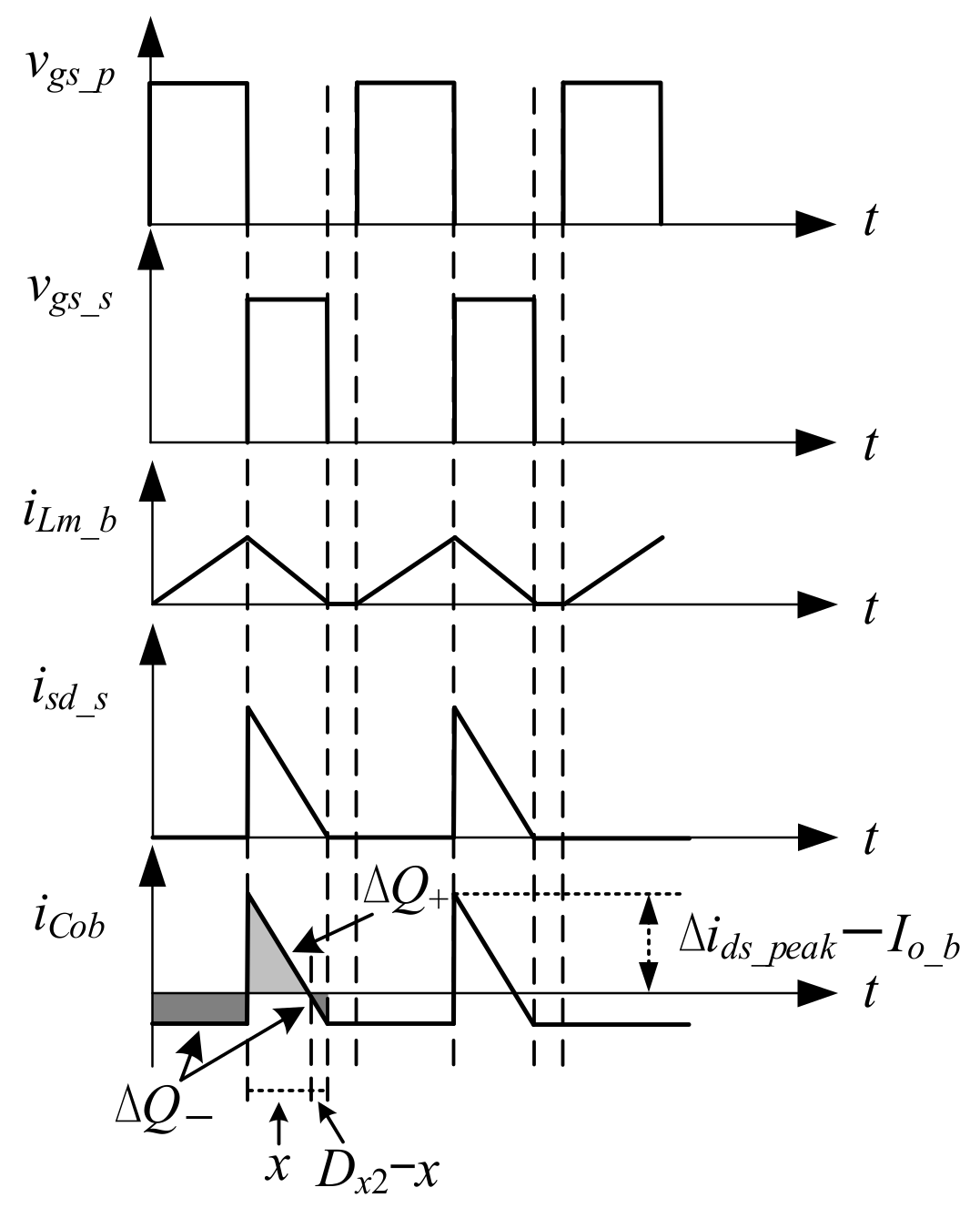
4.1.4. Output Capacitance Design for Flyback Converter
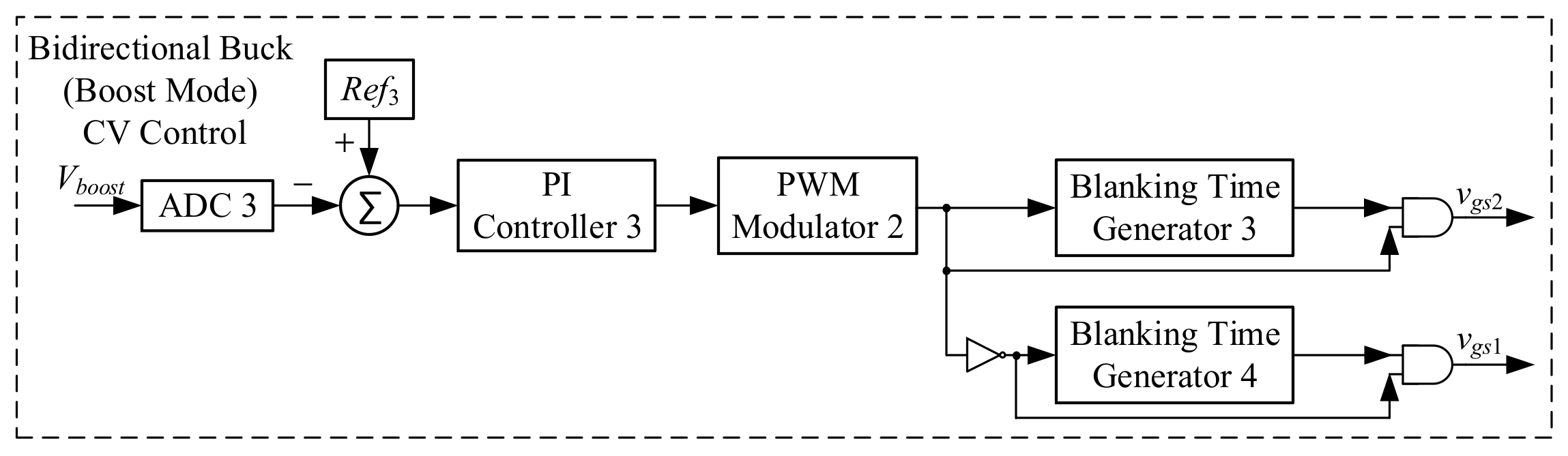
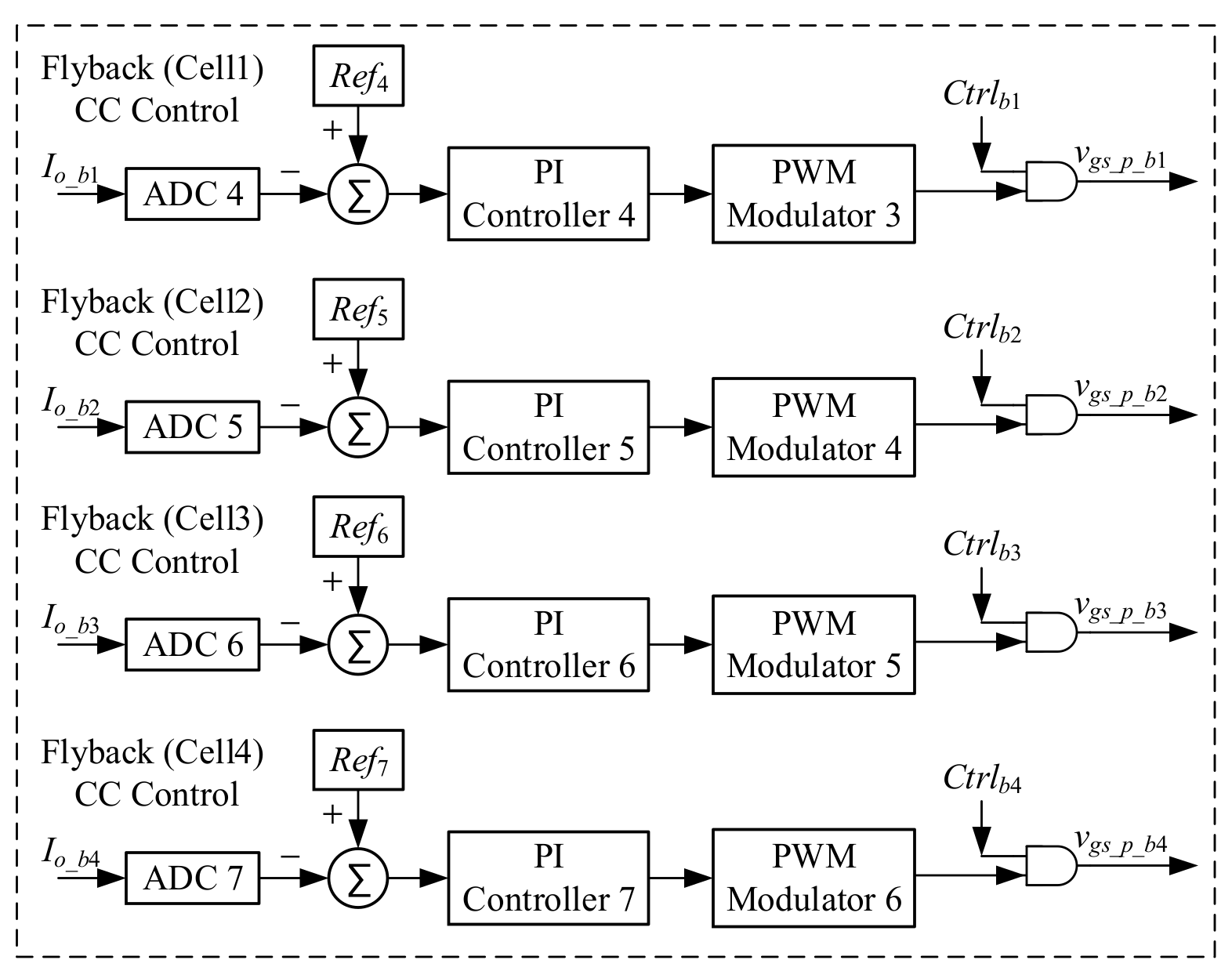
5. Control Considerations
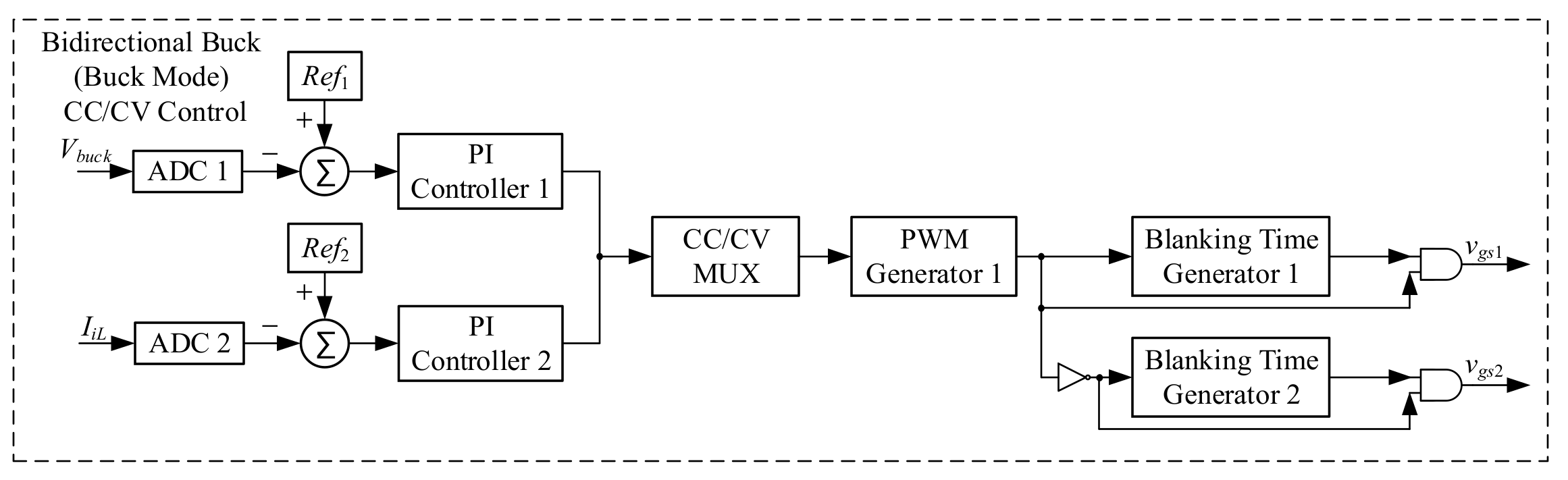
5.1. Control Strategies for Converters in Different Modes
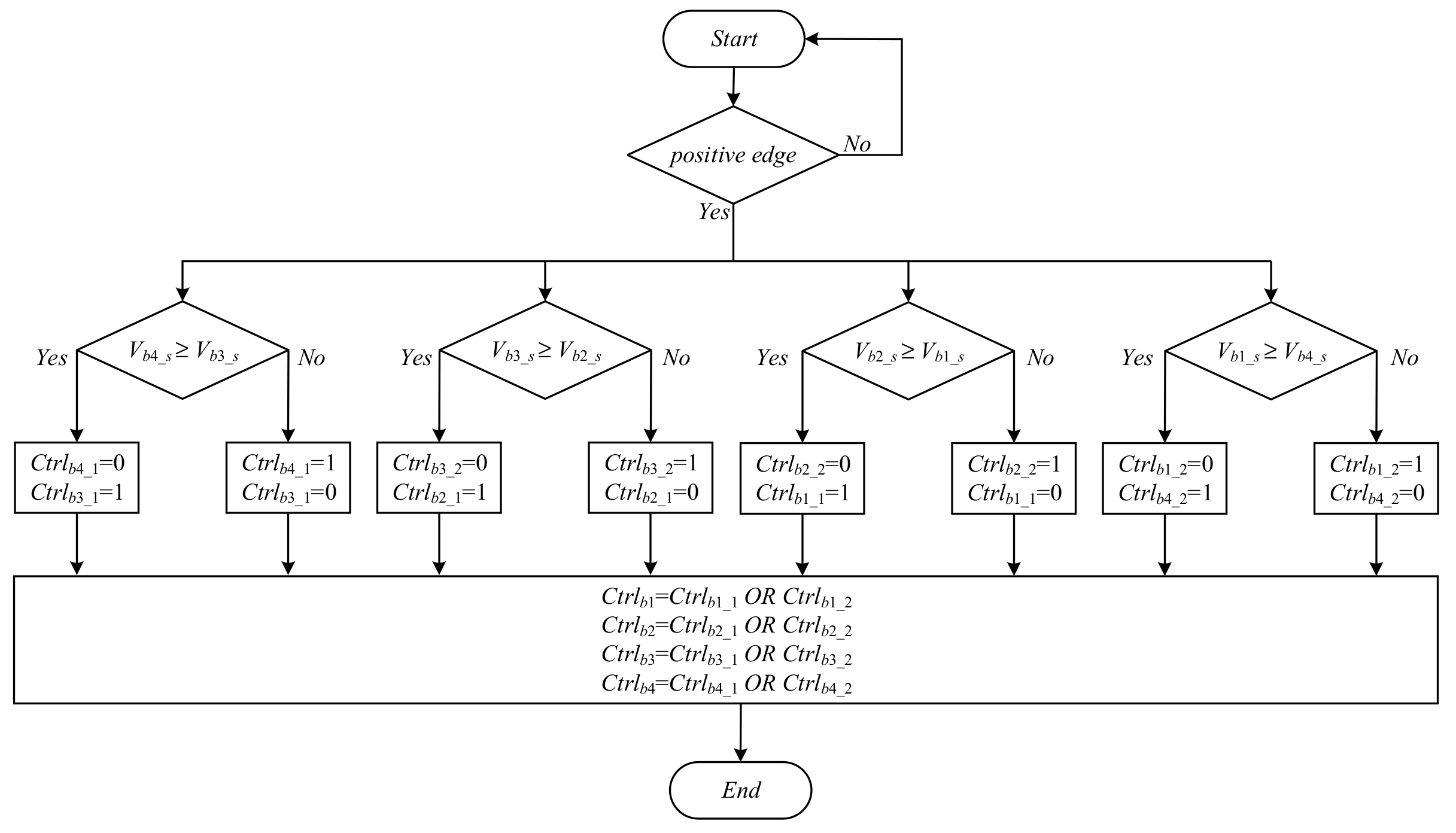
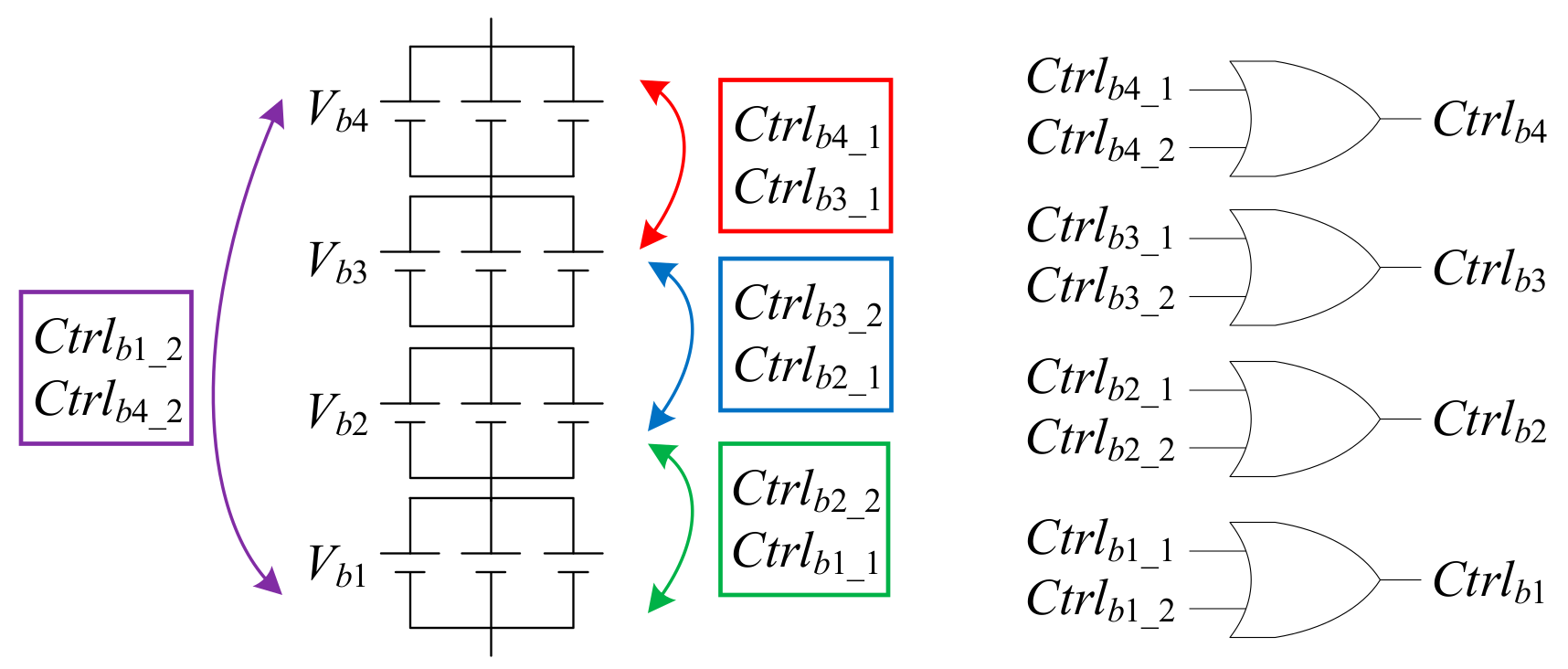
5.2. Chain-Loop Comparison Signals
6. Experimental Results
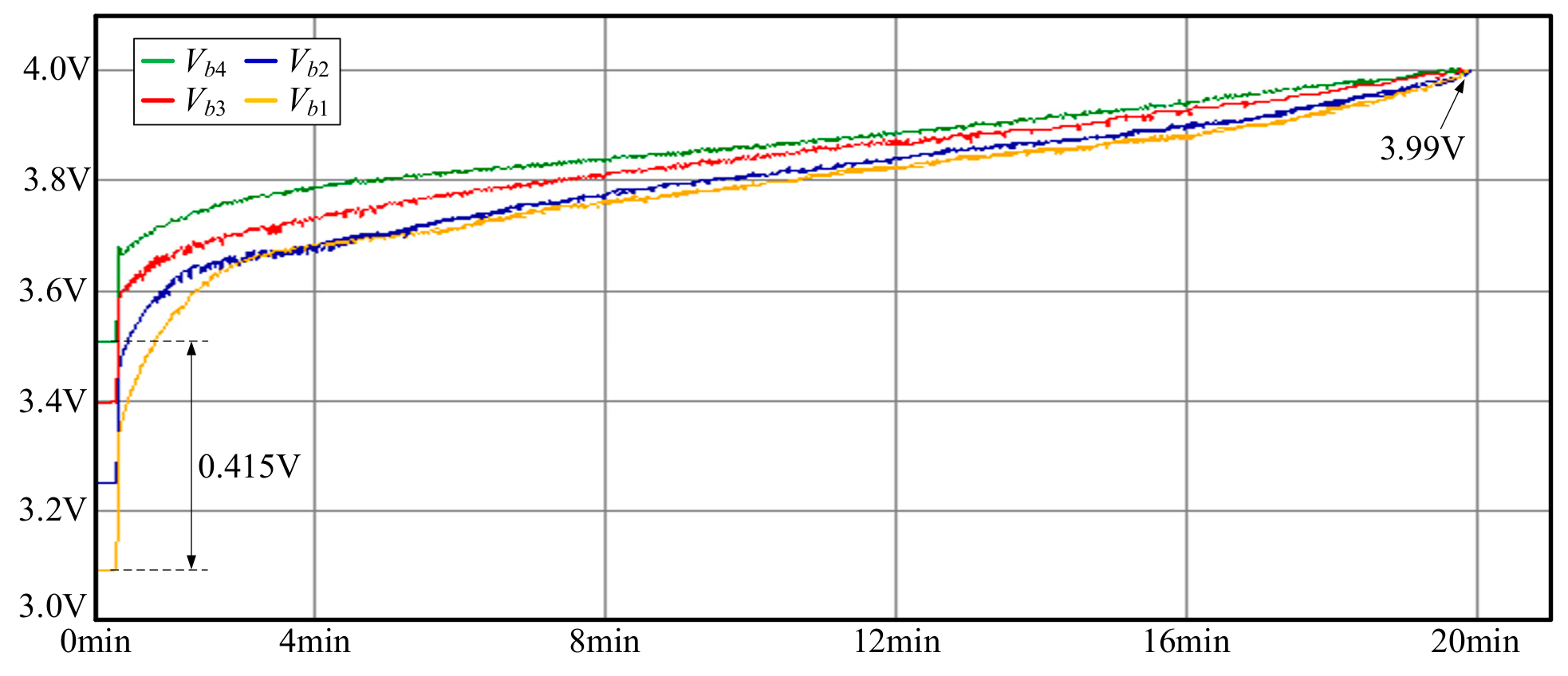
6.1. Experimental Results for Charging Balance
6.2. Experimental Results for Discharging Balance
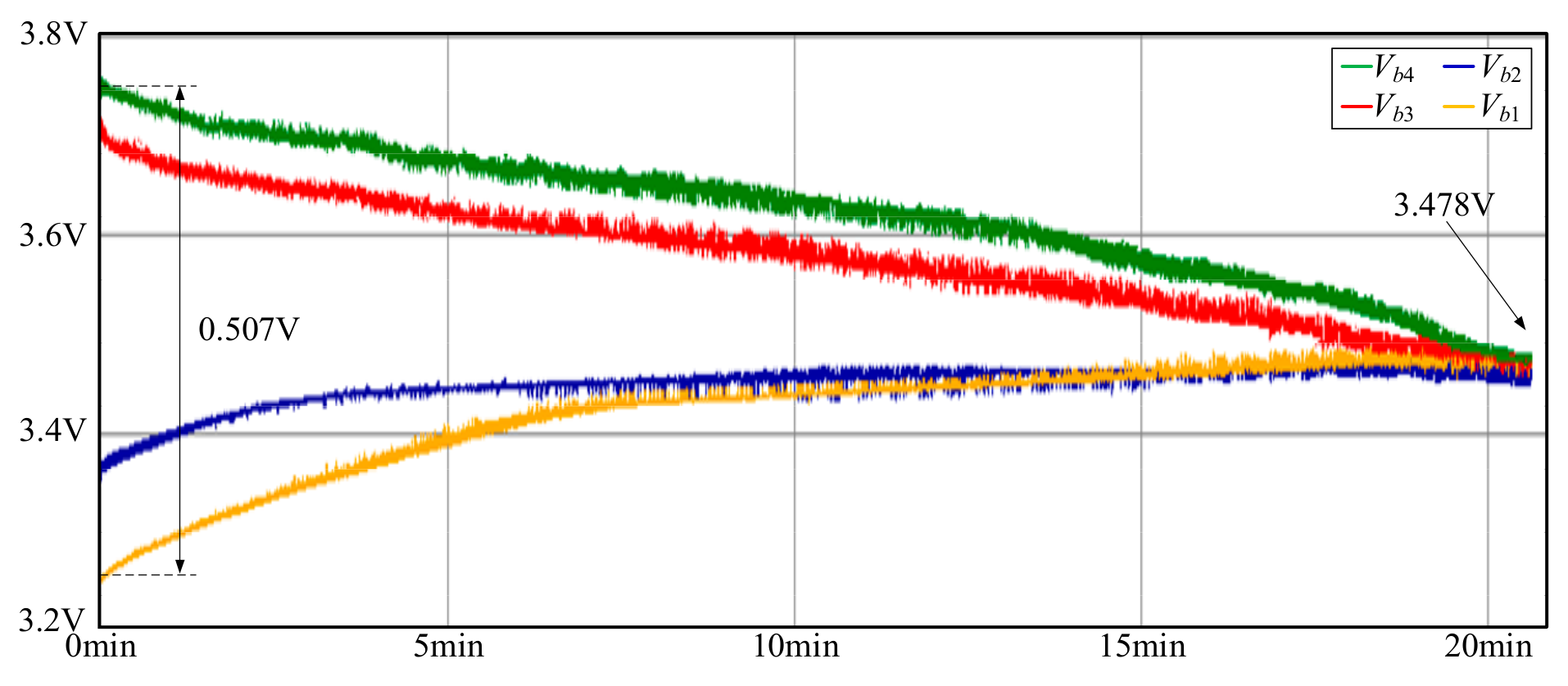
6.3. Experimental Results for Static Balance
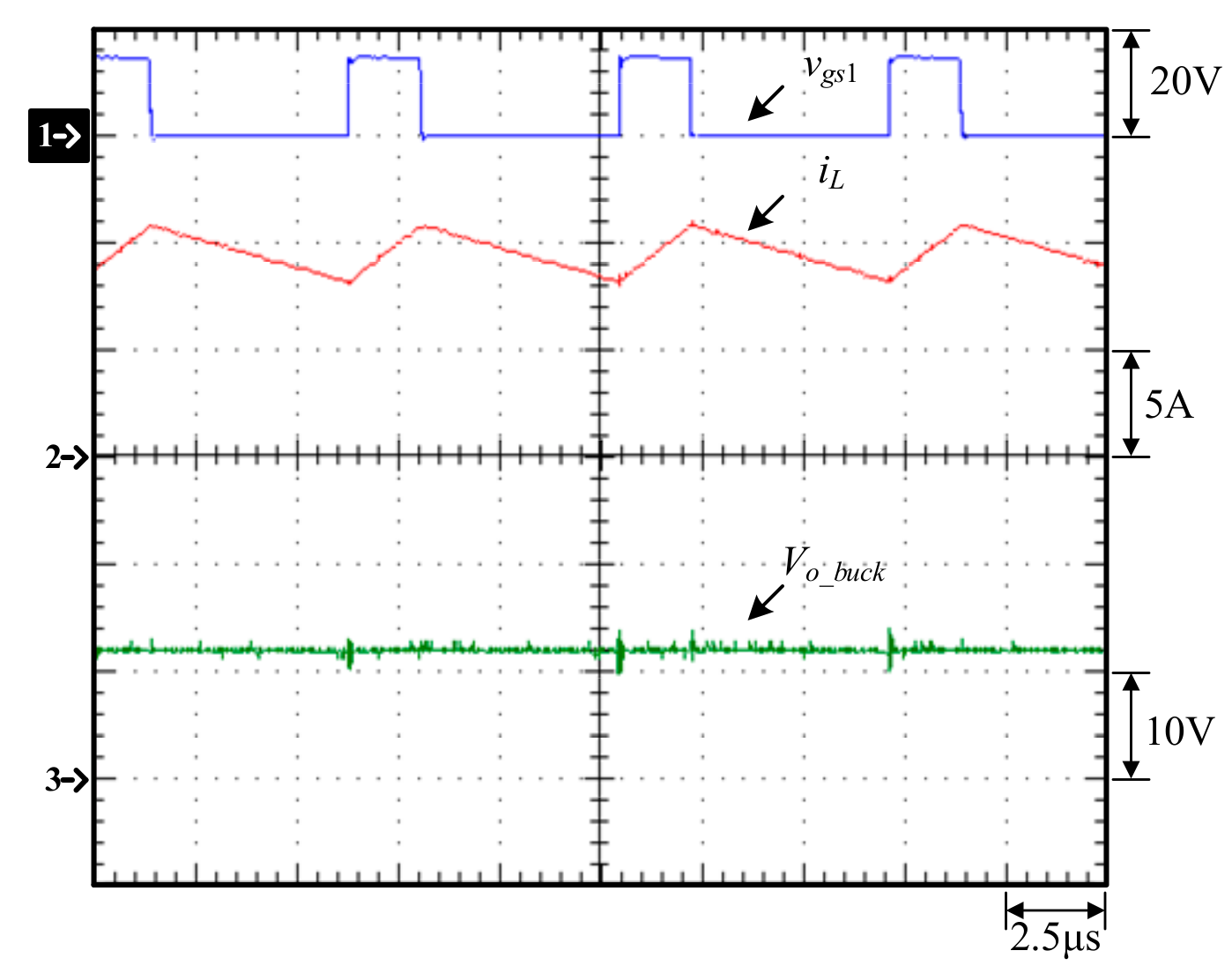
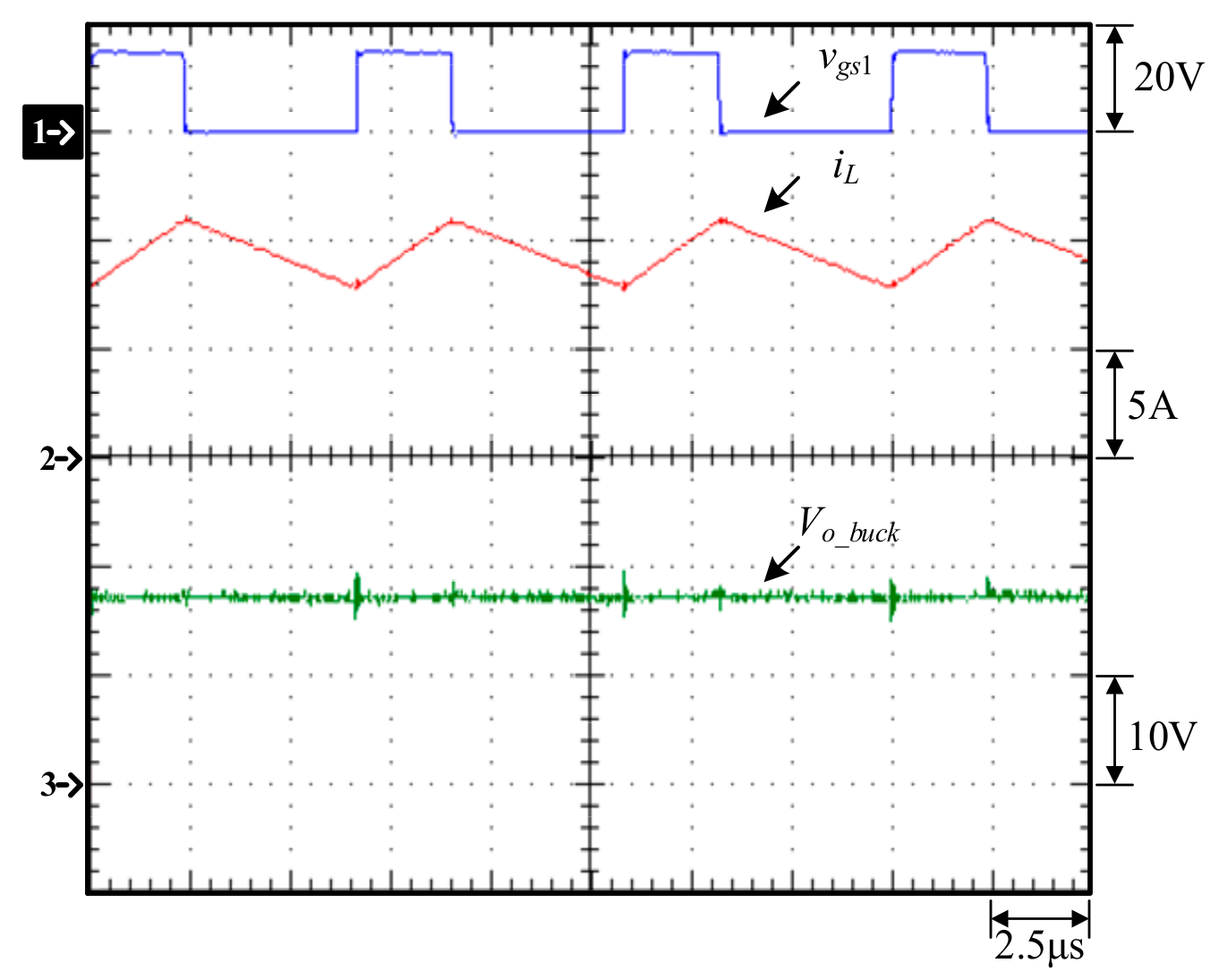
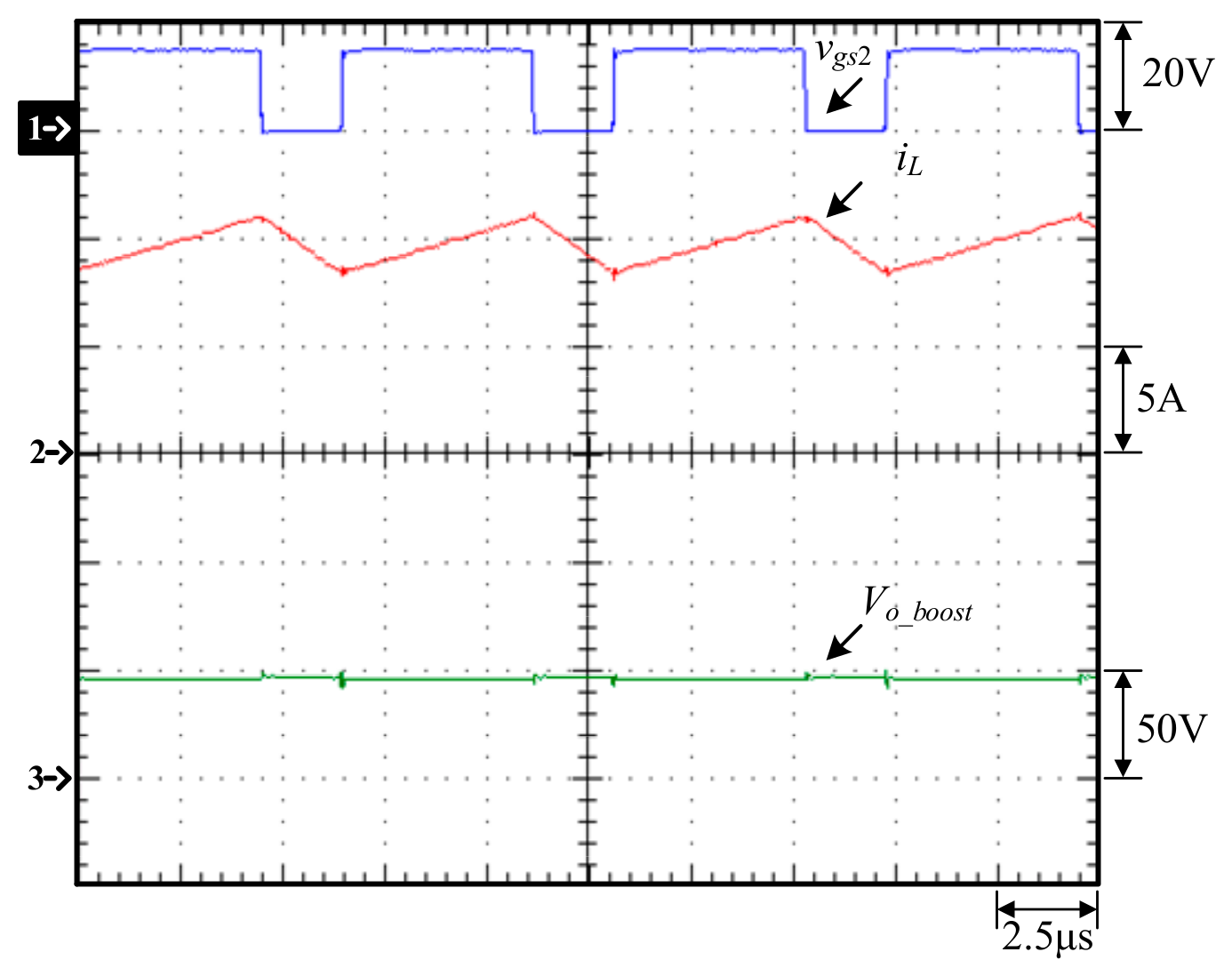
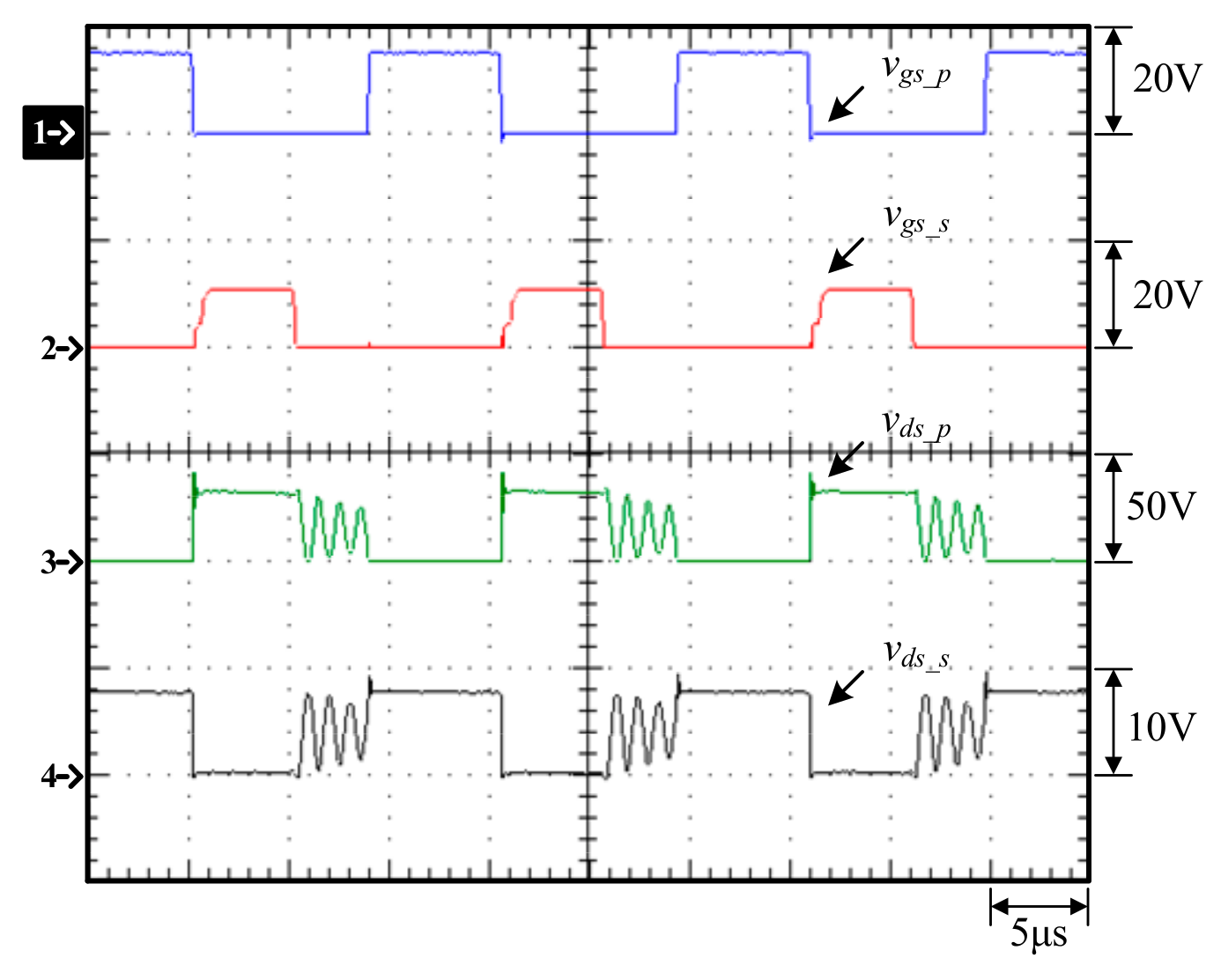
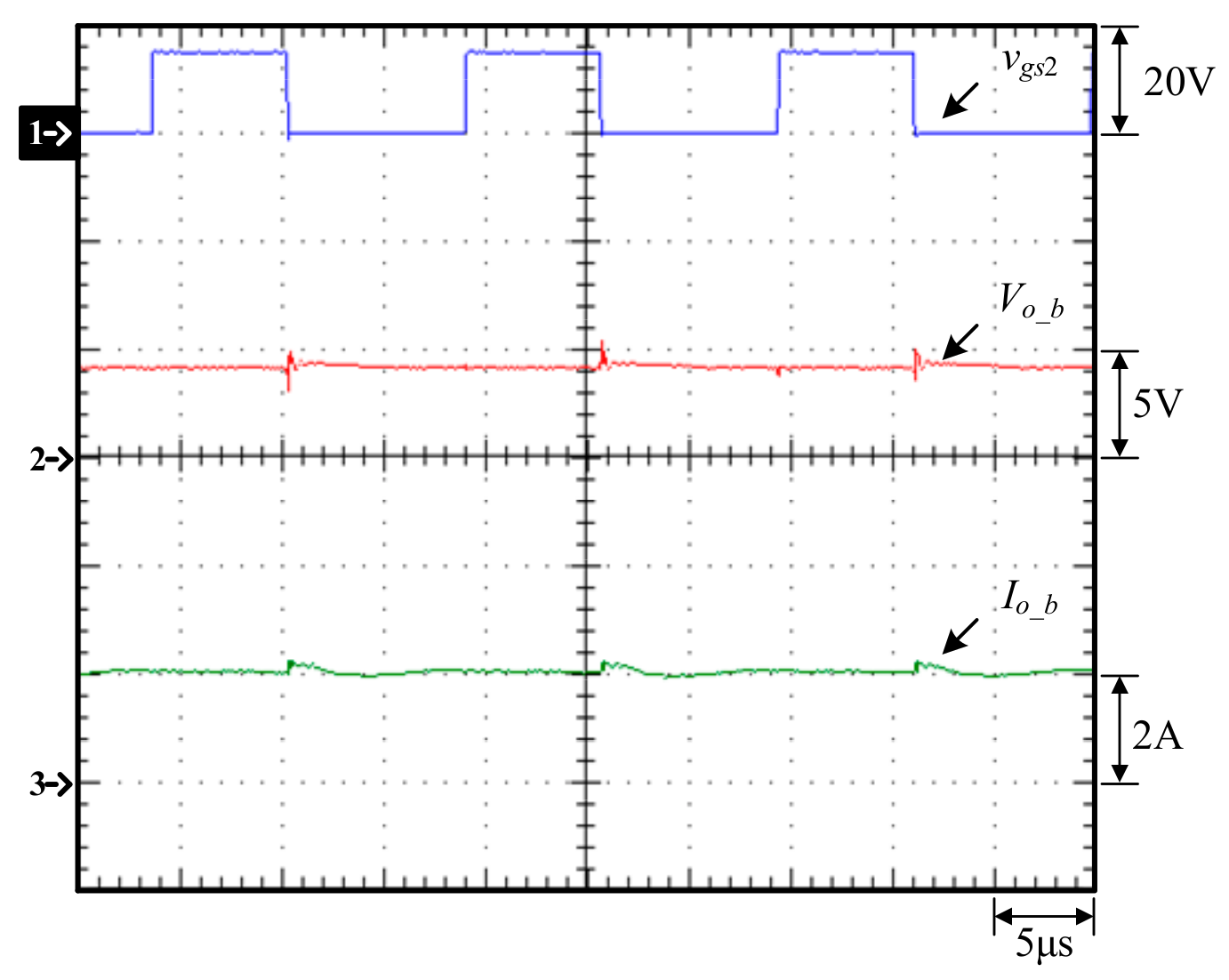
6.4. Experimental Waveforms of Converters
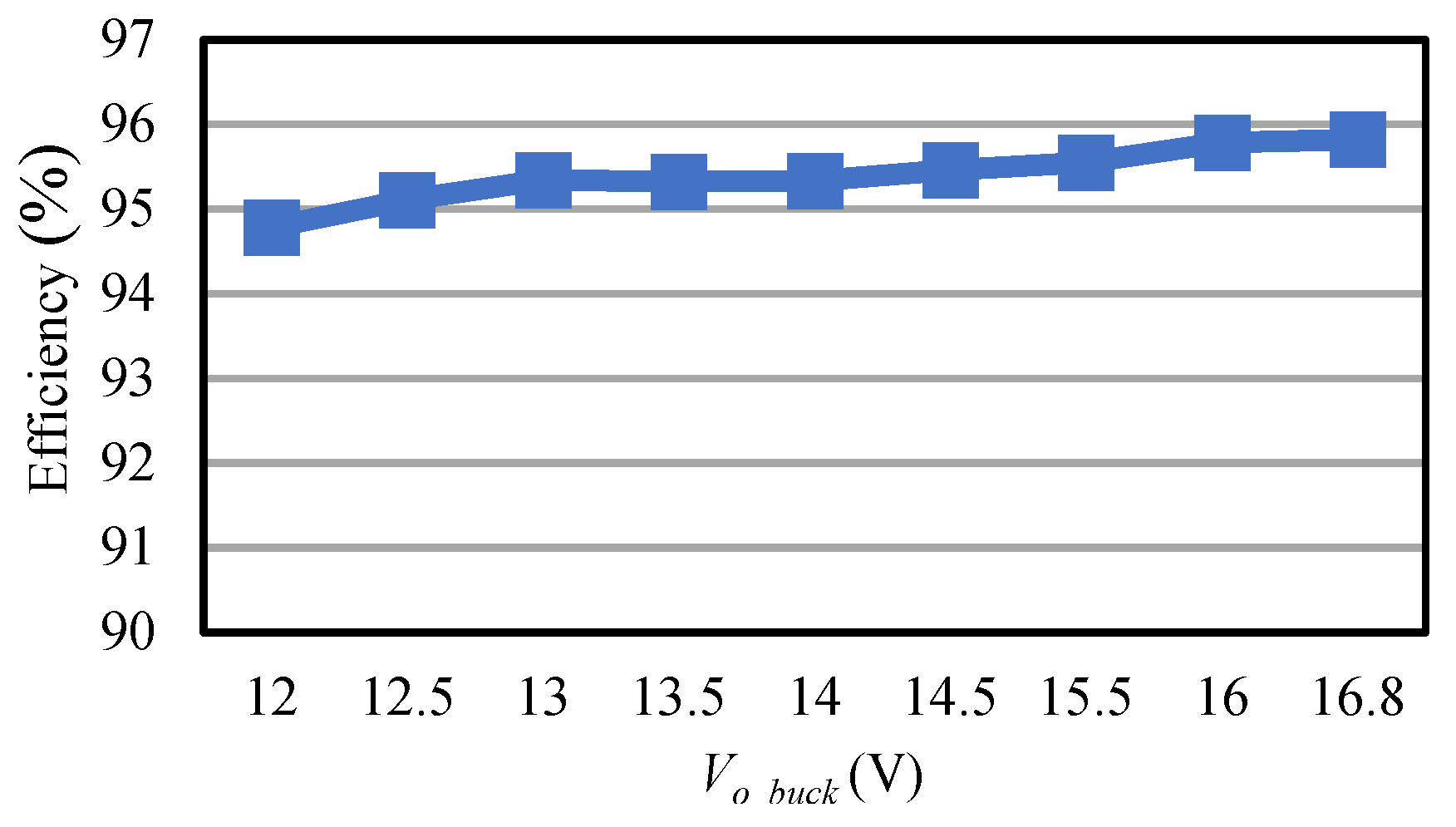
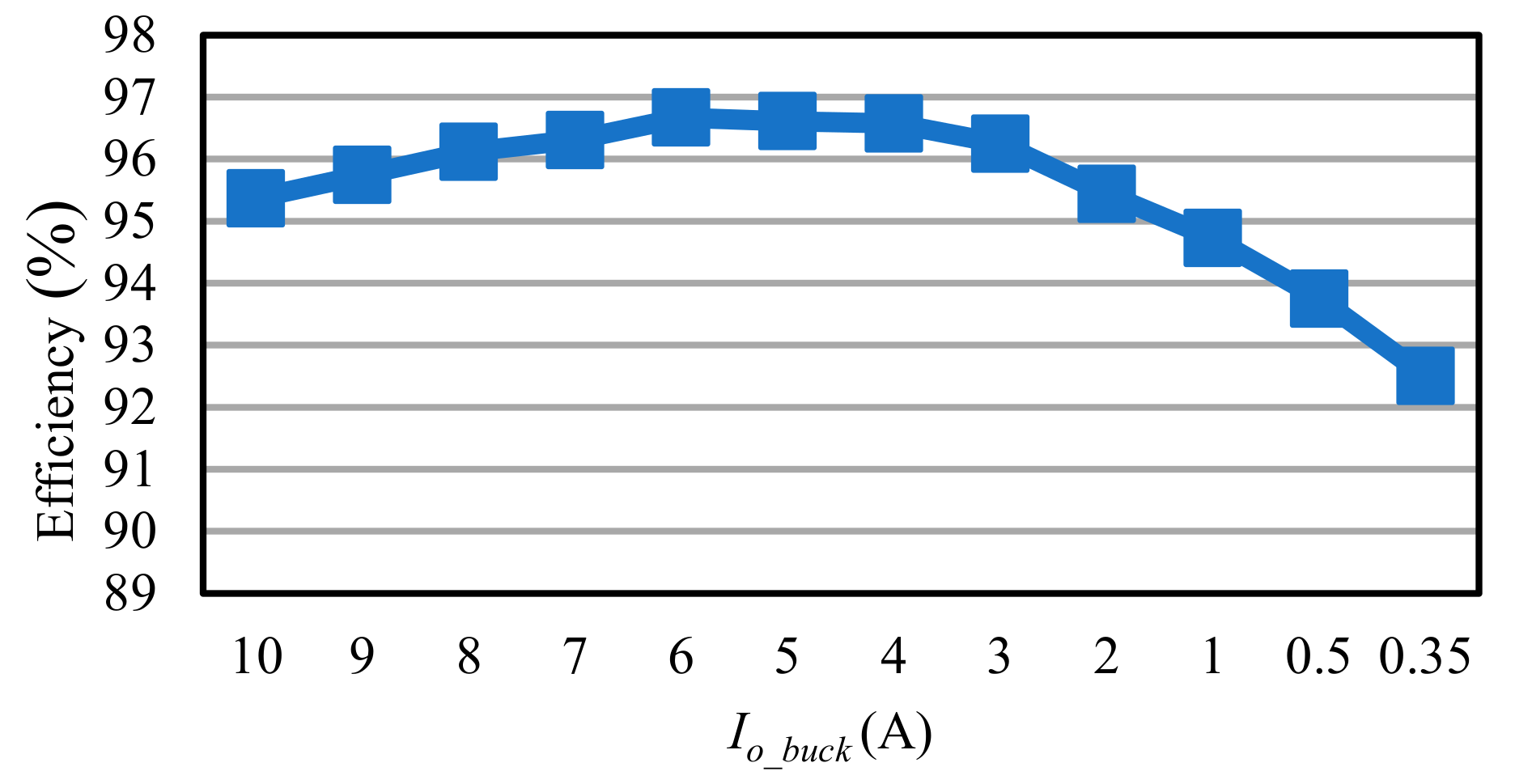
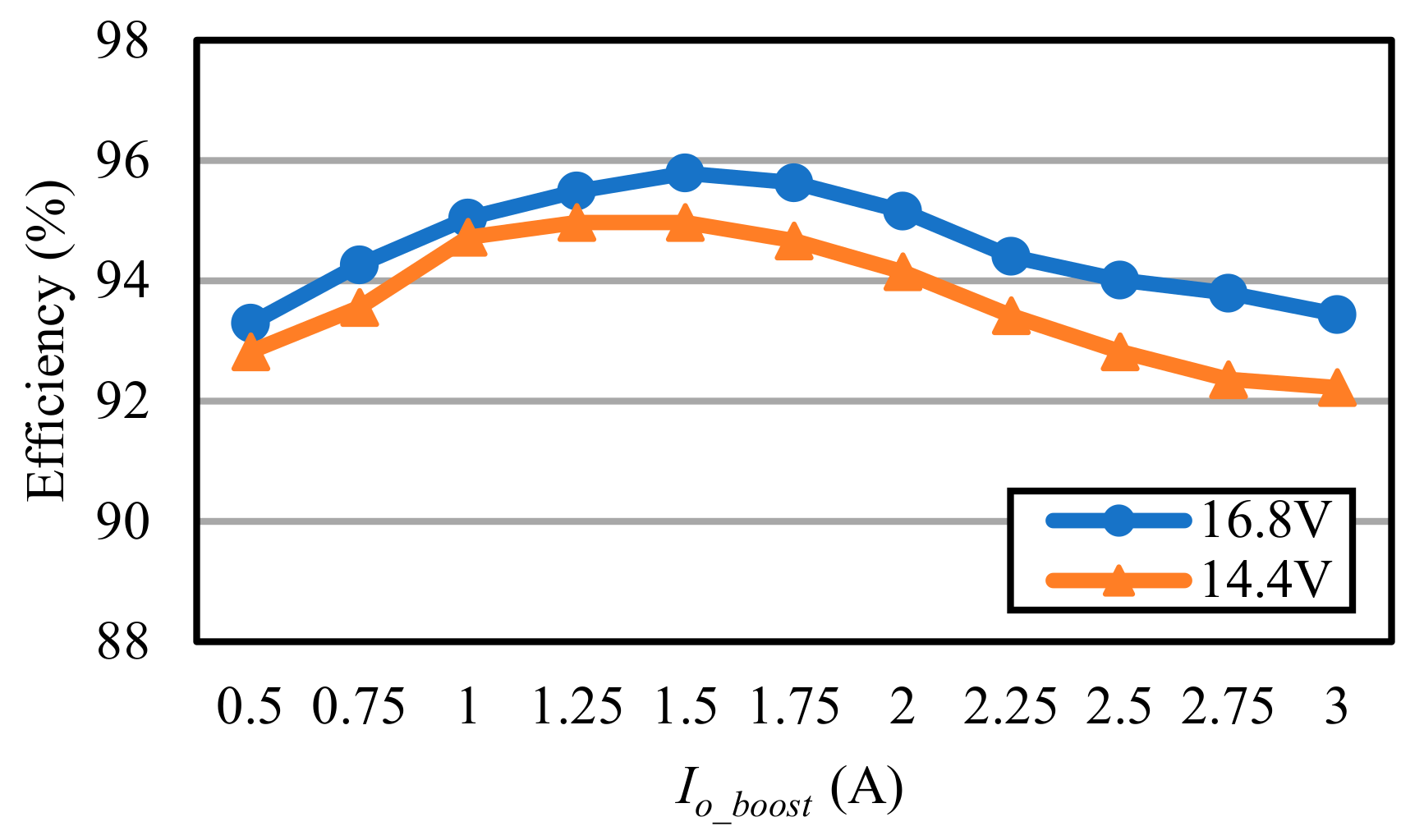
6.5. Converter Efficiency Measurement
7. Literature Comparison
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| S1, S2 | Switches of bidirectional buck converter |
| Cboost | Output capacitance of bidirectional buck converter in boost mode |
| Cbuck | Output capacitance of buck mode of bidirectional buck converter |
| L | Inductance of bidirectional buck converter |
| Tb1, Tb2, Tb3, Tb4 | Coupling inductors of flyback converters |
| Sb1_p, Sb2_p, Sb3_p, Sb4_p | Primary switches of flyback converter |
| Sb1_s, Sb2_s, Sb3_s, Sb4_s | Secondary switches of flyback converters |
| Co_b1, Co_b2, Co_b3, Co_b4 | Output capacitances of flyback converters |
| Lm_b1, Lm_b2, Lm_b3, Lm_b4 | Magnetizing inductances of flyback converters |
| Np_b1, Np_b2, Np_b3, Np_b4 | Primary coils of flyback converters |
| Ns_b1, Ns_b2, Ns_b3, Ns_b4 | Primary coils of flyback converters |
| Vin_buck | Input voltage for buck mode of bidirectional buck converter |
| Vin_boost | Input voltage for boost mode of bidirectional buck converter |
| Vin_b | Input voltage for buck mode of bidirectional buck converter |
| Vo_buck | Output voltage for buck mode of bidirectional buck converter |
| Vo_boost | Output voltage for boost mode of bidirectional buck converter |
| Vo__b | Output voltage of flyback converter |
| Iin_buck | Input current for buck mode of bidirectional buck converter |
| Iin_boost | Input current for boost mode of bidirectional buck converter |
| Iin_b | Input current of flyback converter |
| iL | Current flowing through L |
| Io_buck | Output current for buck mode of bidirectional buck converter |
| Io_boost | Output current for boost mode of bidirectional buck converter |
| Io_b | Output current of flyback converter |
| Ro_boost | Output resistance for boost mode of bidirectional buck converter |
| iCbuck | Current in output capacitor Cbuck |
| iCboost | Current in output capacitor Cboost |
| vL | Voltage of inductor L |
| vLm_b | Voltage of magnetizing inductance Lm_b |
| vNp_b | Voltage of coil Np_b |
| vNs_b | Voltage of coil Ns_b |
| Coss1, Coss2, Coss_p | Parasitic output capacitances of S1, S2, Sb_s |
| vgs1, vgs2, vgs_p, vgs_s | Gate driving signals for switches S1, S2, Sb_s, Sb_p |
| vds1, vds2, vds_p, vds_s | Voltages of S1, S2, Sb_s, Sb_p |
| Dbuck | Duty cycle for buck mode of bidirectional buck converter |
| Ts1 | Switching period of flyback converter |
| Mbuck | Voltage conversion ratio for buck mode of bidirectional buck converter |
| Dboost | Duty cycle for boost mode of bidirectional buck converter |
| Mboost | Voltage conversion ratio for buck mode of bidirectional buck converter |
| Dx1 | On-time ratio of switch Sb_p |
| Dx2 | On-time ratio of switch Sb_s |
| Dx3 | Duration ratio of magnetizing inductance Lm_b when no energy is stored |
| Ts2 | Switching period of flyback converter |
| Mb | Voltage conversion ratio of the flyback converter |
| Ids_s_peak | Peak current in switch Sb_s |
| ILm_b_peak | Peak current in magnetizing inductor Lm_b |
| Ipack | Current in battery pack |
| Iin_bT | Total input current of flyback converter |
| Vb1, Vb2, Vb3, Vb4 | Voltages of battery cell |
| Ib1_T, Ib2_T, Ib3_T, Ib4_T | Currents in battery cell |
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Accelerated charge-discharge cycling test and cycle life prediction model for super capacitors in alternative battery applications. IEEE Trans. Ind. Electron. 2012, 59, 4704–4712. [Google Scholar] [CrossRef]
- Park, H.; Kim, C.; Park, K.; Moon, G.; Lee, J. Design of a charge equalizer based on battery modularization. IEEE Trans. Veh. Technol. 2009, 58, 3216–3223. [Google Scholar] [CrossRef]
- Kim, J.; Shin, J.; Chun, C.; Cho, B.H. Stable configuration of a Li-ion series battery pack based on a screening process for improved voltage/SOC balancing. IEEE Trans. Power Electron. 2021, 27, 411–424. [Google Scholar] [CrossRef]
- Kelkar, A.; Dasari, Y.; Williamson, S.S. A comprehensive review of power electronics enabled active battery cell balancing for smart energy management. In Proceedings of the IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Rui, L.; Lizhi, W.; Xueli, H.; Qiang, D.; Jie, Z. A review of equalization topologies for lithium-ion battery packs. In Proceedings of the IEEE 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 7922–7927. [Google Scholar]
- Daowd, M.; Omar, N.; Bossche, P.V.; Mierlo, J.V. A review of passive and active battery balancing based on MATLAB Simulink. Int. Rev. Electr. Eng. 2011, 6, 2974–2989. [Google Scholar]
- Ghaeminezhad, N.; Ouyang, Q.; Hu, X.; Xu, G.; Wang, Z. Active cell equalization topologies analysis for battery packs: A systematic review. IEEE Trans. Power Electron. 2021, 36, 9119–9135. [Google Scholar] [CrossRef]
- Cao, J.; Schofield, N.; Emadi, A. Battery balancing methods: A comprehensive review. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar]
- Daowd, M.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Passive and active battery balancing comparison based on matlab simulation. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar]
- Ci, S.; Lin, N.; Wu, D. Reconfigurable battery techniques and systems: A survey. IEEE Access 2016, 4, 1175–1189. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Sun, D. Review of battery cell balancing methodologies for optimizing battery pack performance in electric vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
- Qi, J.; Dah-Chuan Lu, D. Review of battery cell balancing techniques. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Perth, WA, Australia, 28 September–1 October 2014; pp. 1–6. [Google Scholar]
- Vardwaj, V.; Vishakha, V.; Jadoun, V.K.; Jayalaksmi, N.S.; Agarwal, A. Various methods used for battery balancing in electric vehicles: A comprehensive review. In Proceedings of the IEEE International Conference on Power Electronics & IoT Applications in Renewable Energy and Its Control (PARC), Mathura, India, 28–29 February 2020; pp. 208–213. [Google Scholar]
- Phung, T.H.; Crebier, J.C.; Lembeye, Y. Voltage balancing converter network for series-connected battery stack. In Proceedings of the IEEE Conference on Industrial Electronics Society (IECON), Montreal, QC, Canada, 25–28 October 2012; pp. 3007–3013. [Google Scholar]
- Lindemark, B. Individual cell voltage equalizers (ICE) for reliable battery performance. In Proceedings of the IEEE International Telecommunications Energy Conference (INTELEC), Kyoto, Japan, 5–8 November 1991; pp. 196–201. [Google Scholar]
- Wei, L.; Jie, L.; Wenji, S.; Ziping, F. Study on passive balancing characteristics of serially connected lithium-ion battery string. In Proceedings of the IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 489–495. [Google Scholar]
- Du, J.; Wang, Y.; Tripathi, A.; Lam, J.S.L. Li-ion battery cell equalization by modules with chain structure switched capacitors. In Proceedings of the IEEE Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 25–26 October 2016; pp. 1–6. [Google Scholar]
- Mahardiono, N.A.; Setiawan, D.; Purnama, I. A study on transfer element in single switched capacitor battery balancer system. In Proceedings of the International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 1–2 November 2018; pp. 64–68. [Google Scholar]
- Moral, C.G.; Laborda, D.F.; Alonso, L.S.; Guerrero, J.M.; Fernandez, D.; Pereda, C.R.; Reigosa, D.D. Battery internal resistance estimation using a battery balancing system based on switched capacitors. IEEE Trans. Ind. Appl. 2020, 56, 5363–5374. [Google Scholar] [CrossRef]
- Shang, Y.; Xia, B.; Yang, J.; Zhang, C.; Cui, N.; Mi, C. A delta-structured switched-capacitor equalizer for series-connected battery strings. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4493–4496. [Google Scholar]
- Shang, Y.; Zhang, Q.; Cui, N.; Duan, B.; Zhang, C. An optimized mesh-structured switched-capacitor equalizer for lithium-ion battery strings. IEEE Trans. Transp. Electrif. 2019, 5, 252–261. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Fong, Y.C.; Xue, X.; Lin, J. Topology, modeling, and design of switched-capacitor-based cell balancing systems and their balancing exploration. IEEE Trans. Power Electron. 2017, 32, 4444–4454. [Google Scholar] [CrossRef]
- Singh, H.R.; Pandey, K.; Prakash, A. Active cell balancing using microcontroller. In Proceedings of the IEEE International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 82–84. [Google Scholar]
- Moghaddam, A.F.; Van Den Bossche, A. An active cell equalization technique for lithium-ion batteries based on inductor balancing. In Proceedings of the IEEE International Conference on Mechanical and Aerospace Engineering (ICMAE), Budapest, Hungary, 10–13 July 2018; pp. 274–278. [Google Scholar]
- Wang, S.; Yang, S.; Yang, W.; Wang, Y. A new kind of balancing circuit with multiple equalization modes for serially connected battery pack. IEEE Trans. Ind. Electron. 2021, 68, 2142–2150. [Google Scholar] [CrossRef]
- Cao, X.; Zhong, Q.-C.; Qiao, Y.-C.; Deng, Z.-Q. Multilayer modular balancing strategy for individual cells in a battery pack. IEEE Trans. Energy Convers. 2018, 33, 526–536. [Google Scholar] [CrossRef]
- Narayanaswamy, S.; Steinhorst, S.; Lukasiewycz, M.; Kauer, M.; Chakraborty, S. Optimal dimensioning and control of active cell balancing architectures. IEEE Trans. Veh. Technol. 2019, 68, 9632–9646. [Google Scholar] [CrossRef]
- Ouyang, Q.; Chen, J.; Zheng, J.; Hong, Y. SOC estimation-based quasi-sliding mode control for cell balancing in lithium-ion battery packs. IEEE Trans. Ind. Electron. 2018, 65, 3427–3436. [Google Scholar] [CrossRef]
- Imtiaz, A.M.; Khan, F.H. Time shared flyback converter based regenerative cell balancing technique for series connected li-ion battery strings. IEEE Trans. Power Electron. 2013, 28, 5960–5975. [Google Scholar] [CrossRef]
- Lim, C.; Lee, K.; Ku, N.; Hyun, D.; Kim, R. A modularized equalization method based on magnetizing energy for a series-connected lithium-ion battery string. IEEE Trans. Power Electron. 2014, 29, 1791–1799. [Google Scholar] [CrossRef]
- Narayanaswamy, S.; Kauer, M.; Steinhorst, S.; Lukasiewycz, M.; Chakraborty, S. Modular active charge balancing for scalable battery packs. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 974–987. [Google Scholar] [CrossRef]
- Peng, F.; Wang, H.; Yu, L. Analysis and design considerations of efficiency enhanced hierarchical battery equalizer based on bipolar CCM buck-boost units. IEEE Trans. Ind. Appl. 2019, 55, 4053–4063. [Google Scholar] [CrossRef]
- Shang, Y.; Cui, N.; Duan, B.; Zhang, C. A global modular equalizer based on forward conversion for series-connected battery strings. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1456–1469. [Google Scholar] [CrossRef]
- Ouyang, Q.; Han, W.; Zou, C.; Xu, G.; Wang, Z. Cell balancing control for lithium-ion battery packs: A hierarchical optimal approach. IEEE Trans. Ind. Inform. 2020, 16, 5065–5075. [Google Scholar] [CrossRef]
- Han, W.; Zou, C.; Zhou, C.; Zhang, L. Estimation of cell SOC evolution and system performance in module-based battery charge equalization systems. IEEE Trans. Smart Grid 2019, 10, 4717–4728. [Google Scholar] [CrossRef]
- Liu, K.; Yang, Z.; Tang, X.; Cao, W. Automotive battery equalizers based on joint switched-capacitor and buck-boost converters. IEEE Trans. Veh. Technol. 2020, 69, 12716–12724. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, X.; Gao, K.; Tian, Q.; Xu, S. Two-mode active balancing circuit based on switched-capacitor and three-resonant-state LC units for series-connected cell strings. IEEE Trans. Ind. Electron. 2022, 69, 4845–4858. [Google Scholar] [CrossRef]
- Nazi, H.; Babaei, E. A modularized bidirectional charge equalizer for series-connected cell strings. IEEE Trans. Ind. Electron. 2021, 68, 6739–6749. [Google Scholar] [CrossRef]
- Chang, C.-H.; Cheng, C.-A.; Chang, E.-C.; Cheng, H.-L.; Yang, B.-E. An integrated high-power-factor converter with ZVS transition. IEEE Trans. Power Electron. 2016, 31, 2326–2371. [Google Scholar] [CrossRef]
- Raeber, M.; Heinzelmann, A.; Abdeslam, D.O. Analysis of an active charge balancing method based on a single nonisolated DC/DC converter. IEEE Trans. Ind. Electron. 2021, 68, 2257–2265. [Google Scholar] [CrossRef]
- Guo, X.; Geng, J.; Liu, Z.; Xu, X.; Cao, W. A flyback converter-based hybrid balancing method for series-connected battery pack in electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 6626–6635. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, K.; Tsai, C. Digital battery management design for point-of-load applications with cell balancing. IEEE Trans. Ind. Electron. 2020, 67, 6365–6375. [Google Scholar] [CrossRef]
- Xie, D.; Lin, C.; Deng, Q.; Lin, H.; Cai, C.; Basler, T.; Ge, X. Simple vector calculation and constraint-based fault-tolerant control for a single-phase CHBMC. IEEE Trans. Power Electron. 2024. early access. [Google Scholar] [CrossRef]












| Flyback_1 | Flyback_2 | Flyback_3 | Flyback_4 | |
|---|---|---|---|---|
| Case 1 | 0 | 0 | 0 | 0 |
| Case 2 | 0 | 0 | 0 | 1 |
| Case 3 | 0 | 0 | 1 | 0 |
| Case 4 | 0 | 0 | 1 | 1 |
| Case 5 | 0 | 1 | 0 | 0 |
| Case 6 | 0 | 1 | 0 | 1 |
| Case 7 | 0 | 1 | 1 | 0 |
| Case 8 | 0 | 1 | 1 | 1 |
| Case 9 | 1 | 0 | 0 | 0 |
| Case 10 | 1 | 0 | 0 | 1 |
| Case 11 | 1 | 0 | 1 | 0 |
| Case 12 | 1 | 0 | 1 | 1 |
| Case 13 | 1 | 1 | 0 | 0 |
| Case 14 | 1 | 1 | 0 | 1 |
| Case 15 | 1 | 1 | 1 | 0 |
| Mode | Constant Current | Constant Voltage |
|---|---|---|
| Operation Mode | CCM | CCM |
| Input Voltage (Vin_buck) | 48 V | 48 V |
| Output Voltage (Vo_buck) | 12~16.8 V | 16.8 V |
| Output Current (Io_buck) | 10 A | 0.35~10 A |
| Output Power (Po_buck) | 120~168 W | 5.88~168 W |
| Mode | Constant Voltage |
|---|---|
| Operation Mode | CCM |
| Input Voltage (Vin_boost) | 12~16.8 V |
| Output Voltage (Vo_boost) | 48 V |
| Output Current (Io_boost) | 0.5~3.5 A |
| Output Power (Po_boost) | 24~168 W |
| Switching Frequency (fs1) | 150 kHz |
| Mode | Constant Current |
|---|---|
| Operation Mode | DCM |
| Input Voltage (Vin_b) | 12~16.8 V |
| Output Voltage (Vo_b) | 3~4.19 V |
| Output Current (Io_b) | 2 A |
| Output Power (Po_boost) | 6~8.38 W |
| Turns Ratio (Np_b/Ns_b) | 4 |
| Switching Frequency (fs1) | 65 kHz |
| Model | NCR18650GA |
|---|---|
| Charge | 3300 mAh |
| Nominal Voltage | 3.6 V |
| Full Charge Voltage | 4.2 V |
| Discharge Cut-Off Voltage | 2.5 V |
| Battery Pack | 4 Series, 3 Parallel (=12 pcs) |
| Battery Pack Voltage | 12~16.8 V |
| [42] | Proposed | ||
|---|---|---|---|
| Before Balancing | Vb_max_before | 3.774 V | 3.507 V |
| Vb_min_before | 3.464 V | 3.092 V | |
| ∆Vb_before | 0.31 V | 0.415 V | |
| After Balancing | Vb_max_after | 3.871 V | 4.0 V |
| Vb_min_after | 3.823 V | 3.993 V | |
| ∆Vb_after | 0.048 V | 0.007 V | |
| Balancing time | 140 min | 19.7 min | |
| [42] | [43] | Proposed | ||
|---|---|---|---|---|
| Before Balancing | Vb_max_before | 4.027 V | 4.1 V | 3.985 V |
| Vb_min_before | 3.693 V | 3.99 V | 3.566 V | |
| ∆Vb_before | 0.334 V | 0.11 V | 0.419 V | |
| After Balancing | Vb_max_after | 3.543 V | 3.99 V (Balanced Voltage) | 3.338 V |
| Vb_min_after | 3.494 V | 3.333 V | ||
| ∆Vb_after | 0.049 V | None | 0.005 V | |
| Balancing time | 140 min | 41.67 min | 24 min | |
| [39] Case 1 | [39] Case 2 | [43] | Proposed | ||
|---|---|---|---|---|---|
| Before Balancing | Vb_max_before | 3.846 V | 3.86 V | 4.08 V | 3.756 V |
| Vb_min_before | 3.79 V | 3.8 V | 3.98 V | 3.249 V | |
| ∆Vb_before | 0.056 V | 0.06 V | 0.1 V | 0.507 V | |
| After Balancing | Vb_max_after | 3.84 V (Balanced Voltage) | 3.84 V (Balanced Voltage) | 4.04 V (Balanced Voltage) | 3.482 V |
| Vb_min_after | 3.475 V | ||||
| ∆Vb_after | None | None | None | 0.007 V | |
| Balancing time | 30 min | 55 min | 33.33 min | 20 min | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwu, K.-I.; Lin, Y.-H.; Shieh, J.-J. Active Battery Voltage Equalization Based on Chain-Loop Comparison Strategy. Energies 2024, 17, 5156. https://doi.org/10.3390/en17205156
Hwu K-I, Lin Y-H, Shieh J-J. Active Battery Voltage Equalization Based on Chain-Loop Comparison Strategy. Energies. 2024; 17(20):5156. https://doi.org/10.3390/en17205156
Chicago/Turabian StyleHwu, Kuo-Ing, Yuan-Hua Lin, and Jenn-Jong Shieh. 2024. "Active Battery Voltage Equalization Based on Chain-Loop Comparison Strategy" Energies 17, no. 20: 5156. https://doi.org/10.3390/en17205156
APA StyleHwu, K.-I., Lin, Y.-H., & Shieh, J.-J. (2024). Active Battery Voltage Equalization Based on Chain-Loop Comparison Strategy. Energies, 17(20), 5156. https://doi.org/10.3390/en17205156








