Review of Low Voltage Ride-Through Capabilities in Wind Energy Conversion System

Abstract

The significance of low voltage ride-through (LVRT) capability in wind energy conversion systems (WECSs) is paramount for ensuring grid stability and reliability during voltage dips. This systematic review delves into the advancements, challenges, and methodologies associated with LVRT capabilities in WECSs. By synthesizing recent research findings, this review highlights technological innovations, control strategies, and regulatory requirements that influence LVRT performance. Key insights include the efficacy of various LVRT techniques, the role of grid codes in shaping LVRT standards, and the integration of advanced control algorithms to improve system resilience. The study offers a comprehensive understanding of the current landscape of LVRT in WECSs and pinpoints future research directions to optimize their performance in increasingly complex grid environments. During the LVRT process, the stator of a double-fed induction generator (DFIG) is directly linked to the power grid. When the external power grid experiences a failure, the stator flux produces a significant transient component, resulting in substantial overvoltage and overcurrent on the rotor side of the DFIG. Failure to implement preventative measures may result in damage to the converter, therefore compromising the safety and stability of how the power system functions.

1. Introduction

Energy plays a critical role in nations’ socioeconomic advancement while also serving as a fundamental element of the Sustainable Development Goals (SDGs) [1,2]. Located in the southern region of Africa, South Africa boasts a population of over 59 million individuals and an average annual growth rate of 1.43% [3]. The growing population exerts continuous strain on the power system infrastructure due to the concurrent rise in energy requirements [4,5]. The electricity system in South Africa has historically been characterized by a significant reliance on coal-fired thermal generators [6,7]. However, in light of the detrimental impact of fossil fuels and the increasing environmental apprehensions around greenhouse gas emissions (GHGs), there is a necessity for a shift in the composition of the power system [8,9]. Moreover, the existence of readily available and plentiful sources of renewable energy necessitates the implementation of novel energy policies aimed at fostering power generation from renewable sources and guaranteeing the preservation of a more environmentally sustainable ecosystem. Factors such as poor management, population growth, and the inadequate maintenance of existing power stations have led to the adoption of “rolling blackouts” and load-shedding occurrences across the country. We have observed significant adverse impacts on society from the phenomenon of load shedding [10,11]. In 2021, the South African populace and industrial sectors experienced a significant power deficit, resulting in regular load-shedding episodes lasting for more than 48 days throughout the year [12]. Apart from the load-shedding phenomenon, utility companies also face challenges due to the overloading of transformers and substations caused by illegal connections, overloading, and acts of vandalism. The aforementioned factor contributes to the occurrence of unplanned outages, also referred to as non-technical losses, within certain sections of the network, constituting around 10% of the overall non-technical losses. Utility companies incur energy losses as a result of metre tempering, inaccurate billing, and cable theft [13,14]. The excessive strain on electrical infrastructure necessitates the compulsory separation of towns from the distribution network. The absence of an adequate power supply or the necessity for sudden load shedding results in observable alterations in power grid frequency, which serves as a prominent characteristic of a power grid infrastructure [15,16]. The power grids that utilize alternating current (AC) function at a designated frequency, such as 50 Hz in the case of South Africa. Consequently, all traditional power-generating units are equipped with a mechanical rotating generator that is specifically calibrated to operate at this frequency. When the power generation is insufficient to meet the demand, a phenomenon known as frequency sag occurs [17,18].

Renewable Energy Resources (RESs) and distributed generators (DGs), such as solar and wind, have garnered significant interest as a viable option to fulfil the world’s energy needs due to their plentiful supply and environmental friendliness [19]. Wind conversion systems (WECSs) are becoming more popular compared to other forms of RESs due to their positive impact on the environment and economic benefits [20]. Wind farms provide a substantial proportion of the electricity produced in contemporary power networks. The variability of electricity provided by wind farms creates uncertainty, making the efficient regulation of these energy sources a significant challenge [21,22].

The frequency of the system decreases when the generator consumes more electricity than it generates [23,24]. The opposite is true when the produced power exceeds the consumed power, resulting in an increase in system frequency. Therefore, as the level of wind power integration in an electrical grid rises, the likelihood of the grid’s frequency deviating from its normal operating frequency likewise increases during a system event [25,26]. Several frequency control methods are available to ensure that the grid’s frequency remains within the designated operating range [27,28].

Consistent electrical frequency is essential for synchronous machines to efficiently and securely transmit electricity to a load or electrical system [29,30]. Moreover, the proper synchronization and operation of loads with reactive properties is necessary [31]. In order to maintain a consistent frequency, various techniques can be employed, including speed governors, electronic power circuits for variable speed generation sources, and power system stabilizers in interconnected systems [32,33]. These measures ensure the stability of the system in the presence of low-frequency electrical power fluctuations. The purpose of the speed governor is to maintain the electric frequency within an acceptable range of tolerance [34,35]. In order to achieve this, the power generated by the unit generator must be approximately equal to the power generated by the main machine. During this procedure, the regulator is required to use a speed sensor in order to identify and measure changes in velocity, whether it be an increase (acceleration) or a decrease (deceleration). Subsequently, the regulator will adjust the mechanical power sent to the rotor of the synchronous machine, either decreasing or increasing it.

Our daily activities rely heavily on energy; therefore, energy research is critical and sensitive. Intensive research has led to the extensive use of wind energy in electrical power production. It is important to highlight the methodologies and characteristics that various researchers used while evaluating WECSs. This is to enable the visibility and identification of certain untapped areas of interest for future deployment [36].

In [37], the author examined the forecasting models for wind energy conversion systems. This projection is critical for ensuring the grid’s effective functioning and management, particularly in the presence of installed renewable energy sources. The research paper outlined two strategies for short-term prediction models: statistical models and machine learning models. The amalgamation of models, which includes deep learning and principal component analysis-based models, in conjunction with the random forest algorithm, illustrates superior performance in terms of prediction accuracy and stability. Nonetheless, this study has pinpointed a gap in data pre-processing techniques within the domain that necessitates additional exploration in the future.

In [38], the study’s purpose is to evaluate the energy storage system as a means of enhancing the stability of renewable energy sources. This article presents the energy storage system (ESS) for both stand-alone and grid-connected microgrid systems. Moreover, the article delves into a comprehensive analysis of the diverse control systems applied in ESS. The primary aim of the research was to present a thorough evaluation of control strategies utilized to enhance ESS coordination in the context of a hybrid energy storage system (HESS), thereby streamlining the integration of RESs into the power grid.

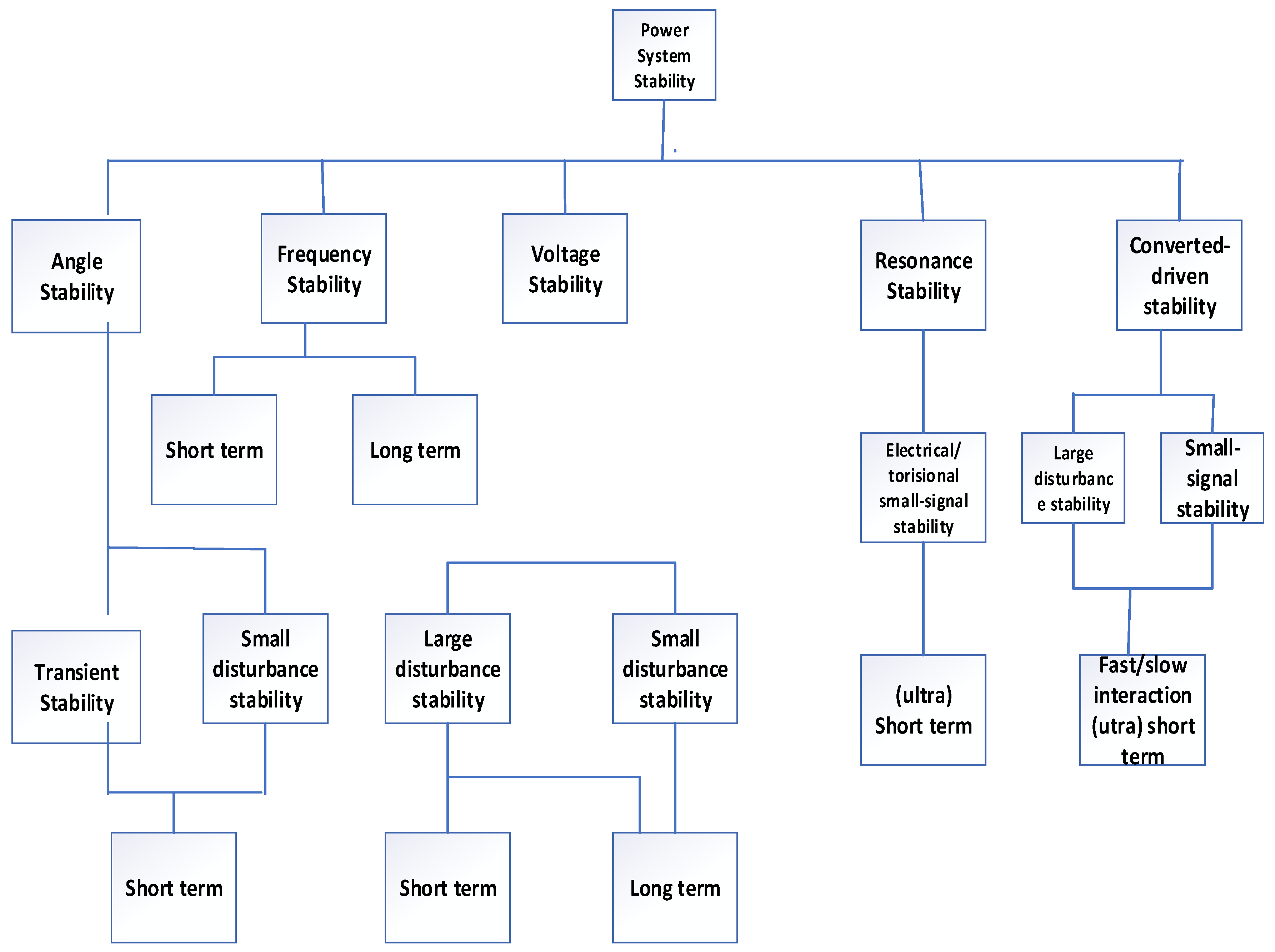
2. Examining the Effects of Wind Turbines on Power System Dynamics

The variable speed wind turbine with a doubly fed induction generator (DFIG) has garnered considerable interest due to its several benefits, including a lower power converter rating and the capability to regulate the output power. There are, however, some problems that can occur when DFIG wind turbines are frequently used in power systems [39]. These problems include less system inertia, problems with how the DFIG converter controls work together, and a weak synchronized coupling that can make frequency stability, power oscillation, and transient stability worse [40,41].

Several studies have been undertaken to quantify the consequences of a large penetration of wind power on interarea power oscillations and transient stability [42,43].

In [44], the author examined many perspectives. The first perspective is that the integration of wind power will enhance the damping of power oscillations. The opposing perspective is that greater integration of wind power will reduce damping and perhaps destabilize the system. The third perspective asserts that the system’s reaction is contingent upon the location and pre-disturbance operating circumstances of the wind power plant. The objective of the paper was to assess the transient stability of numerous wind power facilities integrated into a large-scale system.

Studying the influence of diverse wind turbine connections to the grid on the transient stability of the system is of utmost importance.

In [45], the author conducted comparative research on the stability of two types of wind turbines: constant speed wind turbines and DFIG wind turbines. The objective of the research was to develop a wind turbine that has little influence on grid stability. The DFIG wind turbine exhibited superior performance in terms of transient stability response compared to a constant speed wind turbine.

The main source of any wind energy conversion system (WECS) is the wind, which is sporadic, unpredictable, and beyond human control [46,47]. As a result, a wind turbine produces varying levels of mechanical power. Thus, the electrical generator connected to the shaft of a wind turbine likewise generates fluctuating electrical power [48]. An inherent issue with RESs that are linked to the power grid is their lack of inertia [49,50]. A back-to-back power electronic converter is used in the design of wind turbines. Due to the absence of a direct connection between DFIG and PMSG and the grid, synchronizing them with the network poses a significant challenge [51]. Integrating a wind farm with the main grid will reduce the overall inertia of the system. Consequently, the rate at which interruptions are addressed diminishes. Disruption in the voltage and frequency stability of the power system may lead to a significant disturbance in the bulk power system. Hence, conducting dynamic analyses of the power system in conjunction with RESs presents significant difficulties [52,53]. Disruptions in the system, such as the sudden disconnection of power generators, can disconnect wind turbines from the grid on a massive scale, leading to grid instability. During a failure or fault, the converter may be unable to handle the currents in both the rotor and stator, resulting in wind turbines being disconnected from the grid [54]. In the context of a power grid, inertia is the term used to describe the amount of kinetic energy that is stored in the revolving generators. This inertia is generated by many synchronized generators, all rotating at the same frequency and in perfect coordination [55]. Traditional generators are coupled by an electromagnetic chain, enabling each generator to contribute to the total inertia of the grid while it is spinning and connected. Due to the significant growth in the use of RESs that rely on power electronic converters, the power grids experience a loss of system inertia, leading to various technical problems [56]. In future power systems, there may be numerous challenges that arise, including the potential difficulties in obtaining frequency stability, voltage instability, and the maloperation of the protective system. The power grid may be categorized as a robust or fragile power grid, where a robust power grid is capable of withstanding the majority of abrupt changes in operating circumstances [57]. Conversely, a fragile power grid is highly responsive to abrupt alterations in operating circumstances, which can cause substantial fluctuations in voltage and frequency, ultimately resulting in an unstable system [58].

The paramount problem in modern electrical systems is the stability of voltage [59,60]. Voltage stability is the capacity of a power system to sustain a consistent voltage across all buses in the system following a disturbance from a specific starting operating condition. Voltage stability is primarily classified into two categories: major disturbance and minor disturbance, based on the size of the disturbance [61]. Large voltage instability caused by lengthy transmission lines or generator tripping is a common occurrence. During a significant voltage instability caused by a large disturbance, the voltages at various bus nodes tend to decrease as the reactive power demand increases. As a result, the operating point and steady-state operating points move further apart from each other. Small disturbance voltage stability refers to the power system’s capacity to maintain a stable voltage level when faced with a slight increase in load demand [62].

Interruptions have a major impact on the key performance indicators (KPIs) related to frequency, voltage, and rotor [63]. These KPIs play a role in stability mechanisms such as voltage stability, rotor angle stability, and frequency stability. The stability of the power system can be categorized based on the response duration, including both long-term and short-term periods. The different categories of power system stability are shown in Figure 1 [64].

Stability may be categorized into two main states: the steady state and the dynamic state [65,66]. Steady-state stability refers to the wind plant’s maximal capacity to transmit power. Dynamic stability refers to the capacity of a wind plant to restore its initial condition following fluctuations caused by changes in load variations, speed, or flux. Phase lead–lag power system stability is commonly employed to enhance dynamic stability [67].

The transmission network, often known as the grid, is a high-voltage infrastructure that links and transports electrical energy from power plants to the distribution network. The transmission network in South Africa operates at a nominal frequency of 50 Hz [68]. The equilibrium between generation and consumption maintains the nominal frequency of a transmission network. Put simply, a generator must adjust the active power it produces in response to any deviations from the normal system frequency, whether that means increasing or decreasing the power. A significant difference in the transmission network’s frequency may result in system instability or harm to linked devices. In relation to the subject of this study, it might result in generating units losing synchronization and triggering out-of-step protection relays, which then disconnect the generator units from the grid. If this frequency of occurrence persists, it will put additional pressure on the remaining generators and possibly result in grid failure [69].

Wind power generation is becoming increasingly significant in global energy production, impacting the stability of power grids. The incorporation of high-penetration electronic-interfaced technologies, such as wind power, enhances grid stability. Traditional stability approaches are evolving as a result of these technologies, leading to new challenges in modelling dynamic phenomena in power systems. The IEEE’s 2020 stability classification includes angle, frequency, voltage, resonance, and converter-driven stability, as illustrated in Figure 2 [70].

3. Standard Grid Codes

The incorporation of RESs into the electricity grid is seeing significant global growth. The transmission system operators (TSOs) regularly update the grid code requirements for connecting RESs to the grid. These standards are utilized to guarantee dependable and consistent grid performance. The grid coding standards vary between countries, and their stringency is contingent upon the extent of RES penetration. The primary goal of establishing grid codes is to guarantee the grid’s stability and consistent operation [71].

Grid codes primarily consist of rules and recommendations for regulating active and reactive electricity within the system [72,73]. It is unpleasant to have wind farms interrupted due to power quality difficulties, especially when a significant portion of the overall network production relies on wind power. Therefore, wind farms must adhere to grid codes in order to maintain uninterrupted operation throughout various fault scenarios. The capacity of a wind turbine to remain connected to the power grid for a predetermined duration in the event of a malfunction or voltage imbalance is referred to as its low voltage ride-through (LVRT) capability. The immediate requirement for LVRT capacity arises from the necessity to consider the fault percentage and the duration during which wind farms must be able to endure the fault [74].

Wind turbines must adhere to strict frequency range standards set by grid regulation [75]. They are only permitted to disconnect if the frequency deviates from the specified limits. The power system needs to meet various frequency range requirements and monitor each turbine’s status. Through active power control, wind turbines can adjust power production to meet the transmission system operators’ demands [76,77]. This adjustment can be achieved through frequency control or power reduction. Frequency control regulates the generation of active power based on variances in frequency. The profile of active power restriction differs among distinct countries. In South Africa, it is mandatory for RESs to maintain a constant operational frequency within the range of 49 to 51 Hz [78]. Nevertheless, the RES will disconnect if the frequency surpasses 51.5 Hz for a duration of more than 4 s or drops below 47 Hz for more than 200 milliseconds.

The South African grid code mandates specific procedures for LVRT, as seen in Figure 3 and Figure 4.

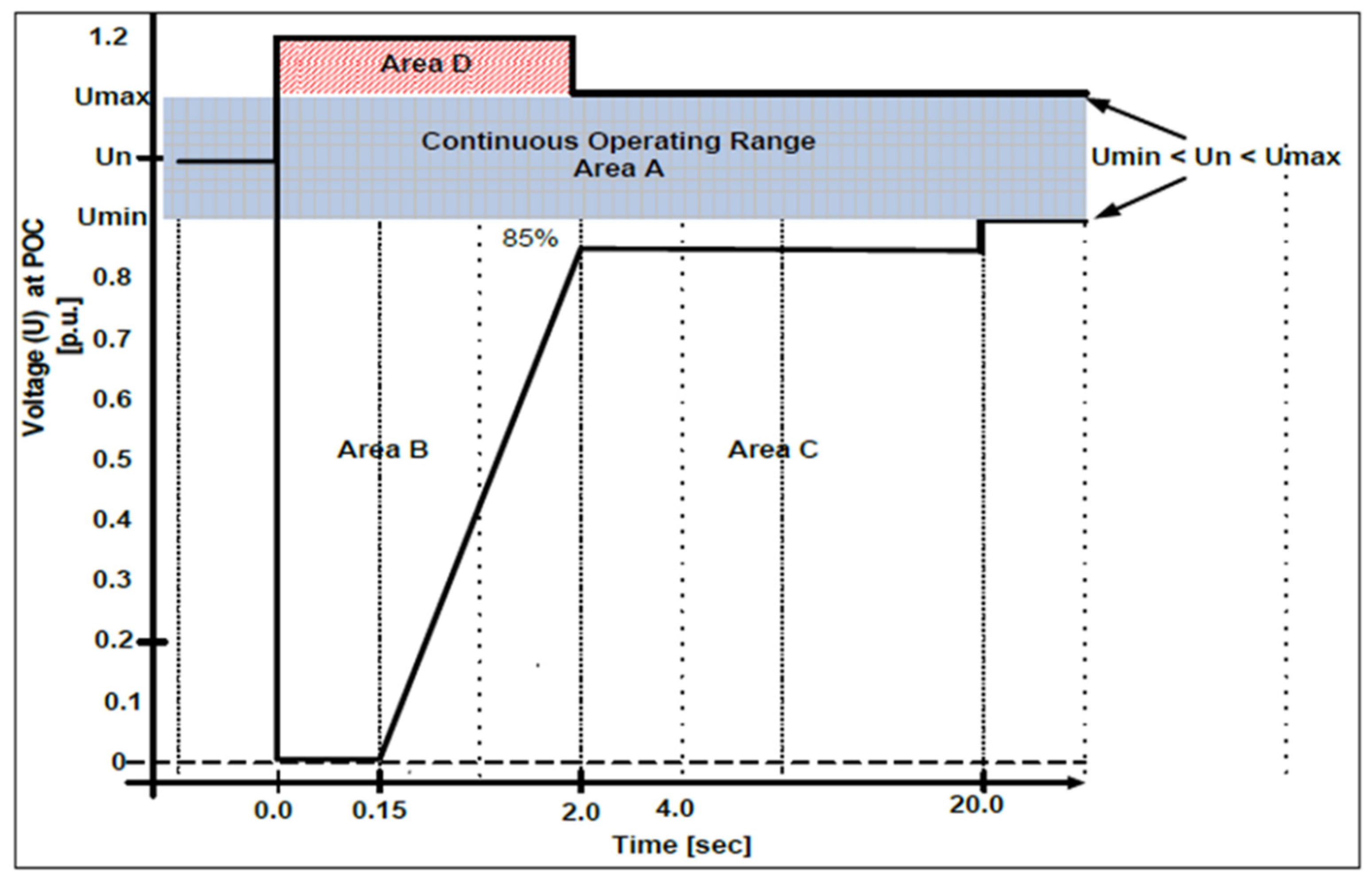
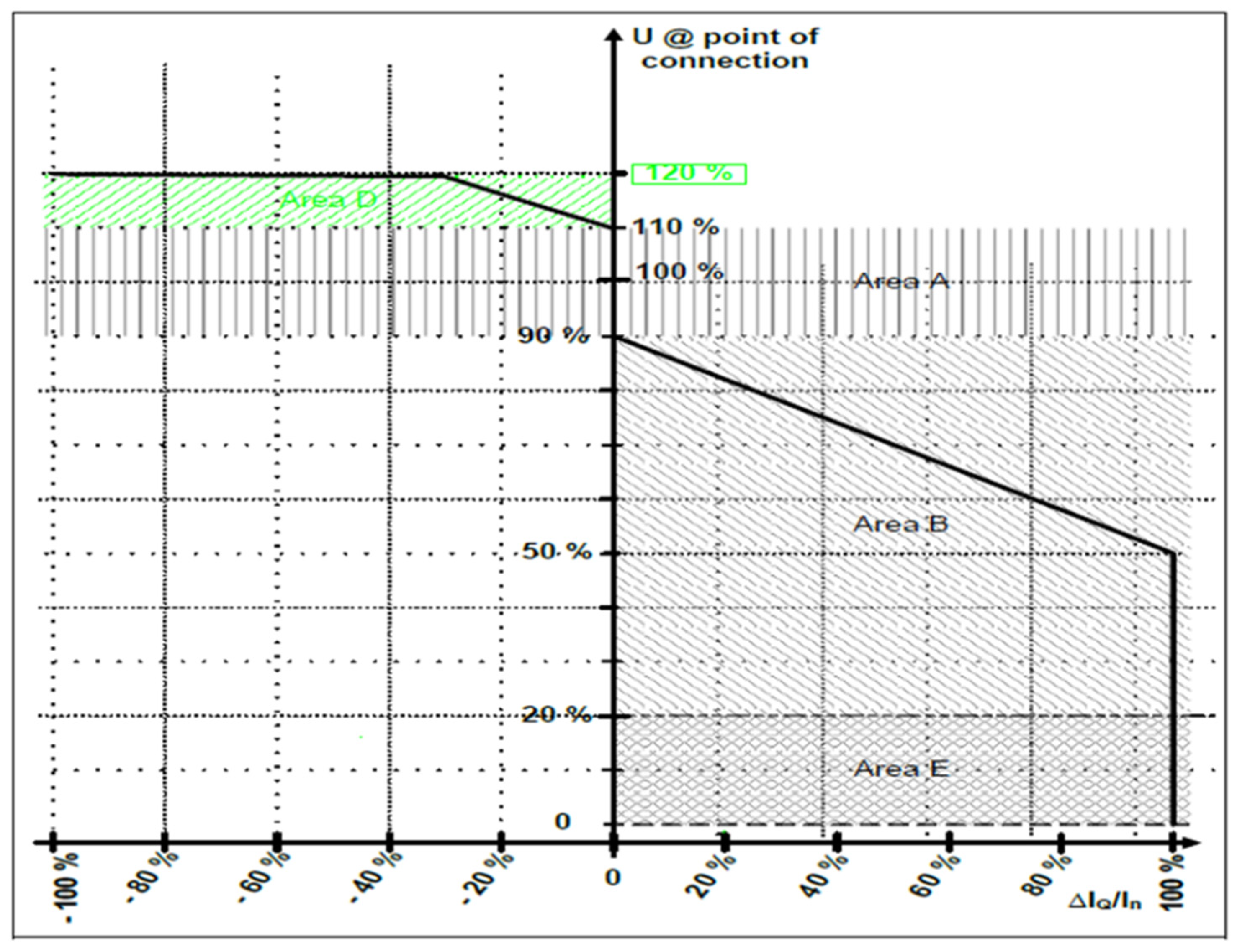
• In Area B, it is necessary for the RESs to remain connected to the network. Additionally, the RESs should provide maximum voltage support by supplying a controlled amount of reactive current to help stabilize the voltage. It should also be able to withstand a voltage drop to zero at the Point of Connection (POC) for a period of 0.15 s without disconnecting. In this area, the supply of reactive power takes precedence over active power. The RES design specifications require a reduction in active power proportionate to the voltage drop for voltages below 85% while maintaining active power during voltage drops. Furthermore, the RESs should have the capability to disable the functionality of providing reactive current support upon request from the system operator or local network operator [80,81].
• In Area C, the RES has permission to disconnect.
• In Area D, it is necessary for the RESs to remain connected to the network. Furthermore, in order to stabilize the voltage, the RESs should be able to provide maximum voltage support by absorbing a regulated amount of reactive current. Furthermore, the RESs should be able to endure voltage peaks up to 120% of the nominal voltage at the POC for at least 2 s without disconnecting.
• Area E (Figure 4): The RESs must maintain their ability to produce reactive current within their technical design limits in order to contribute to the stabilization of voltage. Disconnection is permissible only upon fulfilment of the aforementioned requirements.

The grid links several types of RESs. However, this study will primarily concentrate on two types of WECSs: DFIG-based WECSs and permanent magnet synchronous generator (PMSG)-based WECSs. Figure 5 demonstrates DFIG-based WECSs connected to the power grid.

Figure 6 demonstrates a PMSG-based WECS connected to the power grid.

The equations below provide the mathematical expressions for a WECS’s mechanical power and mechanical torque.

Mechanical power:

$$P_m={\displaystyle \frac{1}{2}}\rho A{\nu }^3{C}_p(\lambda ,\beta )$$

(1)

In the above equation, the significance of each variable and coefficient is as follows:

• C_p: Coefficient of performance.
• $\rho$: Air density.
• A: Rotor blades swept area.
• $\nu$: Wind speed.
• $\lambda$: Tip speed ratio.
• $\beta$: Pitch angle.

The following equation describes how the pitch angle and the tip speed ratio affect the power coefficient of a specific rotor blade:

$$C_p(\lambda ,\beta )=0.5176\left({\displaystyle \frac{116}{{\lambda }_i}}-0.4\beta -5\right){\mathcal{l}}^{{\displaystyle \frac{-21}{{\lambda }_1}}}+0.0068\lambda$$

(2)

${\lambda }_i$ is given by the following equation:

$${\displaystyle \frac{1}{{\lambda }_i}}={\displaystyle \frac{1}{\lambda +0.08\beta }}-{\displaystyle \frac{0.035}{{\beta }^3+1}}$$

(3)

The following equation expresses the tip speed ratio, which is the difference between the rotor’s speed and the wind’s speed:

$$\lambda ={\displaystyle \frac{R{\omega }_m}{\nu }}$$

(4)

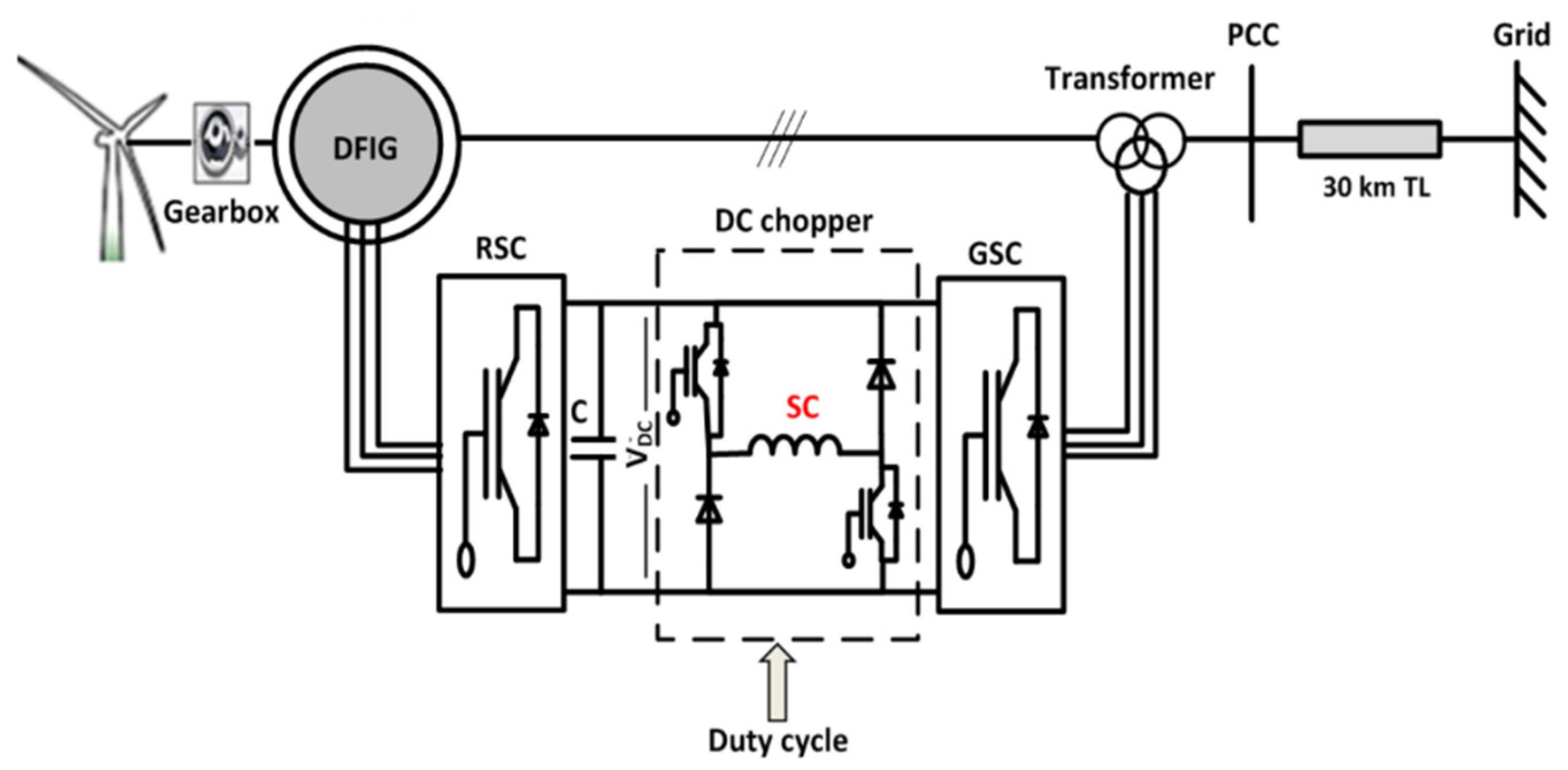
3.1. DFIG-Based WECS LVRT Capabilities

The LVRT approach is crucial for the DFIG to maintain connection in the event of a fault occurrence [83,84]. Fluctuations in voltage pose significant disruptions for DFIG. A decrease in these sags leads to an increase in stator and rotor currents, thereby reducing the power supply to the DFIG. The approaches for LVRT in DFIG-based WECSs may be classified into two categories. The first category pertains to alterations made to the hardware, while the second category pertains to adjustments made to the traditional controllers for the converters of DFIG. This study focuses on both traditional controllers and hardware.

DFIG control techniques may be categorized as either rotor-side converter control (RSC) or grid-side converter control (GSC). The primary purpose of a rotor-side converter is to autonomously modify the actual and reactive power of the stator. The maximum power tracking method (Pref) is used to monitor the reference active power. When a DFIG is connected to a power system, the RSC may be used to regulate the reactive power and ensure a steady stator voltage without the need for auxiliary support. In the stator field reference, the maintenance of reactive power is achieved by regulating the direct axis current (Idr) of the rotor, while the management of active power is achieved by regulating the quadrature axis current (Iqr) When the wind turbine generator contributes electricity to a stable or robust grid, the reactive power is often reduced to zero. The primary purpose of the grid-side converter is to provide a stable direct current (DC) link voltage to protect the DFIG against excessive increases in rotor current.

DFIG control may be readily accomplished by converting the ABC conventional form into a d-q reference frame, as shown by the following equations:

$$V_{ds}=R_s{I}_{ds}+{\displaystyle \frac{d}{dt}}{\phi }_{ds}-{\omega }_s{\phi }_{qs}$$

(5)

In the above equation, the significance of each variable and coefficient is as follows:

• $V_{ds}$: Direct-axis stator voltage.
• $R_s$: Stator equivalent resistance.
• $I_{ds}$: Stator inductance along the direct axis.
• ${\phi }_{ds}$: Flux linkage along the direct axis.
• ${\omega }_s$: Stator angular velocity.
• ${\phi }_{qs}$: Flux linkage along the quadrature.

$$V_{qs}=R_s{I}_{qs}+{\displaystyle \frac{d}{dt}}{\phi }_{qs}+{\omega }_s{\phi }_{ds}$$

(6)

In the above equation, the significance of the variable and coefficient is as follows:

• $V_{qs}$: Quadrature-axis stator voltage.
• $I_{qs}$: Stator inductance along the quadrature.

$$V_{dr}=R_r{I}_{dr}+{\displaystyle \frac{d}{dt}}{\phi }_{dr}-{\omega }_r{\phi }_{qr}$$

(7)

In the above equation, the significance of the variable and coefficient is as follows:

• $V_{dr}$: Direct-axis rotor voltage.
• $R_r$: Rotor equivalent resistance.
• $I_{dr}$: Direct-axis rotor currents.
• ${\phi }_{dr}$: Direct-axis rotor flux-linkage.
• ${\omega }_r$: Electrical rotor angular velocity.
• ${\phi }_{qr}$: Quadrature-axis rotor flux-linkage.

$$V_{qr}=R_r{I}_{qr}+{\displaystyle \frac{d}{dt}}{\phi }_{qr}+{\omega }_r{\phi }_{dr}$$

(8)

In the above equation, the significance of the variable and coefficient is as follows:

• $V_{qr}$: Quadrature-axis rotor voltage.
• $I_{qr}$: Quadrature-axis rotor voltage.
• where

$${\phi }_{ds}=L_s{i}_{ds}+L_m{i}_{dr}$$

(9)

$${\phi }_{qs}=L_s{i}_{qs}+L_m{i}_{dr}$$

(10)

$${\phi }_{dr}=L_m{i}_{ds}+L_r{i}_{dr}$$

(11)

$${\phi }_{qr}=L_m{i}_{qs}+L_r{i}_{qr}$$

(12)

The modification of converter control procedures has led to the development of various techniques that provide LVRT capabilities in WECSs [54,84]. Control strategies for regulating the converters on the grid side (GS) and rotor side (RS) influence the performance of LVRT techniques. The controller’s appropriate adjustment also influences the LVRT capacity of the DFIG [85,86]. Modifying the control of the DFIG converter, which involves changing the reference values of the control system, can improve the LVRT. The control methods mentioned are highly cost-effective for enhancing LVRT due to their advantageous features, including simple implementation, seamless transition to normal operation, constant control over DFIG, and reduced expenses. Figure 7 presents DFIG-based categorizations of several LVRT strategies employed by wind power facilities [87].

3.2. PMSG-Based WECS LVRT Capabilities

When there are grid faults for a WECS based on a PMSG, the transmission power from a wind turbine to the electrical grid decreases [88]. Consequently, the grid-side converter’s controller is unable to notice a decrease in voltage at the PCC. Meanwhile, the machine-side converter continues to provide active power to the DC-link capacitor. The uneven distribution of active power raises the DC-link voltage, which could damage capacitors, overwork the generators, and put more voltage stress on the grid and machine-side converters. We utilize LVRT techniques to address these issues.

Field-oriented control (FOC) and direct torque control (DTC) are the two most often used control systems for PMSG. The degree of freedom of a PMSG enables the optimization of many performance indices, including electromagnetic torque, power factor, and efficiency. The prevailing FOC technique used for PMSG assumes that the direct-axis current is equal to zero. The absence of d-axis current results in a direct correlation between the stator current and electromagnetic torque for a surface-amount PMSG across all operating conditions. In order to effectively regulate a PMSG, the dynamics of the stator voltage and electromagnetic torque are characterized in the synchronous (dq) reference frame as follows:

$$V_{ds}=-R_s{i}_{ds}+{\omega }_r{L}_{qs}{i}_q-L_{ds}{\displaystyle \frac{d{i}_{ds}}{dt}}$$

(13)

$$V_{qs}=-R_s{i}_{qs}-{\omega }_r{L}_{ds}{i}_{ds}-L_{qs}{\displaystyle \frac{d{i}_{qs}}{dt}}+{\omega }_r{\phi }_r$$

(14)

$$T_e=1.5P_p[{\phi }_r{i}_{qs}-(L_{qs}-L_{qs})i_{ds}{i}_{qs}]$$

(15)

where

• $i_{ds},i_{qs}$: PMSG dq-frame stator currents.
• $V_{ds},V_{qs}$: PMSG stator voltages.
• ${\phi }_r$: PMSG rotor flux linkage.
• $R_s$: Stator equivalent resistance.
• $L_{ds},L_{qs}$: PMSG dq-axis inductances
• ${\omega }_r$: Machine rotor speed.
• $P_p$: Machine number of poles.
• $T_e$: Electric torque.

3.3. Hardware LVRT Methods for Wind

Table 1. Summary of hardware LVRT strategies.

Reference	LVRT Strategies	Advantages	Drawback
[89,90]	Energy Storage System to improve the LVRT for wind farms.	This design eliminates the requirement for a bi-directional voltage source inverter (VSI) and just requires a buck/boost DC-DC converter to regulate the actual power, resulting in reduced system cost.	It is very suitable for a standalone system. During a malfunction, the voltage in the grid decreases, causing the grid-side inverter to be unable to transmit power from the rotor-side converter to the grid. Consequently, the excess energy charges the DC-bus capacitor, resulting in a swift rise in bus voltage.
[91,92,93,94]	Crowbar Protection	The crowbar control approach enhances the LVRT capabilities of the DFIG-based turbine. In order to safeguard the power converter, the crow restricts the rotor current during a failure.	The generator-side converter deactivates upon crowbar activation, eliminating independent control over active and reactive power.
[95,96,97]	Stator Damping Resistor (SDR) and Rotor Current Limiter (RCL)	During a fault occurrence, we use the SDR and RCL to restrict the stator and rotor currents. The purpose of this measure is to improve the LVRT capacity and protect the power converters and DC-link capacitors. The DFIG remains interconnected with the grid and has the capability to provide both active and reactive electricity to the grid even in the event of a fault.	During the fault state, the RCL resistor activation does not effectively dampen the stator modes, resulting in increased settling time and variations in the DFIG transient responses.
[98]	PMSG installed in the farm with fixed speed wind turbine.	This approach aims to enhance the LVRT capacity of a fixed speed wind turbine during network disruptions by including a variable speed wind turbine inside the same wind farm.	This technology offers a cost-effective way to enhance the LVRT capacity and reduce voltage fluctuations in both fixed speed and variable speed wind turbines. It eliminates the need for additional expenses associated with installing flexible AC transmission system devices at the wind farm’s terminal.
[99,100]	DC-link chopper	It is used to safeguard electronic devices during severe voltage drop circumstances.	Under severely defective conditions, the DFIG undergoes a conversion process and becomes a squirrel cage induction generator. Consequently, it loses its controllability and begins to absorb more reactive power from the grid. This leads to a further drop in voltage at the Point of Common Coupling (PCC).
[101,102,103,104]	Dynamic voltage restorer	Despite its high cost and complexity, DVR is capable of efficiently allowing DFIG to withstand large power drops. The planned use involves using it in conjunction with the generator to augment the stator voltage. Therefore, it is possible to keep the rotor current below the maximum allowable limit. The generator can optimize the reactive power it injects by controlling the voltage of the DVR, which not only enhances the terminal voltage but also absorbs a significant portion of the active power it provides. While implementing DVR simplifies the DFIG system, it also increases the total cost.	High cost and complexity.
[105,106,107]	Static Synchronous Compensator	The primary purpose of STATCOM is to provide reactive power to the system in order to control and stabilize the voltage at the point of common coupling (PCC). STATCOMs provide superior performance compared to SVCs, with quicker response, decreased disturbances, and improved operation even at lower voltage levels.	The switching frequency and the inductor’s dimensions limit the response time.
[108,109,110]	Series Dynamic Braking Resistors.	Regulating the voltage at the connection point and making up for changes in voltage during the fault is an effective way to fix problems caused by grid faults in WT generators and make them better able to handle these faults. A dynamic voltage restorer (DVR), a power electronic compensator, can maintain a constant voltage at the point of common coupling (PCC) and synchronize it with the network. The DVR injects a suitable voltage into the grid bus by connecting it in series, ensuring that the generator voltage remains constant and in phase with the network.	The DVR must be able to absorb a portion of the excess active power provided by the wind generator during a fault in order to maintain the DC-link voltage (Vdc) at the desired level. However, this capability to dissipate energy is the fundamental disadvantage of the DVR.
[111]	DC-link switchable resistive-type FCL.	To limit excessive current flow, the Reactive Power Support Controller (RSC) is connected to the DC side. It effectively addresses the issue of crowbar protection by completely mitigating the negative outcomes, even in situations where the grid voltage is zero. It does not utilize superconducting inductance, resulting in lower costs.	Temperature and current density affect it, necessitating the use of compensating equipment.
[112]	Bridge-type FCL	When switching, minimize power losses. It is useful for reducing high voltage drops, minimizing rotor speed fluctuations, and minimizing conduction losses.	Utilization of a mechanical bypass switch. It is necessary to use a coupling transformer of significant size, maintain a high level of reactance, and avoid the undesirable saturation of the DC reactance.
[113,114]	Saturated Amorphous Alloy Core Based Fault Current Limiter.	Compared to typical cores used in fault current limiters (FCL), the B-H loop in amorphous alloy cores is significantly smaller. In other words, the SAACFCL (Saturated Amorphous Alloy Core Fault Current Limiter) needs a smaller DC excitation current, which means that there are fewer core losses. Under typical conditions, this advanced SAACFCL achieves a low impedance and has little effect on the network’s operation. Grid faults result in a significant decrease in voltage, which leads to high fault currents that reduce the magnetic properties of the SAACFCL core. This increase in impedance restricts fault currents and enhances the capacity of wind farm systems to withstand low LVRT conditions.	Despite the aforementioned benefits, these FCLs still lack the ability to effectively handle voltage sags.

presents a concise overview of the findings from previous studies about hardware techniques for LVRT.

In order to address the limitations of individual hardware-based LVRT methods, researchers in the literature have suggested the implementation of a hybrid system that combines multiple hardware strategies to improve LVRT performance. Here are some examples of LVRT hardware hybridization for WECSs:

This approach synergizes the efficacy of the rotor crowbar and DC hopper circuits [115,116]. A crowbar is employed to restrict the oscillations and maximum values of stator and rotor overcurrent, while a DC chopper is utilized to regulate the oscillations and maximum values of the DC-link voltage and electromagnetic torque within a desired range [117,118,119]. Alternatively, the same method is used in conjunction with the crowbar and DC chopper control systems to prevent the system from needlessly using reactive power [99,120]. The control system operates based on the fundamental premise that if the signals acquired do not align with the reference threshold values, either the rotor current or the DC-link voltage will activate the IGBT to engage the protective circuits. The control system has enhanced the reactive power compared to the approach discussed earlier, resulting in an advantage. The control system utilizes the “on” and “off” signals to activate the protective circuitry in the event of a failure and to deactivate it in order to restore control of the DFIG.

This approach synergizes the efficacy of DC chopper and series dynamic resistance circuits. The DC chopper is employed to restrict the fluctuations and maximum levels of the DC-link voltage, while the SDR (Series Dynamic Resistance) is utilized to sustain the peak values of rotor current, rotor voltage, and DC-link voltage, as well as provide reactive power support to the network. The SDR circuit possesses a distinctive capability to directly regulate the rotor current. Additionally, SDR can restrict the occurrence of DC-link overvoltage by regulating the rotor current, which serves as the charging current for the DC-link capacitance. Furthermore, the hybrid combination of DC chopper and SDR not only serves its distinct function but also effectively reduces oscillations and peak values of the stator current. Additionally, it initially decreases the electromagnetic torque. Meanwhile, the rotor-side converter remains connected to the system to control the active and reactive power output of the generator [117,121,122] and displays graphs of the generator’s reactive power, rotor speed, and electrical torque. These graphs were produced using PSCAD and illustrate the distinction between the utilization of SDR and crowbar circuits. The author highlighted the usage of the SDR circuit as a substitute for the crowbar circuit due to its superior overall performance compared to the crowbar. However, it should be noted that the SDR circuit has the drawback of experiencing more torque variation compared to the crowbar [123].

3.4. Control Techniques for Wind Conversion System

Control approaches have gained more attention due to the drawbacks of hardware devices. They lower the cost of hardware components and improve the WECS’s ability to withstand faults. They are advantageous in the development of WECSs because they help overcome drawbacks. They are inexpensive. Control approaches are highly efficient in mitigating minor voltage decreases, but for more severe voltage dips, hardware devices are necessary.

In [124], the author Implemented a nonlinear adaptive controller for the ESS integrated DVR to improve LVRT capabilities for WECSs. The suggested control system was used to efficiently regulate the grid voltage dips in order to sustain the voltage at the point of common coupling (PCC) and store excess wind power to mitigate potential fluctuations in wind energy.

In [125], the author suggested an innovative control method for the rotor-side converter (RSC) in DFIGs to equip WECSs with effective LVRT capability in the presence of significant drops in both unbalanced and balanced grid voltages. The suggested control relied on the principles of nonlinear control theory to create a controller that reduces oscillations in rotor voltages and currents. This control system ensures that the system remains connected and does not disconnect for protection.

In [126], the author suggested a simple control method to improve the LVRT capabilities of WECSs, which relies on PMSG. The main concept of this strategy was to alternate between adjusting the variables of the reference control’s GSC and SSC. This was carried out to ensure that the DC-link voltage remains within a safe range when there are decreases in the grid voltage. This is achieved by storing surplus actual power in the system’s inertia.

In [127], Implemented a parallel switched DVR with modified feedback control to enhance the FRT capabilities in DFIG-based WECSs under abnormal situations.

In [128], Proposed a model-free adaptive control strategy for the Unified Power Flow Controller (UPFC) to enhance the FRT capabilities of DFIG-based WECSs during various disturbance events and to improve the overall dynamic performance during wind gusts. The proposed control regulates the shunt and series converters of the unified power flow controller.

In [128], the proposed model-free adaptive control for UPFC has improved the FRT capabilities of the DFIG-based WECS throughout multiple disturbance occurrences and the overall dynamic performance during wind gusts. The unified power flow controller uses the suggested control to regulate both the shunt and series converters. The suggested technique sought to make a system resilient and responsive to various operating circumstances and disruptions. The paper [128] presents research on optimizing an optimal PI controller using the elephant herding technique in a WECS. This controller’s design enhances the grid-tie switching reluctance generator’s (SRG) LVRT capabilities during faults that affect the SRG output voltage. This is achieved by adjusting the generator’s off-delay angle.

In [129], the author developed a control technique that incorporates an energy-dissipating circuit on the machine side and reactive power compensation on the grid. The author uses the Braking Chopper (BC) circuit for machine-side energy dissipation and the Port-Controlled Hamiltonian Algorithm (PCH) for grid-side reactive power adjustment. When the grid voltage decreases, the BC circuit absorbs surplus power generated during the fault to maintain stability in the DC bus voltage, while the PCH provides reactive power compensation.

To attain LVRT capability, the author [130] proposed optimal reference magnitude and angle values for the injected DFIG rotor voltage and reference pitch angles, which maximize DFIG mechanical power while ensuring that rotor and stator currents remain within rated limits and deliver maximum reactive power to support grid voltage during faults across all operating wind speeds. The Bonobo optimizer (BO) was used to fulfil the objectives of the article. To verify the correctness of the findings, the BO outcomes were compared with two other optimization algorithms: PSO and DTA.

In [131], the author presents a nonlinear controller for DFIG wind turbines using the partial feedback linearization (PFL) approach. The controller produces switching signals to concurrently operate both the rotor side converter and the grid side converter, hence improving the LVRT capacity throughout a broad spectrum of operating circumstances. The suggested PFL approach has been integrated into a partly linearized version of a nonlinear system, resulting in an autonomous and reduced-order transformed system.

4. Converter Control Strategies

Power electronic converters establish the connection between the WECS and the utility system. The WECS employs various power electronics interfaces to transform the generator’s electricity into an appropriate format. Modern wind turbines have used controlled rectifiers and inverters with diverse inverter switching systems. Each of them has distinct advantages and disadvantages. The primary concern in the converter-based grid-linked wind energy conversion system is voltage variability and harmonic distortion. Ensuring that the grid remains within the operating voltage and frequency constraints for all anticipated combinations of WECSs and consumer loads while also ensuring transient stability is of utmost importance. The controllers for generator-side (GSC) and grid-side converters (GSC) are the principal controllers that are utilized in grid-linked WECSs [132]. The usual controls are mentioned below:

4.1. Generator Side Control Strategy

The controller’s primary objectives for the GSC are to achieve precise control over the machine’s magnetic flux and torque, thereby regulating its speed, optimizing wind power extraction, and controlling the active and reactive components of the machine’s current [133,134]. Direct torque control and field-oriented control are two primary control methods used to efficiently attain these objectives [135,136].

In [137], used field-oriented control to manage the generator’s speed by adjusting the stator current amplitude, phase, and frequency. This technique has many benefits, such as reduced fluctuations in reactive and active power, excellent performance in steady-state conditions, minimum loss during switching, a consistent and low frequency of converter switching, and resilience against measurement noise [138,139,140]. Nevertheless, there are several drawbacks to this system. These include the need for frequent online calculations due to pulse width modulation, slow response to sudden changes in the power grid due to the limited control bandwidth of PI controllers, reliance on the grid filter parameters, which can change over time, challenges in tuning the system’s parameters, and reduced reliability when operating conditions vary.

Direct torque control has many benefits over vector control, including less compensation load, faster dynamic response, no need for an internal current control loop, a totally decoupled system, and simplicity [141,142,143]. Modifying the torque angle, or flux can change the generator’s torque. This control has many disadvantages, including variable switching frequency, high current total harmonic distortion, tracking inaccuracy, and high filter inductance [139,144,145]. Using space vector modulation for direct torque control alleviates the challenges of variable switching frequency operation and reduces filter inductance [146].

4.2. Grid Side Control Strategy

The grid-side converter performs several key roles, including regulating reactive and actual power in the grid, adjusting the DC-link voltage, synchronizing with the grid, and ensuring high-quality injected power [147,148,149]. The grid-side converter’s configuration is not dependent on the type of generator. There are two methods of control for the grid-side converter can be controlled using two methods: voltage-oriented control and direct power control [150].

A voltage-oriented control strategy employs a synchronous reference frame phase-locked loop to achieve grid synchronization [151,152]. It has many advantages, such as the ability to track things more quickly, be more sensitive to sudden changes in parameters, provide better power quality while injecting power, do away with the need for voltage vector switching states, and work at both variable and fixed switching frequencies [153,154]. The disadvantages of utilizing this method of control include a limited ability to respond quickly to changes, a complicated process of implementation, and the need for a coordinated transformation block [145,155].

The direct power control technique bears resemblance to the direct torque control employed in the generator-side converter. The control of reactive and active power is achieved by utilizing a voltage vector state. The device offers several benefits, including simplicity as it does not require an internal current control loop, robustness, quick responsiveness to changes, a power factor close to unity, no requirement for pulse width modulation or coordinate translation, and stable functioning even when there are changes in parameters. This approach has several drawbacks, including an increase in total harmonic distortion, significant current fluctuations, an increase in filter dimensions, and suboptimal performance when the converters operate at their maximum power capacity [156,157,158].

4.3. Popular Control Strategies for Electronic Converters

Converters and their associated management systems are becoming increasingly important in the effective collection of wind energy [140,159]. They are substantial contributions to the energy conversion process. Wind energy continues to have poor conversion efficiency. As a result, the development of efficient converter devices and resilient controllers will guarantee a power supply that is both high-quality and dependable [160]. Due to the increasing integration of wind turbines into the electrical system, it is necessary to generate electricity efficiently to adhere to the grid code. To achieve this objective, the wind energy conversion system has designed numerous converter devices. A thorough examination of the function of converters in wind power systems, including energy conversions, controls, and applications, was extensively emphasized.

In [161], Proposed an enhanced sensorless control algorithm for a variable speed-constant frequency generation system utilizing DFIG. A modified phase-locked loop (MPLL) serves as the mechanism for estimating the position and speed of the rotor. The proposed approach utilizes the measured stator voltages and rotor currents to directly calculate the rotor position and speed through basic arithmetic operations based on the PLL principle. Regardless of the machine characteristics, the technique estimates the speed without differentiation, significantly enhancing control robustness and increasing resistance to noise.

In [162], the authors introduced an innovative approach to sensor-less maximum power point tracking for wind energy conversion systems (WECSs); a fuzzy logic-based solution was provided. Compared to standard procedures, the proposed method significantly decreases the range of speed variation in the wind generator, resulting in a reduction of around 40% in the size of the PWM back-to-back converters. The approach also enhances the system’s reliability by reducing the converter’s losses. We estimated the speed of the DFIG rotor using a model reference adaptive system that applied a fuzzy logic technique. Subsequently, a Fuzzy Logic Maximum Power Point Tracking algorithm was utilized to determine the desired electromagnetic torque.

Disturbance observer-based integral sliding mode control for wind energy conversion systems is presented in [163]. The observers estimated the aerodynamic torque and disturbances on the d- and q-axes. The implemented aerodynamic torque observer has the ability to accurately measure wind speed, even in situations where the wind speed is rapidly fluctuating. The stability analysis of the suggested observers and controller was conducted utilizing the Lyapunov stability theory.

In [164], This work presents an approach for controlling grid-connected DFIG using fractional order sliding mode control (FOSMC). Field-Oriented Sliding Mode Control (FOSMC) is used in this one-of-a-kind method to directly control the active and reactive power output of a DFIG-based WECS. An approach to control systems, known as fractional order sliding mode control, was utilized to address disturbances. The Caputo derivative was used in the construction of the sliding surface. The primary goal was to attain exceptional, robust performance.

The Takagi-Sugeno (T-S) fuzzy model-based integral sliding mode control (ISMC) is described in [165]. The ISMC approach exhibits resilience to external disturbances and noises. An essential concern about the WECSs is the fluctuating wind speed, which undergoes significant variations within brief time intervals. The wind speed estimation challenge was solved using the disturbance observer application, which was also employed for estimating the wind speed. The utilization of a T-S fuzzy model was justified due to its ability to withstand mismatched perturbations with resilience. The proposed combination of control techniques offers a novel solution to address issues related to nonlinearity, the calculation of aerodynamic torque, and the inherent chattering phenomenon associated with sliding mode control.

In [166], presents a second-order sliding mode control approach for regulating the generator and grid sides of a variable speed experimental wind energy conversion system. The rotational speed at the generator side is regulated to align with a profile derived from the wind turbine’s power curve, aiming for optimal power extraction. The grid side regulates the DC-link voltage to ensure efficient power transfer. The control technique relies on a perturbed single input-single output error model and a second-order sliding mode control algorithm. The suggested second-order sliding mode control technique exhibits notable attributes, including resilience to parametric errors in both the turbine and the generator, as well as resistance to external disturbances.

In [167], The study demonstrated the application of return control technology in a feedback proportional-integral (FPI) controller for controlling a variable speed multi-rotor wind turbine (VSMRWT) conversion system equipped with a double-powered asynchronous generator (DPAG). Direct vector control (DVC) operates this generator. The FPI controller was employed to enhance the performance of the DPAG. Utilizing the DVC-FPI to improve the DPAG’s effectiveness and durability is highlighted by the study. The DPAG is a mechanism for turning mechanical energy into electrical energy. Utilizing the FPI controller to increase the DPAG’s power output can reduce power fluctuations and improve the quality of the network’s current. Furthermore, the utilization of the DVC-FPI results in a reduction of overshoot and steady-state error. During transient and steady-state errors, the DPAG allows for independent manipulation of the system’s interacting and active forces.

In [168], Engaged in managing the power usage of nonessential devices by applying DC electric springs. A genetic algorithm (GA)-based learning design process is proposed for identifying the parameters of the ANFIS model. The system being investigated is meticulously modelled, including its control methods. The performance of the ANFIS-GA controller was compared to that of other controllers, such as artificial neural networks (ANN), model predictive controllers (MPC), and fuzzy logic controllers (FLC), as well as optimized proportional-integral controllers.

The study in [169], investigated the use of integral terminal sliding mode control for WECSs. The study’s goal was to create a system that performs at a high level. Improve durability while maintaining excellent and reliable temporary properties. The paper [170], presents a proposal for a robust control architecture for a DFIG-based wind turbine employing a discrete-time neural sliding mode controller with field-oriented control. A recurrent high-order neural network model based on the field-oriented model of the DFIG is utilized for system identification. The simulated results demonstrate successful identification of the DFIG’s actual rotor currents. An extended Kalman filter-based approach is employed to train the neural model. The discrete-time neural sliding mode controller and the discrete-time conventional sliding mode controller, both utilizing field-oriented control, have been compared. The simulation results show that the suggested controller is strong and works well, even when the desired output changes, decoupling happens, and stability and convergence are reached. Moreover, it demonstrates robustness against changes in DFIG parameters, and it outperforms the discrete-time conventional sliding mode controller in terms of response time.

5. Frequency Monitoring

Currently, the inertia of power networks has decreased due to the increased integration of wind energy into the existing power grid [171,172]. If there is a significant frequency disruption, the ability to regulate system frequency tends to decline. Wind turbines may contribute to the regulation of network frequency in order to ensure network frequency stability [173,174]. Inertia and droop controls, which employ derivative and proportional control methods, often achieve frequency control. In order to ensure that variable speed wind turbines effectively carry out frequency regulation according to specific requirements, it is necessary to develop and integrate supplemental controllers into both the existing pitch angle control loop and the converter power control loop [175,176]. These controllers will manipulate the reference set points for real power, torque, or rotor speed. A variable speed wind turbine must operate in a suboptimal mode, using deloaded control, to engage in secondary, primary, and tertiary frequency control. This ensures that a certain amount of spinning reserve margin is always available to provide extra actual power in the event of a frequency contingency. Balance, delta, or fixed reserve management often determines primary reserves. While the delta control mechanism reserves a certain percentage of the maximum actual power now available, the balance control mechanism sets aside a fixed proportion of the rated power. Fixed reserve control entails retaining a consistent amount of actual power. The reserve margin level is contingent upon the prevailing wind speed’s magnitude, the accuracy of wind speed predictions, and the top allowable limit of the variable speed wind turbine rotor speed. The principal frequency control of a wind energy conversion system (WECS) operates in a manner similar to that of a conventional generator. When the grid frequency deviates above the allowed threshold, it typically initiates within a few tens of seconds and continues for up to 15 min. In order to mimic the typical reaction of a traditional governor, variable speed wind turbines use droop control. This control mechanism allows for the correlation between fluctuations in the grid frequency and the corresponding adjustments in the production of actual power via the power converter’s controller. It modulates the power output in response to significant grid frequency fluctuations [177].

Trending Frequency Control Strategies

In [178], the proposed approach utilizes a modified inertial control scheme to leverage the rapid response capability of electronically controlled WECSs. This allows for the partial and temporary release of the kinetic energy stored in rotating masses, enabling earlier frequency support. Furthermore, the transmission of the WECS reaction to traditional generators achieves an even greater improvement, empowering them to finally tackle the entire load imbalance.

In [179], researchers conducted a study on a hybrid intelligent control system that enables frequency support regulation in wind turbines using permanent magnet synchronous generators (PMSGs). The suggested technique for a wind energy conversion system (WECS) is planned to include the modelling of a Permanent Magnet Synchronous Generator (PMSG) and the use of full-scale back-to-back Insulated-Gate Bipolar Transistor (IGBT) converters for both the machine and grid sides. The controllers for the machine side converter (MSC) and the grid side converter (GSC) are intended to accomplish maximum power point tracking (MPPT) using an enhanced hill climb searching (IHCS) control algorithm and de-loaded (DL) operation to ensure a power margin. The Integrated Hybrid Control System (IHCS) not only provides extensive control over the maximum power tracking mode but also devises a technique to manage the discharge of kinetic energy (KE) in the primary frequency control scheme through Distributed Ledger (DL) operation. This method aims to regulate the short-term frequency response and ensure the reliable operation of the power system.

The paper introduces a unique droop control loop that is based on kinetic energy [180]. A novel linear-gain droop control loop is suggested for the DFIG wind farm. In the proposed control loop, the droop gain is directly proportional to the wind turbine rotor speed. By carefully choosing the coefficients of the linear function, the suggested linear droop gain may closely approximate the quadratic droop gain. The effectiveness of the suggested droop control loop is shown using three different wind speed scenarios. Four indicators have been created to validate the system frequency responses and WT power output. The simulation findings indicate that the proposed linear-gain droop control loop has a frequency control capacity that is comparable to that of KE-based droop control.

A coordinated frequency control technique, which utilizes the rotor kinetic energy and supercapacitor, is introduced in reference [181]. To guarantee the DFIG delivers both rapid and sustained power supply, a supercapacitor was used to provide the droop characteristic, while the inertia characteristic, similar to that of a synchronous generator (SG), was achieved using the rotor’s kinetic energy. In addition, the supercapacitor is regulated to offset the power decrease in the Do DFIG as the rotor’s kinetic energy transitions from providing inertia support in order to prevent a further decrease in frequency. In addition, a novel tracking curve for the DFIG rotor speed and output power was implemented in order to minimize power loss during rotor speed recovery.

In [182], the author introduced a novel fractional-order fuzzy control (FOFC) for DFIG-based multi-rotor wind energy systems. This control integrates fractional-order control with fuzzy control to achieve a highly robust technique. The proposed control seeks to enhance the efficacy of the DFIG-based multi-rotor WECS regarding various performance metrics, including power quality and resilience to variations in system parameters.

6. Application of Artificial Intelligence in Wind Energy Conversion Systems

This section offers a concise summary of artificial intelligence (AI) methods used in grid-connected WECSs. Efficient management of expansive wind farms and their integration into power grids is a critical endeavour to ensure the provision of dependable, efficient, and protected electrical energy. Consequently, the use of AI techniques and soft computing methods in combination with traditional control methodologies may significantly improve the performance of WECSs [183,184].

The teaching-learning-based optimization method is examined in [185]. The research aimed to mitigate the adverse impacts of the wake and optimize the power production of the wind farm. The suggested method is structured in parallel rather than series in order to expedite convergence and enhance algorithm efficiency. The study in [186], focuses on the grouped grey wolf optimizer, a unique approach that determines the optimal parameters of interactive proportional-integral controllers for DFIG-based WECSs. The proposed technique’s objective was to harness the most efficient wind energy in order to achieve maximum power point tracking.

In [187], introduced a new adaptation and use of the salp swarm algorithm (SSA), which draws inspiration from the collective behaviour of salp fish residing in the depths of the ocean. The expanded salp swarm algorithm (ESSA) is introduced as a solution to address the limitations of the SSA in producing subpar results, particularly for functions with large dimensions. The ESSA is validated by conducting tests on twenty-three benchmark test functions and then comparing its performance with that of the original SSA technique as well as other algorithms. The statistical analysis of the findings demonstrated a considerable improvement in the ESSA method. The convergence curves indicated a rapid convergence towards the optimal solution. In addition, the SSA and ESSAs are used to improve the efficiency of maximum power point tracking and the capacity to withstand faults in a grid-connected permanent magnet synchronous generator powered by a variable speed wind turbine (PMSG-VSWT).

The multi-stage PID controller is described in [188]. The controller parameters were tuned using a moth-flame optimization process. The objective of the suggested method was to fine-tune the PID control to its best operating state. The study’s primary goal was to control the microgrid frequency deviation under various disturbance conditions.

In [189], the author focused on the optimum control methods that may enhance the LVRT capacity of grid-tied wind power stations. They emphasized the importance of using optimal control techniques to improve these stations’ LVRT performance. The study showed the effectiveness of a PI controller in regulating a 9-MW DFIG grid-connected wind power system. The suggested design approach involves using the mountain gazelle optimizer (MGO) to create optimum PI controllers for grid-connected wind power systems’ RSC or GSC converters. This technique aims to improve the LVRT capacity. The proposed control system made the wind system more responsive than what was required by the grid code to improve LVRT capabilities in both symmetrical and unsymmetrical fault situations. The efficacy of the simulated optimization approach is validated by comparing its outcomes to those generated by traditional PSO and GA. Implementing the recommended MGO significantly improved the system’s performance. This improvement was seen in several aspects, including reduced computation time, decreased overshoot, improved settling time, and decreased steady-state inaccuracy. The suggested innovative optimization approach yielded good outcomes, indicating that these gain controller solutions are well-suited for both symmetrical and unsymmetrical stator voltage dips. Compared to standard approaches, the suggested controllers demonstrated superior speed, reduced fluctuations, and improved damping.

In [190], the author proposed the use of FAMSANFIS, a technique that combines the fertile field algorithm, the momentum search algorithm, and the adaptive neuro-fuzzy inference system to enhance WECSs with DFIG at LVRT. The suggested approach combines the fertile field algorithm (FFA) and momentum search algorithm (MSA) with the adaptive neuro-fuzzy inference system (ANFIS) to improve performance. The suggested technique enhanced the grid fault condition’s capacity to withstand LVRT. The suggested technique generates the data set using the FFA-MSA approach and then predicts the control signal using the ANFIS approach. The proposed technique effectively achieves the system’s objectives by employing this approach. The author examines the performance of the suggested technique in two scenarios: under fault conditions and under normal conditions.

In [191], the author introduces an approach called autonomous group particle swarm optimization. The suggested method’s goal was to make the DFIG better at handling faults by making a PI controller’s settings work better.

The GVSS-DCMPN-FLC, which stands for generalized variable step size diffusion continuous mid-p-norm fuzzy logic controller, is examined in [192]. The suggested GVSS-DCMPN-FLC effectively reduces the transient stator and rotor current of the DFIG during grid disturbance, resulting in improved responsiveness. The GVSS-DCMPN algorithm effectively reduces torque ripple, but the PSO-PI controller fails to achieve the same reduction. The stator active power of the DFIG is varied using a particle swarm optimization (PSO)-based adaptive proportional-integral (PI) controller, while it remains stable utilizing the suggested Generalized Variable Structure System (GVSS), Direct Current Model Predictive Control (DCMPN), and Fuzzy Logic Controller (FLC). In addition, the examination of the transient responses of the given parameter of the DFIG using the suggested GVSS-DCMPN-FLC method demonstrates a shorter settling time, reduced overshoot, and decreased steady-state error compared to the results obtained using a PI controller based on the Particle Swarm Optimization (PSO) algorithm. The suggested approach exhibits higher capabilities in improving LVRT compared to existing optimization and adaptive filtering algorithms (AFAs).

In [193], the author used STATCOM as an LVRT solution for a wind farm that is linked to the power grid. The author employed two optimization approaches, ant colony and particle swarm optimization, to improve the dynamic performance of STATCOM.

In [194], the author introduced a nature-inspired meta-heuristic method called the water cycle algorithm (WCA) for the optimum adjustment of PI controllers in DFIG-based wind systems. The author examined two scenarios to analyze the control efficacy of improved PI controllers.

A grey wolf optimizer (GWO), Artificial Grey Wolf Optimization (AGWO) and particle swarm optimization (PSO) method is used in [195], to improve the efficiency of a grid-connected permanent magnet synchronous generator that is powered by a variable speed wind turbine (PMSG-VSWT). The AGWO method demonstrated the smallest integral squared error (ISE) for the input errors of the PI controllers, which regulate the RMS voltage of the PMSG and grid, the DC-link voltage, and the generated real power. A PSCAD simulation examines the optimal parameters for GWO and PSO. We simulated the dynamic and transient stability of the grid-connected Permanent Magnet Synchronous Generator Variable Speed Wind Turbine (PMSG-VSWT). The results showed that the AGWO method was more effective than both the GWO and PSO algorithms.

In [196], the author conducted a study on the optimum design of multiple Sugeno FLCs using the Whale Optimization Algorithm (WOA). The goal of the developed WOA-FLC is to enhance the FRT capability of grid-connected gearless VSWT equipped with PMSG. The VSWT-PMSG is connected to the grid using a frequency converter due to its changing frequency. The frequency converter consists of two voltage source converters (VSCs), namely the modular multilevel converter (MSC) and the grid-side inverter (GSI). Eight Wavelet-Optimized Adaptive Fuzzy Logic Controllers (WOA-FLCs) are used in the cascaded control of the MSC and Grid-Side Inverter (GSI) to enhance the FRT capability and maximize power extraction from the wind. The design process of WOA-FLCs is accomplished by minimizing the high-dimensional cost function, which consists of the integral squared errors of the inputs of the outer FLCs. The enhancement of Fault Ride using the FRT capability of a grid-connected VSWT with a PMSG is confirmed using PSCAD and EMTDC simulations, both in the presence of balanced and unbalanced faults. The simulation findings demonstrated that the transient responses of grid voltage, real power, DC voltage, and reactive power achieved using WOA-FLCs outperformed the responses obtained using a genetic algorithm (GA-FLCs) and grey wolf optimizer (GWO-FLCs). The WOA-FLC method has lower overshoot and steady-state errors compared to the GA-FLC and GWO-FLC methods. Furthermore, the maximum power attained by the use of WOA-FLCs surpasses that reached with GA-FLCs and GWO-FLCs.

7. LVRT Impact on Wind Turbines and Practical Application of Controllers and FACTs Devices

The DFIG-based WECS connected to the grid is susceptible to defects such as voltage dips and voltage surges. When voltage dips at the grid, the stator flux linkage breaks down into natural and forced components. The natural components rotate simultaneously, while the forced components remain motionless with regard to the stator. Furthermore, the natural components generate significant EMF in the rotor winding.

Table 2. Control strategies for DFIG-based WECSs.

Control Type	Application
Sliding mode	It ensures that the rotor current and DC-link voltage remain constant. It regulates both active and reactive power, ensuring that there is no reactive power during a malfunction.
Stator Flux Oriented Reference frame	The device reduces excessive currents on both the rotor and stator sides. Isolate the electromagnetic torque from the rotor excitation current.
Fuzzy controller	Overcurrent is mitigated. The DC-link voltage is kept constant.

summarizes the different controllers in the low voltage ride-through mechanism of a DFIG-based wind turbine generator. Table 2 also provides an overview of how these control devices may help with practical work.

Power electronic systems have a significant impact on wind turbine generator power system applications. The DFIG rotor windings link with the grid through a converter, enabling bidirectional power transmission. A configuration of two voltage source converters (VSCs) and a DC-link capacitor mitigates torque pulsations of the generator and enhances output power quality.

The grid connects the PMSG with a power electronic converter to manage both active and reactive power comprehensively. Grid faults impact the PMSG-based WECSs with a full rating converter, leading to an increase in voltage at the DC-link capacitor. The disparity in the mechanical and electrical components of WECSs causes damage to the generator and power electronic converter by producing over currents and overvoltages inside the system. Specifically, addressing overcurrent and overvoltages indirectly improves the LVRT capabilities. Grid characteristics such as fault voltage, voltage recovery, and reaction time during overshoots, along with turbine factors like rotor speed, rotor current, and DC bus voltage, determine the LVRT capacity.

Table 3. Control strategies of PMSG-based PMSG.

Control Type	Application
Type-2 fuzzy control	It regulates the DC-link voltage. It controls the flow of both active and reactive electricity into the grid.
Field-oriented control	It regulates the generator’s speed. The stator current is regulated.
Direct predictive torque control approach	It regulates torque and mitigates ripple. The system meets the maximum torque per ampere specification.

summarizes the different controllers in the low voltage ride-through mechanism of a PMSG-based wind turbine generator. Table 3 also provides an overview of how these control devices may help with practical work.

Short circuit problems significantly harm grid-connected wind turbine turbines. The literature has published several solutions to mitigate these impacts using the LVRT capabilities. MATLAB/Simulink has been used to calculate the performance of several LVRT augmentation controllers. The simulation results demonstrate many techniques to enhance the LVRT capabilities. The author of this work discussed the various controller techniques and FACTS devices described in the literature for improving LVRT. This study sets itself apart by classifying the various techniques as rotor side and grid side controllers and classifying FACTS devices as series, shunt, and series-shunt connecting devices. The FACTS devices are critical in providing reactive power assistance to the grid during imbalanced conditions. During LVRT augmentation, the controller approaches are more important for increasing MPPT and optimizing parameters.

8. Recommendations

Most researchers’ primary focus in a literature review is to regulate the active and reactive power of a renewable energy source. The literature study revealed that all the recommended control techniques for LVRT had both benefits and drawbacks. Researchers are currently showing little interest in power distribution within the power system. This paper proposes that researchers investigate the power contribution of each generator following a load change on the power system. Studying techniques for regulating power division may greatly aid in maintaining power system stability. Furthermore, it is essential to do research on standby renewable energy sources that function similarly to operating diesel standby generators. These sources would just monitor the grid frequency and only become active when there is a change in grid frequency. Load shifting necessitates changes in the mechanical power of each machine’s primary mover. Governor Droop is well-regarded for managing the distribution of power among parallel alternators. Figure 8 illustrates the power deviation shared between two generators.

If generator A wants to handle a higher active power load, it needs to boost the prime mover’s power output. The power of generator B’s primary mover must decrease, or the system frequency will rise. If the electrical load on a system grows without any governor control, the system frequency will decrease. The governor’s automatic management of the no-load speed compensates for changes in the load by adjusting the characteristics of the machines, either increasing or decreasing them. Researchers have only investigated governor control on two parallel generators. This research aims to investigate the number of generators connected to a power system. Additionally, communication among the distributed generators should be investigated for better performance of the governor droop control system.

The following equations illustrate how two generators, as shown in Figure 8, send active power into a grid in response to a load change:

$$GD={\displaystyle \frac{GSR.F_{rated}}{P_{rated}}}={\displaystyle \frac{\Delta F}{\Delta P}}$$

(16)

where

• GD—Governor droop.
• GSR—Governor speed regulation.
• $\Delta f$—Change in f due to change in load.
• $\Delta P$—Change in load.

$$P_{Anew}=\Delta P_A+P_A$$

(17)

$$P_{Bnew}=\Delta P_B+P_B$$

(18)

In [197], the author investigated the implementation of governor droop control on a system consisting of a steam turbine and a hydro turbine connected by power lines. The research’s primary goal was to achieve power deviation among the generators. However, the proposed method continued to encounter a consistent frequency inaccuracy during the steady state phase. The load distribution of two generators using the governor droop method is studied in [198]. Nevertheless, the communication between the two controllers continues to present a challenge. Therefore, it presents an opportunity for academics to explore ways to enhance the control technique.

The research on load sharing in an autonomous microgrid is examined in [199]. The author found that implementing high gain angle droop control guarantees accurate load sharing, particularly in situations when the system is weak. Nevertheless, it adversely affects overall stability. Frequency-domain modelling, eigenvalue analysis, and time-domain simulations demonstrated this disagreement. The author suggested adding an extra loop to each DG converter’s traditional droop control to stabilize the system while using large-angle droop gains. Control loops depend on measuring local power and adjusting the d-axis voltage reference for each converter. The author poses the coordinated design of supplemental control loops for each distributed generation (DG) as a parameter optimization issue and addresses it using an evolutionary approach. The supplemental droop control loop is shown to stabilize the system across various operating situations while guaranteeing appropriate load sharing.

In [200], the author examined the inertia emulation controller. The objective was to enhance the current wind turbine by including inertia response and primary frequency control (PFC) capabilities. The author constructed two controllers, an inertial controller and a droop controller, and evaluated their frequency control capabilities in an isolated power system. The power system comprises a conventional steam turbine generator and a wind farm. The findings indicate that the proposed controllers contribute to improved frequency control performance in the microgrid.

In [201], the author developed a simulation model to optimize the speed droop regulator’s function in a gas turbine cogeneration unit. This study used a quantitative approach and utilized descriptive statistical analysis methods. The author used the simulation model as a simulator to operate the speed droop governor, which controls frequency in the electrical system. The author conducted an analysis using operational data of the speed droop values from gas turbine cogeneration unit 2 to examine how frequency variations affect the generating unit’s reaction. The study and simulation findings revealed that the gas turbine cogeneration unit 2 maintains a speed droop value of 4%, considered optimal for maintaining the stability of the 60 Hz nominal frequency that consumers demand.

A simulation and experimental evaluation of the controller’s design and application were presented in [202]. To emulate hydraulic turbines, a small-scale testbed system used this controller. The goal was to address the speed regulation issues faced by existing hydraulic turbines in hydroelectric power generation systems. The author studied two controllers, one with integer order and one with fractional order. The author tested both controllers in a computational environment as well as on a nonlinear system that replicates a small-scale power generation system. The controllers were implemented using a development platform that combines the speed governor with the Arduino Due controller in the testbed system. The results of the real-world tests conducted in a non-minimum phase system showed that the fractional order speed regulator made the system less likely to overshoot and undershoot, and it also made speed oscillations less common in all tests. Nevertheless, in some instances, the settling times of both controllers showed similarities.

Changes in load and fluctuations in active power can have a significant impact on frequency levels, which may lead to instability in the electric power system. Therefore, it is necessary to enhance the speed-droop model in order to optimize its performance. Additionally, the integration of trending AI strategies could potentially enhance the improvement even further. In addition, implementing governor droop in all distributed generators and fostering communication among these generators could enhance the overall system stability. This can be accomplished using the same method that protection relays use to communicate on the power system.

9. Conclusions

This study conducted a comprehensive analysis of the proposed LVRT solutions implemented in WECSs, covering both established engineering strategies and the latest theoretical advancements. This study examines the advantages and disadvantages of various topologies or techniques for incorporating specific circuits into WECSs by adjusting the operation of electronic power switches during grid faults. Modifying the configurations of WECSs can help mitigate stator and rotor overcurrent, provide power support, and regulate overvoltage, thereby enhancing the LVRT capacity of WECSs. While future LVRT solutions may not prioritize external modifications, the installation of external LVRT devices with specific functions is essential. Internal control methods utilize advanced control theories to enhance the LVRT capabilities of WECSs. By adjusting voltage and current compensation, or improving control performance in uncertain, nonlinear systems through internal control modifications, changes can enhance control effectiveness during grid voltage fluctuations. Newly established WECS now have the option to boost their LVRT capacity through internal control methods in the absence of external auxiliary circuits. These techniques demonstrate promising potential for future development despite encountering some limitations. Our study proposes a hybrid control strategy that integrates governor droop control to address these challenges.