Ultra-Short-Term Wind Power Forecasting in Complex Terrain: A Physics-Based Approach
Abstract
:1. Introduction
2. Wind Energy Extraction Latency Model—Theoretical Framework
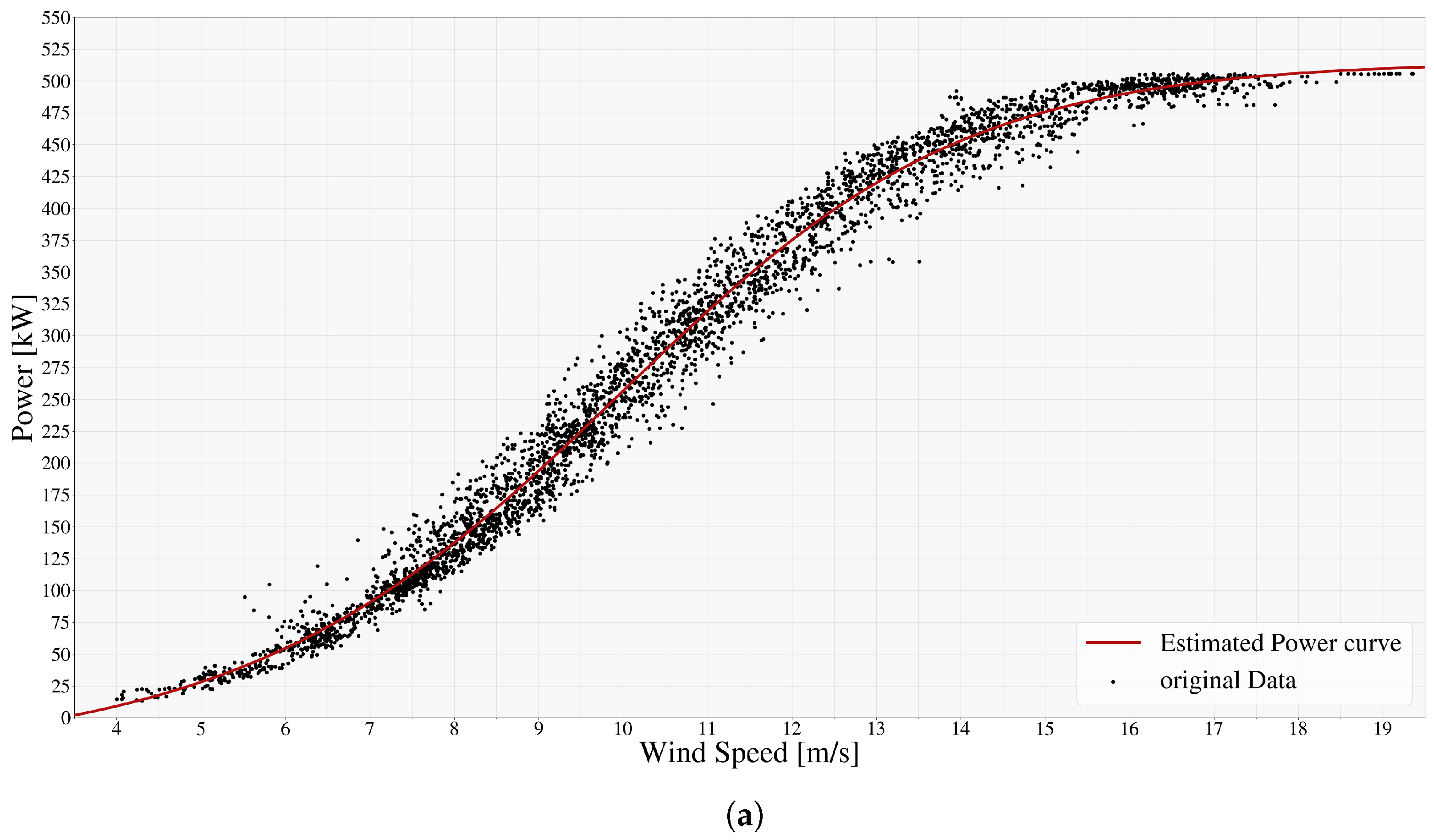
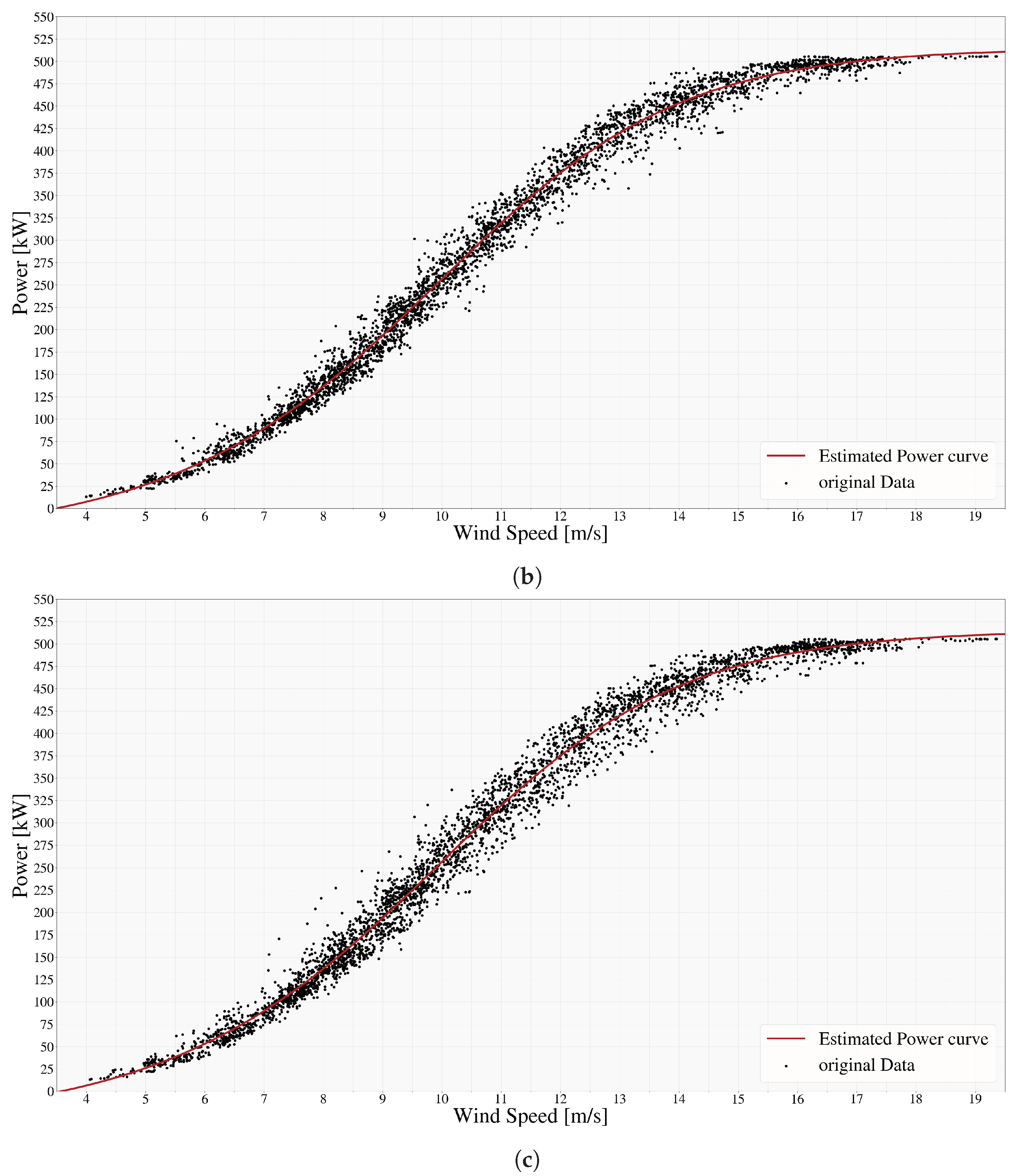
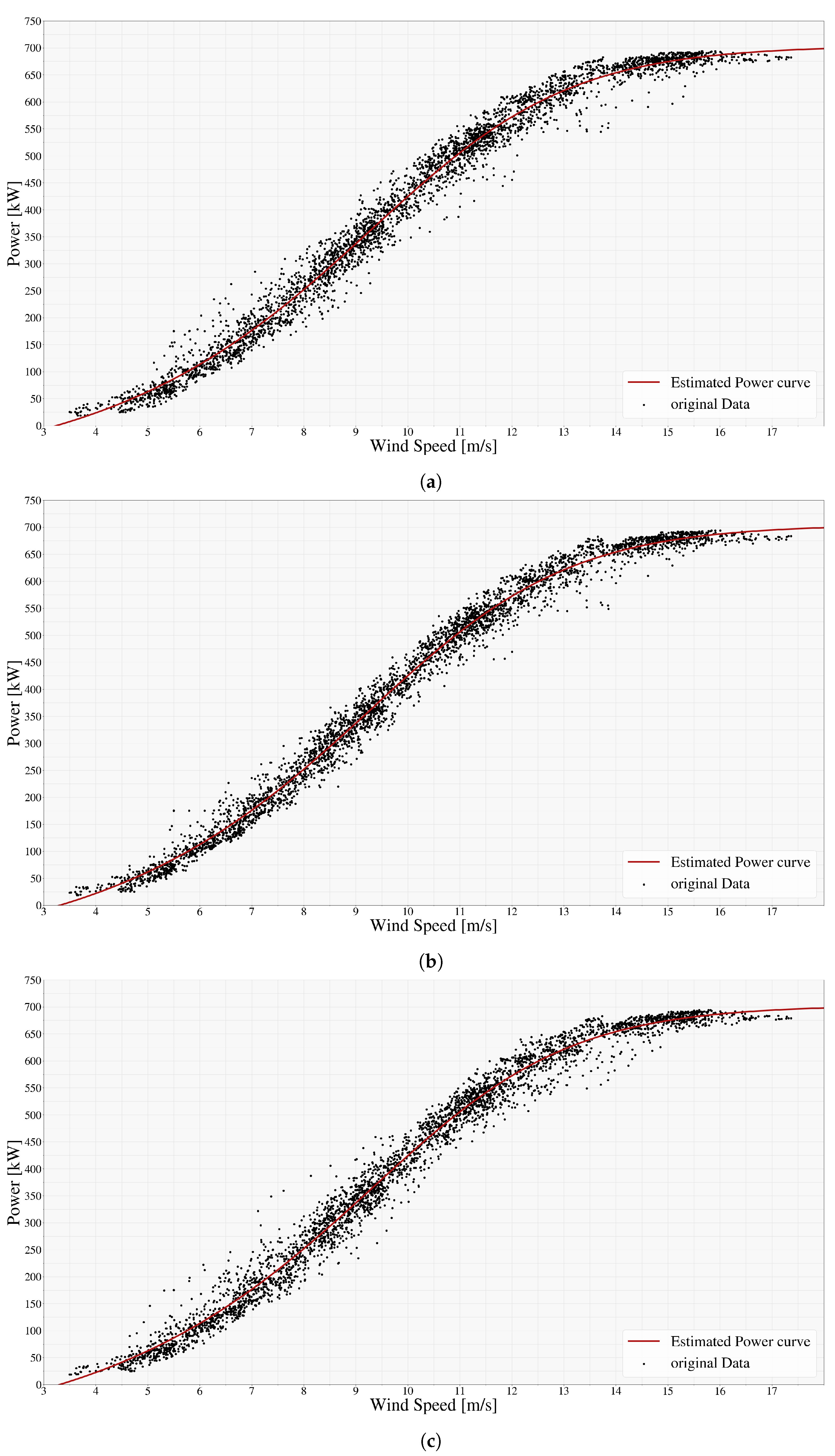
2.1. Power Curve Equation Modeling
2.2. ShiVa Detection
3. Data and Methodology
3.1. CRES Wind Farm
3.2. WiSpEx
3.3. WEEL
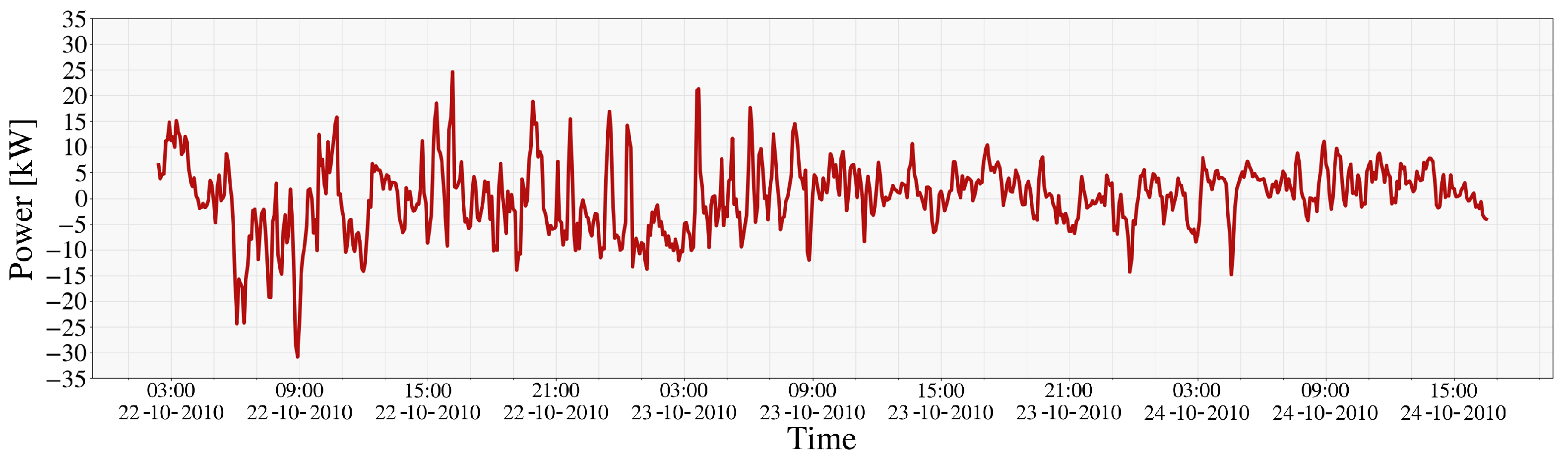
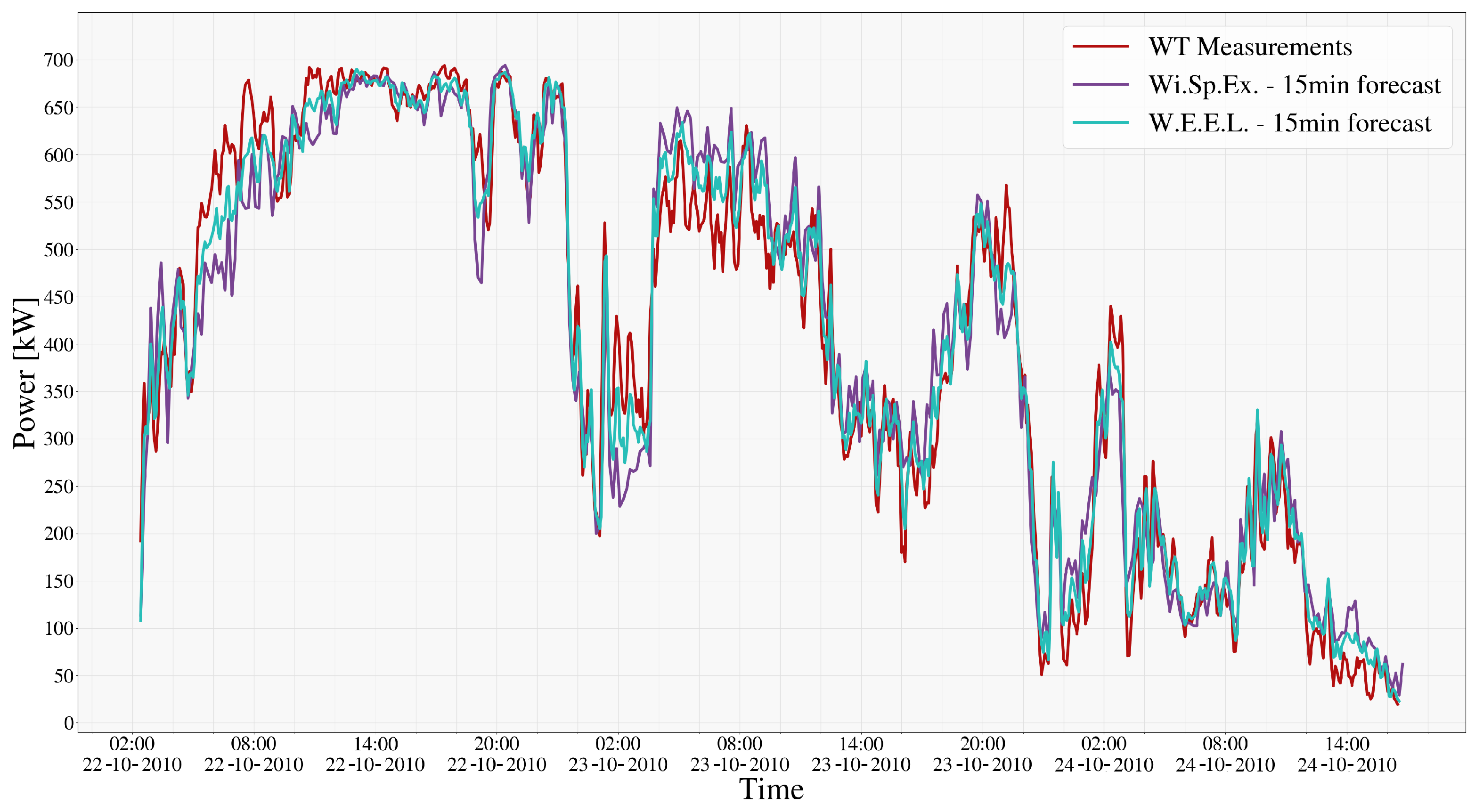
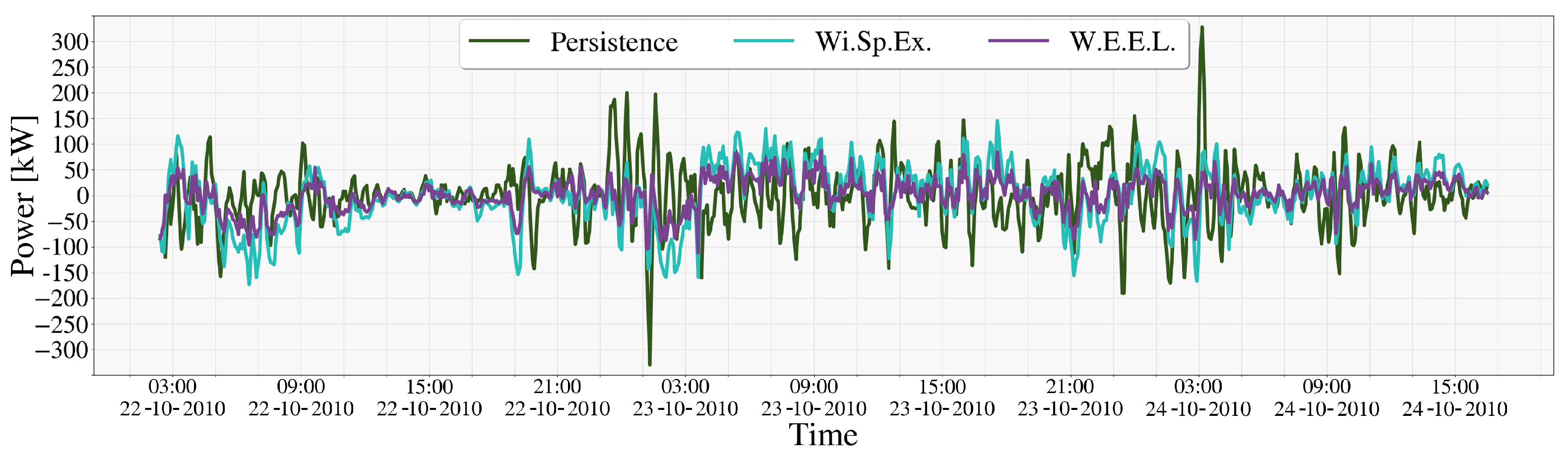
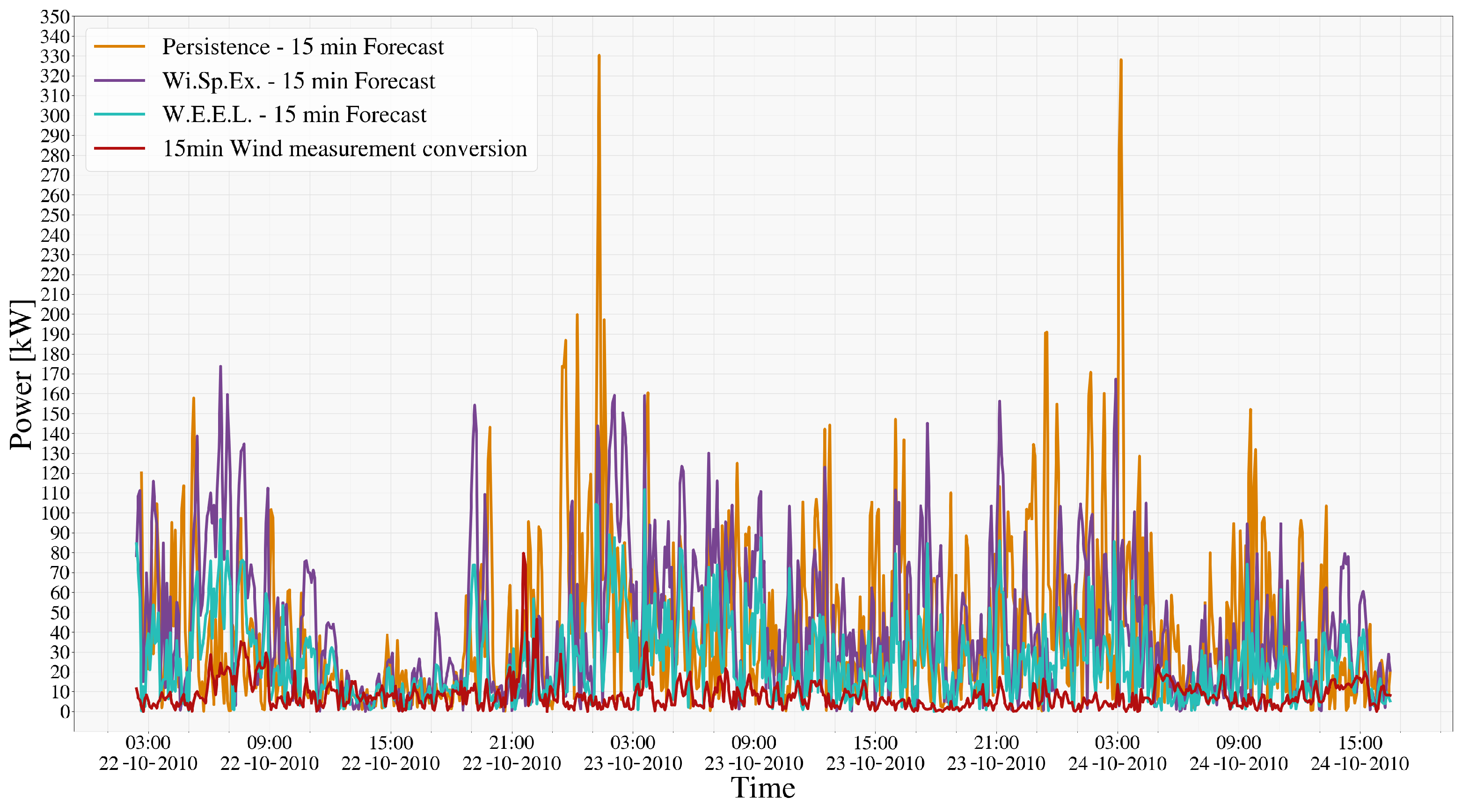
4. Results
4.1. Shiva Detection
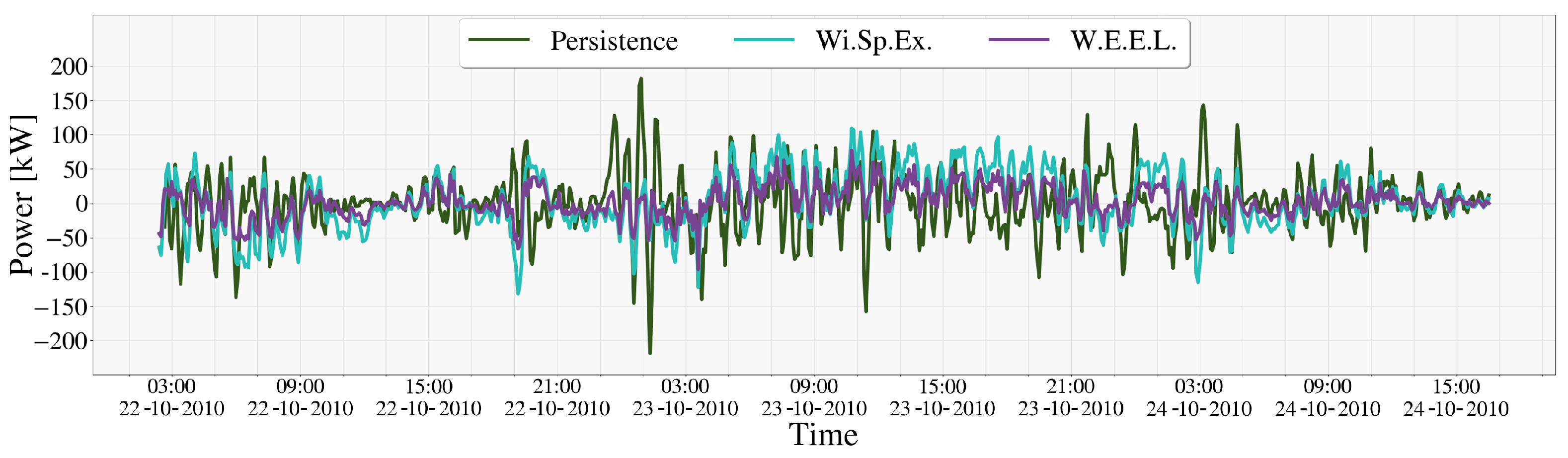
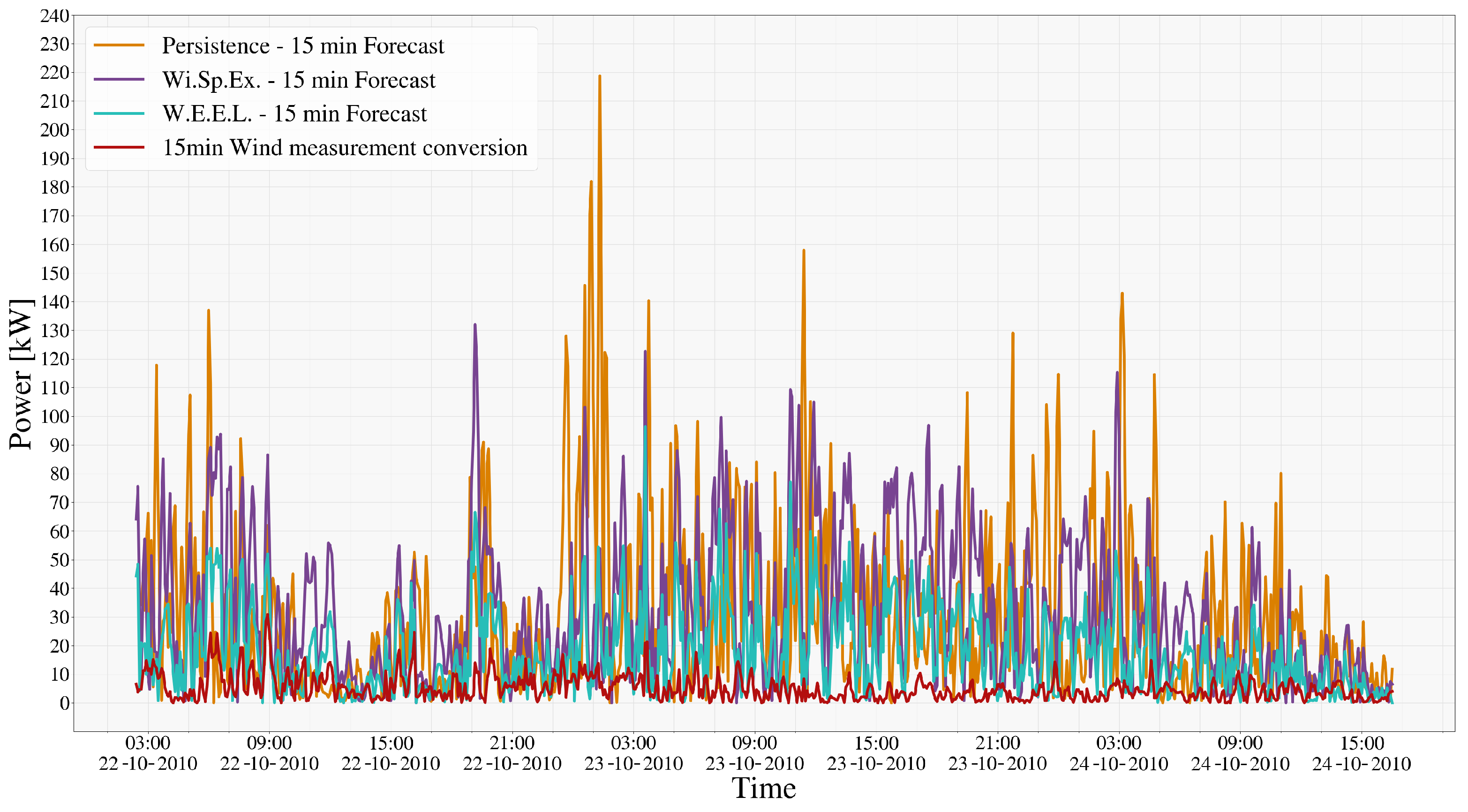
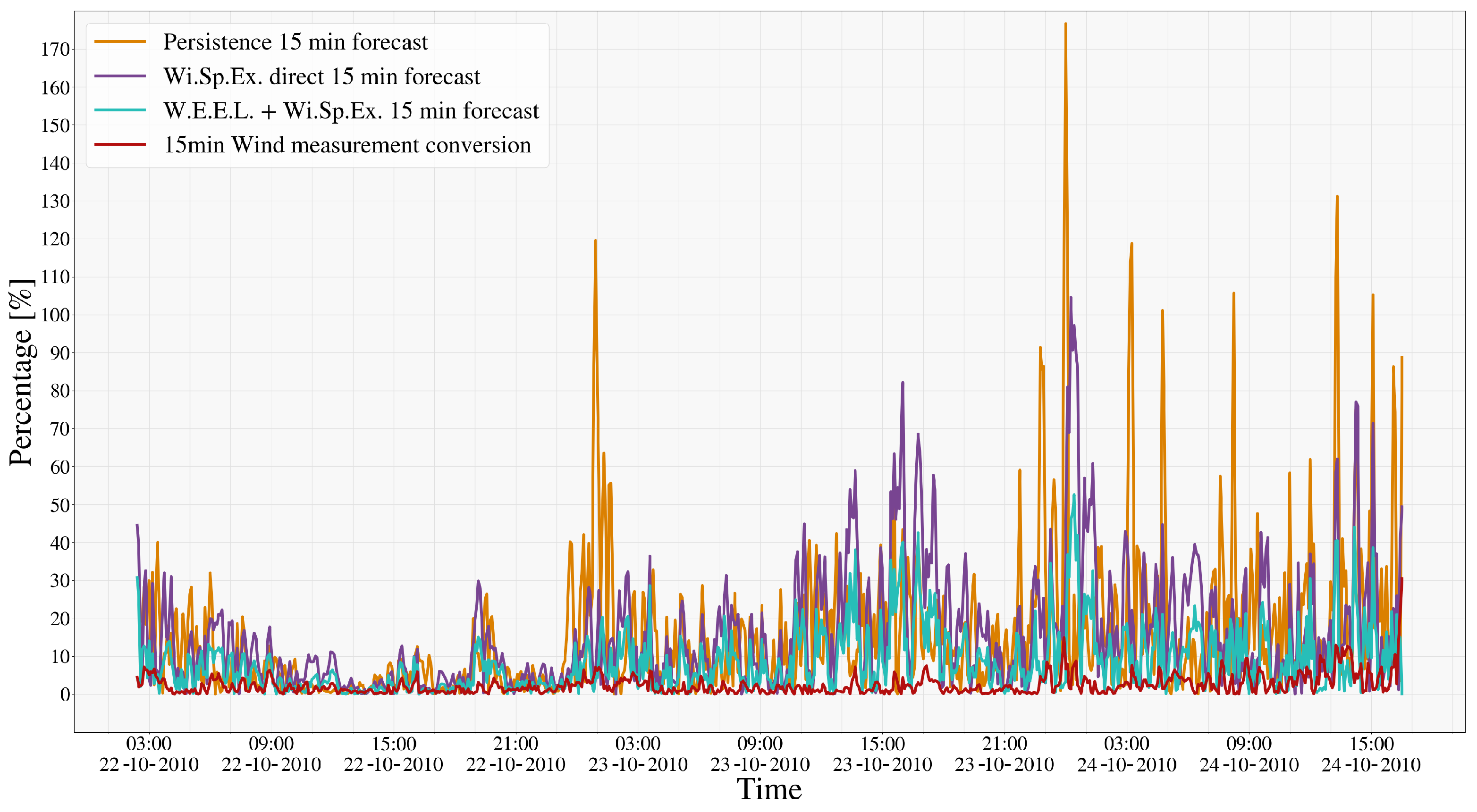
4.2. Power Forecasting
4.2.1. Enercon
4.2.2. NEG
4.3. Comparative Analysis and Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CRES | Center For Renewable Energy Sources |
| LIDAR | Light Detection and Ranging |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Square Error |
| NMAE | Normalized Mean Absolute Error |
| NRMSE | Normalized Root Mean Square Error |
| NWP | Numerical Weather Prediction |
| RMSE | Root Mean Square Error |
| ShiVa | Shift Value |
| ShiVa | Shifted Value |
| SMAPE | Symmetric Mean Absolute Percentage Error |
| SSE | Sum of Squared Errors |
| UST | Ultra-Short-Term |
| WF | Wind Farm |
| WiSpEx | Wind Spatial Extrapolation model |
| WEEL | Wind Energy Extraction Latency model |
| WT | Wind Turbine |
References
- Quiñones, J.J.; Pineda, L.R.; Ostanek, J.; Castillo, L. Towards smart energy management for community microgrids: Leveraging deep learning in probabilistic forecasting of renewable energy sources. Energy Convers. Manag. 2023, 293, 117440. [Google Scholar] [CrossRef]
- Manfren, M.; Caputo, P.; Costa, G. Paradigm shift in urban energy systems through distributed generation: Methods and models. Appl. Energy 2011, 88, 1032–1048. [Google Scholar] [CrossRef]
- Nallolla, C.A.; P, V.; Chittathuru, D.; Padmanaban, S. Multi-objective optimization algorithms for a hybrid AC/DC microgrid using RES: A comprehensive review. Electronics 2023, 12, 1062. [Google Scholar] [CrossRef]
- Polimeni, S.; Nespoli, A.; Leva, S.; Valenti, G.; Manzolini, G. Implementation of different PV forecast approaches in a multiGood microGrid: Modeling and experimental results. Processes 2021, 9, 323. [Google Scholar] [CrossRef]
- Michos, D.; Catthoor, F.; Foussekis, D.; Kazantzidis, A. A CFD Model for Spatial Extrapolation of Wind Field over Complex Terrain—Wi. Sp. Ex. Energies 2024, 17, 4139. [Google Scholar] [CrossRef]
- Wei, J.; Wu, X.; Yang, T.; Jiao, R. Ultra-short-term forecasting of wind power based on multi-task learning and LSTM. Int. J. Electr. Power Energy Syst. 2023, 149, 109073. [Google Scholar] [CrossRef]
- Dai, X.; Liu, G.P.; Hu, W. An online-learning-enabled self-attention-based model for ultra-short-term wind power forecasting. Energy 2023, 272, 127173. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.; Wang, J.; Shu, H.; Zhang, X.; Yu, T.; Sun, L. State-of-the-art one-stop handbook on wind forecasting technologies: An overview of classifications, methodologies, and analysis. J. Clean. Prod. 2021, 283, 124628. [Google Scholar] [CrossRef]
- Xiang, L.; Liu, J.; Yang, X.; Hu, A.; Su, H. Ultra-short term wind power prediction applying a novel model named SATCN-LSTM. Energy Convers. Manag. 2022, 252, 115036. [Google Scholar] [CrossRef]
- Liu, L.; Liu, J.; Ye, Y.; Liu, H.; Chen, K.; Li, D.; Dong, X.; Sun, M. Ultra-short-term wind power forecasting based on deep Bayesian model with uncertainty. Renew. Energy 2023, 205, 598–607. [Google Scholar] [CrossRef]
- Niu, D.; Sun, L.; Yu, M.; Wang, K. Point and interval forecasting of ultra-short-term wind power based on a data-driven method and hybrid deep learning model. Energy 2022, 254, 124384. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Pan, G.; Xu, Y.; Wang, F. A multi-stage predicting methodology based on data decomposition and error correction for ultra-short-term wind energy prediction. J. Clean. Prod. 2021, 292, 125981. [Google Scholar] [CrossRef]
- Sezer-Uzol, N.; Long, L. 3-D time-accurate CFD simulations of wind turbine rotor flow fields. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006; Volume 394. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound.-Layer Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Yan, B.; Li, Q. Coupled on-site measurement/CFD based approach for high-resolution wind resource assessment over complex terrains. Energy Convers. Manag. 2016, 117, 351–366. [Google Scholar] [CrossRef]
- Yan, S.; Shi, S.; Chen, X.; Wang, X.; Mao, L.; Liu, X. Numerical simulations of flow interactions between steep hill terrain and large scale wind turbine. Energy 2018, 151, 740–747. [Google Scholar] [CrossRef]
- Valldecabres, L.; Peña, A.; Courtney, M.; von Bremen, L.; Kühn, M. Very short-term forecast of near-coastal flow using scanning lidars. Wind Energy Sci. 2018, 3, 313–327. [Google Scholar] [CrossRef]
- Kajishima, T.; Taira, K. Computational Fluid Dynamics: Incompressible Turbulent Flows; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics, 4th ed.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Wendt, J. Computational Fluid Dynamics: An Introduction; A von Karman Institute Book; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind Power Forecasts Using Gaussian Processes and Numerical Weather Prediction. IEEE Trans. Power Syst. 2014, 29, 656–665. [Google Scholar] [CrossRef]
- Du, P. Ensemble machine learning-based wind forecasting to combine NWP output with data from weather stations. In Renewable Energy Integration for Bulk Power Systems: ERCOT and the Texas Interconnection; Springer International Publishing: Cham, Switzerland, 2023; pp. 263–281. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nasiri, F.; Menon, R.P.; Monsalvete, P.; Kaifel, A.; Eicker, U. Smart Urban Wind Power Forecasting: Integrating Weibull Distribution, Recurrent Neural Networks, and Numerical Weather Prediction. Energies 2023, 16, 6208. [Google Scholar] [CrossRef]
- Chang, Y.; Yang, H.; Chen, Y.; Zhou, M.; Yang, H.; Wang, Y.; Zhang, Y. A Hybrid Model for Long-Term Wind Power Forecasting Utilizing NWP Subsequence Correction and Multi-Scale Deep Learning Regression Methods. IEEE Trans. Sustain. Energy 2024, 15, 263–275. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, G.; Tse, K.T.; He, X. Twisted-wind effect on the flow field of tall building. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104778. [Google Scholar] [CrossRef]
- Xiaoxia, G.; Luqing, L.; Shaohai, Z.; Xiaoxun, Z.; Haiying, S.; Hongxing, Y.; Yu, W.; Hao, L. LiDAR-based observation and derivation of large-scale wind turbine’s wake expansion model downstream of a hill. Energy 2022, 259, 125051. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: La Cañada, CA, USA, 2006. [Google Scholar]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Choukulkar, A.; Pichugina, Y.; Clack, C.T.; Calhoun, R.; Banta, R.; Brewer, A.; Hardesty, M. A new formulation for rotor equivalent wind speed for wind resource assessment and wind power forecasting. Wind Energy 2016, 19, 1439–1452. [Google Scholar] [CrossRef]
- Shourangiz-Haghighi, A.; Haghnegahdar, M.A.; Wang, L.; Mussetta, M.; Kolios, A.; Lander, M. State of the art in the optimisation of wind turbine performance using CFD. Arch. Comput. Methods Eng. 2020, 27, 413–431. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® (CFD). COMSOL Multiphysics® CFD Module User’s Guide, Version 5.6; COMSOL: Burlington, MA, USA, 2020. [Google Scholar]
- COMSOL Multiphysics® (CYCLOPEDIA). COMSOL Multiphysics® CYCLOPEDIA; COMSOL: Burlington, MA, USA, 2017. [Google Scholar]
- COMSOL Multiphysics® (Reference Manual). COMSOL Multiphysics® Reference Manual, Version 5.6; COMSOL: Burlington, MA, USA, 2020. [Google Scholar]
- Tavner, P.; Edwards, C.; Brinkman, A.; Spinato, F. Influence of wind speed on wind turbine reliability. Wind Eng. 2006, 30, 55–72. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; De Haan, S.W. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Hassan, A.; Rehman, A.U.; Shabbir, N.; Hassan, S.R.; Sadiq, M.T.; Arshad, J. Impact of inertial response for the variable speed wind turbine. In Proceedings of the IEEE 2019 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 21–22 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Besseau, R.; Jansen, M.; Staffell, I.; Troccoli, A.; Dubus, L.; Schmidt, J.; Gruber, K.; Simões, S.G.; Heier, S. A parametric model for wind turbine power curves incorporating environmental conditions. Renew. Energy 2020, 157, 754–768. [Google Scholar] [CrossRef]
- Bingöl, F.; Mann, J.; Foussekis, D. 2.3 Lidar in complex terrain. In Advancements in Wind Energy Metrology—UPWIND 1A2.3; Danmarks Tekniske Universitet: Copenhagen, Denmark, 2011; p. 11. [Google Scholar]
- CRES. Technical Specs of the WTs; CRES: Kansas City, MI, USA, 2024. [Google Scholar]
- He, B.; Ye, L.; Pei, M.; Lu, P.; Dai, B.; Li, Z.; Wang, K. A combined model for short-term wind power forecasting based on the analysis of numerical weather prediction data. Energy Rep. 2022, 8, 929–939. [Google Scholar] [CrossRef]
- Yang, M.; Wang, D.; Zhang, W. A short-term wind power prediction method based on dynamic and static feature fusion mining. Energy 2023, 280, 128226. [Google Scholar] [CrossRef]
- Yakoub, G.; Mathew, S.; Leal, J. Intelligent estimation of wind farm performance with direct and indirect ‘point’ forecasting approaches integrating several NWP models. Energy 2023, 263, 125893. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.; Mei, S.; Zhou, Q.; Fan, H. Series-wise attention network for wind power forecasting considering temporal lag of numerical weather prediction. Appl. Energy 2023, 336, 120815. [Google Scholar] [CrossRef]




| Specification | E40-500 | NM 750/48 | |
|---|---|---|---|
| Rotor | Diameter | 40 m | 48.2 m |
| Area swept | 1275 m2 | 1824 m2 | |
| Number of blades | 3 | 3 | |
| Type | Upwind rotor with active pitch control | Upwind Rotor | |
| Tower | Hub height (approx.) | 44 m | 45 m |
| Generator | Type | Direct-driven ENERCON ring generator (with drive train) | Asynchronous, 4/6 pole |
| Name plate rating | 500 kW | 750/200 kW | |
| Nominal Voltage | 500 V | 690 V | |
| Nominal Frequency | 50 Hz | 50 Hz | |
| Operational Data | Nominal output | 500 kW | 750 kW |
| Cut-in wind speed | 2.5 m/s | 4 m/s | |
| Nominal wind speed | 12 m/s | 16 m/s | |
| Power regulation | Variable Speed + Pitch | Stall |
| Metric | +0 min Shift | +1 min Shift | +2 min Shift | +3 min Shift | +4 min Shift | +5 min Shift |
|---|---|---|---|---|---|---|
| MAE | 12.961 | 11.577 | 10.838 | 10.675 | 11.129 | 12.353 |
| MSE | 293.660 | 231.483 | 204.463 | 201.226 | 220.992 | 274.580 |
| RMSE | 17.136 | 15.214 | 14.299 | 14.185 | 14.865 | 16.570 |
| MAPE | 6.342 | 5.664 | 5.317 | 5.225 | 5.416 | 5.988 |
| Metric | +0 min Shift | +1 min Shift | +2 min Shift | +3 min Shift | +4 min Shift | +5 min Shift |
|---|---|---|---|---|---|---|
| MAE | 18.385 | 16.930 | 16.384 | 16.490 | 17.179 | 18.653 |
| MSE | 614.732 | 511.373 | 470.061 | 472.260 | 518.871 | 629.909 |
| RMSE | 24.793 | 22.613 | 21.680 | 21.731 | 22.778 | 25.097 |
| MAPE | 7.561 | 6.872 | 6.601 | 6.652 | 6.988 | 7.74 |
| Method | 15 min MA | WEEL (Direct) | Persistence Power Interpolated | WEEL | Persistence | WEEL (Wi.Sp.Ex.) | Wi.Sp.Ex. | Persistence |
|---|---|---|---|---|---|---|---|---|
| MAE [kW] | 5.06 | 12.23 | 15.32 | 12.96 | 24.85 | 17.81 | 31.58 | 31.82 |
| MSE [kW2] | 45.18 | 271.15 | 450.05 | 294.81 | 1188.44 | 532.48 | 1643.36 | 1938.99 |
| RMSE [kW] | 6.72 | 16.47 | 21.21 | 17.17 | 34.47 | 23.08 | 40.54 | 44.03 |
| MAPE [%] | 2.4 | 5.91 | 7.41 | 6.1 | 12.2 | 8.44 | 15.36 | 16.01 |
| NMAE | 0.0101 | 0.0245 | 0.0306 | 0.0259 | 0.0497 | 0.0356 | 0.0632 | 0.0636 |
| NRMSE | 0.0134 | 0.0330 | 0.0424 | 0.0343 | 0.0690 | 0.0462 | 0.0811 | 0.0881 |
| SMAPE [%] | 2.39 | 5.88 | 7.29 | 5.99 | 11.72 | 8.18 | 14.51 | 15.03 |
| time step | live | +5 min | +5 min | +10 min | +10 min | +15 min | +15 min | +15 min |
| Method | 15 min MA | WEEL (Direct) | Persistence | WEEL Power Interpolated | Persistence | WEEL (Wi.Sp.Ex.) | Wi.Sp.Ex. | Persistence |
|---|---|---|---|---|---|---|---|---|
| MAE [kW] | 8.15 | 18.48 | 20.75 | 18.99 | 32.84 | 24.93 | 43.19 | 42.75 |
| MSE [kW2] | 121.24 | 603.92 | 843.16 | 611.47 | 2195.32 | 1039.3 | 3176.67 | 3635.62 |
| RMSE [kW] | 11.01 | 24.57 | 29.04 | 24.73 | 46.85 | 32.24 | 56.36 | 60.3 |
| MAPE [%] | 3.86 | 7.67 | 8.21 | 7.95 | 13.65 | 10.25 | 17.71 | 18.14 |
| NMAE | 0.0109 | 0.0246 | 0.0277 | 0.0253 | 0.0438 | 0.0332 | 0.0576 | 0.0570 |
| NRMSE | 0.0148 | 0.0328 | 0.0387 | 0.0329 | 0.0626 | 0.0430 | 0.0751 | 0.0804 |
| SMAPE [%] | 3.71 | 7.53 | 8.0 | 7.44 | 12.68 | 9.26 | 15.28 | 16.12 |
| time step | live | +5 min | +5 min | +10 min | +10 min | +15 min | +15 min | +15 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michos, D.; Catthoor, F.; Foussekis, D.; Kazantzidis, A. Ultra-Short-Term Wind Power Forecasting in Complex Terrain: A Physics-Based Approach. Energies 2024, 17, 5493. https://doi.org/10.3390/en17215493
Michos D, Catthoor F, Foussekis D, Kazantzidis A. Ultra-Short-Term Wind Power Forecasting in Complex Terrain: A Physics-Based Approach. Energies. 2024; 17(21):5493. https://doi.org/10.3390/en17215493
Chicago/Turabian StyleMichos, Dimitrios, Francky Catthoor, Dimitris Foussekis, and Andreas Kazantzidis. 2024. "Ultra-Short-Term Wind Power Forecasting in Complex Terrain: A Physics-Based Approach" Energies 17, no. 21: 5493. https://doi.org/10.3390/en17215493
APA StyleMichos, D., Catthoor, F., Foussekis, D., & Kazantzidis, A. (2024). Ultra-Short-Term Wind Power Forecasting in Complex Terrain: A Physics-Based Approach. Energies, 17(21), 5493. https://doi.org/10.3390/en17215493







