Analysis of the Impact of Volt/VAR Control on Harmonics Content and Alternative Harmonic Mitigation Methods
Abstract
1. Introduction
- -
- Level of voltage;
- -
- Slow and fast voltage changes, rapid voltage changes;
- -
- Asymmetry of voltage;
- -
- Voltage distortions.
2. Harmonics in the Distribution System Network
2.1. Basics of Harmonics Load Flow
- I group—entities whose devices, installations, and networks are connected directly to networks with a rated voltage higher than 110 kV;
- II group—entities whose devices, installations, and networks are connected directly to the network with a rated voltage of 110 kV;
- III group—entities whose devices, installations, and networks are connected directly to networks with a rated voltage higher than 1 kV but lower than 110 kV;
- IV group—entities whose devices, installations, and networks are connected directly to the network with a rated voltage not higher than 1 kV and a connection power higher than 40 kW or the rated current of the pre-meter protection in the current path higher than 63A;
- V group—entities whose devices, installations, and networks are connected directly to the network with a rated voltage not higher than 1 kV, a connection power not higher than 40 kW, and a rated current of the pre-meter protection not higher than 63A;
- VI group—entities whose devices, installations, and networks are connected to the network through a temporary connection, which will be, under the terms specified in the contract, replaced by a target connection, or entities whose devices, installations, and networks are connected to the network for a specified period, but not longer than a year.
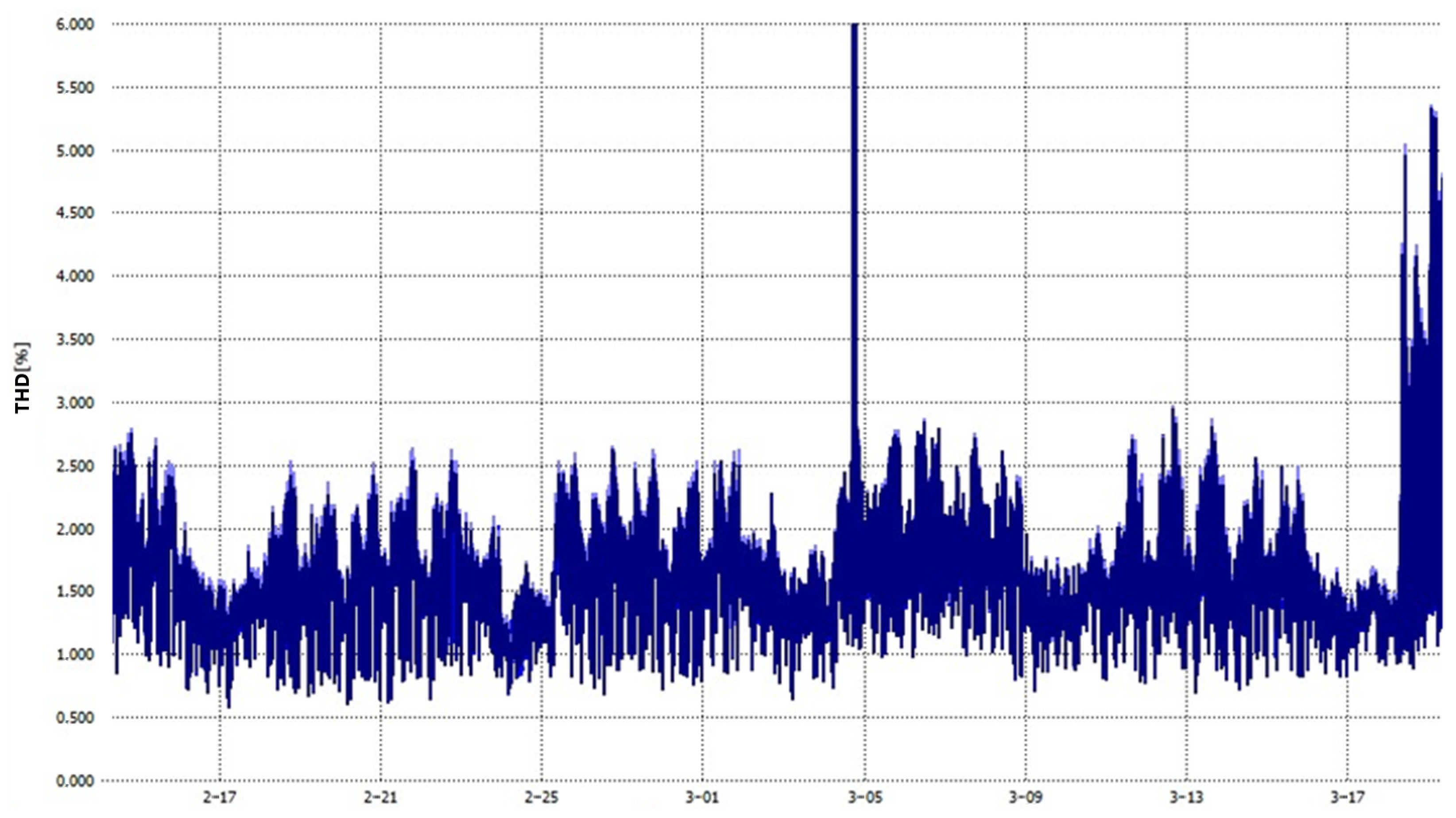
Current Situation in the Distribution System
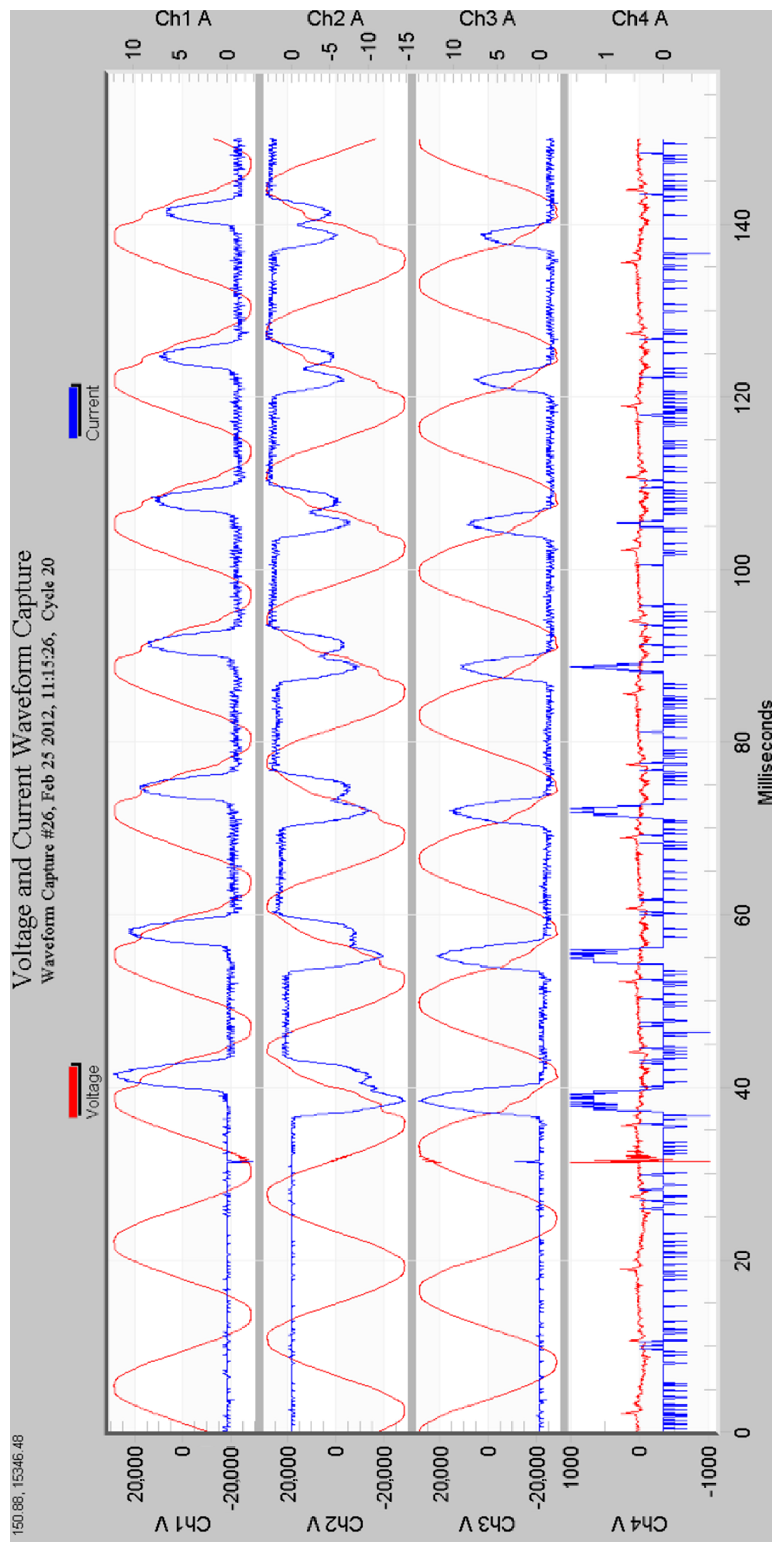
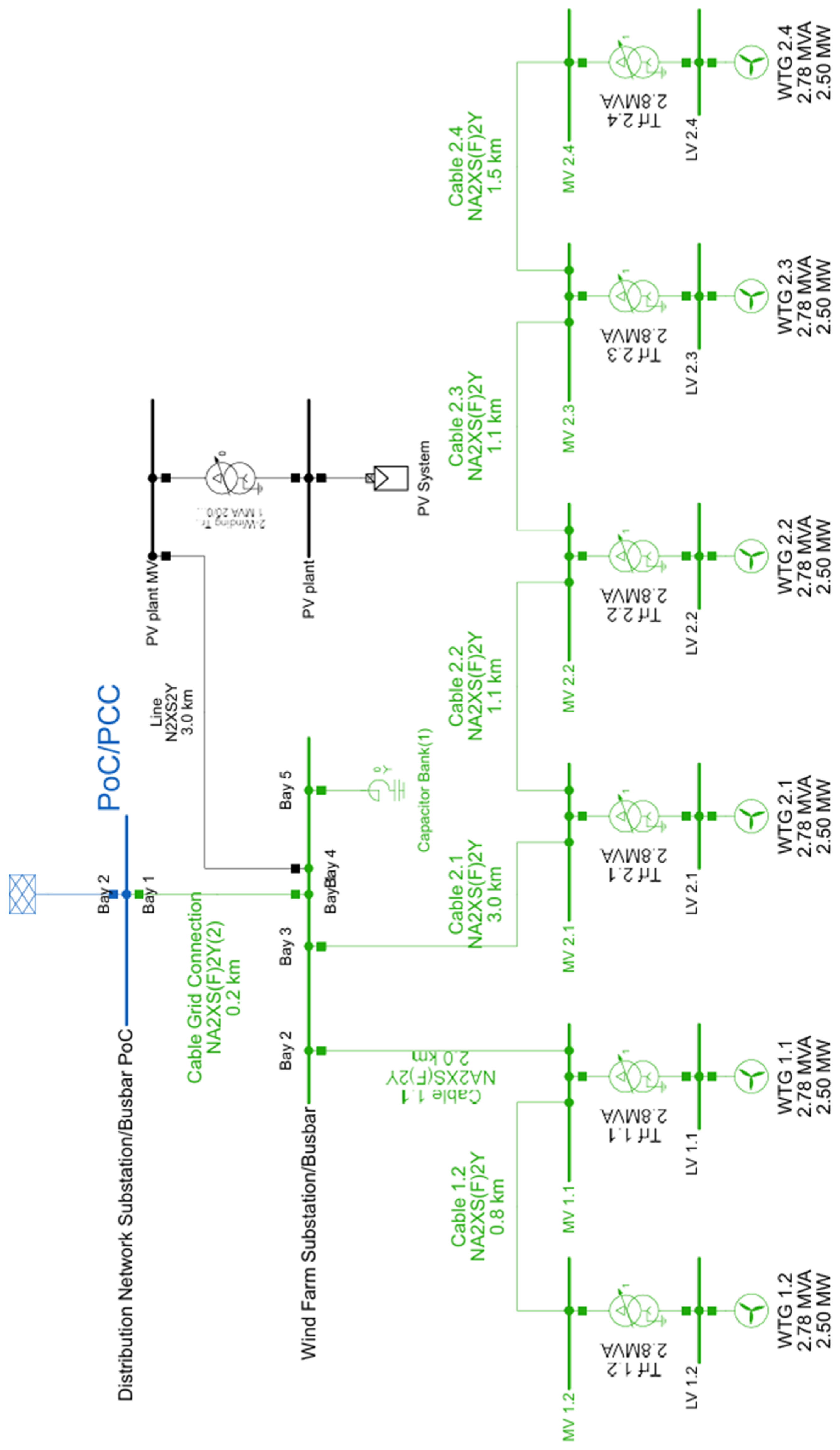
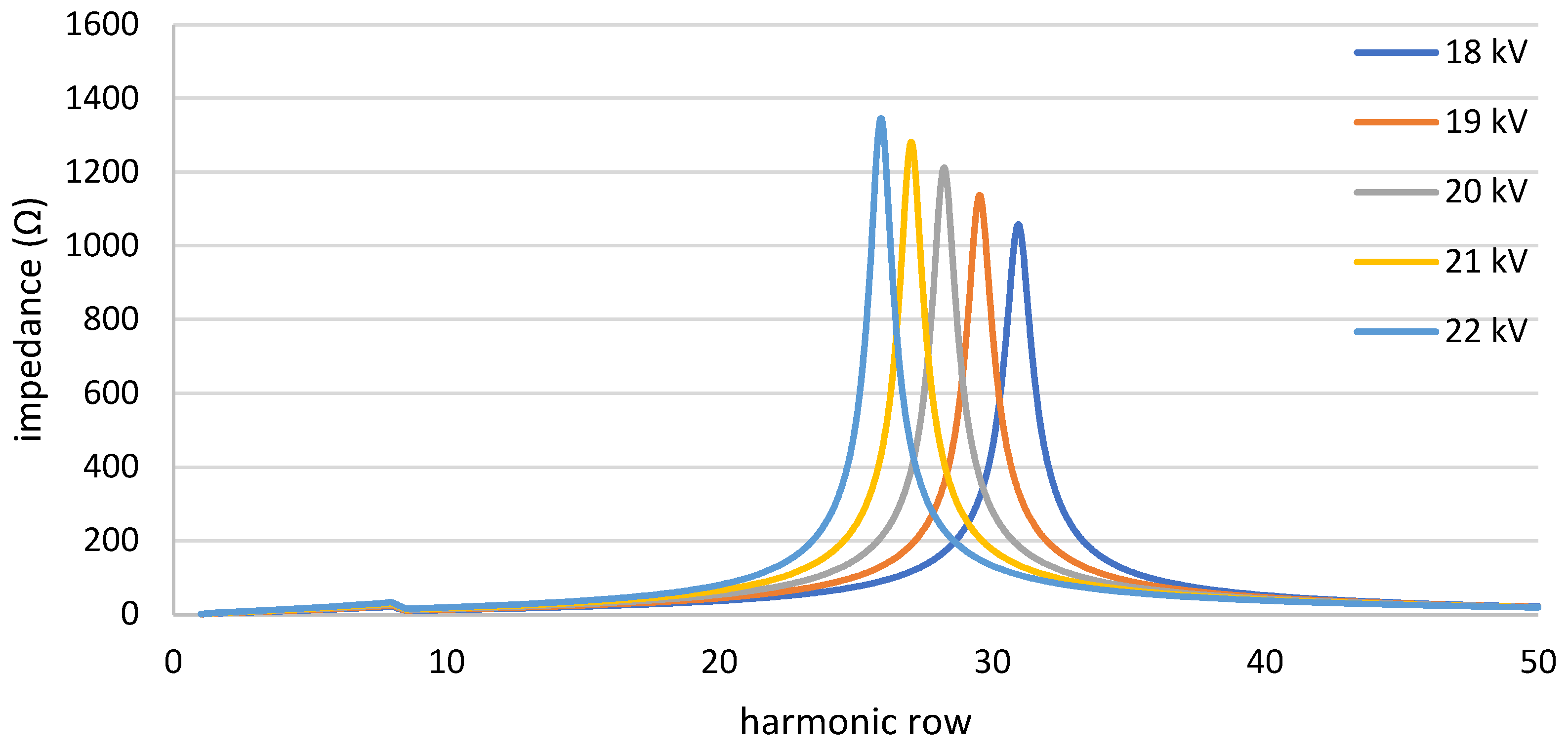
3. Harmonic Analysis—Simulations
4. Harmonic Mitigation—Alternative Methods
- -
- An A-class power quality analyzer, which is characterized by measurement uncertainty equal to 0.1% of the declared input voltage;
- -
- A high-accuracy instrument transformer, e.g., 0.2 class (0.2 amplitude error) [55].
- -
- Different transformers’ phase shifts may be used only in the case of twin PV designs, and it may be difficult to find transformers with different phase shifts in the market;
- -
- The harmonic spectrum of energy sources is one of many parameters e.g., short circuit power, cost, warranty, etc.; therefore, it may not always be possible to find an optimal harmonic spectrum for the location. Moreover, it is often difficult to obtain the harmonic spectrum for analysis;
- -
- Active changing the reactive power to mitigate harmonics is effective in case of high-frequency harmonics; however, in the case of low-frequency resonances, the method requires high reactive power, which could have an impact on voltage level or energy losses. The effectiveness of the proposed method may be different depending on the inverter type; therefore, a special test may be required to confirm that the solution is effective, e.g., the harmonic angle changes as a function of the generated power.
5. Conclusions
- −
- Pointing out the potential problem in the power system—the risk of resonance under various conditions like control actions in the power system and power system extension;
- −
- Providing measurements that show examples of resonances;
- −
- Development of simulation study cases that present the interaction between volt/VAR control and harmonics interactions;
- −
- Recommendations about the need to monitor harmonics in case of volt/VAR regulation;
- −
- Alternative passive and active harmonics mitigation methods are proposed:
- -
- Utilization of transformers with different phase shifts for mitigation of harmonics emitted by twin PV plants and proof of concept measurements are presented;
- -
- Active reactive power regulation is proposed in order to shift harmonics in the resonance band to reduce the risk of serious issues. The general methodology and further research are presented;
- -
- The adaptation of the design to mitigate harmonic issues is presented, e.g., utilization of different line types or sources that are the sources of harmonics outside the potential resonance band.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| R (Ω) | X (Ω) | B (mS) | |
|---|---|---|---|
| Cable Grid Connection | 0.0204 | 0.033 | 23.12 |
| Cable 1.1 | 0.422 | 0.244 | 159.59 |
| Cable 1.2 | 0.168 | 0.098 | 63.92 |
| Cable 2.1 | 0.633 | 0.367 | 239.39 |
| Cable 2.2 | 0.232 | 0.134 | 87.78 |
| Cable 2.3 | 0.232 | 0.134 | 87.78 |
| Cable 2.4 | 0.317 | 0.183 | 119.69 |
| PV 1 km 70 mm2 | 0.446 | 0.137 | 61.57 |
| PV 1.5 km 95 mm2 | 0.501 | 0.196 | 101.79 |
| PV 2.5 km 120 mm2 | 0.641 | 0.317 | 197.07 |
| Wind Turbine Transformer | PV Transformer | |
|---|---|---|
| Voltage | 20/0.69 | 20/0.8 |
| Short circuit voltage | 6% | 6% |
| Cooper losses | 20 kW | 14 kW |
| No load loss | 10 kW | 2.4 kW |
| No load current | 0.8% | 0.15% |
| Harmonic Row | Harmonic Content (%) | Interharmonic Row | Interharmonic Content |
|---|---|---|---|
| 2 | 0.28 | 1.5 | 0.11 |
| 3 | 0.41 | 2.5 | 0.12 |
| 4 | 0.25 | 3.5 | 0.18 |
| 5 | 0.91 | 4.5 | 0.35 |
| 6 | 0.29 | 5.5 | 0.85 |
| 7 | 0.43 | 6.5 | 0.29 |
| 8 | 0.24 | 7.5 | 0.72 |
| 9 | 0.06 | 8.5 | 0.1 |
| 10 | 0.02 | 9.5 | 0.05 |
| 11 | 0.08 | 10.5 | 0.05 |
| 12 | 0.02 | 11.5 | 0.05 |
| 13 | 0.07 | 12.5 | 0.08 |
| 14 | 0.02 | 13.5 | 0.05 |
| 15 | 0.01 | 14.5 | 0.04 |
| 16 | 0.1 | 15.5 | 0.04 |
| 17 | 0.2 | 16.5 | 0. |
| 18 | 0.01 | 17.5 | 0. |
| 19 | 0.1 | 18.5 | 0. |
| 20 | 0.01 | 19.5 | 0. |
| 21 | 0.01 | 20.5 | 0. |
| 22 | 0.01 | 21.5 | 0. |
| 23 | 0.1 | 22.5 | 0. |
| 24 | 0.01 | 23.5 | 0. |
| 25 | 0.05 | 24.5 | 0. |
| 26 | 0.01 | 25.5 | 0. |
| 27 | 0 | 26.5 | 0. |
| 28 | 0 | 27.5 | 0. |
| 29 | 0 | 28.5 | 0. |
| 30 | 0 | 29.5 | 0. |
| 31 | 0 | 30.5 | 0. |
| 32 | 0 | 31.5 | 0. |
| 33 | 0 | 32.5 | 0. |
| 34 | 0 | 33.5 | 0. |
| 35 | 0 | 34.5 | 0. |
| 36 | 0 | 35.4 | 0. |
| 37 | 0 | 36.5 | 0. |
| 38 | 0.02 | 37.5 | 0. |
| 39 | 0.02 | 38.5 | 0.05 |
| 39.5 | 0 |
References
- Miller, P.; Wancerz, M. Praca zrodeł fotowoltaicznych przy zmianach i zanikach napiecia w sieci nn. Rynek Energii 2017, 1, 56–61. [Google Scholar]
- Fantana, N.L.; Lowczowski, K.; Javora, R.; Myrda, P.; Gegot, F.; Brun, P.; Carpenter, J.; Beaudry, J.; Kaiser, N.; Yusa, H.; et al. Substation Servicing and Supervision Using Moblie Devices and Smart Sensing; CIGRE: Paris, France, 2020; ISBN 978-2-85873-528-0. [Google Scholar]
- Musial, E. Ocena jakosci energii elektrycznej w sieciach przemyslowych. Autom. Zaklocenia 2010, 1, 30–45. [Google Scholar]
- Barros, J.; de Apráiz, M.; Diego, R.I. A review of international limits for rapid voltage changes in public distribution networks. Renew. Sustain. Energy Rev. 2021, 144, 110966. [Google Scholar] [CrossRef]
- Lodetti, S.; Azcarate, I.; Gutierrez, J.J.; Leturiondo, L.A.; Redondo, K.; Saiz, P.; Melero, J.J.; Bruna, J. Flicker of Modern Lighting Technologies Due to Rapid Voltage Changes. Energies 2019, 12, 865. [Google Scholar] [CrossRef]
- Kostic, M.; Nikolic, A. Negative Consequence of Motor Voltage Asymmetry and Its Influence to the Unefficient Energy Usage. WSEAS Trans. Circuits Syst. 2010, 9, 547–552. [Google Scholar]
- Mariscotti, A.; Mingotti, A. The Effects of Supraharmonic Distortion in MV and LV AC Grids. Sensors 2024, 24, 2465. [Google Scholar] [CrossRef]
- Grady, M. Understanding Power System Harmonics. IEEE Power Eng. Rev. 2012, 21, 8–11. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A Review of Total Harmonic Distortion Factors for the Measurement of Harmonic and Interharmonic Pollution in Modern Power Systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Pinyol, R. Harmonics: Causes, Effects and Minimization; Salicru: Barcelona, Spain, 2015. [Google Scholar]
- Landis Gyr. Landis+Gyr S650 Smart Grid Terminal A Smart Grid Innovation; Landis Gyr: Zug, Switzerland, 2013. [Google Scholar]
- Tran, Q.-T.; Truong, A.V.; Le, P.M. Reduction of harmonics in grid-connected inverters using variable switching frequency. Int. J. Electr. Power Energy Syst. 2016, 82, 242–251. [Google Scholar] [CrossRef]
- Prodanovic, M.; Green, T. Control of Power Quality in Inverter-Based Distributed Generation. In Proceedings of the 28th Annual Conference of the IEEE Industrial Electronics Society, Sevilla, Spain, 5–8 November 2002; Volume 2, pp. 1185–1189. [Google Scholar] [CrossRef]
- Liu, W.; Chung, I.-Y.; Liu, L.; Leng, S.; Cartes, D.A. Real-time particle swarm optimization based current harmonic cancellation. Eng. Appl. Artif. Intell. 2011, 24, 132–141. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Zhang, S.; Gao, L.; Guo, X.; Chen, L.; Xu, Y. Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics 2023, 12, 3684. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Liu, Z.; Gao, Y.; Leon, J.I.; Vazquez, S.; Wu, L.; Franquelo, L.G. Sliding-Mode Control of Neutral-Point-Clamped Power Converters with Gain Adaptation. In IEEE Transactions on Power Electronics; IEEE: New York, NY, USA, 2024; Volume 39, pp. 9189–9201. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Kalair, A.R.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Jha, K.; Shaik, A.G. A comprehensive review of power quality mitigation in the scenario of solar PV integration into utility grid, e-Prime—Advances in Electrical Engineering. Electron. Energy 2023, 3, 100103. [Google Scholar] [CrossRef]
- Micallef, A. Review of the current challenges and methods to mitigate power quality issues in single-phase microgrids. IET Gener. Transm. Distrib. 2019, 13, 2044–2054. [Google Scholar] [CrossRef]
- Michalec, Ł.; Jasinski, M.; Sikorski, T.; Leonowicz, Z.; Jasinski, L.; Suresh, V. Impact of Harmonic Currents of Nonlinear Loads on Power Quality of a Low Voltage Network–Review and Case Study. Energies 2021, 14, 3665. [Google Scholar] [CrossRef]
- Zagrajek, K.; Paska, J.; Klos, M.; Pawlak, K.; Marchel, P.; Bartecka, M.; Michalski, L.; Terlikowski, P. Impact of Electric Bus Charging on Distribution Substation and Local Grid in Warsaw. Energies 2020, 13, 1210. [Google Scholar] [CrossRef]
- Baraniak, J.; Starzynski, J. Modeling the Impact of Electric Vehicle Charging Systems on Electric Power Quality. Energies 2020, 13, 3951. [Google Scholar] [CrossRef]
- Miller, P.; Wancerz, M. Wpływ sposobu wyznaczania parametrów linii 110 kV na dokładność obliczeń sieciowych. Prz. Elektrotech. 2014, 4, 187–190. [Google Scholar]
- ABB. Technical Guide No. 6 Guide to Harmonics with AC Drives. Available online: https://library.e.abb.com/public/bc35ffb4386c4c039e3a8ec20cef89c5/Technical_guide_No_6_3AFE64292714_RevF_EN.pdf (accessed on 10 September 2024).
- Dziennik Ustaw Rzeczypospolitej Polskiej, Rozporzadzenie Ministra Klimatu I Srodowiska z dnia 22 Marca 2023 r. w Sprawie Szczegolowych Warunkow Funkcjonowania Systemu Elektroenergetycznego. Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20230000819/O/D20230819.pdf (accessed on 10 September 2024).
- Energa Operator. Available online: https://energa-operator.pl/przylaczenie-do-sieci/definicje (accessed on 10 September 2024).
- IEEE. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE: New York, NY, USA, 2014; Volume 519. [Google Scholar]
- Villanueva, I.; Vazquez, N.; Vaquero, J.; Hernandez, C.; Lopez, H.; Osorio, R. L vs. LCL Filter for Photovoltaic Grid-Connected Inverter: A Reliability Study. Int. J. Photoenergy 2020, 2020, 7872916. [Google Scholar] [CrossRef]
- EMC/EMI Filter for PV Inverters. Available online: https://www.schaffner.com/product/FN2200/Schaffner_datasheet_FN2200.pdf (accessed on 10 September 2024).
- Dash, D.K.; Sadhu, P.K. A Review on the Use of Active Power Filter for Grid-Connected Renewable Energy Conversion Systems. Processes 2023, 11, 1467. [Google Scholar] [CrossRef]
- Enea Operator, Instrukcja Ruchu I Eksploatacji Sieci Dytaustrybucyjnej. 2024. Available online: https://www.operator.enea.pl/bricks/instrukcja-ruchu (accessed on 15 August 2024).
- Fiorina, J.N. Inverters and Harmonics (Case Studies of Non-Linear Loads); Cahier Technique Merlin Gerin: Lyon, France, 1993. [Google Scholar]
- Lowczowski, K. Wplyw odksztalcenia napiecia na przepiecia ziemnozwarciowe. Prz. Elektrotech. 2018, 94, 41–44. [Google Scholar] [CrossRef]
- Zheng, R.; Bollen, M. Harmonic Resonances Associated with Wind Farms; Lules University of Technology: Skelleftes, Sweden, 2010. [Google Scholar]
- Rozporządzenie Komisji (UE) 2016/631 z dnia 14 Kwietnia 2016 r. Ustanawiające Kodeks Sieci Dotyczący Wymogów w Zakresie Przyłączenia Jednostek Wytwórczych do Sieci. Available online: https://eur-lex.europa.eu/legal-content/PL/TXT/PDF/?uri=CELEX:32016R0631&from=SK (accessed on 10 September 2024).
- Bollen, M.; Mousavi-Gargari, S.; Bahramirad, S. Harmonic resonances due to transmission-system cables. Renew. Energy Power Qual. J. 2014, 712–716. [Google Scholar] [CrossRef]
- PN-EN 50160:2023-10; Supply Voltage Parameters in Public Power Grids. Polish Committee for Standardization: Warsaw, Poland, 2023.
- Tauron Dystrybucja, Kryteria Techniczne Oceny Możliwości Przyłączenia Jednostek Wytwórczych, Magazynów Energii Oraz OSDn do Sieci Dystrybucyjnej Średniego Napięcia, Krakow. 2014. Available online: https://www.tauron-dystrybucja.pl/przylaczenie-do-sieci/przylaczenie/zrodla-wytworcze (accessed on 15 August 2024).
- Enea Operator, Kryteria Techniczne Oceny Mozliwosci Przylaczenia Jednostek Wytworczych, Magazynow Energii oraz OSDn do Sieci Dystrybucyjnej Sredniego Napiecia ENEA Operator sp. z o.o. August 2023. Available online: https://www.operator.enea.pl/uploads-ev2/Operator/ospolce/raporty/Kryteria%20przy%C5%82%C4%85czania%20obiekt%C3%B3w%20do%20sieci%20SNna%20stronk%C4%99.pdf (accessed on 15 August 2024).
- Available online: https://forum.huawei.com/enterprise/en/Harmonic-spectrum-for-SUN2000-100-KTL-M1-inverter/thread/667249710882242560-667213868771979264 (accessed on 10 September 2024).
- Available online: https://pgeenergetykakolejowa.pl/kolej/1-3-zielona-kolej (accessed on 10 September 2024).
- PLK SA, Standardy Techniczne, Tom IV Urzadzenia Trakcji Elektrycznej/Elektroenergetyki Trakcyjnej. Available online: https://www.plk-sa.pl/files/public/user_upload/pdf/Akty_prawne_i_przepisy/Standardy_techniczne/11.04.2022/3_TOM_IV.pdf (accessed on 10 September 2024).
- Rojek, A. Jakosc Energii Elektrycznej w Kolejowym Systemie Elektroenergetycznym; Z. 137/138; Problemy Kolejnictwa: Warszawa, Polnad, 2003. [Google Scholar]
- Kuznetsov, V.; Hubskyi, P.; Rojek, A.; Udzik, M.; Lowczowski, K. Progress and Challenges Connected with the Integration of Renewable Energy Sources with Railway Distribution Networks. Energies 2024, 17, 489. [Google Scholar] [CrossRef]
- Lowczowski, K.; Nadolny, Z. Voltage Fluctuations and Flicker in Prosumer PV Installation. Energies 2022, 15, 2075. [Google Scholar] [CrossRef]
- Power Monitors. White Paper: Key Issues with DG/DER Monitoring; Power Monitors: Mt Crawford, VA, USA, 2016. [Google Scholar]
- DigSilent. Power Factory User Manual; DigSilent: Gomaringen, Germany, 2023. [Google Scholar]
- Han, G.; Sang, S.; Cai, X. Impedance analysis and stabilization control of the LCL-type wind power inverter under weak grid conditions. J. Renew. Sustain. Energy 2018, 10, 035301. [Google Scholar] [CrossRef]
- Andrieu, C.; Dauphant, E.; Boss, D. A Frequency Dependent Model For a MV/LV Transformer. In Proceedings of the International Conference on Power System Transients, Budapest, Hungary, 20–24 June 1999. [Google Scholar]
- Bula, D.; Grabowski, D.; Maciazek, M. A Review on Optimization of Active Power Filter Placement and Sizing Methods. Energies 2022, 15, 1175. [Google Scholar] [CrossRef]
- Bollen, M.; Yang, K. Harmonics—Another Aspect of the Integration between Wind-Power Installations and the Grid. In Proceedings of the 22nd International Conference on Electricity Distribution, Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Qian, G.; Wang, Q.; He, S.; Dai, W.; Wei, N.; Zhou, N. Harmonic Modeling and Analysis for Parallel 12-Pulse Rectifier under Unbalanced Voltage Condition in Frequency-Domain. Energies 2022, 15, 3946. [Google Scholar] [CrossRef]
- Parmar, J. Understanding Vector Group of Transformer. 2012. Available online: https://electrical-engineering-portal.com/understanding-vector-group-transformer-1 (accessed on 15 August 2024).
- Zainuddin, M.; Putra Surusa, F.E.; Syafaruddin, S.; Manjang, S. Constant Power Factor Mode of Grid-Connected Photovoltaic Inverter for Harmonics Distortion Assessment. Int. J. Renew. Energy Res. 2020, 10, 1525–1535. [Google Scholar] [CrossRef]
- ABB. Instrument Transformers, Technical Information and Application Guide. 2004. Available online: https://library.e.abb.com/public/e2462bd7f816437ac1256f9a007629cf/ITTechInfoAppGuide.pdf (accessed on 15 August 2024).
- CIGRE/CIRED, Guidelines for Power Quality Monitoring WG C4.112 TECHNICAL BROCHURE 596. 2014. Available online: https://www.e-cigre.org/publications/detail/596-cigrecired-guidelines-for-power-quality-monitoring-measurement-locations-processing-and-presentation-of-data.html (accessed on 15 August 2024).
- Lumbreras, D.; Gálvez, E.; Collado, A.; Zaragoza, J. Trends in Power Quality, Harmonic Mitigation and Standards for Light and Heavy Industries: A Review. Energies 2020, 13, 5792. [Google Scholar] [CrossRef]
- Olczykowski, Z.; Starula, P. Power quality in the circuits of traction substation. J. Civ. Eng. Transp. 2023, 5, 29–52. [Google Scholar] [CrossRef]
- Kazem, H.A. Harmonic Mitigation Techniques Applied to Power Distribution Networks. Adv. Power Electron. 2013, 2013, 591680. [Google Scholar] [CrossRef]
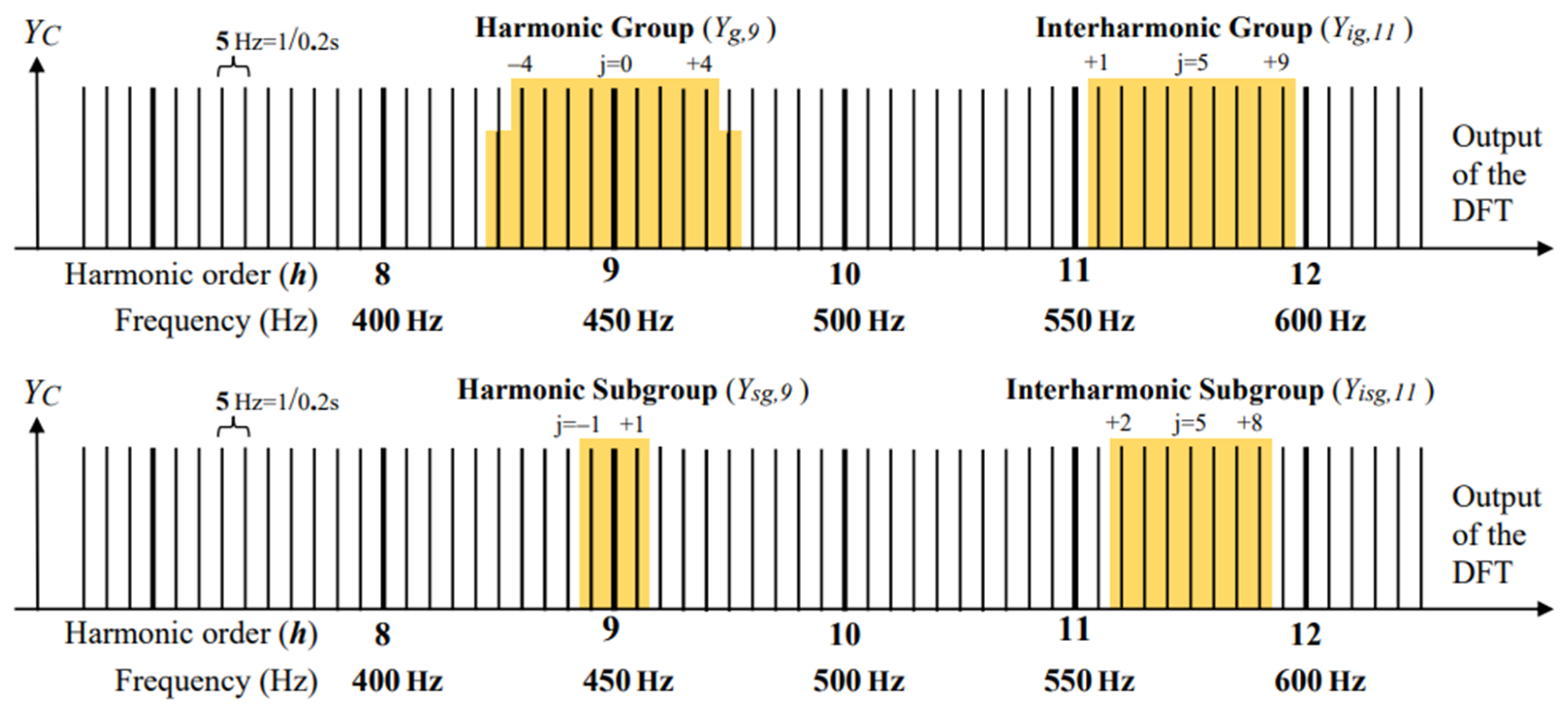
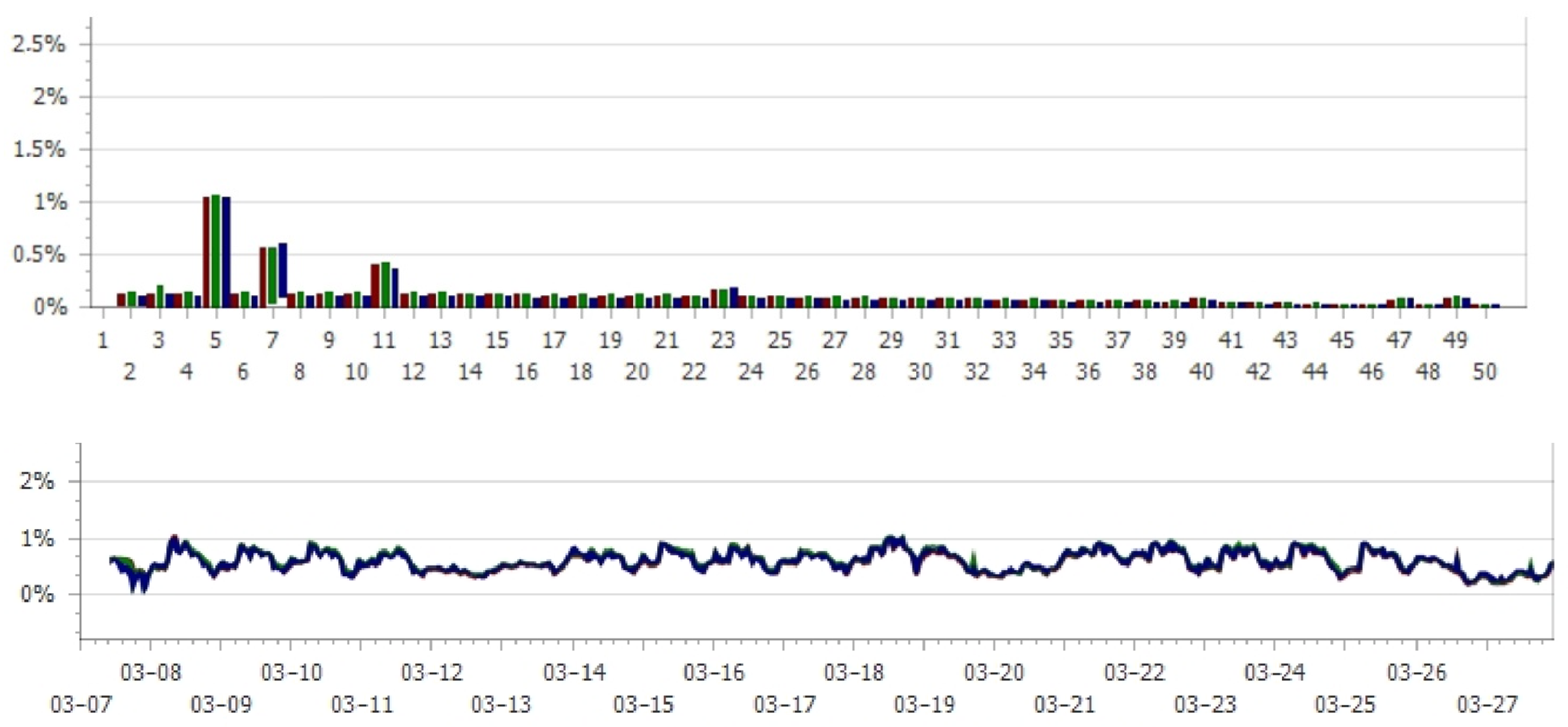
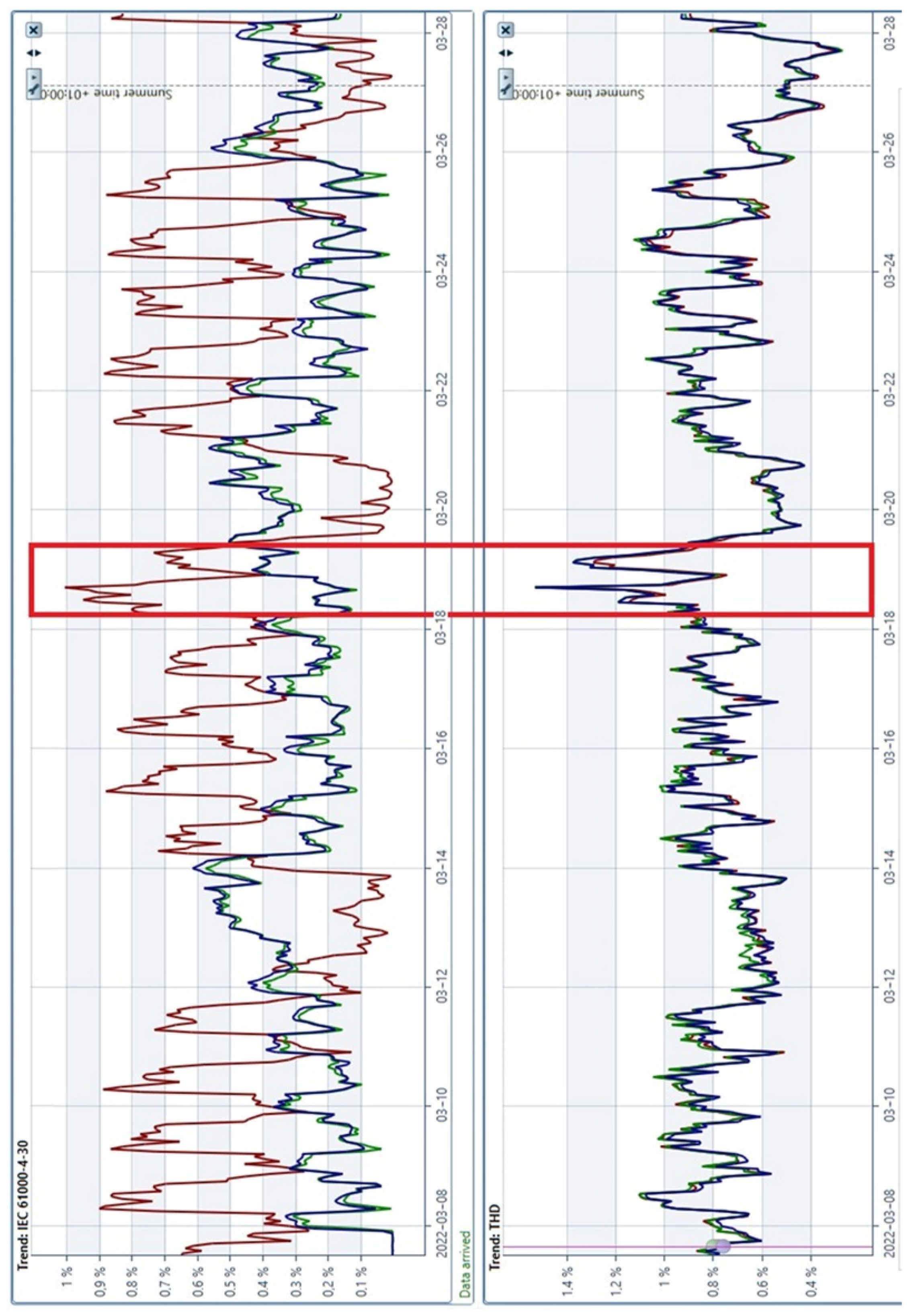
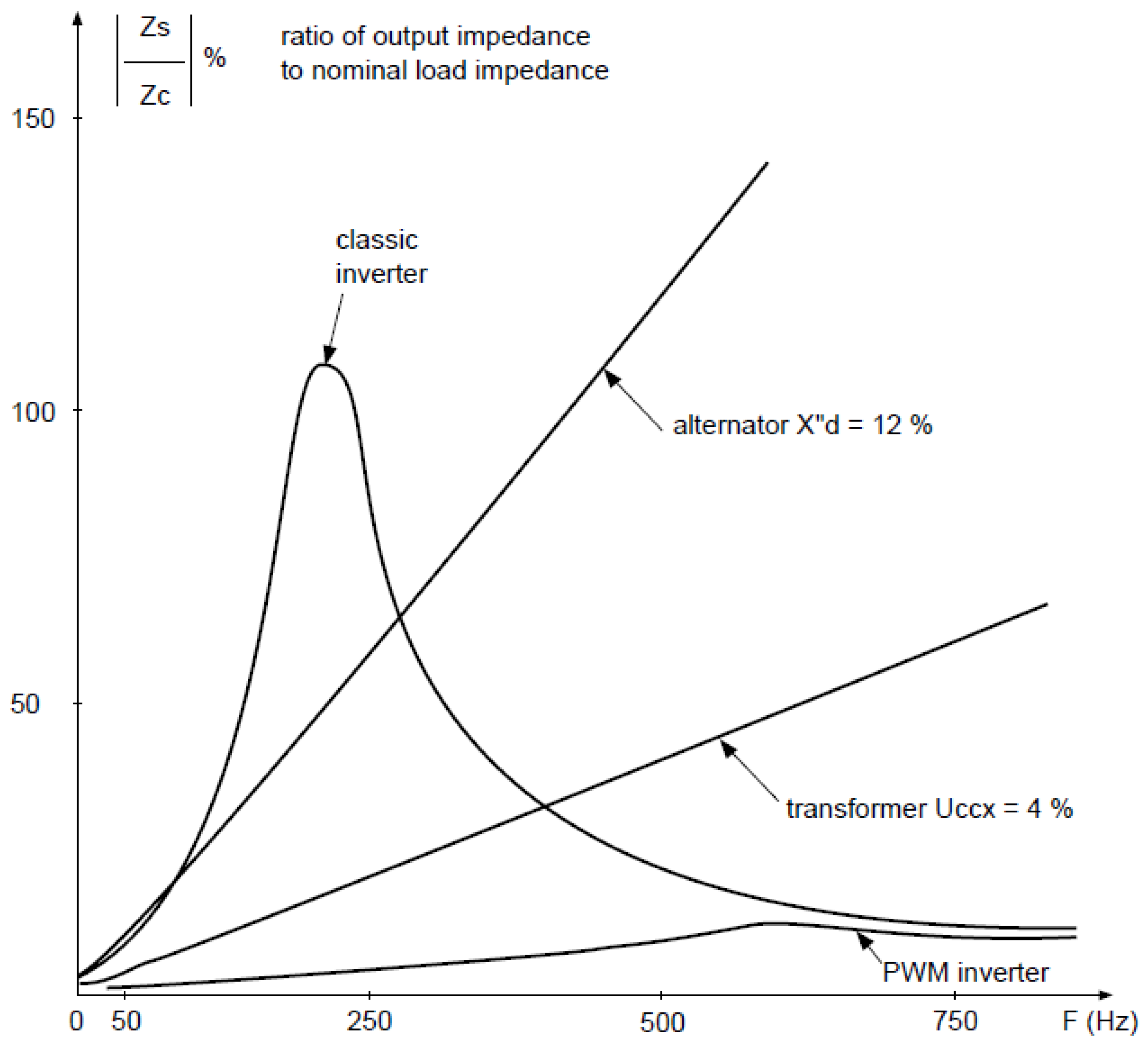
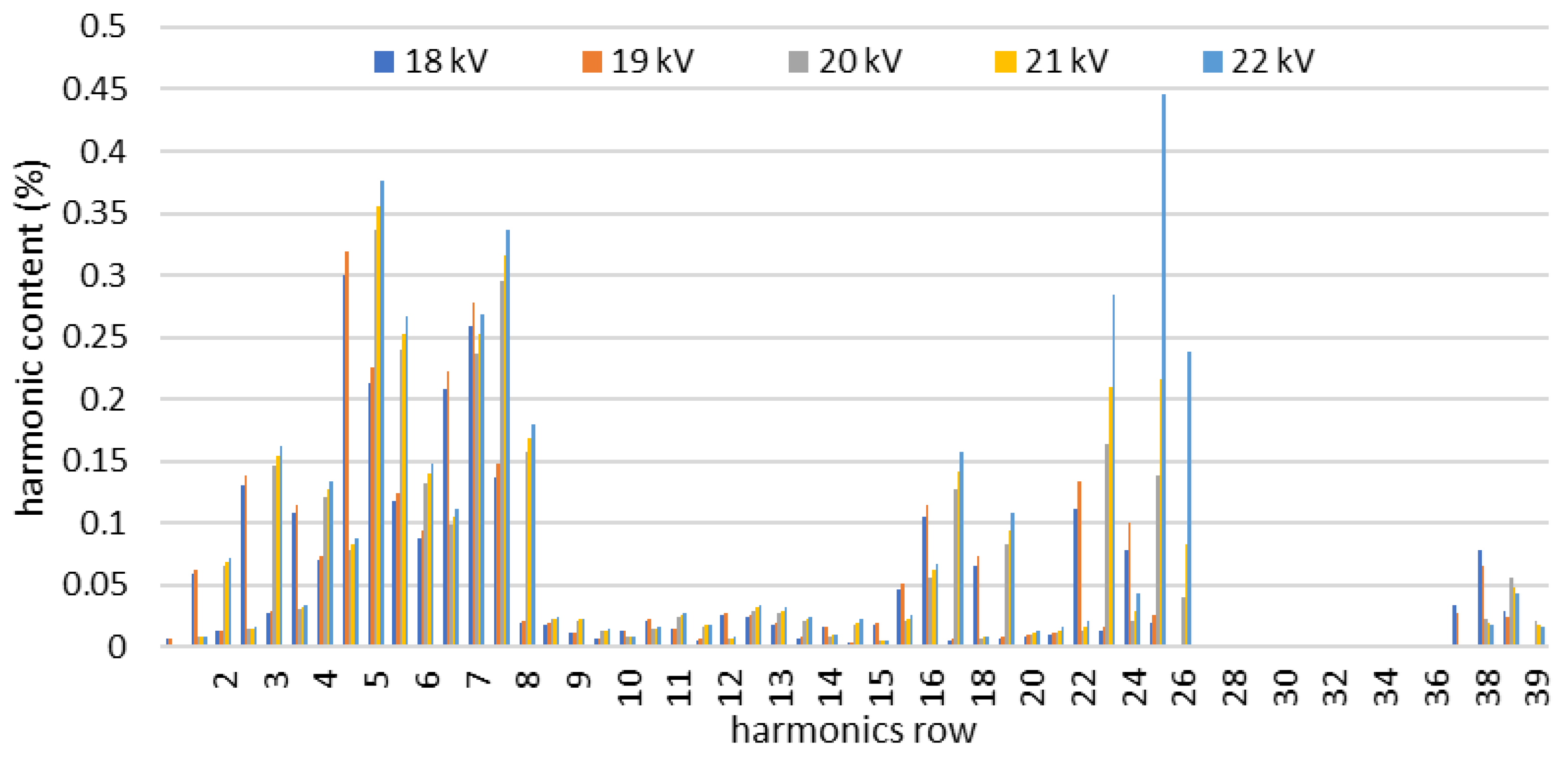
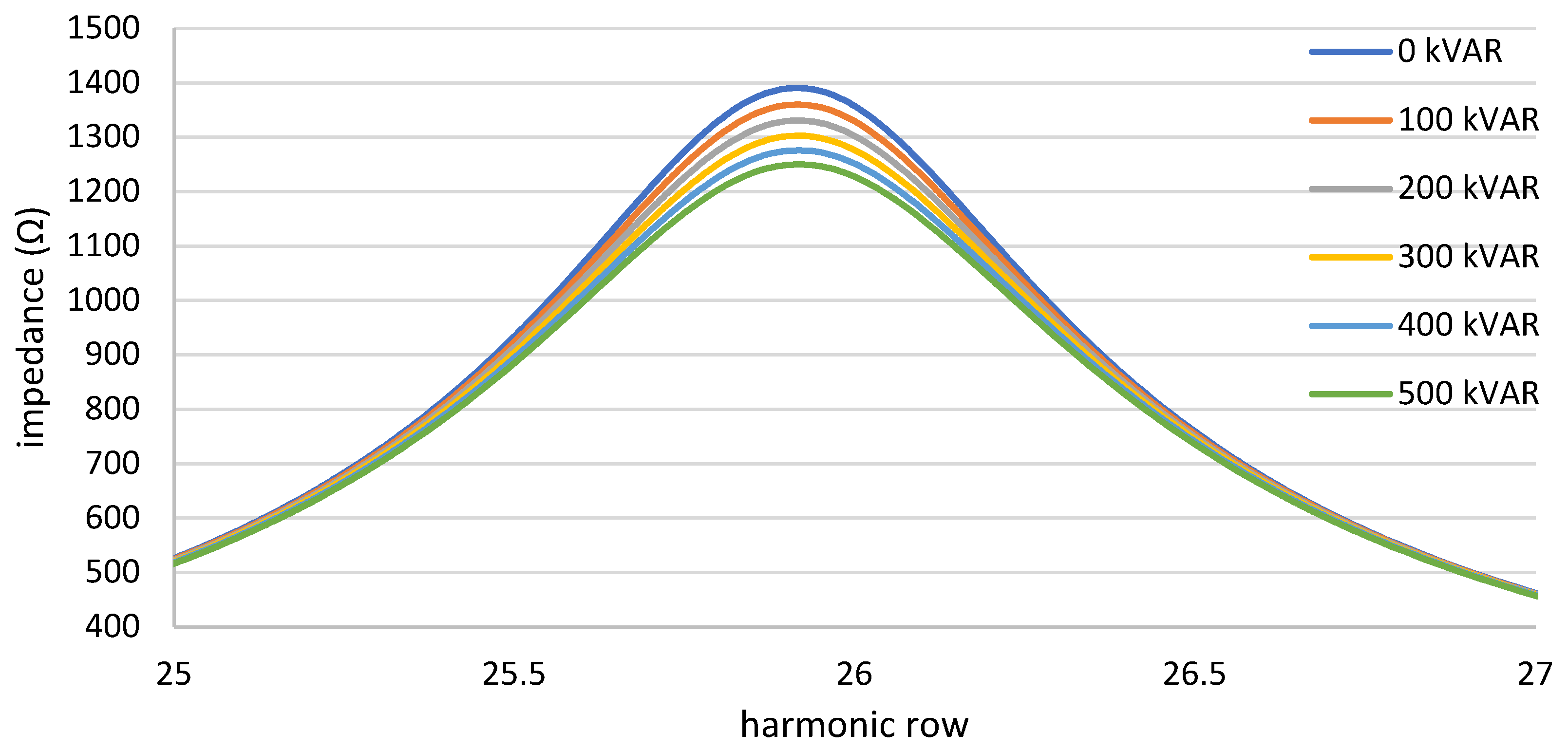

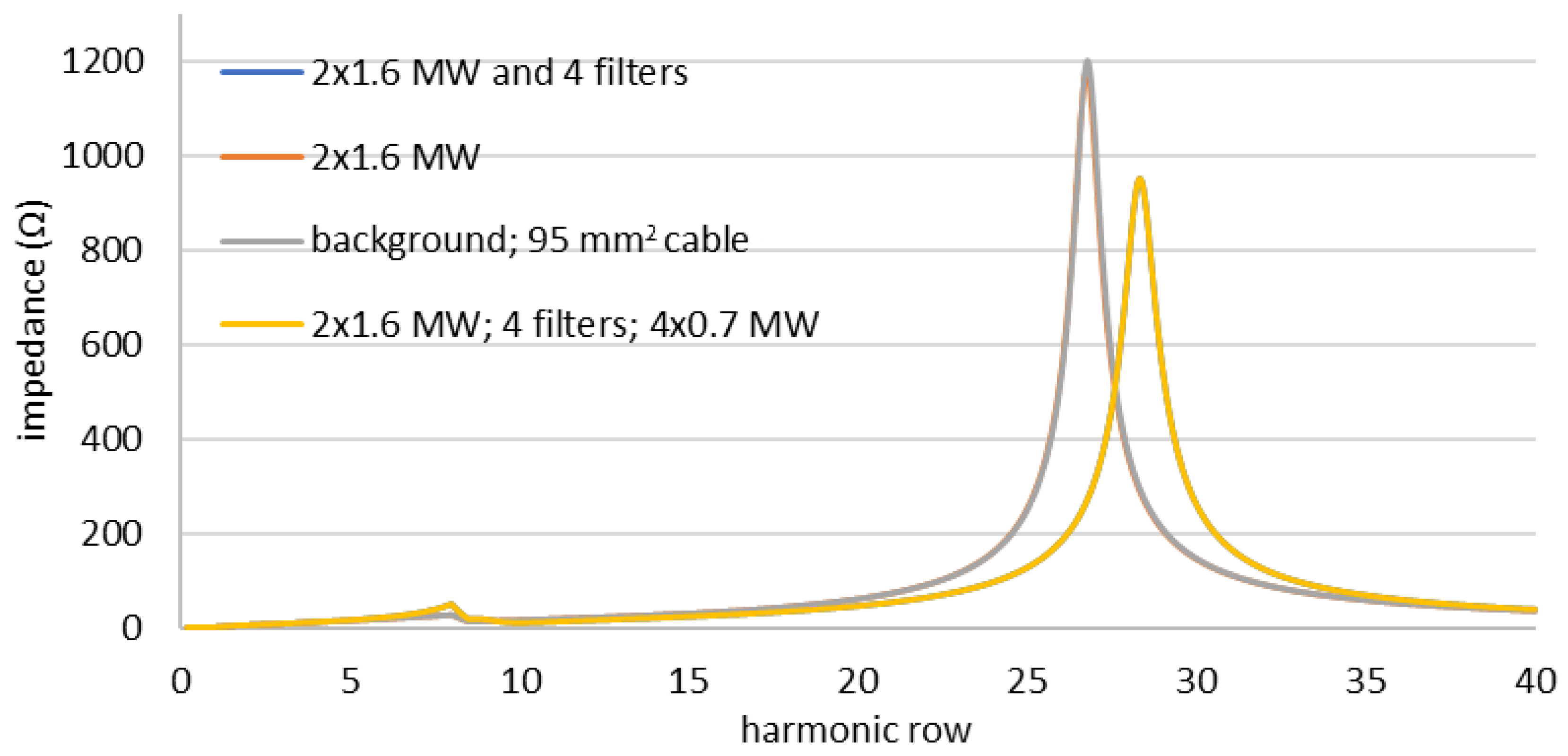

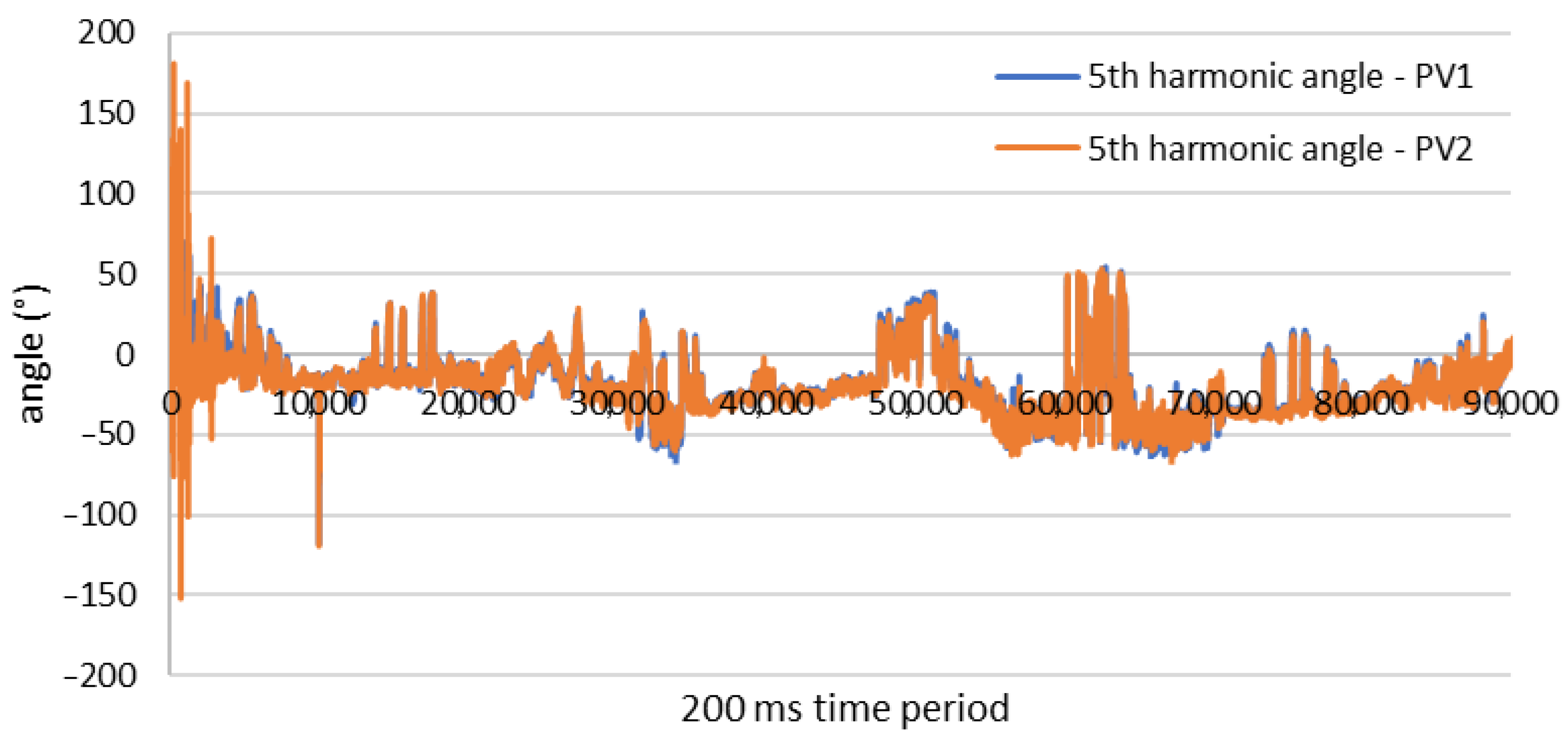
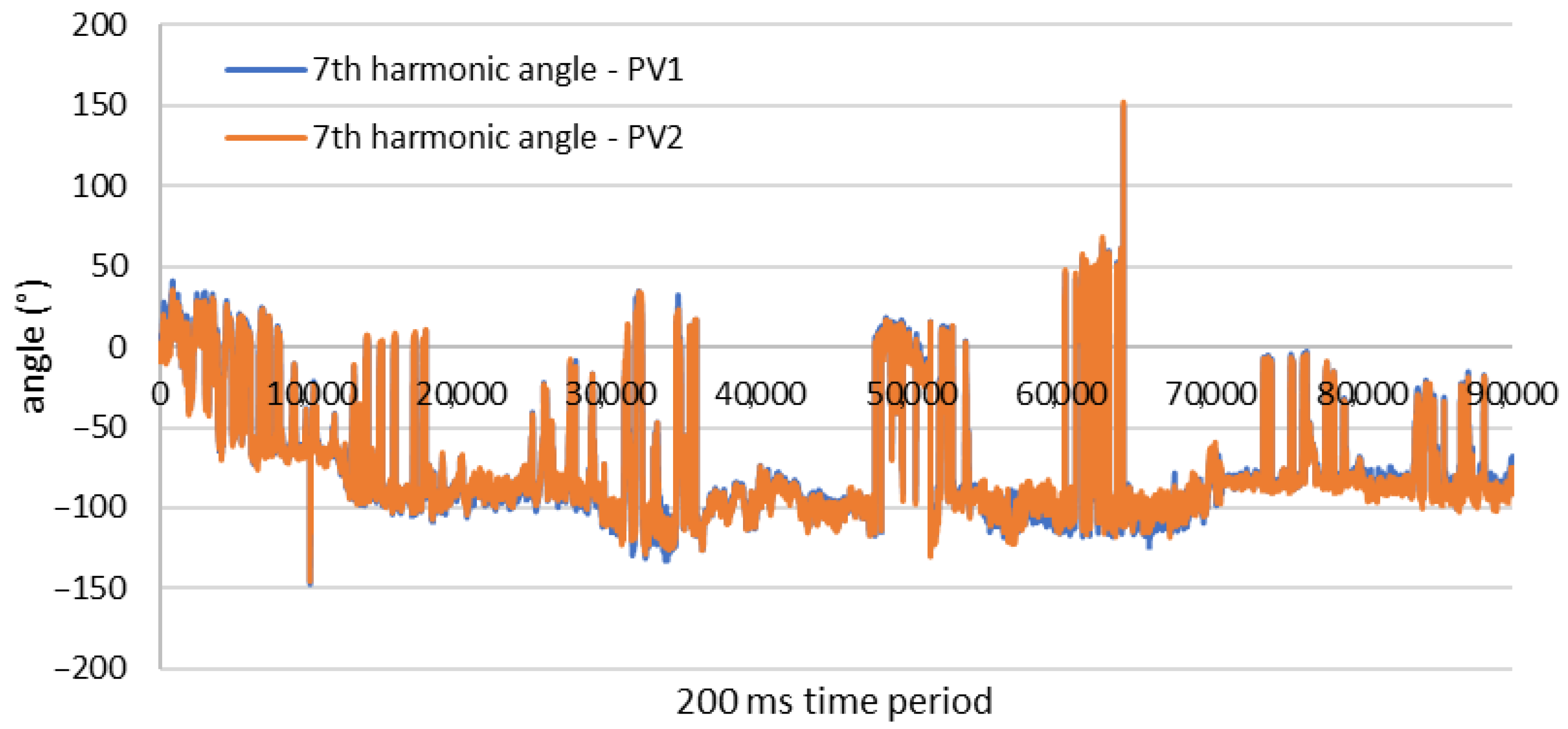
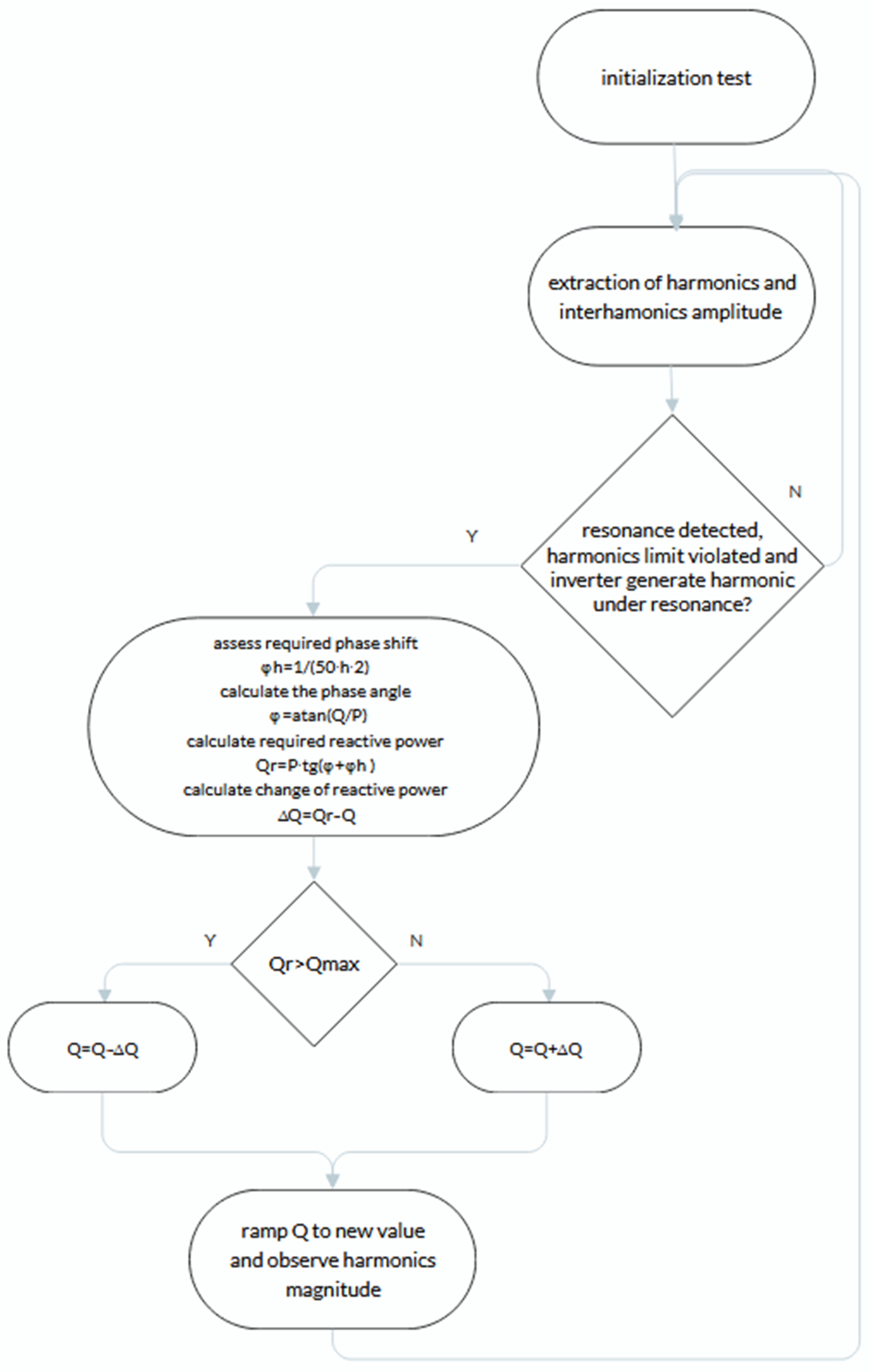

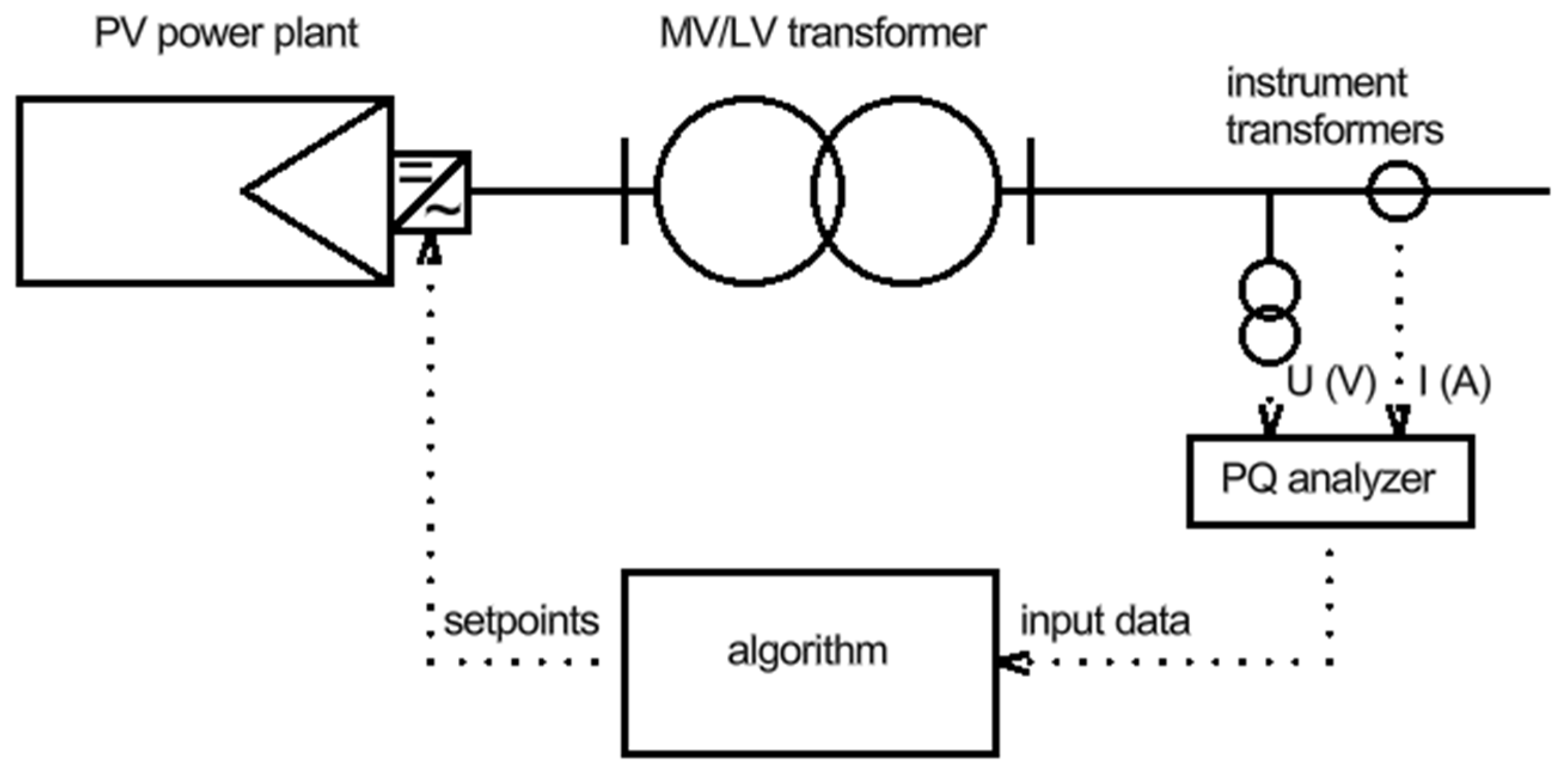
| For I and II Connection Group | |||||
|---|---|---|---|---|---|
| Odd Harmonics | Even Harmonics | ||||
| Not Being a Multiplicity of 3 | Being a Multiplicity of 3 | Harmonic Order | Relative Voltage Value in Percent of the Fundamental Component (uh) | ||
| Harmonic Order | Relative Voltage Value in Percent of the Fundamental Component (uh) | Harmonic Order | Relative Voltage Value in Percent of the Fundamental Component (uh) | ||
| 5 | 2% | 3 | 2% | 2 | 1.5% |
| 7 | 2% | 9 | 1% | 4 | 1% |
| 11 | 1.5% | 15 | 0.5% | >4 | 0.5% |
| 13 | 1.5% | >15 | 0.5% | ||
| 17 | 1% | ||||
| 19 | 1% | ||||
| 23 | 0.7% | ||||
| 25 | 0.7% | ||||
| >25 | 0.2 + 0.5·25/h | ||||
| for III to V connection group | |||||
| 5 | 6% | 3 | 5% | 2 | 2% |
| 7 | 5% | 9 | 1.5% | 4 | 1% |
| 11 | 3.5% | 15 | 0.5% | >4 | 0.5% |
| 13 | 3% | >15 | 0.5% | ||
| 17 | 2% | ||||
| 19 | 1.5% | ||||
| 23 | 1.5% | ||||
| 25 | 1.5% | ||||
| >25 | 0.5 + 25/h | ||||
| Harmonic Row | Current Magnitude [A] | % Of Fundamental | ||||
|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L1 | L2 | L3 | |
| 1 | 134,856 | 134,736 | 134,840 | 100,940 | 100,851 | 100,928 |
| 2 | 0.252 | 0.139 | 0.299 | 0.187 | 0.103 | 0.221 |
| 3 | 0.380 | 0.209 | 0.215 | 0.282 | 0.155 | 0.159 |
| 4 | 0.107 | 0.200 | 0.095 | 0.079 | 0.148 | 0.071 |
| 5 | 0.278 | 0.226 | 0.239 | 0.206 | 0.168 | 0.177 |
| 6 | 0.076 | 0.066 | 0.044 | 0.056 | 0.049 | 0.033 |
| 7 | 0.070 | 0.096 | 0.083 | 0.052 | 0.072 | 0.062 |
| 8 | 0.047 | 0.036 | 0.061 | 0.035 | 0.027 | 0.046 |
| 9 | 0.122 | 0.039 | 0.100 | 0.091 | 0.029 | 0.074 |
| 10 | 0.040 | 0.061 | 0.071 | 0.030 | 0.045 | 0.052 |
| 11 | 0.224 | 0.167 | 0.175 | 0.166 | 0.124 | 0.130 |
| 12 | 0.075 | 0.055 | 0.044 | 0.055 | 0.041 | 0.033 |
| 13 | 0.261 | 0.245 | 0.286 | 0.193 | 0.182 | 0.212 |
| 14 | 0.042 | 0.038 | 0.058 | 0.031 | 0.028 | 0.043 |
| 15 | 0.053 | 0.102 | 0.079 | 0.039 | 0.076 | 0.059 |
| 16 | 0.043 | 0.065 | 0.073 | 0.032 | 0.048 | 0.054 |
| 17 | 0.235 | 0.170 | 0.197 | 0.175 | 0.126 | 0.146 |
| 18 | 0.107 | 0.066 | 0.053 | 0.079 | 0.049 | 0.039 |
| 19 | 0.281 | 0.242 | 0.229 | 0.208 | 0.180 | 0.170 |
| Passive Filters | Active Filters | Inverters’ Built-in Algorithms | Proposed Solution | |
|---|---|---|---|---|
| Cost | Big | Big | No extra cost | No extra cost |
| Experience | Big | Big | Depending on the solution | Low |
| Analysis required | Project needed | Sizing of device and limitations of sizes | No extra project | No extra project |
| Individual harmonics limitation | Harmonics designed to be damped | Yes, the full spectrum of problematic harmonics | Depending on the construction | Yes, but only the resonance band |
| THD reduction | Yes if sized properly | Yes | Yes | Yes, under resonance conditions |
| Losses | Extra losses | Extra losses | Switching losses could increase | Change of reactive power could have an impact on losses however in general the impact is minimal |
| Impact of power system reconfiguration | Big impact | No, until power limitations are met | Yes, could be reduced if adaptive algorithms are used | Effectiveness could drop in case of multi resonance point |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowczowski, K.; Gielniak, J.; Nadolny, Z.; Udzik, M. Analysis of the Impact of Volt/VAR Control on Harmonics Content and Alternative Harmonic Mitigation Methods. Energies 2024, 17, 5561. https://doi.org/10.3390/en17225561
Lowczowski K, Gielniak J, Nadolny Z, Udzik M. Analysis of the Impact of Volt/VAR Control on Harmonics Content and Alternative Harmonic Mitigation Methods. Energies. 2024; 17(22):5561. https://doi.org/10.3390/en17225561
Chicago/Turabian StyleLowczowski, Krzysztof, Jaroslaw Gielniak, Zbigniew Nadolny, and Magdalena Udzik. 2024. "Analysis of the Impact of Volt/VAR Control on Harmonics Content and Alternative Harmonic Mitigation Methods" Energies 17, no. 22: 5561. https://doi.org/10.3390/en17225561
APA StyleLowczowski, K., Gielniak, J., Nadolny, Z., & Udzik, M. (2024). Analysis of the Impact of Volt/VAR Control on Harmonics Content and Alternative Harmonic Mitigation Methods. Energies, 17(22), 5561. https://doi.org/10.3390/en17225561










