Research on Heat Transfer Characteristics of Plate Evaporators for Cold Storage
Abstract
:1. Introduction
2. Establishment of Heat Transfer Model for Evaporator
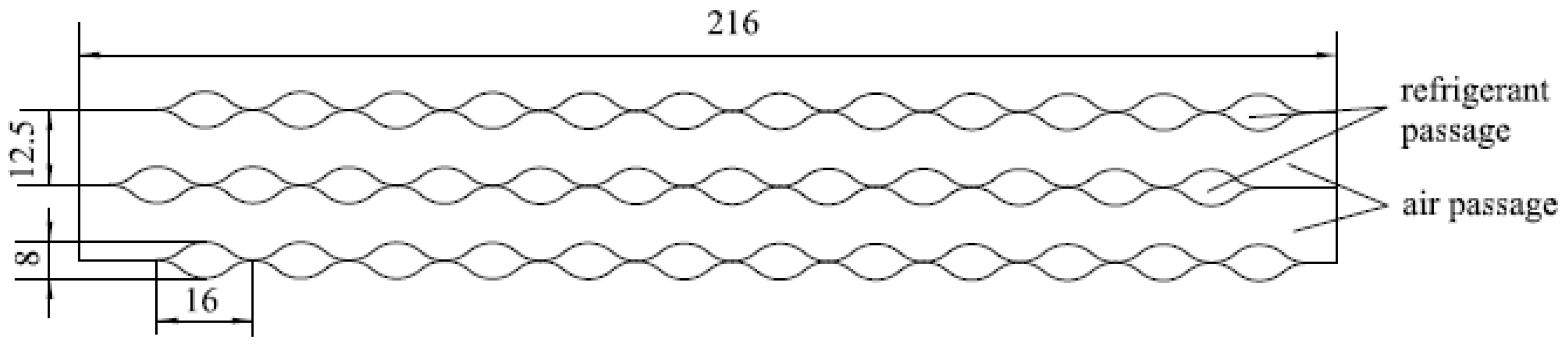
2.1. Physical Model
2.2. Mathematical Models
2.2.1. Refrigerant Domain
2.2.2. Air Domain
2.2.3. Solid Domain
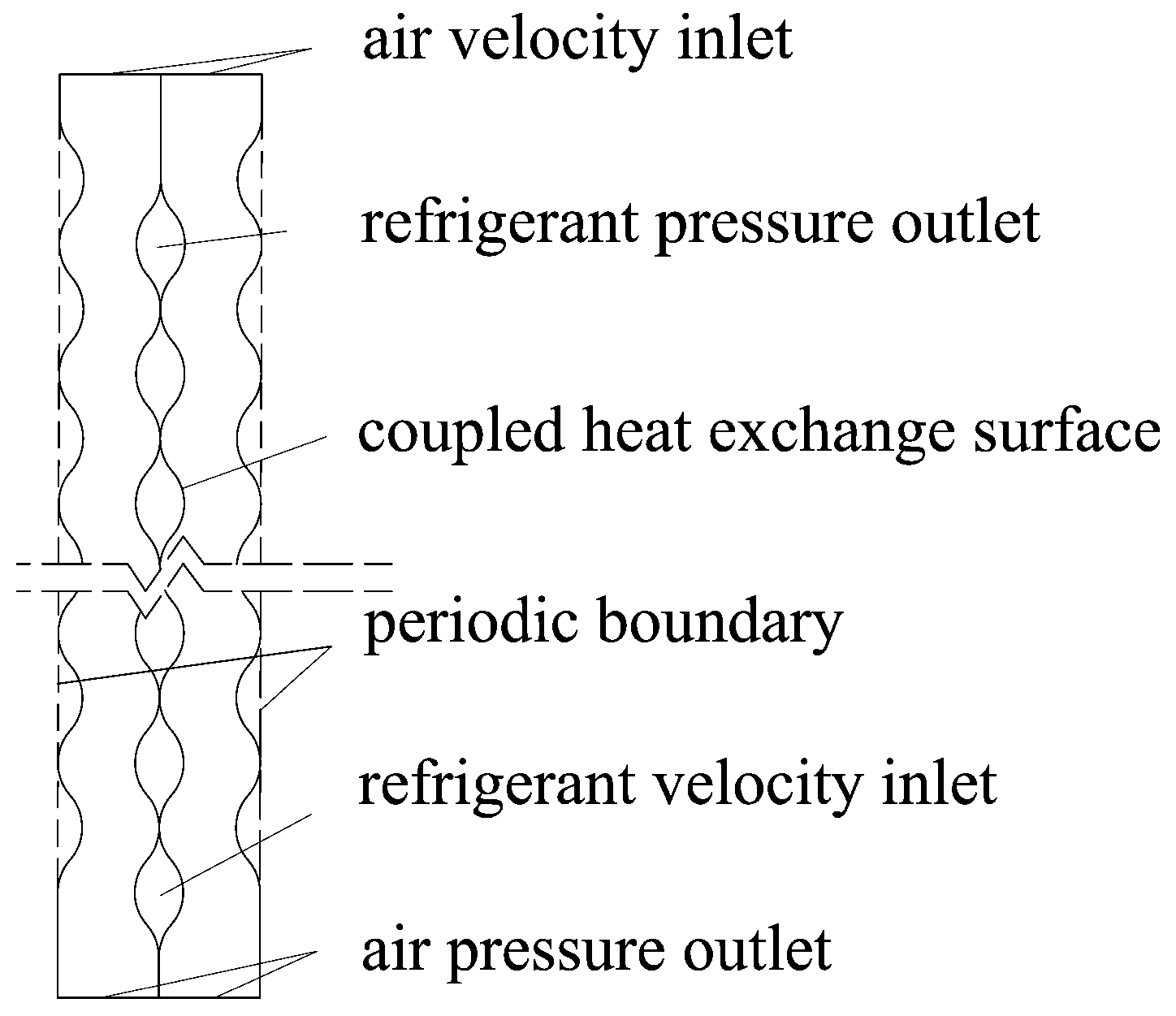
2.3. Boundary Conditions
3. Numerical Simulation Results and Analysis
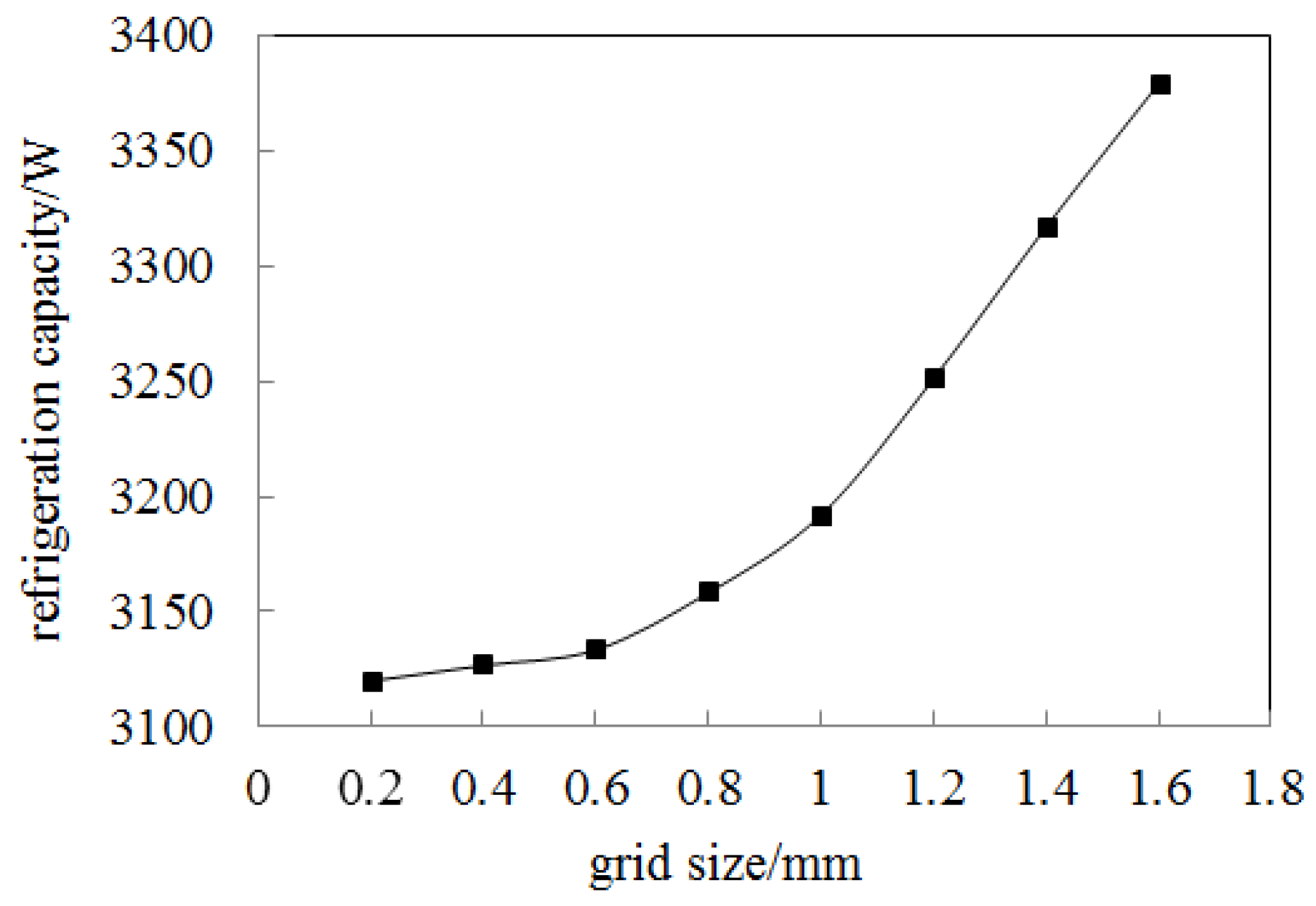
3.1. Grid Independence Verification
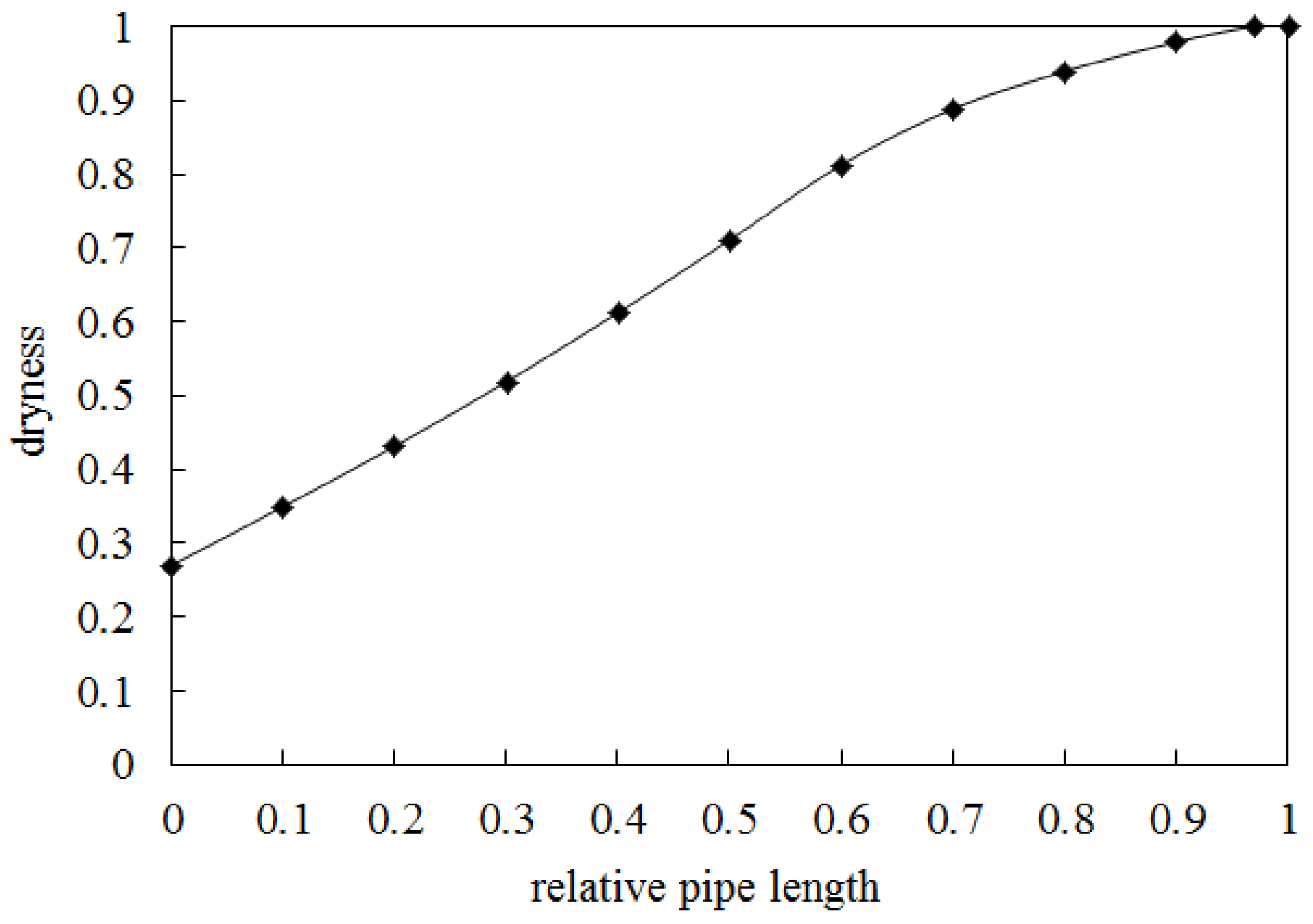
3.2. Calculation Results
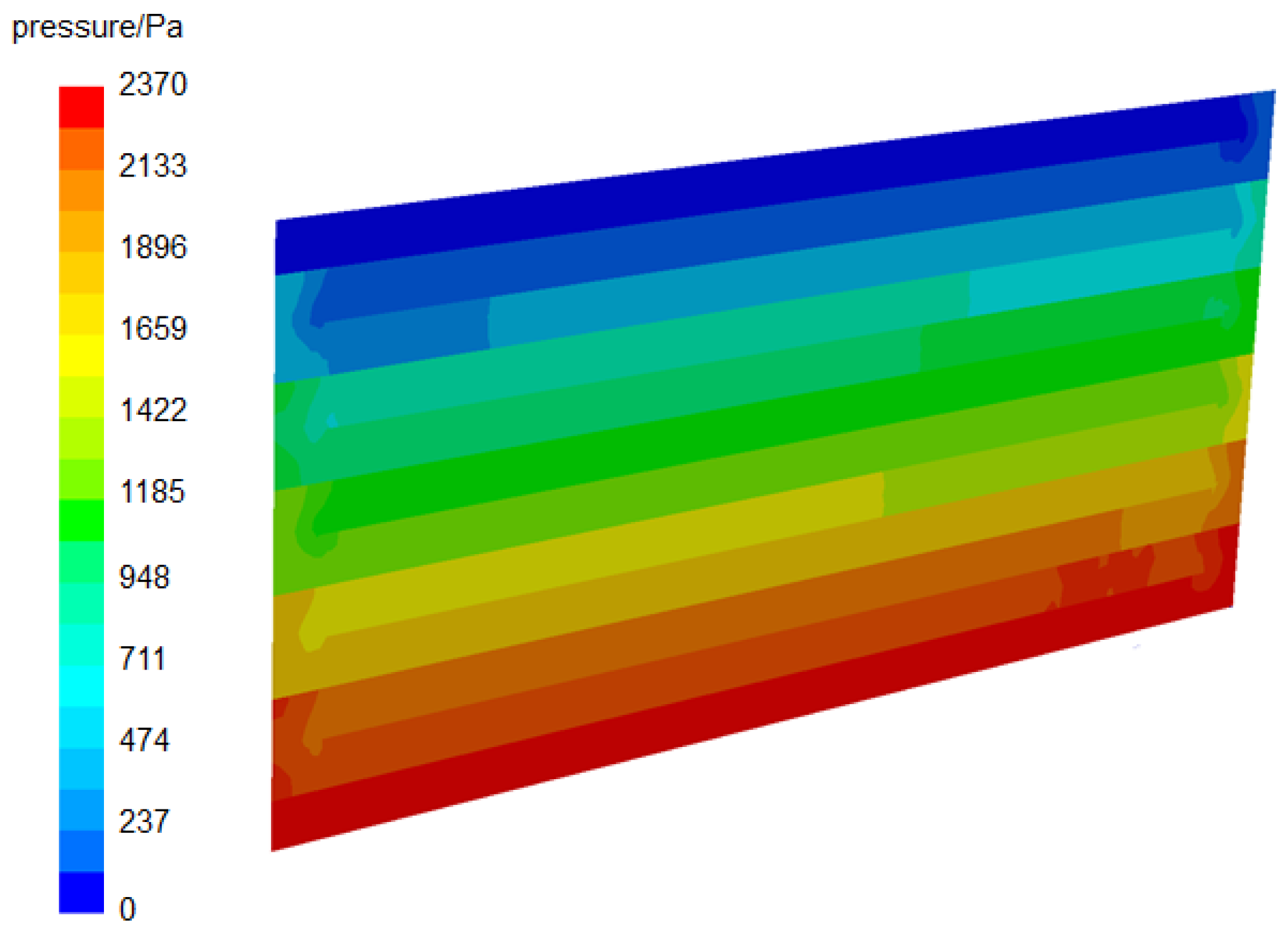
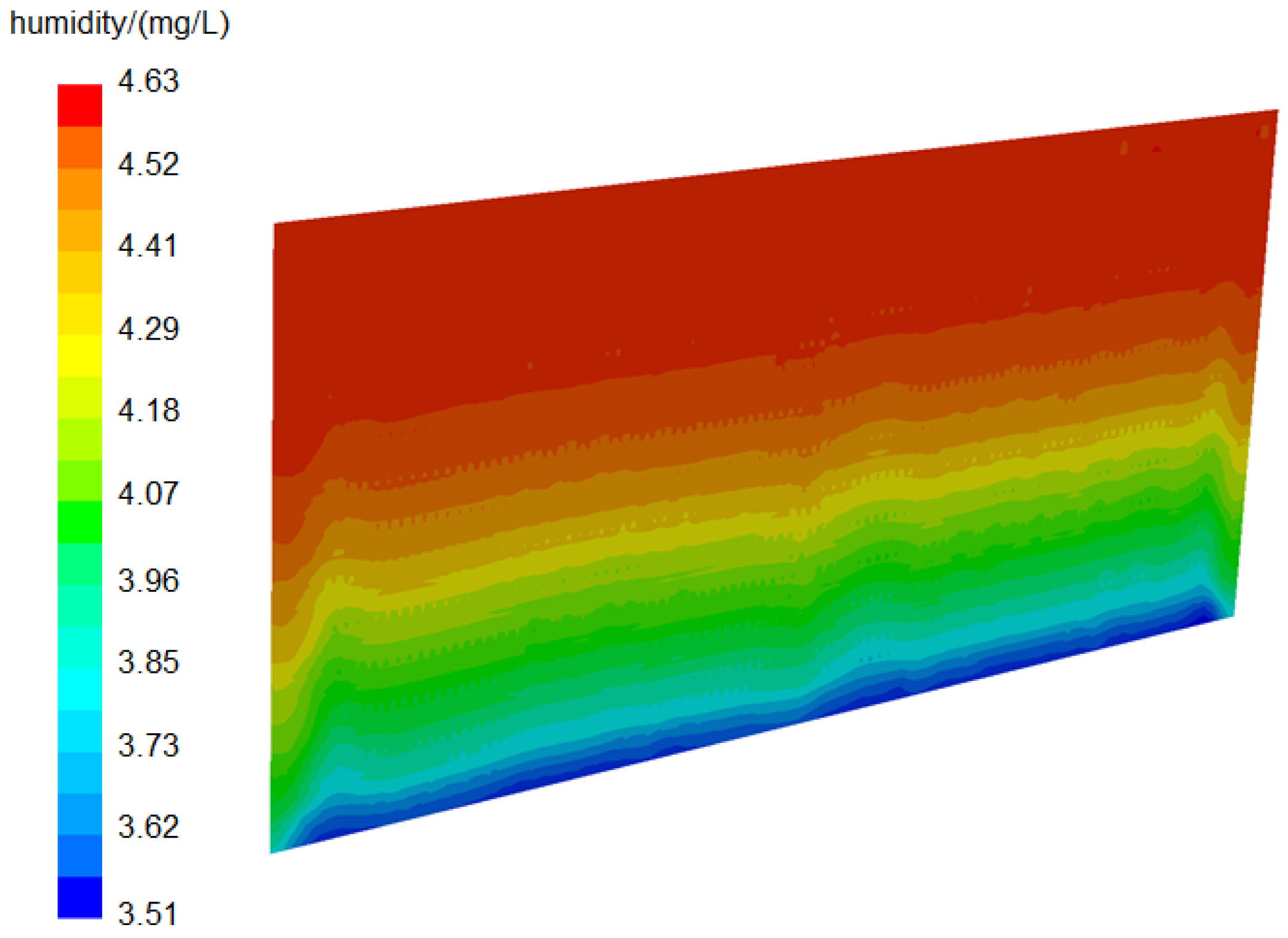
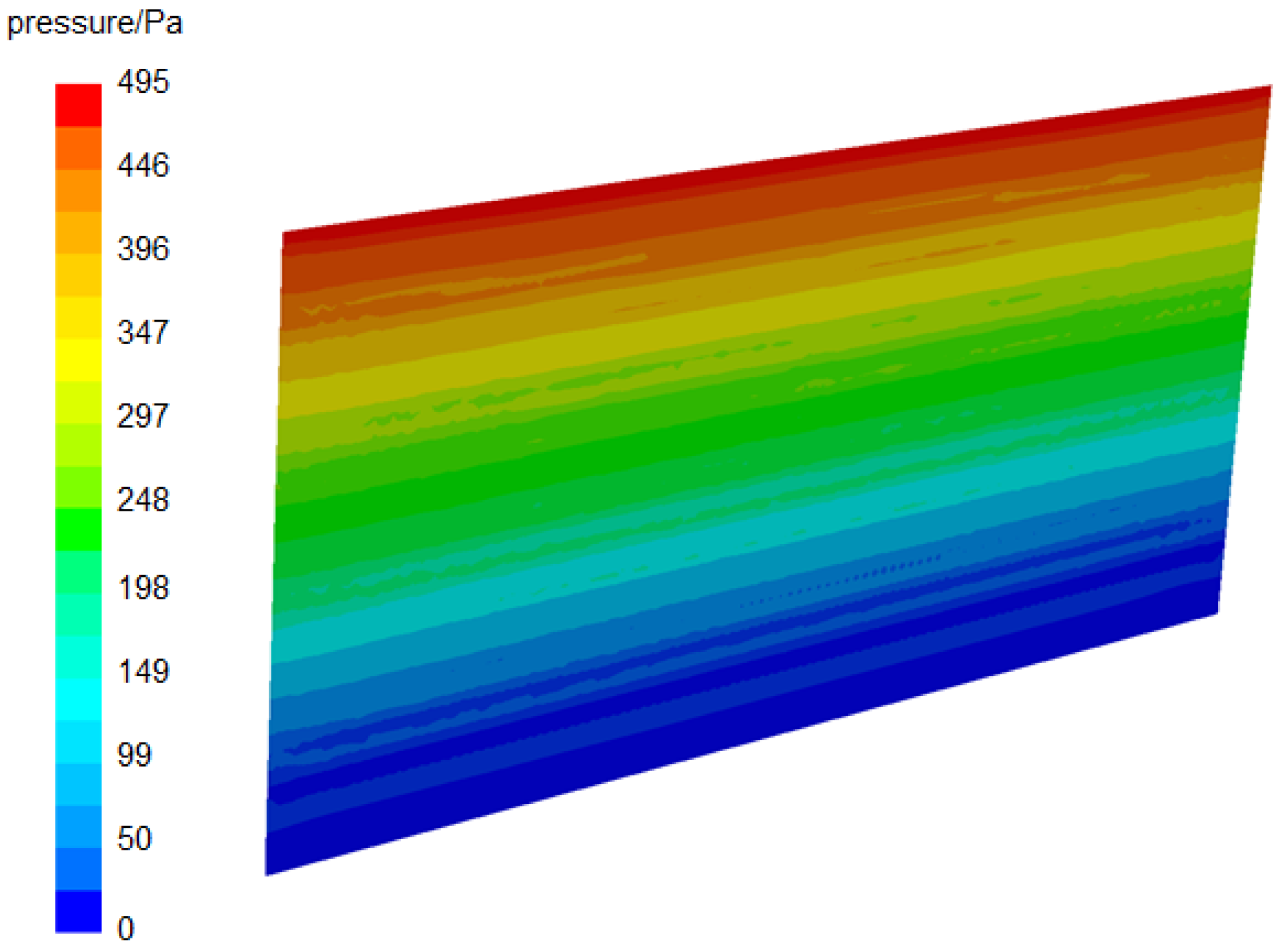
3.3. Analysis of Heat Transfer and Pressure Drop Characteristics
4. Experimental Study on Plate Evaporator
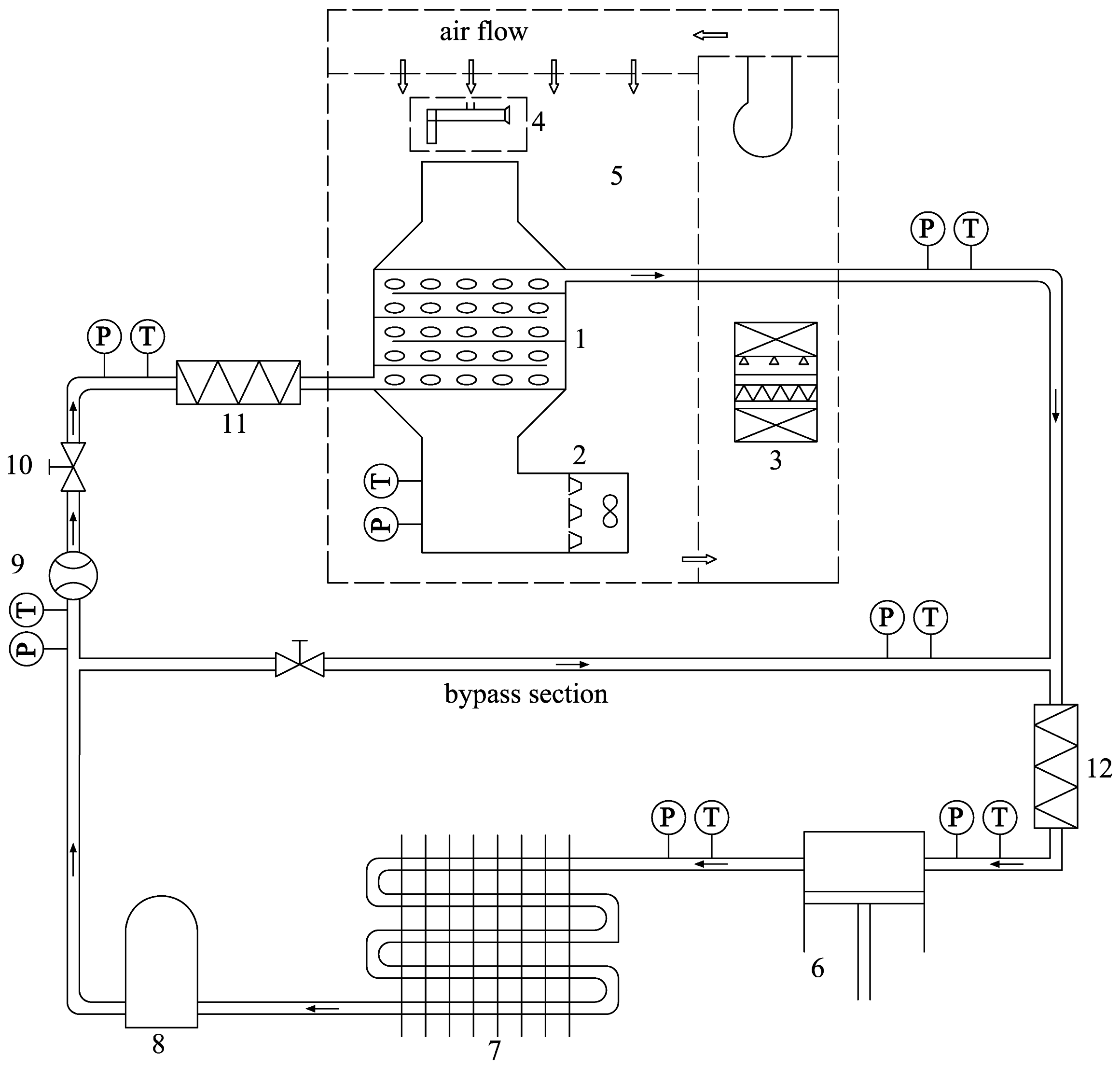
4.1. Experimental System
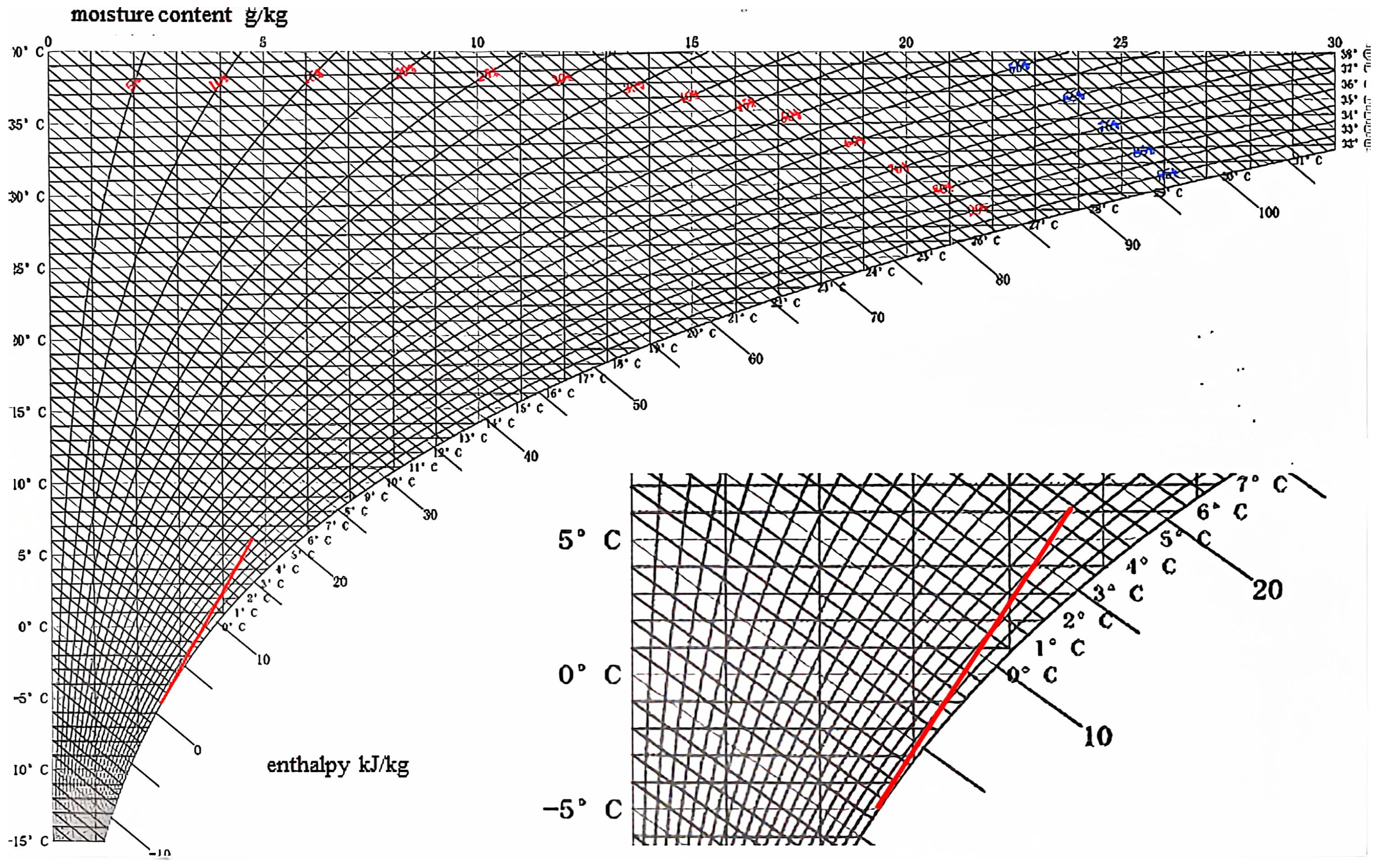
4.2. Uncertainty Analysis
4.3. Test Results and Analysis
5. Conclusions
- The design working condition is that the inlet dryness of refrigerant R22 is 0.27, the temperature is −5 °C, the pressure is the saturation pressure at this temperature, the mass flow rate is 0.0187 kg/s, the air inlet temperature is 6 °C, the relative humidity is 80%, and the flow rate is 3 m/s. The new plate evaporator has a cooling capacity of 3.13 kW, a refrigerant side pressure drop of 1.36 kPa, and an air side pressure drop of 495 Pa.
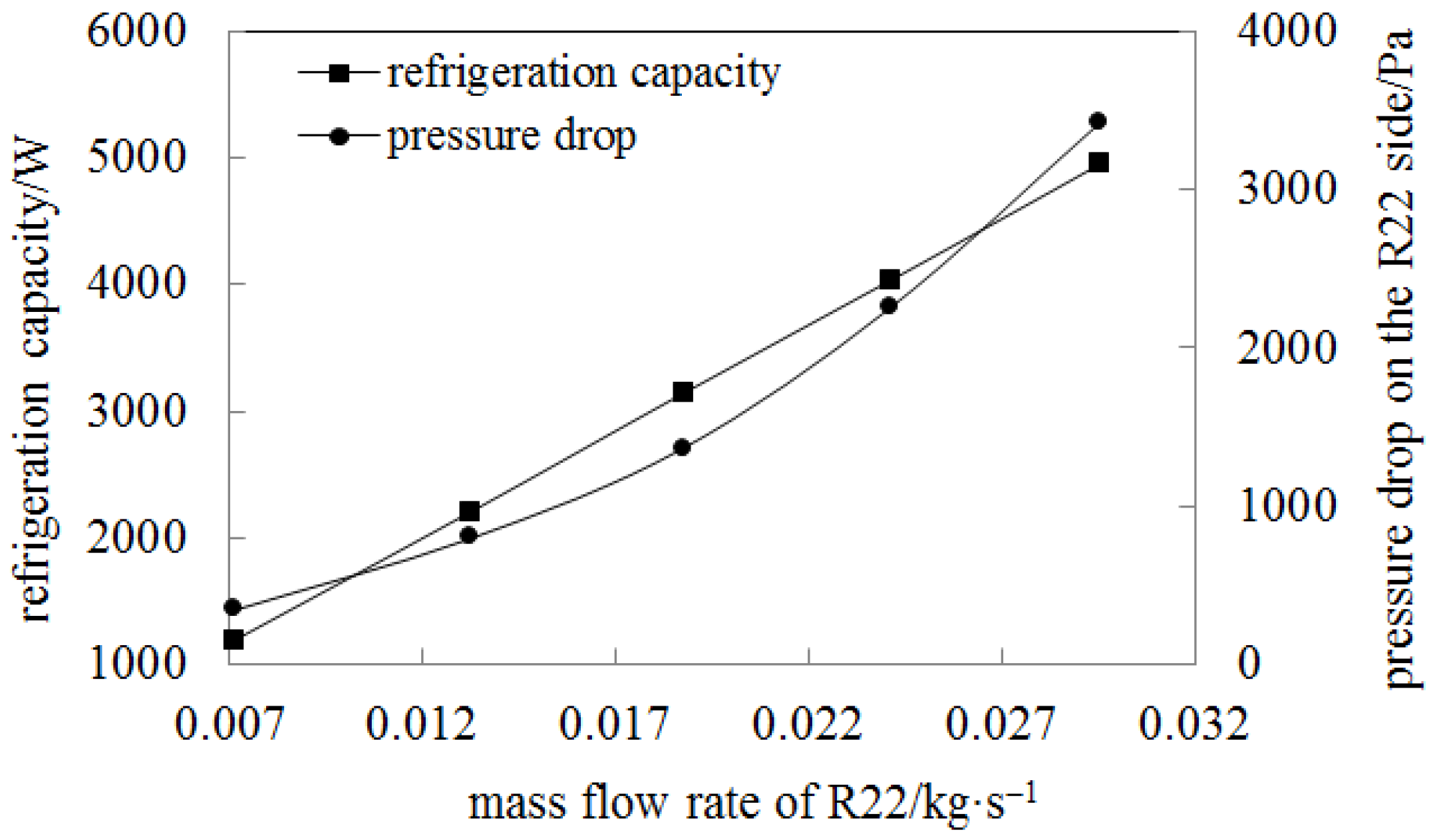
- The refrigeration capacity increases linearly with the increase in refrigerant mass flow rate. The pressure drop on the refrigerant side increases with the increase in R22 mass flow rate, and the growth rate gradually increases.
- The cooling capacity increases linearly with the increase in the frontal wind speed. The air side pressure drop increases with the increase in air inlet flow rate.
- The refrigerant mass flow rate and air inlet conditions should match each other.
- A reasonable and systematic calculation and experimental plan will be designed; sufficient data samples will be collected, and the heat transfer correlation equations will be fit on both sides of the plate evaporator.
- Due to its destruction of the ozone layer and high greenhouse effect, refrigerant R22 will be replaced by other new refrigerants. Therefore, the next step will be to study the performance of plate evaporators using new refrigerants as working fluids.
- The structure of the plate evaporator should be optimized to improve its heat transfer performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | total heat exchange area, m2 |
| Dm | mass diffusion coefficient |
| DT | thermal diffusion coefficient. |
| F | volumetric force, N·m−3 |
| Gk | turbulent kinetic energy generated by the average velocity gradient, J |
| h | enthalpy of the substance |
| ha1 | specific enthalpy of the indoor unit inlet air, kJ/kg |
| ha2 | specific enthalpy of the indoor unit outlet air, kJ/kg |
| J | diffusion flow rate, kg/s |
| K | total heat transfer coefficient/W(m2·K) |
| k | coverage factor |
| keff | effective thermal conductivity, W/(m·K) |
| M | dry air molar mass, kJ/mol |
| ma | mass flow rate of air, kg/s |
| mr | mass flow rate of R22 |
| n | number of phases |
| P | atmospheric pressure, Pa |
| PW | partial pressure of water vapor at the exit wet bulb temperature, Pa. |
| q | indoor unit air volume, m3/s |
| Qa | cooling capacity on air side, kW; |
| Qr | cooling capacity on R22 side, kW |
| R | ideal gas constant, J/(kg·K) |
| RH | relative humidity |
| r | phase transition coefficient, s−1. |
| Sct | turbulent Schmidt number |
| Sd | source term generated by the condensation of steam components |
| SE | energy source term, W/m3 |
| Sm | quality source term, kg/(m3·s). |
| Sl | mass transfer quantities during the evaporation process, kg/(m3·s) |
| Sv | mass transfer quantities during the condensation process, kg/(m3·s) |
| T | fluid temperature, K |
| t | dry bulb temperature of the air, °C |
| td | dew point temperature of the air, °C |
| Tsat | saturation temperature, K |
| U | the expanded relative standard uncertainty |
| u(x) | uncertainty |
| um | average mass velocity, m/s |
| udr,k | slip velocity of the k-th phase, m/s |
| Y | mass fraction of the substance |
| ρ | density of each phase, kg/m3 |
| ρm | density of the mixture, kg/m3 |
| μm | viscosity of the mixture, Pa·s |
| τeff | stress tensor, Pa |
| μt | turbulent viscosity coefficient |
| ε | dissipation rate |
| σk | turbulent Prandtl number for k |
| σε | turbulent Prandtl number for ε |
| α | volume fraction of each phase |
| Φ | cooling capacity, W |
References
- Qin, Y. Cold storage construction boom: Seven causes and eight trends. China Food Ind. 2021, 11, 61–63. [Google Scholar]
- Wei, D.; Jiang, S. Experimental study on performance test of cold storage finned tube evaporator. Cryog. Supercond. 2019, 47, 72–76. [Google Scholar]
- Zhang, J.; Gao, E.; Liang, C.; Lv, N.; Shao, Z. Effect of structure parameters on frosting characteristics of air cooler at different cold storage temperatures. J. Cent. South Univ. (Sci. Technol.) 2022, 12, 4905–4914. [Google Scholar]
- Ma, Y.; Zang, R.; Sun, Z.; Wu, G. Comparative study on the performance of variable fin spacing cooling fan and fixed fin spacing cooling fan. Fluid Mach. 2019, 47, 6–10. [Google Scholar]
- Jiang, S.; Yujun, B.; Meng, Y. Simulation study on the influence of structure parameters of CO2 air cooler on the heat transfer. Refrigeration 2018, 45, 79–85. [Google Scholar]
- Mehmet, D.A.S.; Pektezel, O. Experimental and numerical comparison of thermodynamic performance of new and old generation refrigerants in the same cooling system. Therm. Sci. 2022, 26, 4841–4854. [Google Scholar]
- Sun, H.; Jin, T.; Hu, K.; Yang, W.; Tian, S.; Tian, Q. Summary of Frost Retarding Technology of Evaporator in Cold Storage. J. Refrig. Technol. 2023, 46, 4–10. [Google Scholar]
- Dong, C.; Chen, S.; Zhu, M.; Jin, S.; Wu, Z. Effect of Double-wall Heat Transfer Tube on Frosting Characteristics of Finned-tube Vaporizer. J. Refrig. 2022, 43, 100–107. [Google Scholar]
- Gu, Y.; Yang, H.; Wu, Y.; Zuo, T. The Realization Mechanism of Carbon Neutralization in the Evolution of China’s Copper Industry. Environ. Conform. Assess. 2023, 4, 61–71. [Google Scholar]
- Lee, D.; Kim, D.; Park, S.; Lim, J.; Kim, Y. Evaporation heat transfer coefficient and pressure drop of R-1233zd(E) in a brazed plate heat exchanger. Appl. Therm. Eng. 2018, 130, 1147–1155. [Google Scholar] [CrossRef]
- Kim, D.; Lee, D.; Jang, D.S.; Jeon, Y.; Kim, Y. Comparative evaluation of flow boiling heat transfer characteristics of R-1234ze(E) and R-134a in plate heat exchangers with different Chevron angles. Appl. Therm. Eng. 2018, 132, 719–729. [Google Scholar] [CrossRef]
- Qiu, C.; Wu, L.; Wu, S. Numerical Study of Evaporator’s Heat Transfer Characteristics in ORC System. Energy Conserv. Technol. 2020, 38, 9–15. [Google Scholar]
- Wu, L.; Liang, X.; Wei, Z.; Yuan, Z. Heat Transfer Characteristics of Corrugated Plate Condenser in Organic Rankine Cycle for Blast Furnace Slag Flushing Water. J. Tongji Univ. (Nat. Sci.) 2021, 49, 1778–1788. [Google Scholar]
- Wu, X.H.; Li, C.; Gong, Y.; Zhang, J.; Zhao, M. Heat transfer and pressure drop characteristic of phase change flow in plate heat exchanger. Chin. J. Chem. Eng. 2017, 68, 133–140. [Google Scholar]
- Belman-Flores, J.M.; Gallegos-Munoz, A. Analysis of the flow and temperature distribution inside the compartment of a small refrigerator. Appl. Therm. Eng. 2016, 106, 743–752. [Google Scholar] [CrossRef]
- Wu, L.; Yuan, Z.; Yuan, Z. Optimization on the Structure of Plate Economizer Based on Orthogonal Design and Grey Relational Theory. J. Tongji Univ. (Nat. Sci.) 2017, 45, 1694–1700. [Google Scholar]
- Fan, J.; Peng, H. Advanced Applications and Example Analysis of Fluent; Tsinghua University Press: Beijing, China, 2008. [Google Scholar]
- Ye, X.; Zhang, J.; Lu, L.; Dai, A.; Yin, J. Research of source models by numerical simulation in wall condensation of water vapor. Energy Conserv. 2021, 6, 66–70. [Google Scholar]
- Deng, H.; Bai, Y. Numerical Simulation for Flow and Condensation in Air Cooled Condenser Reflux Tube with Diffusion Layer Model and Multiphase-flow Approach. Proc. CSEE 2017, 37, 826–837. [Google Scholar]
- Zhang, Q. Numerical Simulation of Flue Gas Condensation Heat Transfer in the Tail of Natural Gas Boiler. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Zhou, M.; Yu, B.; Cao, Y. Numerical Study on Condensation Behaviors of Air-vapor Mixture within and outside of Heat Exchange Pipes. Petro-Chem. Equip. 2019, 48, 40–47. [Google Scholar]
- Lee, W.H. Computational Methods for Two-Phase Flow and Particle Transport; World Scientific Publishing Company: Singapore, 1980; pp. 407–431. [Google Scholar]
- Ding, Q. Simulation of Steam Condensation and Flow in Horizontal Tube; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Qiu, G.; Cai, W.; Wu, Z.; Jiang, Y.; Yao, Y. Analysis on the value of coefficient of mass transfer with phase change in Lee′s equation. J. Harbin Inst. Technol. 2014, 46, 15–19. [Google Scholar]
- Liu, X.; Chen, H.; Zhu, L.; Cheng, K.; Wang, G. Numerical simulation of heat transfer law of flue gas with steam condensation. Energy Conserv. 2018, 433, 125–128. [Google Scholar]
- Li, M.; Huang, Y.S.; Huang, H. Analysis of the main deviation sources of measuring the cooling capacity of air conditioners by the air enthalpy method and the evaluation of measurement uncertainty. J. Insp. Quar. 2017, 27, 7–9. [Google Scholar]





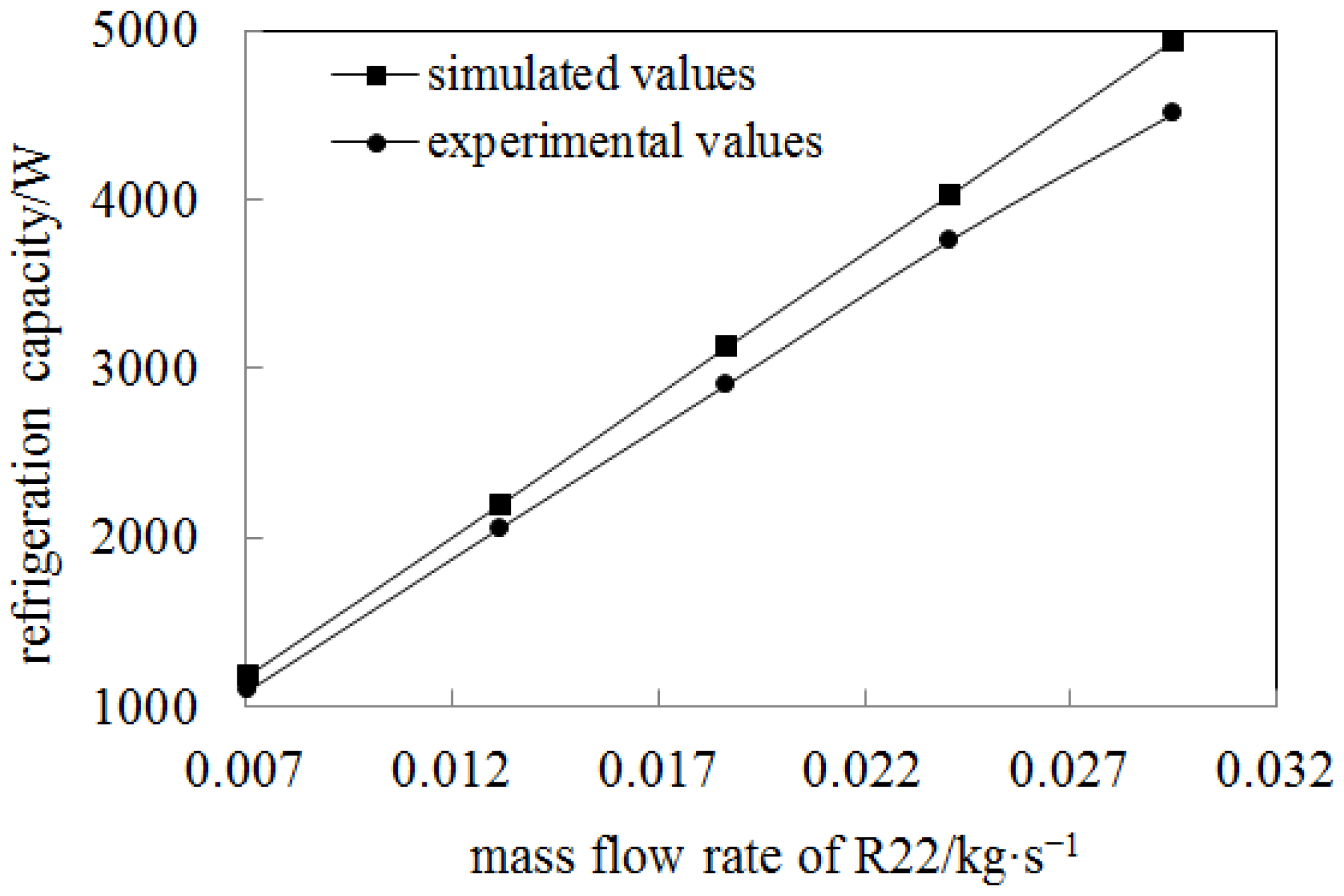
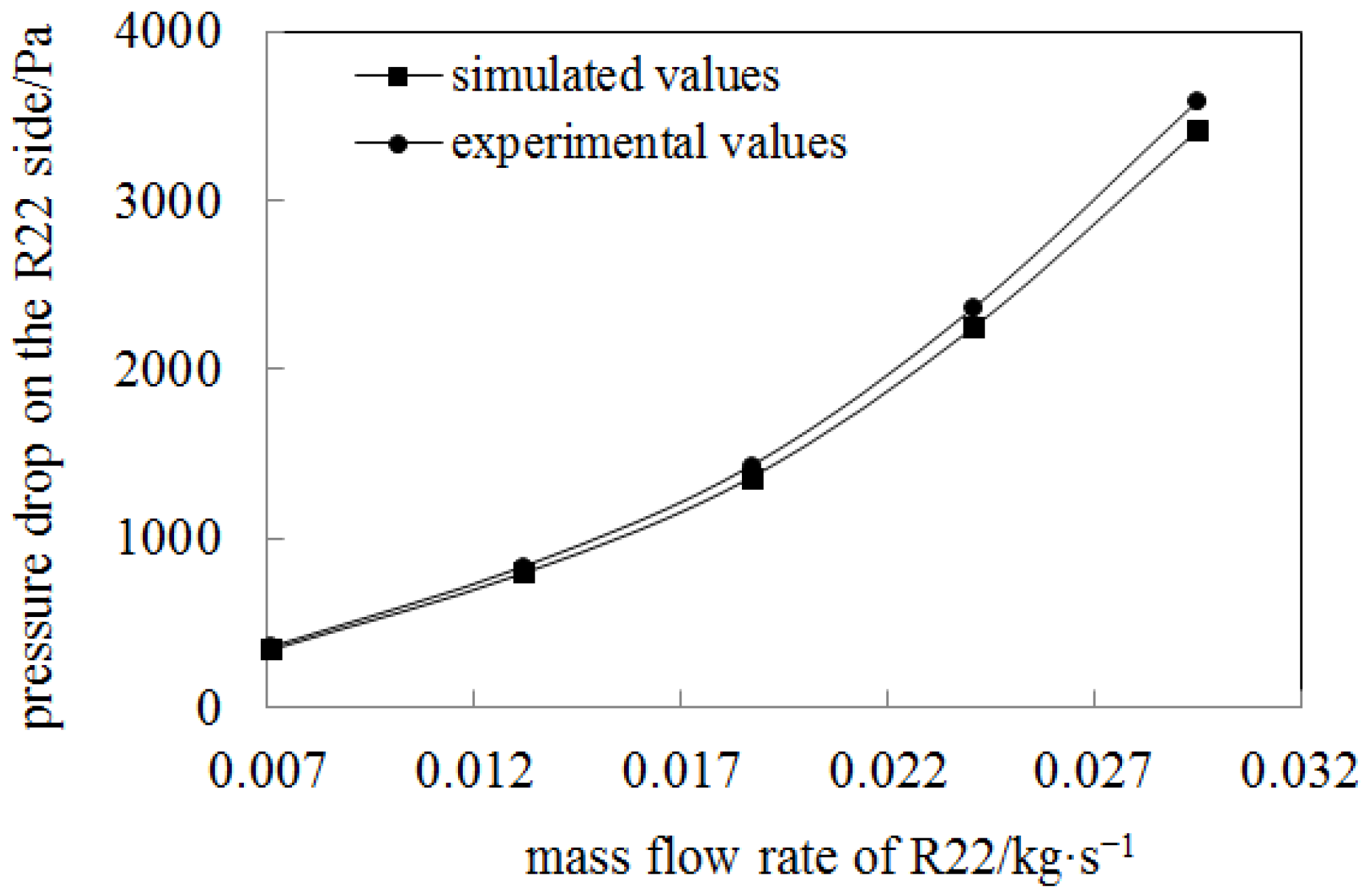
| Air Inlet Velocity/m·s−1 | Air Outlet Temperature/°C | Relative Humidity at the Air Outlet | R22 Mass Flow Rate/kg·s−1 |
|---|---|---|---|
| 1 | −0.5 | 0.93 | 0.0071 |
| 2 | 0 | 0.92 | 0.0132 |
| 3 | 0.3 | 0.91 | 0.0187 |
| 4 | 0.5 | 0.91 | 0.0241 |
| 5 | 0.6 | 0.91 | 0.0295 |
| Air Inlet Velocity/m·s−1 | R22 Mass Flow Rate/kg·s−1 | Refrigeration Capacity/W | Pressure Drop on the R22 Side/Pa | Pressure Drop on Air Side/Pa | Total Heat Transfer Coefficient/W·m−2·K−1 |
|---|---|---|---|---|---|
| 1 | 0.0071 | 1191 | 343 | 113 | 40 |
| 2 | 0.0132 | 2200 | 794 | 236 | 72 |
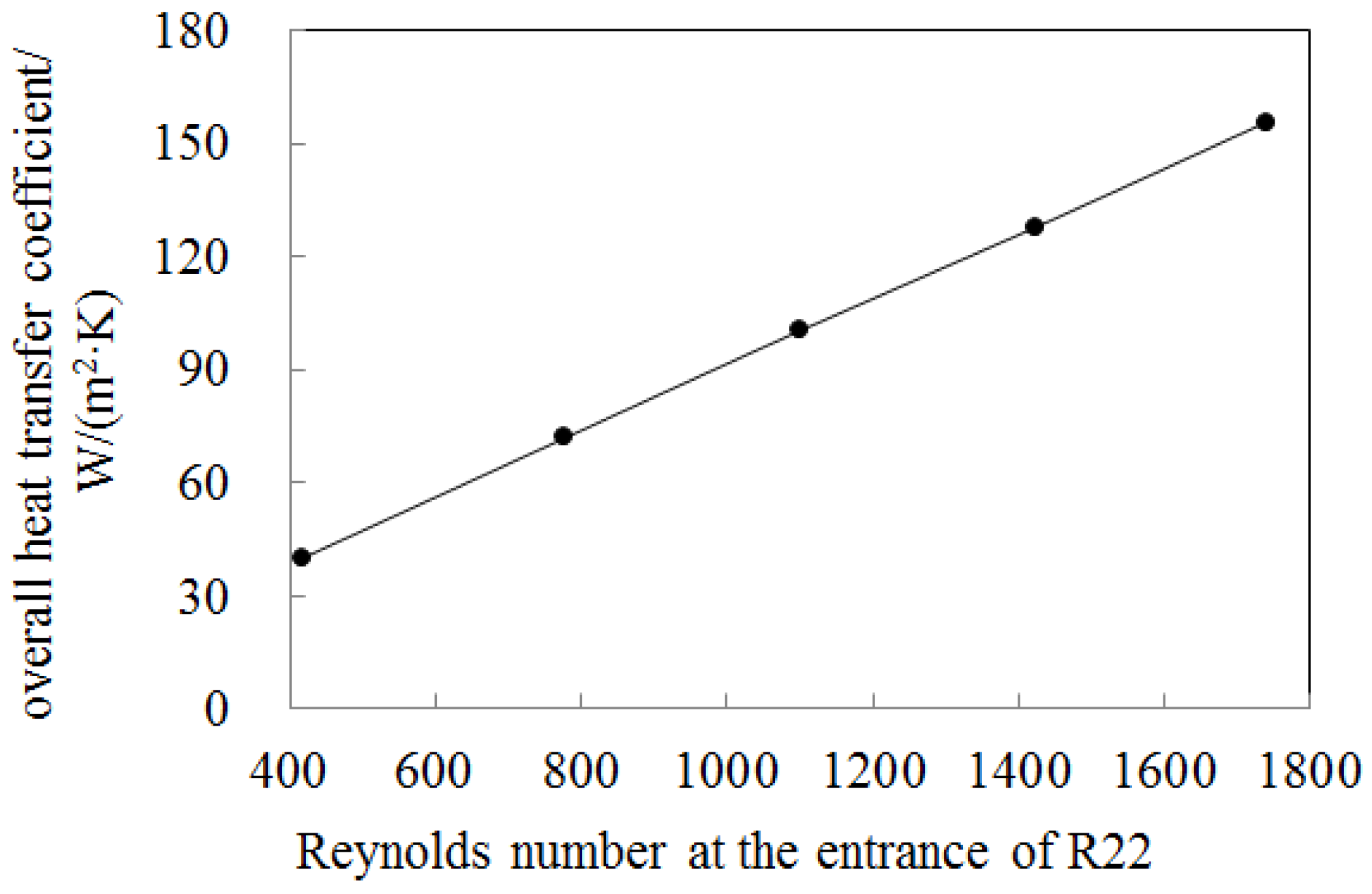
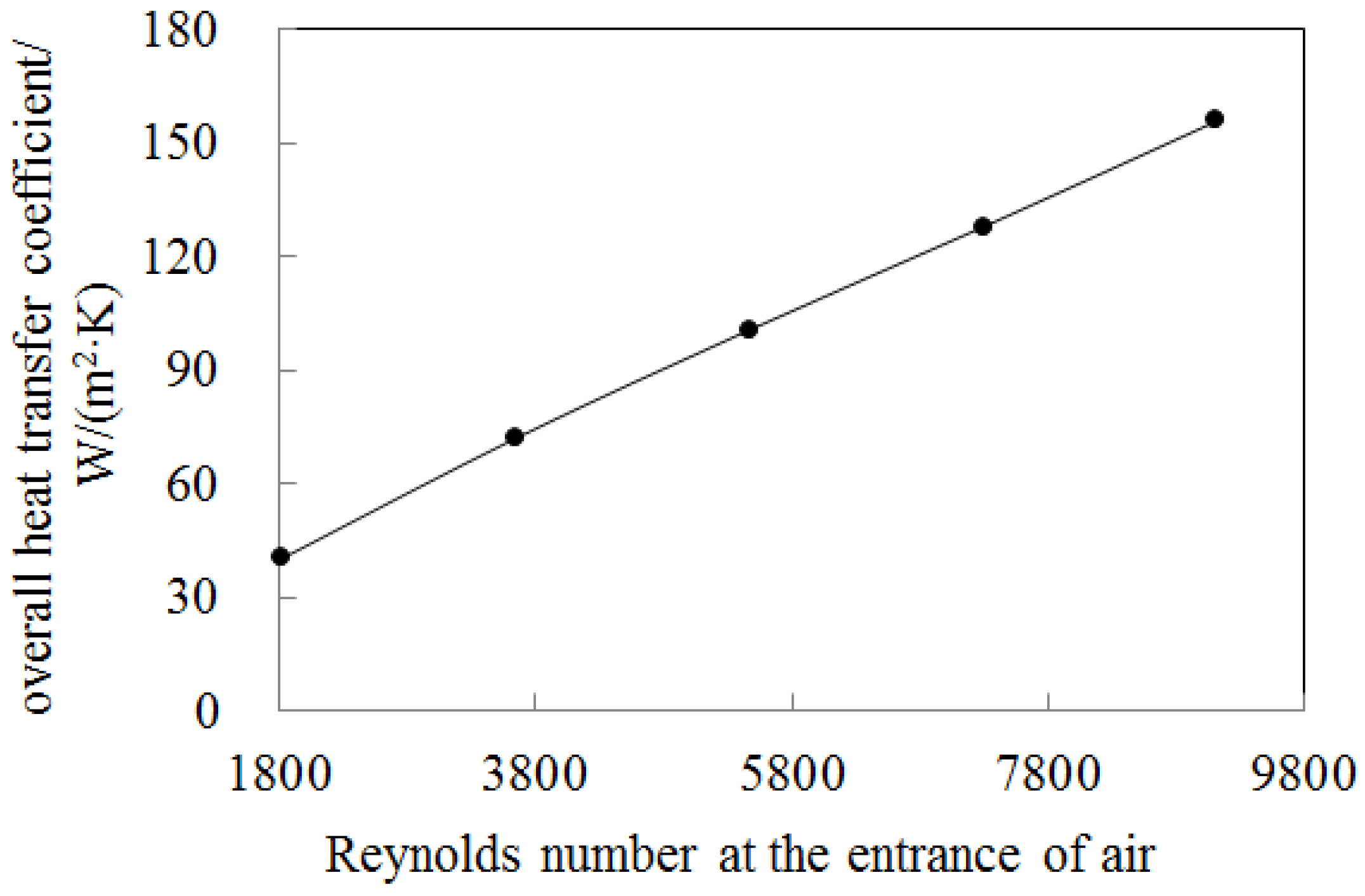
| 3 | 0.0187 | 3133 | 1360 | 495 | 101 |
| 4 | 0.0241 | 4029 | 2250 | 853 | 128 |
| 5 | 0.0295 | 4940 | 3410 | 1310 | 156 |
| Instrument | Measurement Range | Accuracy |
|---|---|---|
| T-type thermocouple | −200–350 °C | ±0.2 °C |
| CAREL SPKT00B1C0 pressure transmitter (Blue Gate Refrigeration Equipment Co., Ltd., Shanghai, China) | 0~44.8 Bar | ±0.1 Bar |
| Coriolis Mass Flowmeter (Yinuo Instrument Co., Ltd., Shanghai, China) | 0–10 kg/h | ±0.2% |
| Source of Uncertainty | Uncertainty | Relative Uncertainty/% |
|---|---|---|
| q | 32.4 m3/h | 1.50 |
| ha1 | 0.48 kJ/kg | 2.32 |
| ha2 | 0.21 kJ/kg | 1.80 |
| T | 0.2 K | 0.04 |
| P | 1000 Pa | 0.50 |
| PW | 10 Pa | 0.02 |
| Air Flow Rate/m·h−1 | Air Outlet Temperature/°C | Air Outlet Relative Humidity/% | Air Heat Lost/W | R22 Mass Flow Rate/kg·h−1 | R22 Heat Gain/W | Error/% |
|---|---|---|---|---|---|---|
| 360 | 0.1 | 93 | 1084 | 27.25 | 1117 | 3.09 |
| 720 | 0.5 | 92 | 2027 | 49.88 | 2096 | 3.42 |
| 1080 | 0.8 | 92 | 2856 | 71.18 | 2963 | 3.76 |
| 1440 | 1 | 91 | 3696 | 91.32 | 3828 | 3.57 |
| 1800 | 1.2 | 91 | 4406 | 113.83 | 4609 | 4.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Yuan, Z. Research on Heat Transfer Characteristics of Plate Evaporators for Cold Storage. Energies 2024, 17, 5837. https://doi.org/10.3390/en17235837
Xu X, Yuan Z. Research on Heat Transfer Characteristics of Plate Evaporators for Cold Storage. Energies. 2024; 17(23):5837. https://doi.org/10.3390/en17235837
Chicago/Turabian StyleXu, Xun, and Zhaokuo Yuan. 2024. "Research on Heat Transfer Characteristics of Plate Evaporators for Cold Storage" Energies 17, no. 23: 5837. https://doi.org/10.3390/en17235837
APA StyleXu, X., & Yuan, Z. (2024). Research on Heat Transfer Characteristics of Plate Evaporators for Cold Storage. Energies, 17(23), 5837. https://doi.org/10.3390/en17235837





