A Fusion Model for Predicting the Vibration Trends of Hydropower Units
Abstract
1. Introduction
- An EMD endpoint effect suppression method based on waveform matching extended (W-EMD) is proposed.
- Combining the proposed endpoint effect suppression method with LSTMNN and reconstructing the decomposed signal by the method of extreme point division greatly improves the quality of signal decomposition as well as the prediction accuracy of the algorithmic model.
- The validity of the proposed method for predicting the vibration trend of hydropower units is demonstrated through validation tests on specific examples.
2. Model Construction and Related Evaluation Indicators
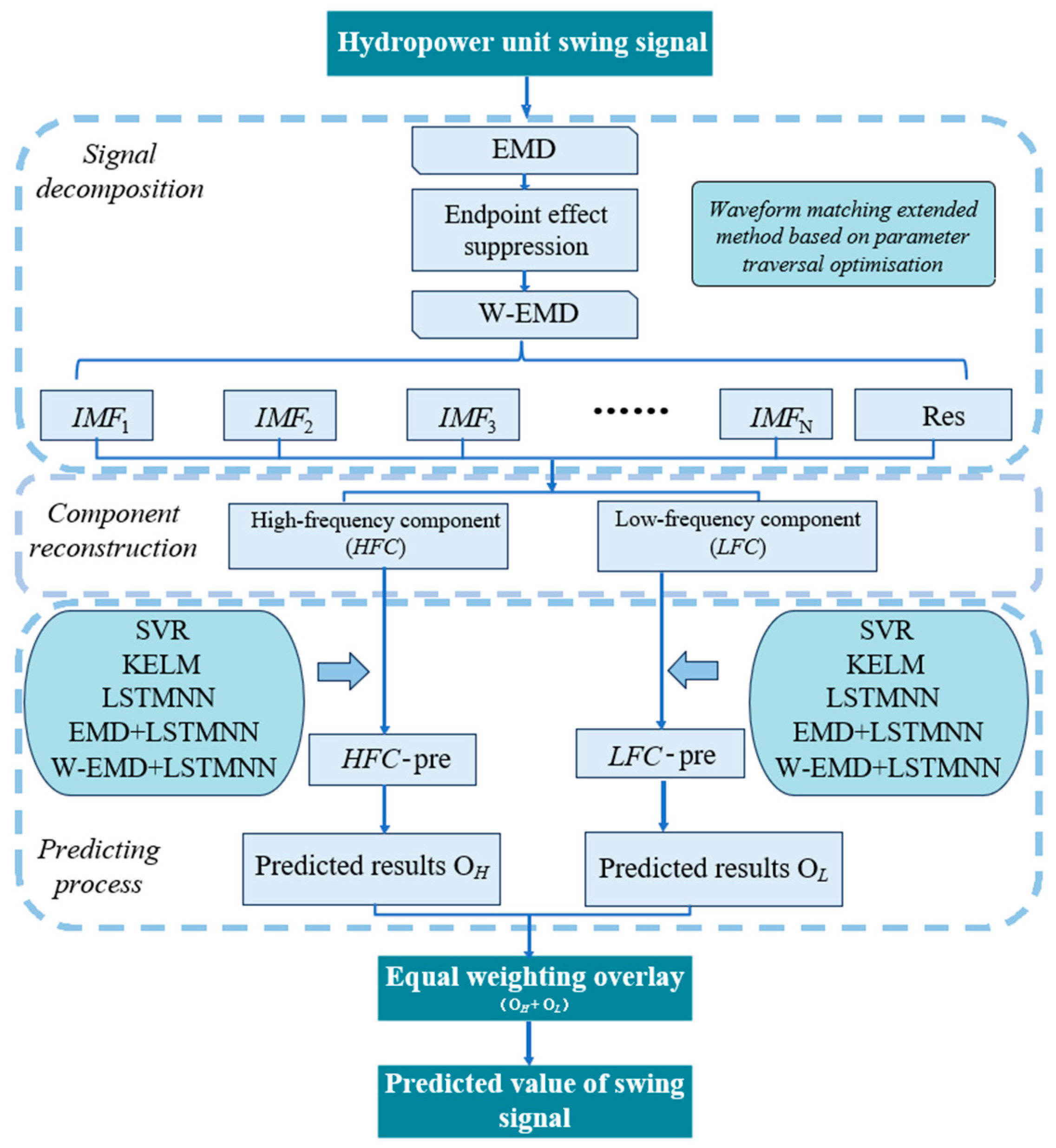
2.1. Establishment of Vibration and Swing Signals Trend Prediction Model for Hydropower Units
2.2. Evaluation Indicators for Endpoint Effects
2.3. Predictive Model Evaluation Indicators
3. Improvement of EMD Algorithm
3.1. Waveform Matching Extended Method Based on Parameter Traversal Optimization
3.1.1. Definition of Waveform Matching Related Parameters
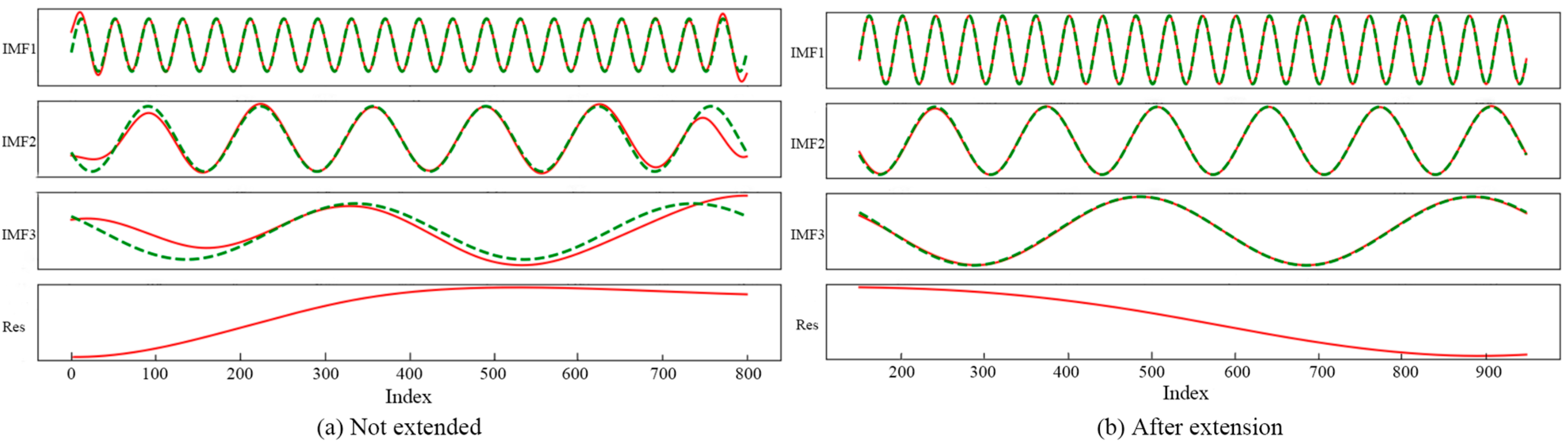
3.1.2. Verification of Simulated Signals
- (1)
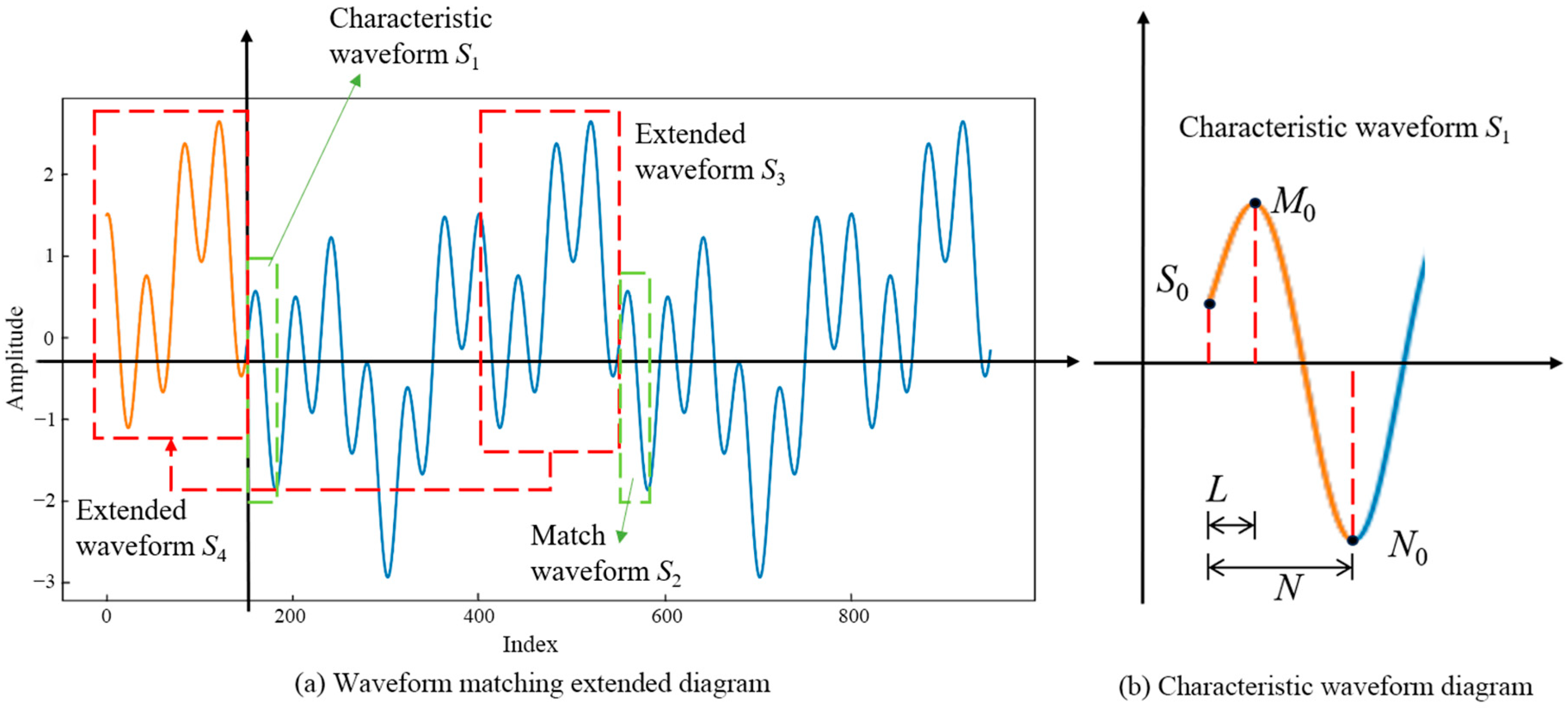
- Taking the extended extension of the left endpoint of the simulated signal x(t) as an example, the characteristic wave S1 (shown in Figure 3b) is defined, which has a very large value point followed by a very small value point. Denote the left endpoint corresponding to the eigenwave as S0, the first extreme value point as M0, and the first minimal value point as N0; the length of the eigenwave is N, and the distance between the left endpoint S0 and the first extreme value point M0 is L. For practical analysis, the characteristic wavelength can be defined according to the measured signal characteristics.
- (2)
- Mark the extremely large and extremely small points within the index range of the simulated signal x(t), and denote the set consisting of all extremely large points as Mmax and the set consisting of all extremely small points as Mmin. Set the initial value of the waveform match parameter and the traversal step, take the first maximal point M0 as a reference point, such that the length of the matching wave is the same as the length of the eigenwave, and calculate the composite index of waveform matching P for different values of the matching parameter .
- (3)
- The signal before the maximum value of the waveform matching index Pmax corresponding to the matching wave is used as the extended wave to extend the original signal. Record that the coordinate of the extreme value corresponding to M0 at this point is Mp, and the coordinate corresponding to S0 is Xp = Mp- − L.
- (4)
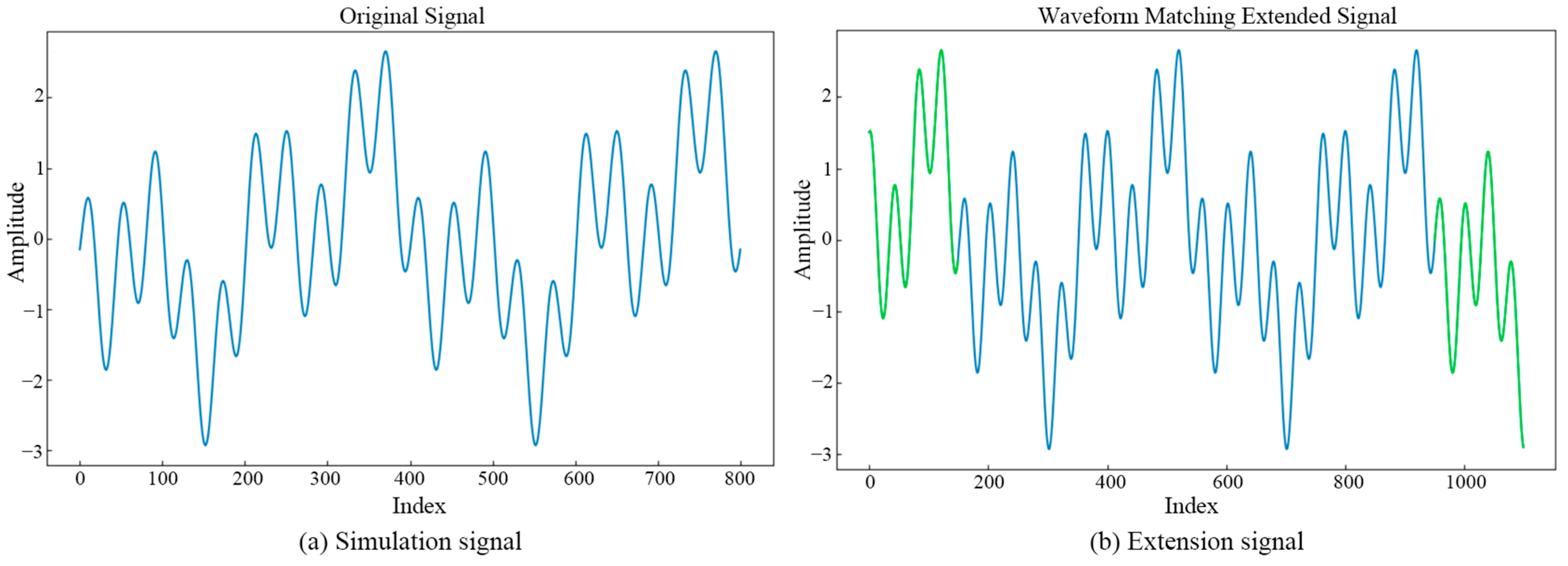
- Set in advance the number of points to be extended n, and using the waveform corresponding to the first n points of Xp as the extended wave S3, the extension of the left end of the signal x(t) is completed by moving this extended wave to just before S0. Figure 3a shows the schematic diagram of the left endpoint of the simulated signal after it is extended. Similarly, an extended extension of the right end of the simulated signal can be achieved.
4. Instance Validation
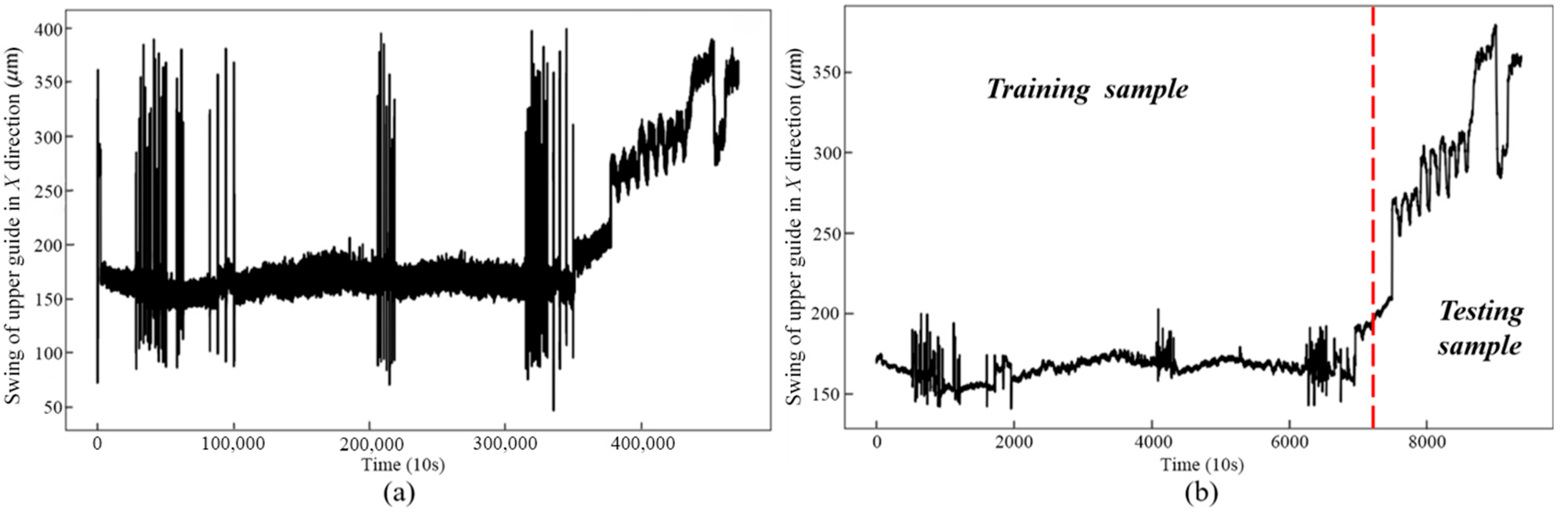
4.1. Trend Prediction Analysis of Upper Guide Swing Signal on Hydropower Units
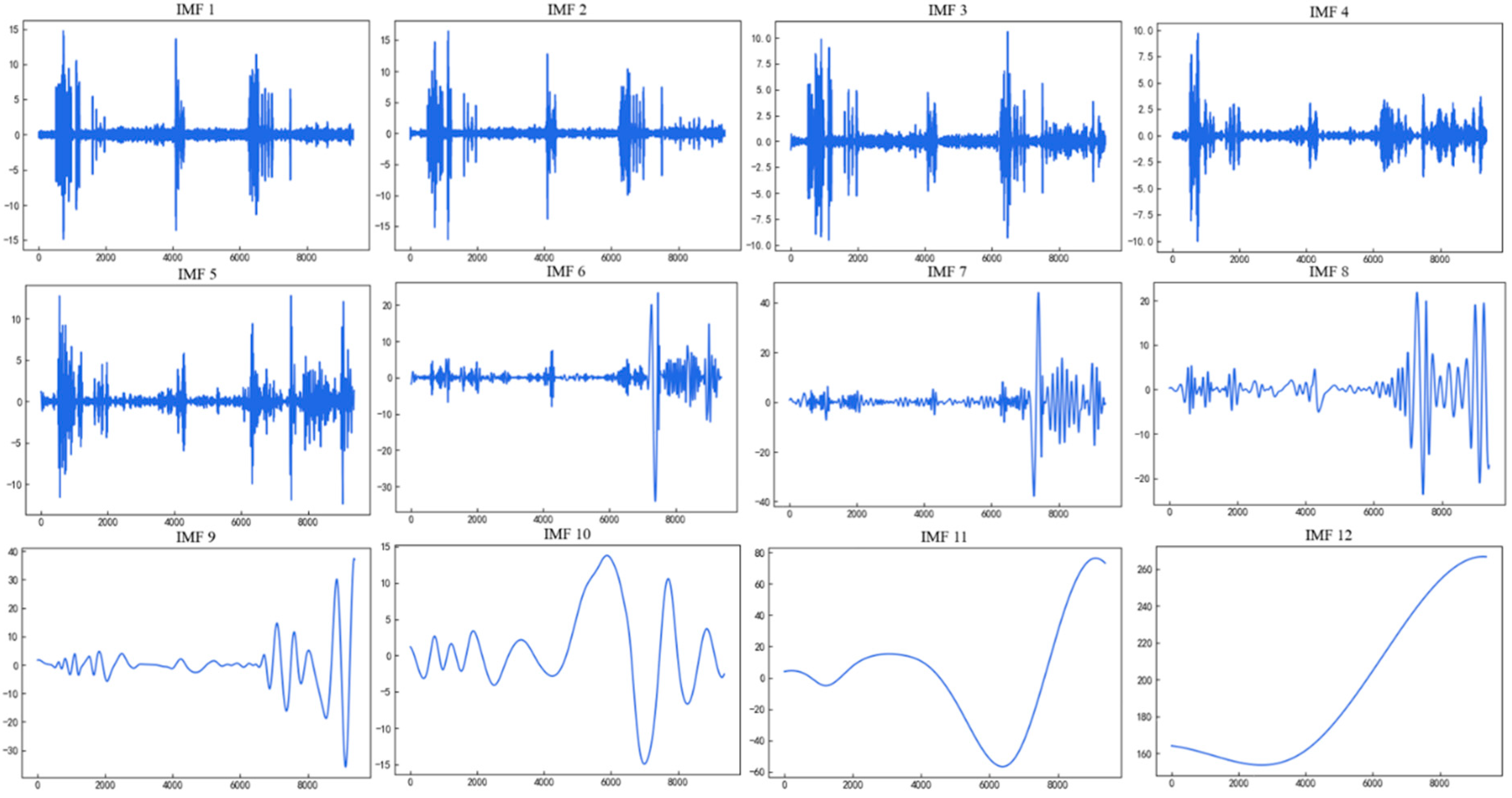
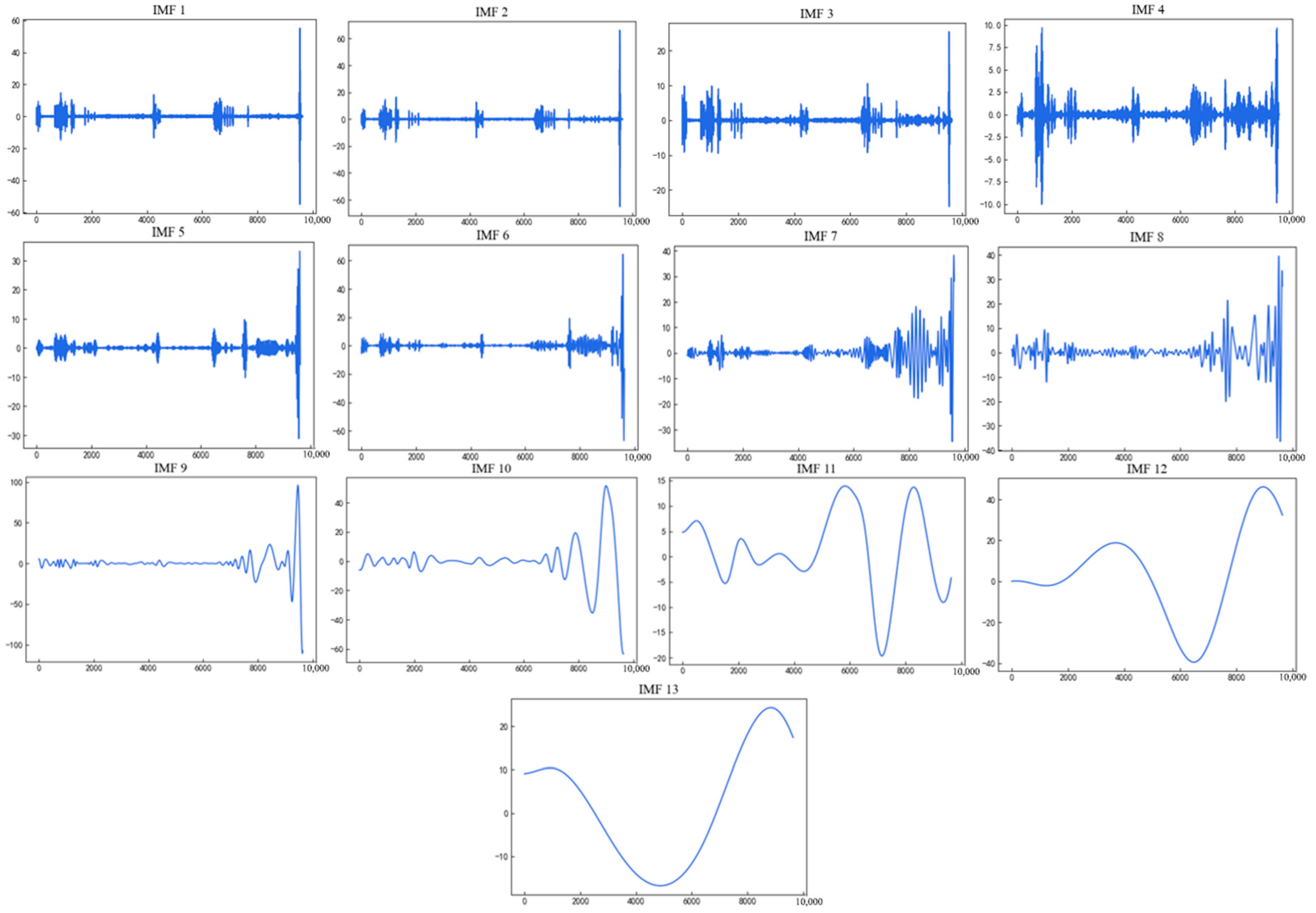
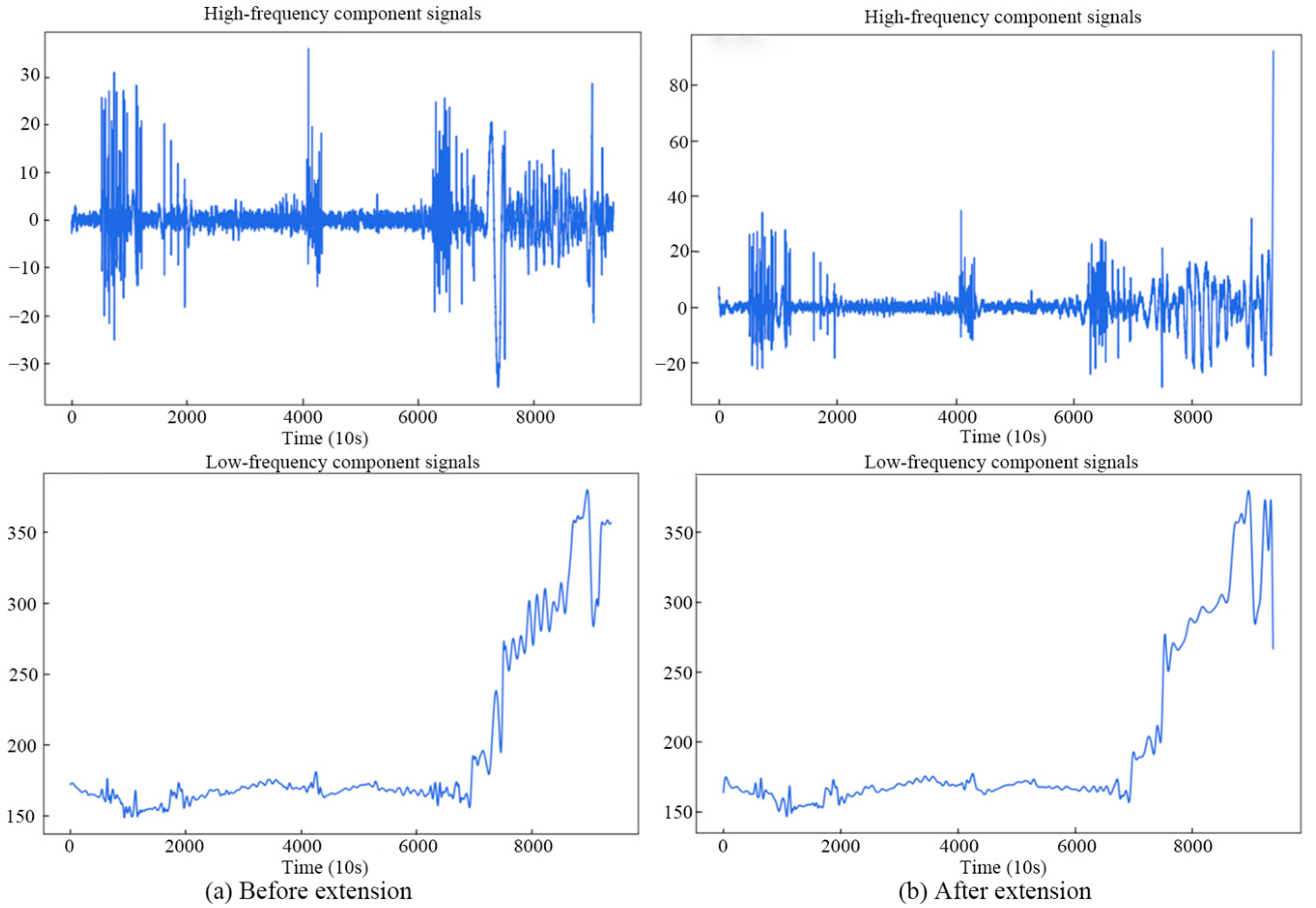
4.2. Swing Signal Decomposition and Component Reconstruction
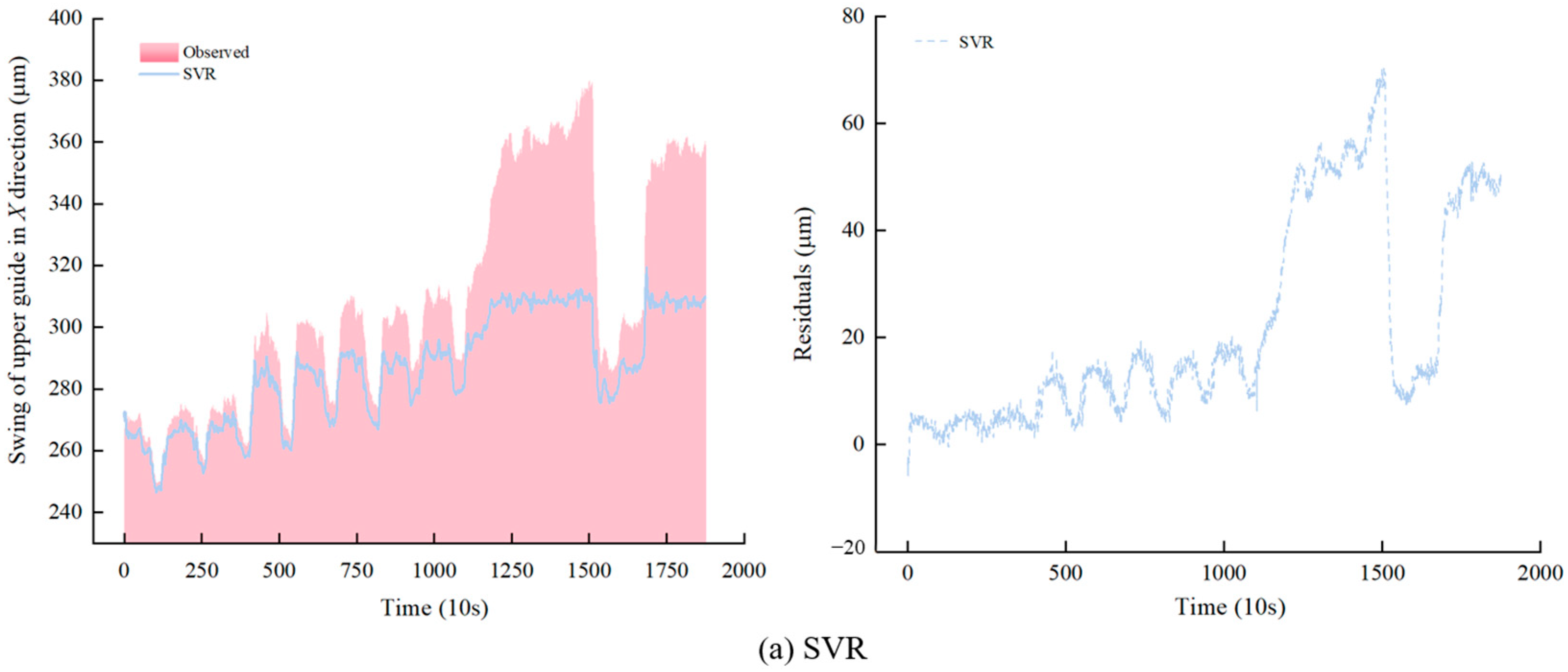
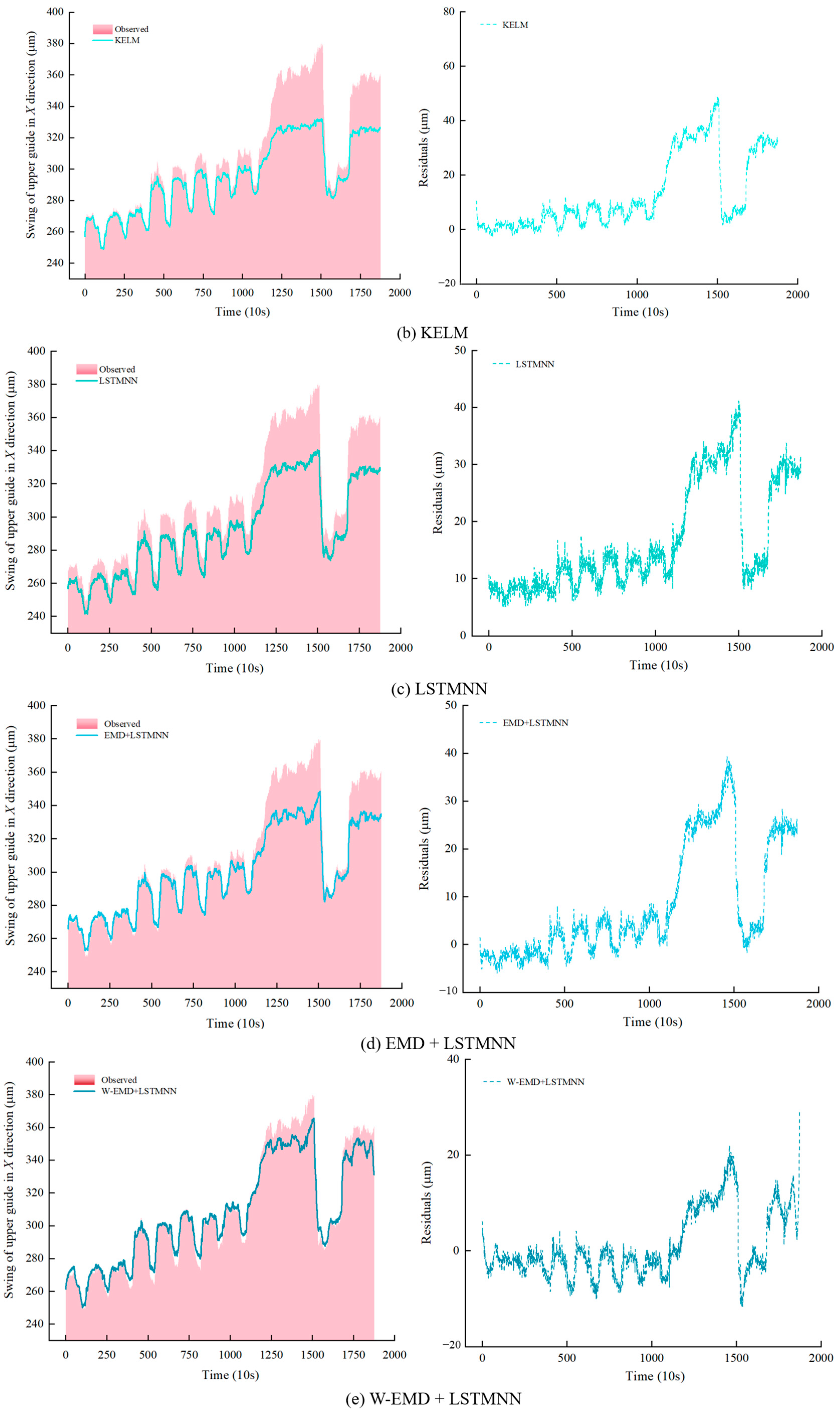
4.3. Analysis of Experimental Results
5. Conclusions, Recommendations, Policy Insights, and Future Works
- (1)
- The waveform matching extended method based on parameter traversal optimization is used to process the x(t) of the simulated signal, and by comparing the similarity coefficient of EMD before and after extension, the method effectively suppresses the endpoint effect of EMD in the short-term data. Compared with the traditional method of predicting each component separately after EMD, the method of component reconstruction reduces the noise and interference in the prediction process, and effectively improves the stability and accuracy of the prediction model.
- (2)
- In order to verify the effectiveness of the proposed fusion model W-EMD + LSTMNN in improving the prediction accuracy, we studied the actual case of a sudden upward movement of the upper conductance slip rotor of unit 16F of a hydropower station in China, which led to the increase of the upper guide X direction swing. The fusion model effectively avoids the endpoint effect problem caused by the traditional empirical mode decomposition process, and compared with SVR, KELM, the single LSTMNN model, and the traditional EMD + LSTMNN combination model, it was found that W-EMD + LSTMNN, with the advantages of high prediction accuracy and strong generalization ability, successfully analyzed and predicted the increasing trend of an X direction pendulum of the upper guide, and discovered the potential hidden danger of the unit. The results show that the proposed W-EMD + LSTMNN fusion model has important application prospects in hydropower system operation state monitoring, and provides a reliable reference for hydropower unit trend prediction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Poudyal, R. Renewable Energy and Other Strategies for Mitigating the Energy Crisis in Nepal. 2021. Available online: https://www.semanticscholar.org/paper/Renewable-Energy-and-Other-Strategies-for-the-in-Poudyal/fcded2d9d9cdadba02cb4dec0414787bde41818c#related-papers (accessed on 12 November 2024).
- Quaranta, E.; Bonjean, M.; Cuvato, D.; Nicolet, C.; Dreyer, M.; Gaspoz, A.; Rey-Mermet, S.; Boulicaut, B.; Pratalata, L.; Pinelli, M. Hydropower case study collection: Innovative low head and ecologically improved turbines, hydropower in existing infrastructures, hydropeaking reduction, digitalization and governing systems. Sustainability 2020, 12, 8873. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Fan, X.; Cheng, Z. Hydropower development situation and prospects in China. Renew. Sustain. Energy Rev. 2018, 82, 232–239. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, Y.; Hu, W.; Chen, J.; Xiao, Z. Intelligent fault diagnosis of hydroelectric units based on radar maps and improved GoogleNet by depthwise separate convolution. Meas. Sci. Technol. 2023, 35, 025103. [Google Scholar] [CrossRef]
- Kumar, K.; Saini, R. A review on operation and maintenance of hydropower plants. Sustain. Energy Technol. Assess. 2022, 49, 101704. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Z.; Wang, X.; Wu, Q.; Zhang, L. Transient vibration of shafting in coupled hydraulic-mechanical-electrical-structural system for hydropower station during start-up process. Appl. Math. Model. 2023, 124, 860–880. [Google Scholar] [CrossRef]
- Singh, V.K.; Singal, S.K. Operation of hydro power plants—A review. Renew. Sustain. Energy Rev. 2017, 69, 610–619. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Wang, B.; Jiang, H. China’s hydropower resources and development. Sustainability 2023, 15, 3940. [Google Scholar] [CrossRef]
- Tong, K.; Zhang, G.; Huang, H.; Qin, A.; Mao, H. A novel combined model for vibration trend prediction of a hydropower generator unit. Insight Non-Destr. Test. Cond. Monit. 2023, 65, 43–51. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Zou, Y.; Li, X.; Qian, J. Acoustic vibration approach for detecting faults in hydroelectric units: A review. Energies 2021, 14, 7840. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zare, M.; Nouri, N.M. End-effects mitigation in empirical mode decomposition using a new correlation-based expansion model. Mech. Syst. Signal Process. 2023, 194, 110205. [Google Scholar] [CrossRef]
- Chai, K.; Feng, S.W. Processing method of EMD endpoint effect based on SVRM extension. Vibroengineering Procedia 2020, 35, 70–75. [Google Scholar] [CrossRef]
- Xu, W.; Chen, S.H.; Wang, M.; Yang, W.; Wang, L. Eliminating the end effect of empirical mode decomposition using a cubic spline based method. Digit. Signal Process. 2021, 110, 102936. [Google Scholar] [CrossRef]
- Lv, C.; Zhao, J.; Wu, C.; Guo, T.; Chen, H. Optimization of the end effect of Hilbert-Huang transform (HHT). Chin. J. Mech. Eng. 2017, 30, 732–745. [Google Scholar] [CrossRef]
- Liang, L. Estimation of EMD Envelope Based on MQ Interpolation. Acad. J. Sci. Technol. 2022, 1, 36–39. [Google Scholar] [CrossRef]
- Song, S.D.; Yao, Z.C.; Wang, X.N. The summary of Hilbert-Huang transform. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Infrared Imaging and Applications, Beijing, China, 25–27 June 2013; SPIE: Dalian, China, 2013; pp. 748–754. [Google Scholar]
- Meng, S.; Kang, J.; Chi, K.; Die, X. Fault diagnosis of rolling bearing based on improved EMD algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 12069. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Zhou, K.B.; Zhang, J.Y.; Shan, Y.; Ge, M.F.; Ge, Z.Y.; Cao, G.N. A hybrid multi-objective optimization model for vibration tendency prediction of hydropower generators. Sensors 2019, 19, 2055. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Zhou, J.; Jiang, W.; Liu, J.; Xu, Y.; Zhao, Y. Vibration Tendency Prediction of Hydroelectric Generator Unit Based on Fast Ensemble Empirical Mode Decomposition and Kernel Extreme Learning Machine with Parameters Optimization. In Proceedings of 2018 11th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 8–9 December 2018; pp. 287–290. [Google Scholar]
- Hu, N.; Kong, L.; Zheng, H.; Zhou, X.; Wang, J.; Tao, J.; Li, W.; Lin, J. Trend Prediction of Vibration Signals for Pumped-Storage Units Based on BA VMD and LSTM. Energies 2024, 17, 5331. [Google Scholar] [CrossRef]
- Qin, Q.; Lai, X.; Zou, J. Direct multistep wind speed forecasting using LSTM neural network combining EEMD and fuzzy entropy. Appl. Sci. 2019, 9, 126. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, Z.; Liu, D.; Chen, J.; Liu, D.; Hu, X. Degradation Trend Prediction of Hydropower Units Based on a Comprehensive Deterioration Index and LSTM. Energies 2022, 15, 6273. [Google Scholar] [CrossRef]
- Zhao, Q.; Lou, L.; Ouyang, B. Short-Time Traffic Flow Prediction Based on a Combined Model of EMD and LSTM. In Proceedings of the 2023 4th International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Nanjing, China, 16–18 June 2023; pp. 424–429. [Google Scholar]
- Rong, Q. Research on EMD Method for Improving End Effect and Suppressing Modal Mixing. Ph.D. Thesis, Tianjin University, Tianjin, China, 2018. [Google Scholar]
- Zhang, C.; Zhou, J.; Li, C.; Fu, W.; Peng, T. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. [Google Scholar]
- Danielsson, P.E. Euclidean distance mapping. Comput. Graph. Image Process. 1980, 14, 227–248. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Feng, J. On the Euclidean distance of images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1334–1339. [Google Scholar] [CrossRef]


| Before Extension | After Extension | |
|---|---|---|
| IMF1 similarity coefficients | 0.9921 | 1.0012 |
| IMF2 similarity coefficients | 0.9685 | 1.0009 |
| IMF3 similarity coefficients | 0.8944 | 1.0008 |
| Upper guide swing signal | Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
| Number of extreme points | 6341 | 4063 | 2347 | 1334 | 803 | 384 | |
| Component | IMF7 | IMF8 | IMF9 | IMF10 | IMF11 | IMF12 | |
| Number of extreme points | 194 | 94 | 39 | 15 | 5 | 2 | |
| After extension upper guide swing signal | Component | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
| Number of extreme points | 6498 | 4197 | 2457 | 1407 | 840 | 522 | |
| Component | IMF7 | IMF8 | IMF9 | IMF10 | IMF11 | IMF12 | |
| Number of extreme points | 263 | 145 | 67 | 35 | 10 | 5 | |
| Component | MF13 | - | - | - | - | - | |
| Number of extreme points | 2 | - | - | - | - | - |
| MAPE (%) | MSPE (%) | |||
|---|---|---|---|---|
| SVR | 21.7025 | 0.0646 | 0.6708 | 0.0019 |
| KELM | 13.1596 | 0.0386 | 0.4351 | 0.0012 |
| LSTMNN | 11.3469 | 0.0345 | 0.3285 | 0.0009 |
| EMD + LSTMNN | 9.4108 | 0.0285 | 0.2713 | 0.0007 |
| W-EMD + LSTMNN | 5.1112 | 0.0160 | 0.1489 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Pi, Y.; Tang, Z.; Hua, H.; Wang, X. A Fusion Model for Predicting the Vibration Trends of Hydropower Units. Energies 2024, 17, 5847. https://doi.org/10.3390/en17235847
Liu D, Pi Y, Tang Z, Hua H, Wang X. A Fusion Model for Predicting the Vibration Trends of Hydropower Units. Energies. 2024; 17(23):5847. https://doi.org/10.3390/en17235847
Chicago/Turabian StyleLiu, Dong, Youchun Pi, Zhengyang Tang, Hongpeng Hua, and Xiaopeng Wang. 2024. "A Fusion Model for Predicting the Vibration Trends of Hydropower Units" Energies 17, no. 23: 5847. https://doi.org/10.3390/en17235847
APA StyleLiu, D., Pi, Y., Tang, Z., Hua, H., & Wang, X. (2024). A Fusion Model for Predicting the Vibration Trends of Hydropower Units. Energies, 17(23), 5847. https://doi.org/10.3390/en17235847






