Power Quality Control Using Superconducting Magnetic Energy Storage in Power Systems with High Penetration of Renewables: A Review of Systems and Applications
Abstract
1. Introduction
- Reviewing the different SMES systems that perform power quality control and regulation services for several power applications. The following main power quality control and regulation services are addressed: Frequency regulation; Power oscillation damping; Power fluctuation suppression; Voltage sags and flickering compensation; and Active harmonics filtering.
- For each type of service that SMES can provide, the main gaps and research trends are identified. This analysis is crucial for guiding future developments in the field.
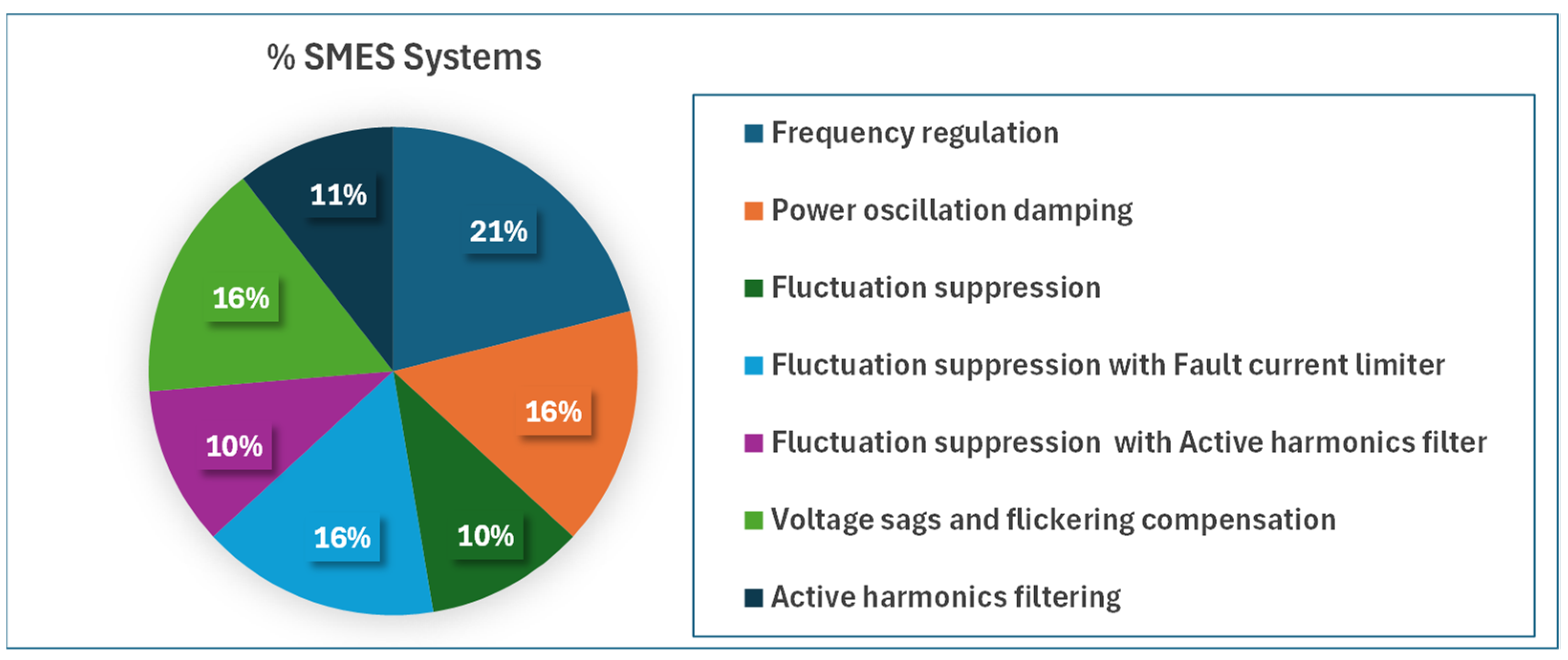
- An overview of the literature is quantified allowing a visual perspective of the works published about the use of SMES in power quality control and regulation services.
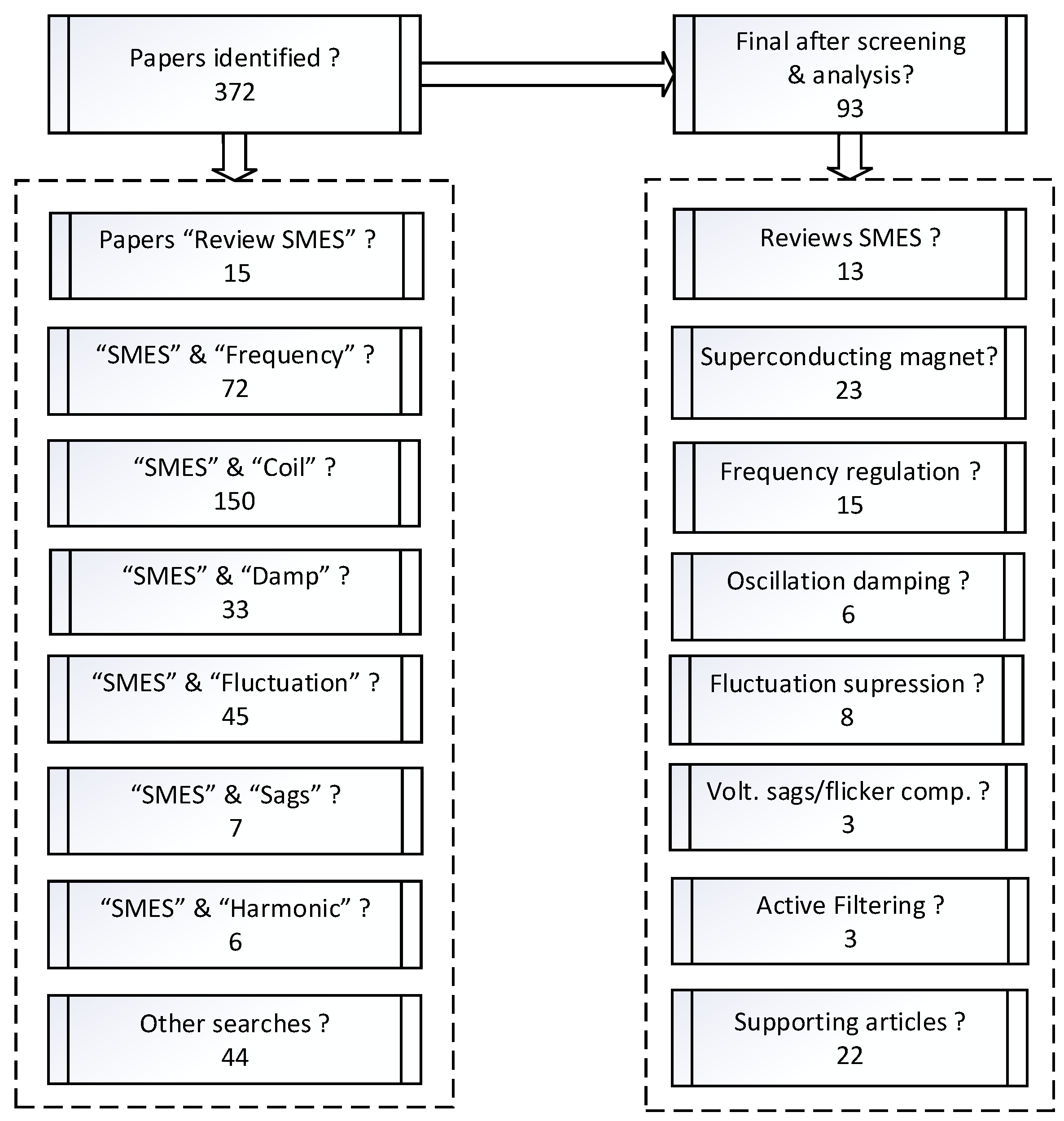
2. Review Methodology
3. Superconducting Magnetic Energy Storage System Components
3.1. Superconducting Magnets
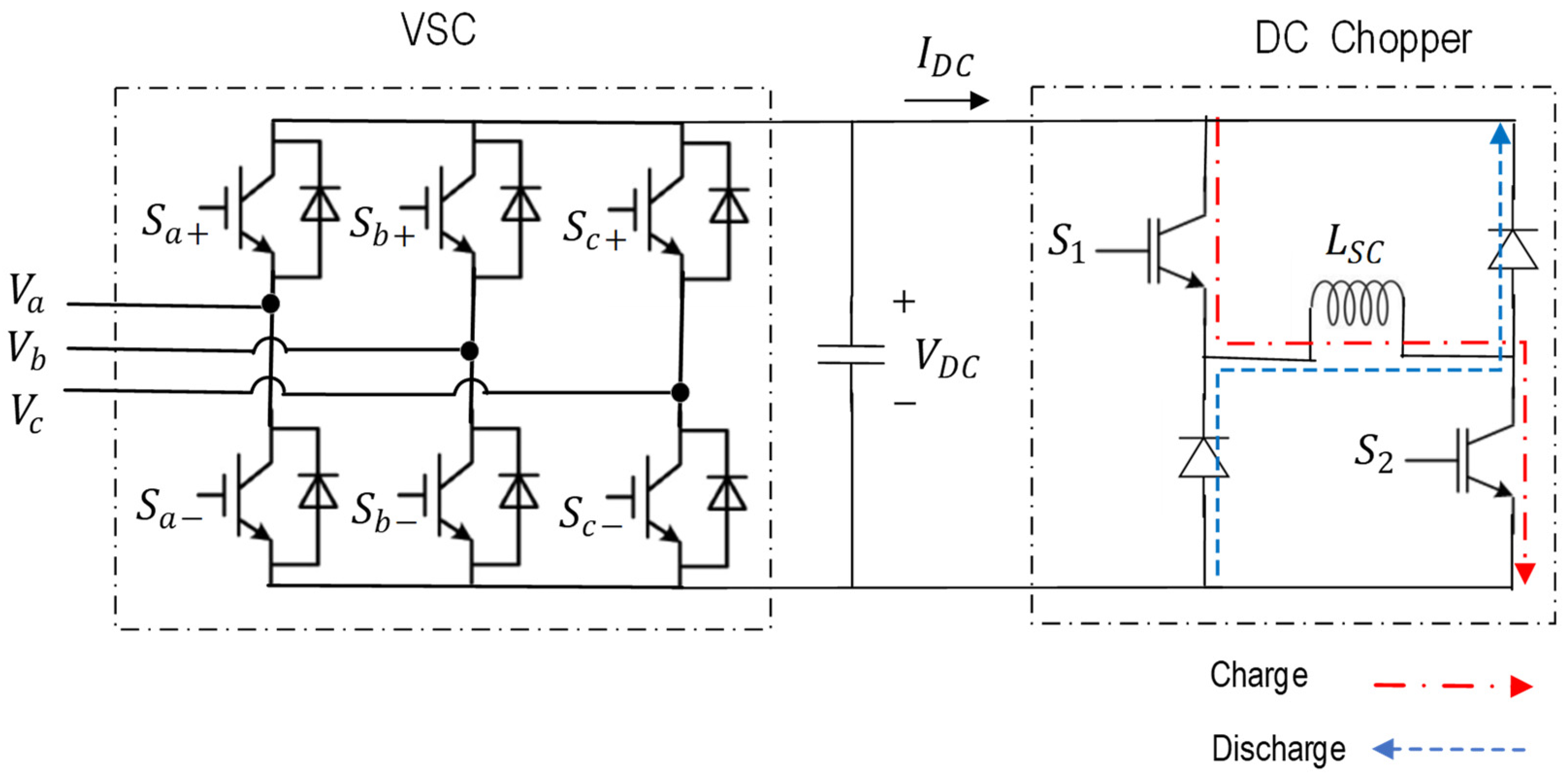
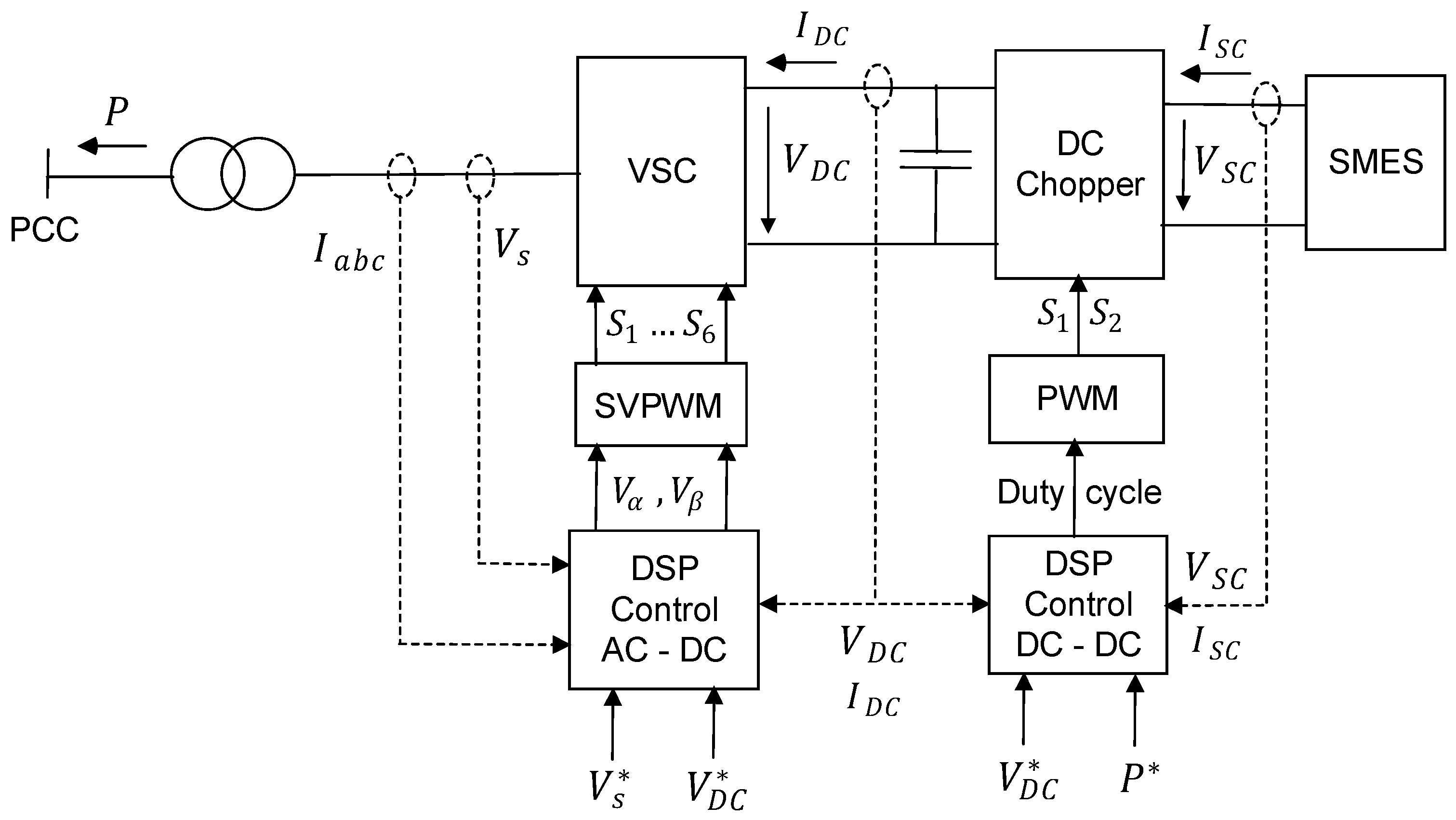
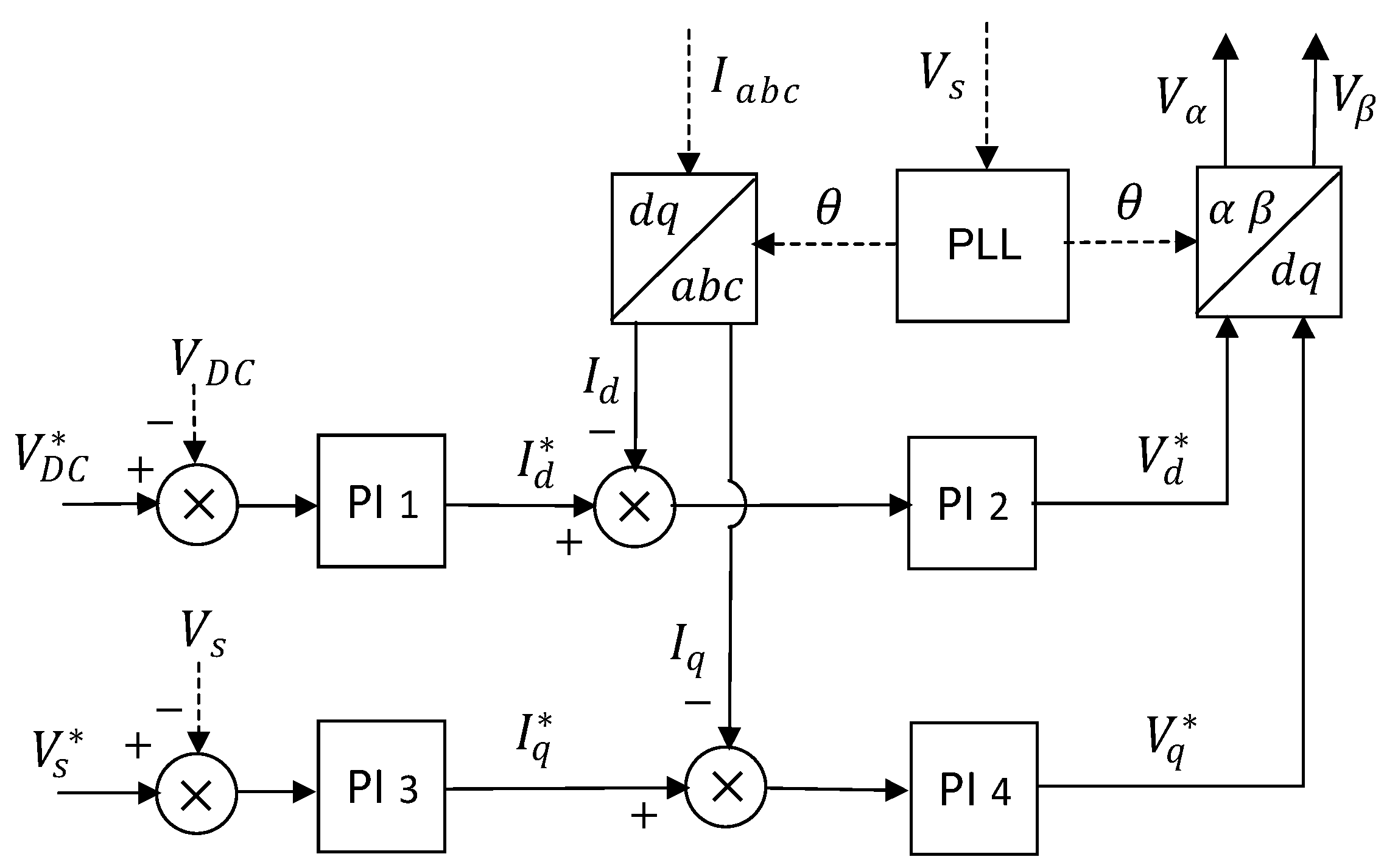
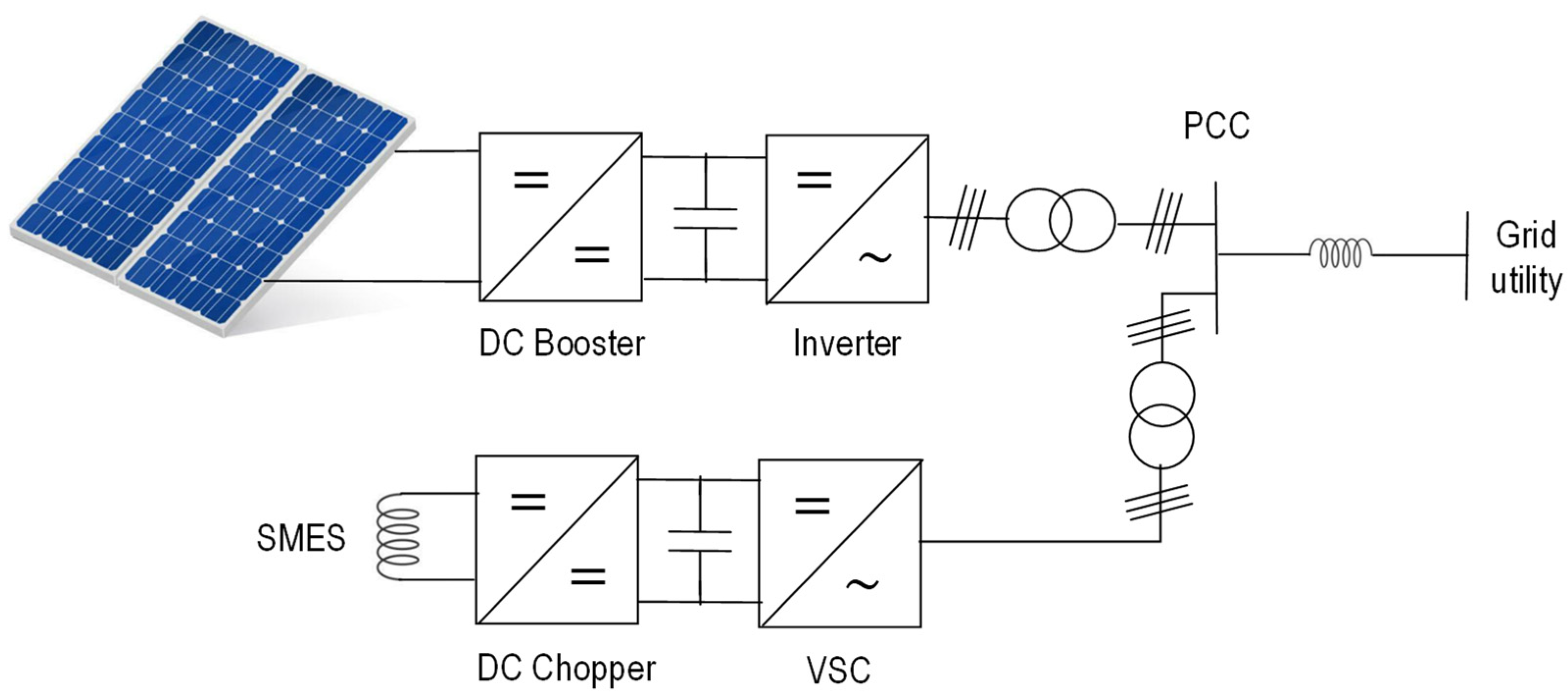
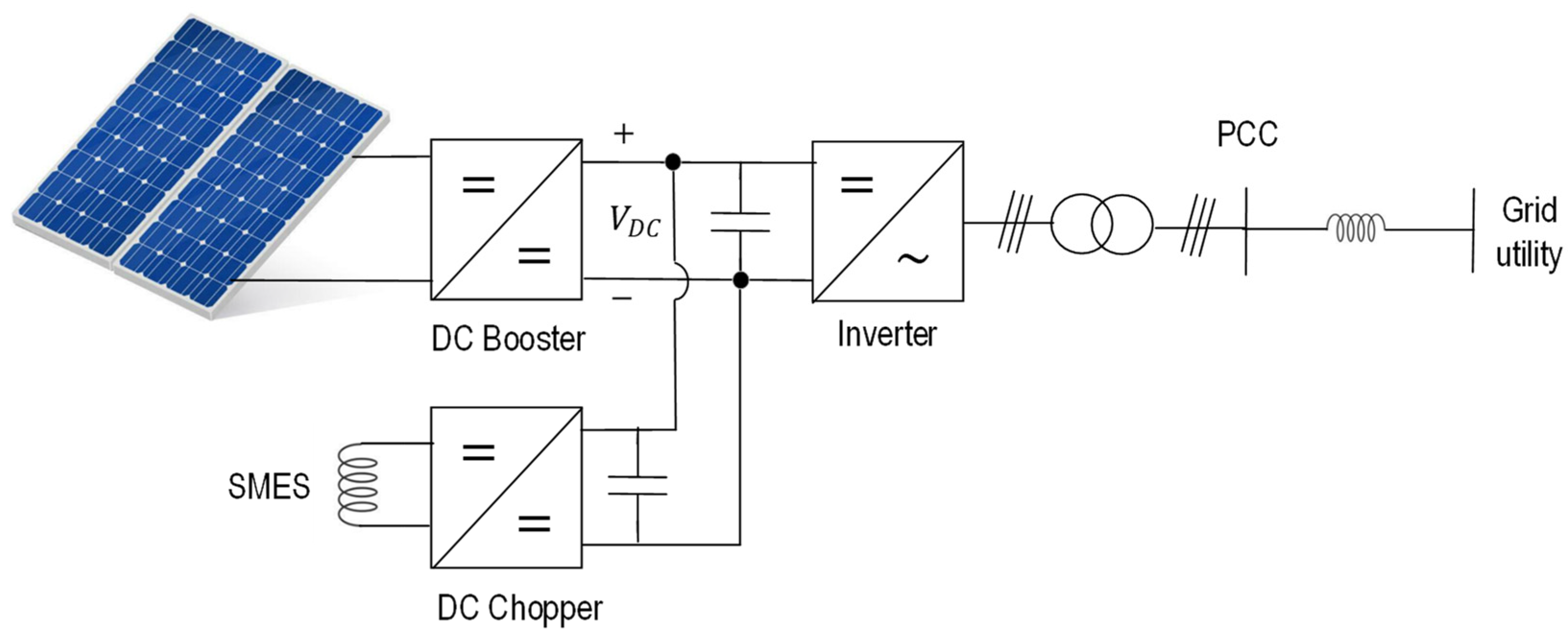
3.2. Current Conversion Circuits and Systems
3.3. Performance and Investment Indicators for Real Systems
4. Frequency Regulation
4.1. Global Frequency Regulation System Models and Parameters
4.2. Superconducting Magnetic Energy Storage System Models
4.3. Systems Overview and Development Challenges in Frequency Control
- (1)
- Optimization of the SMES energy storage capacity looking for the renewable resources potential and expected load demanding profile.
- (2)
- Use of predictive control for anticipating the possibility that the maximum frequency deviation is exceeded based on the prediction of renewable resources evolution.
- (3)
- Study and assessment of SMES system control techniques for frequency regulation on grids with significant renewable power generation.
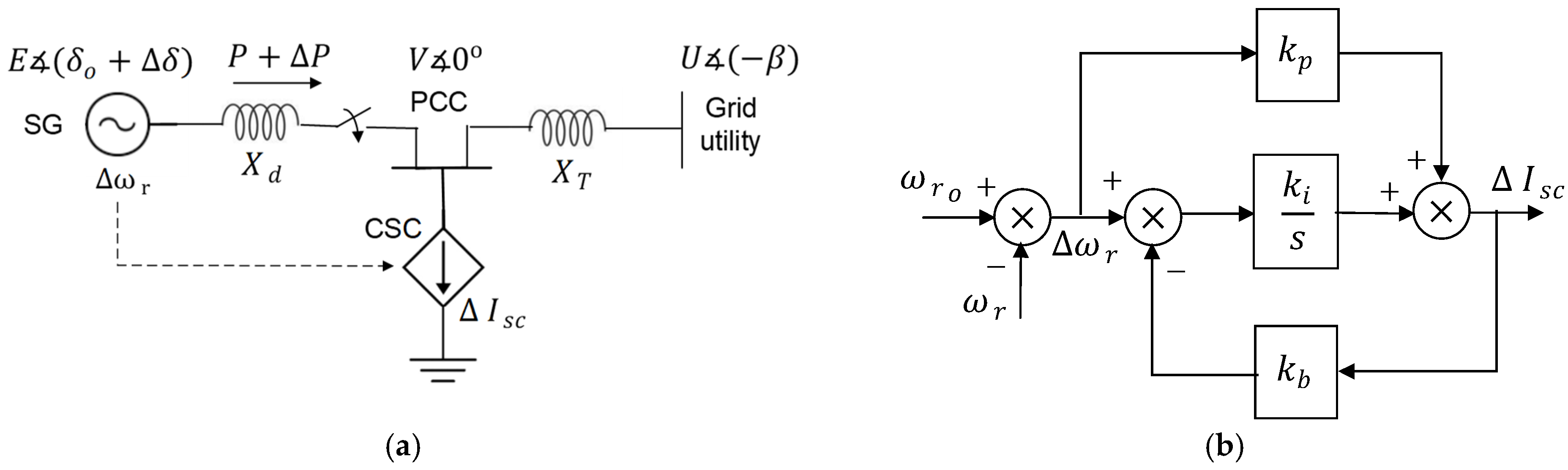
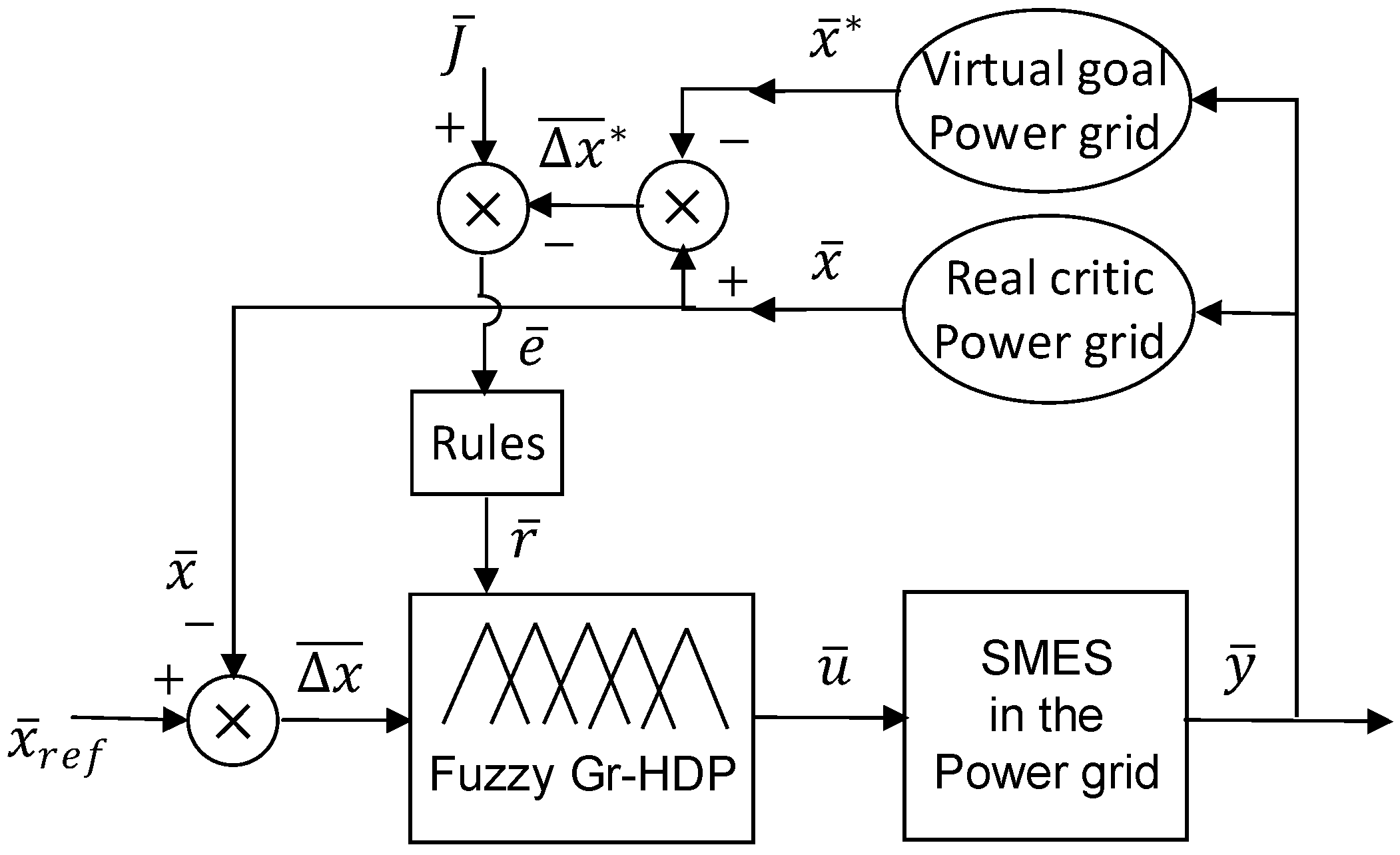
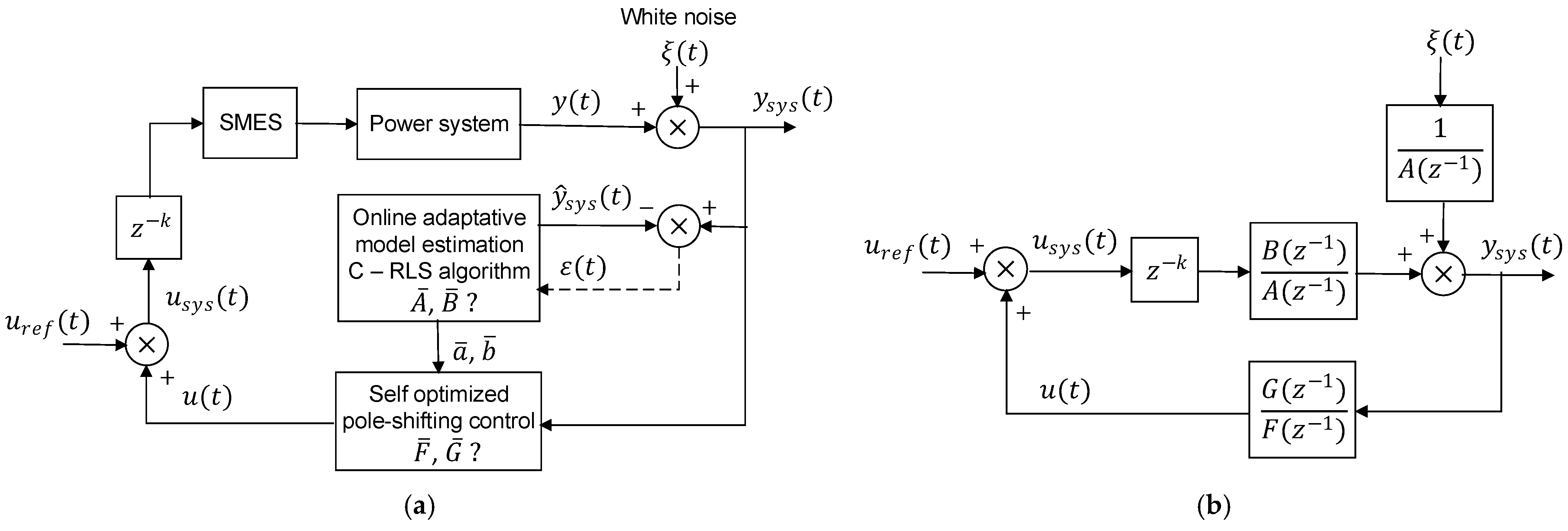
5. Power Oscillation Damping
5.1. Power Oscillation Damping Systems Using Superconducting Magnetic Energy Storage
5.2. Systems Overview and Development Challenges in Oscillation Damping
- (1)
- Optimization of the SMES energy storage capacity for a specific damping coefficient.
- (2)
- Analysis of the damping gain from using the distributed Fuzzy-GrHDP on a grid with several SG, looking for the synchronous deviations between different SG, instead of performing the power oscillation damping based only on the local generator phase angle.
- (3)
- Use of distributed adaptative control SMES systems, with adaptative algorithms based on the measurements of power oscillations also from other decentralized renewable power generation plants in the same distribution grid.
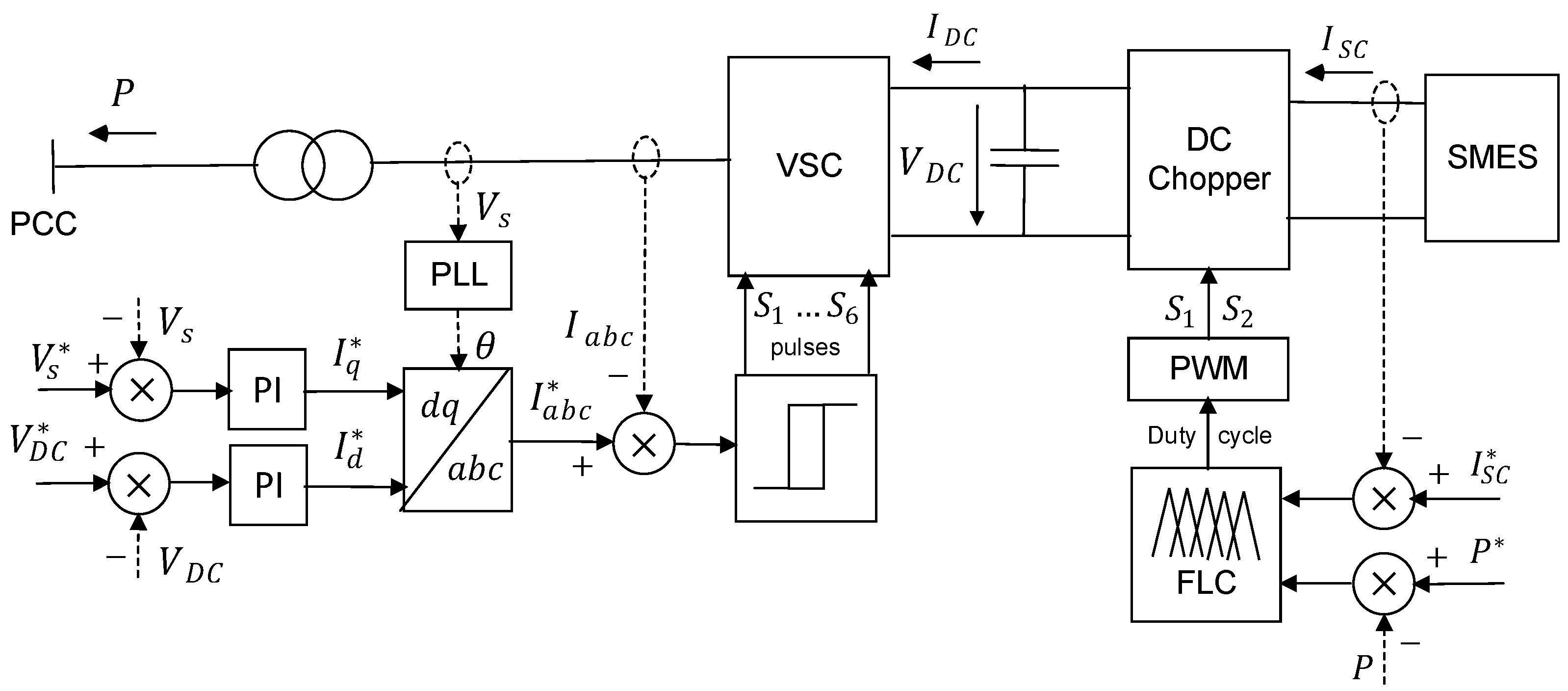
6. Power Fluctuation Suppression
6.1. Power Fluctuation Suppression Systems Using Superconducting Magnetic Energy Storage
6.1.1. Wind Power Generation
6.1.2. Photovoltaic Power Generation
6.2. Systems Overview and Development Challenges in Fluctuation Suppression
- (1)
- Studies comparing the efficiency, time-response and fluctuation suppression precision of SMES systems connected via VSC and DC chopper to the AC grid bus or via only a DC-Chopper to the DC-link of DFIG or to the DC -grid of wind or PV generation plants.
- (2)
- Studies of the transient effects when a superconducting magnet with both SMES and SFCL functionalities, changes from a specific stored magnetic energy to support a short-circuit fault current.
- (3)
- Studies comparing the precision of SVPWM and HCC modulations on the control of VSC in an SMES system for power suppression.
- (4)
- The proposal and study of adaptative control techniques that continuously adapt to the system response and improve the power fluctuation suppression.
7. Voltage Sags and Flickering Compensation
8. Active Harmonics Filtering
8.1. Active Harmonics Filtering Systems Using Superconducting Magnetic Energy Storage
8.2. Active Harmonics Filtering Challenges
- (1)
- Determination of the minimum optimum SMES energy storage capacity that is necessary to generate cancellation currents equal in magnitude but opposite in phase to the detected harmonics.
- (2)
9. Quantitative Overview
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hjalmarsson, J.; Thomas, K.; Boström, C. Service stacking using energy storage systems for grid applications—A review. J. Energy Storage 2023, 60, 106639. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Luongo, C.A.; Baldwin, T.; Ribeiro, P.; Weber, C.M. A 100 MJ SMES demonstration at FSU-CAPS. IEEE Trans. Appl. Supercond. 2003, 13, 1800–1805. [Google Scholar] [CrossRef]
- Sparacio, S.; Napolitano, A.; Savoldi, L.; Viarengo, S.; Laviano, F. Design of a Module for a 10 MJ Toroidal YBCO Superconducting Magnetic Energy Storage. IEEE Trans. Appl. Supercond. 2022, 32, 5700105. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Y.; Gao, Y.; Yang, Z.; Li, Z.; Pi, W. Mechanical characterization of a 10-MJ HTS SMES magnet wound by quasi-isotropic strands and directly stacked tape conductors. Superconductivity 2023, 5, 100042. [Google Scholar] [CrossRef]
- Katagiri, T.; Nakabayashi, H.; Nijo, Y.; Tamada, T.; Noda, T.; Hirano, N.; Nagata, T.; Nagaya, S.; Yamane, M.; Ishii, Y.; et al. Field Test Result of 10MVA/20MJ SMES for Load Fluctuation Compensation. IEEE Trans. Appl. Supercond. 2009, 19, 1993–1998. [Google Scholar] [CrossRef]
- Singh, H.; Vadhera, S. Comparative analysis between SMES and BESS in application of VSC-HVDC system. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Adetokun, B.B.; Oghorada, O.; Abubakar, S.J. Superconducting magnetic energy storage systems: Prospects and challenges for renewable energy applications. J. Energy Storage 2022, 55, 105663. [Google Scholar] [CrossRef]
- Molina-Ibáñez, E.-L.; Rosales-Asensio, E.; Pérez-Molina, C.; Pérez, F.M.; Colmenar-Santos, A. Analysis on the electric vehicle with a hybrid storage system and the use of Superconducting magnetic energy storage (SMES). Energy Rep. 2021, 7, 854–873. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Huang, Y.; Ru, Y.; Shen, Y.; Zeng, Z. Characteristics and Applications of Superconducting Magnetic Energy Storage. J. Phys. Conf. Ser. 2021, 2108, 012038. [Google Scholar] [CrossRef]
- Jin, J.X.; Chen, X.Y. Study on the SMES Application Solutions for Smart Grid. Phys. Procedia 2012, 36, 902–907. [Google Scholar] [CrossRef]
- Alkhafaji, A.S.; Trabelsi, H. Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions. Energies 2022, 15, 8597. [Google Scholar] [CrossRef]
- Yunus, A.M.S.; Saini, M. Overview of SMES units application on smart grid systems. In Proceedings of the 2016 International Seminar on Intelligent Technology and Its Applications (ISITIA), Lombok, Indonesia, 28–30 July 2016; pp. 465–470. [Google Scholar]
- Jacques, B.J.; Armel, T.K.F.; Astrid, M.N.B.; René, T. Contribution to the improvement of the performances of PV/wind microgrids integrating a hybrid SMES/battery energy storage unit. J. Energy Storage 2024, 85, 111011. [Google Scholar] [CrossRef]
- Wang, P.; Lu, J.; Wu, Y.; Xu, L.; Li, J.; Mao, H.; Tian, Y.; Xu, B.; Huang, J. A Novel Cooperative Control for SMES/Battery Hybrid Energy Storage in PV Grid-Connected System. IEEE Trans. Appl. Supercond. 2024, 34, 5401605. [Google Scholar] [CrossRef]
- Papageorgiou, P.G.; Papafilippou, P.T.; Oureilidis, K.O.; Christoforidis, G.C. An Adaptive Controller of a Hybrid Storage System for Power Smoothing with Enlarged Battery Lifetime. IEEE Trans. Sustain. Energy 2024, 15, 2567–2580. [Google Scholar] [CrossRef]
- Hernando, C.; Munilla, J.; García-Tabarés, L.; Pedraz, G. Optimization of High Power SMES for Naval Applications. IEEE Trans. Appl. Supercond. 2023, 33, 5700205. [Google Scholar] [CrossRef]
- Jin, J.X.; Xu, W.; Chen, X.Y.; Zhou, X.; Zhang, J.Y.; Gong, W.Z.; Ren, A.L.; Xin, Y. Developments of SMES devices and potential applications in smart grids. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar]
- Bevrani, H.; Golpîra, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- Khan, I.A.; Mokhlis, H.; Mansor, N.N.; Illias, H.A.; Awalin, L.J.; Wang, L. New trends and future directions in load frequency control and flexible power system: A comprehensive review. Alex. Eng. J. 2023, 71, 263–308. [Google Scholar] [CrossRef]
- Filippidis, S.; Bouhouras, A.; Poulakis, N.; Christoforidis, G. A Review of the Cryocooler-Based Cooling Systems for SMES. IEEE Trans. Appl. Supercond. 2021, 31, 4902713. [Google Scholar] [CrossRef]
- Zhang, H.; Nie, Z.; Xiao, X.; Aggarwal, R.; Kang, Q.; Ainslie, M.; Zhu, J.; Coombs, T.; Yuan, W. Design and Simulation of SMES System Using YBCO Tapes for Direct Drive Wave Energy Converters. IEEE Trans. Appl. Supercond. 2013, 23, 5700704. [Google Scholar] [CrossRef]
- Zimmermann, A.W.; Sharkh, S.M. Design of a 1 MJ/100 kW high temperature superconducting magnet for energy storage. Energy Rep. 2020, 6, 180–188. [Google Scholar] [CrossRef]
- Wang, Q.; Dai, Y.; Song, S.; Wen, H.; Bai, Y.; Yan, L.; Kim, K. A 30 kJ Bi2223 High Temperature Superconducting Magnet for SMES with Solid-Nitrogen Protection. IEEE Trans. Appl. Supercond. 2008, 18, 754–757. [Google Scholar] [CrossRef]
- Atomura, N.; Takahashi, T.; Amata, H.; Iwasaki, T.; Son, K.; Miyagi, D.; Tsuda, M.; Hamajima, T.; Shintomi, T.; Makida, Y.; et al. Conceptual design of MgB2 coil for the 100 MJ SMES of advanced superconducting power conditioning system (ASPCS). Phys. Procedia 2012, 27, 400–403. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.-H.; Kim, W.-S.; Lee, J.-K.; Lee, S.; Park, C.; Bae, J.-H.; Kim, S.-H.; Seong, K.-C.; Choi, K.; et al. Analysis of Eddy Current Losses and Magnetization Losses in Toroidal Magnets for a 2.5 MJ HTS SMES. IEEE Trans. Appl. Supercond. 2011, 21, 1354–1357. [Google Scholar] [CrossRef]
- Kim, K.; Kim, A.-R.; Kim, J.-G.; Park, M.; Yu, I.-K.; Sohn, M.-H.; Eom, B.-Y.; Sim, K.; Kim, S.; Kim, H.-J.; et al. Analysis of Operational Loss Characteristics of 10 kJ Class Toroid-Type SMES. IEEE Trans. Appl. Supercond. 2011, 21, 1340–1343. [Google Scholar] [CrossRef]
- Kim, A.-R.; Kim, G.-H.; Kim, K.-M.; Kim, J.-G.; Kim, D.-W.; Park, M.; Yu, I.-K.; Kim, S.-H.; Sim, K.; Seong, K.-C. Design and Manufacturing of a SMES Model Coil for Real Time Digital Simulator Based Power Quality Enhancement Simulation. IEEE Trans. Appl. Supercond. 2010, 20, 1339–1343. [Google Scholar] [CrossRef]
- Trillaud, F.; Cruz, L.S. Conceptual Design of a 200-kJ 2G-HTS Solenoidal μ-SMES. IEEE Trans. Appl. Supercond. 2014, 24, 5700205. [Google Scholar] [CrossRef]
- Kamada, H.; Ninomiya, A.; Nomura, S.; Yagai, T.; Nakamura, T.; Chikaraishi, H. Development of 1-T Class Force-Balanced Helical Coils Using REBCO Tapes. IEEE Trans. Appl. Supercond. 2020, 30, 4600905. [Google Scholar] [CrossRef]
- Kimura, Y.; Kamada, H.; Nomura, S.; Yagai, T.; Nakamura, T.; Tsutsui, H.; Chikaraishi, H.; Yanagi, N.; Imagawa, S. Development of a Prototype Winding Machine for Helical Coils Using High-Temperature Superconducting Tapes. IEEE Trans. Appl. Supercond. 2016, 26, 4202104. [Google Scholar] [CrossRef]
- Kim, A.-R.; Jung, H.-Y.; Kim, J.-H.; Park, M.; Yu, I.-K.; Kim, S.-H.; Sim, K.; Kim, H.-J.; Seong, K.-C. Design of a 10 kJ Class SMES Model Coil for Real Time Digital Simulator Based Grid Connection Study. IEEE Trans. Appl. Supercond. 2009, 19, 2023–2027. [Google Scholar] [CrossRef]
- Wang, Q.; Song, S.; Lei, Y.; Dai, Y.; Zhang, B.; Wang, C.; Lee, S.; Kim, K. Design and Fabrication of a Conduction-Cooled High Temperature Superconducting Magnet for 10 kJ Superconducting Magnetic Energy Storage System. IEEE Trans. Appl. Supercond. 2006, 16, 570–573. [Google Scholar] [CrossRef]
- Zheng, Z.-X.; Chen, X.-Y.; Xiao, X.-Y.; Huang, C.-J. Design and Evaluation of a Mini-Size SMES Magnet for Hybrid Energy Storage Application in a kW-Class Dynamic Voltage Restorer. IEEE Trans. Appl. Supercond. 2017, 27, 5700911. [Google Scholar] [CrossRef]
- Jubleanu, R.; Cazacu, D. Design and Numerical Study of Magnetic Energy Storage in Toroidal Superconducting Magnets Made of YBCO and BSCCO. Magnetochemistry 2023, 9, 216. [Google Scholar] [CrossRef]
- Vialle, J.; Badel, A.; Tixador, P.; Ciceron, J.; Forest, F.; Pasquet, R. Preliminary Tests of Pancakes From a 12 T REBCO Insulated Solenoid Magnet. IEEE Trans. Appl. Supercond. 2021, 31, 4600805. [Google Scholar] [CrossRef]
- Kim, H.J.; Seong, K.C.; Cho, J.W.; Bae, J.H.; Sim, K.D.; Kim, S.; Lee, E.Y.; Ryu, K.; Kim, S.H. 3 MJ/750 kVA SMES System for Improving Power Quality. IEEE Trans. Appl. Supercond. 2006, 16, 574–577. [Google Scholar] [CrossRef]
- Nomura, S.; Kasuya, K.; Tanaka, N.; Tsuboi, K.; Tsutsui, H.; Tsuji-Iio, S.; Shimada, R. Experimental Results of a 7-T Force-Balanced Helical Coil for Large-Scale SMES. IEEE Trans. Appl. Supercond. 2008, 18, 701–704. [Google Scholar] [CrossRef]
- Nomura, S.; Kasuya, K.; Tanaka, N.; Tsuboi, K.; Tsutsui, H.; Tsuji-Iio, S.; Shimada, R.; Arai, K.; Ninomiya, A.; Ishigohka, T. Quench Properties of a 7-T Force-Balanced Helical Coil for Large-Scale SMES. IEEE Trans. Appl. Supercond. 2009, 19, 2004–2007. [Google Scholar] [CrossRef]
- Hayashi, H.; Hatabe, Y.; Nagafuchi, T.; Taguchi, A.; Terazono, K.; Ishii, T.; Taniguchi, S. Test Results of Power System Control by Experimental SMES. IEEE Trans. Appl. Supercond. 2006, 16, 598–601. [Google Scholar] [CrossRef]
- Ali, M.H.; Wu, B.; Dougal, R.A. An Overview of SMES Applications in Power and Energy Systems. IEEE Trans. Sustain. Energy 2010, 1, 38–47. [Google Scholar] [CrossRef]
- Sun, Q.; Lv, H.; Gao, S.; Wei, K.; Mauersberger, M. Optimized Control of Reversible VSC with Stability Mechanism Study in SMES Based V2G System. IEEE Trans. Appl. Supercond. 2019, 29, 5401106. [Google Scholar] [CrossRef]
- Chen, X.; Xie, Q.; Bian, X.; Shen, B. Energy-saving superconducting magnetic energy storage (SMES) based interline DC dynamic voltage restorer. J. Power Energy Syst. 2022, 8, 238–248. [Google Scholar] [CrossRef]
- Jin, J.X.; Wang, J.; Yang, R.H.; Zhang, T.L.; Mu, S.; Fan, Y.J.; Xing, Y.Q. A superconducting magnetic energy storage with dual functions of active filtering and power fluctuation suppression for photovoltaic microgrid. J. Energy Storage 2021, 38, 102508. [Google Scholar] [CrossRef]
- Zhu, J.; Bao, X.; Yang, B.; Chen, P.; Yang, Y.; Qiu, M. Dynamic Simulation Test Research on Power Fluctuation Compensation Using Hybrid SMES of YBCO and BSCCO Tapes. IEEE Trans. Appl. Supercond. 2012, 22, 5700404. [Google Scholar] [CrossRef]
- Abdalrahman, G.; Abdalla, O.H.; Jibril, M.I.; Awad, A.A. Space Vector Pulse Width Modulation Technique Applied to Two Level Voltage Source Inverter. SUST J. Eng. Comput. Sci. 2018, 19, 10–17. [Google Scholar]
- Shen, Y.; Zheng, Z.; Wang, Q.; Liu, P.; Yang, X. DC Bus Current Sensed Space Vector Pulsewidth Modulation for Three-Phase Inverter. IEEE Trans. Transp. Electrif. 2021, 7, 815–824. [Google Scholar] [CrossRef]
- Abraham, R.J.; Das, D.; Patra, A. Automatic generation control of an interconnected hydrothermal power system considering superconducting magnetic energy storage. Int. J. Electr. Power Energy Syst. 2007, 29, 571–579. [Google Scholar] [CrossRef]
- Elmelegi, A.; Mohamed, E.A.; Aly, M.; Ahmed, E.M.; Mohamed, A.-A.A.; Elbaksawi, O. Optimized Tilt Fractional Order Cooperative Controllers for Preserving Frequency Stability in Renewable Energy-Based Power Systems. IEEE Access 2021, 9, 8261–8277. [Google Scholar] [CrossRef]
- Pappachen, A.; Fathima, A.P. Load frequency control in deregulated power system integrated with SMES–TCPS combination using ANFIS controller. Int. J. Electr. Power Energy Syst. 2016, 82, 519–534. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Alhasheem, M. Superconducting energy storage technology-based synthetic inertia system control to enhance frequency dynamic performance in microgrids with high renewable penetration. Prot. Control Mod. Power Syst. 2021, 6, 36. [Google Scholar] [CrossRef]
- Bhatt, P.; Ghoshal, S.P.; Roy, R. Coordinated control of TCPS and SMES for frequency regulation of interconnected restructured power systems with dynamic participation from DFIG based wind farm. Renew. Energy 2012, 40, 40–50. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Molina-Ibáñez, E.-L.; Rosales-Asensio, E.; Blanes-Peiró, J.-J. Legislative and economic aspects for the inclusion of energy reserve by a superconducting magnetic energy storage: Application to the case of the Spanish electrical system. Renew. Sustain. Energy Rev. 2018, 82, 2455–2470. [Google Scholar] [CrossRef]
- Soman, R.; Ravindra, H.; Huang, X.; Schoder, K.; Steurer, M.; Yuan, W.; Zhang, M.; Venuturumilli, S.; Chen, X. Preliminary Investigation on Economic Aspects of Superconducting Magnetic Energy Storage (SMES) Systems and High-Temperature Superconducting (HTS) Transformers. IEEE Trans. Appl. Supercond. 2018, 28, 5400805. [Google Scholar] [CrossRef]
- European Union. Commission Regulation (EU) 2017/1485 of 2 August 2017 Establishing a Guideline on Electricity Transmission System Operation; European Union: Brussels, Belgium, 2017. [Google Scholar]
- Mohamed, E.A.; Ahmed, E.M.; Elmelegi, A.; Aly, M.; Elbaksawi, O.; Mohamed, A.-A.A. An Optimized Hybrid Fractional Order Controller for Frequency Regulation in Multi-Area Power Systems. IEEE Access 2020, 8, 213899–213915. [Google Scholar] [CrossRef]
- Banerjee, S.; Chatterjee, J.K.; Tripathy, S.C. Application of magnetic energy storage unit as load-frequency stabilizer. IEEE Trans. Energy Convers. 1990, 5, 46–51. [Google Scholar] [CrossRef]
- Chandrakala, V.; Sukumar, B.; Sankaranarayanan, K. Load Frequency Control of Multi-source Multi-area Hydro Thermal System Using Flexible Alternating Current Transmission System Devices. Electr. Power Compon. Syst. 2014, 42, 927–934. [Google Scholar] [CrossRef]
- Vyshna, K.; Thresia, M.M.; Shahin, M. Design of SMES for Load Frequency Control in Power Systems with Renewable Integration. In Proceedings of the 2023 5th International Conference on Energy, Power and Environment: Towards Flexible Green Energy Technologies (ICEPE), Shillong, India, 15–17 June 2023; pp. 1–6. [Google Scholar]
- Khan, I.A.; Mokhlis, H.; Mansor, N.N.; Illias, H.A.; Usama, M.; Daraz, A.; Wang, L.; Awalin, L.J. Load Frequency Control Using Golden Eagle Optimization for Multi-Area Power System Connected Through AC/HVDC Transmission and Supported with Hybrid Energy Storage Devices. IEEE Access 2023, 11, 44672–44695. [Google Scholar] [CrossRef]
- Ali, H.H.; Kassem, A.M.; Al-Dhaifallah, M.; Fathy, A. Multi-Verse Optimizer for Model Predictive Load Frequency Control of Hybrid Multi-Interconnected Plants Comprising Renewable Energy. IEEE Access 2020, 8, 114623–114642. [Google Scholar] [CrossRef]
- Pati, S.S.; Subudhi, U. Frequency regulation of Solar-Wind integrated multi-area system with SMES and SSSC. In Proceedings of the 2021 IEEE International Power and Renewable Energy Conference (IPRECON), Kerala, India, 24–26 September 2021; pp. 1–4. [Google Scholar]
- Alam, M.S.; Al-Ismail, F.S.; Abido, M.A. PV/Wind-Integrated Low-Inertia System Frequency Control: PSO-Optimized Fractional-Order PI-Based SMES Approach. Sustainability 2021, 13, 7622. [Google Scholar] [CrossRef]
- Tripathy, S.C.; Juengst, K.P. Sampled data automatic generation control with superconducting magnetic energy storage in power systems. IEEE Trans. Energy Convers. 1997, 12, 187–192. [Google Scholar] [CrossRef]
- Tran, X.K.; Chen, Y.; Phan, G.T.; Huynh, D.H. Optimal Design for Frequency Fluctuation Control System with SMES Unit. In Proceedings of the 2020 4th International Conference on Robotics and Automation Sciences (ICRAS), Chengdu, China, 14–16 June 2020; pp. 50–54. [Google Scholar]
- Li, T.; Xie, J.; Gong, X.; Chen, M.; Zeng, Q.; Chen, X. Mechanism Analysis and Controller Design of SMES-Based Power Oscillation Damping. IEEE Trans. Appl. Supercond. 2021, 31, 5403704. [Google Scholar] [CrossRef]
- Li, T.; Hu, W.; Zhang, B.; Zhang, G.; Zhang, Z.; Chen, Z. SMES Damping Controller Design and Real-Time Parameters Tuning for Low-Frequency Oscillation. IEEE Trans. Appl. Supercond. 2021, 31, 3800604. [Google Scholar] [CrossRef]
- Tang, Y.; Mu, C.; He, H. SMES-Based Damping Controller Design Using Fuzzy-GrHDP Considering Transmission Delay. IEEE Trans. Appl. Supercond. 2016, 26, 5701206. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, H.; Jiang, L.; Zeng, P. A SMES-based adaptive damping controller design in wind power system. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 212–216. [Google Scholar]
- Rai, D.; Gokaraju, R.; Faried, S.O. Adaptive Control Using Constrained RLS and Dynamic Pole-Shift Technique for TCSCs. IEEE Trans. Power Deliv. 2014, 29, 224–234. [Google Scholar] [CrossRef]
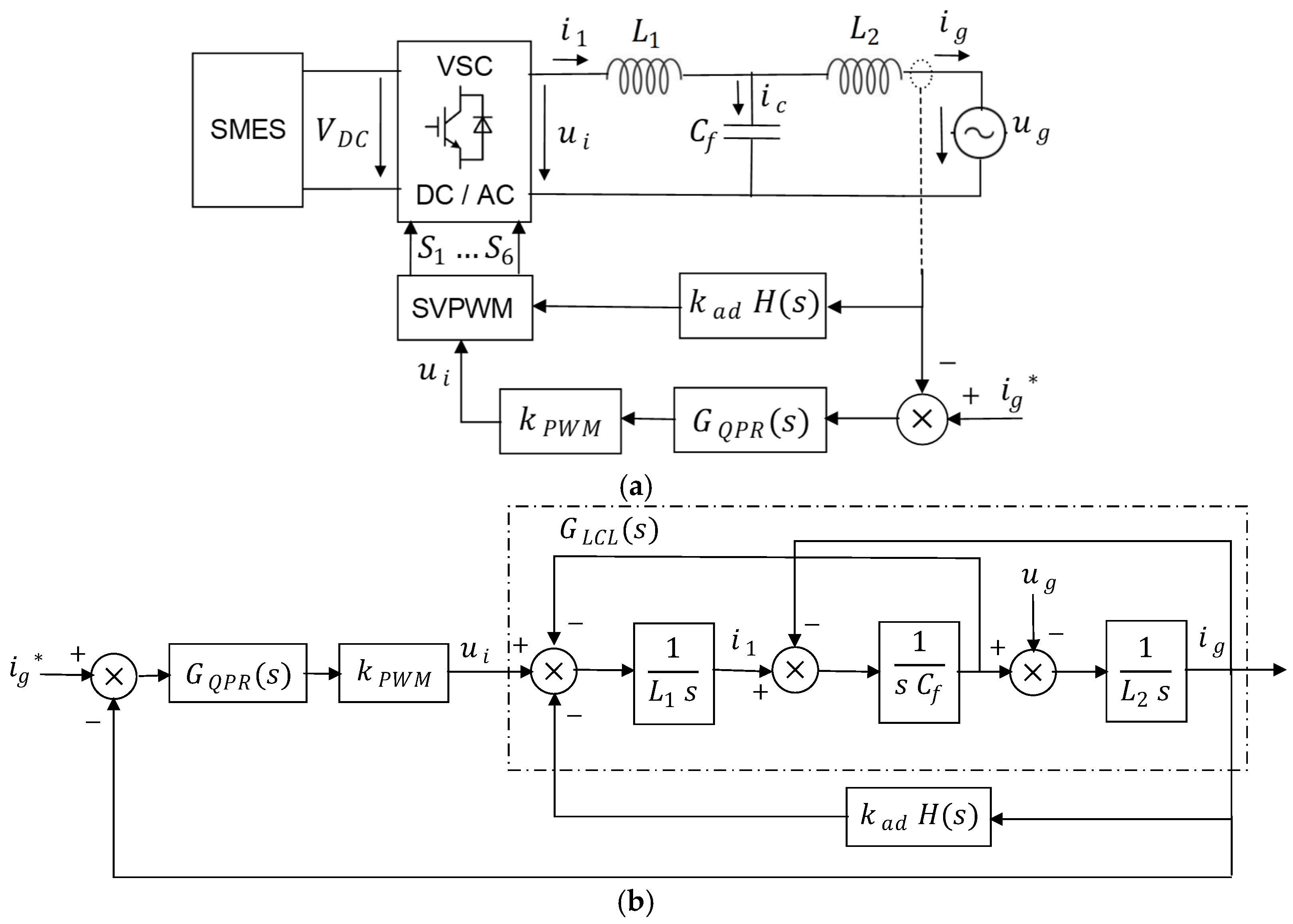
- Sun, Q.; Miao, Y.; Zhao, L.; Xu, J.; Gao, S.; Wei, K.; Wang, L. Study on LCL-Type Grid-Connected VSC Based on Optimized Active Damping with NBPF for SMES System. IEEE Trans. Appl. Supercond. 2024, 34, 5701505. [Google Scholar] [CrossRef]
- dos Santos Costa, A.J.A.; Valério, D.; da Costa Branco, P.J. Predictive control model to manage power flow on a hybrid wind-photovoltaic and diesel microgeneration power plant with additional storage capacity. IET Cyber-Phys. Syst. Theory Appl. 2018, 3, 206–211. [Google Scholar] [CrossRef]
- Amezquita, H.; Carvalho, P.M.S.; Morais, H. Wind Forecast at Medium Voltage Distribution Networks. Energies 2023, 16, 2887. [Google Scholar] [CrossRef]
- Amezquita, H.; Guzman, C.P.; Morais, H. Forecasting Electric Vehicles’ Charging Behavior at Charging Stations: A Data Science-Based Approach. Energies 2024, 17, 3396. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, D.; Mu, B.; Wang, L.Y.; Bao, Y.; Jiang, J.; Morais, H. Decentralized Electric Vehicle Charging Strategies for Reduced Load Variation and Guaranteed Charge Completion in Regional Distribution Grids. Energies 2017, 10, 147. [Google Scholar] [CrossRef]
- Yunus, A.M.S.; Abu-Siada, A.; Mosaad, M.I.; Albalawi, H.; Aljohani, M.; Jin, J.X. Application of SMES Technology in Improving the Performance of a DFIG-WECS Connected to a Weak Grid. IEEE Access 2021, 9, 124541–124548. [Google Scholar] [CrossRef]
- Salama, H.S.; Vokony, I. Voltage and Frequency Control of Balanced/Unbalanced Distribution System Using the SMES System in the Presence of Wind Energy. Electricity 2021, 2, 205–224. [Google Scholar] [CrossRef]
- Ngamroo, I.; Karaipoom, T. Cooperative Control of SFCL and SMES for Enhancing Fault Ride Through Capability and Smoothing Power Fluctuation of DFIG Wind Farm. IEEE Trans. Appl. Supercond. 2014, 24, 5400304. [Google Scholar] [CrossRef]
- Ngamroo, I.; Karaipoom, T. Improving Low-Voltage Ride-Through Performance and Alleviating Power Fluctuation of DFIG Wind Turbine in DC Microgrid by Optimal SMES with Fault Current Limiting Function. IEEE Trans. Appl. Supercond. 2014, 24, 5700805. [Google Scholar] [CrossRef]
- Karaipoom, T.; Ngamroo, I. Optimal Superconducting Coil Integrated into DFIG Wind Turbine for Fault Ride Through Capability Enhancement and Output Power Fluctuation Suppression. IEEE Trans. Sustain. Energy 2015, 6, 28–42. [Google Scholar] [CrossRef]
- Jin, J.X.; Yang, R.H.; Zhang, R.T.; Fan, Y.J.; Xie, Q.; Chen, X.Y. Combined low voltage ride through and power smoothing control for DFIG/PMSG hybrid wind energy conversion system employing a SMES-based AC-DC unified power quality conditioner. Int. J. Electr. Power Energy Syst. 2021, 128, 106733. [Google Scholar] [CrossRef]
- Shivashankar, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M. Mitigating methods of power fluctuation of photovoltaic (PV) sources—A review. Renew. Sustain. Energy Rev. 2016, 59, 1170–1184. [Google Scholar] [CrossRef]
- Wang, J.; Mu, S.; Zhou, Q.; Li, Y.J.; Zhang, T.L. Design and Performance Analysis of PV-SMES-Based Microgrid Integrated with Power Fluctuation Suppression and Active Filtering Control. IEEE Trans. Appl. Supercond. 2021, 31, 5402705. [Google Scholar] [CrossRef]
- Masetti, C. Revision of European Standard EN 50160 on power quality: Reasons and solutions. In Proceedings of the 14th International Conference on Harmonics and Quality of Power—ICHQP 2010, Bergamo, Italy, 26–29 September 2010; pp. 1–7. [Google Scholar]
- Jiang, X.; Zhu, X.; Cheng, Z.; Ren, X.; He, Y. A 150 kVA/0.3 MJ SMES voltage sag compensation system. IEEE Trans. Appl. Supercond. 2005, 15, 1903–1906. [Google Scholar] [CrossRef]
- Zheng, Z.X.; Xiao, X.Y.; Li, C.S.; Chen, Z.; Zhang, Y. Performance Evaluation of SMES System for Initial and Steady Voltage Sag Compensations. IEEE Trans. Appl. Supercond. 2016, 26, 5701105. [Google Scholar] [CrossRef]
- Yunus, A.M.S.; Habriansyah, I.; Abu-Siada, A.; Masoum, M.A.S. Sag and Flicker Reduction Using Hysteresis-Fuzzy Control-Based SMES Unit. Can. J. Electr. Comput. Eng. 2019, 42, 52–57. [Google Scholar] [CrossRef]
- IEEE Std 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014. [CrossRef]
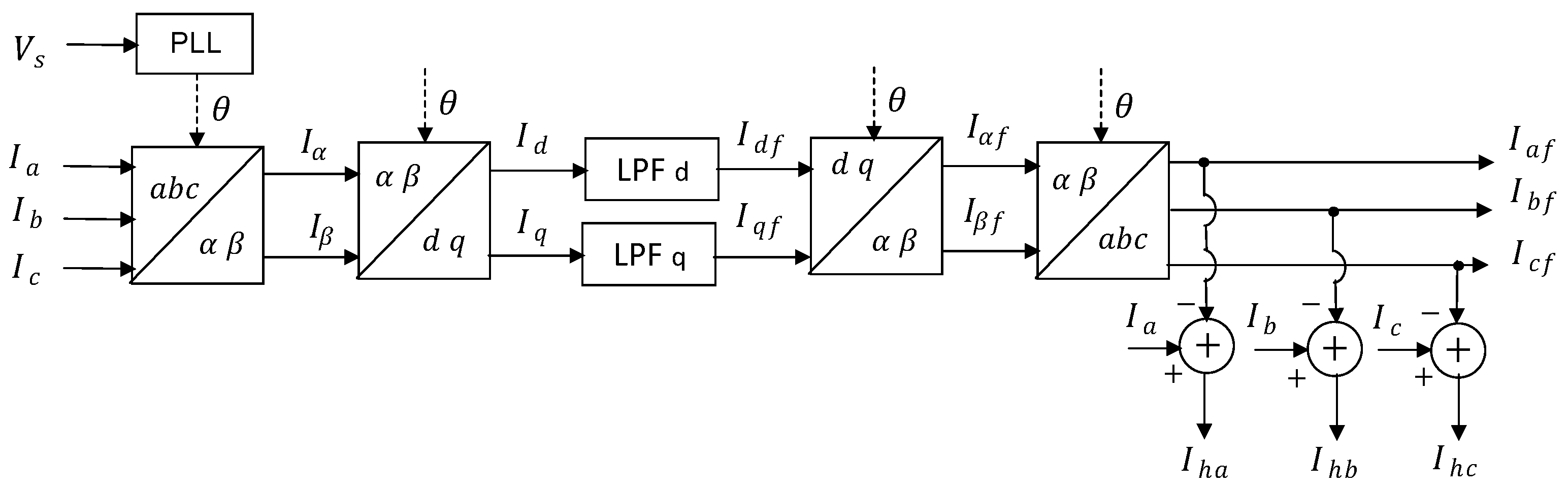
- Tong, L.; Qian, Z.; Kuang, N.; Lingxiao, X.; Peng, F.Z. Optimal Design of Synchronous Reference Frame Harmonic Detection Method. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1071–1076. [Google Scholar]
- Wang, X.; Liu, J.; Hu, J.; Meng, Y.; Yuan, C. Frequency characteristics of the d-q synchronous-frame current reference generation methods for active power filter. In Proceedings of the 2007 7th International Conference on Power Electronics, Daegu, Republic of Korea, 22–26 October 2007; pp. 945–950. [Google Scholar]
- Simoesõ, F.; Pires, V.F.; Murta-Pina, J. Assessment of Using Superconducting Magnetic Energy Storage for Current Harmonic Compensation. In Proceedings of the 2020 International Young Engineers Forum (YEF-ECE), Costa da Caparica, Portugal, 3 July 2020; pp. 73–77. [Google Scholar]
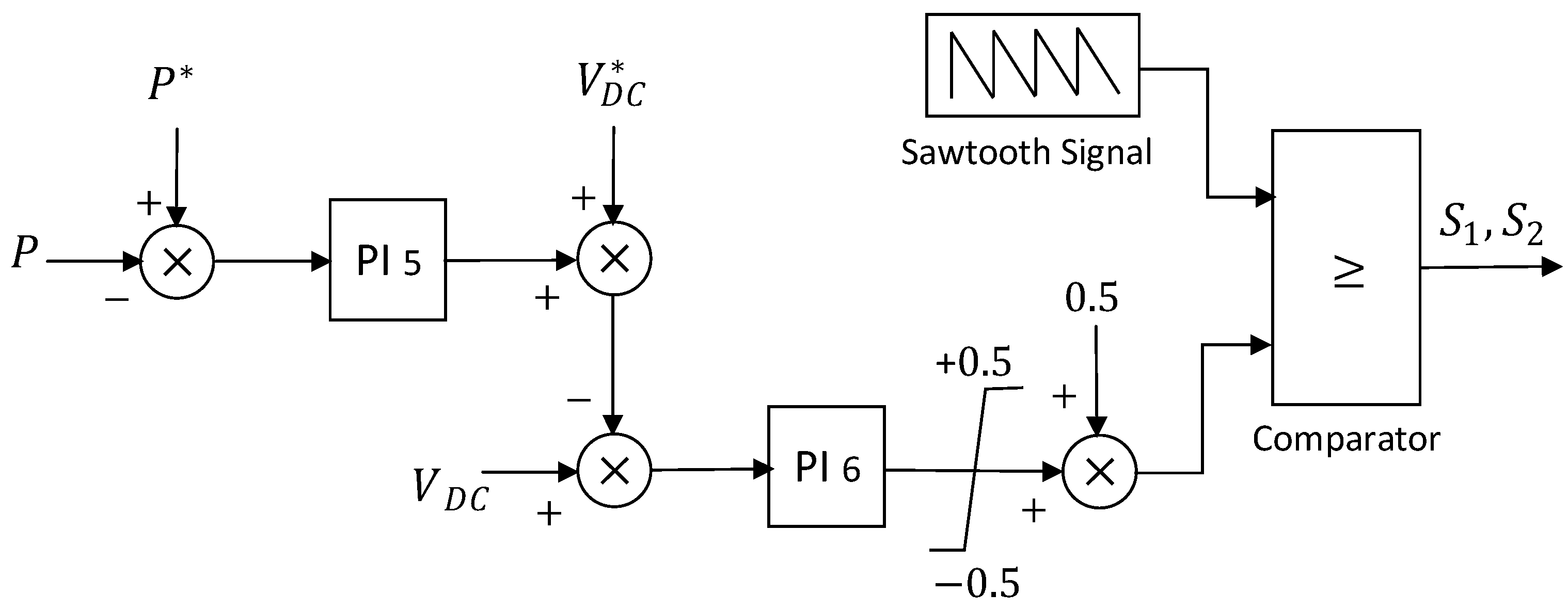
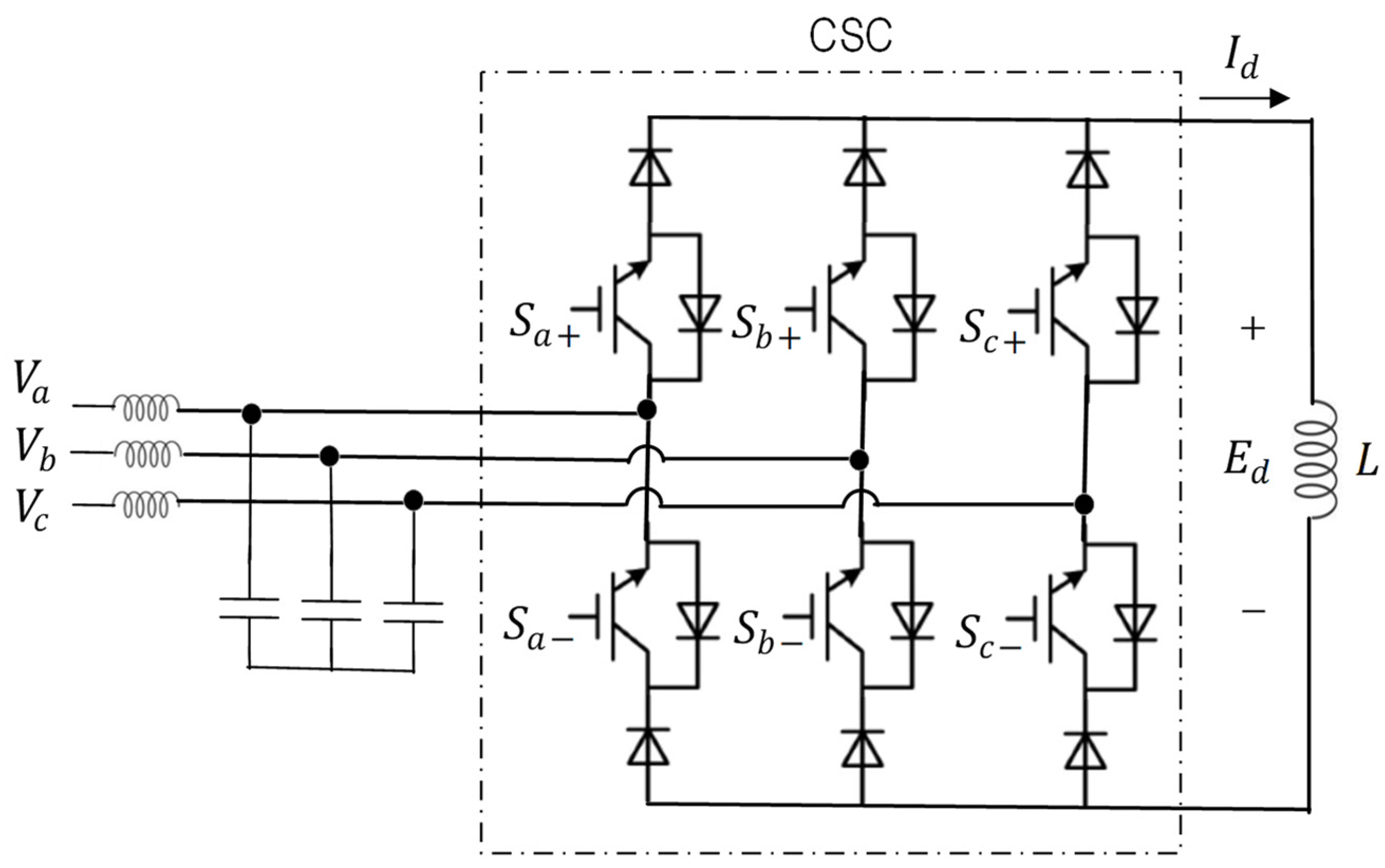

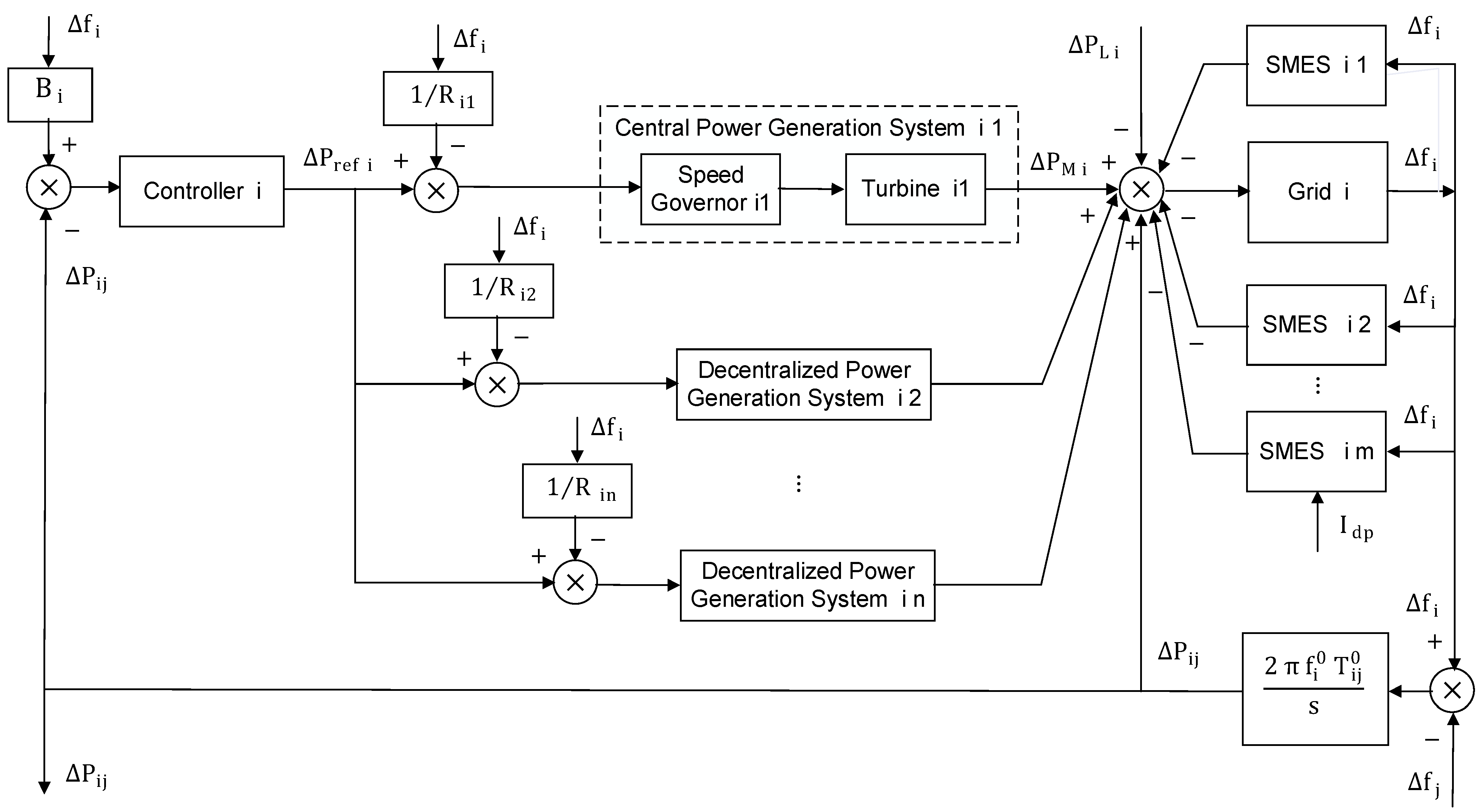

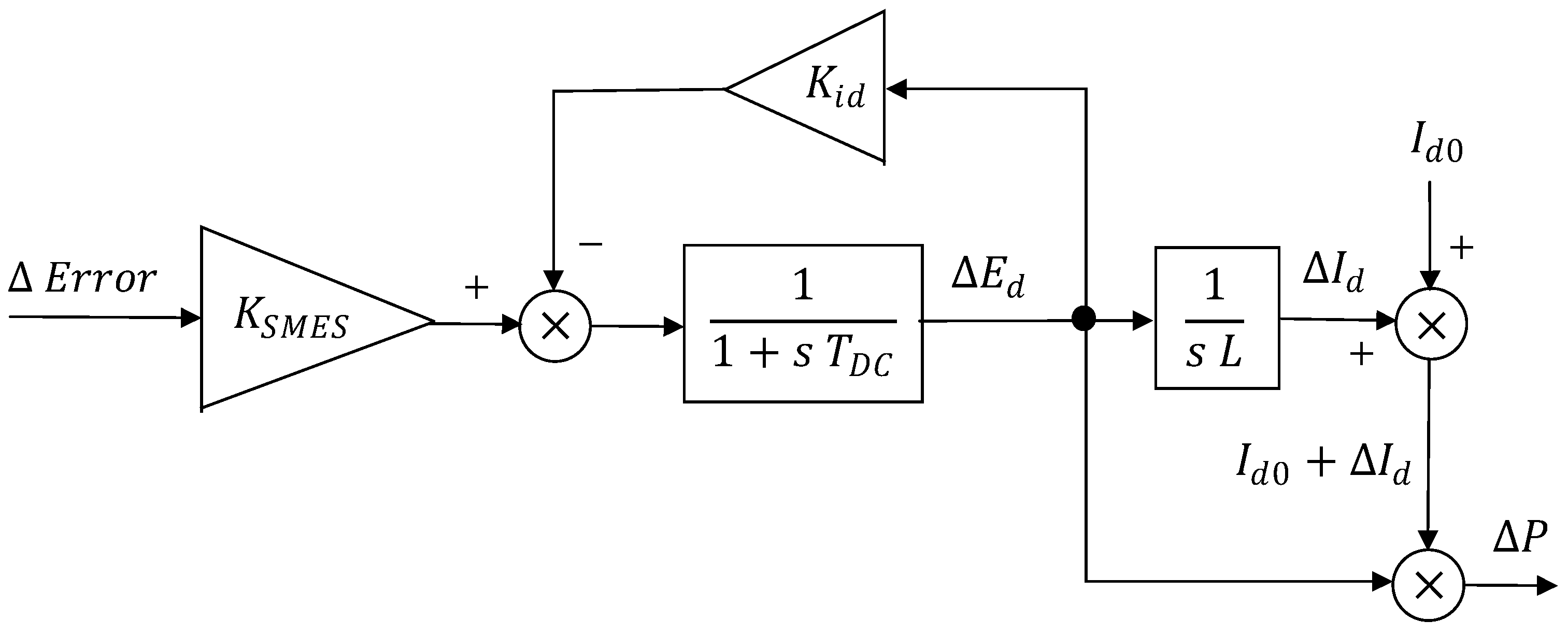

| Magnet | Superconductor | Ref. | ||||
|---|---|---|---|---|---|---|
| double pancake coils | YBCO 4 mm tape | [23] | ||||
| double pancake coils | YBCO 12 mm tape | [24] | ||||
| double pancake coils | BSCCO tape | [25] | ||||
| single coils | MGB2 cable | [26] | ||||
| double pancake coils | YBCO 12 mm tape | [27] | ||||
| double pancake coils | BSCCO tape | [28,29] | ||||
| double pancake coils | YBCO 12 mm tape | [30] | ||||
| Toroid, 52-layer coils | YBCO 12 mm tape | [4] | ||||
| helicoidal coils | YBCO 5 mm tape | [31,32] | ||||
| double pancake coils | YBCO 4 mm tape | [33] | ||||
| Solenoid, 13 double pancake coils | BSCCO tape | [34] | ||||
| single coils | GDBCO wire | [35] | ||||
| Toroid, 16 double pancake coils | BSCCO tape | [36] | ||||
| double pancake coils | ReBCO 12 mm tape | [37] | ||||
| coils | YBCO 4 mm tape | [5] | ||||
| -layer coils | NbTi wires cable | [38] | ||||
| double pancake coils | NbTi/Cu strand cable | [3] | ||||
| poles coil configuration | NbTi wires cable | [6] | ||||
| helical coils | NbTi/Cu strand cable | [39,40] | ||||
| Solenoid, 16 layers coil | NbTi wires cable | [41] |
| Parameter | Values | References |
|---|---|---|
| [49,50,51,57,58,59,60,61,62,65] | ||
| [49,50,51,57,58,59,60,61,62,65] | ||
| [49,50,51,57,58,59,60,61,62,65] | ||
| [49,50,51,52,57,58,59,60,61,62,65] | ||
| [49,50,51,52,57,58,59,60,61,62,65] | ||
| [51,62,65] | ||
| [51,62,65] | ||
| [s] | [49,50,51,57,59] | |
| [49,50,51,57,59] | ||
| [49,50,51,57,59] | ||
| [49,50,51,57,59] | ||
| [49,51,58,59,61,62,65] | ||
| [49,51,58,59,61,62,65] |
| Wind | PV | Diesel | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [s] | [s] | ||||||||
| - | |||||||||
| [1] | Reference | |||||
|---|---|---|---|---|---|---|
| [53] | ||||||
| [51,59] | ||||||
| [21,61,62,63] |
| Reference | |||||
|---|---|---|---|---|---|
| [49,51,64] | |||||
| [50] | |||||
| [52] | |||||
| 100 | [58] | ||||
| 10 | [65] |
| Ref. | # Areas | Centralized Generation | Decentralized Generation | System Control | SMES Interface | SMES System Control |
|---|---|---|---|---|---|---|
| [21] | 1 | 1: Thermal | 1: PV + Wind | Secondary | Not specified | PI Lead-Lag |
| [49] | 2 | 1: Thermal 2: Hydro | - | Secondary | pulse SCR bridge | FOPI |
| [50] | 2 | 1: Thermal 2: Hydro | 1: Wind; 2: PV | Secondary | Not specified | FOPI |
| [51] | 2 | 1: Thermal 2: Hydro | - | Secondary | pulse SCR bridge | FOPI |
| [52] | 1 | 1: Thermal | 1: PV + Wind | Secondary | pulse SCR bridge | FOPI |
| [53] | 2 | 1: Steam reheat 2: Hydro | 1: Wind | Secondary | pulse SCR bridge | PI Lead-Lag |
| [57] | 2 | 1: Thermal 2: Hydro | 1: Wind; 2: PV | Secondary | Not specified | PID |
| [58] | 2 | 1: Thermal reheat 2: Thermal reheat | - | Secondary | pulse SCR bridge | FOPI |
| [59] | 2 | 1: Hydro + Thermal 2: Hydro + Thermal | - | Secondary | pulse SCR bridge | PI Lead-Lag |
| [60] | 2 | 1: Thermal 2: Thermal reheat | - | Secondary | pulse SCR bridge | PI Lead-Lag |
| [61] | 4 | 1, 2, 3, 4: Thermal | - | Secondary | Not specified | PI Lead-Lag |
| [62] | 6 | 1: Thermal; 2: Hydro 3: Thermal; 4: Hydro 5: Thermal; 6: Hydro | 1: PV; 2: Wind 3: Diesel; 4: PV 5: Wind; 6: Diesel | Secondary | pulse SCR bridge | PI Lead-Lag |
| [63] | 2 | 1: Thermal + Hydro 2: Thermal + Hydro | 1: Wind; 2: Diesel | Secondary | Not specified | PI Lead-Lag |
| [64] | 2 | 1: Thermal 2: Hydro | 1: PV; 2: Wind 1: PV; 2: Wind | Secondary | pulse SCR bridge | FOPI |
| [65] | 2 | 1: Thermal reheat 2: Thermal reheat | - | Primary | VSC + DC Chopper | FOPI |
| [66] | 1 | 1: Thermal | - | Primary | Not specified | PI-FLC |
| References | Quality Control | SMES System Connection | SMES Interface | SMES System Control Strategy |
|---|---|---|---|---|
| [67,68] | Power oscillation damping | PCC | CSC | PI-IA |
| [69] | Power oscillation damping | PCC | CSC | Distributed FLC Fuzzy GrHDP |
| [70,71] | Power oscillation damping | WTG AC or DC bus | Adaptable | Adaptative |
| References | Quality Control | SMES System Connection | SMES Interface | SMES System Control Strategy |
|---|---|---|---|---|
| [46] | Fluctuation suppression | PCC | VSC + DC chopper | PI ()SVPWM + PI PWM |
| [77] | Fluctuation suppression | PCC | VSC + DC chopper | PI ()HCC + FLCPWM |
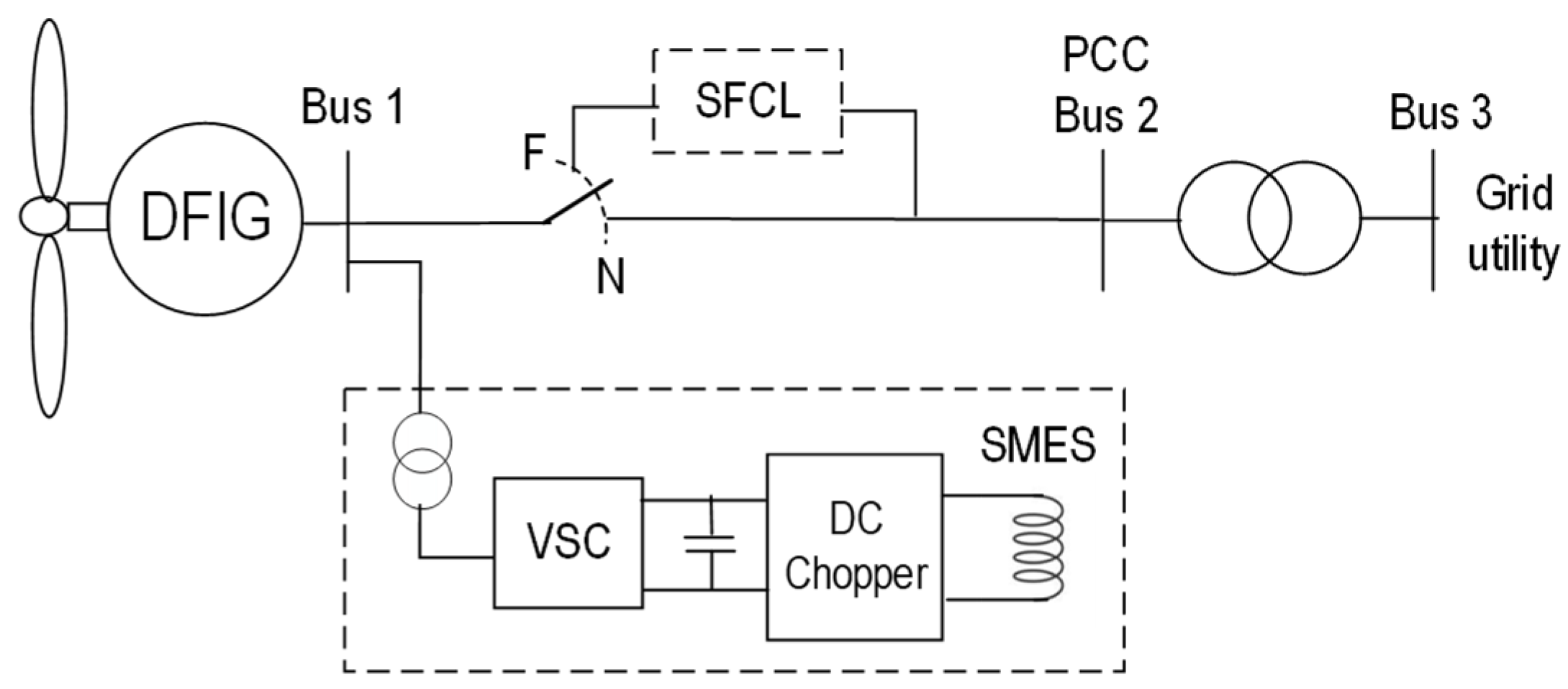
| [79] | Fluctuation suppression + Fault limiter | DFIG Stator terminal | VSC + DC chopper + SFCL | PI ()SVPWM + PI PWM + comparator |
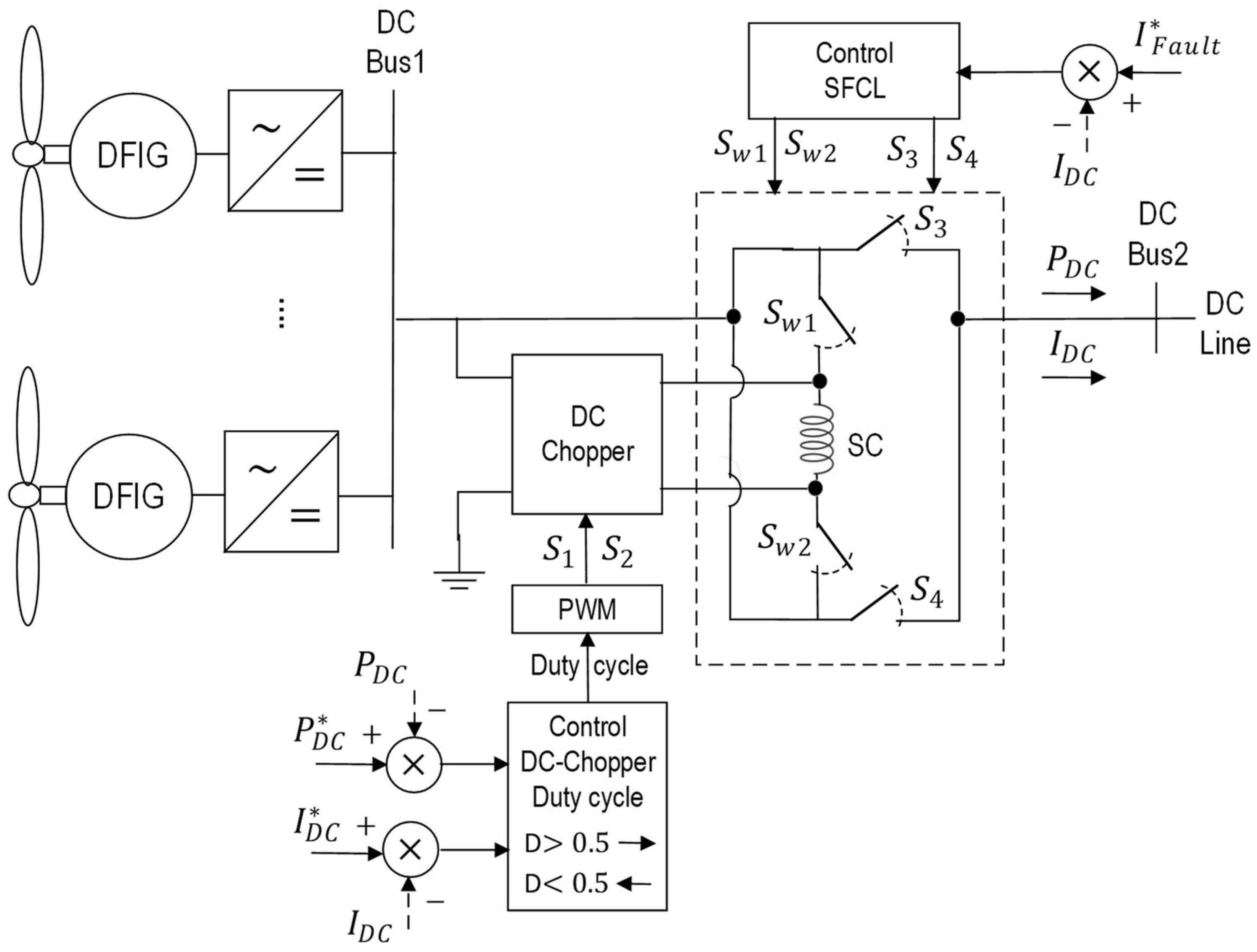
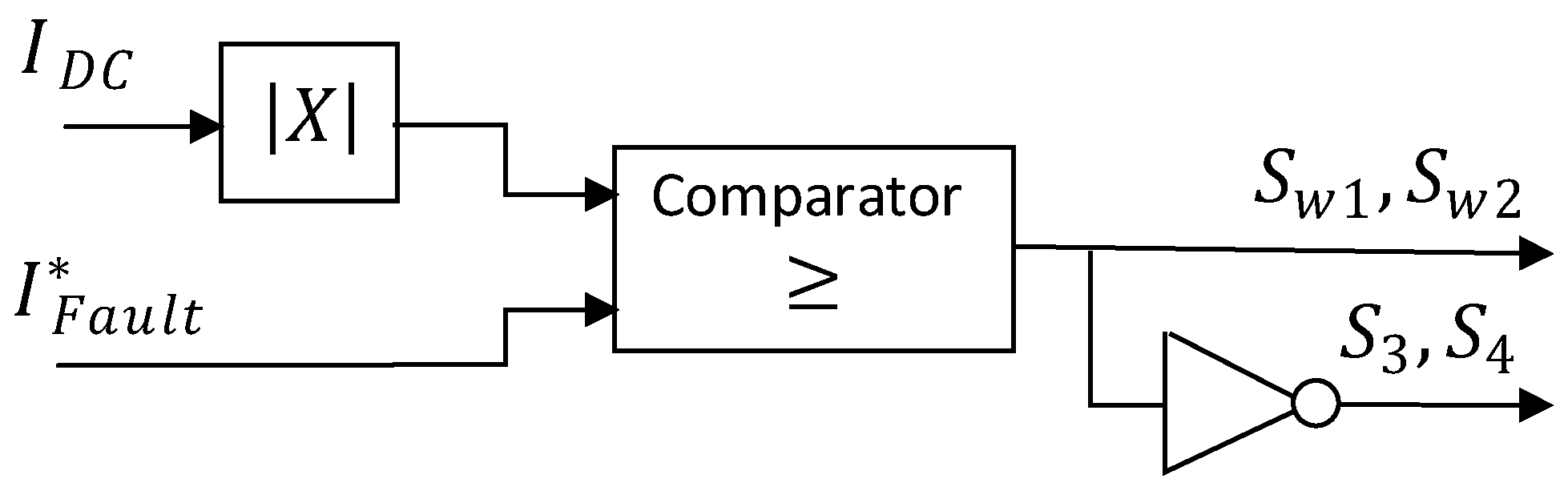
| [80] | Fluctuation suppression + Fault limiter | WTG DC grid | DC chopper + SFCL | PI PWM+ comparator |
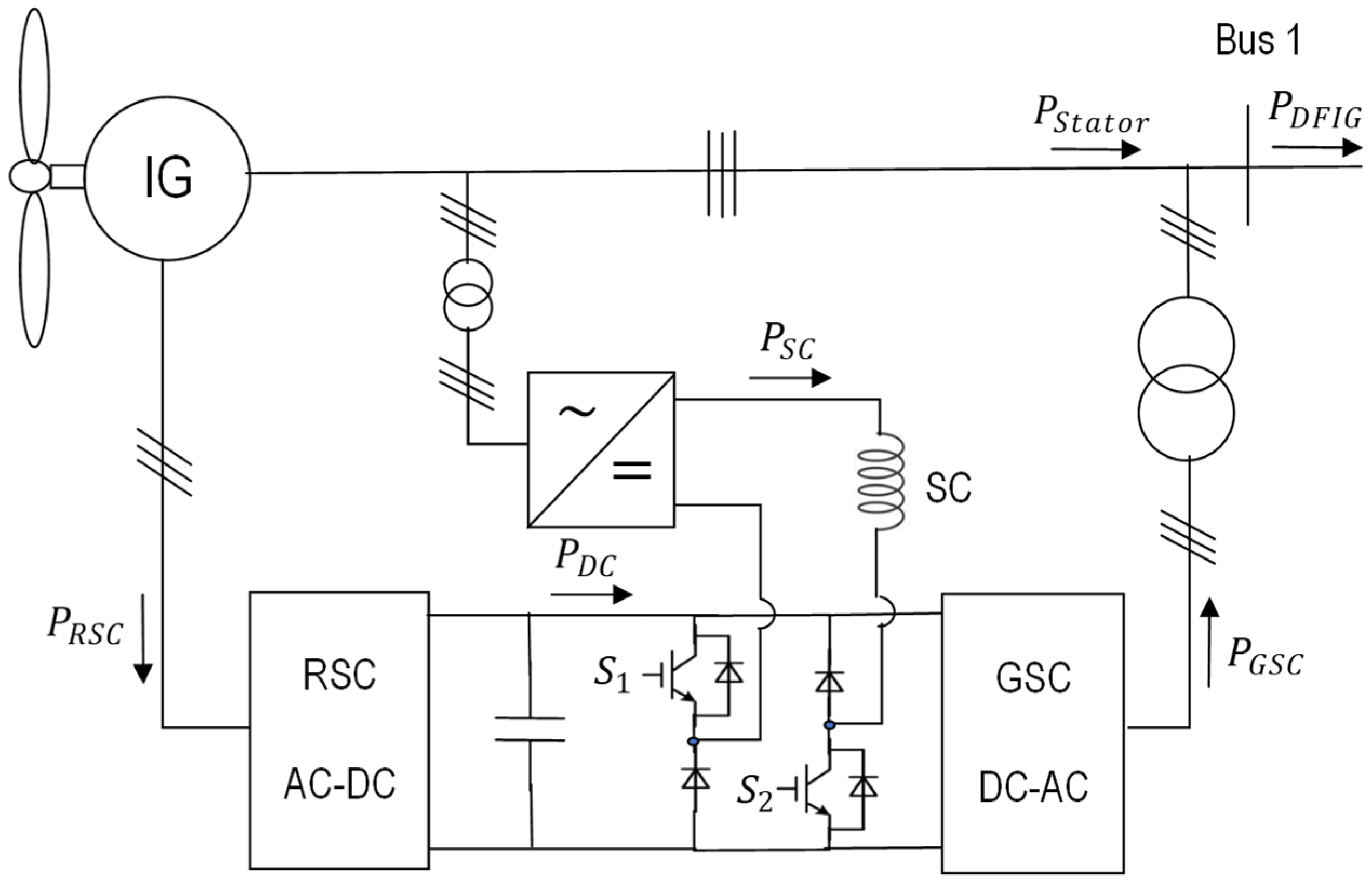
| [81] | Fluctuation suppression + Fault limiter | DFIG DC link RSC-GSC | AC-DC converter DC Chopper | PI ()SVPWM + comparator |
| [45,83] | Fluctuation suppression + Harmonics filter | PV PCC | VSC + DC chopper | PI ()HCC + FLCPWM + Active filtering |
| [84] | Fluctuation suppression + Harmonics filter | PV DC link Boost-Inverter | DC Chopper | SMCPWM Lyapunov stability Active filtering |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arsénio Costa, A.J.; Morais, H. Power Quality Control Using Superconducting Magnetic Energy Storage in Power Systems with High Penetration of Renewables: A Review of Systems and Applications. Energies 2024, 17, 6028. https://doi.org/10.3390/en17236028
Arsénio Costa AJ, Morais H. Power Quality Control Using Superconducting Magnetic Energy Storage in Power Systems with High Penetration of Renewables: A Review of Systems and Applications. Energies. 2024; 17(23):6028. https://doi.org/10.3390/en17236028
Chicago/Turabian StyleArsénio Costa, António J., and Hugo Morais. 2024. "Power Quality Control Using Superconducting Magnetic Energy Storage in Power Systems with High Penetration of Renewables: A Review of Systems and Applications" Energies 17, no. 23: 6028. https://doi.org/10.3390/en17236028
APA StyleArsénio Costa, A. J., & Morais, H. (2024). Power Quality Control Using Superconducting Magnetic Energy Storage in Power Systems with High Penetration of Renewables: A Review of Systems and Applications. Energies, 17(23), 6028. https://doi.org/10.3390/en17236028









