Comparative Study of OLGA and LedaFlow Models for Mechanistic Predictions of Hydrate Transport Dynamics
Abstract
:1. Introduction
2. Multiphase Flow Simulators and Hydrate Effects
3. Methodology
4. Hydrate Module Comparison Used in Simulators
4.1. Hydrate Models Used in OLGA and LedaFlow
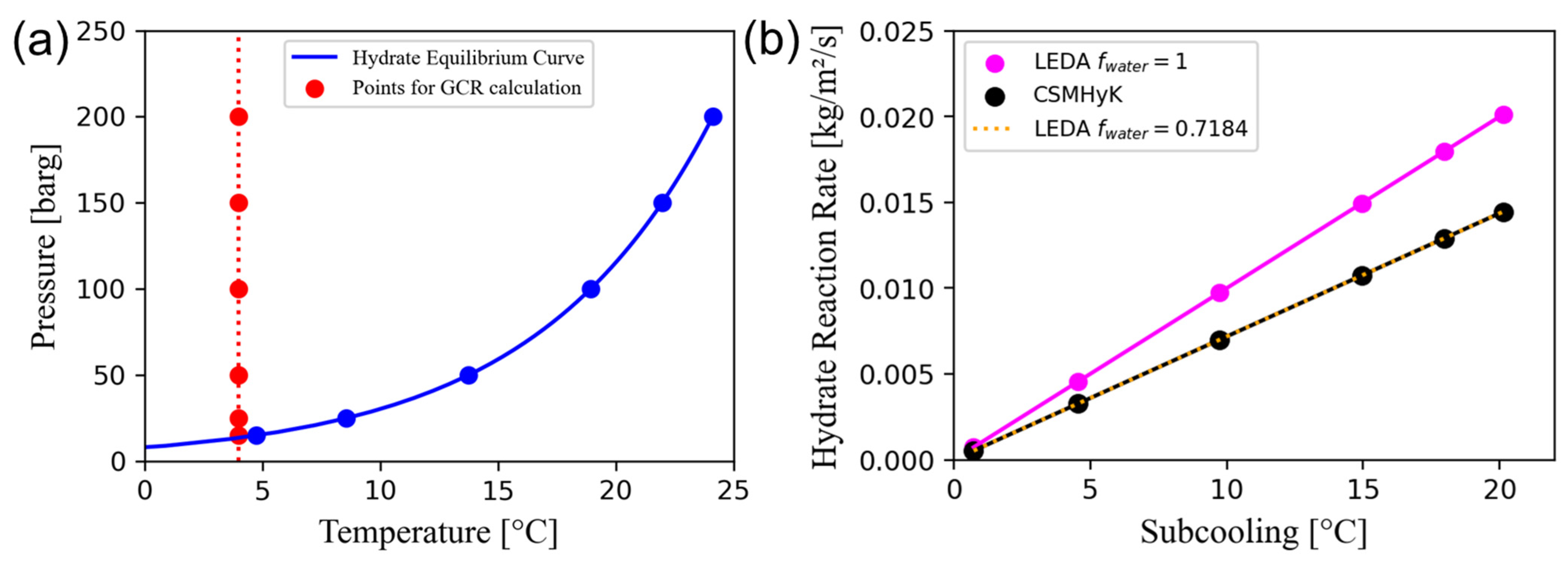
4.1.1. Hydrate Kinetics Model
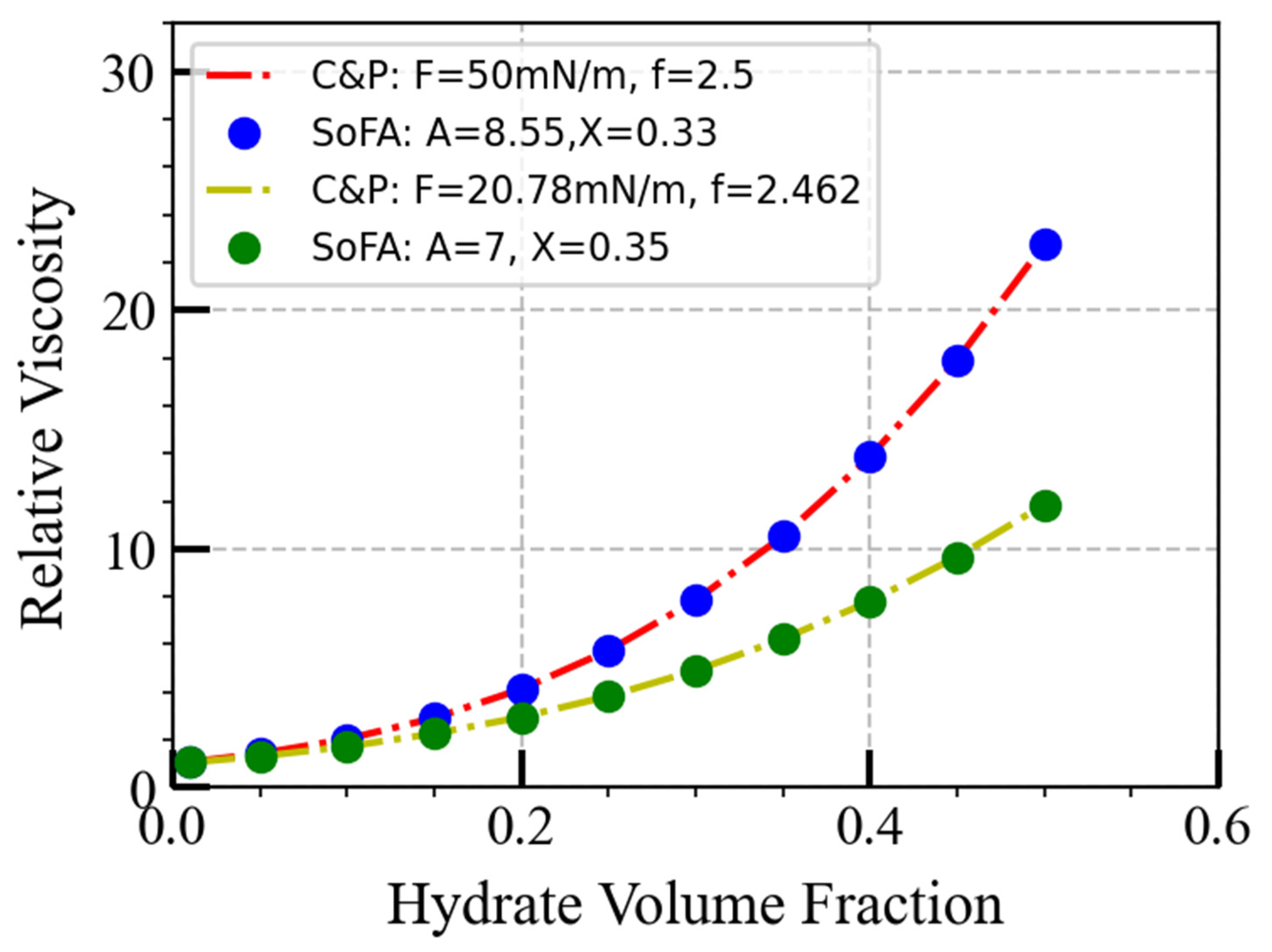
4.1.2. Hydrate Viscosity Model
4.2. Hydrate-Relevant Parameters Implemented in OLGA and LedaFlow
4.3. Coupling of Hydrate Models with the Multiphase Flow Simulator
5. Application of OLGA and LedaFlow into Field Case
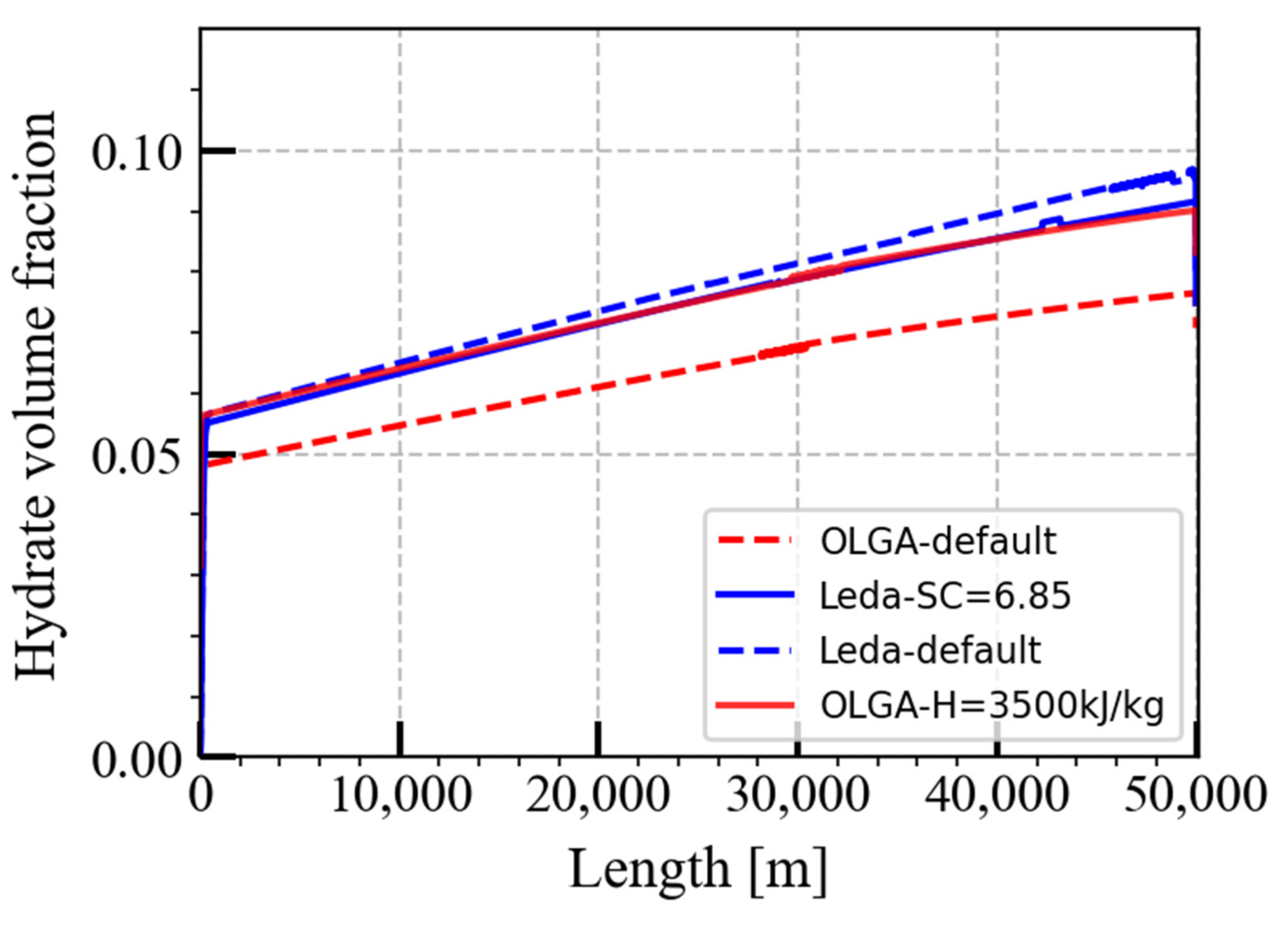
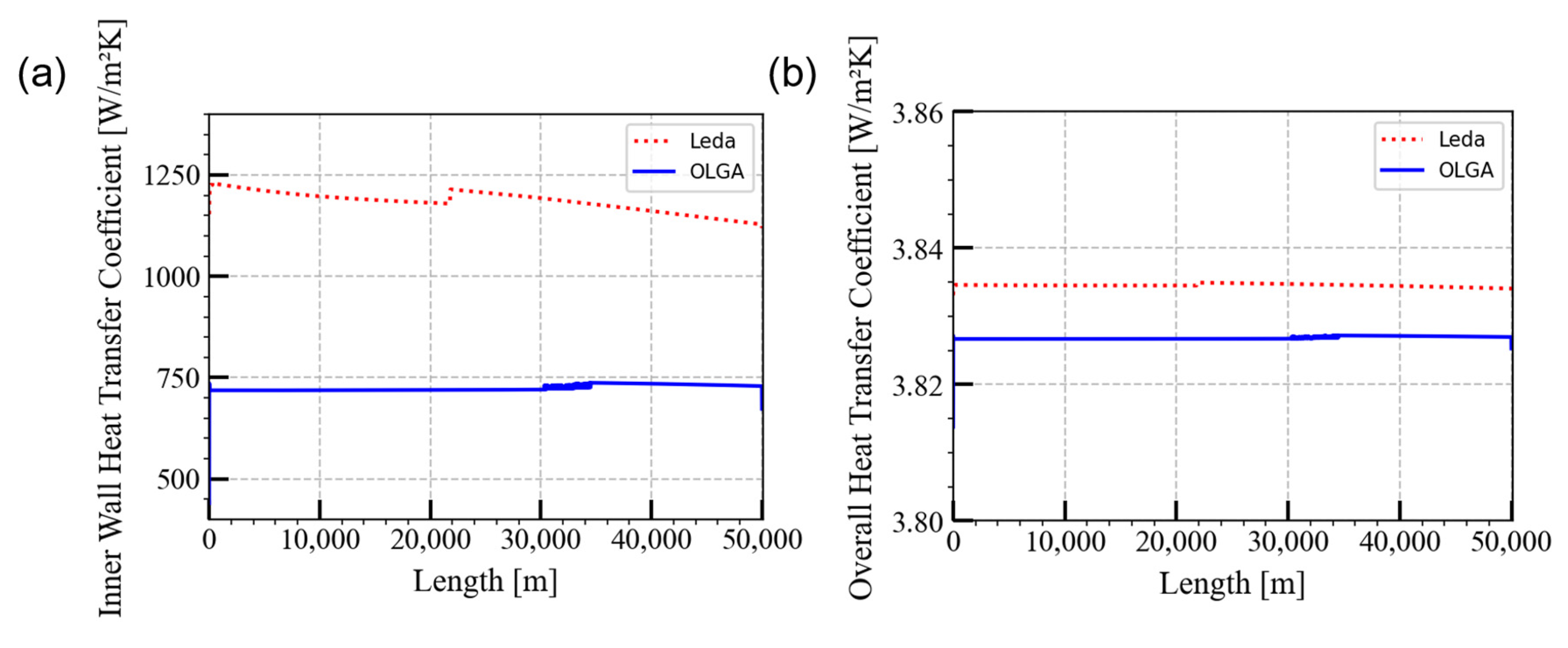
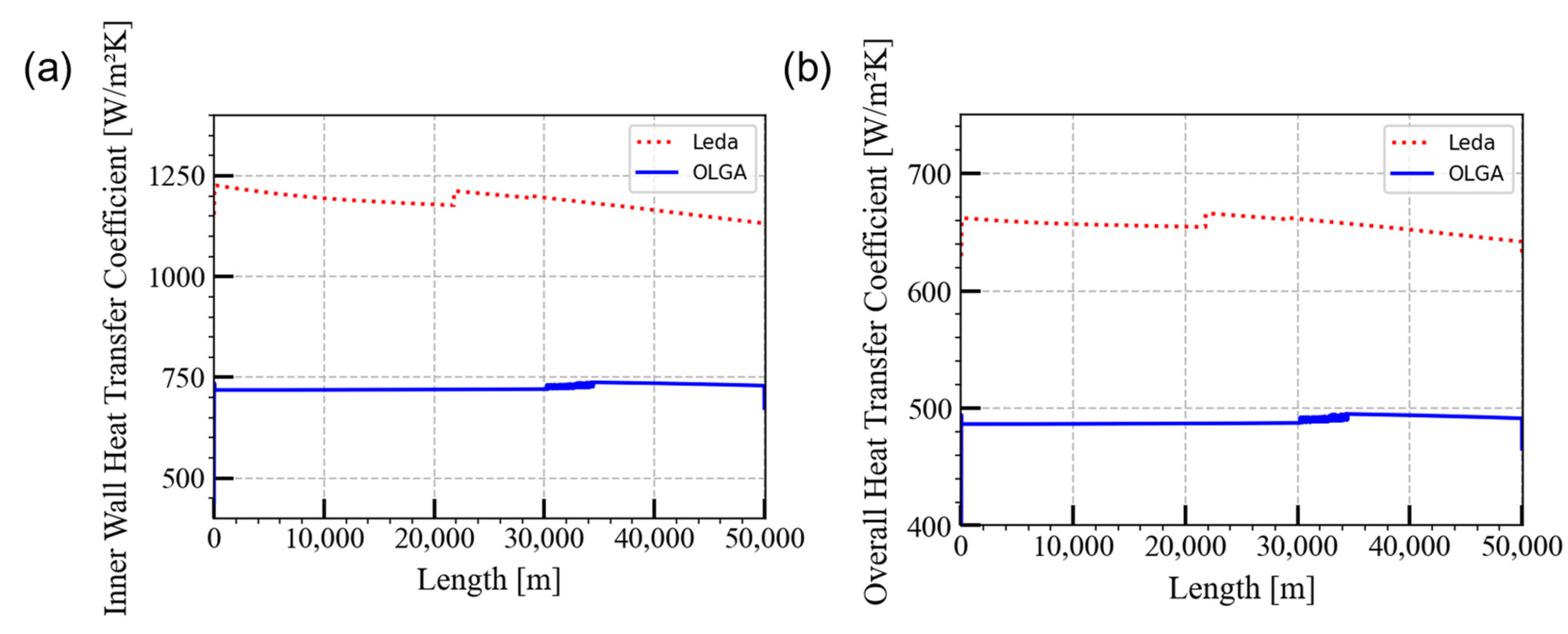
5.1. Steady-State Preprocessor Comparison
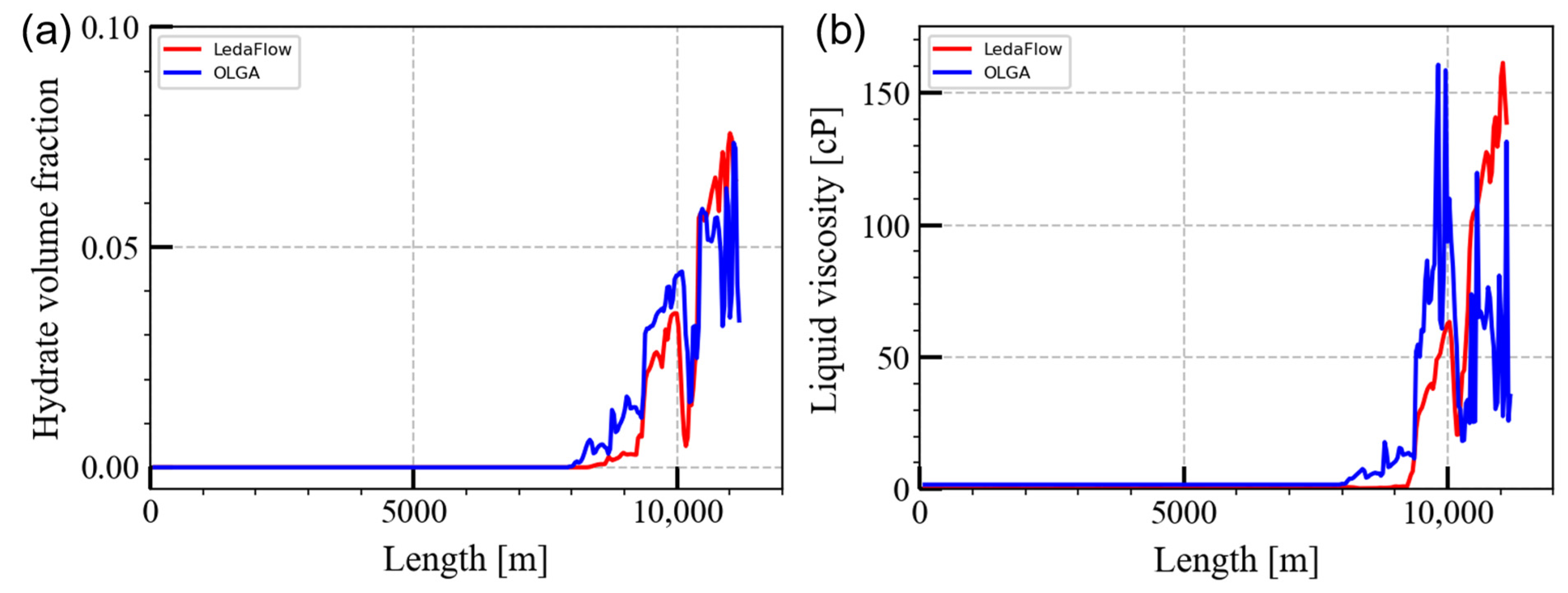
5.2. Initial Condition Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakrabarti, S.K. Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005; pp. 15–200. [Google Scholar] [CrossRef]
- Makogon, T.Y. Handbook of Multiphase Flow Assurance; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128130629. [Google Scholar]
- Sloan, E.D., Jr.; Koh, C.A. Clathrate Hydrates of Natural Gases; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–548. [Google Scholar] [CrossRef]
- Turner, D.J. Clathrate Hydrate Formation in Water-in-Oil Dispersions. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2005. [Google Scholar]
- Camargo, R.; Palermo, T. Rheological Properties of Hydrate Suspensions in an Asphaltenic Crude Oil. In Proceedings of the 4th International Conference on Gas Hydrates, Yokohama, Japan, 9–23 May 2002; pp. 880–885. [Google Scholar]
- Zerpa, L.E. A Practical Model to Predict Gas Hydrate Formation, Dissociation and Transportability in Oil and Gas Flowlines. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2013. [Google Scholar]
- Bassani, C.L.; Barbuto, F.A.A.; Morales, R.E.M.; Cameirão, A.; Herri, J.M.; Sum, A.K. Predicting Gas Hydrate Formation during Three-Phase Gas-(Water-in-Oil) Flow. In Proceedings of the BHR 19th International Conference on Multiphase Production Technology, Cannes, France, 5–7 June 2020; pp. 201–215. [Google Scholar]
- Bassani, C.L.; Kakitani, C.; Herri, J.M.; Sum, A.K.; Morales, R.E.M.; Cameiraõ, A. A Multiscale Approach for Gas Hydrates Considering Structure, Agglomeration, and Transportability under Multiphase Flow Conditions: III. Agglomeration Model. Ind. Eng. Chem. Res. 2020, 59, 15357–15377. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Gao, S. Gas Hydrate Management. In Flow Assurance; Gulf Professional Publishing: Cambridge, MA, USA, 2022; ISBN 9780128220108. [Google Scholar]
- Ballard, L.; Sloan, E.D. The next Generation of Hydrate Prediction IV: A Comparison of Available Hydrate Prediction Programs. Fluid Phase Equilib. 2004, 216, 257–270. [Google Scholar] [CrossRef]
- Lv, X.; Shi, B.; Wang, Y.; Gong, J. Study on Gas Hydrate Formation and Hydrate Slurry Flow in a Multiphase Transportation System. Energy Fuels 2013, 27, 7294–7302. [Google Scholar] [CrossRef]
- Zhou, L.; Upchurch, E.R.; Liu, Y.; Anfinsen, B.-T.; Hashemian, Y.; Yuan, Z. Evaluating Subsea Capping Stack Usage for CO2 Blowouts. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2024. [Google Scholar] [CrossRef]
- Qin, H. Hydrate Film Growth and Risk Management in Oil/Gas Pipelines Using Experiments, Simulations, and Machine Learning. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2020. [Google Scholar]
- Wang, Y. The Development and Application of Hydrate Formation, Transportation and Bedding Models in Liquid-Dominated Systems. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2019. [Google Scholar]
- Kannan, S.N. Modeling and Experiments of Gas Hydrates and Other Solids Management. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2024. [Google Scholar]
- Danielson, T.J.; Bansal, K.M.; Hansen, R.; Leporcher, E. LEDA: The next Multiphase Flow Performance Simulator. In Proceedings of the 12th International Conference on Multiphase Production Technology ’05, Barcelona, Spain, 25–27 May 2005; pp. 477–492. [Google Scholar]
- Puente, P.; Martinez, V.; Richon, V.; Morud, J.; Zambare, N. Wax Deposition and Hydrate Transport Dynamic Simulations on an Oil Pipeline-Experiences Applying Novel Models for Flow Assurance Assessment. In Proceedings of the Society of Petroleum Engineers-Abu Dhabi International Petroleum Exhibition & Conference 2018, ADIPEC 2018, Abu Dhabi, United Arab Emirates, 12–15 November 2018. [Google Scholar] [CrossRef]
- Giacchetta, G.; Marchetti, B.; Leporini, M.; Terenzi, A.; Dall’Acqua, D.; Capece, L.; Cocci Grifoni, R. Pipeline Wax Deposition Modeling: A Sensitivity Study on Two Commercial Software. Petroleum 2019, 5, 206–213. [Google Scholar] [CrossRef]
- Leporini, M.; Terenzi, A.; Marchetti, B.; Giacchetta, G.; Corvaro, F. Experiences in Numerical Simulation of Wax Deposition in Oil and Multiphase Pipelines: Theory versus Reality. J. Pet. Sci. Eng. 2019, 174, 997–1008. [Google Scholar] [CrossRef]
- Belt, R.; Djoric, B.; Kalali, S.; Duret, E.; Larrey, D. Comparison of Commercial Multiphase Flow Simulators with Experimental and Field Databases. In Proceedings of the BHR Group-15th International Conference on Multiphase Production Technology, Cannes, France, 15–17 June 2011; pp. 413–427. [Google Scholar]
- Akselsen, A.H. Efficient Numerical Methods for Waves in One-Dimensional Two-Phase Pipe Flows. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- OLGA Plugin User Model Numerics and Programmers Guide; Schlumberger: Sagamihara, Japan, 2014.
- Laux, H. Modeling of Dilute and Dense Dispersed Fluid-Particle Flow. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1998. [Google Scholar]
- Danielson, T.J. Transient Multiphase Flow: Past, Present, and Future with Flow Assurance Perspective. Energy Fuels 2012, 26, 4137–4144. [Google Scholar] [CrossRef]
- LedaFlow Engineering Version 2.8.264.024-User Manual; Kongsberg Digital: Houston, TX, USA, 2011.
- Bendiksen, K.; Espedal, M.; Malnes, D. Physical and numerical simulation of dynamic two-phase flow in pipelines with application to existing oil-gas field lines. In Proceedings of the Conference on Multiphase Flow in Industrial Plants, Bologna, Italy, 29–30 September 1988. [Google Scholar]
- Bendiksen, K.H.; Maines, D.; Moe, R.; Nuland, S. The Dynamic Two-Fluid Model OLGA: Theory and Application. SPE Repr. Ser. 1991, 6, 171–180. [Google Scholar]
- Beggs, H.D.; Brill, J.P. A Study of Two-Phase Flow in Inclined Pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Wang, Y.; Koh, C.A.; White, J.; Patel, Z.; Zerpa, L.E. Hydrate Formation Management Simulations with Anti-Agglomerants and Thermodynamic Inhibitors in a Subsea Tieback. Fuel 2019, 252, 458–468. [Google Scholar] [CrossRef]
- Qu, A.; Ravichandran, S.; Hatscher, S.; Ugueto, L.; Torsvik, M.; Zerpa, L.E.; Koh, C. Predicting Hydrate Formation and Plugging in a Gas Condensate Subsea Tieback Using a Transient Hydrate Simulation Tool. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 16–18 October 2023. [Google Scholar] [CrossRef]
- Vysniauskas, A.; Bishnoi, P.R. A Kinetic Study of Methane Hydrate Formation. Chem. Eng. Sci. 1983, 38, 1061–1072. [Google Scholar] [CrossRef]
- Kalogerakis, N.; Englezos, P.; Dholabhai, P.D. Kinetics of Gas Hydrate Formation from Mixtures of Methane and Ethane. Chem. Eng. Sci. 1987, 42, 2659–2666. [Google Scholar]
- Boxall, J.; Davies, S.; Koh, C.A.; Sloan, E.D. Predicting When and Where Hydrate Plugs Form in Oil-Dominated Flowlines. SPE Proj. Facil. Constr. 2009, 4, 80–86. [Google Scholar] [CrossRef]
- Clausse, D.; Gomez, F.; Dalmazzone, C.; Noik, C. A Method for the Characterization of Emulsions, Thermogranulometry: Application to Water-in-Crude Oil Emulsion. J. Colloid Interface Sci. 2005, 287, 694–703. [Google Scholar] [CrossRef] [PubMed]
- Matthews, P.N.; Notz, P.K.; Widener, M.W.; Prukop, G. Flow Loop Experiments Determine Hydrate Plugging Tendencies in the Field. Ann. N. Y. Acad. Sci. 2000, 912, 330–338. [Google Scholar] [CrossRef]
- Boxall, J.A. Hydrate Plug Formation from <50% Water Content Water-in-Oil Emulsions. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2009. [Google Scholar]
- Palermo, T.; Tournis, E. Viscosity Prediction of Waxy Oils: Suspension of Fractal Aggregates (SoFA) Model. Ind. Eng. Chem. Res. 2015, 54, 4526–4534. [Google Scholar] [CrossRef]
- Muhle, K. Floc Stability in Laminar and Turbulent Flow. In Coagulation and Flocculation: Theory and Applications (Surfactant Science Book 47); CRC Press: New York, NY, USA, 1993; pp. 355–390. [Google Scholar]
- Mills, P. Non-Newtonian Behaviour of Flocculated Suspensions. J. Phys. Lett. Edp Sci. 1985, 46, 301–309. [Google Scholar] [CrossRef]
- Potanin, A.A. On the Mechanism of Aggregation in the Shear Flow of Suspensions. J. Colloid Interface Sci. 1991, 145, 140–157. [Google Scholar] [CrossRef]




| Pipeline length | 50 km |
| Pipeline inner diameter | 30 cm |
| Water cut | 20 vol.% |
| Gas–oil ratio | 180 Sm3/Sm3 |
| Flowline length | 11.2 km |
| Flowline inner diameter | 30.48 cm |
| Water cut | 15 vol.% |
| Gas–oil ratio | 2500 Sm3/Sm3 |
| Options | Settings | Descriptions | |
|---|---|---|---|
| OLGA | LedaFlow | ||
| 1 | Temperature = OFF | Temperature calculations = No | Constant temperature, the energy equation is disabled |
| 2 | Temperature = Ugiven Heat transfer coefficient = Uvalue | Wall heat transfer = Uvalue | User-defined overall heat transfer coefficient |
| 3 | Temperature = Fastwall Heat transfer coefficient = HOuterOption | Wall heat transfer = Walls (static) | The heat transfer coefficient is defined or calculated; heat storage is neglected in the wall |
| 4 | Temperature = Wall Heat transfer coefficient = HOuterOption | Wall heat transfer = Walls (dynamic) | The heat transfer coefficient is defined or calculated; heat storage in the wall is included |
| Parameters | OLGA | LedaFlow |
|---|---|---|
| Hydrate distribution phase | Oil (embedded) | Hydrate distribution coefficient (fraction in oil) = 1 |
| Hydration number | 6.85 (embedded) | 6.85 |
| Enthalpy | 3500 kJ/kg gas | 477.4 kJ/kg hydrate (embedded) |
| Kinetics correction factor | 0.02 | = 10.2 |
| Viscosity model | Camargo and Palermo model: = 2.5 | SoFA model: = 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, A.; Dalla, L.F.R.; Zerpa, L.E.; Palermo, T.; Mateen, K.; Fidel-Dufour, A.; Koh, C.A. Comparative Study of OLGA and LedaFlow Models for Mechanistic Predictions of Hydrate Transport Dynamics. Energies 2024, 17, 6101. https://doi.org/10.3390/en17236101
Qu A, Dalla LFR, Zerpa LE, Palermo T, Mateen K, Fidel-Dufour A, Koh CA. Comparative Study of OLGA and LedaFlow Models for Mechanistic Predictions of Hydrate Transport Dynamics. Energies. 2024; 17(23):6101. https://doi.org/10.3390/en17236101
Chicago/Turabian StyleQu, Anqi, Luiz F. R. Dalla, Luis E. Zerpa, Thierry Palermo, Khalid Mateen, Annie Fidel-Dufour, and Carolyn A. Koh. 2024. "Comparative Study of OLGA and LedaFlow Models for Mechanistic Predictions of Hydrate Transport Dynamics" Energies 17, no. 23: 6101. https://doi.org/10.3390/en17236101
APA StyleQu, A., Dalla, L. F. R., Zerpa, L. E., Palermo, T., Mateen, K., Fidel-Dufour, A., & Koh, C. A. (2024). Comparative Study of OLGA and LedaFlow Models for Mechanistic Predictions of Hydrate Transport Dynamics. Energies, 17(23), 6101. https://doi.org/10.3390/en17236101







