Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis of Heat Exchanger
Abstract
:1. Introduction
2. Failure Mode and Effect Analysis of Heat Exchanger
- (1)
- Fouling fault
- (2)
- Internal leakage
- (3)
- External leakage
3. The Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis
3.1. Data Acquisition and Processing
3.2. Inference Rules for Fault Qualitative Identification
3.3. Model-Data Fusion-Driven Fault Quantification Index
3.3.1. Quantification Index for Fouling
3.3.2. Quantification Index for Leakage
- (a)
- Q1: Heat loss caused by the leakage of hot fluid flowing from the tube to the shell through the leakage hole, as is shown in Equation (12).
- (b)
- Q2: The released heat during the process that the hot fluid leaking from tubes flows into the shell, as is shown in Equation (13).
- (c)
- Q3: Heat brought by an external heat source that leads to the temperature increase of the cold side fluid in the shell, as is shown in Equation (14).
- (d)
- Q4: Absorbed heat as hot fluid flowing into the shell and causing the cold fluid temperature to rise, as is shown in Equation (15).
4. Experimental Study
4.1. Experiment Setup and Data Acquisition
4.2. Data Analysis
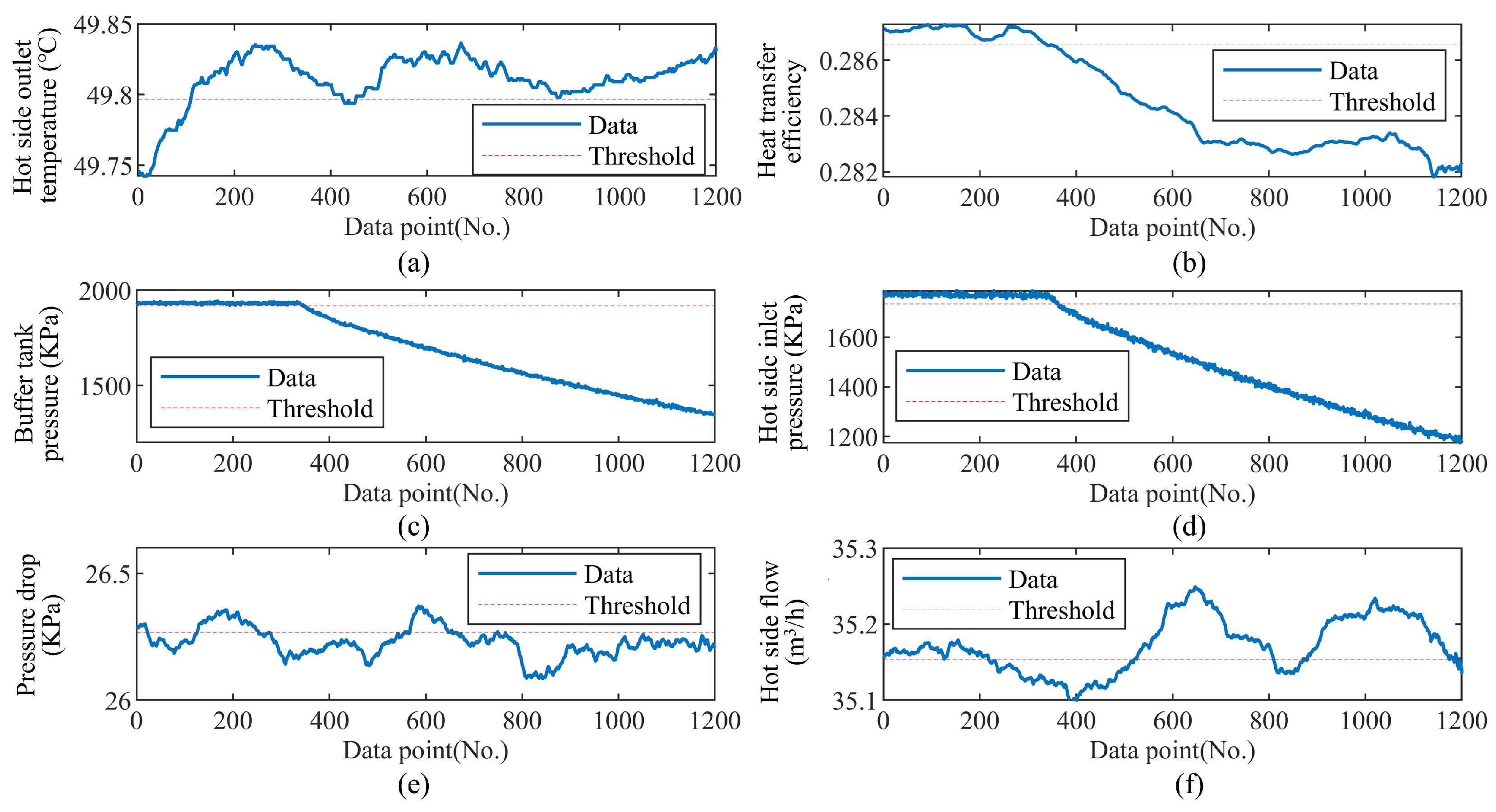
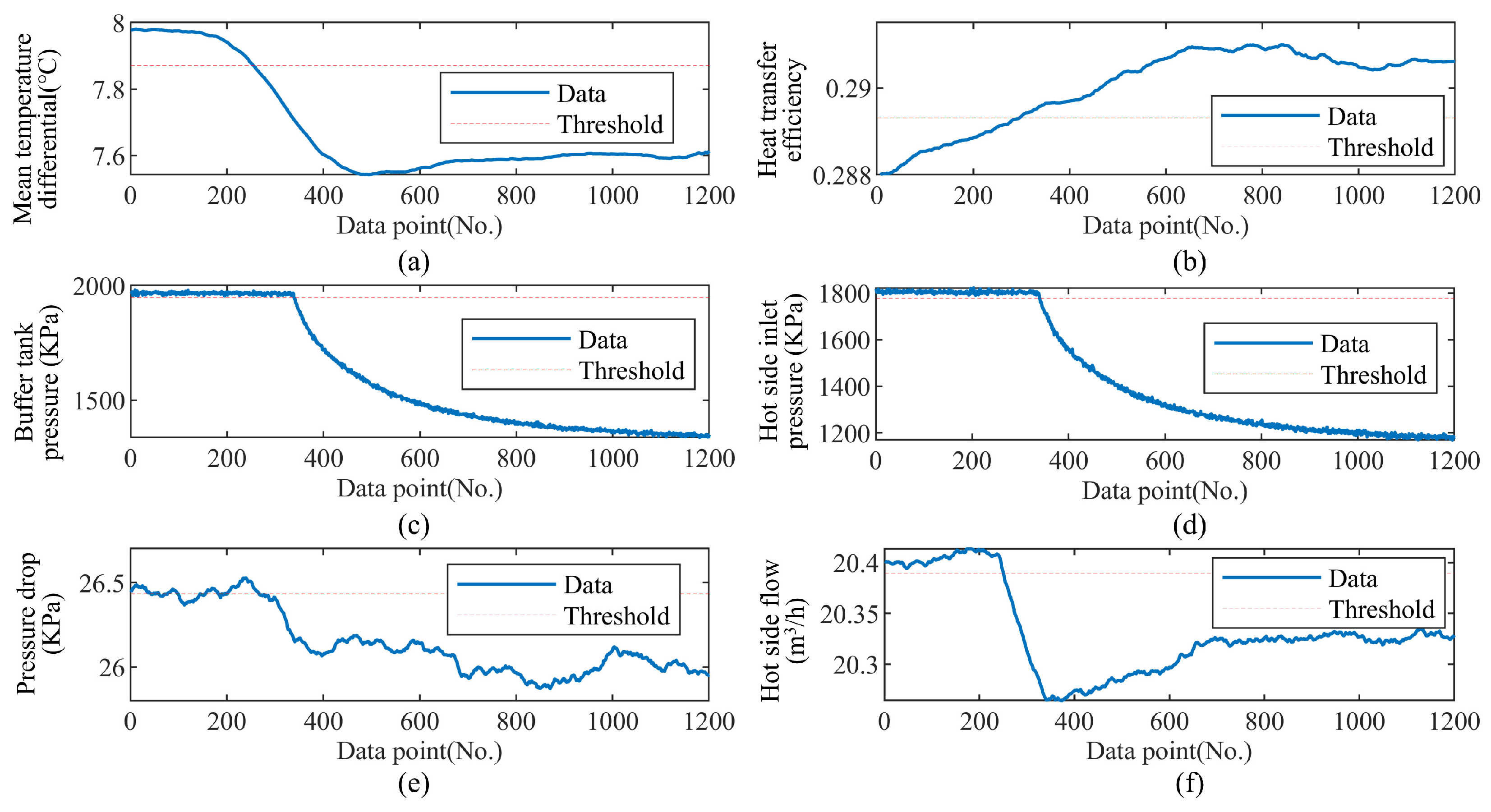
4.2.1. Data Analysis for Leakage Fault
4.2.2. Data Analysis for Fouling Fault
4.3. Fault Reasoning and Qualitive Identification
4.4. Fault Degree Quantification
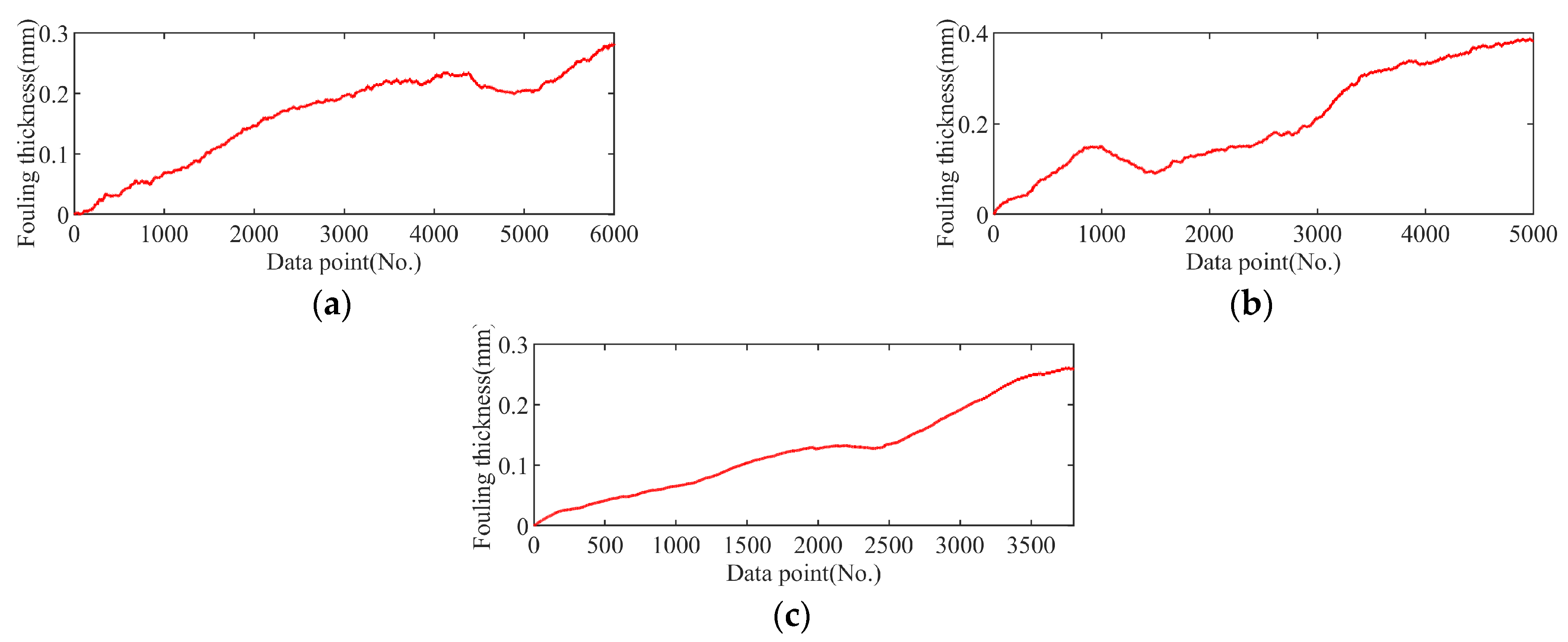
4.4.1. Fouling Thickness Quantification Analysis
4.4.2. Leakage Quantification Analysis
5. Discussions
- (1)
- Comparation of the methods in fault detection
- (2)
- Comparation of the methods in fault quantification
- (3)
- Scalability and limitation analysis of the proposed method
6. Conclusions
- (1)
- Based on failure modes and effect analysis of heat exchangers, a fault symptoms and reasoning rule base for fault identification is constructed. By introducing parameter weights, the model has excellent sensitivity to fault recognition.
- (2)
- The direct fault quantification index of the heat exchanger is constructed by an integrate fault mechanism and the actual monitored data, which can achieve fault quantitative analysis of a heat exchanger with a leakage rate less than 1% and scale thickness less than 0.5 mm, within a 0.017 m3/h and 0.013 mm mean calculated error, respectively.
- (3)
- Compared with the traditional fault diagnosis method, the proposed method integrates fault qualitative identification and quantification analysis, which can not only realize an accurate identification of different fault modes, but also has good performance on fault degree assessment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steinhagen, R.; Müller-steinhagen, H.; Maani, K. Problems and Costs Due to Heat Exchanger Fouling in New Zealand Industries. Heat Transf. Eng. 1993, 14, 19–30. [Google Scholar] [CrossRef]
- Fguiri, A.; Marvillet, C.; Jeday, M.R. Estimation of Fouling Resistance in a Phosphoric Acid/Steam Heat Exchanger Using Inverse Method. Appl. Therm. Eng. 2021, 192, 116935. [Google Scholar] [CrossRef]
- Al Hadad, W.; Schick, V.; Maillet, D. Fouling Detection in a Shell and Tube Heat Exchanger Using Variation of Its Thermal Impulse Responses: Methodological Approach and Numerical Verification. Appl. Therm. Eng. 2019, 155, 612–619. [Google Scholar] [CrossRef]
- Jonsson, G.R.; Lalot, S.; Palsson, O.P.; Desmet, B. Use of Extended Kalman Filtering in Detecting Fouling in Heat Exchangers. Int. J. Heat Mass Transf. 2007, 50, 2643–2655. [Google Scholar] [CrossRef]
- Delrot, S.; Guerra, T.M.; Dambrine, M.; Delmotte, F. Fouling Detection in a Heat Exchanger by Observer of Takagi–Sugeno Type for Systems with Unknown Polynomial Inputs. Eng. Appl. Artif. Intell. 2012, 25, 1558–1566. [Google Scholar] [CrossRef]
- Afgan, N.H.; Carvalho, M.G. Knowledge-Based Expert System for Fouling Assessment of Industrial Heat Exchangers. Appl. Therm. Eng. 1996, 16, 203–208. [Google Scholar] [CrossRef]
- Patil, P.D.; Kozminski, M.; Peterson, J.; Kumar, S. Fouling Diagnosis of Pennsylvania Grade Crude Blended with Opportunity Crude Oils in a Refinery Crude Unit’s Hot Heat Exchanger Train. Ind. Eng. Chem. Res. 2019, 58, 17918–17927. [Google Scholar] [CrossRef]
- Wallhäußer, E.; Hussein, M.A.; Becker, T. Detection Methods of Fouling in Heat Exchangers in the Food Industry. Food Control 2012, 27, 1–10. [Google Scholar] [CrossRef]
- Di Pretoro, A.; D’Iglio, F.; Manenti, F. Optimal Cleaning Cycle Scheduling under Uncertain Conditions: A Flexibility Analysis on Heat Exchanger Fouling. Processes 2021, 9, 93. [Google Scholar] [CrossRef]
- Wang, K.; Chen, J.; Song, Z.; Wang, Y.; Yang, C. Deep Neural Network-Embedded Stochastic Nonlinear State-Space Models and Their Applications to Process Monitoring. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7682–7694. [Google Scholar] [CrossRef]
- Hacene, H.; Michel, K.; Mimoun, Z. A Complete Procedure for Leak Detection and Diagnosis in a Complex Heat Exchanger Using Data-Driven Fuzzy Models. ISA Trans. 2009, 48, 354–361. [Google Scholar] [CrossRef]
- Davoudi, E.; Vaferi, B. Applying Artificial Neural Networks for Systematic Estimation of Degree of Fouling in Heat Exchangers. Chem. Eng. Res. Des. 2018, 130, 138–153. [Google Scholar] [CrossRef]
- Tian, W.; Liu, N.; Sui, D.; Cui, Z.; Liu, Z.; Wang, J.; Zou, H.; Zhao, Y. Early Warning of Internal Leakage in Heat Exchanger Network Based on Dynamic Mechanism Model and Long Short-Term Memory Method. Processes 2021, 9, 378. [Google Scholar] [CrossRef]
- Jallal, M.A.; Vallée, M.; Lamaison, N. Fouling Fault Detection and Diagnosis in District Heating Substations: Validation of a Hybrid CNN-Based PCA Model with Uncertainty Quantification on Virtual Replica Synthesis and Real Data. Energy 2024, 312, 133590. [Google Scholar] [CrossRef]
- Ingimundardóttir, H.; Lalot, S. Detection of Fouling in a Cross-Flow Heat Exchanger Using Wavelets. Heat Transf. Eng. 2011, 32, 349–357. [Google Scholar] [CrossRef]
- Elwerfalli, A.; Alsadaie, S.; Mujtaba, I.M. Estimation of Shutdown Schedule to Remove Fouling Layers of Heat Exchangers Using Risk-Based Inspection (RBI). Processes 2021, 9, 2177. [Google Scholar] [CrossRef]
- Wang, F.-L.; Tang, S.-Z.; He, Y.-L.; Kulacki, F.A.; Yu, Y. Heat Transfer and Fouling Performance of Finned Tube Heat Exchangers: Experimentation via on Line Monitoring. Fuel 2019, 236, 949–959. [Google Scholar] [CrossRef]
- Cid, N.; Patiño, D.; Porteiro, J.; Eiroa, D. Validation of a Fouling Measurement Procedure. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Withers, P.M. Ultrasonic, Acoustic and Optical Techniques for the Non-Invasive Detection of Fouling in Food Processing Equipment. Trends Food Sci. Technol. 1996, 7, 293–298. [Google Scholar] [CrossRef]
- Guépié, B.K.; Grall-Maës, E.; Beauseroy, P.; Nikiforov, I.; Michel, F. Reliable Leak Detection in a Heat Exchanger of a Sodium-Cooled Fast Reactor. Ann. Nucl. Energy 2020, 142, 107357. [Google Scholar] [CrossRef]
- Samantray, J.S.; Goswami, S.; Sharma, V.K.; Biswal, J.; Pant, H.J. Leak Detection in a High-Pressure Heat Exchanger System in a Refinery Using Radiotracer Technique. J. Radioanal. Nucl. Chem. 2014, 302, 979–982. [Google Scholar] [CrossRef]
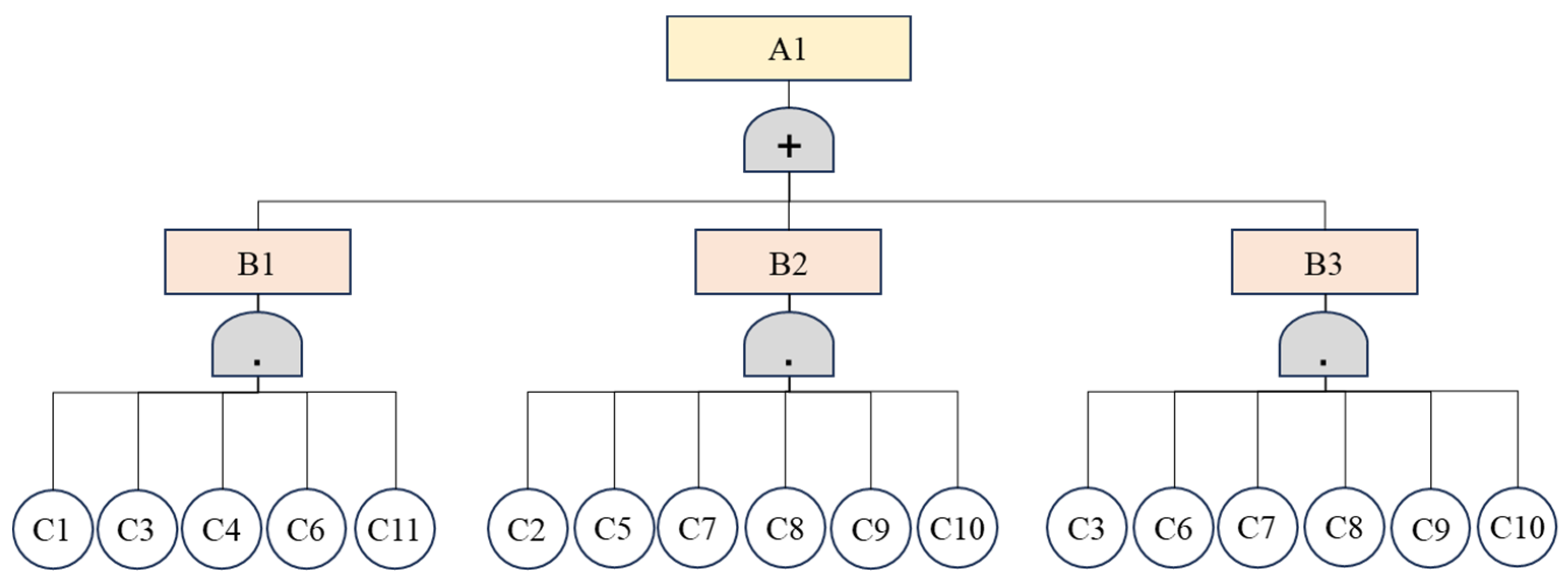

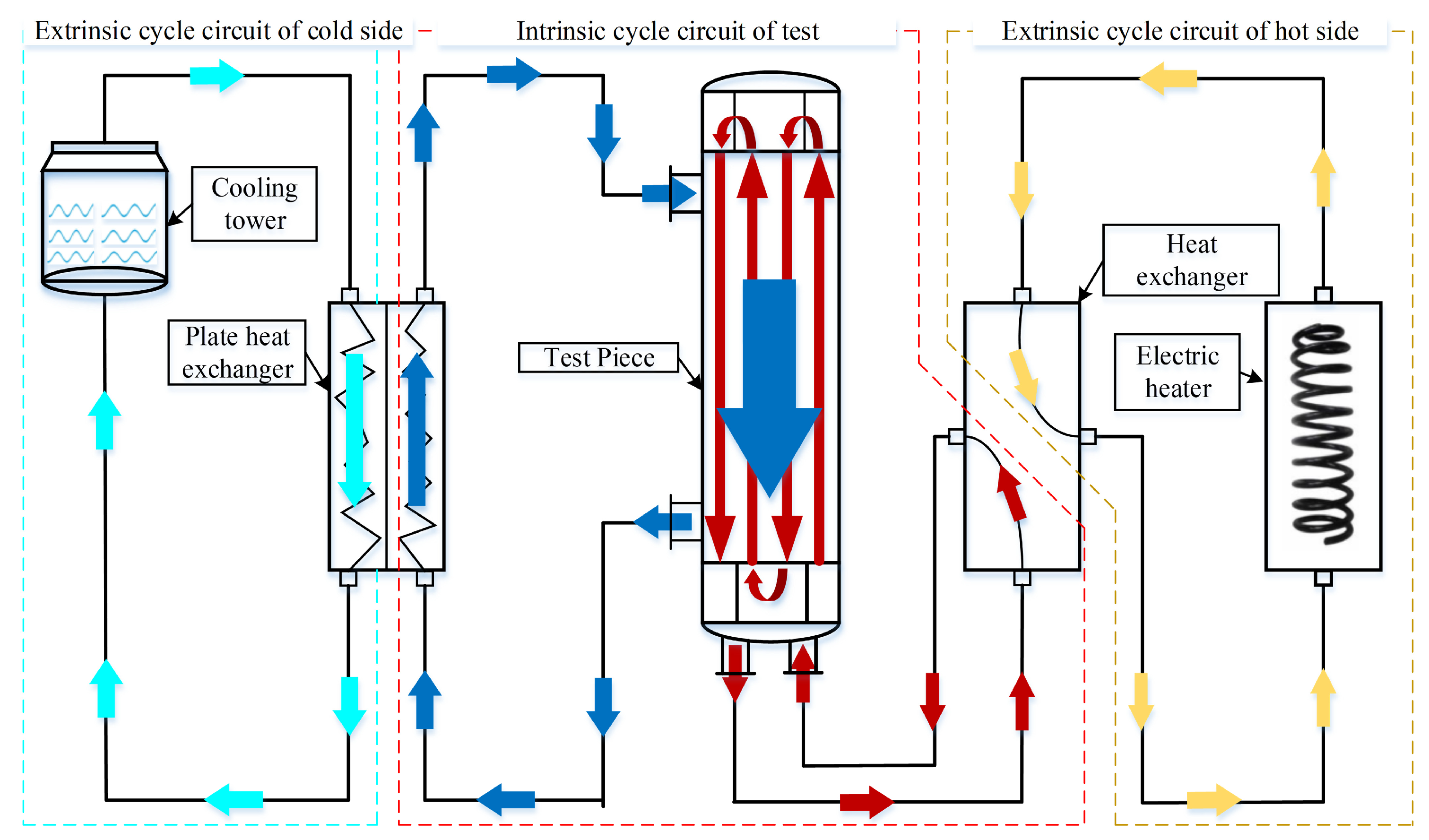

| Event | Symbol | Event Name |
|---|---|---|
| Top event | A1 | Fault of heat exchanger occurs |
| Intermediate event | B1 | Fouling |
| B2 | Internal leakage | |
| B3 | External leakage | |
| Bottom event | C1 | Abnormal increase in average mean temperature |
| C2 | Abnormal decrease in average mean temperature | |
| C3 | Abnormal increase in hot side outlet temperature | |
| C4 | Abnormal decrease in cold side outlet temperature | |
| C5 | Abnormal increase in heat transfer efficiency | |
| C6 | Abnormal decrease in heat transfer efficiency | |
| C7 | Abnormal decrease in buffer tank water level L | |
| C8 | Abnormal decrease in inlet pressure | |
| C9 | Abnormal decrease in pressure drop | |
| C10 | Abnormal decrease in flow rate V | |
| C11 | Abnormal decrease in heat transfer efficiency K |
| Parameter | Name | Equation |
|---|---|---|
| Hot side inlet temperature | ||
| Monitored online data | Hot side outlet temperature | / |
| Cold side inlet temperature | ||
| Cold side outlet temperature | ||
| Buffer tank water level L | ||
| Inlet pressure | ||
| Pressure drop | ||
| Flow rate V | ||
| Secondary parameters | Average temperature differential | |
| Heat transfer coefficient K | ||
| Heat transfer efficiency |
| Fault Type | Fault Symptom | Score | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 (w1) | 2 (w2) | 3 (w3) | 4 (w4) | 5 (w5) | 6 (w6) | 7 (w7) | 8 (w8) | 9 (w9) | 10 (w10) | 11 (w11) | ||
| Fouling | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | S1 |
| Internal leakage | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | S2 |
| External leakage | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | S3 |
| Parameters | Working Condition 1 | Working Condition 2 | Working Condition 3 |
|---|---|---|---|
| Hot/cold side inlet temperature (°C) | 55/35 | 55/35 | 55/35 |
| Hot/cold side inlet pressure (MPa) | 1.0/0.1 | 1.5/0.1 | 2.0/0.1 |
| Hot/cold side flow rate (m3/h) | 30/20 | 35/20 | 30/20 |
| Internal medium leakage rate (%) | 0.04 | 0.6 | \ |
| External leakage rate of flange (%) | \ | \ | 0.12 |
| Parameters | Working Condition 1 | Working Condition 2 | Working Condition 3 |
|---|---|---|---|
| Hot/cold side inlet temperature (°C) | 60/25 | 70/30 | 75/35 |
| Hot/cold side inlet pressure (MPa) | 0.1 | 0.1 | 0.1 |
| Hot/cold side flow rate (m3/h) | 8/5 | 7/4 | 6/3 |
| Medium in the shell | Water | ||
| Medium in tubes | CaSO4 | ||
| Fault and Dataset | Fault Symptoms and Weight Coefficients | Score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 (0.3) | 2 (0.3) | 3 (0.3) | 4 (0.3) | 5 (0.3) | 6 (0.3) | 7 (0.3) | 8 (0.3) | 9 (0.3) | 10 (0.1) | 11 (0.4) | |||
| Fouling | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| Internal leakage | 4 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1.5 |
| 5 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1.8 | |
| External leakage | 6 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1.7 |
| Working Condition | Actual Fouling Thickness (mm) | Calculated Fouling Thickness (mm) | Calculated Error (mm) |
|---|---|---|---|
| 1 | 0.288 | 0.282 | 0.006 |
| 2 | 0.401 | 0.382 | 0.019 |
| 3 | 0.244 | 0.259 | 0.015 |
| Working Condition | Leakage Rate | Actual Leakage (m3/h) | Calculated Leakage (m3/h) | Calculated Error (m3/h) |
|---|---|---|---|---|
| 1 | 0.04% | 0.012 | 0.013 | 0.001 |
| 2 | 0.60% | 0.217 | 0.170 | 0.047 |
| 3 | 0.12% | 0.0428 | 0.039 | 0.004 |
| Working Condition | Actual Leakage (m3/h) | Value When Fault Occurs | Time Delay for Fault Detection Using Value (s) | Time Delay for Fault Detection Using the Proposed Method (s) |
|---|---|---|---|---|
| 1 | 0.012 | 0.756 | 40 | 10 |
| 2 | 0.217 | 0.579 | 60 | 10 |
| 3 | 0.0428 | 0.462 | 70 | 10 |
| Working Condition | Actual fouling Thickness (mm) | Value When Fault Occurs | Time Delay for Fault Detection Using Value (s) | Time Delay for Fault Detection Using the Proposed Method (s) |
|---|---|---|---|---|
| 1 | 0.319 | 0.921 | 160 | 240 |
| 2 | 0.223 | 0.942 | 210 | 260 |
| 3 | 0.265 | 0.913 | 410 | 460 |
| Fault Mode | Working Condition | Calculated Error | ||
|---|---|---|---|---|
| The Proposed Method | Traditional Fouling Model | Traditional Leakage Model | ||
| Fouling | 1 | 0.006 mm | 0.119 mm | / |
| 2 | 0.019 mm | 0.205 mm | ||
| 3 | 0.015 mm | 0.213 mm | ||
| Leakage | 1 | 0.001 m3/h | / | 0.008 m3/h |
| 2 | 0.047 m3/h | 0.175 m3/h | ||
| 3 | 0.004 m3/h | 0.001 m3/h | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Yan, S.; Xu, H.; Gao, Y.; Yu, Y.; Wang, J. Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis of Heat Exchanger. Energies 2024, 17, 6113. https://doi.org/10.3390/en17236113
Qin X, Yan S, Xu H, Gao Y, Yu Y, Wang J. Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis of Heat Exchanger. Energies. 2024; 17(23):6113. https://doi.org/10.3390/en17236113
Chicago/Turabian StyleQin, Xiaogang, Shiwei Yan, Haibo Xu, Yi Gao, Yanbing Yu, and Jinjiang Wang. 2024. "Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis of Heat Exchanger" Energies 17, no. 23: 6113. https://doi.org/10.3390/en17236113
APA StyleQin, X., Yan, S., Xu, H., Gao, Y., Yu, Y., & Wang, J. (2024). Data-Model Fusion-Driven Method for Fault Quantitative Diagnosis of Heat Exchanger. Energies, 17(23), 6113. https://doi.org/10.3390/en17236113





