Optimal Scheduling Strategies for EV Charging and Discharging in a Coupled Power–Transportation Network with V2G Scheduling and Dynamic Pricing
Abstract
1. Introduction
- A DTRN model is developed by an OD matrix method to simulate the travel movement features of EVs. By incorporating a dynamic Dijkstra algorithm, the travel paths of EVs are accurately modeled. Furthermore, the charging loads are predicted through interactions between the TN and PDN.
- An MTDEP mechanism is proposed that optimizes the charging plan of EVs. By segmenting the load into multiple time periods and calculating the price for each period based on the actual load conditions, the proposed MTDEP mechanism can accurately and efficiently facilitate load transfer in accordance with varying base load conditions and enhance economic efficiency.
- An optimal scheduling strategy for EV charging and discharging in a CPTN with V2G scheduling and dynamic pricing is proposed using DTRN information from the coupled system. This model optimizes the charging and discharging of EVs according to the predicted spatial–temporal distribution of charging loads, in conjunction with the MTDEP-guided V2G model. It effectively meets EV charging demands while reducing costs, minimizing load fluctuations, and enhancing grid stability.
2. Problem Formulation
2.1. Modeling for the Spatial–Temporal Distribution Simulation of EV Charging Loads
2.1.1. DTRN Model
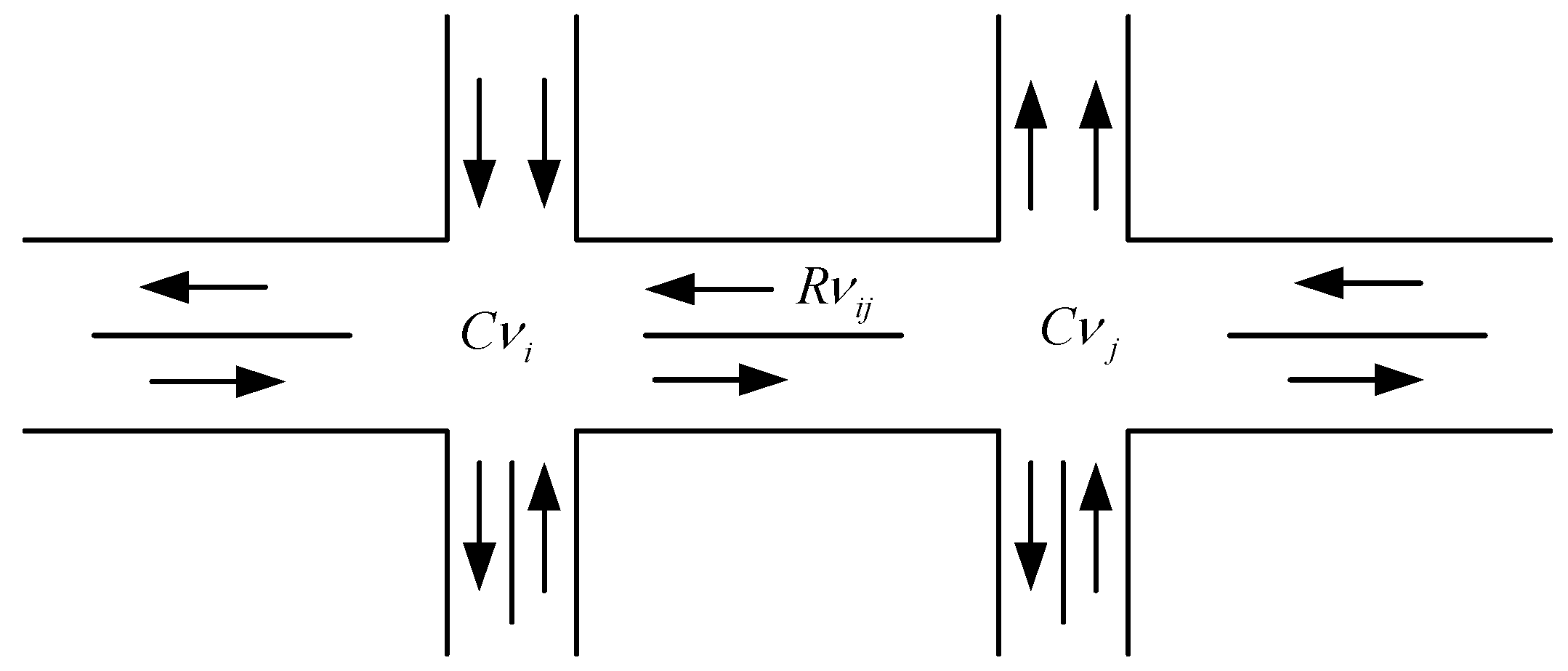
2.1.2. Road Resistance Model
- (1)
- The road segment impedance model is as follows:
- (2)
- The node impedance model is as follows:where is the signal cycle; is the green ratio; and is the vehicle arrival rate at the road segment.
- (3)
- The road resistance model is as follows:
2.1.3. EV Driving Characteristics
2.1.4. EV Charging Characteristics
2.1.5. Charging Demand Model
2.2. Optimal Power Flow Model for the PDN
2.2.1. EV Grid Connection Model
2.2.2. MTDEP Mechanism
2.2.3. Network Loss Model
2.2.4. Objective Function and Constraints
3. Model-Solving Method
4. Case Analysis
4.1. Test System
4.2. Experimental Results and Analysis
4.2.1. Comparison of Electricity Price Strategies
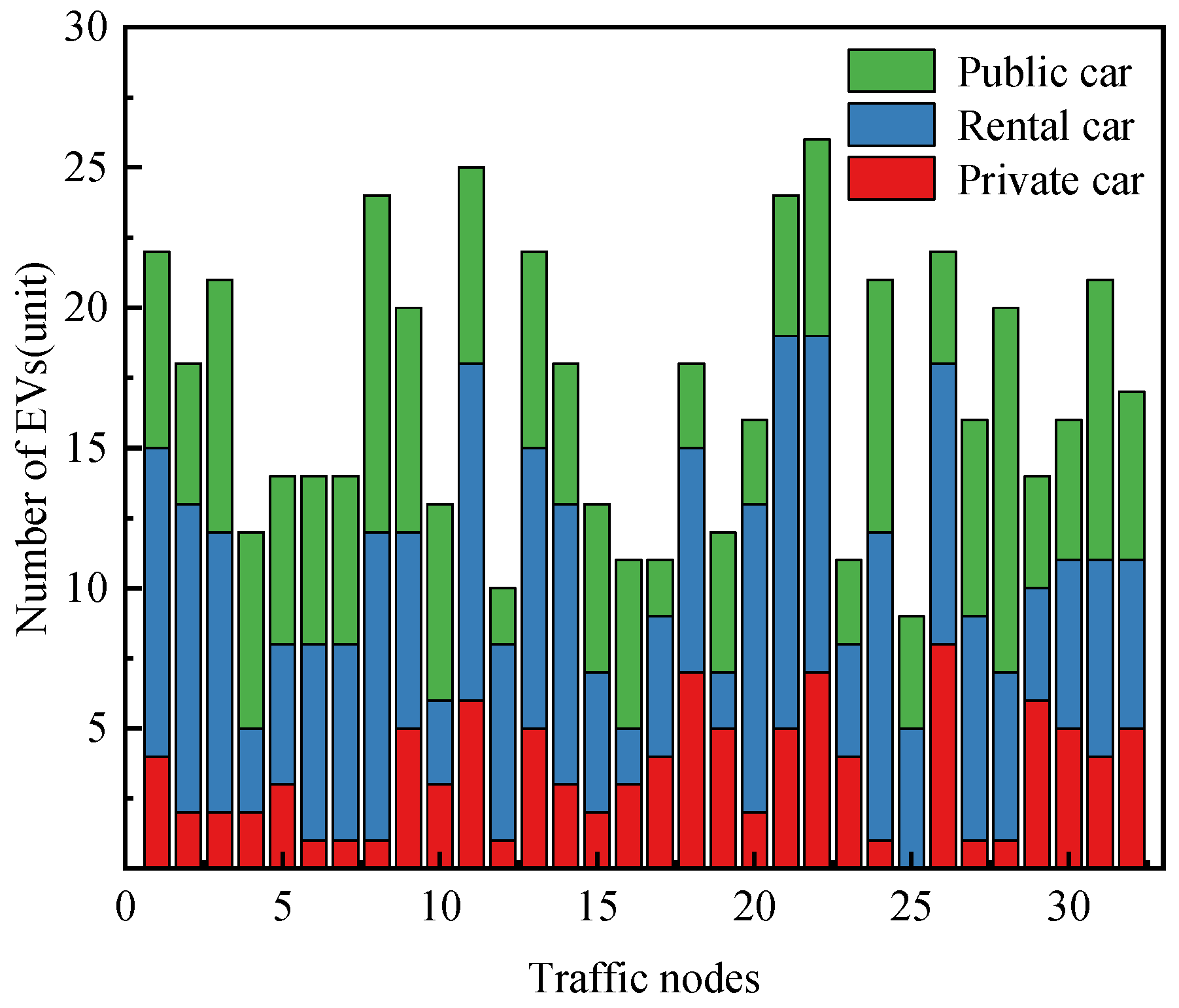
4.2.2. Initial Distribution of EVs at Traffic Nodes
4.2.3. Spatial–Temporal Distribution of EV Charging Loads
4.2.4. Comparison of Charging Strategies
4.2.5. NLS Analysis
4.2.6. Cost Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, T.; Wei, X.; Zhang, X.; Wang, G.; Qiu, J.; Xia, S. Carbon-oriented expansion planning of integrated electricity-natural gas systems with EV fast-charging stations. IEEE Trans. Transp. Electr. 2022, 8, 2797–2809. [Google Scholar] [CrossRef]
- Keegan, G.; Nelendran, P.; Oluwafemi, O. Modeling and Simulation of Hybrid Electric Vehicles for Sustainable Transportation: Insights into Fuel Savings and Emissions Reduction. Energies 2024, 17, 5225. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Jin, H.; Lee, S.; Nengroo, S.H.; Har, D. Development of charging/discharging scheduling algorithm for economical and energy-efficient operation of multi-EV charging station. Appl. Sci. 2022, 12, 4786. [Google Scholar] [CrossRef]
- Li, J.; He, S.; Yang, Q.; Ma, T.; Wei, Z. Optimal design of the EV charging station with retired battery systems against charging demand uncertainty. IEEE Trans. Ind. Inf. 2022, 19, 3262–3273. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, C.; Cai, G.; Koh, L.H. Charging and Discharging Optimization Strategy for Electric Vehicles Considering Elasticity Demand Response. eTransportation 2023, 18, 100262. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized Operational Cost Reduction for an EV Charging Station Integrated with Battery Energy Storage and PV Generation. IEEE Trans. Smart Grid 2018, 10, 2096–2106. [Google Scholar] [CrossRef]
- Xu, Z.; Su, W.; Hu, Z.; Song, Y.; Zhang, H. A Hierarchical Framework for Coordinated Charging of Plug-in Electric Vehicles in China. IEEE Trans. Smart Grid 2015, 7, 428–438. [Google Scholar] [CrossRef]
- Li, Y.; Hu, B. An Iterative Two-Layer Optimization Charging and Discharging Trading Scheme for Electric Vehicle Using Consortium Blockchain. IEEE Trans. Smart Grid 2019, 11, 2627–2637. [Google Scholar] [CrossRef]
- Pourazarm, S.; Cassandras, C.G. Optimal Routing of Energy-Aware Vehicles in Transportation Networks with Inhomogeneous Charging Nodes. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2515–2527. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Shang, Y.; Jian, L. Modeling the temporal and economic feasibility of electric vehicles providing vehicle-to-grid services in the electricity market under different charging scenarios. J. Energy Storage 2023, 68, 107579. [Google Scholar] [CrossRef]
- Lei, X.; Yu, H.; Yu, B.; Shao, Z.; Jian, L. Bridging electricity market and carbon emission market through electric vehicles: Optimal bidding strategy for distribution system operators to explore economic feasibility in China’s low-carbon transitions. Sustain. Cities Soc. 2023, 94, 104557. [Google Scholar] [CrossRef]
- Shang, Y.; Shang, Y.; Yu, H.; Shao, Z.; Jian, L. Achieving efficient and adaptable dispatching for vehicle-to-grid using distributed edge computing and attention-based LSTM. IEEE Trans. Ind. Inform. 2021, 18, 6915–6926. [Google Scholar] [CrossRef]
- Yu, H.; Shang, Y.; Niu, S.; Cheng, C.; Shao, Z.; Jian, L. Towards energy-efficient and cost-effective DC nanaogrid: A novel pseudo hierarchical architecture incorporating V2G technology for both autonomous coordination and regulated power dispatching. Appl. Energy 2022, 313, 118838. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, X.; Shao, Z.; Jian, L. A Reliable Evaluation Metric for Electrical Load Forecasts in V2G Scheduling Considering Statistical Features of EV Charging. IEEE Trans. Smart Grid 2024, 15, 4917–4931. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, Z.; Duan, X. Optimal Pricing of Public Electric Vehicle Charging Stations Considering Operations of Coupled Transportation and Power Systems. IEEE Trans. Smart Grid 2021, 12, 3278–3288. [Google Scholar] [CrossRef]
- Xie, S.; Wu, Q.; Hatziargyriou, N.D.; Zhang, M.; Zhang, Y.; Xu, Y. Collaborative Pricing in a Power-Transportation Coupled Network: A Variational Inequality Approach. IEEE Trans. Power Syst. 2022, 38, 783–795. [Google Scholar] [CrossRef]
- Cao, Z.; Han, Y.; Zhao, Q.; Wang, J.; Li, Y.; Zhao, S. Traffic and Power Flow Optimization of Coupled Power-Transportation Networks Considering Environment-Aware User Behavior. IEEE Trans. Transp. Electrif. 2023, 10, 3940–3955. [Google Scholar] [CrossRef]
- Gan, W.; Wen, J.; Yan, M.; Zhou, Y.; Yao, W. Enhancing resilience with electric vehicles charging redispatching and vehicle-to-grid in traffic-electric networks. IEEE Trans. Ind. Appl. 2023, 60, 953–965. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Wei, W.; Wu, L. A Bilevel EV Charging Station and DC Fast Charger Planning Model for Highway Network Considering Dynamic Traffic Demand and User Equilibrium. IEEE Trans. Smart Grid 2023, 15, 714–728. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Z.; Li, Z.; Tian, W.; Shahidehpour, M. EV Charging Schedule in Coupled Constrained Networks of Transportation and Power System. IEEE Trans. Smart Grid 2018, 10, 4706–4716. [Google Scholar] [CrossRef]
- He, C.; Zhu, J.; Lan, J.; Li, S.; Wu, W.; Zhu, H. Optimal planning of electric vehicle battery centralized charging station based on EV load forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6557–6575. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Cao, Y.; Li, L.; Yan, K.; Wu, L.; Liang, K. Electric vehicle charging schedule considering shared charging pile based on generalized Nash game. Int. J. Electr. Power Energy Syst. 2022, 136, 107579. [Google Scholar] [CrossRef]
- Ngo, H.; Kumar, A.; Mishra, S. Optimal positioning of dynamic wireless charging infrastructure in a road network for battery electric vehicles. Transp. Res. Part D 2020, 85, 102385. [Google Scholar] [CrossRef]
- Li, B.; Chang, X. EV charging station load prediction in coupled urban transportation and distribution networks. Energy Eng. 2024, 121, 3001–3018. [Google Scholar] [CrossRef]
- Chen, L.; Xie, C.; Ma, D.; Yang, Y.; Li, Y. A short-term traffic flow prediction model for road networks using inverse isochrones to determine dynamic spatiotemporal correlation ranges. Phys. A Stat. Mech. Its Appl. 2024, 657, 130244. [Google Scholar] [CrossRef]
- Mahmoudi, E.; dos Santos Barros, T.A.; Ruppert Filho, E. Forecasting urban electric vehicle charging power demand based on travel trajectory simulation in the realistic urban street network. Energy Rep. 2024, 11, 4254–4276. [Google Scholar] [CrossRef]
- Tang, D.; Wang, P. Probabilistic modeling of nodal charging demand based on spatial-temporal dynamics of moving electric vehicles. IEEE Trans. Smart Grid 2015, 7, 627–636. [Google Scholar] [CrossRef]
- Jabbar, L.S.; Abass, E.I.; Hasan, S.D. A modification of shortest path algorithm according to adjustable weights based on Dijkstra algorithm. Eng. Technol. J. 2023, 41, 359–374. [Google Scholar] [CrossRef]
- Mu, Y.; Wu, J.; Jenkins, N.; Jia, H.; Wang, C. A spatial-temporal model for grid impact analysis of plug-in electric vehicles. Appl. Energy 2014, 114, 456–465. [Google Scholar] [CrossRef]
- Shao, C.; Li, K.; Qian, T.; Shahidehpour, M.; Wang, X. Generalized user equilibrium for coordination of coupled power-transportation network. IEEE Trans. Smart Grid 2022, 14, 2140–2151. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, X.; Yu, H. Electric vehicle charging load prediction considering spatio-temporal node importance information. Energies 2024, 17, 4840. [Google Scholar] [CrossRef]
- Zhang, D.; Jiang, Y.; Wang, S.; Li, H.; Bai, J.; Zhang, R.; An, Z. Performance analysis of the comprehensive energy system based on active energy storage-discharge technology under time-sharing electricity price operation strategy. J. Clean Prod. 2024, 436, 140654. [Google Scholar] [CrossRef]
- Tian, X.; Cheng, B.; Liu, H. V2G optimized power control strategy based on time-of-use electricity price and comprehensive load cost. Energy Rep. 2023, 10, 1467–1473. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, X.; Zhu, L.; Li, Z. Optimal allocation method for energy storage capacity considering dynamic time-of-use electricity prices and on-site consumption of new energy. Processes 2023, 11, 1725. [Google Scholar] [CrossRef]
- Nam, I.; Kim, J.H.; Yoo, Y.; Jung, S. An EV-based wind power curtailment scheme utilizing the power sensitivity of the distribution network. IEEE Access 2022, 10, 61124–61134. [Google Scholar] [CrossRef]
- Xu, F.; Wei, S.; Li, J.; Yuan, D. Sensitivity analysis of a double-layer coupling structure for an electric vehicle wireless power transfer system. World Electr. Veh. J. 2023, 14, 322. [Google Scholar] [CrossRef]
- Khosravi, M.; Monsef, H.; Aliabadi, M.H. Network loss management and allocating the transmission losses to loads and generation units according to their transactions. IET Gener. Transm. Distrib. 2020, 14, 1540–1551. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities 2023, 6, 3161–3191. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Eltamaly, A.M. Upgrading conventional power system for accommodating electric vehicle through demand side management and V2G concepts. Energies 2022, 15, 6541. [Google Scholar] [CrossRef]







| Pricing Strategy | Peak Value/kW | Valley Value/kW | Peak–Valley Difference/kW |
|---|---|---|---|
| TSSEP | 2982.443 | 1962.628 | 1019.815 |
| MPDEP | 2928.748 | 2001.147 | 927.601 |
| Scheduling Strategy | Total Cost/CNY |
|---|---|
| Disorderly charging and discharging | 10,526.087 |
| The proposed scheduling strategy | 9502.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Y.; Liao, H.; Liang, H.; Lu, L.; Zhong, J. Optimal Scheduling Strategies for EV Charging and Discharging in a Coupled Power–Transportation Network with V2G Scheduling and Dynamic Pricing. Energies 2024, 17, 6167. https://doi.org/10.3390/en17236167
Ran Y, Liao H, Liang H, Lu L, Zhong J. Optimal Scheduling Strategies for EV Charging and Discharging in a Coupled Power–Transportation Network with V2G Scheduling and Dynamic Pricing. Energies. 2024; 17(23):6167. https://doi.org/10.3390/en17236167
Chicago/Turabian StyleRan, Yunzheng, Honghua Liao, Huijun Liang, Luoping Lu, and Jianwei Zhong. 2024. "Optimal Scheduling Strategies for EV Charging and Discharging in a Coupled Power–Transportation Network with V2G Scheduling and Dynamic Pricing" Energies 17, no. 23: 6167. https://doi.org/10.3390/en17236167
APA StyleRan, Y., Liao, H., Liang, H., Lu, L., & Zhong, J. (2024). Optimal Scheduling Strategies for EV Charging and Discharging in a Coupled Power–Transportation Network with V2G Scheduling and Dynamic Pricing. Energies, 17(23), 6167. https://doi.org/10.3390/en17236167





