Finite Element Analysis and Validation of Wind Turbine Bearings
Abstract
:1. Introduction
2. Research Methodology
2.1. Bearing Information
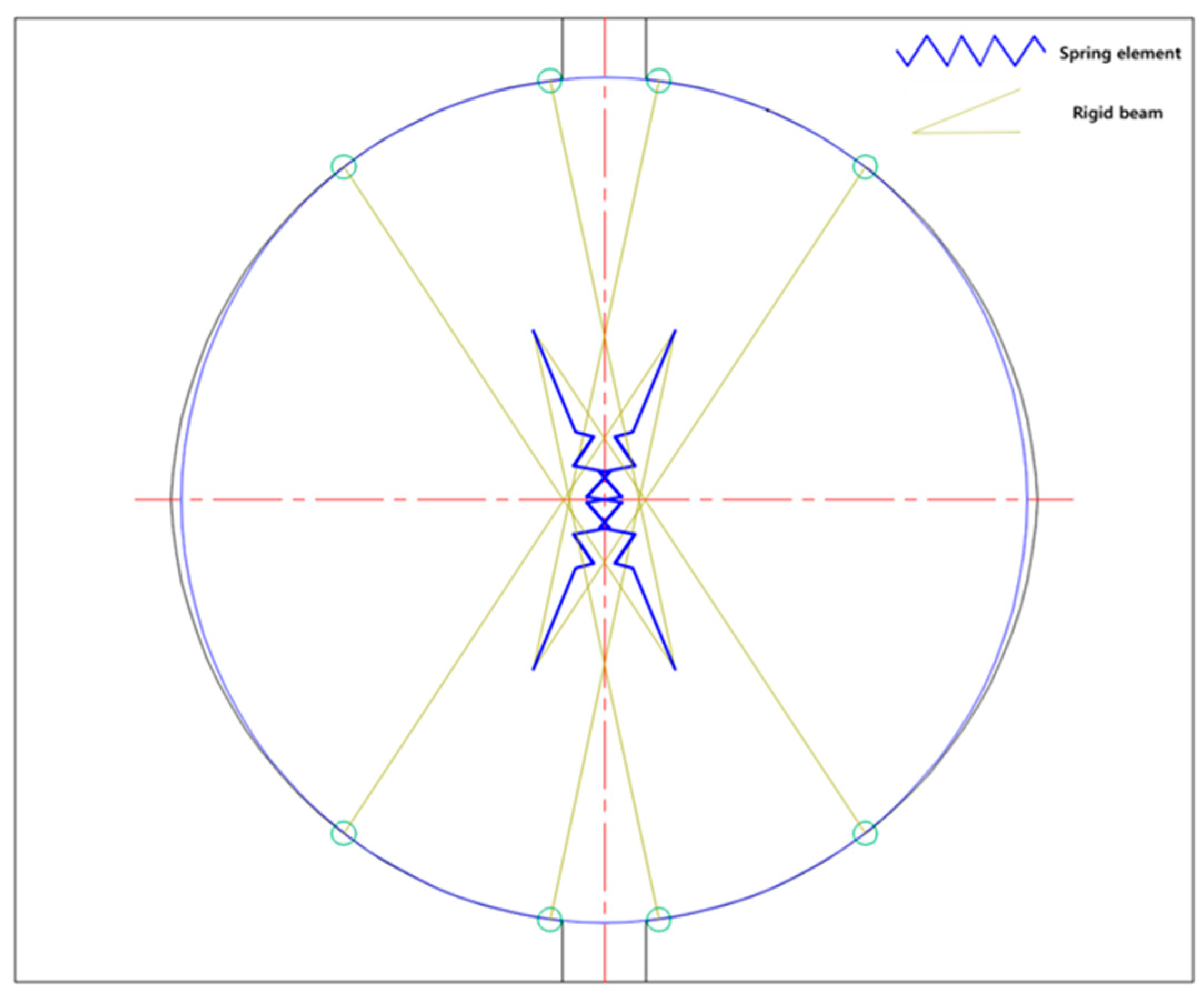
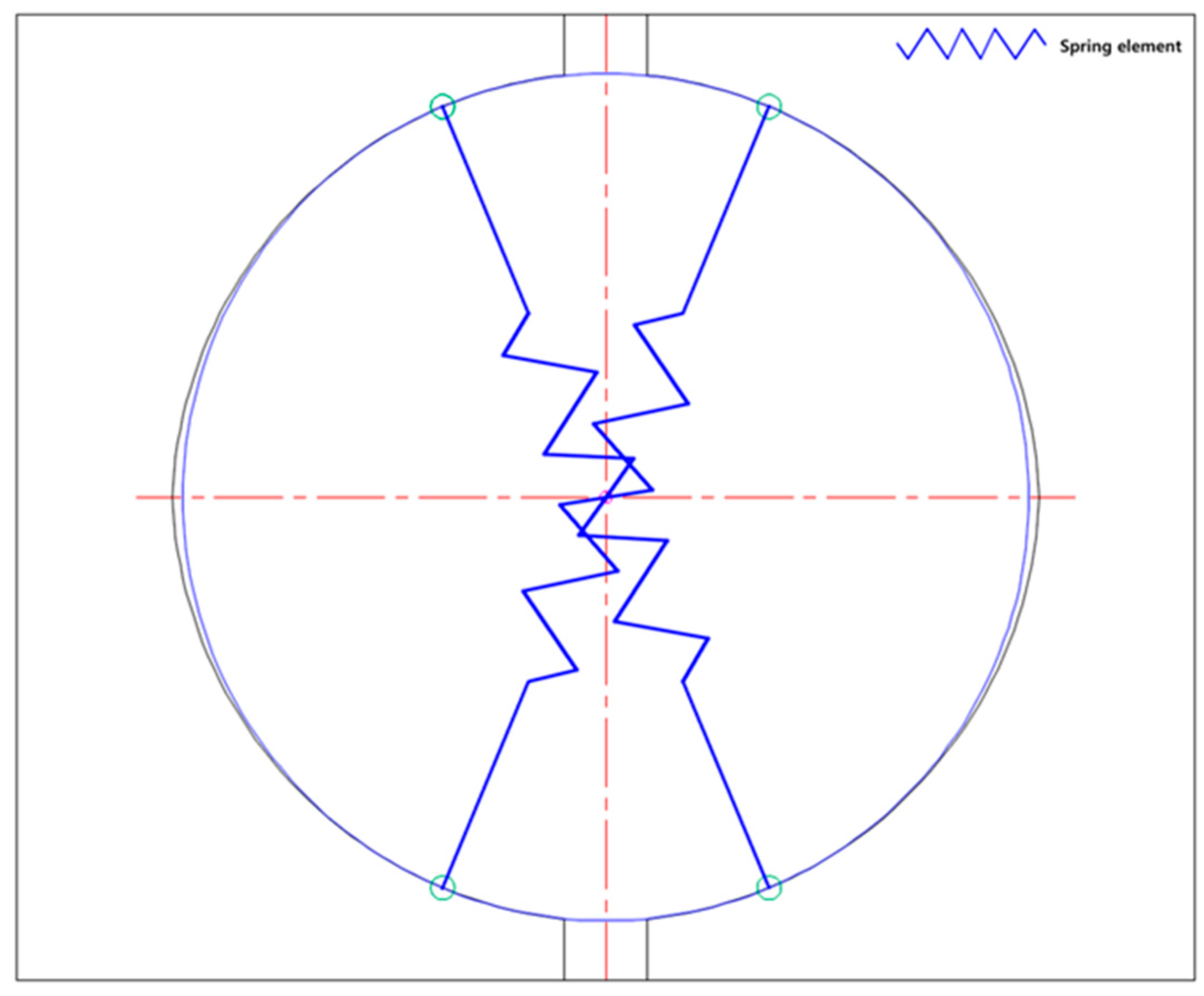
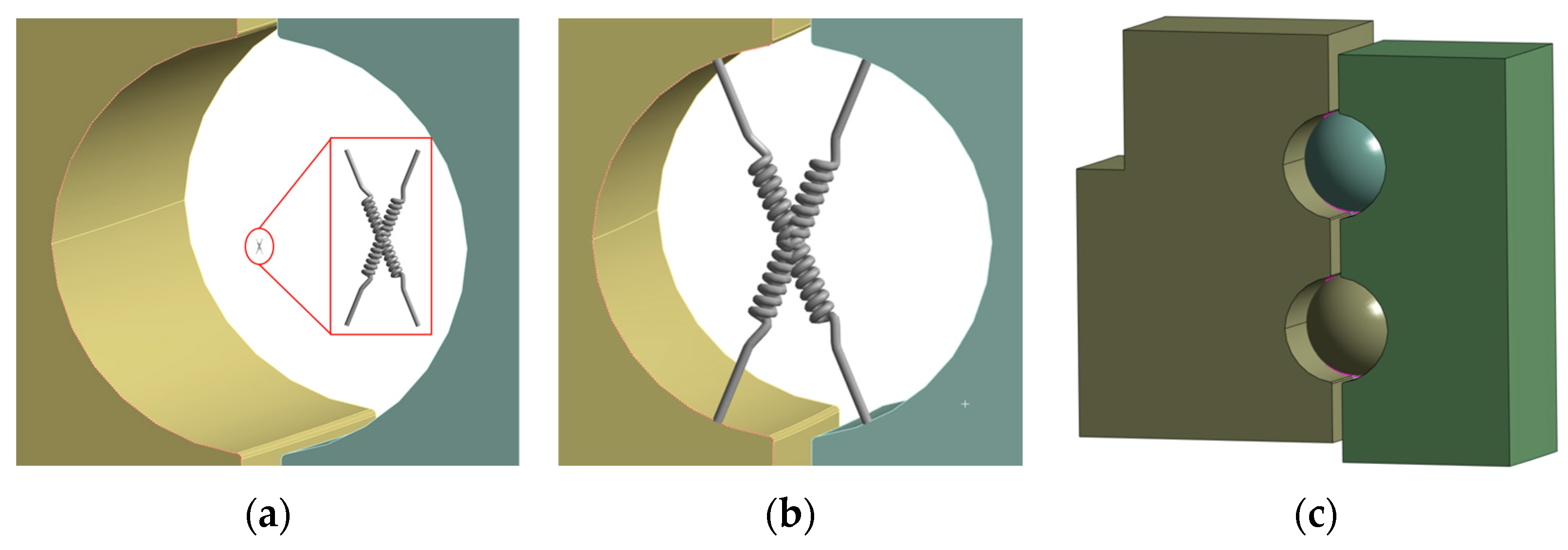
2.2. Four-Contact FE Bearing Model
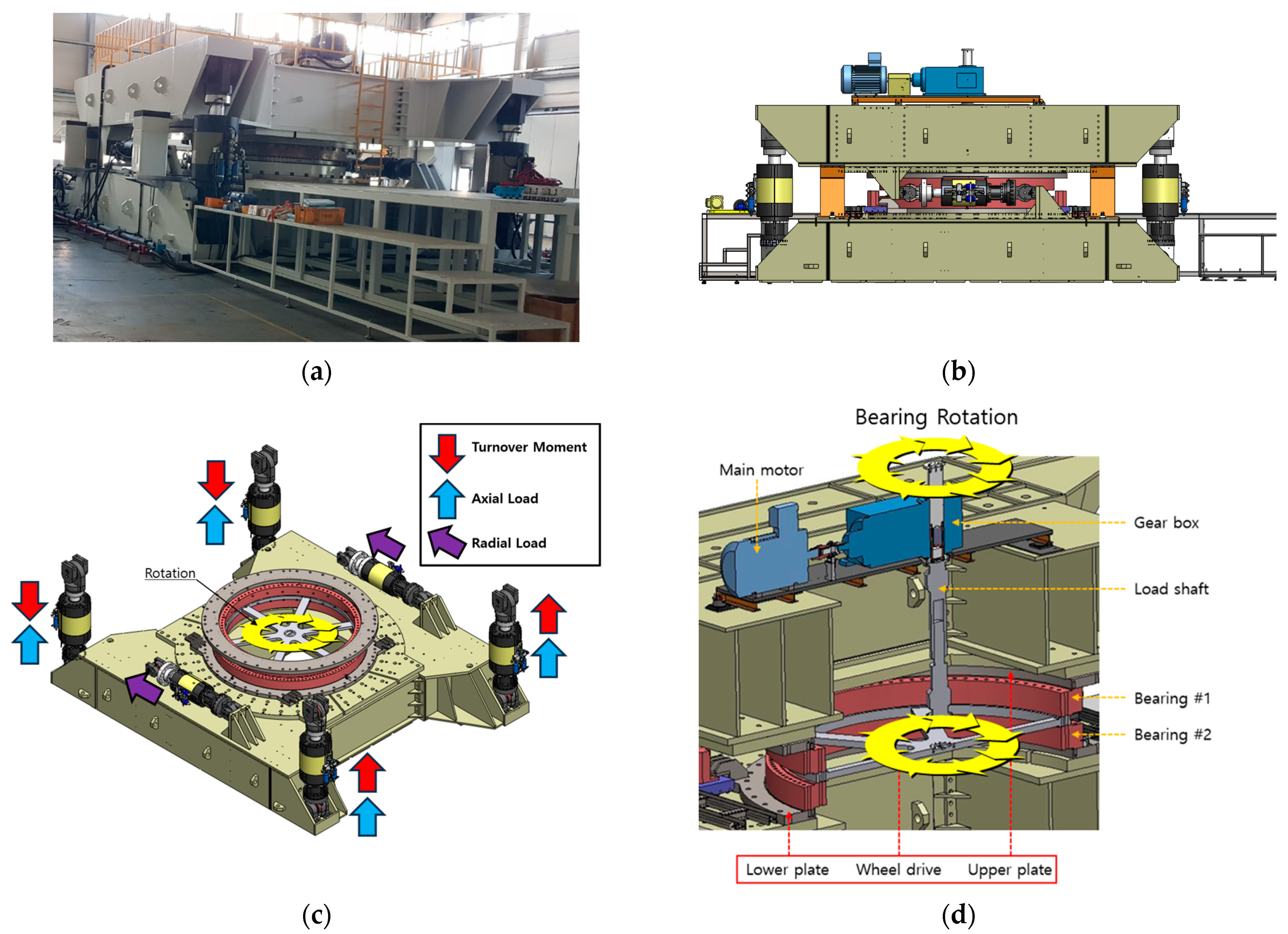
2.3. Test Bench of Pitch Bearing
3. Finite Element Analysis of Pitch Bearing
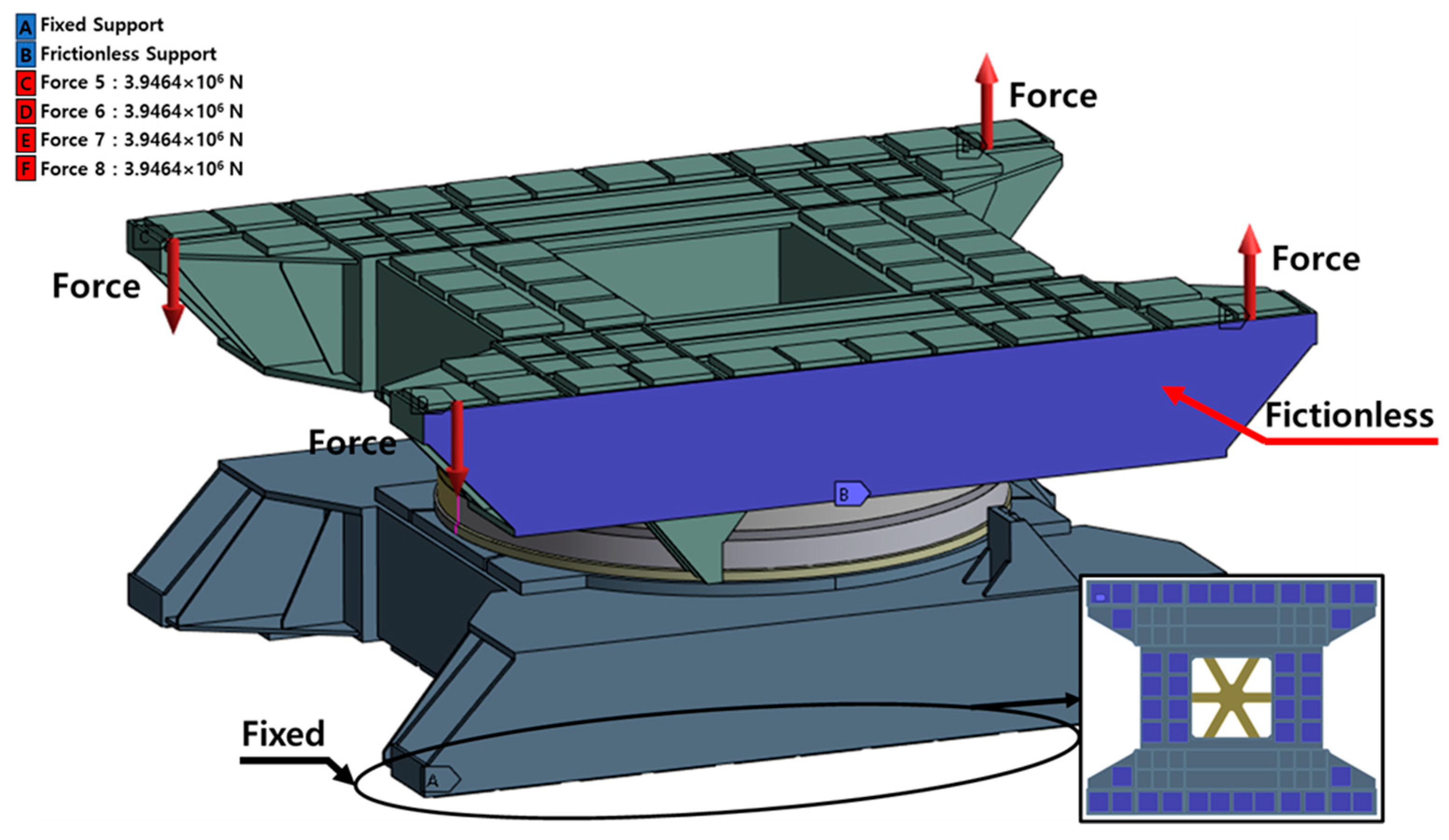
3.1. Global Model Finite Analysis Condition
3.2. Sub-Model Finite Analysis Condition
4. Results
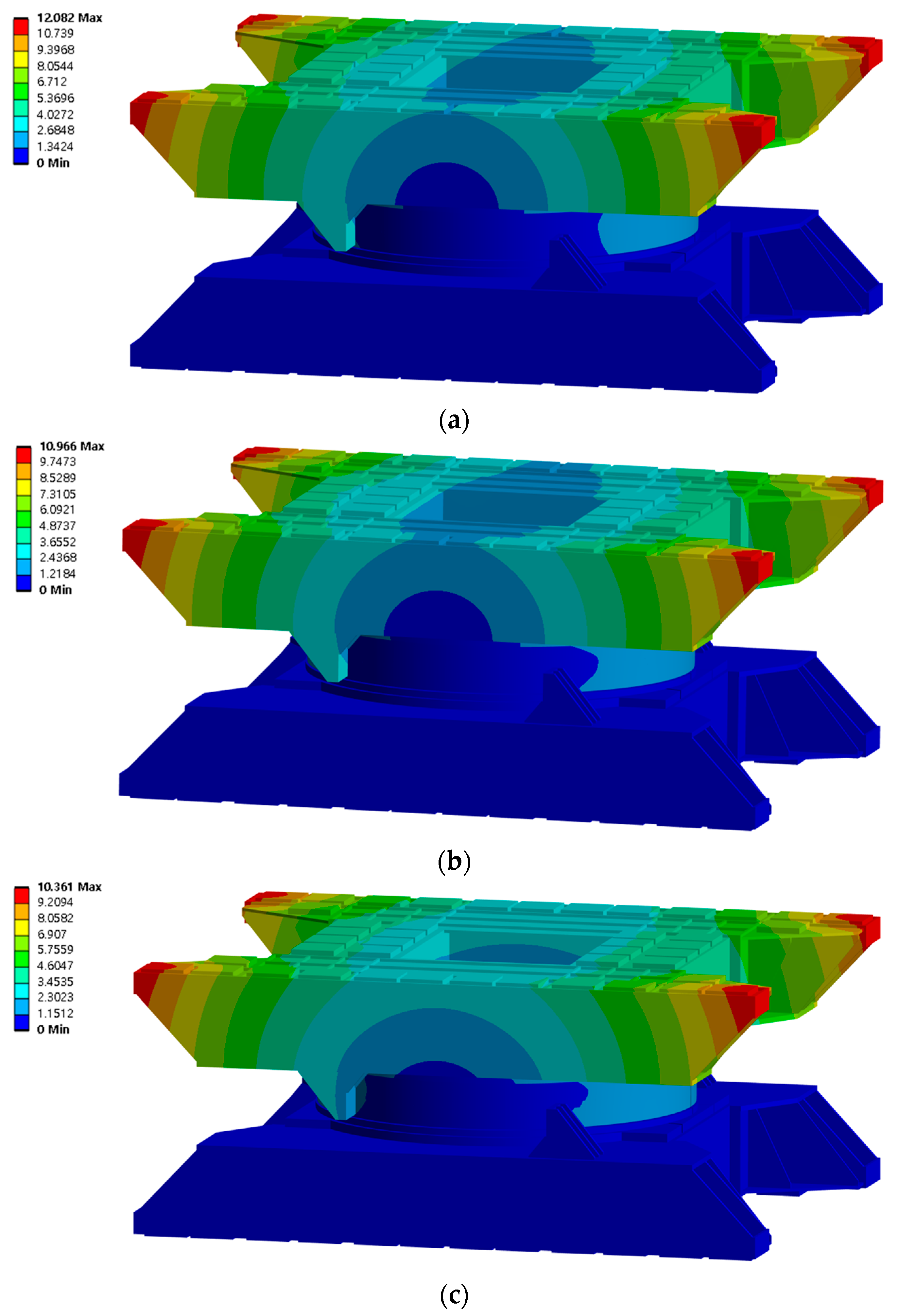
4.1. Global Model Analysis Results
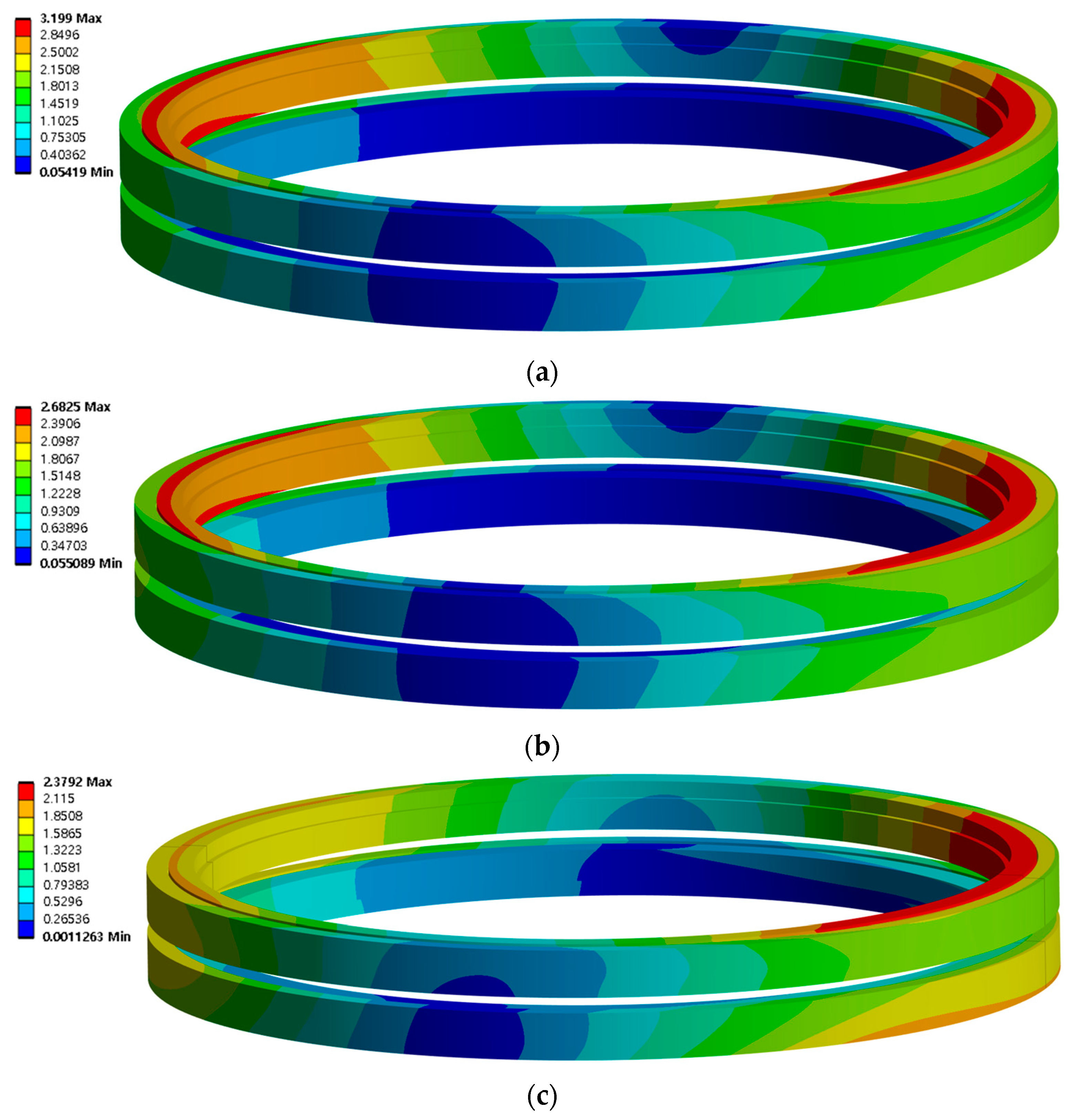
4.2. Sub-Model Analysis Result
4.3. Comparison of Results between FEAs and the Test with the Test Bench
4.4. Discussion of the Analysis Results
5. Conclusions
- (1)
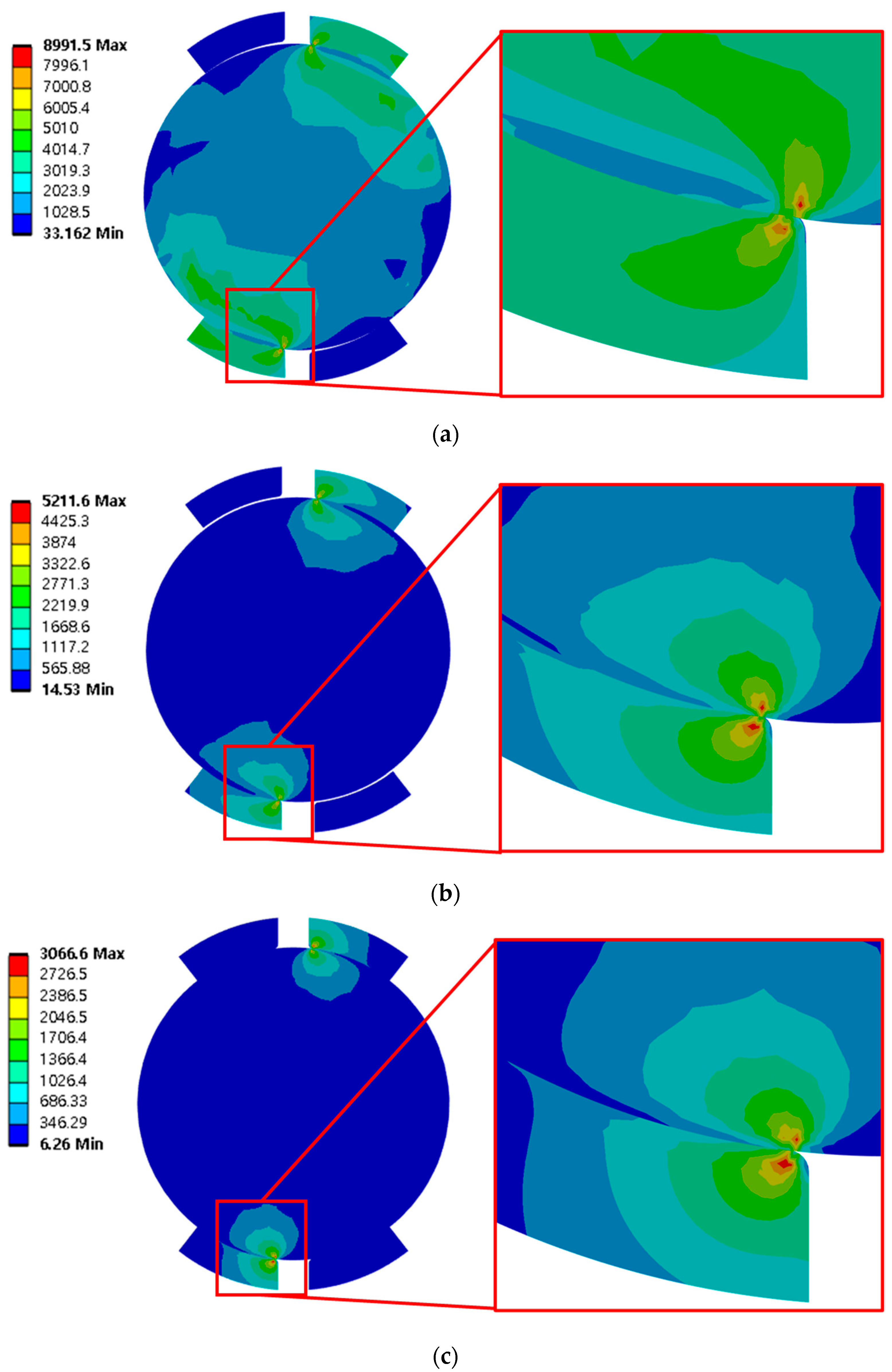
- According to the results of the global model analysis, the differences in displacement from the test results were 2.0 mm (17%) in the single-spring model, 0.97 mm (9%) in the Daidie spring model, and 0.36 mm (3%) in the FE mesh ball model. Therefore, the results from the FE mesh ball model were the most similar to the test results.
- (2)
- According to the results of the sub-model analysis, carried out based on the results of the global model analysis, the contact stress was 8991 MPa in the single-spring model, 4675 MPa in the Daidie spring model, and 3067 MPa in the ball model. The ball model shows the lowest contact stress. The single-spring model and the Daidie spring model showed high stress values, probably because they failed to simulate contact angle changes caused by turnover moments.
- (3)
- To evaluate the safety of bearings, a safety factor was calculated using the contact stress of the model that exhibited results most similar to the bearing test results based on the static allowable stress of ball bearings at 4200 MPa, presented in the NREL DG:03 Bearing Guideline. The calculated safety factor was 2.271 for the inner ring and 2.721 for the outer ring.
- (4)
- Further studies may need to be conducted to measure the displacement of both the bearing test bench and the bearings, considering the composite loads together, including the axial load, radial load, and turnover moment. The FEA results can be compared among the spring models and the FE mesh ball models with or without a preload for validation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abhijith, S. Study of Pitch Bearings in Wind Turbines—A Model Based Approach. Master’s Thesis, KTH Industrial Engineering and Management Machine Design, Stockhol, Sweden, 2018. [Google Scholar]
- Harris, T.A. Rolling Bearing Analysis, 3rd ed.; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Houpert, L. An Engineering Approach to Hertzian Contact Elasticity—Part I. J. Tribol. 2000, 123, 582–588. [Google Scholar] [CrossRef]
- Antoine, J.-F.; Abba, G.; Molinari, A. A New Proposal for Explicit Angle Calculation in Angular Contact Ball Bearing. J. Mech. Des. 2005, 128, 468–478. [Google Scholar] [CrossRef]
- Aguirrebeitia, J.; Avilés, R.; de Bustos, I.F.; Abasolo, M. Calculation of General Static Load-Carrying Capacity for the Design of Four-Contact-Point Slewing Bearings. J. Mech. Des. 2010, 132, 064501. [Google Scholar] [CrossRef]
- Aguirrebeitia, J.; Plaza, J.; Abasolo, M.; Vallejo, J. General static load-carrying capacity of four-contact-point slewing bearings for wind turbine generator actuation systems. Wind. Energy 2012, 16, 759–774. [Google Scholar] [CrossRef]
- Zupan, S.; Prebil, I. Carrying angle and carrying capacity of a large single row ball bearing as a function of geometry parameters of the rolling contact and the supporting structure stiffness. Mech. Mach. Theory 2001, 36, 1087–1103. [Google Scholar] [CrossRef]
- Daidié, A.; Chaib, Z.; Ghosn, A. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearing. J. Mech. Des. 2008, 130, 082601. [Google Scholar] [CrossRef]
- Duijvendijk, M.; Van, M.; Kalverboer, A.; De Gruiter, T. Benchmark of Bolted Bearing Connection Models in Wind Turbines. In Proceedings of the European Wind Energy Conference and Exhibition, Athens, Greece, 27 February–2 March 2006; pp. 1–7. [Google Scholar]
- Gao, X.H.; Huang, X.D.; Wang, H.; Chen, J. Modelling of ball raceway contacts in a slewing bearing with nonlinear springs. Proc Inst. Mech. Eng. Part C 2011, 225, 827–831. [Google Scholar] [CrossRef]
- Starvin, M.S.; Babu, S.; Aithal, S.; Manisekar, K.; Chellapandi, P. Finite element simulation of nonlinear deformation behaviour in large diameter angular contact thrust bearing. Sci. Res. Essays 2013, 8, 128–138. [Google Scholar] [CrossRef]
- Aguirrebeitia, J.; Plaza, J.; Abasolo, M.; Vallejo, J. Effect of the preload in the general static load-carrying capacity of four-contact-point slewing bearings for wind turbine generators: Theoretical model and finite element calculations. Wind Energy 2013, 17, 1605–1621. [Google Scholar] [CrossRef]
- Plaza, J.; Abasolo, M.; Coria, I.; Aguirrebeitia, J.; Ferna’ndez de Bustos, I. A new finite element approach for the analysis of slewing bearings in wind turbine generators using superelement techniques. Meccanica 2015, 50, 1623–1633. [Google Scholar] [CrossRef]
- Schwack, F.; Flory, H.; Poll, G.; Stammler, M. Free contact angles in pitch bearings and their impact on contact and stress conditions. In Proceedings of the Wind Europe, SUMMIT 2016, Hamburg, Germany, 27–30 September 2016; pp. 27–29. [Google Scholar]
- Zhang, H.; Chen, S.; Dou, Y.; Fan, H.; Wang, Y. Mechanical model and contact properties of double row slewing ball bearing for wind turbine. Rev. Adv. Mater. Sci. 2021, 60, 112–126. [Google Scholar] [CrossRef]
- Porziani, S.; Biancolini, M.E.; Brutti, C. Analysis of Wind Turbine Pitch 4-Point Contact Bearing. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1275, 012034. [Google Scholar] [CrossRef]
- He, P.; Hong, R.; Wang, H.; Ji, X.; Lu, C. Calculation analysis of yaw bearings with a hardened raceway. Int. J. Mech. Sci. 2018, 144, 540–552. [Google Scholar] [CrossRef]
- Graßmann, M.; Schleich, F.; Stammler, M. Validation of a finite-element model of a wind turbine blade bearing. Finite Elements Anal. Des. 2023, 221, 103957. [Google Scholar] [CrossRef]
- He, P.; Qian, Q.; Wang, Y.; Liu, H.; Guo, E.; Wang, H. Influence of finite element mesh size on the carrying capacity analysis of single-row ball slewing bearing. Adv. Mech. Eng. 2021, 13, 16878140211009030. [Google Scholar] [CrossRef]
- Saint-Vanant, D. Mémoire sur la flexion des prismes. J. Math. Pures Appl. 1856, 1, 89–189. [Google Scholar]
- Liu, Y.; Glass, G. Effects of Mesh Density on Finite Element Analysis. In Proceedings of the SAE 2013 World Congress & Exhibition, Detroit, MI, USA, 16–19 April 2013. [Google Scholar]
- Chang, S.; Liu, K.; Yang, M.; Yuan, L. Theory and implementation of sub-model method in finite element analysis. Heliyon 2022, 8, e11427. [Google Scholar] [CrossRef] [PubMed]
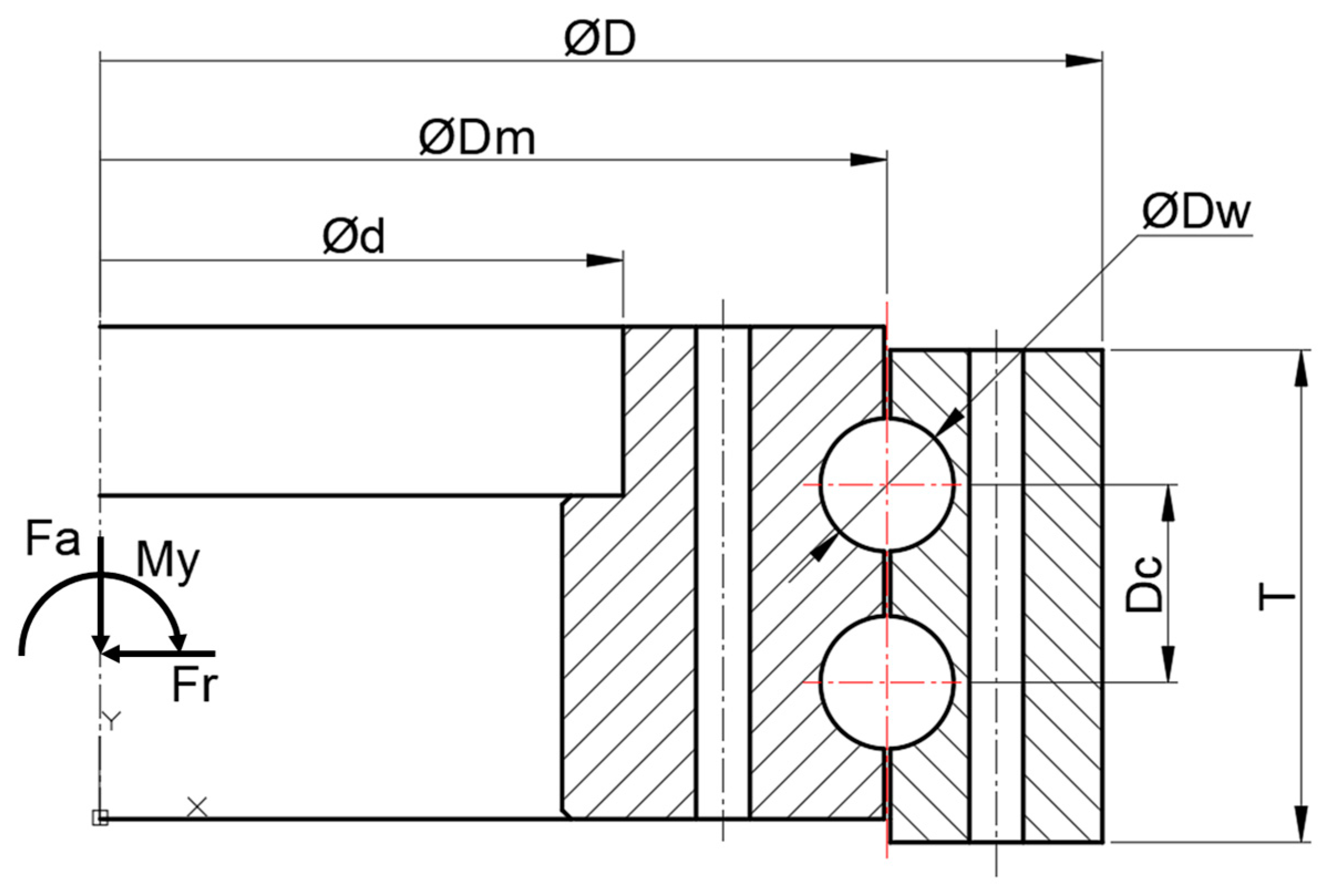


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Outer ring, outer diameter | D | 5200 | mm |
| Ball center, ball center diameter | Dm | 4957 | mm |
| Inner ring | d | 4660 | mm |
| Ball diameter | Dw | 71.32 | mm |
| Ball center interval | Dc | 110 | mm |
| Outer ring height | T | 274 | mm |
| Contact angle | α | 67.29 | Deg |
| Maximum moment | My | 63,142 | kNm |
| Bearing Test Bench | ||
|---|---|---|
| Maximum load | Moment | 76,000 kNm |
| Radial load | 2900 kN | |
| Axial load | 9500 kN | |
| Full assembly | Width | 9385 mm |
| Length | 17,200 mm | |
| Height | 4835 mm | |
| Total weight | 270,000 kg | |
| Max Contact Stress [MPa] | Static Load Factor | |
|---|---|---|
| Inner raceway | 3195.4 | 2.271 |
| Outer raceway | 3008.4 | 2.721 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-W.; Song, J.-W.; Hong, J.-P.; Kim, H.-J.; Kang, J.-H. Finite Element Analysis and Validation of Wind Turbine Bearings. Energies 2024, 17, 692. https://doi.org/10.3390/en17030692
Kim S-W, Song J-W, Hong J-P, Kim H-J, Kang J-H. Finite Element Analysis and Validation of Wind Turbine Bearings. Energies. 2024; 17(3):692. https://doi.org/10.3390/en17030692
Chicago/Turabian StyleKim, Seung-Woo, Jung-Woo Song, Jun-Pyo Hong, Hyun-Jong Kim, and Jong-Hun Kang. 2024. "Finite Element Analysis and Validation of Wind Turbine Bearings" Energies 17, no. 3: 692. https://doi.org/10.3390/en17030692
APA StyleKim, S.-W., Song, J.-W., Hong, J.-P., Kim, H.-J., & Kang, J.-H. (2024). Finite Element Analysis and Validation of Wind Turbine Bearings. Energies, 17(3), 692. https://doi.org/10.3390/en17030692






