Research on Excitation Estimation for Ocean Wave Energy Generators Based on Extended Kalman Filtering
Abstract
:1. Introduction
2. Materials and Methods
2.1. WEC Model
2.2. Radiative Force
2.3. Hydrostatic Restoring Force and PTO Force
2.4. Mooring Force
2.5. Modeling the WEC System
3. Methods
3.1. Kalman Filter Estimation
3.2. Discretization
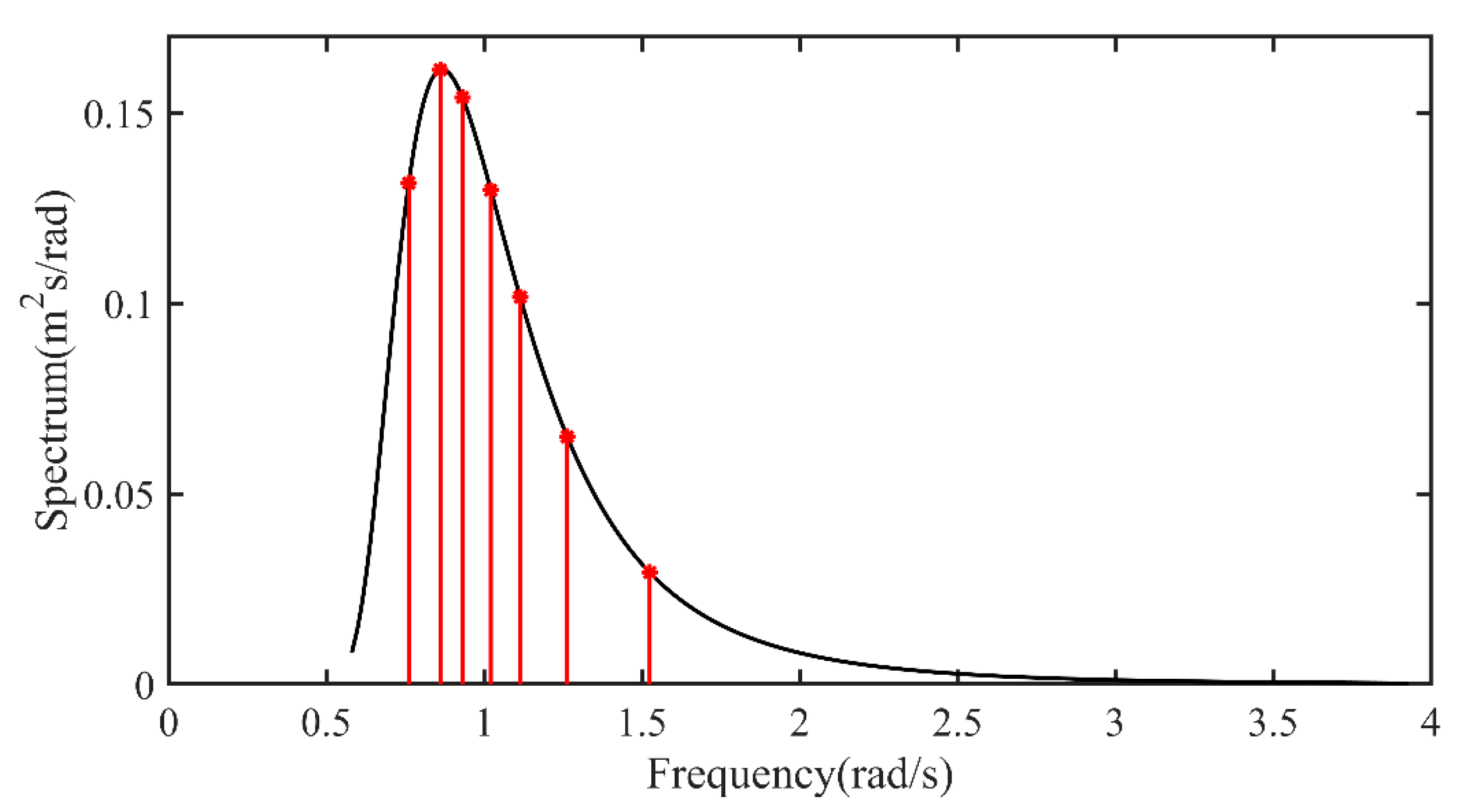
3.3. Equal-Energy Method
4. Results and Discussion
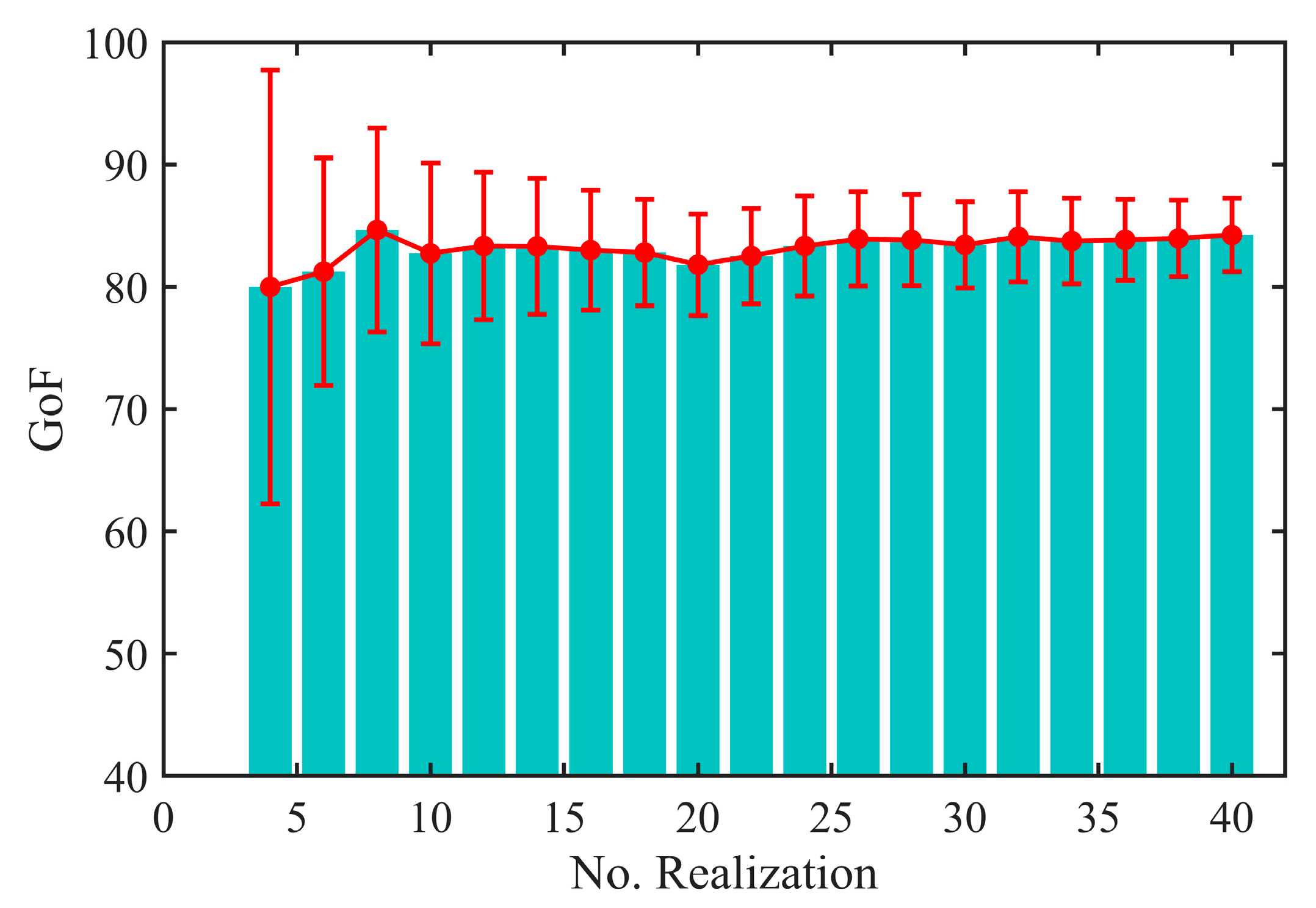
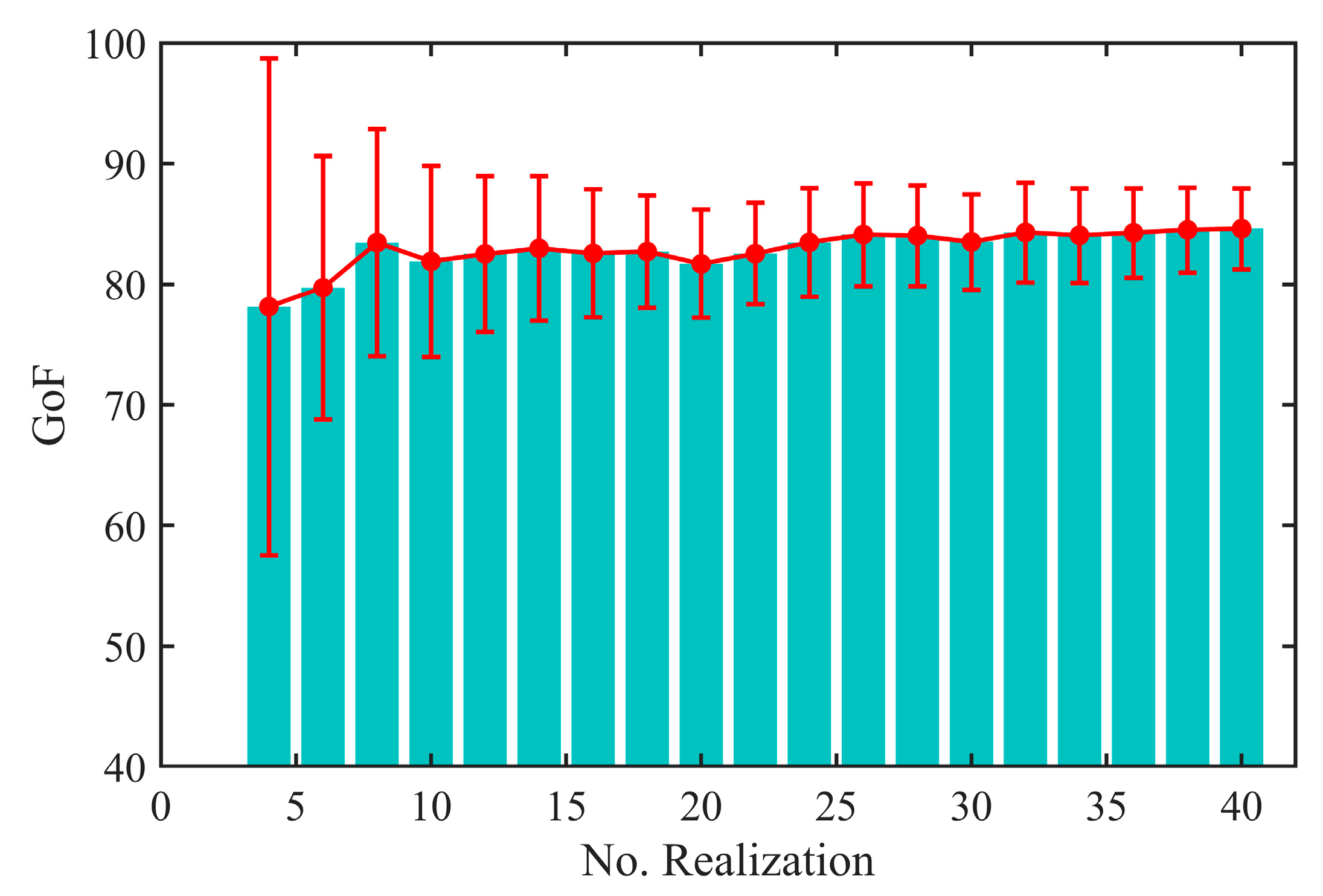
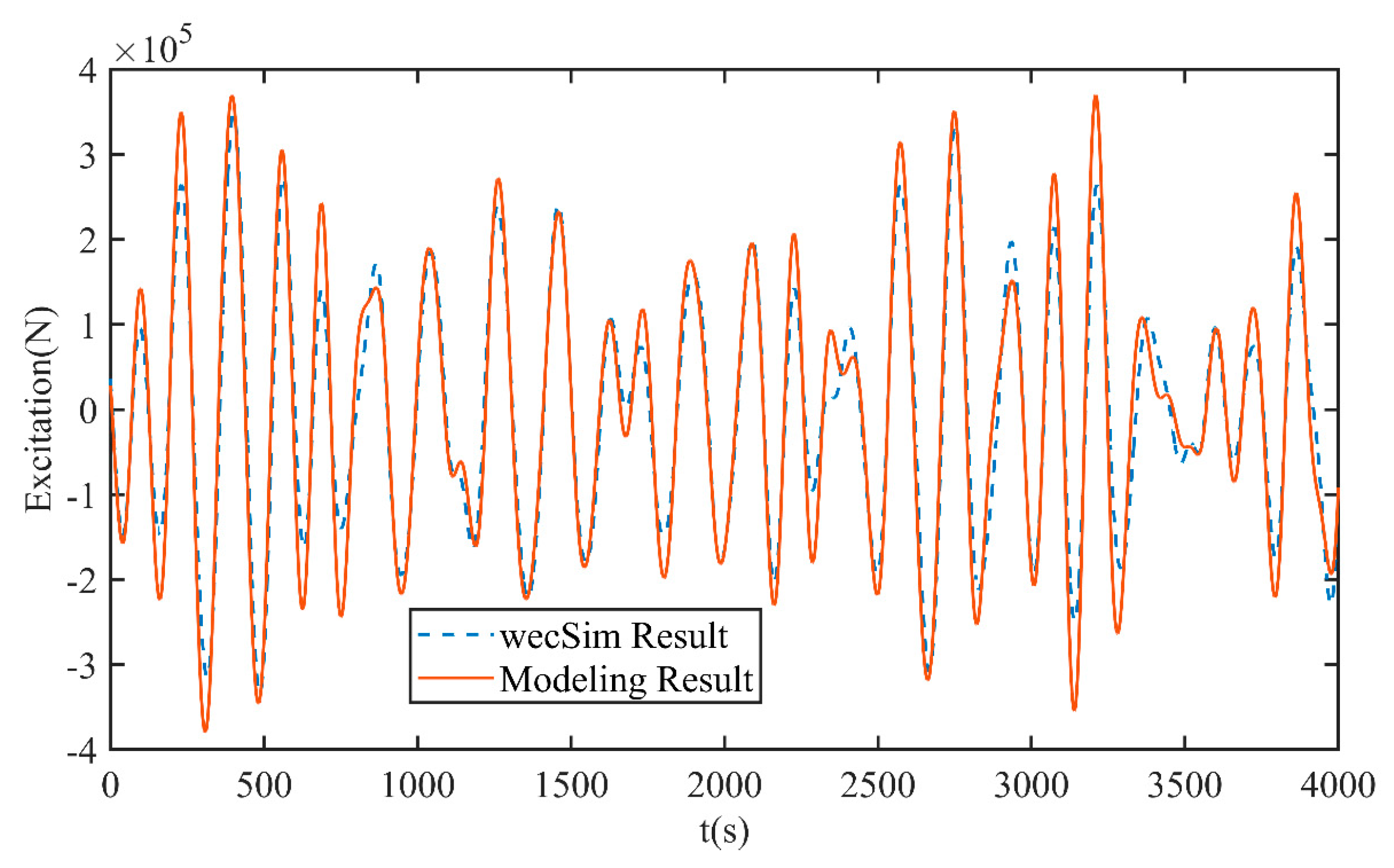
4.1. The Effect of Random Phase on the Estimation Results
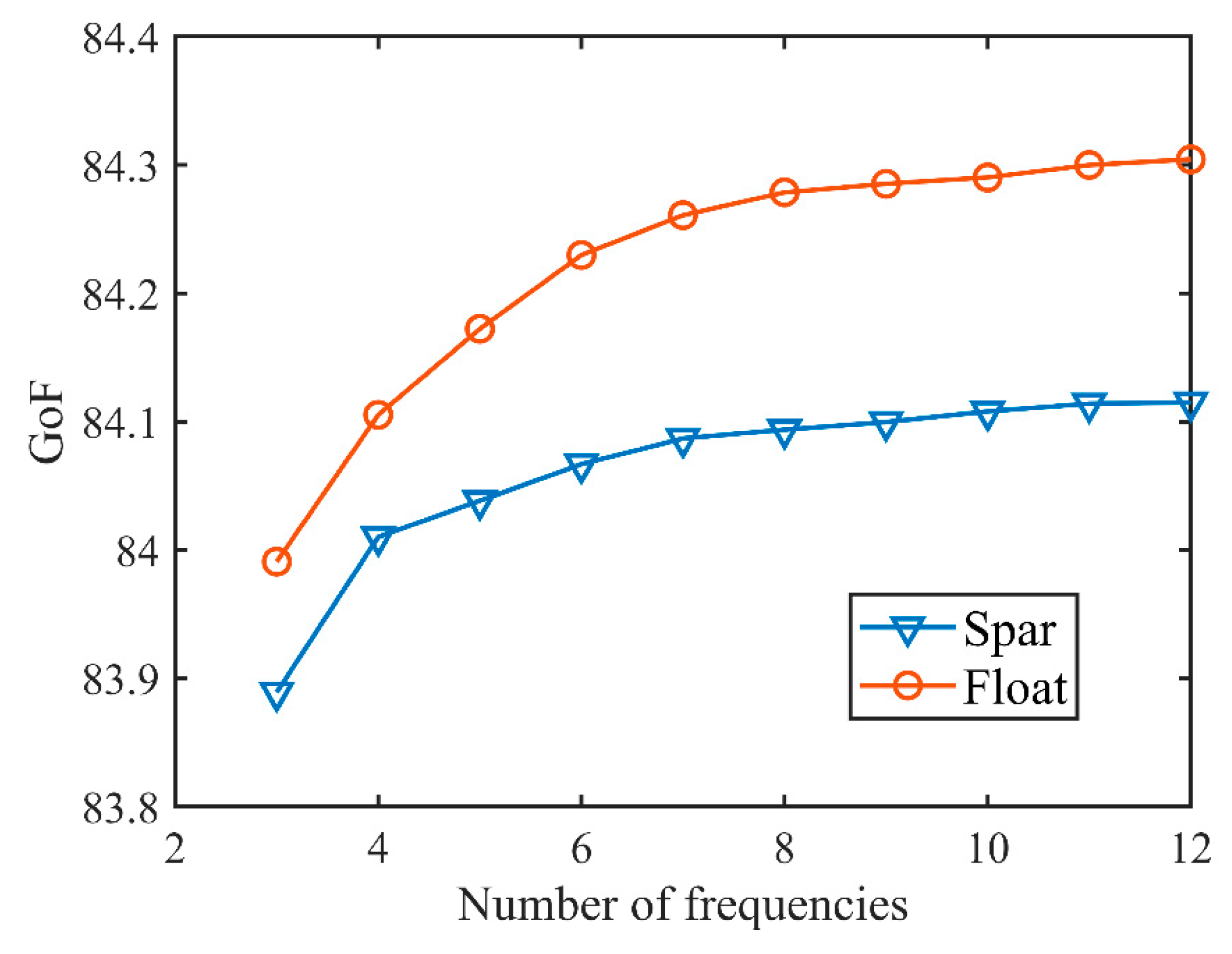
4.2. Impact of Dividing the Number of Frequencies on the Estimation Results
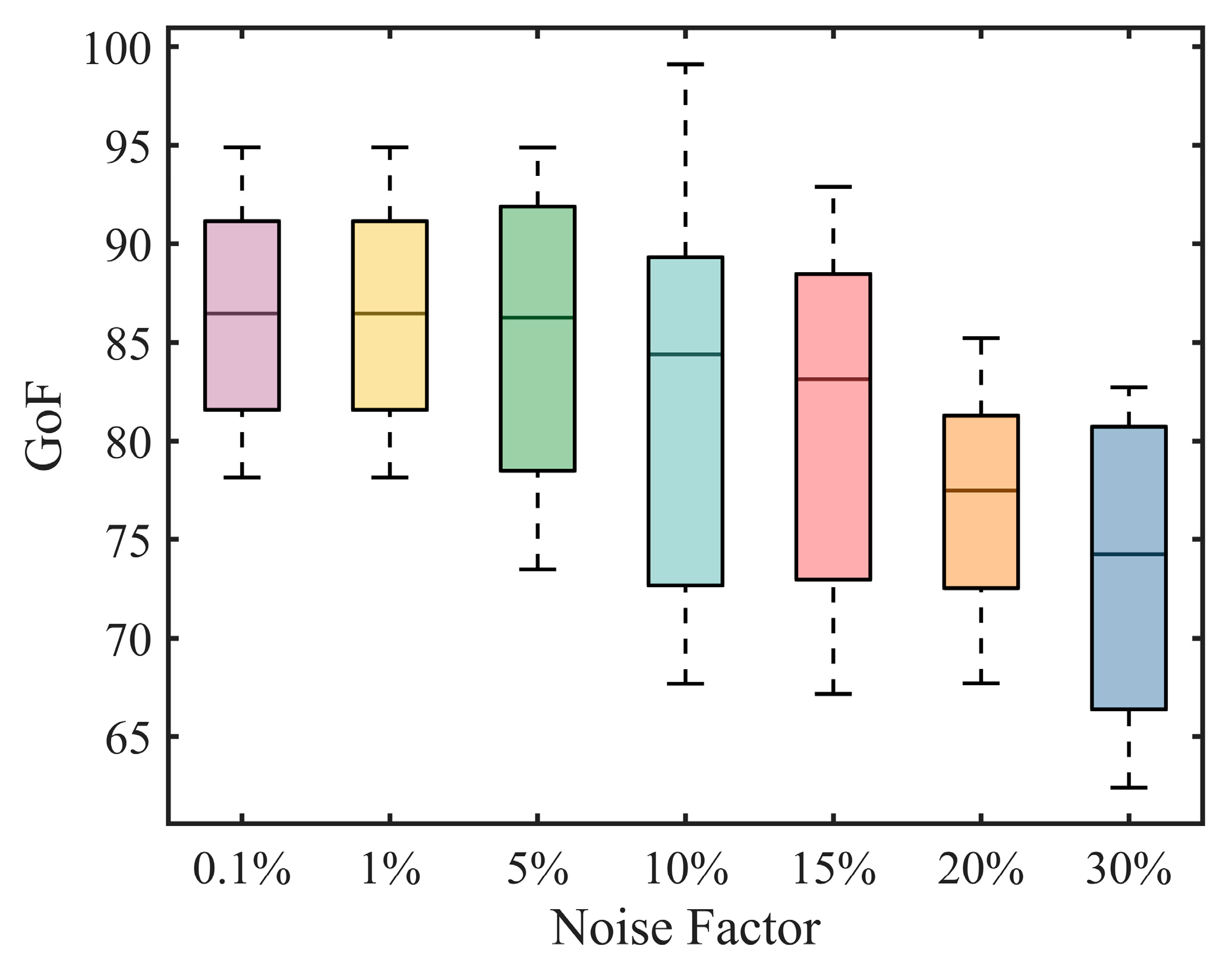
4.3. Effect of Noise Factor on Estimation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, S.; Li, F. Introduction to Marine Science; Higher Education Press: Beijing, China, 2006; p. 185. [Google Scholar]
- Mork, G.; Barstow, S.; Kabuth, A.; Pontes, M.T. Assessing the global wave energy potential. In Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, OMAE, Shanghai, China, 6–11 June 2010. [Google Scholar]
- IEA. Data and Statistics: Electricity[DB/OL]. Available online: https://www.iea.org (accessed on 12 February 2022).
- Gao, D.; Wang, F.; Shi, H.; Chang, Z.; Zhao, L. Research Progress of Wave Energy Generators in Foreign Countries. Ocean. Dev. Manag. 2012, 29, 21–26. [Google Scholar]
- Wang, Z.; Zhou, L.; Dong, S.; Wu, L.; Li, Z.; Mou, L.; Wang, A. Wind wave characteristics and engineering environment of the South China Sea. J. Ocean. Univ. China 2014, 13, 893–900. [Google Scholar] [CrossRef]
- Han, B.; Chu, J.; Xiong, Y.S.; Yao, F. Progress of Research on Ocean Wave Energy Power Generation. Power Syst. Clean Energy 2012, 28, 61–66. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave energy in Europe: Current status and perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Wang, C.; Lu, W. Ocean Energy Resource Analysis Methodology and Reserve Assessment; Ocean Press: Beijing, China, 2009; pp. 106–129. [Google Scholar]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- Rusu, L.; Onea, F. The performance of some state-of-the-art wave energy converters in locations with the worldwide highest wave power. Renew. Sustain. Energy Rev. 2017, 75, 1348–1362. [Google Scholar] [CrossRef]
- Pena-Sanchez, Y.; Windt, C.; Davidson, J.; Ringwood, J.V. A critical comparison of excitation force estimators for wave-energy devices. IEEE Trans. Control. Syst. Technol. 2020, 28, 2263–2275. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.J.; Jin, S. Numerical and experimental studies of excitation force approximation for wave energy conversion. Renew. Energy 2018, 125, 877–889. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Zou, S.; Bacelli, G.; Robinett, R.D.; Wilson, D.G.; Coe, R.G. Estimation of excitation force on wave energy converters using pressure measurements for feedback control. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, OCE, Monterey, CA, USA, 19–23 September 2016. [Google Scholar]
- Gao, J.; He, Z.; Zang, J.; Chen, Q.; Ding, H.; Wang, G. Numerical investigations of wave loads on fixed box in front of vertical wall with a narrow gap under wave actions. Ocean Eng. 2020, 206, 107323. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, J.; Wang, J.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on Transient Gap Resonance with Consideration of the Motion of Floating Body. China Ocean. Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Fusco, F.; Ringwood, J.V. Short-term wave forecasting for real-time control of wave energy converters. IEEE Trans. Sustain. Energy 2010, 1, 99–106. [Google Scholar] [CrossRef]
- Paparella, F.; Monk, K.; Winands, V.; Lopes, M.F.P.; Conley, D.; Ringwood, J.V. Up-wave and autoregressive methods for short-term wave forecasting for an oscillating water column. IEEE Trans. Sustain. Energy 2015, 6, 171–178. [Google Scholar] [CrossRef]
- Merigaud, A.; Ringwood, J.V. Incorporating ocean wave spectrum information in short-term free-surface elevation forecasting. IEEE J. Ocean. Eng. 2019, 44, 401–414. [Google Scholar] [CrossRef]
- Ma, Y.; Sclavounos, P.D.; Cross-Whiter, J.; Arora, D. Wave forecast and its application to the optimal control of offshore floating wind turbine for load mitigation. Renew Energy 2018, 128, 163–176. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- Desouky, M.A.A.; Abdelkhalik, O. Wave prediction using wave rider position measurements and NARX network in wave energy conversion. Appl. Ocean Res. 2019, 82, 10–21. [Google Scholar] [CrossRef]
- Mahmoodi, K.; Nepomuceno, E.; Razminia, A. Wave excitation force forecasting using neural networks. Energy 2022, 247, 123322. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Zou, S.; Robinett, R.; Bacelli, G.; Wilson, D. Estimation of excitation forces for wave energy converters control using pressure measurements. Int. J. Control 2016, 90, 1793–1805. [Google Scholar] [CrossRef]
- Brekken, T.K.A. On model predictive control for a point absorber wave energy converter. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Ling, B.A. Real-Time Estimation and Prediction of Wave Excitation Forces for Wave Energy Control Applications. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Nguyen, H.-N.; Tona, P. Wave Excitation Force Estimation for Wave Energy Converters of the Point-Absorber Type. IEEE Trans. Control. Syst. Technol. 2018, 26, 2173–2181. [Google Scholar] [CrossRef]
- Abril, M.G.; Paparella, F.; Ringwood, J.V. Excitation force estimation and forecasting for wave energy applications. In International Federation of Automatic Control; Elsevier: Amsterdam, The Netherlands, 2017; pp. 14692–14697. [Google Scholar]
- Mahmoodi, K.; Ghassemi, H.; Razminia, A. Performance assessment of a two-body wave energy converter based on the Persian Gulf wave climate. Renew. Energy 2020, 159, 519–537. [Google Scholar] [CrossRef]
- Yu, Z.; Falnes, J. State-space modelling of a vertical cylinder in heave. Appl. Ocean Res. 1995, 17, 265–275. [Google Scholar]
- Kristiansen, E.; Hjulstad, Å.; Egeland, O. State-space representation of radiation forces in time-domain vessel models. Ocean Eng. 2005, 32, 2195–2216. [Google Scholar] [CrossRef]
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency–time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K.A. Nonlinear Model Predictive Control of a Point Absorber Wave Energy Converter. IEEE Trans. Sustain. Energy 2013, 4, 118–126. [Google Scholar] [CrossRef]
- Bonfanti, M.; Hillis, A.; Sirigu, S.A.; Dafnakis, P.; Bracco, G.; Mattiazzo, G.; Plummer, A. Real-Time Wave Excitation Forces Estimation: An Application on the ISWEC Device. J. Mar. Sci. Eng. 2020, 8, 825. [Google Scholar] [CrossRef]
- Yerai, S.P.; Marina, A.G.; Francesco, P.; Ringwood, J.V. Estimation and Forecasting of Excitation Force for Arrays of Wave Energy Devices. IEEE Trans. Sustain. Energy 2018, 9, 1672–1680. [Google Scholar]
- Davis, A.F.; Fabien, B.C. Wave excitation force estimation of wave energy floats using extended Kalman filters. Ocean. Eng. 2020, 198, 106970. [Google Scholar] [CrossRef]
- Gao, J.; Chen, H.; Zang, J.; Chen, L.; Wang, G.; Zhu, Y. Numerical investigations of gap resonance excited by focused transient wave groups. Ocean. Eng. 2020, 212, 107628. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, J.; Wang, D.; Wang, W.; Liu, Y.; Xue, G. Research on wave excitation estimators for arrays ofwave energy converters. Energy 2023, 264, 126133. [Google Scholar] [CrossRef]
- Kazantzis, N.; Chong, K.T.; Park, J.H.; Parlos, A.G. Control-relevant discretization of nonlinear systems with time-delay using taylor-lie series. J. Dyn. Sys. Meas. Control 2005, 127, 153–159. [Google Scholar] [CrossRef]
- Bosma, B.; Thiebaut, F.; Sheng, W. Comparison of a catenary and compliant taut mooring system for marine energy systems. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]

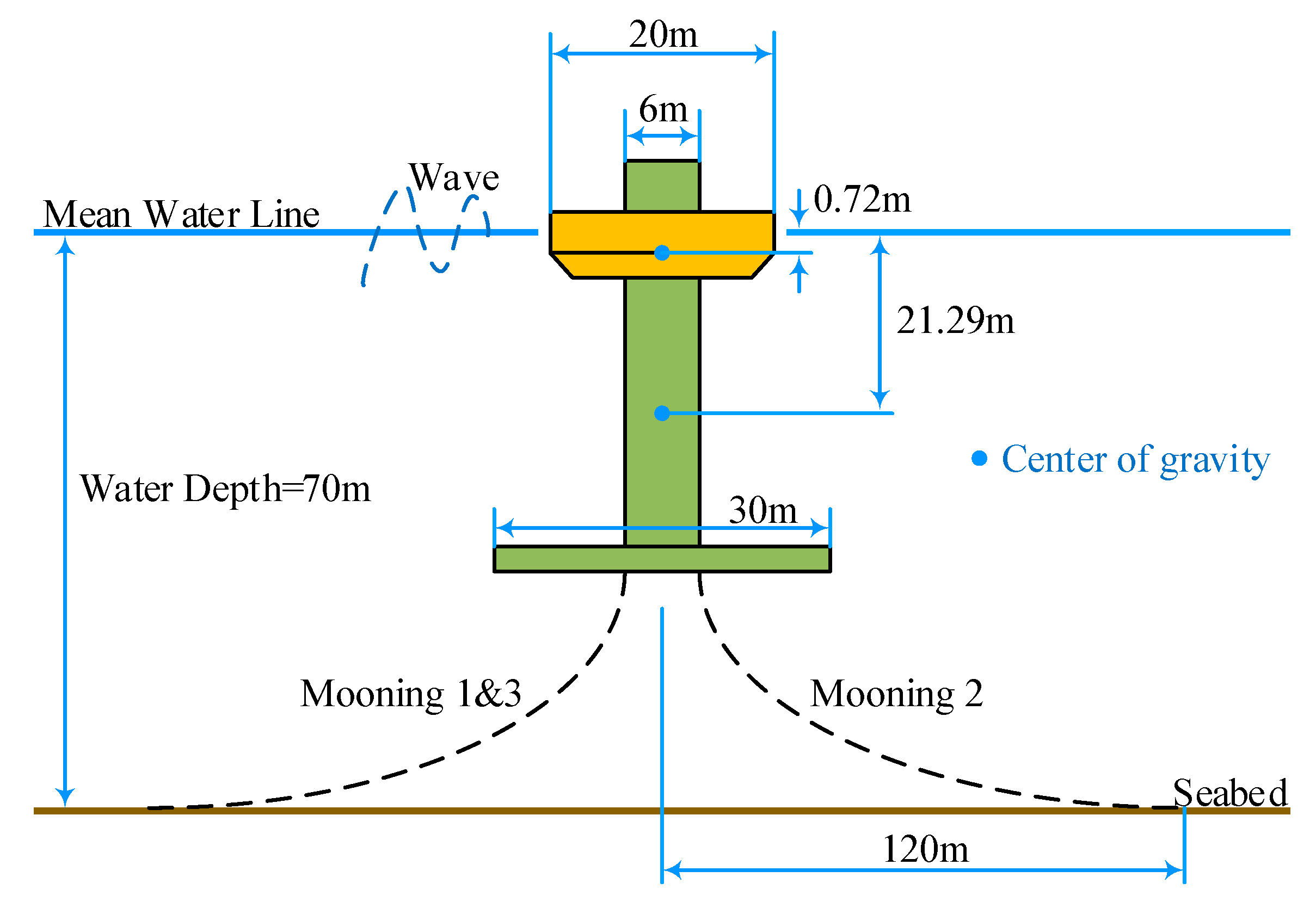


| Body | Mass (Tonne) | Direction | Center of Gravity (m) | Inertia Tensor (kg·m2) | ||
|---|---|---|---|---|---|---|
| Float | 727.01 | x | 0 | 20,907,301 | 0 | 0 |
| y | 0 | 0 | 21,306,091 | 0 | ||
| z | −0.72 | 0 | 0 | 37,085,481 | ||
| Spar | 878.30 | x | 0 | 94,419,615 | 0 | 0 |
| y | 0 | 0 | 94,407,091 | 0 | ||
| z | −21.29 | 0 | 0 | 28,542,225 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, Z.; Wang, J.; Qin, J.; Huang, S.; Xue, G.; Liu, Y. Research on Excitation Estimation for Ocean Wave Energy Generators Based on Extended Kalman Filtering. Energies 2024, 17, 704. https://doi.org/10.3390/en17030704
Zhang Y, Zhang Z, Wang J, Qin J, Huang S, Xue G, Liu Y. Research on Excitation Estimation for Ocean Wave Energy Generators Based on Extended Kalman Filtering. Energies. 2024; 17(3):704. https://doi.org/10.3390/en17030704
Chicago/Turabian StyleZhang, Yuchen, Zhenquan Zhang, Jun Wang, Jian Qin, Shuting Huang, Gang Xue, and Yanjun Liu. 2024. "Research on Excitation Estimation for Ocean Wave Energy Generators Based on Extended Kalman Filtering" Energies 17, no. 3: 704. https://doi.org/10.3390/en17030704





