Design and Optical Performance Evaluation of the Three-Dimensional Solar Concentrators with Multiple Compound Parabolic Profiles and Elliptical and Rectangular Receiver Shapes

Abstract

The compound parabolic concentrator (CPC) is a core technology in the field of solar concentration. Nevertheless, it only has one degree of freedom in the choice of its half-acceptance angle. In this study, extending the idea of the three-dimensional CPC, a design method for new kinds of concentrators having a CPC shape at each profile with various acceptance angles in all directions is proposed. The feature of this method is that the receiver can take any shape. Here, elliptical and rectangular receivers are assumed, and the shape and concentration performance of the concentrators with multiple CPC profiles and an elliptical receiver (MultiPro-ECPCs) and the concentrators with multiple CPC profiles and a rectangular receiver (MultiPro-RCPCs) are derived. The new designs are compared to the conventional CPC and a mirrorless flat receiver through ray-tracing simulations in terms of energy distribution on the receiver, optical efficiency, and optical concentration ratio based on axial and solar angles. The results show that in terms of optical efficiency, the MultiPro-RCPCs cover a wider range of incident angles after the 3DCPC. In terms of the optical concentration ratio, the MultiPro-ECPC with a longitudinal half-acceptance angle of 15° has the highest peak value of 19.5, followed by the MultiPro-RCPC. This study enlightens that with the concentration system settings adapted to the acceptance range of the proposed concentrators, a higher concentration can be achieved with the MultiPro-ECPC and MultiPro-RCPC compared to the conventional CPC.

1. Introduction

More energy from the sun falls on the earth in one hour than is used by everyone in the world in one year [1]. Humans have been harnessing solar energy for thousands of years to grow crops, stay warm, and dry foods and clothes. Today, solar energy is used to heat and cool buildings [2], dry [3], cook [4], and produce electricity [5]. Therefore, the use of mirrors to concentrate solar energy is necessary to increase the collection intensity and enable an efficient use of the available resources. This high concentration of solar heat can also be used in a variety of industrial applications, such as water desalination, enhanced oil recovery, food processing, chemical production, and mineral processing [6]. Nowadays, new photovoltaic technologies, which are more resistant to heat and can work with mirrors, such as the bifacial photovoltaic (BPV) panels [7] and concentrated photovoltaic (CPV) systems [8], are emerging. In all these cases, the optical concentration ratio and mirror incidence acceptance range are determinants in the concentrating mirror shape selection.

The compound parabolic concentrator (CPC), designed by Winston et al. and consisting of a combination of two parabolic mirrors, is a concentrator with the function of advancing obliquely incident rays to the receiver [9]. The CPC is the core design for many solar concentrators resulting from its rotation [10,11,12,13,14] or translation transformation [15,16,17,18]. The shapes created by rotating the CPC curve around an axis are called three-dimensional CPCs (3DCPCs) and the ones created by translating the CPC curve in a direction are called two-dimensional CPCs (2DCPCs). The energy concentration ratio of the 3DCPC is found to be the square of the one of the 2DCPCs [19]. Nevertheless, one disadvantage of the CPC and its derivatives is that they have only one degree of freedom in designing the acceptance angle at which they can receive rays. Due to that, hourly tracking technologies are often used with concentrators to increase their energy collection since the position of the sun changes during the day and throughout the year. Therefore, it is necessary to develop a concentrator with more degrees of freedom in terms of their acceptance angle based on the concept of the three-dimensional CPC. From this perspective, Cooper et al. studied the energy collection performance of a 3DCPC with the same aperture and receiver polygonal shape [20]. Cooper et al. found that, especially for large acceptance angles, the performance of polygonal CPCs with reasonable numbers of sides approaches that of the revolved CPC. On the other hand, the flux distributions at the exit aperture of polygonal CPCs were shown to be less uniform than that of the revolved CPC, with dark spots forming near the corners. The polygonal shapes are of particular interest for applications where the concentrators must be uniformly tiled over a plane since the revolved CPC would result in significant gap losses in such an application. Nevertheless, the cases where the shape of the aperture and receiver were different were not studied, and the directional acceptance angles had the same value.

Concerning the use of ellipses in the field of solar concentration, Garcia-Botella et al. developed a new family of non-imaging concentrators called elliptical concentrators, where the receiver and aperture shapes are elliptical or circular [21]. This new family of concentrators provides new capabilities and can have different configurations, either homofocal or non-homofocal. Considering the transmission curves, the non-homofocal concentrator is found to fit the maximum theoretical longitudinal acceptance better than the homofocal concentrator, but both are worse than the 3DCPC. In addition, only the concentrator profiles at the longitudinal and transversal cross-sectional views are CPC profiles, and the intermediate profiles are unknown. Furthermore, Nazmi et al. and Ali et al., respectively, investigated a three-dimensional static square elliptical hyperboloid concentrator and a three-dimensional static elliptical hyperboloid concentrator [22,23]. Their results, respectively, showed low optical efficiencies of 0.70 and 0.27 when the sun was right on top of the concentrator.

The exploration of static three-dimensional solar concentrator geometries without the need for daily solar tracking mechanisms is paramount in advancing solar energy harvesting technologies. Non-tracking systems offer the potential to simplify solar energy systems, reduce initial and maintenance costs, and improve overall system robustness [24]. In addition, tracking systems, in some cases, come with tracking errors due to their low tracking accuracy [25] or weather dependency [26]. Investigating non-tracking geometries, including their optical efficiencies and flux concentration, becomes imperative as it seeks sustainable and cost-effective solutions to harness solar energy for a greener future. Under that perspective, Vaidya and al. developed a non-tracking immersion-graded index optical concentrator. This concentrator, with a square aperture and receiver, uses glass and polymers as its mirror material to enable inner refraction and demonstrates an optical concentration ratio of 3 with over 90% efficiency [27]. Nevertheless, the technology without refraction can only achieve an optical concentration ratio around one.

To overcome the concentration limits in a simpler way without considering refraction and to extend the ideas developed in these previous studies, in this study, a new family of three-dimensional solar concentrators with different directional acceptance angles is proposed. Another characteristic of this new family of concentrators, the MultiPro-CPCs, is that they are multi-profiled CPCs. In addition, the uniqueness of the proposed concentrators resides in the fact that their receivers can take any shape, except circular. This non-utilization of a circular receiver enables the variation of the directional acceptance angles. Specifically, in this study, the focus is on slender receivers such as elliptical and rectangular-shaped receivers, considering that the sun mainly moves in one direction during the day, i.e., the East–West direction. Thus, the shape and concentration performance of the concentrators with multiple CPC profiles and an elliptical receiver (MultiPro-ECPCs) and the concentrators with multiple CPC profiles and a rectangular receiver (MultiPro-RCPCs) are studied. In addition, the use of different East–West and North–South directional acceptance angles results in aperture shapes different from the receiver shapes. The motivation behind this study is that such a revolutionary concentrator shape could have major benefits to the solar concentration field by combining high optical concentration, a variation in the directional acceptance range, and the compactness of the receiver.

Based on the conventional CPC design principles, the objective of this study is to design and evaluate, through optical simulation, the MultiPro-CPCs with elliptical and rectangular receivers following the steps below:

• Develop a design method for the proposed concentrators with customizable receiver shapes.
• Assume elliptical receivers for the MultiPro-ECPCs and rectangular receivers for the MultiPro-RCPCs.
• Define the simulation conditions and evaluation indices.
• Evaluate the optical efficiency based on the axial angles and solar angles.
• Assess the irradiance distribution on the receiver and the axial angle coverage limits of the newly designed MultiPro-CPCs.
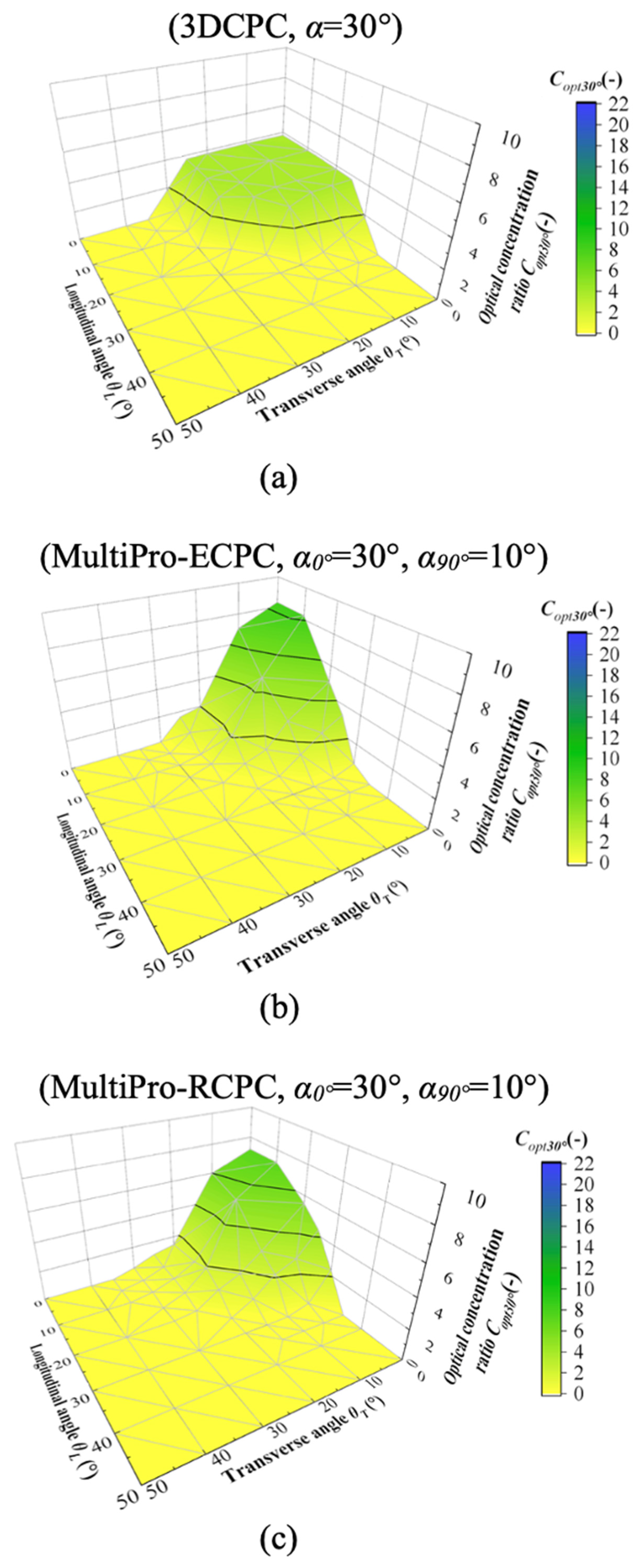
• Evaluate the optical concentration ratio based on the solar angles and a spatiotemporal interpretation.

2. Design of the Proposed Solar Concentrator

Non-tracking three-dimensional solar concentrators need to have different half-acceptance angles α to capture solar incident rays as the sun moves from time to time. The moving range in the East–West direction is much larger than the range in the North–South direction. Therefore, it is reasonable for concentrators to have different acceptance angles for each direction. In addition, in the case of optical applications, higher concentration ratios help in reducing the number of concentrators needed for a single receiver. Conventional 3DCPCs only have one acceptance angle, i.e., the same angle for both the East–West direction and North–South direction. Additionally, therefore, it is also hard to maximize their ideal concentration ratio expressed in Equation (1) [9]. To address this problem, this study proposes CPC-based concentrator designs allowing different acceptance angles in the East–West and North–South directions and, consequently, the use of non-rotationally symmetric receiver shapes such as an ellipse and a rectangle. With elliptical and rectangular receivers, the incidence acceptance range of the longitudinal direction becomes smaller than that of the transverse direction due to the existence of unequal major and minor axes in an ellipse and unequal length and width in a rectangle. Based on Equation (1), when the value of the half-acceptance angle α is between 0° and 90°, i.e., sin(α) is between 0 and 1, a decrease in α results in an increase in C_geo for a conventional 3DCPC that has a circular receiver. This way, for the same α in the longitudinal direction and a smaller one in the transverse direction, C_geo is expected to increase. Furthermore, the idea is that any diagonal cross-section of the concentrator has the shape of a CPC.

First, the CPC profiles and receiver shapes were determined using mathematical formulas. Then, the geometries were generated through a computer-aided design. Finally, the optical efficiency and optical concentration of the concentrators were assessed through ray-tracing simulations.

$$C_{geo}=\frac{A_{Ap}}{A_{Abs}}=\frac{1}{{\left(\sin \alpha \right)}^2}$$

(1)

2.1. Design of the Profile

Figure 1 shows the CPC profile at any diagonal cross-section of the solar concentrator. The red bold lines represent the parabolic segments AF and BC. Here, AF and BC are the mirror profiles, and C and F are, respectively, their focuses. Thanks to the characteristics of the parabola, the rays entering the AB aperture with an incidence angle smaller than the half-acceptance angle α_γ, can be focused onto the FC receiver. The equations used in the design of the CPC are shown below, where D_γ is the diameter of the aperture of the CPC, d_γ is the diameter of its receiver, and H is its height (see Figure 1 for details) [9].

$$y=\frac{x^2}{4f}=\frac{x^2}{2d_{\gamma }\left(1+\sin {\alpha }_{\gamma }\right)}$$

(2)

$$D_{\gamma }=d_{\gamma }/\sin {\alpha }_{\gamma }$$

(3)

$$H=\frac{D_{\gamma }+d_{\gamma }}{2\tan {\alpha }_{\gamma }}$$

(4)

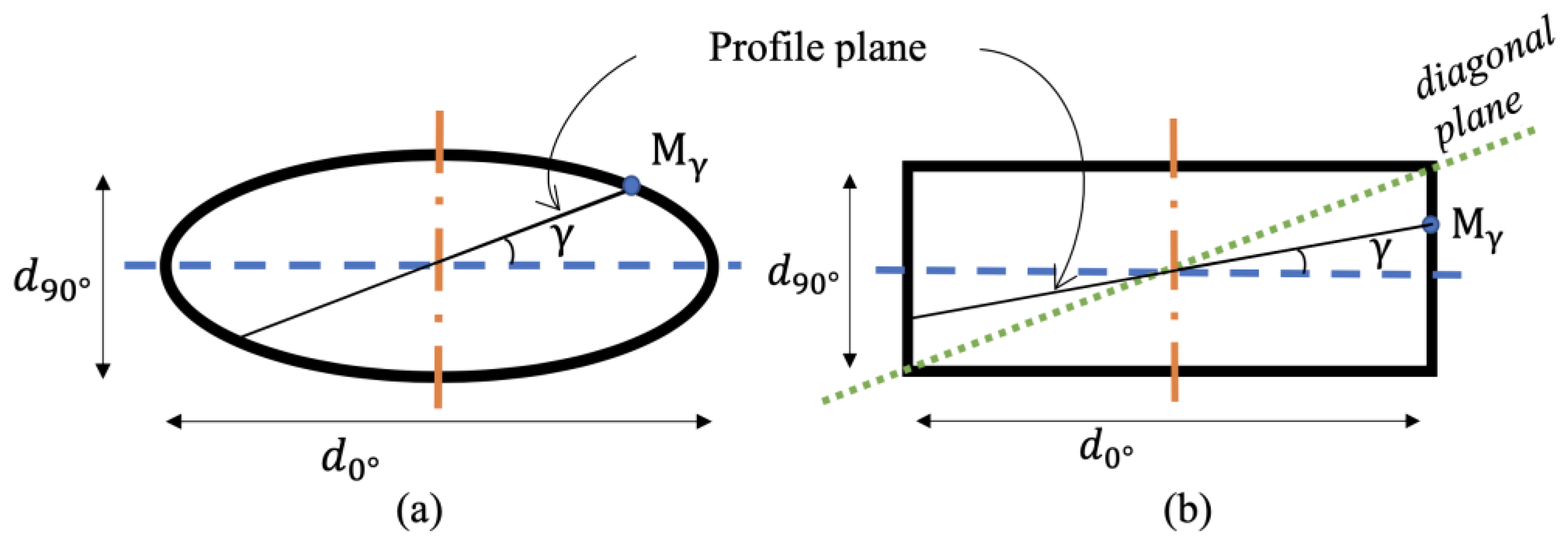
2.2. Design of the Receiver

The novel geometries for the CPC-type concentrators analyzed in this study find their applications in various fields, including fluid heating, photovoltaic generation, and building illumination. Considering the requirement for receivers to have varying dimensions in each of the North–South and East–West directions, this study suggests analyzing two receiver types: elliptical and rectangular. Therefore, two representative shapes are adopted, an elliptical receiver for the MultiPro-ECPC and a rectangular receiver for the MultiPro-RCPC, as illustrated in Figure 2. The acceptance angle changes continuously depending on the angle between the profile plane and the longitudinal direction, γ, as shown in Figure 2. The parameters considered in this design are the aperture diameter D_γ, the receiver diameter d_γ, the half-acceptance angle α_γ, and the height H. The point M_γ represents a position on the receiver at γ. The half-acceptance angle of the longitudinal direction α_0° was set to 15°, 30°, and 45°, and the half-acceptance angle of the transversal direction α_90° to 10°, 20°, and 30°. The length of the receiver major axis d_0° was fixed at 50 mm. Three-dimensional CPCs with a receiver diameter of 50 mm and a half-acceptance angle of α_0° were also simulated as a reference to be compared. In this study, the longitudinal direction corresponds to the East–West direction and the transversal direction to the North–South direction.

2.3. Steps in the Geometry Generation of Novel CPCs and Conventional CPCs

The novel solar concentrators are designed following the steps shown in Figure 3.

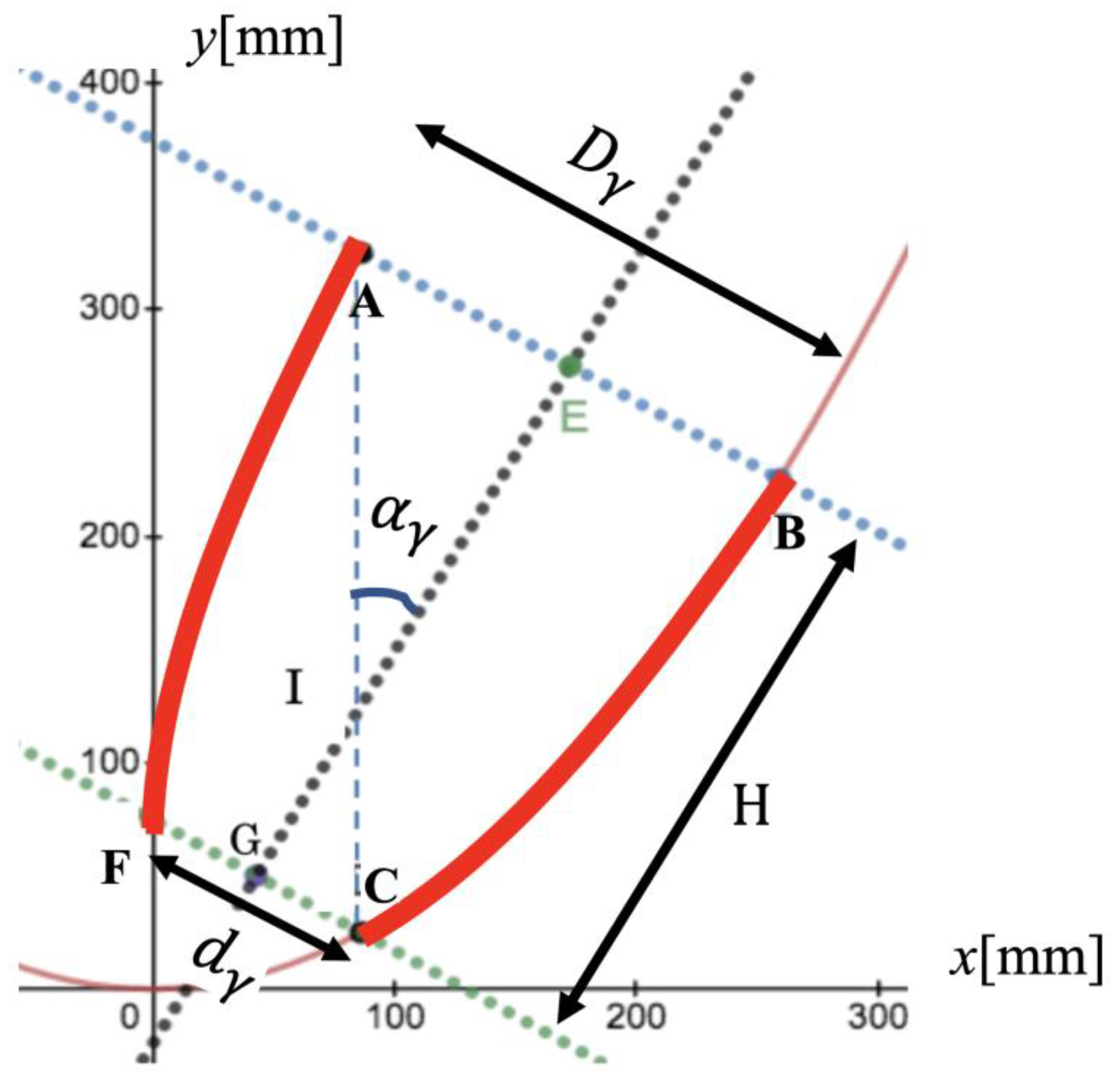
• First, the receiver shape was chosen. In Figure 3, the receiver is rectangular. Then, the receiver length of the East–West direction d_0°, the half-acceptance angle of the East–West direction α_0°, and the half-acceptance angle of the North–South direction α_90° were fixed.
• Secondly, the value of H and the East–West profile of the solar concentrator were determined from the fixed α_0° and d_0°, respectively.
• Thirdly, with H and α_90°, the length of the receiver minor axis d_90° was calculated and used to determine the North–South direction profile.
• Fourthly, the same method was repeated to design the CPC profile at each γ profile with $H$ and $d_{\gamma }$ as the inputs and ${\alpha }_{\gamma }$ as the output. The receiver diameter $d_{\gamma }$ is expressed in Equation (5) for the elliptical receiver and in Equation (7) for the rectangular receiver. Here, t_γ, represented in Equation (6), is the angular parameter of the elliptical receiver at γ, and γ_diag, represented in Equation (8), is the value of γ at the diagonal plane of the rectangular receiver. All equations are derived from the trigonometric relationships in an ellipse and a rectangle with the parameters shown in Figure 2.
• Finally, all the profiles were joined to form the concentrator, where γ varies from 0 to 90° every 15°.

The conventional CPCs are designed by rotating the CPC profile around its axis after applying Steps 1 and 2, as shown in Figure 3. Here, the shape of the receiver is circular and there is only one half-acceptance angle α that is equal to the one of the East–West direction α_0°. Furthermore, the elliptical and rectangular receiver lengths of the East–West direction d_0° become the diameter of the circular receiver.

All geometries were generated using the computer-aided design (CAD) software SolidWorks 2019 [28]. More precisely, a combination of the equation of a parabola shown in Equation (2) with the parameters α_0° and d_0° were inputted to form the profiles using the loft function of SolidWorks. To form the elliptical and rectangular receivers, the shapes already available in SolidWorks were used, considering a major axis length of d_0° and a minor axis length of d_90°.

$$d_{\gamma Ell}=2\sqrt{{(\frac{d_{0°}}{2}cos{t}_{\gamma })}^2+{(\frac{d_{90°}}{2}sin{t}_{\gamma })}^2}$$

(5)

$$t_{\gamma }={\tan }^{-1}(\frac{d_{0°}}{d_{90°}}\ast tan\gamma )$$

(6)

$$d_{\gamma Rec}=\left\{\begin{array}{c}\frac{d_{0°}}{\cos \left(\gamma \right)} 0°\le \gamma \le {\gamma }_{diag}\\ \frac{d_{90°}}{\sin \left(\gamma \right)} {\gamma }_{diag}\le \gamma \le 90°\end{array}\right.$$

(7)

$${\gamma }_{diag}={\mathit{tan}}^{-1}(\frac{d_{90°}}{d_{0°}})$$

(8)

2.4. Designed Solar Concentrators

Table 1. The parameter values and resulting shapes of the MultiPro-ECPCs with an elliptical receiver.

α0°	15°	30°	45°
H/d0°	9.1	2.6	1.2
α90°= 10°
α90°= 20°
α90°= 30°

and

Table 2. The parameter values and resulting shapes of the MultiPro-RCPCs with a rectangular receiver.

α0°	15°	30°	45°
H/d0°	9.1	2.6	1.2
α90°= 10°
α90°= 20°
α90°= 30°

, respectively, show the designed shapes with elliptical receivers and rectangular receivers for each combination of longitudinal half-acceptance angle α_0° = 15°, 30°, and 45° and transversal half-acceptance angle α_90° = 10° when the longitudinal axis length d_0° is 50 mm. In both cases, the height H and geometric concentration ratio C_geo calculated using Equation (1) decrease with α_0° and α_90°. The slim shape of the receivers is reflected in the aperture’s shape. Therefore, in the case of the elliptical receiver, as depicted in Figure 2, the receiver length $d_{\gamma }$ decreases continuously as the angle between the profile plane and the longitudinal direction γ increases from 0 to 90°, resulting in a corresponding decrease in the aperture length $D_{\gamma }$. Nevertheless, when the receiver shape is rectangular, the length of the receiver first increases as γ increases from 0° to γ_diag and then decreases as γ increases from γ_diag to 90°. The aperture length also follows the same trend.

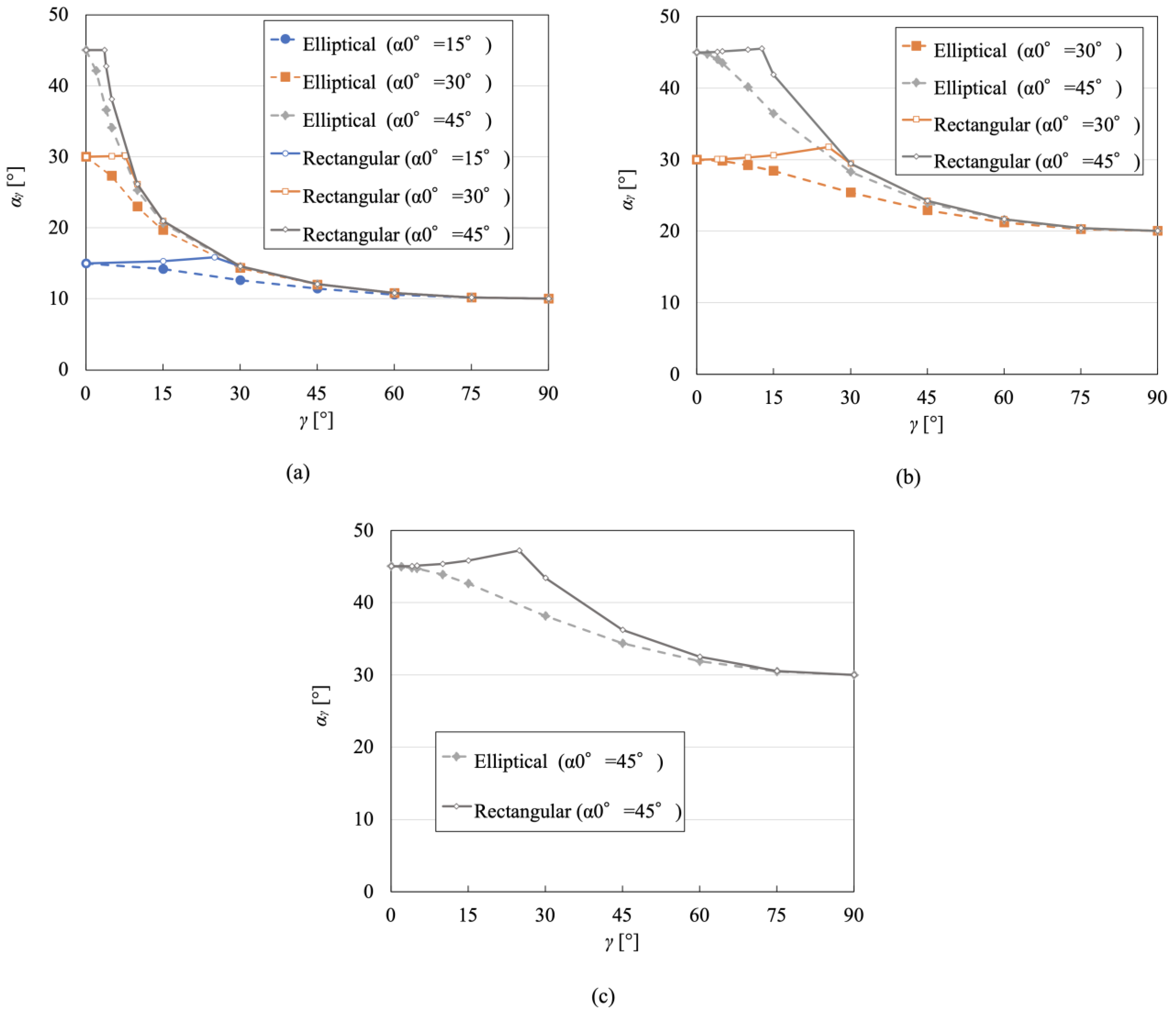
2.4.1. Variation of the Half-Acceptance Angle According to γ

In the case of the CPC, the half-acceptance angle α_γ does not change with γ. In contrast, in the case of the two newly proposed designs, it changes, as shown in Figure 4. In the case of the newly proposed design with an elliptical receiver, the MultiPro-ECPCs, α_γ decreases gradually. On the other hand, in the case of the MultiPro-RCPCs, α_γ keeps almost the same maximum value up to γ_diag and then decreases gradually. With the increase in α_90° from Figure 4a–c, the decrease rate of the half-acceptance angle decreases, and the value of γ_diag increases. The comparison also shows that the concentrators with rectangular receivers have slightly larger half-acceptance angles compared to the ones with elliptical receivers.

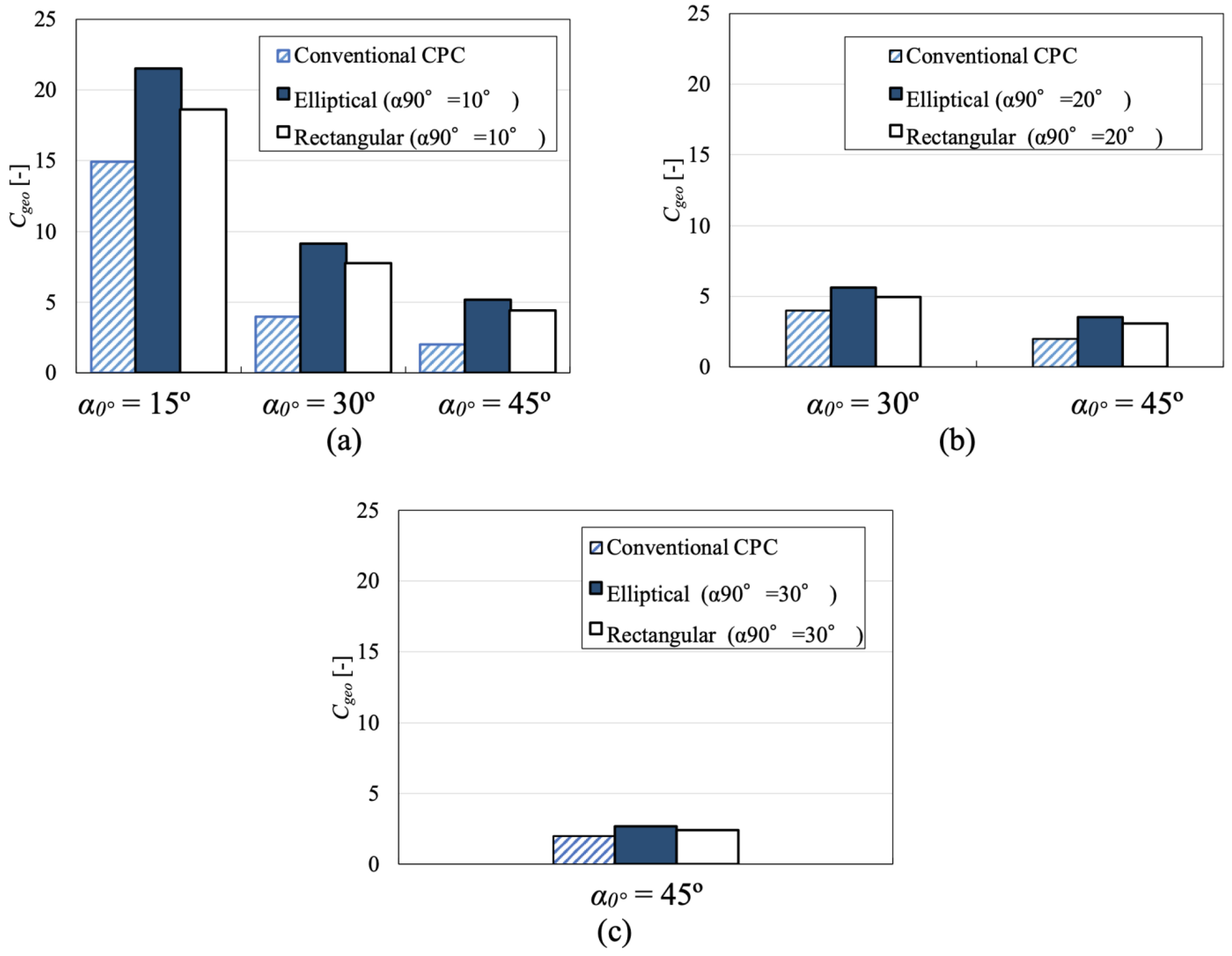
2.4.2. Geometric Concentration Ratio

For an aperture area of A_Ap (m²) and a receiver area of A_Abs (m²), for each shape, the geometric concentration ratio C_geo is expressed as A_Ap/A_Abs, as shown in Figure 5. The geometric concentration ratio decreases as the half-acceptance angle α_0° increases, which is understandable as a similar tendency is observed for the conventional CPC. It is also observed that for any value of α_0° or α_90°, the geometric concentration ratio of the proposed design with an elliptical receiver is larger than that of the rectangular type. For each value of α_0°, the geometric concentration ratios of the MultiPro-ECPCs are larger than that of the CPCs up to 2.5 times. Under these conditions, a maximum of 22.0 was obtained with the MultiPro-ECPC with a longitudinal half-acceptance angle α_0° of 15°, and a minimum of 2 was obtained with the conventional CPC with a half-acceptance angle α of 45°. It can be said that the proposed MultiPro-CPCs have the advantage of having larger geometric concentration ratios for a given half-acceptance angle.

3. Optical Simulation of the Designed Solar Concentrators

Optical ray-tracing simulations are employed under the following simulation conditions on all newly designed MultiPro-CPCs, on the corresponding 3DCPCs, and on a circular flat plate receiver of diameter d_0° without a mirror. In the following, specific parameters such as the solar angles and axial angles are also defined to assess the optical performance of the proposed designs, with the optical efficiency and the optical concentration ratio as evaluation indices.

3.1. Simulation Conditions

The ray-tracing simulation software used in this simulation was TracePro LC 2022, which is based on the Monte Carlo ray-tracing method [29]. As for the concentration device, the reflectance of the mirror was set to 95%, and the absorptance of the receiver was set to 100%. Concerning the emitter, 100,000 rays were launched from a surface of 0.25 m² with an intensity of 1 kW/m². The light was monochromatic with a wavelength of 550 nm. Only the direct radiation of the sun was considered. The objective of these simulations was to assess optical efficiency as a function of the solar position while also investigating concentration performance when varying incident solar angles.

Figure 6 provides a visual representation of the solar concentrator under investigation, along with the solar source, illustrating their respective angular positions relative to the sun angles. Here, the projection of the incidence angles on the longitudinal plane and transversal plane of the concentration are, respectively, the longitudinal angle θ_L expressed in Equation (9) and the transversal angle θ_T expressed in Equation (10). In this study, the longitudinal angle θ_L and transversal angle θ_T were changed every 5° from 0 to 90°, and the concentrator was vertically positioned. The direction at θ_L = 0° and θ_T = 0° was the normal direction to the aperture of the concentrators.

Since the longitudinal direction corresponds to the East–West direction and the transversal direction corresponds to the North–South direction, based on Figure 6, the solar elevation angle θ_El and solar azimuth φ can be expressed as functions of θ_L and θ_T, as shown in Equations (11) and (12):

$${\theta }_L={\tan }^{-1}(\frac{x}{z}), \frac{x}{z}=\tan {\theta }_L$$

(9)

$${\theta }_T={\tan }^{-1}(\frac{y}{z}), \frac{y}{z}=\tan {\theta }_T$$

(10)

$${\theta }_{Elevation}={\tan }^{-1}\left(\frac{z}{\sqrt{x^2+y^2}}\right)={\tan }^{-1}\left(\frac{1}{\sqrt{{(\tan {\theta }_L)}^2+{(\tan {\theta }_T)}^2}}\right)$$

(11)

$$\phi ={\tan }^{-1}(\frac{x}{y})={\tan }^{-1}(\frac{\tan {\theta }_L}{\tan {\theta }_T})$$

(12)

3.2. Evaluation Indices

When considering the assessment of the optical behavior of the concentrator designs, it is important to define the key evaluation indices. The first index encompasses the optical efficiency, which quantifies the effectiveness of the concentrator in capturing incident light. The second index focuses on the optical concentration ratio, which measures the degree of light concentration achieved by the concentrator. During the ray-tracing simulations, the number of rays transmitted by the aperture and the number of rays absorbed by the receiver were obtained. The optical efficiency η, which is expressed in Equation (13), indicates the ratio of absorbed energy from the transmitted energy. Additionally, the optical concentration ratio is defined in Equation (14). The simulation results were validated using OTSunWebApp [30], a web-based application offering optical simulations of arbitrary geometries, which showed similar values for the optical concentration ratio. In the case of the mirrorless flat plate receiver, both indices constantly took the value of 1.

$$\eta =\frac{Energy absorbed by the receiver}{Energy transmitted by the aperture}$$

(13)

C_opt = η·A_Ap/A_Abs

(14)

4. Results and Discussion

Here, the optical performance based on the axial and solar incidence angle coverage, the irradiance distribution on the receiver, and the absorbed rays’ path inside the concentrator are presented. For visualization purposes, only the graphs for the cases, when α = α_0° = 30° and the α_90° = 10°, are represented. The remaining graphs can be found in the Supplementary Materials.

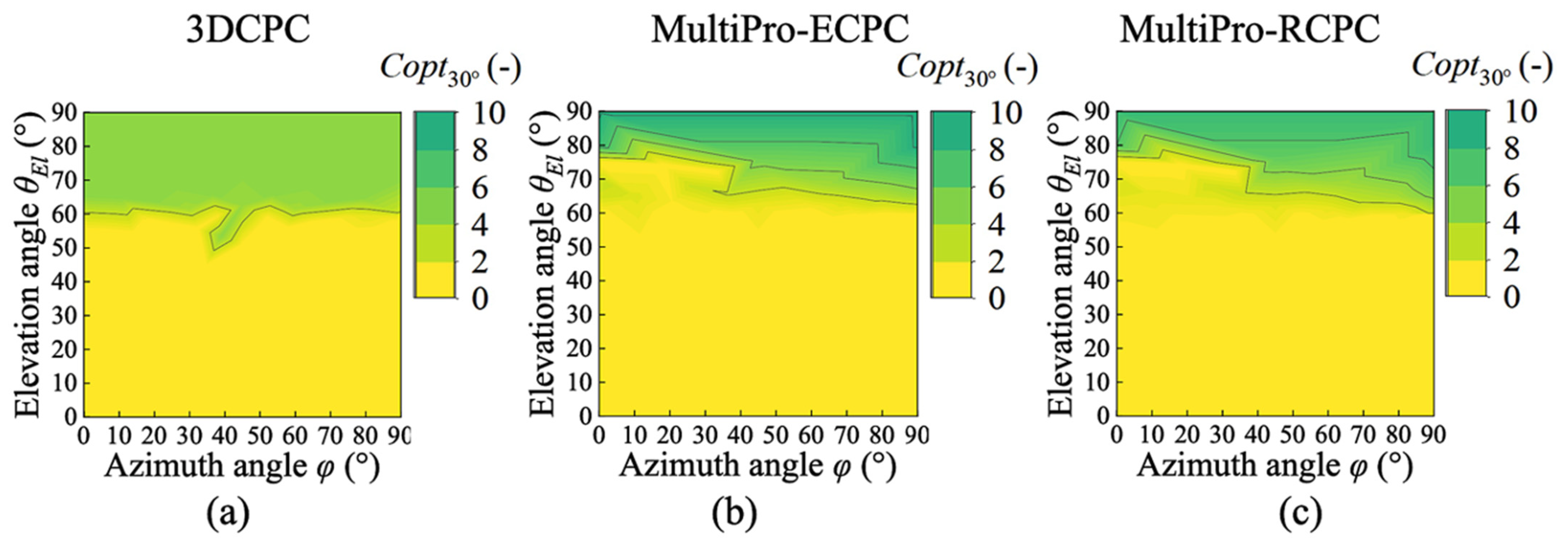
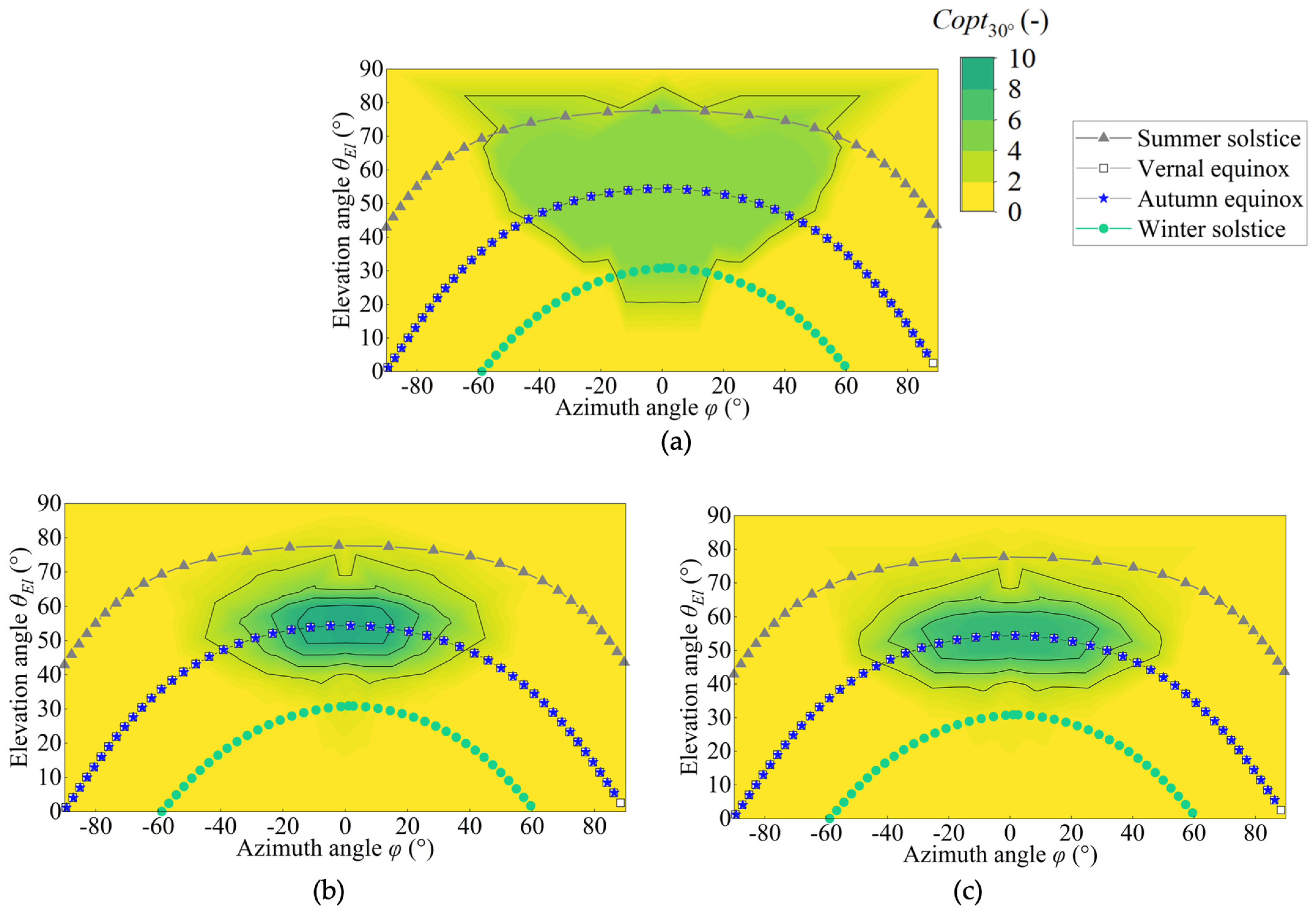
4.1. Optical Performance Based on the Axial Incidence Angle Coverage

The axial incidence angle coverage is an important factor in terms of optical applications. Figure 7 shows the optical efficiency η for the MultiPro-CPCs shown in Table 1 and Table 2 and the corresponding 3DCPC as a reference. The peak optical efficiency is obtained for all cases when the longitudinal angle θ_L and transversal angle θ_T are both equal to 0°, i.e., when the emitter is right on top of the concentrator. The maximum optical efficiency of 0.95, obtained by the conventional CPC when α = 45°, is in accordance with the reflectance of 95% set in the simulation conditions. In the case of the MultiPro-CPCs, it is noticeable that the values of the optical efficiency for each (MultiPro-CPC, α_0° and α_90°) combination decrease with the longitudinal angle θ_L and transversal angle θ_T. For the MultiPro-ECPC and MultiPro-RCPC, the maximum optical efficiency of 0.95 is obtained when α_0° = 45° and α_90° = 30°. Compared with the conventional CPCs, which have a wide axial incidence angle coverage and maintain optical efficiencies bigger than 0.9 up to θ_L = α_0° − 5° and θ_T = α_90°, the designed MultiPro-CPCs have moderate filtering performances, particularly in terms of θ_L. Following the difference in the receiver shape, the MultiPro-RCPCs that have a rectangular receiver capture a wider range of oblique incidence in the East–West direction compared to the MultiPro-ECPCs. It is also observed that the rays with a transversal incidence angle θ_T equal to the designed angle for the North–South direction α_90° are captured when θ_L = 0° for both the elliptical and rectangular receivers. In contrast, when the transversal angle θ_T = 0°, rays with an incidence angle θ_L equal to the designed angle for the East–West direction α_0° cannot be collected similarly to the case of the 3DCPC. Nevertheless, for the MultiPro-CPCs, optical efficiencies bigger than 0.9 can only be obtained up to θ_L = α_0° − 10° and θ_T = α_90° for the case (MultiPro-RCPC, α_0° = 45° and α_90° = 30°) that has the widest axial incidence angle coverage.

Figure 8 shows the optical concentration ratio C_opt of the simulation targets as a function of the longitudinal and transversal incidence angles. Here, it is noticeable that the trend in terms of axial incidence coverage is maintained. For each concentrator, the values of the optical concentration ratio also decrease with the axial incidence angles θ_L and θ_T. Among the simulated concentrators, the MultiPro-ECPCs have the highest values of the optical concentration ratio, followed by the MultiPro-RCPCs. Here, the maximum optical concentration ratio of 19.5 is obtained with the MultiPro-ECPC when α_0° = 15° and α_90° = 10°, followed by 16.8 for the MultiPro-RCPC with α_0° = 15° and α_90° = 10°, and by 13.8 for the conventional CPC with α = 15°. When α = α_0° = 45° and α_90° = 10°, the peak optical concentration ratios are 4.9 for the MultiPro-ECPC, 4.2 for the MultiPro-RCPC, and 1.9 for the conventional CPC.

Although the CPCs show their ability to cover wider ranges compared to the MultiPro-CPCs, the values of their optical concentration ratio are still very low. These findings suggest that although capturing rays from the North–South direction is restricted at the edges, the new MultiPro-CPCs can concentrate rays up to 10 times more effectively than the conventional CPCs when θ_L = 0° and θ_T = 0°. Therefore, by utilizing efficient concentration system settings, MultiPro-CPCs may offer a distinct advantage over conventional CPCs.

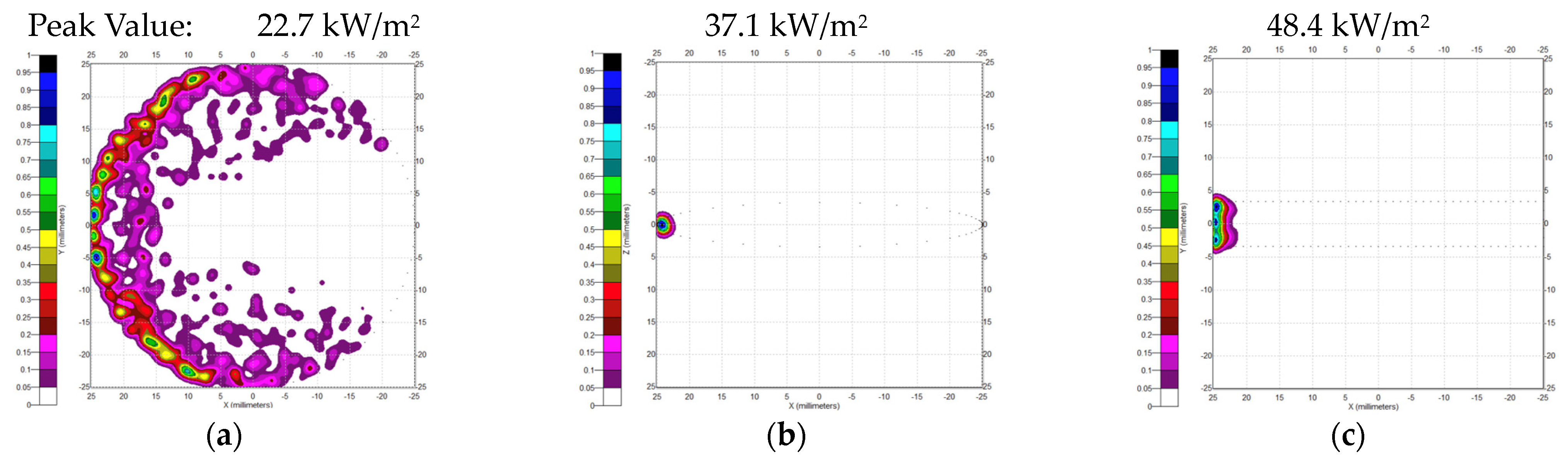
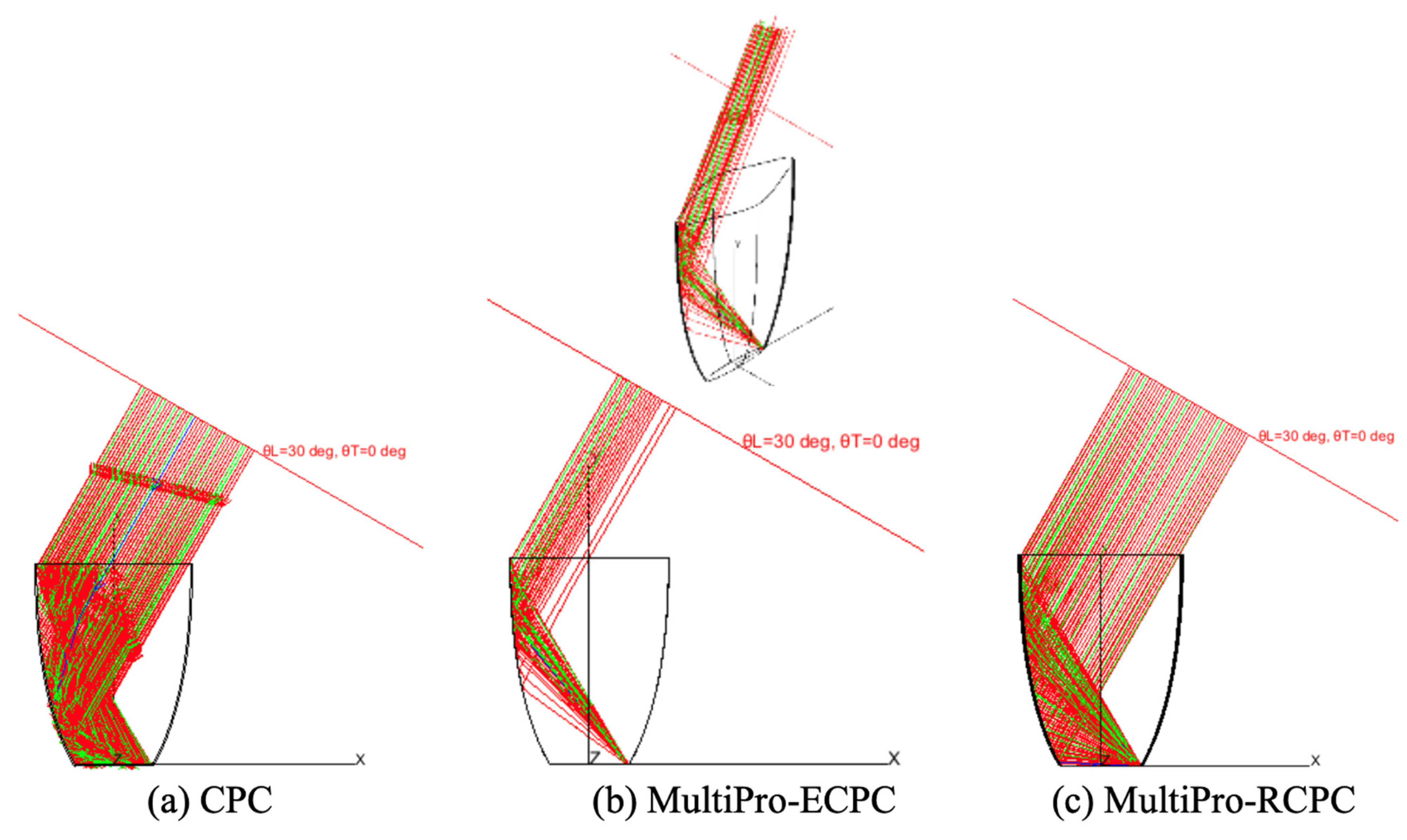
4.2. Irradiance Distribution on the Receiver and Absorbed Ray Path Inside the Concentrator

Figure 9 compares the irradiance distribution on the receivers of each design when α_0° = 30° and α_90° = 10° for the incident angles (θ_L, θ_T) of (0°, 0°). In each case, the irradiance is normalized by its peak value. When (θ_L = 0°, θ_T = 0°), the rays are mainly concentrated at the tips of the elliptical and rectangular receivers, while in the case of the conventional CPC with a circular receiver, the rays are mainly concentrated in the shape of a circle a little further from the extremity. Concerning the irradiance, the peak values for the newly designed shapes are higher, and the intensity on the center part of the circular receiver is very low. Figure 10 compares the irradiance distribution on the receivers of each design when α_0° = 30° and α_90° = 10° for the incident angles (θ_L, θ_T) of (α_0°, 0°). From Figure 9, it is observed that under these conditions, the rays are reflected at one edge of the receiver. The rectangle, which has a larger edge width, obtained a higher irradiance peak value. Since the new design with an elliptical receiver has a smaller edge width compared to the new design with a rectangular receiver and the 3DCPC, the rays cannot reflect well within it. Figure 11 shows the path of the absorbed rays inside the concentrator under the same conditions as Figure 10. The results in Figure 11 confirm the ones in Figure 10 since the amount of energy variation and the rays’ path follow the same trend and direction. The tightness of the lower part of the MultiPro-ECPC is the reason behind the impossibility of reflecting into the receiver all rays passing through the aperture. This explains the low amount of absorbed rays in Figure 11b, resulting in a small irradiance distribution in Figure 10b. Correlations are also noticeable between the size of the concentrators in Figure 11 and between the size of the receiver and the irradiance peak value in Figure 10. The peak value decrease rate between α_0° = 15° and α_0° = 45° cases are, respectively, 6.0, 37.0, and 10.7 for the conventional CPC, for the new design with an elliptical receiver, and for the new design with a rectangular receiver.

The combined analysis of Figure 9, Figure 10 and Figure 11 elucidates the necessity to consider the characteristics of the new designs in the solar concentration system to mainly have the focus in the middle and avoid any concentration at the edge of the receiver, specifically in the case of the MultiPro-ECPC.

4.3. Optical Performance Based on the Solar Incidence Angle Coverage

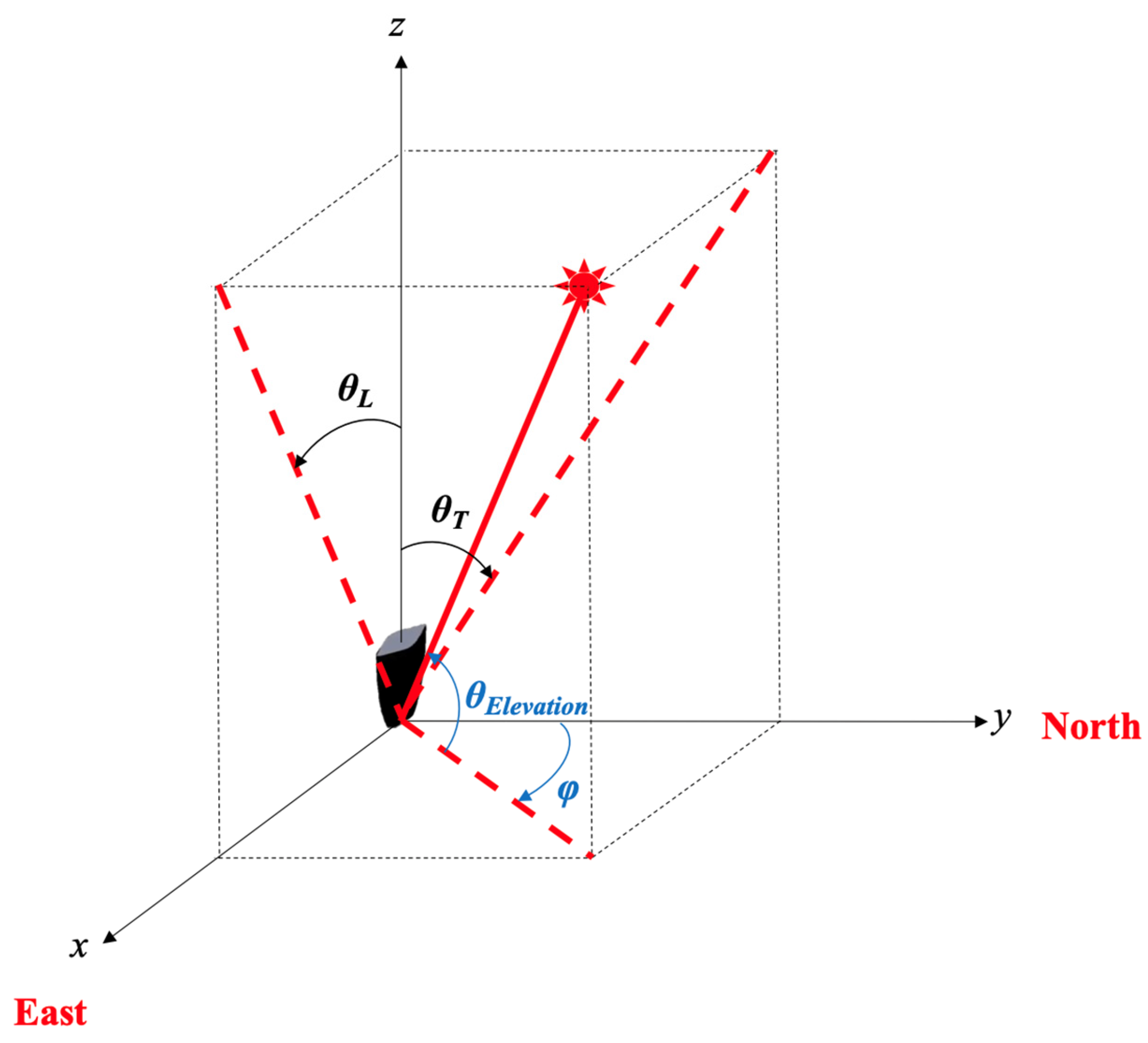
The coverage of solar incidence angles is an important factor for daily use. Figure 12 shows the optical concentration ratio of the proposed MultiPro-CPCs and 3DCPCs based on the solar azimuth angle φ and solar elevation angle θ_El. Here, too, the conventional CPC still has a wider coverage, and the variation in the maximum optical concentration ratio by case is conserved. The MultiPro-ECPCs also have the highest optical concentration ratios, followed by the MultiPro-RCPCs, for each half-acceptance angle. In addition, when comparing the solar angle coverage of all shapes, the MultiPro-RCPCs still showed the ability to cover wider ranges compared to the MultiPro-ECPCs. For all azimuth angles, the 3DCPC covers the solar incidence up to θ_El = 90° − α. Nevertheless, in the case of the MultiPro-CPCs, increases in solar elevation angle coverage with the azimuth angle are noticeable. These increases are generally from θ_El = 90° − α_90° when φ = 0° to θ_El = 90° − α_0° when φ = 90°. This variation can be explained by the changes in the aperture shapes when the difference between α_0° and α_90° is superior to 5°, as shown in Table 1 and Table 2. In addition, it fits the variation in the acceptance angle according to γ applied in the design of the MultiPro-CPCs. These findings indicate that although capturing sunlight from the North–South direction is restricted at the edges of the MultiPro-CPCs, elevation angles within the acceptable range of θ_El = 90° − α_90° are still covered when the azimuth angle is less than 90°.

Figure 13 represents the daily variation in the solar angles in Tokyo during the solstices and equinoxes of 2023 [31] combined with the optical concentration ratio of the 54°-tilted MultiPro-ECPC, 3DCPC, and MultiPro-RCPC when α_0° =30° and α_90° =10°. In Tokyo, the elevation angle at noon varies from 76° on the summer solstice to 54° on the equinoxes to 33° on the winter solstice. Through analyzing the daily variation in the solar angles in Tokyo, it is understandable that for a concentrator to cover the elevation angles throughout the year in Tokyo, its smallest acceptance angle, 2α_90°, should be 2° bigger than the difference of 43° between the peak elevation angles on the summer solstice (76°) and the winter solstice (33°). Thus, the smallest acceptance angle of the concentrator α_90° should be at least 23°. In Figure 13, the MultiPro-ECPC is 54° tilted from the horizontal to equal the peak elevation angle of the equinoxes. Accordingly, the elevation angle coverage shifted to a lower range compared to Figure 12b. In fact, the MultiPro-ECPC obtains a concentration ratio higher than 2 and up to 8.3 between 38° and 75° elevation and between -46° and 46° azimuth. The coverage is centered at 54° elevation and 0° azimuth, following an elliptical shape in accordance with the receiver shape. Nevertheless, under the conditions set, it is still challenging for the MultiPro-ECPC to cover most of the variation in terms of elevation angle, specifically in the early morning and evening. In contrast, the MultiPro-RCPC covers 8 more degrees in terms of azimuth angle for the same elevation range, with a maximum concentration centered at 7.2. On the other hand, with much lower intensities and a maximum concentration ratio of 3.8, the 3DCPC demonstrates coverage expanding from noon during the winter to most of the day during the summer in addition to the equinoxes. This complementary analysis points to the necessity for further research concerning the seasonal tilting and adjustment of the incidence based on the geographical position of a selected location for an effective operation of the MultiPro-CPCs.

5. Conclusions

In this study, the concept of CPCs is extended, and a design method for new kinds of concentrators with various acceptance angles in all directions, the MultiPro-CPCs, is proposed. The feature of this method is that the receiver can take any shape, and all profiles are compound parabolic. In this study, elliptical and rectangular receivers are assumed, and the shape and concentration performance of the MultiPro-ECPCs and MultiPro-RCPCs are derived. The energy distribution on the receiver, the optical efficiency η, and the optical concentration ratio C_opt, as a function of solar angles and axial angles, were compared by fixing the length of the receiver major axis to 50 mm. A flat receiver with a diameter of 50 mm and 3DCPCs with half-acceptance angles equal to the East–West half-acceptance angles α_0° and a receiver diameter of 50 mm are also simulated for reference. Here, the half-acceptance angle in the East–West direction is set to 15°, 30°, and 45°, and that in the North–South direction to 10°, 20°, and 30°.

In terms of optical efficiency, the conventional 3DCPCs have the highest values and widest incidence coverage for each East–West half-acceptance angle α_0°. The designed MultiPro-CPCs have moderate filtering performances, particularly in terms of their longitudinal incidence angle θ_L. When comparing the proposed designs, the MultiPro-RCPCs cover a wider range of incidence angles than the MultiPro-ECPCs. The optical concentration ratio is also compared, and it is found that the newly designed MultiPro-ECPC has the highest peak value of 19.5 when θ_L = 0° and θ_T = 0°, followed by the MultiPro-RCPCs, which is up to 10 times more concentrated than the conventional CPCs.

The irradiance distribution on the receivers of each design when α_0° = 30° and α_90° = 10° for the incident angles (θ_L, θ_T) of (0°, 0°) showed that the rays are mainly concentrated at the tips of the elliptical and rectangular receivers, while in the conventional CPC, they are mainly concentrated in the shape of a circle a little further away from the extremity. In addition, when α_90° = 10° with the incident angles (θ_L, θ_T) of (α_0°, 0°), the rays are reflected at one edge of the receivers. In this case, the rectangle, which also has a large edge width, allowed more incidence, and this fact, combined with its high concentration ratio, enabled a higher irradiance peak value. In contrast, the rays cannot enter well in the elliptical receiver, which has the smallest edge widths.

In terms of solar incidence angle coverage, the conventional CPCs still showed a wider coverage area for each half-acceptance angle, followed by the MultiPro-RCPCs. Nevertheless, the variation in the maximum optical concentration ratio by case is conserved. The MultiPro-ECPCs have the highest optical concentration ratios, followed by the MultiPro-RCPCs, for each half-acceptance angle. For all azimuth angles between 0 and 90°, all 3DCPCs and MultiPro-CPCs with α_0° = 15° cover the solar elevation up to θ_El = 90° − α. Nevertheless, the remaining cases generally showed increases from θ_El = 90° − α_90° when φ = 0° to θ_El = 90° − α_0° when φ = 90°. Complementary spatiotemporal analyses pointed the necessity of seasonal tilting and adjustment to the latitude and longitude of a selected place of use.

This study enlightens the need for a concentration system setting adapted to the acceptance range of the proposed concentrators. In this case, a higher concentration can be achieved with the MultiPro-ECPCs and MultiPro-RCPCs compared to the conventional CPCs. Furthermore, the comparison of these three receiver shapes—circular, elliptical, and rectangular—gives some insights into the potential for further investigation of the MultiPro-CPCs with different shapes of receivers.

In Section 4 of this article, for visualization purposes, only the graphs for the cases when α = α_0° = 30° and α_90° = 10° are represented. However, in the Supplementary Materials, the optical performance based on the axial and solar incidence angle coverage, the irradiance distribution on the receiver, and the absorbed rays’ path inside the concentrator are presented for the remaining cases.