Study of the Thermal and Hydraulic Performance of Porous Block versus Gyroid Structure: Experimental and Numerical Approaches
Abstract
1. Introduction
2. Experimental Measurements
2.1. General Description of the Experiment
2.2. Uncertainty Analysis of the Measurement
3. Numerical Modelling
3.1. Flow Formulation in Porous Media
3.1.1. Darcy–Brinkman in the x Direction
3.1.2. Darcy–Brinkman in the y Direction
3.1.3. Darcy–Brinkman in the z Direction
3.1.4. The Energy Equation
3.2. Flow Formulation for Gyroid Structure
3.2.1. Navier–Stokes Formulation in the x Direction
3.2.2. Navier–Stokes Formulation in the y Direction
3.2.3. Navier–Stokes Formulation in the z Direction
3.2.4. Energy Formulation
3.3. Boundary Conditions of the System
- (i)
- The velocity u = uin in the x direction is applied at the inlet;
- (ii)
- At the inlet, the temperature of the fluid enters the test section at T = Tin;
- (iii)
- At the outlet, an open boundary is applied where the stresses are equal to zero;
- (iv)
- The bottom surface of the Aluminum block is heated with a heat flux q″ shown in red;
- (v)
- All external surfaces are assumed adiabatic, and for the flow, no-slip boundary conditions are applied.
3.4. Non-Dimensional Parameters
3.5. Solution Technique and Convergence Criteria
4. Results and Discussion
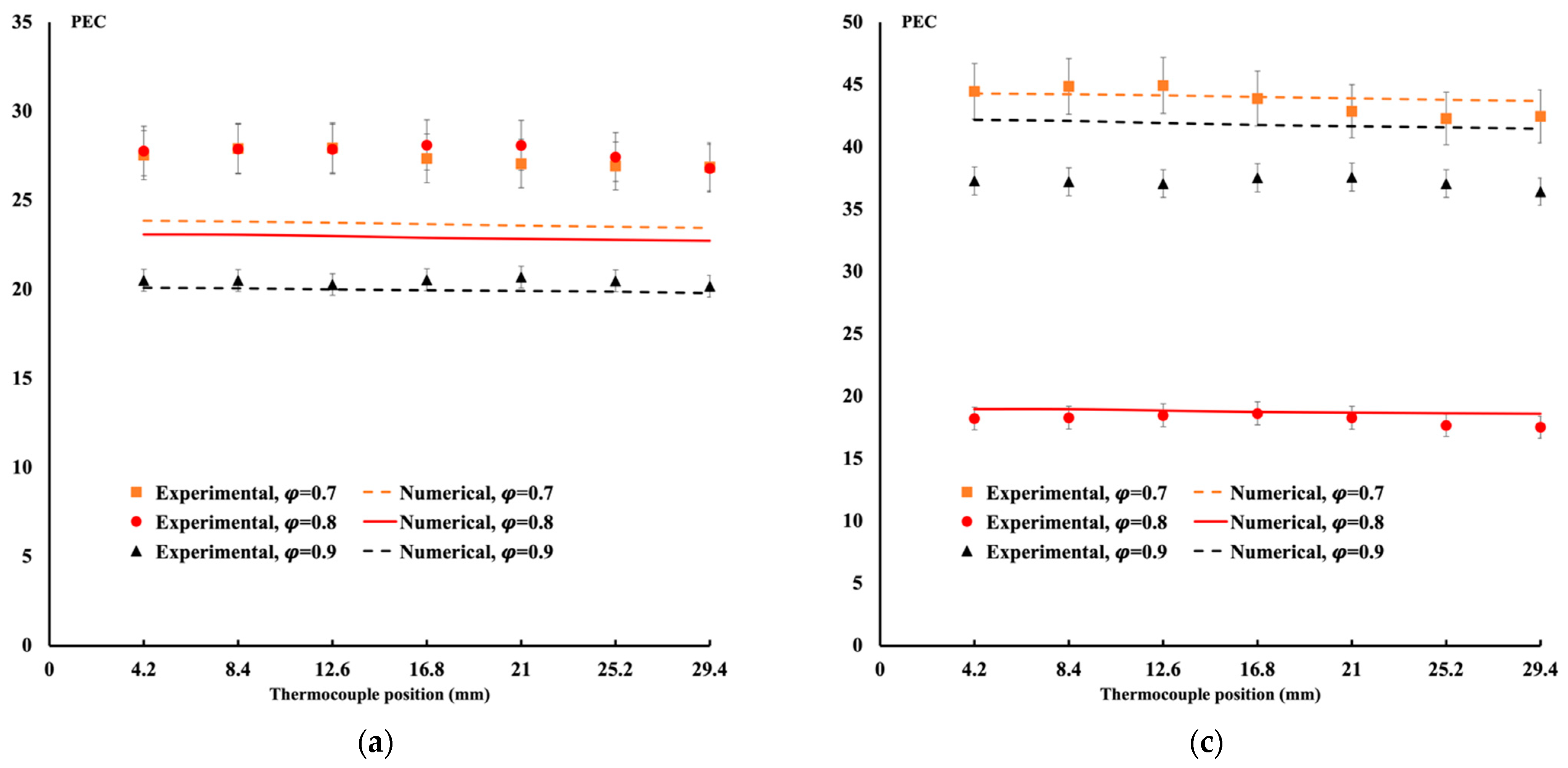
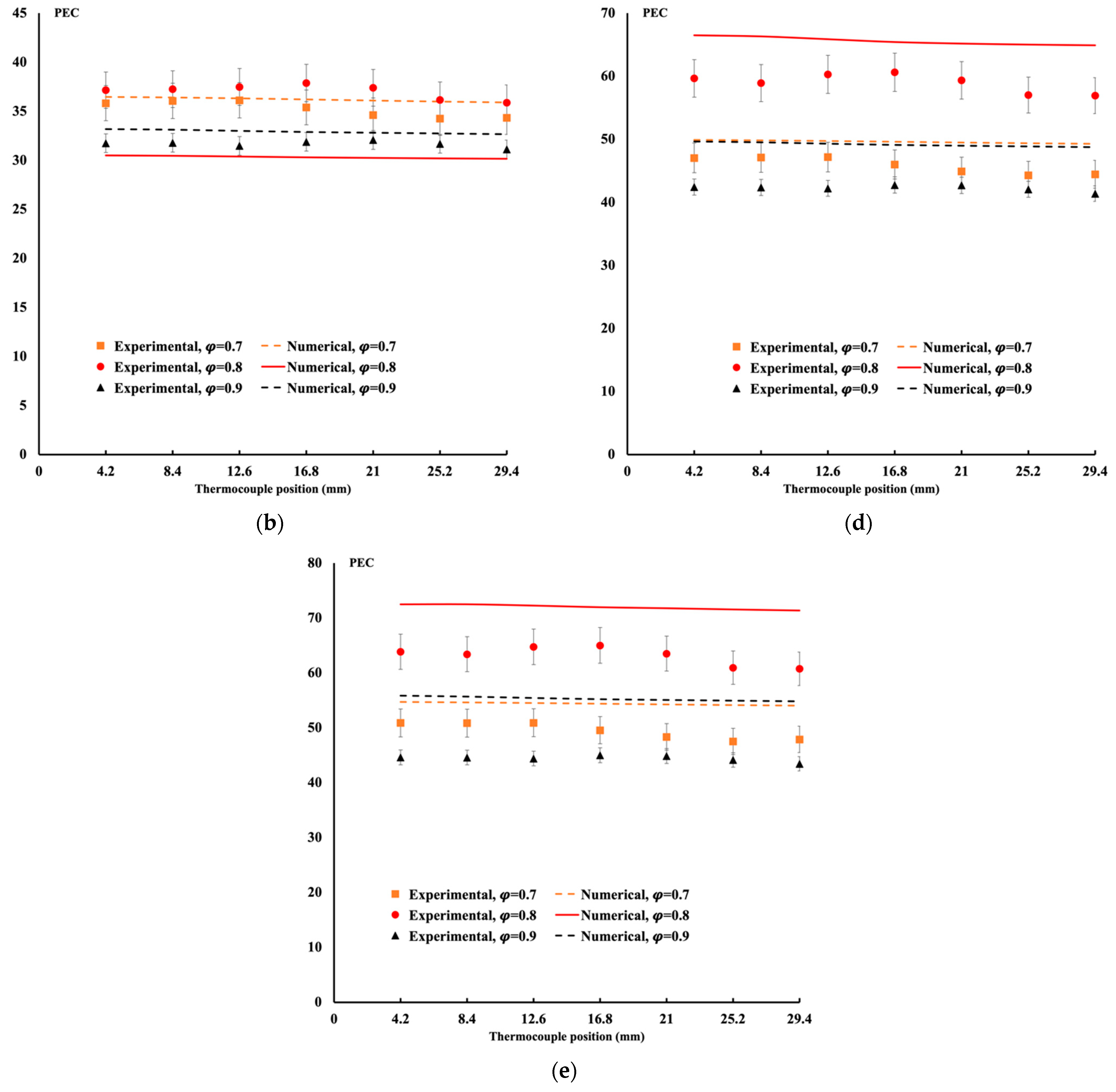
4.1. Comparison between Experimental Data and Numerical Results for the Porous Block
4.2. Comparison between Experimental Data and Numerical Results for the Gyroid Structure Case
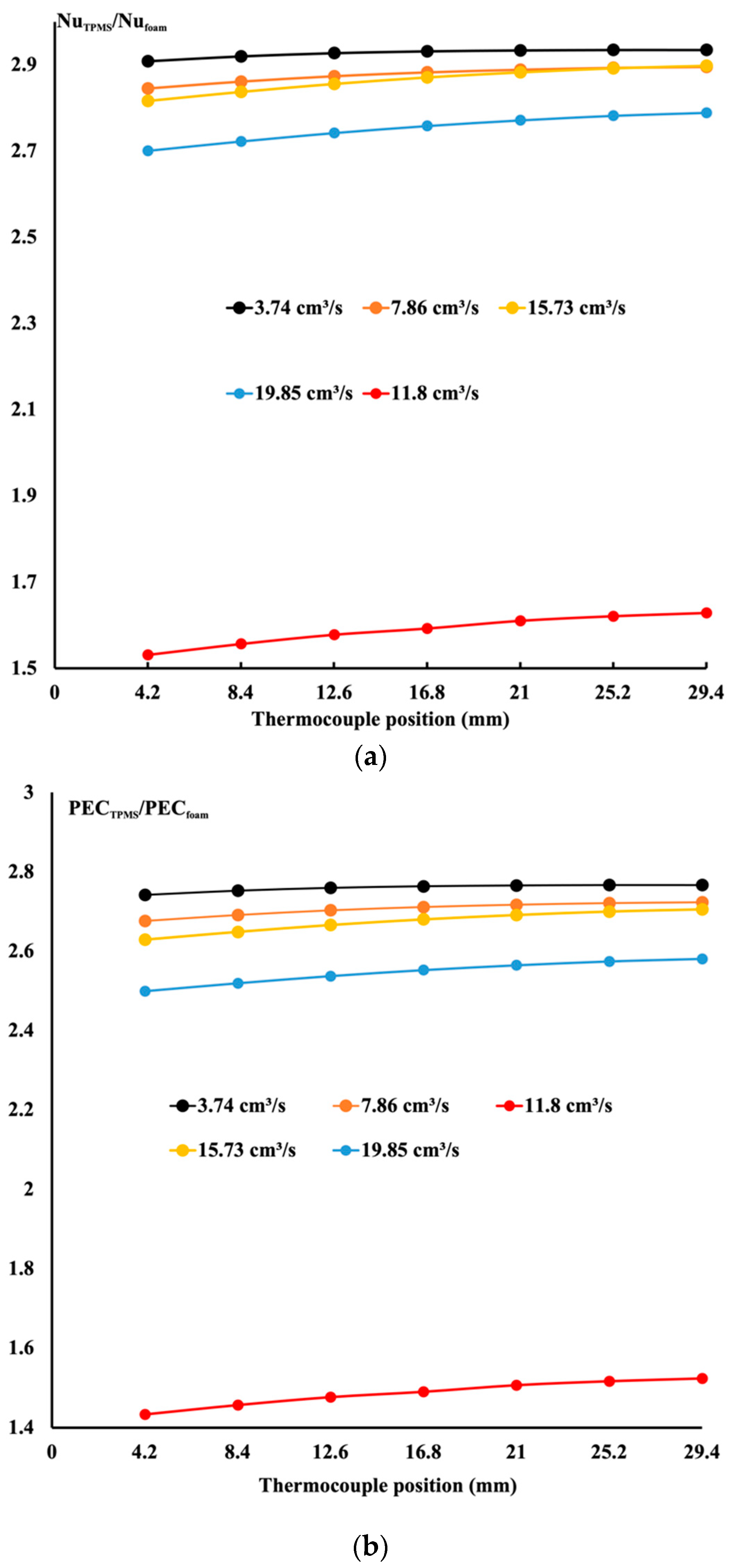
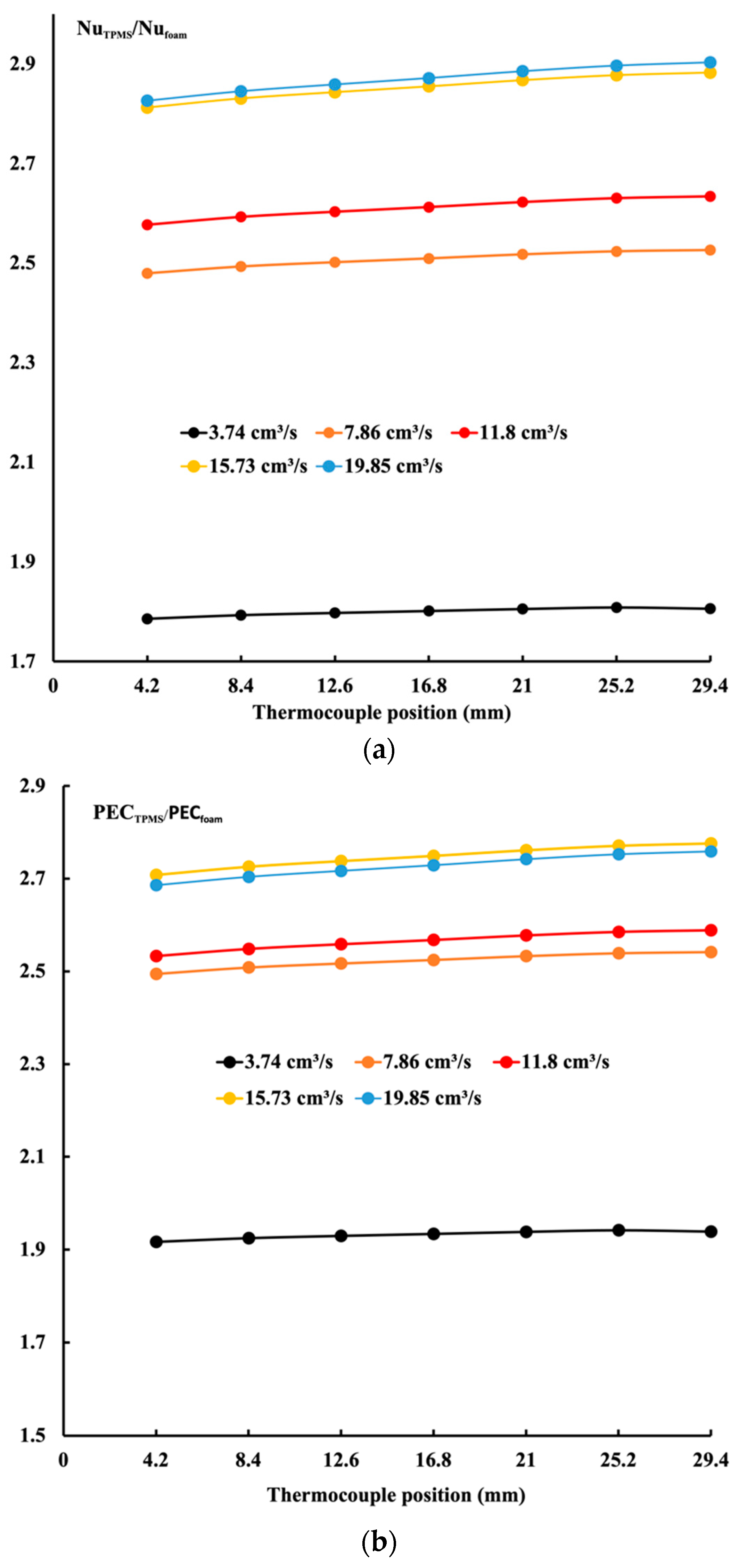
4.3. Comparison of Performance between Porous Block and Gyroid Structure for Different Permeabilities and Porosities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | Fluid dynamic viscosity in kg/m.s | ||
| p | Fluid pressure in Pa | Fluid density in kg/m3 | |
| u,v,w | Fluid velocity in m/s | Permeability in metal foam in m2 | |
| x,y,z | Coordinate system in m | Permeability in TPMS in m2 | |
| g | Gravity acceleration in m/s2 | Porosity of TPMS | |
| q″ | Heat Flux in W/m2 | Porosity of metal foam [1] | |
| T | Temperature in degrees C | Subscript | |
| k | Thermal conductivity in W/m.K | in | Inlet |
| Cp | Heat Capacity in J/kg.K | out | Outlet |
| Non-dimensional | f | Fluid | |
| Re | Reynolds number | s | Solid |
| MOGA | Multi-objective genetic algorithm optimization | o | Reference |
| Nu | Nusselt number | eff | effective |
| f | Friction coefficient | TPMS | Triply periodic minimum surfaces |
| PEC | Performance Evaluation Criterion | Foam | Metal foam porous media |
| Greek letter | Iwp | I-graph and wrapped package graph |
References
- Bayomy, A.M. Electronic Cooling Using ERG Aluminum Foam Subjected to Steady/Pulsating Water and γ-Al2O3–Water Nanofluid Flows: Experimental and Numerical Approach. Ph.D. Thesis, Ryerson University, Toronto, Canada, 2017. [Google Scholar]
- Al-Ketan, O.; Abu Al-Rub, R.K. MSLattice: A free software for generating uniform and graded lattices based on triply periodic minimal surfaces. Mater. Des. Process. Commun. 2021, 3, e205. [Google Scholar] [CrossRef]
- Saghir, M.Z.; So, J.; Rasheed, H.; Ilesaliev, D. Forced Convection in Porous Medium Using Triply Periodical Minimum Surfaces. Fluids 2023, 8, 311. [Google Scholar] [CrossRef]
- COMSOL Manual; COMSOL Inc.: Burlington, MA, USA, 2023.
- Sélo, R.R.; Catchpole-Smith, S.; Maskery, I.; Ashcroft, I.; Tuck, C. The thermal conductivity of AlSi10Mg and lattice structures made by laser powder bed fusion. Addit. Manuf. 2020, 34, 101214. [Google Scholar] [CrossRef]
- Piedra, S.; Gómez-Ortega, A.; Pérez-Barrera, J. Prediction of Flow Properties of Porous Triply Periodic Minimal Surface (TPMS) Structures. Fluids 2023, 8, 312. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, Z.; Li, Q.; Zhou, S. On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. Mater. Des. 2019, 183, 108109. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Sélo, R.R.J.; Davis, A.W.; Ashcroft, I.A.; Tuck, C.J.; Clare, A. Thermal conductivity of TPMS lattice structures manufactured via laser powder bed fusion. Addit. Manuf. 2019, 30, 100846. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Attarzadeh-Niaki, S.H.; Duwig, C. Multi-objective optimization of TPMS-based heat exchangers for low-temperature waste heat recovery. Appl. Therm. Eng. 2022, 212, 118448. [Google Scholar] [CrossRef]
- Vignoles, G.L.; Rochais, D.; Chupin, S. Computation of the conduct-radiative effective heat conductivity of porous media defined by Triply Periodic Minimal Surfaces. Int. J. Therm. Sci. 2021, 159, 106598. [Google Scholar] [CrossRef]
- Wei, H.; Bao, H.; Ruan, X. Machine learning prediction of thermal transport in porous media with physics-based descriptors. Int. J. Heat Mass Transf. 2020, 160, 120176. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, X.; Xu, R.; Jiang, P. Investigations on porous media customized by triply periodic minimal surface: Heat transfer correlations and strength performance. Int. Commun. Heat Mass Transf. 2021, 129, 105713. [Google Scholar] [CrossRef]
- Daish, C.; Blanchard, R.; Pirogova, E.; Harvie, D.J.E.; Pivonka, P. Numerical calculation of permeability of periodic porous materials: Application to periodic arrays of spheres and 3D scaffold microstructures. Int. J. Numer. Methods Eng. 2019, 118, 783–803. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, H.; Zeng, Y.; Yan, M.; Jiang, C.; Yang, P.; Li, Q.; Li, Z.; Fu, J.; Huang, Y.; et al. Analysis of the convective heat transfer process and performance evaluation of Triply Periodic Minimal Surface (TPMS) based on Diamond, Gyroid and Iwp. Int. J. Heat Mass Transf. 2023, 201, 123642. [Google Scholar] [CrossRef]
- Cheng, Z.; Xu, R.; Jiang, P.X. Morphology, flow and heat transfer in triply periodic minimal surface-based porous structures. Int. J. Heat Mass Transf. 2021, 170, 120902. [Google Scholar] [CrossRef]
- Niknam, S.A.; Mortazavi, M.; Li, D. Additively manufactured heat exchangers: A review on opportunities and challenges. Int. J. Adv. Manuf. Technol. 2021, 112, 601–618. [Google Scholar] [CrossRef]
- Thompson, S.M.; Aspin, Z.S.; Shamsaei, N.; Elwany, A.; Bian, L. Additive manufacturing of heat exchangers: A case study on a multi-layered Ti–6Al–4V oscillating heat pipe. Addit. Manuf. 2015, 8, 163–174. [Google Scholar] [CrossRef]
- Arie, M.A.; Shooshtari, A.H.; Tiwari, R.; Dessiatoun, S.V.; Ohadi, M.M.; Pearce, J.M. Experimental characterization of heat transfer in an additively manufactured polymer heat exchanger. Appl. Therm. Eng. 2017, 113, 575–584. [Google Scholar] [CrossRef]
- Iyer, J.; Moore, T.; Nguyen, D.; Roy, P.; Stolaroff, J. Heat transfer and pressure drop characteristics of heat exchangers based on triply periodic minimal and periodic nodal surfaces. Appl. Therm. Eng. 2022, 209, 118192. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Rovira, M.; Duwig, C. Design analysis of the “Schwartz D” based heat exchanger: A numerical study. Int. J. Heat Mass Transf. 2021, 177, 121415. [Google Scholar] [CrossRef]
- Reynolds, B.W.; Fee, C.J.; Morison, K.R.; Holland, D.J. Characterisation of Heat Transfer within 3D Printed TPMS Heat Exchangers. Int. J. Heat Mass Transf. 2023, 212, 124264. [Google Scholar] [CrossRef]





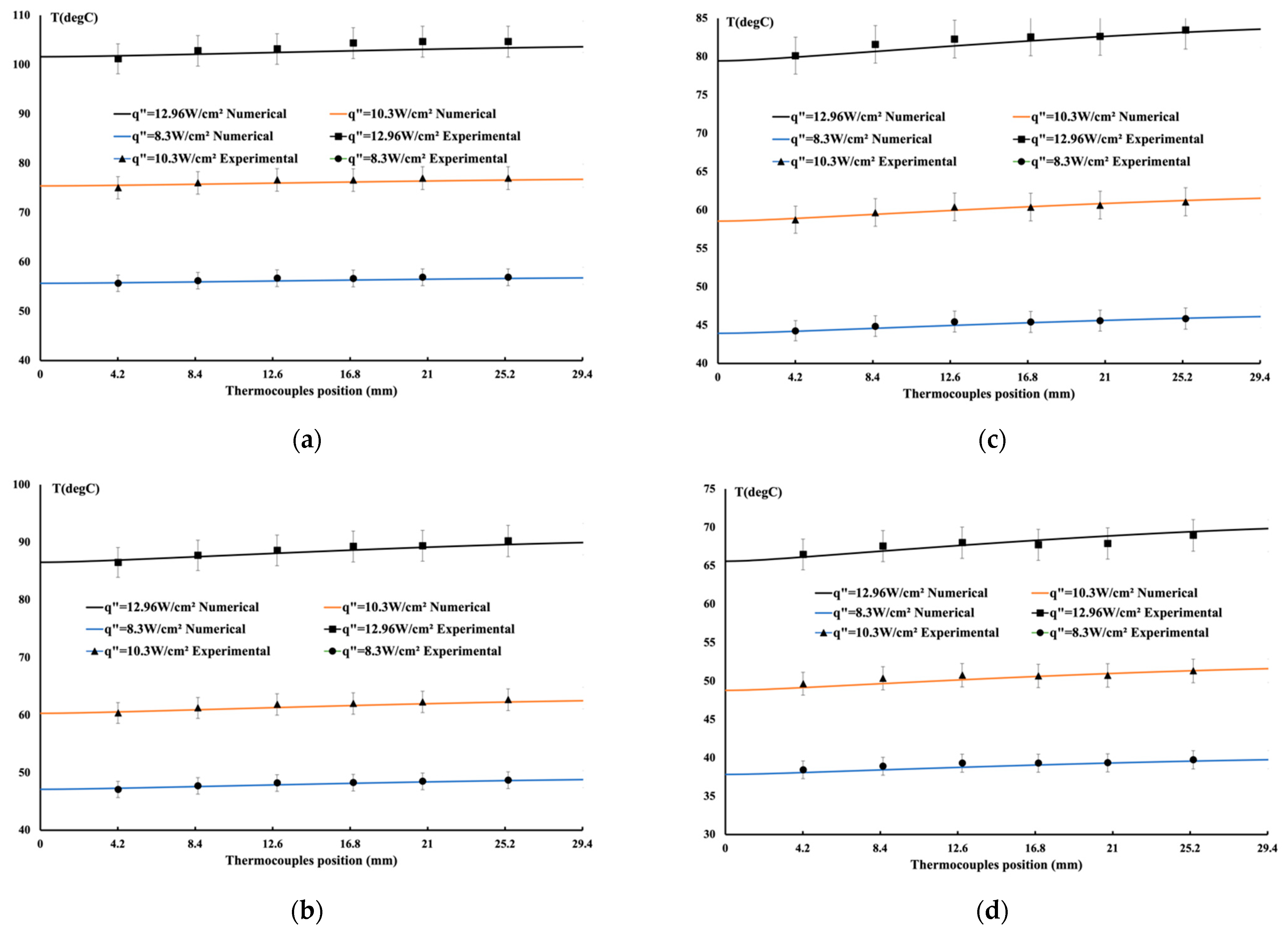
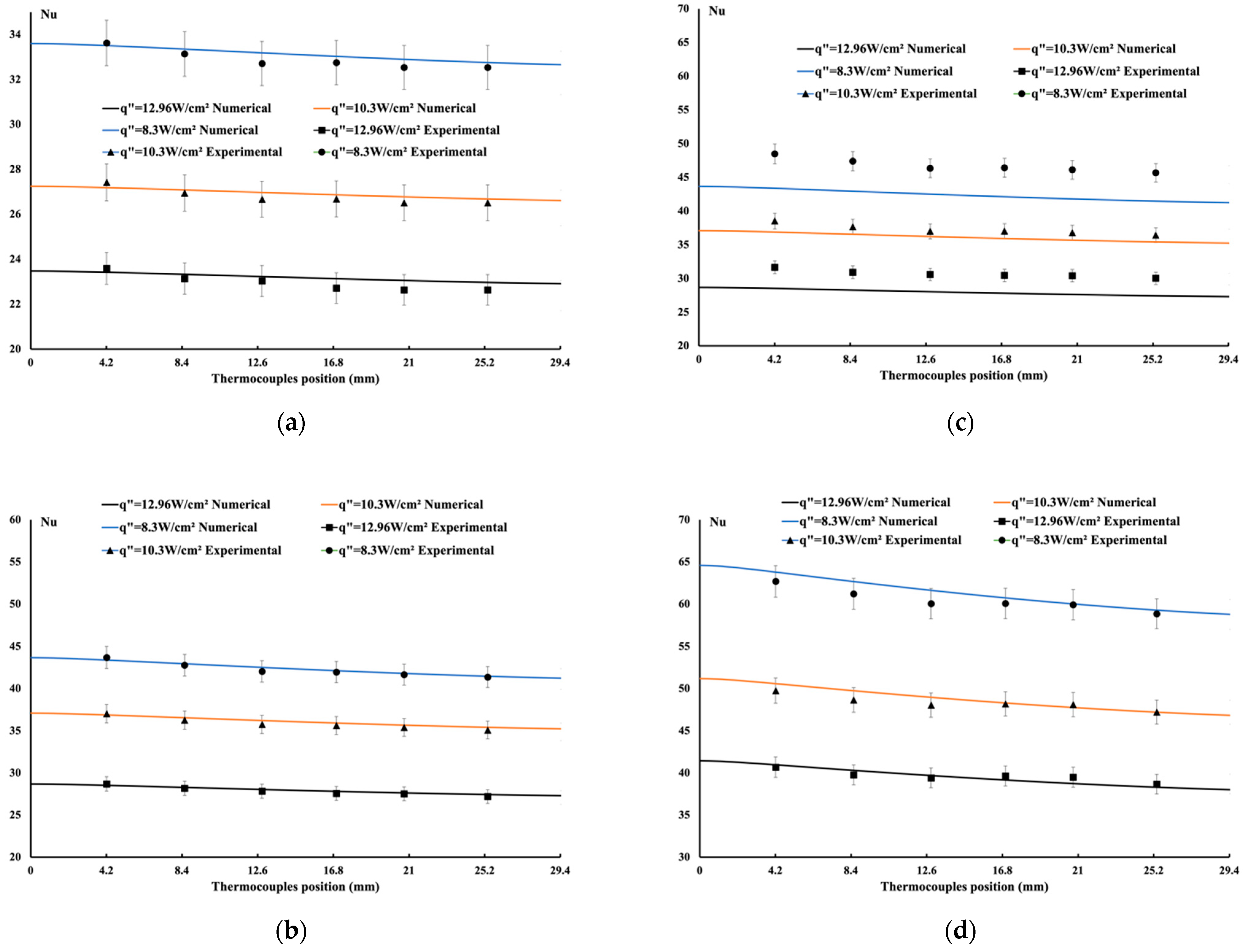

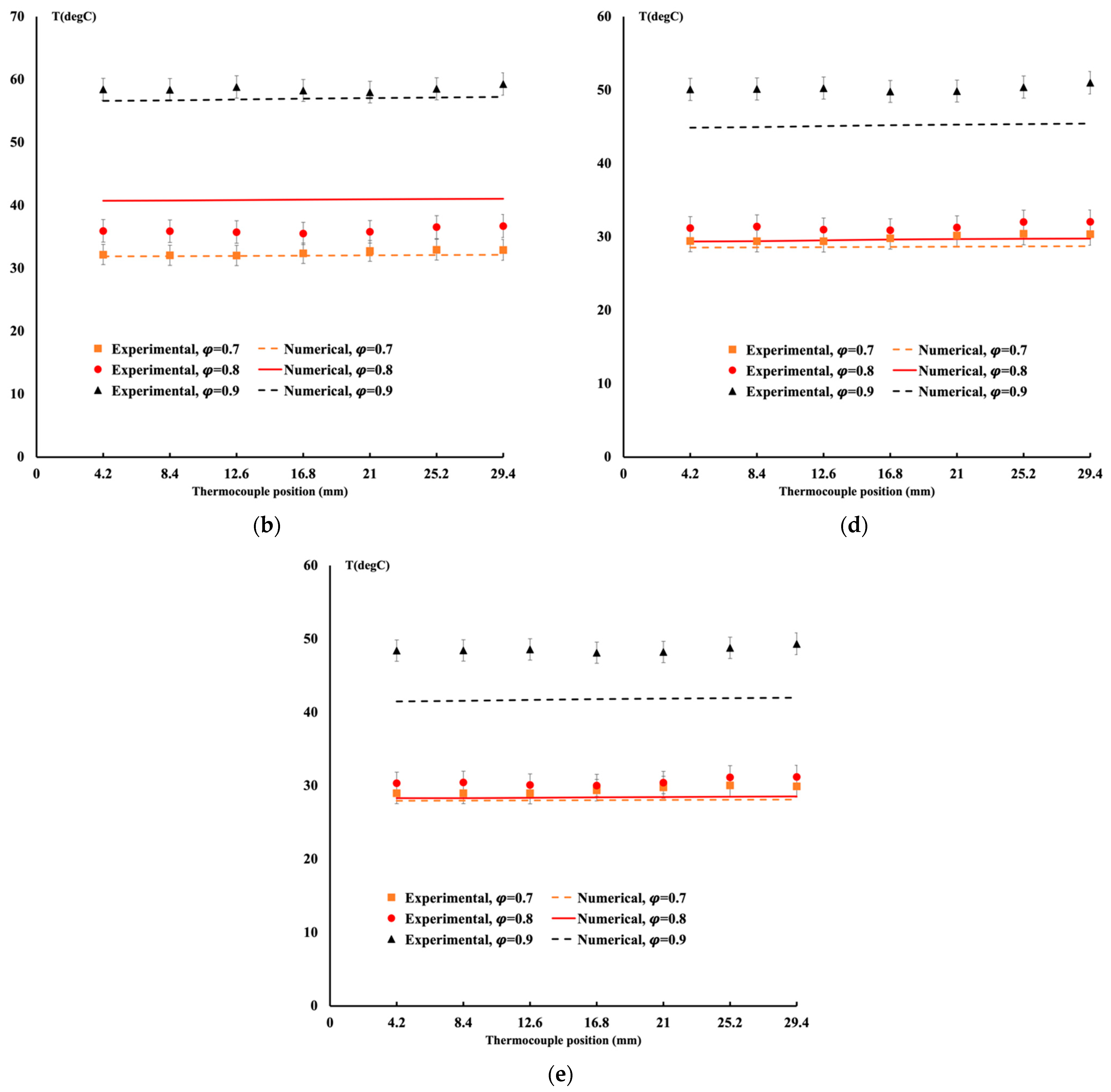

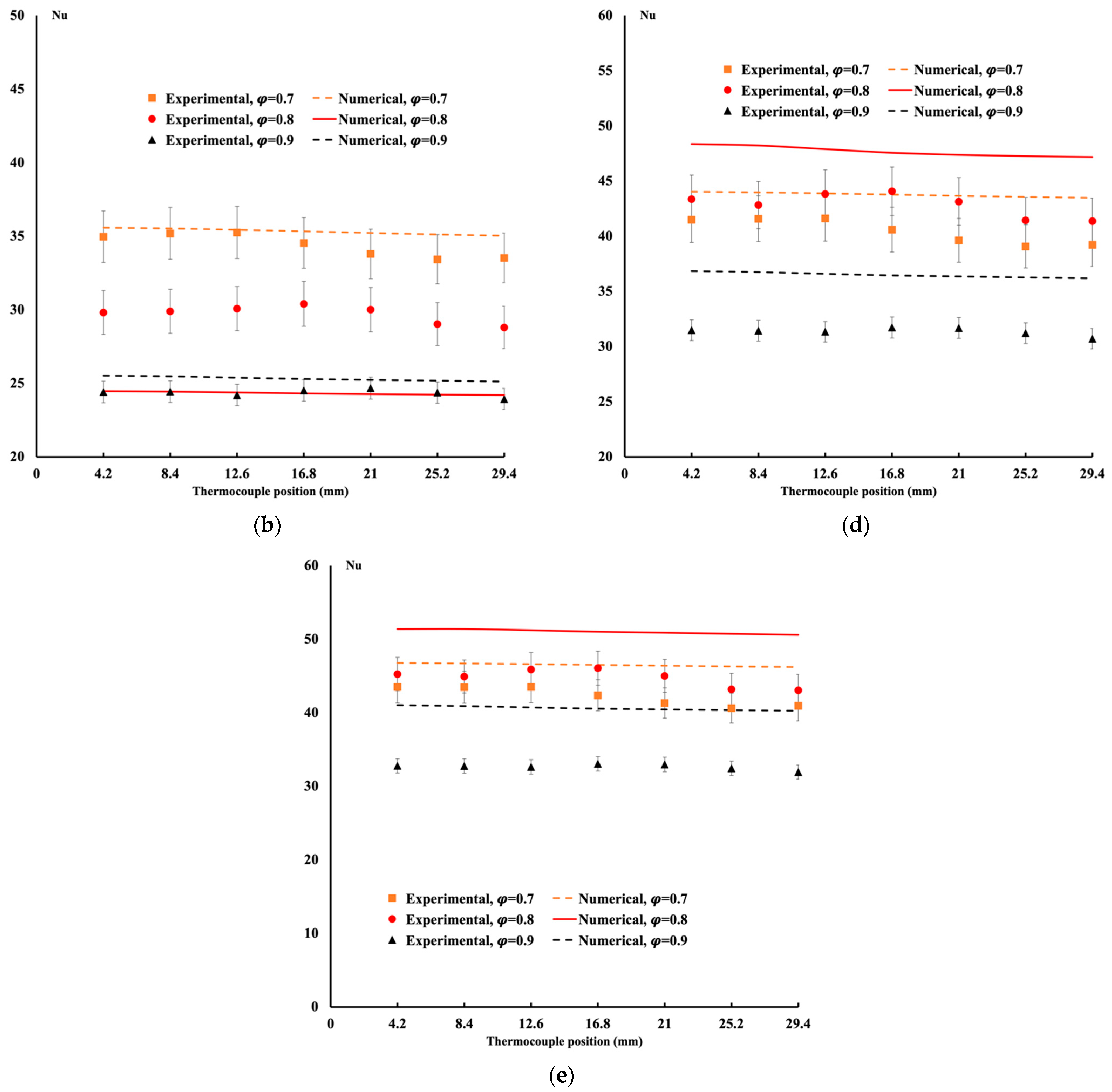

| Maximum Difference | Temperature (%) |
|---|---|
| Flow rate = 11.35 cm3/s q″ = 8.3 W/cm2 | 1.11 |
| Flow rate = 11.35 cm3/s q″ = 10.3 W/cm2 | 0.77 |
| Flow rate = 11.35 cm3/s q″ = 12.96 W/cm2 | 1.17 |
| Flow rate = 13.88 cm3/s q″ = 8.3 W/cm2 | 1.4 |
| Flow rate = 13.88 cm3/s q″ = 10.3 W/cm2 | 1.42 |
| Flow rate = 13.88 cm3/s q″ = 12.96 W/cm2 | 1.49 |
| Maximum Difference in % | Nusselt Number (%) |
|---|---|
| Flow rate = 6.31 cm3/s q″ = 8.3 W/cm2 | 1.5 |
| Flow rate = 6.31 cm3/s q″ = 10.3 W/cm2 | 1.31 |
| Flow rate = 6.31 cm3/s q″ = 12.96 W/cm2 | 2.49 |
| Flow rate = 9.46 cm3/s q″ = 8.3 W/cm2 | 1.16 |
| Flow rate = 9.46 cm3/s q″ = 10.3 W/cm2 | 1.34 |
| Flow rate = 9.46 cm3/s q″ = 12.96 W/cm2 | 0.93 |
| Maximum Difference | Temperature (%) |
|---|---|
| Flow rate = 7.86 cm3/s Porosity = 0.7 | 2.58 |
| Flow rate = 11.8 cm3/s Porosity = 0.7 | 1.84 |
| Flow rate = 11.8 cm3/s Porosity = 0.8 | 3.42 |
| Flow rate = 15.73 cm3/s Porosity = 0.8 | 7.17 |
| Flow rate = 7.86 cm3/s Porosity = 0.9 | 3.46 |
| Flow rate = 11.8 cm3/s Porosity = 0.9 | 8.84 |
| Maximum Difference in % | Nusselt Number (%) |
|---|---|
| Flow rate = 7.86 cm3/s Porosity = 0.7 | 5.03 |
| Flow rate = 11.8 cm3/s Porosity = 0.7 | 3.52 |
| Flow rate = 11.8 cm3/s Porosity = 0.8 | 5.5 |
| Flow rate = 15.73 cm3/s Porosity = 0.8 | 7.17 |
| Flow rate = 7.86 cm3/s Porosity = 0.9 | 4.85 |
| Flow rate = 11.8 cm3/s Porosity = 0.9 | 13.9 |
| Flow Rate | = 0.7 | = 0.8 | = 0.9 |
|---|---|---|---|
| 3.74 cm3/s | 1.4019 × 10−7 m2 | 2.4696 × 10−7 m2 | 3.517 × 10−7 m2 |
| 7.86 cm3/s | 9.61798 × 10−8 m2 | 1.7305 × 10−7 m2 | 1.9663 × 10−7 m2 |
| 11.8 cm3/s | 7.69154 × 10−8 m2 | 5.7362 × 10−9 m2 | 1.3928 × 10−7 m2 |
| 15.73 cm3/s | 6.50458 × 10−8 m2 | 1.1638 × 10−7 m2 | 1.0933 × 10−7 m2 |
| 19.85 cm3/s | 5.66955 × 10−8 m2 | 9.955 × 10−8 m2 | 8.9289 × 10−8 m2 |
| Average | 8.7 × 10−8 m2 | 1.2834 × 10−7 m2 | 1.772 × 10−7 m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saghir, M.Z.; Kerme, E.D.; Hajialibabei, M.; Rasheed, H.; Welsford, C.; Al-Ketan, O. Study of the Thermal and Hydraulic Performance of Porous Block versus Gyroid Structure: Experimental and Numerical Approaches. Energies 2024, 17, 861. https://doi.org/10.3390/en17040861
Saghir MZ, Kerme ED, Hajialibabei M, Rasheed H, Welsford C, Al-Ketan O. Study of the Thermal and Hydraulic Performance of Porous Block versus Gyroid Structure: Experimental and Numerical Approaches. Energies. 2024; 17(4):861. https://doi.org/10.3390/en17040861
Chicago/Turabian StyleSaghir, Mohamad Ziad, Esa D. Kerme, Mahsa Hajialibabei, Heba Rasheed, Christopher Welsford, and Oraib Al-Ketan. 2024. "Study of the Thermal and Hydraulic Performance of Porous Block versus Gyroid Structure: Experimental and Numerical Approaches" Energies 17, no. 4: 861. https://doi.org/10.3390/en17040861
APA StyleSaghir, M. Z., Kerme, E. D., Hajialibabei, M., Rasheed, H., Welsford, C., & Al-Ketan, O. (2024). Study of the Thermal and Hydraulic Performance of Porous Block versus Gyroid Structure: Experimental and Numerical Approaches. Energies, 17(4), 861. https://doi.org/10.3390/en17040861







