A Novel Method for Line Selection for Cross-Line Two-Point Successive Grounding Faults Utilizing Transient and Steady-State Information
Abstract
1. Introduction
- (1)
- The active method is identified by injecting signals or artificially creating disturbances, which requires additional devices for implementation and increases the workload of the operation and maintenance. Hence, the application of this method in the field is relatively limited. Ref. [2] uses the transient measurement information after arc extinction to determine the operating state of the distribution network. Ref. [3] proposes to regulate the arc suppression coil to obtain the trajectory matrix, for which a gray correlation analysis is used to identify faults. Ref. [4] identifies faulty lines based on the voltage and current variations under multiple disturbances. Ref. [5] uses a single-phase flexible arc elimination device to detect fault phases, providing a new method for detecting faulty lines. Ref. [6] uses the injected characteristic signal to detect the fault location. Ref. [7] uses the transient voltage and current variations that are generated by the regulation of the arc suppression coil to achieve fault line selection.
- (2)
- The passive method is divided into the steady-state quantity method and the transient quantity method, which only uses the electrical quantity of the fault process itself. The amount of equipment renovation is small, but it has been widely used in the field. Steady-state quantity method: Ref. [8] calculates the power factor of each line to detect the faulty line. Ref. [9] uses three fault characteristics to detect the fault location. Ref. [10] uses the complete residual current magnitude after the fault has occurred to detect the faulty line. Transient quantity method: Ref. [11] makes full use of the transient component after the grounding fault and distinguishes the faulty line from the healthy line by comparing the magnitude and polarity of the projected component of the transient current. Ref. [12] uses the cumulative generation operator to preprocess the transient currents while identifying the faulty lines by improving the cosine similarity. Ref. [13] uses the fault characteristics of the third harmonic amplitude and phase angle to detect faulty lines. Ref. [14] extracts voltage and current information in the characteristic frequency band range after a grounding fault occurrence to construct a dynamic trajectory of voltage–current characteristics to carry out fault line selection. Ref. [15] combines the instantaneous energy of the transient signal with the cosine similarity to achieve fault line selection. Ref. [16] distinguishes the fault from the healthy section based on the third harmonic phase difference. Ref. [17] uses the zero-crossing time difference of the transient currents to detect the faulty line. In [18], the inner product is calculated for the transient current of each line, and the fault location is distinguished based on the symbol of the inner product. Ref. [19] uses the magnitude and sign of the integrated inner product’s value to distinguish between faulty and healthy lines, and the method is adapted to various extreme conditions. Ref. [20] detects faulty lines based on the integrated harmonic energy and correlation of transient signals. In [21], the cosine similarity between the bus voltage and line current is calculated for the fault’s initial phase to distinguish the faulty line. Ref. [22] detects the fault location by comparing the amplitude characteristics of the transient components. Ref. [23] uses mathematical morphology to extract the fault characteristics and adopts correlation analysis to achieve fault detection. Ref. [24] proposes advanced distortion detection techniques for waveform analysis to distinguish and detect high-impedance faults. Ref. [25] combines three typical transient fault characteristics with D-S evidence fusion theory to achieve fault line selection. In [26], a multi-terminal traveling wave location network is developed. Ref. [27] uses the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) algorithm to extract transient signals and develops three complementary fault line selection methods. Ref. [28] identifies the fault location based on the fault characteristics of voltage and current in the characteristic frequency band. Ref. [29] uses the voltage traveling wave after the fault occurs to measure the fault location. Ref. [30] uses the transient energy difference between the faulty and healthy lines in the characteristic frequency band. Ref. [31] combines clustering methods with similarity analysis, thus detecting faulty lines with a high degree of sensitivity. Ref. [32] uses the variational mode decomposition (VMD) algorithm to extract transient characteristics after the occurrence of faults. Ref. [33] uses stochastic resonance to extract transient signals under strong noise. Ref. [34] uses transient voltage and current features and combines these with neural networks to achieve detection of the fault location. Ref. [35] uses the disturbance generated by the small resistance input of a flexible grounding system to achieve fault location detection.
2. Adaptation Analysis of Transient and Steady-State State Quantity Methods for CTSGs
2.1. Transient Quantity Method
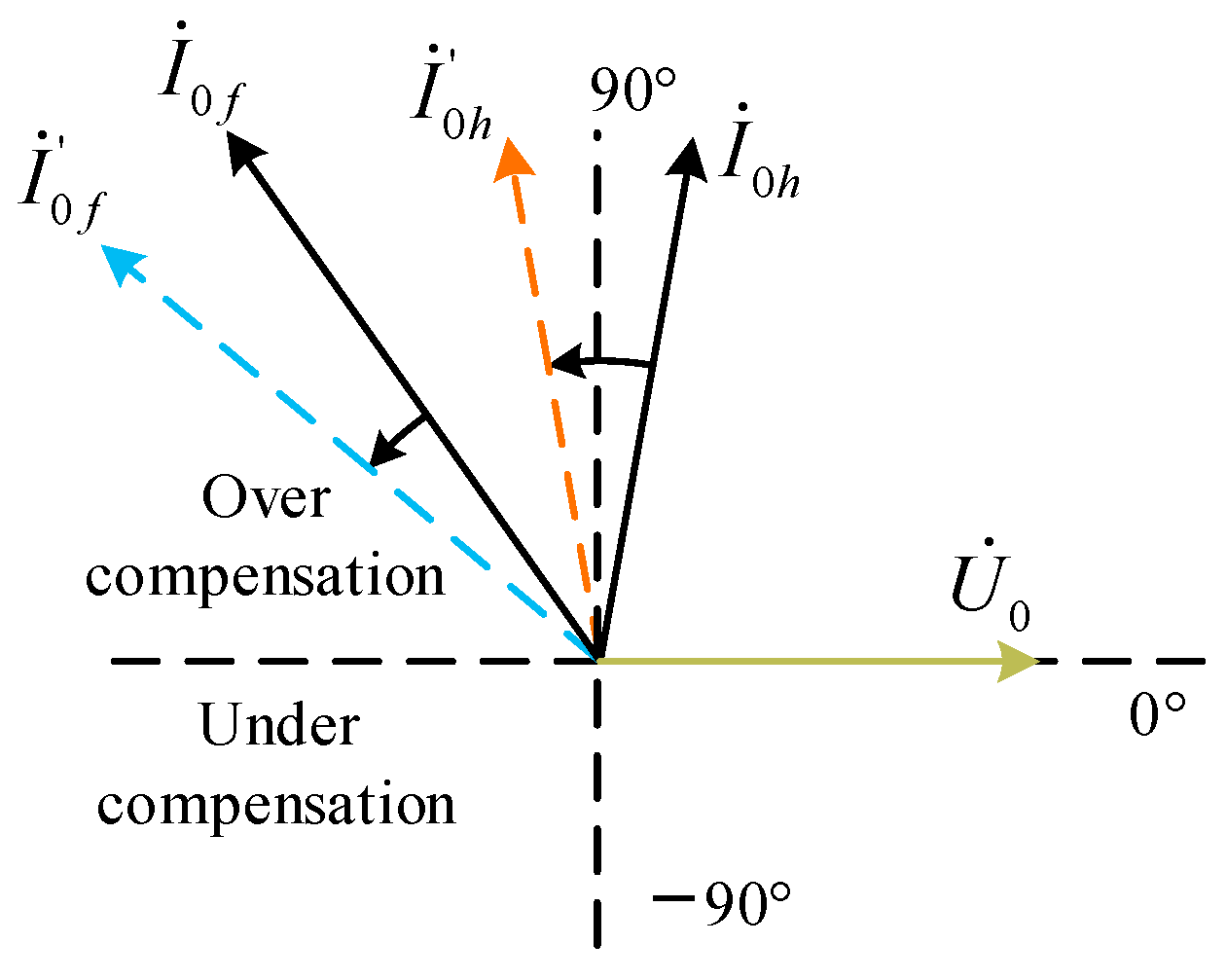
2.2. Steady-State Quantity Method
- (1)
- Analysis of steady-state fault characteristics and the adaptability of the steady-state quantity method for SP-CTSGs
- (2)
- Analysis of steady-state fault characteristics and the adaptability of the steady-state quantity method for DP-CTSGs
3. New Method of Line Selection for CTSGs
3.1. Analysis of Calculation Amount for Continuous Detection in Transient Quantity Method
3.2. Analysis of the Accuracy of the Steady-State Quantity Method of Detection
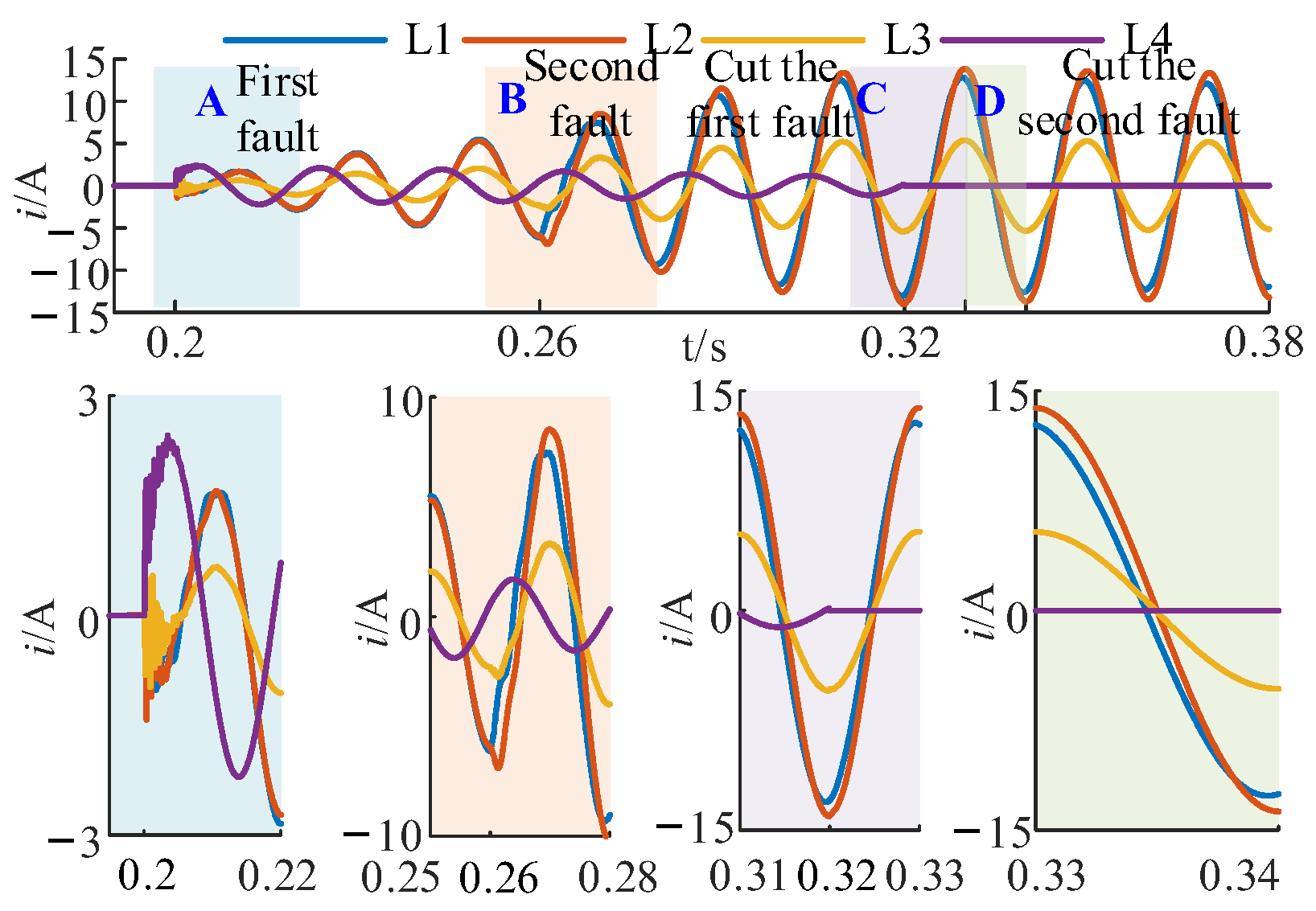
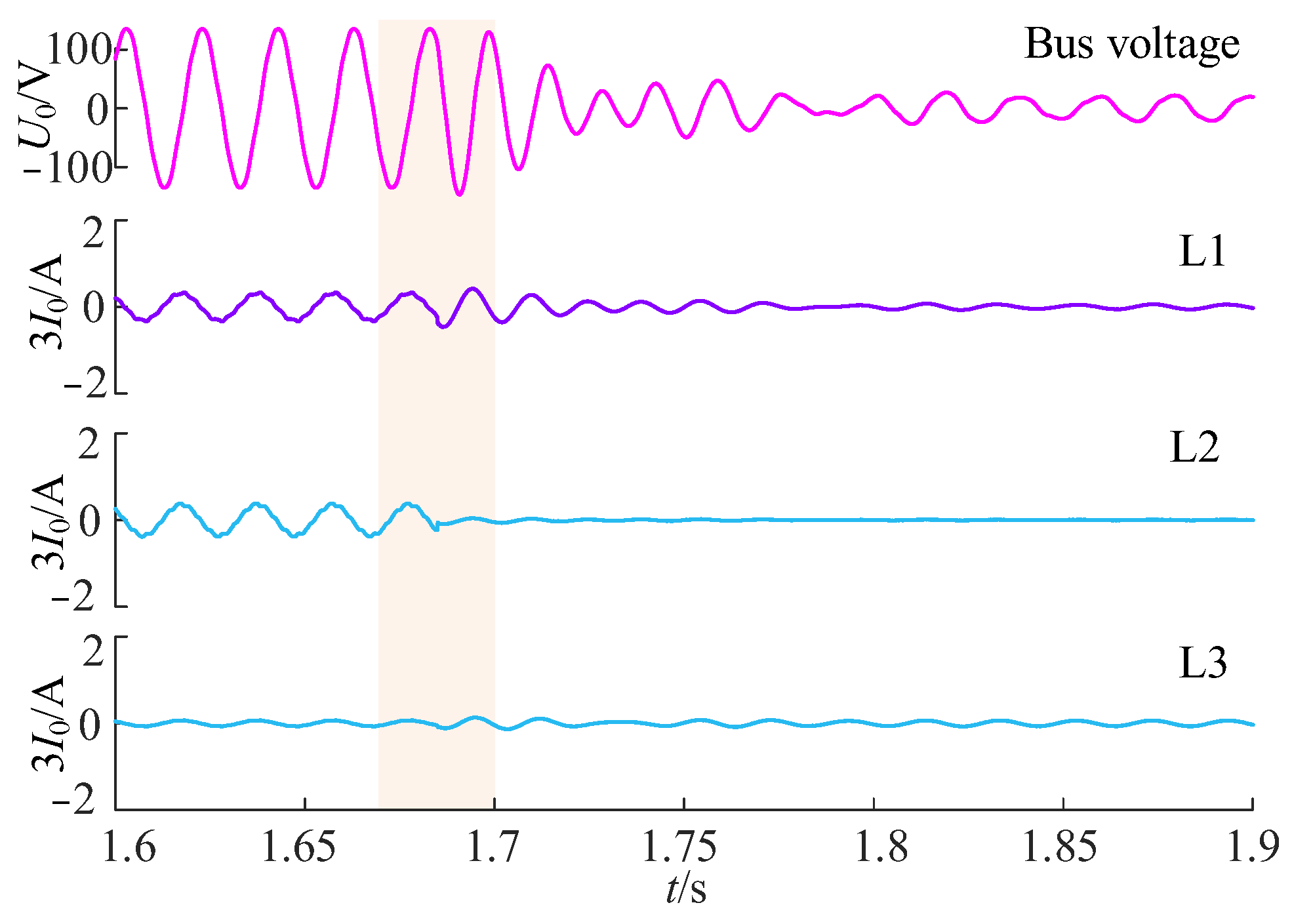
4. Simulation Testing
- (1)
- Condition ①:
- (2)
- Condition ②:
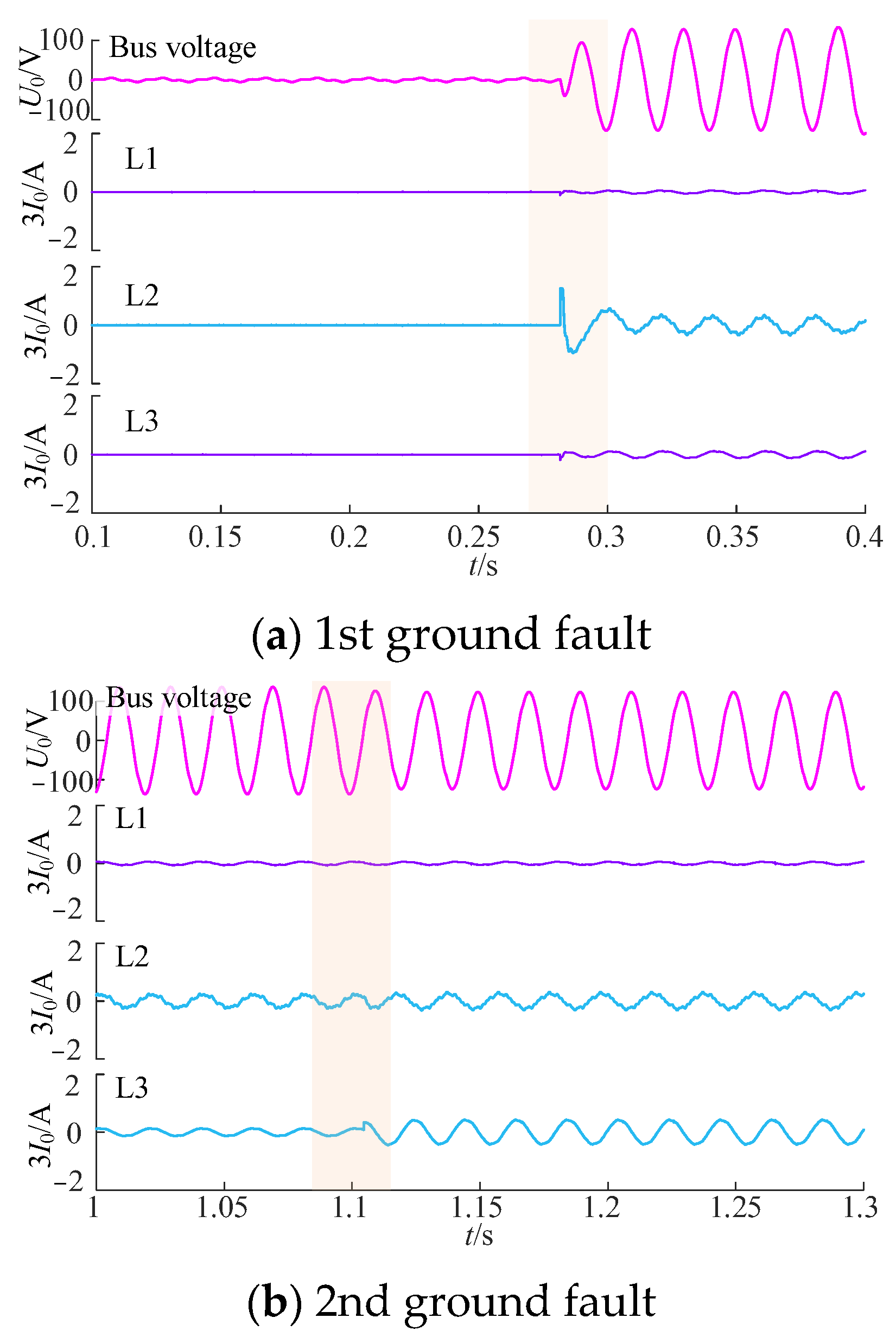
5. Full-Scale Test Field Testing
6. Field Recording Test

7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Recording Data of SP-CTSGs and DP-CTSGs
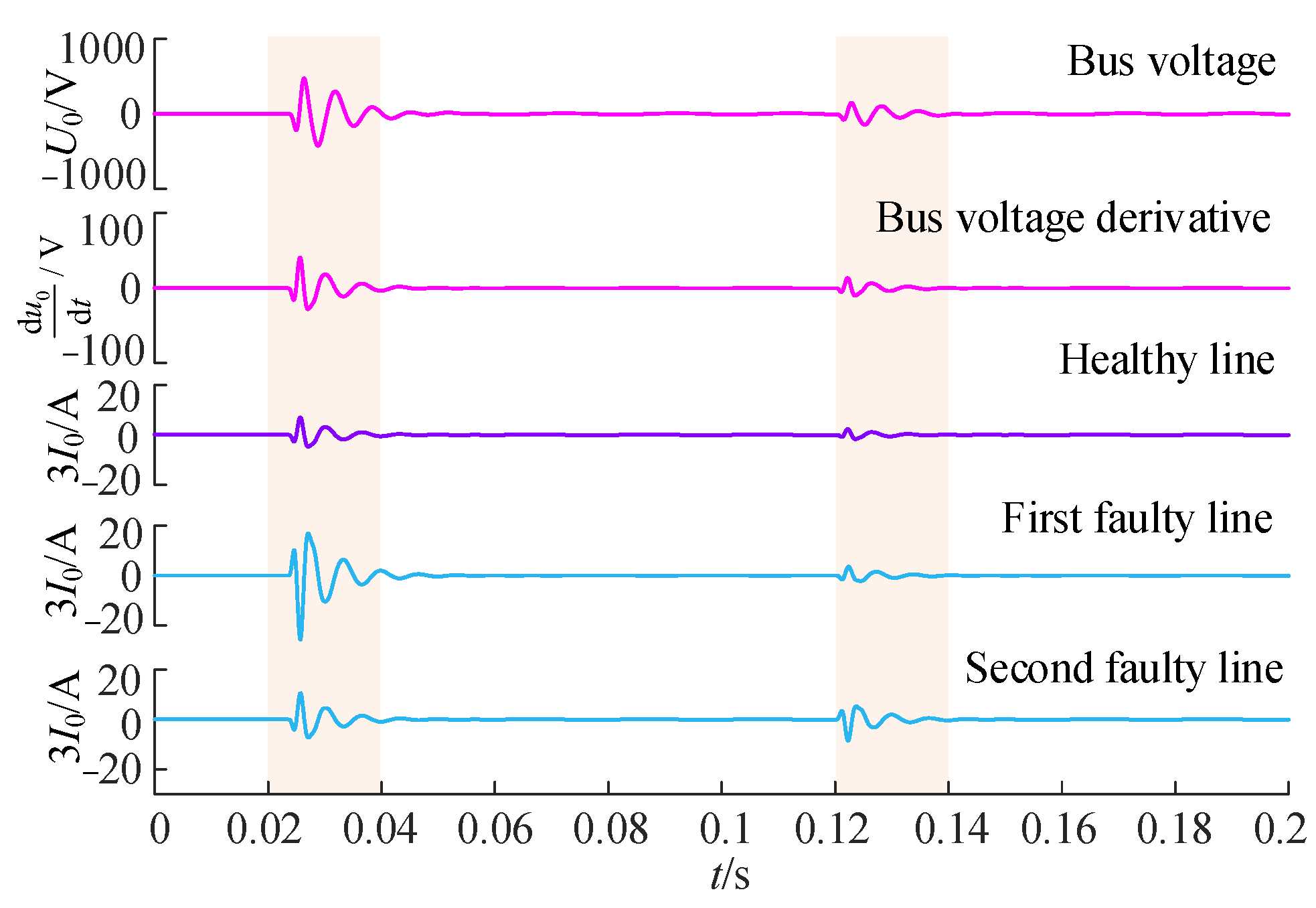
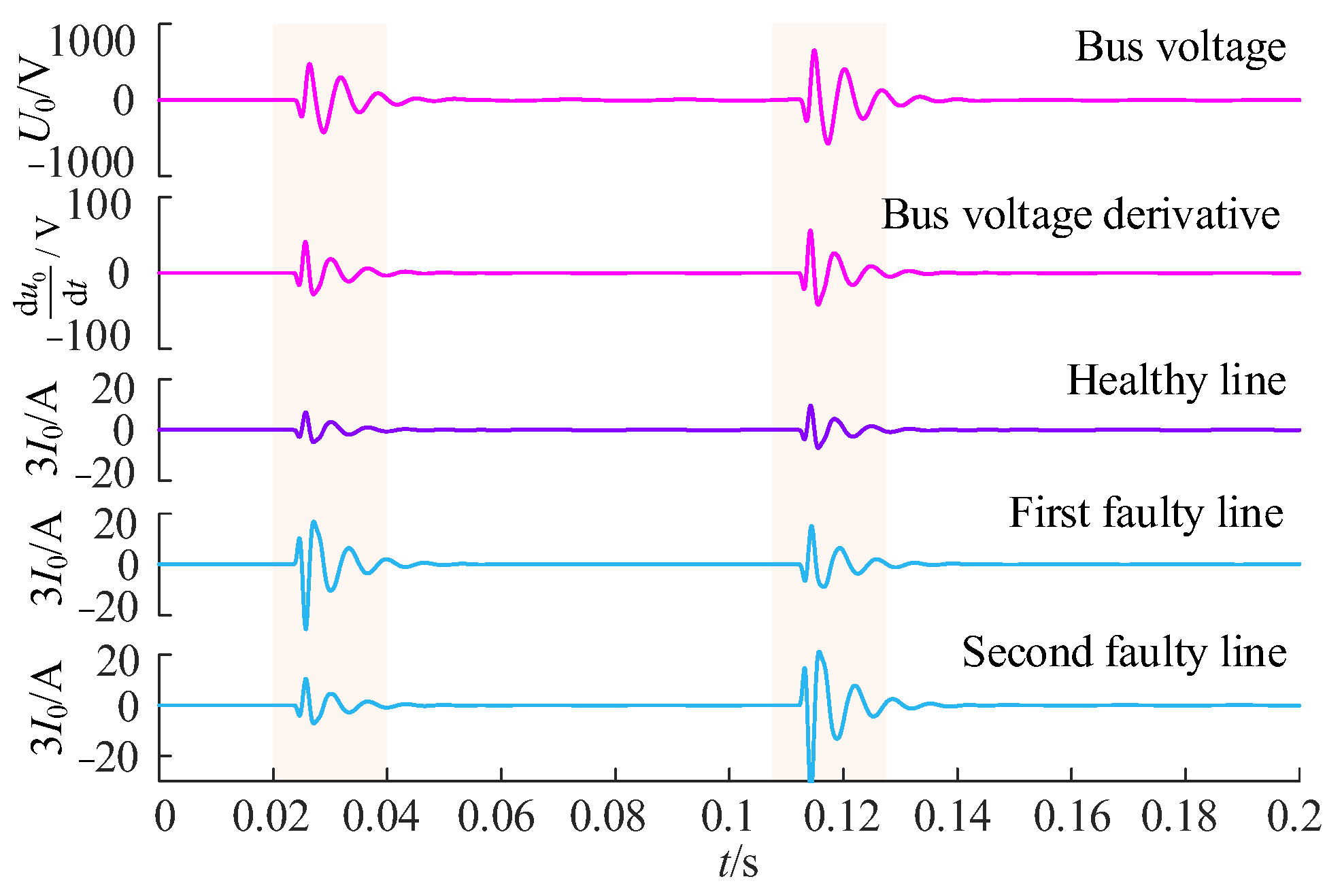
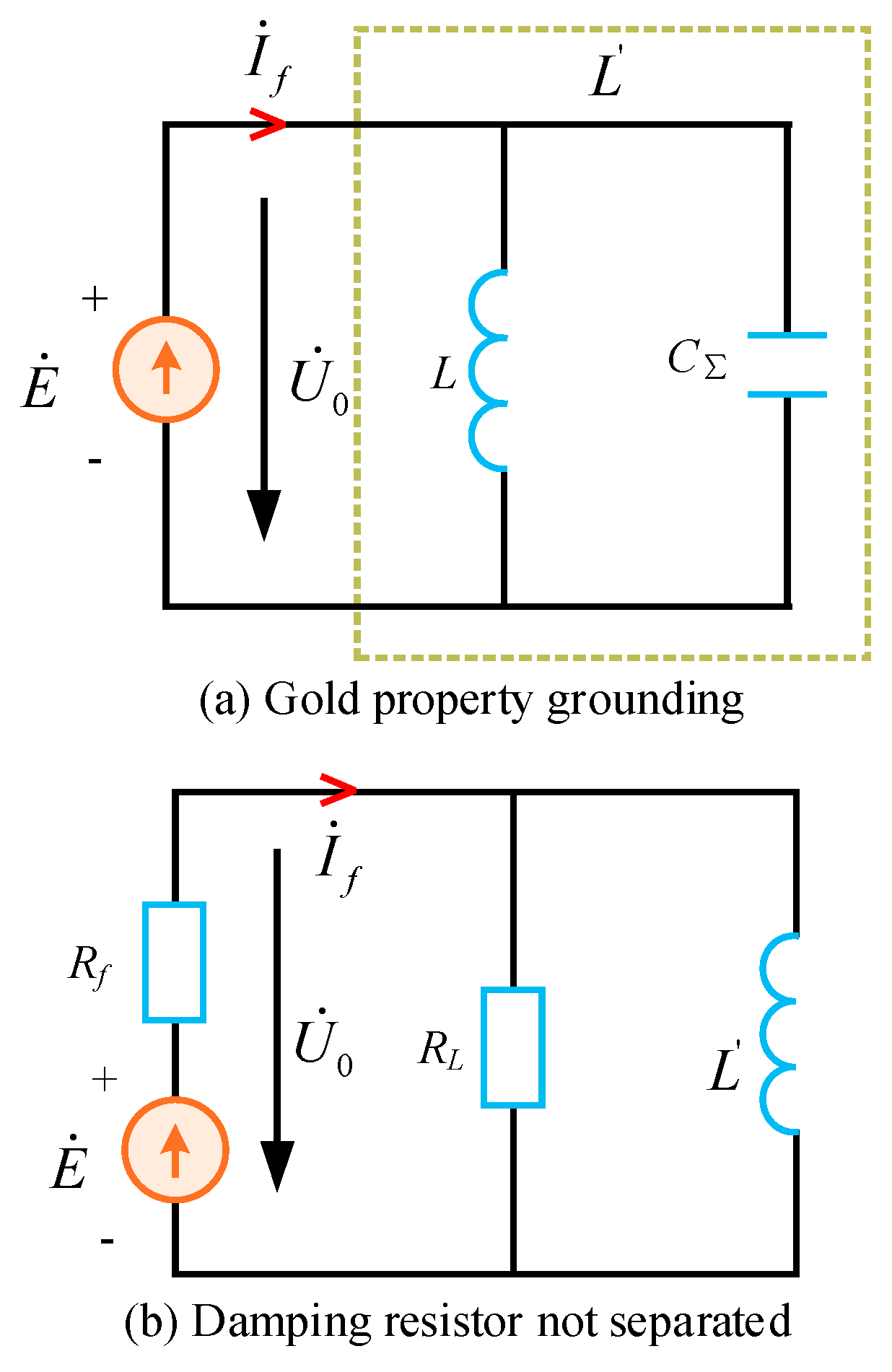
Appendix A.2. Process for Deriving the Relationship between Bus’s Zero-Sequence Voltage and Grounding Resistance Rf
References
- Xiao, Y.; Ouyang, J.; Xiong, X.; Wang, Y.; Luo, Y. Fault protection method of single-phase break for distribution network considering the influence of neutral grounding modes. Prot. Control Mod. Power Syst. 2020, 5, 10. [Google Scholar] [CrossRef]
- Zhang, F.; Xue, Y.; Li, G.; Xu, B. A Method for Measuring and Adjusting the Detuning of Resonant Grounding Systems with Transient Information After Arc Extinction. IEEE Trans. Power Deliv. 2022, 38, 496–504. [Google Scholar] [CrossRef]
- Tang, J.; Xiong, B.; Li, Y.; Yuan, C.; Qiu, Y. Faulted Feeder Identification Based on Active Adjustment of Arc Suppression Coil and Similarity Measure of Zero-Sequence Currents. IEEE Trans. Power Deliv. 2021, 36, 3903–3913. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, J.; Shao, W.; Wang, Y. Fault line selection using multiple disturbance characteristics of fault phase active grounding in resonant grounded distribution networks. Int. J. Electr. Power Energy Syst. 2022, 138, 107931. [Google Scholar] [CrossRef]
- Guo, M.-F.; Cai, W.-Q.; Zheng, Z.-Y.; Wang, H. Fault Phase Selection Method Based on Single-Phase Flexible Arc Suppression Device for Asymmetric Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 4548–4558. [Google Scholar] [CrossRef]
- Li, Z.; Ye, Y.; Ma, X.; Lin, X.; Xu, F.; Wang, C.; Ni, X.; Ding, C. Single-phase-to-ground fault section location in flexible resonant grounding distribution networks using soft open points. Int. J. Electr. Power Energy Syst. 2020, 122, 106198. [Google Scholar] [CrossRef]
- Huang, C.; Tang, T.; Jiang, Y.; Hua, L.; Hong, C. Faulty feeder detection by adjusting the compensation degree of arc-suppression coil for distribution network. IET Gener. Transm. Distrib. 2018, 12, 807–814. [Google Scholar] [CrossRef]
- Chen, J.; Li, H.; Deng, C.; Wang, G. Detection of Single-Phase to Ground Faults in Low-Resistance Grounded MV Systems. IEEE Trans. Power Deliv. 2020, 36, 1499–1508. [Google Scholar] [CrossRef]
- Wang, X.; Du, H.; Gao, J.; Wei, X.; Liang, Z.; Guo, L.; Liu, W. Grounding fault location method of overhead line based on dual-axis magnetic field trajectory. Prot. Control Mod. Power Syst. 2023, 8, 4. [Google Scholar] [CrossRef]
- Granizo Arrabe, R.; Granados, J.M.G.; Gomez, F.A.; Gaona, C.A.P. New Selective Directional Ground Fault Protection Method for Ungrounded Systems. IEEE Trans. Power Deliv. 2022, 37, 5234–5243. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, X.; Song, H.; Xu, B. Resonance Analysis and Faulty Feeder Identification of High-Impedance Faults in a Resonant Grounding System. IEEE Trans. Power Deliv. 2017, 32, 1545–1555. [Google Scholar] [CrossRef]
- Wei, X.; Wang, X.; Gao, J.; Yang, D.; Wei, K.; Guo, L.; Wei, Y. Faulty Feeder Identification Method Considering Inverter Transformer Effects in Converter Dominated Distribution Network. IEEE Trans. Smart Grid 2022, 14, 939–953. [Google Scholar] [CrossRef]
- Wei, M.; Shi, F.; Zhang, H.; Chen, W. Wideband Synchronous Measurement-Based Detection and Location of High Impedance Fault for Resonant Distribution Systems with Integration of DERs. IEEE Trans. Smart Grid 2022, 14, 1117–1134. [Google Scholar] [CrossRef]
- Wang, B.; Cui, X. Nonlinear Modeling Analysis and Arc High-Impedance Faults Detection in Active Distribution Networks With Neutral Grounding via Petersen Coil. IEEE Trans. Smart Grid 2022, 13, 1888–1898. [Google Scholar] [CrossRef]
- Wei, X.; Wang, X.; Gao, J.; Yang, D.; Wei, K.; Guo, L. Faulty Feeder Detection for Single-Phase-to-Ground Fault in Distribution Networks Based on Transient Energy and Cosine Similarity. IEEE Trans. Power Deliv. 2022, 37, 3968–3979. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, H.; Shi, F.; Chen, W.; Terzija, V. Nonlinearity Characteristic of High Impedance Fault at Resonant Distribution Networks: Theoretical Basis to Identify the Faulty Feeder. IEEE Trans. Power Deliv. 2021, 37, 923–936. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Zhang, Z.; Zheng, T.; Ren, S.; Chen, J. A faulty line detection method for single phase-to-ground fault in resonant grounding system with CTs reversely connected. Int. J. Electr. Power Energy Syst. 2023, 147, 108873. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Wei, X.; Guo, L.; Song, G.; Wang, P. Faulty Feeder Detection Under High Impedance Faults for Resonant Grounding Distribution Systems. IEEE Trans. Smart Grid 2022, 14, 1880–1895. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Liang, Z.; Guo, L.; Du, H.; Gao, J.; Li, C. Faulty feeder detection based on the integrated inner product under high impedance fault for small resistance to ground systems. Int. J. Electr. Power Energy Syst. 2022, 140, 108078. [Google Scholar] [CrossRef]
- Yuan, J.; Hu, Y.; Liang, Y.; Jiao, Z. Faulty Feeder Detection for Single Line-to-Ground Fault in Distribution Networks with DGs Based on Correlation Analysis and Harmonics Energy. IEEE Trans. Power Deliv. 2022, 38, 1020–1029. [Google Scholar] [CrossRef]
- Pandakov, K.; Høidalen, H.K.; Trætteberg, S. An additional criterion for faulty feeder selection during ground faults in compensated distribution networks. IEEE Trans. Power Deliv. 2018, 33, 2930–2937. [Google Scholar] [CrossRef]
- Li, Z.; Wan, J.; Wang, P.; Weng, H.; Li, Z. A novel fault section locating method based on distance matching degree in distribution network. Prot. Control Mod. Power Syst. 2021, 6, 20. [Google Scholar] [CrossRef]
- Busik, M.A.; Gargoom, A.; Mahmud, M.A.; Haque, M.E.; Al-Khalidi, H.; Than Oo, A.M. A decentralized fault detection technique for detecting single phase to ground faults in power distribution systems with resonant grounding. IEEE Trans. Power Deliv. 2018, 33, 2462–2473. [Google Scholar]
- Bhandia, R.; Chavez, J.D.J.; Cvetkovic, M.; Palensky, P. High Impedance Fault Detection using Advanced Distortion Detection Technique. IEEE Trans. Power Deliv. 2020, 35, 2598–2611. [Google Scholar] [CrossRef]
- Wei, X.; Yang, D.; Wang, X.; Wang, B.; Gao, J.; Wei, J. Faulty Feeder Detection Based on Fundamental Component Shift and Multiple-Transient-Feature Fusion in Distribution Networks. IEEE Trans. Smart Grid 2020, 12, 1699–1711. [Google Scholar] [CrossRef]
- Deng, F.; Zeng, X.; Pan, L. Research on multi-terminal traveling wave fault location method in complicated networks based on cloud computing platform. Prot. Control Mod. Power Syst. 2017, 2, 19. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Wei, X.; Zeng, Z.; Wei, Y.; Kheshti, M. Single Line to Ground Fault Detection in a Non-Effectively Grounded Distribution Network. IEEE Trans. Power Deliv. 2018, 33, 3173–3186. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, T.; Mohamed, M.A.; Deb, D. A Novel Linear Optimization Method for Section Location of Single-Phase Ground Faults in Neutral Noneffectively Grounded Systems. IEEE Trans. Instrum. Meas. 2021, 70, 3513410. [Google Scholar] [CrossRef]
- Deng, F.; Zhong, Y.; Zeng, Z.; Zu, Y.; Zhang, Z.; Huang, Y.; Feng, S.; Zeng, X. A Single-Ended Fault Location Method for Transmission Line Based on Full Waveform Features Extractions of Traveling Waves. IEEE Trans. Power Deliv. 2023, 38, 2585–2595. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Shi, F.; Wu, Q.; Terzija, V.; Xie, W.; Fang, C. Location of Single Phase to Ground Faults in Distribution Networks Based on Synchronous Transients Energy Analysis. IEEE Trans. Smart Grid 2019, 11, 774–785. [Google Scholar] [CrossRef]
- Ni, Y.; Zeng, X.; Liu, Z.; Yu, K.; Xu, P.; Wang, Z.; Zhuo, C.; Huang, Y. Faulty feeder detection of single phase-to-ground fault for distribution networks based on improved K-means power angle clustering analysis. Int. J. Electr. Power Energy Syst. 2022, 142, 108252. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Wei, X.; Song, G.; Wu, L.; Liu, J.; Zeng, Z.; Kheshti, M. High Impedance Fault Detection Method Based on Variational Mode Decomposition and Teager–Kaiser Energy Operators for Distribution Network. IEEE Trans. Smart Grid 2019, 10, 6041–6054. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Gao, J.; Song, G.; Kheshti, M.; Guo, L. High-Impedance Fault Detection Method Based on Stochastic Resonance for a Distribution Network with Strong Background Noise. IEEE Trans. Power Deliv. 2021, 37, 1004–1016. [Google Scholar] [CrossRef]
- Jamali, S.; Bahmanyar, A.; Ranjbar, S. Hybrid classifier for fault location in active distribution networks. Prot. Control Mod. Power Syst. 2020, 5, 17. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Wei, X.; Gao, J.; Guo, L.; Wang, Y. Fault location of flexible grounding distribution system based on multivariate modes and kurtosis calibration. Int. J. Electr. Power Energy Syst. 2023, 150, 109108. [Google Scholar] [CrossRef]
- Gao, J.; Wang, X.; Wang, X.; Yang, A.; Yuan, H.; Wei, X. A High-Impedance Fault Detection Method for Distribution Systems Based on Empirical Wavelet Transform and Differential Faulty Energy. IEEE Trans. Smart Grid 2021, 13, 900–912. [Google Scholar] [CrossRef]
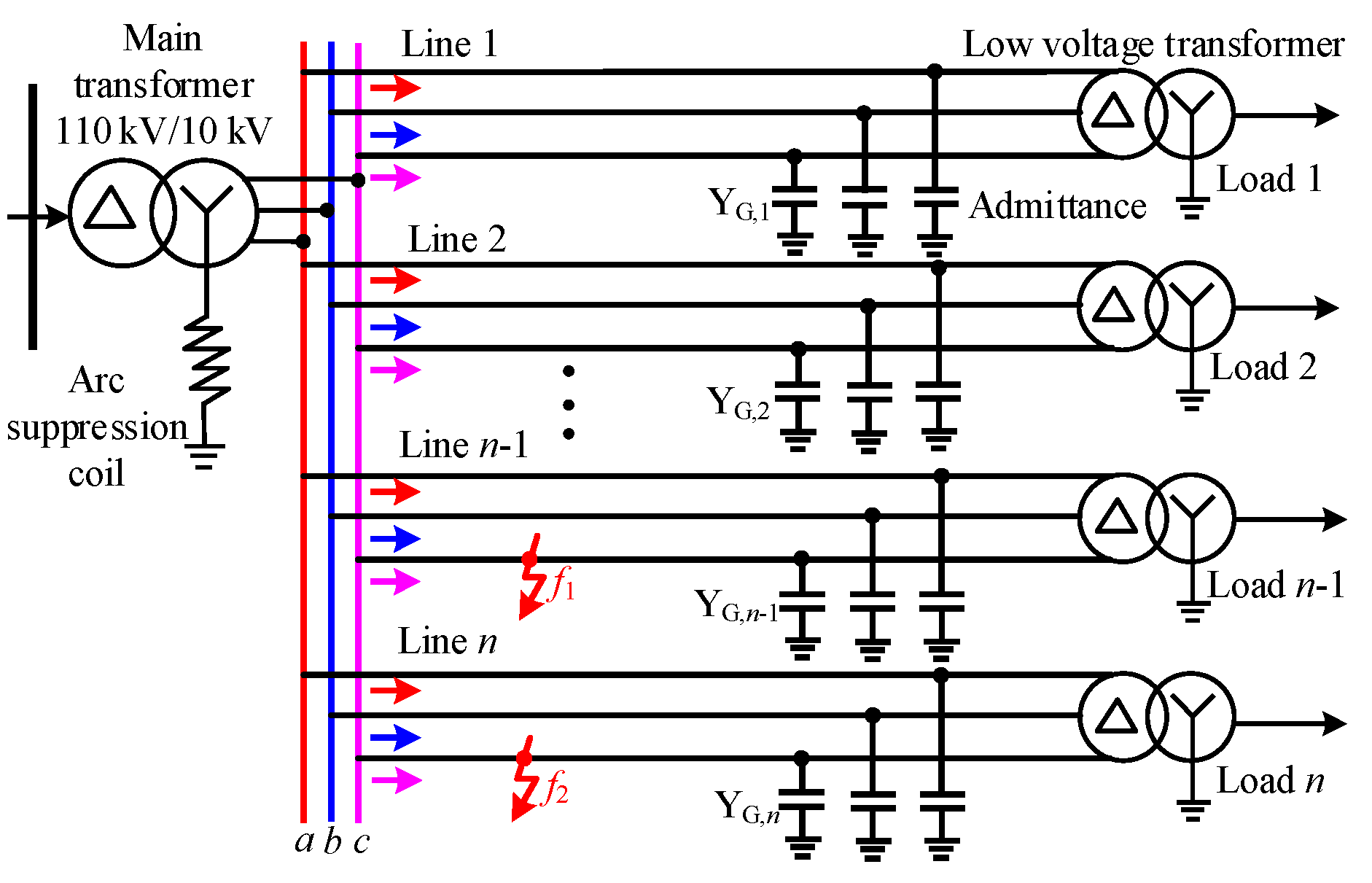
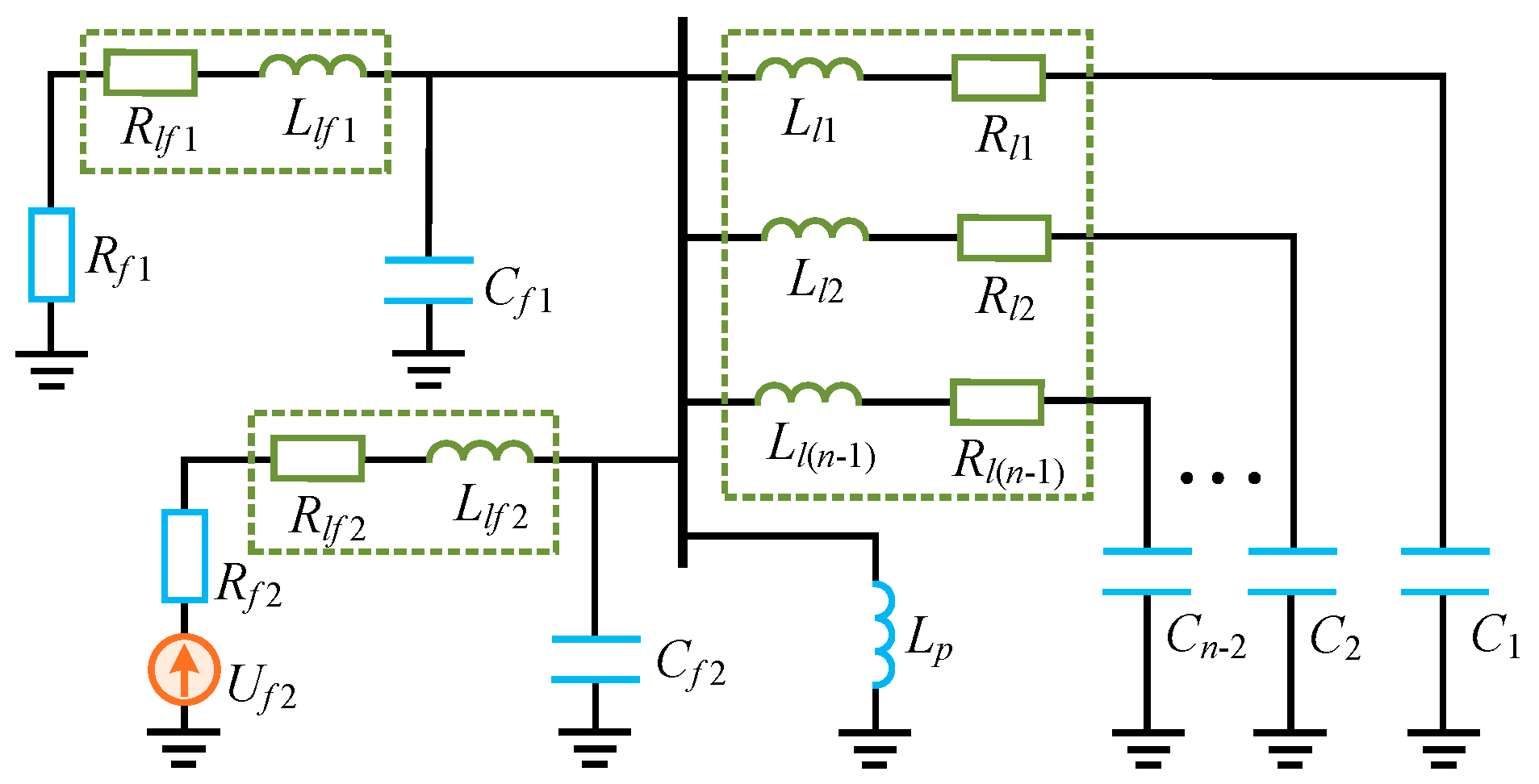
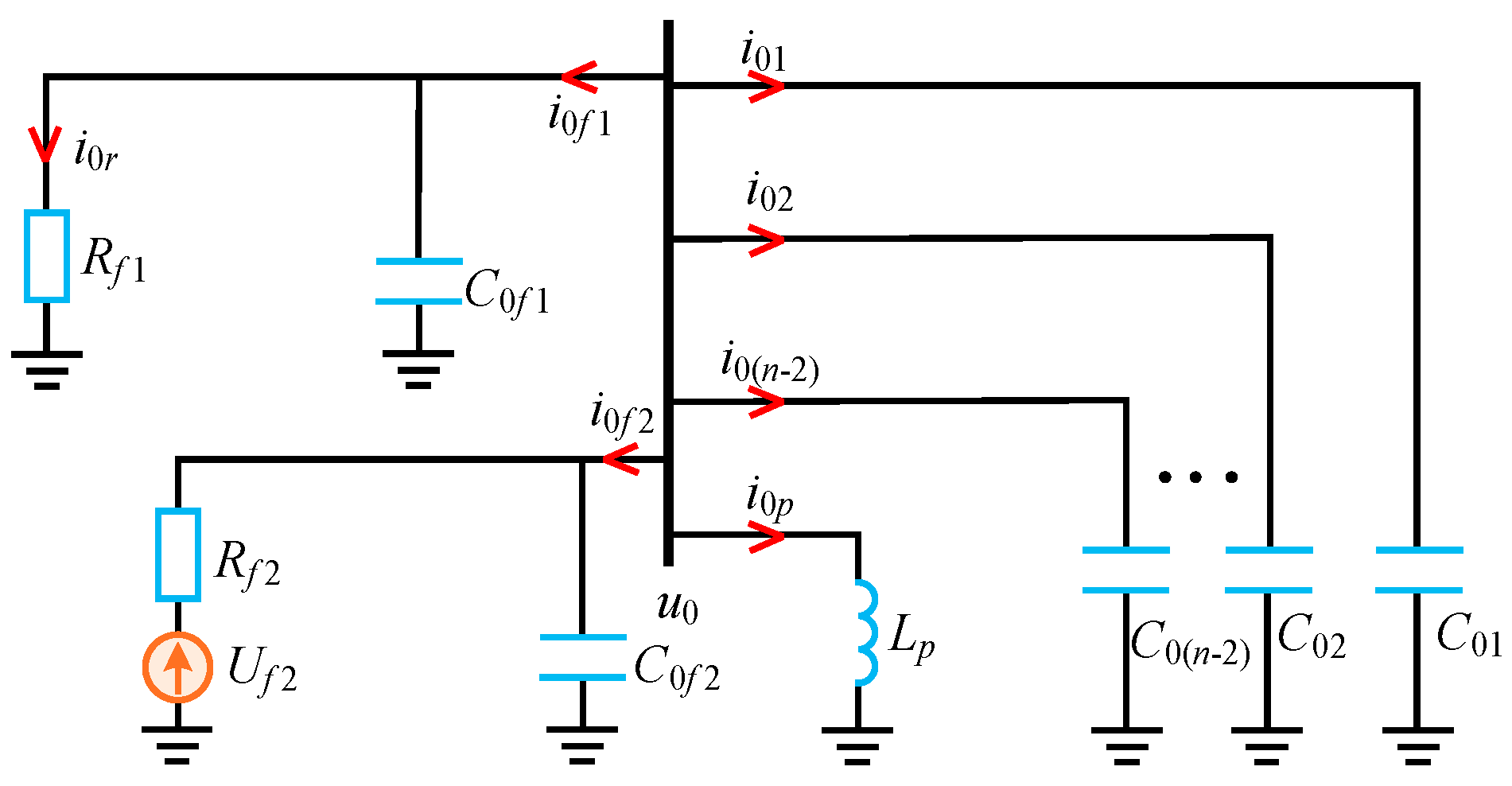

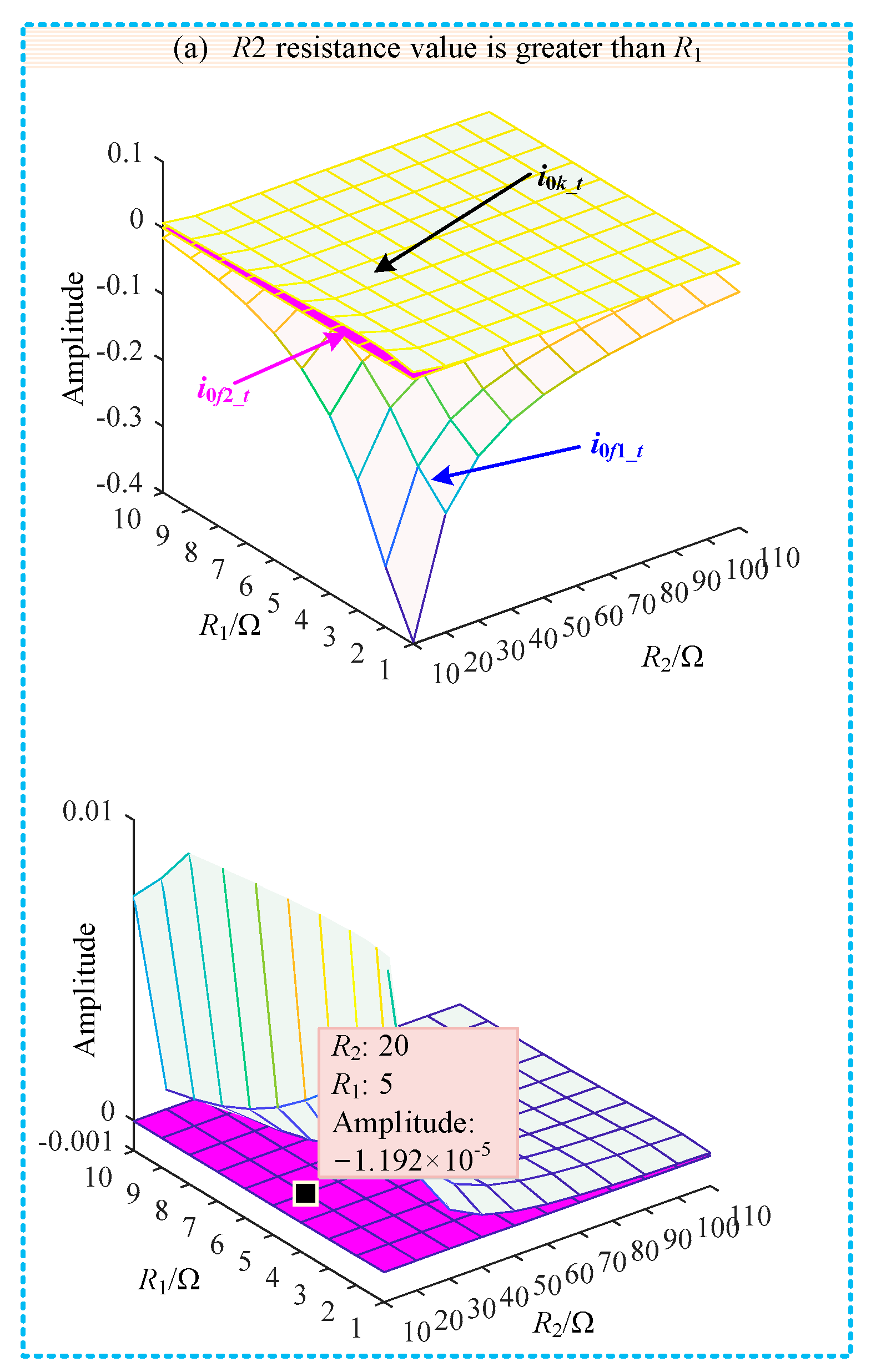
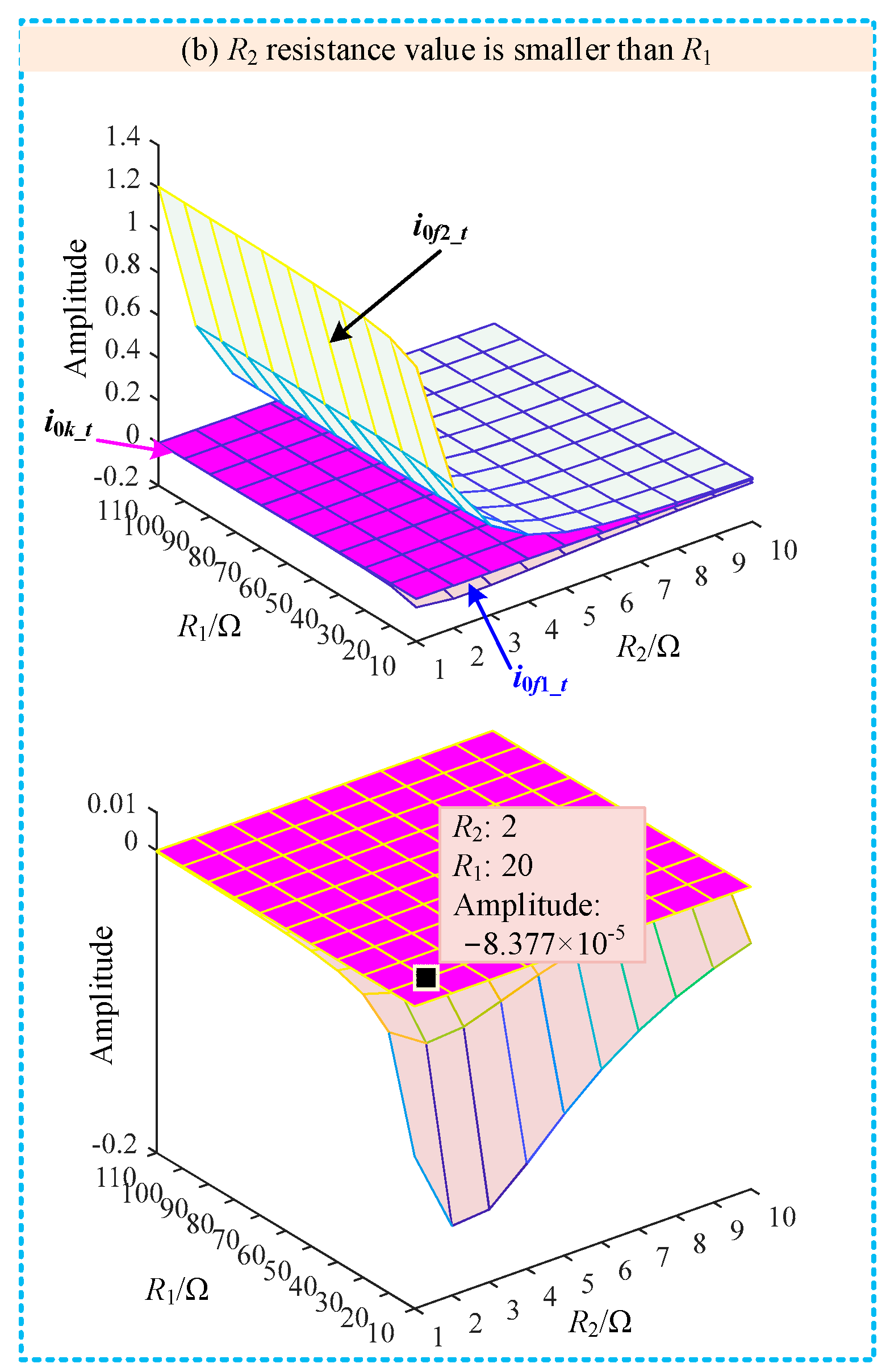
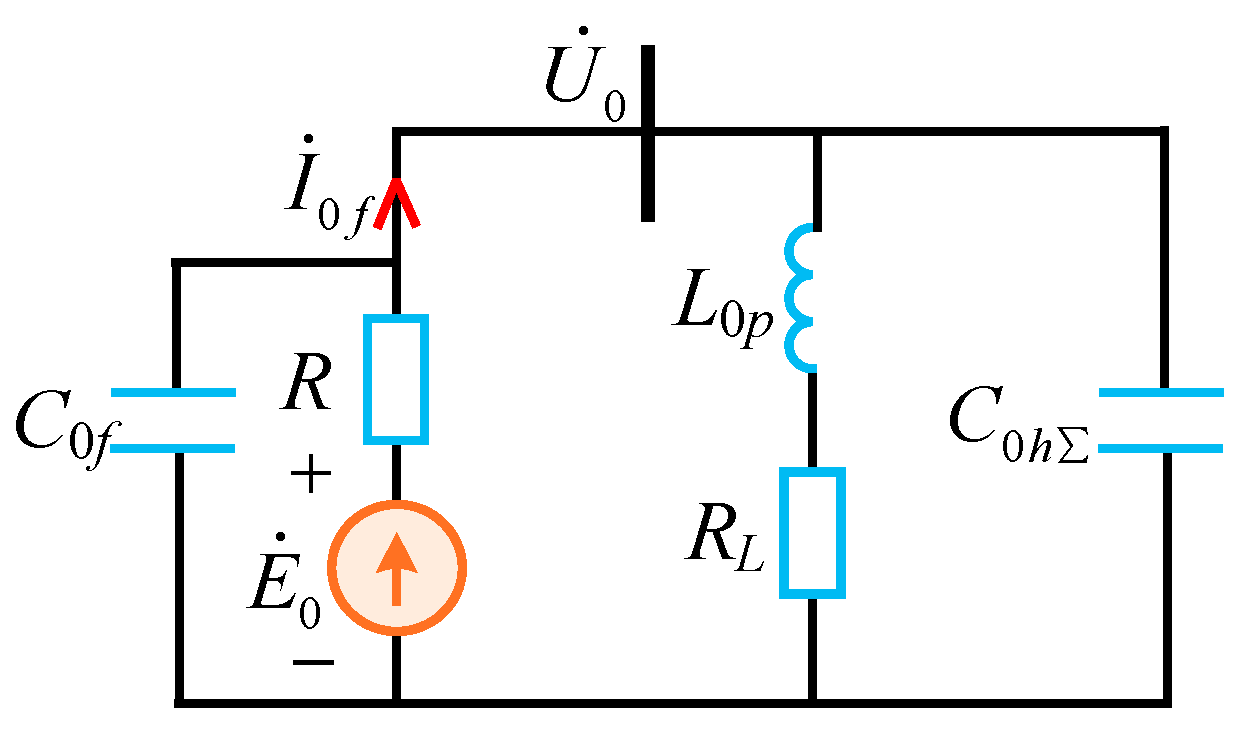

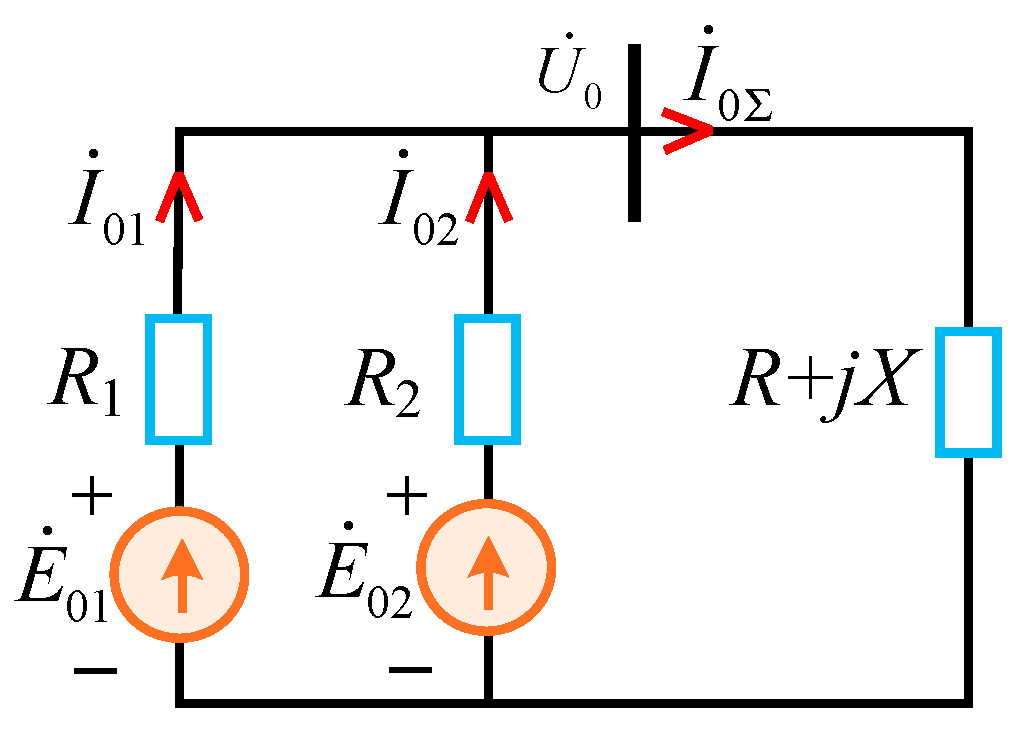
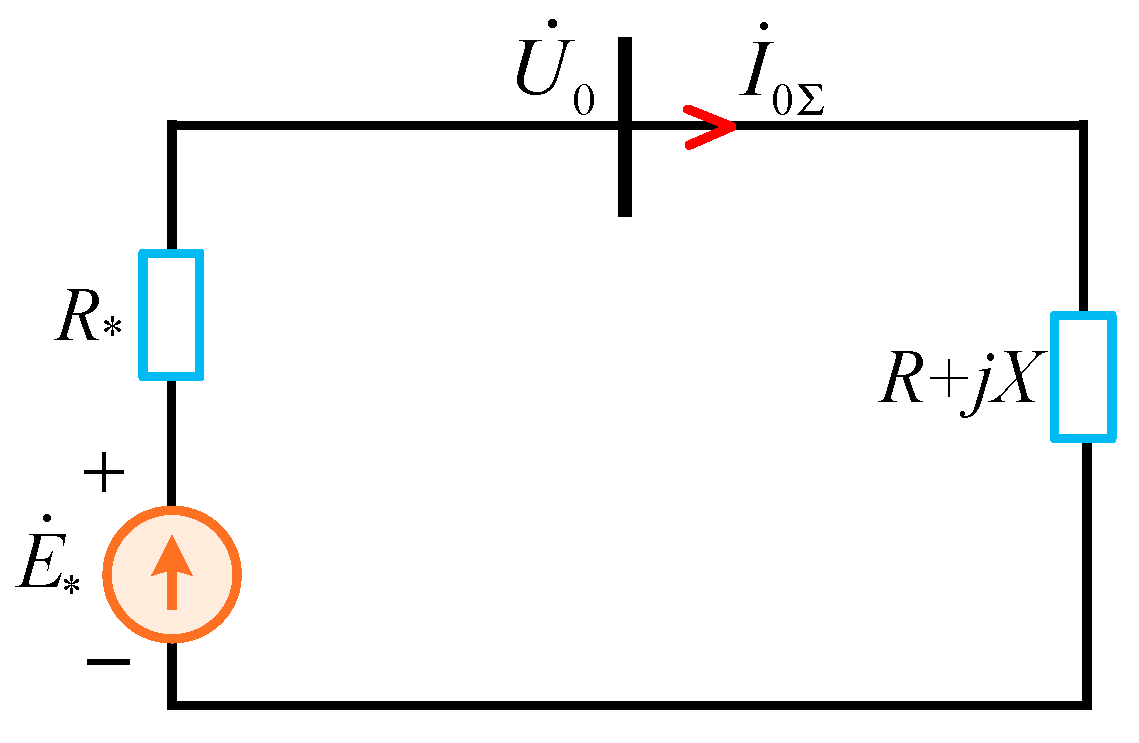




| Line | Phase Sequence | R (Ω/km) | L (mH/km) | C (μF/km) |
|---|---|---|---|---|
| Cable line | Positive sequence | 0.2700 | 0.2550 | 0.3390 |
| Zero-sequence | 2.7000 | 1.0190 | 0.2800 | |
| Overhead line | Positive sequence | 0.1700 | 1.2100 | 0.0097 |
| Zero-sequence | 0.2300 | 5.4780 | 0.0080 |
| Arc Types | Vρ | Vρ | Rp | Rp |
|---|---|---|---|---|
| Cement | 4.5 ± 10% kV | 2.0 ± 20% kV | 800 Ω | 750 Ω |
| Dry grass | 3.8 ± 10% kV | 3.6 ± 10% kV | 400 Ω | 350 Ω |
| Wet grass | 1.2 ± 10% kV | 1.0 ± 10% kV | 1200 Ω | 1100 Ω |
| Initial Phase Angle | 1st Fault | 2nd Fault | Transient Current at 1st Fault/A [L1 L2 L3 L4] | Transient Current at 2nd Fault/A [L1 L2 L3 L4] | Transient Method Results | Phase Ahead at Steady-State [L1 L2 L3 L4] | Steady-State Method Results | Wheel Cut |
|---|---|---|---|---|---|---|---|---|
| 0° | L3 1500 Ω B | L2 1000 Ω A | [3.58 1.99 −5.18 0.43] | [−12.60 −6.00 −5.88 −0.70] | L3 | [85.38° 105.36°/86.41°] | L2 | / |
| 0° | L2 2000 Ω A | L1 1000 Ω A | [−1.11 1.53 −1.3 −0.21] | [−8.83 −7.3 −3.7 −0.43] | L2 | [98.05°/88.56° 89.43°] | L1 | / |
| 0° | L3 2000 Ω A | L2 500 Ω C | [−0.43 −1.85 1.33−0.16] | [−11.37 −7.72 −4.87 −0.73] | L3 | [83.33° 99.85°/84.78°] | L2 | / |
| 30° | L3 1500 Ω A | L2 3000 Ω B | [−0.94 −3.66 4.75 −0.36] | [−8.99 −10.95 2.21 −0.25] | L3 | [92.61° 93.12°/91.82°] | / | L2 |
| 30° | L2 1000 Ω B | L1 500 Ω A | [−0.11 5.31 −5.03 −0.41] | [−0.21 −22.31 −5.88 −0.7] | L2 | [94.37°/91.51°92.92°] | L1 | / |
| 30° | L4 100 Ω C | L2 500 Ω A | [12.52 10.79 4.09 −37.54] | [42.31 33.33 5.89 −9.19] | L4 | [88.34° 100.4° 89.67°/] | L2 | / |
| 60° | L4 500 Ω B | L2 1000 Ω B | [0.39 4.49 4.5 −10.25] | [−14.28 −13.61 −5.42 −1.71] | L4 | [89.64° 94.99° 91.17°/] | L2 | / |
| 60° | L3 2000 Ω C | L2 1000 Ω A | [0.44 1.056 −2.34 0.17] | [9.41 15.37 −3.68 0.035] | L3 | [88.11° 102°/89.65°] | L2 | / |
| 60° | L3 300 Ω A | L2 1300 Ω A | [−5.11 −20.1 25.84 −1.91] | [−1.81 −0.98 4.4 −0.06] | L3 | [88.56° 92.03°/89.91°] | / | L2 |
| 90° | L4 1500 Ω B | L3 100 Ω A | [−0.1 −0.55 −0.19 0.86] | [−44.76 −21.63 48.54 −2.69] | L4, L3 | / | / | / |
| 90° | L4 100 Ω A | L2 100 Ω A | [−5.03 −44.33 −27.81 63.48] | [13.5 14.54 5.14 2.17] | L4 | [88.26° 100.88° 89.59°/] | L2 | / |
| Initial Phase Angle | 1st Fault | 2nd Fault | Transient Current at 1st Fault/A [L1 L2 L3 L4] | Transient Current at 2nd Fault/A [L1 L2 L3 L4] | Transient Method Results | Phase Ahead at Steady-State [L1 L2 L3 L4] | Steady-State Method Results | Wheel Cut |
|---|---|---|---|---|---|---|---|---|
| 0° | L2 Cement C | L3 Wet grass A | [−0.21 −2.99 5.27 −0.43] | [0.23 4.36 9.87 0.55] | L3 | [90.59° 127.49°/88.42°] | L2 | / |
| 30° | L2 Cement B | L3 Dry grass C | [0.36 −5.52 4.73 0.70] | [−0.17 −13.93 −3.29 −0.39] | L2 | [89.62°/93.99° 90.06°] | L3 | / |
| 60° | L2 Dry grass A | L3 Wet grass A | [−0.04 7.33 −6.26 −1.01] | [0.59 11.22 7.48 0.10] | L2 | [76.47°/94.30° 76.54°] | L3 | / |
| 90° | L2 Dry grass B | L3 Wet grass C | [−0.05 5.88 −1.55 −0.32] | [0.42 5.43 −8.95 1.08] | L2, L3 | / | / | / |
| 0° | L1 Cement A | L4 Cement B | [3.94 −3.98 −1.95 −0.27] | [1.96 16.29 8.01 −14.5] | L1, L4 | / | / | / |
| 30° | L1 Cement A | L4 Dry grass C | [8.85 −7.34 −4.00 −0.37] | [6.51 9.26 3.99 −2.64] | L1, L4 | / | / | / |
| 60° | L1 Cement B | L4 Wet grass C | [−3.85 1.75 1.90 0.14] | [−3.98 −1.41 −2.92 −6.03] | L1 | [/81.58° 89.03° 91.19°] | L4 | / |
| 90° | L1Dry grass C | L4 Wet grass C | [−7.54 4.21 1.82 0.33] | [−1.22 −6.91 −2.45 −1.06] | L1 | [/99.87° 80.70° 100.88°] | L4 | / |
| 0° | L2 Cement A | L4 Cement B | [−0.16 2.29 −1.94 −0.14] | [0.10 6.84 2.14 1.26] | L2 | [85.27°/89.88° 188.85°] | L4 | / |
| 30° | L2 Cement A | L4 Dry grass C | [−0.13 1.90 −1.61 −0.12] | [0.04 4.30 0.97 1.44] | L2 | [85.39°/89.76° 193.70°] | L4 | / |
| 60° | L2 Cement B | L4 Wet grass C | [0.46 −6.39 5.48 0.85] | [−0.38 −18.13 −5.14 4.58] | L2, L4 | / | / | / |
| 90° | L2 Dry grass C | L4 Wet grass C | [−0.01 4.27 −0.60 −0.21] | [0.46 6.14 3.43 −11.18] | L2, L4 | / | / | / |
| Initial Phase Angle | 1st Fault | 2nd Fault | Transient Current at 1st Fault/A [L1 L2 L3 L4] | Transient Current at 2nd Fault/A [L1 L2 L3 L4] | Transient Method Results | Phase Ahead at Steady-State [L1 L2 L3 L4] | Steady-State Method Results | Wheel Cut |
|---|---|---|---|---|---|---|---|---|
| 90° | L2 Wet grass A | L2 750 Ω C | [0.28 −4.44 0.61 0.27] | [0.20 6.78 8.39 0.28] | L2 | [61.57°/94.61° 60.04°] | L3 | / |
| 0° | L1 Dry grass A | L2 1000 Ω B | [9.74 −5.12 −1.86 −0.35] | [12.23 1.61 3.06 0.78] | L1 | [/105.85° 86.32° 86.38°] | L2 | / |
| 30° | L2 Dry grass B | L3 2000 Ω A | [0.42 −6.40 5.39 0.43] | [−0.16 −17.01 0.90 −0.73] | L2, L3 | / | / | / |
| 60° | L3 Dry grass C | L1 500 Ω B | [0.31 5.67 −7.24 0.14] | [23.16 −18.76 −9.91 −2.16] | L3, L1 | / | / | / |
| 90° | L4 Dry grass A | L1 750 Ω C | [0.10 3.26 1.57 −3.08] | [−9.71 12.28 4.27 7.79] | L4, L1 | / | / | / |
| 0° | L1 Cement A | L2 2500 Ω B | [7.42 −3.57 −1.42 −0.33] | [7.21 5.38 2.66 0.54] | L1 | [/91.37° 78.29° 79.92°] | / | L2 |
| 30° | L2 Cement B | L3 1500 Ω C | [0.35 −5.25 4.50 0.66] | [−0.22 −11.19 −3.77 −0.12] | L2 | [82.74°/109.72° 82.14°] | L3 | / |
| 60° | L3 Cement C | L4 2000 Ω A | [0.13 3.22 −3.39 0.28] | [−0.37 −8.06 −6.48 6.92] | L3, L4 | / | / | / |
| 90° | L4 Cement A | L1 750 Ω B | [−0.33 −3.78 −4.20 8.39] | [11.72 −2.65 −0.83 −0.25] | L4, L1 | / | / | / |
| 0° | L1 Wet grass A | L3 1000 Ω B | [4.39 −2.03 −2.20 −0.17] | [2.03 11.6 −7.84 0.98] | L1, L3 | / | / | / |
| 30° | L2 Wet grass B | L1 750 Ω B | [0.29 −4.51 3.83 0.29] | [−10.21 −5.11 −1.11 −1.12] | L1 | [95.73°/80.45° 83.73°] | L1 | / |
| 60° | L3 Wet grass C | L2 1500 Ω B | [0.23 2.66 −3.17 0.23] | [−0.61 −11.00 −0.01 −0.77] | L3 | [83.73° 92.72°/82.78°] | / | L2 |
| Initial Phase Angle | 1st Fault | 2nd Fault | Transient Current at 1st Fault/A [L1 L2 L3 L4] | Transient Current at 2nd Fault/A [L1 L2 L3 L4] | Transient Method Results | Phase Ahead at Steady-State [L1 L2 L3 L4] | Steady-State Method Results | Wheel Cut |
|---|---|---|---|---|---|---|---|---|
| 0° | L1 750 Ω C | L2 Wet grass A | [8.36 −4.44 −2.11 −0.55] | [3.19 2.49 0.73 0.06] | L1 | [80.08° 96.83°/87.07°] | L2 | / |
| 0° | L1 1000 Ω B | L4 Dry grass A | [−11.00 4.71 4.13 0.41] | [−8.32 −10.05 −4.61 11.60] | L1, L4 | / | / | / |
| 0° | L1 2000 Ω C | L2 Dry grass B | [3.11 −1.45 −1.54 −0.12] | [2.89 −4.47 6.69 0.55] | L1, L2 | / | / | / |
| 30° | L2 500 Ω A | L3 Dry grass C | [−0.06 4.46 −2.83 −1.37] | [0.20 16.73 3.44 0.33] | L2 | [65.92°/96.17° 62.19°] | L3 | / |
| 30° | L2 750 Ω B | L4 Dry grass A | [0.46 −7.50 5.56 0.89] | [−0.48 −20.23 −6.21 30.97] | L2, L4 | / | / | / |
| 30° | L2 1000 Ω C | L1 Cement A | [0.03 −0.14 0.14 0.01] | [6.42 −2.23 −5.44 −0.37] | L2, L1 | / | / | / |
| 60° | L3 1000 Ω A | L2 Cement B | [−0.52 −6.13 7.23 −0.66] | [0.45 5.86 13.82 0.62] | L3 | [46.27° 93.30 °/47.49°] | / | L2 |
| 60° | L3 1500 Ω B | L1 Cement C | [0.05 1.92 −2.30 0.17] | [−6.84 −0.74 −1.10 7.29] | L3, L4 | / | / | / |
| 60° | L3 2000 Ω C | L4 Cement A | [0.16 1.90 −2.17 0.21] | [−0.54 −7.92 −2.02 10.11] | L3, L4 | / | / | / |
| 90° | L4 500 Ω A | L1 Wet grass A | [−0.26 −6.20 −1.69 8.05] | [0.62 −3.72 −1.58 −1.37] | L4, L1 | / | / | / |
| 90° | L4 1000 Ω B | L2 Wet grass B | [0.42 4.34 1.56 −5.22] | [−12.15 13.11 −2.90 −6.59] | L4, L2 | / | / | / |
| 90° | L4 1500 Ω C | L3 Wet grass C | [0.25 5.42 2.88 −6.47] | [0.15 −8.03 1.68 −3.47] | L4 | [90.66° 85.75° 94.45°/] | L3 | / |
| No. | Test Project | F1/Ω | F2/Ω |
|---|---|---|---|
| 1 | The 2nd grounding occurs | 60 | 60 |
| 2 | before the 1st grounding line | 60 | 3000 |
| 3 | trips (same phase) | 3000 | 60 |
| 4 | The 2nd grounding occurs | 60 | 2000 |
| 5 | before the 1st grounding line | 60 | 3000 |
| 6 | trips (different phase) | 3000 | 60 |
| 7 | The 2nd grounding occurs after | 60 | 60 |
| 8 | the 1st grounding line trips | 60 | 3000 |
| 9 | (same phase) | 3000 | 60 |
| 10 | The 2nd grounding occurs after | 60 | 2000 |
| 11 | the 1st grounding line trips | 60 | 3000 |
| 12 | (different phase) | 3000 | 60 |
| Line No. | Transient Zero-Sequence Current for Each Line of the 1st Ground Fault/A | Transient Zero-Sequence Current for Each Line of the 2nd Ground Fault/A |
|---|---|---|
| 163 | 0.876 | −0.272 |
| 122 | 2.408 | −0.69 |
| 165 | 1.553 | −0.388 |
| 124 | 0.639 | −0.162 |
| 125 | 0.589 | −0.224 |
| 126 | 0.576 | −0.271 |
| 171 | −14.16 | −13.04 |
| 128 | 1.923 | −0.51 |
| 141 | 1.055 | −0.328 |
| 134 | 2.238 | −0.65 |
| 167 | 2.207 | 14.15 |
| r | Transient Zero-Sequence Current for Each Line of the 1st Ground Fault/A | Transient Zero-Sequence Current for Each Line of the 2nd Ground Fault/A |
|---|---|---|
| 179 | 0.119 | 0.353 |
| 114 | 0.761 | −14.16 |
| 115 | 0.380 | 0.967 |
| 189 | 0.496 | 1.671 |
| 193 | 0.494 | 1.472 |
| 178 | 0.507 | 1.22 |
| 180 | 0.147 | 0.521 |
| 188 | −9.252 | 12.49 |
| 190 | 0.289 | 0.68 |
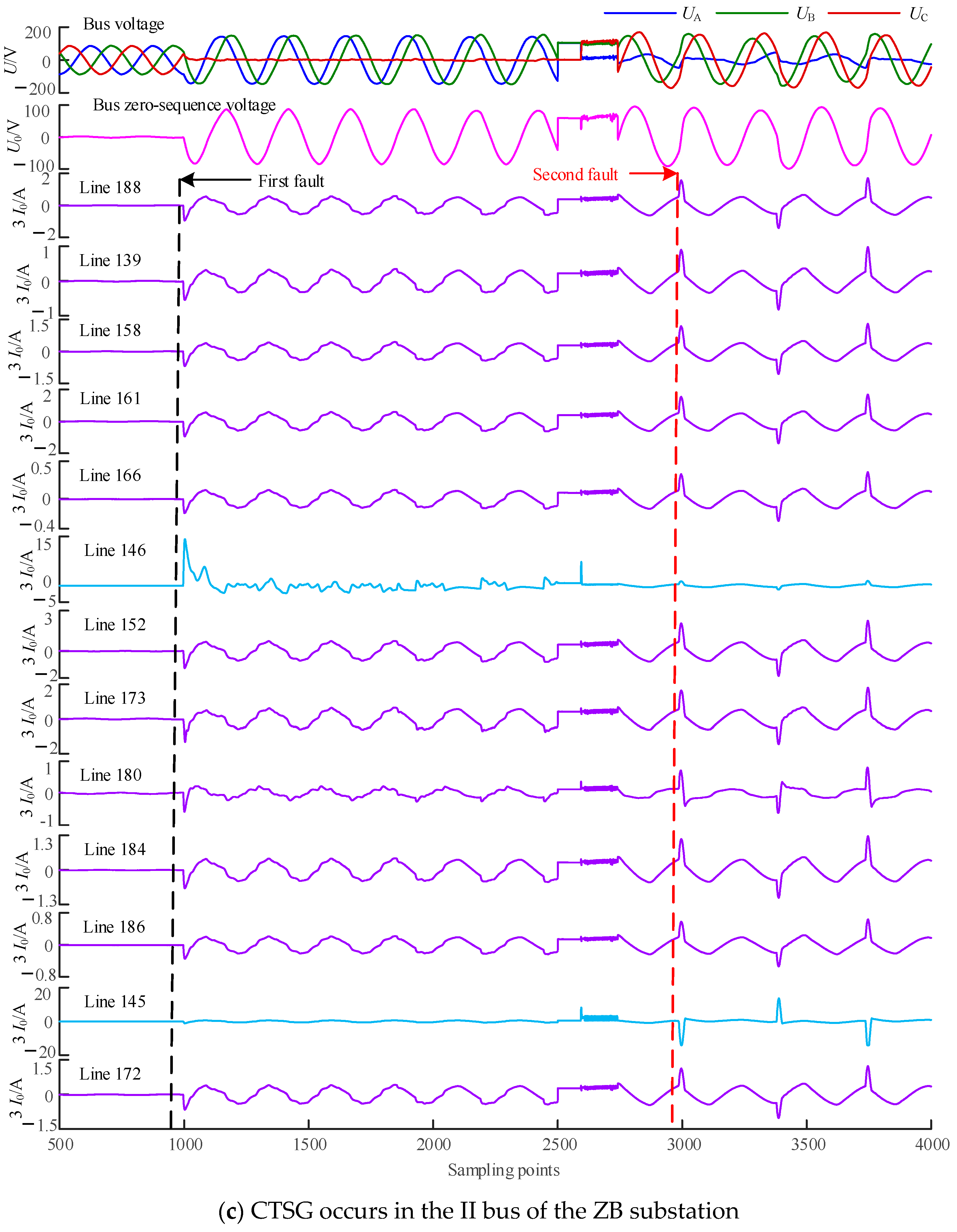
| Line No. | Transient Zero-Sequence Current for Each Line of the 1st Ground Fault/A | Transient Zero-Sequence Current for Each Line of the 2nd Ground Fault/A |
|---|---|---|
| 188 | −0.94 | 1.398 |
| 139 | −0.415 | 0.835 |
| 158 | −0.616 | 1.124 |
| 161 | −0.924 | 1.496 |
| 166 | −0.162 | 0.322 |
| 146 | 14.15 | 1.339 |
| 152 | −1.234 | 1.684 |
| 173 | −0.863 | 1.642 |
| 180 | −0.438 | 0.709 |
| 184 | −0.687 | 1.165 |
| 186 | −0.294 | 0.544 |
| 145 | −0.703 | −13.93 |
| 172 | −0.575 | 1.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, J.; Zhang, Z.; Ren, S. A Novel Method for Line Selection for Cross-Line Two-Point Successive Grounding Faults Utilizing Transient and Steady-State Information. Energies 2024, 17, 950. https://doi.org/10.3390/en17040950
Wang Y, Liu J, Zhang Z, Ren S. A Novel Method for Line Selection for Cross-Line Two-Point Successive Grounding Faults Utilizing Transient and Steady-State Information. Energies. 2024; 17(4):950. https://doi.org/10.3390/en17040950
Chicago/Turabian StyleWang, Yizhao, Jian Liu, Zhihua Zhang, and Shuangxue Ren. 2024. "A Novel Method for Line Selection for Cross-Line Two-Point Successive Grounding Faults Utilizing Transient and Steady-State Information" Energies 17, no. 4: 950. https://doi.org/10.3390/en17040950
APA StyleWang, Y., Liu, J., Zhang, Z., & Ren, S. (2024). A Novel Method for Line Selection for Cross-Line Two-Point Successive Grounding Faults Utilizing Transient and Steady-State Information. Energies, 17(4), 950. https://doi.org/10.3390/en17040950





