Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle
Abstract
1. Introduction
2. Motivation and Applications
3. Mathematical Modelling
3.1. Governing Equations
- At channel inlet, u = 1, v = 0, θ = 0.
- At the bottom and inclined wall of the cavity (hot wall), θ = 1.
- At adiabatic walls, ∂θ/∂n = 0; where n refer to normal direction
3.2. Numerical Investigation
3.2.1. The Procedure
3.2.2. Grid Independence Test
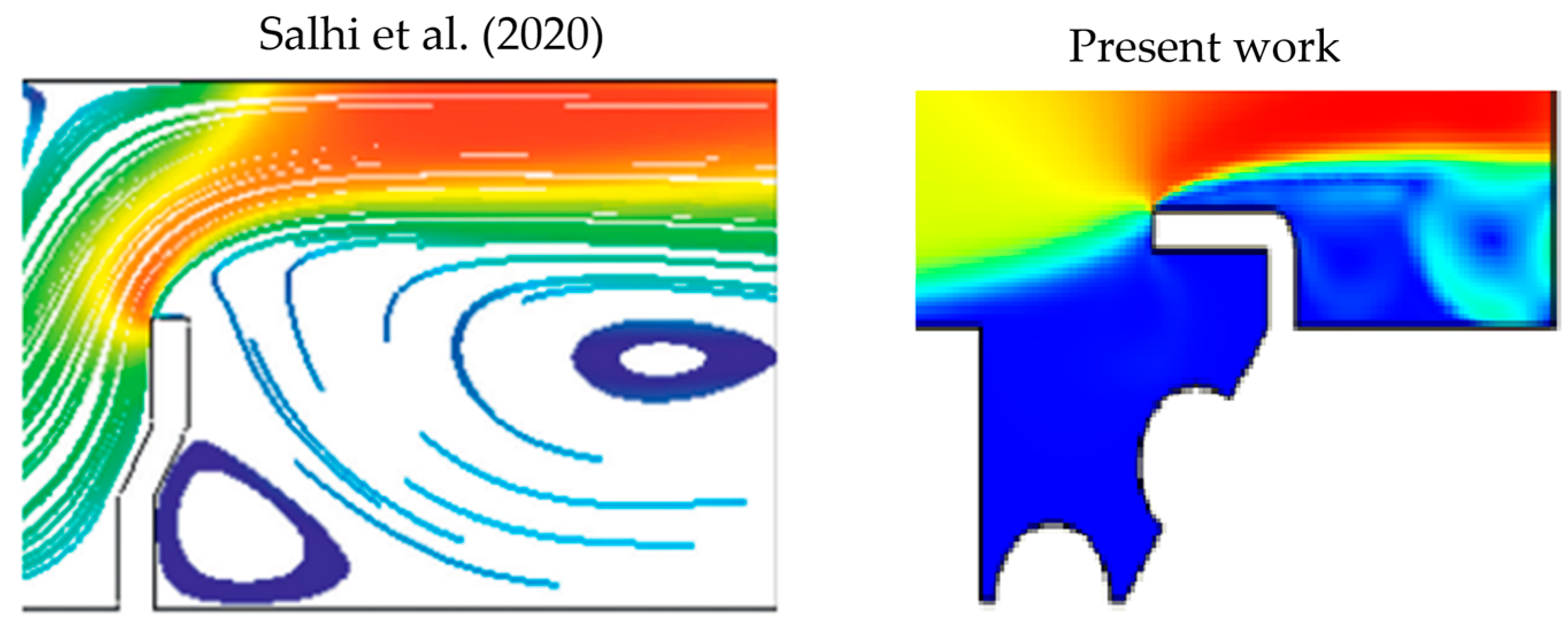
3.2.3. Validation of the Results
4. Results and Discussion
5. Conclusions
- (1)
- Analysis reveals dominant heat transfer mechanisms: convection within the duct, dispersion at the cavity’s base, and convection in the contact zone. Temperature gradients and flow velocities (e.g., 10–150 cm/s) illustrate the complex interplay of these mechanisms.
- (2)
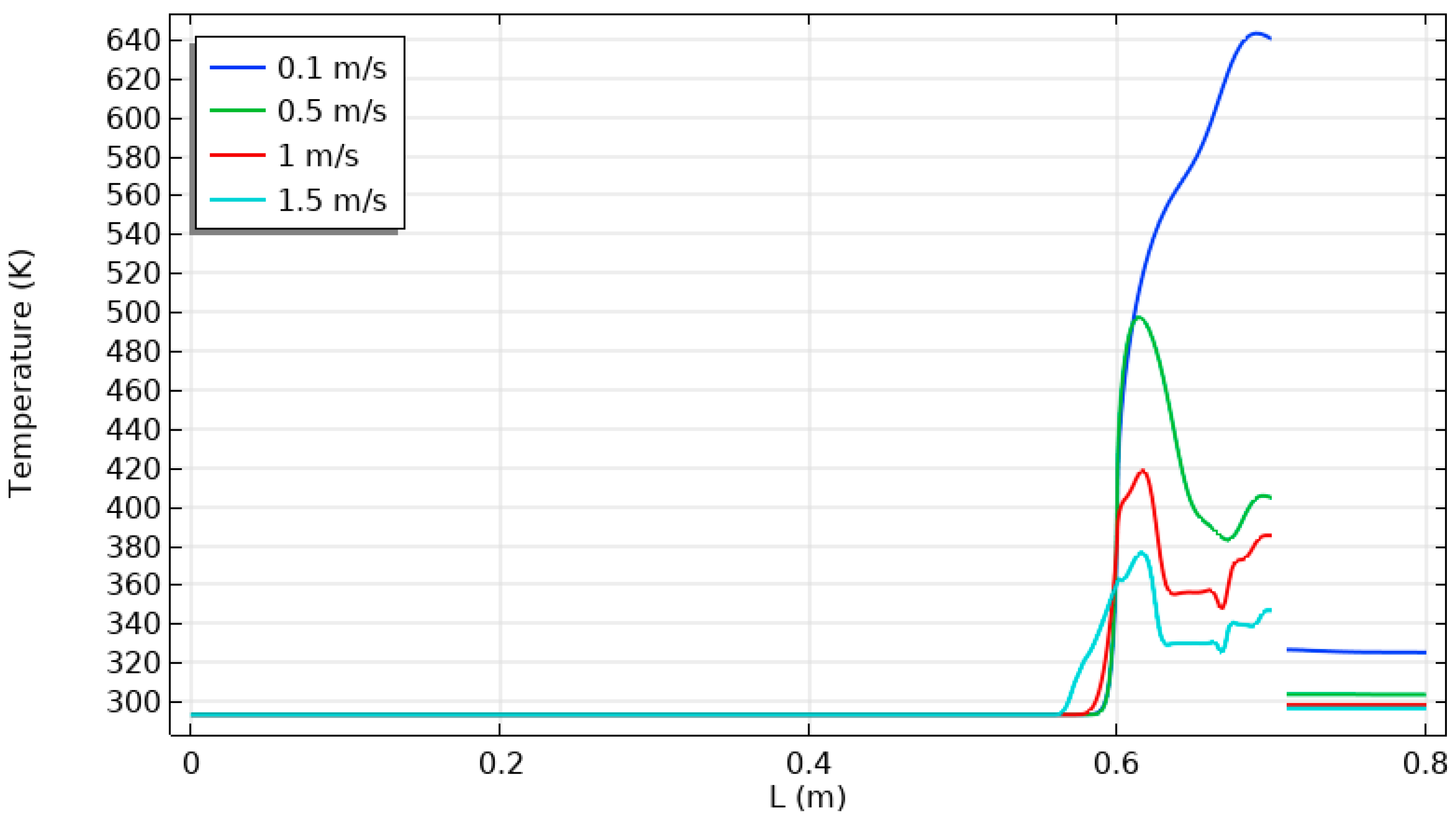
- Varying inlet air velocity (10–150 cm/s) significantly alters temperature fields and flow dynamics. Temperature profiles show shifts with increased velocity, impacting both forced and natural convection processes. Thus, the cavity neck temperature ranges from 380 to 640 K, with inflow air velocities varying from 0.1 to 1.5 m/s, respectively.
- (3)
- The presence of a 90° unheated baffle enhances recirculation and modifies velocity profiles. Pressure and velocity distributions demonstrate how the baffle alters flow characteristics, improving heat transfer efficiency.
- (4)
- Thermal sources induce recirculating air zones and buoyancy effects, influencing flow directionality. Temperature gradients and heat transfer rates highlight the spatial distribution of thermal energy (e.g., 20 W sources).
- (5)
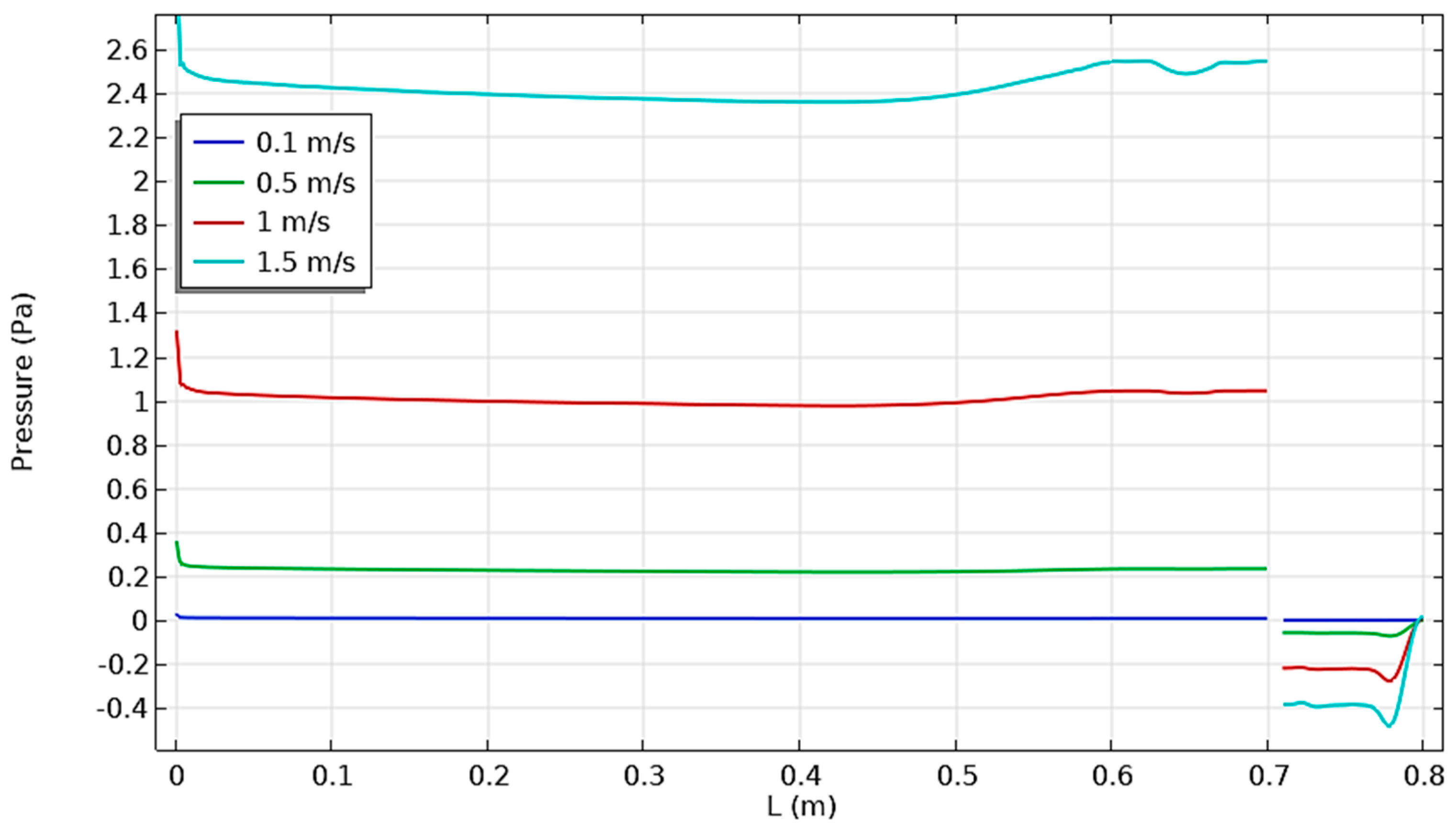
- The cavity neck pressure varies from 0.01 to 2.5 Pa, with inflow air velocities changing from 0.1 to 1.5 m/s, respectively.
- (6)
- Incorporating a 90° unheated baffle optimises heat transfer by promoting recirculation. Pressure profiles and Nusselt numbers validate design interventions, ensuring efficient heat transfer and temperature uniformity. As the input air velocity increases, more heat is transported from the thermal source into the airflow, lowering the temperature.
- (7)
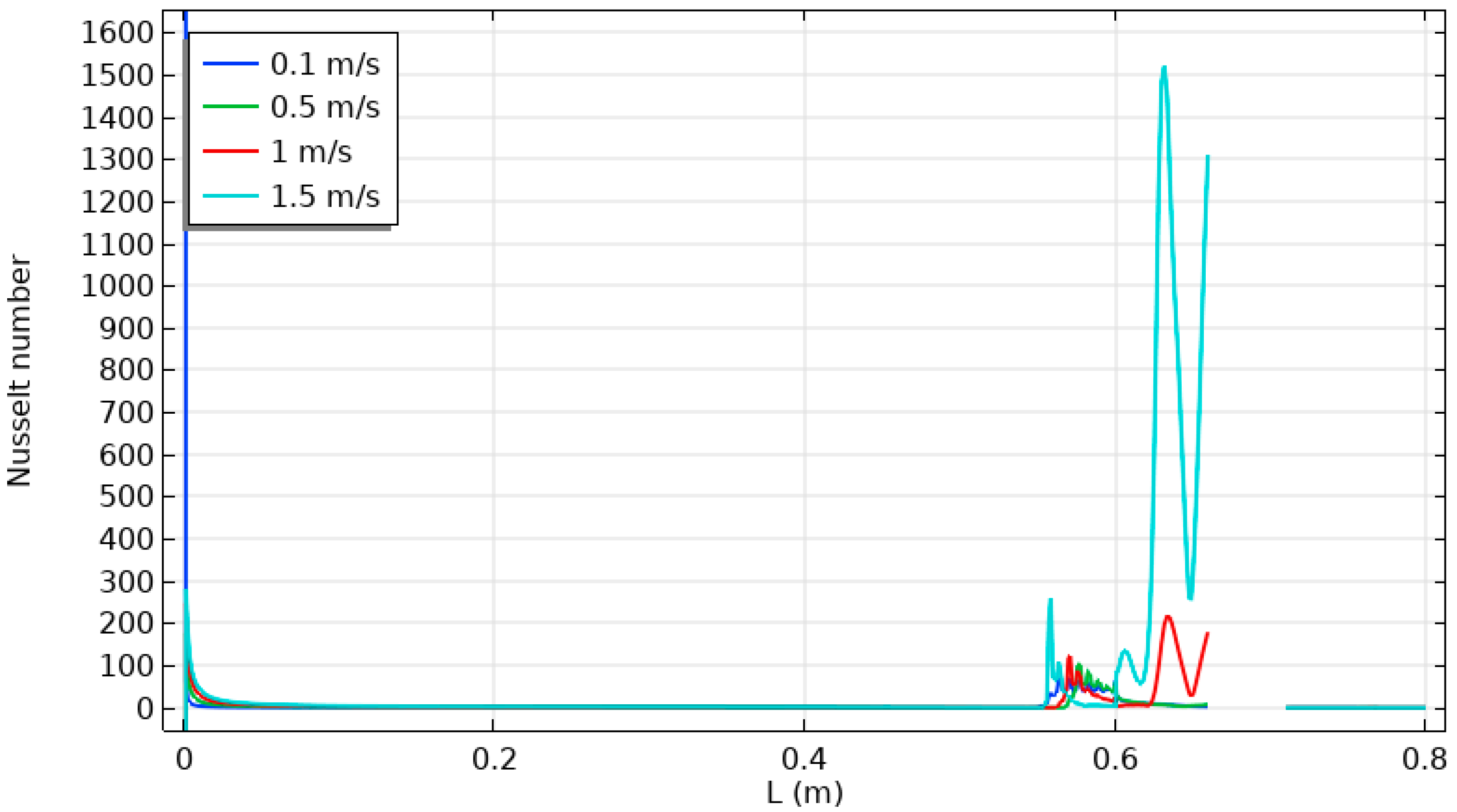
- The mean Nusselt number is obtained at about 1500 when the inflow velocity reaches 1.5 m/s.
- (8)
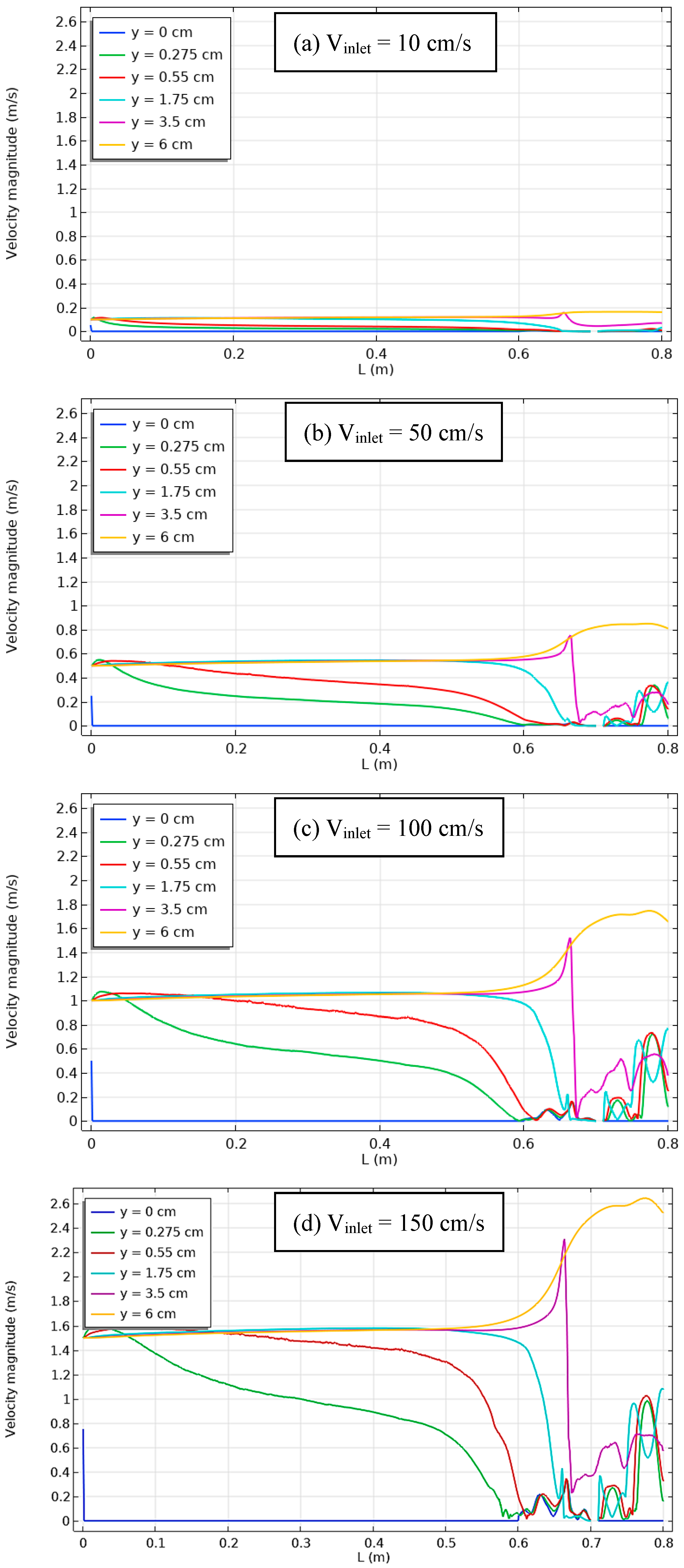
- Shear force from the channel wall had the largest impact on the local velocity distribution near the channel inlet, where it suddenly broke down. In the middle of the interface, it peaked, varied, and finally dropped to its lowest position towards the end of the cavity, where air recirculation was at work.
- (9)
- There is a pressure difference when the channel meets the hollow, higher than anywhere else along the channel’s path.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-aswadi, A.A.; Mohammed, H.A.; Shuaib, N.H.; Campo, A. Laminar Forced Convection Flow over a Backward Facing Step Using Nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 950–957. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Al-Shamani, A.N.; Sheriff, J.M. Thermal and Hydraulic Characteristics of Turbulent Nanofluids Flow in a Rib–Groove Channel. Int. Commun. Heat Mass Transf. 2012, 39, 1584–1594. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eriksen, V.L.; Olson, R.M.; Eckert, E.R.G. Laminar Separation, Reattachment, and Transition of the Flow over a Downstream-Facing Step. J. Fluids Eng. 1970, 92, 732–739. [Google Scholar] [CrossRef]
- Ilis, G.G.; Mobedi, M.; Öztop, H.F. Heat Transfer Reduction Due to a Ceiling-Mounted Barrier in an Enclosure with Natural Convection. Heat Transf. Eng. 2011, 32, 429–438. [Google Scholar] [CrossRef]
- Louhibi, A.M.; Salhi, N.; Bouali, H.; Amghar, K. Numerical Analysis of Heat Transfer in a Channel with Inclined Baffles. Res. Invent. Int. J. Eng. Sci 2015, 4, 12–23. [Google Scholar]
- Yu, L.; Xue, M.-A.; Zhu, A. Numerical Investigation of Sloshing in Rectangular Tank with Permeable Baffle. J. Mar. Sci. Eng. 2020, 8, 671. [Google Scholar] [CrossRef]
- Mahapatra, S.K.; Sarkar, A.; Sarkar, A. Numerical Simulation of Opposing Mixed Convection in Differentially Heated Square Enclosure with Partition. Int. J. Therm. Sci. 2007, 46, 970–979. [Google Scholar] [CrossRef]
- Eleiwi, M.A.; Rashid, F.L.; Khalaf, A.F.; Tuama, S.A. Numerical Investigation of Conjugate Heat Transfer Between Spherical Solid Body and Fluid. Math. Model. Eng. Probl. 2022, 9, 491–497. [Google Scholar] [CrossRef]
- Rahman, M.; Parvin, S.; Rahim, N.; Hasanuzzaman, M.; Saidur, R. Simulation of mixed convection heat transfer in a horizontal channel with an open cavity containing a heated hollow cylinder. Heat Transf.—Asian Res. 2012, 41, 339–353. [Google Scholar] [CrossRef]
- Salhi, J.E.; Amghar, K.; Bouali, H.; Salhi, N. Combined Heat and Mass Transfer of Fluid Flowing through Horizontal Channel by Turbulent Forced Convection. Model. Simul. Eng. 2020, 2020, 1453893. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Safaei, M.R. Combination Effect of Baffle Arrangement and Hybrid Nanofluid on Thermal Performance of a Shell and Tube Heat Exchanger Using 3-D Homogeneous Mixture Model. Mathematics 2021, 9, 881. [Google Scholar] [CrossRef]
- Valencia, A.; Calderon, W. Convective Heat Transfer in Plane Channels with Inline Mounted Rectangular Bars. Int. J. Numer. Methods Heat Fluid Flow 2004, 14, 866–878. [Google Scholar] [CrossRef]
- Kumar, S.; Vengadesan, S. The Effect of Fin Oscillation in Heat Transfer Enhancement in Separated Flow over a Backward Facing Step. Int. J. Heat Mass Transf. 2019, 128, 954–963. [Google Scholar] [CrossRef]
- Stiriba, Y.; Grau, F.; Ferre, J.; Vernet, A. A numerical study of three-dimensional laminar mixed convection past an open cavity. Int. J. Heat Mass Transf. 2010, 53, 4797–4808. [Google Scholar] [CrossRef]
- Thao, P.B.; Truyen, D.C.; Phu, N.M. CFD Analysis and Taguchi-Based Optimization of the Thermohydraulic Performance of a Solar Air Heater Duct Baffled on a Back Plate. Appl. Sci. 2021, 11, 4645. [Google Scholar] [CrossRef]
- Du, S.-Q.; Bilgen, E.; Vasseur, P. Mixed Convection Heat Transfer in Open Ended Channels with Protruding Heaters. Heat Mass Transf. 1998, 34, 263–270. [Google Scholar] [CrossRef]
- How, S.P.; Hsu, T.H. Transient Mixed Convection in a Partially Divided Enclosure. Comput. Math. Appl. 1998, 36, 95–115. [Google Scholar] [CrossRef]
- Hsu, T.H.; How, S.P. Mixed Convection in an Enclosure with a Heat-Conducting Body. Acta Mech. 1999, 133, 87–104. [Google Scholar] [CrossRef]
- Chung, C.-K.; Wu, C.-Y.; Shih, T.R. Effect of Baffle Height and Reynolds Number on Fluid Mixing. Microsyst. Technol. 2008, 14, 1317–1323. [Google Scholar] [CrossRef]
- Radhakrishnan, T.V.; Joseph, G.; Balaji, C.; Venkateshan, S.P. Effect of Baffle on Convective Heat Transfer from a Heat Generating Element in a Ventilated Cavity. Heat Mass Transf. 2009, 45, 1069–1082. [Google Scholar] [CrossRef]
- Asif, M.R.; Hossain, M.S.; Hossain, K.A. Heat Transfer in a Rectangular Enclosure with Baffles. ARPN J. Eng. Appl. Sci. 2011, 6, 29–41. [Google Scholar]
- Sripattanapipat, S.; Promvonge, P. Numerical Analysis of Laminar Heat Transfer in a Channel with Diamond-Shaped Baffles. Int. Commun. Heat Mass Transf. 2009, 36, 32–38. [Google Scholar] [CrossRef]
- Sriromreun, P.; Thianpong, C.; Promvonge, P. Experimental and Numerical Study on Heat Transfer Enhancement in a Channel with Z-Shaped Baffles. Int. Commun. Heat Mass Transf. 2012, 39, 945–952. [Google Scholar] [CrossRef]
- Hamzah, H.K.; Ali, F.H.; Hatami, M.; Jing, D. Effect of Two Baffles on MHD Natural Convection in U-Shape Superposed by Solid Nanoparticle Having Different Shapes. J. Appl. Comput. Mech. 2020, 6, 1200–1209. [Google Scholar]
- Sabbar, W.A.; Ismael, M.A.; Almudhaffar, M. Fluid-Structure Interaction of Mixed Convection in a Cavity-Channel Assembly of Flexible Wall. Int. J. Mech. Sci. 2018, 149, 73–83. [Google Scholar] [CrossRef]
- Heshmati, A.; Mohammed, H.A.; Darus, A.N. Mixed Convection Heat Transfer of Nanofluids over Backward Facing Step Having a Slotted Baffle. Appl. Math. Comput. 2014, 240, 368–386. [Google Scholar] [CrossRef]
- Ashraf, M.; Ullah, Z.; Zia, S.; Alharbi, S.O.; Baleanu, D.; Khan, I. Analysis of the Physical Behavior of the Periodic Mixed-Convection Flow around a Nonconducting Horizontal Circular Cylinder Embedded in a Porous Medium. J. Math. 2021, 2021, 8839146. [Google Scholar] [CrossRef]
- Yaseen, D.T.; Ismael, M.A. Effect of Deformable Baffle on the Mixed Convection of Non-Newtonian Fluids in A Channel-Cavity. Basrah J. Eng. Sci. 2020, 20, 18–26. [Google Scholar] [CrossRef]
- Yasina, N.J.; Jehhefb, K.A.; Shakirc, A.M. Experimental and Numerical Study of Mixed Convection in a Partially Opened Cavity with Tilted Baffle. Univ. Thi-Qar J. Eng. Sci. 2019, 10, 182–193. [Google Scholar]
- Da Silva, A.; Fontana, É.; Mariani, V.C.; Marcondes, F. Numerical Investigation of Several Physical and Geometric Parameters in the Natural Convection into Trapezoidal Cavities. Int. J. Heat Mass Transf. 2012, 55, 6808–6818. [Google Scholar] [CrossRef]
- Al-Hafidh, M.H.; Mohammed, H. Natural Convection of Nanofluid in Cylindrical Enclosure Filled with Porous Media. J. Energy Power Eng. 2013, 7, 2263–2272. [Google Scholar]
- Kumar, A.; Kim, M.-H. Convective Heat Transfer Enhancement in Solar Air Channels. Appl. Therm. Eng. 2015, 89, 239–261. [Google Scholar] [CrossRef]
- Mohammed, H.I.; Giddings, D. Natural Convection Heat and Mass Transfer in the Vertical Cylindrical Porous Channel under the Effects of Time-Periodic Boundary Condition. J. Heat Transf. 2019, 141, 122503. [Google Scholar] [CrossRef]
- Kim, K.M.; Kim, S.H.; Lim, S.T.; Kim, T.; Jerng, D.-W.; Ahn, H.S. Geometrical effect of natural convection in an air channel with a cavity at the turning section on thermal behavior and heat removal performance. Int. J. Heat Mass Transf. 2023, 203, 123792. [Google Scholar] [CrossRef]
- Kato, Y.; Guo, G.; Kamigaki, M.; Fujimoto, K.; Kawaguchi, M.; Nishida, K.; Hongou, H.; Koutoku, M.; Yokohata, H.; Sumi, S.; et al. Correlation Between Wall Heat Transfer and Characteristics of Pulsating Flow in A Rectangular Tube toward an Automobile Exhaust System. In Proceedings of the 8th World Congress on Mechanical, Chemical, and Material Engineering, Prague, Czech Republic, 31 July–2 August 2022. [Google Scholar]
- Khattak, Z.; Muhammad, H.A. Thermal analysis and parametric optimization of plate fin heat sinks under forced air convection. Therm. Sci. 2022, 26, 629–639. [Google Scholar] [CrossRef]
- Mothilal, T.; Pitchandi, K. Influence of inlet velocity of air and solid particle feed rate on holdup mass and heat transfer characteristics in cyclone heat exchanger. J. Mech. Sci. Technol. 2015, 29, 4509–4518. [Google Scholar] [CrossRef]
- Kolchanova, E.A.; Sagitov, R. Throughflow Effect on Local and Large-scale Penetrative Convection in Superposed Air-porous Layer with Internal Heat Source Depending on Solid Fraction. Microgravity Sci. Technol. 2022, 34, 52. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Mohammed, A.A.; Channapattana, S.V. Numerical Study of Convection Air Currents around a Hot Cylinder Inside a Triangular Cavity. Al-Nahrain J. Eng. Sci. 2023, 26, 102–115. [Google Scholar] [CrossRef]
- Gilago, M.C.; Mugi, V.R.; V.P., C.; S., S. Evaluating the performance of an indirect solar dryer and drying parameters of pineapple: Comparing natural and forced convection. J. Therm. Anal. Calorim. 2023, 148, 3701–3709. [Google Scholar] [CrossRef]
- Elangovan, E.; Natarajan, S.K. Convective and evaporative heat transfer coefficients during drying of ivy gourd under natural and forced convection solar dryer. Environ. Sci. Pollut. Res. 2023, 30, 10469–10483. [Google Scholar] [CrossRef]
- Osodo, B.O.; Nyaanga, D.M.; Kiplagat, J.K.; Muguthu, J. Optimum Air Velocity, Air Temperature and Maize Layer Thickness for Highest Moisture Removal Rate and Drying Efficiency in a Forced Convection Grain Dryer. Am. J. Food Sci. Technol. 2018, 6, 263–273. [Google Scholar]
- Patankar, S.V.; Liu, C.H.; Sparrow, E.M. Fully Developed Flow and Heat Transfer in Ducts Having Streamwise-Periodic Variations of Cross-Sectional Area. J. Heat Transf. 1977, 99, 180–186. [Google Scholar] [CrossRef]
- Al-Jibory, M.W.; Rashid, F.L.; Talib, S.M. Numerical Investigation of Heat Transfer Enhancement in Ribbed Elliptical Passage. J. Eng. Appl. Sci. 2018, 13, 7223–7234. [Google Scholar]
- Wang, H.; Chen, J.; Dai, P.; Zhang, F.; Li, Q. Simulation and Experimental Study of the Influence of the Baffles on Solar Chimney Power Plant System. Processes 2021, 9, 902. [Google Scholar] [CrossRef]
- Ashraf, M.; Ilyas, A.; Ullah, Z.; Abbas, A. Periodicmagnetohydrodynamic mixed convection flow along a cone embedded in a porous medium with variable surface temperature. Ann. Nucl. Energy 2022, 175, 109218. [Google Scholar] [CrossRef]
- Berner, C.; Durst, F.; McEligot, D.M. Flow Around Baffles. J. Heat Transf. 1984, 106, 743–749. [Google Scholar] [CrossRef]
- Sivakumar, V.; Sivasankaran, S. Mixed Convection in an Inclined Lid-Driven Cavity with Non-Uniform Heating on Both Sidewalls. J. Appl. Mech. Tech. Phys. 2014, 55, 634–649. [Google Scholar] [CrossRef]
- Stiriba, Y. Analysis of the flow and heat transfer characteristics for assisting incompressible laminar flow past an open cavity. Int. Commun. Heat Mass Transf. 2008, 35, 901–907. [Google Scholar] [CrossRef]
- Ashraf, M.; Ullah, Z. Effects of variable density on oscillatory flow around a non-conducting horizontal circular cylinder. AIP Adv. 2020, 10, 015020. [Google Scholar] [CrossRef]
- AL-Hafidh, M.H.; Mohammed, H.I. Numerical Investigation of Natural Convection Radiation and Magnetohydrodynamic in Vertical Porous Cylindrical Channel. J. Eng. 2011, 17, 1600–1613. [Google Scholar] [CrossRef]
- Elshafei, E.A.M.; Awad, M.M.; El-Negiry, E.; Ali, A.G. Heat Transfer and Pressure Drop in Corrugated Channels. Energy 2010, 35, 101–110. [Google Scholar] [CrossRef]
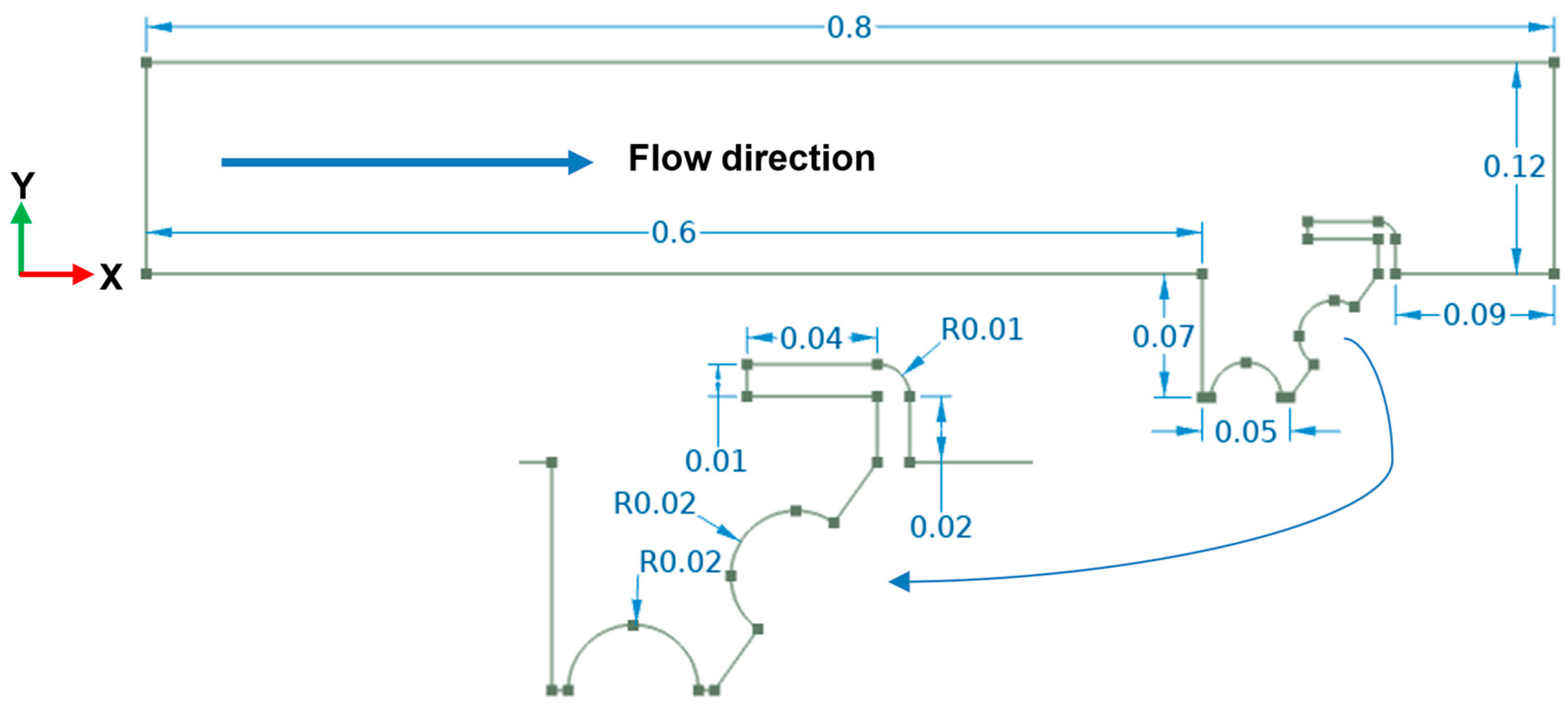












| Symbol | Value | Description |
|---|---|---|
| D | 120 mm | Tube diameter |
| L | 800 mm | Tube length |
| W | 100 mm | Cavity width |
| H | 70 mm | Height of cavity |
| wb1 | 10 mm | Baffle width |
| Lb1 | 20 mm | Baffle height |
| Lb2 | 40 mm | Baffle length |
| R | 20 mm | Heat source’s spherical radius inside cavity |
| Tin | 20 °C | Flow temperature at the inlet |
| Vin | 0.1–1.5 m/s | Inlet velocity |
| Pw | 20 W | Power of heated source |
| Number of Elements | Average Nusselt Number | |
|---|---|---|
| 5203 | 5.65 | -- |
| 9266 | 5.69 | 0.708 |
| 18,196 | 5.772 | 1.441 |
| 66,767 | 5.777 | 0.086 |
| Nusselt Number | |||
|---|---|---|---|
| Re | Exp. of Elshafei et al. [52] | Present Model | Difference |
| 3400 | 16 | 13 | −18.8% |
| 4100 | 22 | 22.5 | +2.3% |
| 5000 | 31 | 32 | +3.2% |
| 6000 | 38 | 41 | +7.9% |
| 6800 | 41 | 45 | +9.8% |
| 8000 | 50 | 53 | +6.0% |
| 9500 | 55 | 59 | +7.3% |
| Figure | Description | Key Findings |
|---|---|---|
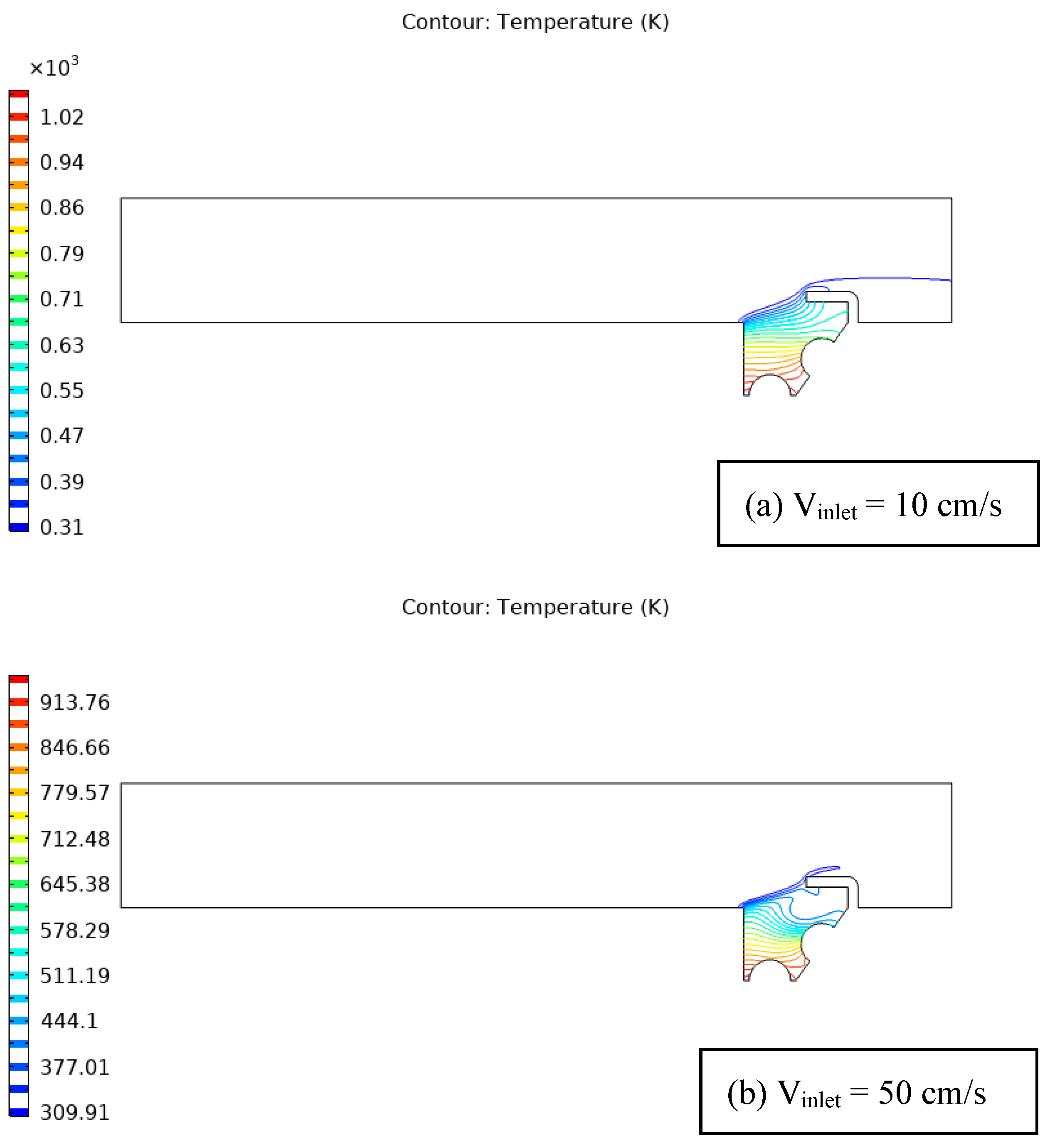
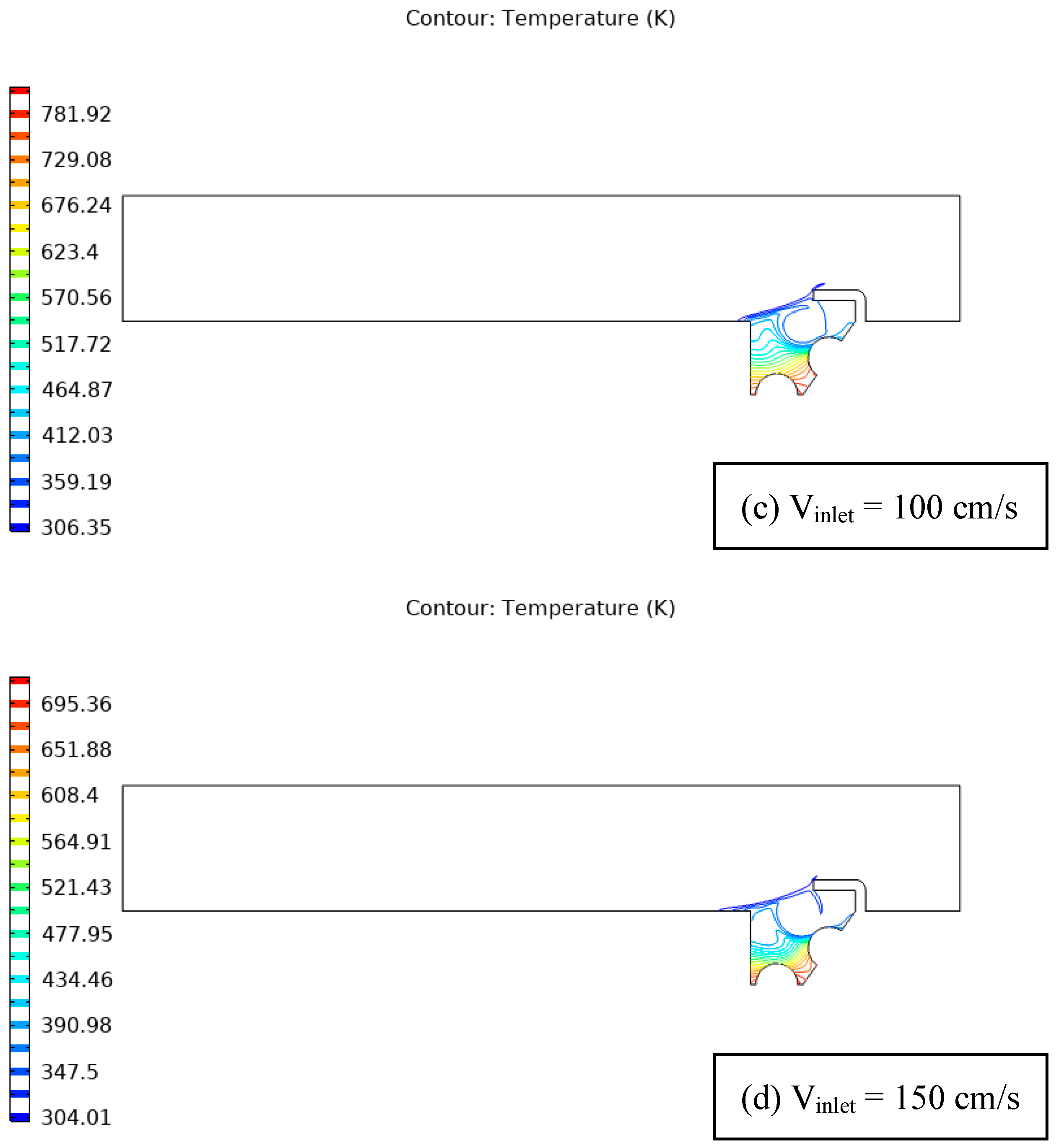
| Figure 4 | Hollow structure with open ducts, thermal energy sources, and an unheated baffle. Includes isotherm contours representing different air velocities. | Convection dominant in cavity; forced convection prevalent in channel; temperature decreases gradually from thermal sources to duct. |
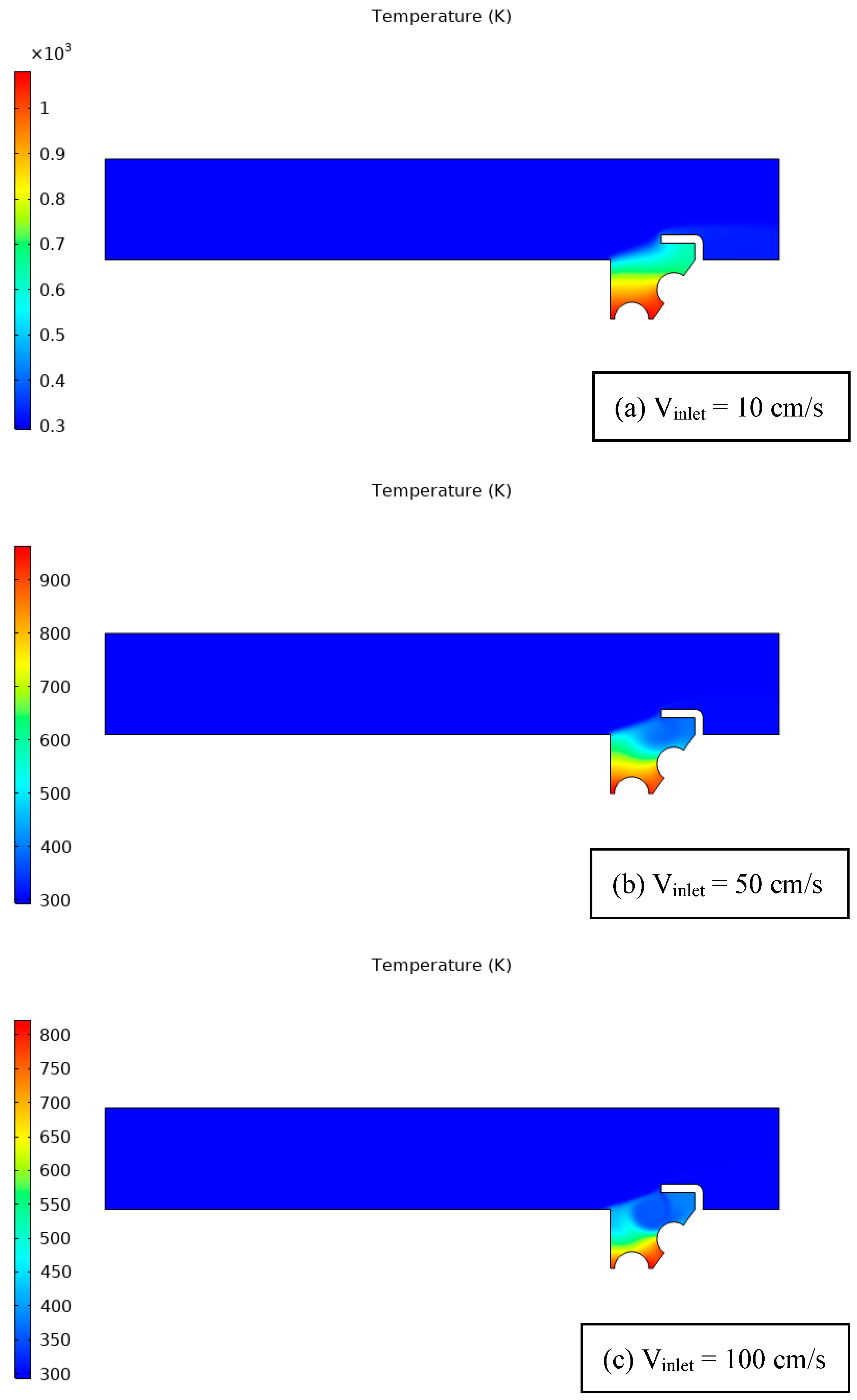
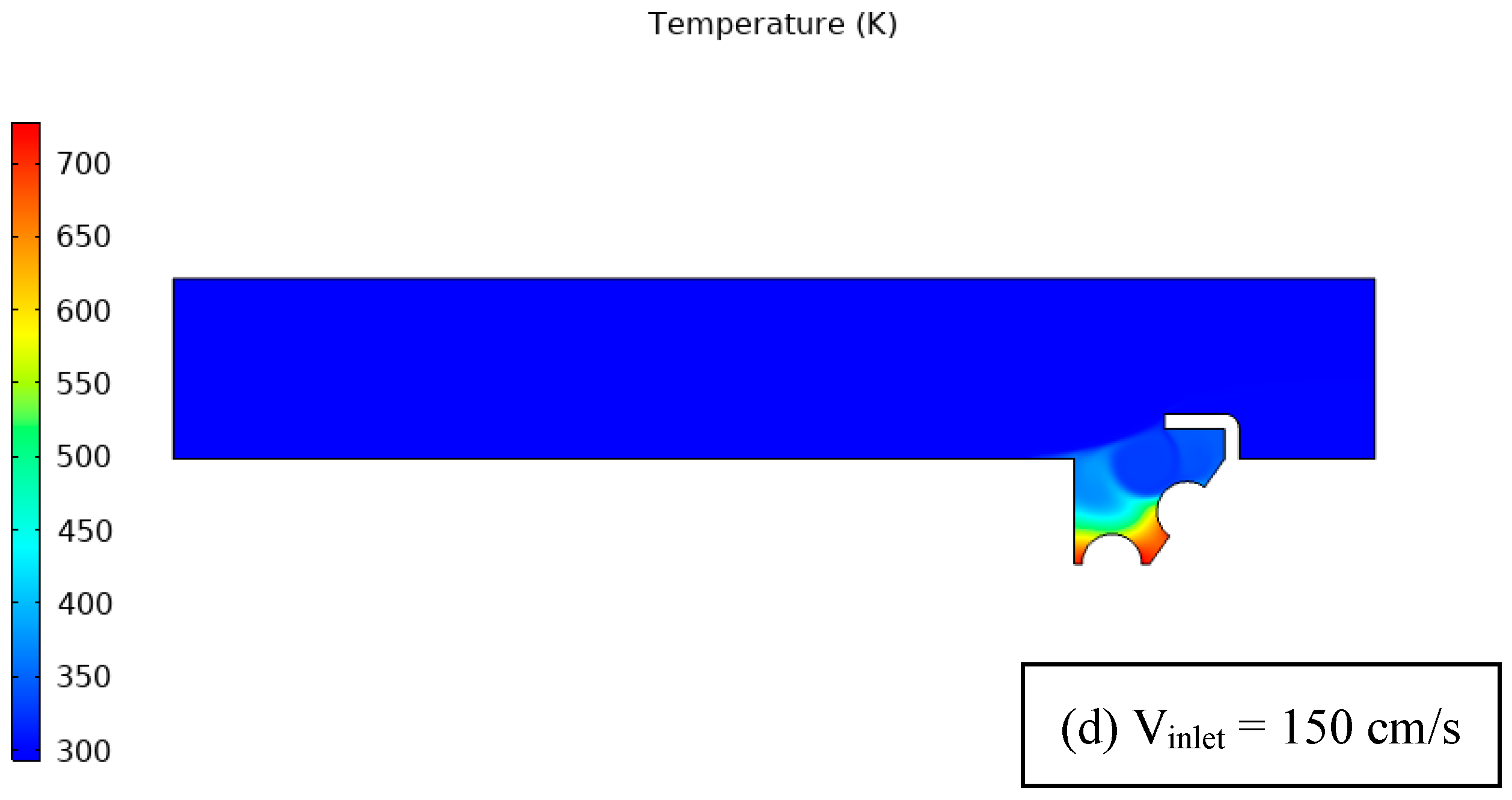
| Figure 5 | Temperature distribution at different air velocities, two thermal sources, and a 90° unheated baffle. | Higher velocities lead to more turbulent flow and improve convective heat transfer. Baffle redirects flow, affecting temperature gradients. Isotherms identify localized heating or cooling. |
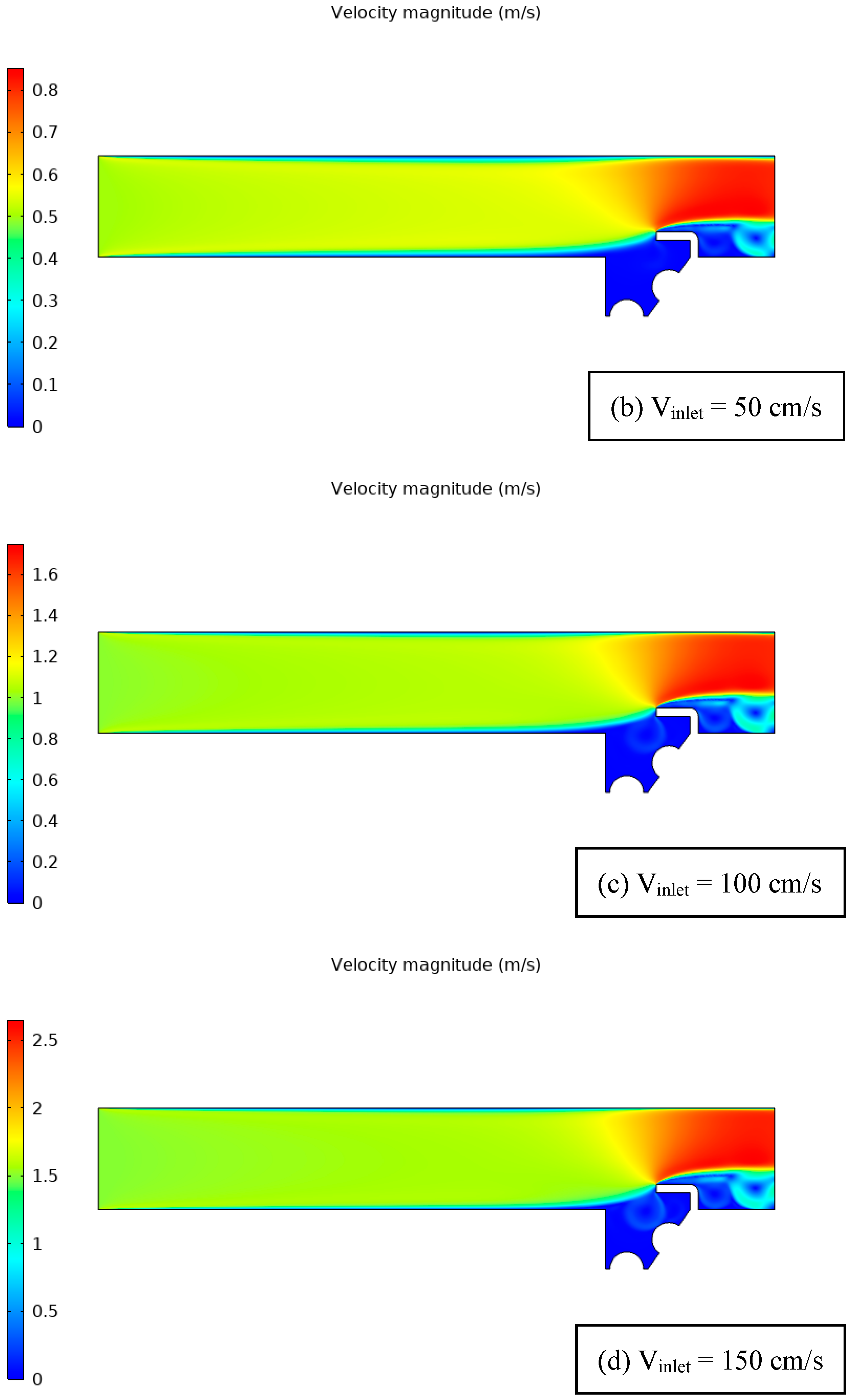
| Figure 6 | Velocity profiles with two heat sources and a 90° unheated baffle at varying air velocities. | Presence of heat sources creates recirculating air zones. Baffle enhances recirculation, improves heat transfer. |
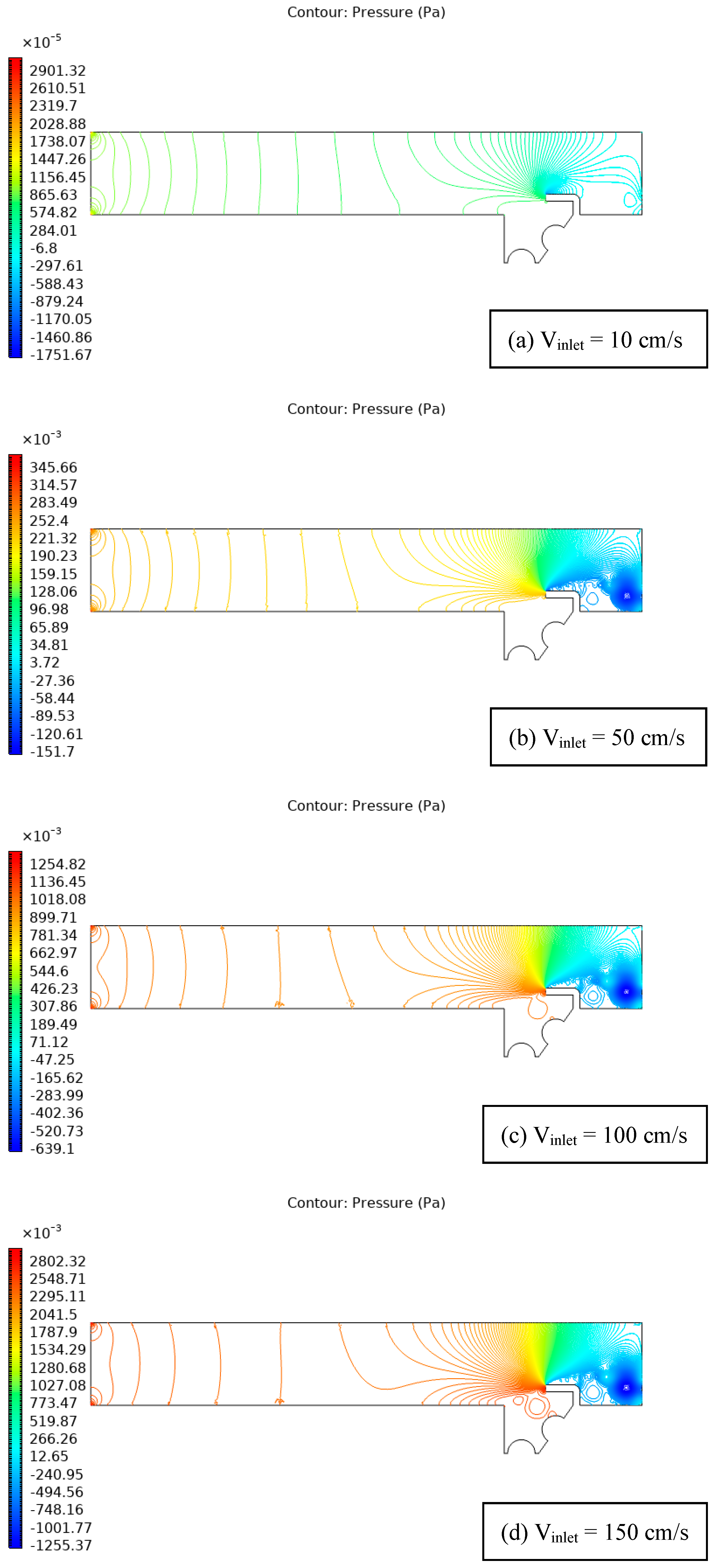
| Figure 7 | Pressure streamlines in channel-cavity system with heat sources and unheated baffle. | Baffle improves recirculation, impacting pressure distributions and flow dynamics. |
| Figure 8 | Inlet velocity contours within cavity, considering two thermal sources and unheated baffle. | Higher velocities lead to increased turbulence and more complex flow patterns. Baffle influences flow direction and velocity profiles. |
| Figure 9 | Pressure distribution along vertical axis in duct with thermal sources and unheated baffle. | Higher inlet velocities result in increased turbulence and pressure fluctuations. Baffle enhances recirculation, impacts pressure distribution. |
| Figure 10 | Temperature distribution along vertical position in cavity with thermal sources and unheated baffle. | Temperature rises with vertical position due to heat sources. Baffle influences recirculation, affects temperature distribution. |
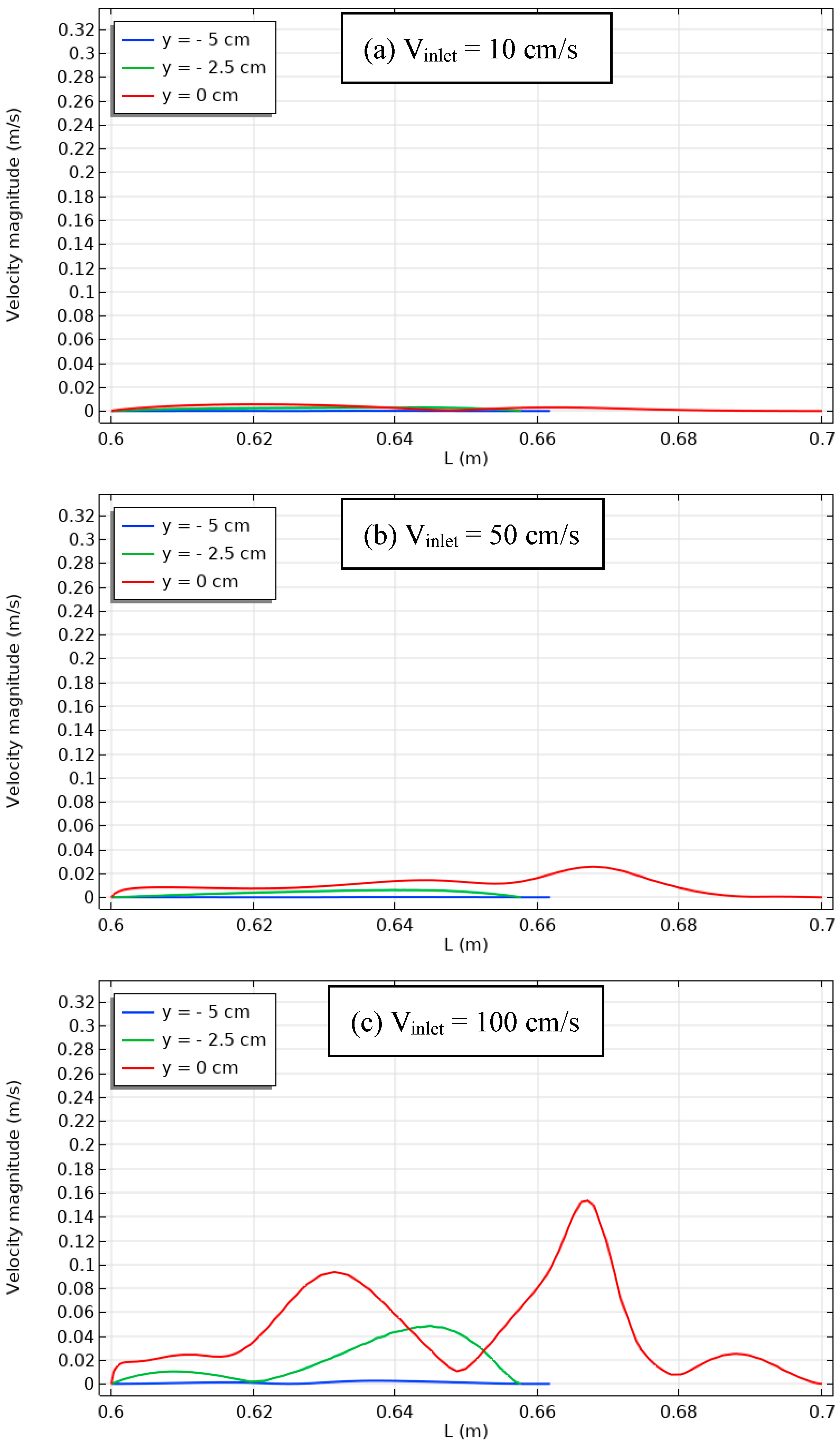
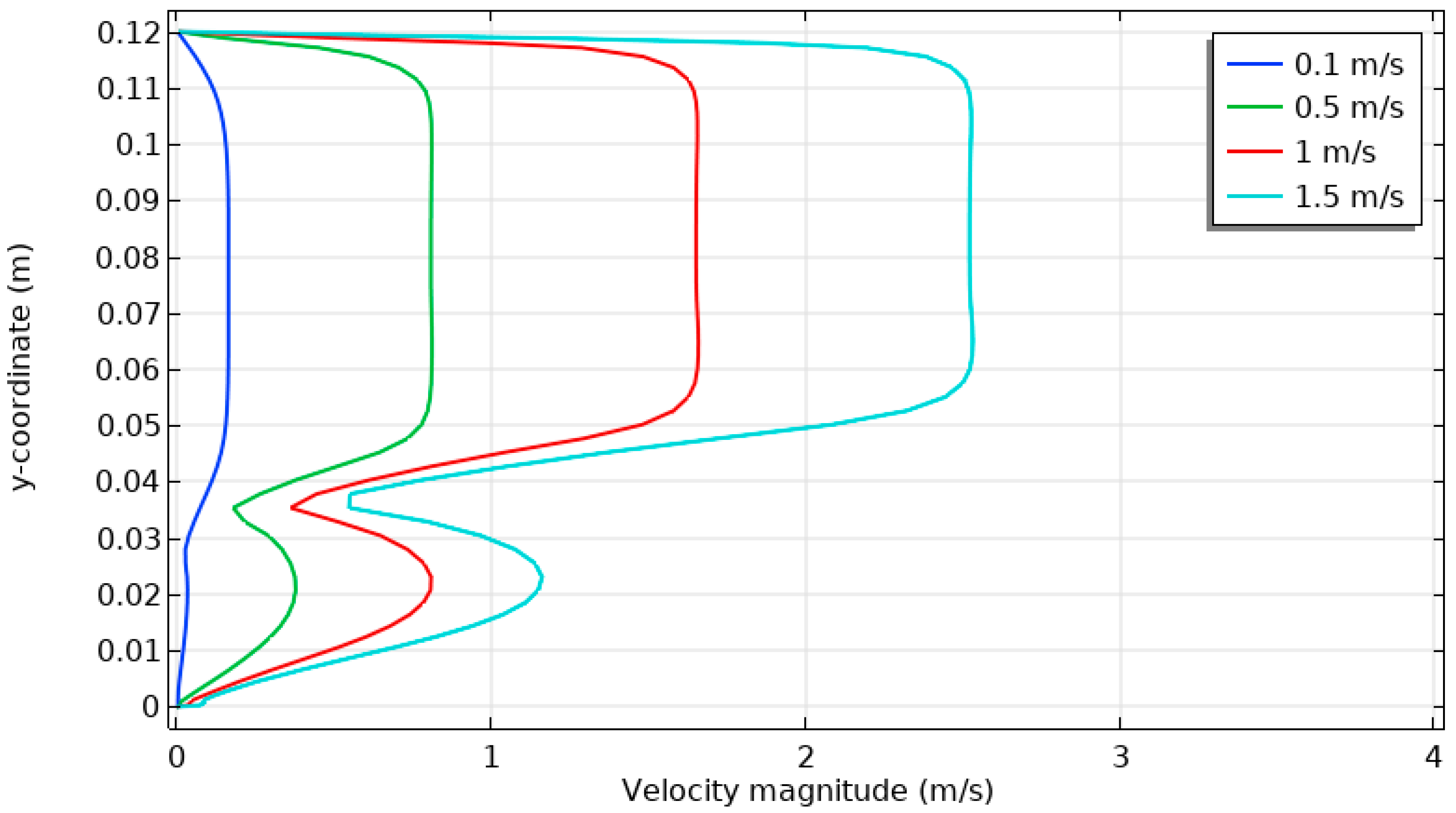
| Figure 11 | Velocity distribution at bottom section of vertical position within cavity with thermal sources and unheated baffle. | Lower velocities exhibit consistent distribution, higher velocities result in distinct velocity profiles. Baffle influences air movement. |
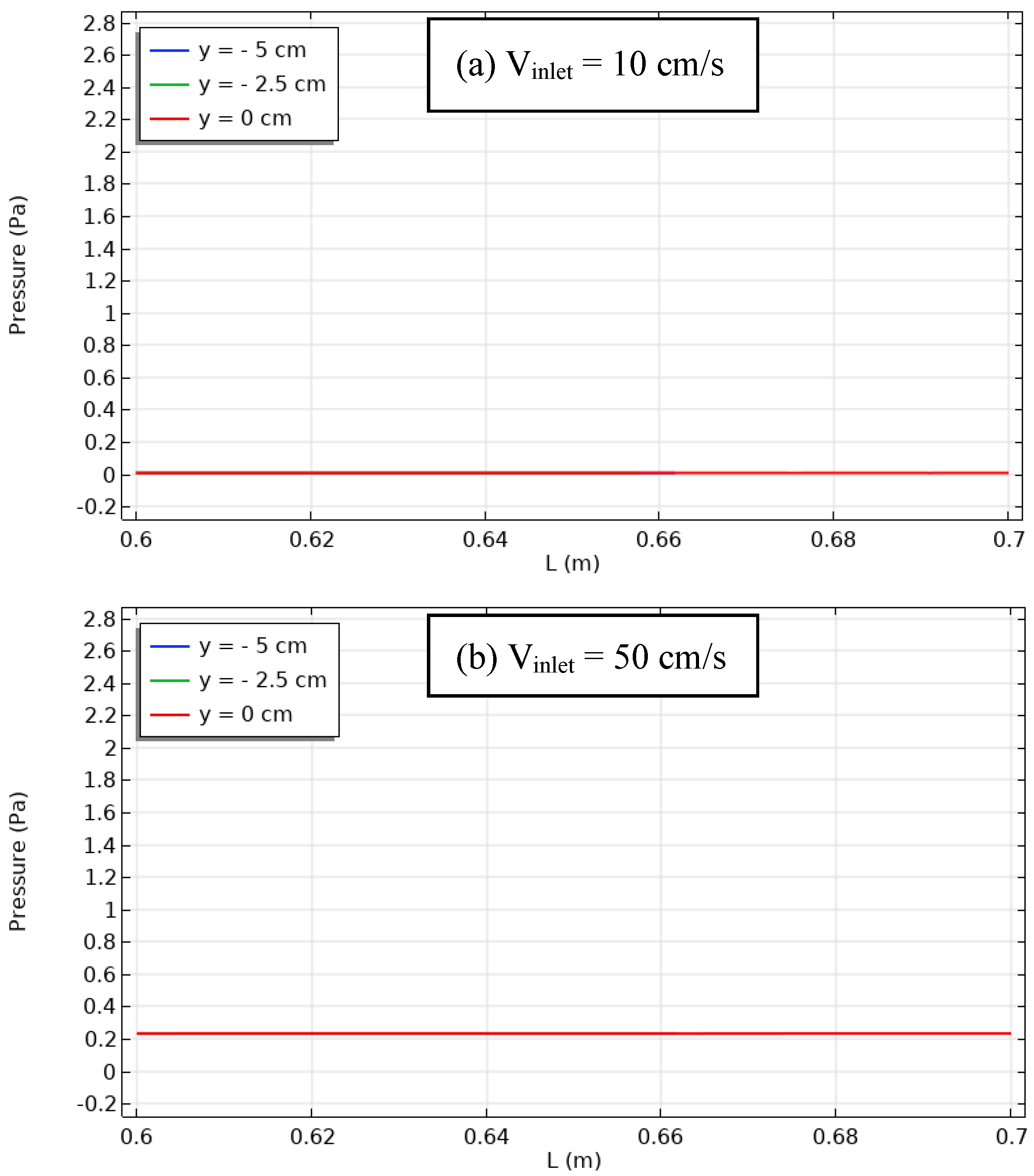
| Figure 12 | Pressure distribution over bottom section of vertical position within cavity with thermal sources and unheated baffle. | Low velocities lead to lower pressure distribution. Increased inlet velocities improve pressure distribution. Baffle affects pressure profile. |
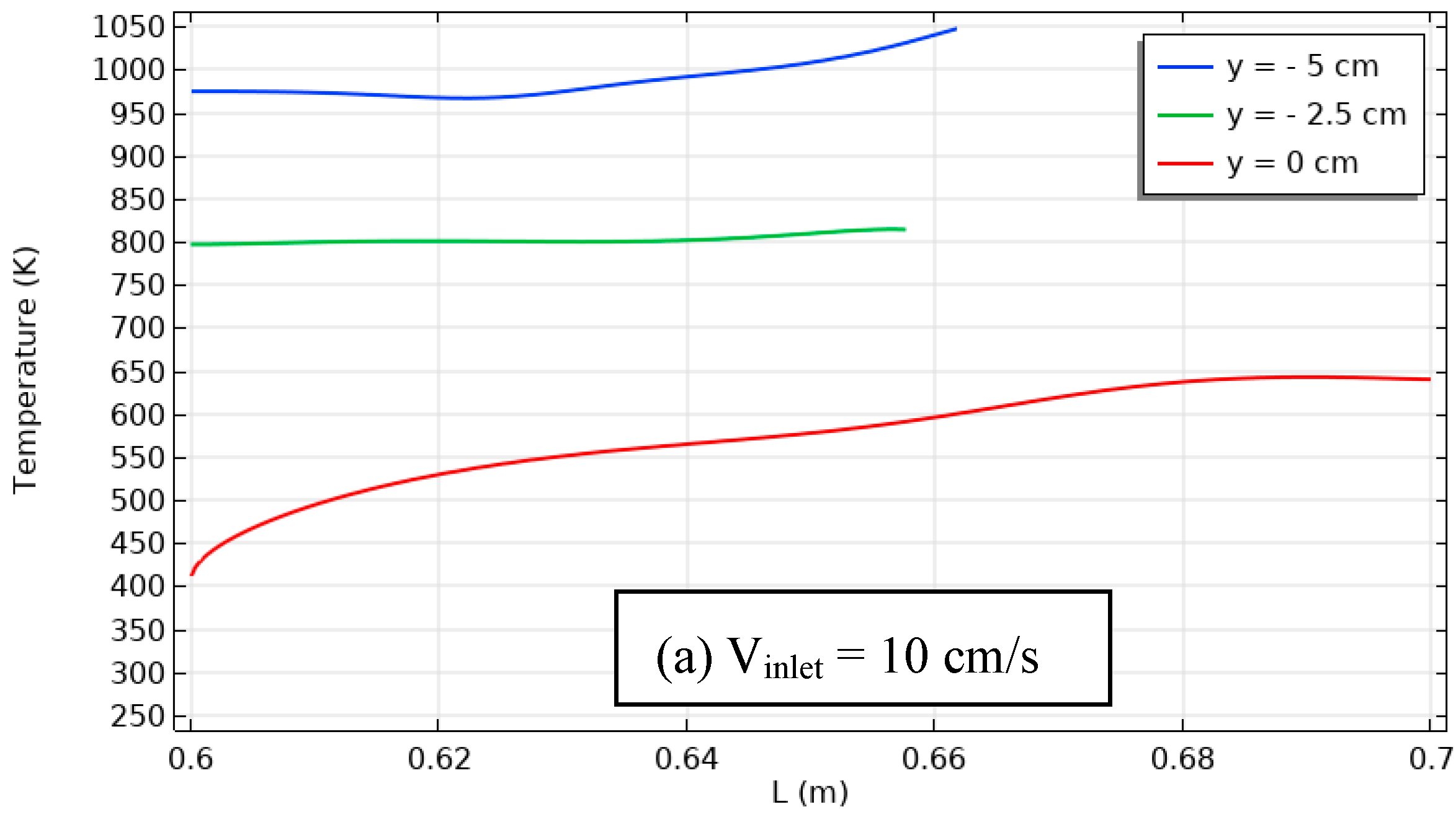
| Figure 13 | Temperature distribution within cavity with thermal sources and unheated baffle, varying inlet air velocities. | Temperature increases with vertical position. Baffle improves recirculation, affects temperature distribution. |
| Figure 14 | The Nusselt number profile within cavity with thermal sources and unheated baffle, varying inlet air velocities. | Higher velocities result in higher Nusselt numbers and improved heat transfer efficiency. Baffle enhances heat transfer. |
| Figure 15 | Velocity distribution within channel-cavity assembly with thermal sources and unheated baffle, varying inlet air velocities. | Velocity fluctuates with inlet air velocity and presence of baffle. Baffle enhances local velocity, influences velocity profile. |
| Figure 16 | Pressure distribution in duct-cavity configuration with thermal sources and unheated baffle, varying inlet air velocities. | Pressure varies along cavity, decreases downstream. Baffle influences pressure distribution, recirculation. |
| Figure 17 | Temperature distribution in channel-cavity system with thermal sources and unheated baffle, varying inlet air velocities. | Higher velocities lead to more effective cooling. Baffle enhances recirculation, reduces temperature gradients. |
| Figure 18 | Average change in the Nusselt number for varying input conditions with thermal sources and unheated baffle. | Higher velocities increase the mean Nusselt number, indicating improved heat transfer efficiency. Baffle enhances heat transfer. |
| Figure 19 | Velocity profile across output channel with thermal source and unheated baffle, varying inlet air velocities. | Velocity varies along channel width, influenced by shear stress and baffle-induced recirculation. |
| Figure 20 | Temperature distribution with varying inlet air velocities, thermal sources, and unheated baffle. | Higher velocities lead to more effective heat transfer, reducing temperature variation. Baffle reduces temperature locally. |
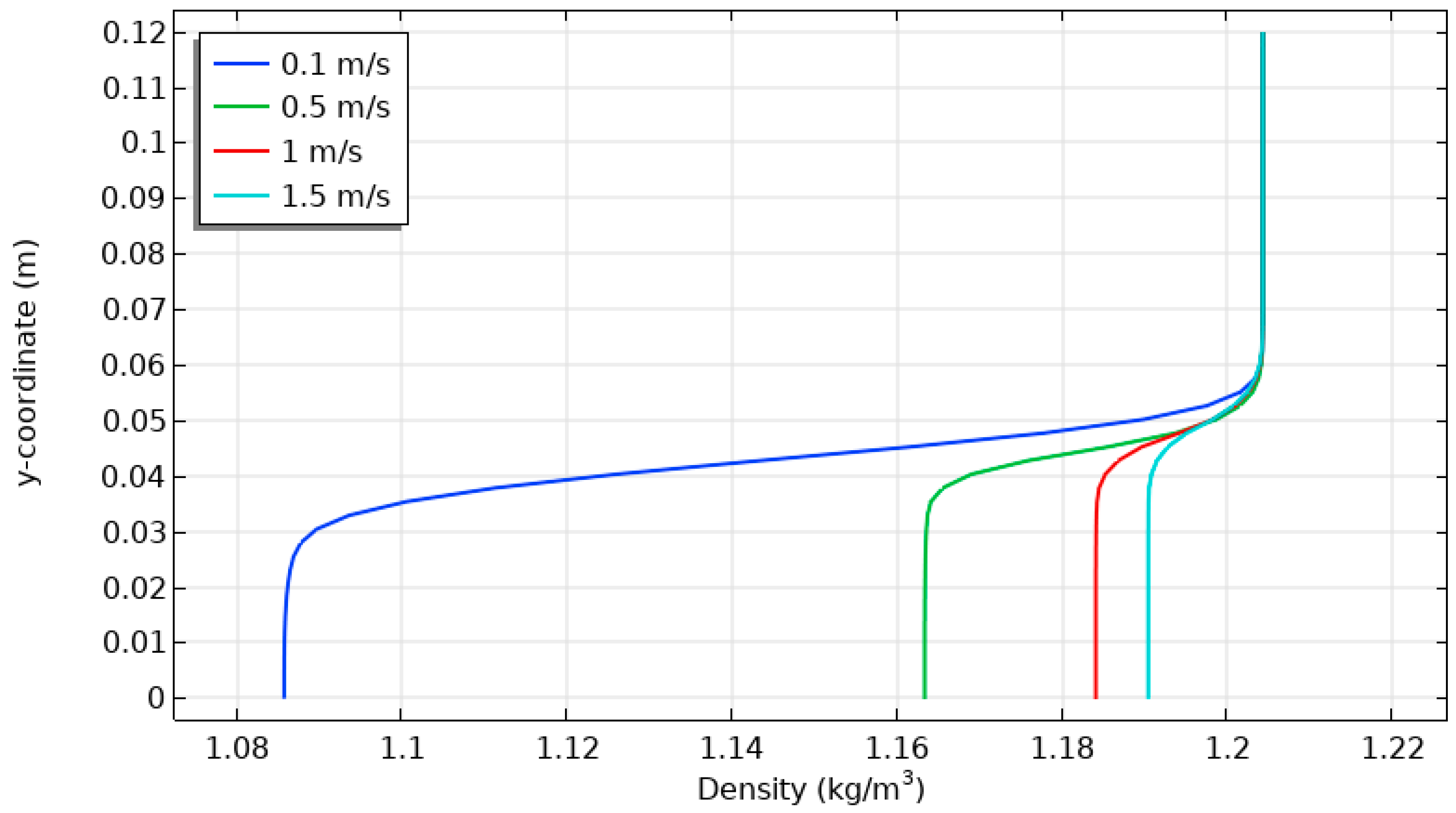
| Figure 21 | Air density distribution in channel flow with varying inlet velocities, thermal sources, and unheated baffle. | Air density increases with distance from thermal sources, higher velocities enhance natural convection and air density. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, F.L.; Al-Gaheeshi, A.M.R.; Mohammed, H.I.; Ameen, A. Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle. Energies 2024, 17, 1209. https://doi.org/10.3390/en17051209
Rashid FL, Al-Gaheeshi AMR, Mohammed HI, Ameen A. Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle. Energies. 2024; 17(5):1209. https://doi.org/10.3390/en17051209
Chicago/Turabian StyleRashid, Farhan Lafta, Asseel M. Rasheed Al-Gaheeshi, Hayder I. Mohammed, and Arman Ameen. 2024. "Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle" Energies 17, no. 5: 1209. https://doi.org/10.3390/en17051209
APA StyleRashid, F. L., Al-Gaheeshi, A. M. R., Mohammed, H. I., & Ameen, A. (2024). Heat Convection in a Channel-Opened Cavity with Two Heated Sources and Baffle. Energies, 17(5), 1209. https://doi.org/10.3390/en17051209









