Research on Flutter Characterization of Flexible Blade Response under Typhoon Operating Conditions
Abstract
:1. Introduction
2. Research Objects and Models
2.1. Wind Turbine Rotor Model of a Wind Turbine
2.2. Aeroelastic Model
2.3. Structural Model
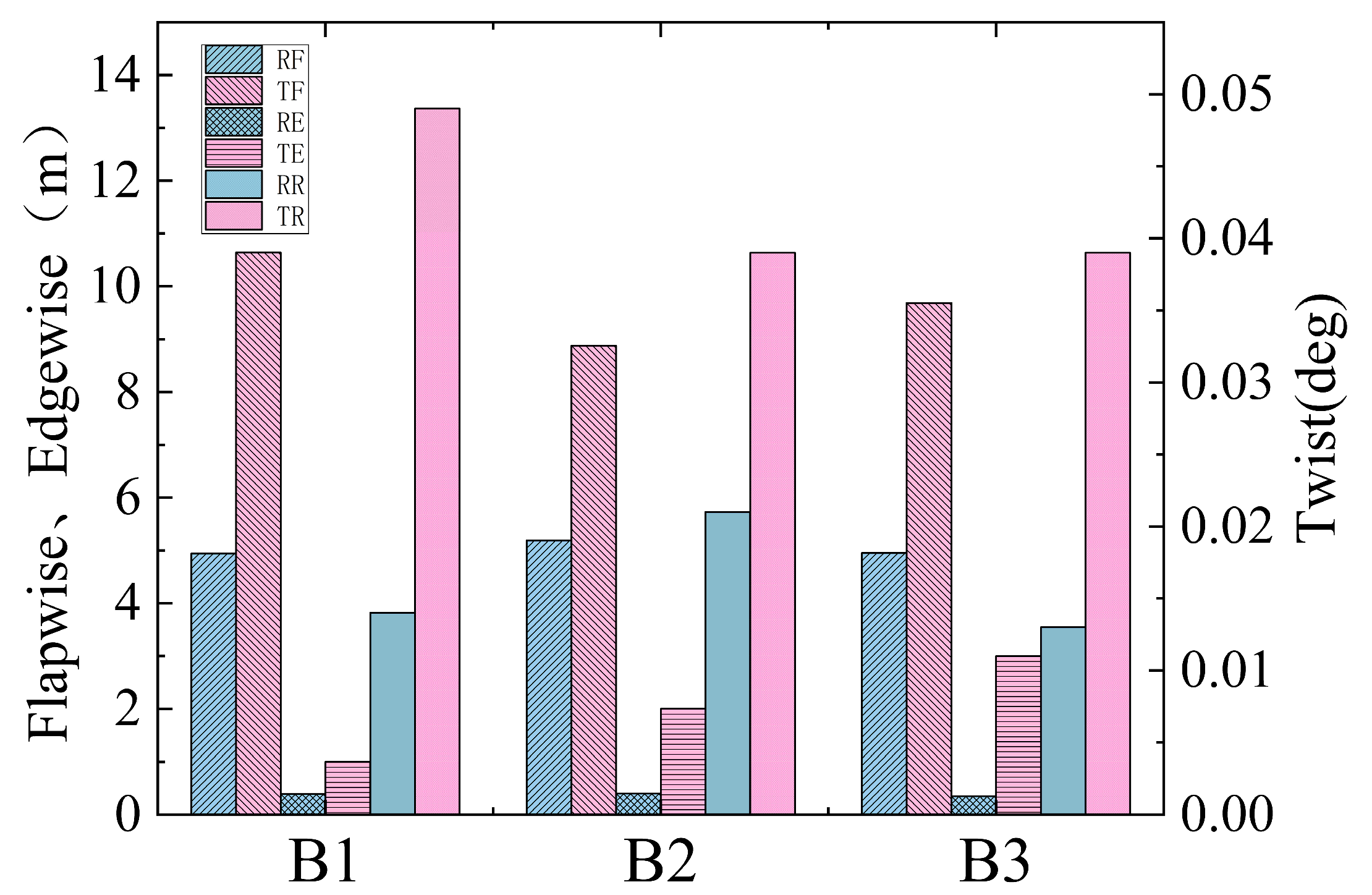
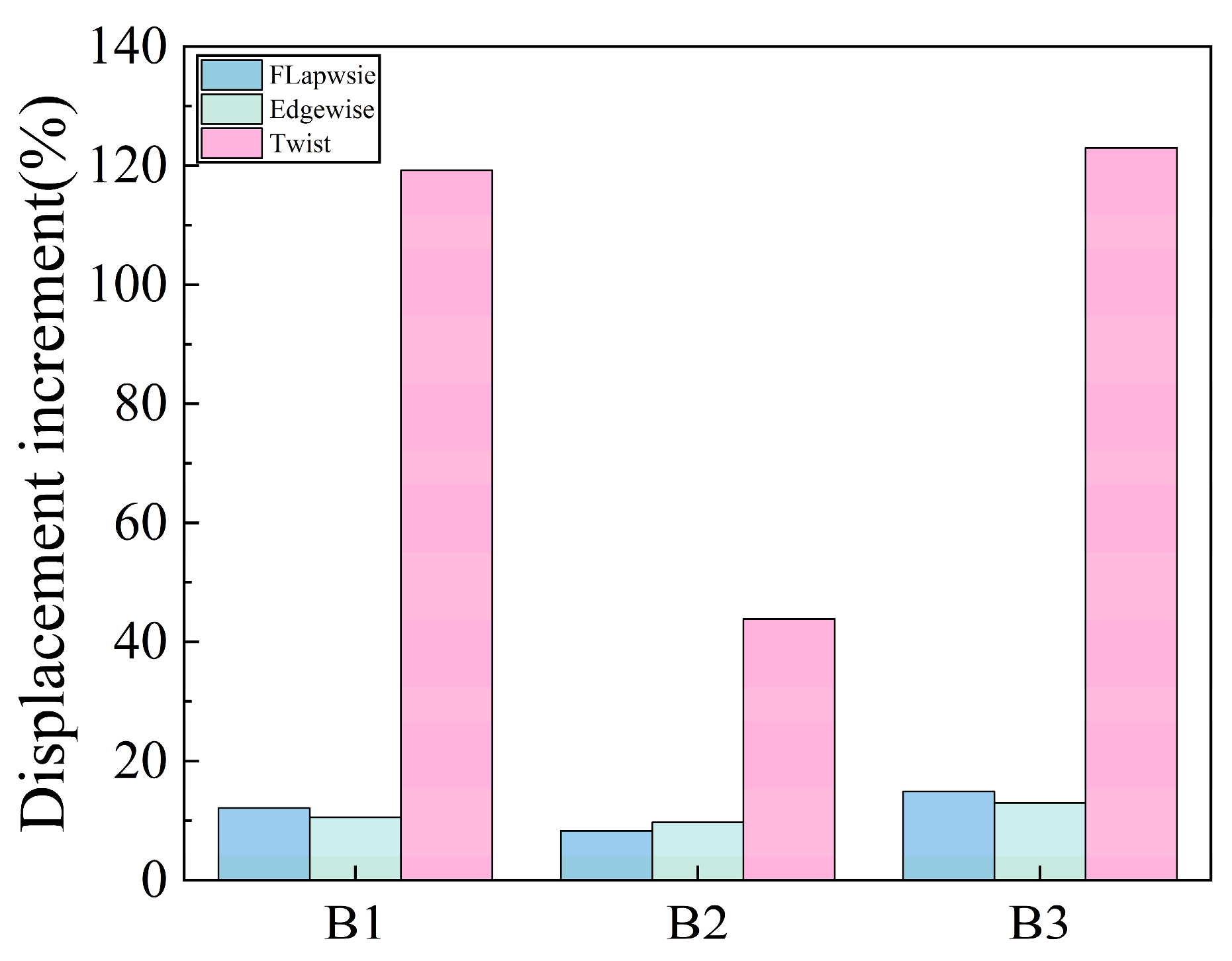
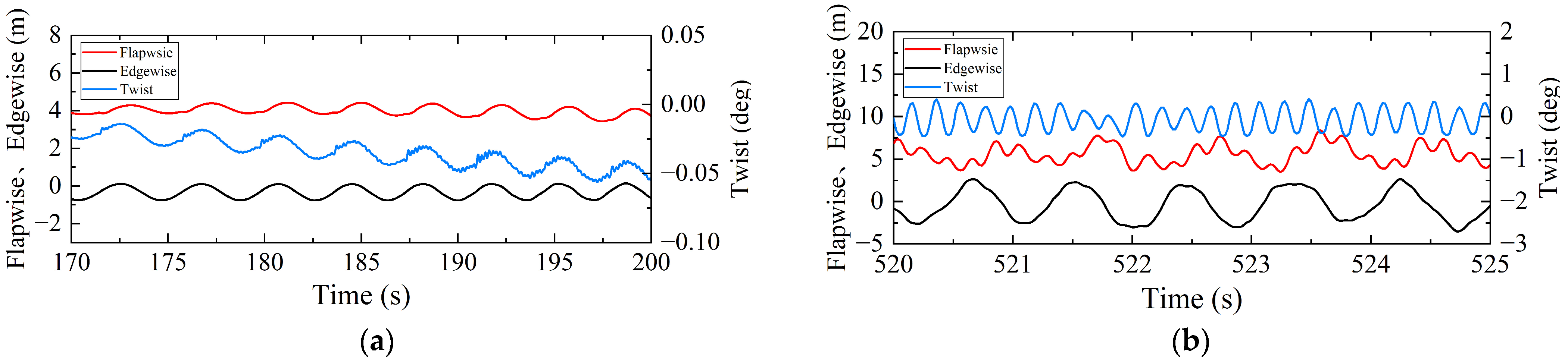
3. Comparative Analysis of the Transient Response of Blade Tip
4. Results and Discussion
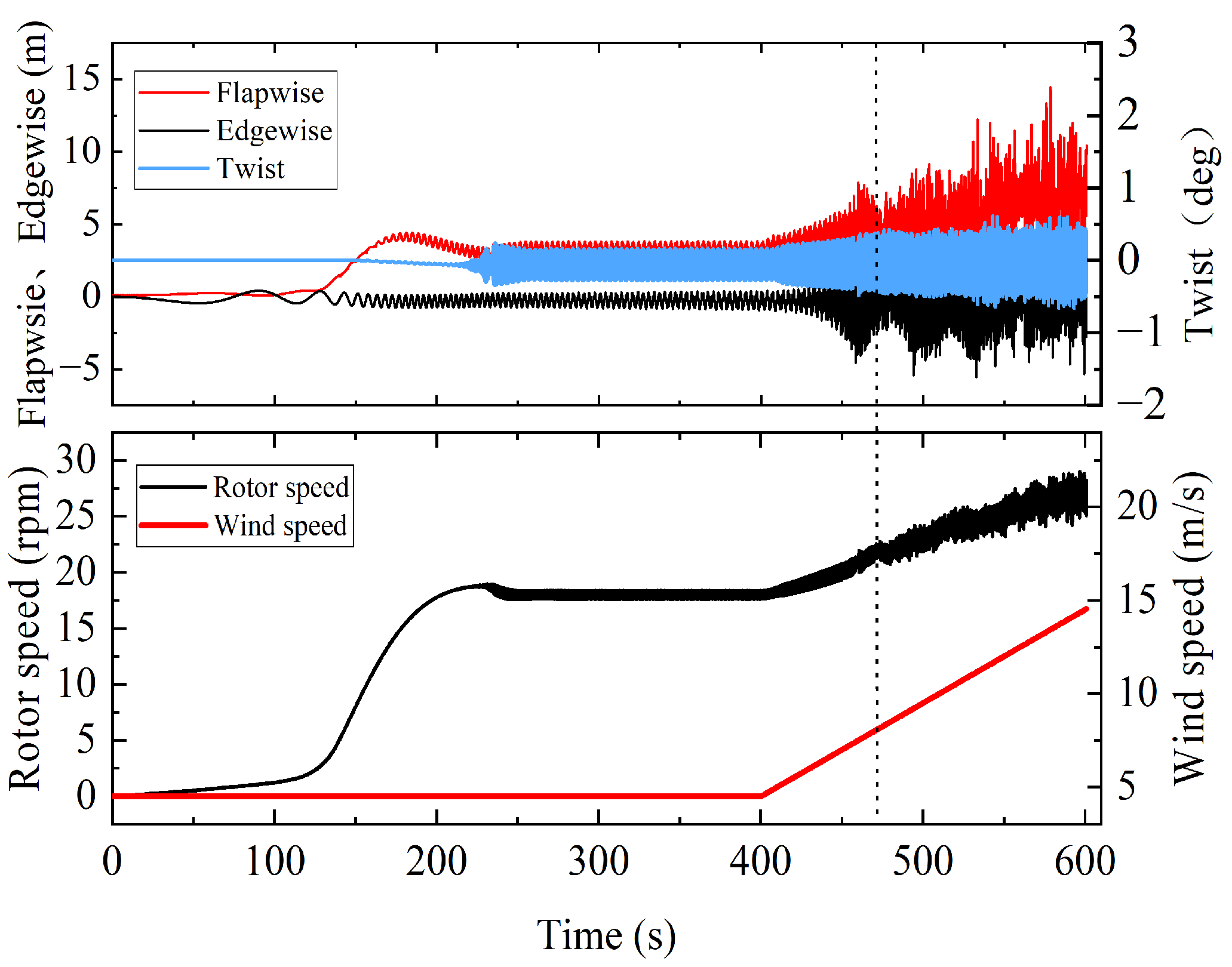
4.1. Time-Domain Analysis of Aeroelastic Stability Boundaries
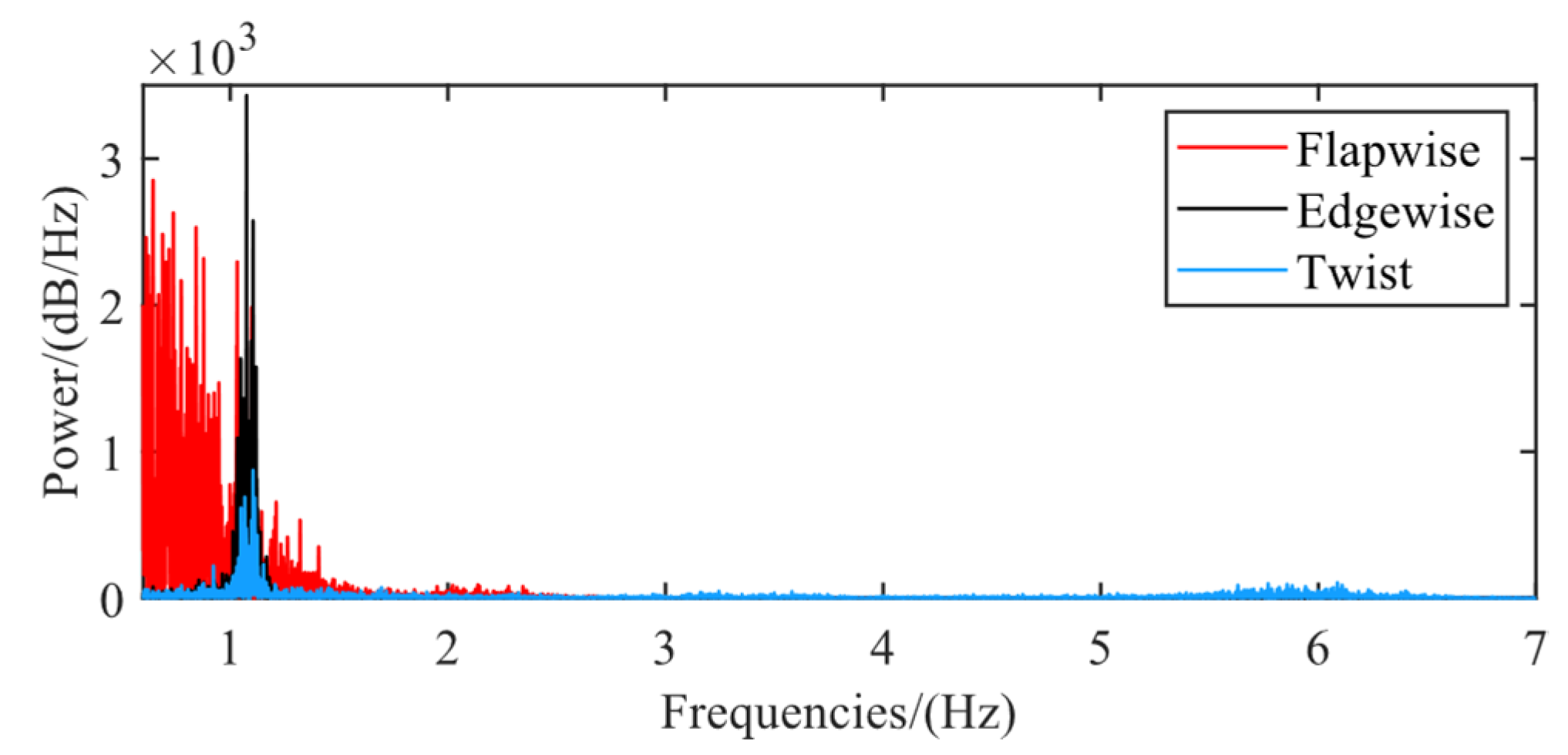
4.2. Aeroelastic Stability Boundary Frequency Domain Analysis
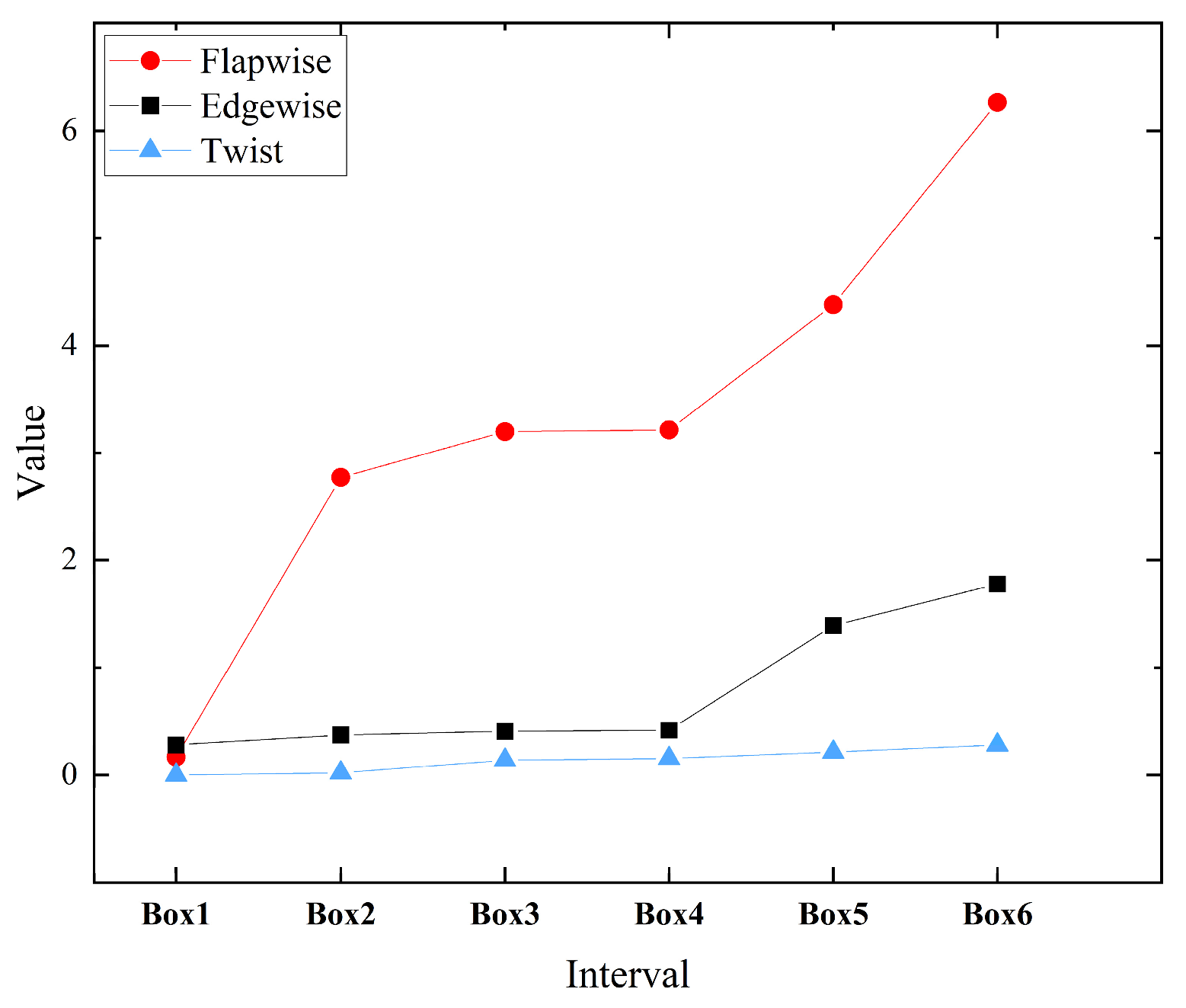
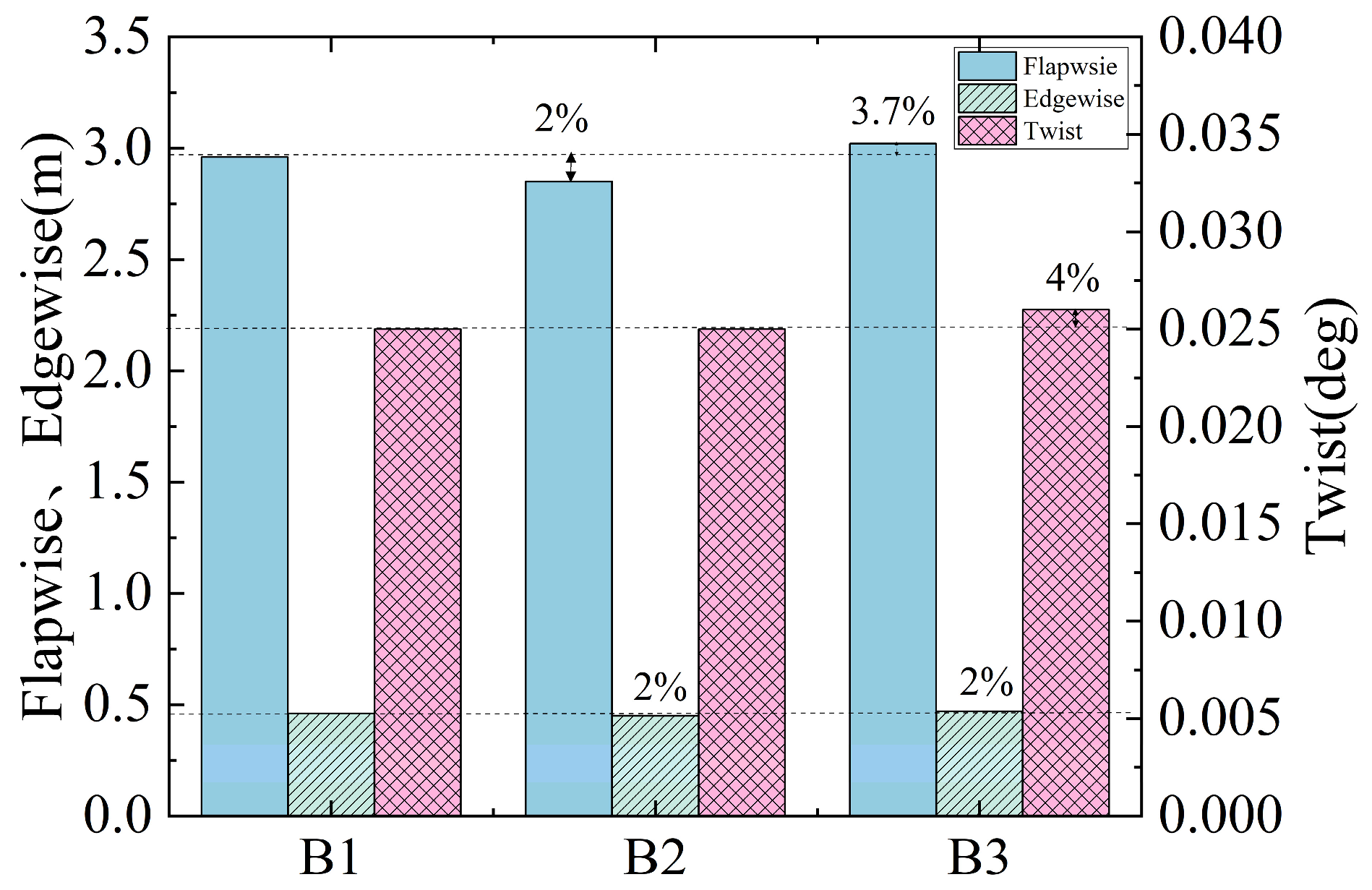
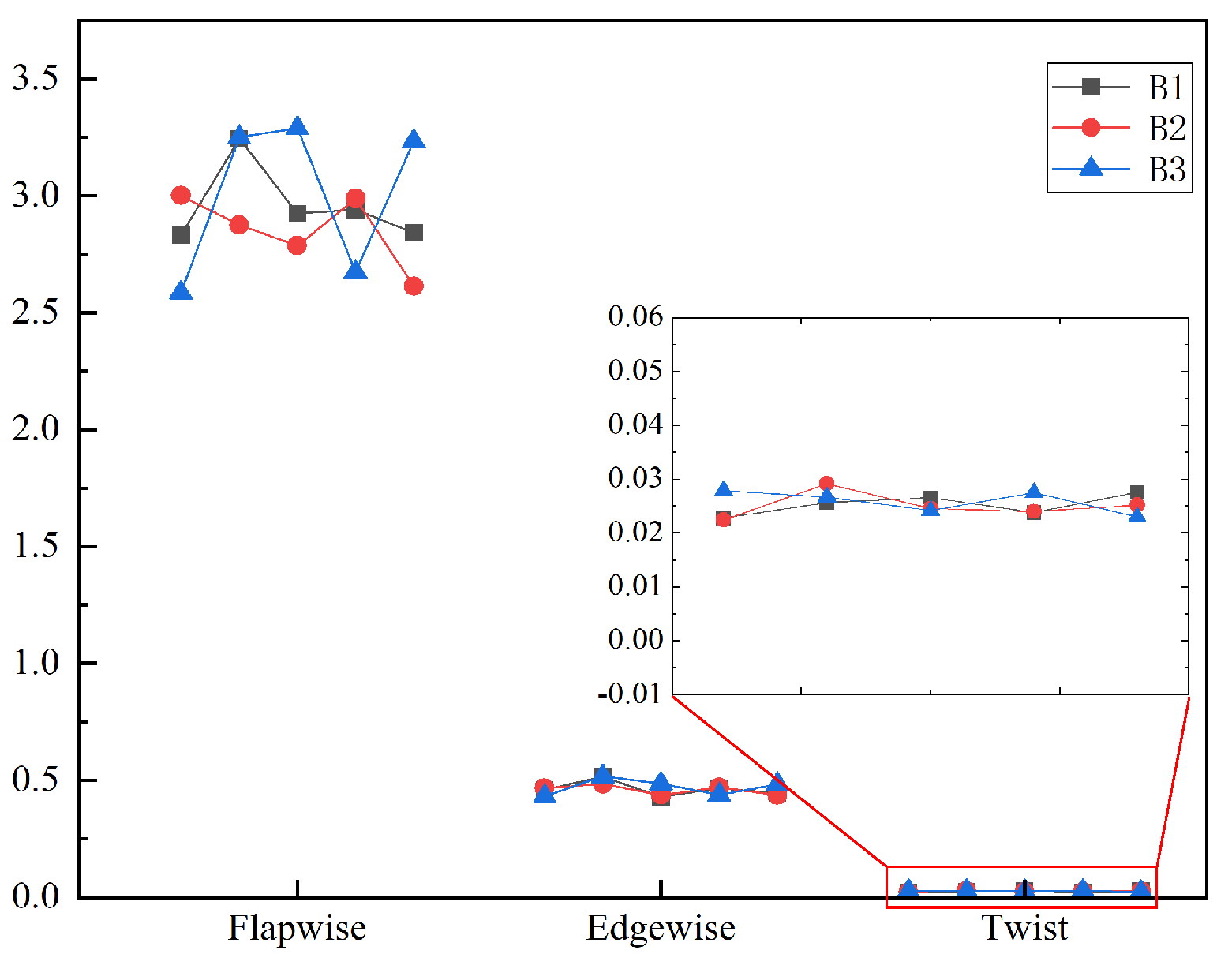
4.3. Aeroelastic Stability Analysis of Blades under Typhoon Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hou, P.; Hu, W.; Soltani, M.; Chen, C.; Zhang, B.; Chen, Z. Offshore wind farm layout design considering optimized power dispatch strategy. IEEE Trans. Sustain. Energy 2016, 8, 638–647. [Google Scholar] [CrossRef]
- Alex. “Global Wind Report 2023”. Global Wind Energy Council (Blog). Available online: https://gwec.net/globalwindreport2023/ (accessed on 14 February 2023).
- Yao, G.; Yang, H.M.; Zhou, L.D.; Li, D.D.; Li, C.B.; Wang, J. Development status and key technologies of large-capacity offshore wind turbines. Autom. Electr. Power Syst. 2021, 45, 33–47. [Google Scholar]
- Chen, X.; Xu, J.Z. Structural Failure Analysis of Wind Turbines Impacted by Super Typhoon Usagi. Eng. Fail. Anal. 2016, 60, 391–404. [Google Scholar] [CrossRef]
- Jingquan, W.; Zhengqing, C. Analysis of risks and measures on the blade damage of offshore wind turbine during strong typhoons—Enlightenment from Red Bay wind farm. Eng. Sci. 2010, 12, 32–34. [Google Scholar]
- Chou, J.-S.; Chiu, C.-K.; Huang, I.-K.; Chi, K.-N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- IEC 61400-1-2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Electrotechnical Commision: Geneva, Switzerland, 2019.
- Li, J.; Li, Z.; Jiang, Y.; Tang, Y. Typhoon Resistance Analysis of Offshore Wind Turbines: A Review. Atmosphere 2022, 13, 451. [Google Scholar] [CrossRef]
- Liu, J.Z.; Ma, L.F.; Wang, Q.H.; Fang, F.; Zhu, Y. Offshore wind power supports China’s energy transition. Strateg. Study Chin. Acad. Eng. 2021, 23, 149–159. [Google Scholar]
- Chen, Y.; Wu, D.; Yu, Y.; Gao, W. Do cyclone impacts really matter for the long-term performance of an offshore wind turbine? Renew. Energy 2021, 178, 184–201. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Branner, K.; Petersen, H.N.; Beauson, J.; McGugan, M.; Sørensen, B.F. Materials for Wind Turbine Blades: An Overview. Materials 2017, 10, 1285. [Google Scholar] [CrossRef] [PubMed]
- Kelley, C.L.; Paquette, J. Investigation of flutter for large, highly flexible wind turbine blades. J. Phys. Conf. Ser. 2020, 1618, 052078. [Google Scholar] [CrossRef]
- Hansen, M.H. Aeroelastic Stability Analysis of Wind Turbines Using an Eigenvalue Approach. Wind Energy 2004, 7, 133–143. [Google Scholar] [CrossRef]
- Jundong, H.; Hongjian, X.; Deyuan, L.; Kunxiang, G. Nonlinear aeroelastic modal analysis of large wind turbine flexible blades. J. Mech. Eng. 2020, 56, 180–187. [Google Scholar] [CrossRef]
- Dai, L.; Bai, X.; Wang, X.; Ye, S. Predictive analysis of large wind turbine blade flutter boundaries. J. Eng. Thermophys. 2022, 43, 2357–2362. [Google Scholar]
- Shakya, P.; Sunny, M.R.; Maiti, D.K. Nonlinear Flutter Analysis of a Bend-Twist Coupled Composite Wind Turbine Blade in Time Domain. Compos. Struct. 2022, 284, 115216. [Google Scholar] [CrossRef]
- Han, R.; Wang, L.; Wang, T.; Gao, Z.; Wu, J. Study of Dynamic Response Characteristics of the Wind Turbine Based on Measured Power Spectrum in the Eyewall Region of Typhoons. Appl. Sci. 2019, 9, 2392. [Google Scholar] [CrossRef]
- Wang, H.; Ke, S.T.; Wang, T.G.; Zhu, S.Y. Typhoon-induced vibration response and the working mechanism of large wind turbine considering multi-stage effects. Renew. Energy 2020, 153, 740–758. [Google Scholar] [CrossRef]
- Tang, D.; Xu, M.; Mao, J.; Zhu, H. Unsteady Performances of a Parked Large-Scale Wind Turbine in the Typhoon Activity Zones. Renew. Energy 2020, 149, 617–630. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Z.; Zhang, L.; Wang, J. Dynamic characterization of megawatt-class wind turbine under extreme wind conditions. Chin. J. Electr. Eng. 2024. accepted. [Google Scholar]
- Ye, K.; Chun, L.; Qinwei, D.; Zhou, Y. Structural dynamic response of large wind turbine under multi-body dynamics simulation. J. Sol. Energy 2018, 5, 1459–1466. [Google Scholar]
- Jonkman, B.; Mudafort, R.M.; Platt, A.; Branlard, E.; Sprague, M.; Vijayakumar, G.; Buhl, M.; Ross, H.; Bortolotti, P.; Ananthan, S.; et al. OpenFAST/Openfast: OpenFAST v3.2.1. Available online: https://zenodo.org/records/6949650 (accessed on 1 August 2022).
- Jonkman, J.M.; Hayman, G.J.; Jonkman, B.J.; Damiani, R.R.; Murray, R.E. AeroDyn V15 User’s Guide and Theory Manual; Renewable Energy: Masdar City, Abu Dhabi, 2015. [Google Scholar]
- Wang, Q.; Sprague, M.A.; Jonkman, J.; Johnson, N.; Jonkman, B. BeamDyn: A High-fidelity Wind Turbine Blade Solver in the FAST Modular Framework. Wind Energy 2017, 20, 1439–1462. [Google Scholar] [CrossRef]
- Vatne, S.R. Aeroelastic Instability and Flutter for a 10 MW Wind Turbine. Bachelor’s Thesis, Institut for Energi- og Procesteknik, Trondheim, Norway, 2011. [Google Scholar]
- Lobitz, D.W. Aeroelastic stability predictions for a MW-sized blade. Wind Energy 2004, 7, 211–224. [Google Scholar] [CrossRef]
- Chen, B.; Hua, X.G.; Zhang, Z.; Basu, B.; Nielsen, S.R. Monitoring of wind turbine blades for flutter instability. Struct. Monit. Maint. 2017, 4, 115–131. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development (No. NREL/TP-500-38060); National Renewable Energy: Golden, CO, USA, 2009.
- Branlard, E.; Jonkman, B.; Pirrung, G.R.; Dixon, K.; Jonkman, J. Dynamic Inflow and Unsteady Aerodynamics Models for Modal and Stability Analyses in OpenFAST. J. Phys. Conf. Ser. 2022, 2265, 032044. [Google Scholar] [CrossRef]
- Hayat, K.; De Lecea, A.G.M.; Moriones, C.D.; Ha, S.K. Flutter Performance of Bend–Twist Coupled Large-Scale Wind Turbine Blades. J. Sound Vib. 2016, 370, 149–162. [Google Scholar] [CrossRef]
- Li, B.; Tian, D.; Wu, X.; Meng, H.; Su, Y. Flutter analysis and parameter sensitivity of ultra-large wind turbine blades. J. Sol. Energy 2023, 16, 295–301. [Google Scholar]
- Shakya, P.; Sunny, M.R.; Maiti, D.K. A parametric study of flutter behavior of a composite wind turbine blade with bend-twist coupling. Compos. Struct. 2019, 207, 764–775. [Google Scholar] [CrossRef]
- Lu, M.-M.; Ke, S.-T.; Wu, H.-X.; Gao, M.-E.; Tian, W.-X.; Wang, H. A Novel Forecasting Method of Flutter Critical Wind Speed for the 15 MW Wind Turbine Blade Based on Aeroelastic Wind Tunnel Test. J. Wind. Eng. Ind. Aerodyn. 2022, 230, 105195. [Google Scholar] [CrossRef]
- Holierhoek, J.G. Aeroelastic Stability Models. In Handbook of Wind Energy Aerodynamics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–45. [Google Scholar]
- Bir, G. User’s Guide to BModes (Software for Computing Rotating Beam-Cupled Modes); Renewable Energy: Masdar City, Abu Dhabi, 2005. [Google Scholar]
- Resor, B.R. Definition of a 5MW/61.5 m Wind Turbine Blade Reference Model; No. SAND2013-2569; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2013.
- Yin, F.-F.; Chen, J.-J.; Chen, X.-J.; Xu, Y.-Q.; Shen, X.; Du, C.-H. Nonlinear aeroelastic stability of wind turbine airfoil structures under nonuniform incoming flow conditions. J. Sol. Energy 2023, 5, 442–448. [Google Scholar]
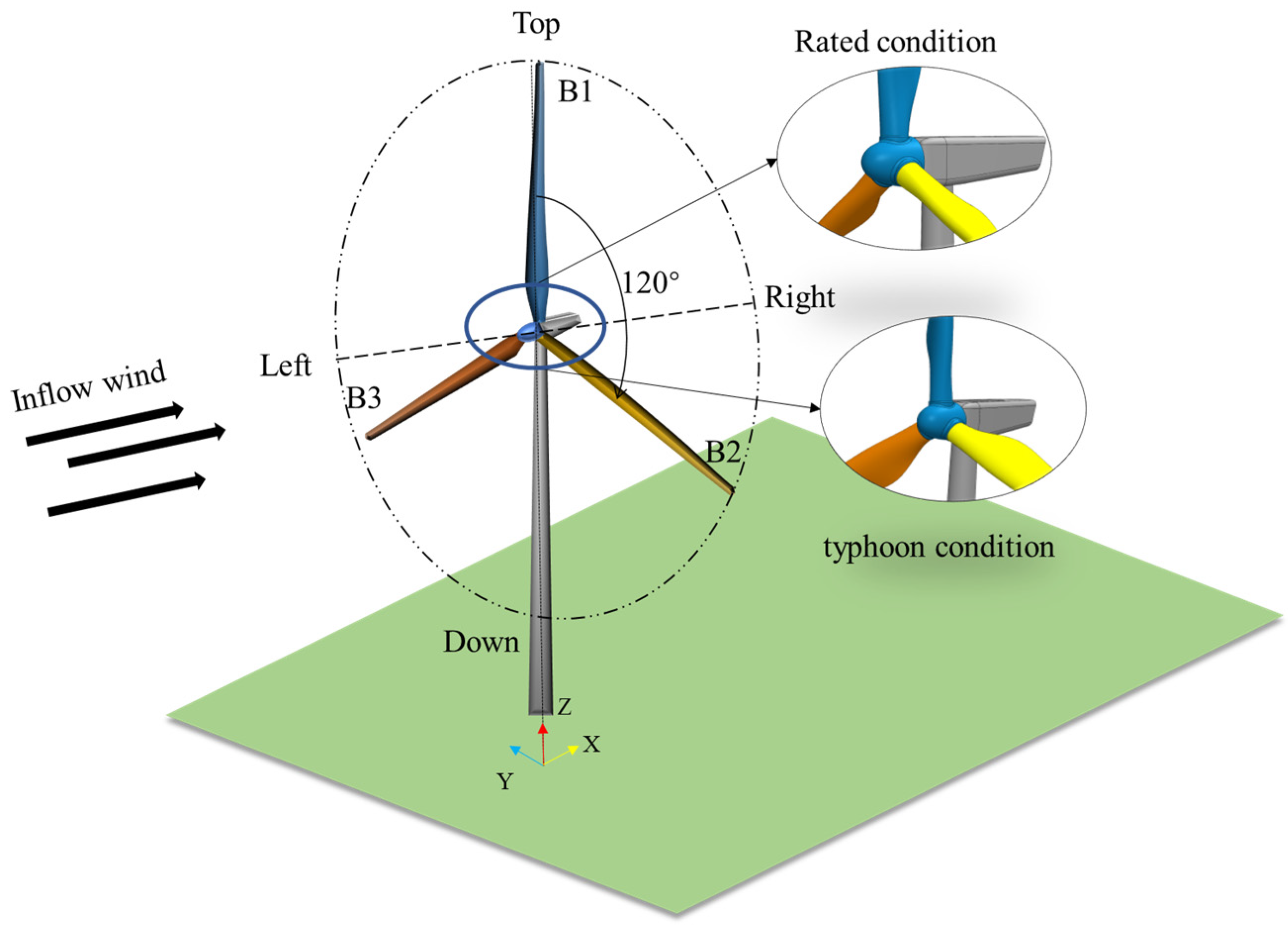

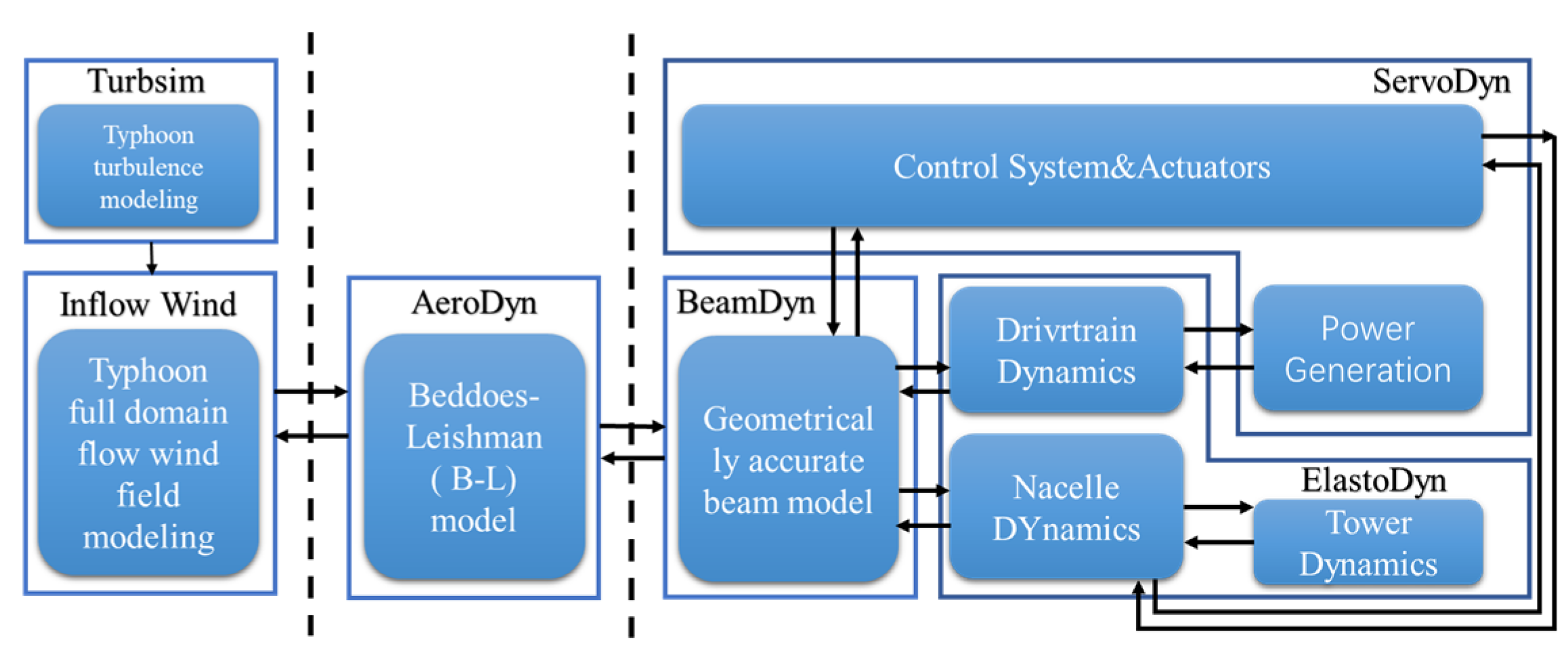
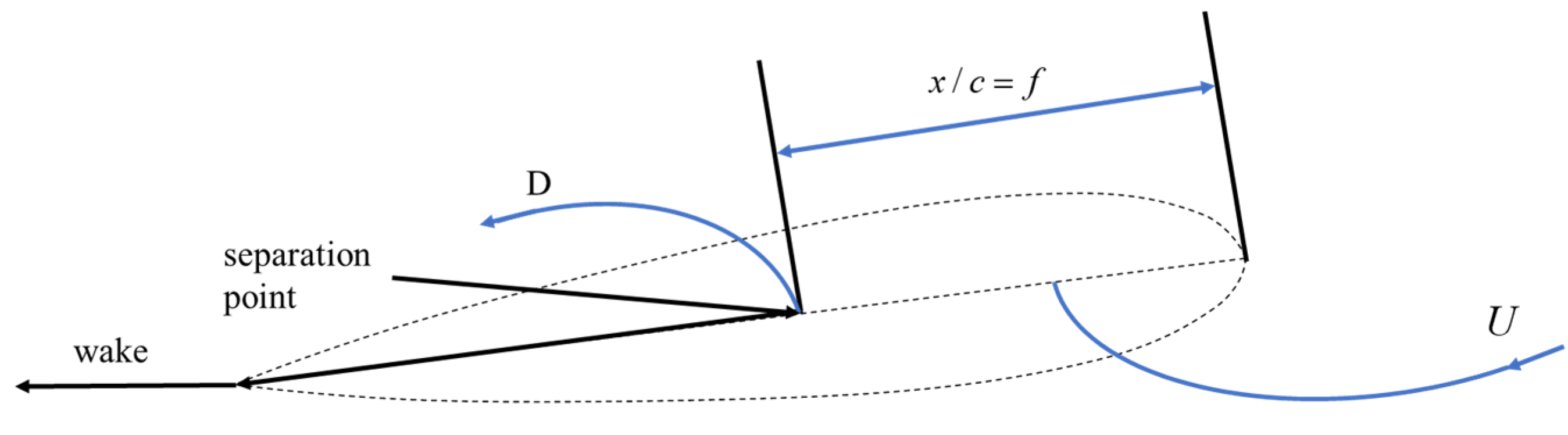
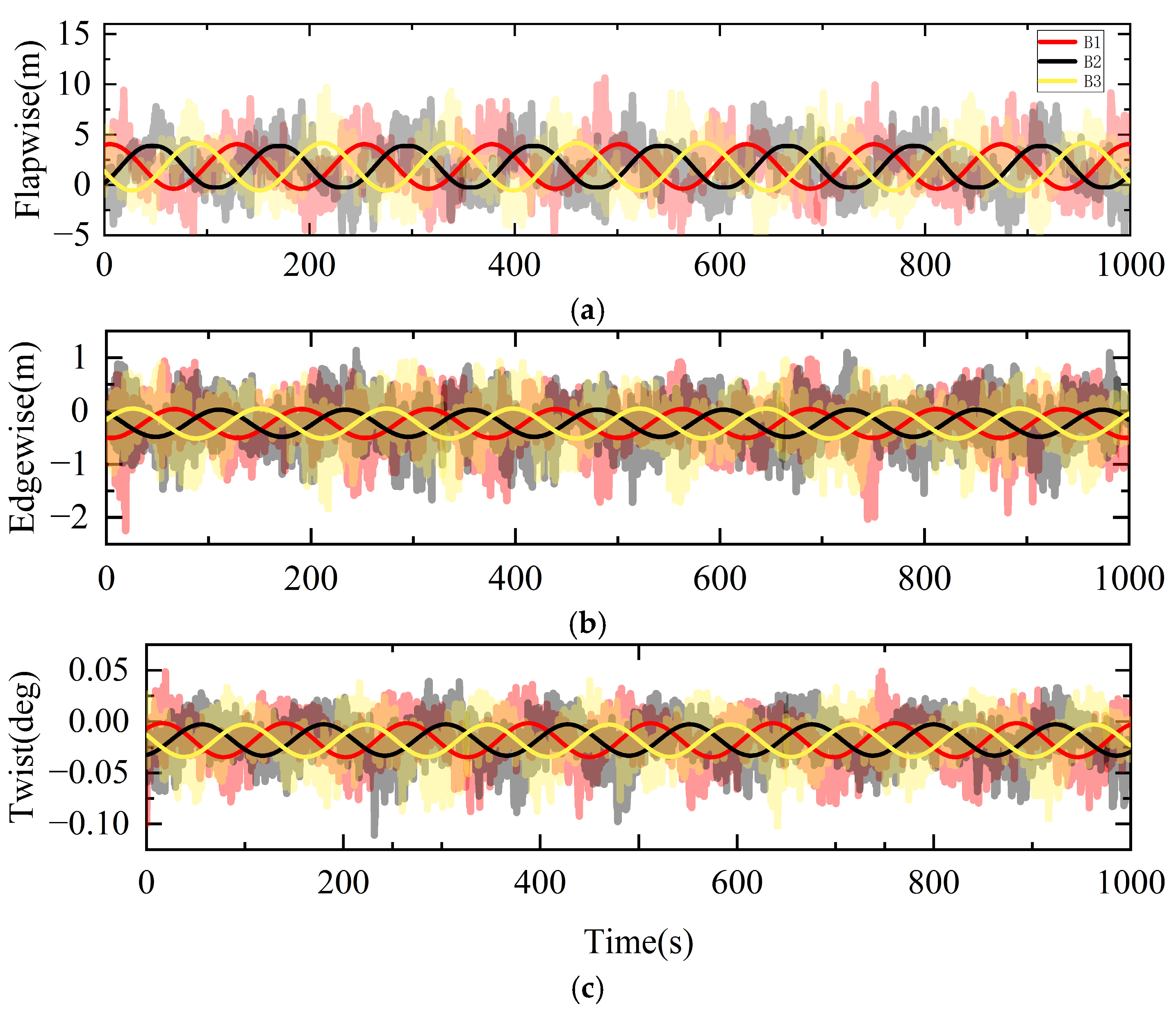


| Parameter/Unit | Numerical Value/Description |
|---|---|
| Rating/(MW) | 5 |
| Rotor Orientation, Configuration | Upwind, 3 Blades |
| Rotor, Hub Diameter/(m) | 126, 3 |
| Hub Height/(m) | 90 |
| Cut-In, Rated, Cut-Out Wind Speed/(m·s−1) | 3, 11.4, 25 |
| Cut-In, Rated Rotor Speed/(m·s−1) | 6.9 rpm, 12.1 rpm |
| Rated Tip Speed/(m·s−1) | 80 |
| Overhang, Shaft Tilt, Precone/(deg) | 5 m, 2.5° |
| Static Tip Clearance/(m) | 13.16 |
| Rotor Mass/(kg) | 110,000 |
| Nacelle Mass/(kg) | 240,000 |
| Tower Mass/(kg) | 347,460 |
| Modality | NREL | OpenFAST | Deviation |
|---|---|---|---|
| 1st Flapwsise | 0.667 Hz | 0.669 Hz | 0.2% |
| 1st Edgewise | 1.079 Hz | 1.110 Hz | 2.8% |
| 2nd Flapwsise | 1.922 Hz | 1.996 Hz | 3.8% |
| 2nd Edgewise | - | 4.096 Hz | - |
| 3rd Flapwsise | - | 4.624 Hz | - |
| 1st Twist | - | 5.815 Hz | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Han, Q.; Tian, D.; Feng, X.; Guo, Z.; Zhang, M. Research on Flutter Characterization of Flexible Blade Response under Typhoon Operating Conditions. Energies 2024, 17, 1254. https://doi.org/10.3390/en17051254
Liu H, Han Q, Tian D, Feng X, Guo Z, Zhang M. Research on Flutter Characterization of Flexible Blade Response under Typhoon Operating Conditions. Energies. 2024; 17(5):1254. https://doi.org/10.3390/en17051254
Chicago/Turabian StyleLiu, Huiyuan, Qiaoli Han, De Tian, Xiaomei Feng, Zhiyong Guo, and Minghui Zhang. 2024. "Research on Flutter Characterization of Flexible Blade Response under Typhoon Operating Conditions" Energies 17, no. 5: 1254. https://doi.org/10.3390/en17051254
APA StyleLiu, H., Han, Q., Tian, D., Feng, X., Guo, Z., & Zhang, M. (2024). Research on Flutter Characterization of Flexible Blade Response under Typhoon Operating Conditions. Energies, 17(5), 1254. https://doi.org/10.3390/en17051254







