Charging Behavior Portrait of Electric Vehicle Users Based on Fuzzy C-Means Clustering Algorithm
Abstract
1. Introduction
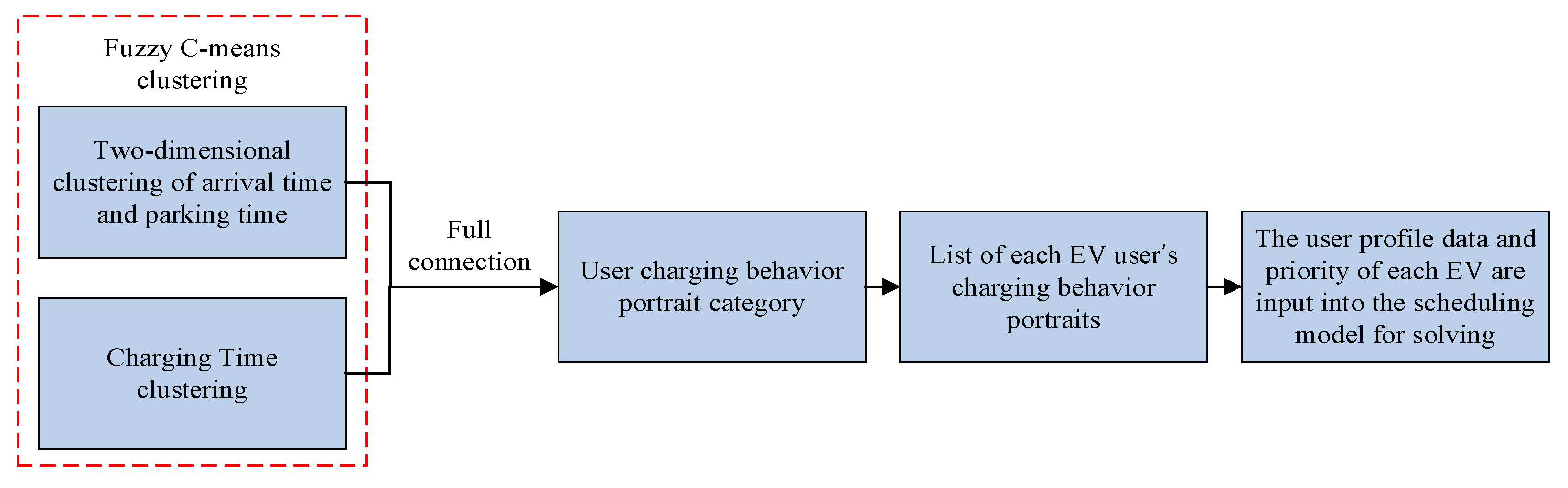
- The charging behavior portraits of EV users are characterized using FCM. The two-dimensional clustering results of the arrival time and parking time of EVs and the clustering results of charging time are aggregated by features, and the charging portrait categories of EVs in the park are obtained.
- This study introduces a portrait model that combines group portrait categories with individual EVs. Each portrait category corresponds to a different range of features, and the charging data of each EV may include one or several portrait categories, thus generating a list of user portraits for each EV. Based on the duration of schedulable time associated with each portrait category, EV users are categorized into four types: high-quality schedulable users, medium-quality schedulable users, low-quality schedulable users, and irregular users.
- In order to enhance the accuracy of the user portraits, this study conducted further statistics based on the charging patterns on weekdays and weekends. The statistics were categorized into weekday charging, weekend charging, and weekday–weekend charging for each EV. This study introduces the classification of dispatchable EVs and their priorities during the peak/flat/valley load periods.
- Based on the priority of user response potential, this study presents a method for calculating the feature data of different user groups. The data are inputted into the EV scheduling optimization model for computation and solution, resulting in optimized scheduling outcomes for each user group. While ensuring user satisfaction is not compromised, the diverse needs of the power grid can be met based on the priority of user groups. This study validates the feasibility of certain user group portraits through three charging scheduling scenarios. The experimental results demonstrate that when considering the charging cost of EV users as a single objective function, the charging cost is reduced by 47.42% compared to unstructured charging. When both the charging cost and load fluctuation of EV users are considered as dual objective functions, the charging cost of EV users and the load fluctuation of the charging station are reduced, respectively, by 41.76% and 31.07%.
2. Research Framework and Methodology
2.1. EV Users’ Charging Behavior Portrait Categories
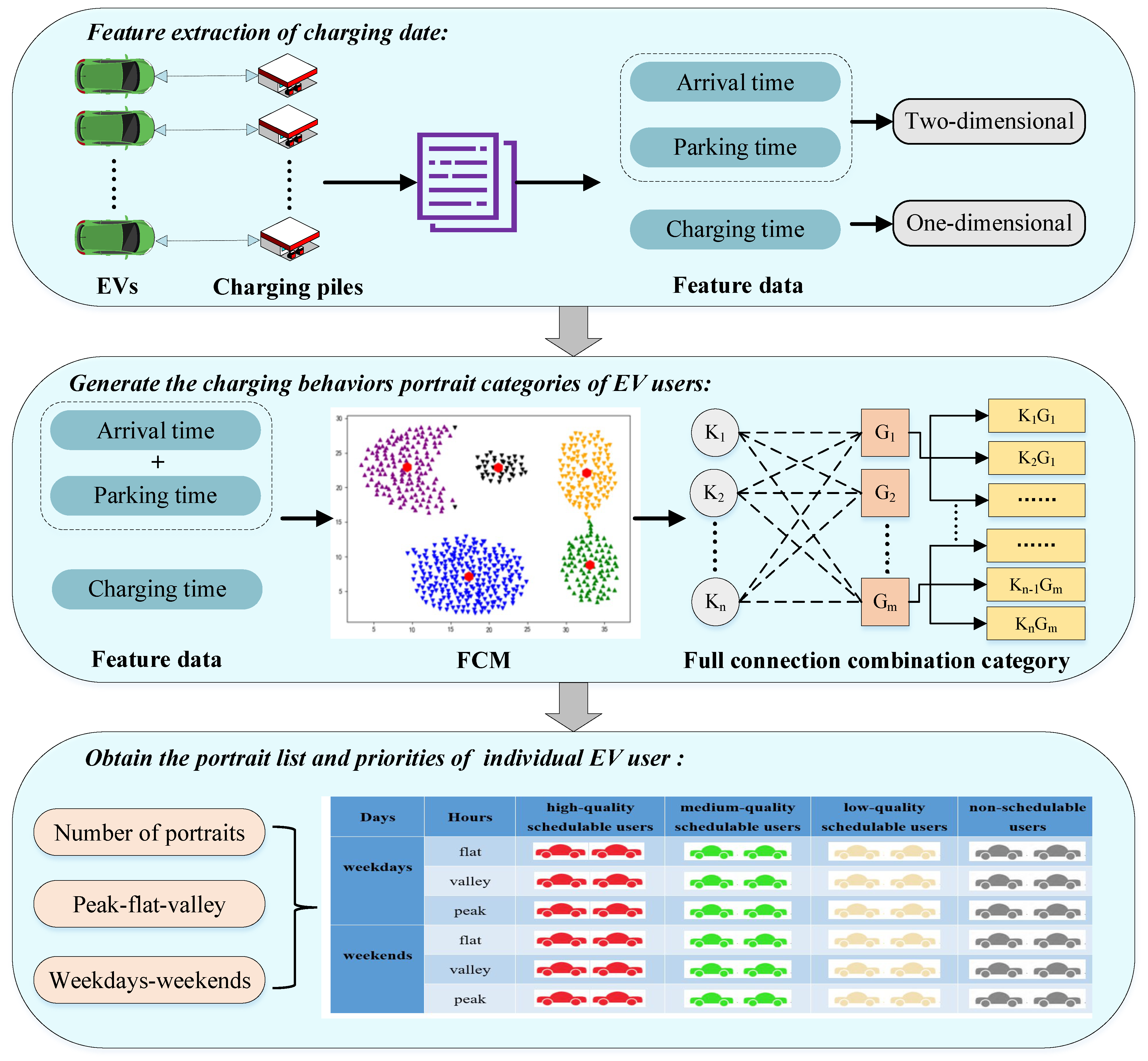
2.1.1. Collection and Preprocessing of Data
2.1.2. Feature Extraction
2.1.3. FCM Clustering
- (1)
- Objective function.
- (2)
- The membership degree matrix and cluster center .
- (3)
- The termination condition of iteration.
- Step 1.
- Initialize the matrix determined by the membership function (initialized between random values [0, 1]) while satisfying the constraints of Formula (3).
- Step 2.
- Calculate the central value of the cluster according to Formula (5).
- Step 3.
- Calculate the new membership matrix according to Formula (4).
- Step 4.
- Calculate the change in the objective function this time and the last time according to Formula (2). If the change is less than a certain threshold, then stop the algorithm; otherwise, go to Step 2.
2.1.4. Feature Aggregation
2.2. Analysis of the Charging Behavior of Each EV
- (1)
- EV charging on weekdays and weekends.
- (2)
- The charging behavior portrait of each EV.
- (3)
- Determine the rules of the user’s charging behavior portrait.
- If the percentage of any single portrait category data reaches between L and 100%, the user is classified as a high-quality user.
- If the combined percentage of any two portrait category data reaches between L and 100%, the user is classified as a medium-quality user.
- If the combined percentage of any three portrait category data reaches between L and 100%, the user is classified as a low-quality user.
- Users who do not fall into the above categories are classified as irregular users.
3. Case Study
3.1. EV Users’ Charging Behavior Portrait Categories
3.1.1. Data Preprocessing
3.1.2. Feature Extraction
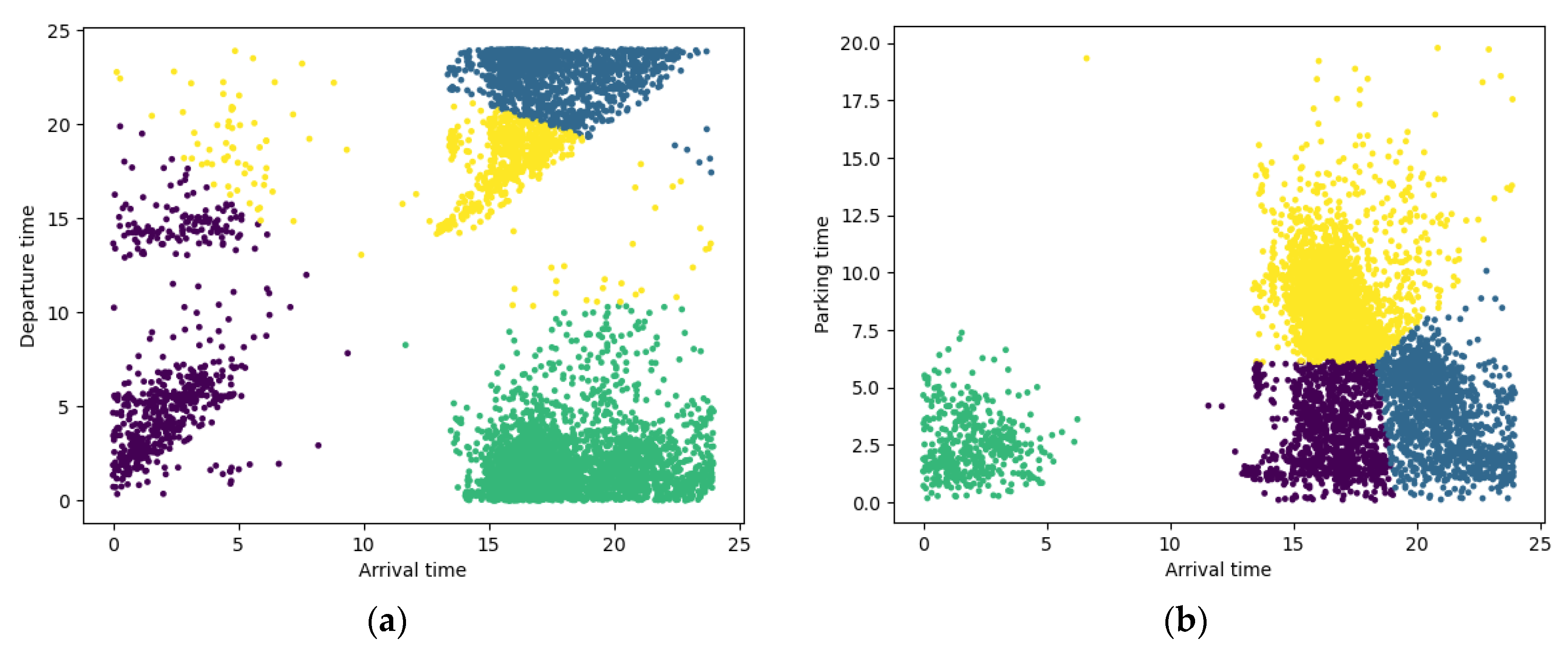
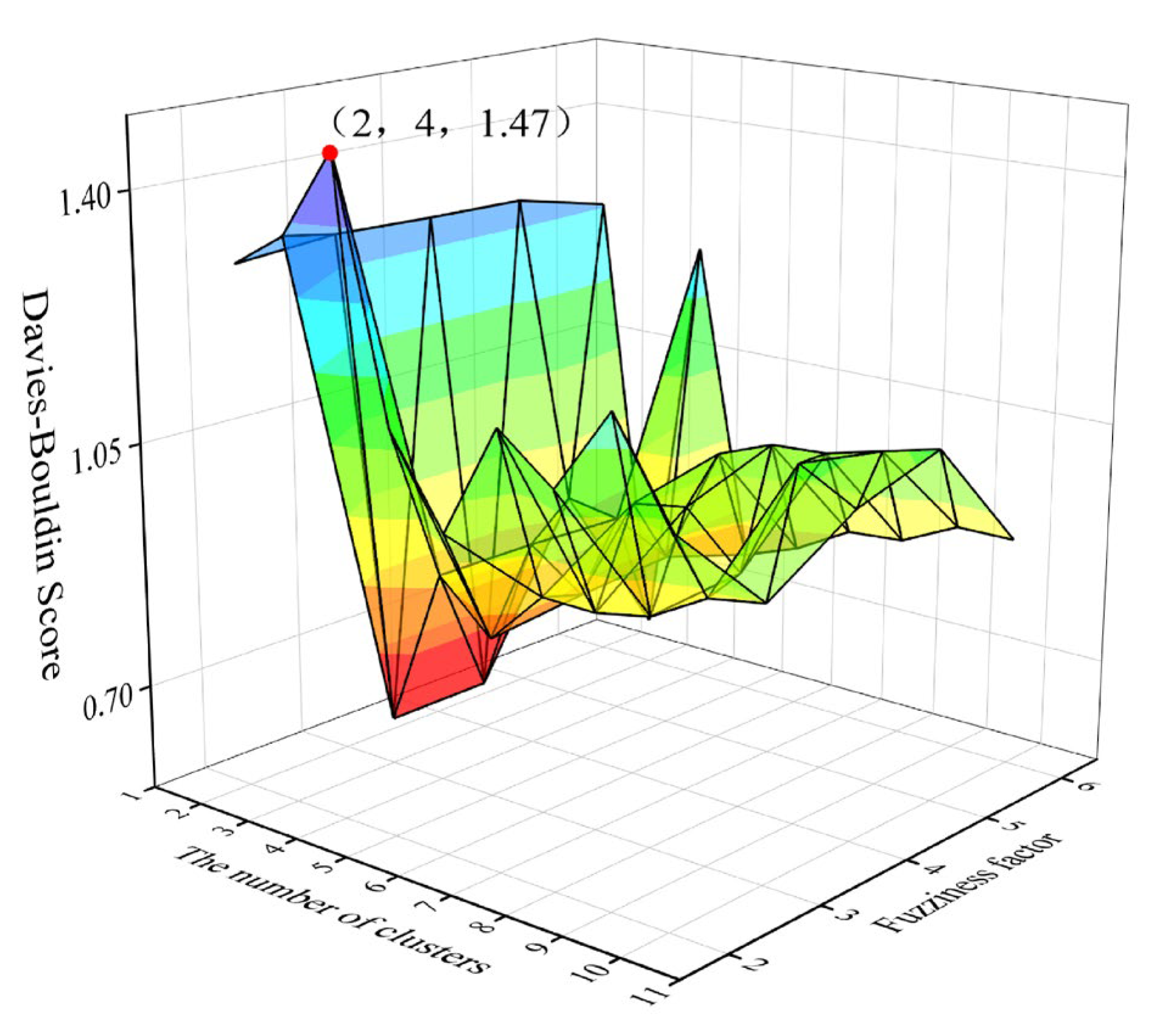
3.1.3. FCM Clustering
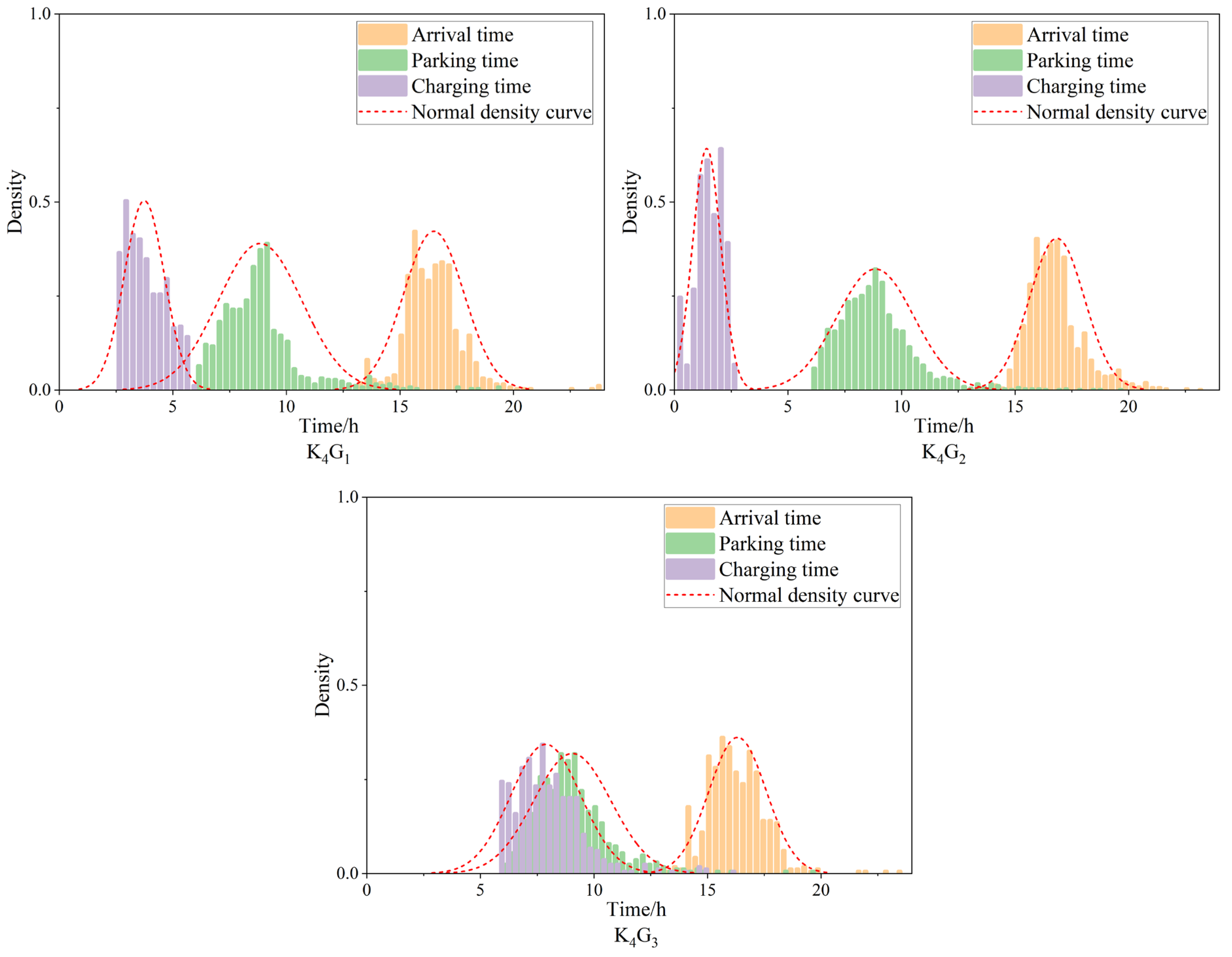
3.1.4. Generate User Charging Behavior Profile Categories
3.1.5. Schedulable Time of User Charging Behavior Profile Category
3.2. Each User’s Charging Behavior Analysis
3.2.1. User Charging Behavior Analysis Based on Weekdays and Weekends
3.2.2. User Charging Behavior Portrait of Each Car
3.3. EV Optimal Scheduling Model
3.3.1. The Calculation Method of Feature Quantities
3.3.2. Time-of-Use Price (TOU)
3.3.3. Decision Variables
3.3.4. Objective Function
3.3.5. Constraints
- (1)
- Charging time constraint:
- (2)
- Integer programming constraints:
- (3)
- Charging Power Constraint:
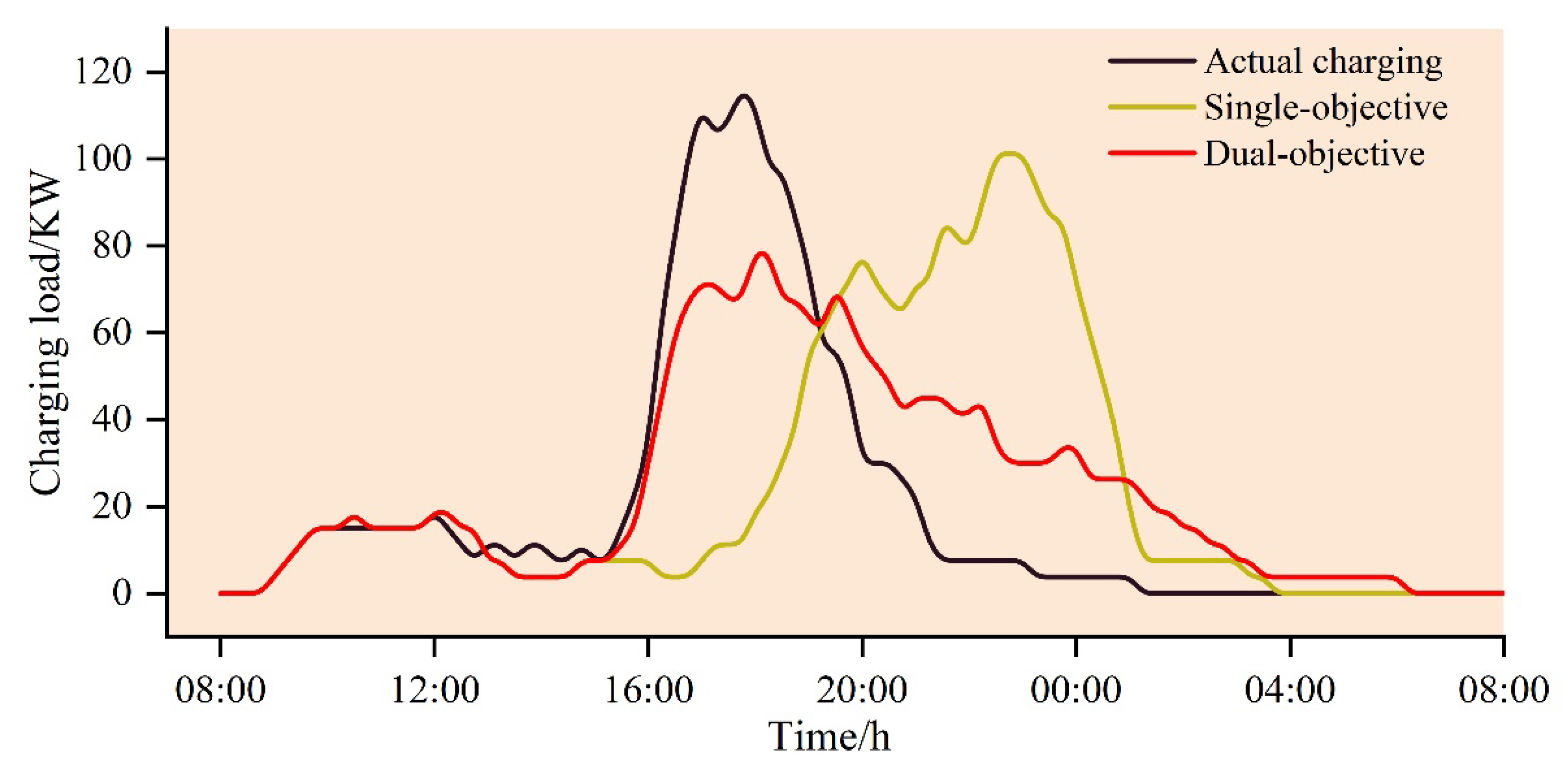
3.3.6. The Experimental Results
4. Results and Analysis
- (1)
- High-quality schedulable EV users (Category 1):
- (2)
- Medium-quality schedulable EV users (Category 2):
- (3)
- Low-quality schedulable EV users (Category 3):
- (4)
- Irregular users:
- Resource allocation: By accurately identifying irregular users as well as high-, medium-, and low-quality schedulable users, resources such as charging stations and grid capacity can be allocated more effectively. High-priority schedulable users could be given priority access to fast charging stations or reserved time slots, while irregular users could be scheduled based on the availability of resources, reducing waiting times, and congestion at charging stations.
- Grid stability: High-priority schedulable users can help grid operators better manage and predict electricity demand. Encouraging these users to charge during periods of low demand or when the generation of renewable energy is high can improve the stability of the grid and maximize the integration of renewable energy sources.
- Demand response programs: Differentiating between user types also enables the implementation of customized demand response programs for each group. Strategies for participating in demand response programs can be formulated based on the priority levels of users, helping to balance grid demand. For irregular users, incentive measures can be introduced to encourage them to adjust their charging patterns, optimizing grid interaction.
5. Conclusions
- (1)
- Based on the user profile model, four types of user groups and their priorities were identified, which formed the basis for the differentiated settings of users in the EV scheduling model.
- (2)
- According to the different priorities of the user groups, the feature values of each EV user were calculated and input into the scheduling model.
- (3)
- By comparing the EV scheduling model before and after optimization, adjusting the charging times of users effectively reduces charging costs, stabilizes grid load fluctuations, and improves the efficiency of orderly charging, preliminarily verifying the effectiveness of the strategy.
- (4)
- Based on satisfying user electricity demand and assessing the potential for user response, this study validates the feasibility of certain user group portraits through three charging scheduling scenarios. The experimental results demonstrate that when considering the charging cost of EV users as a single objective function, the charging cost is reduced by 47.42% compared to unstructured charging. When both the charging cost and load fluctuation of EV users are considered as dual objective functions, the charging cost of EV users and the load fluctuation of the charging station are reduced by 41.76% and 31.07%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| EVs | Electric vehicles |
| DBSCAN | Density-based spatial clustering of applications with noise |
| FCM | Fuzzy c-means |
| GMM | Gaussian mixture model |
| Variables | |
| EV arrival time | |
| EV departure time | |
| EV parking time | |
| Objective function | |
| Fuzzy index | |
| The data volume | |
| The number of clustering centers | |
| -th center | |
| -th sample | |
| . | |
| The similarity (distance) of data | |
| The number of iteration steps | |
| The result of arrival time and parking time clustering | |
| The result of charging time clustering | |
| The error threshold | |
| EV | |
| EV | |
| EV | |
| EV | |
| EV | |
| EV | |
| EV. | |
| EV | |
| EV | |
| time period | |
| time period | |
| The duration of each time period | |
| The variance of the load curve of EVS within the region | |
| The average power consumption of EVS within the region during the day | |
| EV | |
| EV | |
| The charging power of the charging pile | |
| The EV charging efficiency | |
| EV | |
Appendix A
| UserID | K1G1 | K1G2 | K2G1 | K2G2 | K3G1 | K3G2 | K4G1 | K4G2 | K4G3 | Maximum Proportion | Portrait Category | Proportion | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 324 | 0.00% | 4.67% | 0.00% | 11.33% | 0.00% | 0.67% | 0.00% | 83.33% | 0.00% | 83.33% | K4G2 | 83.33% | ||
| 1082 | 0.00% | 7.43% | 0.00% | 0.00% | 0.00% | 6.29% | 0.00% | 82.29% | 3.43% | 82.29% | K4G2 | 82.29% | ||
| 567 | 1.85% | 11.73% | 0.00% | 1.85% | 0.00% | 1.23% | 1.85% | 77.78% | 3.70% | 77.78% | K4G2 | 77.78% | ||
| 754 | 0.00% | 18.18% | 0.00% | 0.00% | 3.03% | 77.27% | 0.00% | 0.00% | 1.52% | 77.27% | K3G2 | 77.27% | ||
| 858 | 1.21% | 3.03% | 3.03% | 9.09% | 0.00% | 1.21% | 4.85% | 76.97% | 0.61% | 76.97% | K4G2 | 76.97% | ||
| 1099 | 0.00% | 0.00% | 0.00% | 0.00% | 23.19% | 76.81% | 0.00% | 0.00% | 0.00% | 76.81% | K3G2 | 76.81% | ||
| 609 | 0.00% | 76.67% | 0.00% | 20.00% | 0.00% | 3.33% | 0.00% | 0.00% | 0.00% | 76.67% | K1G2 | 76.67% | ||
| 1126 | 1.16% | 9.30% | 0.00% | 6.98% | 0.00% | 1.16% | 6.98% | 73.26% | 1.16% | 73.26% | K4G2 | 73.26% | ||
| 743 | 0.00% | 3.82% | 0.00% | 44.71% | 0.00% | 0.88% | 0.88% | 49.71% | 0.00% | 49.71% | K4G2 | K2G2 | 94.41% | |
| 1746 | 0.00% | 61.29% | 0.00% | 3.23% | 2.42% | 33.06% | 0.00% | 0.00% | 0.00% | 61.29% | K1G2 | K3G2 | 94.35% | |
| 1133 | 0.00% | 8.08% | 1.01% | 34.34% | 0.00% | 55.56% | 0.00% | 0.00% | 1.01% | 55.56% | K3G2 | K2G2 | 89.90% | |
| 676 | 3.13% | 1.04% | 1.04% | 0.00% | 0.00% | 1.04% | 56.25% | 3.13% | 33.33% | 56.25% | K4G1 | K4G3 | 89.58% | |
| 712 | 3.27% | 4.67% | 2.34% | 3.27% | 0.00% | 0.00% | 20.56% | 62.15% | 3.74% | 62.15% | K4G1 | K4G2 | 82.71% | |
| 1124 | 10.81% | 68.65% | 0.00% | 0.54% | 0.00% | 0.00% | 2.16% | 14.05% | 1.08% | 68.65% | K1G2 | K4G2 | 82.70% | |
| 559 | 3.65% | 2.19% | 4.38% | 2.19% | 0.00% | 0.73% | 49.64% | 32.85% | 3.65% | 49.64% | K4G1 | K4G2 | 82.48% | |
| 1161 | 4.76% | 45.24% | 1.19% | 5.95% | 1.19% | 36.90% | 2.38% | 2.38% | 0.00% | 45.24% | K1G2 | K3G2 | 82.14% | |
| 777 | 61.11% | 1.39% | 8.33% | 1.39% | 19.44% | 1.39% | 1.39% | 1.39% | 0.00% | 61.11% | K1G1 | K3G1 | 80.56% | |
| 1164 | 0.00% | 9.41% | 1.18% | 4.71% | 0.00% | 36.47% | 3.53% | 43.53% | 1.18% | 43.53% | K4G2 | K3G2 | 80.00% | |
| 620 | 5.56% | 4.44% | 0.00% | 7.78% | 0.00% | 0.00% | 25.56% | 54.44% | 2.22% | 54.44% | K4G2 | K4G1 | 80.00% | |
| 69 | 0.78% | 7.75% | 2.33% | 7.75% | 0.00% | 0.78% | 13.18% | 66.67% | 0.00% | 66.67% | K4G1 | K4G2 | 79.84% | |
| 891 | 0.87% | 19.05% | 0.00% | 23.81% | 0.00% | 0.00% | 1.30% | 54.55% | 0.43% | 54.55% | K2G2 | K4G2 | 78.35% | |
| 558 | 1.13% | 0.56% | 1.69% | 2.82% | 0.00% | 2.26% | 20.34% | 57.06% | 14.12% | 57.06% | K4G1 | K4G2 | 77.40% | |
| 818 | 4.94% | 6.17% | 4.94% | 3.70% | 0.00% | 2.47% | 18.52% | 2.47% | 58.02% | 58.02% | K4G3 | K4G1 | 76.54% | |
| 714 | 3.29% | 4.61% | 1.32% | 2.63% | 0.00% | 0.66% | 33.55% | 42.76% | 10.53% | 42.76% | K4G2 | K4G1 | 76.32% | |
| 945 | 1.22% | 3.66% | 1.22% | 6.10% | 0.00% | 0.00% | 18.29% | 56.10% | 13.41% | 56.10% | K4G1 | K4G2 | 74.39% | |
| 1912 | 1.08% | 19.35% | 2.15% | 23.66% | 0.00% | 0.00% | 2.15% | 50.54% | 1.08% | 50.54% | K4G2 | K2G2 | 74.19% | |
| 562 | 1.14% | 34.22% | 3.80% | 39.92% | 0.00% | 0.00% | 1.14% | 19.77% | 0.00% | 39.92% | K2G2 | K1G2 | 74.14% | |
| 560 | 2.59% | 44.04% | 30.05% | 3.63% | 0.00% | 1.04% | 14.51% | 1.04% | 3.11% | 44.04% | K1G2 | K2G1 | 74.09% | |
| 1534 | 1.03% | 1.03% | 4.12% | 8.25% | 0.00% | 0.00% | 38.14% | 35.05% | 12.37% | 38.14% | K4G1 | K4G2 | 73.20% | |
| 1104 | 2.84% | 9.22% | 9.22% | 1.42% | 0.00% | 0.00% | 59.57% | 4.26% | 13.48% | 59.57% | K4G1 | K4G3 | 73.05% | |
| 1095 | 2.33% | 1.16% | 4.07% | 5.81% | 0.00% | 0.00% | 27.91% | 42.44% | 15.70% | 42.44% | K4G2 | K4G1 | 70.35% | |
| 1222 | 0.00% | 32.14% | 3.57% | 19.64% | 0.00% | 7.14% | 0.00% | 37.50% | 0.00% | 37.50% | K1G2 | K4G2 | 69.64% | |
| 632 | 2.56% | 2.56% | 3.85% | 3.85% | 0.00% | 1.28% | 37.18% | 11.54% | 32.05% | 37.18% | K4G1 | K4G3 | 69.23% | |
| 2170 | 2.88% | 2.88% | 0.00% | 5.77% | 0.00% | 0.00% | 28.85% | 28.85% | 30.77% | 30.77% | K4G3 | K4G1 | K4G2 | 88.46% |
| 1366 | 0.00% | 28.68% | 0.78% | 33.33% | 0.00% | 10.08% | 0.78% | 25.58% | 0.78% | 33.33% | K4G2 | K1G2 | K4G2 | 87.60% |
| 1108 | 7.14% | 5.71% | 0.00% | 41.43% | 25.71% | 18.57% | 1.43% | 0.00% | 0.00% | 41.43% | K4G2 | K3G2 | K3G1 | 85.71% |
| 668 | 2.22% | 22.22% | 5.56% | 41.11% | 0.00% | 0.00% | 6.67% | 21.11% | 1.11% | 41.11% | K4G2 | K1G2 | K4G2 | 84.44% |
| 1202 | 36.59% | 21.95% | 2.44% | 2.44% | 4.88% | 21.95% | 9.76% | 0.00% | 0.00% | 36.59% | K1G1 | K1G2 | K3G2 | 80.49% |
| 1154 | 2.90% | 7.25% | 7.25% | 7.25% | 0.00% | 0.00% | 26.09% | 31.88% | 17.39% | 31.88% | K4G2 | K4G1 | K4G3 | 75.36% |
| 2461 | 1.33% | 12.00% | 4.00% | 25.33% | 0.00% | 0.00% | 12.00% | 37.33% | 6.67% | 37.33% | K4G2 | K4G2 | K4G1 | 74.67% |
| 431 | 5.41% | 24.32% | 6.76% | 28.38% | 0.00% | 4.05% | 10.81% | 20.27% | 0.00% | 28.38% | K4G2 | K1G2 | K4G2 | 72.97% |
| 832 | 45.65% | 6.52% | 13.04% | 2.17% | 0.00% | 0.00% | 13.04% | 2.17% | 11.96% | 45.65% | K1G1 | K2G1 | K4G1 | 71.74% |
| 569 | 5.67% | 4.12% | 11.34% | 8.76% | 0.00% | 0.00% | 8.76% | 13.40% | 46.91% | 46.91% | K4G3 | K4G2 | K2G1 | 71.65% |
| 850 | 8.16% | 6.12% | 8.16% | 8.16% | 2.04% | 2.04% | 48.98% | 14.29% | 2.04% | 48.98% | K4G1 | K4G2 | K1G1 | 71.43% |
| 838 | 34.78% | 8.70% | 1.45% | 8.70% | 23.19% | 11.59% | 8.70% | 0.00% | 0.00% | 34.78% | K1G1 | K3G1 | K3G2 | 69.57% |
| 515 | 16.67% | 31.82% | 7.58% | 16.67% | 0.00% | 0.00% | 7.58% | 13.64% | 6.06% | 31.82% | K1G2 | K1G1 | K2G2 | 65.15% |
| 1135 | 15.24% | 23.81% | 13.33% | 8.57% | 25.71% | 8.57% | 4.76% | 0.00% | 0.00% | 25.71% | K3G1 | K1G2 | K1G1 | 64.76% |
| 1524 | 7.81% | 3.13% | 12.50% | 15.63% | 0.00% | 1.56% | 15.63% | 10.94% | 31.25% | 31.25% | K4G3 | K4G1 | K2G2 | 62.50% |
| 1001 | 7.50% | 10.00% | 8.75% | 15.00% | 0.00% | 0.00% | 12.50% | 26.25% | 20.00% | 26.25% | K4G2 | K4G3 | K2G2 | 61.25% |
| 1470 | 4.47% | 8.38% | 12.29% | 13.97% | 0.00% | 0.00% | 22.35% | 13.97% | 24.58% | 24.58% | K4G3 | K4G1 | K4G2 | 60.89% |
| 1083 | 16.48% | 26.37% | 3.30% | 14.84% | 0.00% | 4.40% | 6.59% | 13.74% | 13.19% | 26.37% | K1G2 | K1G1 | K2G2 | 57.69% |
| 248 | 13.24% | 10.29% | 14.71% | 23.53% | 1.47% | 5.88% | 10.29% | 2.94% | 17.65% | 23.53% | K2G2 | K4G3 | K4G1 | 55.88% |
| 1137 | 13.75% | 15.00% | 17.50% | 15.00% | 0.00% | 0.00% | 11.25% | 10.00% | 16.25% | 17.50% | K1G1 | K1G2 | K2G1 | 48.75% |
References
- Saleh, M.; Milovanoff, A.; Posen, I.D.; MacLean, H.L.; Hatzopoulou, M. Energy and greenhouse gas implications of shared automated electric vehicles. Transp. Res. Part D Transp. Environ. 2022, 105, 103233. [Google Scholar] [CrossRef]
- Ji, Z.; Huang, X. Plug-in electric vehicle charging infrastructure deployment of China towards 2020: Policies, methodologies, and challenges. Renew. Sustain. Energy Rev. 2018, 90, 710–727. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2021; International Energy Agency: Paris, France, 2021. [Google Scholar]
- O’Connell, A.; Flynn, D.; Keane, A. Rolling Multi-Period Optimization to Control Electric Vehicle Charging in Distribution Networks. IEEE PES Gen. Meet. Conf. Expo. 2014, 29, 340–348. [Google Scholar]
- Axsen, J.; Bailey, J.; Castro, M.A. Preference and lifestyle heterogeneity among potential plug-in electric vehicle buyers. Energy Econ. 2015, 50, 190–201. [Google Scholar] [CrossRef]
- Münzel, C.; Plötz, P.; Sprei, F.; Gnann, T. How large is the effect of financial incentives on electric vehicle sales?—A global review and European analysis. Energy Econ. 2019, 84, 104493. [Google Scholar] [CrossRef]
- Yin, W.; Ming, Z.; Wen, T. Scheduling strategy of electric vehicle charging considering different requirements of grid and users. Energy 2021, 232, 121118. [Google Scholar] [CrossRef]
- Muhtadi, A.; Pandit, D.; Nguyen, N.; Mitra, J. Distributed energy resources based microgrid: Review of architecture, control, and reliability. IEEE Trans. Ind. Appl. 2021, 3, 2223–2235. [Google Scholar] [CrossRef]
- Chen, H.; Huang, B. Integrated G2V/V2G switched reluctance motor drive with sensing only switch-bus current. IEEE Trans. Power Electron. 2021, 8, 9372–9381. [Google Scholar] [CrossRef]
- Saber, H.; Ehsan, M.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M.; Lehtonen, M. Network-constrained transactive coordination for plug-in electric vehicles participation in real-time retail electricity markets. IEEE Trans. Sustain. Energy 2021, 2, 1439–1448. [Google Scholar] [CrossRef]
- Dong, C.; Chu, R.; Morstyn, T.; McCulloch, M.D.; Jia, H. Online rolling evolutionary decoder-dispatch framework for the secondary frequency regulation of time-varying electrical-grid-electric-vehicle system. IEEE Trans. Smart Grid 2021, 1, 871–884. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S.H. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 2, 940–951. [Google Scholar] [CrossRef]
- Solanke, T.U.; Ramachandaramurthy, V.K.; Yong, J.Y.; Pasupuleti, J.; Kasinathan, K.; Rajagopalan, A. A review of strategic charging–discharging control of grid-connected electric vehicles. J. Energy Storage 2020, 28, 101193. [Google Scholar] [CrossRef]
- Yong, J.Y.; Tan, W.S.; Khorasany, M.; Razzaghi, R. Electric vehicles destination charging: An overview of charging tariffs, business models and coordination strategies. Renew. Sust. Energy. Rev. 2023, 184, 113534. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, Z.; Shang, D.; Zhao, Z.; Chen, H. Charging Load Prediction and Distribution Network Reliability Evaluation Considering Electric Vehicles’ Spatial-Temporal Transfer Randomness. IEEE Access 2020, 8, 124084–124096. [Google Scholar] [CrossRef]
- Huang, A.; Mao, Y.; Chen, X.; Xu, Y.; Wu, S. A multi-timescale energy scheduling model for microgrid embedded with differentiated electric vehicle charging management strategies. Sustain. Cities Soc. 2024, 101, 105123. [Google Scholar] [CrossRef]
- Singh, S.; Vaidya, B.; Mouftah, H.T. Smart EV Charging Strategies Based on Charging Behavior. Front. Energy Res. 2022, 10, 773440. [Google Scholar] [CrossRef]
- Kim, J.D. Insights into residential EV charging behavior using energy meter data. Energy Pol. 2019, 129, 610–618. [Google Scholar] [CrossRef]
- Weldon, P.; Morrissey, P.; Brady, J.; O’Mahony, M. An investigation into usage patterns of electric vehicles in Ireland. Transp. Res Transp. Env. 2016, 43, 207–225. [Google Scholar] [CrossRef]
- Sun, X.-H.; Yamamoto, T.; Morikawa, T. Charge timing choice behavior of battery electric vehicle users. Transp. Res. Transp. Environ. 2015, 37, 97–107. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, R.; Wang, H.; Cai, H. Optimal battery electric vehicles range: A study considering heterogeneous travel patterns, charging behaviors, and access to charging infrastructure. Energy 2020, 197, 116945. [Google Scholar] [CrossRef]
- Gschwendtner, C.; Knoeri, C.; Stephan, A. The impacts of plug-in behavior on the spatial–temporal flexibility of electric vehicle charging load. Sustain. Cities Soc. 2023, 88, 104263. [Google Scholar] [CrossRef]
- Tian, J.; Lv, Y.; Zhao, Q.; Gong, Y.; Li, C.; Ding, H.; Yu, Y. Electric vehicle charging load prediction considering the orderly charging. Energy Rep. 2022, 8, 124–134. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Hooper, G.; Chase, J. Driving change: Electric vehicle charging behavior and peak loading. Renew. Sustain. Energy Rev. 2024, 189, 113953. [Google Scholar] [CrossRef]
- Chen, J.; Ai, Q.; Xiao, F. Electric vehicle charging station planning based on user travel demand. Electr. Power Autom. Equip. 2016, 36, 34–39. [Google Scholar]
- Philipsen, R.; Brell, T.; Brost, W.; Eickels, T.; Ziefle, M. Running on empty—Users’ charging behavior of electric vehicles versus traditional refueling. Transp. Res. Part F Traffic Psychol. Behav. 2018, 59, 475–492. [Google Scholar] [CrossRef]
- Wei, W.; Wu, D.; Wu, Q.; Shafie-Khah, M.; Catalão, J.P.S. Interdependence between transportation system and power distribution system: A comprehensive review on models and applications. J. Mod. Power Syst. Clean Energy 2019, 7, 433–448. [Google Scholar] [CrossRef]
- Wei, W.; Mei, S.; Wu, L.; Shahidehpour, M.; Fang, Y. Optimal traffic-power flow in urban electrified transportation networks. IEEE Trans. Smart Grid 2017, 8, 84–95. [Google Scholar] [CrossRef]
- Yao, W.; Zhao, J.; Wen, F.; Dong, Z.; Xue, Y.; Xu, Y.; Meng, K. A multi-objective collaborative planning strategy for integrated power distribution and electric vehicle charging systems. IEEE Trans. Power Syst. 2014, 9, 1811–1821. [Google Scholar] [CrossRef]
- Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. Coordinated planning strategy for electric vehicle charging stations and coupled traffic-electric networks. IEEE Trans. Power Syst. 2019, 34, 268–279. [Google Scholar] [CrossRef]
- Hou, K.; Xu, X.; Jia, H.; Yu, X.; Jiang, T.; Zhang, K.; Shu, B. A reliability assessment approach for integrated transportation and electrical power systems incorporating electric vehicles. IEEE Trans. Smart Grid 2018, 9, 88–100. [Google Scholar] [CrossRef]
- Meng, J.; Mu, Y.; Jia, H.; Wu, J.; Yu, X.; Qu, B. Dynamic frequency response from electric vehicles considering travelling behavior in the Great Britain power system. Appl. Energy 2016, 162, 966–979. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Hossain Lipu, M.S.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Xydas, E.; Marmaras, C.; Cipcigan, L.M.; Jenkins, N.; Carroll, S.; Barker, M. A A data driven approach for characterizing the charging demand of electric vehicles: A UK case study. Appl. Energy 2016, 162, 763–771. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J. Multi-source Data Driven Electric Vehicle User Identification Method. Electr. Power Syst. Autom. 2023, 35, 141–147. [Google Scholar]
- Bui, V.-H.; Hussain, A.; Zarrabian, S.; Kump, P.M.; Su, W. Clustering-based optimal operation of charging stations under high penetration of electric vehicles. Sustain. Energy Grids Netw. 2023, 36, 101178. [Google Scholar] [CrossRef]
- Xu, J.; Feng, G.; Zhao, T.; Sun, X.; Zhu, M. Remote sensing image classification based on semi-supervised adaptive interval Type-2 fuzzy C-Means algorithm. Comput. Geosci. 2019, 131, 132–143. [Google Scholar] [CrossRef]
- Li, S.; Cheng, Y.; Lin, S. A FCM-based deterministic forecasting model for fuzzy time series. Comput. Math. Appl. 2008, 12, 3052–3063. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, B.; Chu, C.-C.; Gadh, R. Vehicle grid integration for demand response with mixture user model and decentralized optimization. Appl. Energy 2018, 231, 481–493. [Google Scholar] [CrossRef]
- Chung, Y.-W.; Khaki, B.; Li, T.; Chu, C.; Gadh, R. Ensemble machine learning-based algorithm for electric vehicle user behavior prediction. Appl. Energy 2019, 254, 113732. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Shen, Y. Industrial customer group portrait method based on potential quantization model of load control. Electr. Power Autom. Equip. 2021, 41, 208–216. [Google Scholar]
- Vagropoulos, S.I.; Keranidis, S.D.; Afentoulis, K.D.; Bampos, Z.N.; Laitsos, V.M. Electric vehicle smart charging business case-outcomes and prospects for electric vehicle aggregators. In Proceedings of the 2023 19th International Conference on the European Energy Market (EEM), Lappeenranta, Finland, 6–8 June 2023; pp. 1–7. [Google Scholar]
- Wang, R.; Mu, J.; Sun, Z.; Wang, J.; Hu, A. NSGA-II multi-objective optimization regional electricity price model for electric vehicle charging based on travel law. Energy Rep. 2021, 7, 1495–1503. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, X.C.; Wei, R.; Chen, X.; Dai, J. Electric vehicle charging demand forecasting using deep learning model. J. Intell. Transp. Syst. 2022, 26, 690–703. [Google Scholar] [CrossRef]
- Lee, Z.J.; Pang, J.Z.; Low, S.H. Pricing EV charging service with demand charge. Electr. Power Syst. Res. 2020, 189, 106694. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Song, Z. Joint optimization of electric bus charging infrastructure, vehicle scheduling, and charging management. Transp. Res. D Transp. Environ. 2023, 117, 103653. [Google Scholar] [CrossRef]



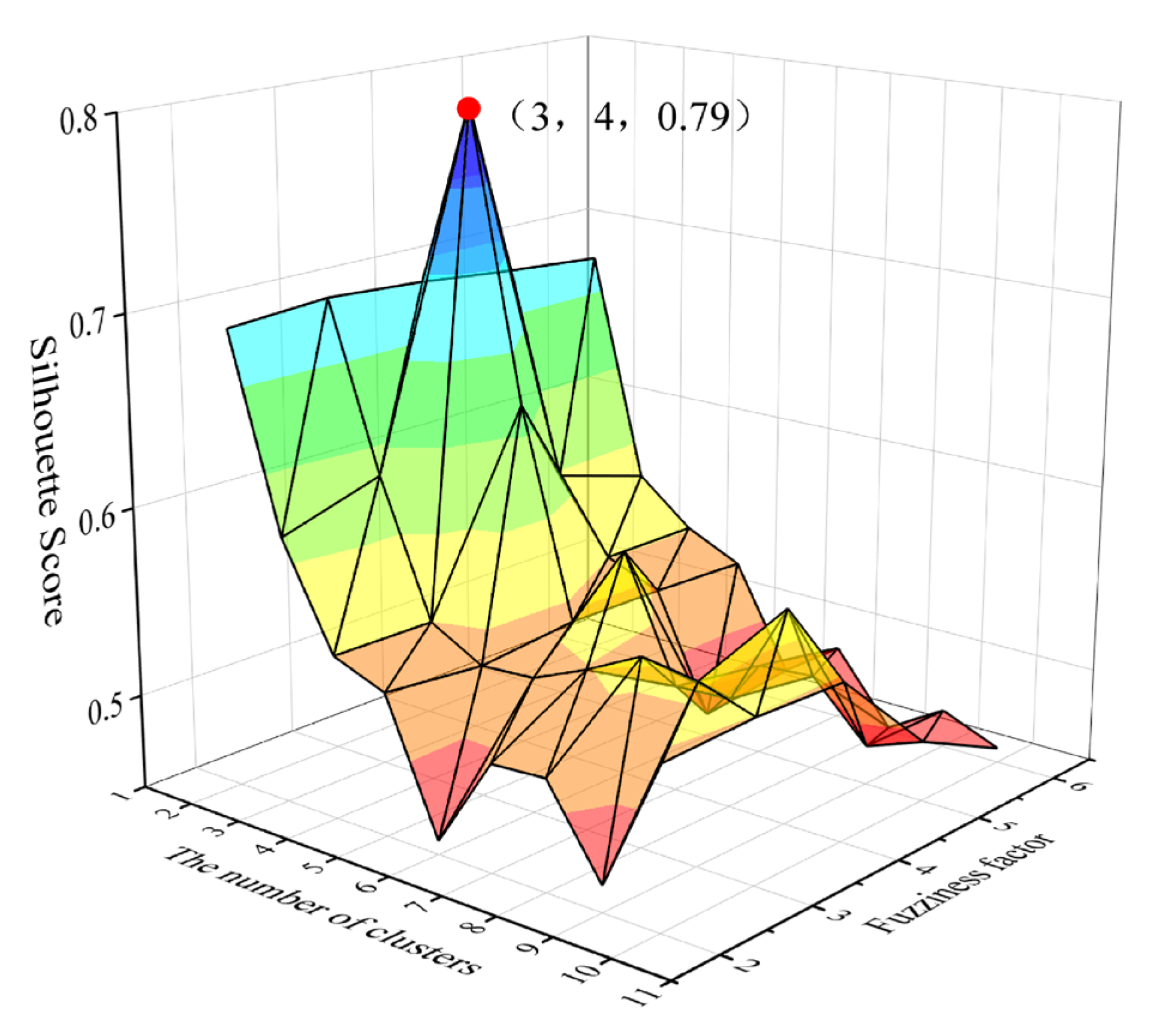
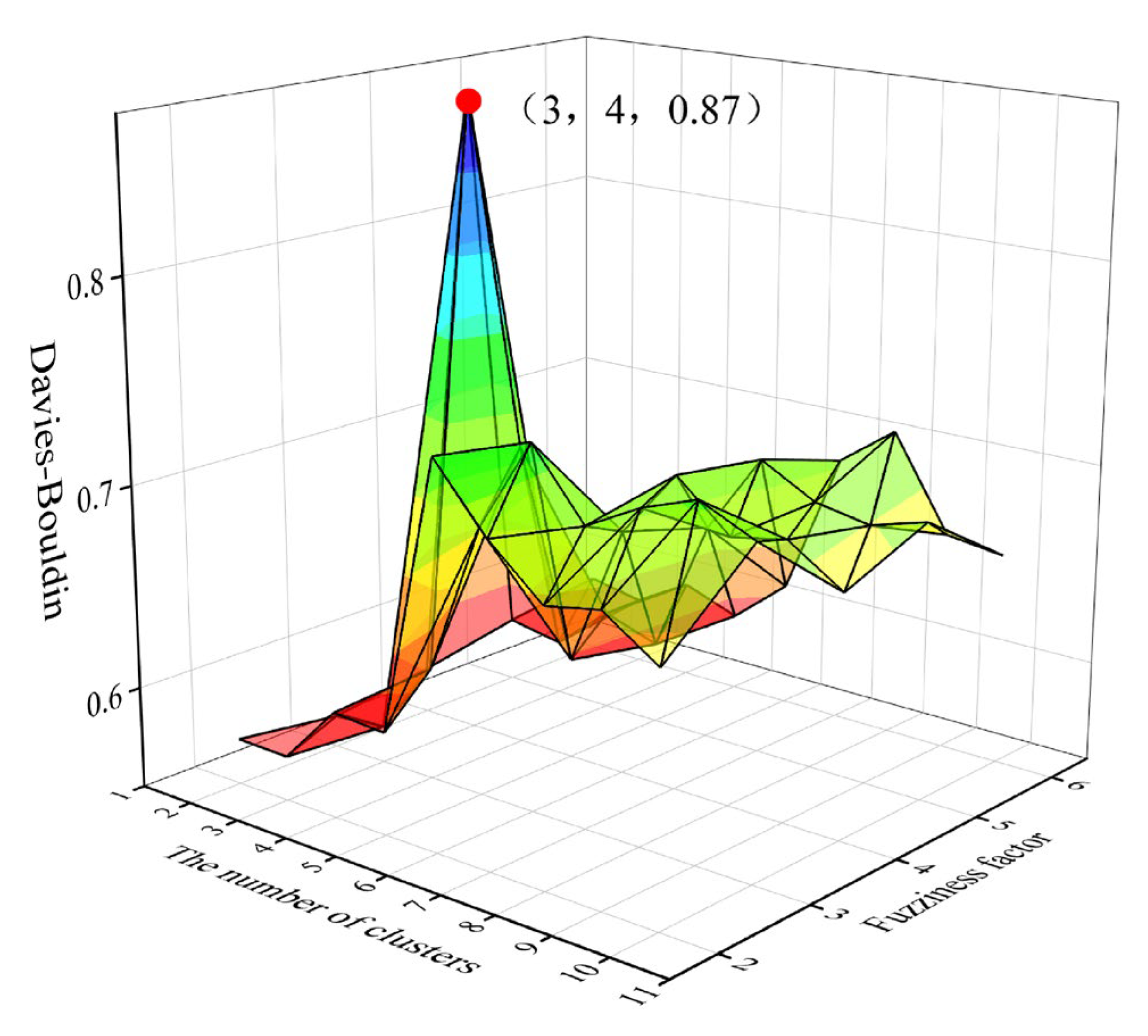



| Fuzziness Factor | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| K | ||||||
| 2 | 0.389443 | 0.395071 | 0.393793 | 0.392867 | 0.392487 | |
| 3 | 0.532903 | 0.531693 | 0.529861 | 0.459066 | 0.234224 | |
| 4 | 0.631191 | 0.382821 | 0.373935 | 0.367385 | 0.272961 | |
| 5 | 0.410918 | 0.405724 | 0.398312 | 0.392735 | 0.195995 | |
| 6 | 0.386903 | 0.344528 | 0.321615 | 0.312594 | 0.306506 | |
| 7 | 0.372883 | 0.337231 | 0.353385 | 0.317599 | 0.142264 | |
| 8 | 0.364074 | 0.337235 | 0.315556 | 0.306669 | 0.294148 | |
| 9 | 0.358419 | 0.327525 | 0.277566 | 0.269329 | 0.171575 | |
| 10 | 0.3556 | 0.330718 | 0.305587 | 0.283643 | 0.27148 | |
| Fuzziness Factor | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| K | ||||||
| 2 | 1.297386 | 1.308402 | 1.302959 | 1.29969 | 1.265925 | |
| 3 | 1.348359 | 0.616996 | 0.618025 | 0.858865 | 0.616264 | |
| 4 | 1.474923 | 0.85197 | 0.851415 | 0.845798 | 1.662239 | |
| 5 | 1.119099 | 0.780511 | 0.796129 | 0.806442 | 0.763778 | |
| 6 | 0.995778 | 0.861625 | 0.950117 | 0.9807 | 0.793255 | |
| 7 | 1.155263 | 0.860409 | 0.963581 | 1.011551 | 0.838428 | |
| 8 | 1.092277 | 0.876527 | 0.88891 | 1.016422 | 0.844842 | |
| 9 | 1.210399 | 0.922233 | 1.061232 | 1.037081 | 0.884294 | |
| 10 | 1.07599 | 0.936428 | 1.017053 | 1.057625 | 0.884567 | |
| Fuzziness Factor | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| K | ||||||
| 2 | 0.691652 | 0.695154 | 0.691652 | 0.686091 | 0.681525 | |
| 3 | 0.590455 | 0.607002 | 0.790455 | 0.576179 | 0.56041 | |
| 4 | 0.536281 | 0.535715 | 0.636281 | 0.536453 | 0.536589 | |
| 5 | 0.525425 | 0.520158 | 0.525425 | 0.524821 | 0.522881 | |
| 6 | 0.457113 | 0.522049 | 0.571373 | 0.462612 | 0.468237 | |
| 7 | 0.506349 | 0.534602 | 0.506349 | 0.498334 | 0.489293 | |
| 8 | 0.508161 | 0.549598 | 0.508161 | 0.500806 | 0.451887 | |
| 9 | 0.463691 | 0.54531 | 0.563691 | 0.470788 | 0.470259 | |
| 10 | 0.533726 | 0.53577 | 0.533726 | 0.482042 | 0.457723 | |
| Fuzziness Factor | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| K | ||||||
| 2 | 0.57263 | 0.565634 | 0.57263 | 0.581957 | 0.588573 | |
| 3 | 0.572094 | 0.568296 | 0.872094 | 0.577003 | 0.583342 | |
| 4 | 0.602113 | 0.605636 | 0.702113 | 0.600107 | 0.599057 | |
| 5 | 0.600321 | 0.682988 | 0.600321 | 0.590946 | 0.589008 | |
| 6 | 0.737542 | 0.73023 | 0.672308 | 0.658926 | 0.612362 | |
| 7 | 0.706368 | 0.696925 | 0.706368 | 0.699832 | 0.685206 | |
| 8 | 0.682917 | 0.711881 | 0.682917 | 0.684912 | 0.705973 | |
| 9 | 0.68834 | 0.722074 | 0.68834 | 0.679799 | 0.659787 | |
| 10 | 0.670146 | 0.709694 | 0.670146 | 0.687916 | 0.655985 | |
| Portrait Category | K1G1 | K1G2 | K2G1 | K2G2 | K3G1 | K3G2 | K4G1 | K4G2 | K4G3 |
|---|---|---|---|---|---|---|---|---|---|
| Scheduling duration | 0:00–1:55 | 0:25–4:13 | 0:00–1:49 | 0:00–2:53 | 0:00–0:53 | 0:00–1:43 | 3:07–7:04 | 5:35–9:15 | 0:00–2:37 |
| Data volume | 338 | 964 | 283 | 833 | 101 | 371 | 821 | 1999 | 543 |
| Arrival time | 19:15–22:07 | 19:35–22:20 | 14:34–17:42 | 14:58–17:46 | 0:34–3:02 | 0:46–3:19 | 15:09–17:49 | 15:37–18:03 | 15:03–17:35 |
| Time of Arrival | User Behavior Portrait Prioritization |
|---|---|
| Valley period | K3G1, K3G2 |
| Flat period | K1G1, K1G2 |
| Peak period | K2G1, K2G2, K4G1, K4G2, K4G3 |
| Weekday–Weekend Charging Categories | User ID |
|---|---|
| Weekdays | 515, 558, 559, 560, 562, 620, 668, 676, 832, 1095, 1124, 1137, 1534, 1912, 1082, 567, 714, 69, 2170, 1126, 632, 2461, 850, 569, 1470, 858, 1104, 945, 1001, 1154, 1164, 1524, 431, 818, 712, 1099, 324, 1366, 1154 |
| Weekdays and Weekends | 1108, 777, 609, 1202, 1222, 754, 1135, 1083, 838, 891, 1161, 743, 1746, 1133 |
| Weekends | 248 |
| Periods | Price/(kWh) |
|---|---|
| 00:00–08:00 | 0.0562 |
| 08:00–12:00 | 0.0925 |
| 12:00–19:00 | 0.2675 |
| 19:00–23:00 | 0.0925 |
| 23:00–24:00 | 0.0562 |
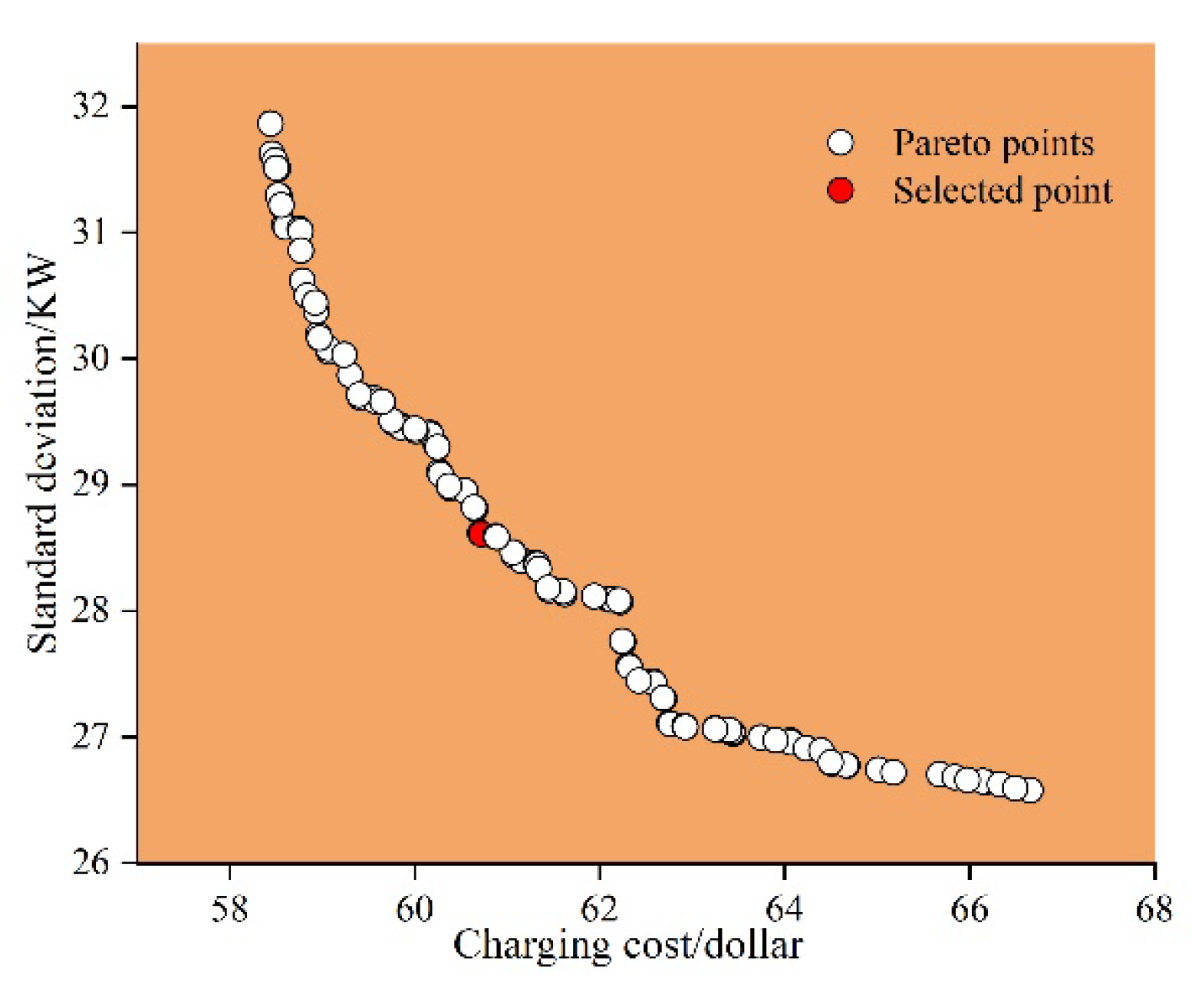
| Scheduling Model | Overall Charging Cost (USD) | Standard Deviation |
|---|---|---|
| Actual charging | 104.25 | 41.5524 kW |
| Single objective | 54.8169 | 38.1269 kW |
| Dual objective | 60.7204 | 28.6401 kW |
| Weekday EVs | Weekend EVs | ||
|---|---|---|---|
| Vehicle ID | 515, 558, 559, 560, 562, 620, 668, 676,832, 1095, 1124, 1137, 1534, 1912, 1083, 567, 714, 69, 2170, 1126, 632, 2461, 850, 569, 1470, 588, 1104, 945, 1001, 1154, 1164, 1524, 431, 818, 712, 1099, 324, 1366, 1154, 777, 609, 1202, 1222, 754, 1135, 1083, 838, 891, 1161, 743, 1746, 1133, 1108 | 777, 609, 248, 1222, 754, 1135, 1083, 838, 891, 1161, 743, 1746, 1133, 1108, 1202 | |
| Valley period (23:00–8:00) | Category 1 | 1099, 754 | 754 |
| Category 2 | 1133, 1746, 1161, 777, 1164 | 1133, 1746, 1161, 777 | |
| Category 3 | 1108, 1202 | 1108, 1202 | |
| Irregular EVs | 1135, 838 | 1135, 838 | |
| Flat period (8:00–12:00) (19:00–23:00) | Category 1 | 324, 1083, 567, 858, 1126 | 1083 |
| Category 2 | 743, 676, 712, 559, 1164, 620, 69, 891, 558, 818, 714, 945, 1912, 562, 1534, 1104, 1095, 632, 1133, 1124, 560, 1222 | 743, 891, 1133, 1222 | |
| Category 3 | 2170, 1366, 1108, 668, 1154, 2461, 569, 850, 431, 832 | 1108 | |
| Irregular EVs | 1524, 1001, 1470, 248 | 248 | |
| Peak period (12:00–19:00) | Category 1 | 609 | 609 |
| Category 2 | 1746, 1124, 1161, 777, 560, 1222, 562 | 1161, 777, 1222 | |
| Category 3 | 1202, 832, 1366, 668, 431, 850 | 1202 | |
| Irregular EVs | 515, 838, 1083, 1137, 1135 | 838, 1135 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, A.; Zhang, G.; Tian, C.; Peng, W.; Liu, Y. Charging Behavior Portrait of Electric Vehicle Users Based on Fuzzy C-Means Clustering Algorithm. Energies 2024, 17, 1651. https://doi.org/10.3390/en17071651
Yang A, Zhang G, Tian C, Peng W, Liu Y. Charging Behavior Portrait of Electric Vehicle Users Based on Fuzzy C-Means Clustering Algorithm. Energies. 2024; 17(7):1651. https://doi.org/10.3390/en17071651
Chicago/Turabian StyleYang, Aixin, Guiqing Zhang, Chenlu Tian, Wei Peng, and Yechun Liu. 2024. "Charging Behavior Portrait of Electric Vehicle Users Based on Fuzzy C-Means Clustering Algorithm" Energies 17, no. 7: 1651. https://doi.org/10.3390/en17071651
APA StyleYang, A., Zhang, G., Tian, C., Peng, W., & Liu, Y. (2024). Charging Behavior Portrait of Electric Vehicle Users Based on Fuzzy C-Means Clustering Algorithm. Energies, 17(7), 1651. https://doi.org/10.3390/en17071651






