Influence of the Skin and Proximity Effects on the Thermal Field in Flat and Trefoil Three-Phase Systems with Round Conductors
Abstract
:1. Introduction
2. Methodology
2.1. Physical Model
2.2. Current Density
2.3. Mathematical Model of Thermal Field
2.4. Solving Methodology
3. Results and Discussion
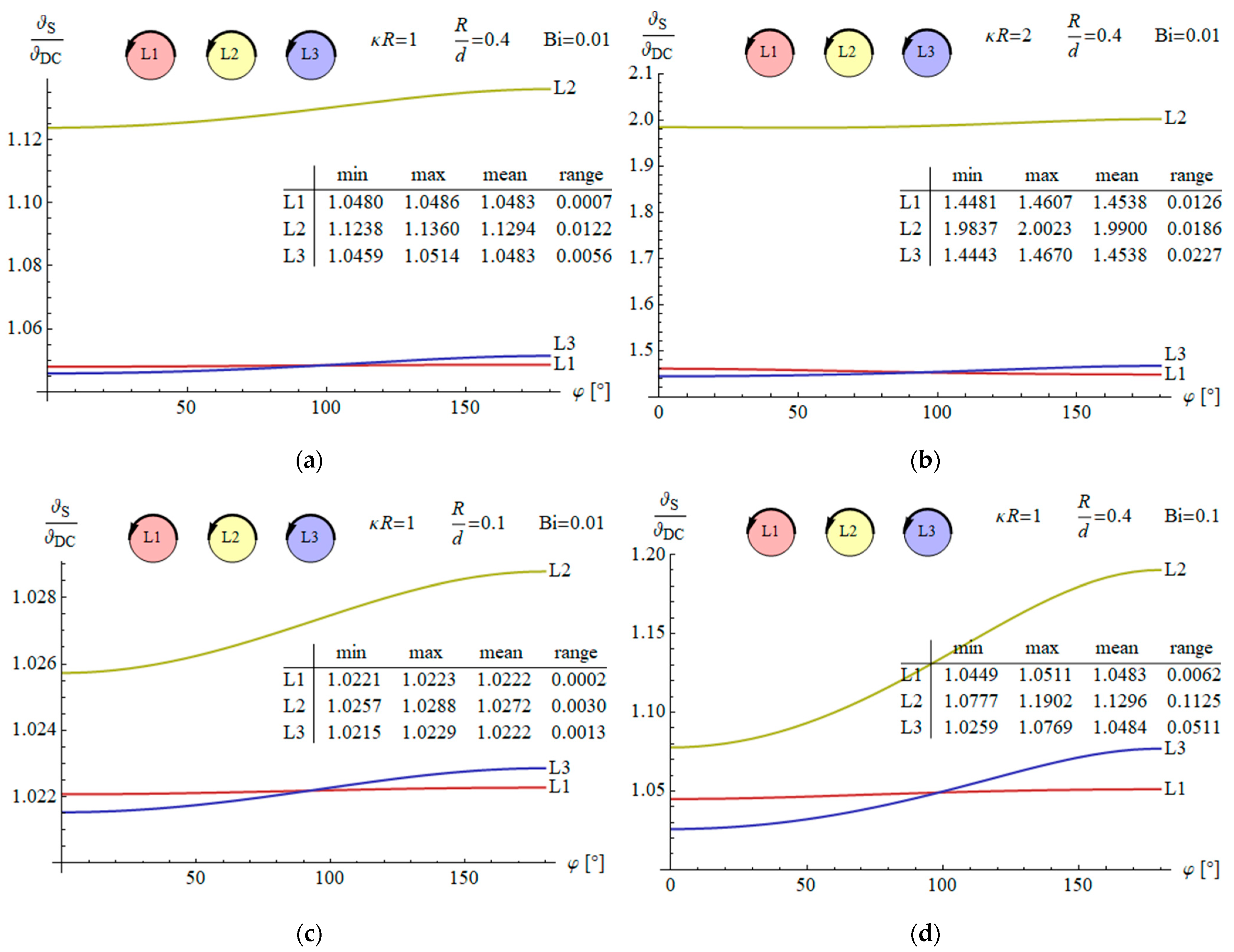
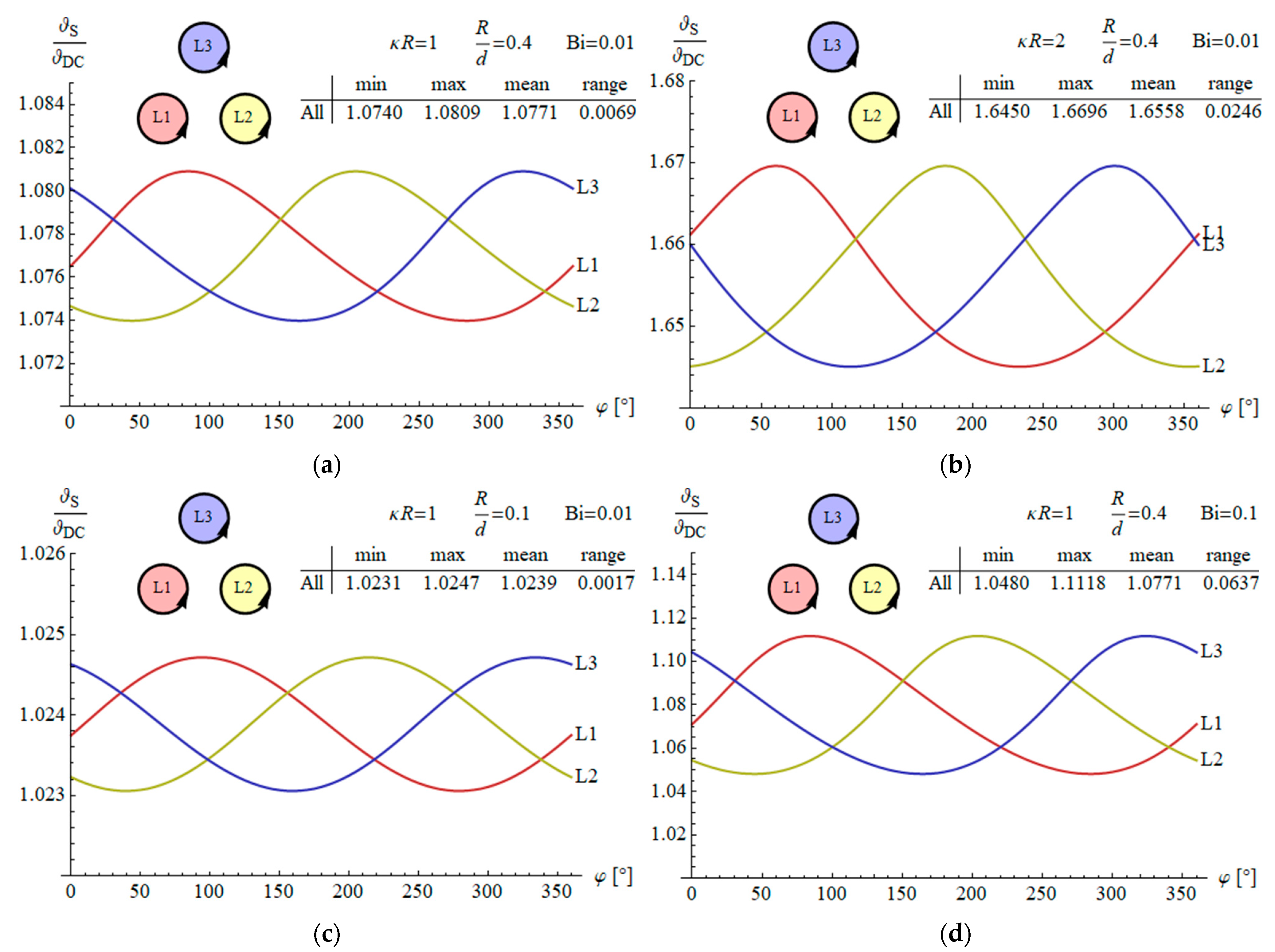
3.1. Temperature Distributions in Wires
3.2. Temperature on Wire Surface
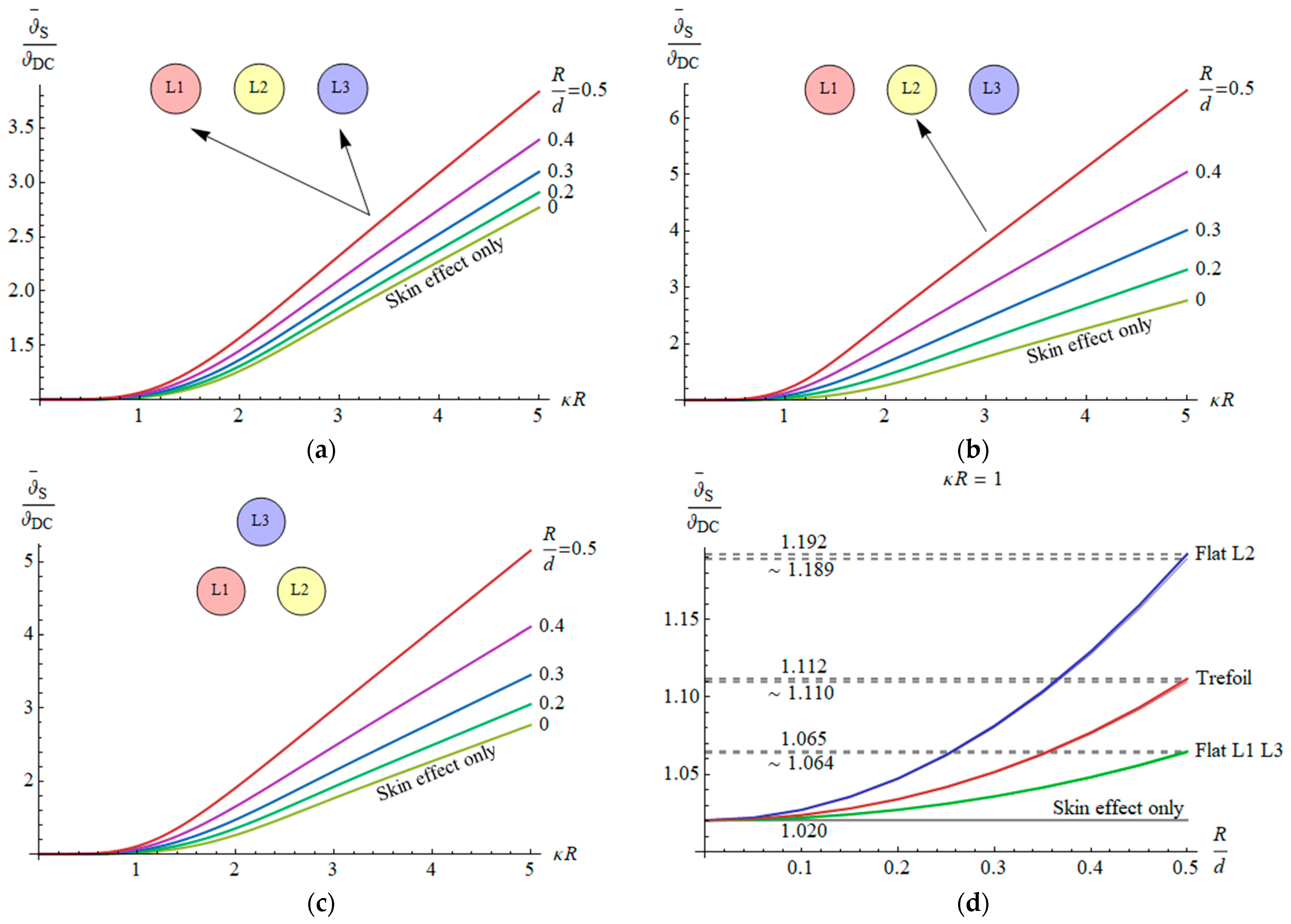
3.3. Mean Temperature on Wire Surface
3.4. Comparison with Other Methods
3.5. Numerical Examples
- ratio: 0.195,
- the skin effect parameter ,
- the Biot number .
4. Conclusions
- The maximum values of the temperature field are shifted towards the highest current densities.
- Current density changes are significantly greater than temperature changes in the wire cross-sections. From the physical side, this is due to the high thermal conductivity of copper (or aluminum), which causes a significant equalization of the temperature values throughout the wire cross-section.
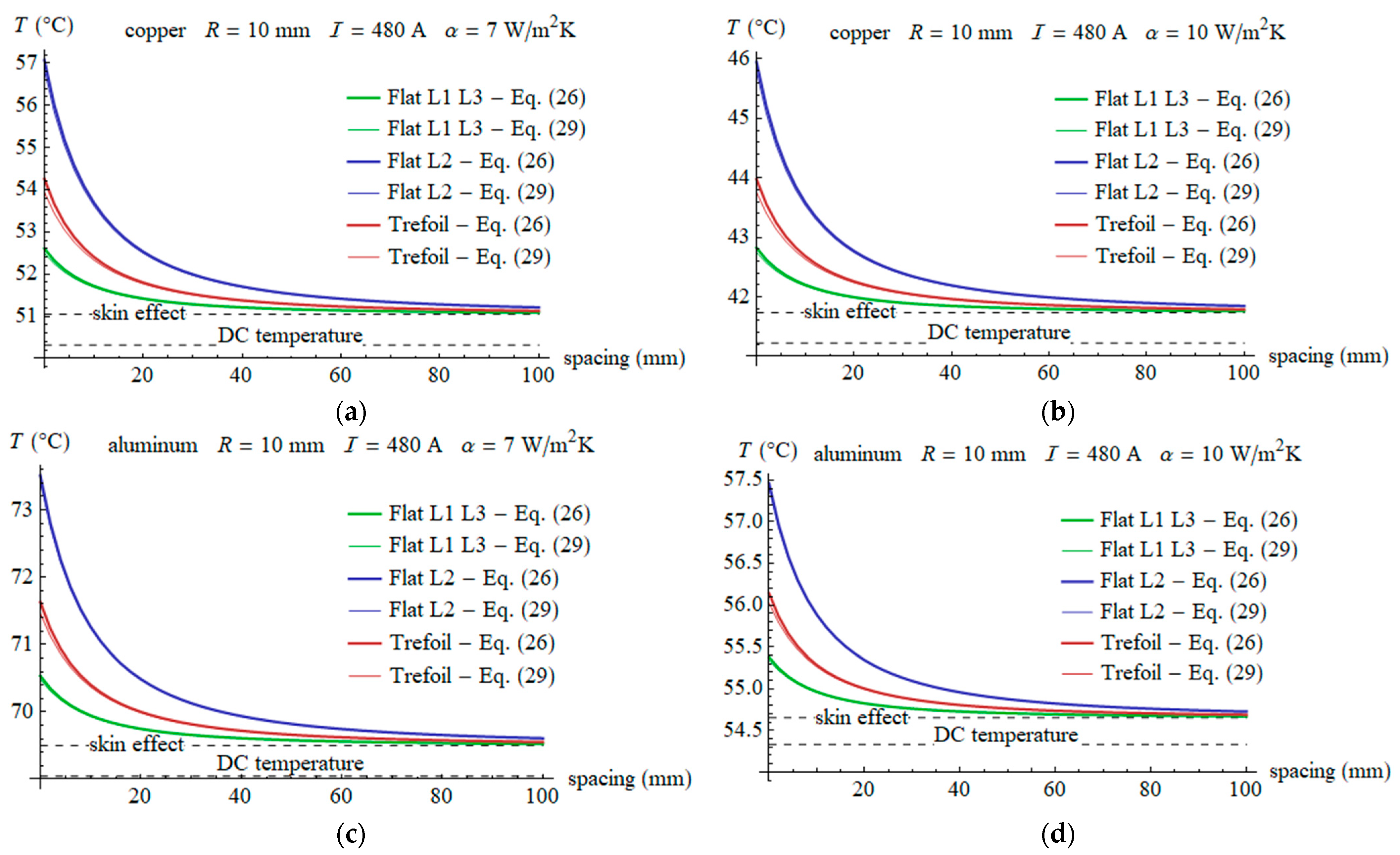
- In a flat configuration, the temperature of the central conductor is noticeably higher than that of the adjacent ones. In turn, in the trefoil configuration, all the wires heat up to approximately the same temperature due to symmetry. It is worth noting that the average temperature in both configurations is approximately the same.
- The temperature increase due to the skin and proximity effects for the skin depth greater than the wire radius can reach around 2% and up to 17% compared to the DC case, respectively. Typically, this may result in an increase of around 1 °C and up to 6 °C, respectively.
- The results of the calculations performed using the Green’s method and finite element methods are consistent. Numerical examples show that temperature distributions by both methods are very similar, with differences below 0.006 °C, which can be attributed to numerical errors or neglecting the higher order reactions in the expression for current density.
- The increase in temperature on the conductor surface depends on the busbar arrangement and three dimensionless parameters: radius to skin depth ratio (), radius to distance between conductors’ axes ratio (), and the Biot number Bi related to heat transfer conditions; however, the mean temperature increase on the conductor surface is independent of the Biot number.
- In typical excitation conditions (symmetrical currents, skin depth greater than wire radius) and cooling conditions (natural convection), the differences in temperature across the conductors’ cross-sections are negligible, whereas the differences between individual wires are clearly noticeable.
- For a skin depth greater than or equal to the wire radius, the temperature increase can be evaluated using the derived approximate formula with an error below 1%.
- The proximity effect can be neglected if the skin depth is greater than the wire radius and the distance between the conductors’ axes is greater than ten wire radii.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| coefficients related to wire arrangement and currents, | |
| operator of complex rotation by 120°, , | |
| Biot number, | |
| coefficients of temperature distribution, | |
| function related to integration over angular coordinate, | |
| coefficients related to wire arrangements, | |
| coefficients related to integration over radial coordinate, | |
| distance between the wires, m, | |
| frequency of currents, Hz, | |
| Green’s function for the temperature in round wire, | |
| heat source density, W/m3, | |
| current root mean square value, A, | |
| modified Bessel function of the first kind of order , | |
| imaginary part of , | |
| current density modulus, A/m2, | |
| imaginary unit, , | |
| coefficients related to the proximity effect, | |
| wire radius, m, | |
| radial coordinate in cylindrical coordinates, m, | |
| coefficients related to wire arrangements, | |
| temperature, °C, | |
| ambient temperature, °C, | |
| conjugate of , | |
| heat transfer coefficient between wires and the surrounding medium, W/Km2, | |
| electromagnetic field penetration coefficient, 1/m, | |
| dimensionless coefficient of electromagnetic field penetration, | |
| Dirac delta, | |
| Kronecker delta, | |
| angular coordinate, | |
| temperature increase above ambient temperature, °C, | |
| temperature increase for DC (uniform) current density distribution, °C, | |
| mean temperature increase on wire surface, °C, | |
| skin depth parameter equal to skin depth reciprocal, 1/m, | |
| thermal conductivity, W/mK, | |
| magnetic permeability of wire material, H/m, | |
| magnetic permeability of vacuum, H/m, | |
| relative magnetic permeability of wire material, | |
| radial coordinate, m, | |
| normalized dimensionless radial coordinate, | |
| electrical conductivity of wire material, S/m, | |
| angular coordinate in cylindrical coordinates, | |
| angular frequency of current, rad/s. |
Appendix A. Coefficients and
References
- Popović, Z.; Popović, B.D. Introductory Electromagnetics; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Lehner, G. Electromagnetic Field Theory; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chatzipetros, J.; Pilgrim, A. Impact of Proximity Effects on Sheath Losses in Trefoil Cable Arrangements. IEEE Trans. Power Deliv. 2020, 35, 455–463. [Google Scholar] [CrossRef]
- IEC 60287-1-1; Electric Cables—Calculation of the Current Rating—Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses—General. IEC: Geneva, Switzerland, 2014.
- Shazly, J.H.; Mostafa, A.M.; Ibrahim, D.K.; Abo El Zahab, E.E. Thermal analysis of high-voltage cables with several types of insulation for different configuration in the presence of harmonics. IET Gener. Transm. Distrib. 2017, 11, 3439–3448. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, J.; Jiang, J.; He, Y.; Wang, Z.; Zhang, H. Development of temperature rise simulation APP for three-phase common enclosure GIS/GIL. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration, Taiyuan, China, 22–25 October 2021. [Google Scholar]
- Li, S.; Han, Y.; Liu, C. Coupled multiphysics field analysis of high-current irregular-shaped busbar. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1805–1814. [Google Scholar] [CrossRef]
- Save, Y.D.; Narayanan, H.; Patkar, S.B. Solution of partial differential equations by electrical analogy. J. Comput. Sci. 2011, 2, 18–30. [Google Scholar] [CrossRef]
- Smirnova, L.; Juntunen, R.; Murashko, K.; Musikka, T.; Pyrhönen, J. Thermal analysis of the laminated busbar system of a multilevel converter. IEEE Trans. Power Electron. 2016, 31, 1479–1488. [Google Scholar] [CrossRef]
- Hu, J.; Xiong, X.; Chen, J.; Wang, J. Transient temperature calculation and multi-parameter thermal protection of overhead transmission lines based on an equivalent thermal network. Energies 2019, 12, 67. [Google Scholar] [CrossRef]
- Anders, G.J. Rating of Electric Power Cables: Ampacity Computations for Transmission, Distribution and Industrial Application; McGraw-Hill Professional: Columbus, OH, USA, 1997. [Google Scholar]
- Baker, A.; De León, F. Equivalent circuit for the thermal analysis of cables in non-vented vertical risers. IET Sci. Meas. Technol. 2015, 9, 606–614. [Google Scholar] [CrossRef]
- Enescu, D.; Colella, P.; Russo, A. Thermal Assessment of Power Cables and Impacts on Cable Current Rating: An Overview. Energies 2020, 13, 5319. [Google Scholar] [CrossRef]
- Henke, A.; Frei, S. Fast analytical approaches for the transient axial temperature distribution in single wire cables. IEEE Trans. Ind. Electron. 2022, 69, 4158–4416. [Google Scholar] [CrossRef]
- Ducluzaux, A. Extra Losses Caused in High Current Conductors by Skin and Proximity Effects; Cahier Technique no. 83; Technical Report; Schneider Electric: Rueil-Malmaison, France, 2002. [Google Scholar]
- Morgan, V.T. The current distribution, resistance and internal inductance of linear power system conductors—A review of explicit equations. IEEE Trans. Power Deliv. 2013, 38, 1252–1262. [Google Scholar] [CrossRef]
- Rolicz, P. Temperature and stresses in cylindrical conductor with an alternating current. J. Appl. Phys. 1978, 49, 4363–4365. [Google Scholar] [CrossRef]
- Moon, P.; Spencer, D.E. Field Theory Handbook; Springer-Verlag: New York, NY, USA, 1988. [Google Scholar]
- Plesca, A. Thermal Analysis of Busbars from a High Current Power Supply System. Energies 2019, 12, 2288. [Google Scholar] [CrossRef]
- Barka, A.; Bernard, J.J.; Benyoucef, B. Thermal behavior of a conductor submitted to skin effect. Appl. Therm. Eng. 2003, 23, 1261–1274. [Google Scholar] [CrossRef]
- Zaręba, M.; Gołębiowski, J. The thermal characteristics of ACCR lines as a function of wind speed—An analytical approach. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e141006. [Google Scholar] [CrossRef]
- Gołębiowski, J.; Zaręba, M. Transient Thermal Field Analysis in ACCC Power Lines by the Green’s Function Method. Energies 2020, 13, 280. [Google Scholar] [CrossRef]
- Gołębiowski, J.; Zaręba, M. Analysis of the influence of current frequency on the thermal field of the insulated busbar. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 89–97. [Google Scholar] [CrossRef]
- Machado, V.M.; Pedro, M.E.; Brandão Faria, J.A.; Van Dommelen, D. Magnetic field analysis of three-conductor bundles in flat and triangular configurations with the inclusion of proximity and skin effects. Electr. Power Syst. Res. 2011, 81, 2005–2014. [Google Scholar] [CrossRef]
- Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Piątek, Z. Analytical–Numerical Solution for the Skin and Proximity Effects in Two Parallel Round Conductors. Energies 2019, 12, 3584. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Greenberg, M.D. Advanced Engineering Mathematics; Prentice Hall: Hoboken, NJ, USA, 1988. [Google Scholar]
- Jabłoński, P.; Kusiak, D.; Szczegielniak, T. Analytical-Numerical Approach to the Skin and Proximity Effect in Lines with Round Parallel Wires. Energies 2020, 13, 6716. [Google Scholar] [CrossRef]
- Dlabač, T.; Filipović, D. Proximity effect in a shielded symmetrical three-phase line. Serbian J. Electr. Eng. 2014, 11, 585–596. [Google Scholar]
- Latif, M.J. Heat Conduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Hahn, D.W.; Ozisik, M.N. Heat Conduction; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cole, K.D.; Beck, J.V.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Functions; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Greenberg, M.D. Applications of Green’s Functions in Science and Engineering; Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- Duffy, D.G. Green’s Functions with Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Zaręba, M.; Szczegielniak, T.; Jabłoński, P. Influence of the Skin and Proximity Effects on the Thermal Field in a System of Two Parallel Round Conductors. Energies 2023, 16, 6341. [Google Scholar] [CrossRef]
- Abramowitz, A.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Wolfram Research Inc. Mathematica; Wolfram Research Inc.: Champaign, IL, USA, 2020. [Google Scholar]
- COMSOL Multiphysics, version 6.2; Reference Manual Release 6.2; COMSOL: Stockholm, Sweden, 2023.
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Sums, Series and Products, 17th ed.; Elsevier Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
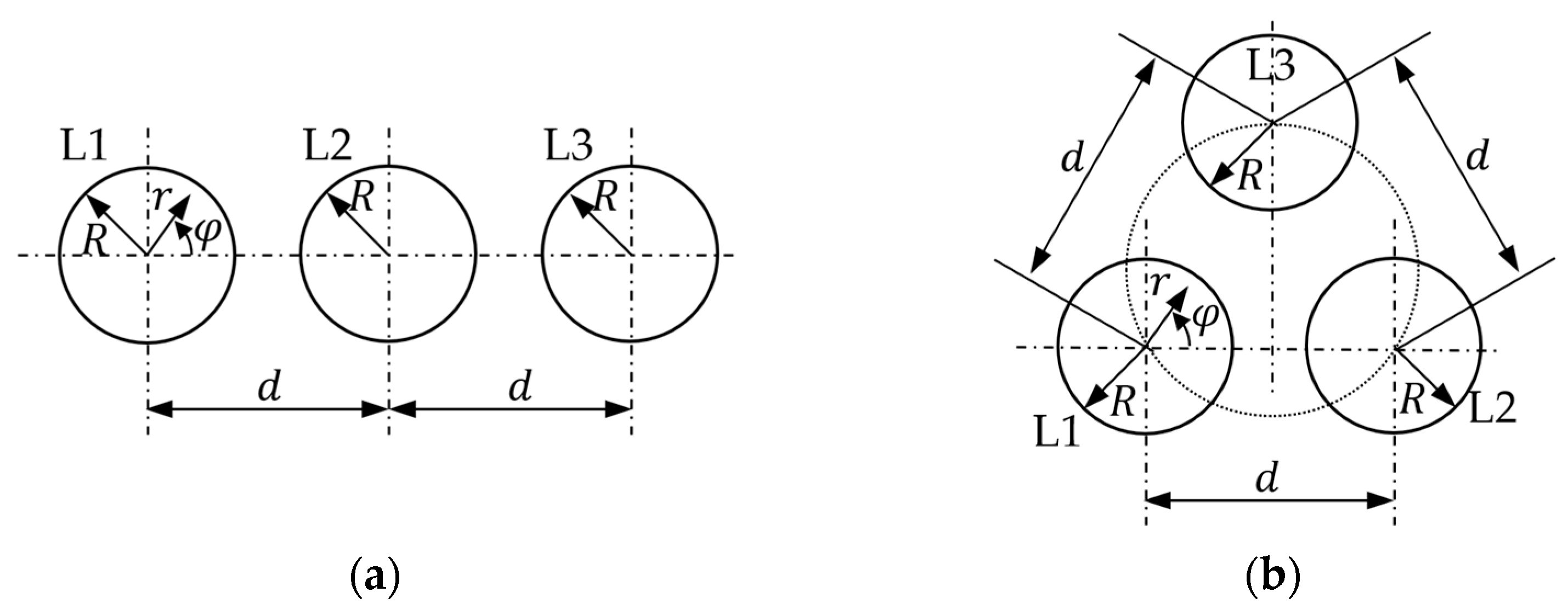


| Flat | Trefoil | |||
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | |
| 0 | ||||
| 0 | ||||
| 0 | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Left/right flat | 1 | 3 | 3.25 | 3.5625 | 3.7656 | 3.8789 | 3.9385 | 3.9690 | 3.9844 | 3.9922 | 3.9961 |
| Middle flat | 1 | 12 | 4 | 12 | 4 | 12 | 4 | 12 | 4 | 12 | 4 |
| Trefoil | 1 | 6 | 10 | 12 | 10 | 6 | 4 | 6 | 10 | 12 | 10 |
| Phase | Point | Temperature, °C | , °C | ||
|---|---|---|---|---|---|
| Equation (13) | FEM | ||||
| L1 | 71.450 | 71.445 | 0.0048 | 0.0067 | |
| 71.445 | 71.441 | 0.0048 | 0.0067 | ||
| 71.445 | 71.441 | 0.0047 | 0.0066 | ||
| L2 | 72.480 | 72.474 | 0.0056 | 0.0077 | |
| 72.472 | 72.466 | 0.0056 | 0.0077 | ||
| 72.475 | 72.469 | 0.0056 | 0.0077 | ||
| L3 | 71.450 | 71.445 | 0.0048 | 0.0067 | |
| 71.444 | 71.440 | 0.0047 | 0.0066 | ||
| 71.445 | 71.441 | 0.0048 | 0.0067 | ||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| [20]—Equation (30) | 1.0000 | 1.0205 | 1.2647 | 1.7681 | 2.2738 | 2.7681 | |
| This work—Equation (26) | 1.0000 | 1.0205 | 1.2647 | 1.7681 | 2.2738 | 2.7681 | |
| Phase | Temperature on Wire Surface, °C | ||||
|---|---|---|---|---|---|
| Min | Max | Mean—Equation (26) | Mean—Equation (29) | Range | |
| Distance between the wires’ axes | |||||
| Flat L1 | 71.444 | 71.444 | 71.444 | 71.436 | <0.001 |
| Flat L2 | 72.470 | 72.476 | 72.473 | 72.448 | 0.006 |
| Flat L3 | 71.443 | 71.445 | 71.444 | 71.436 | 0.003 |
| Trefoil | 71.791 | 71.794 | 71.792 | 71.773 | 0.003 |
| Distance between the wires’ axes | |||||
| Flat L1 | 72.072 | 72.072 | 72.072 | 72.036 | <0.001 |
| Flat L2 | 74.931 | 74.941 | 74.935 | 74.848 | 0.010 |
| Flat L3 | 72.070 | 72.074 | 72.072 | 72.036 | 0.005 |
| Trefoil | 73.065 | 73.071 | 73.068 | 72.973 | 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabłoński, P.; Zaręba, M.; Szczegielniak, T.; Gołębiowski, J. Influence of the Skin and Proximity Effects on the Thermal Field in Flat and Trefoil Three-Phase Systems with Round Conductors. Energies 2024, 17, 1713. https://doi.org/10.3390/en17071713
Jabłoński P, Zaręba M, Szczegielniak T, Gołębiowski J. Influence of the Skin and Proximity Effects on the Thermal Field in Flat and Trefoil Three-Phase Systems with Round Conductors. Energies. 2024; 17(7):1713. https://doi.org/10.3390/en17071713
Chicago/Turabian StyleJabłoński, Paweł, Marek Zaręba, Tomasz Szczegielniak, and Jerzy Gołębiowski. 2024. "Influence of the Skin and Proximity Effects on the Thermal Field in Flat and Trefoil Three-Phase Systems with Round Conductors" Energies 17, no. 7: 1713. https://doi.org/10.3390/en17071713
APA StyleJabłoński, P., Zaręba, M., Szczegielniak, T., & Gołębiowski, J. (2024). Influence of the Skin and Proximity Effects on the Thermal Field in Flat and Trefoil Three-Phase Systems with Round Conductors. Energies, 17(7), 1713. https://doi.org/10.3390/en17071713





