optimHome: A Shrinking Horizon Control Architecture for Bidirectional Smart Charging in Home Energy Management Systems
Abstract
:1. Introduction
2. Literature Review
2.1. Electric Vehicle Integration in Energy Management System
2.2. Model Predictive Control-Based Architectures for EMS
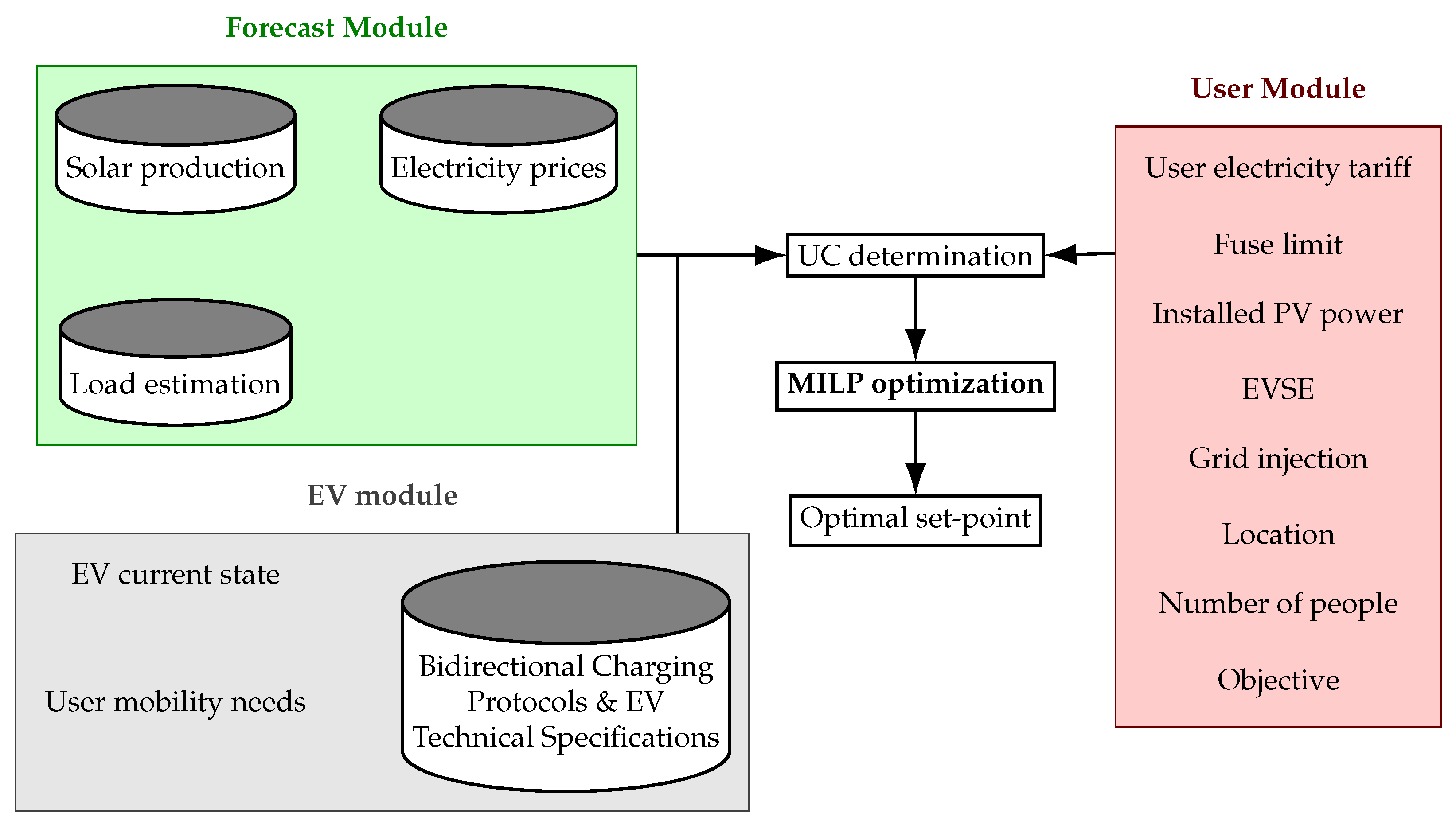
3. Materials and Methods
3.1. System Architecture and Use Cases
- The capability for the user to inject power into the grid, thus shifting from a V2H to V2G paradigm. The latter includes many interactions with the grid, which are aimed at different objectives: the present work is focused on energy arbitrage to maximize user’s benefits;
- The economic value of the energy possibly injected into the grid: optimHome offers the possibility to set the price of the power injected into the grid. As seen in Table 1, options can range from the retail price or any fixed Feed-In Tariff (FIT);
- Operation purpose is not limited to economics: the scheduling can be aimed at maximizing renewable self-consumption on site.
3.2. One-Shot Optimal Scheduling
3.2.1. Battery and Degradation Models
3.2.2. Conventional Constraints
3.2.3. Condition Constraints
- Zone 1 represents a nonoptimized region in which cycling is not allowed. Practically, this region can be entered only at the beginning of the charging process if the arrival SoC is very low. If this is the case, the actual optimized scheduling will not start until the safety value is reached. Operations in this region are governed by a rule-based control algorithm:
- Zone 2 is an intermediate region in which cycling is still not permitted, but the charging power can be the result of the optimization. In other words, the charging can be postponed by waiting for a more convenient moment, but discharging is not permitted even in the presence of a very convenient price. To enforce the condition, a binary decision variable must be designed to be true when belongs to Zone 2 (refer to formulation in Equation (11)). Subsequently, direct implication is enforced by means of Equation (25):
- The core of optimization is represented by the operations in Zone 3, where cycling aimed at maximizing objective function is admitted;
- Zone 4 covers the states between the upper level for cycling and . Zone 5, consequently, represents the remaining region between the size of the battery and EV Maximum energy level. The protocol prescribes that in Zone 5, only discharging is admitted, while you can only enter Zone 4 to reach the departure SoC target. Specifically, in Zone 4, discharging is permitted to enter the cycling zone just once. In other words, no cycling is admitted between Zone 3 and Zone 4. In real-life applications, the arrival SoC is far from being comparable with the above-mentioned levels. As a result of these considerations, Zone 5 has no interest in being defined, as this scenario only occurs with extremely high SoC arrivals. For the purpose of this work, Zone 4 and 5 can be condensed into a single zone, within which only charging is allowed. Clearly, this simplifies what is described in the protocol, which, however, by its nature and given its purposes, must include as many case scenarios as possible by establishing constraints and conditions valid for even the most extreme circumstances. Similarly to Zone 2, the condition is enforced by introducing a new binary variable, , thus referring to Equations (11) and (25).
3.2.4. Objective Functions
- The objective function of this first UC purely quantifies the cost of operations within the control volume (Equation (26)). Total cost is given by the sum of two distinct addends and is homogeneous in terms of unit of measurement: Firstly, the cost for electricity is given by the scalar product between the variable that quantifies the power bought from the grid and the parameter that collects the electricity tariff for each considered time step. Secondly, in accordance with other related studies [11], battery deterioration can be related to an economic cost and thus included in the objective function to counterbalance discharge operations. It was chosen to assess degradation under a differential perspective: charging the vehicle up to a target SoC represents a benchmark, which is an inevitable deterioration of battery performance induced by simple car use, and therefore, it should not affect the optimal scheduling. For this reason, the optimal charging control sequence is affected, thus accounting for two times the discharged energy considered as the deviation from the reference unidirectional charging process.
- A multiobjective function to maximize self-consumption is employed in UC 2 to deal with heterogeneous terms. The quantification of renewable overproduction from PV is the additional term to the total cost of operation already discussed for UC 1. is an auxiliary variable that quantifies the excess of renewable energy.
3.3. Receding Horizon Optimization
4. Case Study
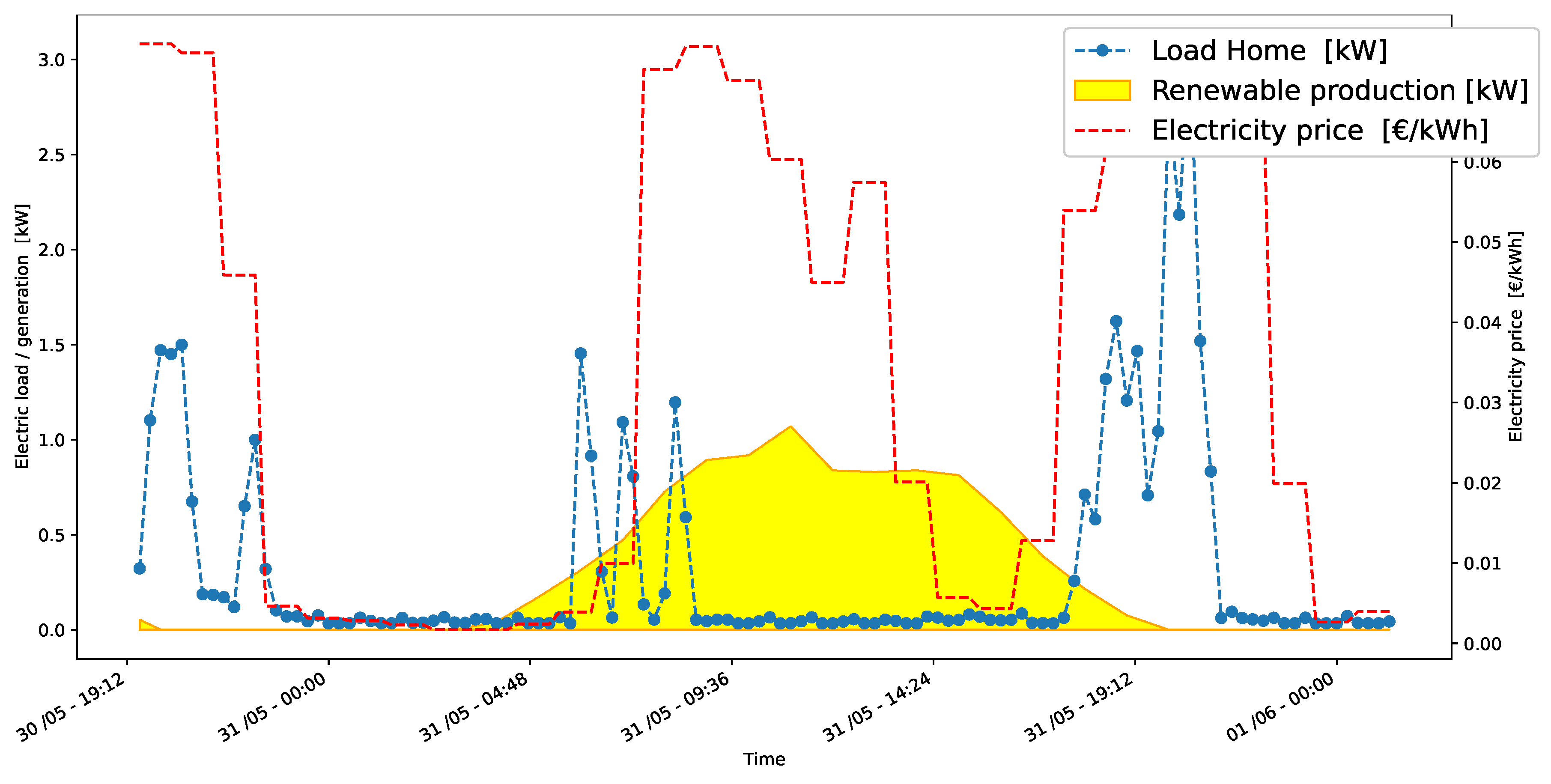
4.1. Electric Load and PV Production Estimation
4.2. Electricity Tariff
5. Results and Discussion
5.1. Economic Profitability in Bidirectional Smart Charging
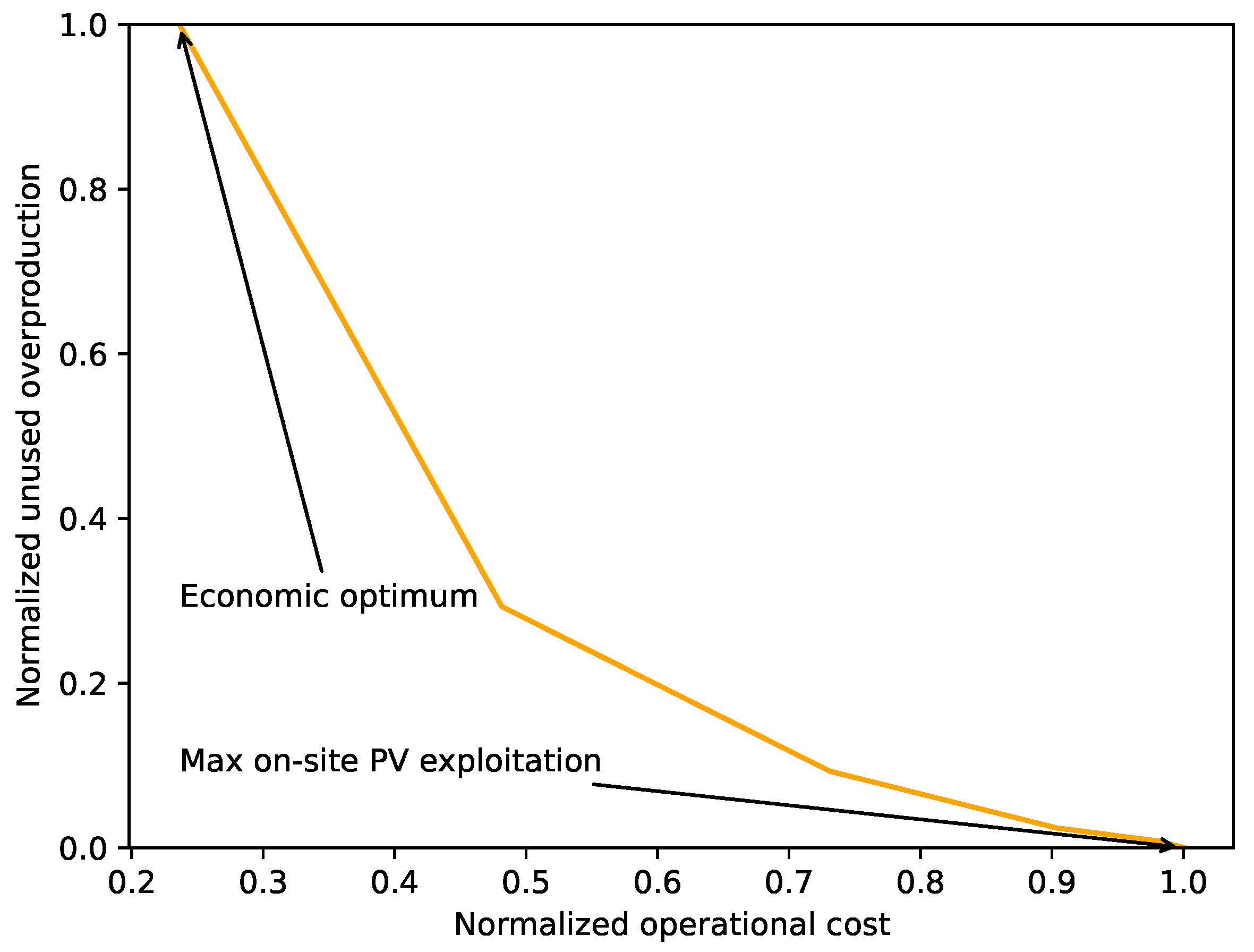
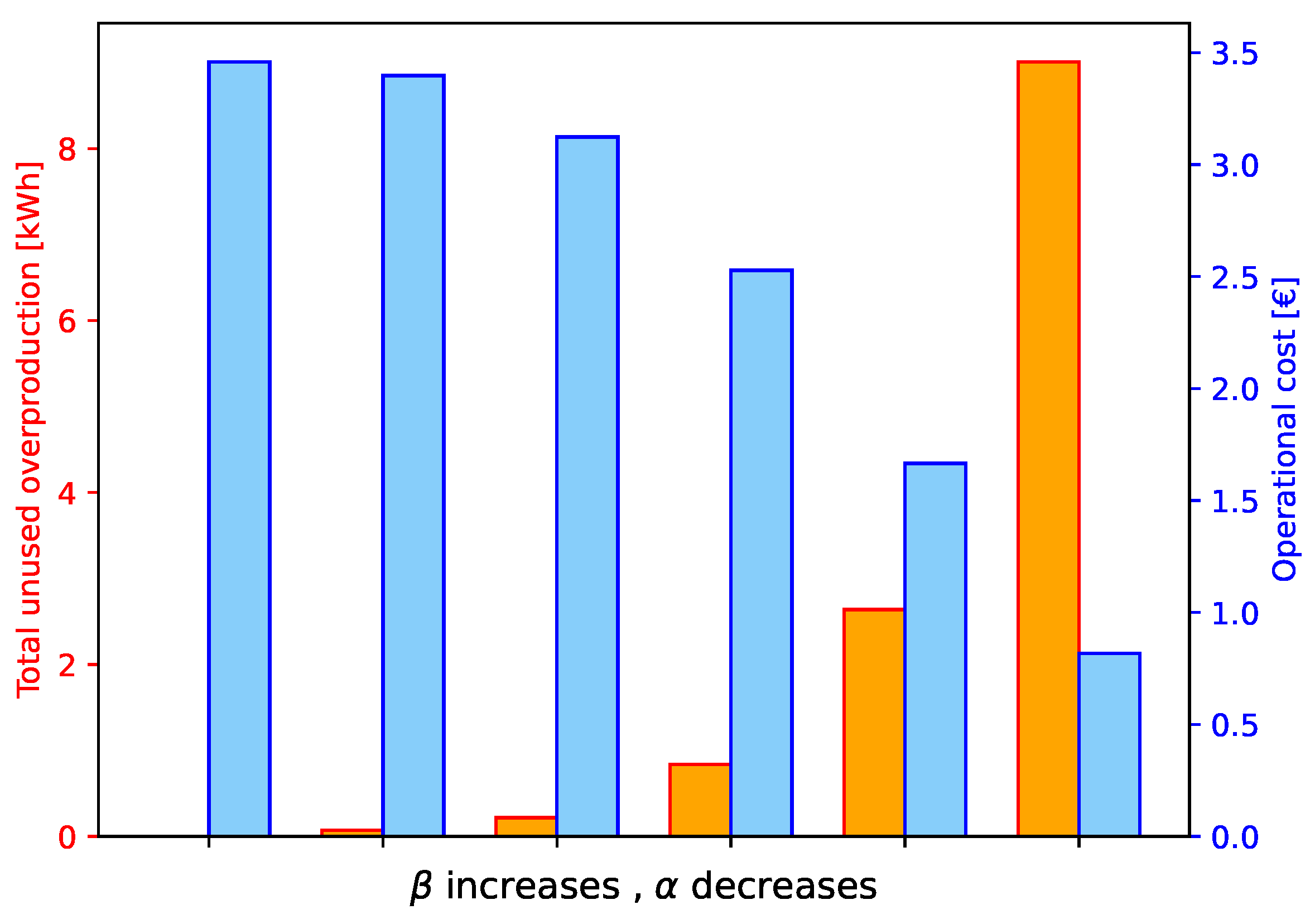
5.2. Maximization of PV Self-Consumption
5.3. Fuse Limit Sensitivity
5.4. Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| HEMS | Home Energy Management System |
| EMS | Energy Management System |
| EVSE | Electric Vehicle Supply Equipment |
| DERs | Distributed Energy Resources |
| DSO | Distribution System Operator |
| dToU | Dynamic Time of Use |
| FIT | Feed-In Tariff |
| KPI | Key Performance Indicator |
| OCP | Optimal Control Problem |
| MILP | Mixed Integer Linear Programming |
| MG | Microgrid |
| LP | Linear Programming |
| RH | Rolling Horizon |
| RES | Renewable Energy Sources |
| RMPC | Robust Model Predictive Control |
| SoC | State Of Charge |
| sMPC | Stochastic Model Predictive Control |
| SH-MPC | Shrinking Horizon MPC |
| sToU | Static Time of Use |
| TSO | Trasmission System Operator |
| UC | Use Case |
| V2H | Vehicle to Home |
| V2X | Vehicle to Everything |
| V2G | Vehicle to Grid |
Nomenclature
| The following nomenclature is employed in this manuscript: | |
| Sets: | |
| /t | Set and index for time steps |
| /g | Grid modes buy or sell |
| /b | Battery mode charge or discharge |
| Variables: | |
| Power drawn from the grid [kW] | |
| Power injected into the grid [kW] | |
| Charging power [kW] | |
| Discharging power [kW] | |
| Renewable overproduction [kW] | |
| Binary for power drawn | |
| Binary for power injected | |
| Binary for charging | |
| Binary for discharging | |
| Binary for Zone 2 | |
| Binary for Zone 4 | |
| State of charge [−] | |
| Parameters: | |
| PV production [kW] | |
| Load demand [kW] | |
| Net demand [kW] | |
| Upper bound of the grid [kW] | |
| EV maximum charging power [kW] | |
| EVSE maximum charging power | |
| Minimum charging power [kW] | |
| Available power [kW] | |
| High SoC threshold [−] | |
| Arrival SoC [−] | |
| Target/Departure SoC [−] | |
| Minimum SoC [−] | |
| Minimum SoC for V2X [−] | |
| Maximum SoC for V2X [−] | |
| Maximum SoC [−] | |
| EV battery capacity [kWh] | |
| Electricity price [€/kWh] | |
| FIT | Feed-In Tariff [€/kWh] |
| Discretization time step [min] | |
| Prediction time steps [−] | |
| T | Time for V2X [min] |
| , | Weight coefficient [−] |
| D | Degradation coefficient [€/kWh] |
| q | Percentage capacity loss [%] |
| Specific cost of battery [€/kWh] | |
| Remaining capacity at end life [−] | |
| Degradation cost [€] | |
References
- Van Kriekinge, G.; De Cauwer, C.; Sapountzoglou, N.; Coosemans, T.; Messagie, M. Peak shaving and cost minimization using model predictive control for uni- and bi-directional charging of electric vehicles. Energy Rep. 2021, 7, 8760–8771. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2023. Available online: https://www.iea.org/reports/global-ev-outlook-2023 (accessed on 10 March 2024).
- Weiss, X.; Xu, Q.; Nordström, L. Energy Management of Smart Homes with Electric Vehicles Using Deep Reinforcement Learning. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hannover, Germany, 5–9 September 2022; pp. 1–9. [Google Scholar]
- Fit for 55 Policy, European Green Deal. Available online: https://www.consilium.europa.eu/en/policies/green-deal/ (accessed on 3 May 2023).
- Hatziargyriou, N.; Sakis Meliopoulos, A. Distributed energy sources: Technical challenges. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 2, pp. 1017–1022. [Google Scholar] [CrossRef]
- Maree, J.P.; Gros, S.; Lakshmanan, V. Low-complexity Risk-averse MPC for EMS. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; pp. 358–363. [Google Scholar] [CrossRef]
- Kanwar, A.; Hidalgo Rodriguez, D.; Von Appen, J.; Braun, M. A Comparative Study of Optimization-and Rule-Based Control for Microgrid Operation; Power and Energy Student Summit (PESS): Dubai, United Arab Emirates, 2015; Volume 1. [Google Scholar]
- Ben Slama, S. Design and implementation of home energy management system using vehicle to home (H2V) approach. J. Clean. Prod. 2021, 312, 127792. [Google Scholar] [CrossRef]
- Daccò, E.; Falabretti, D.; Ilea, V.; Merlo, M.; Nebuloni, R.; Spiller, M. Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation. Electricity 2024, 5, 134–153. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and Distributed Optimal Energy Management of Active Distribution Networks Within Integrated Office Buildings. CSEE J. Power Energy Syst. 2024, 10, 504–517. [Google Scholar] [CrossRef]
- Yousefi, M.; Hajizadeh, A.; Soltani, M.N.; Hredzak, B. Predictive Home Energy Management System with Photovoltaic Array, Heat Pump, and Plug-In Electric Vehicle. IEEE Trans. Ind. Inform. 2021, 17, 430–440. [Google Scholar] [CrossRef]
- Wu, H.; Pratt, A.; Munankarmi, P.; Lunacek, M.; Balamurugan, S.P.; Liu, X.; Spitsen, P. Impact of model predictive control-enabled home energy management on large-scale distribution systems with photovoltaics. Adv. Appl. Energy 2022, 6, 100094. [Google Scholar] [CrossRef]
- Ghazvini, M.A.F.; Antoniadou-Plytaria, K.; Steen, D.; Le, T. Two-stage demand-side management in energy flexible residential buildings. J. Eng. 2024, 2024, e12372. [Google Scholar] [CrossRef]
- Cominesi, S.; La Bella, A.; Farina, M.; Scattolini, R. A multi-layer control scheme for microgrid energy management. IFAC Pap. 2016, 49, 256–261. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Li, X.; Sun, B.; Liao, Q.; Tao, Y.; Wang, Z. Strategic integration of vehicle-to-home system with home distributed photovoltaic power generation in Shanghai. Appl. Energy 2020, 263, 114603. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, H.; Li, D.; Zhang, G. Smart Online Charging Algorithm for Electric Vehicles via Customized Actor–Critic Learning. IEEE Internet Things J. 2022, 9, 684–694. [Google Scholar] [CrossRef]
- Amry, Y.; Elbouchikhi, E.; Le Gall, F.; Ghogho, M.; El Hani, S. Optimal sizing and energy management strategy for EV workplace charging station considering PV and flywheel energy storage system. J. Energy Storage 2023, 62, 106937. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. Stochastic Model Predictive Control for Economic/Environmental Operation Management of Microgrids: An Experimental Case Study. J. Process Control 2016, 43, 24–37. [Google Scholar] [CrossRef]
- Raveendran Nair, U.; Costa-Castelló, R. A Model Predictive Control-Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Pavan, A.M.; Blasuttigh, N.; Petrone, G.; Spagnuolo, G. Real time Energy Management System of a photovoltaic based e-vehicle charging station using Explicit Model Predictive Control accounting for uncertainties. Sustain. Energy Grids Netw. 2022, 31, 100769. [Google Scholar] [CrossRef]
- Panapongpakorn, T.; Banjerdpongchai, D. Model Predictive Control of Energy Management System for Economic Dispatch with Application to MHS Microgrid in Normal Operation. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; pp. 1281–1286. [Google Scholar] [CrossRef]
- Esmaeel Nezhad, A.; Rahimnejad, A.; Nardelli, P.; Gadsden, S.; Sahoo, S.; Ghanavati, F. A Shrinking Horizon Model Predictive Controller for Daily Scheduling of Home Energy Management Systems. IEEE Access 2022, 10, 29716–29730. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.; Steen, D.; Tuan, L.A.; Carlson, O.; Fotouhi Ghazvini, M.A. Market-Based Energy Management Model of a Building Microgrid Considering Battery Degradation. IEEE Trans. Smart Grid 2021, 12, 1794–1804. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel–cobalt–manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Barcellona, S.; Piegari, L. Effect of current on cycle aging of lithium ion batteries. J. Energy Storage 2020, 29, 101310. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- Bisschop, J. AIMMS Optimization Modeling; Paragon Decision Technology: Kirkland, WA, USA, 1993. [Google Scholar]
- ISO 15118-20 Road Vehicles to Grid Communication Interface. Available online: https://www.iso.org/standard/77845.html (accessed on 5 May 2023).
- Electric Vehicle Outlook 2022 Bloomberg NEF. Available online: https://about.bnef.com/electric-vehicle-outlook/ (accessed on 29 May 2023).
- Mazzola, S.; Vergara, C.; Astolfi, M.; Li, V.; Perez-Arriaga, I.; Macchi, E. Assessing the value of forecast-based dispatch in the operation of off-grid rural microgrids. Renew. Energy 2017, 108, 116–125. [Google Scholar] [CrossRef]
- Volvo XC 40. Available online: https://www.volvocars.com/uk/cars/xc40/ (accessed on 5 March 2024).
- LoadProfileGenerator Website. Available online: https://www.loadprofilegenerator.de/ (accessed on 25 May 2023).
- PVsyst Website. Available online: https://www.pvsyst.com/ (accessed on 26 May 2023).
- Nordpool Day-Ahead Prices Website. Available online: https://www.nordpoolgroup.com/en/Market-data1/Dayahead/Area-Prices/ALL1/Hourly/?view=chart (accessed on 26 May 2023).
- Abdi, M.S. Residential Electricity Network Tariffs in Sweden—A Survey and Commentary; KTH Royal Institute of Technology: Stockholm, Sweden, 2020. [Google Scholar]
- Halvgaard, R.; Poulsen, N.; Madsen, H.; Jørgensen, J.; Marra, F.; Bondy, D.E.M. Electric vehicle charge planning using Economic Model Predictive Control. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, IEVC 2012, Greenville, SC, USA, 4–8 March 2012. [Google Scholar] [CrossRef]
- Dcbel: Home Energy Station Website. Available online: https://www.dcbel.energy/uk/?lang=en (accessed on 19 June 2023).
- Tibber Website. Available online: https://tibber.com/en (accessed on 19 June 2023).







| UC | Mode | Objective | Formulation | Sold Electricity Price | Bidirectional Capability |
|---|---|---|---|---|---|
| 1 | V2H | Cost minimization | Single Obj | - | EV |
| 2 | V2H | Self-consumption | Multi-Obj | - | EV |
| 3 | V2G | Cost minimization | Single Obj | Retail price | EV + GRID |
| 4 | V2G | Cost minimization | Single Obj | FIT | EV + GRID |
| Set | Use Cases | ||
|---|---|---|---|
| All | |||
| All | |||
| 3/4 | |||
| 3/4 |
| Relevant Parameters | |||||
|---|---|---|---|---|---|
| [−] | 0.2 1 | [−] | 0.25 1 | [−] | 0.8 1 |
| [−] | 0.97 1 | [€/kWh] | 100 2 | [KWh] | 69 4 |
| [kW] | 11 | [kW] | 2.3 | [−] | 0.8 |
| [−] | 0.97 | [−] | 0.97 | [min] | 15 3 |
| Input Parameters | |||
|---|---|---|---|
| Time window [hours] | 30 | 11 | |
| Arrival SoC [−] | 0.35 | Departure SoC [−] | 0.7 |
| KPI Variation [%] | UC 3 | UC 1 | Benchmark |
|---|---|---|---|
| Operational cost | −205.3 | −89.9 | 8.7 € |
| Total grid power demand | 109.1 | 25.2 | 26.9 kWh |
| BESS energy throughput | 193.1 | 37.2 | 24.2 kWh |
| Fuse Limits | |
|---|---|
| Current Limit [A] | Power Limit [kW] |
| 16 | 11 |
| 20 | 13.8 |
| 25 | 17.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caminiti, C.M.; Merlo, M.; Fotouhi Ghazvini, M.A.; Edvinsson, J. optimHome: A Shrinking Horizon Control Architecture for Bidirectional Smart Charging in Home Energy Management Systems. Energies 2024, 17, 1963. https://doi.org/10.3390/en17081963
Caminiti CM, Merlo M, Fotouhi Ghazvini MA, Edvinsson J. optimHome: A Shrinking Horizon Control Architecture for Bidirectional Smart Charging in Home Energy Management Systems. Energies. 2024; 17(8):1963. https://doi.org/10.3390/en17081963
Chicago/Turabian StyleCaminiti, Corrado Maria, Marco Merlo, Mohammad Ali Fotouhi Ghazvini, and Jacob Edvinsson. 2024. "optimHome: A Shrinking Horizon Control Architecture for Bidirectional Smart Charging in Home Energy Management Systems" Energies 17, no. 8: 1963. https://doi.org/10.3390/en17081963







