Effect of Entrainment on the Liquid Film Behavior in Pipe Elbows
Abstract
:1. Introduction
2. Theories and Modeling
2.1. Entrainment Modeling
2.2. Droplet Size
3. Experimental Background
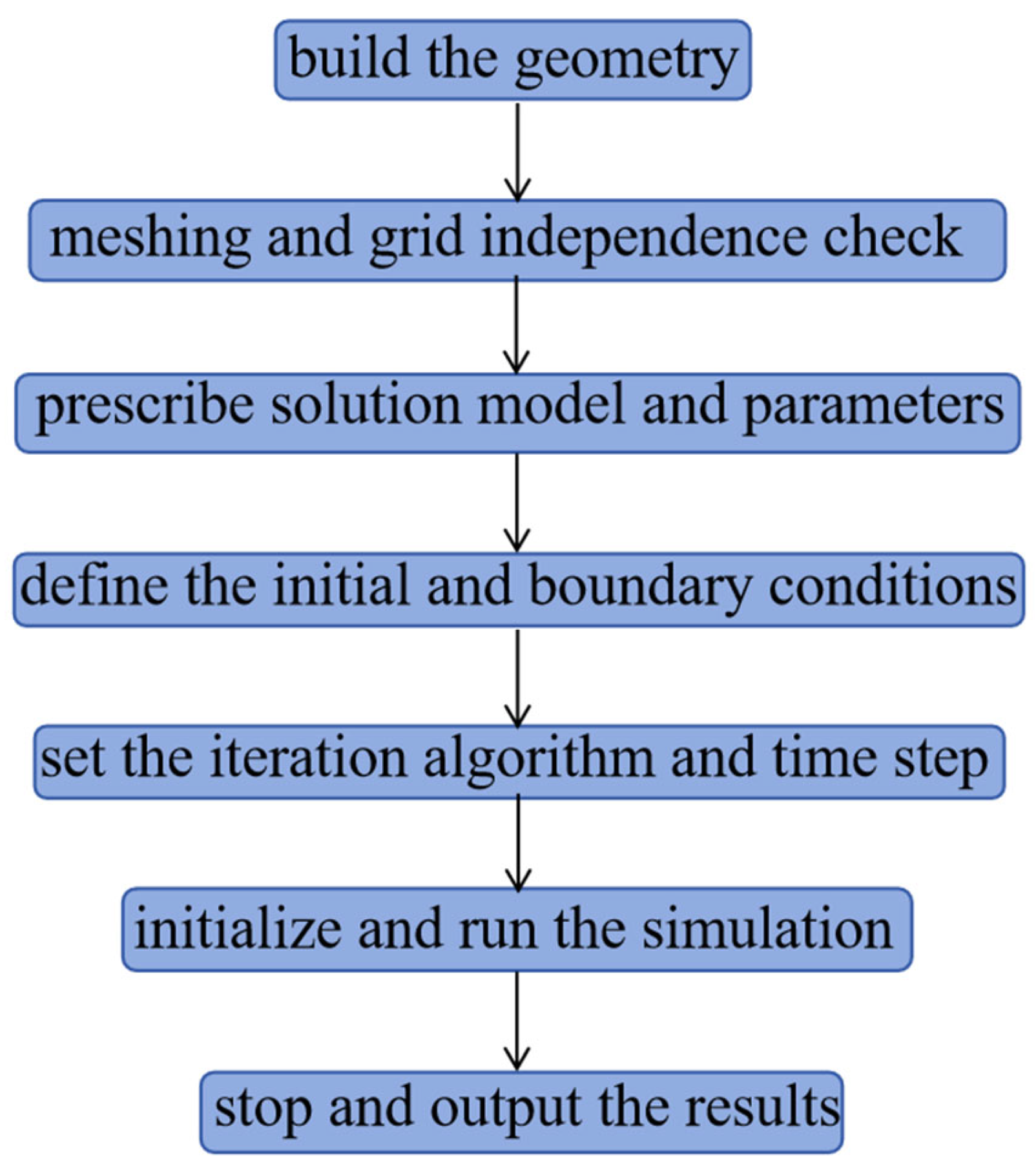
4. CFD Simulation
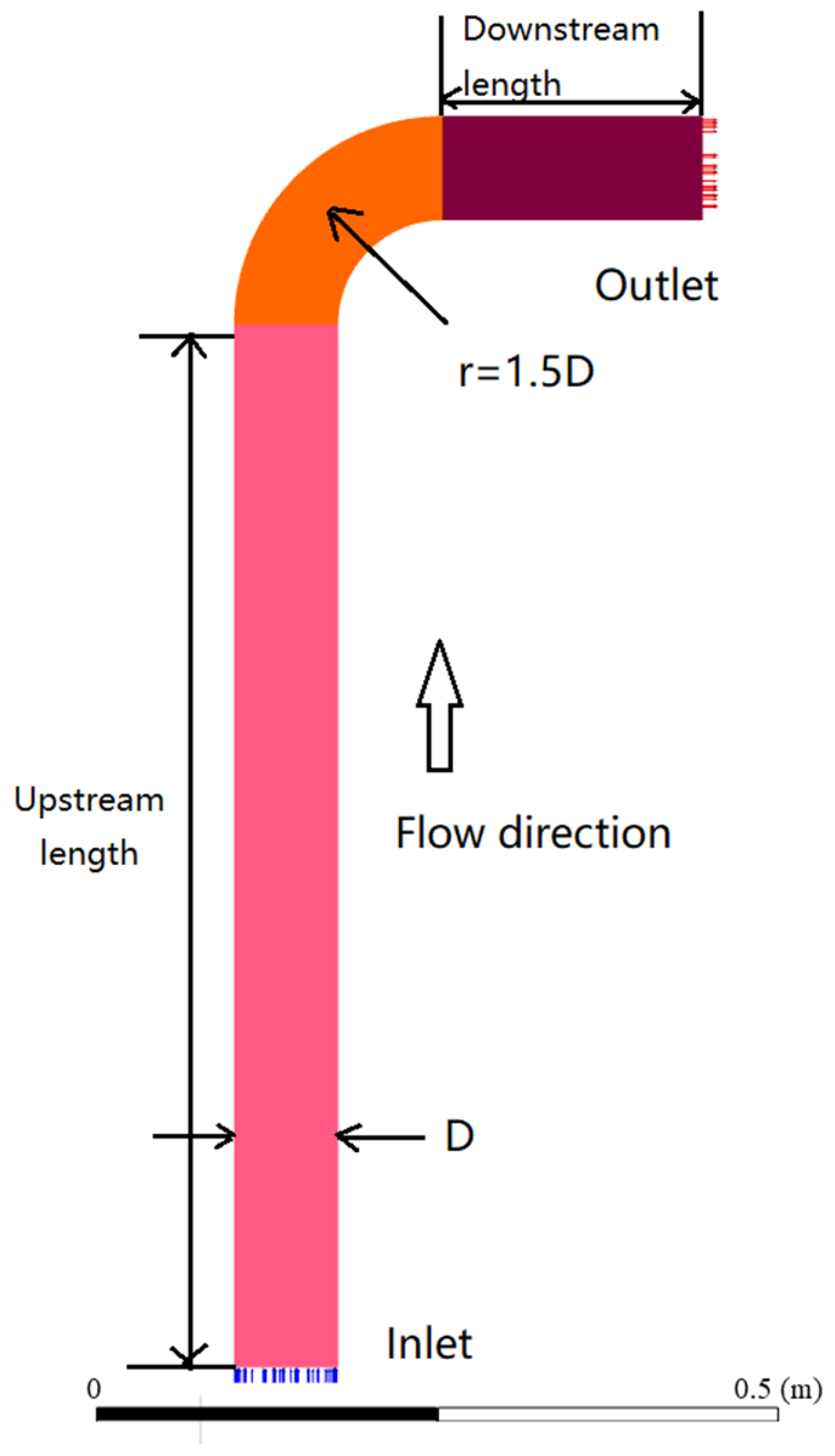
4.1. Geometry
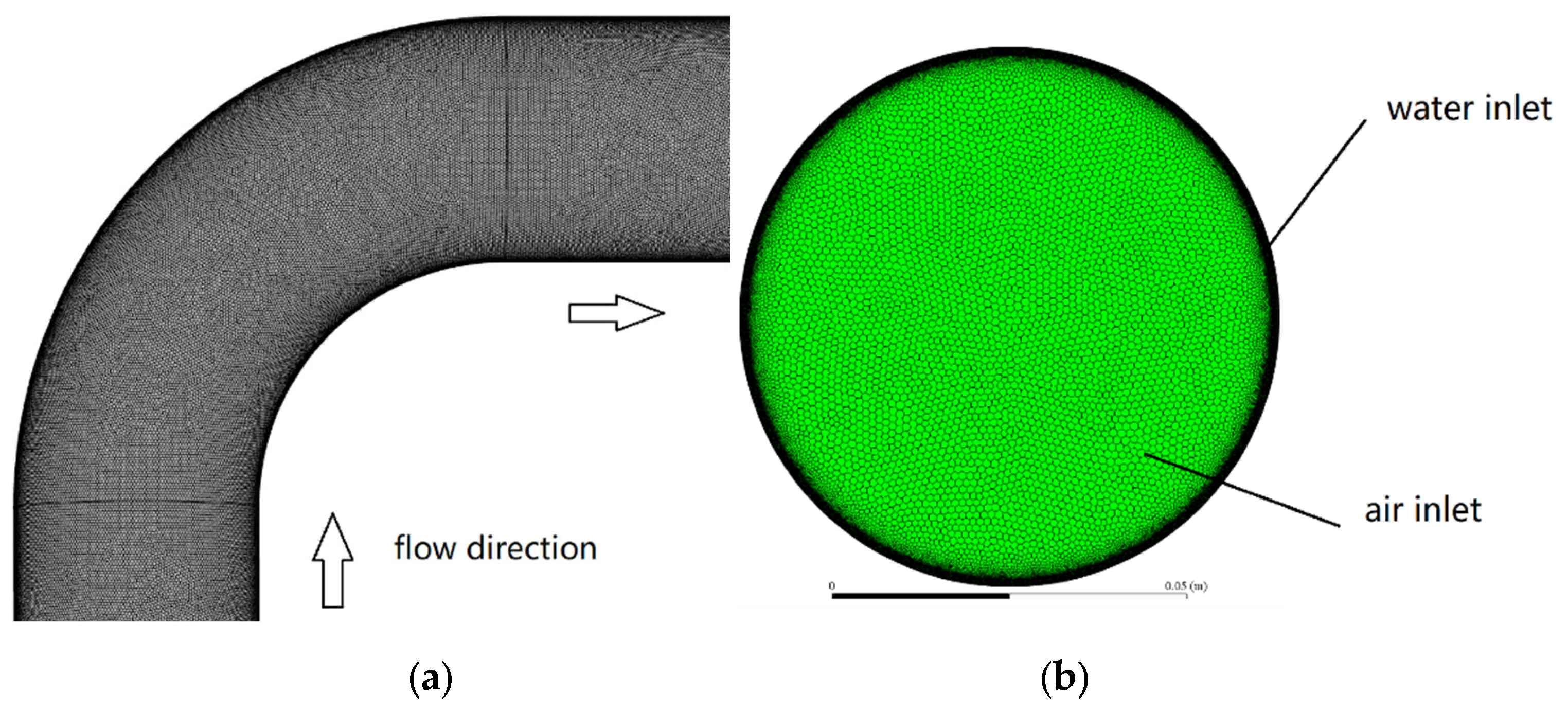
4.2. Meshing
4.3. Simulation Settings and Boundary Conditions
5. Results and Discussion
5.1. Entrainment Fraction Validation
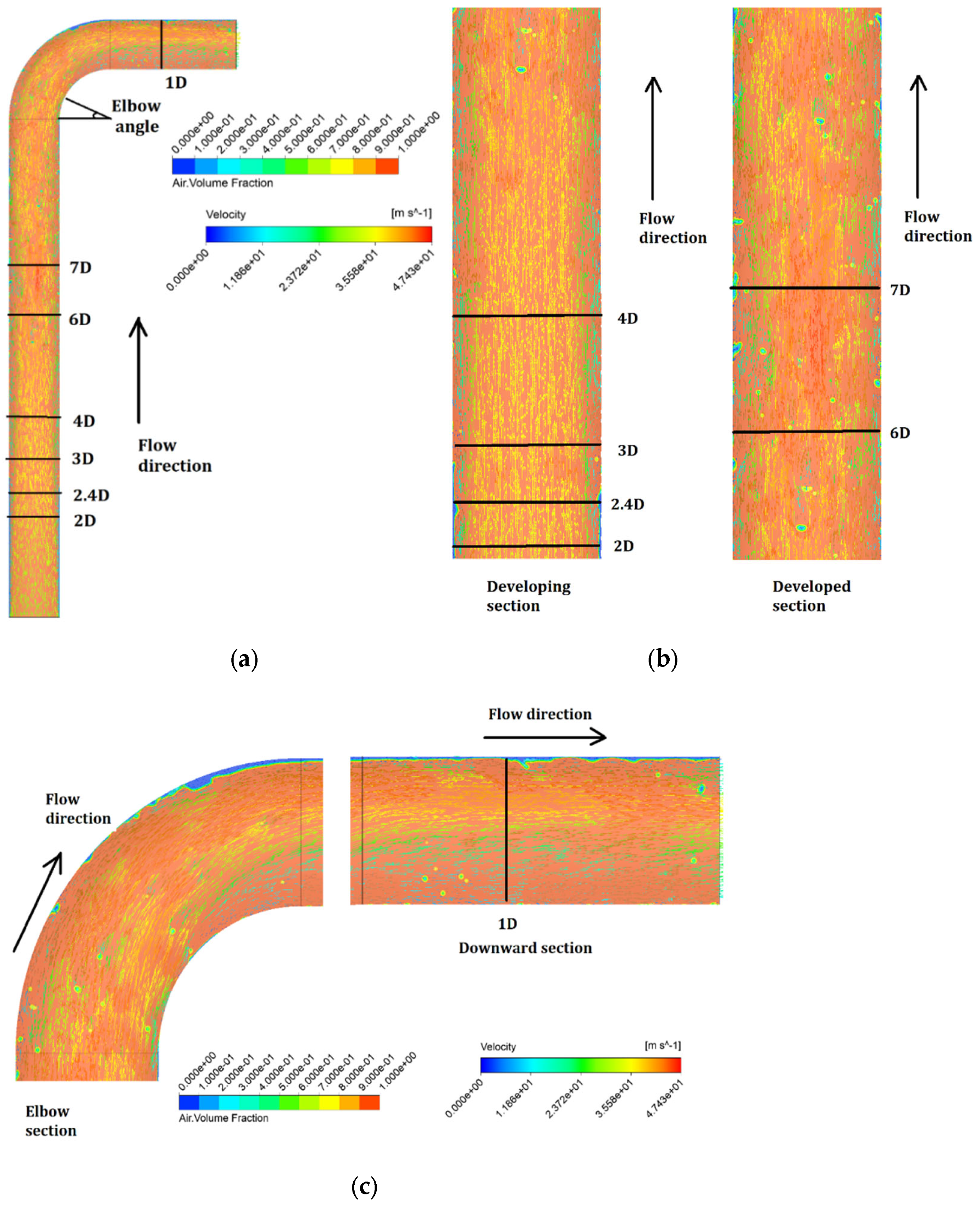
5.2. Entrainment Behavior in the Pipeline
5.2.1. Entrainment Distribution
5.2.2. Entrainment Characteristics
5.2.3. Entrainment Mechanism
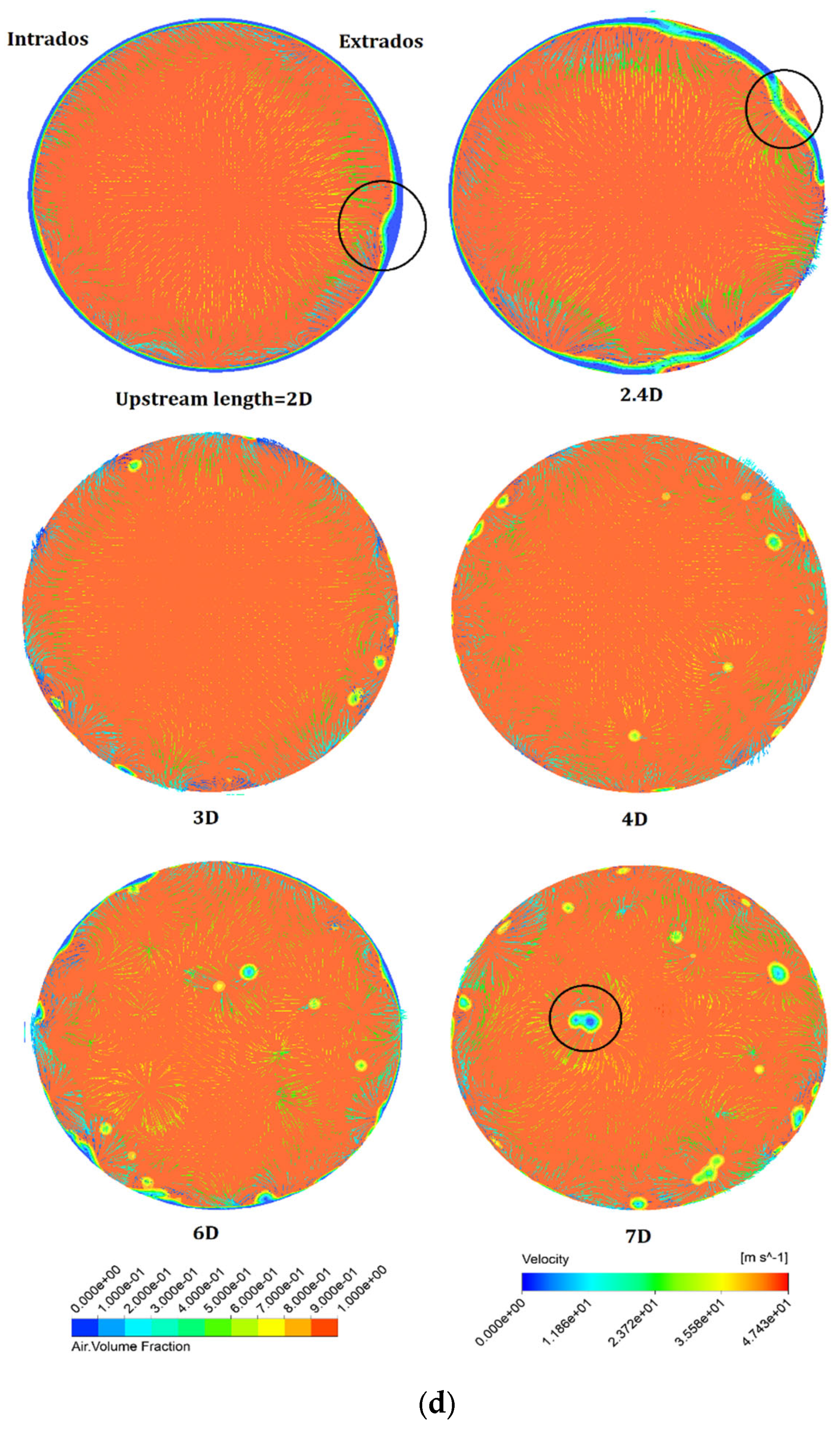
5.3. Entrainment Changes in the Elbow
6. Conclusions
- (1)
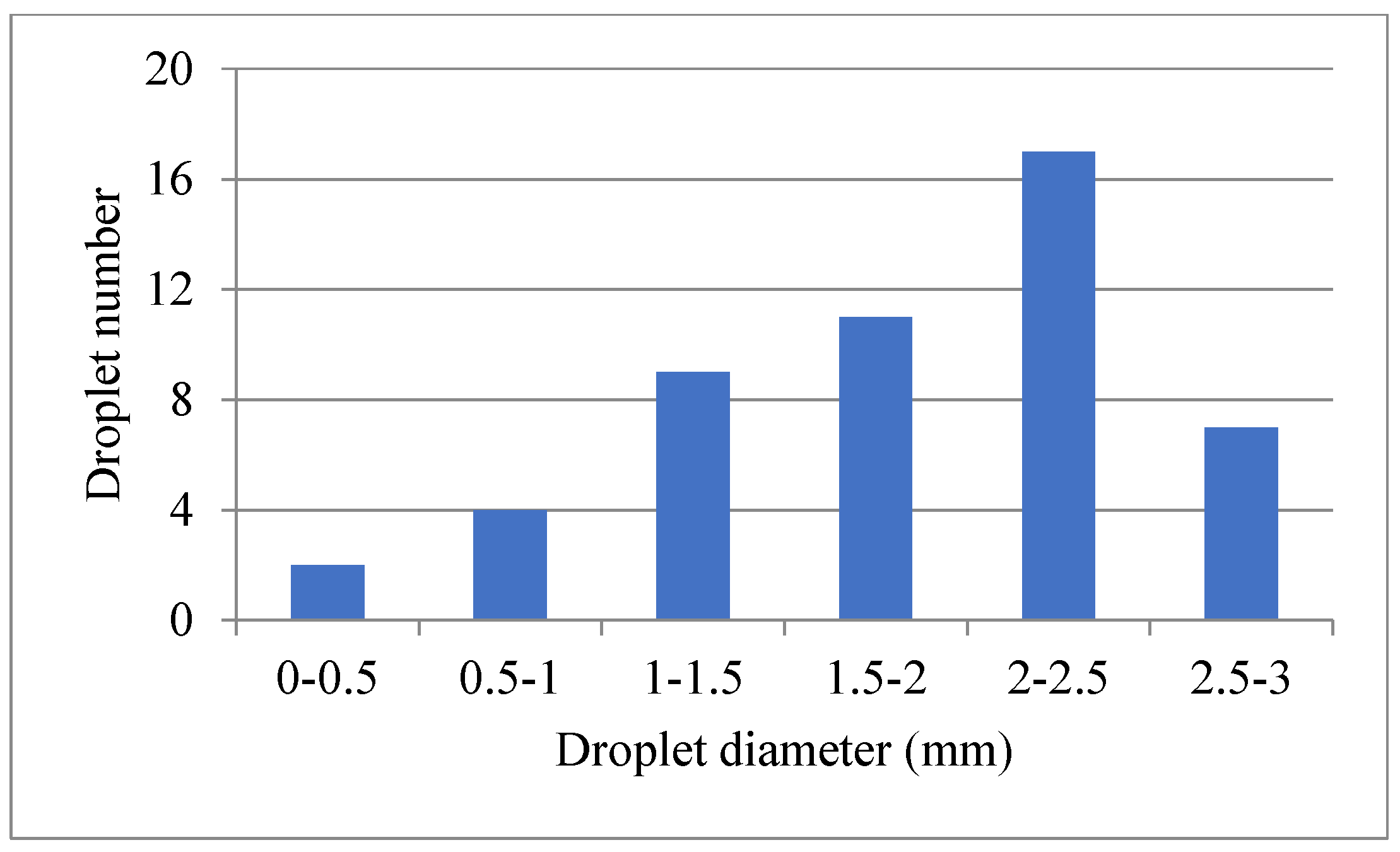
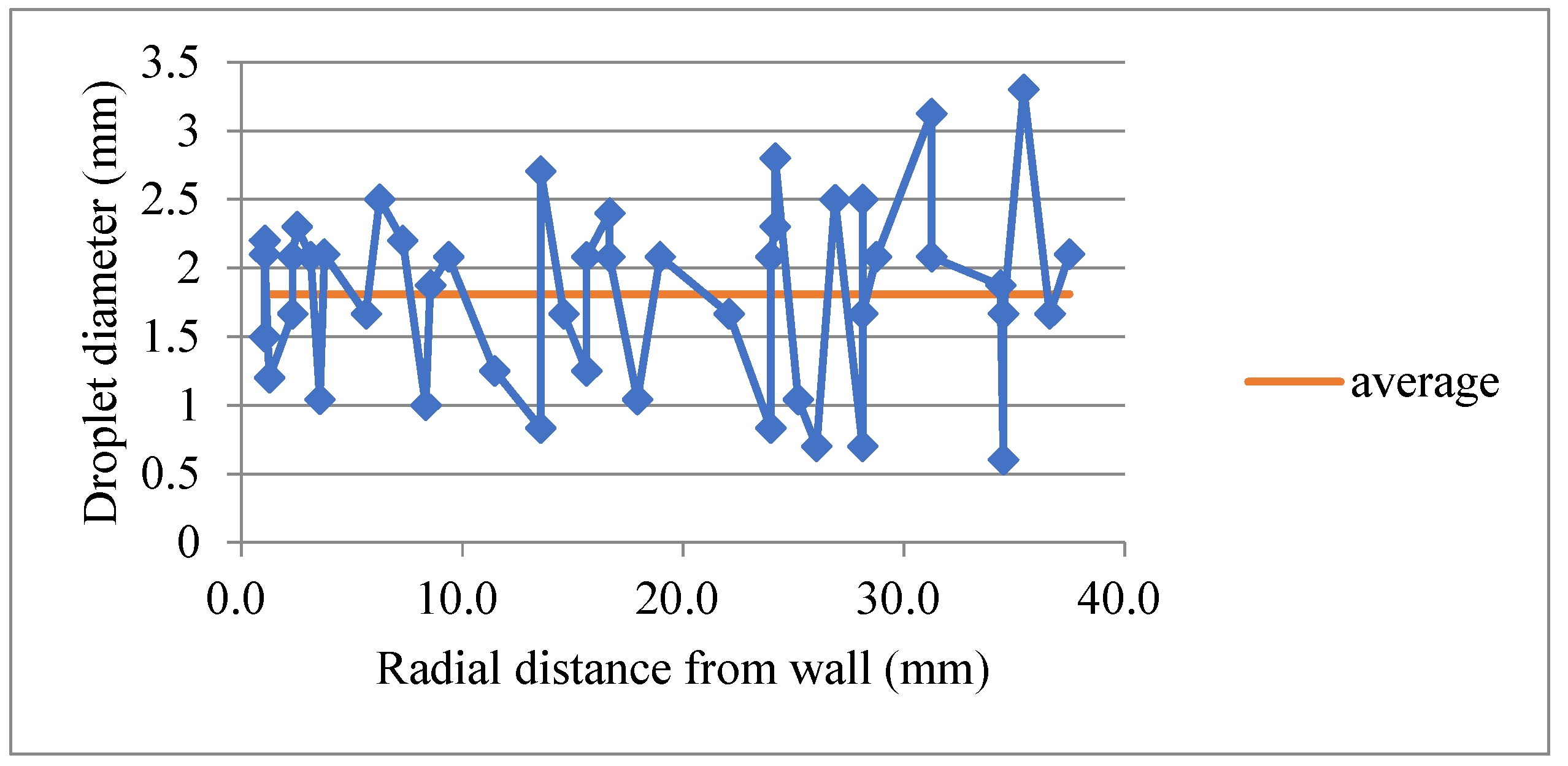
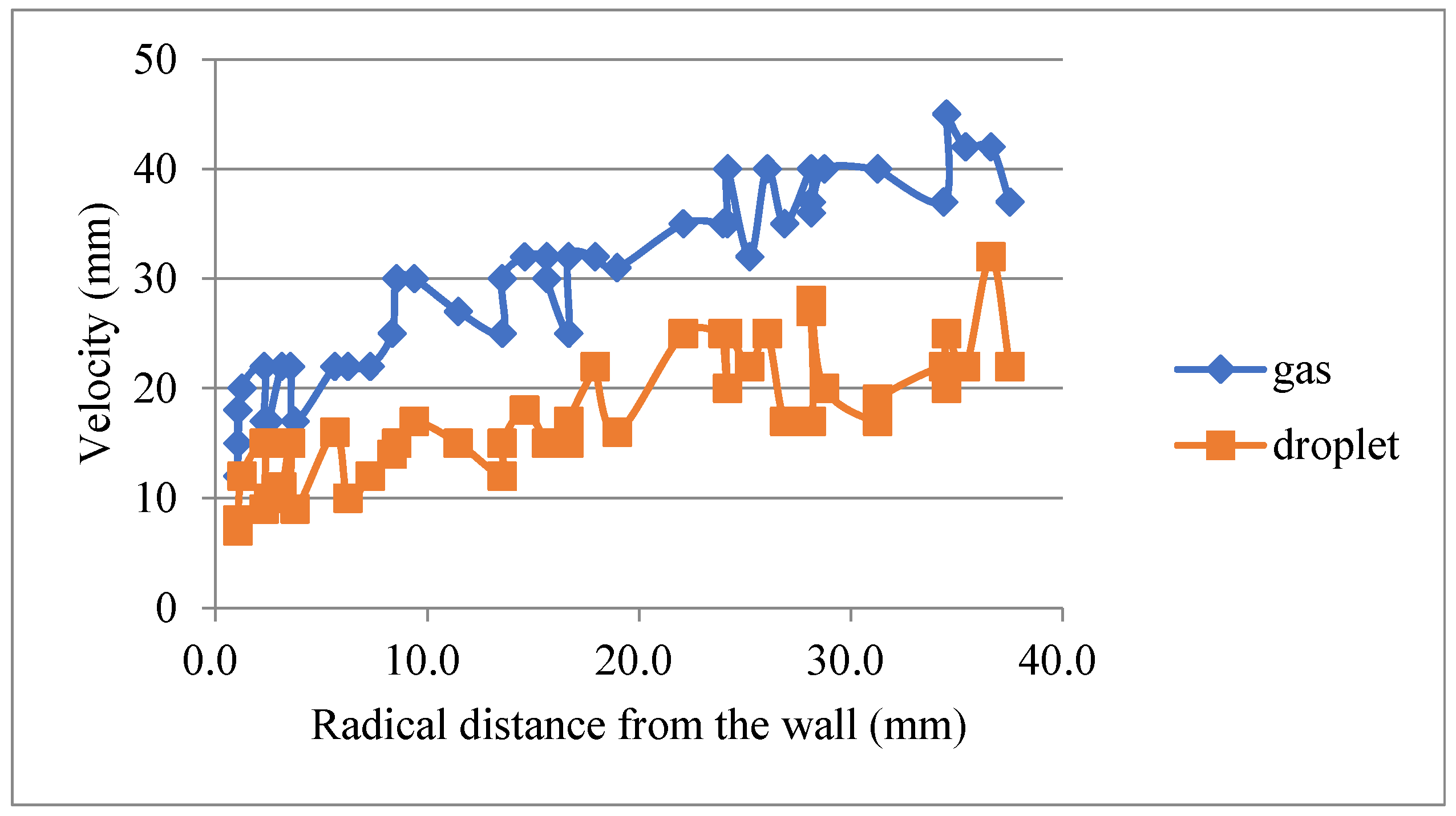
- Under the annular inlet condition, the entrainment distribution along the upstream developing length from the entrance is close to a form of exponential relaxation. The droplet diameter in a developed annular flow follows a negative skewness distribution, with most droplet diameters ranging from 1.5 mm to 2 mm. As the radial distance (from the wall) increases, the fluctuation of the droplets becomes stronger, and the velocity difference between gas and droplets increases linearly.
- (2)
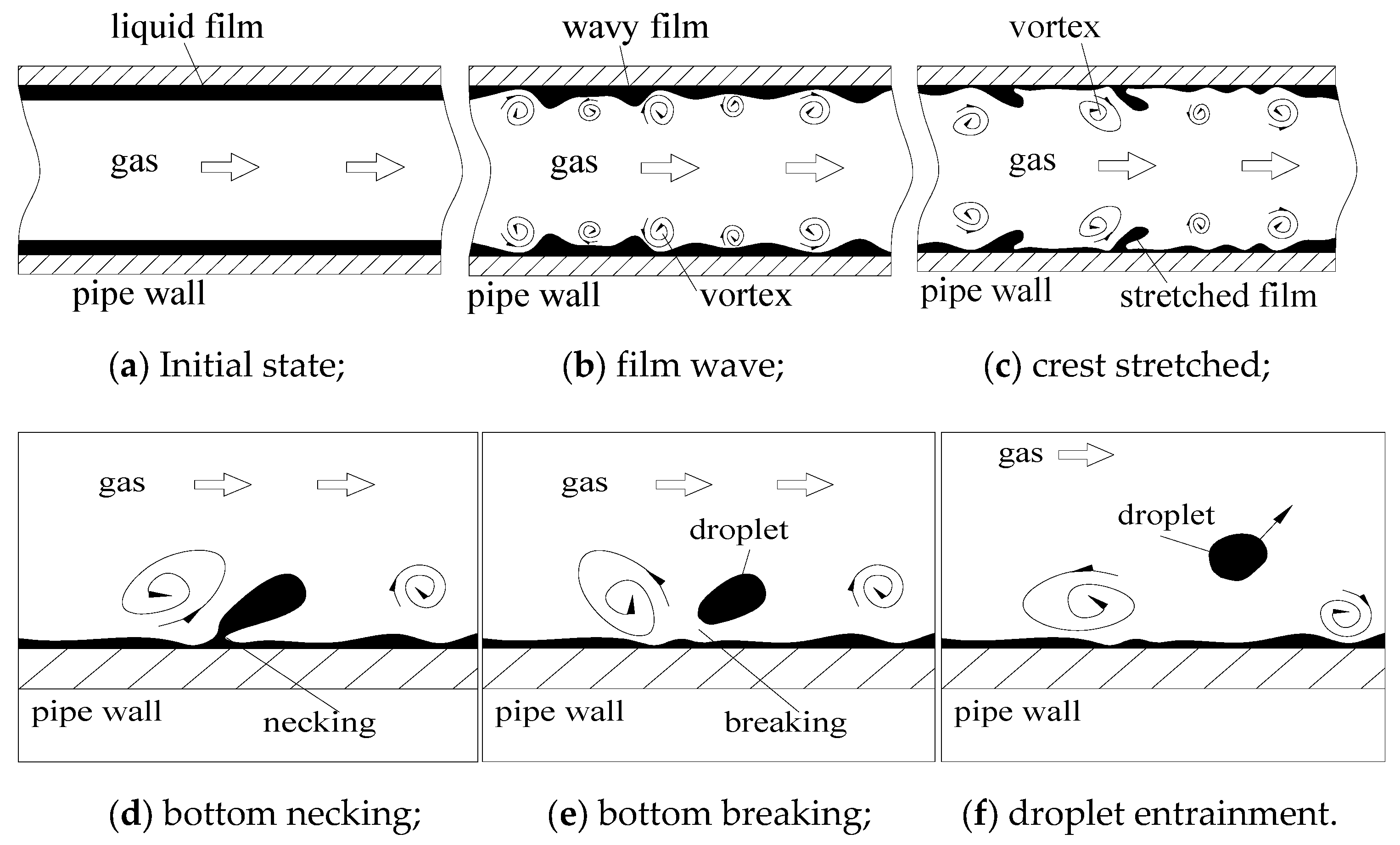
- Turbulence bursts and vortices near the wall jointly deform the liquid film and crest so that they begin to take shape; then, the external stress force acting on the liquid crest overcomes the surface force, and droplets form. Finally, vortices sucking transforms the droplets into gas, and the entrained droplet size is approximately equal to the height of the most unstable wavelength.
- (3)
- As the annular flow enters the elbow, droplets hit the extrados and form a liquid film, the droplet number in gas decreases, and at an elbow angle of 60°, there are no droplets in the pipe. Secondary flow promotes the film formation and expansion of the film to the upper and lower parts of the pipe. However, for an elbow angle of 90°, droplets re-occur near the elbow intrados, and the re-entrained droplet size is much smaller than that in the straight upstream pipe. Vortices sucking at low gas velocity play an important role in this process.
- Unique work description
- Recommendations and future work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Cross sectional area | m2 | |
| Area of the gas core | m2 | |
| Area of droplets on the cross-section | m2 | |
| Area of liquid film on the cross-section | m2 | |
| Pipe diameter | m | |
| Pressure gradient | MPa/m | |
| Entrainment flux | m/s | |
| Entrainment fraction | / | |
| Entrainment fraction calculated by simulation | / | |
| Gravitational acceleration | m/s2 | |
| Liquid holdup of gas core | / | |
| Liquid holdup of pipe cross-section | / | |
| Height of the wavelength | m | |
| L | Distance from the pipe inlet | m |
| Critical Weber number | / | |
| Liquid mass flow rate | kg/h | |
| Gas mass flow rate | kg/h | |
| Entrainment group | ft3/lbf-hr | |
| Gas Reynolds number | / | |
| Reynolds number of the liquid film | / | |
| Droplet slippage ratio | / | |
| Sample time | s | |
| Gas velocity | m/s | |
| Droplet velocity | m/s | |
| Collected liquid volume | m3 | |
| Critical Weber number | / | |
| Gas Weber number | / | |
| Droplet mass flow rate | kg/h | |
| Mixture density of the core | kg/m3 | |
| Gas density | kg/m3 | |
| Liquid density | kg/m3 | |
| Dynamic viscosity of liquid | Pa·s | |
| Dynamic viscosity of gas | Pa·s | |
| Superficial liquid velocity | m/s | |
| Superficial gas velocity | m/s | |
| Surface tension | N·m | |
| Droplet diameter | m | |
| Average maximum droplet size | m | |
| Droplet volume median diameter | m |
References
- Mishima, K.; Ishii, M. Flow regime transition criteria for upward two-phase flow in vertical tubes. Int. J. Heat Mass Transf. 1984, 27, 723–737. [Google Scholar]
- Wu, B.; Firouzi, M.; Mitchell, T.; Rufford, T.E.; Leonardi, C.; Towler, B. A critical review of flow maps for gas-liquid flows in vertical pipes and annuli. Chem. Eng. J. 2017, 326, 350–377. [Google Scholar] [CrossRef]
- Dasgupta, A.; Chandraker, D.K.; Kshirasagar, S.; Reddy, B.R.; Rajalakshmi, R.; Nayak, A.K.; Walker, S.P.; Vijayan, P.K.; Hewitt, G.F. Experimental investigation on dominant waves in upward air-water two-phase flow in churn and annular regime. Exp. Therm. Fluid Sci. 2017, 81, 147–163. [Google Scholar] [CrossRef]
- Ryu, S.H.; Park, G.C. A droplet entrainment model based on the force balance of an interfacial wave in two-phase annular flow. Nucl. Eng. Des. 2011, 241, 3890–3897. [Google Scholar] [CrossRef]
- Kataoka, I.; Ishii, M.; Mishima, K. Generation and size distribution of droplet in annular two-phase flow. J. Fluids Eng. 1983, 105, 230–238. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B. Generalization of droplet entrainment rate correlation for annular flow considering disturbance wave properties. Chem. Eng. Sci. 2017, 164, 279–291. [Google Scholar] [CrossRef]
- Berna, C.; Escriva, A.; Munoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow: Interfacial waves and onset of entrainment. Prog. Nucl. Energy 2014, 74, 14–43. [Google Scholar] [CrossRef]
- Pan, L.; Hanratty, T.J. Correlation of entrainment for annular flow in horizontal pipes. Int. J. Multiph. Flow 2002, 32, 385–408. [Google Scholar] [CrossRef]
- Okawa, T.; Kotani, A.; Kataoka, I.; Natio, M. Prediction of critical heat flux in annular flow using a film flow model. J. Nucl. Sci. Technol. 2003, 40, 388–396. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Cherdantsev, A.V.; Cherdantsev, M.V.; Isaenkov, S.V.; Markovich, D.M. Study of formation and development of disturbance waves in annular gas–liquid flow. Int. J. Multiph. Flow 2015, 77, 65–75. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T. Wave behavior in horizontal annular air-water flow. Int. J. Multiph. Flow 2008, 34, 636–646. [Google Scholar] [CrossRef]
- Belt, R.J.; Westende, J.M.C.V.; Prasser, H.M.; Portela, L.M. Time and spatially resolved measurements of interfacial waves in vertical annular flow. Int. J. Multiph. Flow 2010, 36, 570–587. [Google Scholar] [CrossRef]
- Asali, J.C.; Hanratty, T.J. Ripples generated on a liquid film at high gas velocities. Int. J. Multiph. Flow 1993, 19, 229–243. [Google Scholar] [CrossRef]
- Holowach, M.J.; Hochreiter, L.E.; Cheung, F.B. A model for droplet entrainment in heated annular flow. Int. J. Heat Fluid Flow 2002, 23, 807–822. [Google Scholar] [CrossRef]
- Wicks, M.; Duckler, A.E. Entrainment and pressure drop in concurrent gas-liquid flow: I. Air-water in horizontal flow. AIChE J. 1960, 6, 463–468. [Google Scholar] [CrossRef]
- Paleev, I.I.; Filippovich, B.S. Phenomena of liquid transfer in two-phase dispersed annular flow. Int. J. Heat Mass Tran. 1966, 9, 1089–1093. [Google Scholar] [CrossRef]
- Xu, G.; Cai, L.; Ullmann, A.; Brauner, N. Trapped water flushed by flowing oil in upward-inclined oil pipelines. In Volume 1: Upstream Pipelines; Project Management; Design and Construction; Environment; Facilities Integrity Management; Operations and Maintenance; Pipeline Automation and Measurement, Proceedings of the International Pipeline Conference, Calgary, AB, Canada, 24 September 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 637–647. [Google Scholar]
- Huang, S.; Zhang, B.; Lu, J.; Wang, D. Study on flow pattern maps in hilly-terrain air-water-oil three-phase flows. Exp Therm. Fluid Sci. 2013, 47, 158–171. [Google Scholar] [CrossRef]
- Parsi, M.; Vieira, R.E.; Torres, C.F.; Kesana, N.R.; McLaury, B.S.; Shirazi, S.A. Experimental investigation of interfacial structures within churn flow using a dual wire-mesh sensor. Int. J. Multiph. Flow 2015, 73, 155–170. [Google Scholar] [CrossRef]
- Magnini, M.; Ullmann, A.; Brauner, N.; Thome, J.R. Numerical study of water displacement from the elbow of an inclined oil pipeline. J. Petrol. Sci. Eng. 2018, 166, 1000–1017. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Saffar-Avval, M.; Ahmadi, G. 3D computational modeling of sand erosion in gas-liquid-particle multiphase annular flows in bends. Wear 2020, 450–451, 203241. [Google Scholar] [CrossRef]
- Pshenin, V.V.; Zakirova, G.S. Improving the efficiency of oil vapor recovery units in the commodity transport operations at oil terminals. J. Min. Inst. 2023, 265, 121–128. [Google Scholar] [CrossRef]
- Korshak, A.A.; Pshenin, V.V. Modeling of water slug removal from oil pipelines by methods of computational fluid dynamics. Neft. Khozyaystvo Oil Ind. 2023, 10, 117–122. (In Russian) [Google Scholar] [CrossRef]
- Zhao, X.Y.; Cao, X.W.; Cao, H.G.; Zhang, J.; Zhang, J.N.; Peng, W.S.; Bian, J. Numerical study of elbow erosion due to sand particles under annular flow considering liquid entrainment. Particuology 2023, 76, 122–139. [Google Scholar] [CrossRef]
- Oliemans, R.V.A.; Pots, B.F.M.; Trompe, N. Modelling of annular dispersed two-phase flow in vertical pipes. Int. J. Multiph. Flow 1986, 12, 711–732. [Google Scholar] [CrossRef]
- Ishii, M.; Mishima, K. Droplet entrainment correlation in annular two-phase flow. Int. J. Heat Fluid Flow 1989, 32, 1835–1846. [Google Scholar] [CrossRef]
- Kolev, N.I. Multiphase Flow Dynamics. 2: Thermal and Mechanical Interactions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Azzopardi, B.J. Drops in annular two-phase flow. Int. J. Heat Multiph. Flow 1997, 23, 1–53. [Google Scholar] [CrossRef]
- Wierzba, A. Deformation and breakup of liquid drops in a gas stream at nearly critical Weber numbers. Exp. Fluids 1990, 9, 59–64. [Google Scholar] [CrossRef]
- Fore, L.B.; Ibrahim, B.B.; Beus, S.G. Visual measurements of droplets size in gas-liquid annular flow. Int. J. Multiph. Flow 2002, 28, 1895–1910. [Google Scholar] [CrossRef]
- Ishii, M.; Grolmes, M.A. Inception criteria foe droplet entrainment in two-phase concurrent film flow. AIChE J. 1975, 21, 308–318. [Google Scholar] [CrossRef]
- Magrini, K.L.; Sarica, C.; Al-Sarkhi, A.; Zhang, H.Q. Liquid entrainment in annular gas/liquid flow in inclined pipes. SPE J. 2012, 17, 617–630. [Google Scholar] [CrossRef]
- Fluent Theory Guide, Release 19.2; ANSYS Inc.: Canonsburg, PA, USA, 2018.
- Zahedi, P.; Jun, Z.; Hadi, A.; McLaury, B.S.; Shirazi, S.A. CFD simulation of multiphase flows and erosion predictions under annular flow and low liquid loading conditions. Wear 2017, 376–377, 1260–1270. [Google Scholar] [CrossRef]
- Kataoka, I.; Ishii, M.; Nakayama, A. Entrainment and deposition rates of droplets in annular two-phase flow. Int. J. Heat Mass Transf. 2000, 43, 1573–1589. [Google Scholar] [CrossRef]
- Berna, C.; Escriva, A.; Munoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow: Characterization of the entrained droplets. Prog. Nucl. Energy 2015, 79, 64–86. [Google Scholar] [CrossRef]
- Mugele, R.A.; Evans, H.D. Droplet size distribution in sprays. Ind. Eng. Chem. 1951, 43, 1317–1324. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: Oxford, UK, 1981. [Google Scholar]
- Henstock, W.H.; Hanratty, T.J. The interfacial drag and the height of the wall layer in annular flows. AIChE J. 1976, 22, 990–1000. [Google Scholar] [CrossRef]
- Vieira, R.E.; Parsi, M.; Zahedi, P.; McLaury, B.S.; Shirazi, S.A. Electrical resistance probe measurements of solid particle erosion in multiphase annular flow. Wear 2017, 382, 15–28. [Google Scholar] [CrossRef]



| Authors | Year | Summary of Work | Output |
|---|---|---|---|
| Wicks et al. [15] | 1960 | Isokinetic sampling experimental study on droplet entrainment characteristics | A model to calculate the droplet mass flow rate |
| Paleev et al. [16] | 1966 | Liquid film removal experimental study on entrainment characteristics | An empirical correlation to calculate film flow rate |
| Xu et al. [17] | 2013 | Water displacement characteristics investigation in inclined pipe | Critical value of oil flow rate to flush out trapped water |
| Haung et al. [18] | 2013 | Flow pattern observation in uphill and downhill pipes using high-speed camera | Experimental program to judge flow pattern in hilly-terrain flow |
| Parsi et al. [19] | 2015 | Experimental study on churn flow using wire-mesh sensor | Interfacial structures analysis of liquid film |
| Magnini et al. [20] | 2018 | Numerical study on effects of oil velocity and wall-wetting conditions on flow pattern | A model for predicting the drift velocity along upward pipes |
| Farokhipour et al. [21] | 2020 | Factors affecting elbow erosion and film distribution using simulation | Higher liquid velocity enhances film cushion and weakens erosion |
| Pshenin et al. [22] | 2022 | Hydrocarbon evaporation losses during loading of tanker fleets | A model of hydrocarbon vapor displacement from the inner part of a tanker |
| Korshak et al. [23] | 2023 | Water slug behavior and removal based on pumping liquid simulation | Slug removal algorithms that agree with experiment |
| Zhao et al. [24] | 2023 | Liquid distribution and erosion pattern of elbow under upward annular flow | Wave undercut and roll-wave entrainment mechanism |
| Items | Settings |
|---|---|
| Multiphase model | Volume of fluid |
| Turbulence model | k-e Realizable |
| Pressure–velocity coupling | SIMPLE |
| Interface modeling | Sharp |
| Spatial discretization | Second-order upwind |
| Primary phase | Air |
| Secondary phase | Water |
| Phase interaction | Surface tension force modeling |
| Surface tension coefficient | 0.072 N/m |
| Near-wall treatment | Enhanced wall treatment |
| Items | Settings |
|---|---|
| Air inlet (mass flow inlet) | 0.145 kg/s |
| Water inlet (mass flow inlet) | 0.456 kg/s |
| Outlet (pressure outlet) | Atmosphere |
| Turbulence intensity | 5% |
| Turbulence viscosity ratio | 10 |
| Wall | No slip |
| Wall contact angle | 90° |
| Experimental Data | Oliemans’ Model | Ishii’s Model | CFD Data | ||
|---|---|---|---|---|---|
| 1520 | 2376 | 0.4 | 0.53 | 0.55 | 0.47 |
| Radial Distance from Wall (mm) | Expectation (mm) | Variance |
|---|---|---|
| 0~10 | 1.85 | 0.19 |
| 10~20 | 1.76 | 0.36 |
| 20~30 | 1.76 | 0.51 |
| 30~40 | 1.86 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Cao, X. Effect of Entrainment on the Liquid Film Behavior in Pipe Elbows. Energies 2024, 17, 1983. https://doi.org/10.3390/en17081983
Xie Z, Cao X. Effect of Entrainment on the Liquid Film Behavior in Pipe Elbows. Energies. 2024; 17(8):1983. https://doi.org/10.3390/en17081983
Chicago/Turabian StyleXie, Zhenqiang, and Xuewen Cao. 2024. "Effect of Entrainment on the Liquid Film Behavior in Pipe Elbows" Energies 17, no. 8: 1983. https://doi.org/10.3390/en17081983
APA StyleXie, Z., & Cao, X. (2024). Effect of Entrainment on the Liquid Film Behavior in Pipe Elbows. Energies, 17(8), 1983. https://doi.org/10.3390/en17081983





