Performance Evaluation of Static and Dynamic Compressed Air Reservoirs for Energy Storage
Abstract
1. Introduction
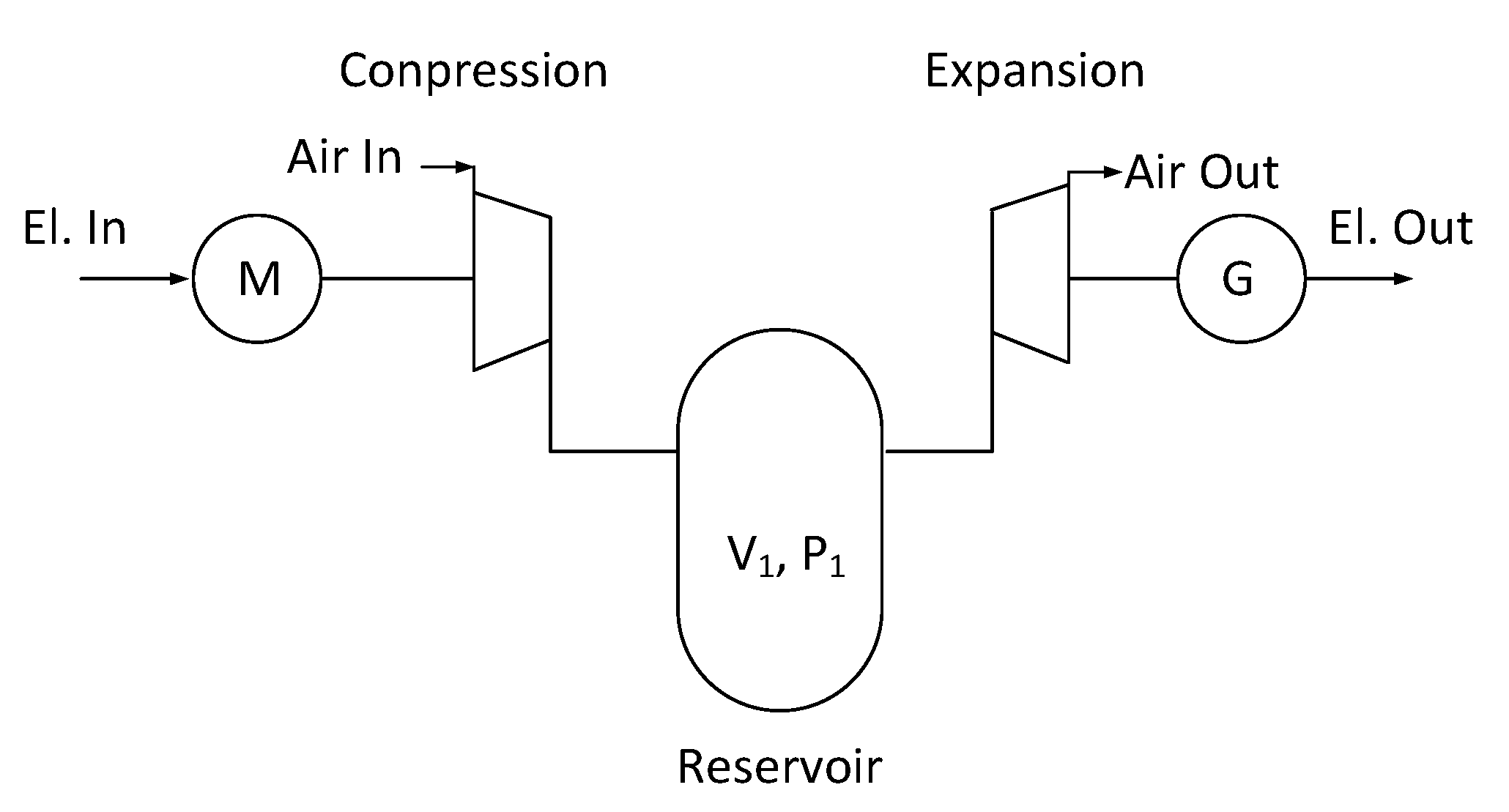
2. Compressed Air Energy System with Accumulation in a Storage Vessel
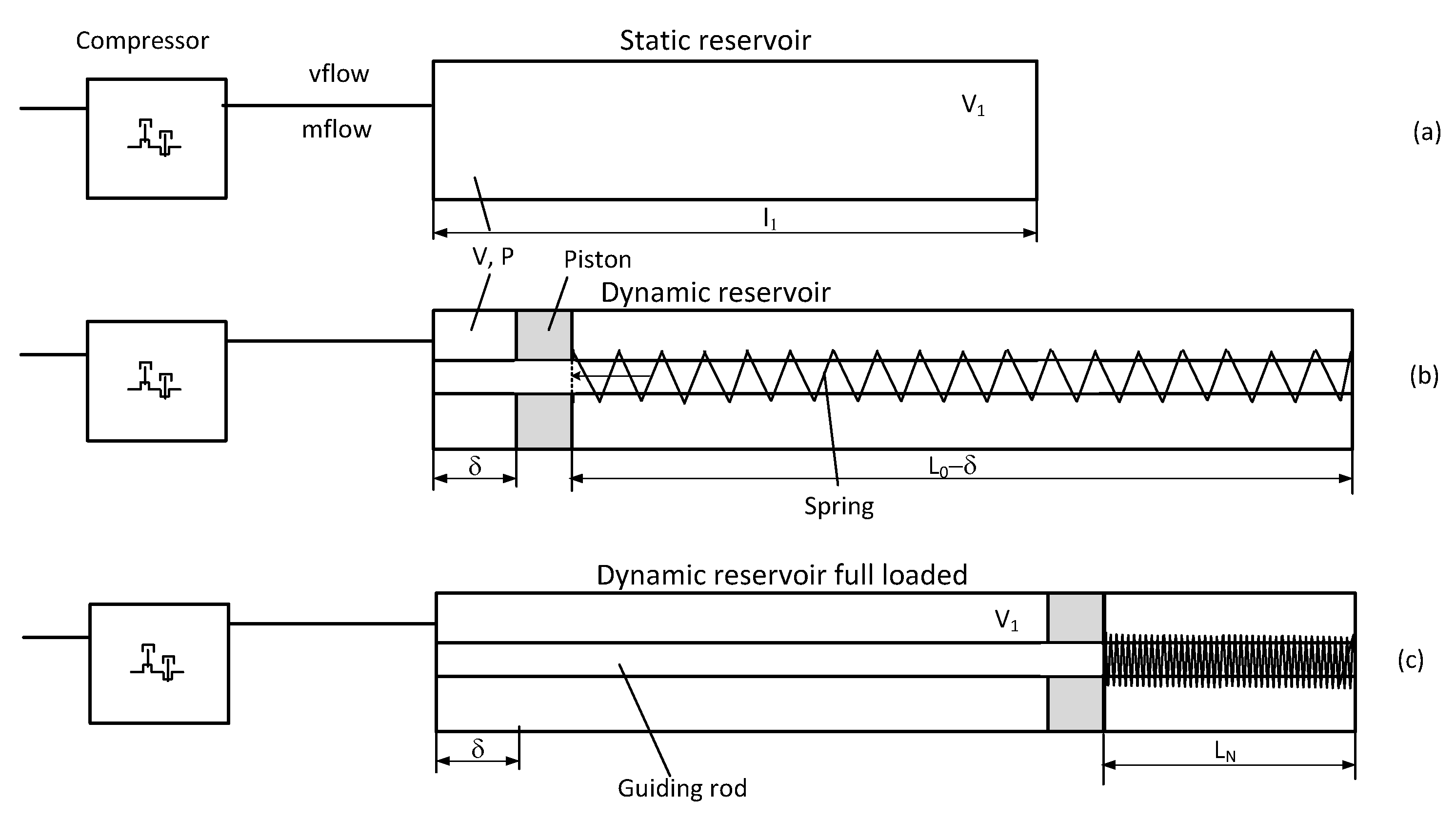
2.1. Static and Dynamic Reservoirs
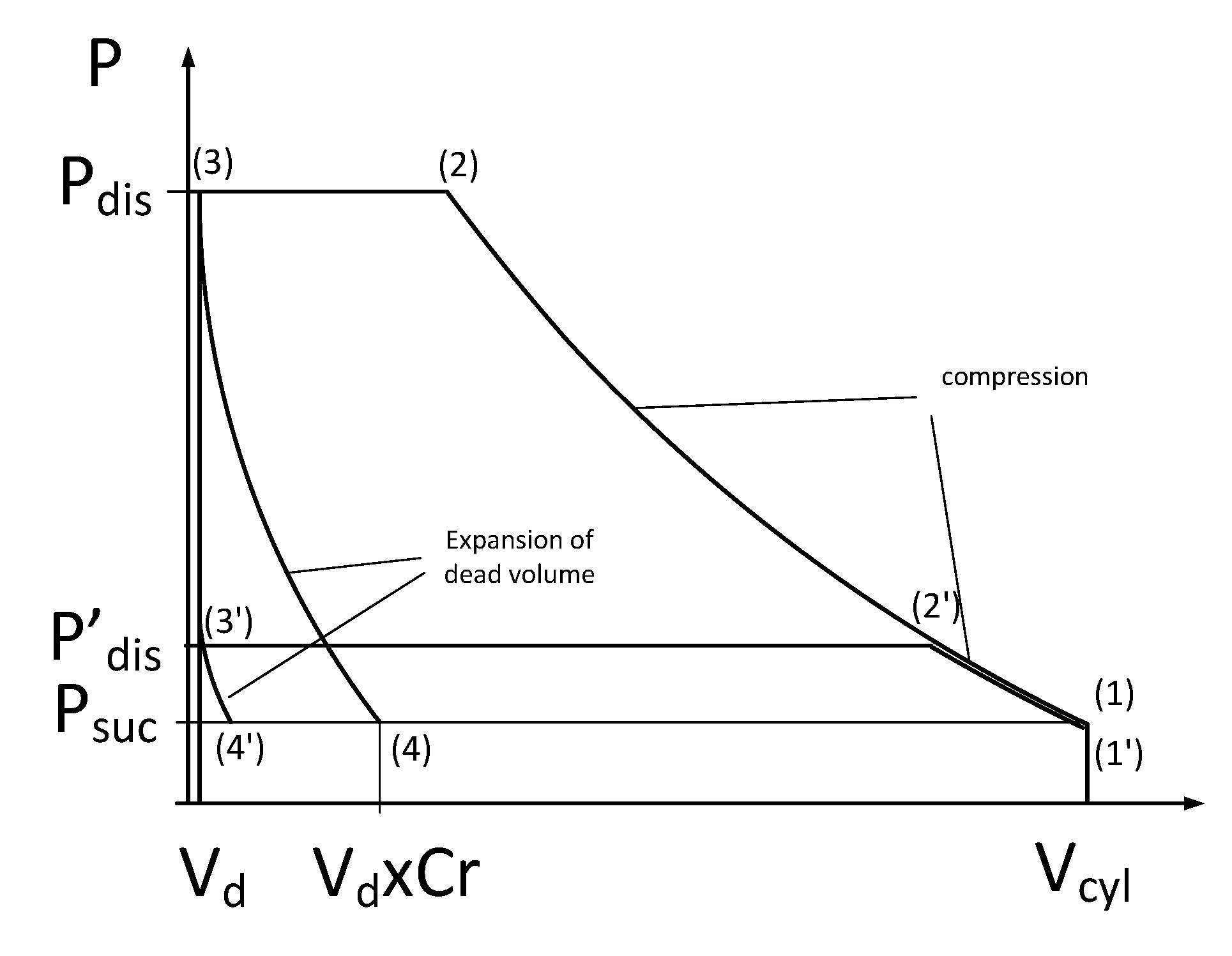
2.2. The Model of the Compressor
2.3. Modeling the Two Reservoirs
2.3.1. Parameters of the Reservoirs
2.3.2. Structural Diagram of the Static Reservoir System
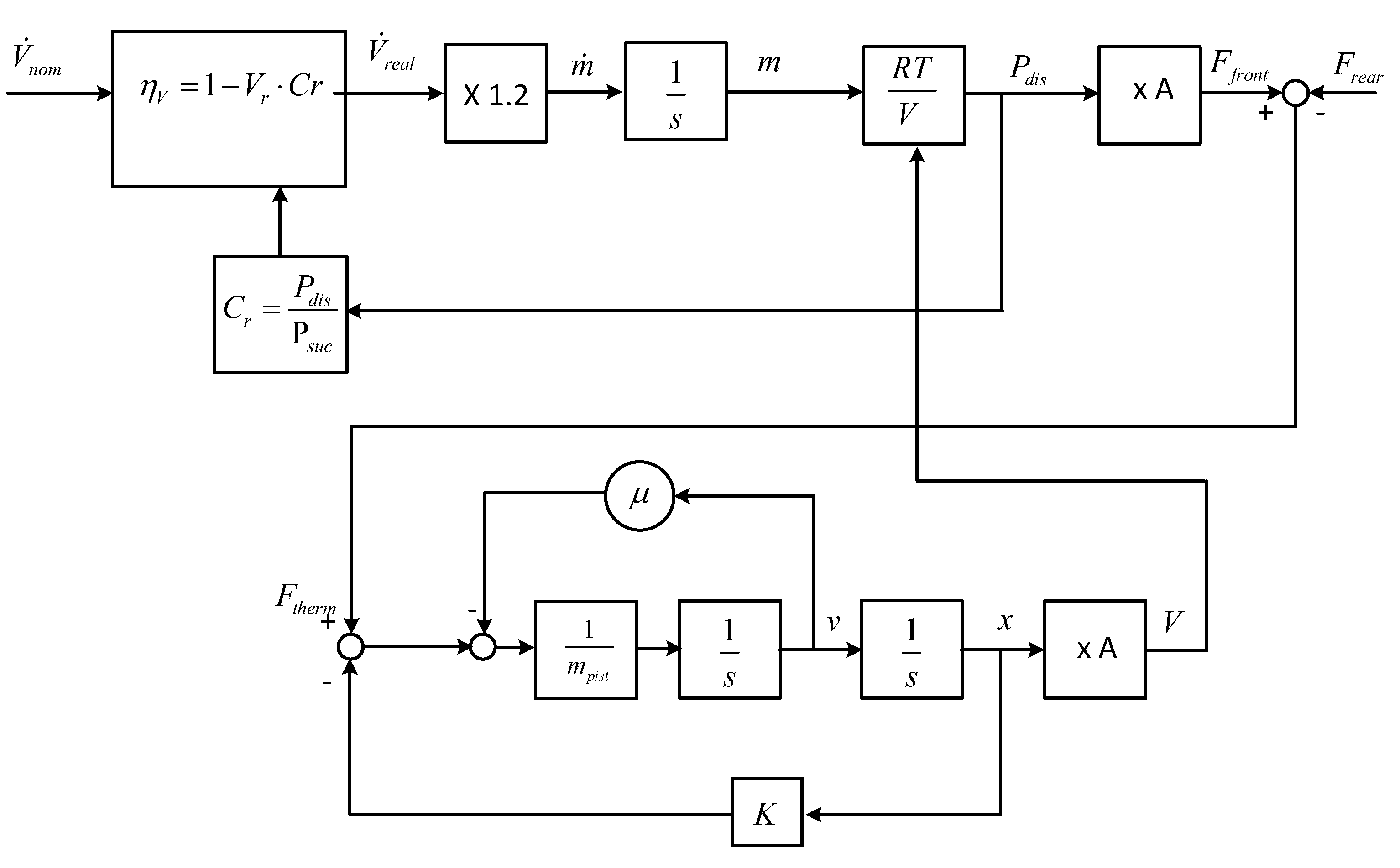
2.3.3. Structural Diagram of the Dynamic Reservoir System
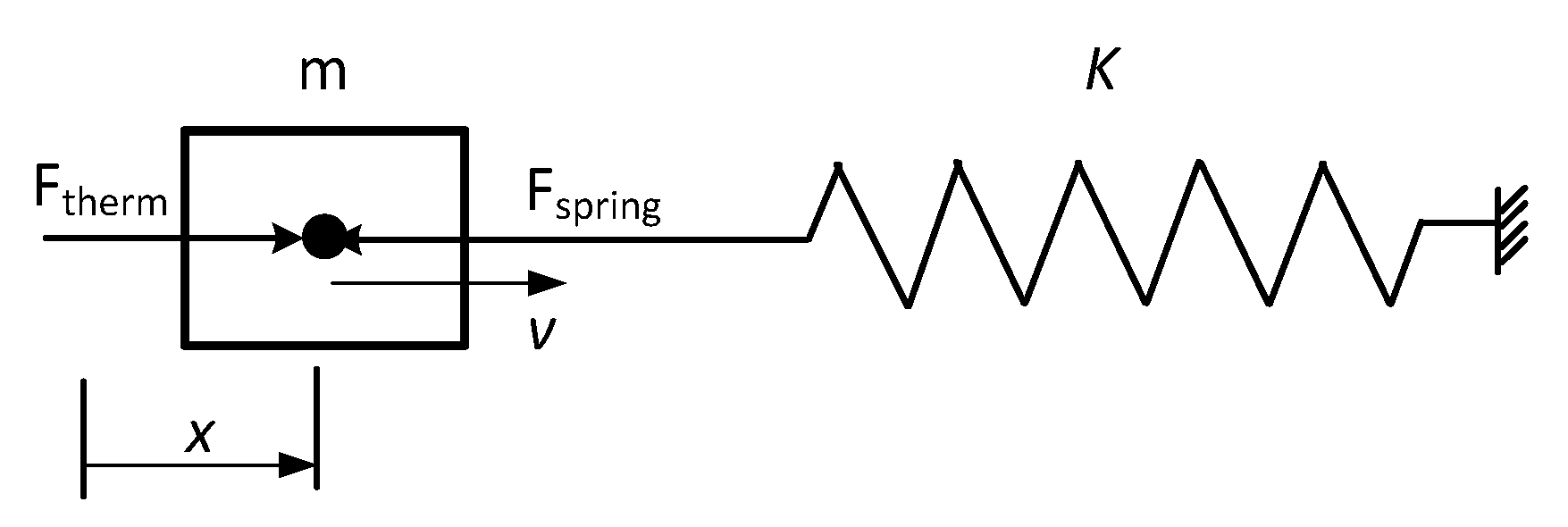
2.3.4. The Model of the Spring–Mass System
2.4. Energies Accumulated
2.4.1. Volume of Air
2.4.2. Energy Accumulated in the Spring
3. Simulation Results
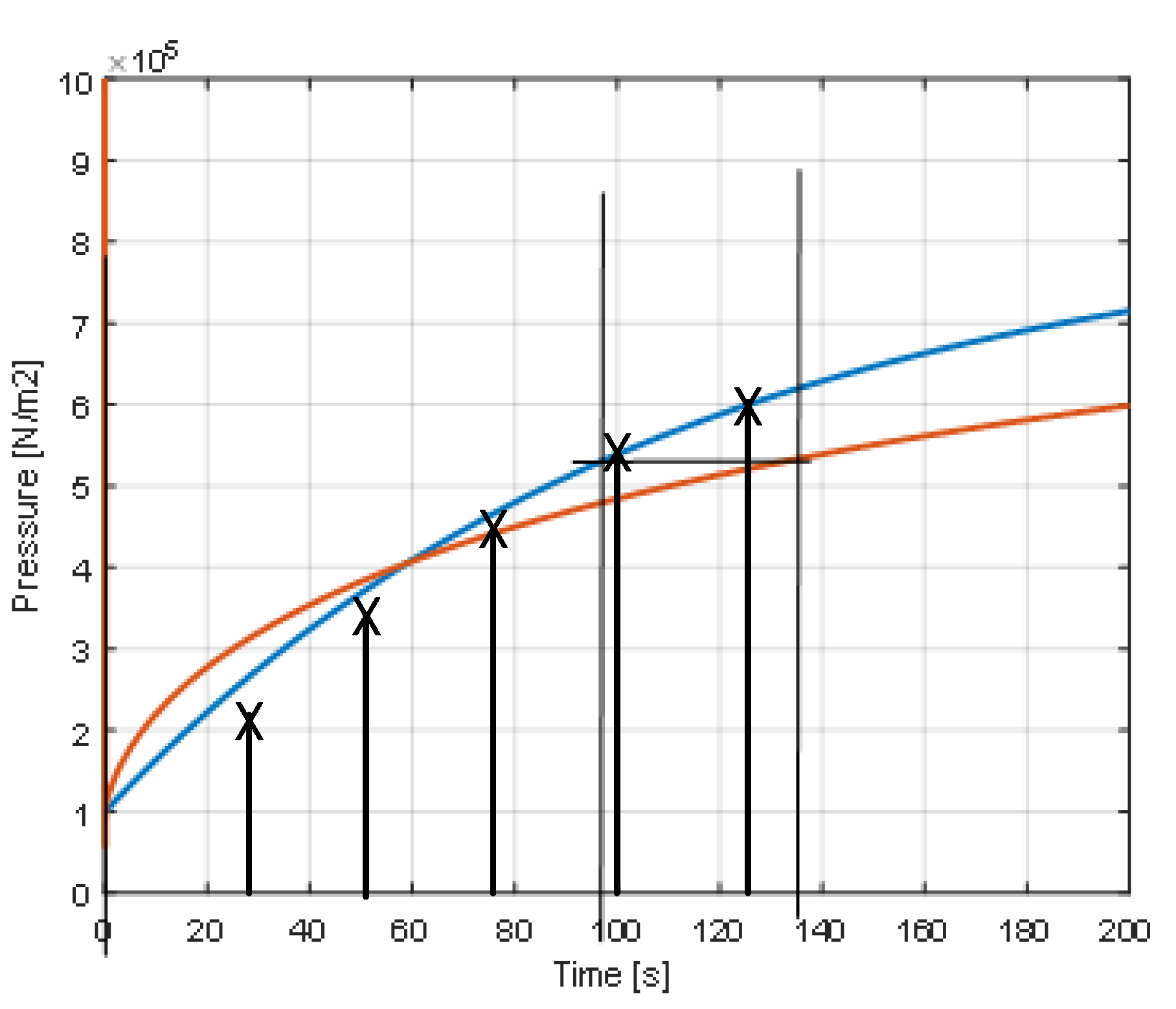
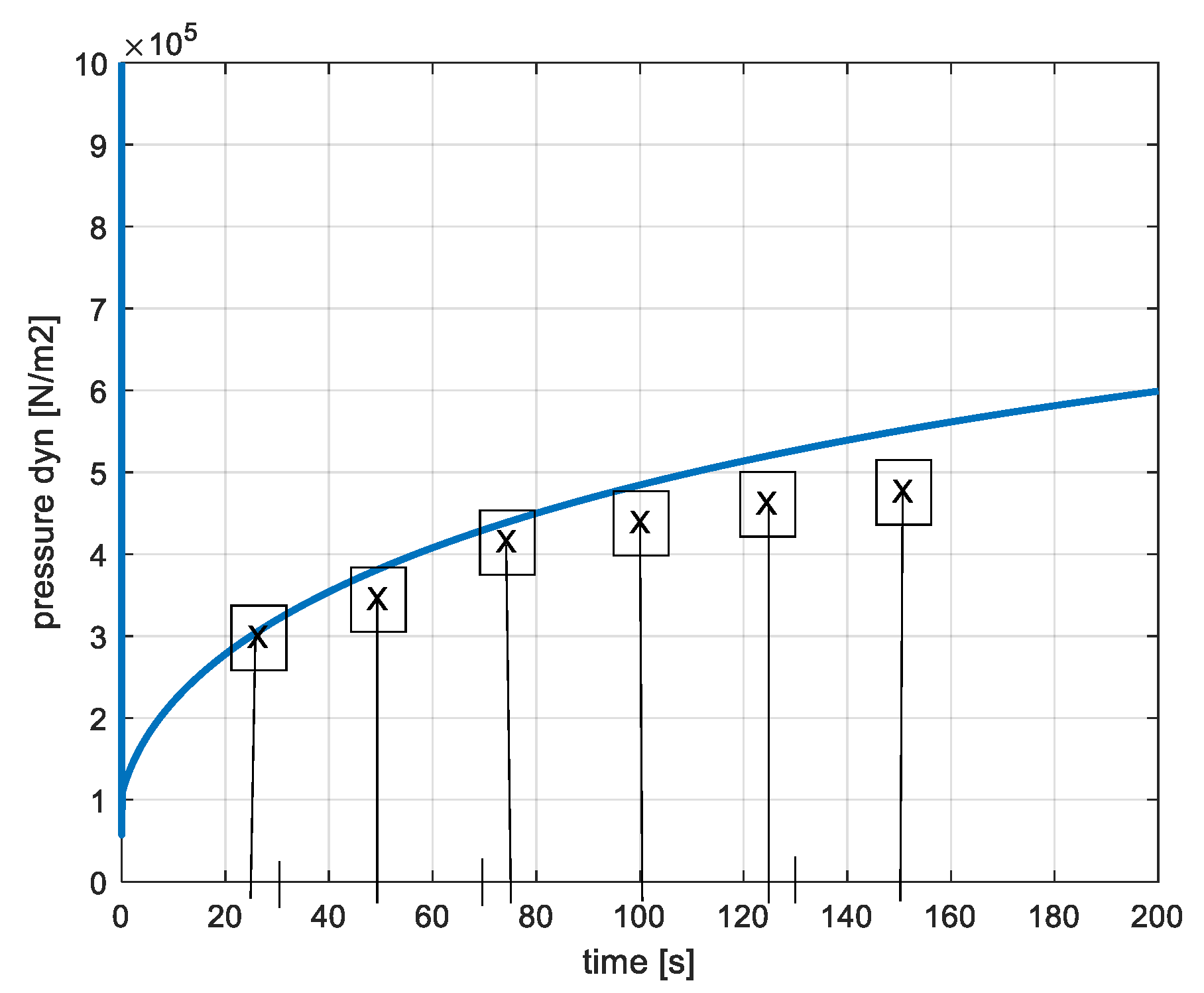
3.1. Evolution of the Pressures and Masses of Air
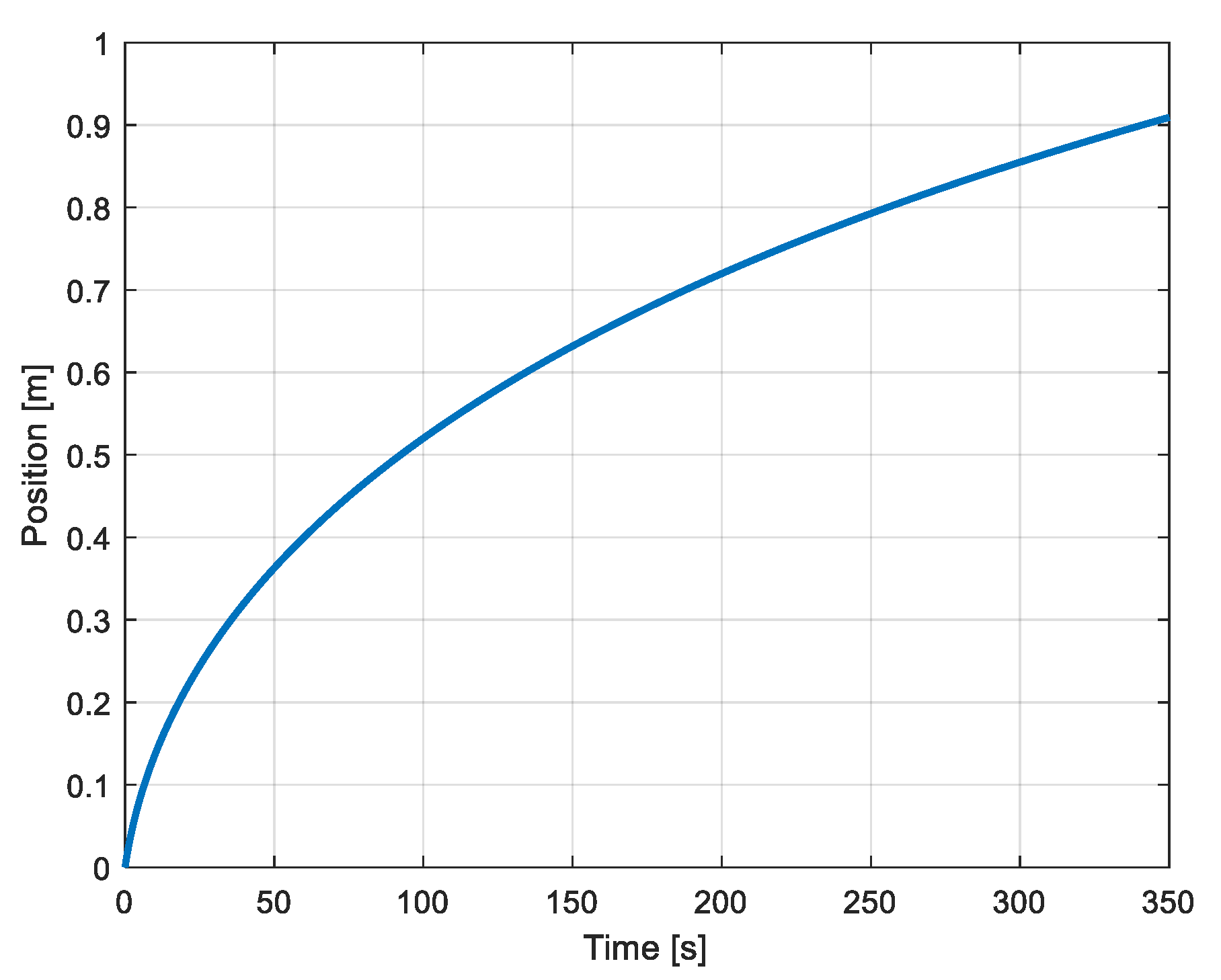
3.2. Evolution of the Mechanical Variables
3.3. Evolution of the Energies Stored in the Systems
4. Analysis and Experimentation with a Small-Scale System
4.1. Numeric Values of the Small Experimental Static Reservoir
- Compression machine
- Diameter of the piston: 12 mm
- Piston stroke: 100 mm
- Volumetric ratio (Vtop/Vdown): 0.12
- Reservoir
- Volume: 0.3 L
- Rotational speed of the drive: 2 revol./s
- The volume of the cylinder of the compressor is calculated (rel. (22)):
4.2. The Small-Scale Dynamic Reservoir
4.3. Experimental Results
5. Discussion
Cost Benefits
6. Conclusions
Funding
Data Availability Statement:
Conflicts of Interest
References
- IPCC Intergovernmental Panel on Climate Change (IPCC) Synthesis Report. 2024. Available online: https://www.ipcc.ch/synthesis-report/ (accessed on 8 July 2025).
- Rufer, A. Energy Storage—Systems and Components; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fang, R.; Zhang, R. Advances in Hybrid Energy Storage Systems and Smart Energy Grid Applications. 2021. Available online: https://www.sciencedirect.com/special-issue/10GRJ69GC0Q (accessed on 4 April 2025).
- International Energy Agency. World Energy Outlook 2024 IEA. Available online: https://iea.blob.core.windows.net/assets/a5ba91c9-a41c-420c-b42e-1d3e9b96a215/WorldEnergyOutlook2024.pdf (accessed on 8 July 2025).
- Adil, A.M.; Ko, Y. Socio-technical evolution of Decentralized Energy Systems: A critical review and implications for urban planning and policy. Renew. Sustain. Energy Rev. 2016, 57, 1025–1037. [Google Scholar] [CrossRef]
- Lehmann, J. Air storage gas turbine power plants, a major distribution for energy storage. In Proceedings of the International Conference on Energy Storage, Brighton, UK, 29 April–1 May 1981; pp. 327–336. [Google Scholar]
- The Mc Intosh CAES Power Plant, Compressed Air Energy Storage Technology: Generating Electricity Out of Thin Air. Available online: https://www.baldwinemc.com/compressed-air-energy-storage-technology-generating-electricity-out-of-thin-air/ (accessed on 22 September 2017).
- Bradshaw, D.T. Pumped hydroelectric storage (PHS) and compressed air energy storage (CAES). In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; Volume 3, pp. 1551–1573. [Google Scholar]
- Allen, K. CAES: The underground portion. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 809–812. [Google Scholar] [CrossRef]
- Ting, D.S.-K.; Stagner, J.A. Compressed Air Energy Storage: Types, Systems and Applications; The Institution of Engineering and Technology: London, UK, 2021; ISBN 978-1-83953-195-8. [Google Scholar]
- Salvini, C.; Mariotti, P.; Giovannelli, A. Compression and Air Storage Systems for Small Size CAES Plants: Design and Off-design Analysis. Energy Procedia 2017, 107, 369–376. [Google Scholar] [CrossRef]
- Rabi, A.M.; Radulovic, J.; Buick, J.M. Comprehensive Review of Compressed Air Energy Storage (CAES) Technologies. Thermo 2023, 3, 104–126. [Google Scholar] [CrossRef]
- Macdonald, J. Compressed Air Energy Storage (CAES): A Comprehensive 2025 Overview. 2025. Available online: https://urbanao.com/post/compressed-air-energy-storage-caes-a-comprehensive-2025-overview (accessed on 17 June 2025).
- Electricity Storage. Heat. Cold. Compressed Air. Combined in a Sustainable System. Available online: https://www.green-y.ch/en/ (accessed on 12 April 2025).
- Radeska, T. The Mekarski System—Compressed-Air Propulsion System for Trams. 2016. Available online: https://www.thevintagenews.com/2016/10/17/the-mekarski-system-compressed-air-propulsion-system-for-trams/ (accessed on 28 July 2017).
- Blain, L. AIRPod: Tiny Air-Powered Commuter Costs Half a Euro Per 100km. 2009. Available online: https://newatlas.com/airpod-compressed-air-car-mdi-zeroemissions/11177/ (accessed on 27 April 2018).
- Lu, M.D.I. Motor Development International. 2018. Available online: https://www.mdi.lu. (accessed on 5 May 2019).
- Kabinga, R.K.N.; Tartibu, L.K.; Okwu, M.O. Development and performance evaluation of a dynamic compressed air energy storage system. In Proceedings of the International Mechanical Engineering Congress and Exposition, Portland, OR, USA, 16–19 November 2020. [Google Scholar]
- Cheng, Y.; Chen, K.; Chan, C.; Bouscayrol, A.; Cui, S. Global modeling and control strategy simulation. IEEE Veh. Technol. Mag. 2009, 4, 73–79. [Google Scholar] [CrossRef]
- Shearer, M.; Gremaud, P.; Kleiner, K. Periodic motion of a mass–spring system. IMA J. Appl. Math. 2009, 74, 807–826. [Google Scholar] [CrossRef]










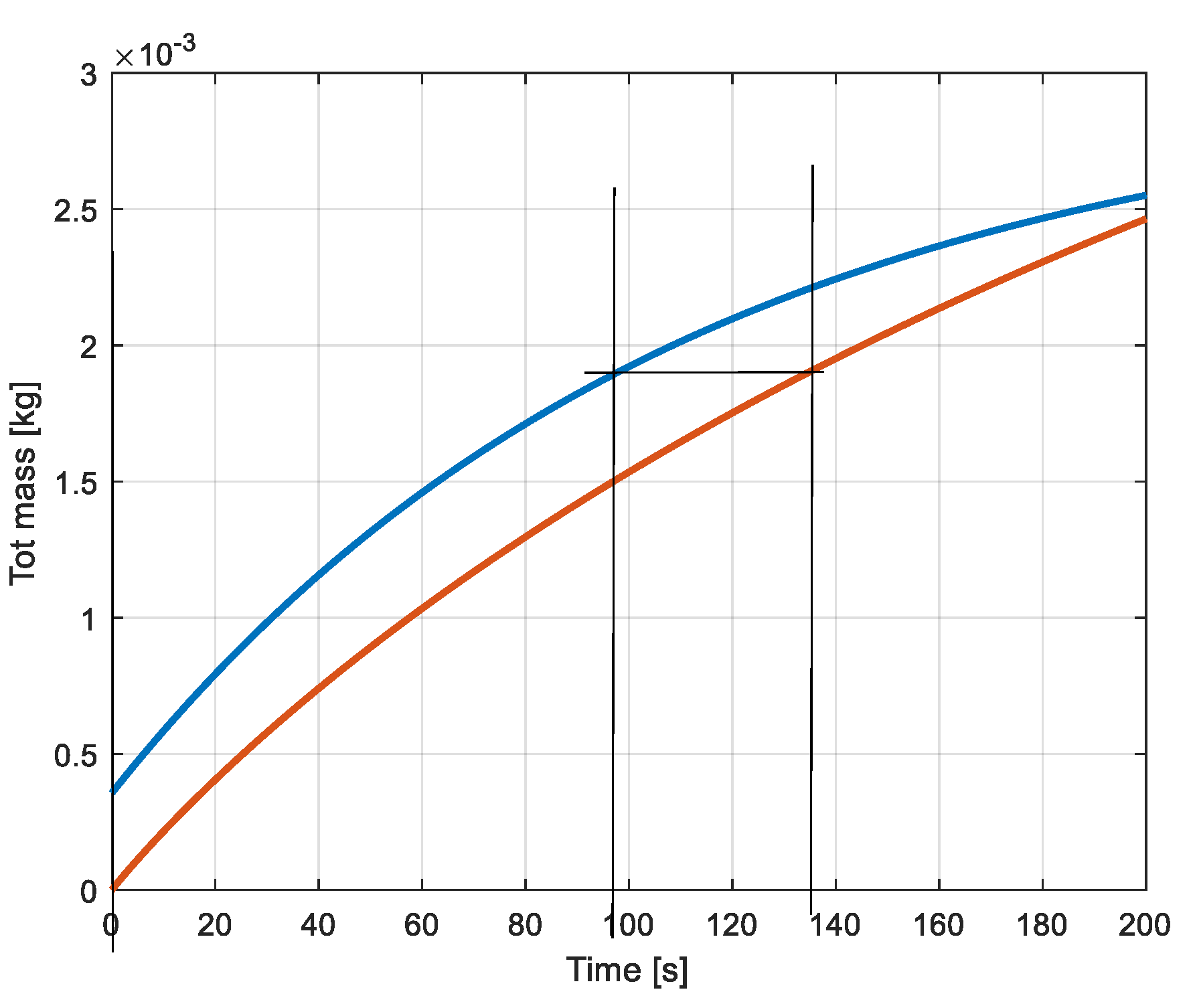
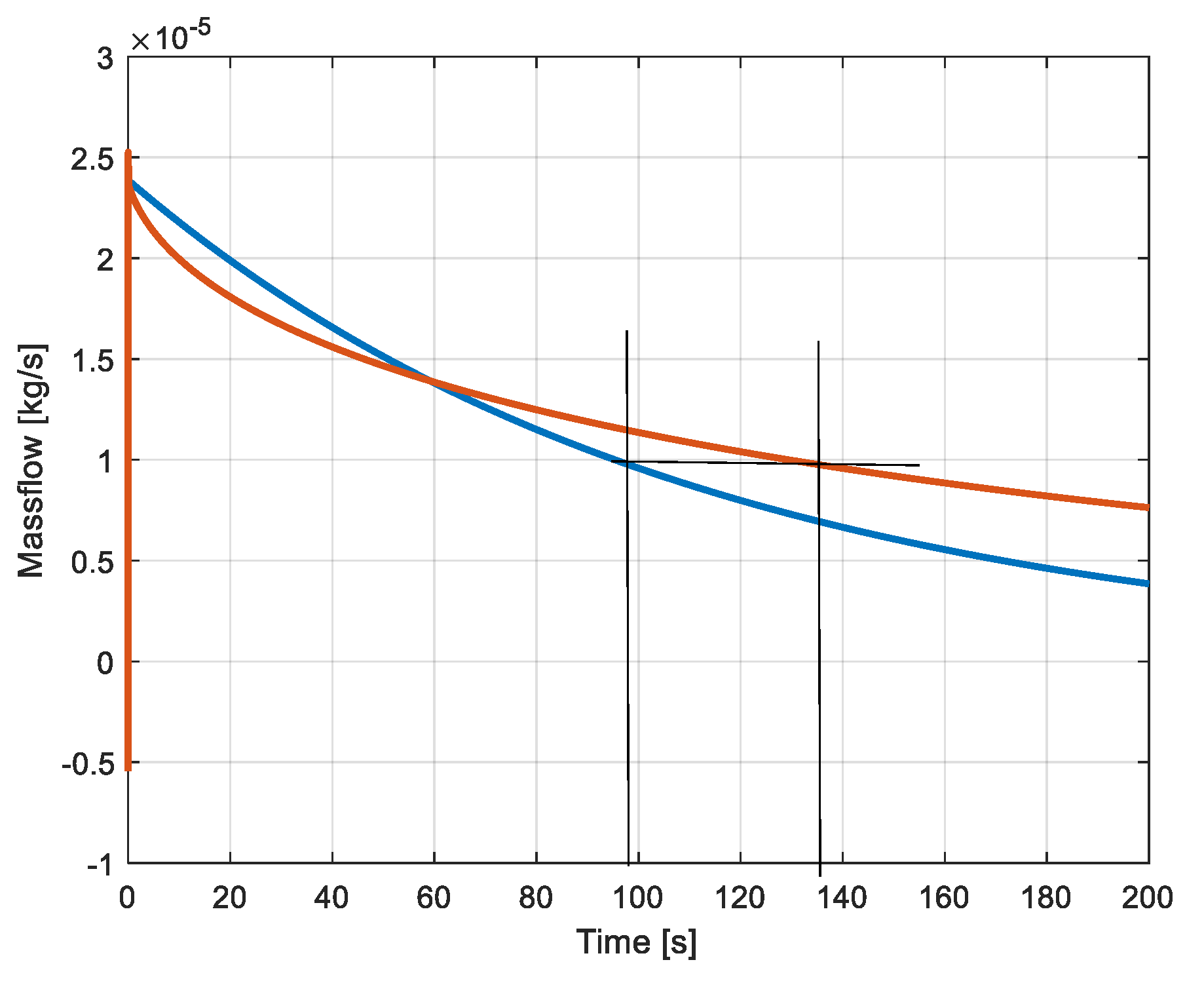


| Static Reservoir | |
| Volume | 0.1 m3 |
| Dynamic reservoir | |
| Variable volume | 0–0.1 m3 |
| Stroke of the piston | 0.9 m |
| Surface of the piston | 0.111 m2 |
| Constant of the spring | 61.7 kN/m |
| Moving mass | 10 kg |
| Pneumatic Cylinder | SC50X175 |
| Diameter of the piston | 50 mm |
| Area of the piston | 0.00196 m2 |
| Maximal stroke | 175 mm |
| Spring | T33220 |
| De (external diameter) | 50 mm |
| D (diameter of the spring wire) | 4.5 mm |
| L0 (initial length) | 142 mm |
| Ln (length under nominal load) | 280 mm |
| Fn (nominal load) | 451 N |
| C (spring constant) | 2.77 × 103 N/m |
| De (external diameter) | 50 mm |
 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rufer, A. Performance Evaluation of Static and Dynamic Compressed Air Reservoirs for Energy Storage. Energies 2025, 18, 3666. https://doi.org/10.3390/en18143666
Rufer A. Performance Evaluation of Static and Dynamic Compressed Air Reservoirs for Energy Storage. Energies. 2025; 18(14):3666. https://doi.org/10.3390/en18143666
Chicago/Turabian StyleRufer, Alfred. 2025. "Performance Evaluation of Static and Dynamic Compressed Air Reservoirs for Energy Storage" Energies 18, no. 14: 3666. https://doi.org/10.3390/en18143666
APA StyleRufer, A. (2025). Performance Evaluation of Static and Dynamic Compressed Air Reservoirs for Energy Storage. Energies, 18(14), 3666. https://doi.org/10.3390/en18143666







